Design and Anti-Impact Performance Study of a Parallel Vector Thruster

Abstract

With the rapid development of unmanned surface vessels (USVs), a vector thruster was designed in this paper to meet their evolving operational demands. The anti-impact capability of the vector thruster, in which the universal joint plays a critical role in attenuating impact loads, directly governs the stability and security of power transmission in USVs. A mechanical model of the vector thruster with a universal joint was established, incorporating length and stiffness ratio coefficients to characterize its key dynamics. Based on this model, numerical simulation using the Newmark method was conducted to systematically evaluate the thruster’s mechanical characteristics, particularly the dynamic variation of the inclination angle, under various working conditions and impact loads. The results indicate that an increase in stiffness ratio amplifies the angular displacement amplitude of the driven shaft but shortens the vibration stabilization time. During the operation of the vector thruster, an increase in the inclination angle leads to greater vibration amplitude. Furthermore, systems with a higher, longer ratio exhibit a more pronounced tendency for amplitude growth as the inclination angle increases. Finally, the theoretical model was validated through a test bench, and the variation pattern of dynamic thrust under impact load was revealed. These results emphasize that the stiffness and dimensional parameters must be carefully considered in the design and control optimization of vector thrusters to ensure reliable performance under demanding operational conditions.

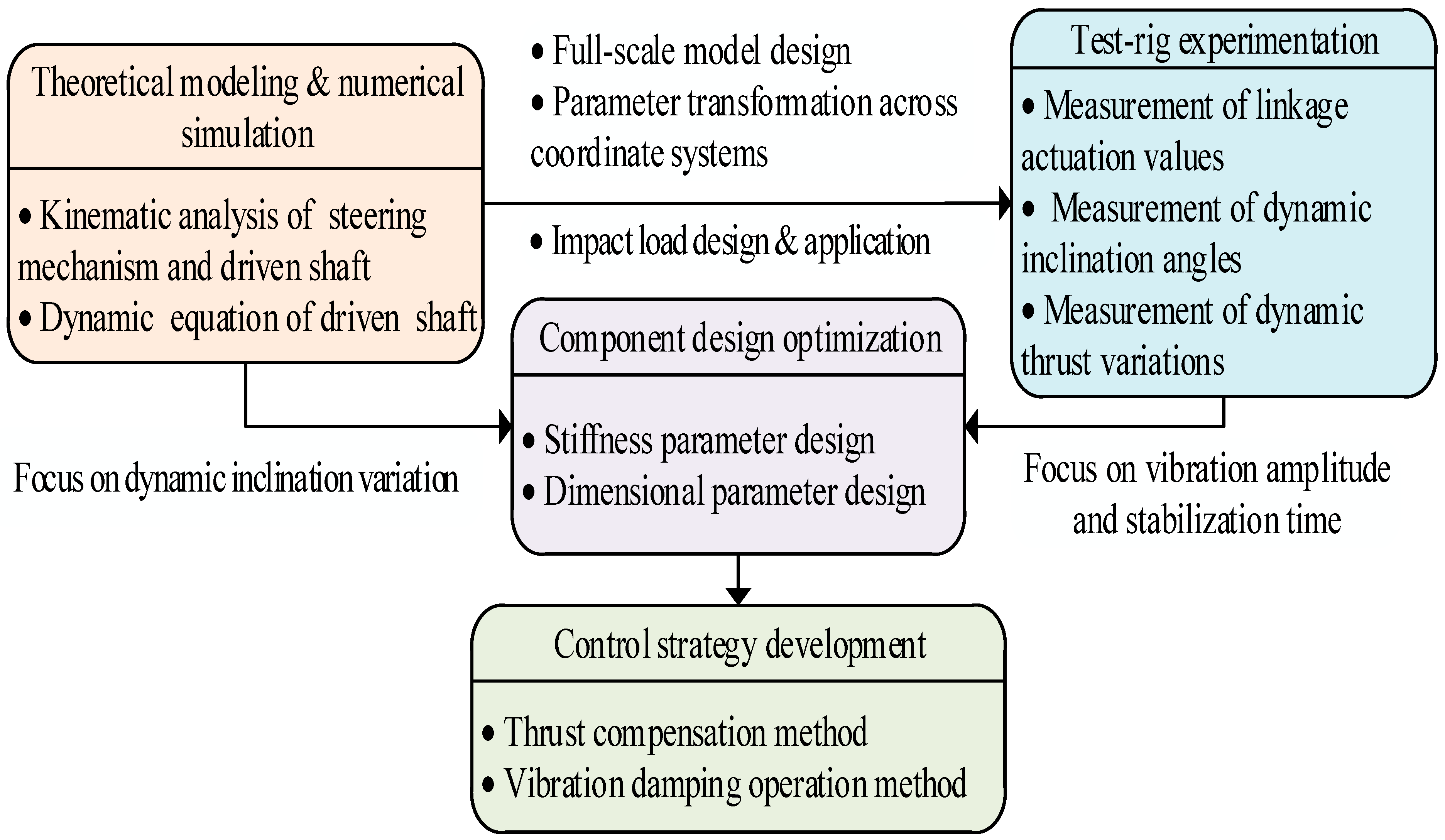
1. Introduction

Vector thrusters enable flexible steering and positioning by adjusting thrust direction, finding wide applications in fighter jets, rockets, and other fields [1]. For example, thrusters developed by researchers like Kadiyam [2] and Desai [3] effectively fulfill vector propulsion functions. In recent years, as autonomous underwater vehicle (AUV) mission requirements grow more complex and diverse, vector thrusters have emerged as a promising underwater navigation technology [4], achieving thrust vectorization by modifying the direction and magnitude of AUV thrust. However, current underwater vector thrusters face issues of structural complexity and poor engineering applicability [5]. The propeller, drive shaft, and steering mechanism in the propulsion system exhibit highly coupled dynamic interactions: propeller-generated pulsating forces induce vibrations in the drive shaft and steering mechanism, which in turn affect thrust characteristics and alter the propeller’s pulsating forces, forming a reinforcing feedback loop. This underscores the critical importance of structural optimization and reliability improvement for the practical application and accurate hydrodynamic calculation of vector thrusters.

The complex spatial motion of a vector thruster’s propeller during operation poses severe challenges to its service performance. This motion stems from two primary sources: the inherent stiffness of the steering mechanism triggers spatial oscillation of the drive shaft under rotational excitation, and the propeller operates in a non-uniform inflow field further disturbed by the shaft’s whirling motion [6,7]. Additionally, pulsating hydrodynamic forces acting on the propeller blades impose substantial dynamic loads. These combined factors create an extreme mechanical environment where impact loads can directly damage structural integrity, leading to performance degradation or even failure [8]. Therefore, enhancing the anti-impact performance of vector thrusters is essential to ensuring their operational stability, structural durability, and long-term reliable service in harsh working conditions.

The drive shaft of a vector thruster generally adopts a shaft with a universal joint and belongs to a high-speed rotor system [9]. In recent years, numerous scholars have studied the response characteristics of thruster shafting under external loads through theoretical analysis, numerical calculation, and experimental research. For example, Zhu [10] explored the interaction between rotational speed and whirling vibration of thruster shafting under impact force and conducted test verification using a heavy hammer. However, these studies assumed that control parameters under different loads remain consistent, ignoring the changes in system stiffness and additional torsion effects under impact loads [11,12], which makes it difficult to match actual working conditions. In fact, the impact response of such high-speed rotor systems is a strong nonlinear process involving phenomena such as jumping, bifurcation, and chaos [13]. Therefore, current research on load response under impact loads mostly focuses on marine shafting, but relevant studies on vector thruster shafting are relatively scarce, and specialized research on vector thruster shafting with universal joints is even rarer. Among existing studies, some scholars have taken universal joint shafting as the research object [14], but failed to consider the characteristic of universal joints that additional elastic torsional vibration may be excited even during stable operation; other studies have considered factors such as the non-constancy of the motion transmission characteristics of universal joints [15] and analyzed vibration behavior by treating the intermediate shaft as a flexible body, but lack an analysis of the influence of the cross shaft.

When a universal joint-based vector thruster is subjected to impact loads, strong coupling vibrations occur due to its complex dynamics and parameter uncertainties, such as varying inclination angles and additional bending moments [16,17]. In recent years, numerous scholars have conducted in-depth research on the coupled vibration induced by impact and operational loads, proposing various advanced analytical methods. For instance, Grządziela [18] analyses the impact of initial conditions on the results of numerical simulations of the fan load with underwater detonation and simultaneously typical harmonic loads from the operating device. Duchemin [19] applied parametric modeling and sensitivity analysis to reveal the influence of structural stiffness and damping ratios on coupled vibration characteristics. Indeed, the impact resistance of vector thrusters represents a crucial metric for both maritime survivability and combat effectiveness. This is particularly critical for unmanned surface vessels, where such thrusters may be required to execute intentional collision missions. In this context, Piperakis [20] established an integrated framework for naval ship survivability assessment during preliminary design phases. Their work developed multiscale computational methodologies that effectively investigate structural parameter coupling mechanisms under complex loading conditions, providing valuable insights for analyzing propulsion system responses to impact scenarios.

In summary, current research lacks both a systematic analysis of steering mechanism spatial positioning effects on universal joint kinematics and an adequate investigation into the coupled mechanism where impact loads induce vibrations while critically causing thrust fluctuations. These limitations consequently hinder the adaptation of vector thrusters to increasingly demanding operational conditions. To address the practical engineering challenges in vector thruster structural design and motion control, this paper presents a vector propulsion device based on a parallel steering mechanism and a universal joint. A corresponding mechanical model is established to analyze the distinct effects of impact forces on the steering mechanism and driven shaft system vibration, introducing both a length coefficient and a stiffness ratio coefficient. An integrated methodology combining mechanical structural analysis, numerical simulation using the Newmark method [21], and experimental testing is employed to systematically investigate the vibration characteristics of the thruster under different operating conditions. The thrust behavior under impact loads is further validated through physical experiments, with results providing theoretical support for performance optimization and practical application of vector propulsion systems in complex marine environments, thereby filling the research gap in coupled vibration–thrust performance analysis for joint-parallel vector thrusters under impact conditions.

The paper is organized as follows: Section 2 derives the kinematic model of the vector thruster based on mechanical structural analysis; Section 3 presents numerical simulations; Section 4 examines the dynamic performance of both the inclination angle and the thrust force using a test rig; and Section 5 provides concluding remarks.

2. Kinematic and Dynamic Analysis of Vector Thruster Components

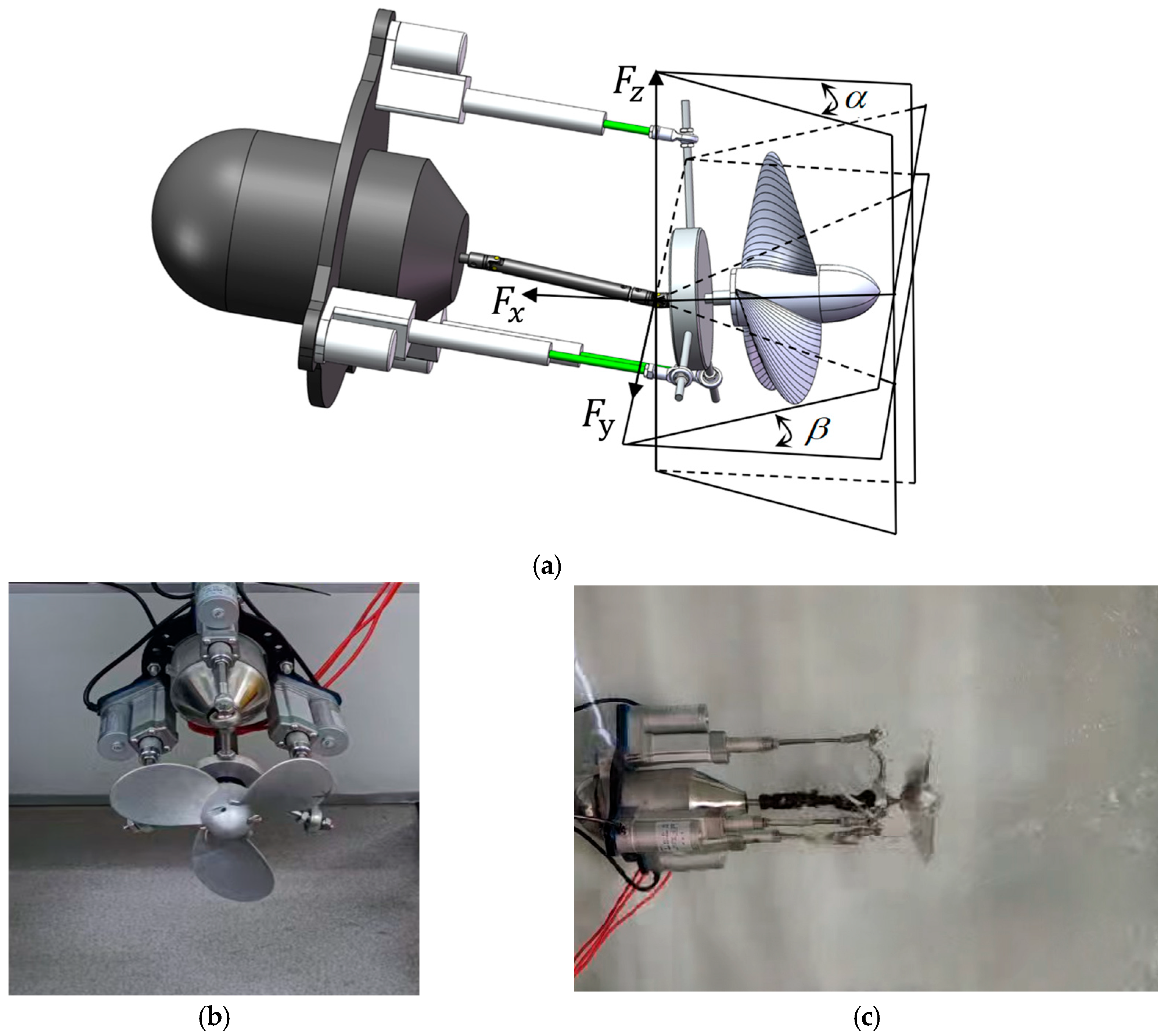
2.1. The Design Philosophy and Implementation

The design of the vector thruster builds upon commonly available commercial configurations. It is mounted externally to the hull, eliminating the need for hull-penetrating seals. Figure 1a illustrates the design objective of enabling propeller deflection in both horizontal and vertical directions, while also presenting the biconical mechanical mechanism that defines the thruster’s workspace. This configuration ensures high maneuverability by allowing the propeller to operate across the full conical range. In the figure, F_x, F_y, and F_z represent the thrust components in the surge, sway, and heave directions, respectively, following the standard convention for vector thrusters. Since the magnitudes of F_y and F_z are significantly smaller compared to F_x, our analysis will primarily focus on F_x, which is designated as the effective thrust. Angles $\alpha$ and $\beta$ denote the inclination angles of the propeller thrust direction relative to the horizontal and vertical planes, respectively.

During the vector thruster’s operation, it experiences fluid excitation forces. These forces cause vibrations in the shaft system, which then interact with the fluid excitation. This further results in complex spatial oscillations of the propeller [22]. Therefore, a reliable variable-direction mechanism must be employed to ensure the accuracy and reliability of the propeller’s position. Figure 1b shows the physical prototype of the thruster, which was constructed to validate the integration of its thrust vectoring mechanism. This mechanism, based on linkage actuation and a double-cross universal joint, accommodates translational and rotational misalignments during orientation adjustments. The key components include a propulsion motor, three steering motors, telescopic rods, a universal joint coupling, and a propeller. Key model parameters are summarized in

Table 1. Main parameters of the vector thruster.

Model	Parameter	Model	Parameter
Model Name	P4119	Maximum Blade Sectional Area (m2)	0.086
Diameter (m)	0.305	Blade Section Shape	NACA66-mod
Blade Number	3	Propeller Hub Length (m)	0.156
Hub Diameter Ratio	0.2	Blade Area Ratio (BAR)	0.6
Vertical Inclination	[−0.436, 0.436]	Horizontal Inclination	[−0.436, 0.436]

[23]. Figure 1c provides a performance visualization of the thruster, which was experimentally investigated in our lab to demonstrate its thrust output and deflection behavior under different actuation conditions, thereby validating its capability to achieve the expected performance.

Based on the working principle of the designed vectored thruster, its steering mechanism requires precise matching with the driven shaft in terms of stiffness and kinematic characteristics, a key distinction from fixed thrusters. Consequently, shock response analysis is identified as the most effective method for observing and evaluating the dynamic performance of this coupled system.

Building on this analytical approach and guided specifically by the objective of assessing anti-impact performance, this paper plans and executes a comprehensive development process spanning from initial design to final control implementation. The specific workflow for this process is illustrated in Figure 2.

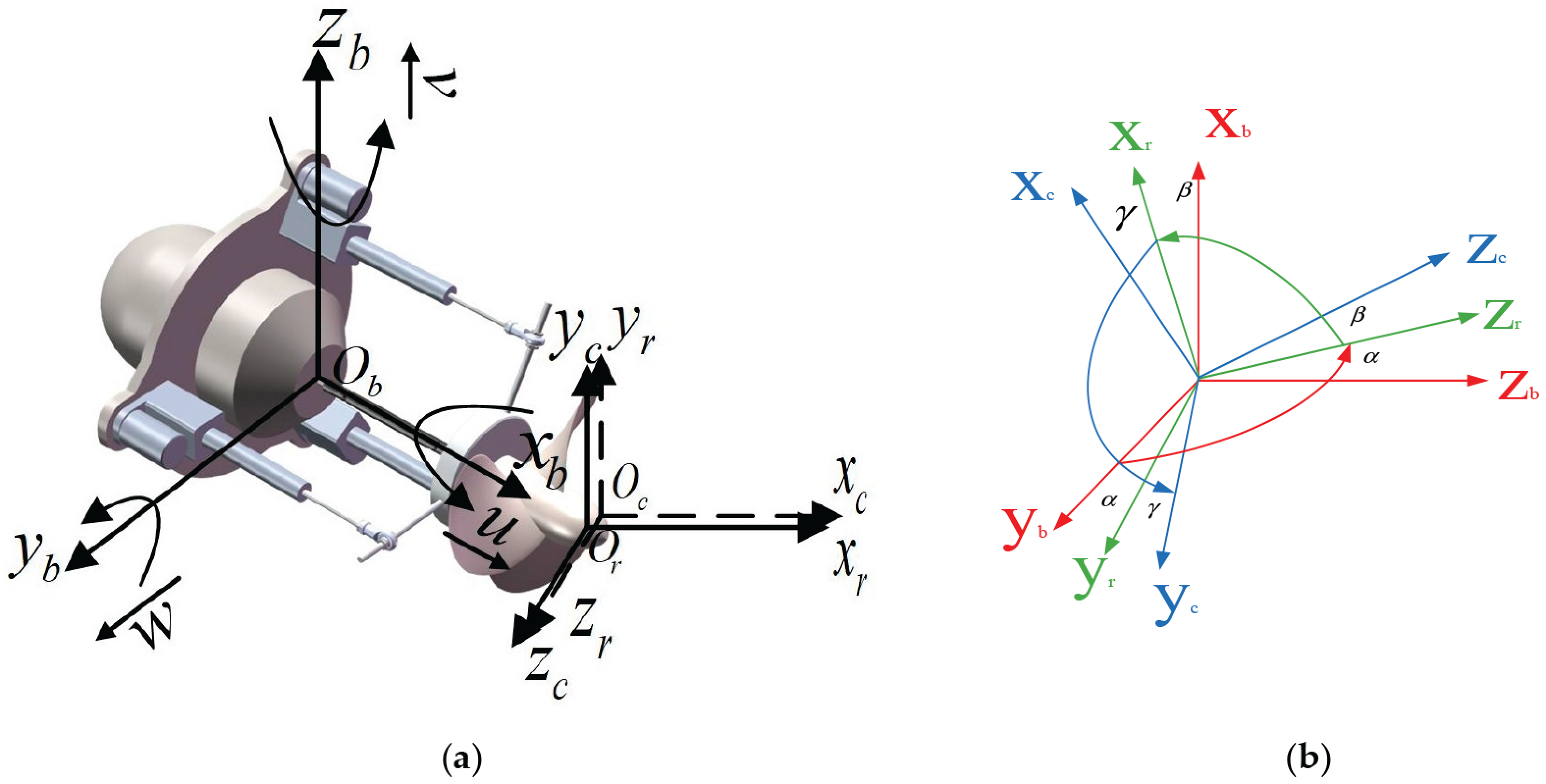
2.2. The Construction of Dynamic Equations

Based on the mechanical model mechanism illustrated in Figure 1, a simplified model of the steering mechanism and propulsive shafting is established, as shown in Figure 3a. To characterize the spatial motion of each vector propeller component, kinematic coordinate systems must first be defined. Subsequently, the kinematic relationships between components are derived through coordinate transformation. The following three coordinate systems are implemented and illustrated in Figure 3b:

(1)

Base coordinate system fixed on AUV $O_b-x_b{y}_b{z}_b$, denoted by $R^b$;

(2)

Rotation coordinate system on the geometry center of the propeller as the original point, $O_r-x_r{y}_r{z}_r$ denoted by $R^r$;

(3)

Rotation coordinate system on the mass center of the propeller as the original point. $O_c-x_c{y}_c{z}_c$, denoted by $R^c$.

Based on the coordinate transformation relationship, the base coordinate system can be obtained by sequentially rotating the angles $\alpha$, $\beta$ and $\gamma$ around the coordinate axes from an initial attitude parallel to the rotation coordinate system, as shown in Figure 3b. The corresponding coordinate transformation matrices for these three rotations are given in Equation (1). The procedure is detailed as follows:

Starting from the coordinate system $O_b-x_b{y}_b{z}_b$, it is first rotated about the x-axis by an angle α to obtain the first intermediate coordinate system, whose transformation matrix is $C_0^1$. It is then rotated about the y-axis by an angle β to obtain the second intermediate coordinate system, with the transformation matrix $C_1^2$. Finally, it is rotated about the z-axis by an angle γ to arrive at the final rotated coordinate system $O_r-x_r{y}_r{z}_r$, whose transformation matrix is $C_2^3$.

Similarly, the spindle coordinate system $R^c$ can be obtained by sequentially rotating the angles $\theta$, $\phi$, and $\psi$ around the coordinate axes starting from an attitude parallel to the base coordinate system. Thus, the transformation matrix from $R^b$ to $R^c$ is derived as Equation (2).

$$C_0^1=\left[\begin{array}{lll}1& 0& 0\\ 0& \cos \alpha & \sin a\\ 0& -\sin \alpha & \cos \alpha \end{array}\right],C_1^2=\left[\begin{array}{lll}\cos \beta & 0& -\sin \beta \\ 0& 1& 0\\ \sin \beta & 0& \cos \beta \end{array}\right],C_2^3=\left[\begin{array}{lll}\cos \gamma & \sin \gamma & 0\\ -\sin \gamma & \cos \gamma & 0\\ 0& 0& 1\end{array}\right]$$

(1)

$$C_b^c=\left[\begin{array}{ccc}\cos \varphi \cos \psi \hfill & \sin \theta \sin \varphi \sin \psi +\cos \varphi \sin \psi & -\cos \theta \sin \varphi \sin \psi +\sin \varphi \sin \psi \\ -\cos \varphi \sin \psi \hfill & -\sin \theta \sin \varphi \sin \psi +\cos \varphi \cos \psi & \cos \theta \sin \varphi \sin \psi +\sin \varphi \cos \psi \\ \sin \varphi \hfill & -\sin \theta \sin \varphi & -\cos \theta \cos \varphi \end{array}\right]$$

(2)

Establishing a unified dynamic model requires determining the propeller’s rotational characteristics in a different coordinate system. For convenience, we denote the propeller rotational movement about a coordinate axis by $\omega$, where the superscript indicates the two relatively moving coordinate systems, while the subscript specifies both the rotation axis and its associated coordinate system.

The propeller’s absolute rotation arises from the superposition of the AUV’s rotation relative to the ground and the propeller’s own rotation relative to the AUV. By applying time-dependent Euler angles, the components of angular velocity ${\omega }^{b0}$ in the coordinate system $R^b$ can be expressed as ${\omega }_{x,b}^{b0},{\omega }_{y,b}^{b0},{\omega }_{z,b}^{b0}$ and is calculated as follows:

$$\left\{\begin{array}{l}{\omega }_{x,b}^{b0}\\ {\omega }_{y,b}^{b0}\\ {\omega }_{z,b}^{b0}\end{array}\right\}=\left[\begin{array}{lll}\cos \beta \cos \gamma & \sin \gamma & 0\\ -\cos \beta \sin \gamma & \sin \gamma & 0\\ \sin \beta & 0& 1\end{array}\right]\left\{\begin{array}{l}\dot{\alpha }\\ \dot{\beta }\\ \dot{\gamma }\end{array}\right\}$$

(3)

According to the given equation, if two or more of ($\dot{\alpha },\dot{\beta },\dot{\gamma }$) are negligible:

$${\omega }^{bo}\approx \left\{\dot{\alpha },\dot{\beta },\dot{\gamma }\right\}$$

(4)

In the same way, the component of ${\omega }^{b0}$ in the $R^c$ system is

$$\left\{\begin{array}{l}{\omega }_{x,c}^{cb}\\ {\omega }_{y,c}^{cb}\\ {\omega }_{z,c}^{cb}\end{array}\right\}=\left[\begin{array}{lll}\cos \varphi \cos \psi & \sin \psi & 0\\ -\cos \varphi \sin \psi & \sin \psi & 0\\ \sin \varphi & 0& 1\end{array}\right]\left\{\begin{array}{l}\dot{\theta }\\ \dot{\varphi }\\ \dot{\psi }\end{array}\right\}$$

(5)

According to the superposition theorem of the angular velocity vector, the vector form of the absolute angular velocity ${\omega }^{co}$ of the propeller in the coordinate system $R^c$ is obtained as follows:

$$\left\{\begin{array}{l}{\omega }_{x,c}^{co}\\ {\omega }_{y,c}^{co}\\ {\omega }_{z,c}^{co}\end{array}\right\}=\left\{\begin{array}{l}{\omega }_{x,c}^{cb}\\ {\omega }_{x,c}^{cb}\\ {\omega }_{x,c}^{cb}\end{array}\right\}+C_b^c\left\{\begin{array}{l}{\omega }_{x,b}^{b0}\\ {\omega }_{y,b}^{b0}\\ {\omega }_{z,b}^{b0}\end{array}\right\}$$

(6)

During the operation of a vector thruster, the propeller rotates about its central axis while simultaneously undergoing spatial oscillations due to unbalanced excitation forces. The resulting motion can be decomposed into three components [24]: (1) rotation about a coordinate axis, (2) translation of its center of mass, and (3) rotation about its center of mass. Given the kinematic complexity of the vector propulsion system, the fundamental dynamic equations of the propeller are derived from multibody dynamics theory, accounting for its spatial motion couplings, as follows:

$$M\ddot{u}+(C+G)\dot{u}+Ku=F_u+P$$

(7)

where $M$ is the mass matrix; $u$ is the matrix of center coordinates; $G$ is the matrix of the gyro; $C$ is the damping matrix; $K$ is the stiffness matrix; $F_u$ is the additional excitation caused by the unbalanced mass of the propeller. $P$ is the impact load. The specific expansion formula for each part is as follows:

$$M=diag(m,m,J_A,J_A),u={\left\{x,y,{\theta }_x,{\theta }_y\right\}}^T,$$

$$G=\left[\begin{array}{l}0000\\ 0000\\ {000\mathrm{J}}_B\omega \\ 0{0\mathrm{J}}_B\omega 0\end{array}\right],F_u=\left\{\begin{array}{l}me{\omega }^2\cos (\omega t+\phi )\\ me{\omega }^2\sin (\omega t+\phi )\\ (J_B-J_A){\omega }^2\delta \sin (\omega t+\phi )\\ (J_A-J_B){\omega }^2\delta \cos (\omega t+\phi )\end{array}\right\}$$

where $m$ is the mass of the propeller; $J_A=(J_{xx}+J_{yy})/2$, $J_B=J_{zz}$, and $J_{xx}$, $J_{yy}$, $J_{zz}$ are the moment of inertia of the propeller, respectively; $K$ is the equivalent stiffness matrix of the propulsion system that can be calculated by the superposition of the support stiffness and the driven shaft itself stiffness in series generally [25].

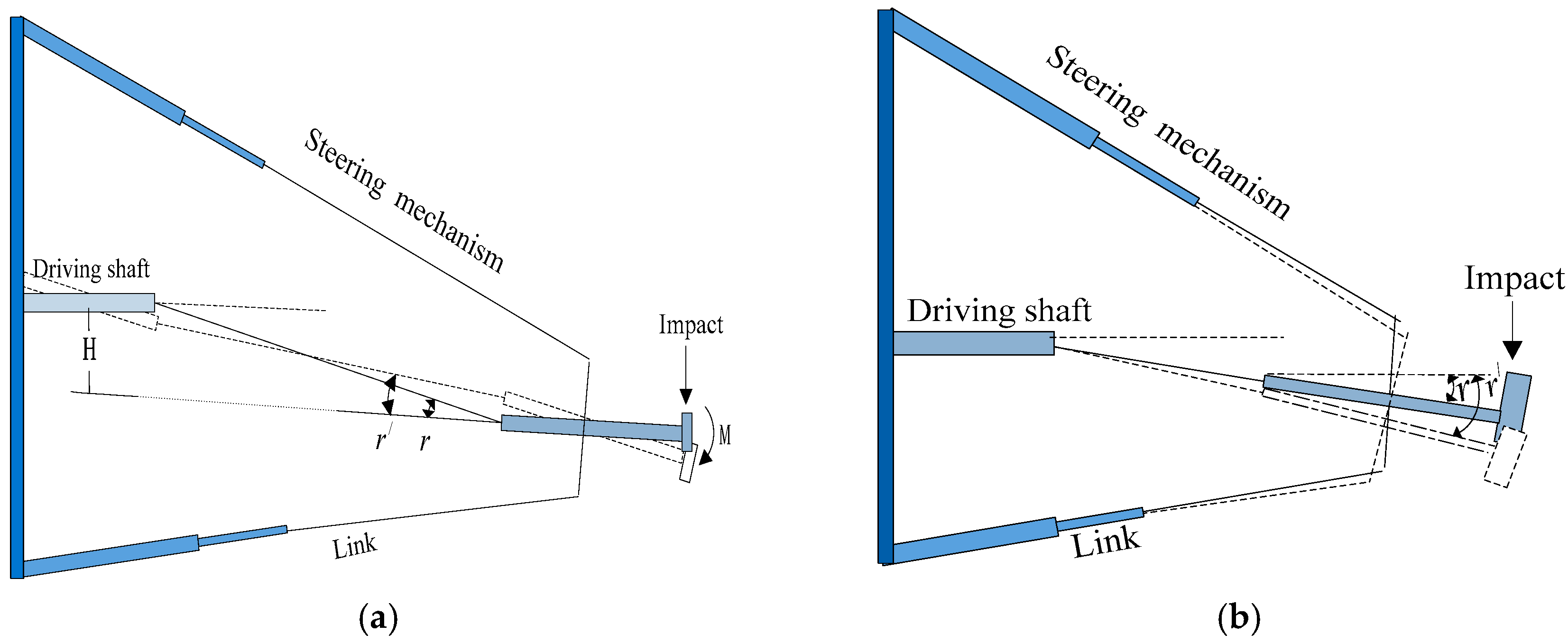
2.3. Dynamic Response of the Steering Mechanism Under Impact Load

To describe the kinematic relationship, a spatial coordinate system is established as shown in Figure 4a. The prismatic joints A₁, A₂, and A₃ are uniformly distributed around the motor spindle, while the spherical joints B₁, B₂, and B₃ are uniformly distributed around the propeller rotation axis. As a result, both triangle ΔA₁A₂A₃ formed by the prismatic joints A₁, A₂, A₃, and triangle ΔB₁B₂B₃ formed by the spherical joints B₁, B₂, and B₃ are equilateral. Let point A be the centroid of ΔA₁A₂A₃, with vectors AA₁, AA₂, and AA₃ connecting it to each vertex; similarly, let point B be the centroid of ΔB₁B₂B₃, with vectors BB₁, BB₂, and BB₃ connecting it to each vertex. A fixed branch coordinate system A-xyz and a moving branch coordinate system A1-x₁y₁z₁ are established at point A, while a moving spherical joint coordinate system B-uvw is established at point B. The deflection distance of the propeller corresponds to the relative spatial position between the two prismatic joints, and the rotation angle represents the relative rotation of the two components about the common axis. The angle between the propeller axis and the w-axis is denoted as $\beta$, which is defined as the thrust angle.

During the motion of the propeller-driven platform, the Euler transformation matrix between the fixed coordinate system A-xyz and the body coordinate system B-uvw is as follows:

$$R=\left[\begin{array}{ccc}\cos \theta \cos \psi & -\sin \psi \cos \phi +\cos \psi \sin \theta \sin \phi & \sin \psi \sin \phi +\cos \theta \cos \psi \cos \phi \\ \sin \psi \cos \theta & \cos \psi \cos \phi +\sin \theta \sin \psi \sin \phi & -\cos \psi \sin \phi +\sin \theta \sin \psi \sin \phi \\ -\sin \theta & \cos \theta \sin \phi & \cos \theta \cos \phi \end{array}\right]$$

(8)

A vector loop equation is established for the polygon A₁B₁BA, as illustrated in Figure 4b. Here, the length of A₁B₁ represents the tie rod length b and is denoted as vector $\overrightarrow{b_1}$; vector AA₁ is denoted as $\overrightarrow{a_1}$, and vector AB is denoted as $\overrightarrow{w_1}$, which is the distance vector between triangles ΔA₁A₂A₃ and ΔB₁B₂B₃. Point B serves as the connection point between the constant-velocity universal joint and the propeller shaft. When the propeller changes its orientation, point A remains stationary. Therefore, based on the configuration in Figure 4b, the vector loop equation can be expressed as follows:

$$\overrightarrow{r_B}=q\overrightarrow{w_1}+\overrightarrow{a_1}-e\overrightarrow{b_1}$$

(9)

Due to the constraint of the mobile part, point B₁ can only rotate around the axis x₁ of the coordinate system A₁-x₁y₁z₁. The vector of the straight line A₁B₁ on the coordinate system A-xyz is perpendicular to the unit vector A₁-x₁y₁z₁ of the axis of the coordinate system. That is,

$${\left(\overrightarrow{r_B}+R\overrightarrow{b_1}\right)}^{{\rm T}}\overrightarrow{x_1}=0$$

(10)

Based on Equation (9), the expression can be written as follows:

$$\left\{\begin{array}{c}\overrightarrow{w_1}={\displaystyle \frac{\overrightarrow{r_B}+R\overrightarrow{b_1}-\overrightarrow{a_1}}{q}}\\ q=‖\overrightarrow{r_B}+R\overrightarrow{b_1}-\overrightarrow{a_1}‖\end{array}\right.$$

(11)

Given that the coordinates of $\overrightarrow{r_B}$ are $\left(0,0,l\right)$, the representation of $q$ in the reference frame $A-xyz$ can therefore be expressed as follows:

$$q=\overrightarrow{r_B}+e\overrightarrow{b_1}-\overrightarrow{a_1}$$

(12)

The length of the tie rod of the vector propeller changes, and the position coordinates of the vector at each point are as follows:

$$A_1=\left(0,a,0\right)A_2=\left({\displaystyle \frac{\sqrt{3}a}{2}},-{\displaystyle \frac{a}{2}},0\right)A_3=\left(-{\displaystyle \frac{\sqrt{3}a}{2}},-{\displaystyle \frac{a}{2}},0\right)$$

(13)

$$B_1=\left(0,b,0\right)B_2=\left({\displaystyle \frac{\sqrt{3}b}{2}}\cos \beta ,-{\displaystyle \frac{b}{2}},{\displaystyle \frac{\sqrt{3}b}{2}}\sin \beta \right)B_3=\left(-{\displaystyle \frac{\sqrt{3}b}{2}}\cos \beta ,-{\displaystyle \frac{b}{2}},-{\displaystyle \frac{\sqrt{3}b}{2}}\sin \beta \right)$$

(14)

When the inclination angle changes, the direction vector e of the propeller axis lies in the plane defined by the v and w coordinate axes, forming an angle β with the w-axis. Given that its projection onto the u-axis is zero, the vector can therefore be expressed as follows:

$$e={\left[0,-\sin \beta ,\cos \beta \right]}^{\mathrm{{\rm T}}}$$

(15)

Substituting Equations (13)–(15) into Equation (12), the relationship between thrust angle and tie rod length can be obtained.

$$q^2={‖\overrightarrow{r_B}+e\overrightarrow{b_1}-\overrightarrow{a_1}‖}^2=\left[\begin{array}{c}\mathrm{\Phi }\\ \mathrm{\Gamma }\\ \mathrm{\Psi }\end{array}\right]{\left[\begin{array}{c}1\\ \sin \left(2\beta \right)\\ \cos \left(4\beta \right)\end{array}\right]}^{\mathrm{{\rm T}}}$$

(16)

The coefficients in the formula are as follows:

$$\mathrm{\Phi }=a^2+l^2+{\displaystyle \frac{4ab+b^2}{32}},\mathrm{\Gamma }={\displaystyle \frac{b^2-8bl+2ab}{16}},\mathrm{\Psi }=-{\displaystyle \frac{b^2}{32}}$$

(17)

Based on the relationship shown in Equation (16), the operating condition with the thruster deflecting only vertically is selected for calculation, where the lengths of q₂ and q₃ are kept equal. Through a straightforward matrix transformation, this relationship can be explicitly written in the following expanded form:

$$\begin{array}{l}{q}_1=‖\overrightarrow{r_B}+e\overrightarrow{b_1}-\overrightarrow{a_1}‖\\ =\sqrt{{\left({\displaystyle \frac{\mathrm{a}\sin 2\beta -7\mathrm{a}\sin \beta +a\tan \beta }{2}}+l\right)}^2+{\left({\displaystyle \frac{\mathrm{a}\sin 2\beta }{4}}-{\displaystyle \frac{3a\sin \beta }{2}}+a\cos \beta -{\displaystyle \frac{a}{2}}\left(1+{\cos }^2\beta \right)\right)}^2}\end{array}$$

(18)

$$\begin{array}{l}{q}_2=q_3=‖\overrightarrow{r_B}+e\overrightarrow{b_2}-\overrightarrow{a_2}‖\\ =\sqrt{{\left({\displaystyle \frac{a\sin 2\beta +a\left(\tan \beta -\sin \beta \right)}{2}}+l\right)}^2+{\left({\displaystyle \frac{a}{4}}\sin 2\beta +{\displaystyle \frac{a}{2}}{\sin }^2\beta +{\displaystyle \frac{a\left(1-\cos \beta \right)}{2}}\right)}^2}\end{array}$$

(19)

Regarding the calculation, based on the bending stiffness of a structure with one end fixed and the other end hinged, the increase in the thrust angle under the impact force can be calculated using Equation (20).

$$\mathrm{\Delta }\beta ={\displaystyle \frac{P}{2E{I}_{link}(q_1^2+q_2^2+q_3^2)}}$$

(20)

where $E{I}_{link}$ is the bending stiffness of the tie rod.

Based on the working principle of the steering mechanism, it can be seen that the length of the tie rod has a significant influence on the response to impact load. This is because, on one hand, the length directly affects the stiffness matrix; on the other hand, it also determines the length of the drive shaft, leading to different deformation modes. Therefore, to account for this influence, a length ratio coefficient has been introduced for subsequent computations $k=\overline{\mathrm{q}}/l$ for the subsequent computations, where $\overline{\mathrm{q}}$ is the arithmetic mean of q₁, q₂, and q₃.

2.4. Dynamic Response of Driven Shaft Under Impact Load

Under impact load, the inclination angle of the vector thruster exhibits two variation patterns due to different deformation mechanisms, as illustrated in Figure 5. The solid lines and dotted lines stand for the initial position and deflection position of the intermediate shaft, in which the inclination angles change from $r$ to $r^{\prime }$. Among these, Figure 5a corresponds to the motion model of the intermediate shaft and the resulting inclination angle variation caused by an additional bending moment on the driven shaft, while Figure 5b addresses the kinematic model and the alternative variation pattern induced by elastic deformation in the steering mechanism links.

In Figure 5a, $H$ is the vertical distance from the driving shaft to the driven shaft, which can be calculated as $H=\mathrm{L}/\sin r$. Under the bending moment, deflection may occur in the intermediate shaft, which further leads to a shorter vertical distance. According to the geometric relation in this process, Equation (21) can be established.

$${\displaystyle \frac{H-\frac{M\sin \left(\omega L\right)}{E{I}_{shaft}}}{H}}={\displaystyle \frac{\sin r^{\prime }}{\sin r}}$$

(21)

where M is the bending moment of the driven shaft, which can be calculated as $M=P\cdot L_3$; $E{I}_{shaft}$ is the bending stiffness of the driven shaft.

Based on the geometric relationship of the drive shaft and assuming equal angular deflection of the universal joints, the relationship between the inclination angle and the position of the propeller is given by Equation (22). Therefore, the axial and radial displacements of the propeller can be calculated using Equation (20). Based on this calculation and to streamline the analysis, the inclination angle is henceforth adopted as the unified metric for evaluating impact response.

$$\left\{\begin{array}{l}x={\mathrm{L}}_2\cos r+{\mathrm{L}}_3\cos (2r)\\ y={\mathrm{L}}_2\sin r+{\mathrm{L}}_3\sin (2r)\end{array}\right.$$

(22)

$$\left[\begin{array}{l}\mathrm{\Delta }x\\ \mathrm{\Delta }y\end{array}\right]=\left[\begin{array}{l}{\mathrm{L}}_2(\cos r-\cos r^{\prime })+{\mathrm{L}}_3[\cos (2r)-\cos (2r^{\prime })]\\ {\mathrm{L}}_2(\sin r-\sin r^{\prime })+{\mathrm{L}}_3[\sin (2r)-\sin (2r^{\prime })]\end{array}\right]$$

(23)

where ${\mathrm{L}}_2$, ${\mathrm{L}}_3$ are the lengths of the intermediate shaft and the driven shaft, respectively; $\mathrm{\Delta }x$, $\mathrm{\Delta }y$ are relative displacements of the propeller center.

Analysis of the deformation behavior reveals distinct responses to impact between the drive shaft and the steering mechanism. Based on the working principle of the steering mechanism, the actual variation in inclination angle during operation results from the superposition of these two deformation modes. The proportion of each mode is primarily governed by the stiffness ratio between the connecting links and the driven shaft. When the link stiffness is significantly lower than the bending stiffness of the shaft, the inclination variation follows the pattern described by Equation (21). Conversely, when the shaft bending stiffness is comparatively lower, Equation (20) provides the dominant model. To simplify the analysis while focusing on vertical vibration in the Y-direction, a stiffness ratio coefficient $g_y=E{I}_{\mathrm{shaft}}/E{I}_{link}$ is introduced for subsequent computational procedures.

3. Vibration Characteristic Analysis Based on Numerical Simulation

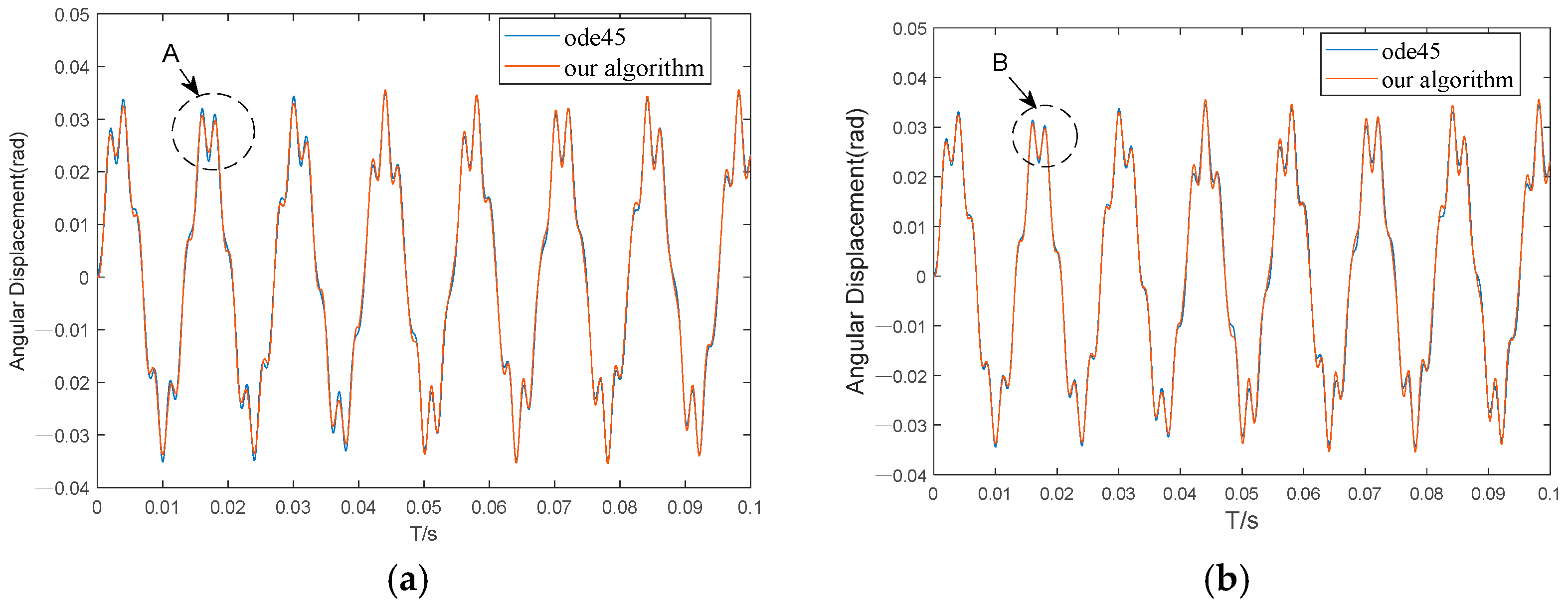
3.1. Numerical Simulation Method

According to the previous kinematic analysis, the drive shaft and the steering mechanism exhibit strong nonlinear characteristics, and their impact response is also highly nonlinear. Therefore, the Newmark method is employed in the numerical simulation, and the iterative steps are described as follows:

(1)

Assign each parameter of the shafting: set the initial inclination angle $r$, set the initial geometric position of the drive shaft and steering mechanism. Set the time t = 0; and set the angular acceleration and angular displacement of the driving shaft, the driven shaft, and the intermediate shaft to all 0.

(2)

Impact load parameters were determined through a combined approach of theoretical calculation and experimental adjustment. Initial baseline load values were obtained by calculating the torque of a four-blade propeller according to DNV standards. Given the system’s high sensitivity to impact loads, iterative experimental adjustments were subsequently performed on the load amplitude, duration, and application point to achieve optimal system response. The parameters ultimately set in this study were an impact force of 0.1 kN and a pulse width of 10 ms. Besides, we applied the impact load at t = 1 s to ensure that the load was imposed on a fully stabilized system, thereby facilitating a consistent and meaningful comparison of the resulting parameters.

(3)

Based on the applied impact loads, a dynamic response analysis was conducted separately for the steering mechanism and the drive shaft. This analysis yielded key parameters including the length of the tie rod, the spatial position of the propeller, and the resulting bending moment.

(4)

The dynamic inclination angle is chosen as the analysis parameter and is designated as $r^{\prime }$. At each time step ($t=t_0+\mathrm{\Delta }t$), the time-varying spatial position of the propeller is calculated and substituted into Equation (8). With the inclination angle updated ($r^{\prime }$→ $r$), the system’s vibration equations at these two angular positions are expressed as follows:

$$\left[M\right]{\left\{\ddot{r}\right\}}_t+\left[C\right]{\left\{\dot{r}\right\}}_t+\left[K\right]{\left\{r\right\}}_t=-\left[M\right]\left\{p\right\}{\left\{\ddot{u}\right\}}_t$$

(24)

$$\left[M\right]{\left\{\ddot{r}\right\}}_{t+\mathrm{\Delta }t}+\left[C\right]{\left\{\dot{r}\right\}}_{t+\mathrm{\Delta }t}+\left[K\right]{\left\{r\right\}}_{t+\mathrm{\Delta }t}=-\left[M\right]\left\{p\right\}{\left\{\ddot{u}\right\}}_{t+\mathrm{\Delta }t}$$

(25)

(5)

Suppose the acceleration varies linearly within the time step $[t,t+\mathrm{\Delta }t]$. Using γ and β as the parameters governing the accuracy and stability of the Newmark algorithm, the update Equations for the state variables $(r,\dot{r})$ can be derived as follows:

$$\left\{\begin{array}{l}{\left\{\dot{r}\right\}}_{t+\mathrm{\Delta }t}={\left\{\dot{r}\right\}}_t+\left[(1-\delta ){\left\{\ddot{r}\right\}}_t+\delta {\left\{\ddot{r}\right\}}_{t+\mathrm{\Delta }t}\right]\mathrm{\Delta }t\\ {\left\{r\right\}}_{t+\mathrm{\Delta }t}={\left\{r\right\}}_t+{\left\{\dot{r}\right\}}_t\mathrm{\Delta }t+\left[(1/2-\gamma ){\left\{\ddot{r}\right\}}_t+\gamma {\left\{\ddot{r}\right\}}_{t+\mathrm{\Delta }t}\right]\mathrm{\Delta }{t}^2\end{array}\right.$$

(26)

After variable substitution according to the Newmark method, Equation (26) becomes Equation (27).

$$\left\{\begin{array}{l}{\left\{\ddot{r}\right\}}_{t+\mathrm{\Delta }t}={\displaystyle \frac{1}{\gamma \mathrm{\Delta }{t}^2}}({\left\{r\right\}}_{t+\mathrm{\Delta }t}-{\left\{r\right\}}_t)-{\displaystyle \frac{1}{\gamma \mathrm{\Delta }t}}{\left\{\dot{r}\right\}}_t-({\displaystyle \frac{1}{2\gamma }}-1)\mathrm{\Delta }t{\left\{\ddot{r}\right\}}_t\\ {\left\{\dot{r}\right\}}_{t+\mathrm{\Delta }t}={\displaystyle \frac{\delta }{\gamma \mathrm{\Delta }t}}({\left\{r\right\}}_{t+\mathrm{\Delta }t}-{\left\{r\right\}}_t)+(1-{\displaystyle \frac{\delta }{\gamma }}){\left\{\dot{r}\right\}}_t+(1-{\displaystyle \frac{\delta }{2\gamma }})\mathrm{\Delta }t{\left\{\ddot{r}\right\}}_t\end{array}\right.$$

(27)

By substituting Equation (27) into Equation (25), we obtain

$$\begin{array}{l}\left[M\right]\left\{{\left\{\dot{r}\right\}}_t+\left[(1-\delta ){\left\{\ddot{r}\right\}}_t+\delta {\left\{\ddot{r}\right\}}_{t+\mathrm{\Delta }t}\right]\mathrm{\Delta }t\right\}+\left[K\right]{\left\{r\right\}}_{t+\mathrm{\Delta }t}+\left[C\right]\\ \left\{{\displaystyle \frac{\delta }{\gamma \mathrm{\Delta }t}}({\left\{r\right\}}_{t+\mathrm{\Delta }t}-{\left\{r\right\}}_t)+(1-{\displaystyle \frac{\delta }{\gamma }}){\left\{\dot{r}\right\}}_t+(1-{\displaystyle \frac{\delta }{2\gamma }})\mathrm{\Delta }t{\left\{\ddot{r}\right\}}_t\right\}=-\left[M\right]\left\{p\right\}{\left\{\ddot{u}\right\}}_{t+\mathrm{\Delta }t}\end{array}$$

(28)

The above Equations can be transformed as follows:

$$\left\{{\displaystyle \frac{1}{\gamma \mathrm{\Delta }{t}^2}}\left[M\right]+{\displaystyle \frac{\delta }{\gamma \mathrm{\Delta }t}}\left[C\right]+\left[K\right]\right\}{\left\{r\right\}}_{t+\mathrm{\Delta }t}=\widehat{T}$$

(29)

where

$$\begin{array}{l}\widehat{T}=-\left[M\right]\left\{p\right\}{\left\{\ddot{r}\right\}}_{t+\mathrm{\Delta }t}+\left[M\right]\left\{{\displaystyle \frac{1}{\gamma \mathrm{\Delta }{t}^2}}{\left\{r\right\}}_t+{\displaystyle \frac{1}{\gamma \mathrm{\Delta }t}}{\left\{\dot{r}\right\}}_t+({\displaystyle \frac{1}{2\gamma }}-1){\left\{\ddot{r}\right\}}_t\right\}\\ +\left[C\right]\left\{{\displaystyle \frac{1}{\gamma \mathrm{\Delta }{t}^2}}{\left\{r\right\}}_t+({\displaystyle \frac{\delta }{\gamma }}-1){\left\{\dot{r}\right\}}_t+({\displaystyle \frac{\delta }{2\gamma }}-1){\left\{\ddot{r}\right\}}_t\right\}\end{array}$$

(30)

So, ${\left\{r\right\}}_{t+\mathrm{\Delta }t}$ can be obtained by solving Equation (30).

(6)

Steps 3–5 are repeated iteratively over each interval until the phase trajectory converges. The resulting state parameters $(r,\dot{r})$ are subsequently used to calculate other vibration characteristics.

The geometric and performance parameters of the vector thruster were obtained from post-fabrication measurements as well as the equipment supplier, among which $L_2=0.1 \mathrm{m}$; $d=0.2 \mathrm{m}$. The initial lengths of links and the propulsion shafting are all $L_3=0.3 \mathrm{m}$, $k_1=5.2\times {10}^4 \mathrm{k}\mathrm{N}/\mathrm{m}$, $k_2=3.4\times {10}^2 \mathrm{k}\mathrm{N}/\mathrm{m}$. The propeller parameters $J_{xx}$, $J_{yy}$, $J_{zz}$ are 0.008 kg·m², 0.053 kg·m², 0.053 kg·m², respectively. During the initial phase, the initial values we set are inconsistent with the actual steady-state values. The simulation undergoes a convergence process to reach a stable operating condition, as the choice of initial values does not affect the final steady state.

To validate the feasibility of the proposed computational method, simulations were conducted under conditions of no impact, at a rotational speed of 200 rpm, and an inclination angle of 5°. The algorithmic parameters were set to $\delta$ = 0.5 and γ = 0.25; the time step of Δt = 0.001 s was adopted for the integration. The relative error tolerances were set to 1 × 10⁻⁶ and 1 × 10⁻⁹, respectively. Figure 6a,b presents a comparison of the angular displacement in the time domain between the proposed algorithm and the ODE45 solver. The results demonstrate that as the relative error decreases, the response curve of the ODE45 algorithm progressively converges toward that of the proposed method. Notably, the peak deviation is significantly reduced, as indicated by labels A and B. However, the computational time required by the ODE45 solver increases substantially with stricter error tolerance. In contrast, the proposed algorithm maintains computational accuracy while achieving improved efficiency.

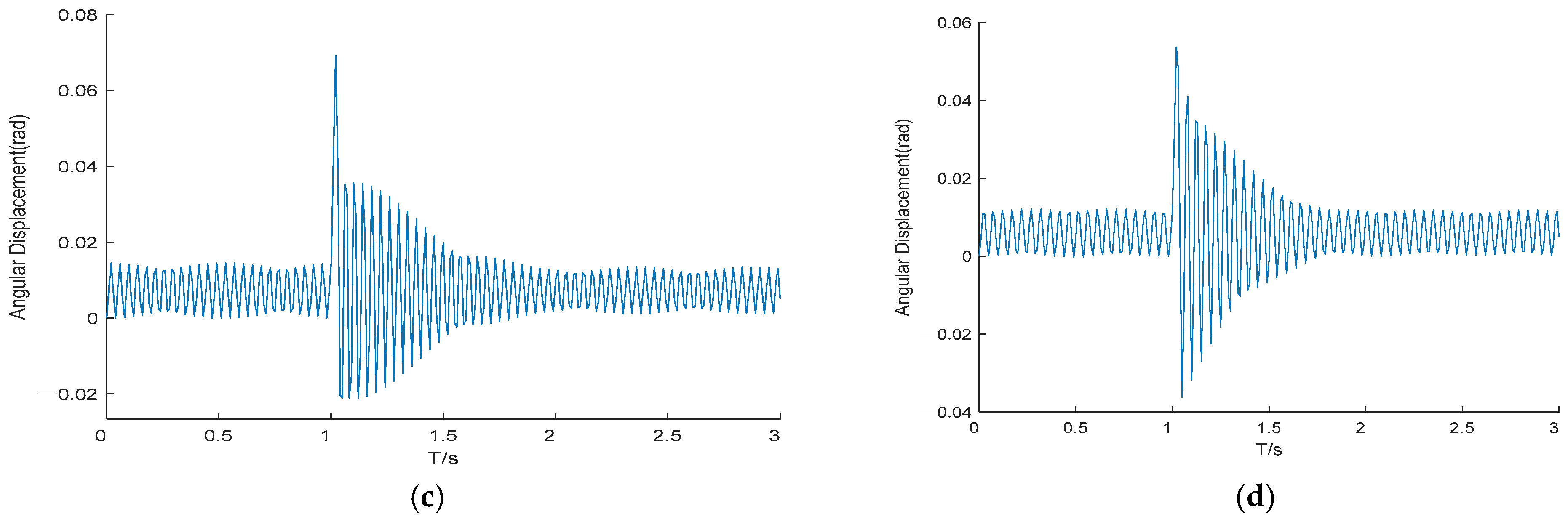
3.2. Vibration Characteristics Under Different Structural Parameters

Based on the force transmission characteristics of the thruster, an impact load triggers significant perturbations in the inclination angle. To systematically assess the influence of structural parameters on the resulting vibration, the effects of the length ratio and stiffness ratio on the dynamic inclination angle should first be analyzed. With the inclination angle fixed at 1 deg and the rotational speed at 400 r/min, an impact load is applied at the initial time of 1 s. The corresponding numerical simulations yield the amplitude–time curves presented in Figure 7. All dynamic response curves in the figure display oscillatory behavior to different degrees. Following the transient impact load applied, the angular displacement of the shafting exhibits irregular motion. After the load dissipates, the shaft motion gradually returns to a quasi-periodic steady state. The overall system undergoes three distinct stages: a quasi-periodic state, a transition to irregular motion, and a recovery to a quasi-periodic state, demonstrating that the influence of the impact load on the propulsive shafting is transient [26].

In terms of impact intensity, thrusters with greater steering mechanism stiffness show smaller amplitude fluctuations and shorter stabilization times. As depicted in Figure 7a, which corresponds to the length ratio 1.0 with a stiffness ratio of 0.1, the amplitude ranges from 0.01 to 0.038 rad, and the shafting resumes periodic motion at 2.8 s, resulting in a stabilization time of 1.8 s. In contrast, Figure 7c, representing the length ratio 1.2, shows the amplitude varying from 0.015 to 0.036 rad, with the shafting returning to periodic motion at 1.9 s. A comparison between Figure 7a,c (k = 1.0) and Figure 7b,d (k = 1.2) reveals that the system with k = 1.0 exhibits smaller amplitude fluctuations and a significantly shorter stabilization time than that with k = 1.2. Therefore, it is advisable to keep the average length of the telescopic link as close as possible to the original length of the drive shaft during the operation of the steering mechanism.

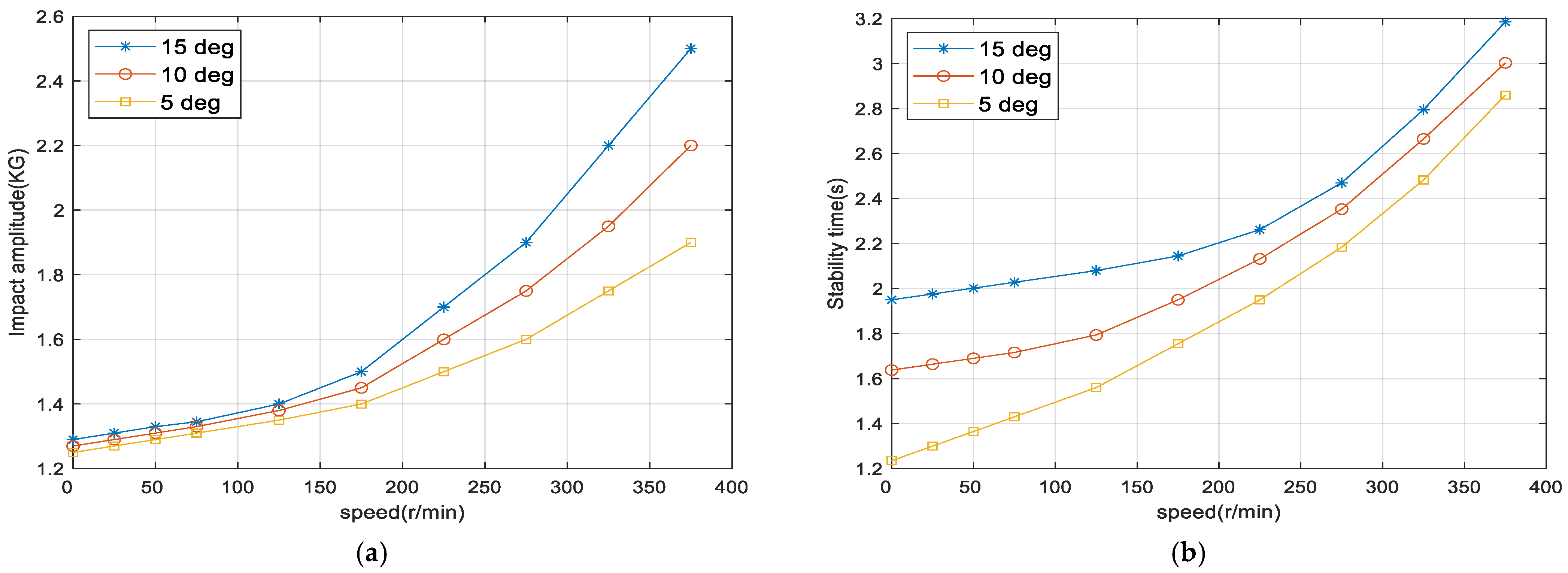
3.3. Vibration Characteristics Under Different Operating Conditions

As a key operational parameter of the vector thruster, the inclination angle affects system dynamics through the universal joint. Variations in the inclination angle alter the natural frequency along the driven shaft, while the support stiffness of the shaft also directly governs its natural frequency. It can therefore be inferred that the stiffness ratio and inclination angle continuously affect both the vibration amplitude and frequency spectrum of the thruster. To observe this relationship, set difference stiffness ratios and successively the inclination angle to 5 deg and 10 deg, respectively. The impact force is applied to the propeller, in which the impact amplitude and width are set at 0.1 KN and 0.01 S, respectively. According to the numerical simulation method above, the load response diagram can be obtained as shown in Figure 8. Figure 8a,c illustrate the time-domain response under impact load, and Figure 8b,d display the corresponding frequency spectra; it can be seen that the amplitude after impact decreases with the increasing inclination angle. Moreover, this phenomenon is more pronounced at a higher stiffness ratio. The overall frequency spectrum shifts to the left with the corresponding increase in the inclination angle, and the amplitude in high frequency decreases, whereas that in low frequency increases. This indicates that the support stiffness primarily affects the low-frequency components, while the inclination angle variation mainly influences the high-frequency components of the system. Notably, since this study focuses specifically on the frequency components associated with the impact load, other higher-frequency vibration components have been intentionally excluded from the presented spectral analysis.

Once the stiffness ratio is determined, it remains fixed during operation, making its appropriate selection a primary task in the design of vector thrusters. Furthermore, if the stiffness ratio is too low during the design phase—meaning the steering mechanism stiffness is too high—it may adversely affect the maneuverability of the steering system. Taking all factors into consideration, a stiffness ratio of 0.5 was selected for this study. Accordingly, the following analysis will focus on examining the influence of the length ratio and other operational parameters on impact resistance performance.

As a key positioning parameter of the steering mechanism, the length ratio directly influences the variation patterns of the universal joint, which in turn affects the change in inclination angles. To analyze this comprehensively in conjunction with operating conditions, multi-group datasets were utilized to compute the variations in vibration amplitude and stabilization time with respect to the inclination angle under different length ratios, as illustrated in Figure 9a,b. As can be observed from the figure, the influence of the inclination angle on the shafting stability is generally limited under normal operating conditions. Specifically, an increase in the inclination angle leads to an increase in both the angular displacement amplitude and the stabilization time, with the growth rate transitioning from rapid to gradual. Furthermore, an increase in the length ratio amplifies these effects to varying degrees. Notably, at smaller length ratios, the displacement response amplitude decreases more markedly as the inclination angle is reduced. The results also indicate that when the inclination angle does not exceed 5 deg, the stabilization time becomes more volatile with variations in the length ratio. Therefore, the action value of the actuators must be reasonably adjusted to ensure it matches the operating conditions.

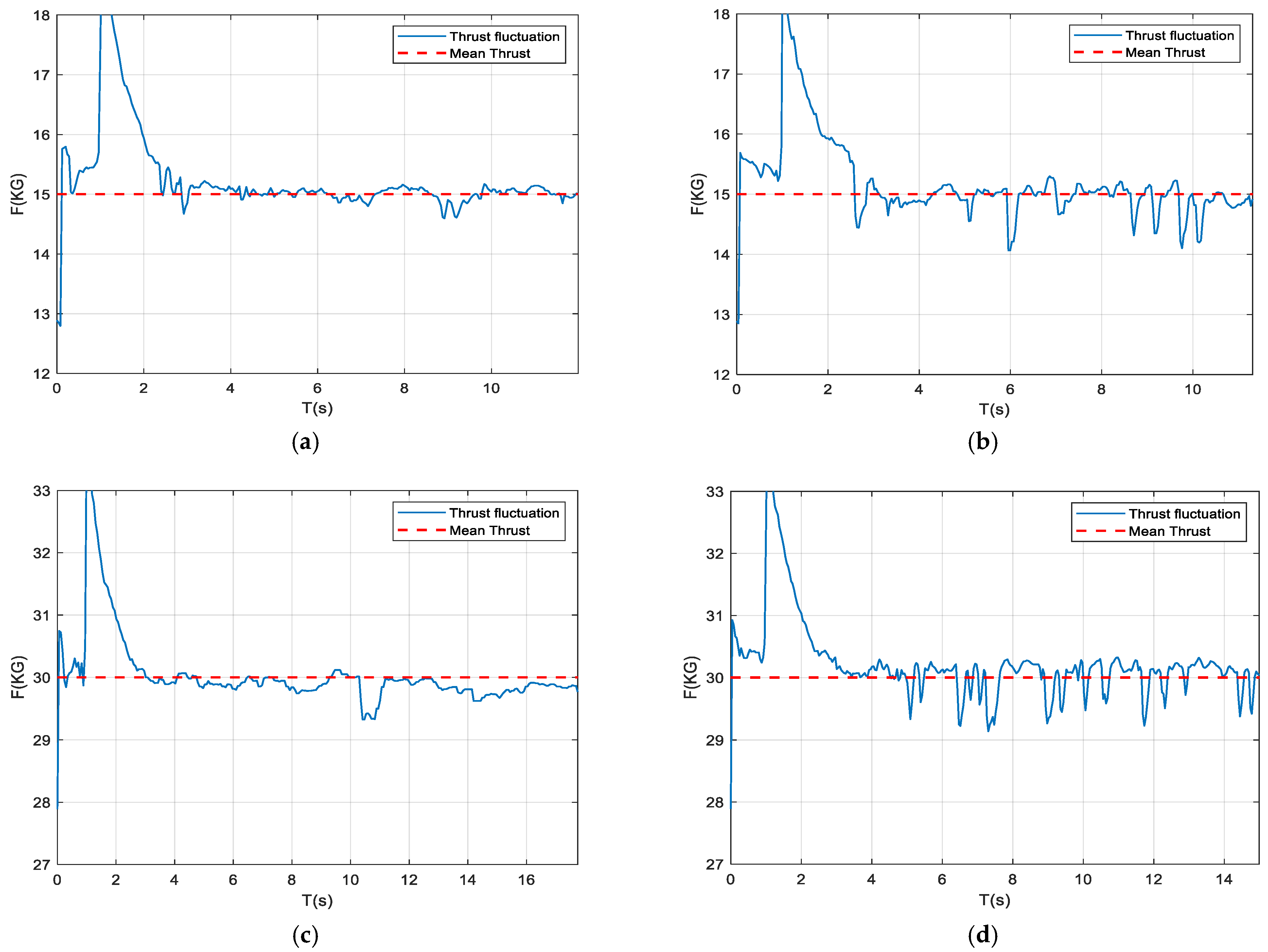
4. Dynamic Inclination Angle and Thrust Analysis Based on a Test Rig

Figure 10a shows the constructed vector thrust test rig. The test bench primarily uses equipment supplied by Shenzhen Quanxiang Power Technology Co., Ltd., and incorporates an impact load application device (shown in Figure 10e) capable of generating impulses with varying periods and pulse widths. It is also instrumented with force, torque, speed, and vibration sensors, along with other equipment (shown in Figure 10b–d), to record real-time data such as the thruster’s thrust, torque magnitude, and propeller speed. The specifications of its key components are shown below.

• The three-axis force sensor (Model: DET G10) has 3 channels, with an accuracy error of ±0.1% ± 30 g, a tension resolution of 0.001 kg, and an internal data update frequency of up to 100 Hz, enabling it to meet the testing standards for underwater vector thrusters.
• The vibration sensor (Model: 5E106) has a range of 10 mm, a sensitivity of 1 V/mm, and a frequency response of 0–10,000 Hz. The sensors were installed on the base, thrust sensor mount, and vectoring mechanism, with specific installation details shown in Figure 10b, Figure 10c, and Figure 10d, respectively.
• The test tank had a diameter of 3L and contained a flow path in which the propeller length was defined as the reference length L; the front section (inlet to thruster) measured 1.5 L and the rear section (thruster to outlet) measured 3.375 L, as illustrated in Figure 11a.
• Figure 12b–d depict three key operational states of the system: (b) the initial standby state before startup; (c) stable underwater operation (side view); and (d) surface-level operation (front view). During the experiments, the load application system integrated into the test bench was capable of applying various types of loads while simultaneously acquiring data, thereby facilitating comprehensive dynamic performance analysis.

To validate the impact load response of the vector thruster, experiments were conducted using an underwater test platform. The tests were performed at a constant inclination angle of 5°, with the propeller speed varying at 200 rpm and 400 rpm. During the experiments, key parameters, including thrust and inclination angle, were monitored in real time. The system recorded numerical data, visualized dynamic performance curves, and automatically archived the results, as shown in Figure 12a,b. As can be seen from the displayed graphs, both the dynamic variation diagram and the spectral diagram are highly complex, making it difficult to observe details clearly. Therefore, to examine the experimental outcomes, the data were processed accordingly. The experimental results and corresponding numerical simulations for the inclination angles are presented in Figure 12c and Figure 12d, respectively. The test rig and the real system exhibit similar change patterns, as evidenced by the close agreement between the observed and simulated values, confirming the validity of the experimental model.

As shown in Figure 12c,d, the maximum amplitude error primarily persists for one period (approximately 1 s) following impact loading. During this interval, the measured values are consistently lower than the simulated results, with the discrepancy becoming more pronounced at higher rotational speeds. This phenomenon can be attributed to propeller-generated pulsating forces, which induce vibrations in both the drive shaft and steering mechanism. These vibrations, in turn, modify the vibration characteristics of the system, thereby influencing the degree of subsequent pulsation. Thus, it is necessary to synergistically apply a set of procedures—calibration, compensation, filtering, and synchronization—in order to collectively control the total experimental uncertainty within acceptable limits. These procedures include the following:

• Signal filtering is employed to manage noise, with the test rig capable of capturing vibrations below 10 kHz. An adjustable software filter is provided to smooth the raw data accordingly.
• Measurement synchronization is achieved through a hardware-triggered procedure, which simultaneously activates all data acquisition channels with a temporal accuracy better than 0.1 ms, thereby minimizing errors caused by timing misalignment.
• Sensor Calibration Adjusted for Environmental Variability: Laboratory tests with vibration isolation remain susceptible to measurement fluctuations in inclination angle due to confined-flow effects such as recirculation and turbulence. Conversely, outdoor experiments—while providing an open flow field—introduce variability from wind, waves, and fixture stability. Therefore, the built-in parameter calibration function must be employed to compensate for these environmental shifts and for drift due to prolonged operation.

The test analysis further indicates that under impact load, both the thrust angle and rotational speed of the vector thruster exhibit certain fluctuations, inevitably affecting thrust output. However, precise thrust analysis requires hydrodynamic simulation for accurate calculation, as such precise simulation is beyond the scope of this paper; to simplify this process and verify the influence pattern of impact load on thrust, the existing test platform was employed in its three-dimensional thrust measurement mode. This configuration employs a three-component force sensor system capable of simultaneously measuring longitudinal (x-axis), vertical (y-axis), and lateral (z-axis) forces within the defined coordinate system. Tests were conducted at inclination angles of 5° and 10° and propeller speeds of 200 rpm and 400 rpm. Following system stabilization, the test platform was activated to record thrust data. Meanwhile, the test bench monitoring interface revealed that the acquired signals contained complex spectral components, attributable to numerous influencing factors. Accordingly, the raw dataset was processed, and the dynamic characteristic curves of thrust amplitude were plotted in MATLAB (Version 2018) for further analysis. Marking t = 0, an impact load was applied at t = 1 s, and the response data were processed to generate the dynamic curves in Figure 13.

In Figure 13a–d, the thrust (reported in kilogram-force, kgf) is plotted against time. The mean values, calculated as the average over the indicated intervals, show that the same impact load produces significantly different effects on thrust fluctuations under different operational parameters. Comparing (a) with (b), and (c) with (d), it is evident that a larger inclination angle (from 5° to 10°) consistently amplifies the thrust oscillation under the same rotational speed. Similarly, comparing (a) with (c), and (b) with (d) reveals that a higher propeller speed (from 200 rpm to 400 rpm) also exacerbates the impact-induced instability. Crucially, sub-figure (d), which combines the highest inclination angle (10°) and rotational speed (400 rpm), exhibits the most severe thrust fluctuations. This demonstrates a coupled effect where high rpm and large inclination angles jointly intensify the impact load. Therefore, this phenomenon must be prioritized in the design and operational protocols for such extreme conditions to ensure system reliability.

To systematically investigate the impact resistance performance of the vectored thruster, we conducted repeated experiments with different structural and operational parameters. By varying parameters such as tie rod length, length ratio K, inclination angle, and rotational speed, we observed changes in anti-impact performance, including the impact amplitude, stabilization time of inclination, and the corresponding thrust amplitude and its stabilization time, as shown in

Table 2. Experimental results under various operating conditions.

Speed (r/min)	Structural Parameters					Amplitude of Fluctuation		Settling Time (s)
	q1 (cm)	q2 (cm)	q3 (cm)	r (deg)	K	Inclination Angle (rad)	Thrust (KG)
100	22.1	22.1	30.3	5	1.0	0.031	1.34	1.5
	22.1	30.3	22.1	5	1.2	0.036	1.40	1.7
200	18.4	18.4	32.5	10	1.0	0.043	1.71	2.0
	14.7	36.0	36.0	20	1.2	0.047	1.94	2.2
300	18.4	18.4	32.5	10	1.0	0.055	2.48	2.6
	14.7	36.0	36.0	20	1.2	0.058	2.51	2.7
400	36.0	14.7	36.0	20	1.0	0.069	3.59	3.5
	14.7	36.0	36.0	20	1.2	0.072	3.65	3.5

.

The inclination angles in Table 2 were obtained from test bench measurements, while the parameters q₁, q₂, and q₃ were derived from actuator data acquisition and conform to Equations (18) and (19). The amplitude of fluctuations and the settling time were acquired via the test bench software. As shown, these output parameters vary with different structural and operational inputs under identical impact loading conditions, which is consistent with the conclusions drawn from the numerical simulations presented earlier. Overall, larger values of K, the inclination angle, and the rotational speed are collectively associated with increased values in the impact response, with the magnitude of increase varying across parameters. To clarify this relationship, we focus on the rotational speed and inclination angle as the key variables. Their combined effect on thrust fluctuation is plotted in Figure 14, based on the experimental data.

As shown in Figure 14, when the rotational speed increases, the impact amplitude under all three inclination angles (5°, 10°, and 15°) shows a continuous increase. The 15° inclination angle results in the most significant amplitude growth, reaching 2.5 KG at high speeds, indicating that a bigger initial impact angle leads to greater sensitivity to speed increases for the vector thruster. Regarding stability time, the vector thruster requires progressively longer to stabilize as the speed rises. Notably, the 5° inclination angle consistently corresponds to the shortest stability time, approximately 2.86 s at 375 r/min, while the 15° condition requires about 3.185 s at the same speed. This indicates that although stabilization time increases with both inclination angle and rotational speed, its dependence on the inclination angle is more pronounced at lower speeds compared to the trend observed for impact amplitude.

5. Discussion

The response of impact loads on the vector thruster with a universal joint exhibits strong coupling vibration characteristics, which intensify inclination angle fluctuations and further affect the stability of power transmission. To effectively evaluate the action intensity and regularity of impact loads, the calculations of loads, inclination angle, motion characteristics, and vibration characteristics are coupled through a mechanical model. The results of numerical simulations and experiments are summarized as follows:

• When impact loads act on the universal-joint vector thruster, they induce distinct dynamic responses in both the driven shaft and the steering mechanism. The dynamic response is highly dependent on factors such as the position, stiffness, and inclination angle of the steering mechanism within the thruster. These two types of responses interact with each other, forming a positive feedback loop that complicates the vibration behavior and ultimately degrades the system’s dynamic performance.
• Due to the strong nonlinear coupling between the universal joint and the steering mechanism under different operating conditions as well as structural parameters, the calculation of the impact load response in the time domain becomes highly complex. However, iterative simulation calculations based on the Newmark method can be effectively applied to the impact load response analysis of the vector thruster. However, as both the numerical simulations and the experimental setup involve significant simplifications, future work should prioritize more sophisticated hydrodynamic calculations, focusing particularly on developing higher-fidelity models through transient fluid–structure interaction analysis to enhance computational precision.
• Both the fluctuation amplitude of the inclination angle and the vibration stabilization time increase with the stiffness ratio, but the increase in stabilization time is more pronounced. During the operation of the vector thruster, both the vibration amplitude and the stabilization time increase with larger inclination angles. However, systems with higher length ratios exhibit a more pronounced growth in amplitude as the inclination angle increases. These fluctuations in inclination angle directly affect the thrust characteristics of the thruster. Therefore, in the design of vector thrusters, stiffness and dimensional parameters must be reasonably selected to enhance anti-impact performance.
• Given the presence of thrust loss and the significant influence of structural parameters on impact response, it remains essential to determine the operational load range through parameter analysis and to promptly increase rotational speed upon impact for compensation. Looking ahead, future implementations should integrate flexible couplings to absorb transient vibrations, incorporate damping materials to dissipate impact energy, and develop active control schemes for real-time compensation. This integrated approach would substantially improve the operational reliability of propulsion systems under dynamic loading conditions.