Design and Validation of a Soft Pneumatic Submodule for Adaptive Humanoid Foot Compliance

Abstract

Achieving stable contact on uneven terrain remains a key challenge in humanoid robotics, as most feet rely on rigid or passively compliant structures with fixed stiffness. This work presents the design, fabrication, and analytical modeling of a compact soft pneumatic submodule capable of tunable longitudinal stiffness, developed as a proof-of-concept unit for adaptive humanoid feet. The submodule features a tri-layer architecture with two antagonistic pneumatic chambers separated by an inextensible layer and reinforced by rigid inserts. A single-step wax-core casting process integrates all materials into a monolithic soft–rigid structure, ensuring precise geometry and repeatable performance. An analytical model relating internal pressure to equivalent stiffness was derived and experimentally validated, showing a linear stiffness–pressure relation with mean error below 10% across 0–30 kPa. Static and dynamic tests confirmed tunable stiffness between 0.18 and 0.43 N·m/rad, a rapid symmetric response (2.9–3.4 ms), and stable stiffness under cyclic loading at gait-relevant frequencies. These results demonstrate the submodule’s suitability as a scalable building block for distributed, real-time stiffness modulation in next-generation humanoid feet.

1. Introduction

Achieving stable locomotion over irregular terrain remains one of the central challenges in humanoid robotics. Most humanoid robots rely on rigid or only passively compliant feet, which cannot conform to uneven ground and thus experience poor contact stability, impact sensitivity, and limited adaptability in unstructured environments. Soft robotics offers a promising alternative by introducing intrinsic compliance, energy absorption, and safer interaction with the environment [1]. However, passive soft components provide fixed mechanical properties once fabricated. For stable and efficient locomotion, the foot should be able to actively adjust its stiffness according to ground conditions and gait phase. This requires compact, lightweight, and fast variable-stiffness mechanisms that can be embedded within the limited volume of a humanoid sole.

A wide range of variable-stiffness technologies have been explored in robotics, including jamming-based systems, mechanically reconfigurable mechanisms, smart materials, and soft fluidic actuators. Jamming structures offer large stiffness changes but require bulky pumps and respond slowly [2,3]. Mechanical VSAs provide precise stiffness control but are difficult to miniaturize for distributed use in a foot [4]. Smart materials such as dielectric elastomers and magnetorheological elastomers offer simple actuation principles but generally suffer from limited bandwidth or complex drive electronics. Soft pneumatic actuators (SPAs), by contrast, are lightweight, manufacturable, and easily scalable [5,6]. Their reliance on pressure-driven deformation makes them particularly suitable for embedding tunable compliance in robotic systems.

SPAs have been widely used in manipulation, wearable robotics, and continuum structures, where their distributed deformation enables safe and adaptive contact [7,8]. Extending these advantages to locomotion, a humanoid foot could similarly benefit from local pneumatic deformation to maintain stable contact on uneven terrain.

Beyond motion-oriented SPAs, several works have explored ways to increase or control stiffness in PneuNet-type pneumatic structures. These include PneuNets with stiffness-variable elements to enhance load capacity [9], modular arrays for combined structural and stiffness control [10], and hybrid PneuNet–jamming systems designed to tune rigidity [11]. Other studies have examined how chamber geometry, internal pressure, and material nonlinearities influence bending and stiffness [12,13]. Additional research has focused on improving response speed and compactness of soft pneumatic systems for integration in wearable or robotic platforms [14,15,16]. Together, these works demonstrate that pneumatic architectures can modulate stiffness, but asymmetric pressurization still produces substantial geometric deformation, and large internal volumes lead to response times of tens to hundreds of milliseconds, too slow for real-time stance-phase stiffness control in humanoid locomotion.

Conventional soft pneumatic actuators such as PneuNets [17,18] and fiber-reinforced designs [19,20] are primarily optimized for producing motion (bending, elongation, or twisting) rather than for stiffness modulation. Their asymmetric pressurization induces unwanted bending, compromising flat stance geometry, while large internal volumes slow down pneumatic response. As a result, existing SPAs struggle to achieve simultaneous geometric symmetry, compact integration, and fast stiffness adaptation—three key requirements for humanoid soles.

To overcome these limitations, we propose a compact dual-chamber pneumatic submodule that modulates longitudinal stiffness through equal pressurization of antagonistic layers. This symmetric architecture enables stiffness tuning without shape change and supports rapid pneumatic actuation compatible with real-time control. The prototype is analyzed here as a stand-alone proof-of-concept submodule (Figure 1), focusing on its design, fabrication, modeling, and experimental validation. Although conceived as a building block for a future pneumatically compliant humanoid foot, this work concentrates exclusively on the submodule-level characterization rather than the integration of a complete sole system.

The step forward achieved in this work with respect to the existing state of the art is summarized in

Table 1. Comparison of existing variable-stiffness actuator technologies.

Type	Geom. Change	Stiffness (N·m/rad)	Resp. Time	Scalability
Layer/particle jamming [2,3,27]	No	0.1–5	0.1–1 s	Poor
Series-elastic (VSA) [4,28]	Yes	1–50	10–100 ms	Limited
Smart materials (DE, MR, SMP) [29,30,31]	Small	<1	0.1–10 s	Low
Fiber-reinforced SPA [19,20]	Yes	0.1–1	50–200 ms	Moderate
PneuNet SPA [17,18]	Yes	0.05–0.5	100–500 ms	Good
Proposed tri-layer	No	0.18–0.43	2.9–3.4 ms	High

. The table compares representative variable-stiffness mechanisms in terms of geometry change, stiffness range, response time, and scalability. Whereas jamming, smart-material, and mechanical approaches provide tunability at the expense of speed, size, or scalability, existing SPAs remain primarily motion generators with slow pneumatic dynamics. The proposed tri-layer submodule instead achieves pure stiffness modulation without geometric deformation, a biologically relevant stiffness range (0.18–0.43 N·m/rad), and a sub-4 ms response time (around one order of magnitude faster than conventional fluidic systems). These values fall within the ranges reported for the human foot arch and ankle quasi-stiffness [21,22,23,24], and correspond to the rapid intrinsic stiffness adjustments observed in human neuromuscular response (2–5 ms) [25,26].

The main contributions of this work are

• Antagonistic Tri-Layer Design: Symmetric pneumatic chambers achieving stiffness modulation without geometric deformation.
• Single-Shot Wax-Core Fabrication: Co-molding of soft, rigid, and inextensible materials for alignment and durability.
• Analytical Pressure–Stiffness Model: Linear closed-form formulation validated experimentally.
• Experimental Validation: Tunable stiffness (0.18–0.43 N·m/rad, 0–30 kPa), fast response (2.9–3.4 ms stable behavior under cyclic loading).

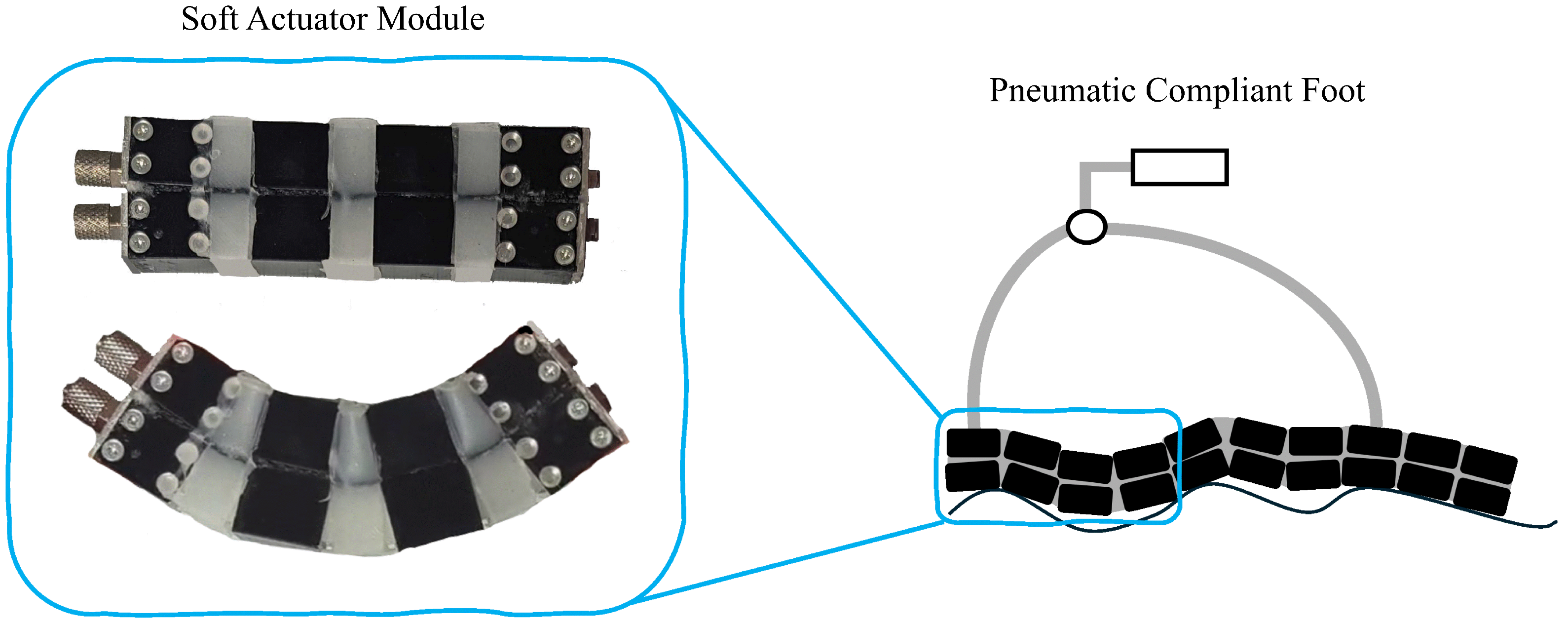
2. Antagonistic Tri-Layer Actuator Design

To achieve tunable stiffness in a compact, load-bearing element suitable for humanoid soles, we developed a tri-layer pneumatic submodule that reproduces the antagonistic behavior of biological muscles. This section details the submodule’s working principle, structural composition, geometric optimization, and prototype implementation.

2.1. Design Concept and Working Principle

Instead of relying on mechanical springs or large external structures, stiffness is modulated internally through pressurized air chambers embedded within a soft–rigid composite. The submodule consists of two mirrored pneumatic layers separated by a thin inextensible nylon sheet that lies along the neutral axis of the structure. Each layer contains a series of longitudinal air chambers made of silicone, while lightweight aluminum inserts reinforce the outer surfaces. This tri-layer arrangement allows the two pneumatic layers to expand in opposite directions during inflation, producing an antagonistic action analogous to paired muscles around a tendon. As shown in Figure 2a, inflating only one side causes the submodule to bend toward the opposite direction, similar to how a single muscle contracts to rotate a joint. When both sides are pressurized equally, the nylon sheet constrains differential expansion, suppressing bending and instead increasing the structure’s longitudinal stiffness. In this state, the internal pressure energy is stored elastically within the soft material rather than being converted into geometric deformation. Manual deformation tests (Figure 2b) illustrate this behavior clearly: at low pressure (2 kPa) the submodule bends easily under load, whereas at high pressure (30 kPa) it resists deflection, demonstrating rapid and reversible stiffness modulation. Unlike conventional soft actuators that exploit shape change for motion, this design intentionally minimizes deformation, focusing instead on controllable stiffness while maintaining a flat, stable geometry, a critical requirement for humanoid feet during stance and locomotion.

2.2. Structural Architecture and Components

The submodule integrates a hyperelastic silicone matrix (Ecoflex 00–30), an inextensible nylon sheet, and lightweight aluminum reinforcements into a compact tri-layer configuration suited for humanoid soles. The nylon layer defines the neutral axis and constrains elongation, coupling the two pneumatic layers so that equal pressurization increases stiffness rather than bending. Each pneumatic layer contains a series of Ecoflex chambers separated by aluminum inserts that act as internal “bones,” locally reinforcing the silicone, limiting radial expansion, and maintaining chamber geometry. This alternating soft–rigid sequence forms discrete spans analogous to human phalanges, combining flexibility with load-bearing capacity. When pressurized, the chambers expand against the nylon interface and rigid frames, generating balanced co-contraction that stiffens the submodule while preserving a flat profile.

Figure 3a shows the submodule’s tri-layer structure which integrates top and bottom rigid blocks with side enclosures around a central inextensible nylon layer. The nylon sheet separates the upper and lower pneumatic sections, while aluminum blocks and Ecoflex regions form alternating soft–rigid spans (Figure 3b). Figure 3c shows the longitudinal section, which reveals paired air chambers above and below the nylon layer, connected by a central air channel that ensures uniform pressurization. The exploded views (Figure 3d,e) show how the nylon layer is clamped between rigid blocks with screws and enclosed laterally by rigid plates, forming a compact soft–rigid module that preserves geometry under load while enabling fast, pressure-dependent stiffness modulation.

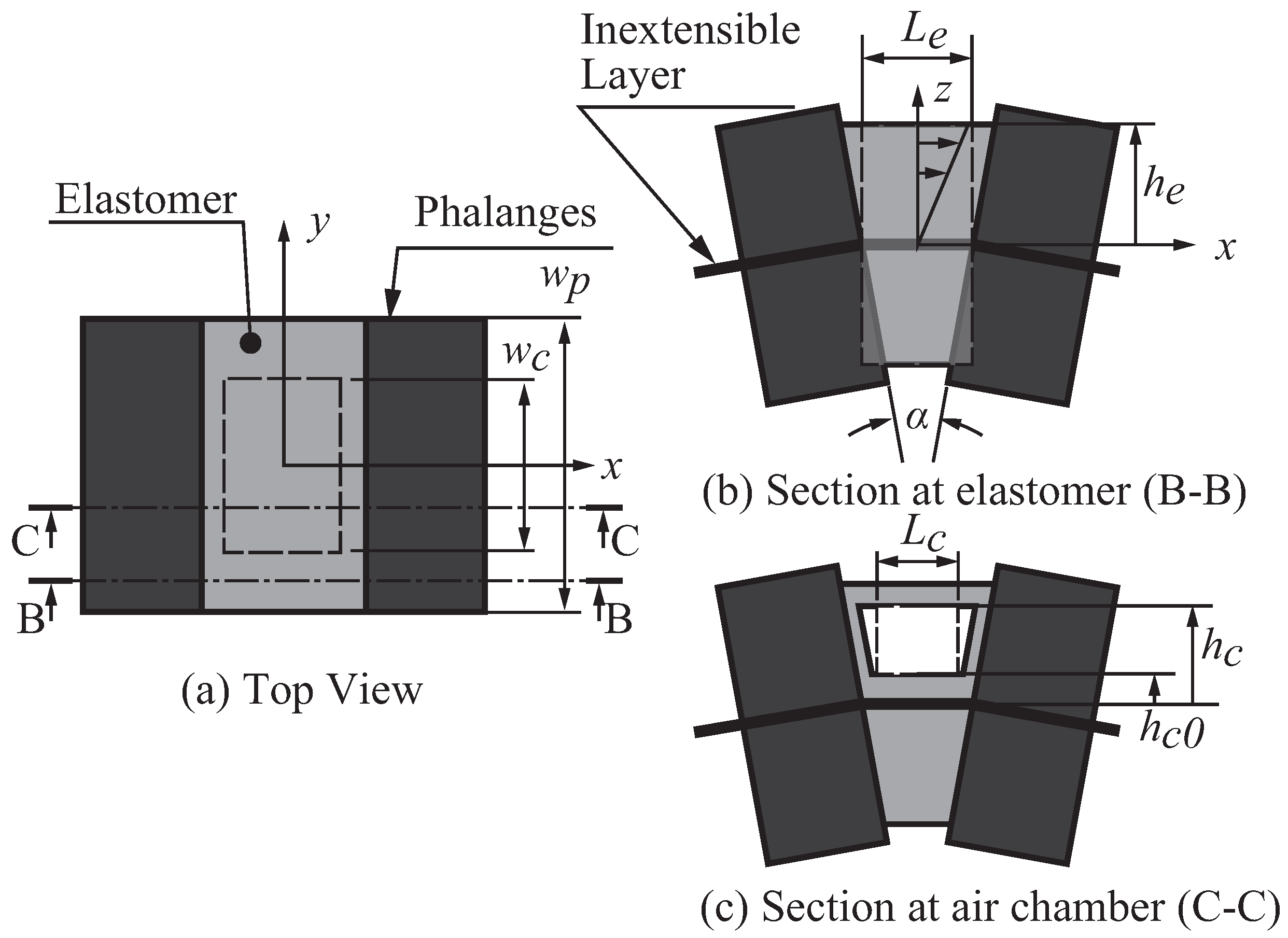
2.3. Geometric Definition

The submodule geometry was designed to balance stiffness tunability, structural robustness, and manufacturability within a compact footprint. It adopts a periodic layout of soft pneumatic chambers alternated with rigid aluminum inserts (Figure 4), enabling local deformation with global alignment, an essential feature for modular humanoid soles. A parametric optimization based on the analytical model in Section 4 was performed to maximize the stiffness variation $\Delta K$ under manufacturing and safety constraints:

$$\underset{h_c,w,l,l_{\mathrm{soft}}}{\mathrm{maximize}}\Delta K(h_c,w,l,l_{\mathrm{soft}})$$

$$\mathrm{subject}\mathrm{to}:\left\{\begin{array}{c}4\mathrm{mm}\le h_c\le 10\mathrm{mm},\hfill \\ 6\mathrm{mm}\le w\le 10\mathrm{mm},\hfill \\ 5\mathrm{mm}\le l\le 9\mathrm{mm},\hfill \\ 8\mathrm{mm}\le l_{\mathrm{soft}}\le 12\mathrm{mm},\hfill \\ t_{\mathrm{wall}}\ge 3\mathrm{mm},P_{\max }\le 30\mathrm{kPa}.\hfill \end{array}\right.$$

Figure 4. Dimensional schematic of the soft pneumatic submodule. The (left panel) shows the top view (top) and lateral view (bottom), while the (right panel) illustrates the frontal view. The geometric parameters, including submodule length ($L_{\mathrm{actuator}}$), chamber width (w), chamber height ($h_c$), inextensible layer thickness ($h_{\mathrm{inex}\_\mathrm{layer}}$), and rigid blocks dimensions, are defined for both modeling and fabrication. The corresponding values are summarized in Table 2.

Figure 4. Dimensional schematic of the soft pneumatic submodule. The (left panel) shows the top view (top) and lateral view (bottom), while the (right panel) illustrates the frontal view. The geometric parameters, including submodule length ($L_{\mathrm{actuator}}$), chamber width (w), chamber height ($h_c$), inextensible layer thickness ($h_{\mathrm{inex}\_\mathrm{layer}}$), and rigid blocks dimensions, are defined for both modeling and fabrication. The corresponding values are summarized in Table 2.

Table 2. Geometric parameters of the pneumatic submodule.

Symbol	Description	Value [mm]
$L_{\mathrm{actuator}}$	Total submodule length	102
$l_p$	Pitch length (rigid + soft span)	17.6
$l_{\mathrm{soft}}$	Length of soft silicone segment	10.6
l	Chamber length	7.0
$w_p$	Total submodule width (including enclosure)	20.0
w	Chamber width	8.0
$h_p$	Half-height (top or bottom section)	15.0
h	Total chamber height (top + bottom)	9.0
$h_c$	Chamber cavity height	5.0
$h_{\mathrm{inex}\_\mathrm{layer}}$	Inextensible layer thickness	1.2

Table 2. Geometric parameters of the pneumatic submodule.

Symbol	Description	Value [mm]
$L_{\mathrm{actuator}}$	Total submodule length	102
$l_p$	Pitch length (rigid + soft span)	17.6
$l_{\mathrm{soft}}$	Length of soft silicone segment	10.6
l	Chamber length	7.0
$w_p$	Total submodule width (including enclosure)	20.0
w	Chamber width	8.0
$h_p$	Half-height (top or bottom section)	15.0
h	Total chamber height (top + bottom)	9.0
$h_c$	Chamber cavity height	5.0
$h_{\mathrm{inex}\_\mathrm{layer}}$	Inextensible layer thickness	1.2

These bounds ensure manufacturability and mechanical integrity: $h_c$, w, and l are limited by mold thickness and allowable expansion before buckling, $l_{\mathrm{soft}}$ guarantees sufficient bonding area without sacrificing flexibility, and $P_{\max }=30$ kPa (equivalent to 0–30,000 Pa in SI units) ensures safe pneumatic operation with compact pumps. The optimal dimensions ($h_c=9$ mm, $w=8$ mm, $l=7$ mm, and $l_{\mathrm{soft}}=10.6$ mm) offered the best trade-off between stiffness range and stability. Larger $h_c$ lowers the required pressure, whereas thicker walls or shorter spans enhance robustness at the cost of adaptability. The influence of $h_c$ on the required pressure was obtained from a parametric sweep of the analytical model (Equation (6)), which shows that a larger chamber height increases the pneumatic moment arm $(h_c-h_{c0})$ and so increases the sensitivity of stiffness to pressure. As a result, larger $h_c$ values require lower pressure to achieve the same stiffness change, a trend that guided the selection of the final geometry. The final prototype represents a balanced configuration optimized for stiffness tunability within safe pneumatic limits. This geometry serves as the physical basis for the analytical and experimental analyses that follow.

2.4. Prototype Implementation

The proof-of-concept prototype was fabricated using the optimized parameters listed in Table 2. It consists of four active spans, each containing an antagonistic pair of pneumatic chambers, yielding a total length of $L_{\mathrm{actuator}}=102$ mm and a mass below $0.4$ kg.

This configuration fulfills the main design goals for humanoid foot integration. When both pneumatic layers are equally pressurized, the submodule maintains a flat geometry, enabling pure stiffness modulation without bending. Stiffness increases monotonically over the 0–30 kPa range, as validated in Section 4, while the rigid inserts and nylon layer distribute compressive loads and suppress bulging, improving durability. The modular layout also supports scalability: identical units can be combined in series or parallel to form a full sole with shared pneumatic routing, enabling spatially distributed stiffness control for adaptive locomotion. Overall, the prototype demonstrates that compact pneumatic co-contraction can achieve precise geometry, robust load support, and rapid, reversible stiffness modulation, providing a strong foundation for next-generation humanoid soles capable of real-time adaptation to uneven terrain.

Finally, given the wall-thickness and pressure limits used in this study, the current geometric pitch represents the minimum size that can still achieve the validated stiffness range (0.18–0.43 N·m/rad). For a humanoid foot comparable in size to the HRP-4C sole, arranging 10 stiffness pixels along the longitudinal axis and 5 pixels transversally would yield a 50-pixel stiffness-tunable sole, preserving the per-pixel stiffness characteristics while enabling distributed, foot-scale modulation.

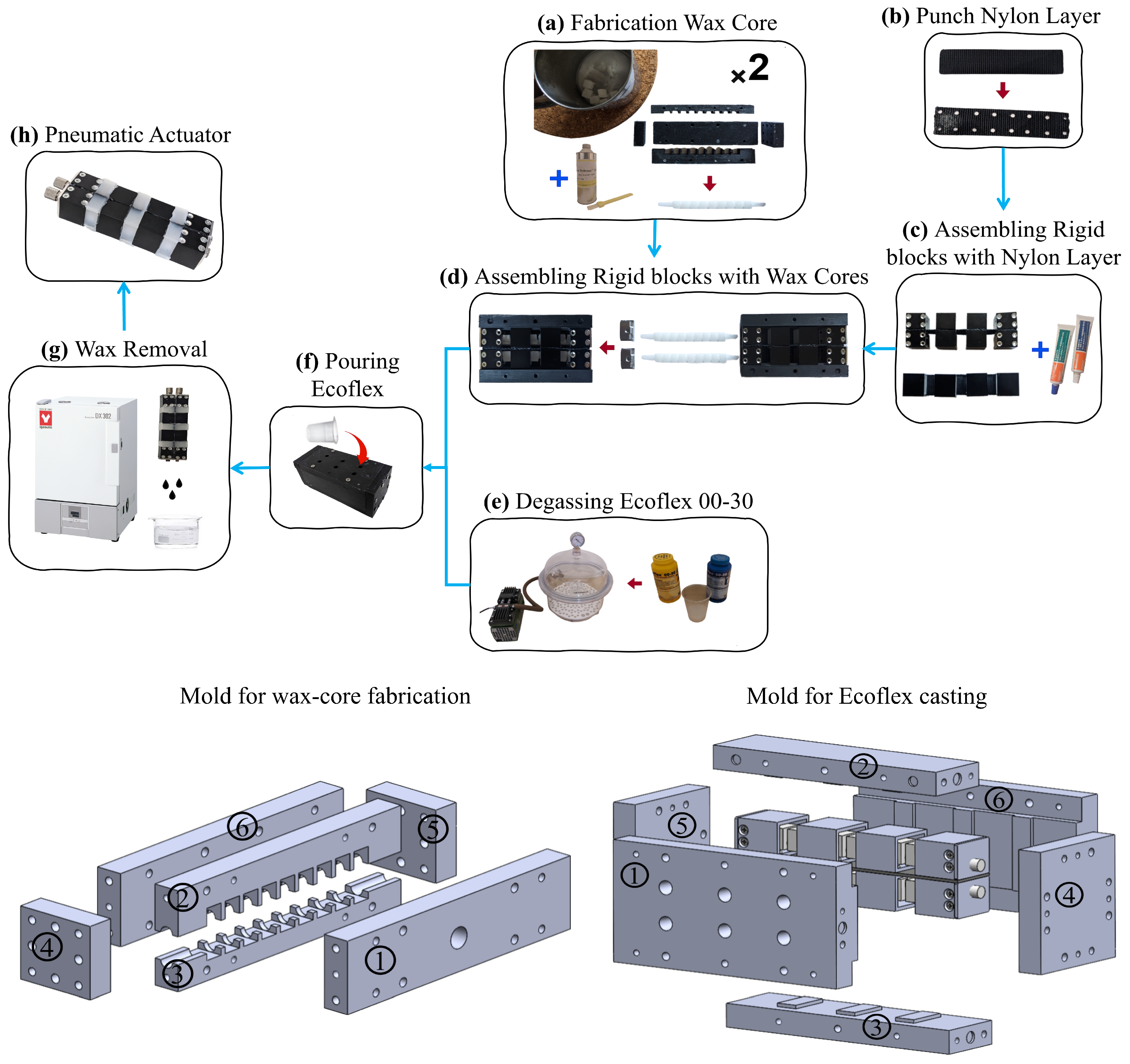
3. Monolithic Wax-Core Fabrication

The soft pneumatic submodule is fabricated using a single-step wax-core casting process that co-molds soft silicone, rigid aluminum, and an inextensible nylon sheet into one monolithic body (Figure 5).

3.1. Fabrication Workflow

The procedure combines casting, assembly, and material integration within a single workflow. First, two identical wax cores are produced using 3D-printed molds, shown in the lower-left part of Figure 5. These molds define the internal air chambers and connecting channels of the submodule, including a lateral port used for wax filling (Figure 5a). A thin layer of release agent is applied to the mold surfaces to ensure clean removal of the solidified wax and to preserve fine internal geometry. Next, the nylon fabric forming the inextensible middle layer is prepared (Figure 5b). Holes are punched along its length to allow mechanical fastening with the rigid aluminum blocks. This layer defines the neutral axis of the pneumatic submodule and mechanically couples the upper and lower pneumatic chambers. The rigid aluminum blocks are then assembled together with the nylon sheet to form the structural skeleton (Figure 5c). Epoxy adhesive and four screws per block ensure precise alignment and strong bonding between the rigid parts and the fabric, creating a stable frame that holds the wax cores during casting. The wax cores are then inserted into this aluminum–nylon assembly (Figure 5d), defining the soft spans where the silicone will later form the pneumatic chambers. Side aluminum plates are attached to close the assembly and maintain the internal geometry. The complete setup is then placed inside the silicone casting mold (shown at the lower right of Figure 5), which includes six side injection ports for uniform filling. The silicone material (Ecoflex 00–30, Smooth-On Inc., Macungie, PA, USA) is prepared by mixing parts A and B in equal proportions (1:1 by weight) and degassed in a vacuum chamber to remove trapped air (Figure 5e). Once homogeneous, the silicone is slowly poured into the closed mold through the inlet ports (Figure 5f). This controlled filling ensures that the material flows evenly around the rigid blocks and wax cores. The mold is then left at room temperature until the silicone solidifies completely. After solidification, the mold is opened, and the entire submodule assembly is heated to $90°\mathrm{C}$ for approximately 20 min (Figure 5g). During this step, the wax melts and drains through the same inlet ports, leaving hollow pneumatic chambers and air channels within the soft body.

The resulting pneumatic submodule (Figure 5h) is a fully integrated soft–rigid composite structure combining the elasticity of silicone, the rigidity of aluminum, and the constraint of the nylon sheet. The process yields a compact, durable pneumatic submodule with precisely defined internal geometry, ready for pressurization and experimental testing.

The molds used for producing the wax cores and for casting the Ecoflex were fabricated using stereolithography (SLA) 3D printing in a standard photopolymer resin. SLA was selected for its high dimensional accuracy and smooth surface finish, which ensures precise chamber geometry and reliable wax release. The printing resolution (≈70 $\mathsf{\mu }$m) is much smaller than the chamber dimensions, so its influence on the actuator’s pneumatic behavior is negligible.

3.2. Advantages over Existing Manufacturing Methods

Soft actuators are commonly fabricated by layer-by-layer casting and bonding or by single-material molding using lost-core or insert-casting techniques. While these methods enable monolithic silicone structures, they cannot readily integrate rigid or inextensible components. The first major advantage of the proposed wax-core process is its ability to co-mold soft silicone, rigid aluminum, and an inextensible nylon layer in a single step. Embedding the rigid blocks and fabric during casting eliminates post-assembly bonding, ensures precise alignment between pneumatic and structural parts, and improves mechanical continuity and fatigue resistance. A second key advantage is about the use of wax as a temporary core material: it is non-abrasive, melts at low temperature, and drains cleanly without damaging the silicone, leaving smooth, well-defined internal chambers. This reduces tearing and delamination issues typical of multi-step fabrication. Overall, the wax-core process extends standard lost-core casting to a practical and scalable method for producing durable, repeatable hybrid soft–rigid submodules.

4. Analytical Modeling of Pressure–Stiffness Relationship

To quantify how internal pressure affects submodule stiffness, we develop an analytical model linking pneumatic pressure to equivalent bending stiffness. The model captures the antagonistic coupling between the upper and lower chambers of the tri-layer structure and serves as the basis for both design optimization and experimental validation.

4.1. Model Assumptions and Geometry

The analytical formulation follows the geometry shown in Figure 6. A single representative span is modeled between two rigid aluminum blocks; this simplification enables an analytical relation between pressure and stiffness while preserving the essential behavior of the full submodule.

To keep the model tractable, the following assumptions are made:

• Internal pressure is uniform and equal in both chambers (no differential bending).
• Deformation remains small (<25% strain), allowing linear elasticity for Ecoflex 00–30.
• Radial expansion is negligible due to confinement from the aluminum blocks and nylon sheet.
• Air behavior is isothermal and follows the ideal gas law.

These assumptions are appropriate for the submodule’s geometry and operating conditions. In fact, the small chamber volume ensures rapid pressure equilibration, validating assumption 1. Silicone strain remains within the linear range [19], supporting assumption 2. Lateral bulging is constrained by the rigid aluminum frames and nylon sheet (assumption 3), and the relatively slow actuation rate maintains thermal equilibrium during operation (assumption 4).

The key geometric parameters used in the derivation are defined as follows:

$$\begin{array}{cc}& w_p:\mathrm{total}\mathrm{module}\mathrm{width},w_c:\mathrm{chamber}\mathrm{width},\hfill \\ & h_{c0}:\mathrm{chamber}\mathrm{height}\mathrm{at}\mathrm{rest},h_c:\mathrm{chamber}\mathrm{height}\mathrm{under}\mathrm{pressure}{p}_0,\hfill \\ & L_c:\mathrm{chamber}\mathrm{length},L_e:\mathrm{soft}\mathrm{span}\mathrm{length}\mathrm{between}\mathrm{rigid}\mathrm{blocks},\hfill \\ & h_e:\mathrm{effective}\mathrm{elastomer}\mathrm{height},E:\mathrm{Young}’\mathrm{s}\mathrm{modulus},\hfill \\ & \alpha :\mathrm{small}\mathrm{bending}\mathrm{angle}\mathrm{around}\mathrm{the}\mathrm{neutral}\mathrm{axis}.\hfill \end{array}$$

Because the submodule comprises identical spans, the total stiffness of the full submodule is obtained by summing the contributions of each span. This modular representation also facilitates scaling to a humanoid sole, where multiple submodules can be arranged in parallel to achieve spatially distributed stiffness control.

4.2. Analytical Derivation

The total bending stiffness of the submodule results from the combined effect of two mechanisms: (i) the elastic resistance of the silicone ribs, and (ii) the pneumatic pressure variations that develop during small bending.

• Elastic contribution

We first consider the bending resistance of the elastomer in the absence of internal pressure. When the submodule bends by a small angle $\alpha$, the upper surface of the elastomer is stretched and the lower surface is compressed, while the inextensible nylon layer defines the neutral axis where the strain is zero. Assuming small deflections, the axial strain at a distance z from the neutral axis is

$${ϵ}_x\left(z\right)={\displaystyle \frac{z\alpha }{L_e}},$$

where $L_e$ is the effective span between two rigid blocks. Applying Hooke’s law for linear elasticity gives the local stress distribution

$${\sigma }_x\left(z\right)=E{ϵ}_x\left(z\right)=E{\displaystyle \frac{z\alpha }{L_e}}.$$

The resulting bending moment is obtained by integrating the stress distribution over the elastomer cross-section:

$$M_e=-{\int }_{-h_e}^{h_e}{\sigma }_x\left(z\right)z{w}_{e}dz,$$

(1)

where $w_e=w_p-w_c$ represents the effective width of the silicone material. Carrying out the integration gives

$$M_e=-{\displaystyle \frac{2E{w}_e{h}_e^3}{3L_e}}\alpha .$$

Differentiating this expression with respect to $\alpha$ yields the elastic stiffness component:

$$K_{\mathrm{elas}}={\displaystyle \frac{2E{w}_e{h}_e^3}{3L_e}}.$$

(2)

This term represents the passive contribution of the silicone to the overall submodule stiffness.

• Pneumatic contribution

We now include the effect of the enclosed air pressure. When the actuator bends, the top chambers experience a small reduction in volume while the bottom chambers expand, producing a pressure differential that generates an additional restoring moment. Assuming an isothermal process ($pV=\mathrm{const}$) and denoting the nominal pressure in the flat state as $p_0$, the instantaneous pressures in the top and bottom chambers are related to their volume changes as follows. For small angles $\alpha$, the effective chamber length of the top and bottom layers becomes

$$L_T=2L_c+\alpha (h_c-h_{c0}),L_B=2L_c-\alpha (h_c-h_{c0}),$$

where $L_c$ is the half-length of one chamber, and $(h_c-h_{c0})$ is the vertical offset between the chamber centroid and the neutral axis. Using $pV=p_0{V}_0$ and cancelling constant geometric factors gives

$$p_T={\displaystyle \frac{2L_c}{2L_c+\alpha (h_c-h_{c0})}}{p}_0,p_B={\displaystyle \frac{2L_c}{2L_c-\alpha (h_c-h_{c0})}}{p}_0.$$

(3)

These relations show that the top layer experiences a slight pressure increase when compressed, while the bottom layer experiences a decrease when stretched.

The differential pressure produces a bending moment that can be obtained by integrating the pressure distribution across the chamber height:

$$M_p={\int }_{h_{c0}}^{h_c}{p}_{T}z{w}_{c}dz-{\int }_{-h_{c0}}^{-h_c}{p}_{B}z{w}_{c}dz.$$

(4)

Evaluating the integrals leads to

$$M_p=-{\displaystyle \frac{2\alpha L_c{w}_c{(h_c-h_{c0})}^3}{4L_c^2-{\alpha }^2{(h_c-h_{c0})}^2}}{p}_0.$$

This expression quantifies the additional pneumatic moment opposing the imposed curvature.

• Total stiffness

The total restoring moment is the sum of the elastic and pneumatic contributions,

$$M\left(\alpha \right)=M_e+M_p.$$

To evaluate the submodule stiffness, we differentiate this moment with respect to the bending angle, obtaining

$$K=-{\displaystyle \frac{\partial M}{\partial \alpha }}=-{\displaystyle \frac{\partial (M_e+M_p)}{\partial \alpha }}.$$

(5)

Substituting the expressions of $M_e$ and $M_p$ into Equation (5) yields

$$K\left(\alpha \right)={\displaystyle \frac{\partial }{\partial \alpha }}\left({\displaystyle \frac{2E(w_p-w_c)h_e^3}{3L_e}}\alpha \right)+{\displaystyle \frac{\partial }{\partial \alpha }}\left[{\displaystyle \frac{2\alpha L_c{w}_c{(h_c-h_{c0})}^3}{4L_c^2-{\alpha }^2{(h_c-h_{c0})}^2}}{p}_0\right].$$

Evaluating both derivatives and taking the small-angle limit ($\alpha \to 0$) gives

$${\left.K\right|}_{\alpha =0}={\displaystyle \frac{2E(w_p-w_c)h_e^3}{3L_e}}+{\displaystyle \frac{w_c{(h_c-h_{c0})}^3}{2L_c}}{p}_0,$$

which corresponds to Equation (6):

$${\left.K\right|}_{\alpha =0}={\displaystyle \frac{2E(w_p-w_c)h_e^3}{3L_e}}+{\displaystyle \frac{w_c{(h_c-h_{c0})}^3}{2L_c}}{p}_0.$$

(6)

The first term corresponds to the passive elastic stiffness of the silicone material, while the second term represents the pneumatic contribution that increases linearly with inflation pressure. Both contributions in Equation (6) yield units of N·m, corresponding to bending moment per unit rotation. Because radians are dimensionless, N·m is equivalent to the usual stiffness notation N·m/rad. This additive structure clearly separates material properties from pressure-dependent effects, highlighting how internal pressurization tunes the effective stiffness of the submodule without altering its geometry.

4.3. Discussion

Equation (6) reveals that the submodule stiffness can be expressed as a linear function of pressure:

$$K\left(p_0\right)=K_{\mathrm{elas}}+k_p{p}_0,$$

where

$$K_{\mathrm{elas}}={\displaystyle \frac{2E(w_p-w_c)h_e^3}{3L_e}},k_p={\displaystyle \frac{w_c{(h_c-h_{c0})}^3}{2L_c}}.$$

The first term represents the passive elastic stiffness governed by material and geometry, while the second term quantifies the pressure-dependent contribution that enables tunable compliance. This linear relation provides a compact and practical way to predict stiffness within the submodule’s operating range (0–30 kPa). Despite its simplicity, the model captures the distinctive feature of this submodule: equal pressurization of antagonistic chambers increases stiffness without producing motion. Unlike most analytical soft-actuator models that predict deformation or tip displacement, this formulation directly links geometry, pressure, and stiffness. It supports both geometry optimization during design and pressure scheduling during control, offering a physically interpretable basis for integrating stiffness modulation into humanoid locomotion algorithms. In summary, the model is both predictive and prescriptive: it explains how stiffness emerges and provides explicit parameters for designing and controlling compliant, pressure-tunable structures. Although Equation (6) closely captures the pressure–stiffness relationship over most of the 0–30 kPa range, small deviations are expected at the boundaries of this interval. At very low pressures (<5 kPa), the chambers are only partially inflated and the silicone operates in the nonlinear toe region of the Ecoflex stress–strain curve, producing a slightly higher stiffness than predicted by a linear-elastic approximation. Also, above ∼25 kPa, the elastomer enters a deformation-induced stiffening regime and the chambers experience minor radial expansion, effects not included in the fixed-geometry, linear formulation. These boundary-region mechanisms explain why the analytical model is most accurate in the mid-pressure range, while still providing an excellent overall fit (R² = 0.97) within the validated operating window.

5. Experimental Validation

We conducted a series of static and dynamic tests to validate the analytical model and quantify the submodule’s pressure-dependent stiffness modulation under representative operating conditions. The objectives were to (i) verify the linear stiffness–pressure relation predicted by Equation (6); (ii) measure response time and repeatability under rapid pressurization; (iii) evaluate actuator rigidity under cyclic loading using pulsed pressure inputs; and (iv) assess suitability for real-time stiffness adaptation in humanoid feet.

5.1. Experimental Setup

The setup (Figure 7) consisted of the pneumatic submodule rigidly clamped at its heel and horizontally loaded at the tip with a calibrated force of $F_{\mathrm{ext}}=1.0\mathrm{N}$ using a handheld digital force gauge (FMT-310, Alluris GmbH & Co. KG, Freiburg, Germany; $\pm 0.01\mathrm{N}$ accuracy). A miniature diaphragm pump (generic DC 6 V unit; 3.5 L/min; 90 kPa maximum pressure) supplied air to both chambers through solenoid valves (three normally closed 12 V valves, SNS Pneumatic, Ningbo, China) controlled by a microcontroller (Arduino Uno, Arduino, Somerville, MA, USA) with an L298N motor driver (STMicroelectronics, Geneva, Switzerland). Two pressure sensors monitored chamber pressure (PSE540, SMC Corporation, Tokyo, Japan; analog output, sampled at 1 kHz and digitally filtered at 50 Hz). The pneumatic circuit operated in three modes (inflate, stabilize, deflate) to maintain each target pressure within $\pm 2\mathrm{kPa}$. Tip deflection ${\delta }_y$ was recorded by a high-resolution camera (RealSense Depth Camera D405, Intel Corporation, Santa Clara, CA, USA; 1280 × 720 pixels, up to 60 fps) and extracted by image analysis using a fiducial marker placed on the submodule tip to obtain sub-millimeter displacement accuracy. Both chambers were always inflated equally to achieve pure stiffness modulation without bending. Each test was repeated ten times per pressure level to quantify repeatability; the pressure sensors were calibrated against a reference chamber prior to testing. This configuration provided precise, repeatable data for quasi-static stiffness estimation, transient response characterization, and high-frequency square-wave pressure stimuli.

5.2. Results for Static Characterization: Stiffness–Pressure Relationship

To determine the quasi-static stiffness, we applied the constant force $F_{\mathrm{ext}}=1.0\mathrm{N}$ at the submodule tip for each pressure value between 0 and 30 kPa. The resulting lateral deflection ${\delta }_y$ was used to compute the bending angle $\theta$ and equivalent stiffness:

$$\theta \approx {\displaystyle \frac{{\delta }_y}{L}},K\left(p_0\right)={\displaystyle \frac{F_{\mathrm{ext}}{L}^2}{{\delta }_y}},$$

where L is the submodule’s free length.

The measured mechanical response of the submodule under a constant lateral tip load is summarized in Figure 8. As the internal pressure increases, the pneumatic submodule becomes progressively stiffer, leading to a clear monotonic reduction in both bending angle and tip deflection, and a corresponding increase in bending stiffness.

At zero pressure, the submodule bends easily under the applied load, exhibiting a mean bending angle of approximately $0.27\mathrm{rad}$ and a lateral deflection of about $27\mathrm{mm}$. When the pressure reaches $30\mathrm{kPa}$, these values drop to $0.14\mathrm{rad}$ and $13\mathrm{mm}$, respectively, corresponding to roughly a $50\%$ reduction in compliance (Figure 8a,b). The measured bending and deflection curves follow the analytical model closely across the full range, with deviations below $8\%$ in the linear region (0–$20\mathrm{kPa}$).

The corresponding stiffness, computed from the measured deflection, increases almost linearly with pressure: from $K\left(0\right)\approx 0.18\mathrm{N}·\mathrm{m}/\mathrm{rad}$ to $K\left(30\right)\approx 0.43\mathrm{N}·\mathrm{m}/\mathrm{rad}$ (Figure 8c). The analytical model reproduces this trend accurately up to about $20\mathrm{kPa}$, while slightly underestimating stiffness at higher pressures due to nonlinear elastic stiffening of the Ecoflex material and small radial expansion effects neglected in the simplified formulation. The model error remains below $10\%$ throughout most of the range (Figure 8d), confirming that the linear approximation and small-deformation assumptions remain valid up to approximately $25\mathrm{kPa}$.

Figure 8e further reports the variation of stored elastic energy, estimated as $U\approx \frac{1}{2}{F}_{\mathrm{ext}}{\delta }_y$. The energy decreases from about $1.9\times {10}^{-5}\mathrm{J}$ at $0\mathrm{kPa}$ to $0.8\times {10}^{-5}\mathrm{J}$ at $30\mathrm{kPa}$, reflecting reduced deformation and higher structural rigidity as pressure rises. This trend confirms that the submodule’s increased stiffness originates from internal pressurization rather than external geometry changes.

Overall, the results in Figure 8 demonstrate a consistent and reproducible pressure-dependent modulation of stiffness. The experimental curves follow the analytical model closely in the quasilinear region, validating the theoretical formulation and confirming that the submodule provides predictable stiffness control over the full 0–30 kPa range.

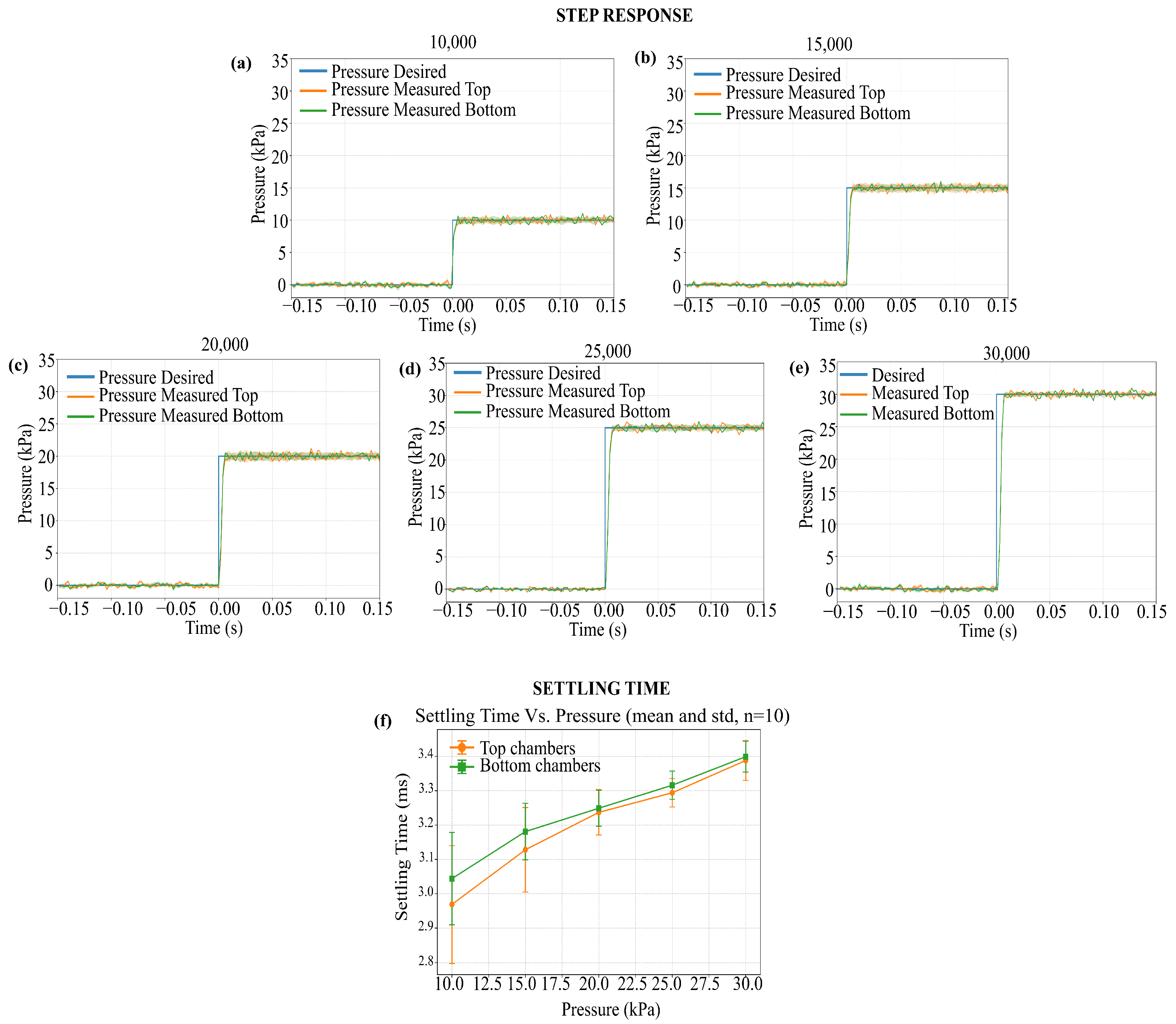
5.3. Results for Dynamic Characterization: Step Response and Timing

To evaluate the pneumatic submodule’s dynamic performance for real-time stiffness modulation, step response tests were performed at target pressures of 10, 15, 20, 25, and 30 kPa. A finite-state controller executed rapid inflation and venting cycles, while the pressures in the upper and lower chambers were recorded at 1 kHz. Each trial was considered settled once both chamber pressures reached and remained within $\pm 5\%$ of the target value. For each pressure level, ten repetitions were carried out to quantify repeatability and to verify symmetry between the top and bottom chambers.

Figure 9 presents representative pressure traces and the corresponding mean settling times. In all cases, the measured pressures follow the commanded step almost instantaneously, with negligible overshoot and no observable oscillation. The top and bottom chambers exhibit nearly identical transients and steady-state values, confirming that the pneumatic manifold maintains symmetric flow distribution. As pressure increases, the steady-state plateau remains stable and well aligned with the desired command, demonstrating the reliability of the FSM-based control.

The lower panel of Figure 9 quantifies the mean and standard deviation of the settling time across all trials. Settling time increases slightly with pressure (from ≈$3.0\mathrm{ms}$ at $10\mathrm{kPa}$ to ≈$3.4\mathrm{ms}$ at $30\mathrm{kPa}$) reflecting the higher air mass that must be displaced at elevated pressures. The standard deviation remains below $0.25\mathrm{ms}$, indicating excellent repeatability across cycles. The absence of measurable delay between the top and bottom chambers (within the $0.1\mathrm{ms}$ resolution of the sampling system) further validates the symmetry and balance of the pneumatic circuit.

Overall, the submodule exhibits fast, symmetric, and repeatable pressure transients, enabling stiffness adjustments well within the real-time constraints of humanoid locomotion. The next section discusses the combined interpretation of static and dynamic results, emphasizing the physical insights and validation of the analytical model.

5.4. Results for Dynamic Loading: Pulsed Stimuli Tests

To evaluate the actuator’s rigidity under cyclic loading, we applied square-wave pressure commands of 0–20, 0–25, and 0–30 kPa at two gait-relevant frequencies (5 Hz and 2 Hz) while maintaining a constant lateral load of $F_{\mathrm{ext}}=1.0\mathrm{N}$. Figure 10 illustrates one-second response of the pneumatic actuator to the six pulsed pressure conditions. Each row corresponds to one pressure–frequency pair and reports four signals: the commanded pressure (blue), the measured pressure in the top and bottom chambers (orange and green), the lateral tip deflection (magenta), and the derived bending stiffness (purple).

Across all conditions, the measured chamber pressures track the commanded input with a settling time of 3–4 ms and a peak overshoot below 4%, calculated as the maximum deviation above the steady-state pressure. The lateral deflection follows these pressure transitions with a slower mechanical response: the deflection reaches its new equilibrium value within 20–25 ms after each pressure step, matching the structural time constant identified in the static loading tests.

The corresponding instantaneous bending stiffness shows the same transition timing and remains nearly constant during each high-pressure phase. The stiffness varies by 5–8% around its mean value during these intervals, reflecting sensor noise and minor viscoelastic relaxation rather than any loss of rigidity.

Overall, the pulsed stimuli experiments demonstrate that (i) pressure transitions occur within 3–4 ms, (ii) the mechanical stiffness settles within 20–25 ms, and (iii) the actuator maintains high and stable stiffness during the entire duration of the high-pressure phases, even under cyclic loading at 5 Hz. These results confirm that the submodule can maintain effective rigidity during stance-like phases of humanoid walking while still allowing rapid stiffness modulation between steps. Importantly, we also observe no cumulative drift, hysteresis buildup, or stiffness degradation across consecutive cycles, indicating that the module can repeatedly stiffen and relax at gait-relevant frequencies without loss of load-bearing capacity.

5.5. Discussion of Experimental Results

The combined static and dynamic tests confirm that the submodule provides predictable, tunable, and fast stiffness modulation in close agreement with the analytical model. The submodule’s small internal volume (≈2 cm³) and short pneumatic lines (<5 cm) result in an exceptionally fast local pneumatic response at the chamber inlet, measured at 2.9–3.4 ms with high repeatability (standard deviation < 0.25 ms). When extrapolated to a full humanoid sole (12.5 × larger internal volume), the expected settling time increases proportionally to ≈38–50 ms (>20 Hz bandwidth), remaining well within the real-time requirements of gait-phase transitions. Overall, the submodule architecture enables stiffness modulation at frequencies around 20 Hz, an order of magnitude faster than the 1–5 Hz range typical of human or prosthetic feet (

Table 3. Comparison between human foot stiffness requirements, prosthetic designs, and the proposed pneumatic submodule.

System/Reference	Metric	Stiffness (N·m/rad)	Resp. Time/Bandwidth
Human ankle–foot (stance) [23,24]	quasi-stiffness	0.2–0.6	1–3 Hz
Human foot arch (passive) [21,22]	longitudinal	0.1–0.4	<2 Hz
Prosthetic feet (ESR type) [32,33]	effective roll-over	0.3–1.0	≲2 Hz
Variable-stiffness prosthetic foot [34,35]	tunable effective	0.2–1.0	∼1–5 Hz
This work (submodule)	pressure-controlled	0.18–0.43	2.9–3.4 ms (>250 Hz)
Projected full sole (from this work)	pressure-controlled	0.09–0.22	38–50 ms (>20 Hz) a

^a Estimated from pneumatic scaling (12.5 × volume) corresponding to ∼38–50 ms sole-level response.

), supporting terrain-responsive impedance control for humanoid locomotion.

The experimentally derived stiffness–pressure curve validates the linear relation predicted by Equation (6), with a mean error below 10% over the 0–25 kPa range. This strong correspondence (R² = 0.97) confirms that the dominant mechanism is the elastic bending of the silicone ribs under symmetric pressurization of the antagonistic chambers. At higher pressures, the model slightly underestimates stiffness (≈8–12% above 25 kPa) due to nonlinear elastic stiffening of Ecoflex and minor radial expansion not captured by the linear formulation. Nevertheless, these deviations remain small and systematic, supporting the use of the analytical model as a compact and reliable tool for design optimization and real-time control.

The simultaneous increase in stiffness and reduction in stored strain energy (from $2.0\times {10}^{-5}\mathrm{J}$ to $0.8\times {10}^{-5}\mathrm{J}$) highlight the submodule’s antagonistic principle: equal inflation of both chambers suppresses bending and transforms pneumatic energy into structural rigidity rather than geometric motion. This behavior, unlike most soft actuators that deform to generate movement, allows the module to function as a controllable load-bearing element with tunable mechanical impedance. Such decoupling of shape and stiffness is particularly advantageous for humanoid feet, where compliance must adapt without compromising stability during stance and push-off.

The pulsed stimuli tests reveal two important characteristics of the submodule’s mechanical behaviour under repeated loading–unloading cycles. First, the pressure and deflection transients occur on time scales more than an order of magnitude faster than the characteristic duration of the stance phase in human or humanoid walking (typically ∼200 ms [26]), indicating that the actuator can complete stiffness adjustments well within a single gait event. Second, once the commanded pressure is reached, the measured stiffness remains effectively constant throughout the high-pressure intervals, with variations confined to approximately 5–$8\%$ and showing no evidence of progressive softening, drift, or hysteresis accumulation over consecutive cycles. This stability suggests that the structural response is dominated by elastic bending of the silicone ribs, with minimal influence from slower viscoelastic relaxation.

Within the validated operating range (0–30 kPa), no degradation, drift, or loss of stability was observed. However, during early prototyping we found that, above this range, the silicone chambers begin to deform and eventually rupture at 33–35 kPa, defining the practical upper pressure limit of the current design.

From a system perspective, the submodule’s fast response and low variability suggest that pneumatic stiffness control can be scaled to multi-submodule soles or leg segments without significant latency. Even when extrapolated to a full humanoid sole (estimated 38–50 ms response; Table 3), the bandwidth remains well above the 20 Hz range required for gait-phase synchronization. The achieved stiffness levels (0.18–0.43 N·m/rad per module, 0.09–0.22 N·m/rad when scaled to a full sole) fall well within the biologically relevant range of the human foot arch (0.1–0.4 N·m/rad) and the lower ankle–foot complex (0.2–0.6 N·m/rad), demonstrating both mechanical sufficiency and biomechanical realism. Although the stiffness range is more restricted than some rigid or high-force prosthetic mechanisms (up to 1 N·m/rad), it is entirely adequate for humanoid walking and provides modulation speeds that exceed any existing variable-stiffness technology. Future work should aim to extend the upper limit of stiffness, by increasing pressure capacity, altering chamber geometry, or using stiffer elastomers, while preserving the same fast, repeatable response.

Regarding the pneumatic submodule design, the combination of wax-core casting and integrated rigid–soft co-molding yields highly reproducible mechanical behavior (repeatability error $<5\%$) with minimal hysteresis. The simple affine stiffness–pressure relation ($K=K_{\mathrm{elas}}+k_p{p}_0$, with $K_{\mathrm{elas}}=0.18\mathrm{N}·\mathrm{m}/\mathrm{rad}$ and $k_p=7.0\times {10}^{-3}\mathrm{N}·\mathrm{m}/(\mathrm{rad}·\mathrm{kPa})$) offers a direct parameterization for controller implementation: stiffness can be commanded through pressure in a linear and invertible manner.

Together, the results demonstrate that the submodule satisfies the three main validation goals: (i) the analytical stiffness–pressure model accurately captures experimental behavior (mean absolute error $<10\%$), (ii) the submodule exhibits sub-5 ms dynamic response suitable for real-time control, and (iii) the integrated fabrication process ensures repeatability and structural robustness. The pneumatic design thus establishes a scalable foundation for adaptive, pressure-controlled stiffness modulation in robotic systems, bridging the gap between soft actuation and rigid support required in humanoid walking.

Finally, the fact that the submodule’s shape is preserved during stiffness modulation, makes it compatible with recent morphing microelectronic meshes [36], as well as with ultrathin flexible sensor networks [37]. Because the module can stiffen or soften without changing its geometry, a conformal electronic mesh laminated or embedded on the top surface would experience minimal strain during stiffness adjustments or during ground contact. This provides a mechanically stable substrate, allowing the sensors to maintain accuracy during the robot walking. Embedding such meshes could enable high-density tactile or curvature sensing directly on a stiffness-tunable structure, while the electronics in turn provide real-time feedback for pneumatic impedance control. This synergy highlights a promising direction for integrating perception with adaptive mechanical response in future humanoid feet.

6. Conclusions

This study presented a compact pneumatic submodule capable of modulating stiffness without geometric deformation. A single-step wax-core co-molding process was developed to integrate soft, rigid, and inextensible materials into a monolithic structure with precise geometry and repeatable behavior. The analytical pressure–stiffness model, validated experimentally with a mean error below 10%, predicts stiffness tunability from 0.18 to 0.43 N·m/rad, while dynamic tests demonstrated symmetric pressure response within 3–4 ms. Figure 1 illustrates the fabricated prototype and its envisioned placement within a pneumatically compliant humanoid foot. In future work, we will assemble multiple submodules into a full-scale sole to evaluate distributed stiffness modulation during stance and walking on uneven terrain. We also plan to improve durability and performance by (i) increasing burst-pressure capacity through modified chamber geometry and (ii) integrating embedded sensing (pressure, curvature, and tactile meshes) to enable closed-loop impedance control.