Research on Task Allocation Method for Dual-Robot Stereoscopic Stone Carving Under Stiffness Constraints
Abstract
1. Introduction
2. Experimental Conditions
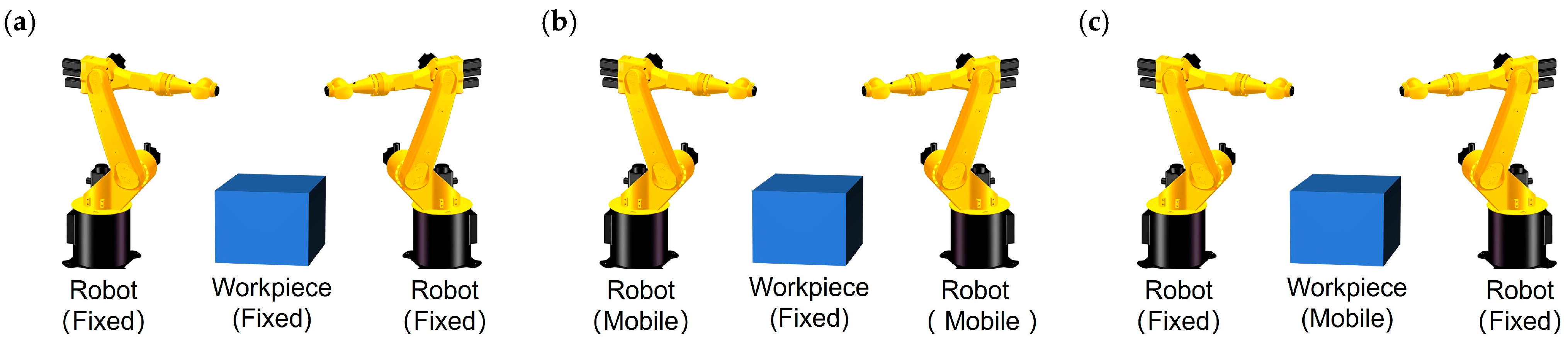
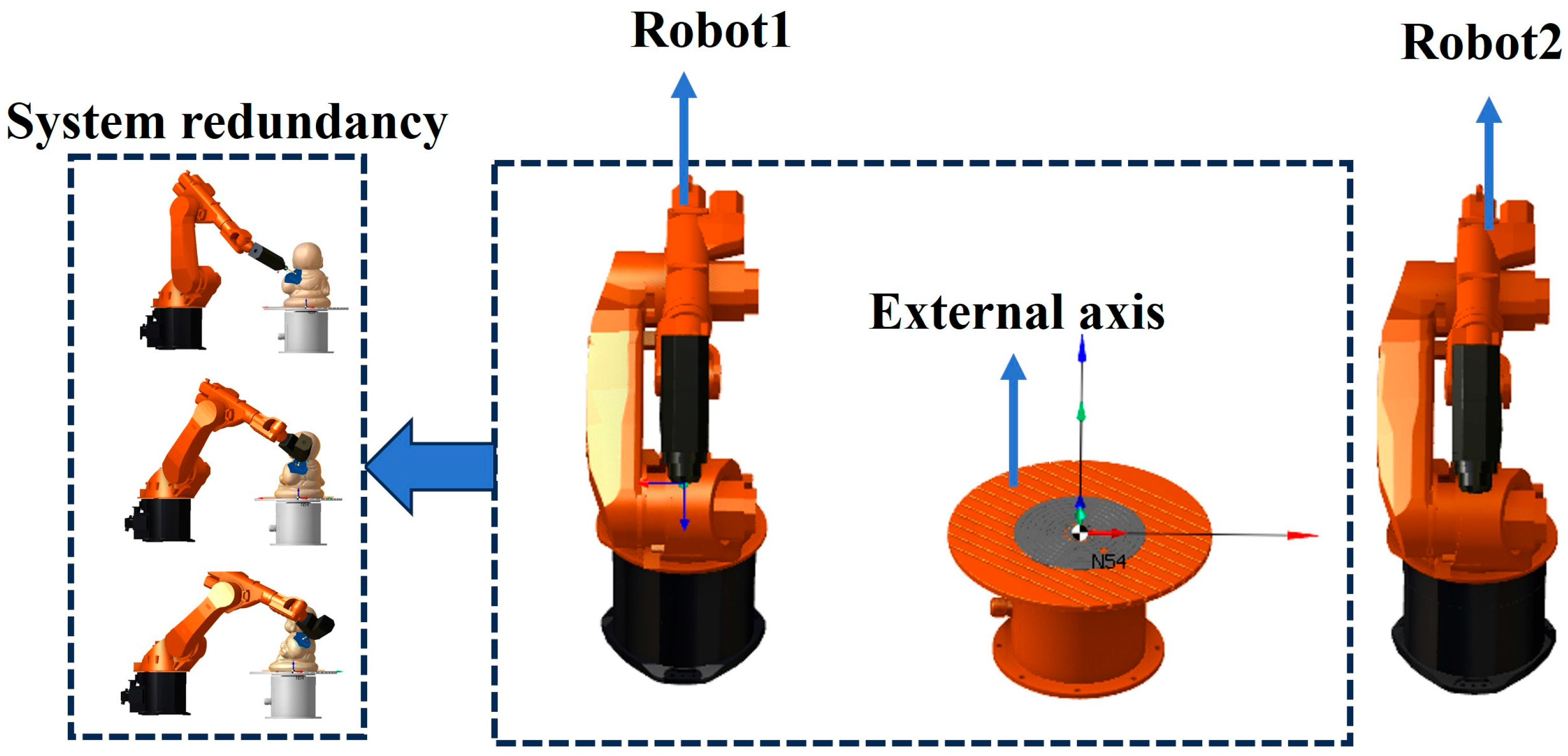
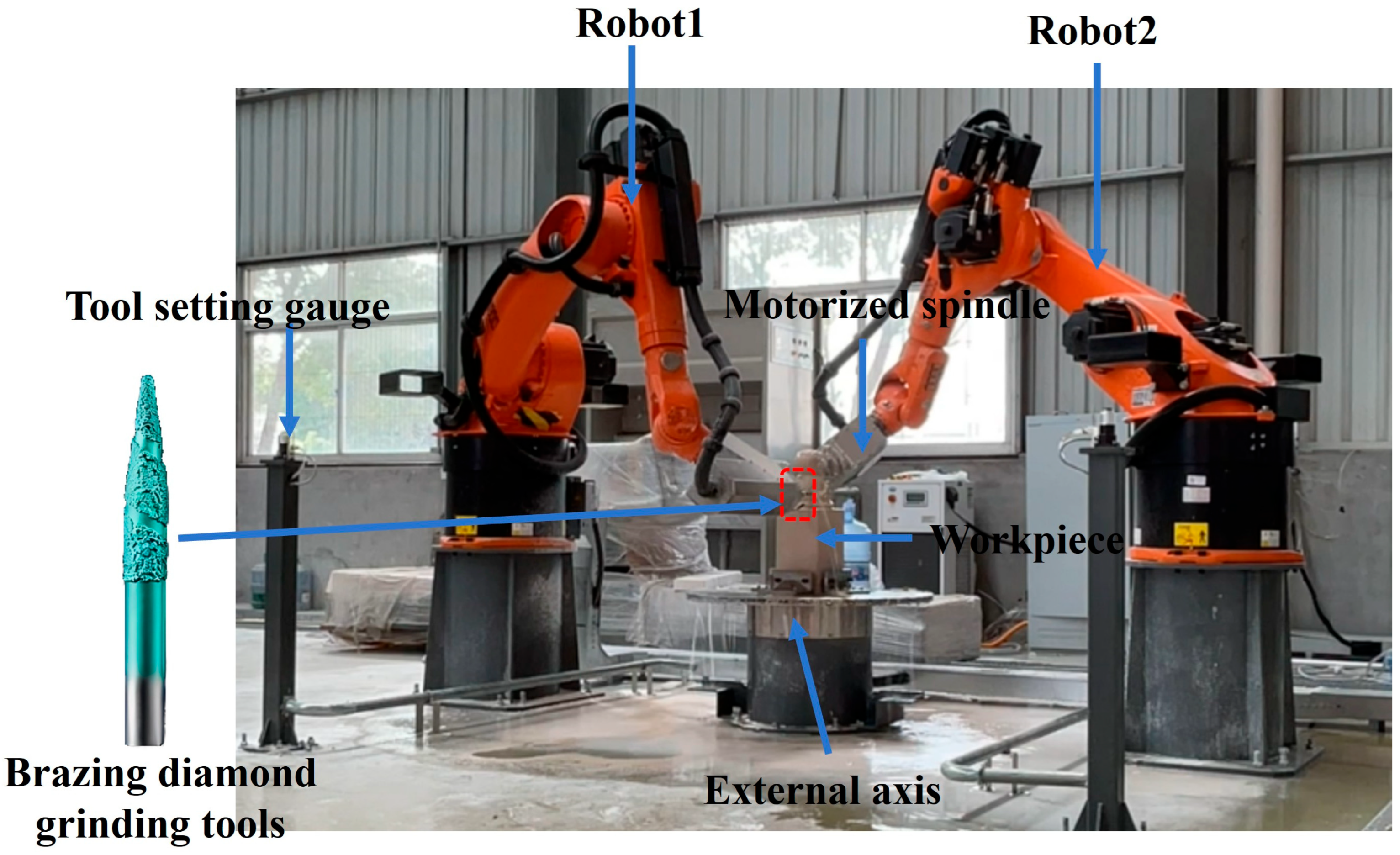
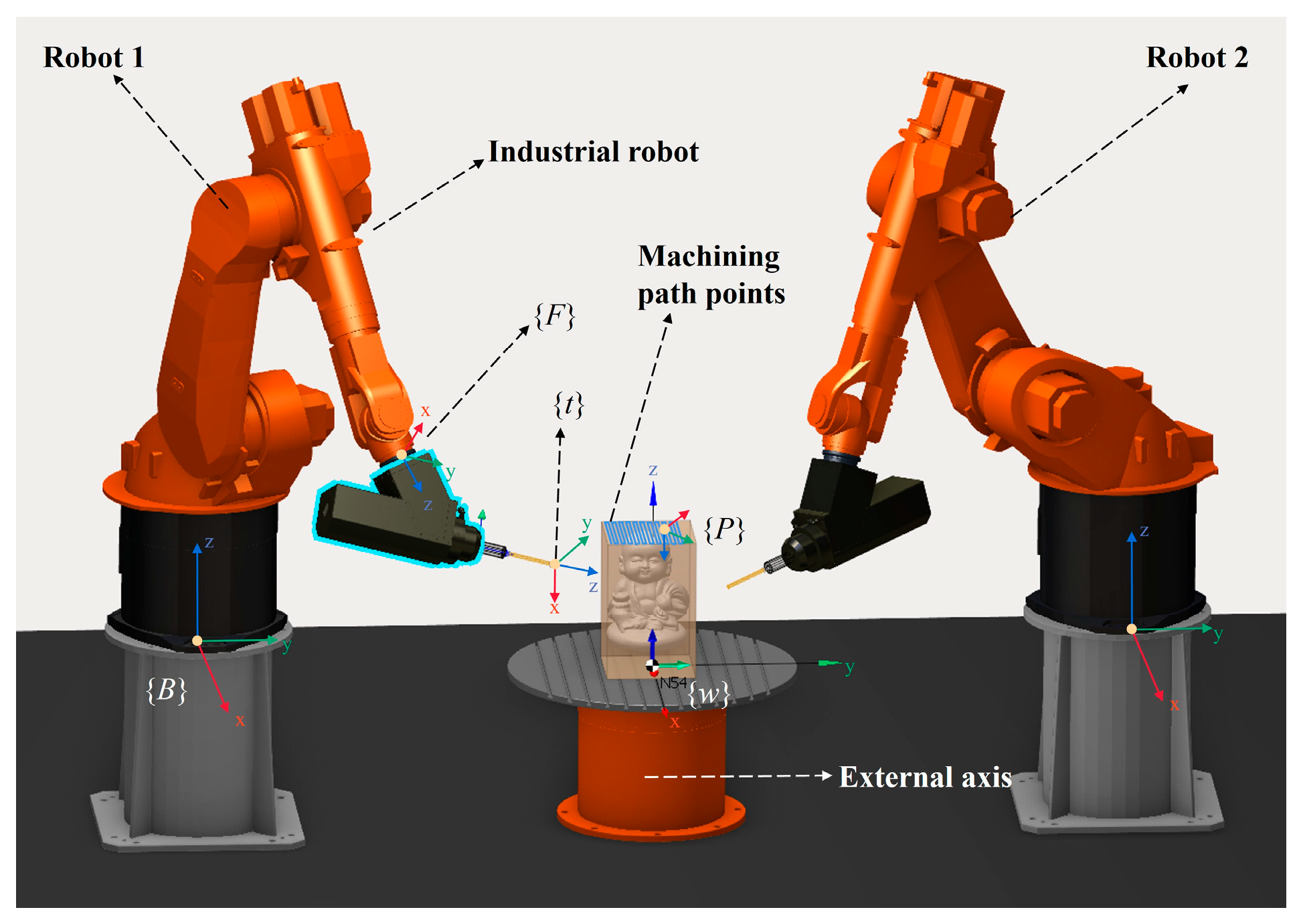
2.1. Description of the Dual-Robot Carving System
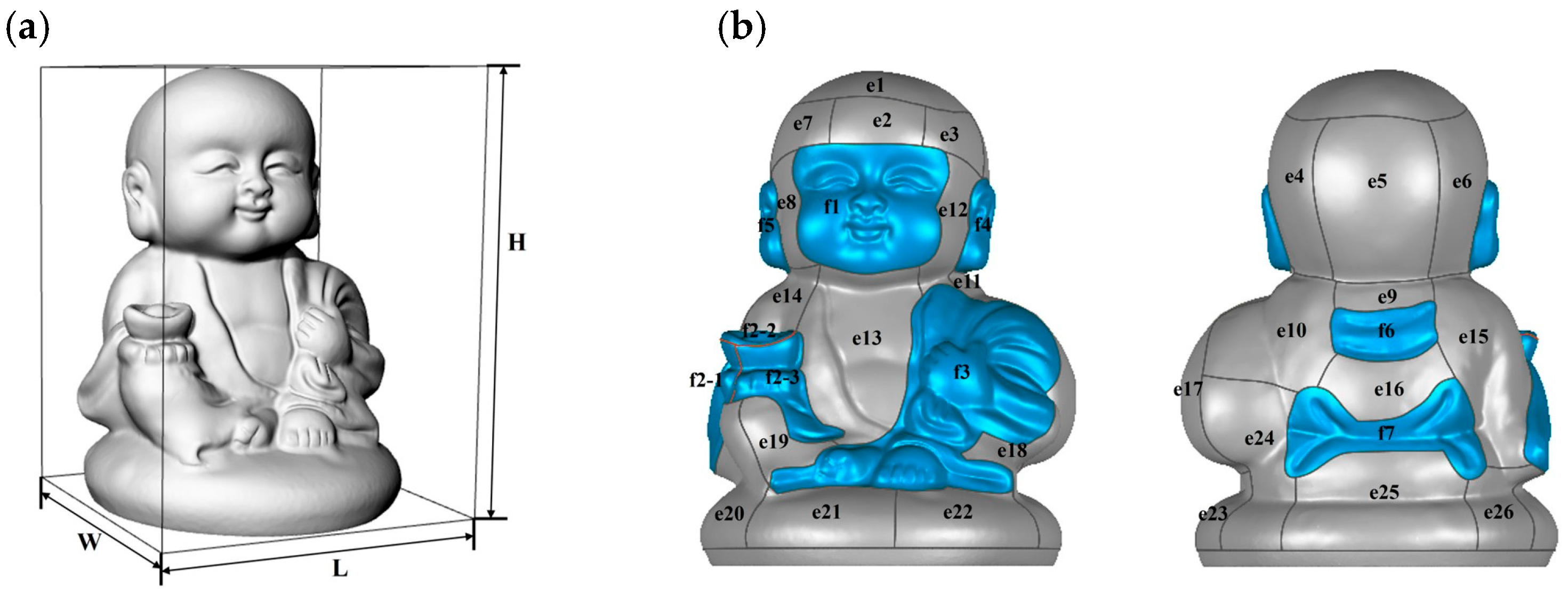
2.2. Machining Model and Parameters
2.2.1. Machining Model
2.2.2. Machining Parameters
2.3. Single-Robot Carving Experiment
3. Task Allocation Method Under Stiffness Performance Constraints
3.1. Workstation Optimization Model Incorporating Stiffness Performance
3.1.1. Description of the Workstation Optimization Model Incorporating Stiffness Performance
3.1.2. Constraints of the Workstation Optimization Model Incorporating Stiffness Performance
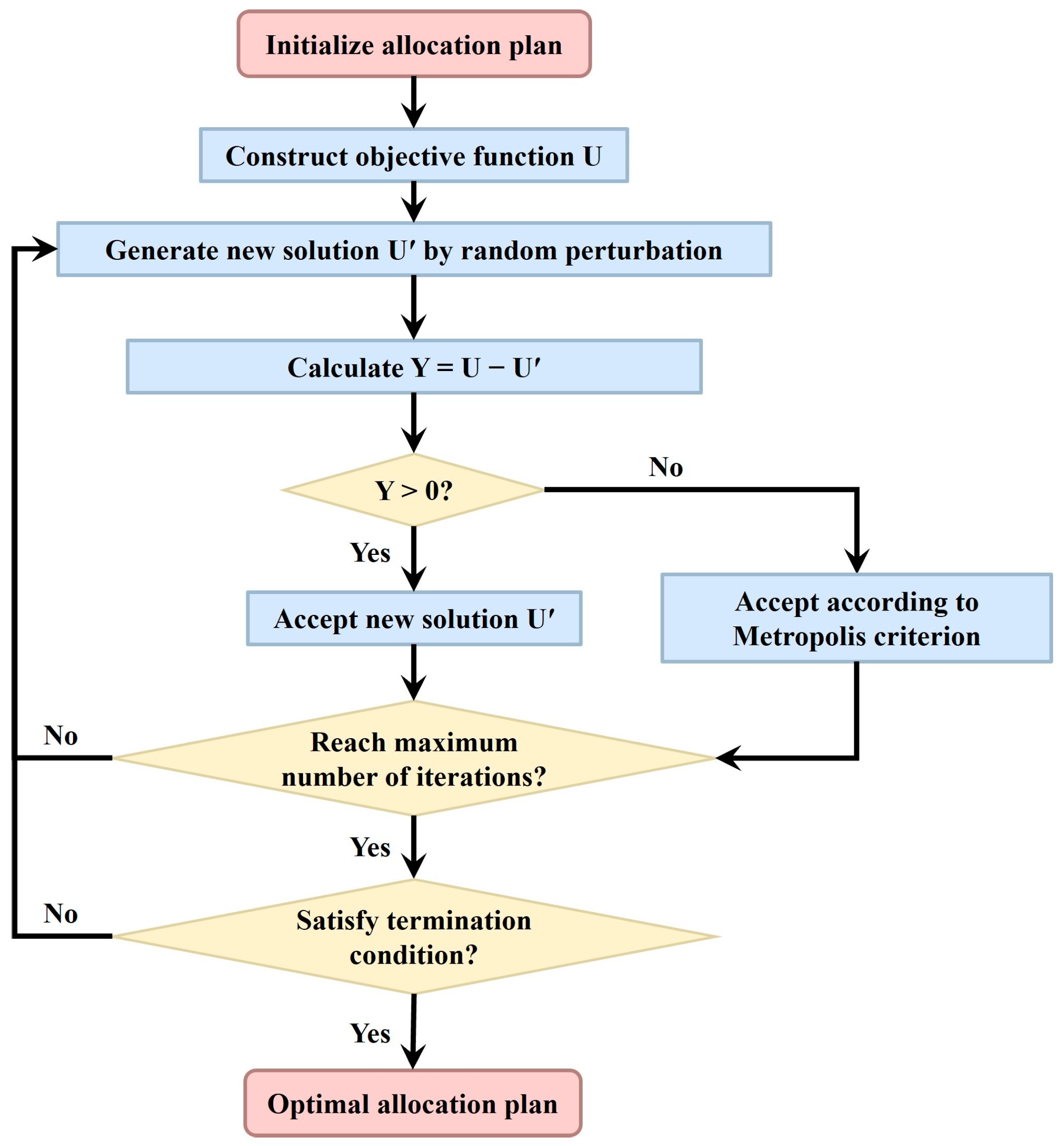
3.2. Task Allocation Method for Workstation Optimization Model
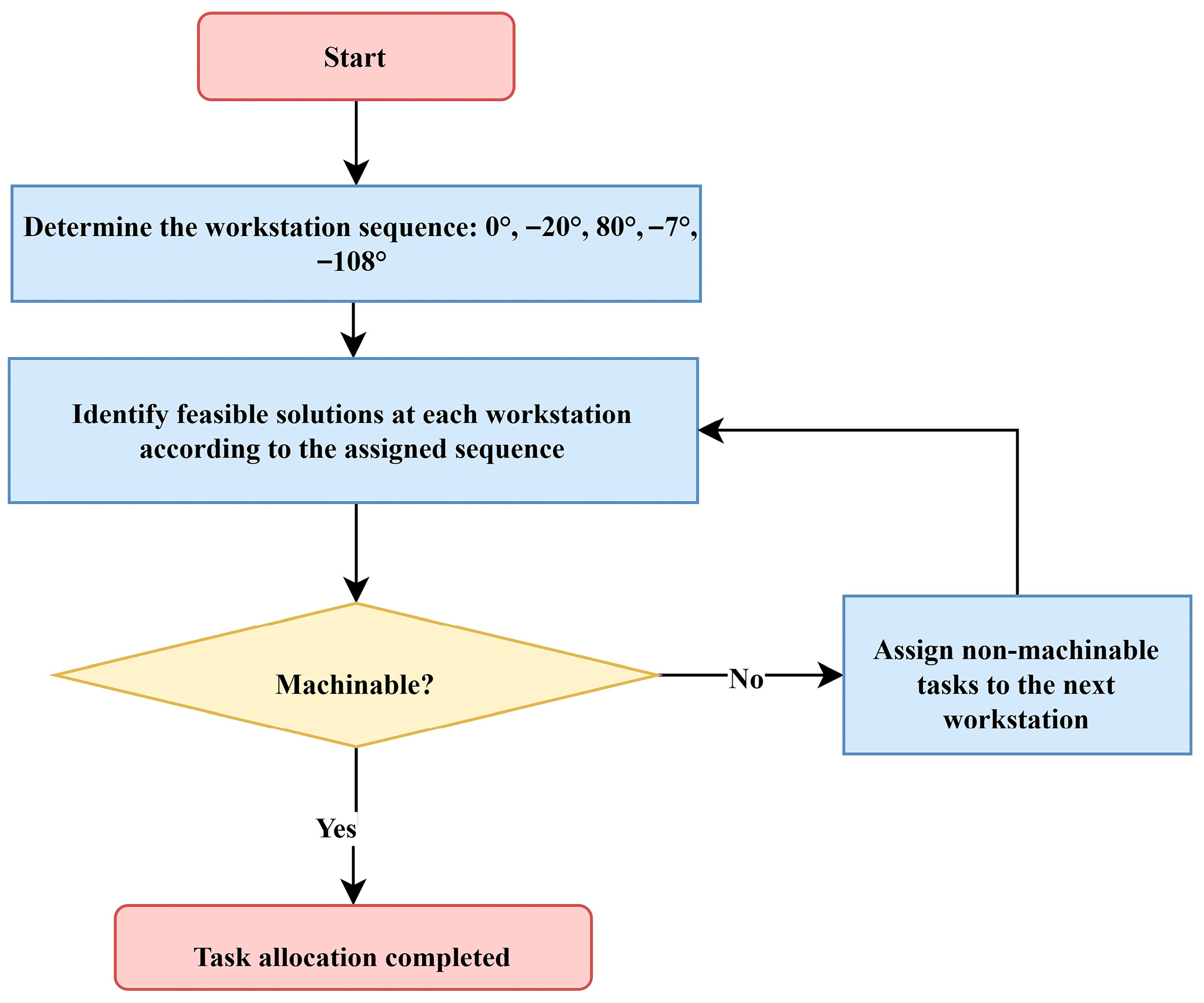
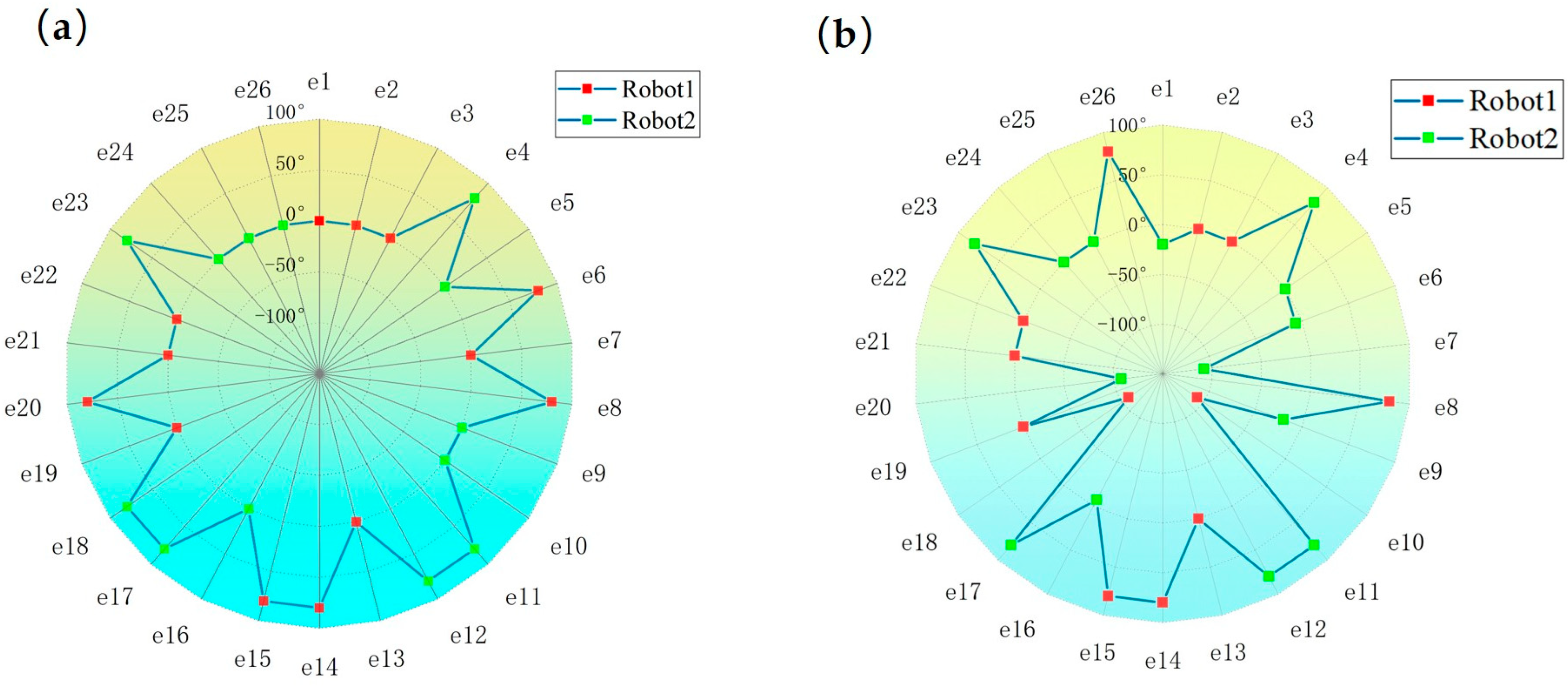
3.2.1. Workstation Angle
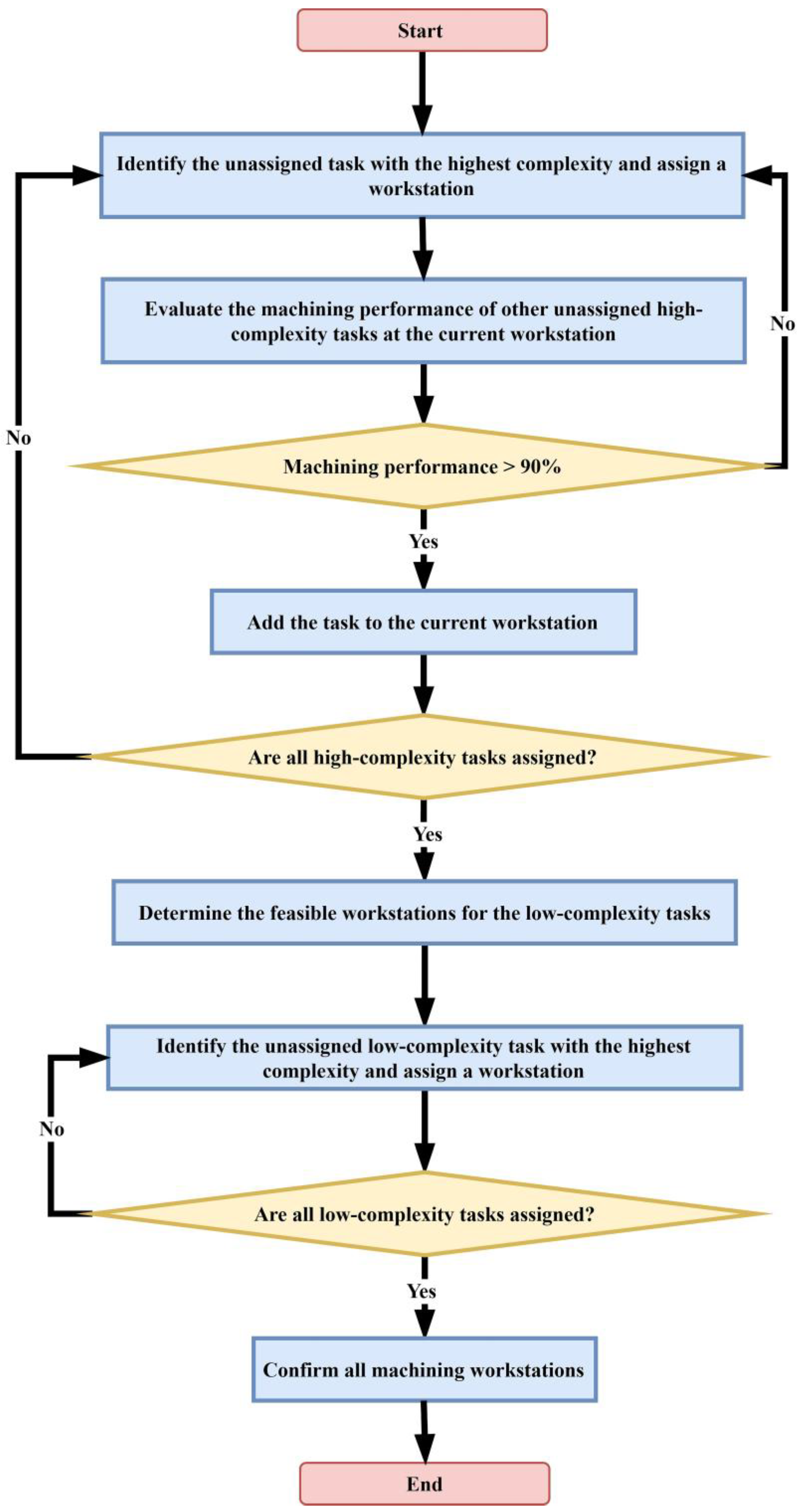
3.2.2. Workstation-Based Task Allocation Based on Machinability
3.2.3. Workstation-Based Task Allocation Based on Machining Time Balancing
4. Results and Discussion
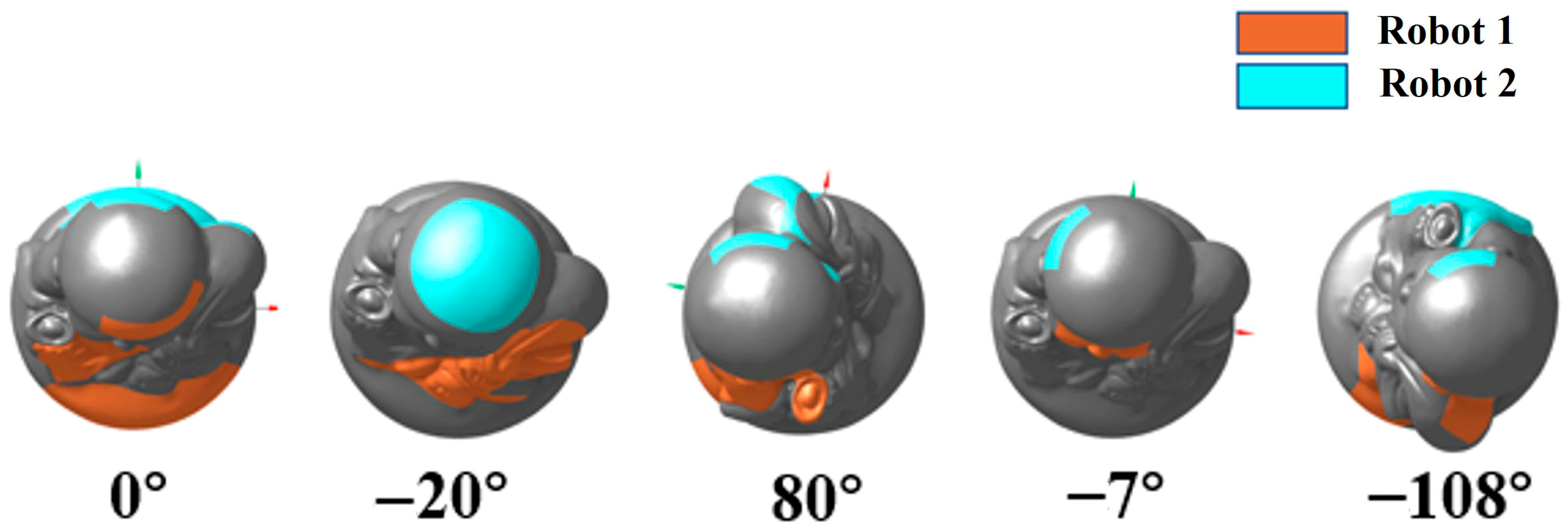
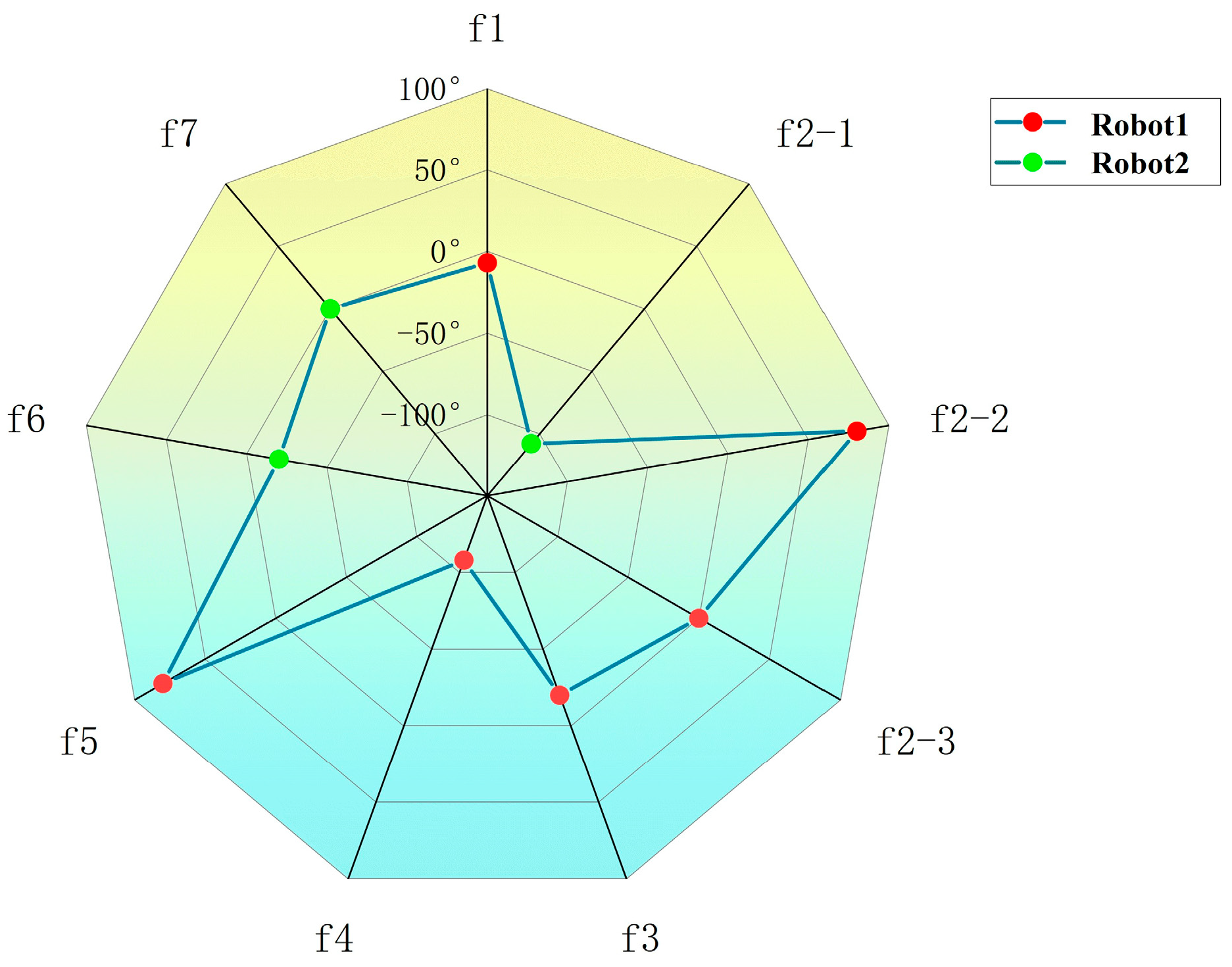
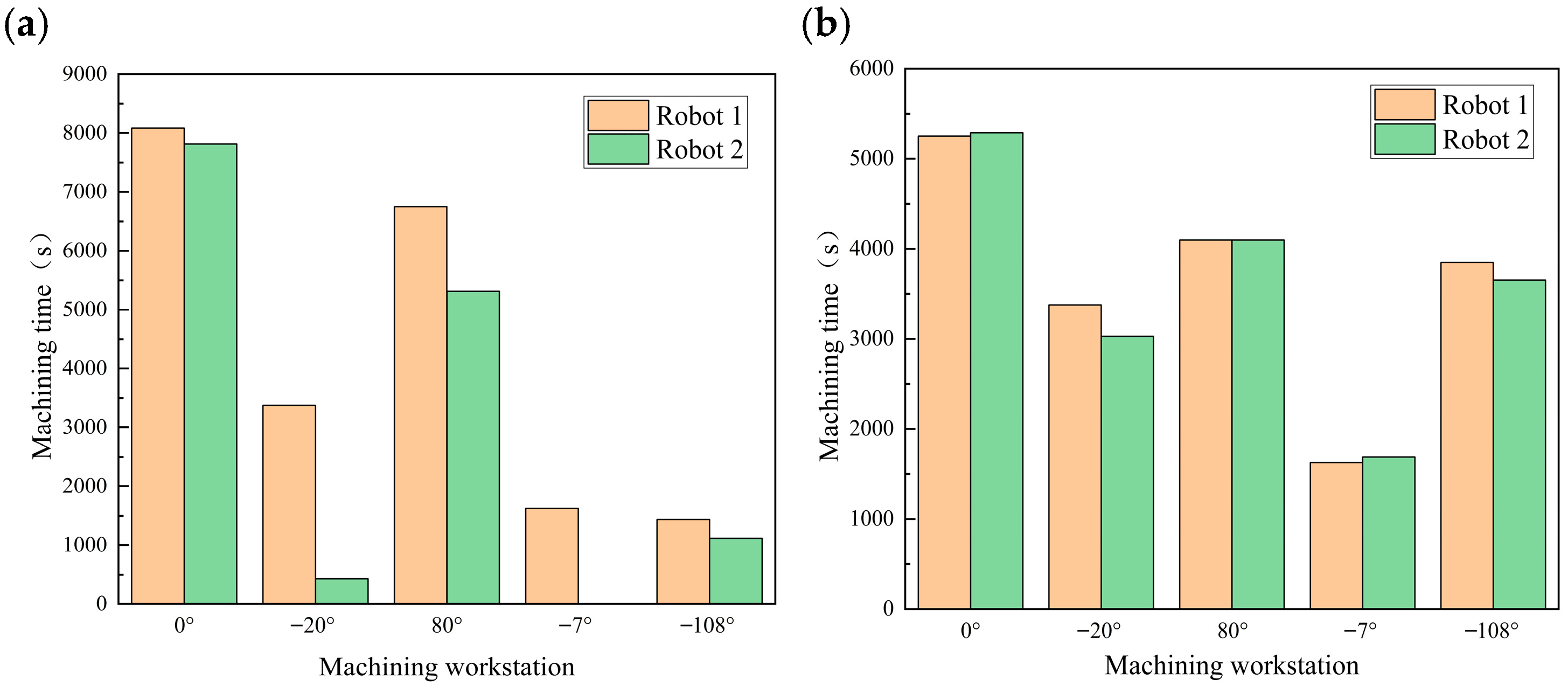
4.1. Workstation Determination Results
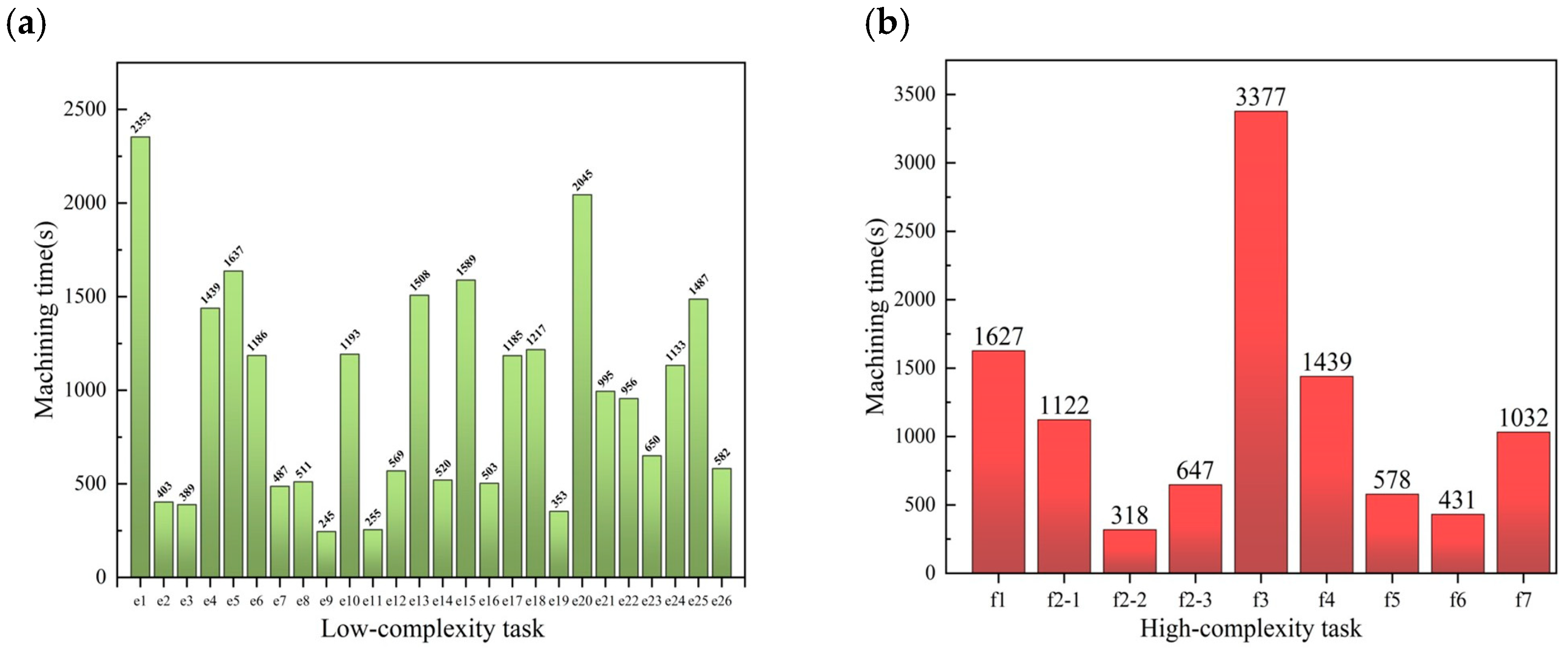
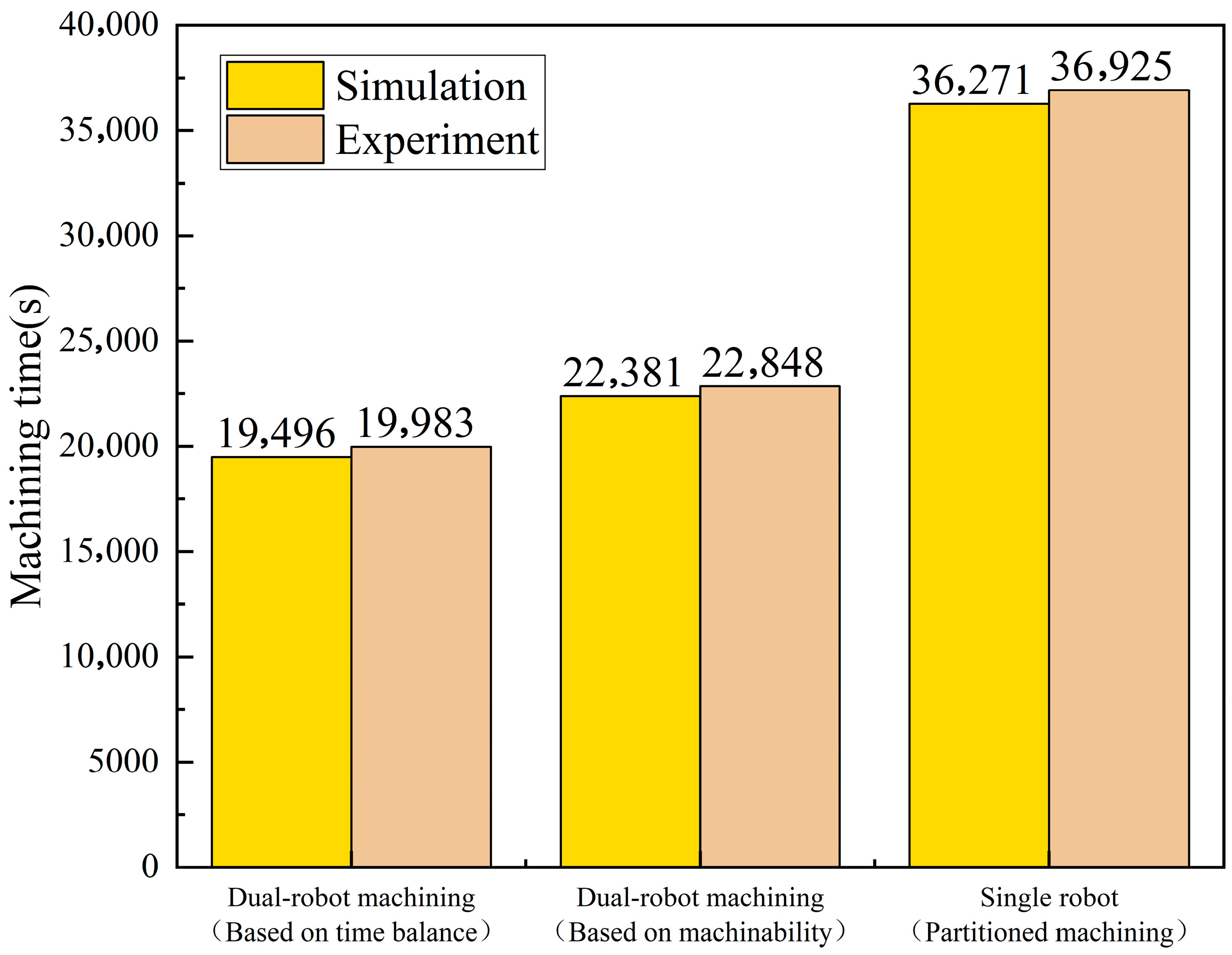
4.2. Comparison of Machining Time Under Different Machining Methods
5. Conclusions and Future Works
- (1)
- To address the machining redundancy caused by the introduction of an external axis in the dual-robot carving system, a workstation optimization model is proposed to determine workstations, enabling the decoupling of the task allocation problem.
- (2)
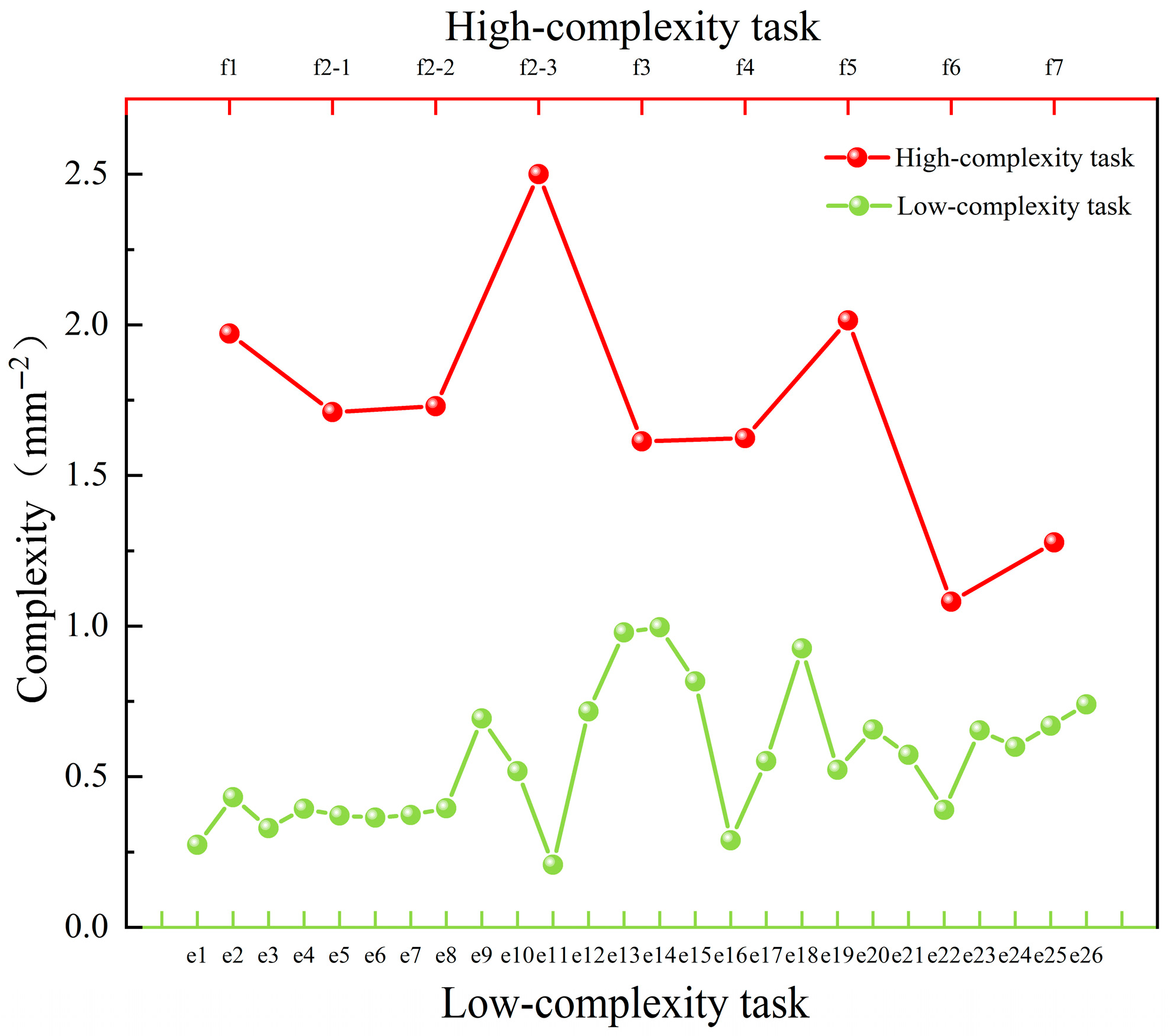
- For the machining accuracy of high-complexity tasks in model segmentation, the proposed stiffness performance-integrated workstation optimization model ensures that these tasks are executed at workstations with better stiffness performance, thereby guaranteeing machining quality.
- (3)
- Considering the machining time balancing of dual robots at each workstation can significantly improve the efficiency of stone carving. The effectiveness of this method is validated through both simulation and physical experiments. Compared with the task allocation method without time balancing and the traditional single-robot partitioned machining approach, experimental results show efficiency improvements of 14.33% and 84.78%, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yin, F.C.; Ji, Q.Z.; Wang, C.Z. Research on machining error prediction and compensation technology for a stone-carving robotic manipulator. Int. J. Adv. Manuf. Technol. 2021, 115, 1683–1700. [Google Scholar] [CrossRef]
- Ji, W.; Wang, L.H. Industrial robotic machining: A review. Int. J. Adv. Manuf. Technol. 2019, 103, 1239–1255. [Google Scholar] [CrossRef]
- Pantscharowitsch, M.; Moser, L.; Kromoser, B. A study of the accuracy of industrial robots and laser-tracking for timber machining across the workspace. Wood Mater. Sci. Eng. 2025, 20, 75–93. [Google Scholar] [CrossRef]
- Cao, Y.J.; Beltrame, G. VIR-SLAM: Visual, inertial, and ranging SLAM for single and multi-robot systems. Auton. Robots 2021, 45, 905–917. [Google Scholar] [CrossRef]
- Kyprianou, G.; Doitsidis, L.; Chatzichristofis, S.A. Towards the achievement of path planning with multi-robot systems in dynamic environments. J. Intell. Robot. Syst. 2021, 104, 15. [Google Scholar] [CrossRef]
- Zhou, Z.Y.; Liu, J.C.; Yu, J.Z. A survey of underwater multi-robot systems. IEEE/CAA J. Autom. Sin. 2022, 9, 1–18. [Google Scholar] [CrossRef]
- Murugappan, E.; Nachiappan, S.; Shams, R.; Mark, G.; Chan, H.K. Performance analysis of clustering methods for balanced multi-robot task allocations. Int. J. Prod. Res. 2022, 60, 4576–4591. [Google Scholar] [CrossRef]
- Mao, W.J.; Liu, Z.J.; Liu, H.; Yang, F.Z.; Wang, M.R. Research progress on synergistic technologies of agricultural multi-robots. Appl. Sci. 2021, 11, 1448. [Google Scholar] [CrossRef]
- Spensieri, D.; Carlson, J.S.; Ekstedt, F.; Bohlin, R. An iterative approach for collision free routing and scheduling in multirobot stations. IEEE Trans. Autom. Sci. Eng. 2016, 13, 950–962. [Google Scholar] [CrossRef]
- Tereshchuk, V.; Stewart, J.; Bykov, N.; Pedigo, S.; Devasia, S.; Banerjee, A.G. An efficient scheduling algorithm for multi-robot task allocation in assembling aircraft structures. IEEE Robot. Autom. Lett. 2019, 4, 3844–3851. [Google Scholar] [CrossRef]
- Behrens, J.K.; Lange, R.; Mansouri, M. A constraint programming approach to simultaneous task allocation and motion scheduling for industrial dual-arm manipulation tasks. In Proceedings of the 2019 IEEE International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 8705–8711. [Google Scholar] [CrossRef]
- Wu, R.J.; Yin, Y.C.; Xu, K. Multi-task collaborative modeling and assignment method of manipulator. Mech. Sci. Technol. Aerosp. Eng. 2020, 39, 433–437. [Google Scholar] [CrossRef]
- Jia, X.H.; Tang, C.R.; Zhang, X.B.; Liu, J.Y. Research on dual robot collaboration method based on improved double ant colony algorithm. Ind. Robot. 2024, 51, 424–435. [Google Scholar] [CrossRef]
- Li, Y.Z.; Meng, L.Y.; Li, M.L.; Zhou, Y.J.; Liu, X.C.; Li, X.L.; Zhang, G.J. Allocation and scheduling of deposition paths in a layer for multi-robot coordinated wire and arc additive manufacturing of large-scale parts. Virtual Phys. Prototyp. 2024, 19, e2300680. [Google Scholar] [CrossRef]
- Liu, W.B.; Kuang, Z.A.; Zhang, Y.C.; Zhou, B.; He, P.F.; Li, S.H. An effective hybrid genetic algorithm for the multi-robot task allocation problem with limited span. Expert Syst. Appl. 2025, 280, 127299. [Google Scholar] [CrossRef]
- Lee, J.; Kim, B.I.; Nam, M. Novel method for welding gantry robot scheduling at shipyards. Int. J. Prod. Res. 2023, 61, 5842–5859. [Google Scholar] [CrossRef]
- Yu, R.; Chen, Y.Y. Coordinated ship welding with optimal lazy robot ratio and energy consumption via reinforcement learning. J. Mar. Sci. Eng. 2024, 12, 1765. [Google Scholar] [CrossRef]
- Liu, S.R.; Tian, W.; Shen, J.X.; Li, B.; Li, P.C. Base position and task assignment optimization concerning productivity and machining performance for multi-robot systems in aerospace manufacturing. Robot. Auton. Syst. 2024, 171, 104536. [Google Scholar] [CrossRef]
- Zhao, G.B.; Wu, J.H. Multi-station and multi-robot welding path planning based on greedy interception algorithm. In Proceedings of the 2020 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Boston, MA, USA, 6–9 July 2020; pp. 1190–1195. [Google Scholar] [CrossRef]
- Zhou, B.; Zhou, R.; Gan, Y.H.; Fang, F.; Mao, Y.J. Multi-robot multi-station cooperative spot welding task allocation based on stepwise optimization: An industrial case study. Robot. Comput.-Integr. Manuf. 2022, 73, 102197. [Google Scholar] [CrossRef]
- Bozma, H.I.; Kalalıoğlu, M.E. Multirobot coordination in pick-and-place tasks on a moving conveyor. Robot. Comput.-Integr. Manuf. 2012, 28, 530–538. [Google Scholar] [CrossRef]
- Arbogast, A.; Nycz, A.; Noakes, M.W.; Wang, P.; Masuo, C.; Vaughan, J.; Love, L.; Lind, R.; Carter, W.; Meyer, L.; et al. Strategies for a scalable multi-robot large scale wire arc additive manufacturing system. Addit. Manuf. Lett. 2024, 8, 100183. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Chen, S.; Gu, X. Multi-station multi-robot welding system planning and scheduling based on STNSGA-D: An industrial case study. IEEE Trans. Autom. Sci. Eng. 2024, 21, 7465–7479. [Google Scholar] [CrossRef]
- Xiao, J.; Huang, K.; Terzi, S.; Bandinelli, R. Towards uncertainty of end-of-use product recycling: A general screw connection-oriented disassembly analysis. Int. J. Prod. Res. 2025, 1–24. [Google Scholar] [CrossRef]
- Xiao, J.; Zhang, Z.; Terzi, S.; Tao, F.; Anwer, N.; Eynard, B. Multi-scenario digital twin-driven human-robot collaboration multi-task disassembly process planning based on dynamic time petri-net and heterogeneous multi-agent double deep Q-learning network. J. Manuf. Syst. 2025, 83, 284–305. [Google Scholar] [CrossRef]
- Xiao, J.; Zhang, Z.; Terzi, S.; Anwer, N.; Eynard, B. Dynamic task allocations with Q-learning based particle swarm optimization for human-robot collaboration disassembly of electric vehicle battery recycling. Comput. Ind. Eng. 2025, 204, 111133. [Google Scholar] [CrossRef]
- Xiao, J.; Gao, J.; Anwer, N.; Eynard, B. Multi-agent reinforcement learning method for disassembly sequential task optimization based on human–robot collaborative disassembly in electric vehicle battery recycling. J. Manuf. Sci. Eng. 2023, 145, 121001. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Z.; Mo, Y.; Pan, H. The path planning of synchronous cooperative motion control between robot and positioner for complex space curve processing. Electronics 2020, 9, 1917. [Google Scholar] [CrossRef]
- Kang, C.; Jia, H.; Zhao, E.; Ma, C. Development of an improved stiffness ellipsoid method for precise robot-positioner collaborative control in friction stir welding. Materials 2025, 18, 1852. [Google Scholar] [CrossRef] [PubMed]
- Unger, K. Carving his own unique niche, in symbols and stone. Science 2006, 314, 412–413. [Google Scholar] [CrossRef][Green Version]
- Wang, H.F.; Luo, Y.Q.; An, C.D.; Chu, S.N.; Shen, Z.X.; Huang, L.X.; Zhang, D.Y. Application of imaging polarimeters to enhanced detection of stone carving. J. Cult. Herit. 2019, 40, 92–98. [Google Scholar] [CrossRef]
- Yin, F.C.; Wu, S.T.; Huang, H.; Cui, C.C.; Ji, Q.Z. Effect of machining trajectory on grinding force of complex-shaped stone by robotic manipulator. Machines 2022, 10, 787. [Google Scholar] [CrossRef]
- Chen, C.; Peng, F.; Yan, R.; Li, Y.; Wei, D.; Fan, Z.; Tang, X.; Zhu, Z. Stiffness performance index-based posture and feed orientation optimization in robotic milling process. Robot. Comput.-Integr. Manuf. 2019, 55, 29–40. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cong, J.; Huang, H.; Yin, F.; Shi, H.; Kang, C. Research on Task Allocation Method for Dual-Robot Stereoscopic Stone Carving Under Stiffness Constraints. Machines 2025, 13, 1097. https://doi.org/10.3390/machines13121097
Cong J, Huang H, Yin F, Shi H, Kang C. Research on Task Allocation Method for Dual-Robot Stereoscopic Stone Carving Under Stiffness Constraints. Machines. 2025; 13(12):1097. https://doi.org/10.3390/machines13121097
Chicago/Turabian StyleCong, Jingbo, Hui Huang, Fangchen Yin, Hongwei Shi, and Cheng Kang. 2025. "Research on Task Allocation Method for Dual-Robot Stereoscopic Stone Carving Under Stiffness Constraints" Machines 13, no. 12: 1097. https://doi.org/10.3390/machines13121097
APA StyleCong, J., Huang, H., Yin, F., Shi, H., & Kang, C. (2025). Research on Task Allocation Method for Dual-Robot Stereoscopic Stone Carving Under Stiffness Constraints. Machines, 13(12), 1097. https://doi.org/10.3390/machines13121097






