Residual Attention-Driven Dual-Domain Vision Transformer for Mechanical Fault Diagnosis
Abstract
1. Introduction
- (1)
- A unified input scheme combines time-domain and frequency-domain signals to enhance complementary feature acquisition and improve reliability under varying and fluctuating conditions.
- (2)
- A residual attention module transmits shallow attention responses to deeper layers, improving local feature perception and maintaining stable feature diversity.
- (3)
- A dual-metric alignment strategy integrates Wasserstein distance and MMD, capturing domain variations from complementary viewpoints and enhancing the extraction of domain-agnostic representations.
2. Theoretical Background
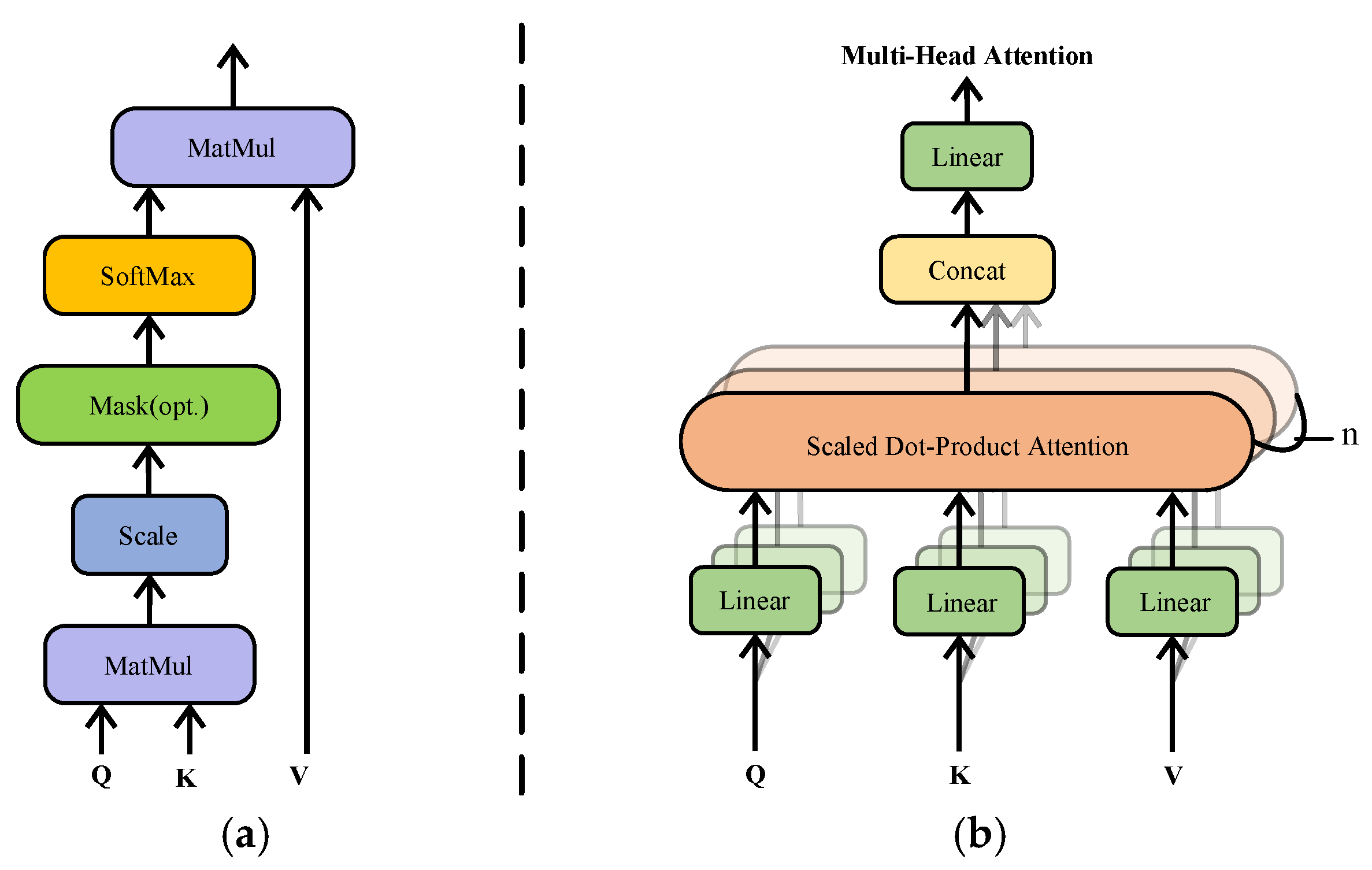
2.1. Multiple Self-Attention Mechanism
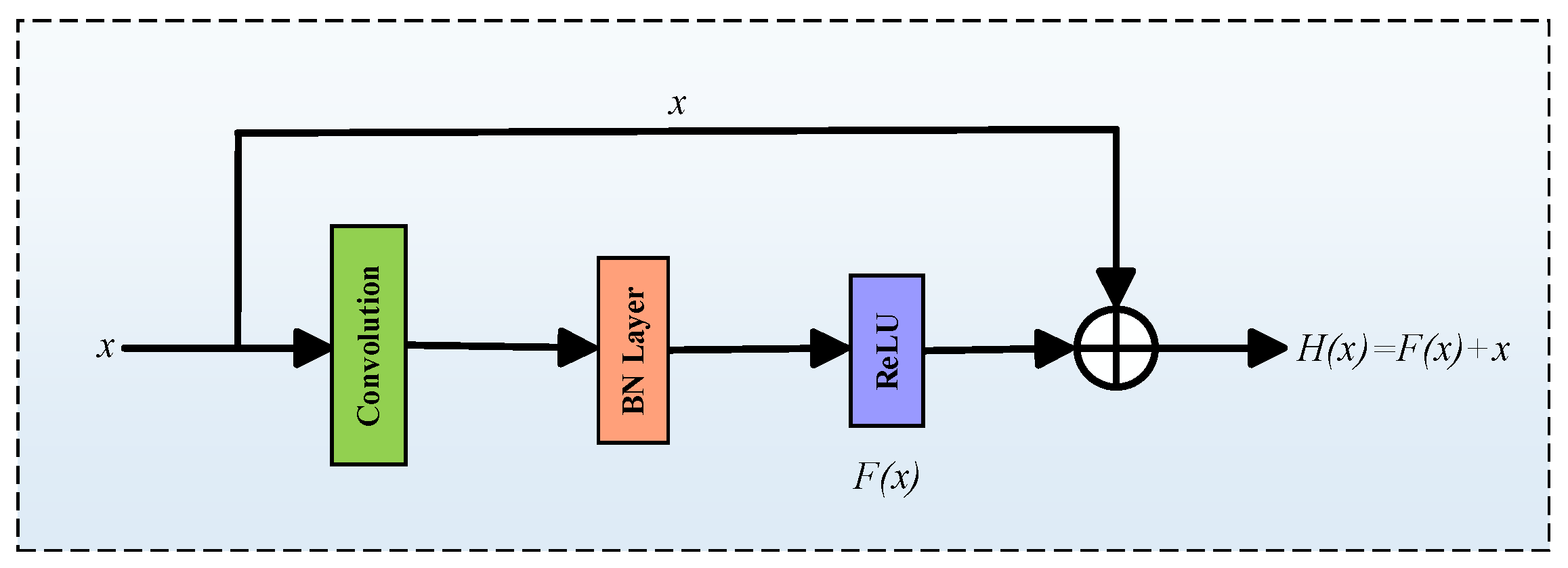
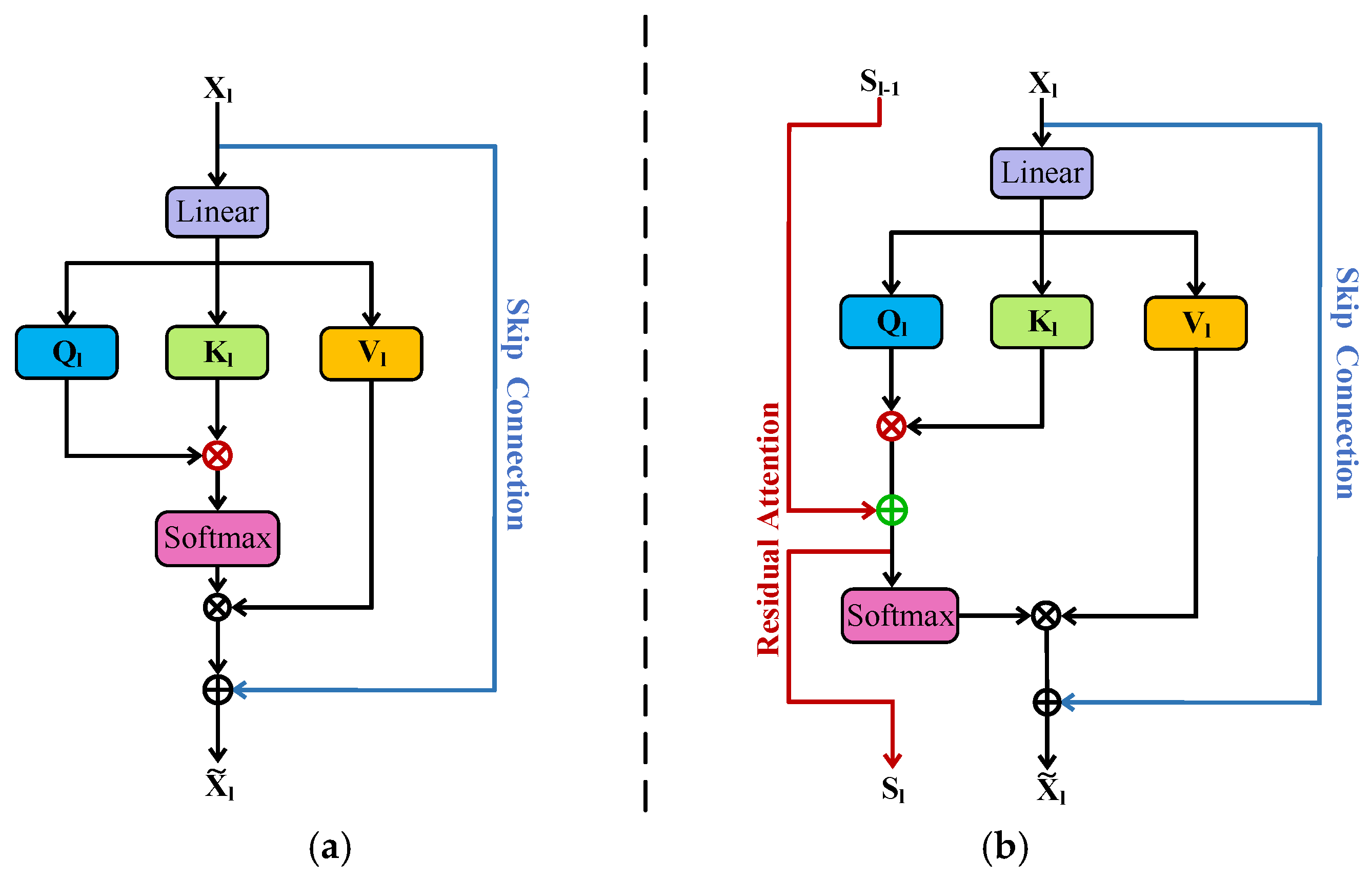
2.2. Residual Connection
2.3. Domain Distance
3. Time–Frequency Fused Vision Transformer Network (TFFViTN)
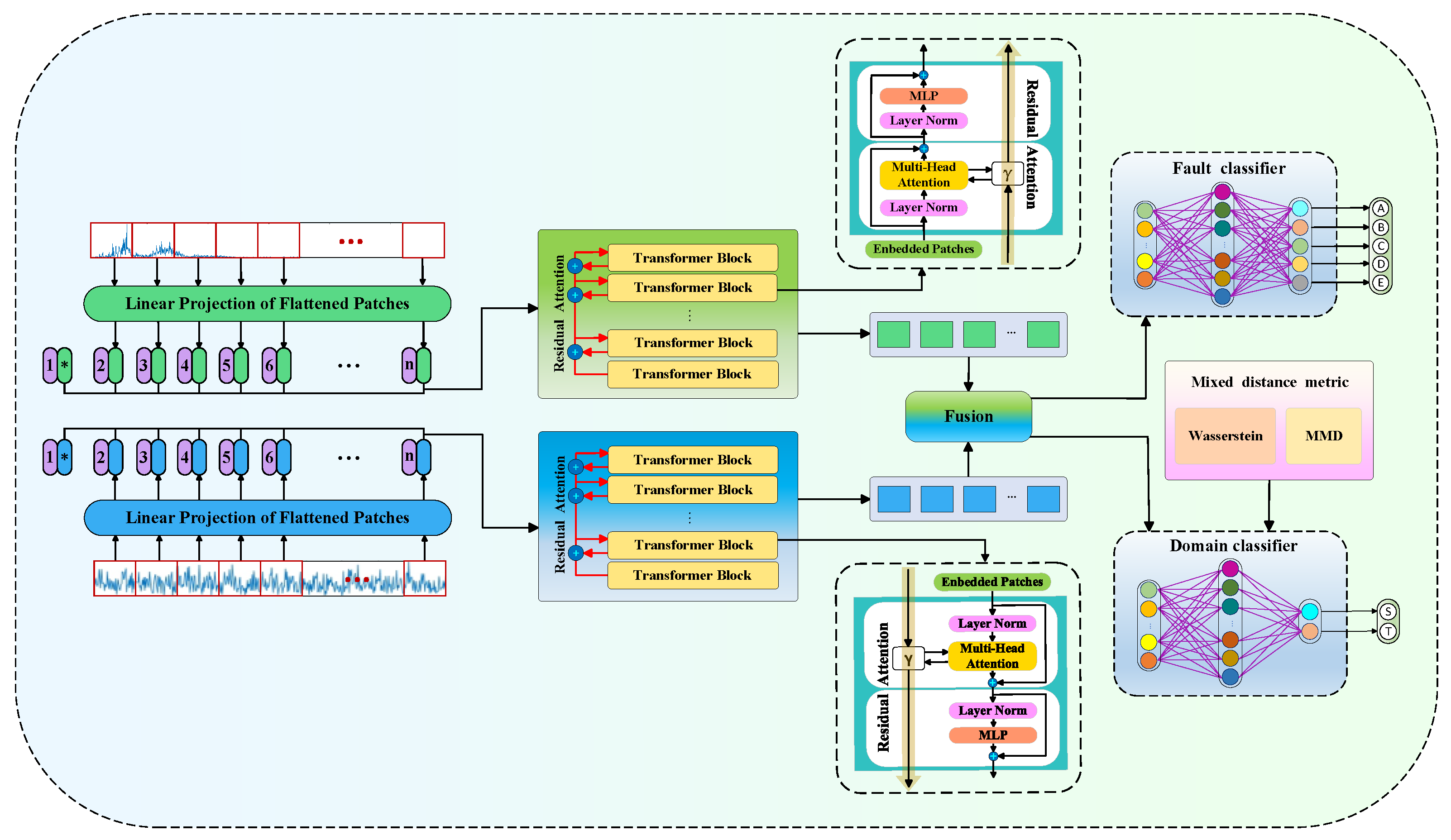
3.1. System Overview
3.2. Concurrent Signal Processing in Time–Frequency Domain
- (1)
- Two types of signals, and are partitioned into equal-length segments at multiple scales (), resulting in and subsequences, respectively. Each segment is mapped into a latent space by linear projection:
- (2)
- To retain temporal order within each segmented sequence, sinusoidal positional encodings are applied as follows:
- (3)
- For each scale , local segment energies are computed as and , and normalized fusion weights are derived as follows:
- (4)
- Fused features from all scales are concatenated to form the multi-scale fused feature:
3.3. Improved Feature Extraction via Residual Attention
3.4. Dual-Domain Distance Metric
- (1)
- To achieve more balanced alignment, an adaptive hybrid domain distance is introduced, combining the strengths of both metrics. The loss functions for Wasserstein distance and MMD are defined as follows:
- (2)
- Instead of fixing and , the model introduces a self-adjusting factor that dynamically reflects the dominant type of domain difference at each iteration. The weights are computed as follows:
- (3)
- The self-adaptive factor is updated through gradient descent according to the overall alignment loss:
- (4)
- By progressively minimizing the adaptive hybrid loss, the model achieves consistent domain alignment across different layers, effectively reducing distribution gaps and enhancing diagnostic robustness under fluctuating operating conditions.
3.5. Integrated Mechanism and Workflow Overview
3.6. TFFViTN Algorithmic Workflow and Architectural Details
| Algorithm 1. Training procedure of TFFViTN |
| Input: Source-domain signals: , and labels Target-domain signals: , ; Maximum epoch ; Accuracy threshold τ; Learning rate η |
| Output: Optimized feature extractor F and classifier C. |
| for epoch = 1 to do |
| 1: Sample mini-batches from source (, ,) and target domains (, ); |
| 2: Pass time-domain and frequency-domain signals separately through corresponding residual attention branches and extract embeddings ; |
| 3: Compute multi-scale fused representations: ; 4: Predict source and target outputs: , Compute classification loss ; 5: Compute hybrid dual-domain alignment loss between and using adaptive Wasserstein + MMD; 6: Aggregate the total loss: L = + 7: Backpropagation and parameter update: Update parameters of F and C with learning rate ; 8: Evaluate target accuracy ; 9: If then save model checkpoint and embedding visualization; break; end for return: optimized parameters F, C. |
4. Experimental Verification
4.1. Data Description of Experiment A
4.2. Experiment A: Fault Diagnosis Under Bearing Data
4.2.1. Data Description of Experiment A
4.2.2. Comparative Evaluation of Experiment A
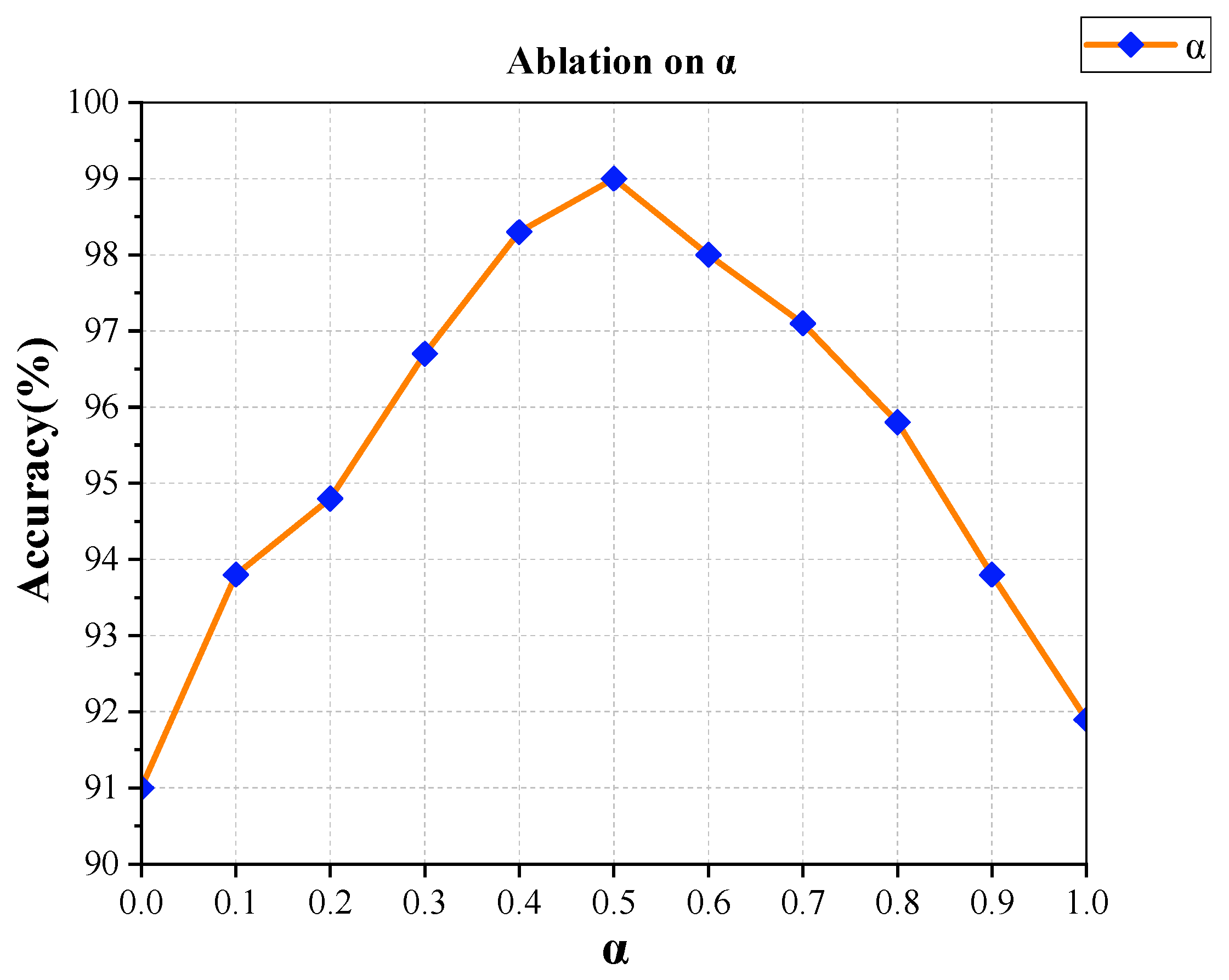
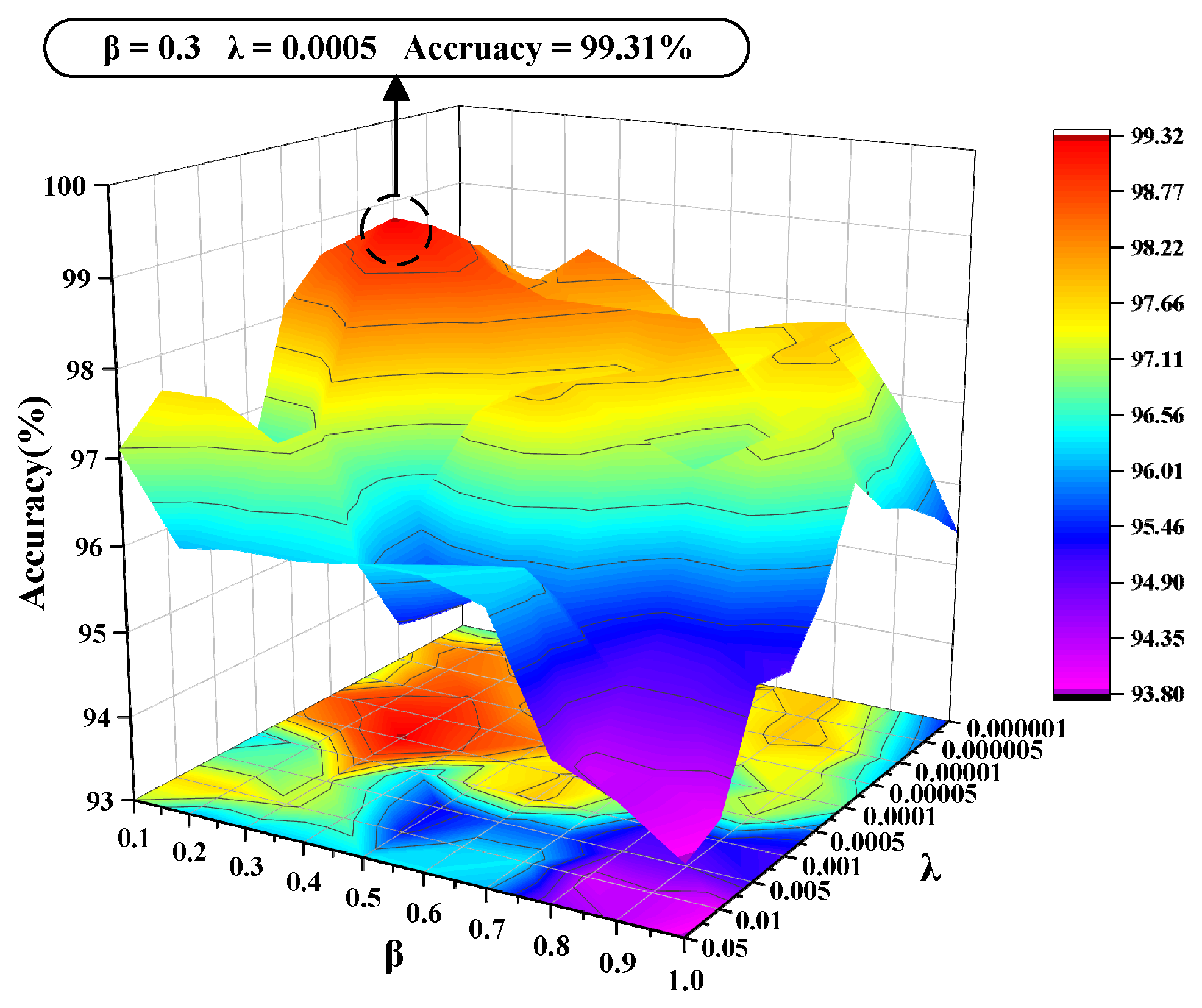
4.2.3. Parameter Sensitivity Analysis
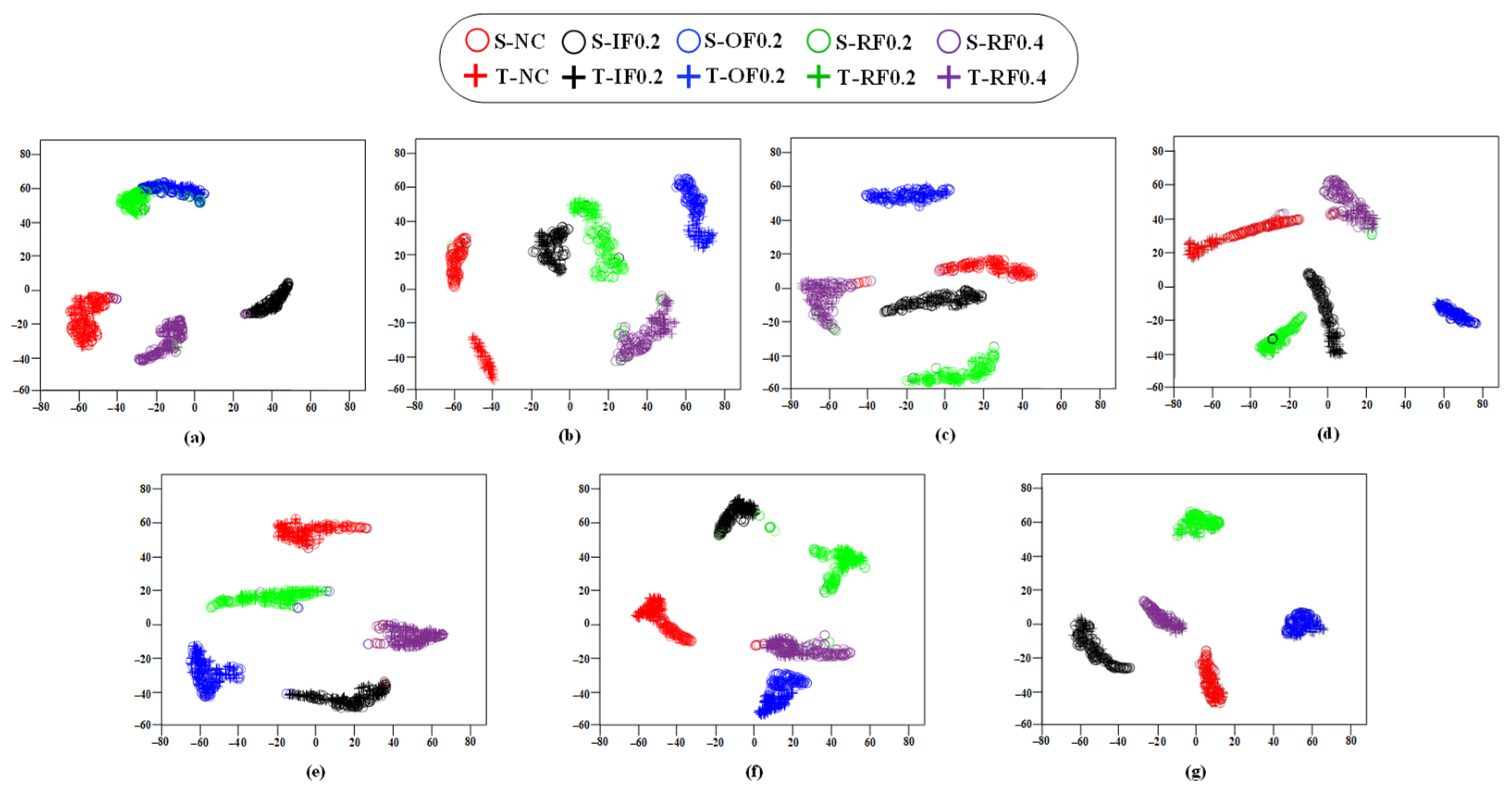
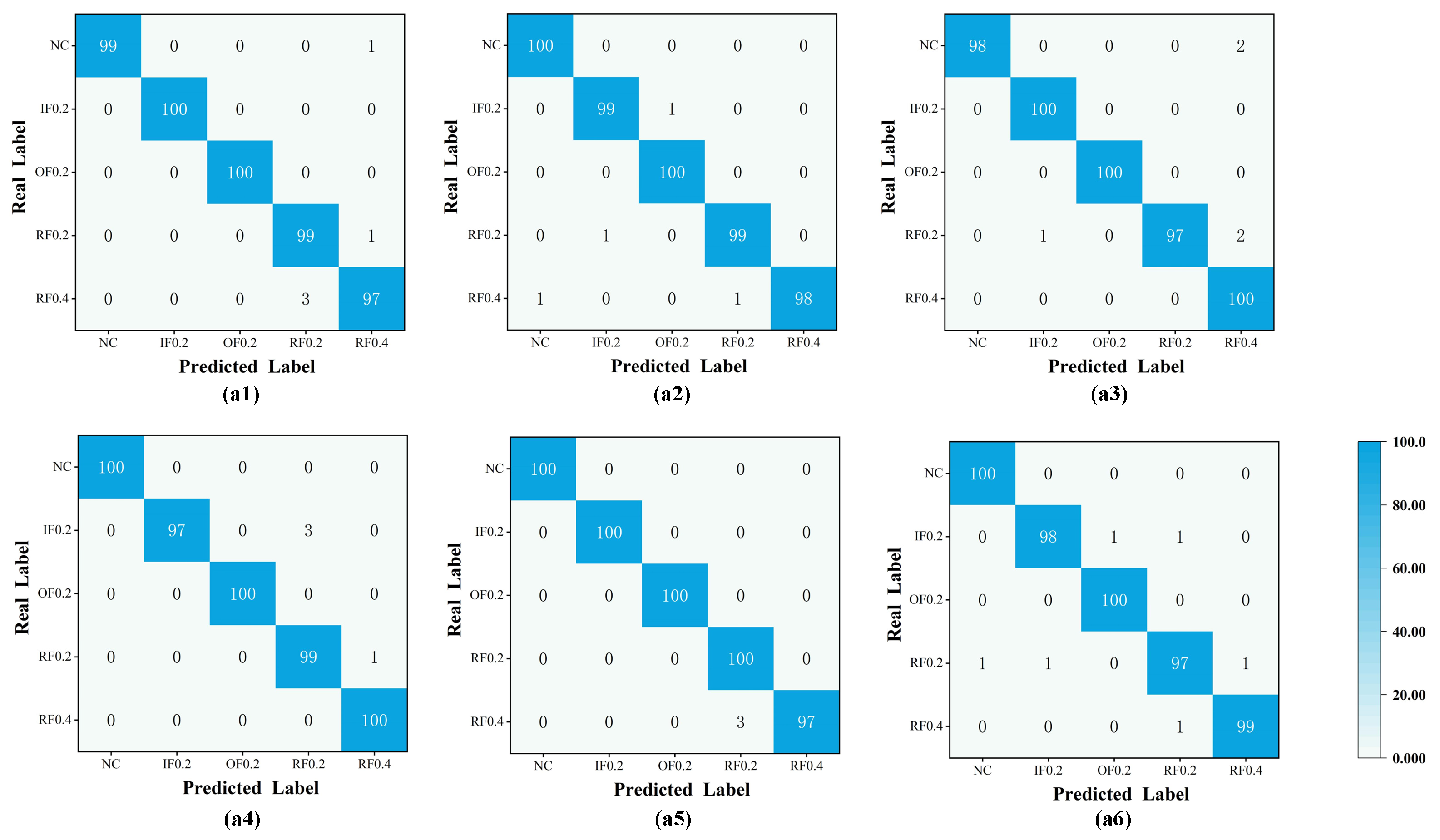
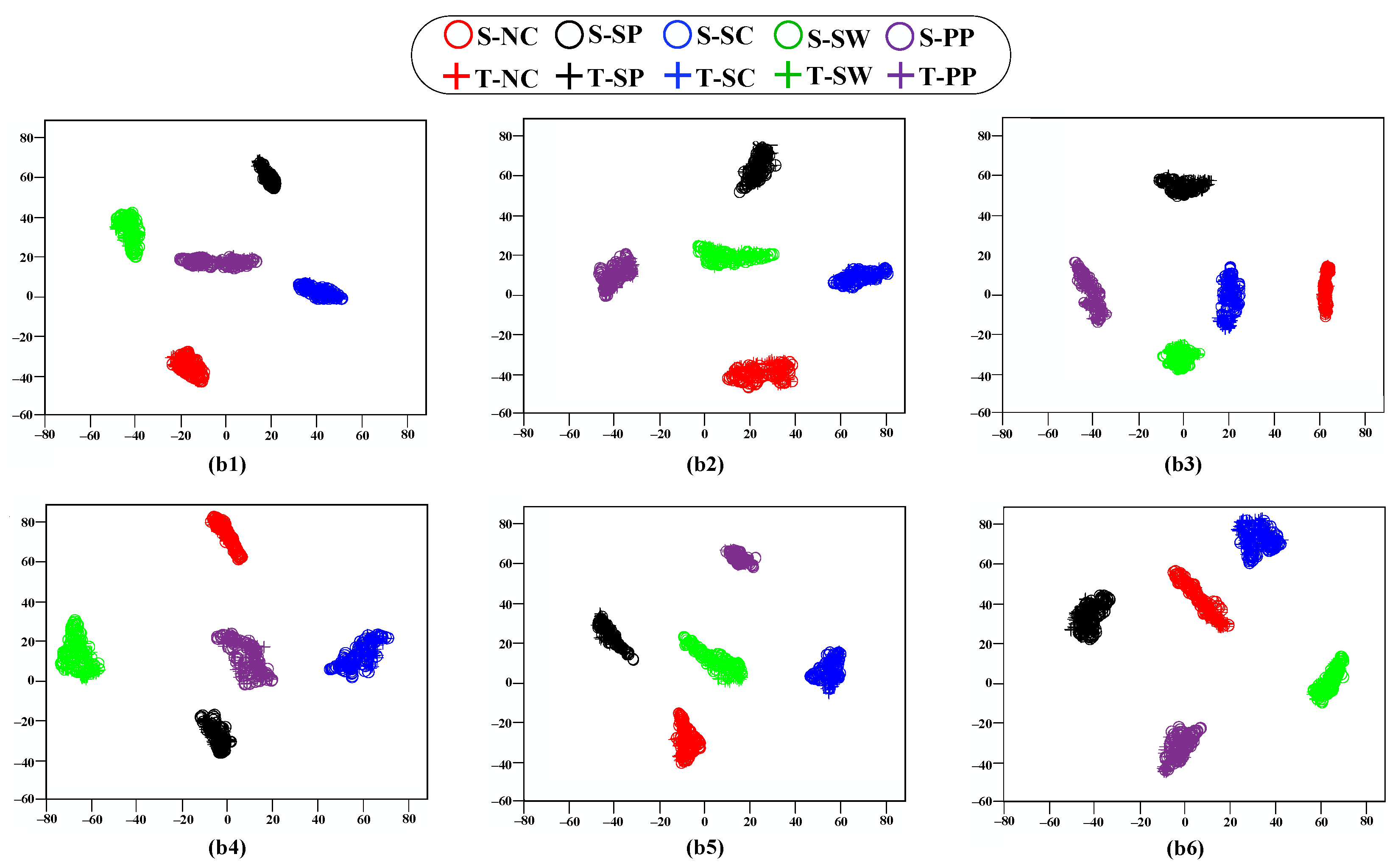
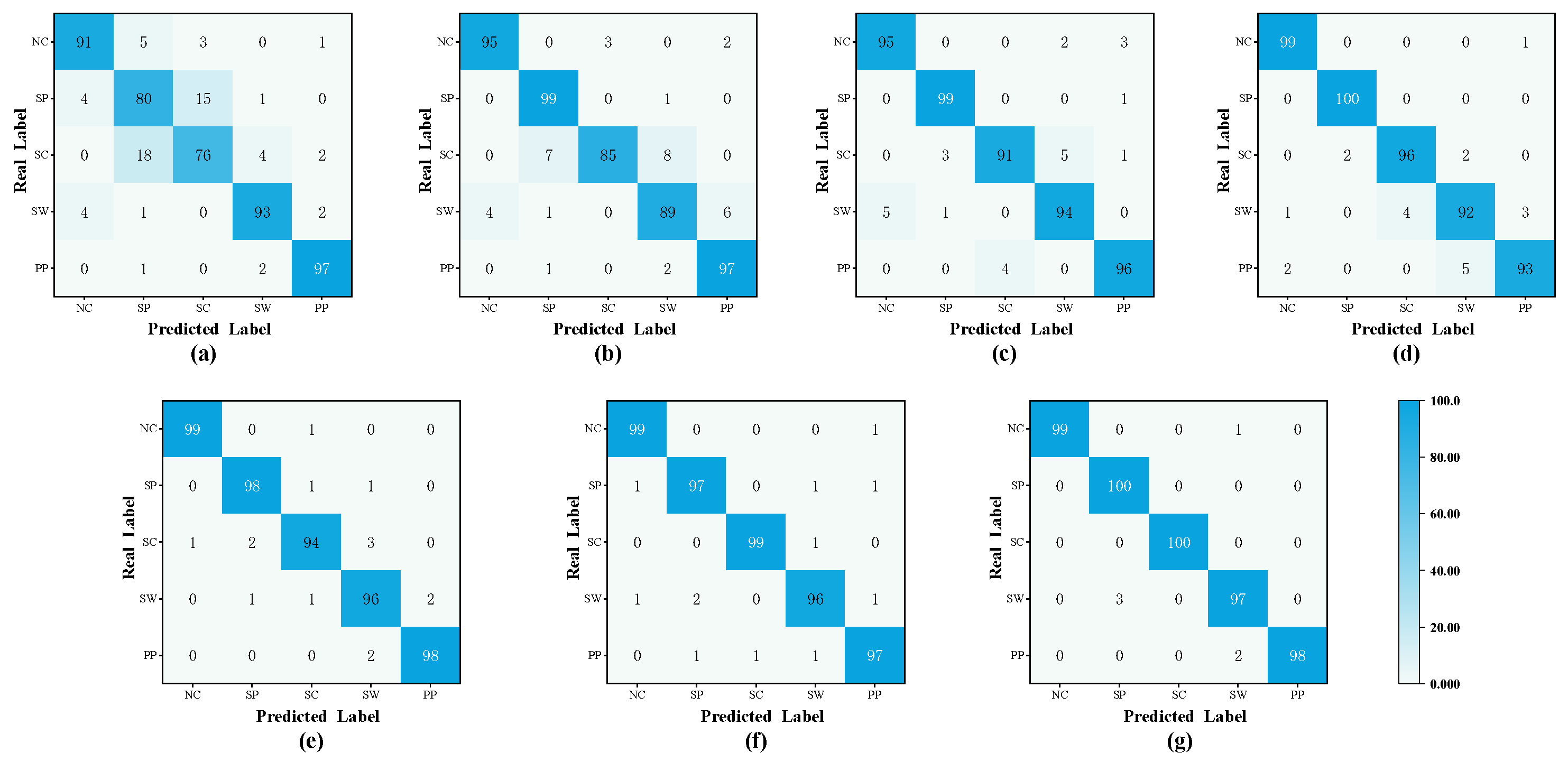
4.2.4. Experimental Results of Experiment A
4.2.5. Computational Complexity Analysis
4.3. Experiment B: Fault Diagnosis Under Gears Data
4.3.1. Data Description of Experiment A
4.3.2. Comparative Evaluation of Experiment B
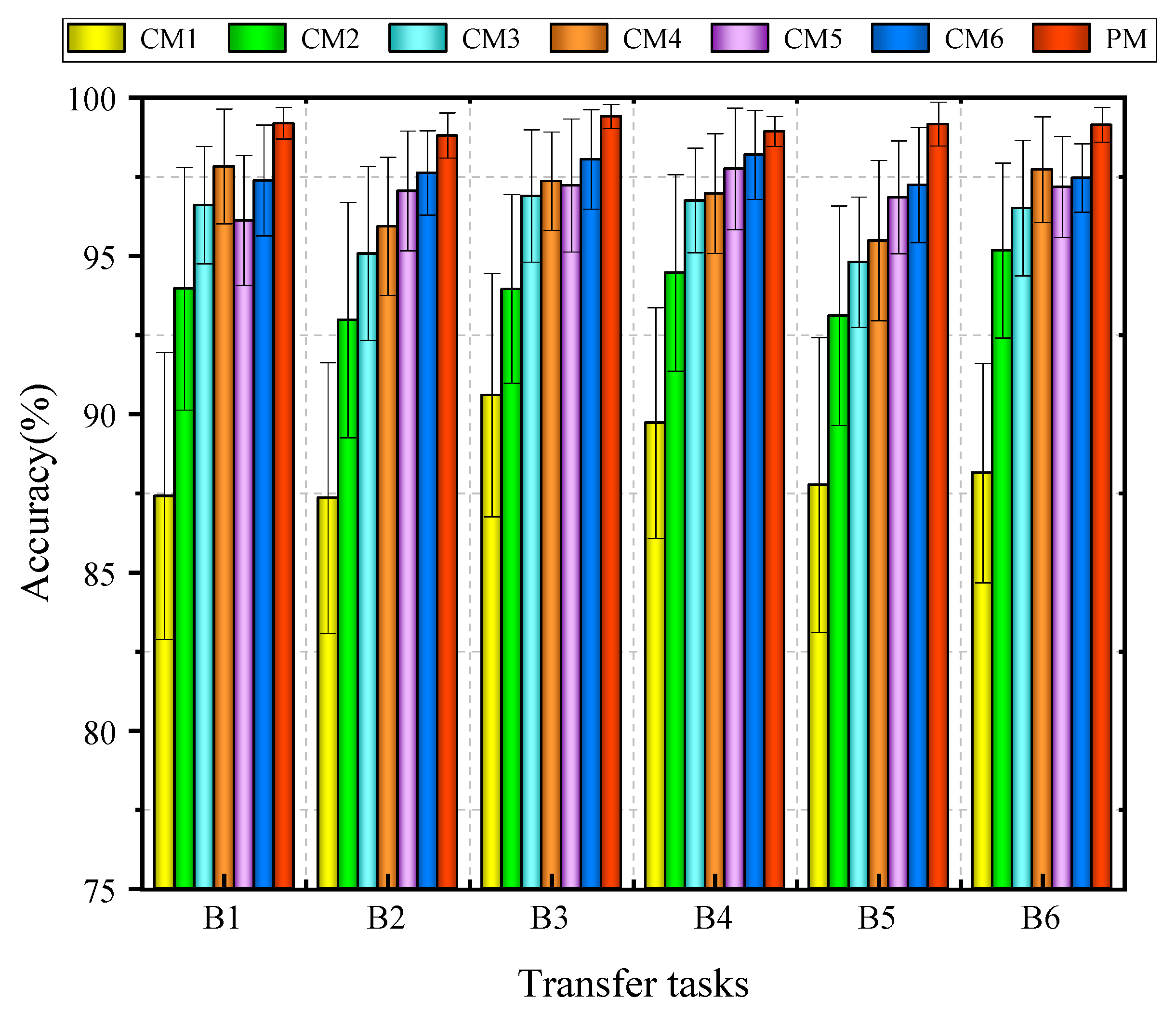
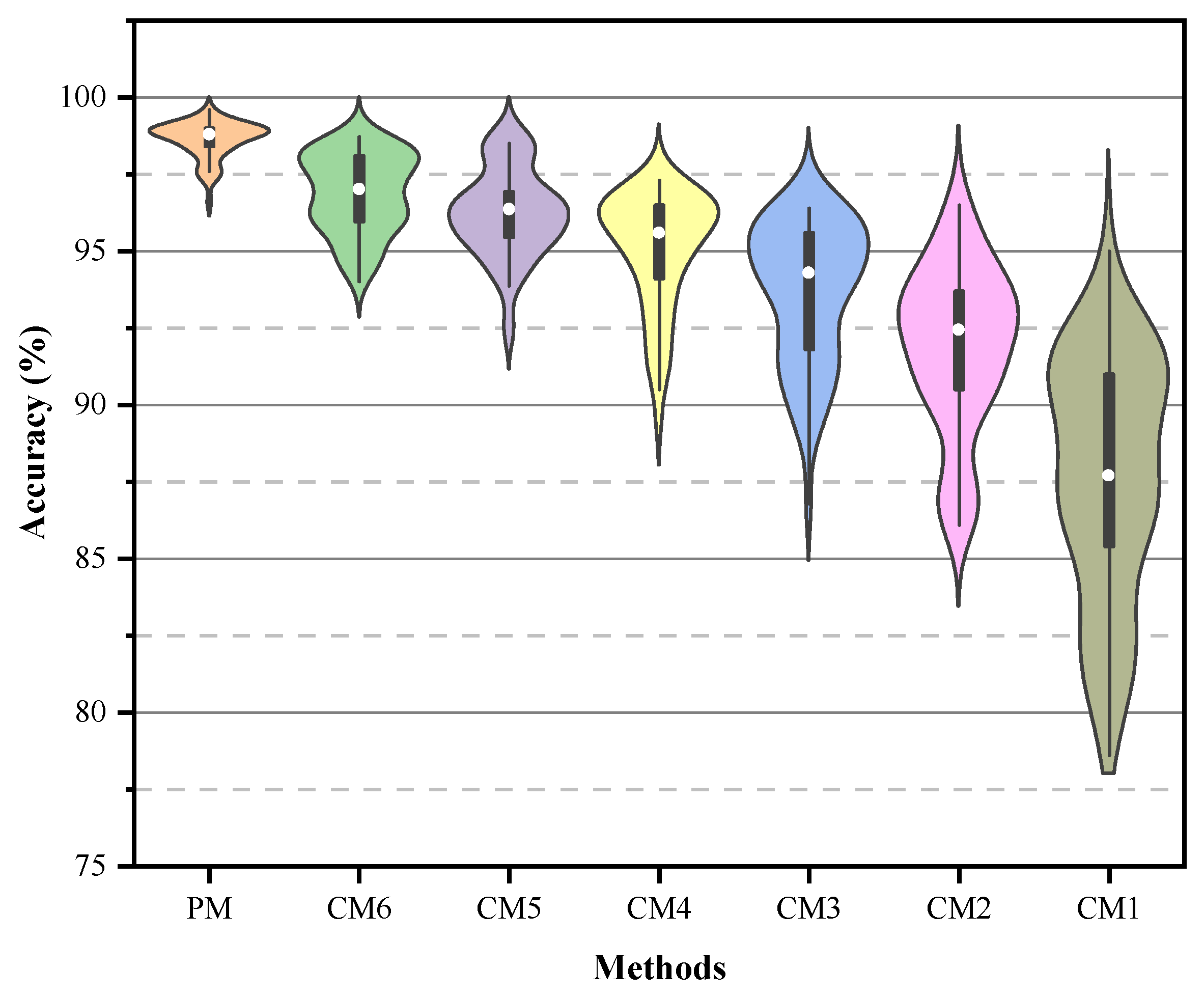
4.3.3. Experimental Results of Experiment B
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, J.; Wu, W.; Huang, X.; Yin, Q.; Yang, K.; Li, S. A modified active learning intelligent fault diagnosis method for rolling bearings with unbalanced samples. Adv. Eng. Inform. 2024, 60, 102397. [Google Scholar] [CrossRef]
- Xu, X.; Ou, X.; Ge, L.; Qiao, Z.; Shi, P. Simulated Data-Assisted Fault Diagnosis Framework with Dual-Path Feature Fusion for Rolling Element Bearings under Incomplete Data. IEEE Trans. Instrum. Meas. 2025, 74, 3542617. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Z.; Liu, Z.; Han, B.; Bao, H.; Ji, S. Digital twin aided adversarial transfer learning method for domain adaptation fault diagnosis. Reliab. Eng. Syst. Saf. 2023, 234, 109152. [Google Scholar] [CrossRef]
- Xu, X.; Yang, X.; He, C.; Shi, P.; Hua, C. Adversarial Domain Adaptation Model Based on LDTW for Extreme Partial Transfer Fault Diagnosis of Rotating Machines. IEEE Trans. Instrum. Meas. 2024, 73, 3538811. [Google Scholar] [CrossRef]
- Jiang, X.; Song, Q.; Wang, H.; Du, G.; Guo, J.; Shen, C.; Zhu, Z. Central frequency mode decomposition and its applications to the fault diagnosis of rotating machines. Mech. Mach. Theory 2022, 174, 104919. [Google Scholar] [CrossRef]
- Almutairi, K.; Sinha, J. A Comprehensive 3-Steps Methodology for Vibration-Based Fault Detection, Diagnosis and Localization in Rotating Machines. J. Dyn. Monit. Diagn. 2024, 3, 49–58. [Google Scholar] [CrossRef]
- Lu, J.; Qian, W.; Li, S.; Cui, R. Enhanced K-Nearest Neighbor for Intelligent Fault Diagnosis of Rotating Machinery. Appl. Sci. 2021, 11, 919. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, J.; Shen, C.; Shi, J.; Huang, W.; Zhu, Z.; Wang, Q. An adaptive and efficient variational mode decomposition and its application for bearing fault diagnosis. Struct. Health Monit. 2021, 20, 2708–2725. [Google Scholar] [CrossRef]
- Wu, Y.; Song, J.; Wu, X.; Wang, X.; Lu, S. Fault Diagnosis of Linear Guide Rails Based on SSTG Combined with CA-DenseNet. J. Dyn. Monit. Diagn. 2024, 3, 1–10. [Google Scholar] [CrossRef]
- Shao, H.; Lai, Y.; Liu, H.; Wang, J.; Liu, B. LSFConvformer: A lightweight method for mechanical fault diagnosis under small samples and variable speeds with time-frequency fusion. Mech. Syst. Signal Process. 2025, 236, 113016. [Google Scholar] [CrossRef]
- Huang, T.; Zhang, Q.; Tang, X.; Zhao, S.; Lu, X. A novel fault diagnosis method based on CNN and LSTM and its application in fault diagnosis for complex systems. Artif. Intell. Rev. 2022, 55, 1289–1315. [Google Scholar] [CrossRef]
- Jiang, X.; Li, X.; Wang, Q.; Song, Q.; Liu, J.; Zhu, Z. Multi-sensor data fusion-enabled semi-supervised optimal temperature-guided PCL framework for machinery fault diagnosis. Inf. Fusion 2024, 101, 102005. [Google Scholar] [CrossRef]
- Chen, Z.; Gryllias, K.; Li, W. Mechanical fault diagnosis using Convolutional Neural Networks and Extreme Learning Machine. Mech. Syst. Signal Process. 2019, 133, 106272. [Google Scholar] [CrossRef]
- Hu, Z.; Han, T.; Bian, J.; Wang, Z.; Cheng, L.; Zhang, W.; Kong, X. A deep feature extraction approach for bearing fault diagnosis based on multi-scale convolutional autoencoder and generative adversarial networks. Meas. Sci. Technol. 2022, 33, 065013. [Google Scholar] [CrossRef]
- Li, X.; Xiao, S.; Zhang, F.; Huang, J.; Xie, Z.; Kong, X. A fault diagnosis method with AT-ICNN based on a hybrid attention mechanism and improved convolutional layers. Appl. Acoust. 2024, 225, 110191. [Google Scholar] [CrossRef]
- Wu, Z.; Jiang, H.; Zhu, H.; Wang, X. A knowledge dynamic matching unit-guided multi-source domain adaptation network with attention mechanism for rolling bearing fault diagnosis. Mech. Syst. Signal Process. 2023, 189, 110098. [Google Scholar] [CrossRef]
- Qian, Q.; Qin, Y.; Luo, J.; Wang, Y.; Wu, F. Deep discriminative transfer learning network for cross-machine fault diagnosis. Mech. Syst. Signal Process. 2023, 186, 109884. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, S.; Zhang, T.; Zhang, H.; Miao, Z. Subdomain adaptation capsule network for unsupervised mechanical fault diagnosis. Inf. Sci. 2022, 611, 301–316. [Google Scholar] [CrossRef]
- Li, J.; Chen, X.; He, Z. Multi-stable stochastic resonance and its application research on mechanical fault diagnosis. J. Sound Vib. 2013, 332, 5999–6015. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, Y.; Zhang, H.; Feng, K.; Wang, Y.; Yang, C.; Ni, Q. Global contextual feature aggregation networks with multiscale attention mechanism for mechanical fault diagnosis under non-stationary conditions. Mech. Syst. Signal Process. 2023, 203, 110724. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Bao, H.; Kong, L.; Lu, L.; Wang, J.; Zhang, Z.; Han, B. A new multi-layer adaptation cross-domain model for bearing fault diagnosis under different operating conditions. Meas. Sci. Technol. 2024, 35, 106116. [Google Scholar] [CrossRef]
- Xing, S.; Wang, J.; Han, B.; Zhang, Z.; Jiang, X.; Ma, H.; Zhang, X.; Shao, H. Dual-domain Signal Fusion Adversarial Network Based Vision Transformer for Cross-domain Fault Diagnosis. In Proceedings of the 2023 Global Reliability and Prognostics and Health Management Conference (PHM-Hangzhou), Hangzhou, China, 12–15 October 2023; IEEE: New York, NY, USA; pp. 1–5. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision 2021, Montreal, QC, Canada, 10–17 October 2021; pp. 9992–10002. [Google Scholar]
- Chen, J.; Kao, S.-H.; He, H.; Zhuo, W.; Wen, S.; Lee, C.-H.; Chan, S.-H.G. Run, don’t walk: Chasing higher FLOPS for faster neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition 2023, Vancouver, BC, Canada, 17–24 June 2023; pp. 12021–12031. [Google Scholar]
- Li, X.; Yu, T.; Wang, X.; Li, D.; Xie, Z.; Kong, X. Fusing joint distribution and adversarial networks: A new transfer learning method for intelligent fault diagnosis. Appl. Acoust. 2024, 216, 109767. [Google Scholar] [CrossRef]
- Zheng, B.; Huang, J.; Ma, X.; Zhang, X.; Zhang, Q. An unsupervised transfer learning method based on SOCNN and FBNN and its application on bearing fault diagnosis. Mech. Syst. Signal Process. 2024, 208, 111047. [Google Scholar] [CrossRef]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]

| Item | Setting/Description |
|---|---|
| Transformer Encoder Layers | 6 |
| Attention Heads per Layer | 4 |
| Input Feature Dimension | D = 1024 (concatenated time–frequency representation) |
| Multi-scale Segmentation | Scales: , segment lengths |
| Fusion Weighting | Energy-based normalization across time and frequency domains |
| Residual Attention | Layer normalization + residual connections + permutation-invariant aggregation |
| Hybrid Domain Distance | Wasserstein + MMD with self-adaptive weighting factor |
| Optimizer | Adam |
| Learning rate | 0.001 (cosine decay schedule) |
| Batch size | 64 |
| Weight decay | 5 × 10−4 |
| Source/Target sampling ratio | 1:1 |
| Number of epochs | 1000 |
| Early stopping | Validation loss not improving for 10 consecutive epochs |
| Hardware | NVIDIA RTX 4060 GPU, Pycharm 1.6 |
| Transfer Task | Source Domain | Target Domain |
|---|---|---|
| Fluctuation Speed (rpm) | Fluctuation Speed (rpm) | |
| A1 | 1000~1500 | 1500~1800 |
| A2 | 1000~1500 | 1800~2000 |
| A3 | 1500~1800 | 1000~1500 |
| A4 | 1500~1800 | 1800~2000 |
| A5 | 1800~2000 | 1000~1500 |
| A6 | 1800~2000 | 1500~1800 |
| Accuracy | CM1 | CM2 | CM3 | CM4 | CM5 | CM6 | PM |
|---|---|---|---|---|---|---|---|
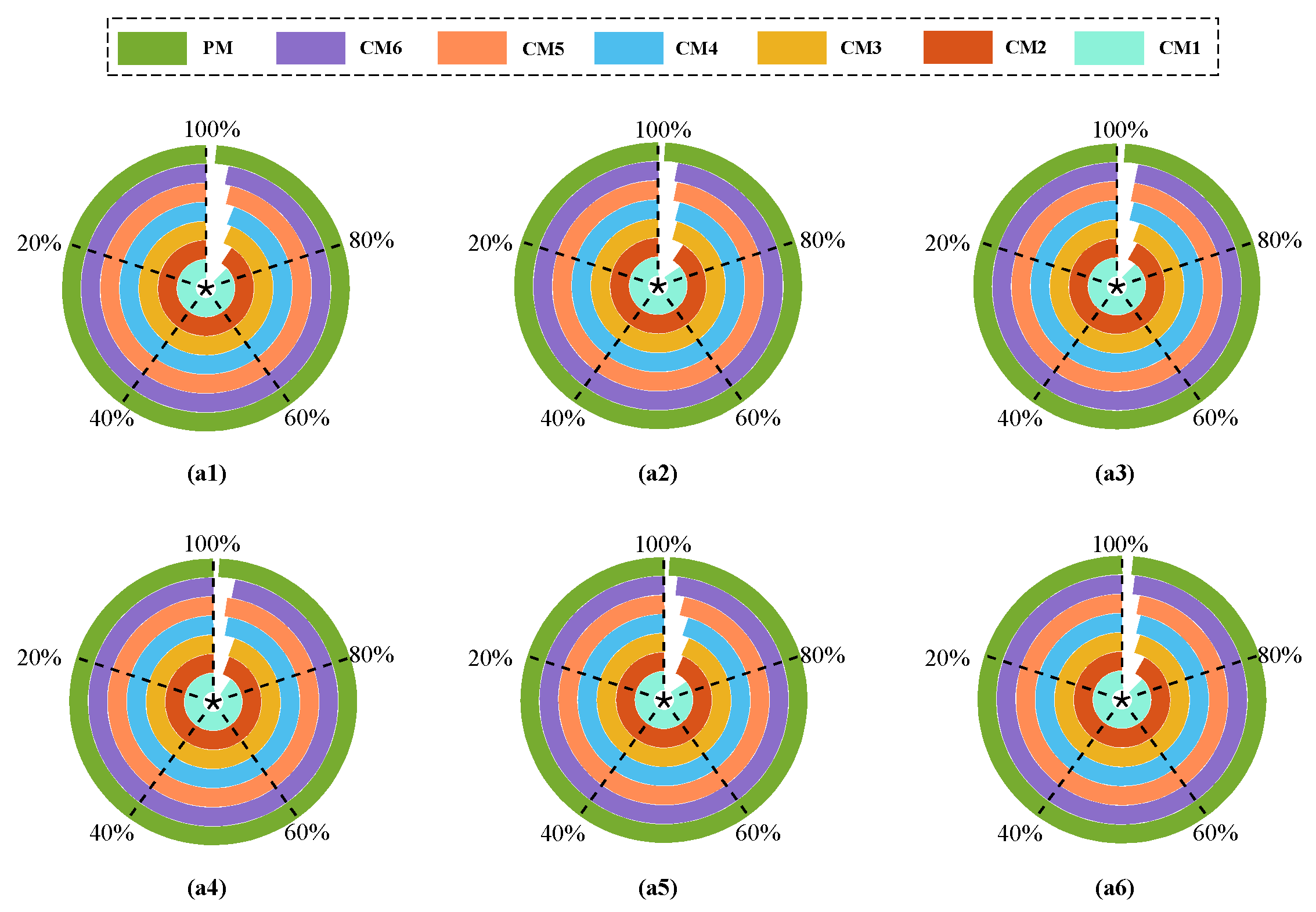
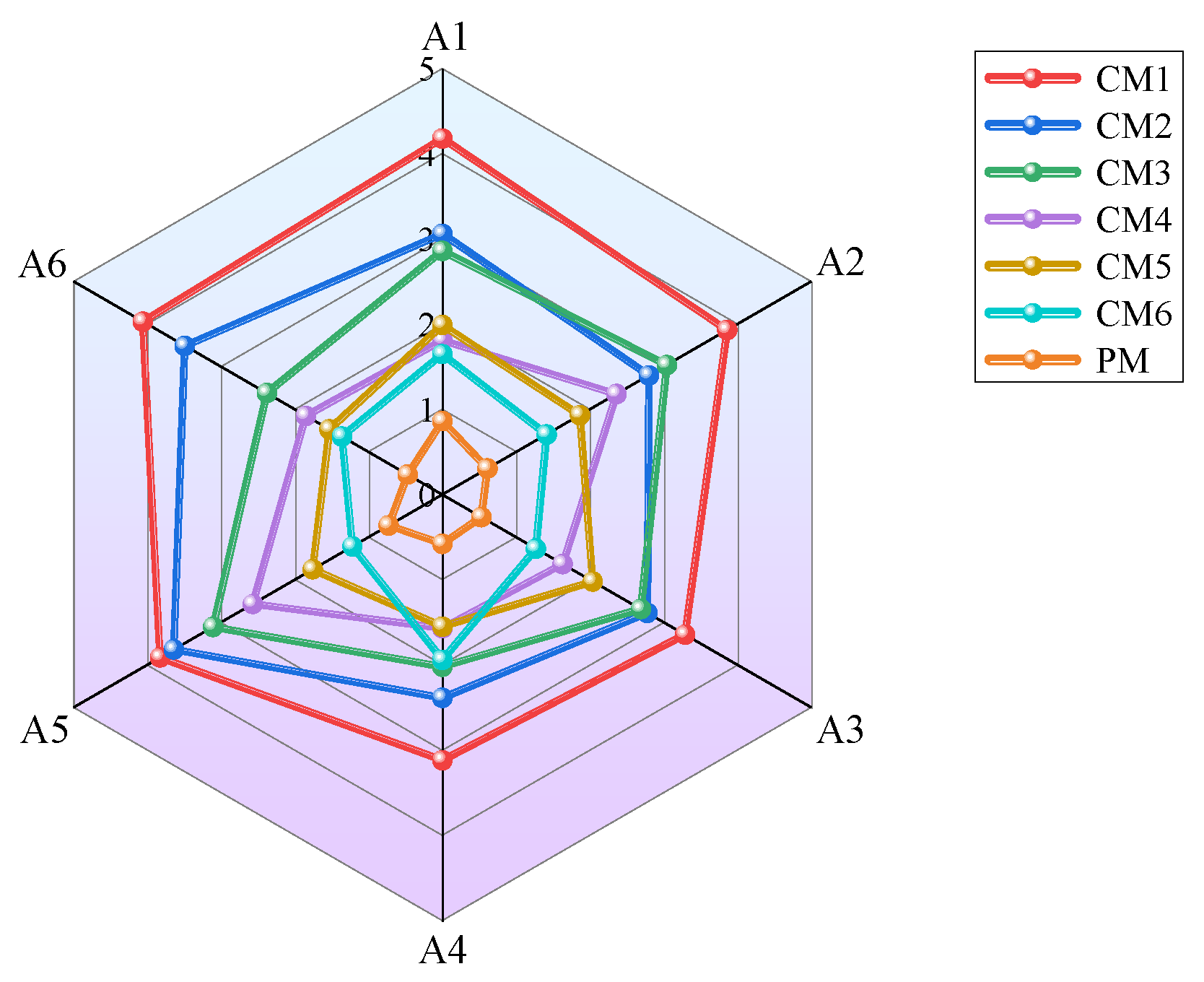
| A1 | 86.72 ± 4.18 | 90.92 ± 3.06 | 93.82 ± 2.86 | 94.72 ± 1.81 | 96.20 ± 1.97 | 97.05 ± 1.65 | 98.80 ± 0.86 |
| A2 | 87.17 ± 3.86 | 91.34 ± 2.80 | 95.30 ± 3.04 | 95.93 ± 2.36 | 97.11 ± 1.86 | 97.48 ± 1.41 | 99.21 ± 0.61 |
| A3 | 89.41 ± 3.29 | 93.15 ± 2.78 | 94.38 ± 2.69 | 96.80 ± 1.63 | 97.34 ± 2.04 | 97.22 ± 1.27 | 99.07 ± 0.53 |
| A4 | 88.94 ± 3.12 | 94.38 ± 2.39 | 94.80 ± 2.02 | 97.16 ± 1.87 | 97.85 ± 1.95 | 97.16 ± 1.94 | 99.28 ± 0.58 |
| A5 | 86.45 ± 3.83 | 93.26 ± 3.64 | 93.89 ± 3.11 | 95.42 ± 2.57 | 96.95 ± 1.76 | 98.21 ± 1.22 | 99.34 ± 0.73 |
| A6 | 87.36 ± 4.06 | 92.16 ± 3.49 | 95.64 ± 2.38 | 96.51 ± 1.85 | 97.25 ± 1.53 | 98.35 ± 1.36 | 98.75 ± 0.47 |
| Metric | PM Value (Approx.) | Interpretation |
|---|---|---|
| Parameter count | ≈9–11 M | Far smaller than ViT-Base (≈86 M), enabling lightweight deployment |
| FLOPs | ≈1.7–2.3 GFLOPs | Reduced computation due to 6-layer × 4-head design |
| Training time per epoch | ≈15–25 s (RTX 4060) | Faster convergence with moderate hardware |
| Inference latency | ≈3–5 ms/sample | Meets real-time industrial monitoring requirements |
| Peak memory usage | ≈2–2.5 GB | Suitable for mid-range GPUs and edge devices |
| Transfer Task | Source Domain | Target Domain |
|---|---|---|
| Fluctuation Load (N) | Fluctuation Load (N) | |
| B1 | 0~0.2 A | 0~0.35 A |
| B2 | 0~0.2 A | 0~0.5 A |
| B3 | 0~0.35 A | 0~0.2 A |
| B4 | 0~0.35 A | 0~0.5 A |
| B5 | 0~0.5 A | 0~0.2 A |
| B6 | 0~0.5 A | 0~0.35 A |
| Accuracy | CM1 | CM2 | CM3 | CM4 | CM5 | CM6 | PM |
|---|---|---|---|---|---|---|---|
| B1 | 87.41 ± 4.53 | 93.96 ± 3.83 | 96.60 ± 1.85 | 97.82 ± 1.81 | 96.12 ± 2.05 | 97.38 ± 1.75 | 99.19 ± 0.50 |
| B2 | 87.35 ± 4.28 | 92.97 ± 3.72 | 95.07 ± 2.75 | 95.93 ± 2.18 | 97.05 ± 1.89 | 97.62 ± 1.33 | 98.80 ± 0.71 |
| B3 | 90.60 ± 3.84 | 93.95 ± 2.98 | 96.89 ± 2.09 | 97.36 ± 1.55 | 97.22 ± 2.10 | 98.05 ± 1.57 | 99.40 ± 0.38 |
| B4 | 89.72 ± 3.64 | 94.46 ± 3.11 | 96.75 ± 1.65 | 96.97 ± 1.89 | 97.75 ± 1.92 | 98.19 ± 1.41 | 98.93 ± 0.47 |
| B5 | 87.76 ± 4.66 | 93.11 ± 3.47 | 94.80 ± 2.06 | 95.48 ± 2.53 | 96.85 ± 1.78 | 97.24 ± 1.82 | 99.16 ± 0.69 |
| B6 | 87.14 ± 3.47 | 95.17 ± 2.76 | 96.51 ± 2.14 | 97.72 ± 1.67 | 97.18 ± 1.60 | 97.46 ± 1.08 | 99.14 ± 0.55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, Y.; Zhang, D.; Zhang, M.; Xin, M.; Wang, Z.; Ding, D.; Huang, F.; Wang, J. Residual Attention-Driven Dual-Domain Vision Transformer for Mechanical Fault Diagnosis. Machines 2025, 13, 1096. https://doi.org/10.3390/machines13121096
An Y, Zhang D, Zhang M, Xin M, Wang Z, Ding D, Huang F, Wang J. Residual Attention-Driven Dual-Domain Vision Transformer for Mechanical Fault Diagnosis. Machines. 2025; 13(12):1096. https://doi.org/10.3390/machines13121096
Chicago/Turabian StyleAn, Yuxi, Dongyue Zhang, Ming Zhang, Mingbo Xin, Zhesheng Wang, Daoshan Ding, Fucan Huang, and Jinrui Wang. 2025. "Residual Attention-Driven Dual-Domain Vision Transformer for Mechanical Fault Diagnosis" Machines 13, no. 12: 1096. https://doi.org/10.3390/machines13121096
APA StyleAn, Y., Zhang, D., Zhang, M., Xin, M., Wang, Z., Ding, D., Huang, F., & Wang, J. (2025). Residual Attention-Driven Dual-Domain Vision Transformer for Mechanical Fault Diagnosis. Machines, 13(12), 1096. https://doi.org/10.3390/machines13121096






