Abstract
To mitigate the inadequate performance of traditional hydraulic systems, mechanical feedback-based digital hydraulic technology is applied to a 3-degree-of-freedom (3-DOF) crane. Digital hydraulic cylinders drive the pitch mechanism, and digital hydraulic motors power the rotary and winch mechanisms. By analyzing the working principles of digital hydraulic cylinders and motors, transfer functions of the 3-DOF actuators are derived. AMESim simulation models are established for each actuator, with model validity verified. Based on these models, simulation analysis of the digital hydraulic system is performed to examine key influencing factors: motor speed, motor subdivision, system flow rate, digital valve opening, and throttle groove shape. System characteristics are obtained, and corresponding optimization schemes are proposed. After optimization, the comprehensive performance of the digital hydraulic system is improved by 1.29%. This study provides theoretical support for the engineering application of digital hydraulic systems in cranes, clarifies their operational specifications and optimization pathways, and exhibits substantial engineering application value.
1. Introduction
In the construction machinery field, intelligent and high-precision control has emerged as a core industrial development trend. As key equipment for material handling and engineering construction, 3-degree-of-freedom (3-DOF) cranes are extensively applied in ports, construction, and logistics. Their operational performance directly impacts engineering project efficiency and safety [1]. In controlling critical 3-DOF crane movements—pitch, rotary, and winch—traditional hydraulic systems have increasingly revealed limitations including inadequate control precision, response lag, and high system complexity. During precision winch operations, traditional systems fail to achieve precise positioning of lifting height and rotary angle, resulting in significant load swing and elevated operational risks. Under complex operating conditions, the response delay of pitch movements impairs crane operational efficiency and stability [2].
As a cutting-edge hydraulic technology, the mechanical feedback-based digital hydraulic system directly maps electrical pulse signals to actuator displacement and speed via unique mechanical-hydraulic closed-loop servo technology, enabling digital control of hydraulic systems. This technology eliminates complex sensor and algorithm debugging, simplifies system structure, reduces costs, and substantially enhances control precision and response speed. Research on the integration of this technology into 3-DOF cranes carries considerable engineering significance, as it helps break through technical bottlenecks of traditional hydraulic systems in crane control and meets the demands for precise control in high-end equipment manufacturing [3].
Existing studies have laid a foundation for digital hydraulic technology and crane hydraulic control. Abdel-Rahman, E. M. et al. [4] reviewed existing crane models in the literature, classified them, discussed their dynamic characteristics, and presented a comprehensive review. Linjama, M. et al. [5] developed a position tracking control system using a series of parallel on/off valves, adopting pulse code modulation for gradual flow control. Results indicate that allowing three or four valve series to open simultaneously—instead of employing classical inflow–outflow control—improves controllability, particularly at low speeds. Liu, Z. H. et al. [6] investigated the precise position control of high-speed on–off valve-controlled hydraulic cylinders, proposing a composite algorithm combining speed feedforward (to address hysteresis) and displacement feedback PI control (to correct position errors); genetic algorithm-optimized parameters further enhanced position accuracy. Drumea, P. et al. [7] elaborated on the principle and operating mode of digital hydraulic motors, while Pedersen, N. et al. [8] proposed the digital direct hydraulic cylinder drive (D-DHCD) concept and its feedback control strategy based on discrete dynamics approximation. Jia, Y. et al. [9] utilized a dual closed-loop control digital hydraulic cylinder to achieve digital motion control, and Pavel, I. et al. [10] noted that digital hydraulics serve as a novel alternative to traditional hydraulic systems. Zhang, Q. et al. [11] provided a precise definition of digital hydraulic technology, analyzed its research status and development history, and predicted future trends. Zhang, H. et al. [12] introduced a digital radial hydraulic motor for heavy-duty vehicle traction, developing a detailed component-level model and feasible application solutions.
Although previous researchers have conducted extensive studies on digital hydraulic components and traditional crane hydraulic systems, existing research exhibits notable limitations. Research on digital hydraulic cylinders and motors primarily focuses on the performance optimization of the components themselves, without integrating with the coordinated operational characteristics of 3-DOF cranes. Studies on crane hydraulic systems mainly target structural modifications to traditional valve-controlled schemes, and no integrated solution has been formed for digital hydraulic components and the overall dynamic control of cranes—hindering the full exploitation of digital technology’s advantages in anti-interference and high-precision control.
To address these gaps, this study innovatively integrates digital hydraulic cylinder and motor technologies into a 3-DOF crane, constructing a full-digital hydraulic drive system. Through deriving the transfer functions of the actuators and establishing AMESim simulation models, the influences of motor speed, flow rate, and valve port parameters on system characteristics are systematically analyzed, and performance optimization strategies are proposed. The research results are anticipated to overcome the technical bottlenecks of traditional hydraulic systems in crane precision control and dynamic response, provide theoretical support and technical reference for the intelligent upgrading of construction machinery, and possess considerable academic value and engineering application significance.
2. Principle of the Digital Hydraulic System for Cranes
As a key equipment for precise material transfer in industrial settings, the 3-degree-of-freedom (3-DOF) crane relies on actuators as core components to execute various operational actions. These actuators mainly comprise three core mechanisms: the pitch mechanism, rotary mechanism, and winch mechanism [13]. The three mechanisms operate collaboratively and synergistically, collectively determining the crane’s operational range, motion flexibility, and positioning precision, while laying the foundation for efficient three-dimensional material transfer. In the physical diagram of the 3-DOF crane (Figure 1), the spatial layout of these mechanisms is clearly illustrated: the rotary mechanism is situated at the crane’s bottom base, serving as the support for overall rotational movement; the pitch mechanism connects to the upper part of the rotary mechanism, enabling boom angle adjustment via its hinge point with the boom; and the winch mechanism is integrated into the boom’s main structure.
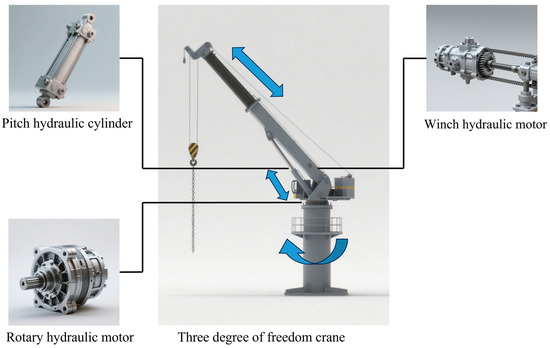
Figure 1.
Image of a three-degree-of-freedom crane.
The pitch mechanism mainly comprises a digital hydraulic cylinder, boom hinges, and limit devices. Its function is to adjust the vertical height of the lifting tackle by changing the boom’s pitch angle (i.e., the angle between the boom and the horizontal plane). When the pitch mechanism drives the boom upward, the lifting tackle’s height increases to facilitate high-position material hoisting; when the boom lowers, the tackle’s height decreases to enable material lowering or short-range picking. This mechanism directly determines the crane’s vertical operational range and is closely associated with hoisting stability. A reasonable pitch angle can effectively reduce sway of the lifting tackle and materials, enhancing operational safety.
The rotary mechanism typically consists of a digital hydraulic motor, a drive motor, and a reduction gear. Its core function is to drive the crane’s boom and lifting tackle to rotate 360° around the vertical axis. Rotational movement allows the crane to adjust the tackle’s horizontal orientation, covering an annular operational area centered on the rotation axis. This function is particularly critical for material loading/unloading in different directions. For instance, at ports and terminals, the rotary mechanism can transfer goods from ship cabins to shore transport vehicles; in workshops, it can move raw materials from storage areas to processing equipment.
As the core executive unit for vertical heavy-load lifting, the winch mechanism’s key drive components usually include a digital hydraulic motor connected in series with a high-reduction-ratio reducer. The digital hydraulic motor efficiently converts hydraulic energy from the hydraulic system into rotational mechanical energy, while the reducer fulfills torque conversion. Through internal multi-stage gear transmission, it significantly reduces the hydraulic motor’s output speed and proportionally increases output torque to meet heavy-load-lifting requirements. The reducer’s final output shaft directly drives the wire rope-carrying drum via rigid coupling, splines, or similar structures. The wire rope is tightly wound in layers within the drum’s rope grooves, with one end firmly anchored to the drum or frame and the other extended through a pulley block (composed of fixed and movable pulleys) to connect to the hook. When the drum rotates clockwise or counterclockwise under the reducer’s drive, the wire rope winds or unwinds accordingly. This winding/unwinding motion is amplified by the pulley block ratio, ultimately achieving precise, controllable vertical ascent or descent of the hook and its load. Thus, the winch mechanism directly determines the crane’s lifting capacity and serves as an indispensable core power transmission component for material vertical displacement.
In engineering applications, load characteristics and control precision requirements are core considerations for drive system selection. For the pitch mechanism, actual operation involves long-term bearing of large gravitational loads, frequent load fluctuations under complex working conditions, and significant impacts of large load inertia on motion stability—all while requiring high-precision control that poses severe challenges to the drive system. After comprehensive evaluation of technical characteristics and performance indicators of various drive schemes, a digital hydraulic cylinder is selected as the pitch mechanism’s drive device [14]. Its high precision, fast response, and strong load-bearing capacity effectively meet the mechanism’s operational requirements under complex conditions. The rotary and winch mechanisms also face significant load inertia issues during operation, which affect motion stability and accuracy. Coupled with strict control precision requirements in practical working conditions, drive system selection must be prudent [15]. Based on comprehensive evaluation of various drive components, both mechanisms adopt digital hydraulic motors as power sources [16]. These motors offer excellent dynamic performance and precise control characteristics, effectively suppressing adverse effects from load inertia. Additionally, to further improve transmission efficiency and control precision, the digital hydraulic motors are driven via reducers.
Figure 2 is a flowchart of the working principle of digital hydraulic components.
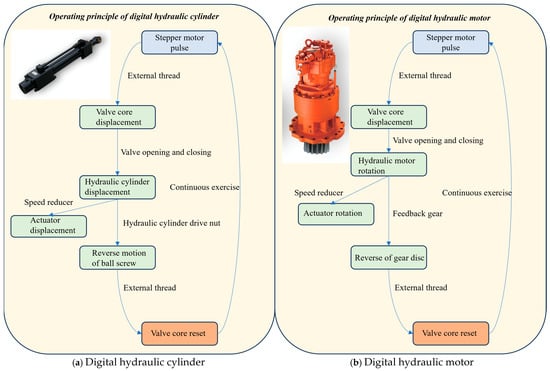
Figure 2.
Operating principle flow charts of digital hydraulic components.
Figure 3 presents the schematic of the digital hydraulic cylinder, with its working principle described as follows: Upon receiving a pulse signal, the stepper motor outputs a specific angular velocity or angular displacement following a defined law. This motion is transmitted to the external thread via the splines and the four-way valve spool. The external thread interfaces with the outer cylinder rotating shaft and outer cylinder rotating disk—where the outer cylinder rotating shaft is fixed in position, enabling rotation but no axial movement. Under the rotation of the external thread, the spool generates axial displacement, prompting the valve port to open and allowing hydraulic oil to be injected into the hydraulic cylinder through the four-way valve. During spool movement, the hydraulic cylinder moves synchronously in the same direction under hydraulic pressure, driving the lead screw nut fixed to the piston to translate rightward. At this point, the ball screw rotates proportionally, with a rotation direction opposite to that of the stepper motor. This further drives the inner cylinder rotating disk to rotate, causing the external thread to move in the opposite direction of the spool and ultimately achieving valve port closure [17].
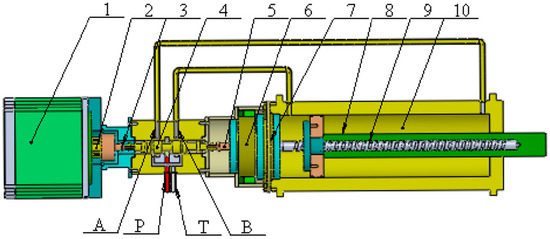
Figure 3.
Schematic diagram of a digital hydraulic cylinder. 1—Stepper motor; 2—Spline; 3—Universal joint; 4—Valve core; 5—Shaft with external thread; 6—Cylinder external shaft with internal thread; 7—End cap; 8—Hollow piston rod: 9—Lead screw; 10—Hydraulic cylinder; P—oil inlet; T—oil return port; A, B—working oil ports.
Figure 4 illustrates the schematic of the digital hydraulic motor, with its working principle described as follows: The stepper motor drives the digital valve spool to rotate within the nut sleeve. Via the thread pair inside the nut sleeve, rotational motion is converted into axial displacement of the spool, enabling valve port opening. Pressurized hydraulic oil from the system enters the hydraulic motor through the digital valve’s port P, driving the motor to rotate. The hydraulic motor outputs torque through the reducer, which drives the rotary gear disk to rotate and thereby achieves rotational movement of the actuator. The feedback gear meshed with the rotary gear disk converts the rotational angle into real-time axial displacement of the spool via the nut sleeve. This displacement direction is opposite to that generated by the stepper motor-driven spool, causing the valve port opening to gradually decrease until closure [18].
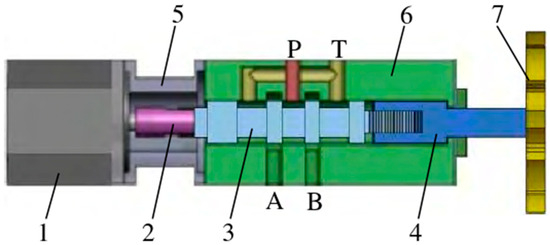
Figure 4.
Schematic diagram of a digital hydraulic motor. 1—Stepper motor; 2—Coupling; 3—Valve core; 4—Nut sleeve; 5—Connecting sleeve; 6—Valve body; 7—Feedback gear; P—oil inlet; T—oil return port; A, B—working oil ports.
3. Mathematical Modeling
Compared with traditional valve-controlled cylinder and valve-controlled motor hydraulic systems, digital hydraulic cylinders and motors differ in structure and control logic. The actuators of these digital components form a unique feedback mechanism with the valve spool. This closed-loop design significantly enhances the system’s response speed and control precision while reducing control deviations induced by factors such as changes in hydraulic oil properties and pipeline pressure loss. Leveraging these characteristics, this study completes the derivation of transfer functions for the 3-DOF actuators. To avoid redundant content, only the key derivation steps of the transfer functions are presented herein [19].
3.1. Pitch Mechanism
After Laplace transformation, the flow continuity equation of the hydraulic cylinder is expressed as Equation (1).
Among them, the total leakage coefficient is expressed as Equation (2).
After Laplace transformation, the force balance equation of the hydraulic cylinder and load is expressed as Equation (3).
It can be seen from the engineering drawing of the digital hydraulic cylinder that a mechanical feedback is composed of a ball screw and a nut inside the cylinder, and the calculation formula of the ball screw is expressed as Equation (4).
It can be known from the mechanism of the valve-controlled cylinder that the displacement of the valve spool is jointly determined by the rotation angle of the stepper motor and the rotation angle of the feedback nut, and Equation (5) can be derived from the ball screw formula.
By combining Equations (1), (3), (4) and (5), the system transfer function of the pitch mechanism can be obtained as Equation (6).
3.2. Rotary Mechanism
The derivation process of the valve-controlled motor’s transfer function is analogous to that of the valve-controlled cylinder. The primary difference lies in the use of distinct actuators, leading to minor variations in their transfer functions. The spool displacement is jointly determined by the stepper motor’s rotation angle and the feedback nut’s rotation angle, as shown in Equation (5). The derived motor rotation angle is expressed in Equation (7).
Since Gear 1 is connected to the connecting shaft of the motor, the rotation angle of Gear 1 is expressed as Equation (8).
Gear 1 and Gear 2 mesh with each other. When Gear 1 rotates, the rotation angle of Gear 2 is expressed as Equation (9).
Gear 2 is connected to a reducer, which has an internal gear ratio. After deceleration, the rotation angle is expressed as Equation (10).
By combining Equations (5), (7) and (10), the system transfer function of the rotary mechanism is obtained as Equation (11).
3.3. Winch Mechanism
Both the winch mechanism and rotary mechanism are driven by digital hydraulic motors, with the sole difference being the gear ratio of their respective reducers. Referring to the derivation process in Section 3.2, the transfer function of the winch mechanism is obtained as Equation (12).
3.4. Simulink Results
With the stepper driver set to 1000 micro-steps, a single input pulse signal rotates the stepper motor by 0.0063 radians. Simulation via the transfer function block in Simulink yields the output of the 3-DOF actuator, as presented in Figure 5 [20].
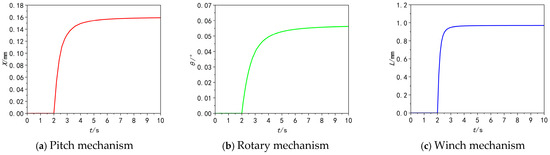
Figure 5.
Output graph of the transfer function of the three-degree-of-freedom actuator.
As illustrated in Figure 5, a single input pulse signal results in a piston displacement of approximately 0.16 mm for the digital hydraulic cylinder in the pitch mechanism, an output angle of about 0.000995 radians (converted from 0.057°) for the rotary mechanism, and an output length of roughly 0.97 mm for the winch mechanism.
4. Simulation of Digital Hydraulic Components
4.1. AMESim Models of Digital Hydraulic Components
Based on the working principles and mathematical models, AMESim models of the digital hydraulic components are established [21]. Figure 6 illustrates the AMESim component models for the pitch, rotary, and winch mechanisms, and Table 1 presents the corresponding component model parameters.
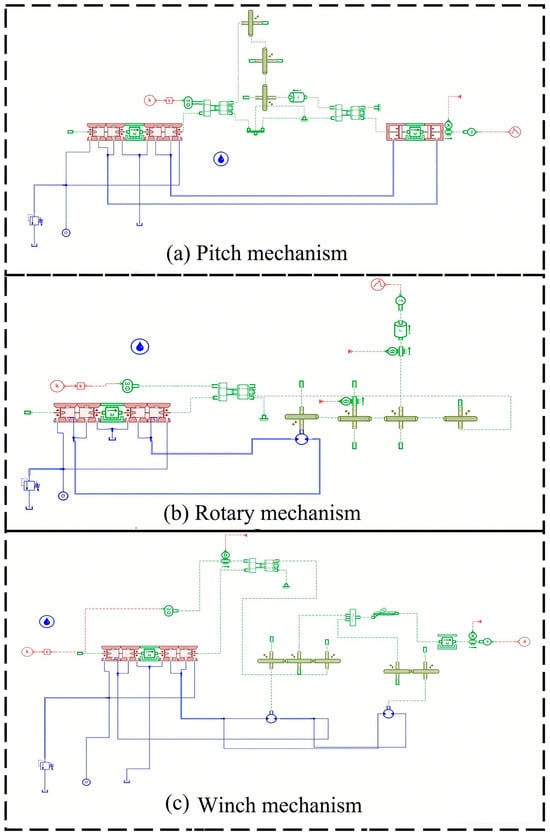
Figure 6.
Three-degree-of-freedom actuator AMESim model diagram.

Table 1.
Parameters of the AMESim model for a three-degree-of-freedom actuator.
4.2. Component Simulation
Model parameters are set according to Table 1, the minimum and maximum motor speeds are set separately based on Table 2, and the simulation step size is set to 0.001 s [22].

Table 2.
Minimum and maximum speeds of stepper motors for three-degree-of-freedom actuators.
When the motor is input with a minimum speed of 0.06 r/min, the output speeds of the 3-DOF actuator are as shown in Figure 7.
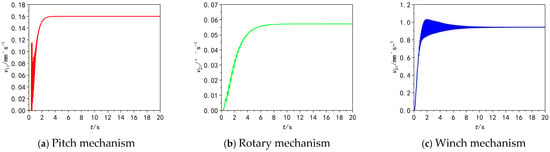
Figure 7.
Speed diagram of the three-degree-of-freedom actuator at the minimum speed of the stepper motor.
In Figure 7, v1l, v2l, v3l represent the speed characteristics of the 3-DOF actuator when the stepper motor speed is 0.06 r/min. At the stable stage, the piston displacement speed of the digital hydraulic cylinder is approximately 0.159 mm/s, the rotational speed of the rotary mechanism is about 0.057°/s, and the speed of the winch mechanism is roughly 0.94 mm/s. These results are basically consistent with the Simulink simulation results presented in Figure 5, confirming the correct establishment of the AMESim models for the digital hydraulic components.
When the motor is input with the maximum speed, the output speeds of the 3-DOF actuator are shown in Figure 8. In Figure 8, v1h, v2h, v3h, respectively, denote the maximum operating speeds of the three-degree-of-freedom actuator.
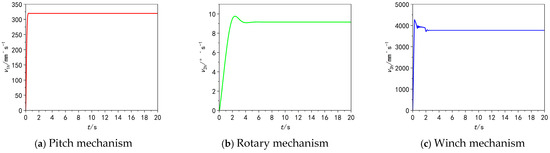
Figure 8.
Speed diagram of the three-degree-of-freedom actuator at the maximum speed of the stepper motor.
5. Simulation of the Digital Hydraulic System
5.1. AMESim Model of the Digital Hydraulic System
The pump station system in this study comprises two tandem pumps, with this structural design enabling efficient power supply distribution and precise regulation [23]. Specifically, the large pump in the tandem pump—characterized by high displacement—primarily supplies high-pressure hydraulic oil to the main system, providing strong driving force for actuator movement. The small pump fulfills a key oil makeup function: it continuously monitors system pressure and flow rate changes during actuator operation. When pressure fluctuations or flow losses occur, it promptly supplements hydraulic oil to ensure stable system operation.
At the actuator level, the hydraulic circuit designs of the pitch, rotary, and winch systems exhibit high consistency and standardization. Each system takes digital hydraulic components as core parts, fully leveraging their high-precision and high-responsiveness performance advantages. They cooperate with 2/4-way directional control valves to achieve precise control of the pilot-operated check valves on the four ports (P, T, A, B) of the digital valve [24]. The specific working principle is as follows: when the 2/4-way directional control valve is energized, electromagnetic force drives the spool to move, allowing hydraulic oil decompressed by the pressure reducing valve to flow smoothly into the pilot-operated check valve. At this point, the pilot-operated check valve opens under hydraulic pressure, forming an unobstructed oil passage to ensure normal oil inflow and outflow along the predetermined path, thereby driving the actuator to complete the corresponding action. When the 2/4-way directional control valve is de-energized, the spool resets, cutting off the hydraulic oil path to the pilot-operated check valve. The pilot-operated check valve closes its port via its own spring force, blocking oil flow and realizing actuator position locking and system pressure holding.
The AMESim model of the digital hydraulic system is illustrated in Figure 9, comprising four subsystems: the pump station system, pitch system, rotary system, and winch system.
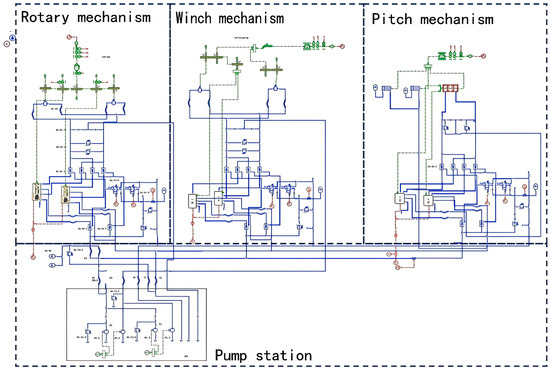
Figure 9.
Three-degree-of-freedom offshore platform digital hydraulic system AMESim model.
To further improve system reliability, each system is equipped with two sets of devices with identical functions. Each set includes one digital valve, one 2/4-way directional control valve, and three pilot-operated check valves, forming a complete hydraulic control unit. These two sets of devices can be arbitrarily switched according to actual needs. In the event of a digital valve or other component failure in one set, the operator can quickly switch to the other set. Maintenance and replacement of faulty equipment can be completed without interrupting system operation, significantly shortening system downtime, effectively avoiding production stagnation caused by equipment failure, and greatly improving the operational reliability and work continuity of the entire hydraulic system.
5.2. System Simulation
Hydraulic system operating speed is directly determined by flow rate, which correlates with valve port opening, and the latter depends on the stepper motor’s angle and speed. Thus, this study constructs a simulation environment consistent with actual working conditions, taking the stepper motor speed corresponding to each mechanism’s maximum operating speed as the core input.
Based on Table 2’s stepper motor speed calculations for each actuator’s maximum operating state: the 320 mm/s pitch mechanism requires the stepper motor to rotate 1518° within 2.12 s (per angular velocity-angle conversion); the 9.12°/s rotary mechanism (matching 9.6 r/min stepper motor speed) is set to rotate 576° within 10 s; the 3760 mm/s winch mechanism configures the stepper motor to rotate 1914° within 1.33 s.
To simulate real working processes, position command timings and operation paths are precisely defined: pitch mechanism (35 s command, 0 m to −0.675 m in 10 s); rotary mechanism (15 s command, 0° to 91.2° in 10 s); winch mechanism (25 s command, 0 m to −5 m in 1.33 s).The simulation step size is set to 0.001 s, and the input position signals are shown in Figure 10, where Xin, in, Lin are the position input signals of the 3-DOF actuator.
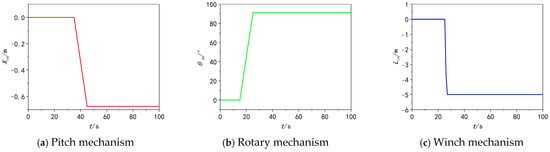
Figure 10.
Three-degree-of-freedom actuator position input diagram.
Figure 11 and Figure 12 show the displacement output and speed output diagrams of each actuator, where Xout, out, Lout are the position outputs of the 3-DOF actuator, and v1l, v2l , v3l are the speed outputs of the 3-DOF actuator.
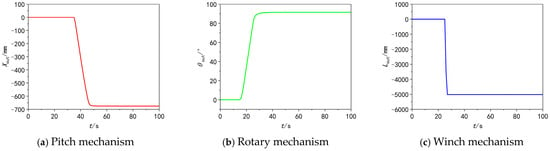
Figure 11.
Three-degree-of-freedom position output diagram.
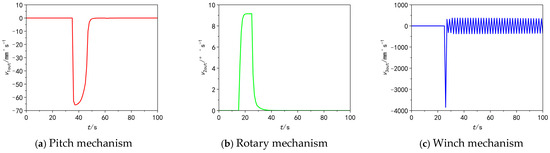
Figure 12.
Three-degree-of-freedom velocity output diagram.
The pitch mechanism moves from 0 m to −0.671 m (35–45 s) with a displacement deviation of 0.004 m (deviation rate: 0.6%), and its speed stabilizes at 67.5 mm/s without obvious fluctuations, benefiting from the real-time dynamic position error correction of the digital hydraulic cylinder’s closed-loop feedback mechanism.
The rotary mechanism rotates from 0° to 91.5° (15–25 s) with an angular deviation of 0.3° (deviation rate: 0.3%), a stable speed of 9.12°/s, and a response delay of only 0.2 s. The feedback gear’s real-time position compensation effectively suppresses rotational inertia-induced hysteresis.
The winch mechanism moves from 0 m to −5.02 m (25–26.33 s) with a length deviation of 0.02 m (deviation rate: 0.4%) but exhibits obvious speed fluctuations. After verifying the simulation settings and numerical methods, it is confirmed that numerical differentiation is not the primary cause. In-depth analysis and literature research reveal that excessive throttle groove gain enhances sensitivity to spool micro-displacements, causing abrupt flow area changes, unregulated oil output, and motor movement deviations. High-frequency oil flow dynamic changes exceed the digital valve’s error correction speed, leading to cumulative errors, exacerbated speed fluctuations, and operational jitter—this finding provides a key basis for subsequent hydraulic system optimization and throttle groove parameter adjustment.
All actuators meet the input position signal requirements, verifying the correctness of the established AMESim model for the digital hydraulic system.
6. Characteristic Analysis
6.1. Motor Speed
As presented in Section 4.2 and Figure 7 and Figure 8, the 3-DOF crane’s digital hydraulic system exhibits superior response characteristics and operational stability under high-speed conditions compared to low-speed operation; at low speeds (Figure 8), dynamic response differences among actuators arise from structural characteristics and load inertia coupling, with the pitch mechanism showing “oscillatory convergence” within 0–3 s (speed fluctuation range: 0.02–0.08 mm/s, amplitude: 0.06 mm/s) due to insufficient initial valve port opening from slow spool movement that causes temporary piston stagnation until flow and pressure balance the load, stabilizing at 0.159 mm/s (0.6% deviation from Simulink results), the rotary mechanism having minimal fluctuation (0.002–0.003°/s) but a 9 s startup delay attributed to high rotational inertia exceeding initial motor torque, with stabilization at 0.057°/s (consistent with theoretical values) occurring after torque overcomes inertial and frictional resistance, and the winch mechanism exhibiting the most severe fluctuations (0.8–1.1 mm/s, 0.1–13 s) due to gear backlash-induced “tooth separation-collision” that generates 0.2 mm impact displacement every 0.5 s, stabilizing at 0.94 mm/s (3.1% deviation from gear deformation modeling simplification) with increased flow. High-speed operation (Figure 9) significantly improves performance: the pitch mechanism’s response time is reduced from 3 s to 0.5 s (6× faster) and fluctuation amplitude from 0.02 mm/s to 0.001 mm/s (95% stability improvement), the rotary mechanism’s response time shortened from 9 s to 5.3 s (1.7× faster) and fluctuation reduced from 0.003°/s to 0.0006°/s (80% stability improvement), and the winch mechanism’s response time cut from 13 s to 10.6 s (1.2× faster) and fluctuation minimized from 0.1 mm/s to 0.005 mm/s (95% stability improvement). The core improvement mechanism lies in high-speed spool movement that rapidly reaches the “flow saturation point,” raising hydraulic pressure to working levels within 0.3 s to overcome inertia and load resistance, which enhances power transmission efficiency, accelerates signal processing, and reduces signal-action delay, while sufficient power supply and rapid adjustment also suppress fluctuations from external interference or load changes—issues prominent at low speeds due to insufficient power and load sensitivity. In summary, high-speed operation endows the 3-DOF crane’s digital hydraulic system with faster response speeds, smaller speed fluctuations, and superior stability, outperforming low-speed conditions in operational performance.
6.2. Motor Micro-Stepping
Mechanism operation accuracy, a core indicator for evaluating system performance, directly relates to the reliability of crane operations. Specifically, the accuracy of the pitch mechanism is jointly determined by the precision of the stepper motor and ball screw, while the accuracy of the rotary and winch mechanisms primarily depends on stepper motor precision. Notably, ball screw precision is fixed post-processing and difficult to adjust via conventional methods. In contrast, stepper motor precision can be flexibly regulated using the driver’s micro-stepping function [25]. The selected stepper motor has a step angle of 1.8°; under different micro-stepping conditions, its pulse equivalent changes accordingly, thereby affecting actuator motion accuracy.
In the simulation settings, the stepper motor remains at zero position for the first 5 s to standardize initial system conditions. It then operates smoothly to the 360° position within 25 s, simulating normal movement. After maintaining the 360° position for 10 s, step angle signals under different micro-stepping modes are applied to trigger the system response.
The number of micro-steps and the corresponding single-pulse rotation angle are shown in Table 3 [26].

Table 3.
Table of fine divisions and corresponding rotary angles.
After simulation, the output displacement results of each actuator under different micro-stepping conditions are obtained, and the specific data are shown in Table 4.

Table 4.
Output displacement results of three-degree-of-freedom actuators under different subdivisions.
As the number of micro-steps increases gradually, the pulse equivalent exhibits a significant linear decreasing trend, indicating that the motor’s rotation amplitude per single pulse signal becomes more refined. Meanwhile, the discrepancy between the simulated and theoretical pulse equivalents continues to narrow. Compared with 1 micro-step, 10 micro-steps reduce the deviations of the 3-DOF actuators by 0.0039 mm, 0.0055 mm, and 0.01 mm, respectively, with precision improved by approximately 63%, 36%, and 50%. These results demonstrate that under large micro-stepping conditions of the stepper motor, the system’s actual operating precision is closer to theoretical expectations, effectively reducing precision loss induced by mechanical errors, control delays, and other factors, thereby enhancing actuator motion precision.
In practical working conditions, if the application scenario prioritizes rotational speed over precision and smoothness, a small number of micro-steps can satisfy operational requirements. Under small micro-stepping conditions, the motor can receive more pulse signals per unit time, enabling higher rotational speed output. Although precision is somewhat compromised, this configuration aligns with the speed-priority demands of such scenarios. When equipment operates at low speeds, issues such as vibration, noise, and unstable operation are prone to occur. In this case, a large number of micro-steps should be adopted. Large micro-stepping further refines the motor’s step angle, smoothing rotation, effectively suppressing vibration and noise during low-speed operation, and ensuring stable and reliable equipment performance to meet the demands of high-precision application scenarios.
In comprehensive consideration, when actual costs permit, selecting a stepper motor with a large number of micro-steps is advisable to improve control precision and reduce errors.
6.3. System Flow Rate
As one of the important parameters of the hydraulic system, the flow rates of the 3-DOF actuator are, respectively, set to 300 L/min, 400 L/min, and 500 L/min. The stepper motor speed is set to the maximum speed, and other parameters are configured in accordance with Table 1. The results are shown in Figure 13.
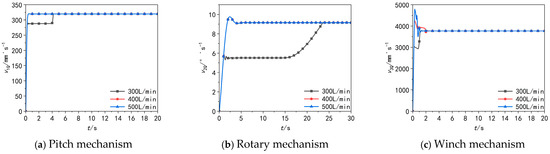
Figure 13.
Speed diagram of the three-degree-of-freedom actuator at different flow rates.
v1Q, v2Q, v3Q represent the speeds of the 3-DOF actuator under different flow rates.
It can be observed that when the system flow rate decreases to 300 L/min, the actuator exhibits significant response hysteresis, which is attributed to the crane’s inherent characteristics of large load inertia and high operational resistance. Specifically, the response time of the pitch mechanism is prolonged by 3.5 s, the delay of the rotary mechanism reaches 18.48 s, and the winch mechanism lags by 1.75 s. This phenomenon is highly consistent with the fundamental principle of “flow rate determining speed” in hydraulic transmission systems. From the perspective of hydraulic transmission theory, under this flow rate condition, the velocity and pressure of hydraulic oil entering the actuator are constrained. The reduced flow velocity delays the pressure build-up process in the actuator’s working chamber, preventing it from quickly overcoming the static frictional resistance and inertial impact of the mechanism itself. Notably, for the rotary mechanism—which is required to drive a large rotational inertia—the torque growth rate of the hydraulic motor is insufficient to rapidly balance the load resistance torque under low-flow conditions. This leads to a significant extension of the adjustment period during the start-up and acceleration phases, serving as the core reason for its most prominent response delay.
When the flow rate is increased to 500 L/min, the improvement in the actuator’s response time fails to meet expectations, revealing a multi-parameter coupling constraint mechanism within the hydraulic system. At this point, the flow rate approaches the upper limit of the digital valve’s rated flow capacity, resulting in a substantial increase in valve port throttling loss, while the proportion of local pressure loss in pipelines relative to the total system loss rises noticeably. Further analysis indicates that once the flow rate exceeds a specific threshold, the system enters a “flow saturation zone.” Continuing to increase the flow rate within this zone not only fails to enhance response speed but also triggers new dynamic issues: the amplitude of pressure pulsation increases (which may induce pipeline resonance), and the incidence of cavitation in hydraulic oil rises concurrently. This verifies the significance of the “flow rate matching” principle in hydraulic system design—namely, parameter co-optimization should be implemented based on the actuator’s load characteristics and the dynamic response requirements of the working conditions.
In conclusion, variations in flow rate exert a significant impact on the performance of the 3-DOF crane’s digital hydraulic system. In particular, a decrease in flow rate substantially prolongs the actuator’s response time and reduces system operating efficiency. To optimize system performance, measures should be taken to minimize or eliminate flow rate fluctuations during the design of digital hydraulic systems.
6.4. Digital Valve Opening
In addition to system flow rate, the spool opening size of digital valves is another critical factor influencing hydraulic system performance. For the 3-DOF crane’s actuators, the sizes of the digital valves’ negative opening, zero opening, and positive opening were set in accordance with the specifications provided in Table 5. To isolate the impact of spool opening size on system behavior, the stepper motor was configured to operate at its maximum speed, while all other system parameters (e.g., reducer gear ratio, hydraulic oil properties) were set consistent with the values outlined in Table 1. The simulation results of the system under these parameter configurations are presented in Figure 14 [27].

Table 5.
Table 1 Opening size.
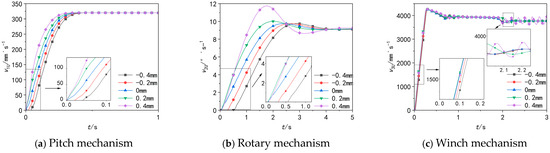
Figure 14.
Speed diagram of the three-degree-of-freedom actuator at different openings.
v1U, v2U, v3U denote the speeds of the 3-DOF actuator under different valve openings. As observed from the simulation results (Figure 14), under the positive opening state, although the actuator achieves fast response speed, the flow gain is excessively high. Owing to the large opening size, the hydraulic oil flow becomes highly sensitive to spool displacement changes—even minor variations in spool position can trigger significant flow fluctuations. These fluctuations further disrupt the actuator’s operational stability, resulting in poor overall system stability that hinders high-precision control and fails to meet the crane’s stability requirements.
The zero opening form theoretically supports higher-precision control but imposes extremely strict requirements on actual manufacturing processes. Achieving absolute zero error in processing is practically challenging; any slight processing deviation may lead to valve port leakage or jamming during operation. This not only degrades system performance but also introduces potential safety hazards, limiting its engineering applicability.
In contrast, the negative opening state exhibits a certain degree of response delay compared to the positive opening: the response time of the pitch mechanism and winch mechanism is delayed by approximately 0.05 s and 0.005 s, respectively, while that of the rotary mechanism is extended by about 0.5 s. However, the negative opening form offers notable advantages: the initial spool position restricts hydraulic oil flow, resulting in smoother flow changes during system operation, smaller actuator fluctuation amplitudes, and effectively guaranteed system stability—thus enabling higher control precision. Meanwhile, the “preload” effect of the negative opening can offset spool thermal deformation caused by temperature variations, making it suitable for marine environments with significant temperature differences. Additionally, the negative opening has relatively lower processing precision requirements, which helps reduce manufacturing difficulty and costs.
Given that cranes demand extremely high system stability and control precision while tolerating a certain degree of response delay, the negative opening form holds greater practical value in actual crane working conditions despite its minor response delay. Its advantages—enhanced system stability, guaranteed control precision, and reduced processing difficulty—are highly prominent. Therefore, in practical engineering applications, after comprehensively weighing various factors, the digital valve should adopt a negative opening form that is as small as possible and close to zero opening. This scheme not only meets the system’s core requirements for stability and precision but also balances processing costs and engineering feasibility, making it the optimal design solution for the crane’s digital hydraulic system.
6.5. Throttle Groove Shape of Digital Valve
To address the problem proposed in Section 5.2—excessively high flow gain caused by the throttle groove shape, which may lead to speed fluctuations of the actuator—this study investigates the throttle groove shape.
Currently, there are various types of throttle groove shapes applied in the main control valves of construction machinery, which can be roughly divided into single-type and composite-type [28]. Among them, the single-type has low processing difficulty and is widely used, while the composite-type has high processing difficulty without significant performance improvement. Therefore, this study compares the existing semicircular throttle groove with single-type throttle grooves (U-shaped, V-shaped, K-shaped). The schematic diagram of the single-type throttle grooves is shown in Figure 15, where L1 and D1 represent the length and depth of the throttle groove, R0 and R1 denote the processing radius of the throttle groove and the radius of the U-shaped throttle groove, respectively, E represents the angle of the V-shaped throttle groove, and W indicates the width of the K-shaped throttle groove [29].
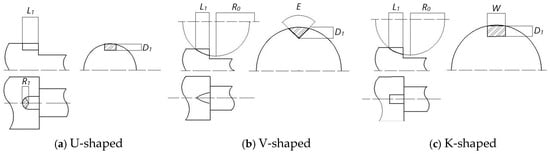
Figure 15.
Schematic diagram of a single-type throttle slot.
The calculation formulas for the flow area of the single-type throttle groove are Equations (13) and (14) [30].
To facilitate a comparative analysis between different throttle groove types and the existing semicircular groove, the design principle is established such that both the groove length and flow area remain identical when the valve port is fully open. The dimensional parameters of various throttle grooves are specified in Table 6.

Table 6.
Single-type throttle slot size parameters.
The original semicircular throttle groove is compared with the common U-shaped, V-shaped, and K-shaped throttle grooves. The stepper motor is set to the maximum speed, and the operating speed of the actuator is observed. The results are shown in Figure 16.
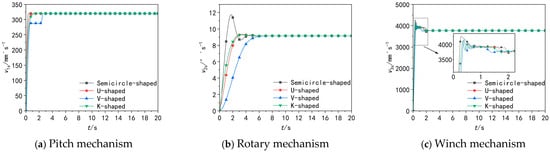
Figure 16.
Speed diagram of a three-degree-of-freedom actuator with different throttle slot shapes.
v1s, v2s, v3s denote the speeds of the 3-DOF actuator with different throttle groove shapes. Analysis of the simulation results reveals that the semicircular throttle groove exhibits significant advantages in overall response speed, allowing the actuator to respond more rapidly to stepper motor signals compared to the U-shaped, V-shaped, and K-shaped alternatives. Among the other single-type grooves, the U-shaped throttle groove demonstrates favorable performance in the pitch mechanism, while the K-shaped throttle groove shows good adaptability to the rotary and winch mechanisms [31]. Notably, the semicircular throttle groove is accompanied by a slight overshoot phenomenon. Combined with the analysis of the winch mechanism’s speed fluctuations in Section 4.2, this overshoot is attributed to excessively high throttle groove gain: when the spool undergoes micro-displacements, the hydraulic oil flows out rapidly, thereby triggering undesirable speed fluctuations of the actuator [32].
To mitigate the slight overshoot of the semicircular throttle groove while retaining its advantages in response speed, this study conducts structural optimization based on its original design. Specifically, under the constraint of maintaining the total cross-sectional area of the semicircular throttle groove unchanged, the radius parameter of the groove is adjusted to two alternative values: 6 mm (increased from the original) and 4 mm (decreased from the original). The optimized structural schematics are presented in Figure 17. To evaluate the effect of this optimization, simulations of the actuator’s operation were conducted with the stepper motor set to its maximum speed; the corresponding simulation results are presented in Figure 18.
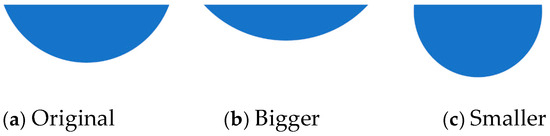
Figure 17.
Schematic diagram of semicircular throttle slots with different radii.
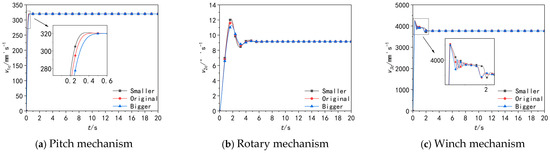
Figure 18.
Speed diagram of a three-degree-of-freedom actuator with semicircular throttle slots of different radii.
v1c, v2c, v3c denote the speeds of the 3-DOF actuator with semicircular throttle grooves of different radii. Analysis of the simulation results (Figure 18) indicates that slight actuator speed fluctuations persist across all configurations: the original semicircular throttle groove, the modified groove with an increased radius, and the modified groove with a decreased radius. When the radius of the semicircular throttle groove is increased, the amplitude of actuator speed fluctuations decreases significantly: for the 3-DOF systems (pitch, rotary, winch), the fluctuations are reduced by 0.2556 mm/s, 0.6289°/s, and 15.1365 mm/s, respectively, with corresponding improvements in system stability of 0.08%, 5.33%, and 0.35%. However, this radius increase is accompanied by a reduction in response speed. In contrast, decreasing the radius enhances response speed—shortening the response time of the 3-DOF systems by 0.02 s, 0.07 s, and 0.03 s, respectively—but further exacerbates speed fluctuations, which is detrimental to system stability.
As a large-scale construction machine, cranes operate in complex environments where system operational stability and working precision are critical to ensuring engineering safety, and their priority far outweighs that of response time. Therefore, despite the existence of slight speed fluctuations, the original semicircular throttle groove remains a relatively optimal choice due to its balanced comprehensive performance (i.e., favorable response speed combined with manageable fluctuations). In practical applications, the radius of the semicircular throttle groove can be appropriately increased to smooth the arc profile. This adjustment optimizes the gradient of valve port area change, mitigating the abrupt nature of flow gain—thereby effectively reducing actuator speed fluctuations and enhancing the system’s operational stability and reliability while minimizing the trade-off in response speed.
7. Performance Optimization
Based on the research in Section 5, during the design and optimization of the digital hydraulic system: the system exhibits better response speed and operational stability when the motor speed is at the maximum value; the optimal flow rate parameter is set to 400 L/min; the system achieves the highest control precision when the motor adopts the large micro-stepping mode; and the semicircular structure is superior for the throttle groove. Therefore, there is no need to conduct comparative analysis between parameters such as motor speed, micro-stepping multiple, and flow rate with other influencing factors. The core adjustment parameters during optimization are the digital valve opening size and the radius of the semicircular throttle groove.
Based on this, considering the synergistic relationship between response speed and system stability, the following optimization schemes are constructed for the digital hydraulic system, and comparative studies are carried out. The interaction mechanism between various influencing factors is explored, and the influence law of parameter adjustment amplitude on the optimization effect is analyzed to finally screen out the optimal optimization scheme. The specific parameters are shown in Table 7.

Table 7.
Different scheme parameter table.
The simulation results of the three-degree-of-freedom actuator of the digital hydraulic system under different schemes are shown in Figure 19.
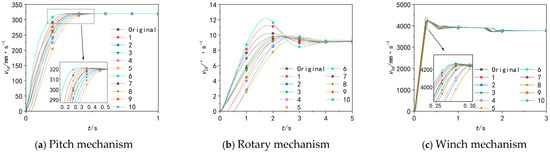
Figure 19.
Speed diagram of three-degree-of-freedom actuators for different schemes.
As shown in the figure, the operating speeds of the 3-DOF actuator under different schemes are presented. It can be seen that the ranking of superiority in response speed of the pitch mechanism is 6, 1, 7, 2, 3, 8, 4, 9, 5, 10; and the ranking of superiority in system stability is 5, 4, 3, 2, 1, 7, 8, 9, 10, 6. For the rotary mechanism, the ranking of superiority in response speed is 7, 2, 6, 1, 8, 3, 9, 4, 10, 5; and the ranking of superiority in system stability is 3, 4, 5, 2, 8, 9, 10, 7, 1, 6. Regarding the winch mechanism, the ranking of superiority in response speed is 6, 7, 1, 2, 8, 3, 9, 4, 10, 5; and the ranking of superiority in system stability is 3, 4, 5, 2, 1, 10, 9, 8, 7, 6. After calculation, the increase/decrease amplitudes of response speed and system stability of each actuator under different schemes are shown in Table 8.

Table 8.
Response speed of the three-degree-of-freedom actuator and system stability increase/decrease table.
The calculation method for the single performance index score is shown in Equations (15) and (16).
Considering that the crane, as a large-scale construction machinery, operates in complex working environments, the system’s operational stability and working precision are directly related to engineering safety, and their importance is higher than that of response time. Therefore, in the weight setting of performance indicators, the weight of response speed is determined as 30%, and the weight of system stability is set to 70%; the calculation method for the overall comprehensive score of a single mechanism is shown in Equation (17).
After calculating the overall comprehensive score of each single mechanism, since the three 3-DOF actuators have the same importance, each is assigned a weight of 1/3. The calculation method for the comprehensive score of different schemes is shown in Equation (18).
The specific calculation process is simple yet tedious, so this study omits the calculation process and presents the results in Table 9.

Table 9.
Comprehensive score table for different schemes.
As evident from the table, Scheme 3 represents the comprehensively optimal solution. With only a minimal sacrifice in response speed, this scheme achieves a significant enhancement in system stability, boosting the overall performance by 1.29%. Additionally, the parameter configuration of Scheme 3 is as follows: the motor operates at maximum speed with a large micro-stepping mode, the flow rate is set to 400 L/min, the digital valve opening is 0 mm, and a semicircular throttle groove with an increased radius is adopted. This configuration aligns with the conclusions on system characteristics derived in Section 6.
The comprehensive optimization plan has improved the overall performance of the crane by 1.29%, reduced positioning deviation by 0.3%, and increased rotational stability by 5.33%. Although the 1.29% overall performance improvement seems modest, it holds significant practical and engineering value when considering the application scenarios and operational characteristics of cranes. Firstly, the crane is mainly used in low-tolerance precision tasks such as port cargo loading and unloading and high-rise building construction, where even minor performance fluctuations may lead to operational interruptions. The 1.29% improvement directly enhances operational stability, especially under heavy load or harsh working conditions (e.g., strong winds, high altitudes), effectively reducing the risk of equipment failure. Secondly, this improvement synergizes with the reduced positioning deviation and enhanced rotational stability: the optimized overall performance provides a reliable foundation for precise positioning and stable rotation, enabling the equipment to meet preset precision standards more consistently and avoiding safety hazards or efficiency losses caused by single-link shortcomings. Thirdly, as a high-investment and long-service-life engineering equipment, the 1.29% performance improvement translates into substantial long-term cumulative benefits. Based on thousands of annual operating hours per crane, this improvement can increase operational efficiency by several hours annually, reduce energy consumption and maintenance costs, and lower the probability of fatigue-induced failures, thereby avoiding potential heavy losses from safety accidents. Finally, the core performance of engineering cranes has reached a high level of maturity, and the performance improvement of similar optimization schemes in the industry generally ranges from 1% to 3%. The 1.29% improvement aligns with the laws of industrial technological development and is achieved without significantly increasing manufacturing costs or modifying the core structure of the equipment, demonstrating strong engineering feasibility and promotion value. Collectively, these improvements are crucial for ensuring operational safety and efficiency in precision tasks, where even small errors may endanger safety or reduce efficiency.
8. Conclusions
This study innovatively integrates digital hydraulic technology based on mechanical feedback into a 3-degree-of-freedom crane, and solves the limitations of traditional hydraulic systems in precision control and dynamic response through mathematical modeling, AMESim simulation, and parameter optimization.
The key performance driving factors include maximum motor speed and 10 micro steps: high-speed operation reduces the response time of pitch, rotation, and winch mechanisms by 83.3%, 41.1%, and 18.5%, respectively (compared to low speed), while 10 micro steps increase their accuracy by 63%, 36%, and 50% (compared to 1 micro step), guiding the adjustment of high-performance parameters.
The optimal parameters were determined to be: a smaller negative digital valve opening (balance stability and responsiveness), an enlarged radius semicircular throttling groove (to suppress winch speed fluctuations by 0.35% and reduce shaking), and a system flow rate of 400 L/min (to avoid delays at lower flow rates or throttling losses/cavitation at higher flow rates).
The comprehensive optimization plan has improved the overall performance of the crane by 1.29%, reduced positioning deviation by 0.3%, and increased rotational stability by 5.33%. This is crucial for precision tasks such as port cargo loading and unloading and high-rise buildings, where even small errors may endanger safety or reduce efficiency.
The limitations of this study include reliance on numerical simulations; Future work should validate research results with physical prototypes and expand models toto achieve better stability performance trade-offs.
This work provides a theoretical and technical foundation for the intelligence of hydraulic systems in cranes, promotes digital hydraulic technology in construction machinery, and improves the safety and accuracy of material handling.
Author Contributions
Conceptualization, S.Z.; methodology, S.Z.; software, S.Z.; validation, S.Z.; formal analysis, Z.W.; investigation, C.Y.; resources, Z.W.; data curation, S.Z.; writing—original draft preparation, S.Z.; writing—review and editing, S.Z.; visualization. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by National Natural Science Foundation of China (51505272).
Data Availability Statement
Data is unavailable due to privacy or ethical restrictions.
Acknowledgments
Thank you to Shenqi Lou and Wei Gao from China Shipbuilding Industry Group No.704 Research Institute for their contributions to the article. They provided relevant technical support. Used AI tools to assist in correcting the language fluency, grammatical accuracy, and logical coherence of the initial draft of the paper, improving the standardization of text expression, but without changing the core ideas, research ideas, data conclusions, and academic connotations of the paper. The ideological core and academic innovation points of the paper are all original creations of myself. AI tools are used to assist in checking the formatting and reference format of the paper to ensure compliance with the journal’s formatting requirements.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| Equation parameters | Meaning | Unit |
| flow entering the hydraulic cylinder | L/min | |
| effective working area of hydraulic cylinder | mm2 | |
| output displacement of pitch mechanism | mm | |
| leakage coefficient inside hydraulic cylinder | m3/s | |
| external leakage coefficient of hydraulic cylinder | m3/s | |
| working capacity of hydraulic cylinder | mm3 | |
| effective bulk modulus of elasticity | MPa | |
| load pressure borne by hydraulic cylinder | Mpa | |
| step signal | dimensionless | |
| mass of hydraulic cylinder piston | kg | |
| viscous damping coefficient | N·m·s | |
| spring elastic coefficient | N/m | |
| external load force, | KN | |
| lead angle of screw | ° | |
| screw angle | ° | |
| thread lead of ball screw | mm | |
| motor angle | ° | |
| valve core angle | ° | |
| motor input radian | rad | |
| feedback nut thread lead | mm | |
| discharge coefficient | m3/s | |
| trim diameter | mm | |
| density of hydraulic oil | kg/m3 | |
| output angle of rotary mechanism | ° | |
| flow gain coefficient | m3/s·A | |
| displacement of motor | mm3/rad | |
| hydraulic natural frequency | rad/s | |
| hydraulic damping ratio | dimensionless. | |
| gear 1 angle | ° | |
| gear 2 angle | ° | |
| section I gear diameter | mm | |
| section II gear diameter | mm | |
| gear diameter of the reducer | mm | |
| gear 2 angle after deceleration | ° | |
| output length of winch mechanism | mm | |
| A1, B1 | surface area and cross-sectional area of throttling groove | mm2 |
| projection angles of V-shaped and K-shaped throttling grooves | ° | |
| response speed score | dimensionless | |
| system stability score | dimensionless | |
| response speed change amplitude | % | |
| change amplitude of system stability | % | |
| overall score of a single institution | dimensionless | |
| comprehensive score of three freely executing agencies | dimensionless | |
| overall score of pitch mechanism | dimensionless | |
| overall score of rotary mechanism | dimensionless | |
| overall score of hoisting mechanism | dimensionless |
References
- Neitzel, R.L.; Seixas, N.S.; Ren, K.K. A review of crane safety in the construction industry. Appl. Occup. Environ. Hyg. 2001, 16, 1106–1117. [Google Scholar] [CrossRef]
- Aneziris, O.N.; Papazoglou, I.A.; Mud, M.L.; Damen, M.; Kuiper, J.; Baksteen, H.; Ale, B.; Bellamy, L.; Hale, A.; Bloemhoff, A.; et al. Toward risk assessment for crane activities. Saf. Sci. 2008, 46, 872–884. [Google Scholar] [CrossRef]
- Lee, H.H. Modeling and control of a three-dimensional overhead crane. J. Dyn. Syst. Meas. Control 1998, 120, 471–476. [Google Scholar] [CrossRef]
- Abdel-Rahman, E.M.; Nayfeh, A.H.; Masoud, Z.N. Dynamics and control of cranes: A review. J. Vib. Control 2003, 9, 863–908. [Google Scholar] [CrossRef]
- Linjama, M.; Vilenius, M. Improved digital hydraulic tracking control of water hydraulic cylinder drive. Int. J. Fluid Power 2005, 6, 29–39. [Google Scholar] [CrossRef]
- Liu, Z.H.; Gao, Q.H.; Li, J.Y.; Niu, H.L. The research of hydraulic cylinder controlled by digital valve. TELKOMNIKA Indones. J. Electr. Eng. 2014, 12, 3873–3886. [Google Scholar] [CrossRef]
- Drumea, P.; Pavel, I.; Matache, G. Digital hydraulic motors. In Proceedings of the 2016 International Conference on Hydraulics and Pneumatics—HERVEX, Baile Govora, Romania, 9–11 November 2016; pp. 9–11. [Google Scholar]
- Pedersen, N.H.; Johansen, P.; Schmidt, L.; Scheidl, R.; Andersen, T.O. Control and performance analysis of a digital direct hydraulic cylinder drive. Int. J. Fluid Power 2019, 20, 295–322. [Google Scholar] [CrossRef]
- Jia, Y.; Shi, Y.; Yuan, Y.; Zhang, Y.; Yao, Z. Analyzing of influencing factors on dynamic response characteristics of double closed-loop control digital hydraulic cylinder. J. Adv. Mech. Des. Syst. Manuf. 2019, 13, JAMDSM0048. [Google Scholar] [CrossRef]
- Pavel, I.; Rădoi, R.; Popescu, A.M.; Marinescu, A. Experimental research on a digital hydraulic cylinder. Int. Multidiscip. Sci. GeoConference SGEM 2019, 19, 271–279. [Google Scholar]
- Zhang, Q.; Kong, X.; Yu, B.; Ba, K.; Jin, Z.; Kang, Y. Review and development trend of digital hydraulic technology. Appl. Sci. 2020, 10, 579. [Google Scholar] [CrossRef]
- Zhang, H.; Wei, W.; Wang, H.; Zhang, Y.; Liu, X. Digital Hydraulic Motor Characteristic Analysis for Heavy-Duty Vehicle Traction. Actuators 2025, 14, 11. [Google Scholar] [CrossRef]
- Nayfeh, T.A.; Nayfeh, A.H.; Mook, D.T. A theoretical and experimental investigation of a three-degree-of-freedom structure. Nonlinear Dyn. 1994, 6, 353–374. [Google Scholar] [CrossRef]
- Samani, A.E.; De Kooning, J.D.; Kayedpour, N.; Singh, N.; Vandevelde, L. The impact of pitch-to-stall and pitch-to-feather control on the structural loads and the pitch mechanism of a wind turbine. Energies 2020, 13, 4503. [Google Scholar] [CrossRef]
- Abdulla, G.; Hasçelik, B.; Palamutcu, S.; Soydan, A.S. Synthesis work about driving mechanism of a novel rotary dobby mechanism. Text. Appar. 2010, 20, 218–224. [Google Scholar]
- Lee, D.; Chang, D.; Shin, Y.I.; Son, D.; Kim, T.W.; Lee, K.Y.; Kim, J. Design and application of a wire-driven bidirectional winch mechanism for workspace expansion with a focus on shipbuilding tasks. Adv. Robot. 2011, 25, 699–715. [Google Scholar] [CrossRef]
- Guo, X.S.; Li, Q.C.; Xiao, J.L. Dynamic Characteristics Simulation of the Digital Hydraulic Cylinder Based on AMESim. Adv. Mater. Res. 2013, 625, 75–78. [Google Scholar] [CrossRef]
- Winkler, B. Recent advances in digital hydraulic components and applications. In Proceedings of the Ninth Workshop on Digital Fluid Power, Aalborg, Denmark, 7–8 September 2017; Tampere University Press: Tampere, Finland, 2017; pp. 1–10. [Google Scholar]
- Yao, J. Model-based nonlinear control of hydraulic servo systems: Challenges, developments and perspectives. Front. Mech. Eng. 2018, 13, 179–210. [Google Scholar] [CrossRef]
- Dabney, J.B.; Harman, T.L. Mastering Simulink, 230; Pearson/Prentice Hall: Upper Saddle River, NJ, USA, 2004; pp. 1–8. [Google Scholar]
- Lebrun, M.; Vasiliu, D.; Vasiliu, N. Numerical simulation of the fluid control systems by AMESim. Stud. Inform. Control 2009, 18, 111–118. [Google Scholar]
- Betin, F.; Pinchon, D.; Capolino, G.A. Fuzzy logic applied to speed control of a stepping motor drive. IEEE Trans. Ind. Electron. 2000, 47, 610–622. [Google Scholar] [CrossRef]
- Ponomareva, E.A.; Tcypkin, A.N.; Smirnov, S.V.; Putilin, S.E.; Yiwen, E.; Kozlov, S.A.; Zhang, X.-C. Double-pump technique–one step closer toward efficient liquid-based THz sources. Opt. Express 2019, 27, 32855–32862. [Google Scholar] [CrossRef]
- Zhang, K.; Wu, D.; Wang, H.; Li, J.; Feng, Z.; Zhu, J.; Lai, Z. Investigation of Effects of Slider Structure on the Reversing Performance of Four-Way Reversing Valve. Processes 2023, 11, 1538. [Google Scholar] [CrossRef]
- Xi, J.; Liao, G.; Yang, W. Study of stepping motor subdivision driver. In Proceedings of the 2010 International Conference on Intelligent Computation Technology and Automation, Changsha, China, 11–12 May 2010; IEEE: New York, NY, USA, 2010; Volume 3, pp. 443–446. [Google Scholar]
- Mengda, Y.; Min, Z. A research of a new technique on hardware implementation of control algorithm of high-subdivision for stepper motor. In Proceedings of the 2010 5th IEEE Conference on Industrial Electronics and Applications, Taichung, Taiwan, 15–17 June 2010; IEEE: New York, NY, USA, 2010; pp. 115–120. [Google Scholar]
- Zhang, G.; Wang, W.W.; Wu, Z.Y.; Chen, D.S.; Kim, H.D.; Lin, Z. Effect of the opening degree on evolution of cryogenic cavitation through a butterfly valve. Energy 2023, 283, 128543. [Google Scholar] [CrossRef]
- Ye, Y.; Yin, C.B.; Li, X.D.; Zhou, W.-J.; Yuan, F.-F. Effects of groove shape of notch on the flow characteristics of spool valve. Energy Convers. Manag. 2014, 86, 1091–1101. [Google Scholar] [CrossRef]
- Zhang, S.Y.; Wang, X.Q.; Wang, N.M.; Wang, Z.Q.; Lu, Y.J. Performance optimization of mechanical hydraulic servo device for marine controllable pitch propeller. Chin. Hydraul. Pneum. 2025, 49, 123–133. [Google Scholar]
- Liping, X.; Haoyi, M.; Liujin, C. Structure improvement and optimization of spool valve throttling grooves of the multiway valve. In Proceedings of the 7th International Conference on Education, Management, Information and Computer Science, Shenyang, China, 16–18 June 2017; Atlantis Press: Dordrecht, The Netherlands, 2016; pp. 257–264. [Google Scholar]
- He, J.; Li, B.; Liu, X. Investigation of flow characteristics in the U-shaped throttle valve. Adv. Mech. Eng. 2019, 11, 1687814019830492. [Google Scholar] [CrossRef]
- Fu, X.; Du, X.; Zou, J.; Ji, H.; Ryu, S.; Ochiai, M. Characteristics of flow through throttling valve undergoing a steep pressure gradient. Int. J. Fluid Power 2007, 8, 29–37. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).