A Discrete Space Vector Modulation MPC-Based Artificial Neural Network Controller for PMSM Drives
Abstract
1. Introduction
- A dataset is generated using the DSVM-MPC controller and employed for offline training of the ANN, thereby effectively alleviating the computational load during real-time operation.
- The proposed ANN-based control strategy achieves superior control performance in both transient response and steady-state accuracy compared with DSVM-MPC.
2. PMSM System Design and DSVM-MPC
2.1. Model of PMSM
2.2. DSVM-MPC

3. Proposed DSVM-MPC-Based ANN Controller for PMSM Drives
3.1. Structure of ANN
3.2. Data Generation and Training Process of ANN
3.3. Comparison of Computational Burden Between DSVM-MPC-Based ANN and DSVM-MPC
4. Results and Analysis
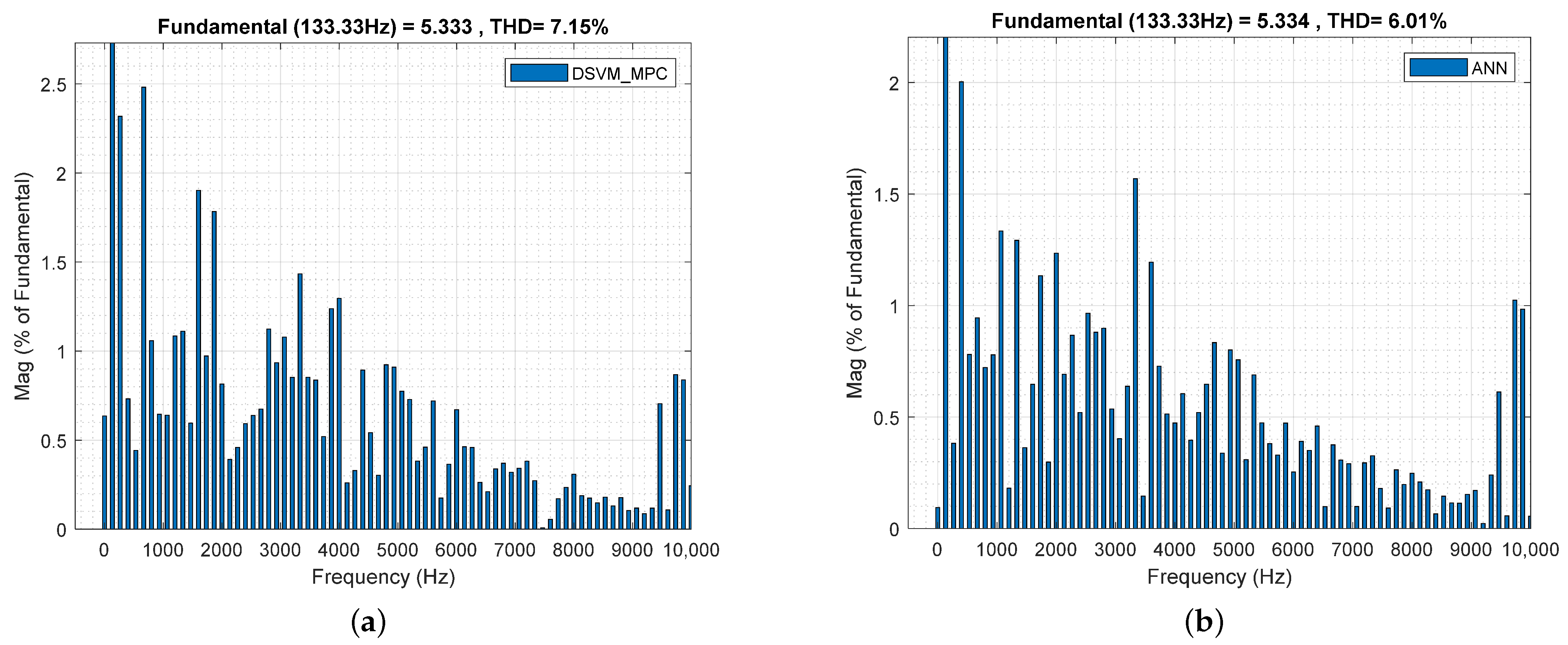
4.1. Steady-State Performance
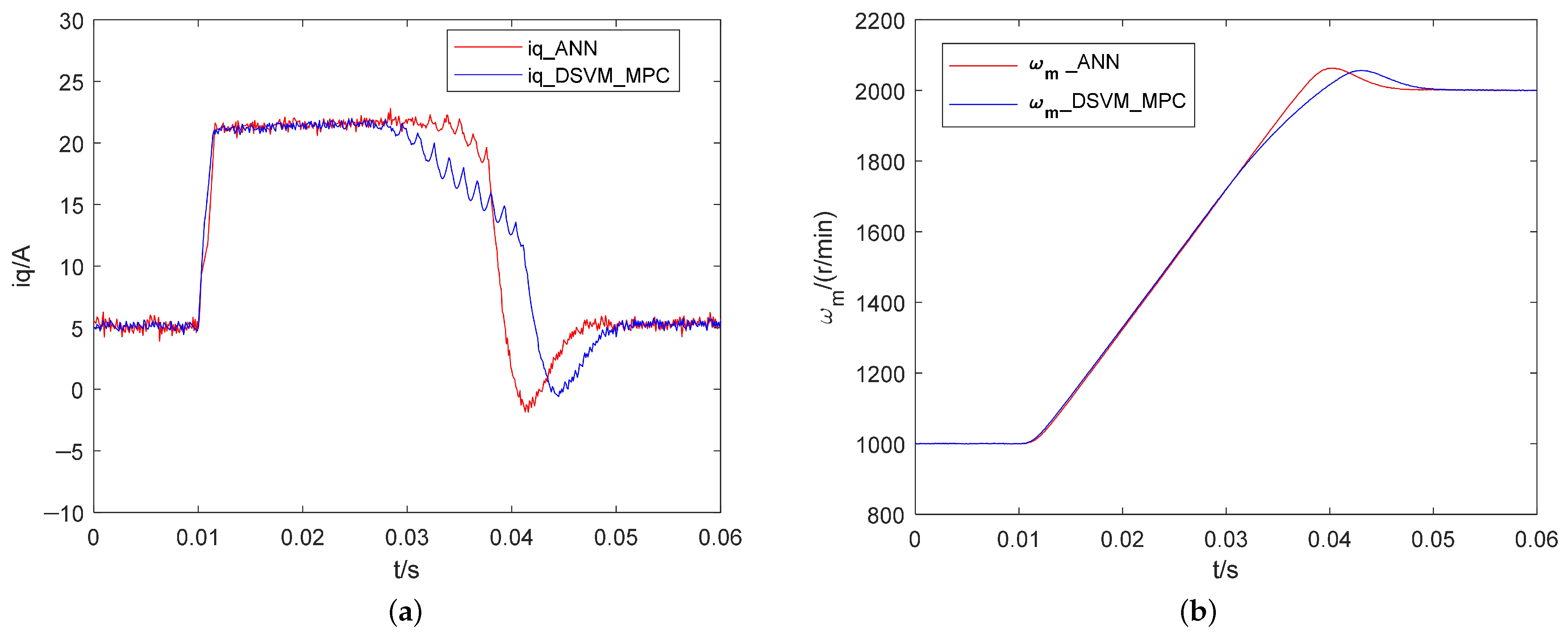
4.2. Dynamic Response
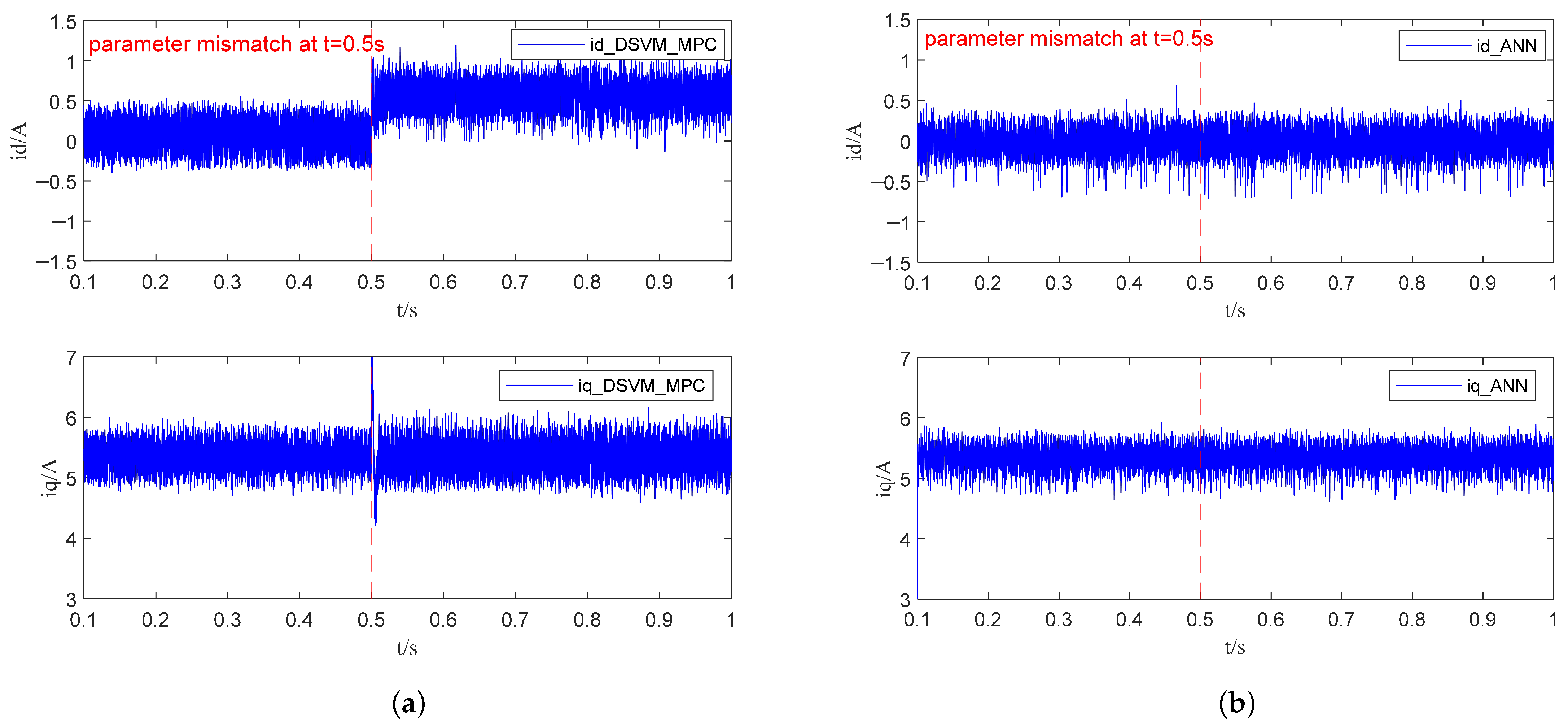
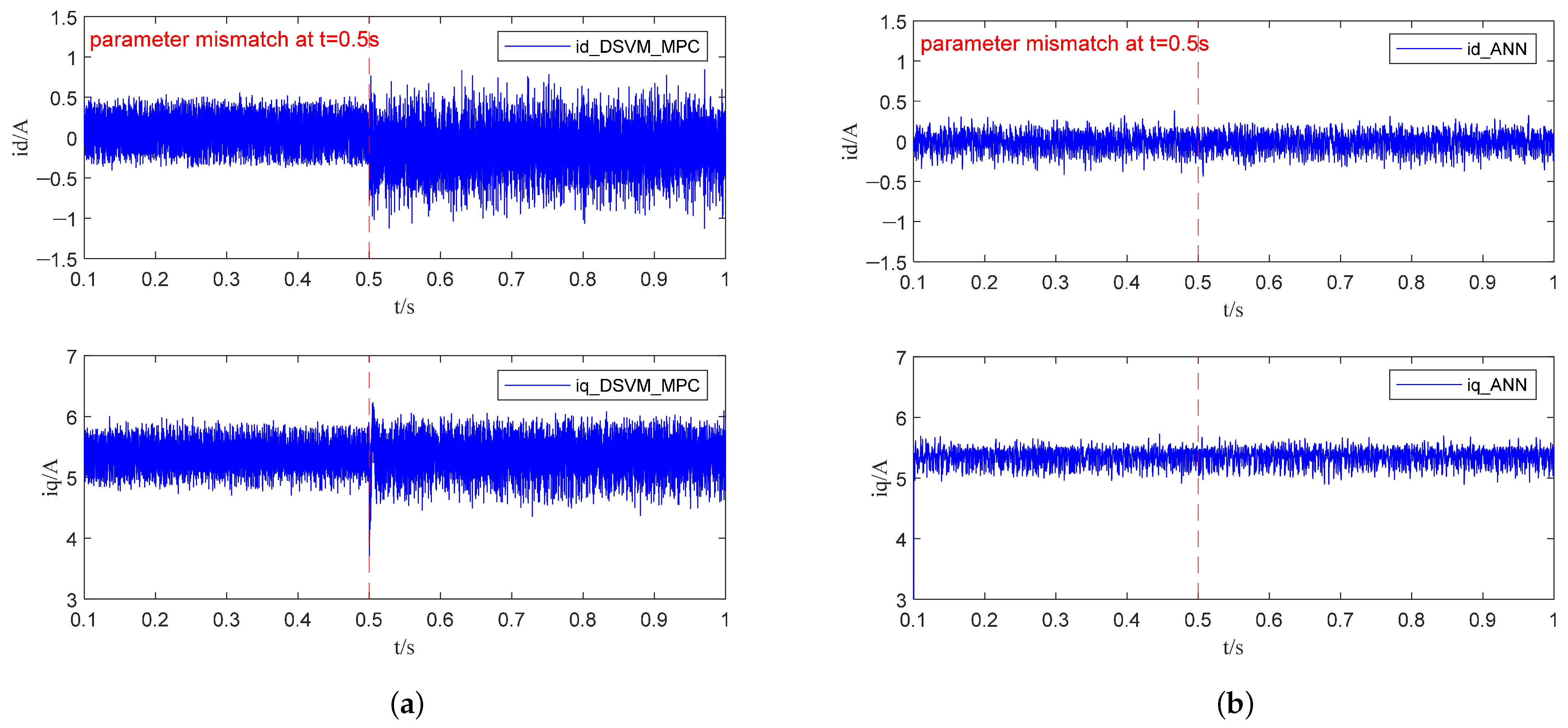
4.3. Performance Under Parameter Mismatches
4.4. Execution Time Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rodriguez, J.; Garcia, C.; Mora, A.; Flores-Bahamonde, F.; Acuna, P.; Novak, M.; Zhang, Y.; Tarisciotti, L.; Davari, S.A.; Zhang, Z.; et al. Latest Advances of Model Predictive Control in Electrical Drives—Part I: Basic Concepts and Advanced Strategies. IEEE Trans. Power Electron. 2022, 37, 3927–3942. [Google Scholar] [CrossRef]
- Fuentes, E.; Silva, C.A.; Kennel, R.M. MPC Implementation of a Quasi-Time-Optimal Speed Control for a PMSM Drive, With Inner Modulated-FS-MPC Torque Control. IEEE Trans. Ind. Electron. 2016, 63, 3897–3905. [Google Scholar] [CrossRef]
- Gao, L.; Chai, F. Model Predictive Direct Speed Control of Permanent-Magnet Synchronous Motors with Compensation for Inverter Nonlinearity and Bus Voltage Uncertainty. Energies 2023, 16, 5128. [Google Scholar] [CrossRef]
- Niu, F.; Wang, B.; Babel, A.S.; Li, K.; Strangas, E.G. Comparative Evaluation of Direct Torque Control Strategies for Permanent Magnet Synchronous Machines. IEEE Trans. Power Electron. 2016, 31, 1408–1424. [Google Scholar] [CrossRef]
- Karamanakos, P.; Liegmann, E.; Geyer, T.; Kennel, R. Model Predictive Control of Power Electronic Systems: Methods, Results, and Challenges. IEEE Open J. Ind. Appl. 2020, 1, 95–114. [Google Scholar] [CrossRef]
- Park, J.-H.; Kim, D.J.; Lee, K.-B. Predictive Control Algorithm Including Conduction-Mode Detection for PFC Converter. IEEE Trans. Ind. Electron. 2016, 63, 5900–5911. [Google Scholar] [CrossRef]
- Vazquez, S.; Rodriguez, J.; Rivera, M.; Franquelo, L.G.; Norambuena, M. Model Predictive Control for Power Converters and Drives: Advances and Trends. IEEE Trans. Ind. Electron. 2017, 64, 935–947. [Google Scholar] [CrossRef]
- Dragičević, T.; Novak, M. Weighting factor design in model predictive control of power electronic converters: An artificial neural network approach. IEEE Trans. Ind. Electron. 2019, 66, 8870–8880. [Google Scholar] [CrossRef]
- Zarei, M.E.; Nicolas, C.V.; Arribas, J.R. Improved Predictive Direct Power Control of Doubly Fed Induction Generator During Unbalanced Grid Voltage Based on Four Vectors. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 695–707. [Google Scholar] [CrossRef]
- Zhang, Z.; Hackl, C.M.; Kennel, R. Computationally efficient DMPC for three-level NPC back-to-back converters in wind turbine systems with PMSG. IEEE Trans. Power Electron. 2017, 32, 8018–8034. [Google Scholar] [CrossRef]
- Kwak, S.; Mun, S. Model predictive control methods to reduce common-mode voltage for three-phase voltage source inverters. IEEE Trans. Power Electron. 2015, 30, 5019–5035. [Google Scholar] [CrossRef]
- Zhang, Z.; Fang, H.; Gao, F.; Rodríguez, J.; Kennel, R. Multiplevector model predictive power control for grid-tied wind turbine system with enhanced steady-state control performance. IEEE Trans. Ind. Electron. 2017, 64, 6287–6298. [Google Scholar] [CrossRef]
- Mohd Alsofyani, I.; Lee, K.-B. Predictive Torque Control Based on Discrete Space Vector Modulation of PMSM without Flux Error-Sign and Voltage-Vector Lookup Table. Electronics 2020, 9, 1542. [Google Scholar] [CrossRef]
- Zhou, S.; Zhu, M.; Lin, J.; Ipoum-Ngome, P.G.; Mon-Nzongo, D.L.; Jin, T. Discrete space vector modulation and optimized switching sequence model predictive control for three-level voltage source inverters. Prot. Control Mod. Power Syst. 2023, 8, 64. [Google Scholar] [CrossRef]
- Boudallaa, A.; Belkhadir, A.; Chennani, M.; Belkhayat, D.; Zidani, Y.; Rhofir, K. Real-Time Implementation of Sensorless DTC-SVM Applied to 4WDEV Using the MRAS Estimator. Energies 2023, 16, 7090. [Google Scholar] [CrossRef]
- Yu, H.; Wang, J.; Xin, Z. Model Predictive Control for PMSM Based on Discrete Space Vector Modulation with RLS Parameter Identification. Energies 2022, 15, 4041. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, X.; Niu, S. A Hybrid Two-Stage Control Solution for Six-Phase PMSM Motor With Improved Performance. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 5435–5445. [Google Scholar] [CrossRef]
- Zhang, F.; Yu, S.; Wang, Y.; Jin, S.; Jovanovic, M.G. Design and Performance Comparisons of Brushless Doubly Fed Generators With Different Rotor Structures. IEEE Trans. Ind. Electron. 2019, 66, 631–640. [Google Scholar] [CrossRef]
- Osman, I.; Xiao, D.; Alam, K.S.; Shakib, S.M.S.I.; Akter, P.; Rahman, M.F. Discrete Space Vector Modulation-Based Model Predictive Torque Control With No Suboptimization. IEEE Trans. Ind. Electron. 2020, 67, 8164–8174. [Google Scholar] [CrossRef]
- Norris, G.; Ducard, G.J.J.; Onder, C. Neural Networks for Control: A Tutorial and Survey of Stability-Analysis Methods, Properties, and Discussions. In Proceedings of the 2021 International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME), Mauritius, Mauritius, 7–8 October 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Xu, H.; Lai, J.G.; Liu, J.Y.; Cao, N.; Zhao, J. Neural Network Pattern Recognition and its Application. Adv. Mater. Res. 2013, 756–759, 2438–2442. [Google Scholar] [CrossRef]
- Novak, M.; Dragicevic, T. Supervised imitation learning of finite-set model predictive control systems for power electronics. IEEE Trans. Ind. Electron. 2021, 68, 1717–1723. [Google Scholar] [CrossRef]
- Mohamed, I.S.; Rovetta, S.; Do, T.D.; Dragicević, T.; Diab, A.A.Z. A neural-network-based model predictive control of three-phase inverter with an output LC filter. IEEE Access 2019, 7, 124737–124749. [Google Scholar] [CrossRef]
- Al-Kaf, H.A.G.; Lee, K.-B. Low Complexity MPC-DSVPWM for Current Control of PMSM Using Neural Network Approach. IEEE Access 2022, 10, 132596–132607. [Google Scholar] [CrossRef]
- Guo, J.; Sun, L.; Kawaguchi, T.; Hashimoto, S. Neural Network Compensator-Based Control for Enhancing IPMSM Dynamics and Copper Loss Efficiency for Air Compressor. IEEE Access 2024, 12, 62986–62996. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Xie, W.; Wang, F.; Dou, M.; Kennel, R.M.; Lorenz, R.D.; Gerling, D. Deadbeat model-predictive torque control with discrete space-vector modulation for pmsm drives. IEEE Trans. Ind. Electron. 2017, 64, 3537–3547. [Google Scholar] [CrossRef]
- Casadei, D.; Serra, G.; Tani, A. Improvement of direct torque control performance by using a discrete SVM technique. In Proceedings of the IEEE Power Electronics Specialist Conference (PESC’98), Fukuoka, Japan, 22 May 1998; Volume 2, pp. 997–1003. [Google Scholar]
- Casadei, D.; Serra, G.; Tani, A. Implementation of a direct control algorithm for induction motors based on discrete space vector modulation. IEEE Trans. Power Electron. 2000, 15, 769–777. [Google Scholar] [CrossRef]
- Keyhani, H.R.; Zolghadri, M.R.; Homaifar, A. An extended and improved discrete space vector modulation direct torque control for induction motors. In Proceedings of the IEEE Power Electronics Specialists Conference (PESC’04), Aachen, Germany, 20–25 June 2004; Volume 5, pp. 3414–3420. [Google Scholar]
- Ocen, D.; Romeral, L.; Ortega, J.A.; Cusido, J.; Garcia, A. Discrete Space Vector Modulation Applied on a PMSM Motor. In Proceedings of the IEEE Power Electronics Specialists Conference (PESC’06), Portoroz, Slovenia, 18–22 June 2004; pp. 1–5. [Google Scholar]
- Singh, B.; Goyal, D. Improved DSVM-DTC Based Current Sensorless Permanent Magnet Synchronous Motor Drive. In Proceedings of the Seventh International Conference on Power Electronics and Drive Systems (PEDS 2007), Portoroz, Slovenia, 27–30 November 2007; pp. 1354–1360. [Google Scholar]
- Zhang, Y.; Huangfu, Y.; Tan, B.; Quan, S.; Li, P.; Tian, C. A Virtual MPC-Based Artificial Neural Network Controller for PMSM Drives in Aircraft Electric Propulsion System. In Proceedings of the 2022 IEEE Industry Applications Society Annual Meeting (IAS), Detroit, MI, USA, 9–14 October 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Ranganathan, A. The Levenberg-Marquardt Algorithm. 2004. Available online: http://www.ananth.in/Notes_files/lmtut.pdf (accessed on 8 June 2004).
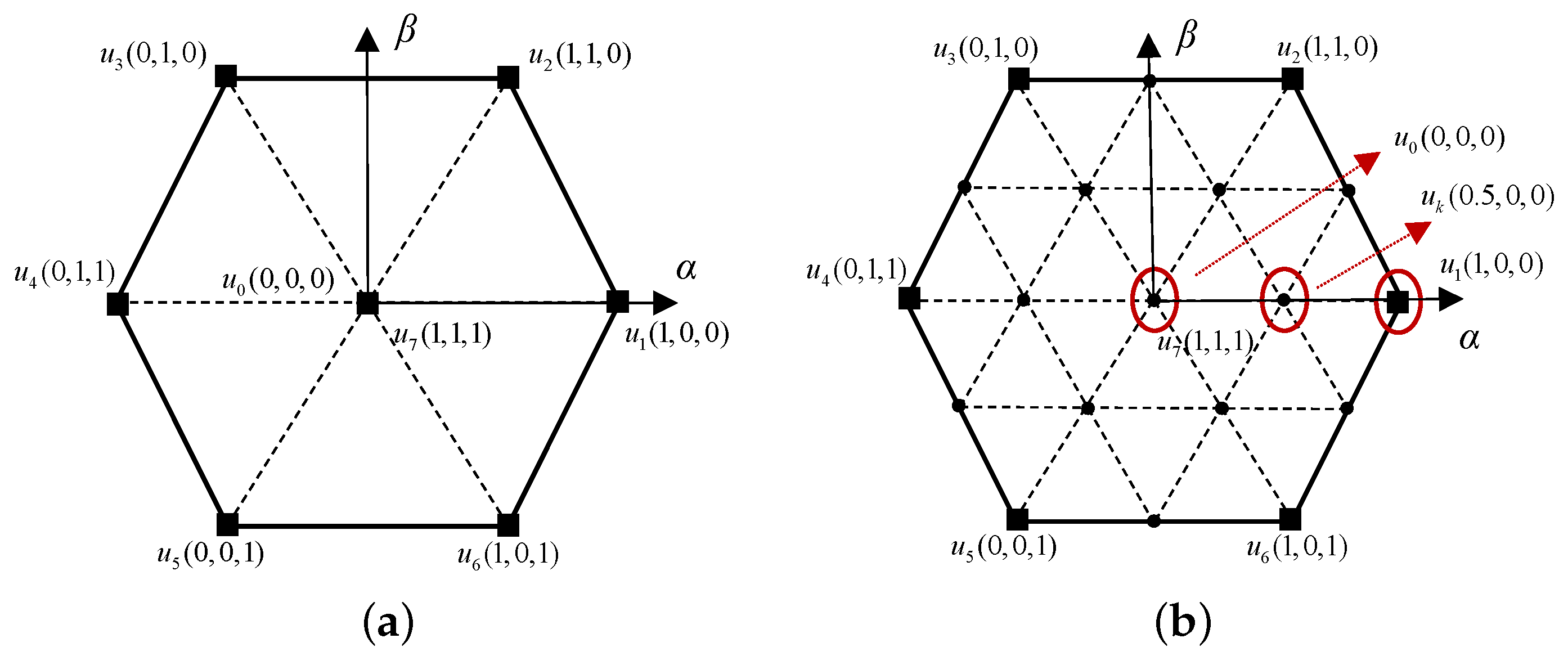

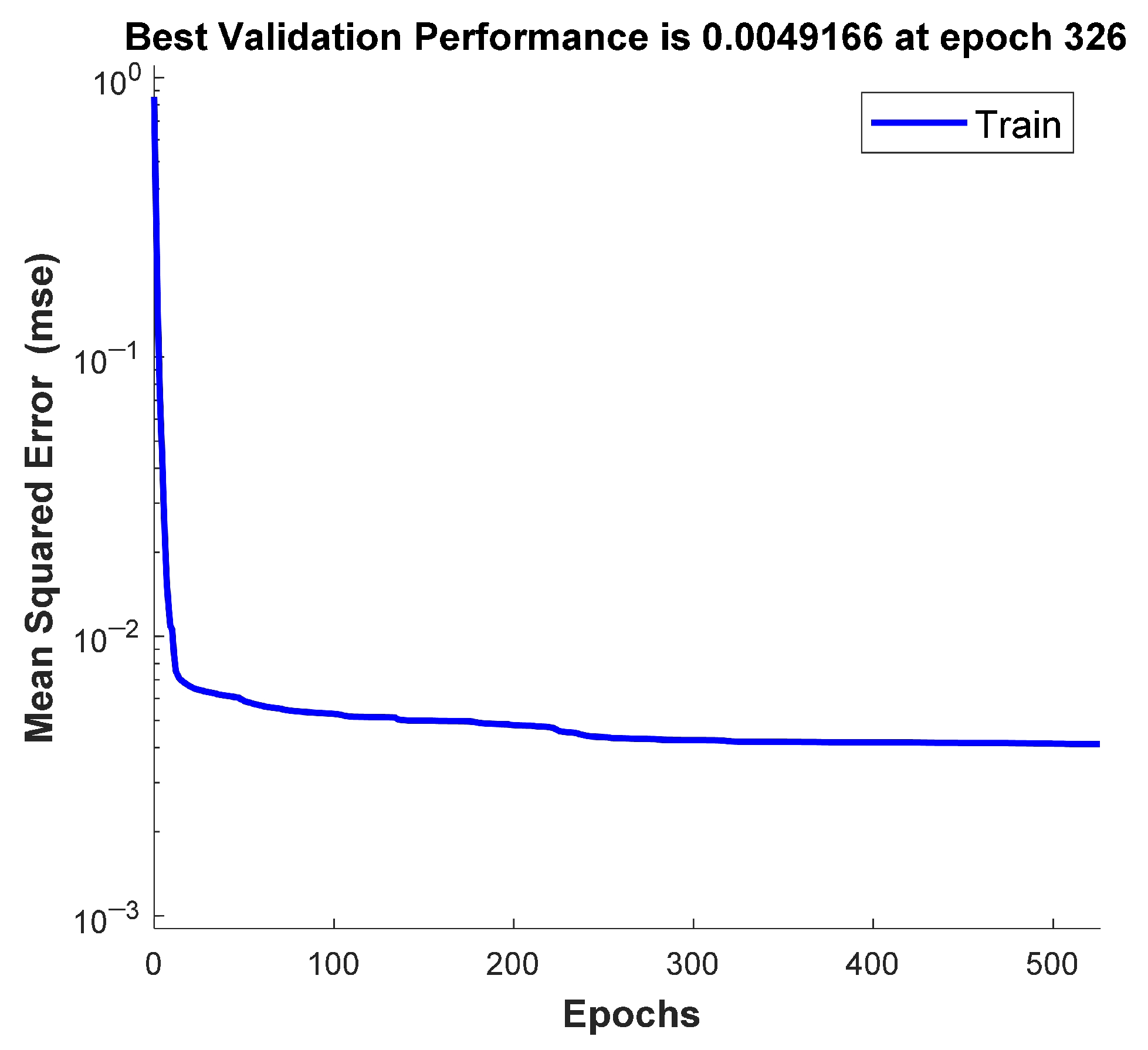
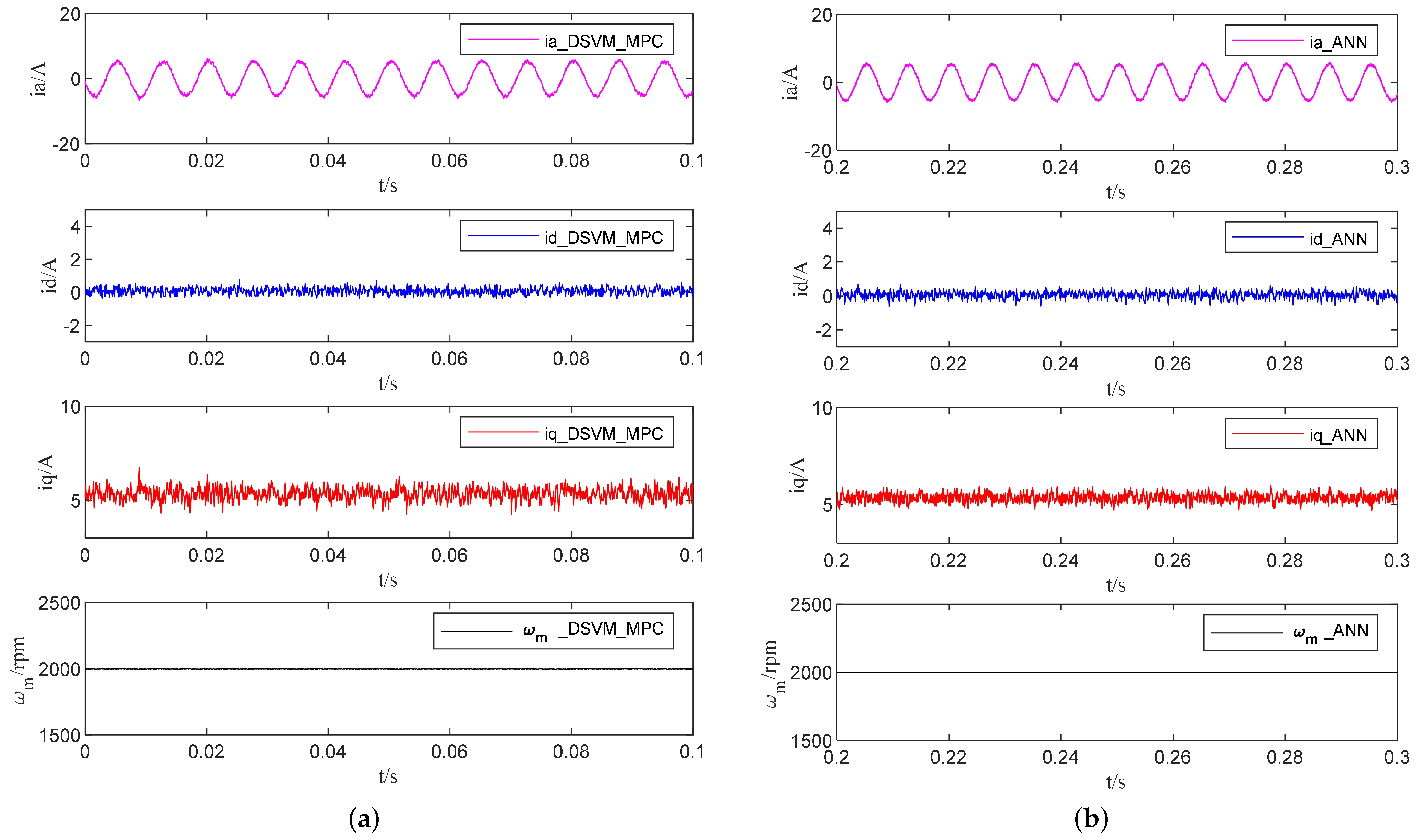
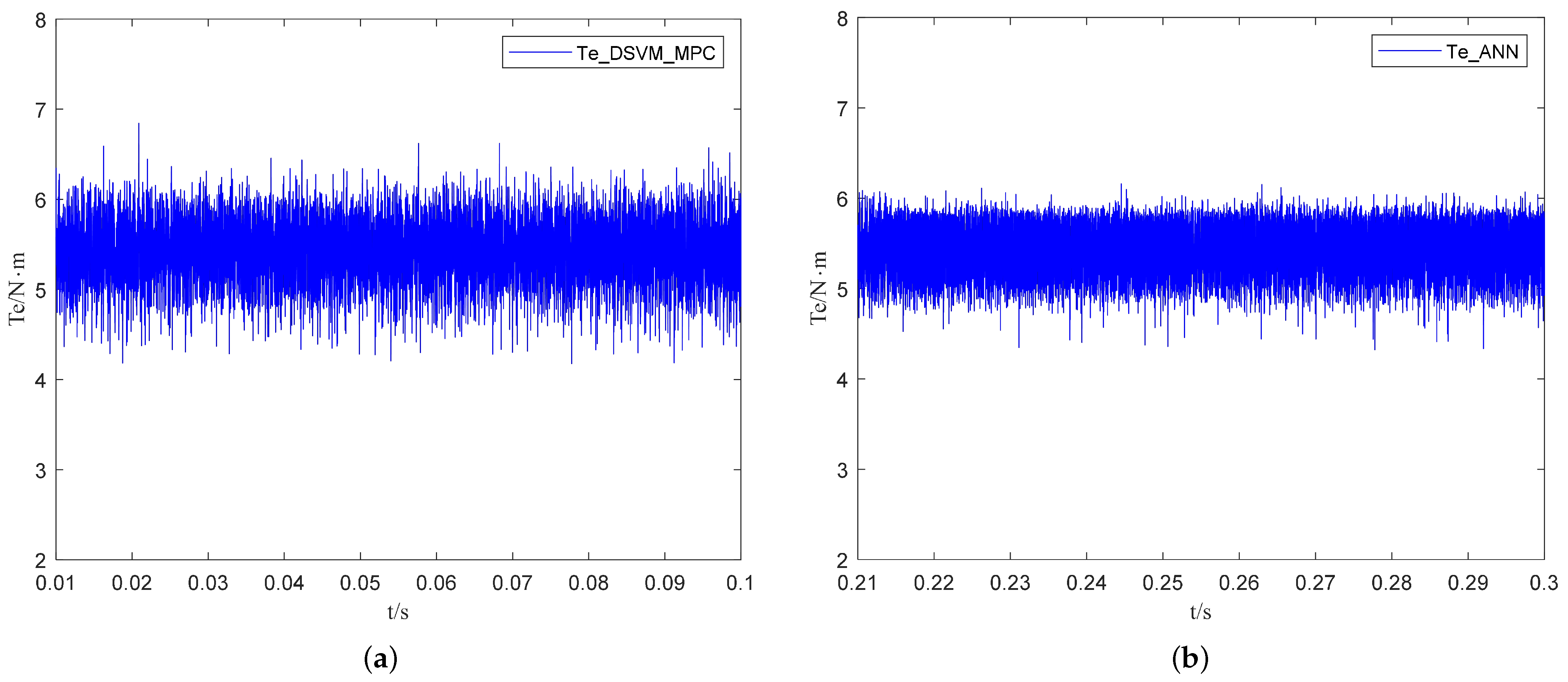
| Parameters | Value | Unit |
|---|---|---|
| DC bus voltage | 311 | V |
| Permanent magnet flux | 0.1688 | Wb |
| Stator inductance | 8.5 | mH |
| Stator copper resistance | 0.998 | |
| Sampling period | 10k | Hz |
| Pole pairs | 4 | / |
| Current | DSVM-MPC | ANN |
|---|---|---|
| ripple rate | 10.58% | 9.83% |
| ripple rate | 11.03% | 10.32% |
| ripple rate | 10.89% | 10.13% |
| Methods | Execution Time (μs) |
|---|---|
| DSVM-MPC | 9.074 |
| ANN | 8.172 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Kawaguchi, T.; Hashimoto, S. A Discrete Space Vector Modulation MPC-Based Artificial Neural Network Controller for PMSM Drives. Machines 2025, 13, 996. https://doi.org/10.3390/machines13110996
Guo J, Kawaguchi T, Hashimoto S. A Discrete Space Vector Modulation MPC-Based Artificial Neural Network Controller for PMSM Drives. Machines. 2025; 13(11):996. https://doi.org/10.3390/machines13110996
Chicago/Turabian StyleGuo, Jiawei, Takahiro Kawaguchi, and Seiji Hashimoto. 2025. "A Discrete Space Vector Modulation MPC-Based Artificial Neural Network Controller for PMSM Drives" Machines 13, no. 11: 996. https://doi.org/10.3390/machines13110996
APA StyleGuo, J., Kawaguchi, T., & Hashimoto, S. (2025). A Discrete Space Vector Modulation MPC-Based Artificial Neural Network Controller for PMSM Drives. Machines, 13(11), 996. https://doi.org/10.3390/machines13110996






