The Diagnosis and Recovery of Faults in the Workshop Environmental Control System Sensor Network Based on Medium-to-Long-Term Predictions
Abstract
1. Introduction
2. The Framework for Fault Diagnosis and Recovery
- (1)
- Data Preprocessing: Missing data are initially filled using a one-dimensional interpolation method, followed by the elimination of unstable data points. Exponential Weighted Moving Average (EWMA) is employed for noise reduction in the acquired data to enhance data quality. Subsequently, the data are normalized to mitigate the influence of varying scales. For the experiment, the data are partitioned into training, testing, and validation sets. The training set is utilized to train the Informer model; the testing set is used to determine the fault threshold; and the validation set is employed for conducting fault diagnosis trials.
- (2)
- Construction of Multivariate Input Medium-to-Long-Term Prediction Model: The preprocessed data are fed into the encoder of the Informer model. Within the encoder, critical features are extracted from the data via a sparse self-attention mechanism, capturing long-term dependencies within the time series and spatial correlations among different sensors. Subsequently, these extracted features are utilized by the decoder, which predicts the entire future time series through a generative decoding mechanism. During model construction, Mean Squared Error (MSE) is adopted as the loss function, and early stopping is implemented to prevent overfitting.
- (3)
- State Prediction: Based on the sensor prediction sequences, these predicted values are utilized as temporary references during the current system operation. This enables the future state of sensors to be anticipated in advance, thereby preventing system failures caused by state delays or unexpected events.
- (4)
- Fault Threshold Analysis: The residual sequences between the outputs of the diagnostic soft sensors and the physical sensors on the testing set are calculated. The method described in Section 3.2 is then applied to determine the fault threshold based on these residuals.
- (5)
- Fault Diagnosis: Fault diagnosis is performed by applying the criterion of consecutive exceedances. A data point is identified as faulty when the residuals of a sensor exceed the fault threshold continuously for five consecutive instances.
- (6)
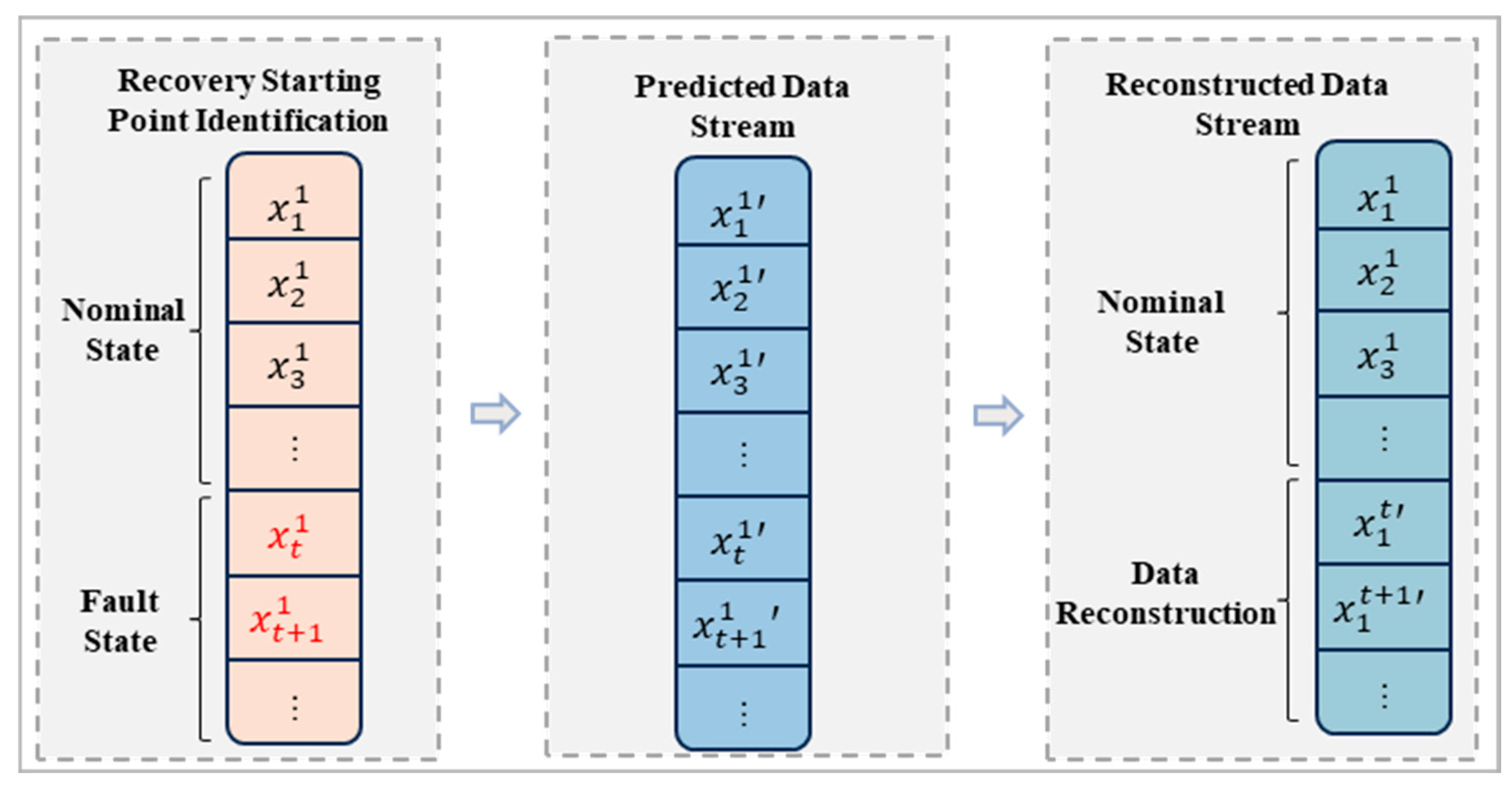
- Fault Data Recovery: Following the identification of faulty data points within a sensor, the predicted values output by the fault diagnosis model are employed to overwrite the faulty values. The predicted values are thus substituted for the faulty ones during the diagnostic process, achieving fault data recovery.
3. A Long-Term Predictive Fault Diagnosis Model for the Sensor Network in the Workshop Environmental Control System
3.1. Long Sequence Prediction Model Informer
- (1)
- Informer Model Input
- (2)
- Probability Sparse Self-Attention Mechanism
- (3)
- Encoder
- (4)
- Decoder
3.2. Sensor System State Prediction
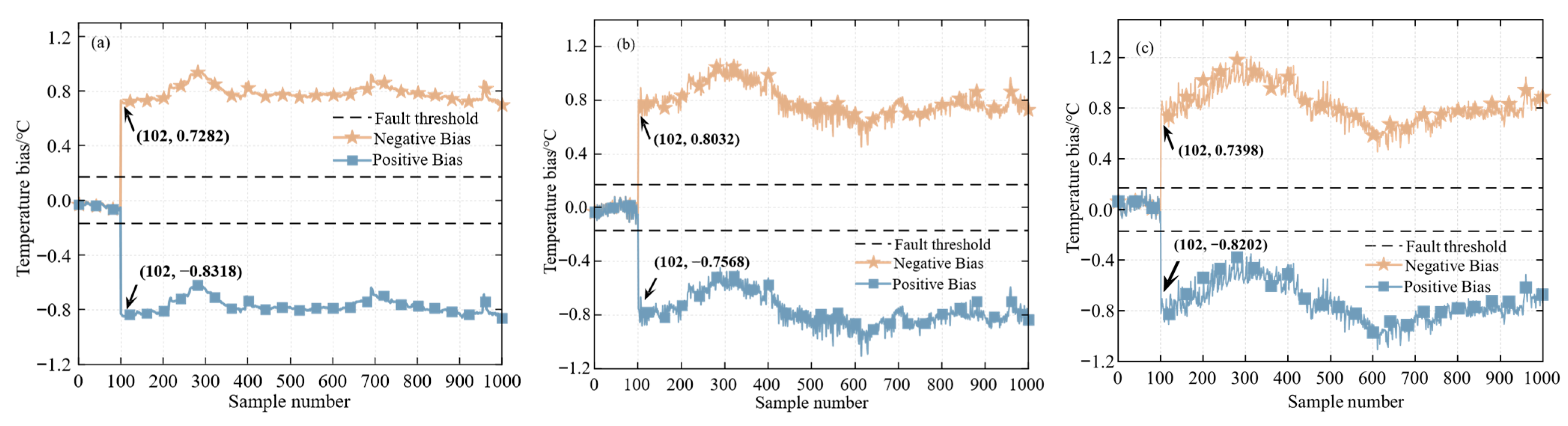
3.3. Fault Threshold Analysis
3.4. Residual-Based Sensor Fault Diagnosis
3.5. Data Recovery for Faulty Sensors
4. Experimental Results and Analysis
4.1. Experimental Data
4.2. Evaluation Indicators
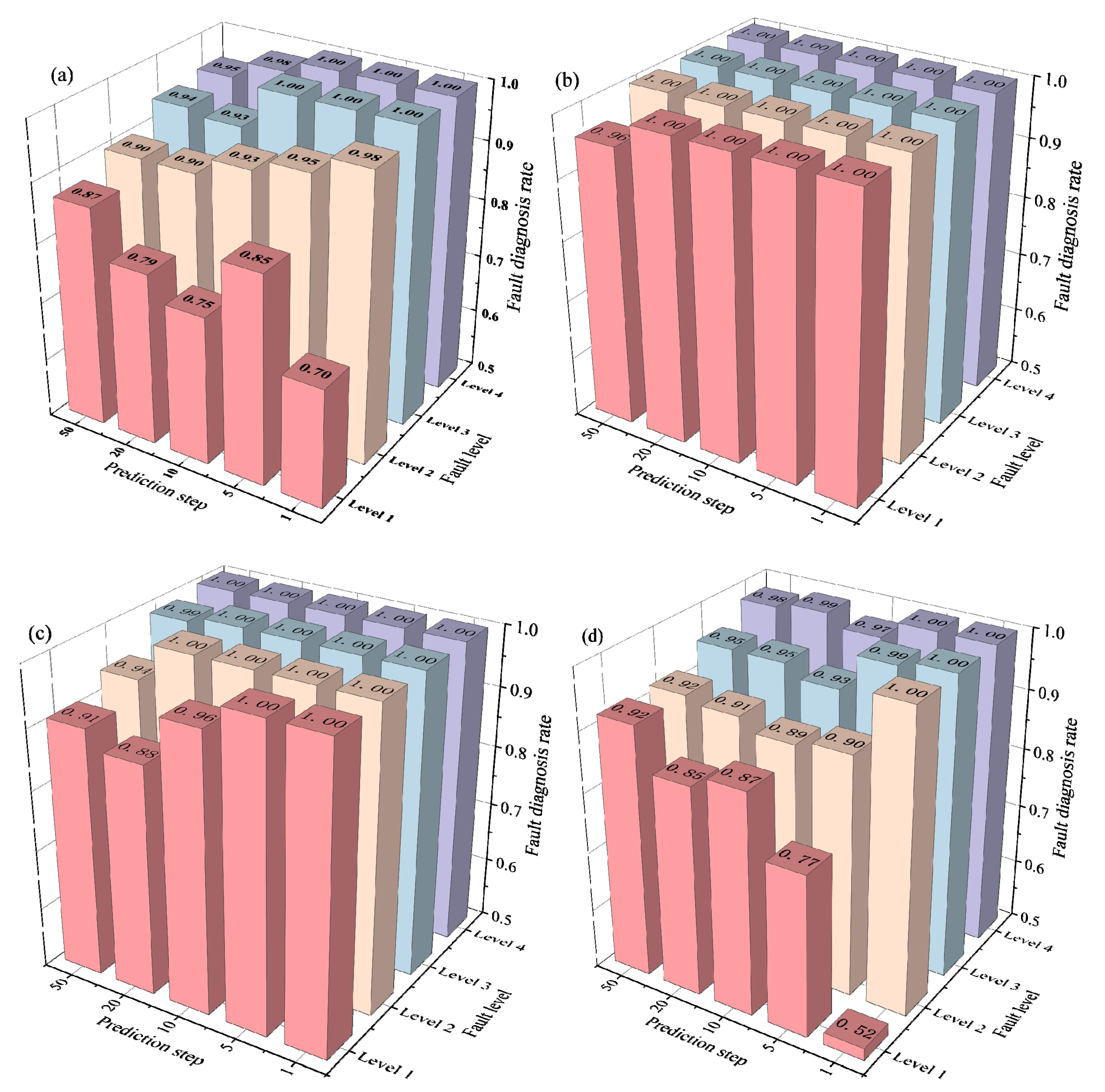
4.3. Analysis of Fault Diagnosis Results
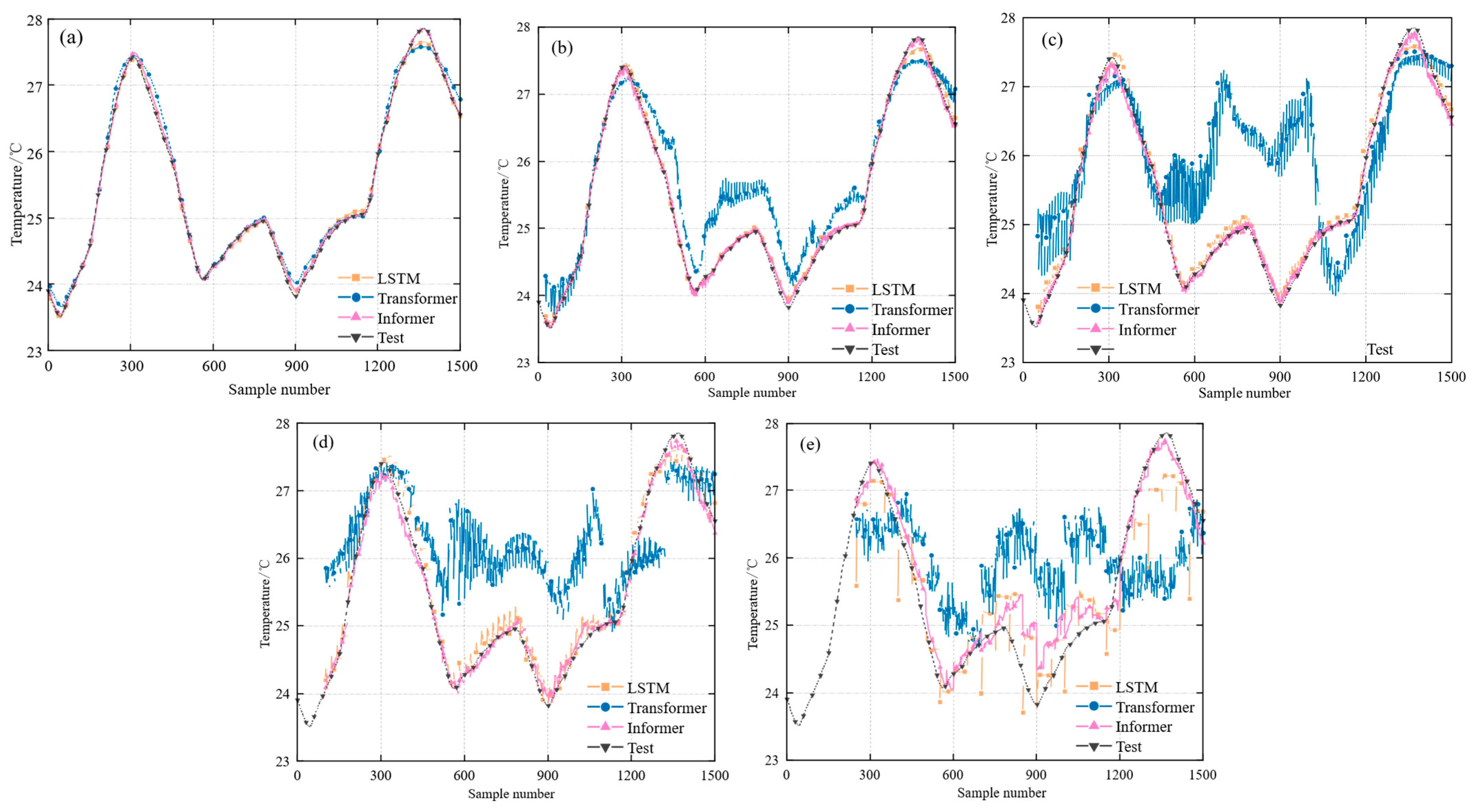
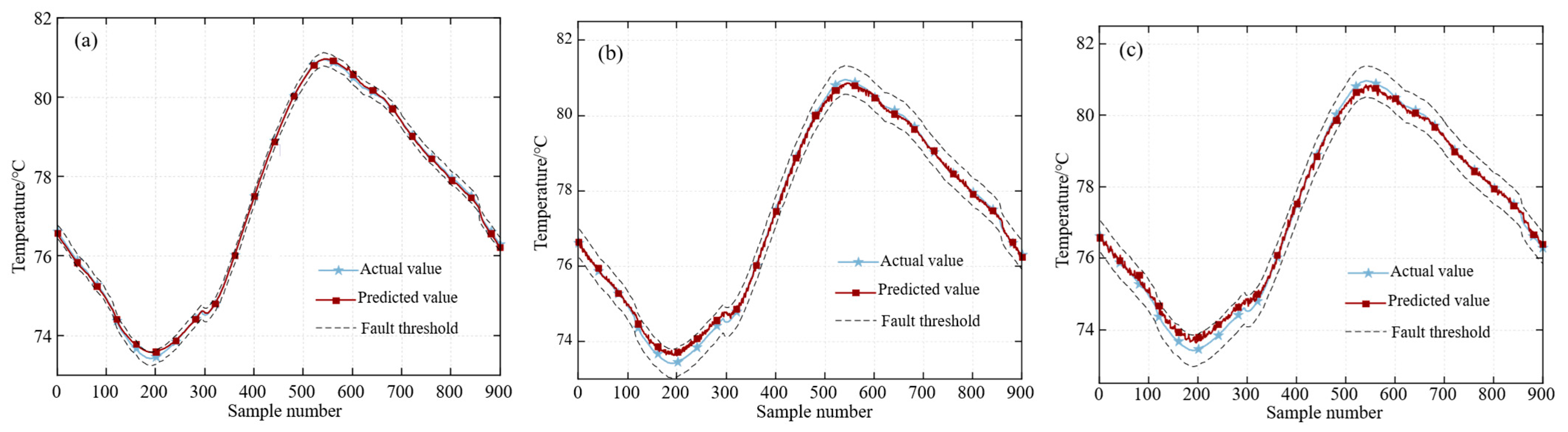
4.3.1. Prediction Results Analysis
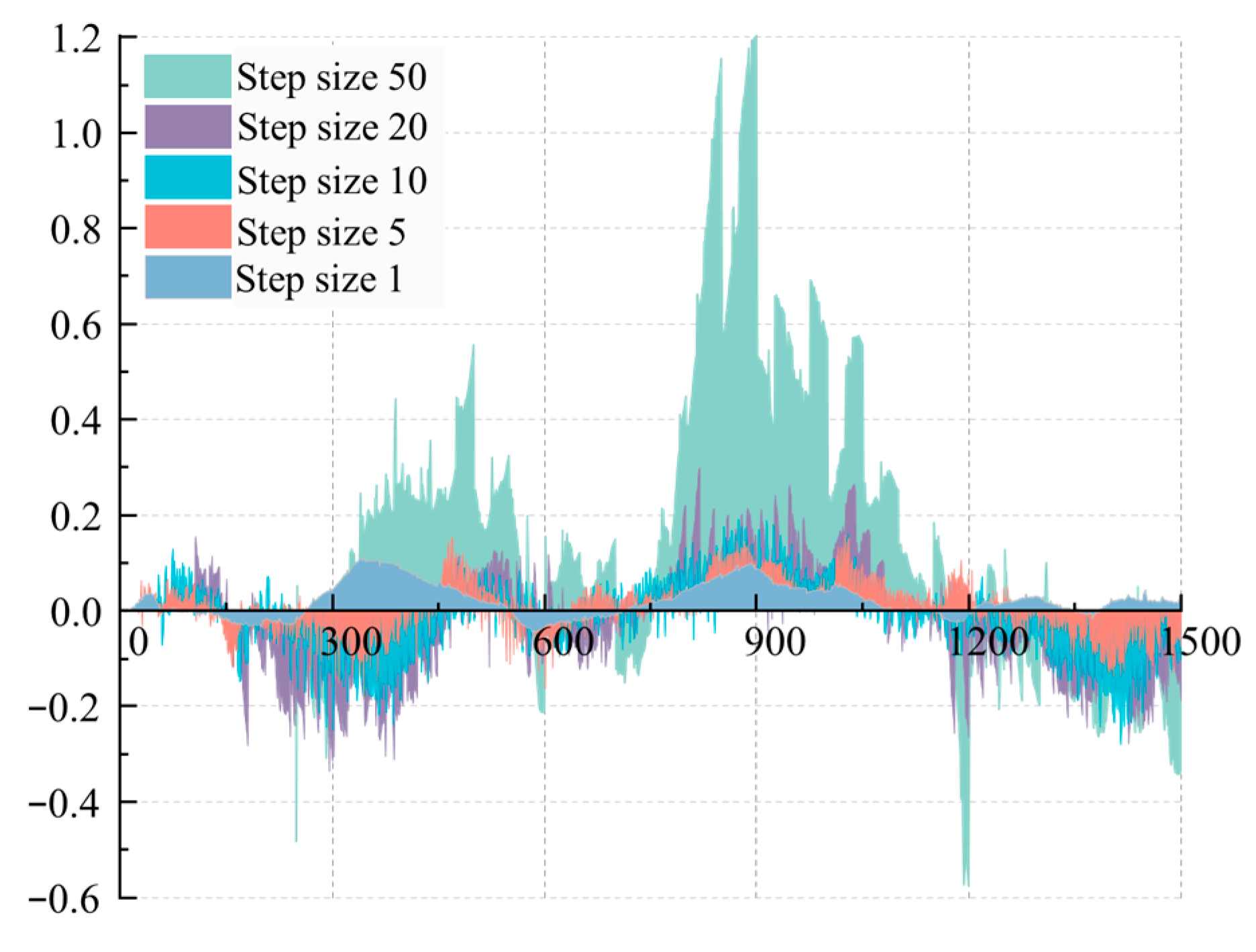
4.3.2. Analysis of Fault Thresholds and Fault Diagnosis Results
4.4. Fault Recovery Result Analysis
5. Conclusions
- (1)
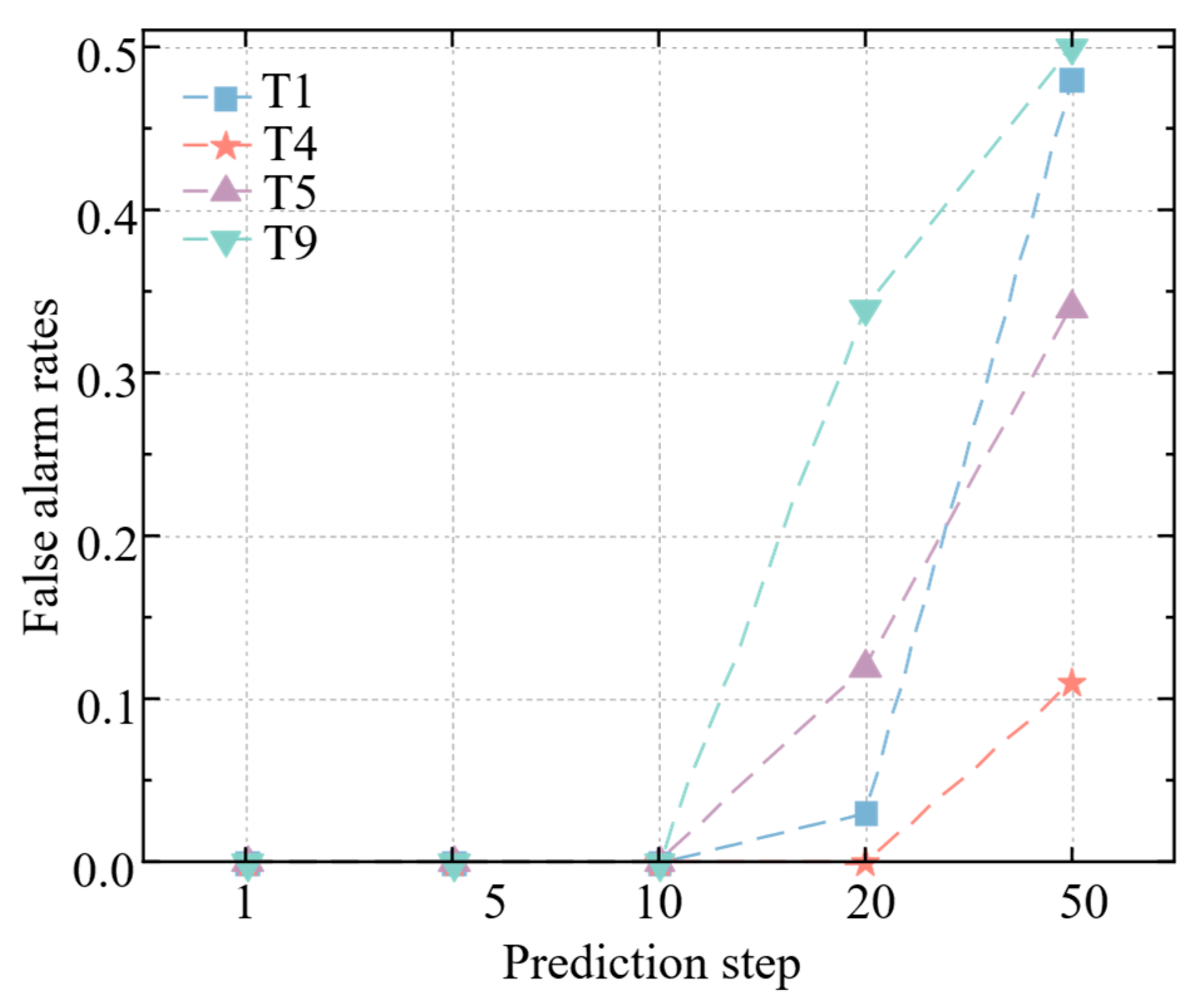
- Compared with the LSTM and Transformer models, the Informer model achieves superior performance on long time series, exhibiting the best prediction results at step lengths of 1, 5, 10, 20, and 50. This capability enables accurate state prediction within the sensor’s prediction horizon. Specifically, the experiment with a prediction step of 10 achieves both high fault diagnosis rates and low false alarm rates, confirming the method’s effectiveness in predicting sensor states for up to 50 s into the future.
- (2)
- For the same sensor, improved fault diagnosis performance is observed with higher fault levels. The average fault diagnosis rates for Level 1 to Level 4 are recorded as 85.69%, 95.17%, 98.71%, and 99.58%, respectively. At prediction steps of 1, 5, 10, 20, and 50, the average diagnosis rates for T1–T9 sensors are maintained at 94.40%, 95.28%, 94.79%, 92.52%, and 93.35%, demonstrating effective fault diagnosis capability across various conditions.
- (3)
- Through medium-to-long-term prediction, faulty data recovery is successfully achieved in this study. The reconstructed data are guaranteed to remain within the fault threshold range, enabling short-term data restoration. System operation can be maintained under sensor fault conditions through this approach. This method has been established as providing a viable medium-to-long-term prediction solution for sensor network fault diagnosis in workshop environmental control systems. Future research should be directed toward exploring methods to increase prediction step lengths while ensuring diagnostic accuracy and reliability.
- (4)
- Adapting this method to new applications does indeed incur a one-time initial model training cost, but its long-term operation and calibration costs are low. Therefore, we believe that this method has significant competitiveness in terms of cost-effectiveness. Its one-time upfront investment can bring long-term reliability and stability improvement to industrial systems, avoiding huge economic losses caused by sudden failures, thus having high practical application value and return rate.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Negi, V.P.S.; Ranganayakulu, C. Energy-efficient three-wheel bleedless electrical environmental control system for a passenger aircraft. J. Appl. Therm. Sci. Eng. Appl. 2025, 17, 021009. [Google Scholar] [CrossRef]
- Jennions, I.; Ali, F.; Miguez, M.E.; Escobar, I.C. Simulation of an aircraft environmental control system. J. Appl. Therm. Eng. 2020, 172, 114925. [Google Scholar] [CrossRef]
- Verma, P.; Kumar, V.; Daim, T.; Sharma, N.K. Design thinking framework toward management control system in environmental dynamism: An innovation perspective. J. IEEE Trans. Eng. Manag. 2024, 71, 4955–4970. [Google Scholar] [CrossRef]
- Petera, P.; Wagner, J.; Paksiova, R. The Influence of environmental strategy, environmental reporting and environmental management control system on environmental and economic performance. J. Energ. 2021, 14, 4637. [Google Scholar] [CrossRef]
- Cozza, A. Low frequency model-based identification of soft impedance faults in cables. J. IEEE Trans. Instrum. Meas. 2019, 68, 3524–3535. [Google Scholar] [CrossRef]
- Ginzarly, R.; Moubayed, N.; Hoblos, G.; Kanj, H.; Alakkoumi, M.; Mawas, A. Assessing HMM and SVM for condition-based monitoring and fault detection in HEV electrical machines. J. Energ. 2025, 18, 3513. [Google Scholar] [CrossRef]
- Yan, K.; Zhong, C.W.; Ji, Z.W.; Huang, J. Semi-supervised learning for early detection and diagnosis of various air handling unit faults. J. Energy Build. 2018, 181, 75–83. [Google Scholar] [CrossRef]
- Orellana, C.; Ortiz, L.; Aguila, A.; Garcia, M.; Ruiz, M. Hybrid algorithm for fault detection in three-phase motors using principal component analysis. J. E-Prime—Adv. Electr. Eng. Electron. Energy 2025, 11, 100916. [Google Scholar] [CrossRef]
- Mao, Q.J.; Fang, X.; Hu, Y.P.; Li, G. Chiller sensor fault detection based on empirical mode decomposition threshold denoising and principal component analysis. J. Appl. Therm. Eng. 2018, 144, 21–30. [Google Scholar] [CrossRef]
- Zhong, X.P.; Zhang, L.; Ban, H. Deep reinforcement learning for class imbalance fault diagnosis of equipment in nuclear power plants. J. Ann. Nucl. Energy 2023, 184, 109685. [Google Scholar] [CrossRef]
- Gins, G.; Kerkhof, D.V.P.; Vanlaer, J.; Van Impe, J.F. Improving classification-based diagnosis of batch processes through data selection and appropriate pretreatment. J. Process Control 2015, 26, 90–101. [Google Scholar] [CrossRef]
- Wang, X.; Shen, C.Q.; Xia, M.; Wang, D.; Zhu, J.; Zhu, Z. Multi-scale deep intra-class transfer learning for bearing fault diagnosis. J. Reliab. Eng. Syst. Saf. 2020, 202, 107050. [Google Scholar] [CrossRef]
- Li, G.N.; Xiong, C.L.; Gao, J.J.; Zhu, H.; Wang, C.; Xiao, J. Fault detection, diagnosis and calibration of heating, ventilation and air conditioning sensors by combining principal component analysis and improved bayesian inference. J. Build. Eng. 2024, 82, 108230. [Google Scholar] [CrossRef]
- Zhou, H.Y.; Zhang, S.H.; Peng, J.Q.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. Proc. AAAI Conf. Artif. Intell. 2021, 35, 11106–11115. [Google Scholar] [CrossRef]
- Li, F.Y.; Wan, Z.B.; Koch, T.; Zan, G.; Li, M.; Zheng, Z.; Liang, B. Improving the accuracy of multi-step prediction of building energy consumption based on EEMD-PSO-Informer and long-time series. J. Comput. Electr. Eng. 2023, 110, 108845. [Google Scholar] [CrossRef]
- Guo, L.; Li, R.Z.; Jiang, B. A data-driven long time-series electrical line trip fault prediction method using an improved stacked-informer network. J. Sens. 2021, 21, 4466. [Google Scholar] [CrossRef] [PubMed]
- Klimek, J.; Jakub, K.; Kraśkiewicz, W.; Topolewski, M. Long-term series forecasting with query selector-efficient model of sparse attention. J. Softw. Impacts 2022, 11, 100187. [Google Scholar] [CrossRef]
- Xu, S.Q.; Yu, H.Y.; Wang, H.; Chai, H.; Ma, M.; Chen, H.; Zheng, W.X. Simultaneous diagnosis of open-switch and current sensor faults of inverters in IM drives through reduced-order interval observer. J. IEEE Trans. Ind. Electron. 2025, 72, 6485–6496. [Google Scholar] [CrossRef]
- Shaheen, K.; Chawla, A.; Rossi, P.S. Trust-Enhanced Distributed Kalman Filtering for Sensor Fault Diagnosis in Sensor Networks. J. IEEE Trans. Signal Inf. Process. Over Netw. 2025, 11, 1178–1187. [Google Scholar] [CrossRef]


| Number | Test Point | Symbol | Unit |
|---|---|---|---|
| 1 | Indoor side air inlet dry-bulb temperature | T1 | °C |
| 2 | Outdoor side air inlet dry-bulb temperature | T2 | °C |
| 3 | Compressor inlet temperature | T3 | °C |
| 4 | Compressor outlet temperature | T4 | °C |
| 5 | Condenser inlet temperature | T5 | °C |
| 6 | Condenser outlet temperature | T6 | °C |
| 7 | Evaporator inlet temperature | T7 | °C |
| 8 | Evaporator outlet temperature | T8 | °C |
| 9 | Expansion valve outlet temperature | T9 | °C |
| Sensors | Level 1 (0.5%) | Level 2 (1%) | Level 3 (1.5%) | Level 4 (2%) |
|---|---|---|---|---|
| T1 | −0.13, 0.13 | −0.25, 0.25 | −0.38, 0.38 | −0.51, 0.51 |
| T2 | −0.17, 0.17 | −0.34, 0.34 | −0.50, 0.50 | −0.67, 0.67 |
| T3 | −0.09, 0.09 | −0.17, 0.17 | −0.26, 0.26 | −0.34, 0.34 |
| T4 | −0.50, 0.50 | −1.00, 1.00 | −1.50, 1.50 | −2.00, 2.00 |
| T5 | −0.39, 0.39 | −0.78, 0.78 | −1.17, 1.17 | −1.56, 1.56 |
| T6 | −0.23, 0.23 | −0.46, 0.46 | −0.69, 0.69 | −0.93, 0.93 |
| T7 | −0.20, 0.20 | −0.40, 0.40 | −0.60, 0.60 | −0.80, 0.80 |
| T8 | −0.04, 0.04 | −0.08, 0.08 | −0.11, 0.11 | −0.15, 0.15 |
| T9 | −0.06, 0.06 | −0.13, 0.13 | −0.19, 0.19 | −0.25, 0.25 |
| Sensor | 1 | 5 | 10 | 20 | 50 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | |
| T1 | 0.0417 | 0.0316 | 0.0536 | 0.0419 | 0.0808 | 0.0636 | 0.1259 | 0.1054 | 0.3566 | 0.2674 |
| T2 | 0.0524 | 0.0383 | 0.1206 | 0.0999 | 0.1252 | 0.0970 | 0.1168 | 0.0911 | 0.2910 | 0.2101 |
| T3 | 0.0248 | 0.0218 | 0.0431 | 0.0349 | 0.0466 | 0.0387 | 0.0680 | 0.0568 | 0.1195 | 0.1017 |
| T4 | 0.0423 | 0.0317 | 0.0549 | 0.0439 | 0.0742 | 0.0579 | 0.1111 | 0.0840 | 0.2504 | 0.1923 |
| T5 | 0.0392 | 0.0299 | 0.0909 | 0.0682 | 0.1317 | 0.1011 | 0.2075 | 0.1608 | 0.5060 | 0.4106 |
| T6 | 0.0663 | 0.0533 | 0.0892 | 0.0727 | 0.1210 | 0.0929 | 0.1840 | 0.1380 | 0.4586 | 0.3204 |
| T7 | 0.0440 | 0.0350 | 0.0961 | 0.0734 | 0.1285 | 0.0964 | 0.1994 | 0.1515 | 0.5260 | 0.3852 |
| T8 | 0.0275 | 0.0222 | 0.0366 | 0.0285 | 0.0494 | 0.0386 | 0.0680 | 0.0511 | 0.2080 | 0.1627 |
| T9 | 0.0252 | 0.0186 | 0.0596 | 0.0470 | 0.0991 | 0.0791 | 0.1671 | 0.1230 | 0.3852 | 0.2829 |
| Sensor | 1 | 5 | 10 |
|---|---|---|---|
| T1 | (−0.11, 0.11) | (−0.18, 0.18) | (−0.28, 0.28) |
| T2 | (−0.15, 0.15) | (−0.37, 0.37) | (−0.47, 0.47) |
| T3 | (−0.06, 0.06) | (−0.13, 0.13) | (−0.14, 0.14) |
| T4 | (−0.13, 0.13) | (−0.17, 0.17) | (−0.30, 0.30) |
| T5 | (−0.17, 0.17) | (−0.38, 0.38) | (−0.44, 0.44) |
| T6 | (−0.18, 0.18) | (−0.33, 0.33) | (−0.44, 0.44) |
| T7 | (−0.12, 0.12) | (−0.34, 0.34) | (−0.46, 0.46) |
| T8 | (−0.04, 0.04) | (−0.12, 0.12) | (−0.16, 0.16) |
| T9 | (−0.06, 0.06) | (−0.15, 0.15) | (−0.24, 0.24) |
| Sensor | 1 | 5 | 10 | 20 | 50 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | |
| T1 | 0.0565 | 0.9982 | 0.0678 | 0.9974 | 0.1111 | 0.9930 | 0.2197 | 0.9730 | 0.5595 | 0.8250 |
| T2 | 0.0623 | 0.9994 | 0.1564 | 0.9965 | 0.1551 | 0.9965 | 0.1713 | 0.9958 | 0.3819 | 0.9793 |
| T3 | 0.0199 | 0.9994 | 0.0484 | 0.9965 | 0.0510 | 0.9961 | 0.0924 | 0.9874 | 0.1103 | 0.9820 |
| T4 | 0.0386 | 0.9992 | 0.0671 | 0.9978 | 0.0698 | 0.9976 | 0.0962 | 0.9956 | 0.2103 | 0.9790 |
| T5 | 0.0500 | 0.9995 | 0.1079 | 0.9978 | 0.1428 | 0.9962 | 0.2261 | 0.9906 | 0.5633 | 0.9416 |
| T6 | 0.0742 | 0.9993 | 0.1216 | 0.9982 | 0.1776 | 0.9962 | 0.2612 | 0.9918 | 0.6655 | 0.9470 |
| T7 | 0.0651 | 0.9992 | 0.1392 | 0.9967 | 0.1823 | 0.9943 | 0.2776 | 0.9869 | 0.7280 | 0.9103 |
| T8 | 0.0261 | 0.9987 | 0.0477 | 0.9958 | 0.0680 | 0.9915 | 0.1136 | 0.9764 | 0.3077 | 0.8274 |
| T9 | 0.0231 | 0.9996 | 0.0715 | 0.9966 | 0.1192 | 0.9905 | 0.2183 | 0.9684 | 0.4905 | 0.8408 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, S.; Ye, F.; Zhang, X.; Tan, M.; Zhang, C. The Diagnosis and Recovery of Faults in the Workshop Environmental Control System Sensor Network Based on Medium-to-Long-Term Predictions. Machines 2025, 13, 975. https://doi.org/10.3390/machines13110975
Xiao S, Ye F, Zhang X, Tan M, Zhang C. The Diagnosis and Recovery of Faults in the Workshop Environmental Control System Sensor Network Based on Medium-to-Long-Term Predictions. Machines. 2025; 13(11):975. https://doi.org/10.3390/machines13110975
Chicago/Turabian StyleXiao, Shaohan, Fangping Ye, Xinyuan Zhang, Mengying Tan, and Canwen Zhang. 2025. "The Diagnosis and Recovery of Faults in the Workshop Environmental Control System Sensor Network Based on Medium-to-Long-Term Predictions" Machines 13, no. 11: 975. https://doi.org/10.3390/machines13110975
APA StyleXiao, S., Ye, F., Zhang, X., Tan, M., & Zhang, C. (2025). The Diagnosis and Recovery of Faults in the Workshop Environmental Control System Sensor Network Based on Medium-to-Long-Term Predictions. Machines, 13(11), 975. https://doi.org/10.3390/machines13110975






