Research Based on a Fuzzy Algorithm for Energy Saving Single-Phased Powered Pumps
Abstract
1. Introduction
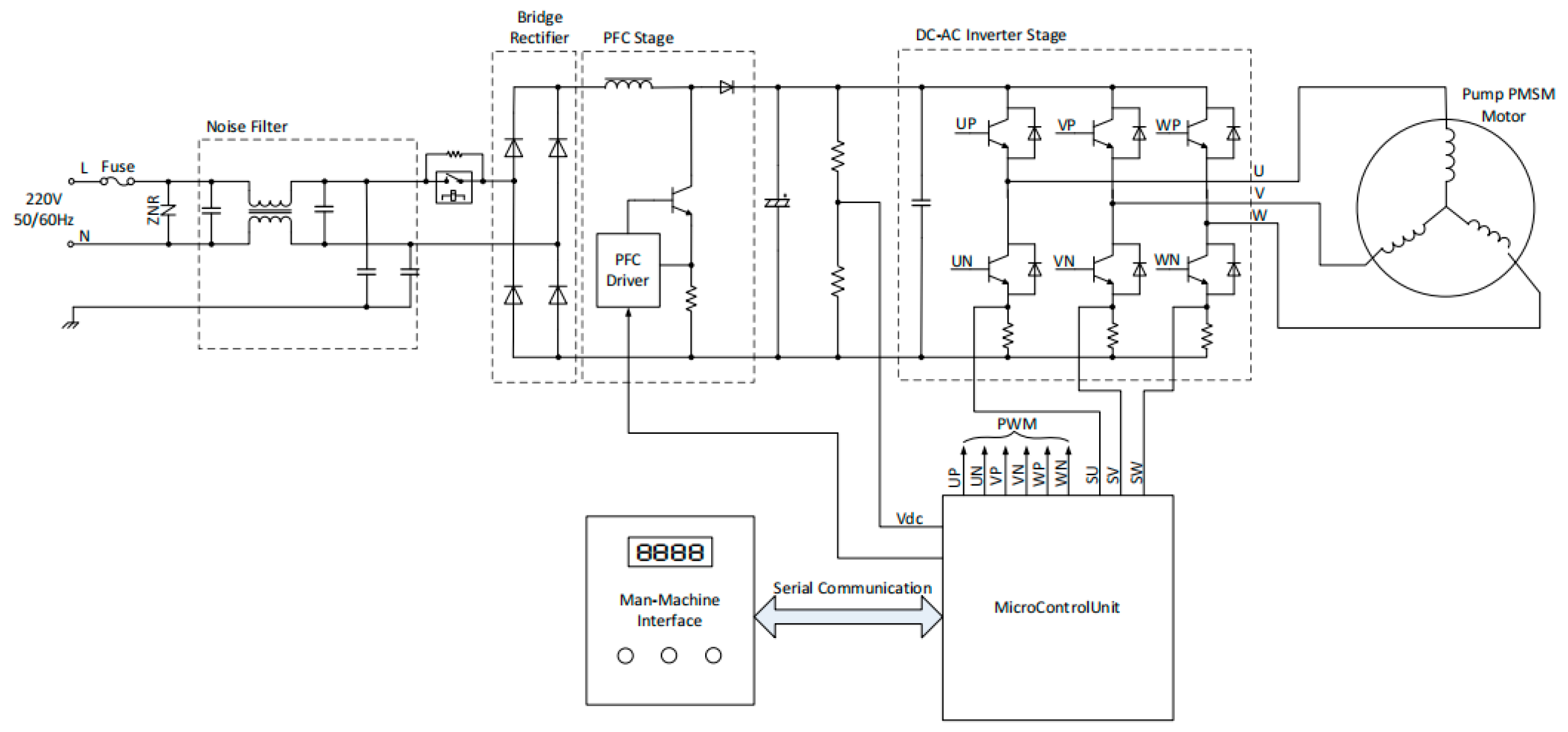
2. The Pump System
2.1. Pumps
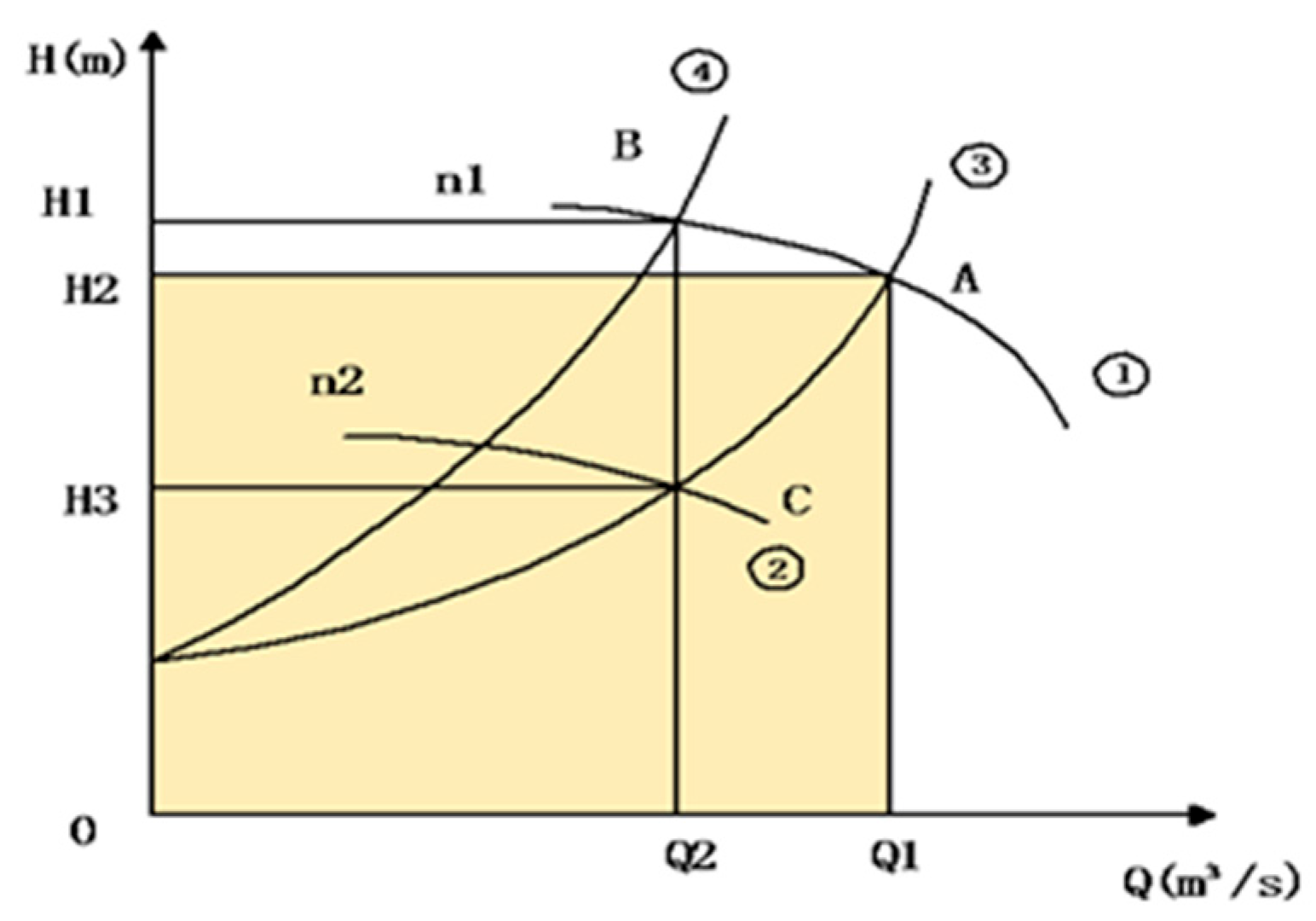
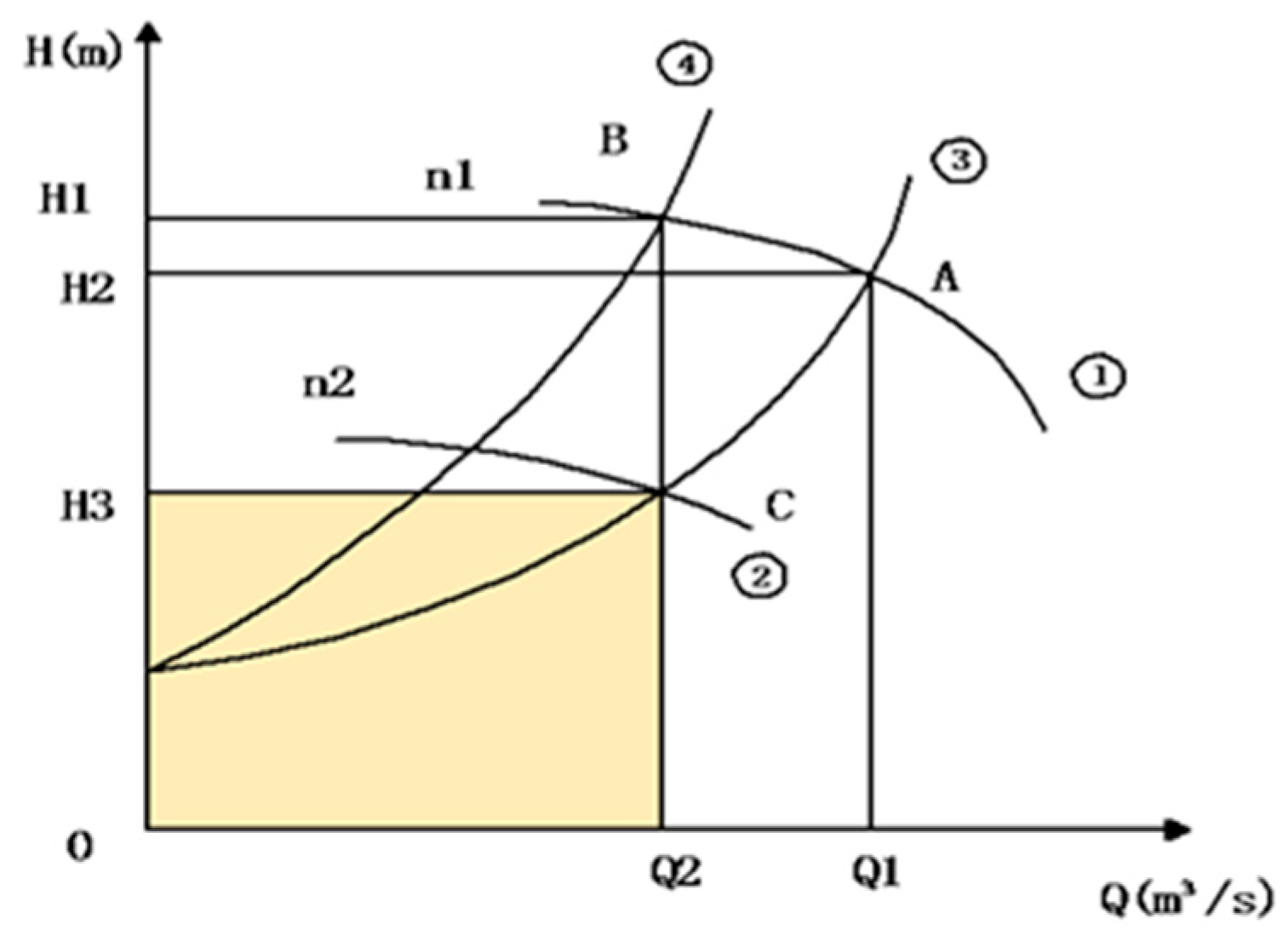
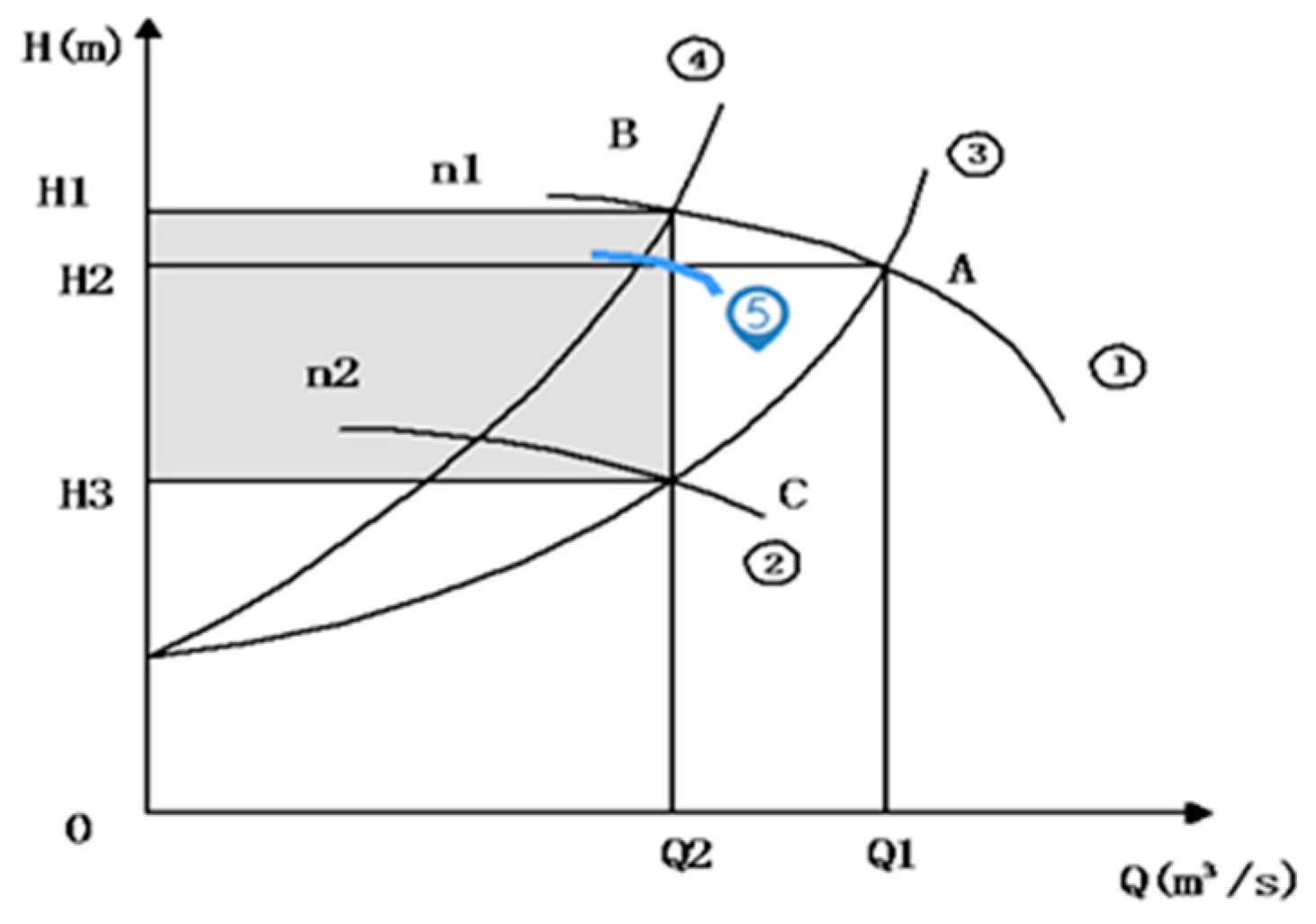
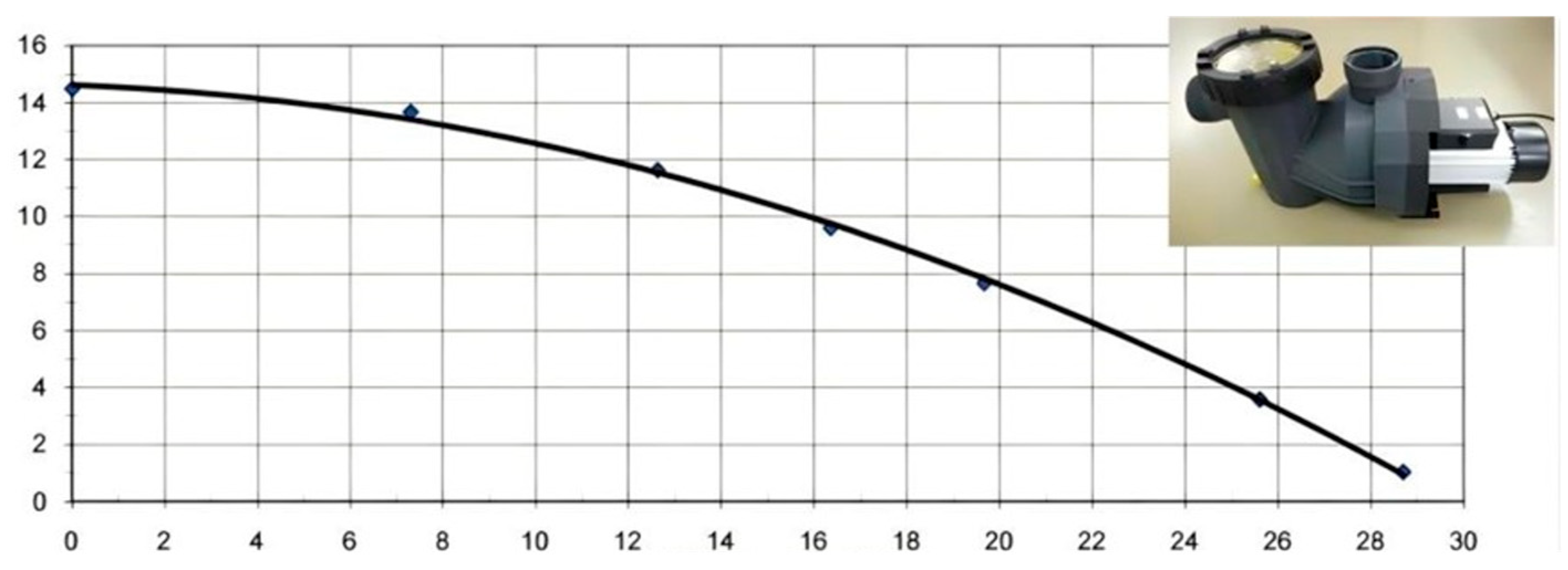
2.1.1. Pumps’ Mechanical Characteristics
2.1.2. The Energy Saving Principle of Pumps
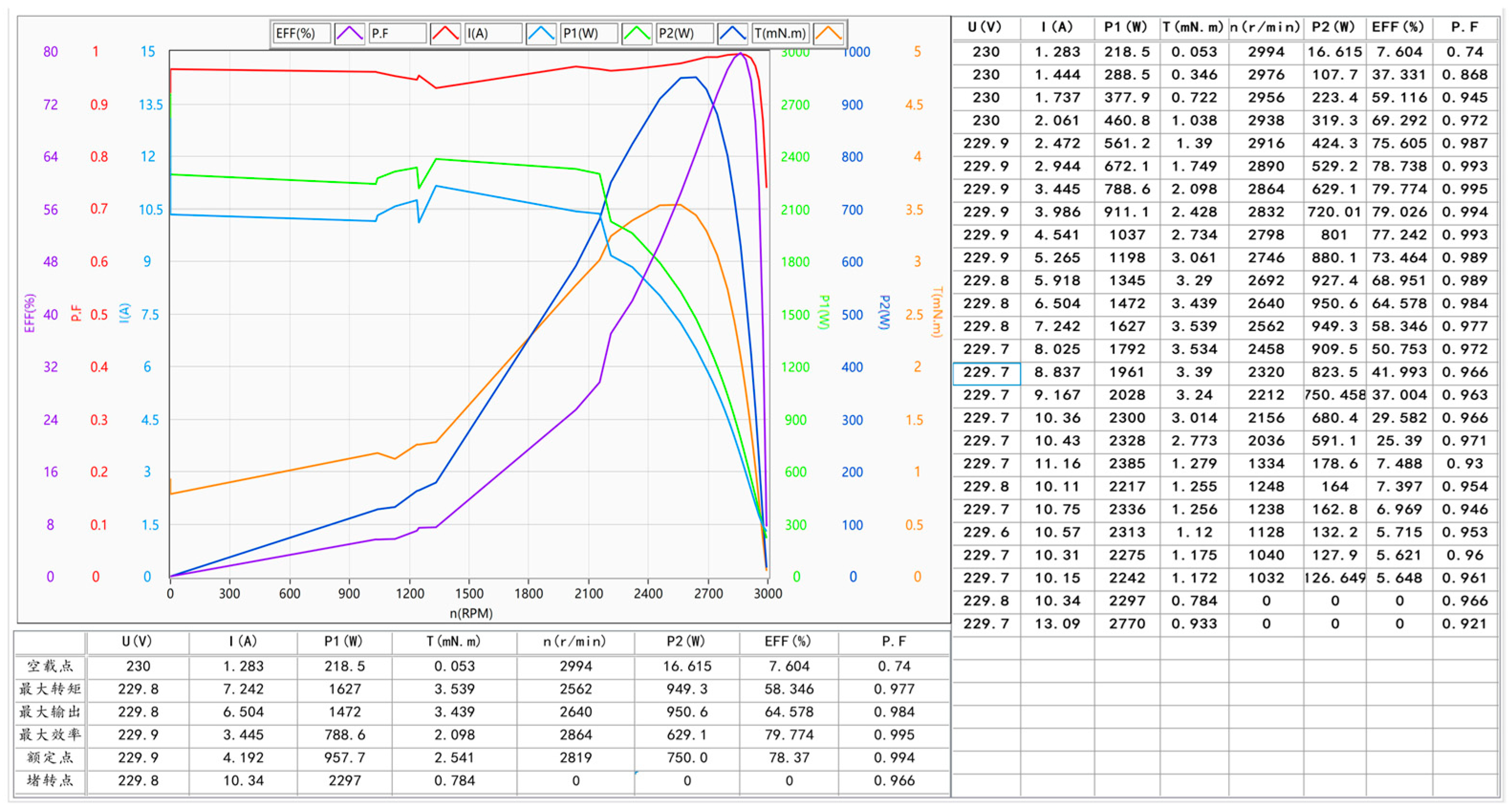
2.2. Permanent Magnet Synchronous Motor
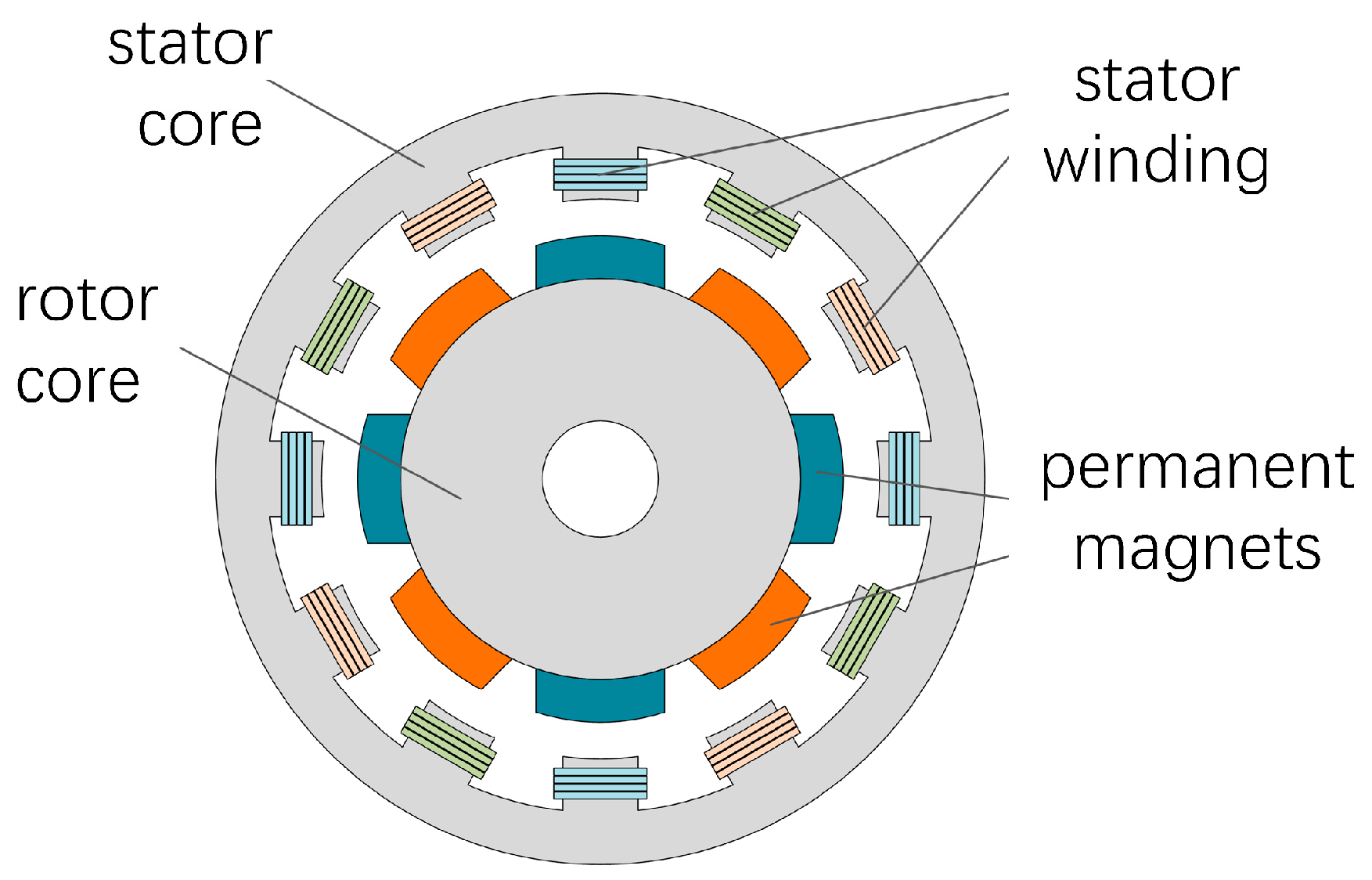
2.2.1. The Structure of PMSM
2.2.2. Field Oriented Control (FOC) Building on PMSM
2.2.3. The Characteristics of Permanent Magnet Motors
- (1)
- Permanent magnet generates a static magnetic field: The permanent magnet creates a constant static magnetic field in the motor.
- (2)
- Current flows through the winding to generate a rotating magnetic field: When current passes through the stator winding, it produces a rotating electromagnetic field.
- (3)
- Interaction between the static and rotating magnetic fields: The interaction between the static and rotating magnetic fields generates torque, driving the rotor to rotate.
- (4)
- The rotor follows the rotating magnetic field: The conductors on the rotor are subjected to magnetic forces, causing the rotor to rotate in sync with the rotating magnetic field.
- (1)
- High efficiency: Since no external excitation is needed, permanent magnet motors achieve higher energy efficiency.
- (2)
- High power density: These motors are smaller and lighter, offering a higher power density for the same power output.
- (3)
- Quick response: They feature rapid start–stop, acceleration, and deceleration, making them suitable for applications that require frequent speed changes.
- (4)
- Low noise: The stable magnetic field generated by the permanent magnet results in low noise during motor operation.
- (5)
- High starting torque: Due to its requirement for rotor-frequency synchronization and the inherent strength of its permanent magnets, the PMSM exhibits a significantly higher starting torque than induction (asynchronous) motors.
- (6)
- Longer life: Due to the high working efficiency at variable speeds, the PMSM could work at different speeds depending on the application request, which lengthens the motor’s life as the motor does not work always at its max speed.
- (7)
- Less maintenance: The longer operational life of the PMSM contributes to reduced bearing maintenance and eliminates the need for capacitor maintenance entirely. This contrasts with most single-phase AC motors, which require capacitors for either starting or running operation.
3. Developing Self-Adaptive Fuzzy PID Control for Pumps
3.1. Normal PID Control
- (1)
- Proportional component
- (2)
- Integral component
- (3)
- Derivative component
3.2. Self-Adaptive Fuzzy PID Control
- Fast response;
- Low overshoot;
- Strong robustness.
- (1)
- There is a nonlinear relationship and uncertainty between the outlet pressure and the pump speed;
- (2)
- There is a certain delay between the water pressure and the pump speed;
- (3)
- The system has high inertia and a long pure delay time.
3.2.1. Principles of Self-Adaptive Fuzzy PID Control
- (1)
- When is large (), the absolute value of the error is significant. To quickly eliminate the error, should be increased to improve the system’s dynamic response speed. To prevent the instantaneous value of from being too large, should be set to a smaller value to avoid large overshoots. Additionally, to prevent integral saturation, the integrator should be limited, and typically ;
- (2)
- When the error is moderate (), to ensure a good response speed and moderate overshoot, should be reduced, should be increased, and should be set to an appropriate value;
- (3)
- When is small , to achieve better stability, both and should be set to larger values. At the same time, to avoid oscillations, the value of should take into account: if is small, can be larger; otherwise, should be smaller.
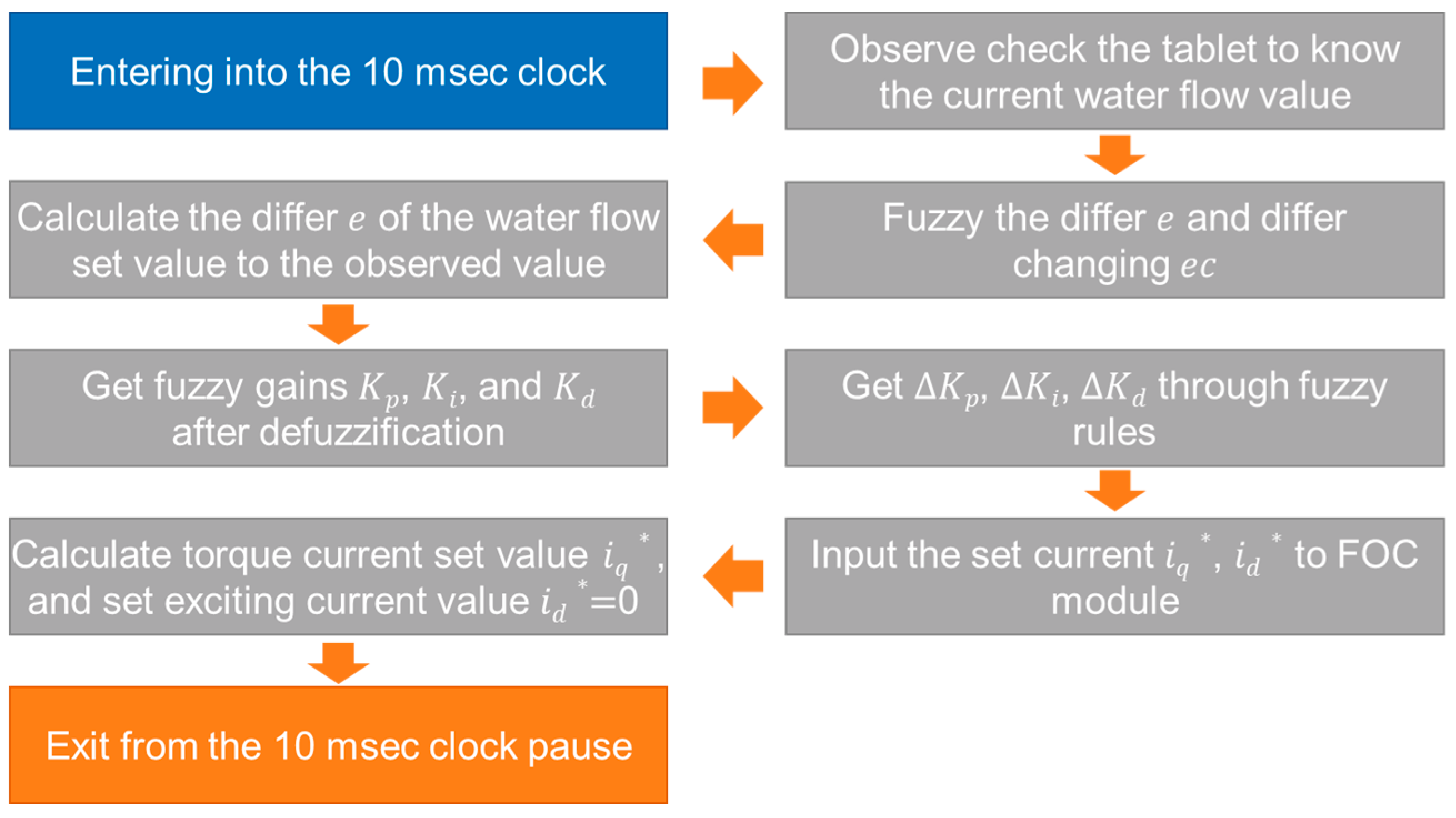
3.2.2. Design of Self-Adaptive Fuzzy PID Controller
- (1)
- Determine the structure and type of the fuzzy controller and the corresponding input and output variables. In this paper, error and rate of change of error are selected as the inputs to the controller, and the incremental PID parameters , , and are selected as the output variables.
- (2)
- Choose scaling factors, quantization factors, and other mapping parameters in the universe of discourse.
- (3)
- Define the fuzzy subsets of the variables and select appropriate membership functions.
- (4)
- Establish fuzzy control rules. Input fuzzy conditional statements to obtain the fuzzy control rules.
- (5)
- Obtain the fuzzy control table. Based on these output values, determine the adjustment values for the PID parameters. By integrating all the logical computation relationships, the control rule table is derived. Since the PID has three parameters, the controller needs to output three output variables as well.
- (6)
- Input the system’s error and error change rate into the fuzzy logic matrix after Steps (2) and (3) to obtain the modification values of the PID parameters. Finally, the final controller output value, i.e., the system’s control quantity, is calculated through the PID algorithm.
- (7)
- Verify the system parameters. By modeling and simulating, the control effect of the system is determined, and then the various system parameters are appropriately adjusted to achieve optimal performance.
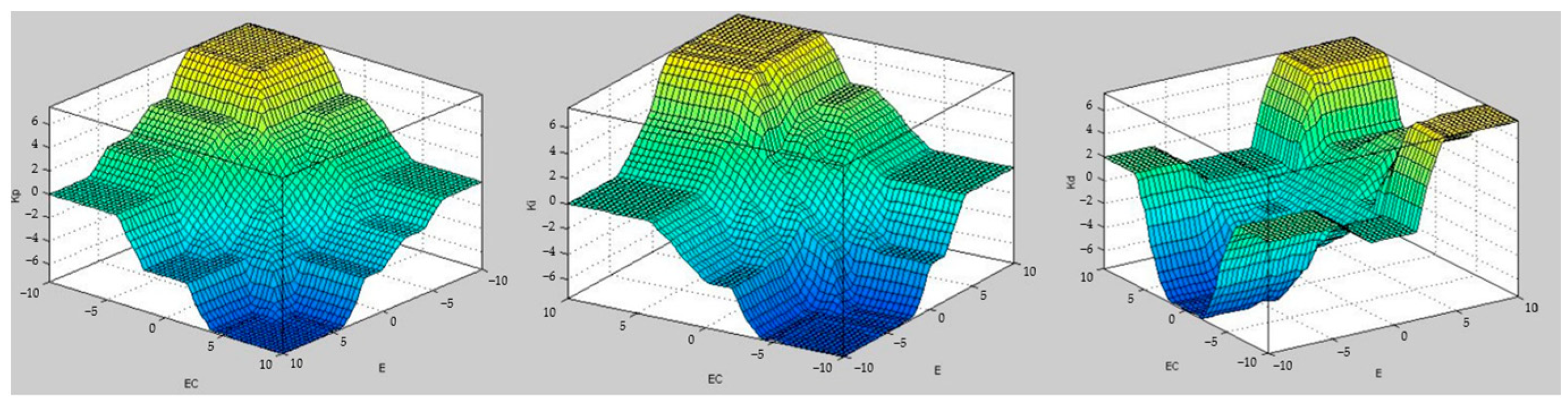
3.2.3. Building up Fuzzy Rules Tablet
3.2.4. Fuzzy Control Rule Lookup Tablet
3.2.5. Self-Adaptive PID Fuzzy Control Chart Design
4. Experiment and Results
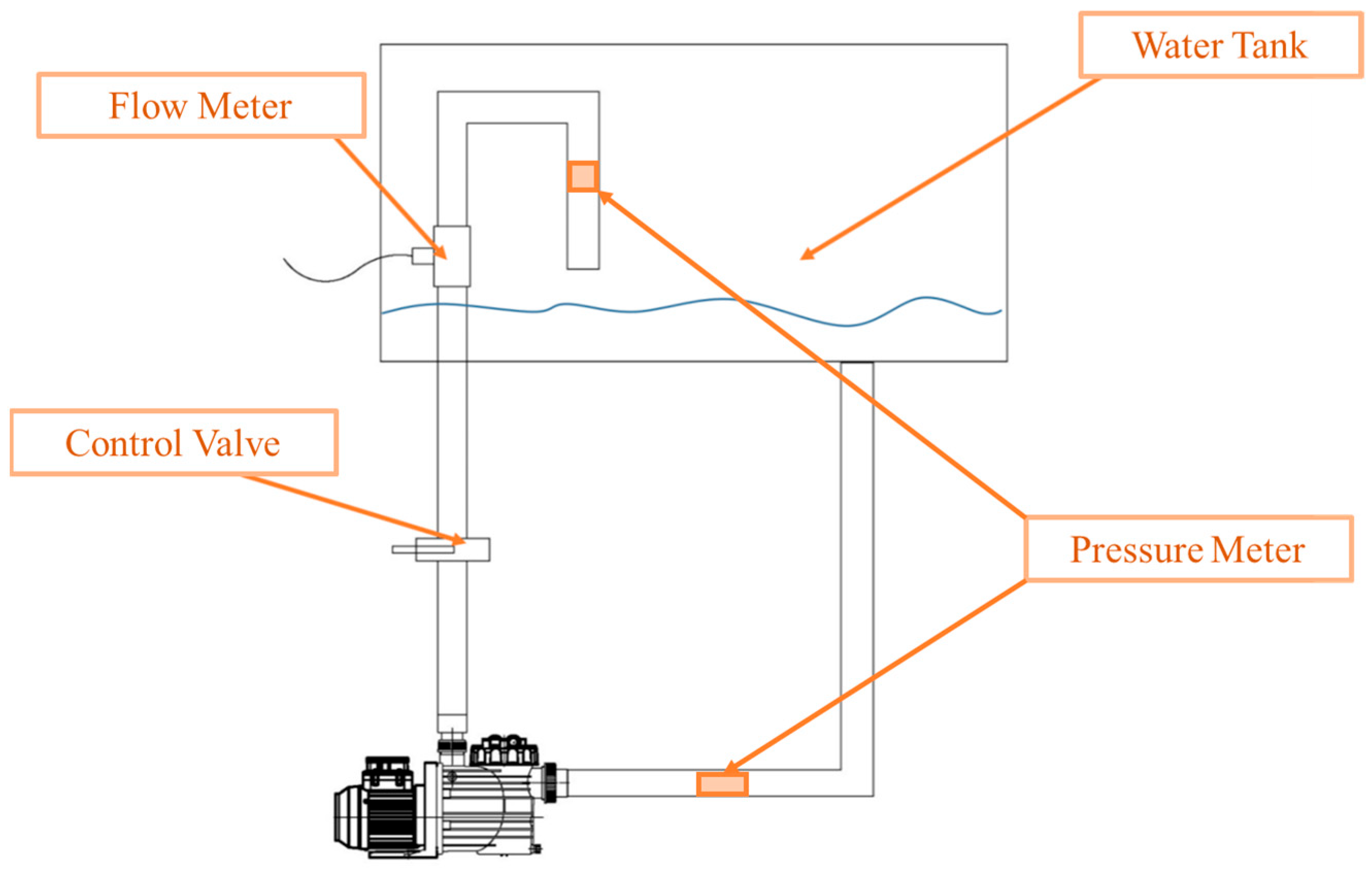
4.1. Testing Sample Building
4.2. Testing Platform Building
4.3. Experiment Method and Results
- (1)
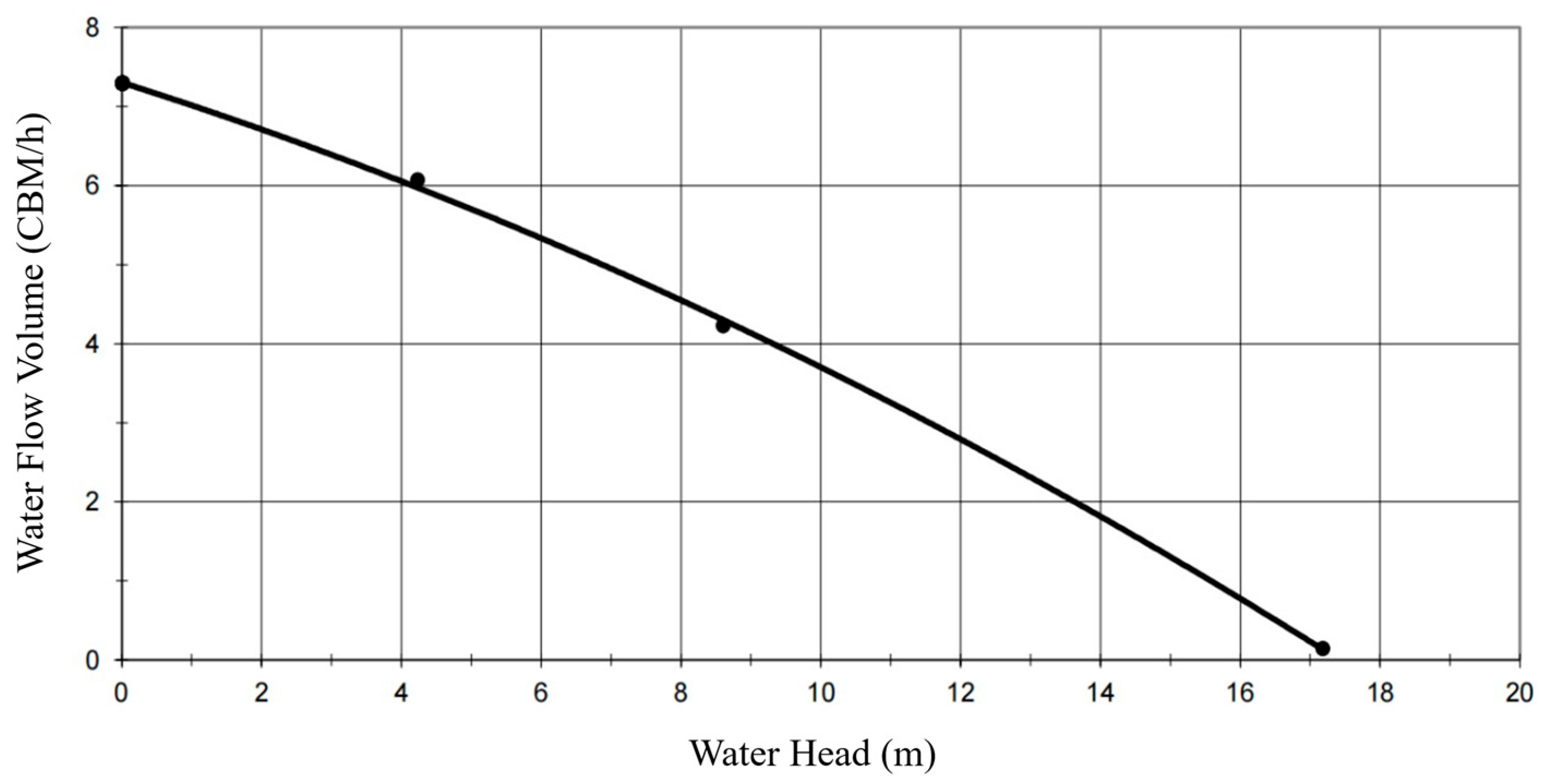
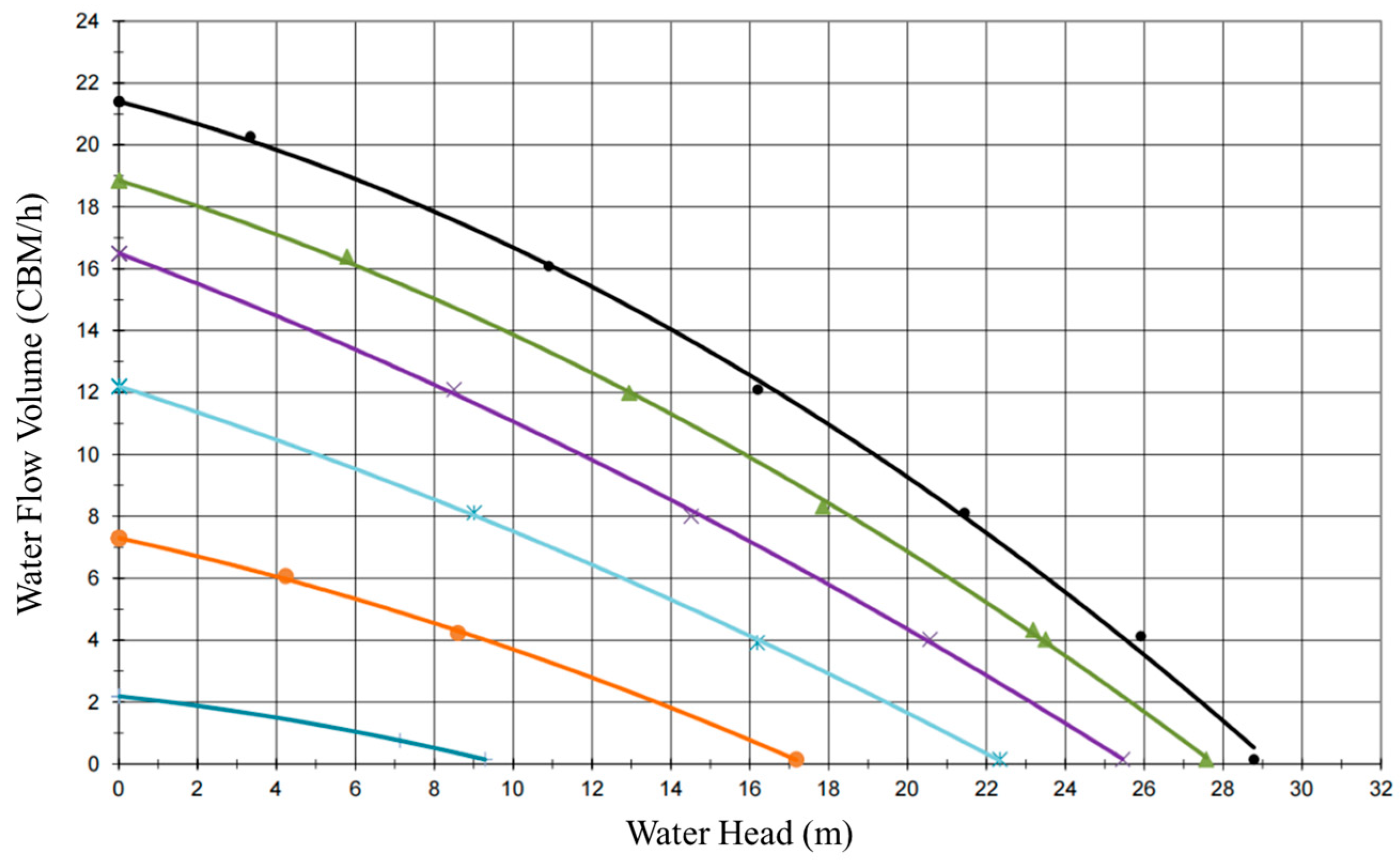
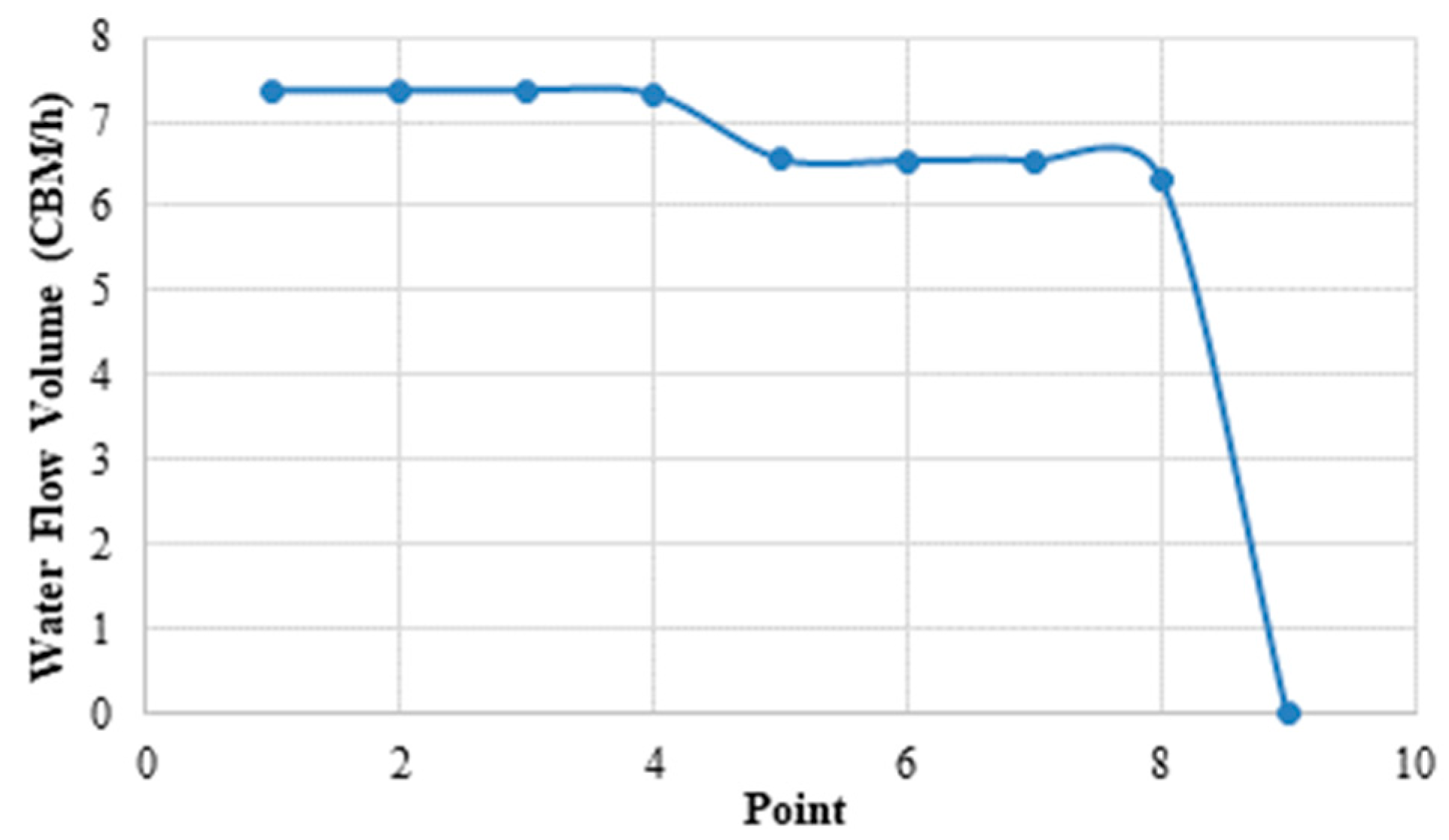
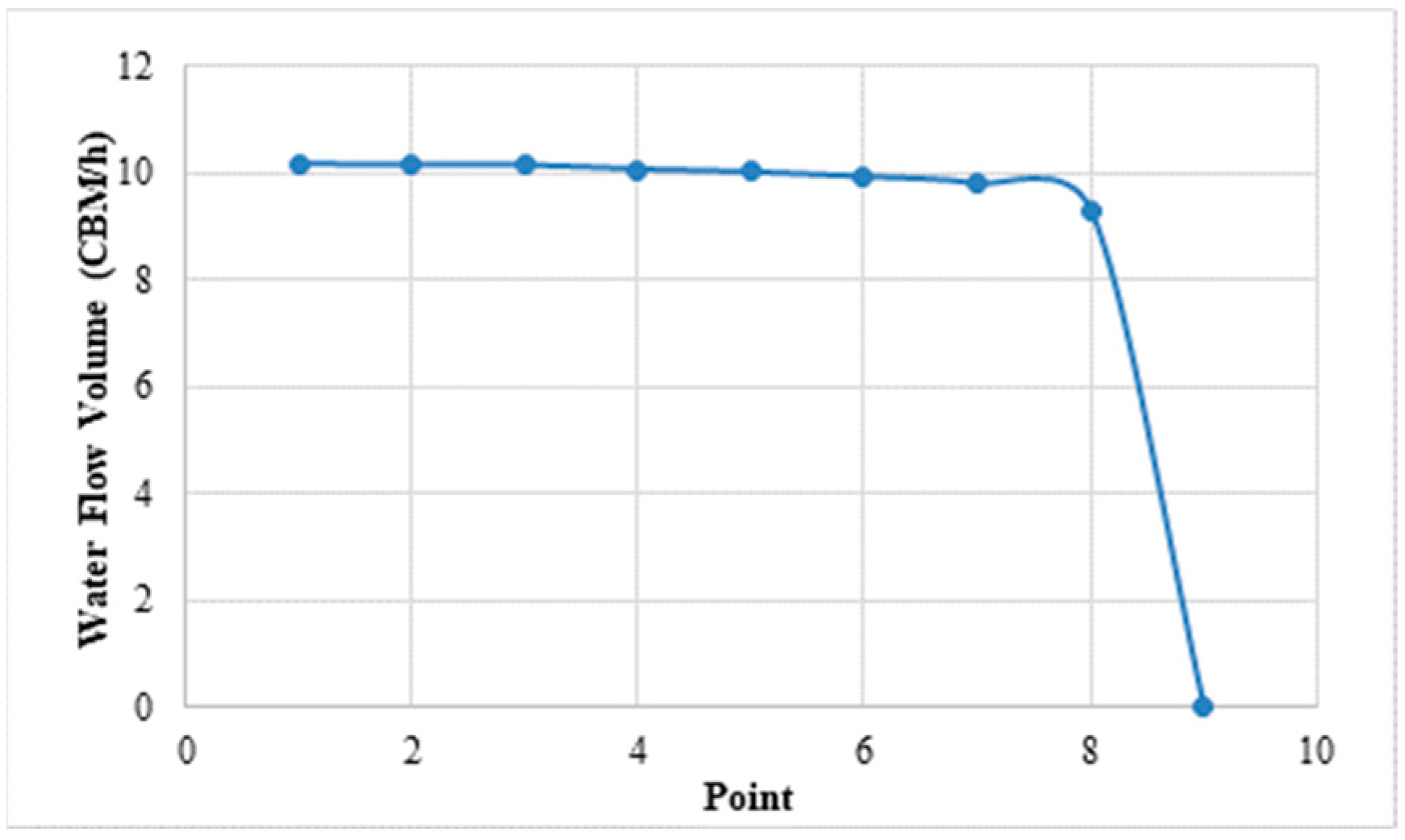
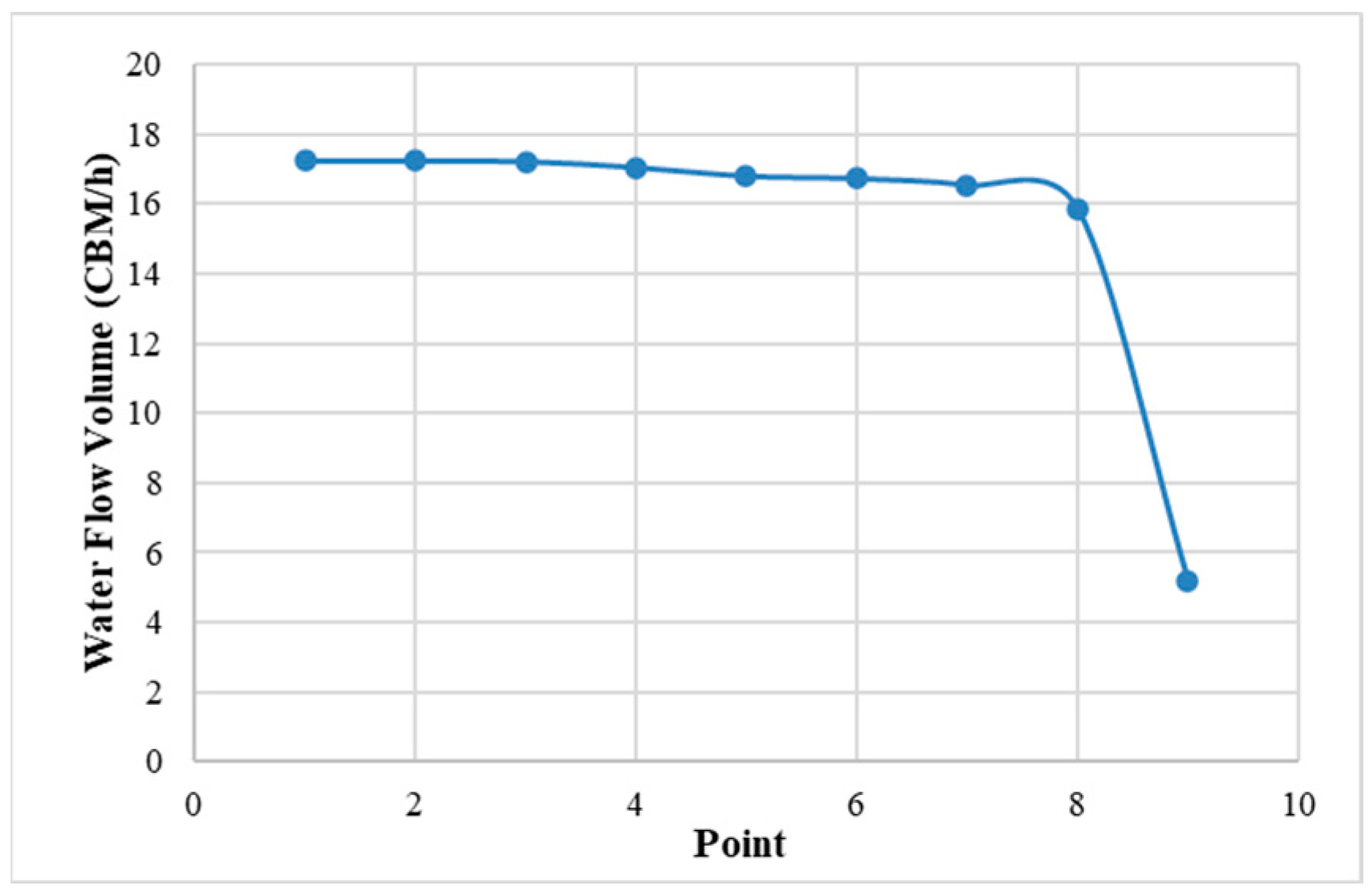
- When the pump system’s input power is a fixed power supply, the pump outputs a constant water flow in a range when the pressure changes. This was verified in the testing: when the motor’s input power was fixed at 100 W, 215 W, 810 W as shown in Figure 21, Figure 22 and Figure 23, the pressure was ignored intentionally in the testing, because in real application, the pressure change would be irregular, so we used a valve to change the water supply pressure, in the same way as a normal water supply’s valve control.
- (2)
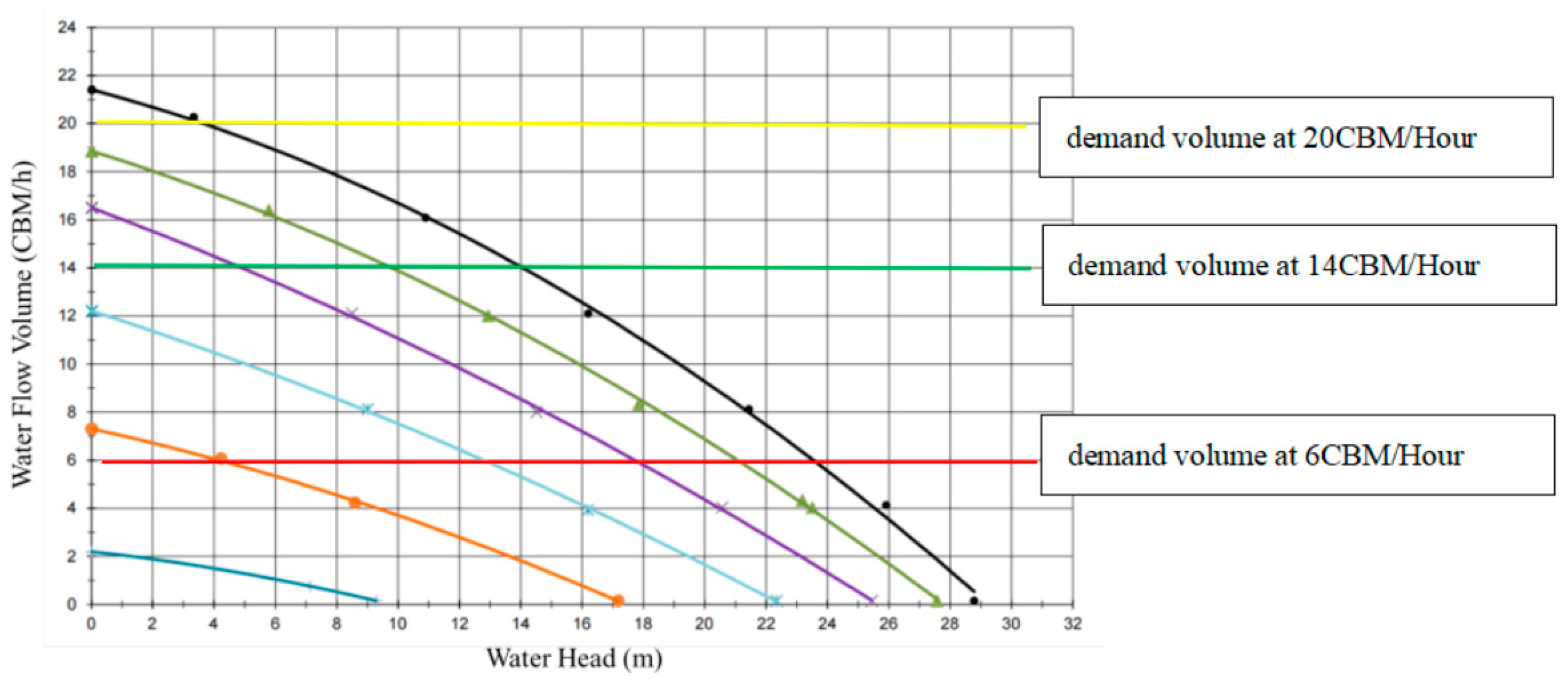
- When the constant water flow was broken or the pressure was too much changed, the pump system automatically switched to a higher input power to achieve a more constant water flow volume or a smaller input power to achieve more energy saving, as Figure 19 shows.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PMSM | Permanent Magnet Synchronous Motor |
| HVAC | Heating, Ventilation, and Air Conditioning |
| VFD | Variable Frequency Drivers |
| PLCs | Programmable Logic Controllers |
| PID | Proportional Integral Derivative |
References
- China Standards Research Institute; United Nations Development Program; Global Environment Facility. China Motor System’s Energy Efficiency and Market Potential Analysis Report; China Standards Research Institute: Beijing, China; United Nations Development Program: New York, NY, USA; Global Environment Facility: Washington, DC, USA, 2008. [Google Scholar]
- Ahmed, A.A.; Moharam, B.A.; Rashad, E.E. Improving energy efficiency and economics of motor-pump-system using electric variable-speed drives for automatic transition of working points. Comput. Electr. Eng. 2022, 97, 107607. [Google Scholar] [CrossRef]
- Luo, Y.; Xiong, Z.; Sun, H.; Guo, Y. Research on energy-saving operation control model of the multi-type configuration centrifugal pump system with single invert. Adv. Mech. Eng. 2017, 9, 1687814017707650. [Google Scholar] [CrossRef]
- Yimchoy, S.; Supatti, U. An energy-savings evaluation method for variable-frequency-drive applications on water pump systems. In Proceedings of the 24th IEEE International Conference on Electrical Machines and Systems, Gyeongju, Republic of Korea, 31 October–3 November 2021. [Google Scholar]
- Rakibuzzaman; Suh, S.; Kim, K.; Kim, H.; Cho, M.T.; Yoon, I.S. A study on multistage centrifugal pump performance characteristics for variable speed drive system. In Proceedings of the 6th BSME International Conference on Thermal Engineering, Dhaka, Bangladesh, 19–21 December 2014. [Google Scholar]
- Zhu, Y. Development and Application of Inverter Controlled Constant Pressure Water Supply System. Master’s Thesis, Zhejiang University, Hangzhou, China, 2005. [Google Scholar]
- Ding, L. Study on Constant Pressure Water Supply Control System of Variable Frequency. Master’s Thesis, Tianjin University, Tianjin, China, 2007. [Google Scholar]
- Gao, M. Constant Pressure Water Supply System Design and Implementation Based on Variable Frequency. Master’s Thesis, University of Electronic Science and Technology of China, Chengdu, China, 2013. [Google Scholar]
- Wang, G. Efficiency degradation detection for VFD-motor-pump systems. Sci. Technol. Built Environ. 2018, 24, 974–981. [Google Scholar] [CrossRef]
- Su, C.L.; Liao, C.H.; Chou, T.C.; Tsai, S.Y.; Yu, K.T. Design and application of variable frequency constant pressure technology in closed system pumps on marine vessels. In Proceedings of the 2015 IEEE IAS Joint Industrial and Commercial Power Systems/Petroleum and Chemical Industry Conference, Hyderabad, India, 19–21 November 2015. [Google Scholar]
- Zhu, G. Constant Pressure Water Supply Control System Using PIC. Master’s Thesis, Zhejiang Sci-Tech University, Hangzhou, China, 2019. [Google Scholar]
- Mo, X. Based on PLC the automatic constant pressure control water supply system design. Appl. Mech. Mater. 2015, 716, 1587–1590. [Google Scholar] [CrossRef]
- Li, S. The design of constant pressure water supply control system for city. Adv. Mater. Res. 2015, 1079, 1018–1021. [Google Scholar] [CrossRef]
- Yu, L. Design and Realization of Constant Pressure Water Supply System Based on PLC. Master’s Thesis, Harbin Engineering University, Harbin, China, 2017. [Google Scholar]
- Wang, H.; Zhang, Y.; An, Z.; Liu, R. An energy-efficient adaptive speed-regulating method for pump-controlled motor hydrostatic drive powertrains. Processes 2024, 12, 25. [Google Scholar] [CrossRef]
- Shankar, V.K.A.; Umashankar, S.; Paramasivam, S.; Norbert, H. Real time simulation of variable speed parallel pumping system. In Proceedings of the 9th International Conference on Applied Energy, Cardiff, UK, 21–24 August 2017. [Google Scholar]
- Shankar, V.K.A.; Umashankar, S.; Padmanaban, S.; Bhaskar, M.S.; Almakhles, D. Investigation for performances comparison PI, adaptive PI, fuzzy speed control induction motor for centrifugal pumping application. In Proceedings of the 2019 IEEE 13th International Conference on Compatibility, Power Electronics and Power Engineering, Sonderborg, Denmark, 23–25 April 2019. [Google Scholar]
- Shen, G.; Sun, B.; Ma, G. A constant pressure water supply system on a fuzzy control basis. Ind. Instrum. Automat 2002, 5, 50–52. [Google Scholar]
- Ramadhan, R.; Fang, X. Enhancing energy efficient water pumping with intelligent control: A comparative study of advanced fuzzy logic and PID controllers on Simulink/Matlab. J. World Sci. 2024, 3, 479–489. [Google Scholar] [CrossRef]
- Yang, X.; Wu, D.; Wang, C.; Gao, C.; Gao, H.; Liu, Y. Adaptive fuzzy PID control of high speed on-off valve for position control system used in water hydraulic manipulators. Fusion. Eng. Des. 2024, 203, 114437. [Google Scholar] [CrossRef]
- Pruna, E.; Andaluz, V.H.; Proaño, L.E.; Carvajal, C.P.; Escobar, I.; Pilatásig, M. Construction and analysis of PID, fuzzy and predictive controllers in flow system. In Proceedings of the 2016 IEEE International Conference on Automatica, Curico, Chile, 19–21 October 2016. [Google Scholar]
- Wang, Z.; Xia, L.; Calautit, J.K.; Wang, X.R.; Jiang, D.W.; Pan, S.; Wu, J.S. Development of an enhanced self-tuning RBF-PID controller for achieving higher energy-efficient process control. J. Build. Constr. Plan. Res. 2021, 9, 272–291. [Google Scholar] [CrossRef]
- Bouchakour, A.; Zarour, L.; Bessous, N.; Bechouat, M.; Borni, A.; Zaghba, L.; Rabehi, A.; Alwabli, A.; El-Abd, M.; Ghoneim, S.S.M. MPPT algorithm based on metaheuristic techniques (PSO & GA) dedicated to improve wind energy water pumping system performance. Sci. Rep. 2024, 14, 17891. [Google Scholar] [CrossRef]
- Hartono, H.; Sudjoko, R.I.; Iswahyudi, P. Speed control of three phase induction motor using universal bridge and PID controller. In Proceedings of the 1st International Conference on Engineering and Applied Science, Madiun, Indonesia, 21 August 2019. [Google Scholar]
- Jin, X.; Zhou, L.; Lang, T.; Jiang, Y. Low-Voltage water pump system based on permanent magnet synchronous motor. Electronics 2024, 13, 3674. [Google Scholar] [CrossRef]
- Bahrami-Fard, M.; Korrani, M.G.; Rastegar, M.; Fahimi, B. Advanced startup and smooth transition to sensorless field oriented control for CSI-Fed PMSM drives in submersible pumps. IEEE Trans. Power Electron. 2025, 40, 12402–12415. [Google Scholar] [CrossRef]
- Nasser, A.; Szemes, P.T. Speed control of three phase induction motor using scalar method and PID controller. Recent. Innov. Mechatron. 2018, 5, 1. [Google Scholar] [CrossRef]
- Anjum, F.; Sharma, N. Speed control of induction motor using hybrid PID fuzzy controller. Int. Res. J. Eng. Technol. 2018, 5, 576–580. [Google Scholar]
- Flores, T.K.S.; Villanueva, J.M.M.; Gomes, H.P. Fuzzy pressure control: A novel approach to optimizing energy efficiency in series-parallel pumping systems. Automation 2023, 4, 11–28. [Google Scholar] [CrossRef]
- AL-washali, T.; Sharma, S.; Kennedy, M. Methods of assessment of water losses in water supply systems: A review. Water Resour. Manag. 2016, 30, 4985–5001. [Google Scholar] [CrossRef]
- Santos de Araújo, J.V.; Villanueva, J.M.M.; Cordula, M.M.; Cardoso, A.A.; Gomes, H.P. Fuzzy control of pressure in a water supply network based on neural network system modeling and IoT measurements. Sensors 2022, 22, 9130. [Google Scholar] [CrossRef] [PubMed]
- Moreira, H.A.M.; Gomes, H.P.; Villanueva, J.M.M.; Bezerra, S.T.M. Real-time neuro-fuzzy controller for pressure adjustment in water distribution systems. Water Supply 2021, 21, 1177–1187. [Google Scholar] [CrossRef]
- Wu, Y.; Zhong, Y.; Chen, J.; Qiu, A.; Cao, L. Design of constant pressure water supply control system based on fuzz-PID. In Proceedings of the 2018 33rd Youth Academic Annual Conference of Chinese Association of Automation, Nanjing, China, 18–20 May 2018. [Google Scholar]
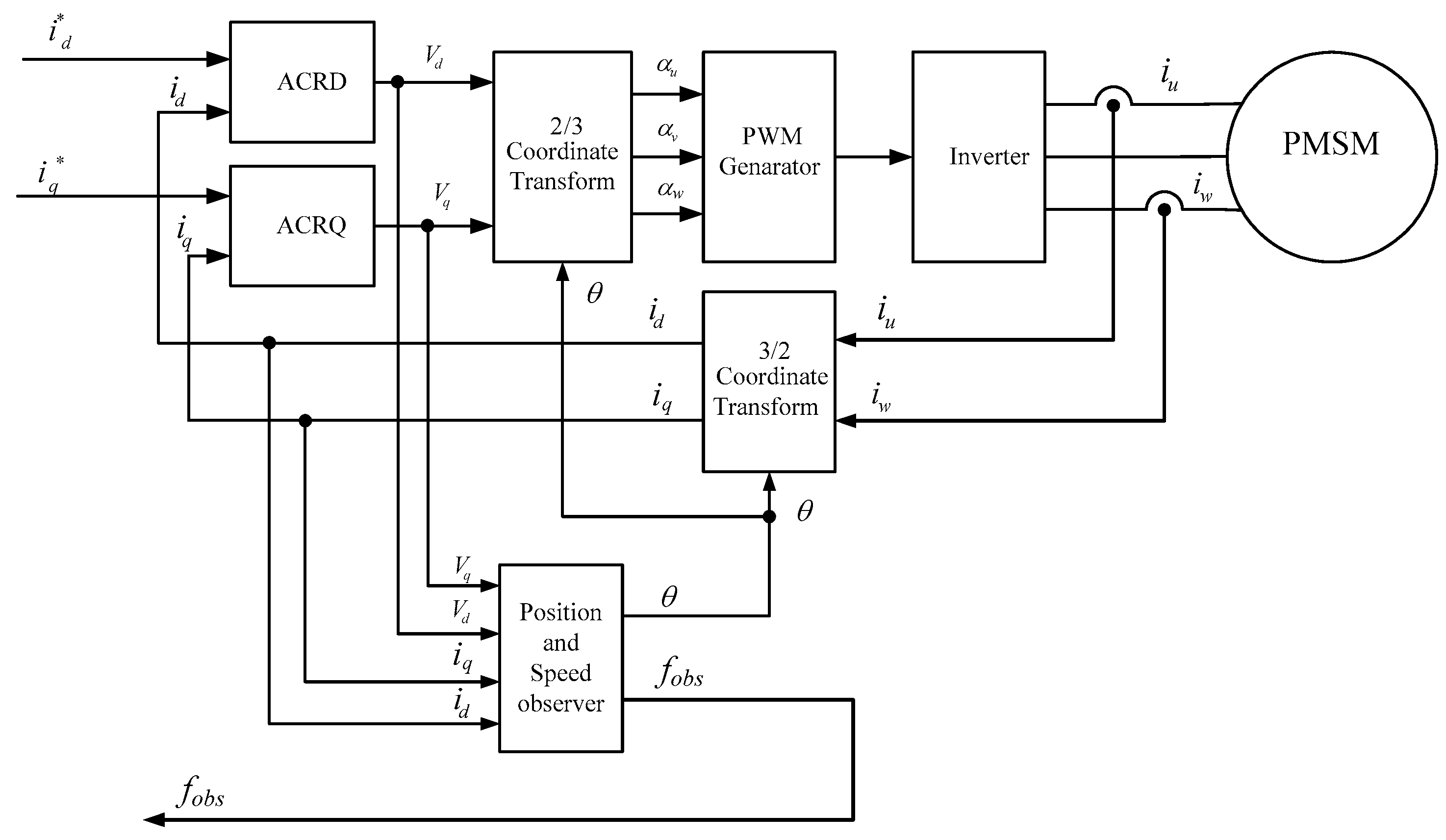
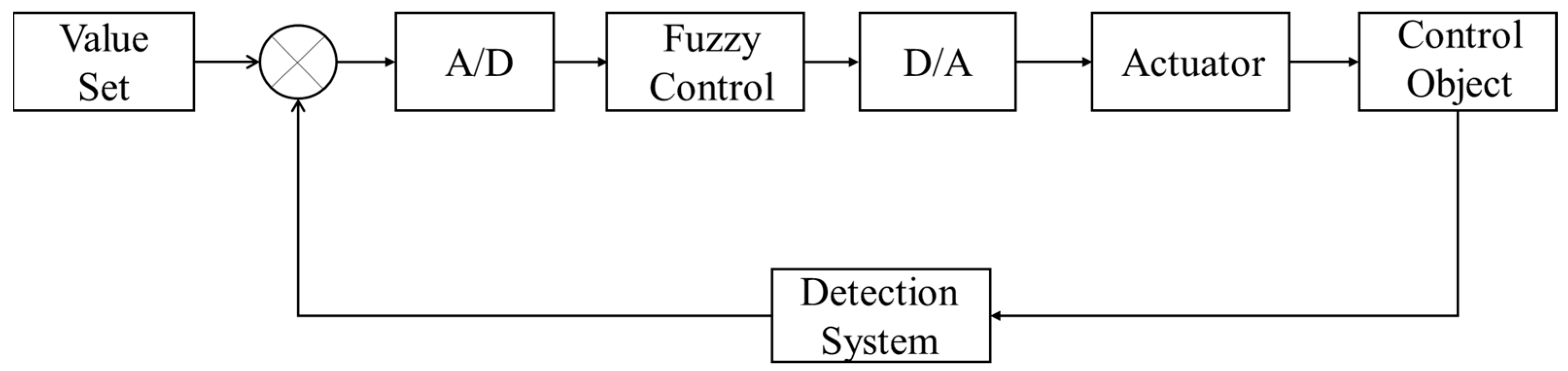
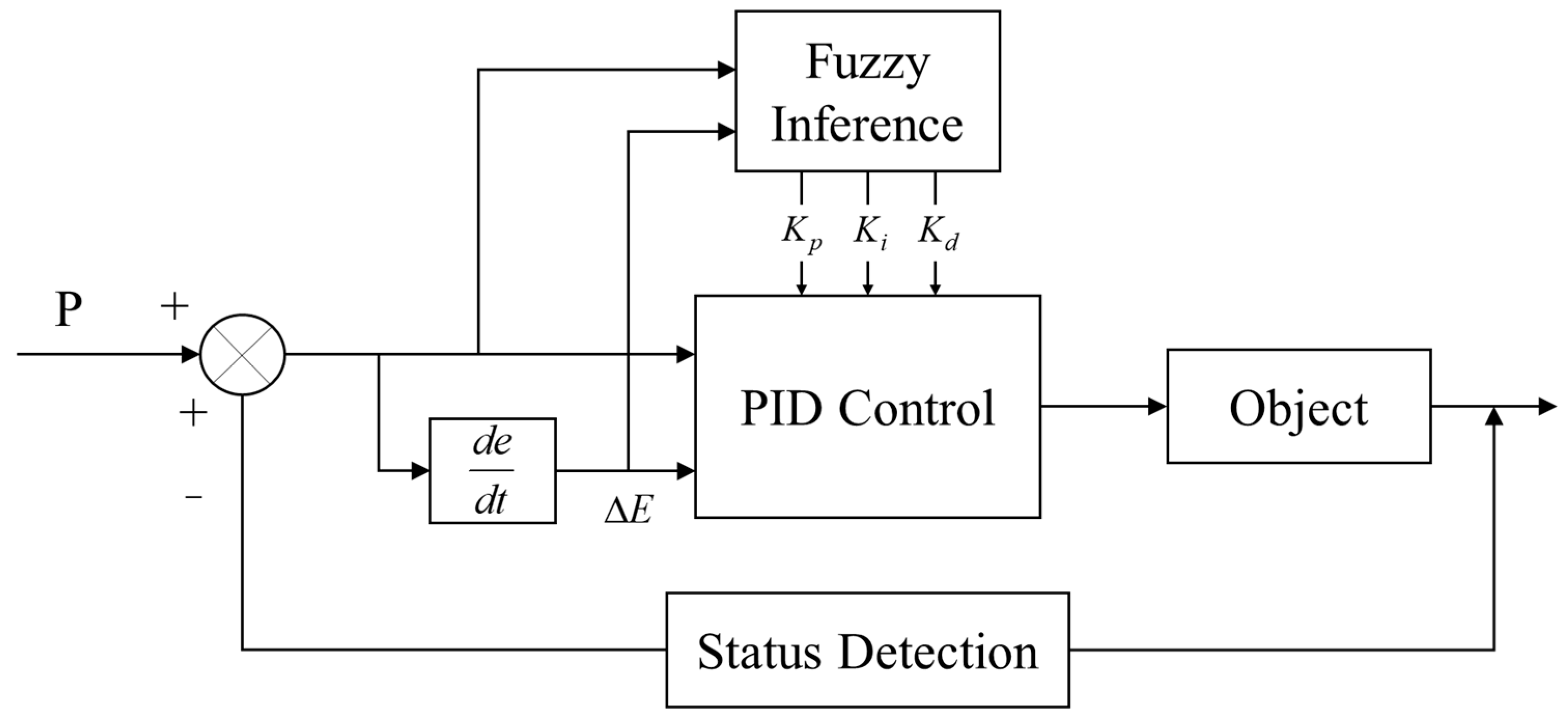
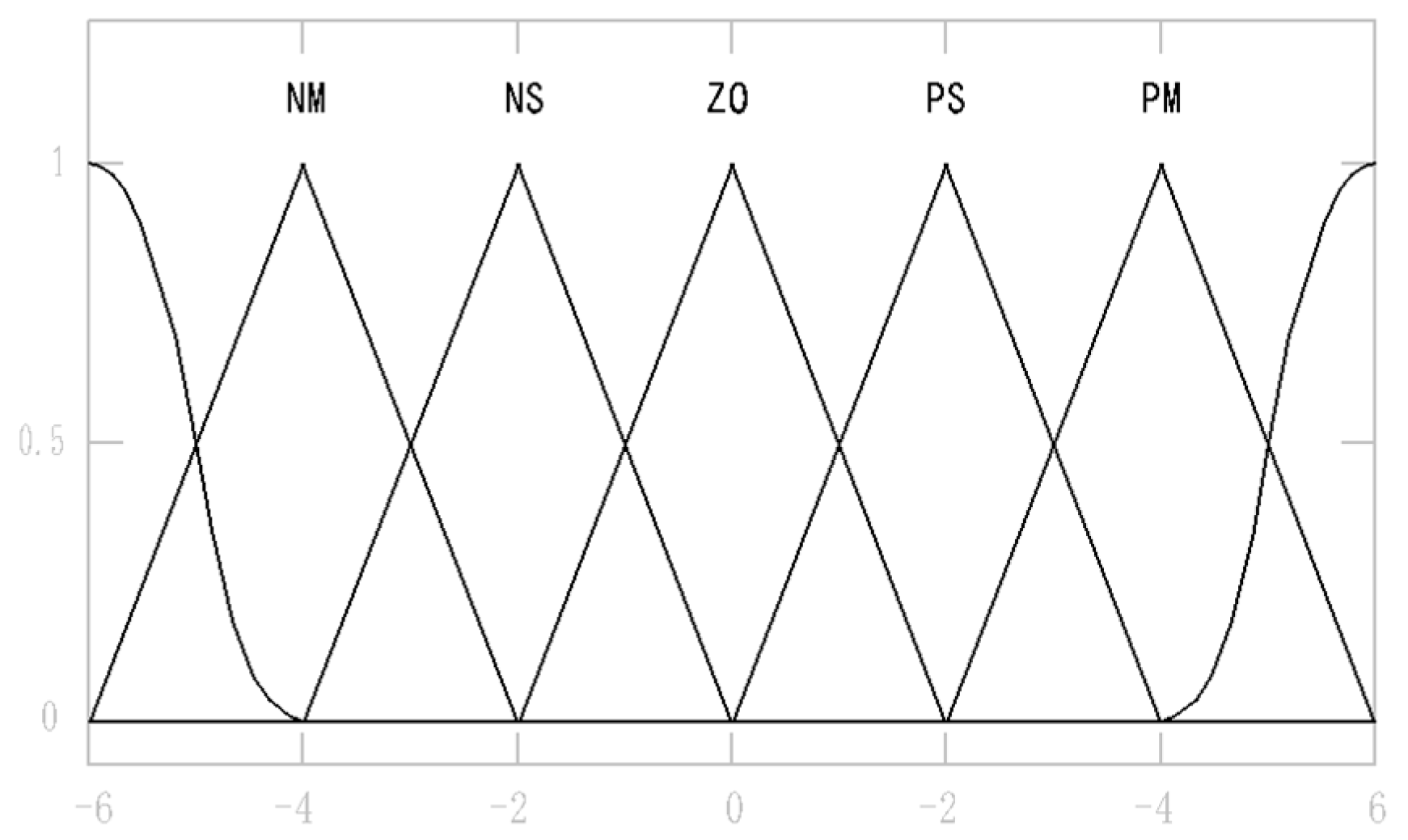



| Part | Function |
|---|---|
| Permanent magnets | The primary magnetic field source, generating a static magnetic field. |
| Stator core | A stationary coil that generates a rotating magnetic field. |
| Rotor core | The rotating part with conductors, which rotates under the interaction of the static and rotating magnetic fields. |
| Stator winding | Coils on the stator that produce the electromagnetic field. |
| Others | Shaft and bearings which support the rotation of the rotor |
| NB | NM | NS | ZO | PS | PM | PB | ||
|---|---|---|---|---|---|---|---|---|
| NB | PB | PB | PM | PM | PS | ZO | ZO | |
| NM | PB | PB | PM | PS | PS | ZO | NS | |
| NS | PM | PM | PM | PS | ZO | NS | NS | |
| ZO | PM | PM | PS | ZO | NS | NM | NM | |
| PS | PS | PS | ZO | NS | NS | NM | NM | |
| PM | PS | ZO | NS | NM | NM | NM | NB | |
| PB | ZO | ZO | NM | NM | NM | NB | NB | |
| NB | NM | NS | ZO | PS | PM | PB | ||
|---|---|---|---|---|---|---|---|---|
| NB | NB | NB | NM | NM | NS | ZO | ZO | |
| NM | NB | NB | NM | NS | NS | ZO | ZO | |
| NS | NB | NM | NS | NS | ZO | PS | PS | |
| ZO | NM | NM | NS | ZO | PS | PM | PM | |
| PS | NM | NS | ZO | PS | PS | PB | PB | |
| PM | ZO | ZO | PS | PS | PM | PB | PB | |
| PB | ZO | ZO | PS | PM | PM | PB | PB | |
| NB | NM | NS | ZO | PS | PM | PB | ||
|---|---|---|---|---|---|---|---|---|
| NB | PS | NS | NB | NB | NB | NM | PS | |
| NM | PS | NS | NB | NM | NM | NS | ZO | |
| NS | ZO | NS | NM | NM | NS | NS | ZO | |
| ZO | ZO | NS | NS | NS | NS | NS | ZO | |
| PS | ZO | ZO | ZO | ZO | ZO | ZO | ZO | |
| PM | PB | NS | PS | PS | PS | PS | PB | |
| PB | PB | PM | PM | PM | PS | PS | PB | |
| −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −6 | 6 | 6 | 5 | 5 | 5 | 5 | 5 | 3 | 3 | 2 | 1 | 0 | 0 | |
| −5 | 6 | 6 | 5 | 5 | 5 | 4 | 3 | 2 | 2 | 1 | 0 | 0 | 0 | |
| −4 | 5 | 5 | 5 | 5 | 4 | 3 | 3 | 1 | 0 | 0 | 0 | 0 | −1 | |
| −3 | 5 | 5 | 5 | 4 | 3 | 3 | 2 | 1 | 0 | 0 | 0 | 0 | −1 | |
| −2 | 4 | 4 | 4 | 4 | 3 | 3 | 2 | 1 | 0 | 0 | 0 | −1 | −2 | |
| −1 | 4 | 4 | 4 | 3 | 3 | 1 | 0 | 0 | 0 | 0 | −1 | −1 | −3 | |
| 0 | 3 | 3 | 3 | 2 | 2 | 1 | 0 | 0 | 0 | 0 | −1 | −2 | −3 | |
| 1 | 3 | 2 | 1 | 0 | 0 | 0 | 0 | −1 | −2 | −2 | −3 | −3 | −3 | |
| 2 | 2 | 1 | 0 | 0 | 0 | 0 | −1 | −2 | −3 | −3 | −4 | −5 | −5 | |
| 3 | 1 | 0 | 0 | 0 | 0 | −1 | −2 | −3 | −4 | −5 | −5 | −5 | −5 | |
| 4 | 0 | 0 | 0 | 0 | −1 | −2 | −3 | −4 | −5 | −5 | −5 | −5 | −5 | |
| 5 | 0 | 0 | 0 | −1 | −2 | −2 | −3 | −4 | −5 | −5 | −5 | −6 | −6 | |
| 6 | 0 | 0 | −1 | −2 | −3 | −3 | −5 | −5 | −5 | −5 | −6 | −6 | −6 | |
| −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −6 | −6 | −6 | −5 | −5 | −5 | −5 | −5 | −3 | −3 | −2 | −1 | 0 | 0 | |
| −5 | −6 | −6 | −5 | −5 | −5 | −4 | −3 | −2 | −2 | −1 | 0 | 0 | 0 | |
| −4 | −5 | −5 | −5 | −5 | −4 | −3 | −3 | −1 | 0 | 0 | 0 | 0 | 1 | |
| −3 | −5 | −5 | −5 | −4 | −3 | −3 | −2 | −1 | 0 | 0 | 0 | 0 | 1 | |
| −2 | −4 | −4 | −4 | −4 | −3 | −3 | −2 | −1 | 0 | 0 | 0 | 1 | 2 | |
| −1 | −4 | −4 | −4 | −3 | −3 | −1 | 0 | 0 | 0 | 0 | 1 | 1 | 3 | |
| 0 | −3 | −3 | −3 | −2 | −2 | −1 | 0 | 0 | 0 | 0 | 1 | 2 | 3 | |
| 1 | −3 | −2 | −1 | 0 | 0 | 0 | 0 | 1 | 2 | 2 | 3 | 3 | 3 | |
| 2 | −2 | −1 | 0 | 0 | 0 | 0 | 1 | 2 | 3 | 3 | 4 | 5 | 5 | |
| 3 | −1 | 0 | 0 | 0 | 0 | 1 | 2 | 3 | 4 | 5 | 5 | 5 | 5 | |
| 4 | 0 | 0 | 0 | 0 | 1 | 2 | 3 | 4 | 5 | 5 | 5 | 5 | 5 | |
| 5 | 0 | 0 | 0 | 1 | 2 | 2 | 3 | 4 | 5 | 5 | 5 | 6 | 6 | |
| 6 | 0 | 0 | 1 | 2 | 3 | 3 | 5 | 5 | 5 | 5 | 6 | 6 | 6 | |
| −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −6 | 1 | 1 | −1 | −2 | −5 | −6 | −6 | −6 | −5 | −4 | −3 | 1 | 1 | |
| −5 | 1 | −1 | −2 | −3 | −4 | −5 | −6 | −5 | −4 | −3 | −2 | −1 | 1 | |
| −4 | 1 | −2 | −2 | −3 | −4 | −5 | −5 | −4 | −4 | −3 | −2 | −1 | 0 | |
| −3 | 1 | −2 | −3 | −4 | −5 | −6 | −5 | −4 | −3 | −2 | −2 | −1 | 0 | |
| −2 | 0 | −1 | −2 | −2 | −3 | −4 | −4 | −4 | −3 | −2 | −1 | 0 | 0 | |
| −1 | 0 | 0 | −1 | −2 | −3 | −3 | −4 | −3 | −3 | −2 | −1 | −1 | 0 | |
| 0 | 0 | 0 | 0 | −1 | −1 | −2 | −2 | −2 | −1 | −1 | −1 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 2 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 3 | 5 | 4 | −1 | −2 | 1 | 1 | 2 | 2 | 2 | 3 | 4 | 5 | 5 | |
| 4 | 5 | 3 | 2 | 1 | 1 | 2 | 3 | 3 | 4 | 5 | 5 | 5 | 5 | |
| 5 | 6 | 5 | 4 | 4 | 4 | 3 | 3 | 3 | 2 | 2 | 2 | 5 | 6 | |
| 6 | 6 | 6 | 5 | 5 | 4 | 4 | 3 | 3 | 3 | 2 | 2 | 6 | 6 | |
| Motor | Input Voltage | Input Frequency | Rated Speed | Rated Output Power | IP Grade | Poles of The Motor |
|---|---|---|---|---|---|---|
| PMSM motor | 230 V | 50/60 Hz | 2850 RPM | 750 W | IP55 | 8 Poles |
| AC asynchronous motor | 230 V | 50 Hz | 2850 RPM | 750 W | IP54 | 2 Poles |
| Symbol | Explanation |
|---|---|
| Water pressure on the discharged side | |
| Water pressure on the suction side | |
| Formula used if suction and discharge pipe side are different, can be ignored if the sizes are same. | |
| Water pressure difference from discharge to suction. | |
| Conversation from bar to meter. | |
| Water flow volume. | |
| Motor output speed. | |
| Motor input current. | |
| Motor input voltage. | |
| Motor input power. | |
| Motor output power. |
[bar] | [bar] | [m] | [bar] | [m] | [m3/h] | [1/min] | [A] | [V] | [kW] |
|---|---|---|---|---|---|---|---|---|---|
| −0.04 | 0.05 | 0.00 | −0.09 | 0.15 | 17.18 | 1586 | 1.02 | 232 | 0.23 |
| 0.36 | 0.05 | 0.00 | 0.31 | 4.23 | 8.60 | 1632 | 1.03 | 231 | 0.23 |
| 0.54 | 0.05 | 0.00 | 0.49 | 6.07 | 4.23 | 1757 | 1.05 | 232 | 0.24 |
| 0.66 | 0.05 | 0.00 | 0.61 | 7.30 | 0.00 | 1766 | 1.06 | 231 | 0.24 |
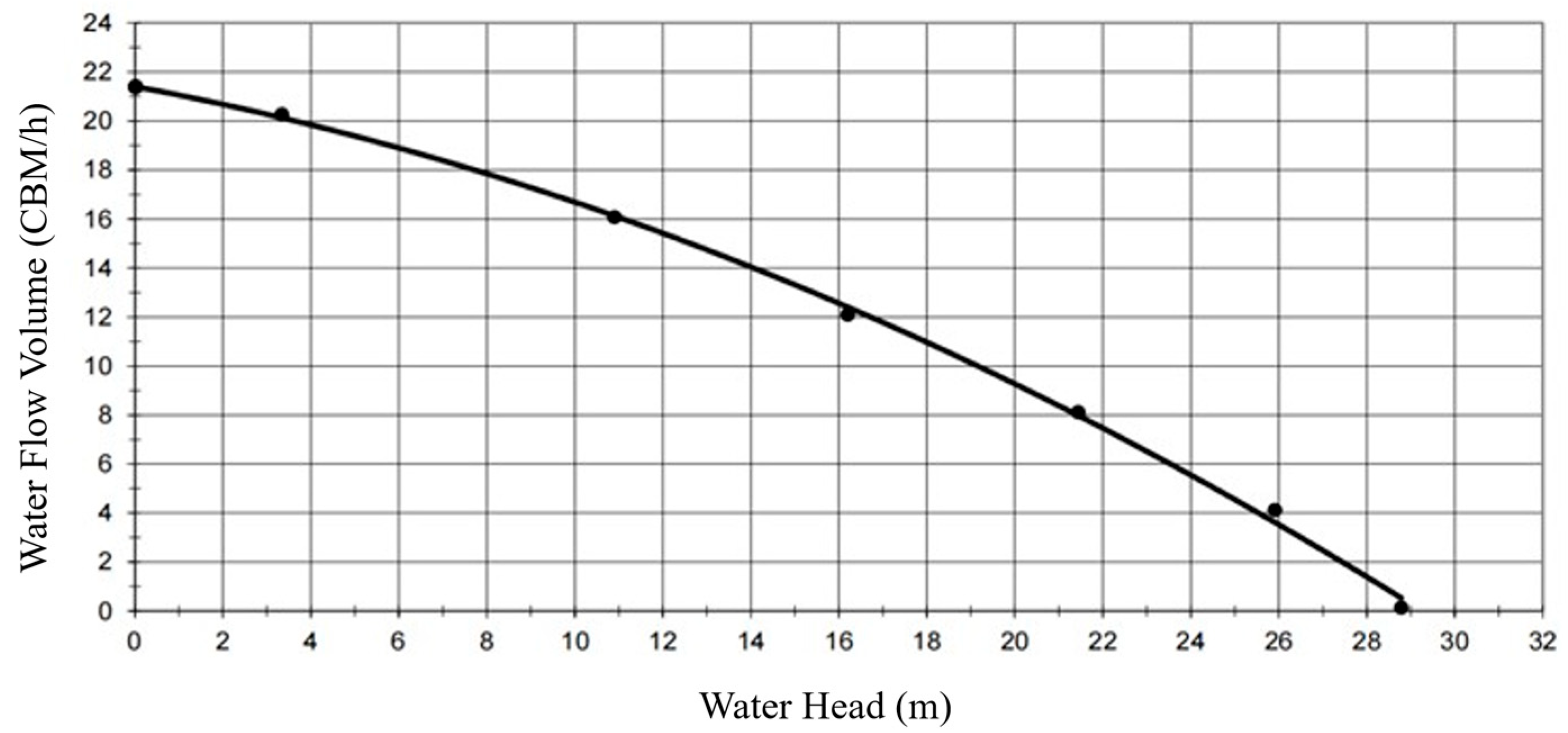
[bar] | [bar] | [m] | [bar] | [m] | [m3/h] | [1/min] | [A] | [V] | [kW] |
|---|---|---|---|---|---|---|---|---|---|
| −0.04 | 0.05 | 0.00 | −0.09 | 0.15 | 28.78 | 2798 | 4.87 | 231 | 1.11 |
| 0.35 | 0.05 | 0.00 | 0.30 | 4.13 | 25.91 | 2777 | 4.90 | 230 | 1.12 |
| 0.74 | 0.05 | 0.00 | 0.69 | 8.12 | 21.44 | 2800 | 4.87 | 231 | 1.11 |
| 1.13 | 0.05 | 0.00 | 1.08 | 12.10 | 16.20 | 2853 | 4.85 | 231 | 1.11 |
| 1.52 | 0.05 | 0.00 | 1.47 | 16.08 | 10.90 | 2978 | 4.81 | 231 | 1.10 |
| 1.93 | 0.05 | 0.00 | 1.88 | 20.27 | 3.34 | 3177 | 4.56 | 231 | 1.05 |
| 2.04 | 0.05 | 0.00 | 1.99 | 21.40 | 0.00 | 3277 | 4.43 | 231 | 1.02 |
[bar] | [bar] | [m] | [bar] | [m] | [m3/h] | [1/min] | [A] | [V] | [kW] | [kW] | [%] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.15 | 0.05 | 0.00 | 0.10 | 1.02 | 28.70 | 2710 | 4.67 | 230.4 | 1.065 | 0.67 | 0.12 |
| 0.40 | 0.05 | 0.00 | 0.35 | 3.57 | 25.61 | 2704 | 4.70 | 230.4 | 1.074 | 0.68 | 0.37 |
| 0.80 | 0.05 | 0.00 | 0.75 | 7.65 | 19.67 | 2709 | 4.67 | 230.4 | 1.063 | 0.67 | 0.61 |
| 1.00 | 0.06 | 0.00 | 0.94 | 9.59 | 16.36 | 2717 | 4.59 | 230.2 | 1.046 | 0.66 | 0.65 |
| 1.20 | 0.06 | 0.00 | 1.14 | 11.63 | 12.63 | 2733 | 4.45 | 230.3 | 1.012 | 0.64 | 0.60 |
| 1.40 | 0.06 | 0.00 | 1.34 | 13.67 | 7.31 | 2778 | 4.05 | 230.6 | 0.914 | 0.58 | 0.47 |
| 1.48 | 0.06 | 0.00 | 1.42 | 14.48 | 0.00 | 2822 | 3.66 | 231.3 | 0.808 | 0.53 | 0.00 |
| Input Power [W] | Valve Close Rate | Water Flow [Q] | Input Voltage [V] | Frequency [Hz] | Input Current [A] | Input Power Actual [W] | Motor Speed [RPM] |
|---|---|---|---|---|---|---|---|
| 100 | 0 | 7.37 | 230 | 50 | 0.75 | 90.2 | 1388 |
| 1/8 | 7.37 | 230 | 50 | 0.77 | 94.8 | 1388 | |
| 1/4 | 7.37 | 230 | 50 | 0.77 | 94.1 | 1390 | |
| 3/8 | 7.32 | 230 | 50 | 0.78 | 96 | 1398 | |
| 1/2 | 6.56 | 230 | 50 | 0.78 | 95.3 | 1400 | |
| 5/8 | 6.54 | 230 | 50 | 0.79 | 96.6 | 1415 | |
| 3/4 | 6.54 | 230 | 50 | 0.8 | 98.8 | 1424 | |
| 7/8 | 6.33 | 230 | 50 | 0.8 | 100.9 | 1436 | |
| 1 | 0 | 230 | 50 | 2.08 | 281 | 2430 |
| Input Power [W] | Valve Close Rate | Water Flow [Q] | Input Voltage [V] | Frequency [Hz] | Input Current [A] | Input Power Actual [W] | Motor Speed [RPM] |
|---|---|---|---|---|---|---|---|
| 215 | 0 | 10.18 | 230 | 50 | 1.65 | 215 | 1948 |
| 1/8 | 10.16 | 230 | 50 | 1.64 | 216 | 1947 | |
| 1/4 | 10.16 | 230 | 50 | 1.64 | 217 | 1946 | |
| 3/8 | 10.08 | 230 | 50 | 1.64 | 215 | 1947 | |
| 1/2 | 10.03 | 230 | 50 | 1.64 | 215 | 1947 | |
| 5/8 | 9.94 | 230 | 50 | 1.63 | 214 | 1947 | |
| 3/4 | 9.81 | 230 | 50 | 1.62 | 215 | 1947 | |
| 7/8 | 9.3 | 230 | 50 | 1.62 | 213 | 1947 | |
| 1 | 0 | 230 | 50 | 4.77 | 704 | 3446 |
| Input Power [W] | Valve Close Rate | Water Flow [Q] | Input Voltage [V] | Frequency [Hz] | Input Current [A] | Input Power Actual [W] | Motor Speed [RPM] |
|---|---|---|---|---|---|---|---|
| 810 | 0 | 17.24 | 230 | 50 | 5.46 | 812 | 3170 |
| 1/8 | 17.24 | 230 | 50 | 5.45 | 810 | 3170 | |
| 1/4 | 17.22 | 230 | 50 | 5.46 | 813 | 3172 | |
| 3/8 | 17.05 | 230 | 50 | 5.45 | 811 | 3172 | |
| 1/2 | 16.8 | 230 | 50 | 5.48 | 814 | 3172 | |
| 5/8 | 16.73 | 230 | 50 | 5.46 | 811 | 3172 | |
| 3/4 | 16.54 | 230 | 50 | 5.44 | 810 | 3172 | |
| 7/8 | 15.87 | 230 | 50 | 5.42 | 806 | 3173 | |
| 1 | 5.2 | 230 | 50 | 6.02 | 908 | 3720 |
| Loading Rated | Motor Output Power [W] | Motor Input Power [W] | Current [A] | Torque [N·m] | Power Factor | N (rpm) | Efficiency |
|---|---|---|---|---|---|---|---|
| 25% | 187.5 | 330 | 2.468 | 0.520 | 0.582 | 195 | 56.82% |
| 50% | 375.0 | 530 | 3.760 | 1.062 | 0.615 | 2550 | 70.75% |
| 75% | 562.5 | 735 | 5.040 | 1.600 | 0.640 | 2930 | 76.53% |
| 100% | 750.0 | 932 | 6.200 | 2.100 | 0.657 | 3250 | 80.47% |
| Max * | 875.0 | 1077 | 6.980 | 2.454 | 0.678 | 3400 | 81.24% |
| Pump Driving Motor | Efficiency Range | Regulating Speed Range |
|---|---|---|
| Normal AC Motor-2poles | 7.48–79.77% | 1334 RPM to 2864 RPM |
| PMSM | 56.82–81.24% | 195 RPM–3400 RPM |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.; Si, H.; Wang, H.; Li, G. Research Based on a Fuzzy Algorithm for Energy Saving Single-Phased Powered Pumps. Machines 2025, 13, 1070. https://doi.org/10.3390/machines13111070
Sun W, Si H, Wang H, Li G. Research Based on a Fuzzy Algorithm for Energy Saving Single-Phased Powered Pumps. Machines. 2025; 13(11):1070. https://doi.org/10.3390/machines13111070
Chicago/Turabian StyleSun, Wangsheng, Haiqing Si, Haibo Wang, and Gen Li. 2025. "Research Based on a Fuzzy Algorithm for Energy Saving Single-Phased Powered Pumps" Machines 13, no. 11: 1070. https://doi.org/10.3390/machines13111070
APA StyleSun, W., Si, H., Wang, H., & Li, G. (2025). Research Based on a Fuzzy Algorithm for Energy Saving Single-Phased Powered Pumps. Machines, 13(11), 1070. https://doi.org/10.3390/machines13111070






