Research on Denoising Methods for Infrasound Leakage Signals Using Improved Wavelet Threshold Algorithm
Abstract
1. Introduction
2. Materials and Methods
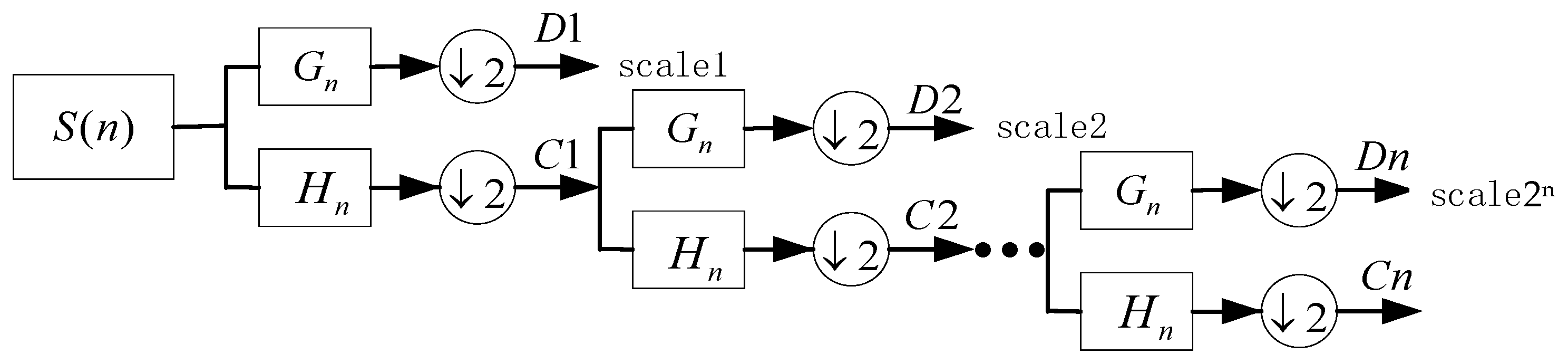
2.1. Wavelet Threshold Denoising Process
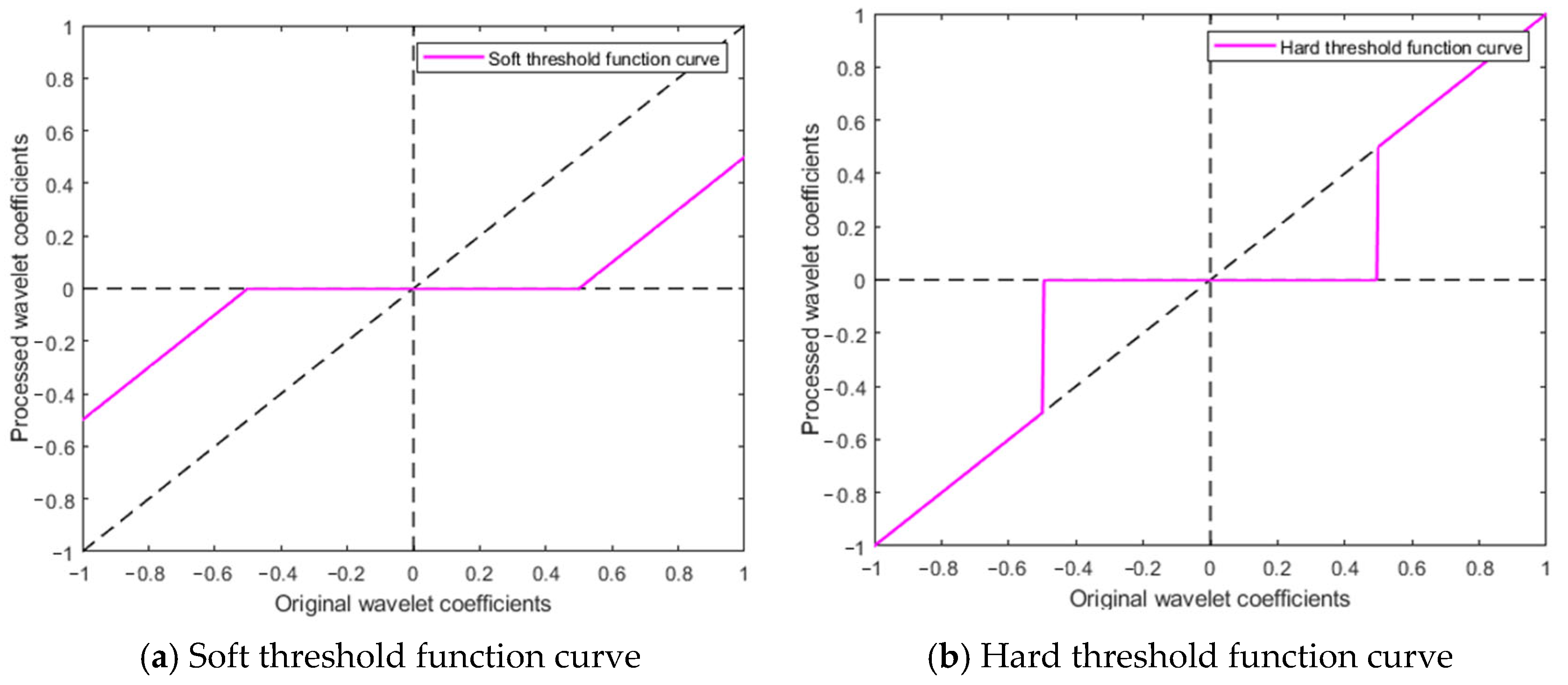
2.2. Classical Threshold Function and Its Limitations
- (1)
- Hard threshold method
- (2)
- Soft threshold method
- (3)
- Semi-soft threshold method
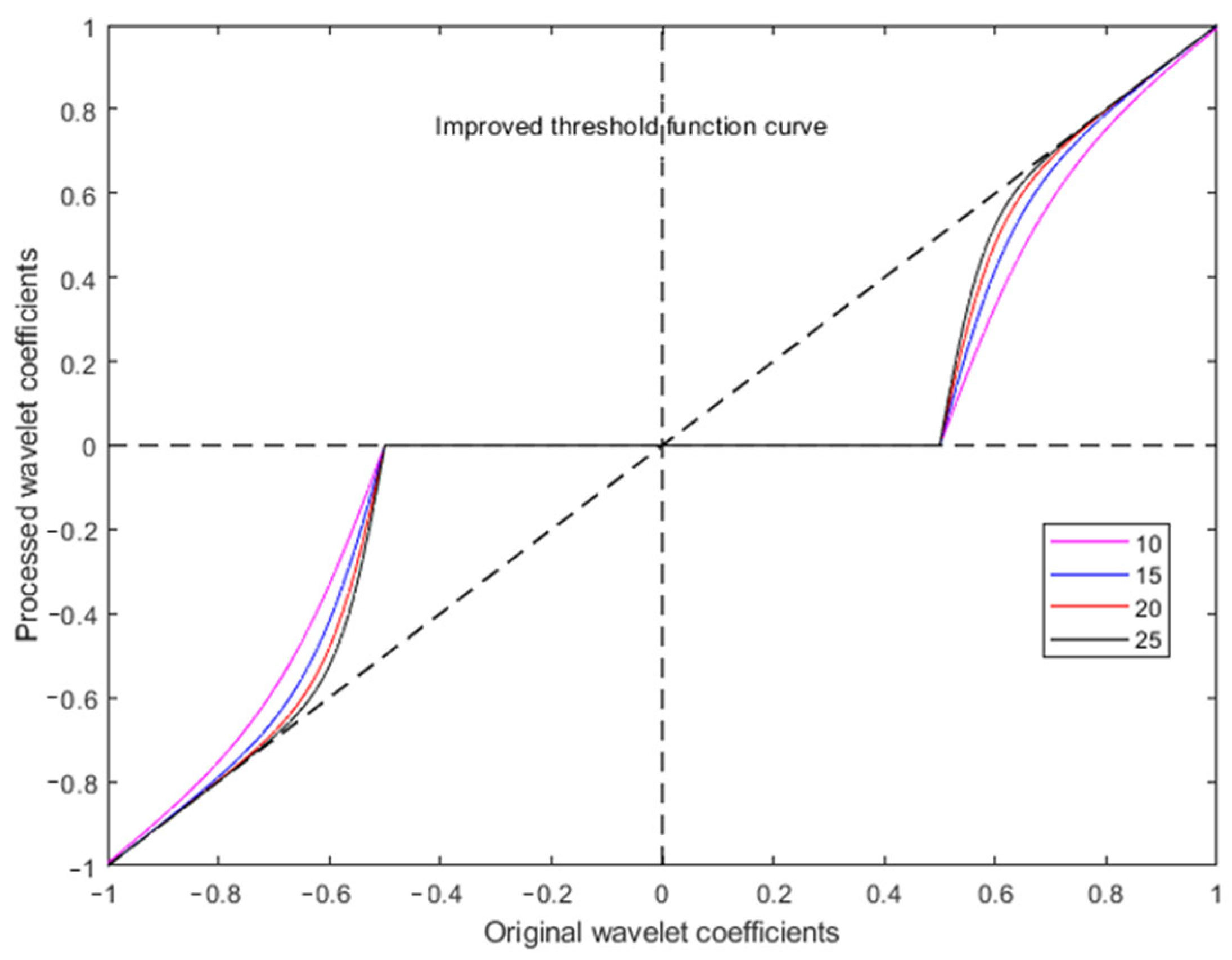
2.3. Improved Threshold Function Algorithm
- (1)
- Proof of continuity
- (2)
- Proof of convergence
3. Experiment
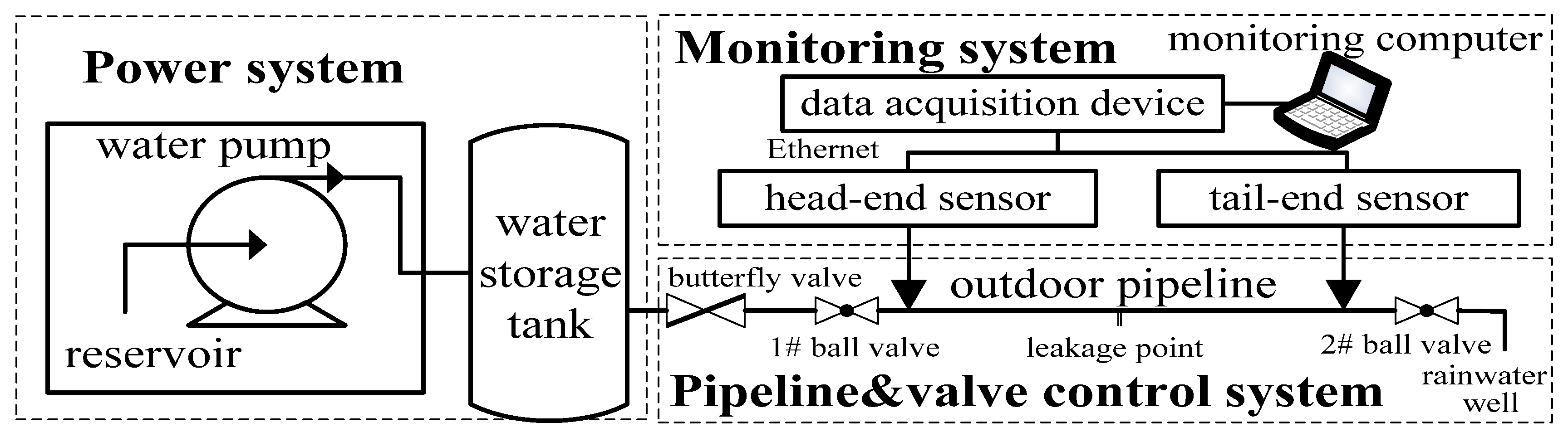
3.1. Establishment of Experimental Platform
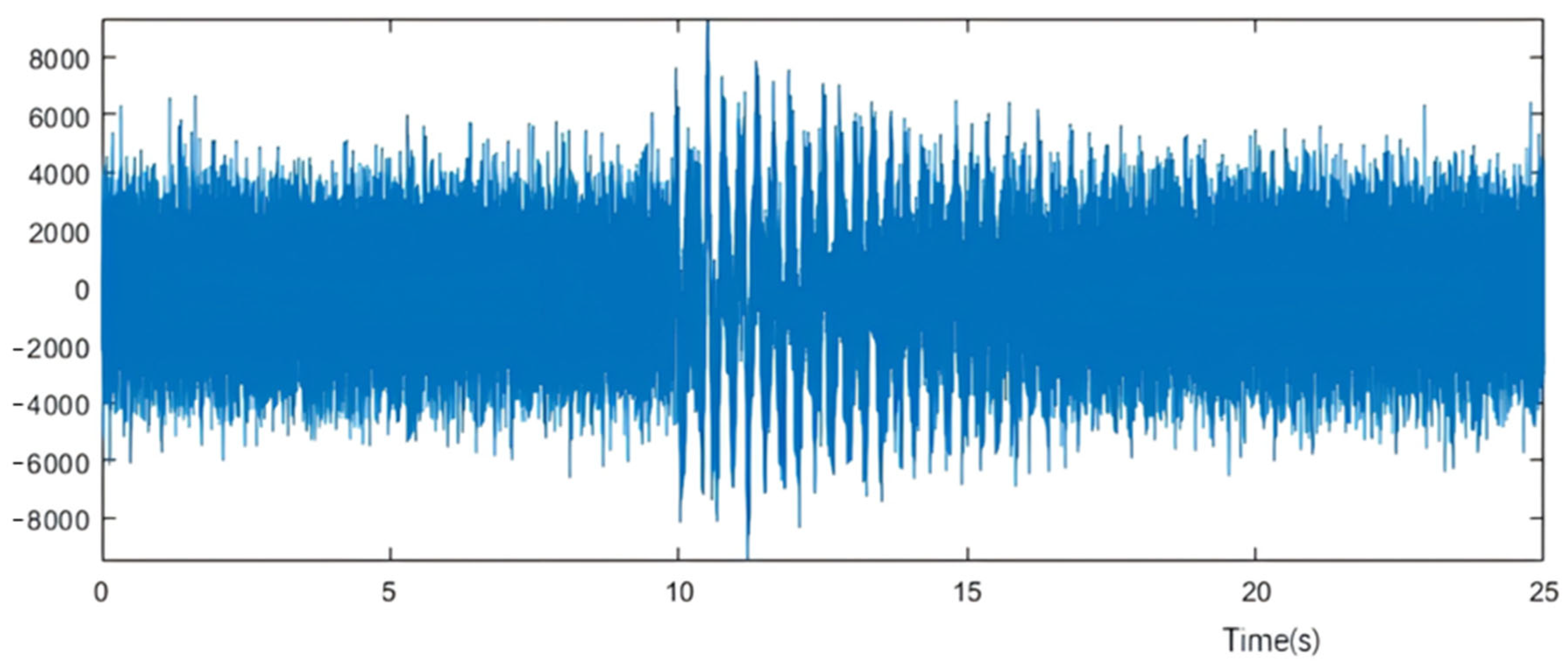
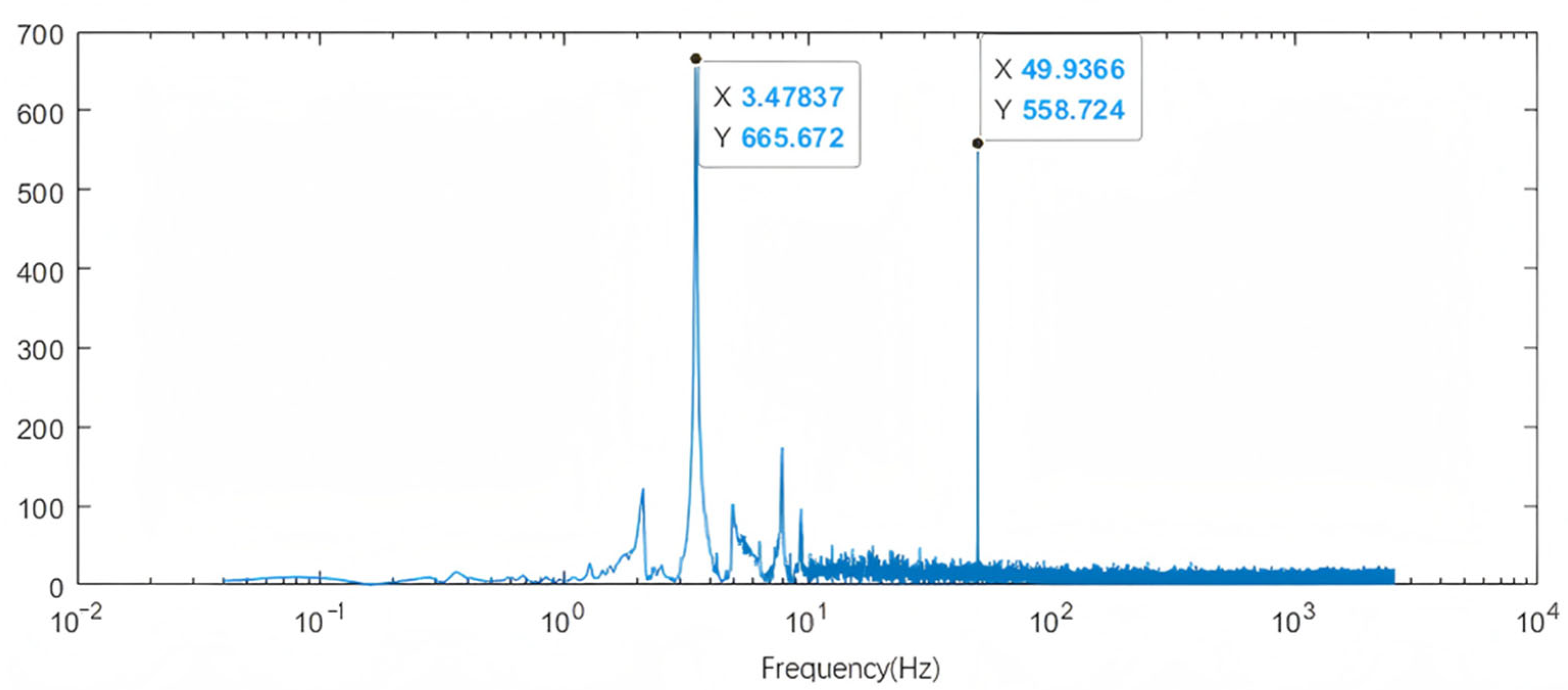
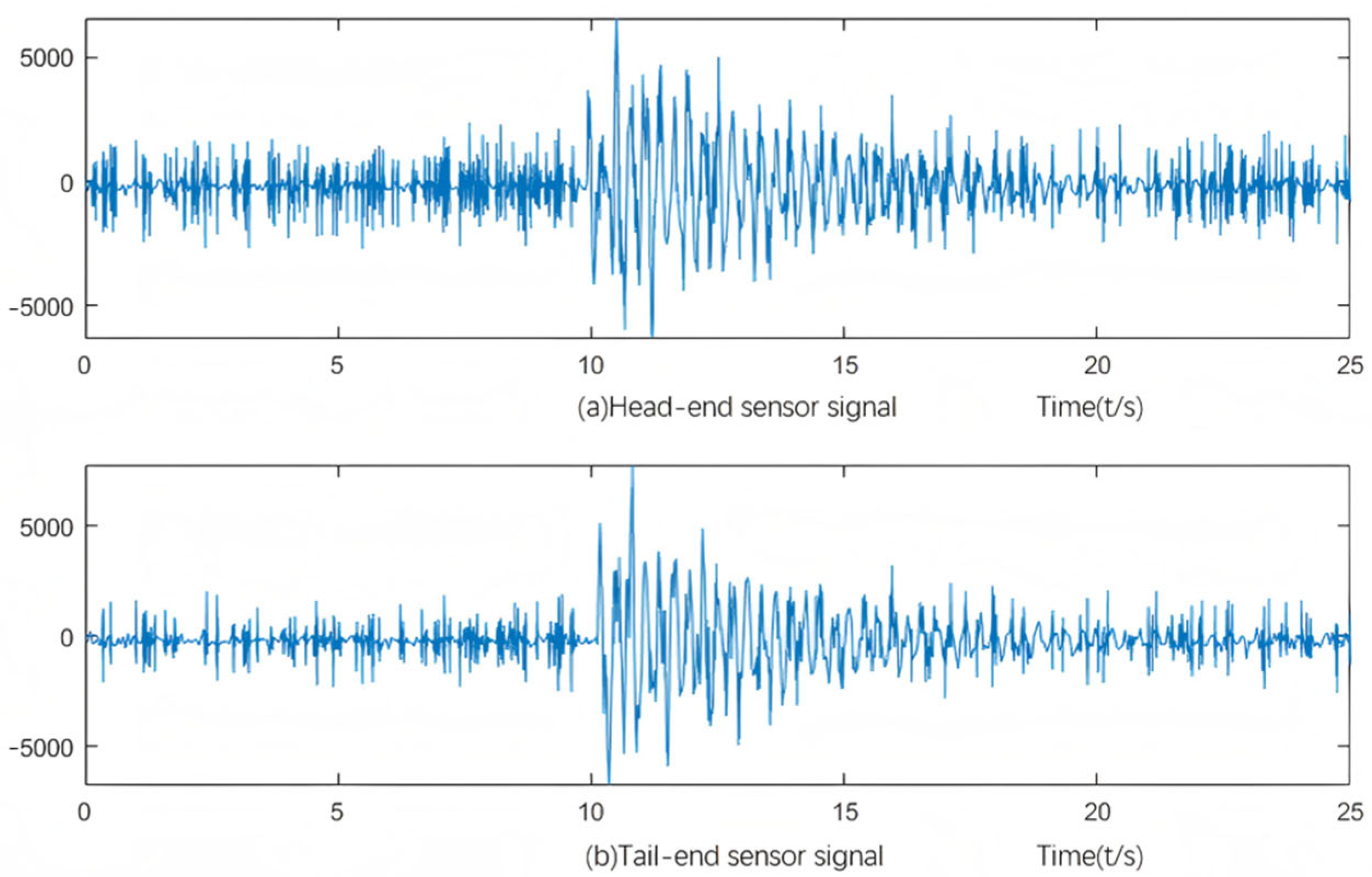
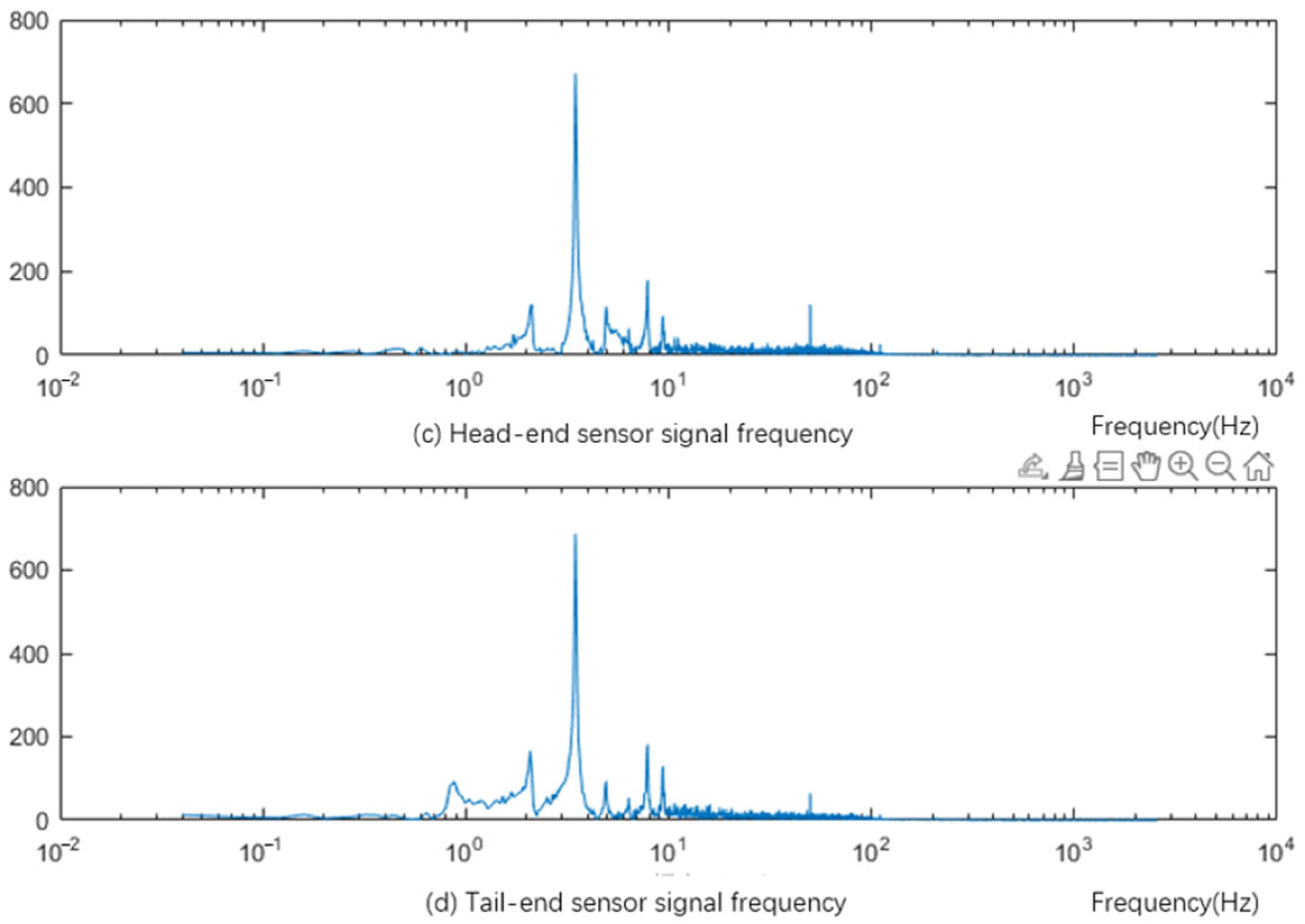
3.2. Analysis of Leakage Infrasound Signal
4. Results and Discussion
- (1)
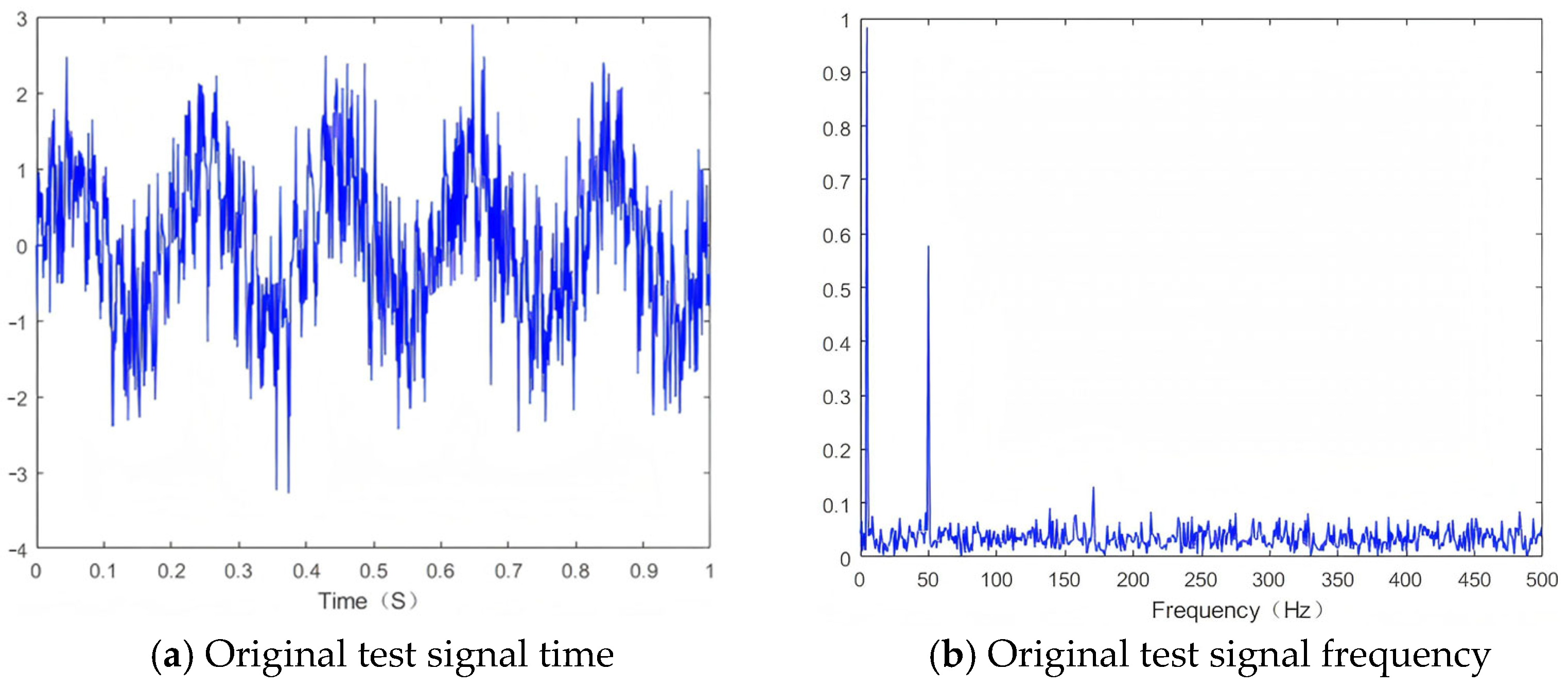
- Discussion of denoising results of simulation signals
- (2)
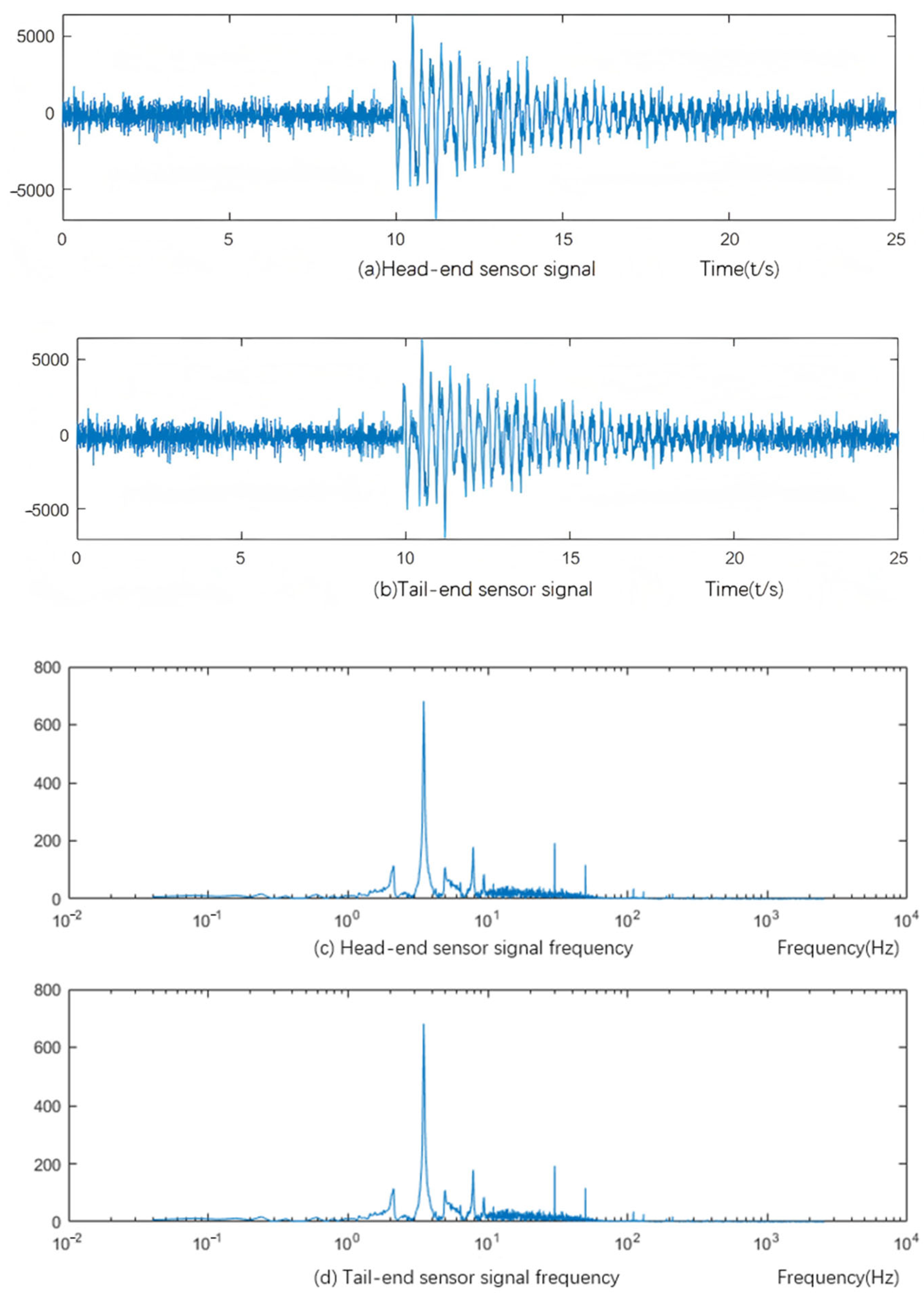
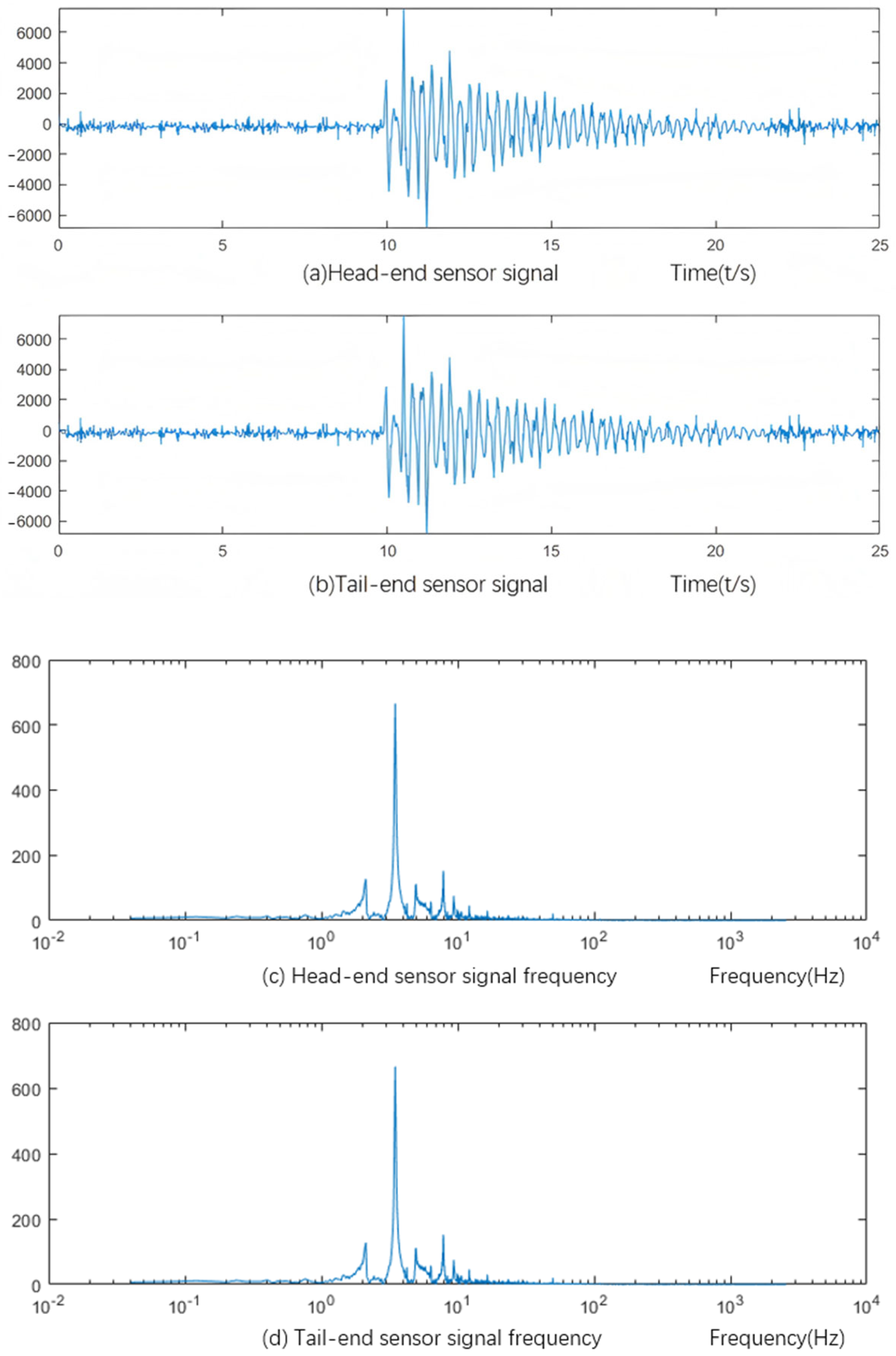
- Discussion of denoising results of measured signals
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wan, J.L.; Deng, Y.L.; Li, Y. A review on detection and defect identification of drainage pipeline. Sci. Technol. Eng. 2020, 20, 13520–13528. [Google Scholar]
- Wang, H.C.; Li, Q.; Luo, Y. A similarity-based locating method of negative pressure wave caused by pipeline leakage. Oil Gas. Storage Transp. 2021, 40, 679–684. [Google Scholar]
- Zhou, Z.M.; Zhang, J.; Yang, K.L.; Zhang, L.L. Development and adaptability of gas transmission pipeline leak detection technology. Oil-Gas. Field Surf. Eng. 2019, 38, 6–12. [Google Scholar]
- Murvay, P.S.; Silea, I. A survey on gas leak detection and localization techniques. J. Loss Prev. Process Ind. 2012, 25, 966–973. [Google Scholar] [CrossRef]
- Hao, Y.M.; Yao, Q.; Jiang, J.C.; Xing, Z.X.; Xu, N. Simulation analysis of influence mechanism on infrasound propagation from urban pipeline leakage. Res. Explor. Lab. 2021, 40, 57–60, 82. [Google Scholar]
- Zhang, Q.; Zhao, P.; Wang, Y. Simulation and experimental study on infrasonic source of gas pipeline leakage. Autom. Instrum. 2023, 44, 116–120. [Google Scholar]
- Chilo, J.; Lindblad, T. Real-Time Signal Processing of Infrasound Data Using 1D Wavelet Transform on FPGA Device. In Proceedings of the 2007 15th IEEE-NPSS Real-Time Conference, Berkeley, CA, USA, 29 April–4 May 2007; pp. 1–6. [Google Scholar]
- Du, X.; Leng, X.; Rao, S.; Feng, L. Debris Flow Infrasound Denoising Based on Improved Wavelet Threshold Algorithm. In Proceedings of the 2022 IEEE International Conference Mechatron Autom, Guilin, China, 7–10 August 2022; pp. 1–6. [Google Scholar]
- Walker, D.; Hedlin, M.A.H. Wind-noise reduction for infrasonic measurements using adaptive line enhancement. J. Atmos. Ocean. Technol. 2010, 27, 1731–1742. [Google Scholar]
- Mallat, S.; Hwang, W.L. Singularity detection and processing with wavelets. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, San Francisco, CA, USA, 23–26 March 1992; IEEE Press: Piscataway, NJ, USA, 1992; pp. 1–20. [Google Scholar] [CrossRef]
- Xu, Y.; Weaver, J.B.; Healy, D.M.J. Wavelet transform domain filters: A spatially selective noise filtration technique. IEEE Trans. Image Process 1994, 3, 747–758. [Google Scholar]
- Donoho, D.L.; Johnstone, J.M. Ideal spatial adaptation by wavelet shrinkage. Biometrika 1994, 81, 425–455. [Google Scholar] [CrossRef]
- Donoho, D.L. De-noising by soft-thresholding. IEEE Trans. Inf. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef]
- Gao, H.; Bruce, A.G. Waveshrink with firm shrinkage. Stat. Sin. 1997, 7, 855–874. [Google Scholar]
- Luisier, F.; Blu, T.; Unser, M. A new SURE approach to image denoising: Interscale orthonormal wavelet thresholding. IEEE Trans. Image Process 2007, 16, 593–606. [Google Scholar] [CrossRef]
- Li, Q.Q.; Qin, B.Y.; Si, W.; Wang, R.Q.; Liu, B.; Ma, S.L.; Wang, X. Wavelet adaptive threshold estimation algorithm optimized by hybrid particle swarm and its application in partial discharge denoising. High. Volt. Eng. 2017, 43, 1485–1492. [Google Scholar]
- Wang, X.X.; Li, Y.Y.; Zhang, Z.Z. Improved wavelet threshold denoising algorithm for acoustic signals based on simulated annealing. Tech. Acoust. 2024, 43, 456–463. (In Chinese) [Google Scholar] [CrossRef]
- Liu, Y.Y.; Chen, K.K.; Zhao, W.W. Pipeline infrasound denoising via Beluga Whale Optimization-VMD combined with wavelet thresholding. Chin. J. Sci. Instrum. 2024, 45, 123–131. [Google Scholar]
- Hao, Y.M.; Yao, Q.; Zhu, Y.L.; Xing, Z.; Jing, J.; Xu, N.; Yang, J. Signal processing of infrasound leakage in urban pipelines based on spectral analysis. J. Pipeline Syst. Eng. Pr. 2023, 14, 04023007. [Google Scholar] [CrossRef]
- Sun, X.X.; Zhou, Y.Y. Pipeline Leakage Signal Processing Method Based on Improved Adaptive Optimal Kernel Time-Frequency Distribution. China Patent CN202410211234.7, 18 March 2024. (In Chinese). [Google Scholar]
- Peng, S.; Xing, J.; Liu, X. A rolling bearing vibration signal noise reduction processing algorithm using the fusion HPO-VMD and improved wavelet threshold. Symmetry 2025, 17, 1316. [Google Scholar] [CrossRef]
- Luan, J.; Liu, L.; Cui, B. Denoising of ceramic detection signals based on the combination of variational modal decomposition optimized by improved secretary bird optimization algorithm and wavelet thresholding. Rev. Sci. Instrum. 2025, 96, 015103. [Google Scholar] [CrossRef] [PubMed]
- Cheng, K.W.; Zhi, F.Z.; Bo, H.C.; Yong, Y. Denoise for propeller acoustic signals based on the improved wavelet thresholding algorithm of CEEMDAN. Cogent Eng. 2024, 11, 2327570. [Google Scholar] [CrossRef]
- Huang, Q.; Deng, Q.; Li, Z.; Luo, P. Application of a modified wavelet threshold denoising algorithm in system identification of WPTS. J. Power Electron. 2024, 24, 1150–1162. [Google Scholar] [CrossRef]
- Zhang, Y.; Ding, W.; Pan, Z.; Qin, J. Improved wavelet threshold for image de-noising. Front. Neurosci. 2019, 13, 39. [Google Scholar] [CrossRef] [PubMed]
- Zhu, G.; Liu, B.; Yang, P.; Fan, X. Image denoising method based on improved wavelet threshold algorithm. Multimed. Tools Appl. 2024, 83, 67997–68011. [Google Scholar] [CrossRef]
- Cui, H.M.; Zhao, R.M.; Hou, Y.L. Improved threshold denoising method based on wavelet transform. Phys. Procedia 2012, 33, 1354–1359. [Google Scholar] [CrossRef]
- Li, X.; Yao, H. Improved signal processing algorithm based on wavelet transform. J. Multimed. 2013, 8, 311–317. [Google Scholar] [CrossRef]
- Gao, X.J.; Gao, Z.G. Research on wavelet threshold denoising algorithm for images. Electron. Opt. Control 2007, 14, 148–151. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, W.Q.; Song, G.X. Signal denoising in wavelet domain based on a new threshold function. J. Xidian Univ. 2004, 31, 296–303. (In Chinese) [Google Scholar] [CrossRef]
- Chen, P.; Zhang, Q. Classification of heart sounds using discrete time-frequency energy feature based on S transform and the wavelet threshold denoising. Biomed. Signal Process. Control. 2020, 57, 101684. [Google Scholar] [CrossRef]
- Ling, T.H.; Liu, H.R.; Zhang, L. Construction method of biorthogonal wavelet basis and its application in blasting vibration signal analysis. J. Vibr Shock. 2018, 37, 8–15. (In Chinese) [Google Scholar] [CrossRef]




| Layers | Soft Threshold Method | Hard Threshold Method | Improved Threshold Method | |
|---|---|---|---|---|
| 4 | SNR RSME | 13.8213 0.14402 | 11.4218 0.18984 | 15.3846 0.09256 |
| 5 | SNR RSME | 14.3781 0.13508 | 15.2959 0.12153 | 19.5107 0.07942 |
| 6 | SNR RSME | 10.7203 0.20581 | 10.8041 0.20383 | 14.3059 0.10020 |
| 7 | SNR RSME | 9.5083 0.2979 | 10.4906 0.21133 | 12.5690 0.13580 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Tang, J.; Li, B.; Li, Y.; Yang, F. Research on Denoising Methods for Infrasound Leakage Signals Using Improved Wavelet Threshold Algorithm. Machines 2025, 13, 1062. https://doi.org/10.3390/machines13111062
Liu Z, Tang J, Li B, Li Y, Yang F. Research on Denoising Methods for Infrasound Leakage Signals Using Improved Wavelet Threshold Algorithm. Machines. 2025; 13(11):1062. https://doi.org/10.3390/machines13111062
Chicago/Turabian StyleLiu, Zunmin, Jingchun Tang, Baogang Li, Yuhuan Li, and Fazhan Yang. 2025. "Research on Denoising Methods for Infrasound Leakage Signals Using Improved Wavelet Threshold Algorithm" Machines 13, no. 11: 1062. https://doi.org/10.3390/machines13111062
APA StyleLiu, Z., Tang, J., Li, B., Li, Y., & Yang, F. (2025). Research on Denoising Methods for Infrasound Leakage Signals Using Improved Wavelet Threshold Algorithm. Machines, 13(11), 1062. https://doi.org/10.3390/machines13111062





