Predicting Real-Time Carbon Emissions for Power Grids Using Graph Convolutional Networks
Abstract
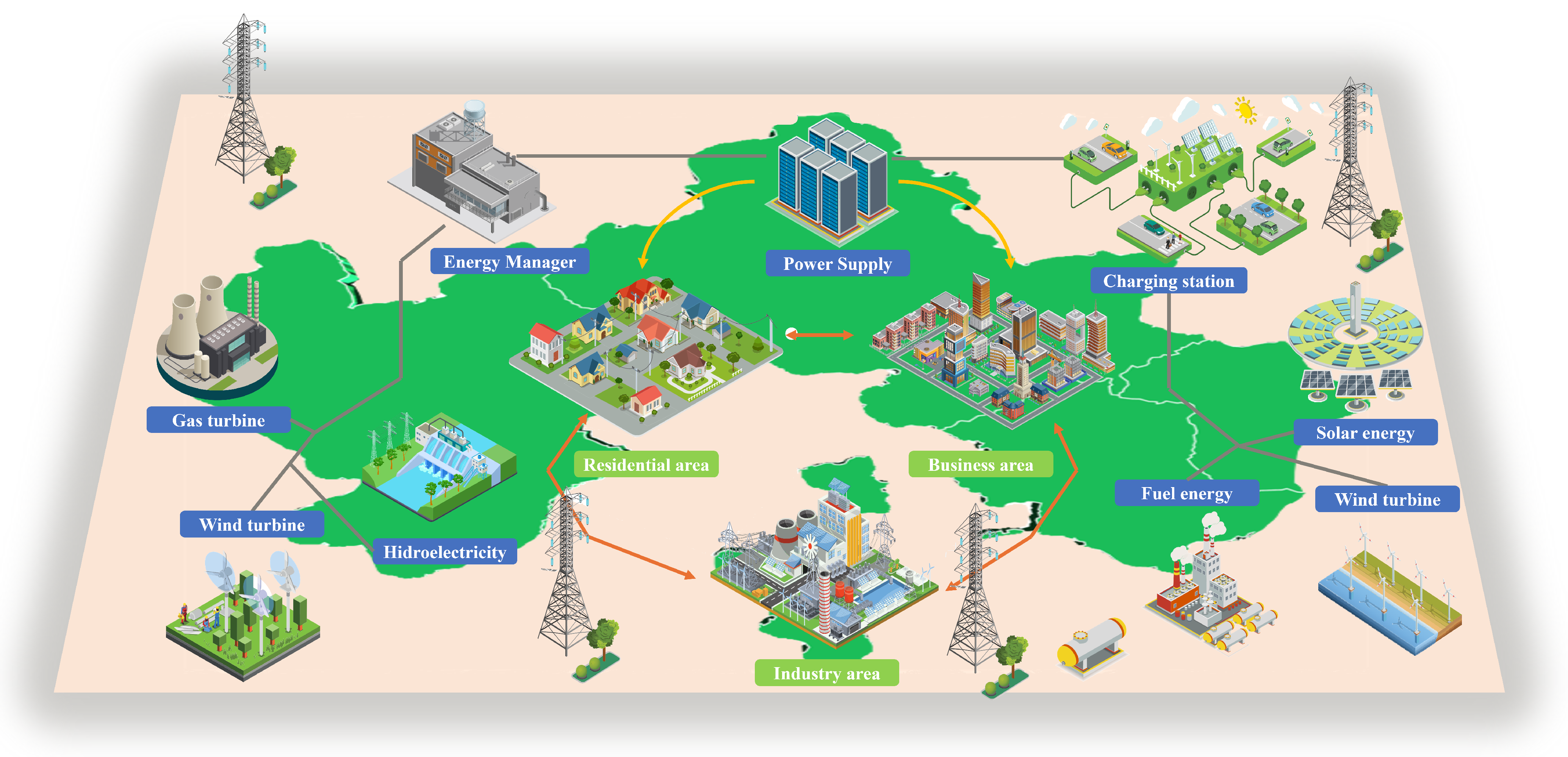
1. Introduction
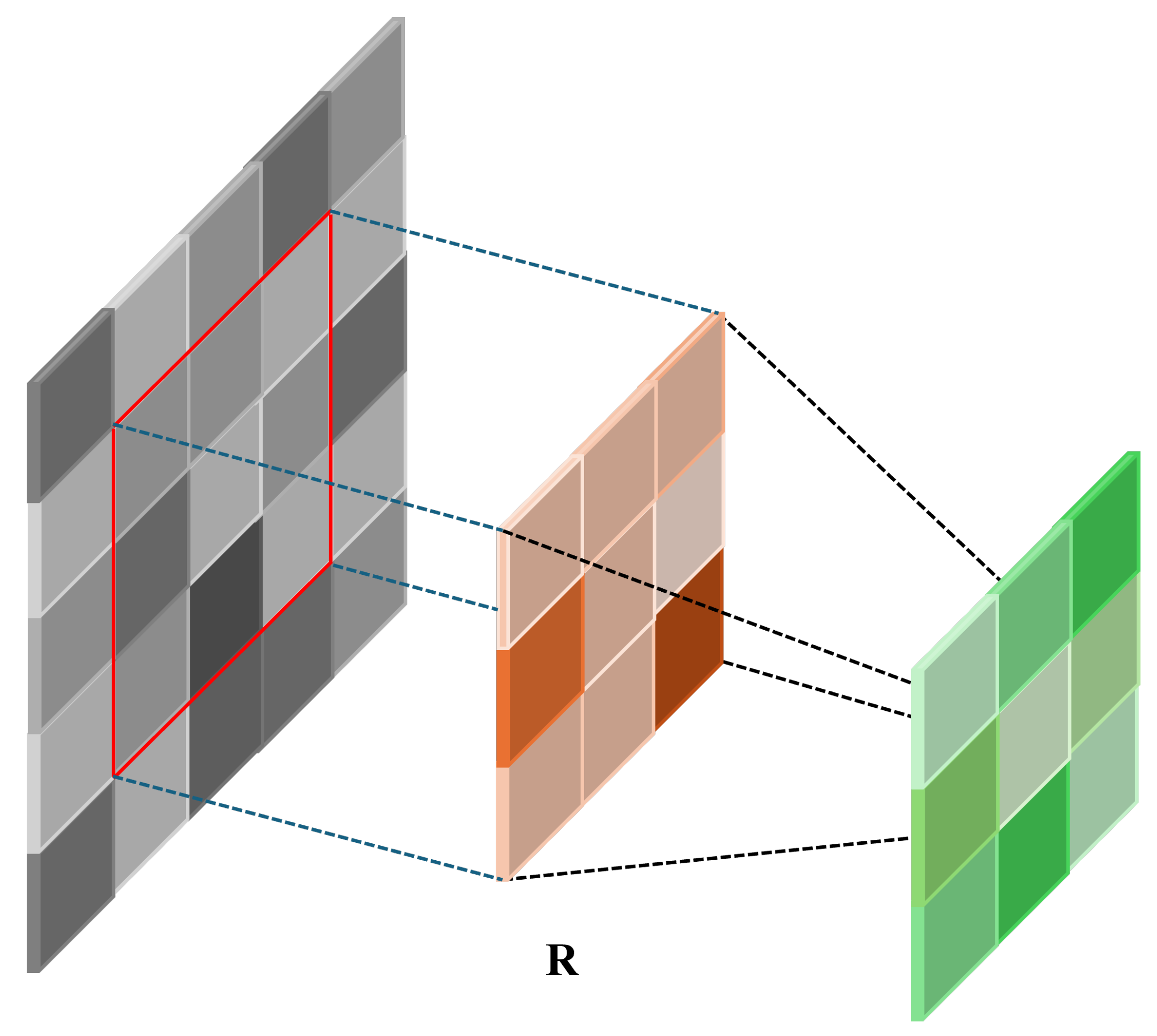
- Complex spatiotemporal data in power grid systems are structured into graph data, leveraging the powerful relational reasoning capabilities of graph neural networks to capture dynamic interactions between regional nodes.
- The TCNs layer captures complex time-dependent relationships, enabling highly accurate predictions of power grid carbon emissions.
2. Preliminaries and Problem Formulation
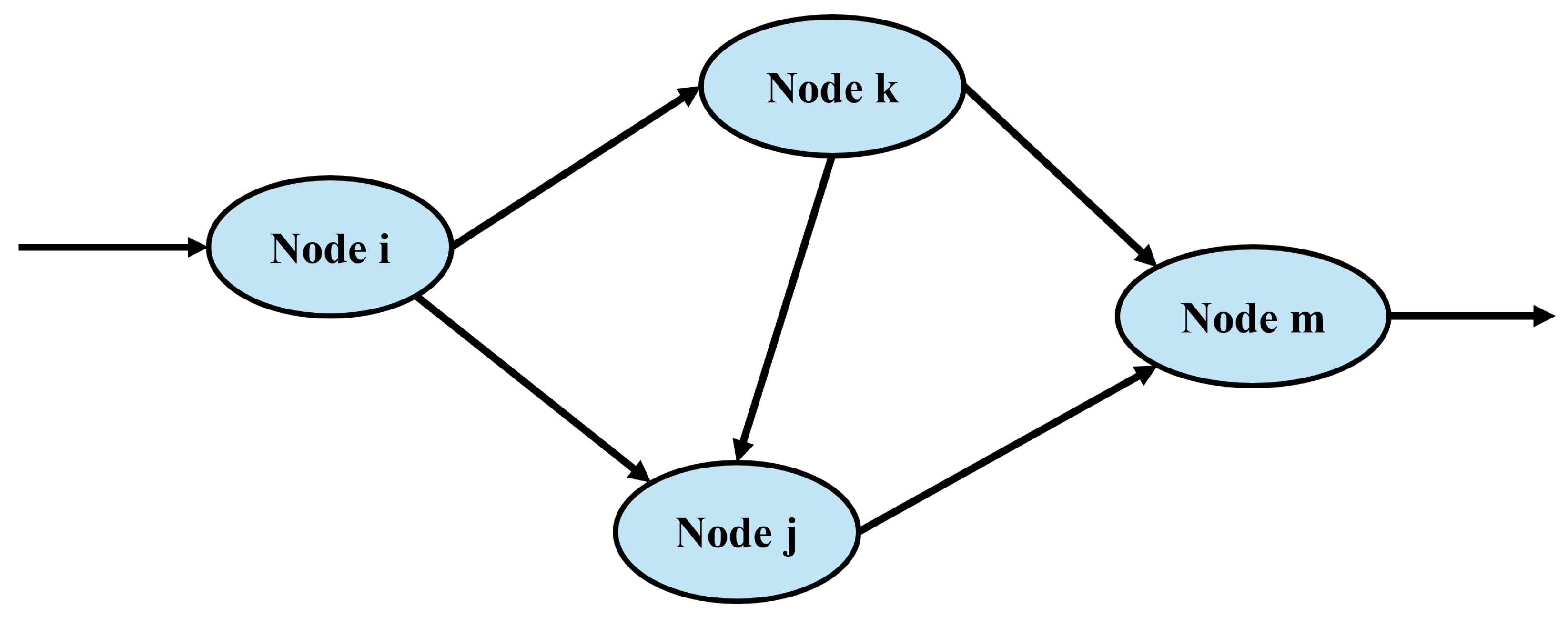
2.1. A Carbon Calculation Model for Power Grid Nodes
2.2. Problem Description
- Establish an accurate measurement model based on graph convolution networks for power grid systems.
- Transform the output of the network topology matrices into a predictive form for carbon emissions.
- Train the entire network to minimize prediction errors for the carbon emissions.
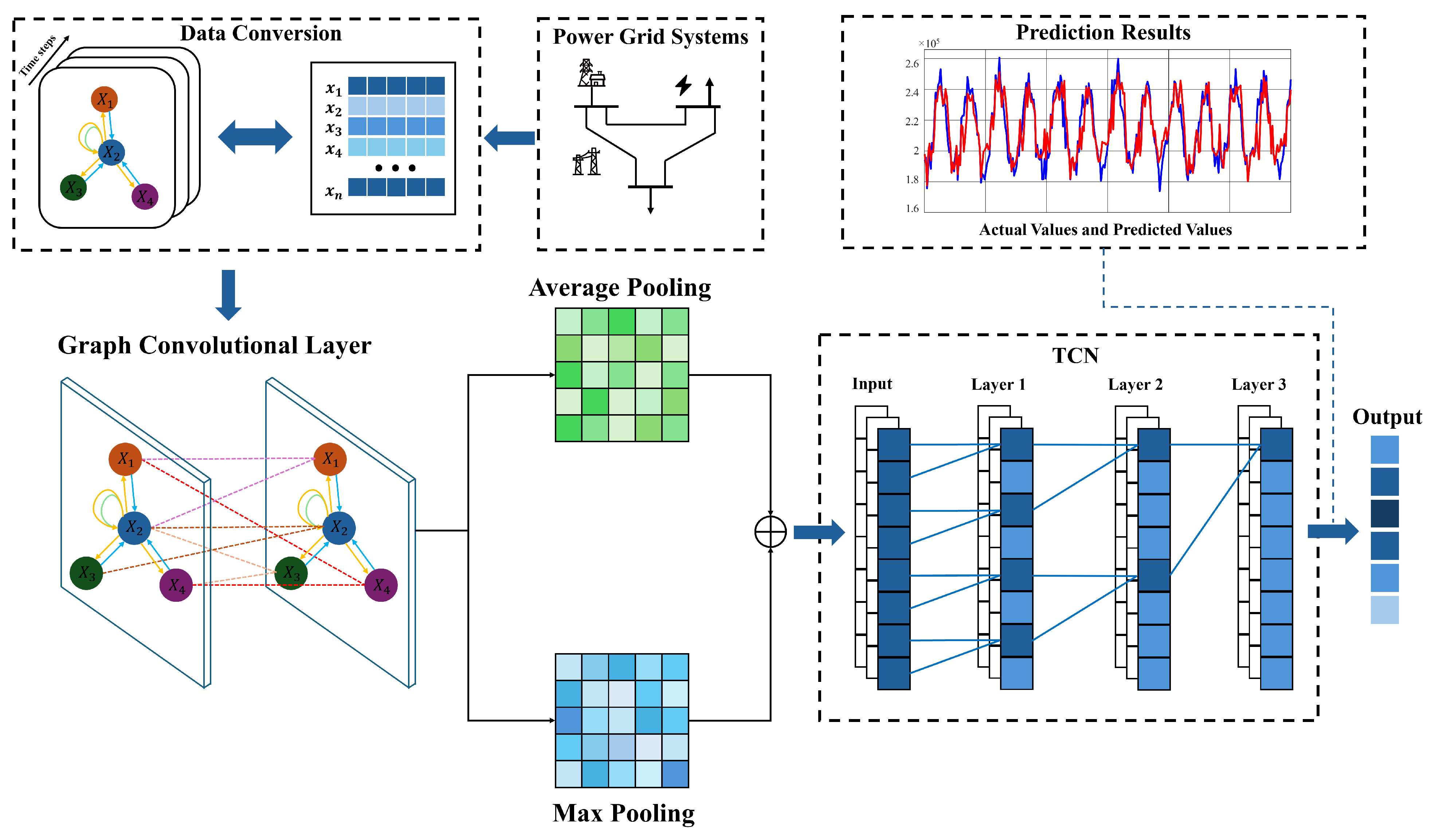
3. GCN-Based Carbon Emissions Prediction
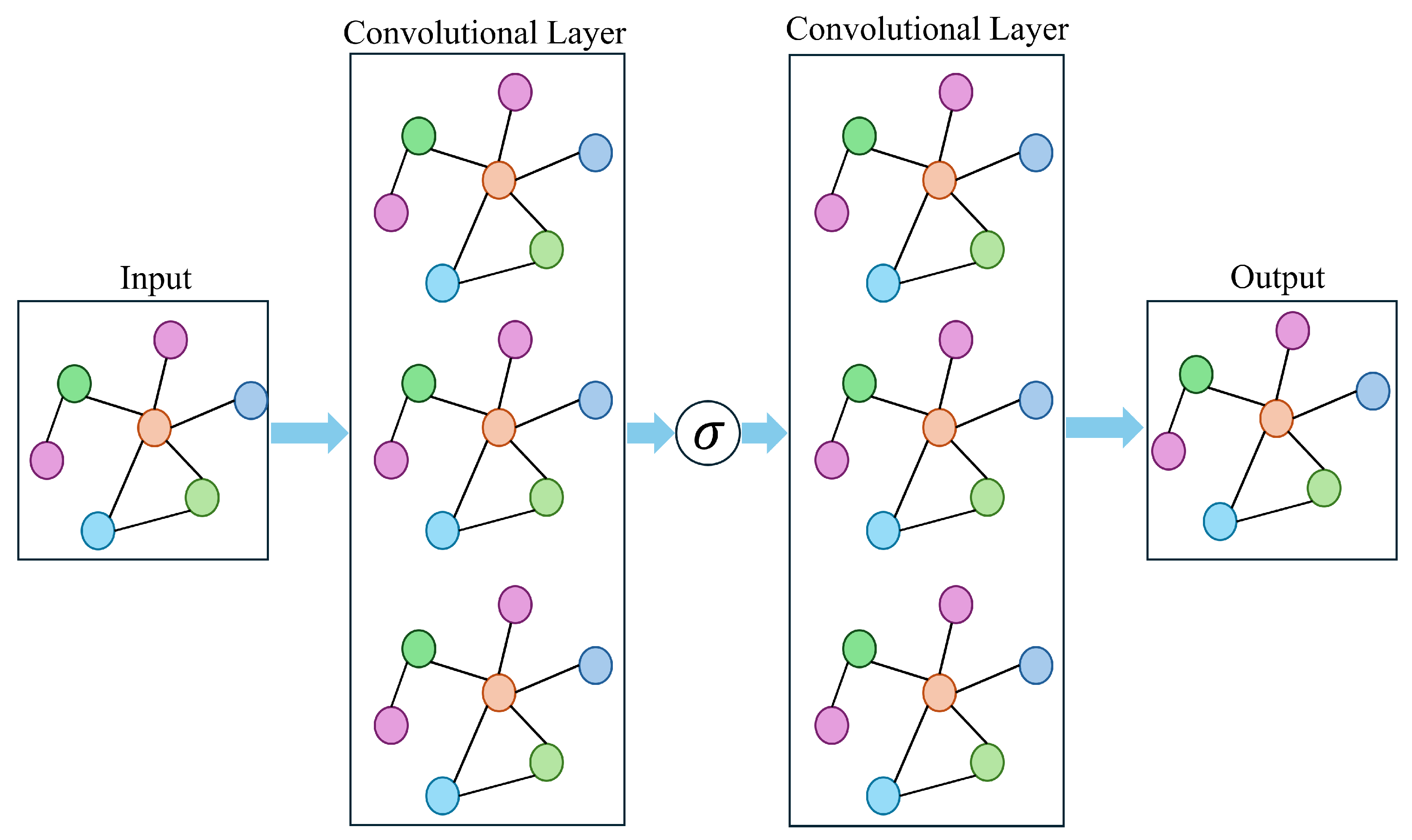
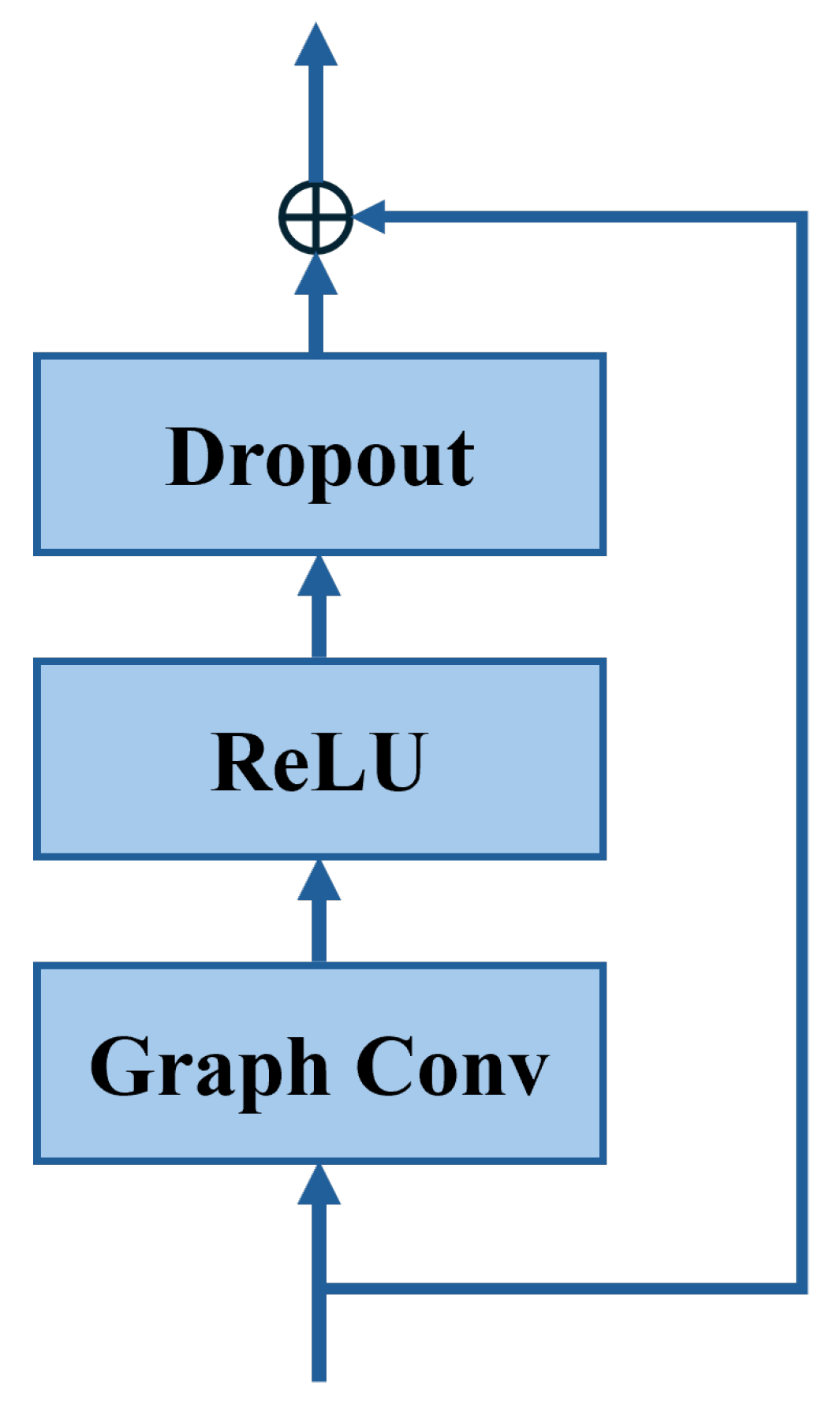
3.1. Graph Convolutional Layer
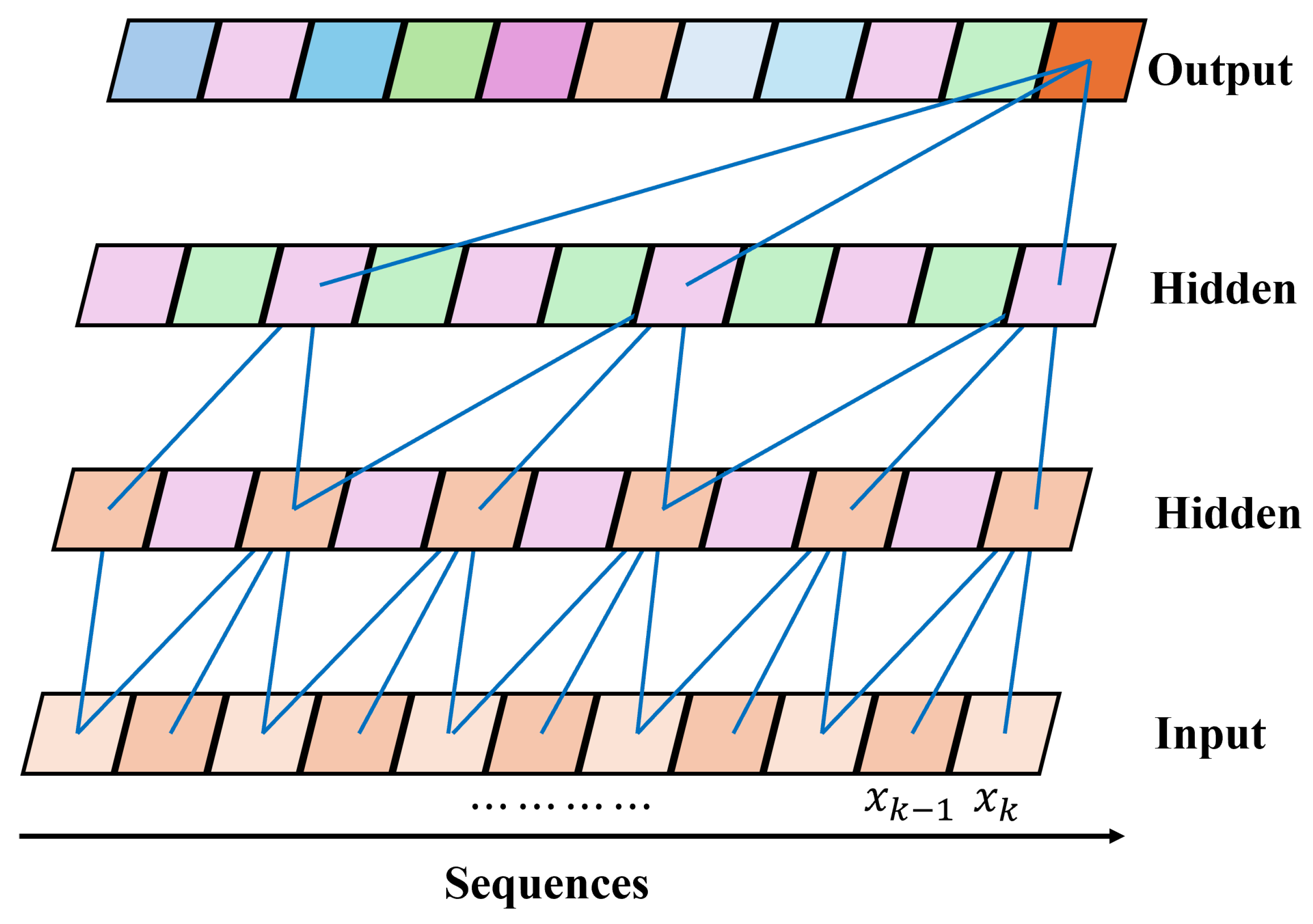
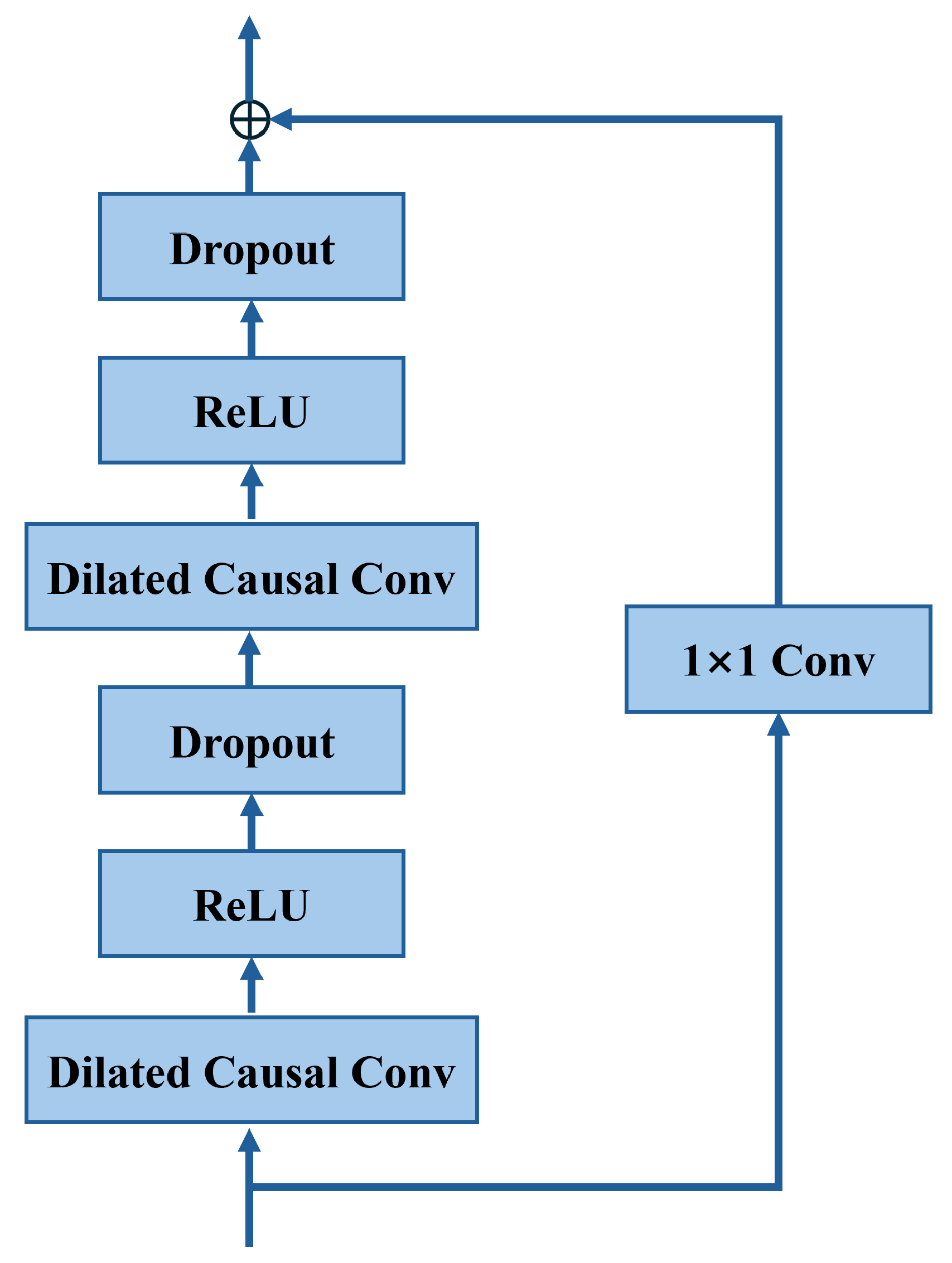
3.2. Temporal Convolutional Layers
- causal convolutions that strictly preserve temporal order and avoid information leakage from future to past.
- dilated convolutions that increase the receptive field and enable long-term dependency modeling.
3.3. Training Method
| Algorithm 1 Training Procedure for GCN-based Model |
| Require: Training data , validation data Ensure: Trained model parameters
|
4. Experimental Studies on GCN-Based Approach
4.1. IEEE 14-Bus Systems Verification
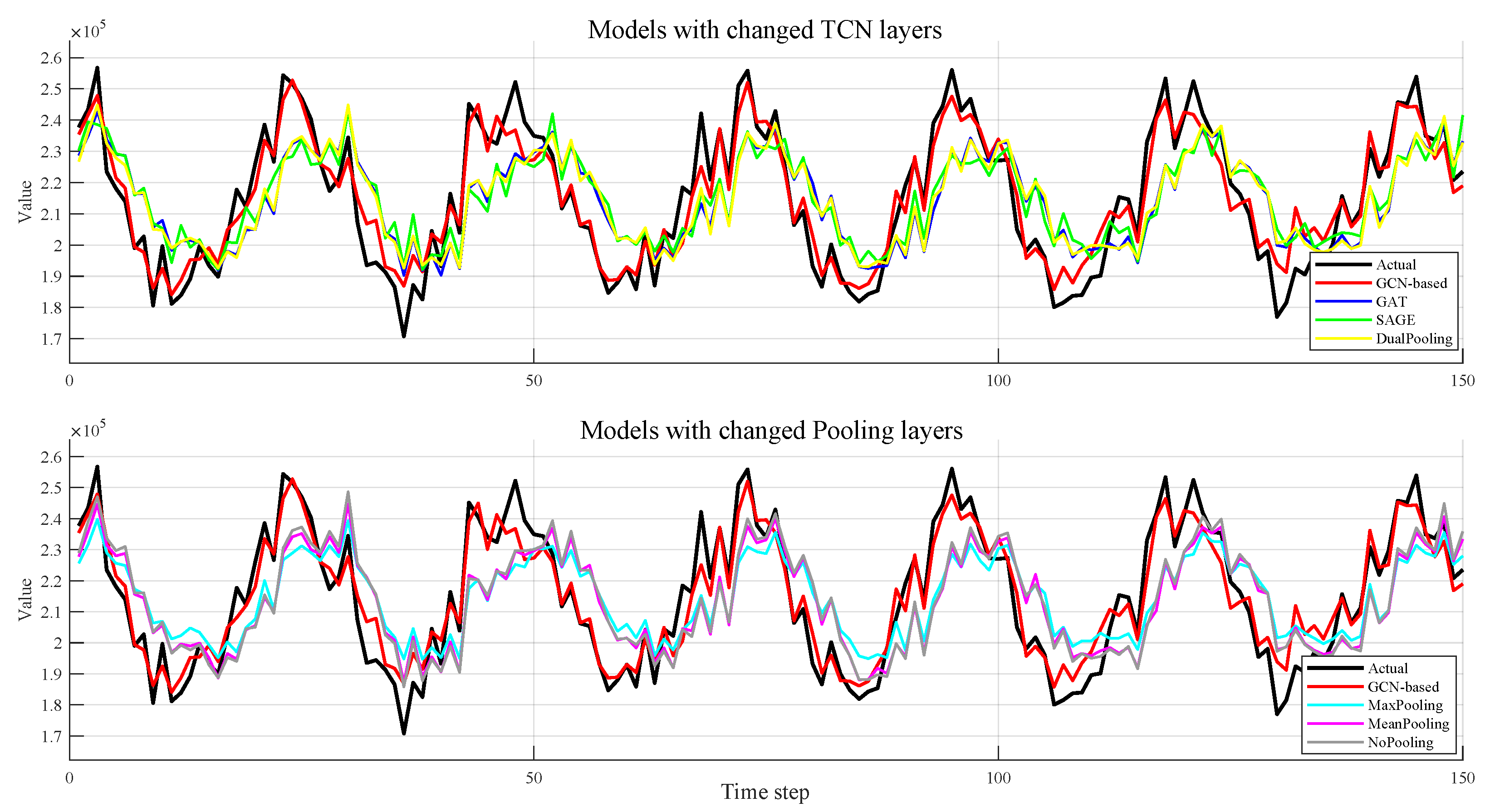
4.2. Robustness Tests
5. Conclusions
- Integrating probabilistic forecasting techniques to handle renewable energy uncertainty, such as using Bayesian neural networks or Monte Carlo dropout within the TCN framework.
- Extending the model to multi-energy coupling systems by incorporating heat and gas network data, using coupled graph structures to capture cross-energy dependencies.
- Exploring model compression and distributed training strategies to enhance scalability for large-scale power grids.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| GCNs | Graph Convolutional Networks |
| TCNs | Temporal Convolutional Networks |
| LEAP | Long-range Energy Alternatives Planning |
| ARIMA | Auto-Regressive Integrated Moving Average |
| LSTM | Long Short-Term Memory |
| SVM | Support Vector Machine |
| GNNs | Graph Neural Networks |
References
- Li, Y.; Yang, X.; Du, E.; Liu, Y.; Zhang, S.; Yang, C.; Zhang, N.; Liu, C. A review on carbon emission accounting approaches for the electricity power industry. Appl. Energy 2024, 359, 122681. [Google Scholar] [CrossRef]
- Albuquerque, B.S.D.; Tostes, M.E.D.L.; Bezerra, U.H.; Carvalho, C.C.M.D.M.; Nascimento, A.L.L.D. Use of Distributed Energy Resources Integrated with the Electric Grid in the Amazon: A Case Study of the Universidade Federal do Pará Poraquê Electric Boat Using a Digital Twin. Machines 2024, 12, 803. [Google Scholar] [CrossRef]
- Guo, Z.; Siew, W.H.; Li, Q.; Shi, W. On the Lightning Attachment Process of Wind Turbine–Observation, Experiments and Modelling. Machines 2025, 13, 704. [Google Scholar] [CrossRef]
- Yang, L.; Mei, L.; Chen, Y.; Hao, Y.; Li, L.; Wu, J.; Mao, X. Prediction Method for Mechanical Characteristic Parameters of Weak Components of 110 kV Transmission Tower under Ice-Covered Condition Based on Finite Element Simulation and Machine Learning. Machines 2024, 12, 652. [Google Scholar] [CrossRef]
- Li, P.; Wu, W.; Wang, X.; Xu, B. A Data-Driven Linear Optimal Power Flow Model for Distribution Networks. IEEE Trans. Power Syst. 2023, 38, 956–959. [Google Scholar]
- Tian, P.; Jin, Y.; Xie, N.; Wang, C.; Huang, C. Power Flow Calculation for VSC-Based AC/DC Hybrid Systems Based on Fast and Flexible Holomorphic Embedding. J. Mod. Power Syst. Clean Energy 2024, 12, 1370–1382. [Google Scholar]
- Ma, M.; Li, Y.; Du, E.; Jiang, H.; Zhang, N.; Wang, W.; Wang, M. Calculating Probabilistic Carbon Emission Flow: An Adaptive Regression-Based Framework. IEEE Trans. Sustain. Energy 2024, 15, 1576–1588. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, H.; Cheng, Z.; Shao, J.; Yu, X.; Jiang, J. A review of carbon emissions accounting and prediction on the power grid. Electr. Eng. 2025, 107, 7561–7574. [Google Scholar] [CrossRef]
- Wang, T.; Watson, J. Scenario analysis of China’s emissions pathways in the 21st century for low carbon transition. Energy Policy 2010, 38, 3537–3546. [Google Scholar] [CrossRef]
- McPherson, M.; Karney, B. Long-term scenario alternatives and their implications: LEAP model application of Panama’s electricity sector. Energy Policy 2014, 68, 146–157. [Google Scholar] [CrossRef]
- Maji, D.; Shenoy, P.; Sitaraman, R.K. Multi-Day Forecasting of Electric Grid Carbon Intensity Using Machine Learning. ACM SIGENERGY Energy Inform. Rev. 2023, 3, 19–33. [Google Scholar]
- Luo, J.; Zhuo, W.; Liu, S.; Xu, B. The Optimization of Carbon Emission Prediction in Low Carbon Energy Economy Under Big Data. IEEE Access 2024, 12, 14690–14702. [Google Scholar] [CrossRef]
- Lau, E.; Yang, Q.; Forbes, A.; Wright, P.; Livina, V. Modelling carbon emissions in electric systems. Energy Convers. Manag. 2014, 80, 573–581. [Google Scholar] [CrossRef]
- Wang, H.; Li, B.; Khan, M.Q. Prediction of Shanghai Electric Power Carbon Emissions Based on Improved STIRPAT Model. Sustainability 2022, 14, 13068. [Google Scholar] [CrossRef]
- Chen, J.; Zheng, L.; Che, W.; Liu, L.; Huang, H.; Liu, J.; Xing, C.; Qiu, P. A method for measuring carbon emissions from power plants using a CNN-LSTM-Attention model with Bayesian optimization. Case Stud. Therm. Eng. 2024, 63, 105334. [Google Scholar]
- Leerbeck, K.; Bacher, P.; Junker, R.G.; Goranović, G.; Corradi, O.; Ebrahimy, R.; Tveit, A.; Madsen, H. Short-term forecasting of CO2 emission intensity in power grids by machine learning. Appl. Energy 2020, 277, 115527. [Google Scholar] [CrossRef]
- Han, Z.; Cui, B.; Xu, L.; Wang, J.; Guo, Z. Coupling LSTM and CNN Neural Networks for Accurate Carbon Emission Prediction in 30 Chinese Provinces. Sustainability 2023, 15, 13934. [Google Scholar] [CrossRef]
- Qiao, W.; Lu, H.; Zhou, G.; Azimi, M.; Yang, Q.; Tian, W. A hybrid algorithm for carbon dioxide emissions forecasting based on improved lion swarm optimizer. J. Clean. Prod. 2020, 244, 118612. [Google Scholar] [CrossRef]
- Wei, X.; Xu, Y. Research on carbon emission prediction and economic policy based on TCN-LSTM combined with attention mechanism. Front. Ecol. Evol. 2023, 11, 1270248. [Google Scholar] [CrossRef]
- Han, Y.; Hao, Y.; Feng, M.; Chen, K.; Xing, R.; Liu, Y.; Lin, X.; Ma, B.; Fan, J.; Geng, Z. Novel STAttention GraphWaveNet model for residential household appliance prediction and energy structure optimization. Energy 2024, 307, 132582. [Google Scholar]
- Lopez-Garcia, T.B.; Domínguez-Navarro, J.A. Optimal Power Flow With Physics-Informed Typed Graph Neural Networks. IEEE Trans. Power Syst. 2025, 40, 381–393. [Google Scholar] [CrossRef]
- Wu, T.; Zhang, Y.J.A.; Liu, Y.; Lau, W.C.; Xu, H. Missing Data Recovery in Large Power Systems Using Network Embedding. IEEE Trans. Smart Grid 2021, 12, 680–691. [Google Scholar] [CrossRef]
- Wu, T.; Scaglione, A.; Arnold, D. Complex-Value Spatiotemporal Graph Convolutional Neural Networks and Its Applications to Electric Power Systems AI. IEEE Trans. Smart Grid 2024, 15, 3193–3207. [Google Scholar] [CrossRef]
- Hossain, R.R.; Huang, Q.; Huang, R. Graph Convolutional Network-Based Topology Embedded Deep Reinforcement Learning for Voltage Stability Control. IEEE Trans. Power Syst. 2021, 36, 4848–4851. [Google Scholar] [CrossRef]
- Chen, L.; Zhou, S.; Liang, X.; Lu, W.; Xia, M.; Weng, L.; Geng, J.; Liu, J. Predicting Power Dispatch for Unit Commitment Problems Using Graph-Temporal Convolutional Networks With Constrained Learning. IEEE Trans. Ind. Inform. 2025, 21, 5734–5745. [Google Scholar] [CrossRef]
- Li, Y.; Song, L.; Zhang, S.; Kraus, L.; Adcox, T.; Willardson, R.; Komandur, A.; Lu, N. A TCN-Based Hybrid Forecasting Framework for Hours-Ahead Utility-Scale PV Forecasting. IEEE Trans. Smart Grid 2023, 14, 4073–4085. [Google Scholar]
- Zhou, X.; Pang, C.; Zeng, X.; Jiang, L.; Chen, Y. A Short-Term Power Prediction Method Based on Temporal Convolutional Network in Virtual Power Plant Photovoltaic System. IEEE Trans. Instrum. Meas. 2023, 72, 1–10. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, J.; Chen, X.; Zeng, X.; Kong, Y.; Sun, S.; Guo, Y.; Liu, Y. Short-Term Load Forecasting for Industrial Customers Based on TCN-LightGBM. IEEE Trans. Power Syst. 2021, 36, 1984–1997. [Google Scholar]
- Ramos, A.C.S.; Freitas, F.D.; Zizzo, G. Economic Dispatch Problem Solution via Holomorphic Embedding Method on IEEE 14-Bus System for Different Loading Scenarios. IEEE Trans. Ind. Appl. 2024, 60, 2664–2672. [Google Scholar] [CrossRef]
- Vazquez-Rodriguez, S.; Duro, R. A genetic based technique for the determination of power system topological observability. In Proceedings of the Second IEEE International Workshop on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications, Lviv, Ukraine, 8–10 September 2003; pp. 48–52. [Google Scholar]
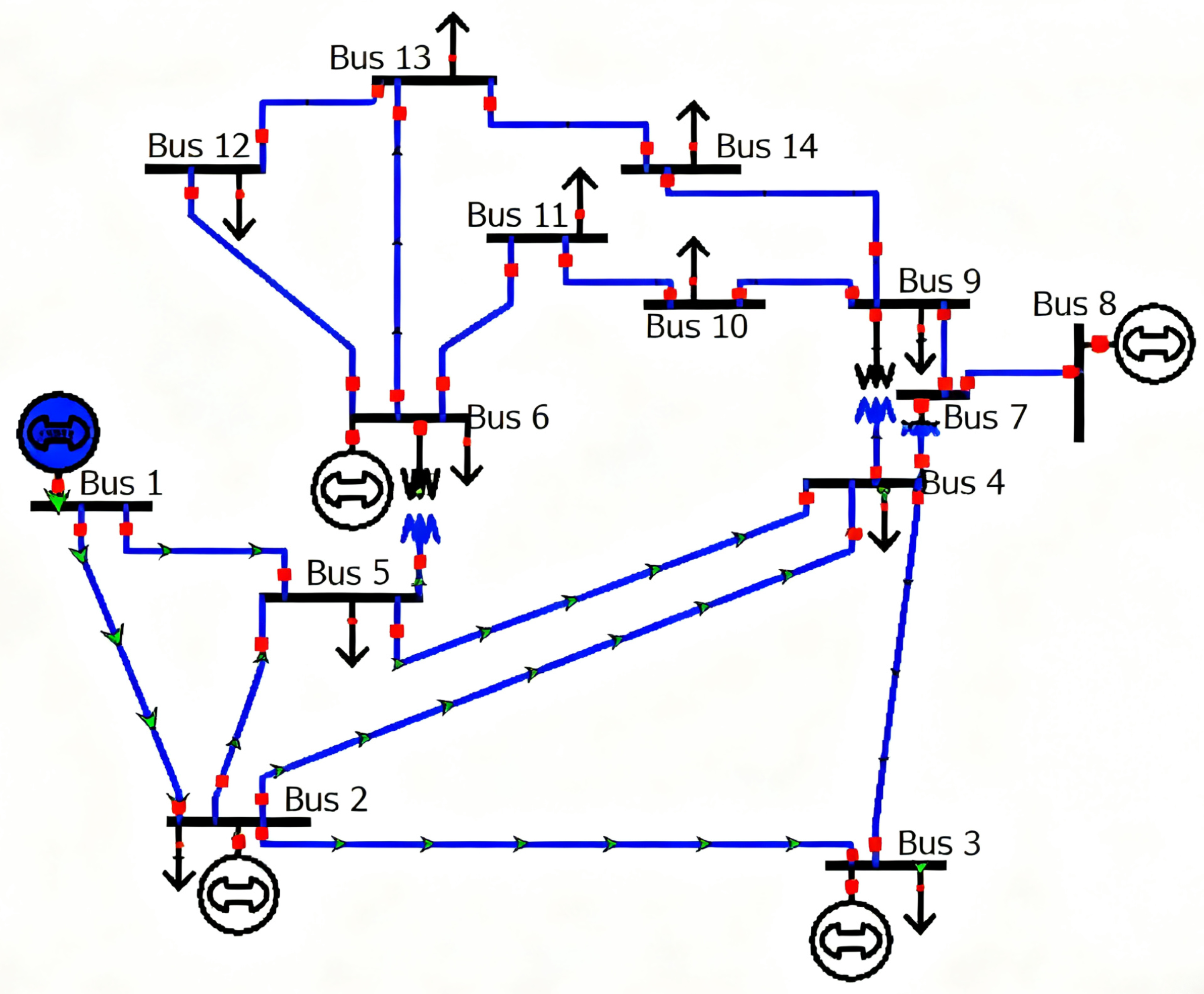
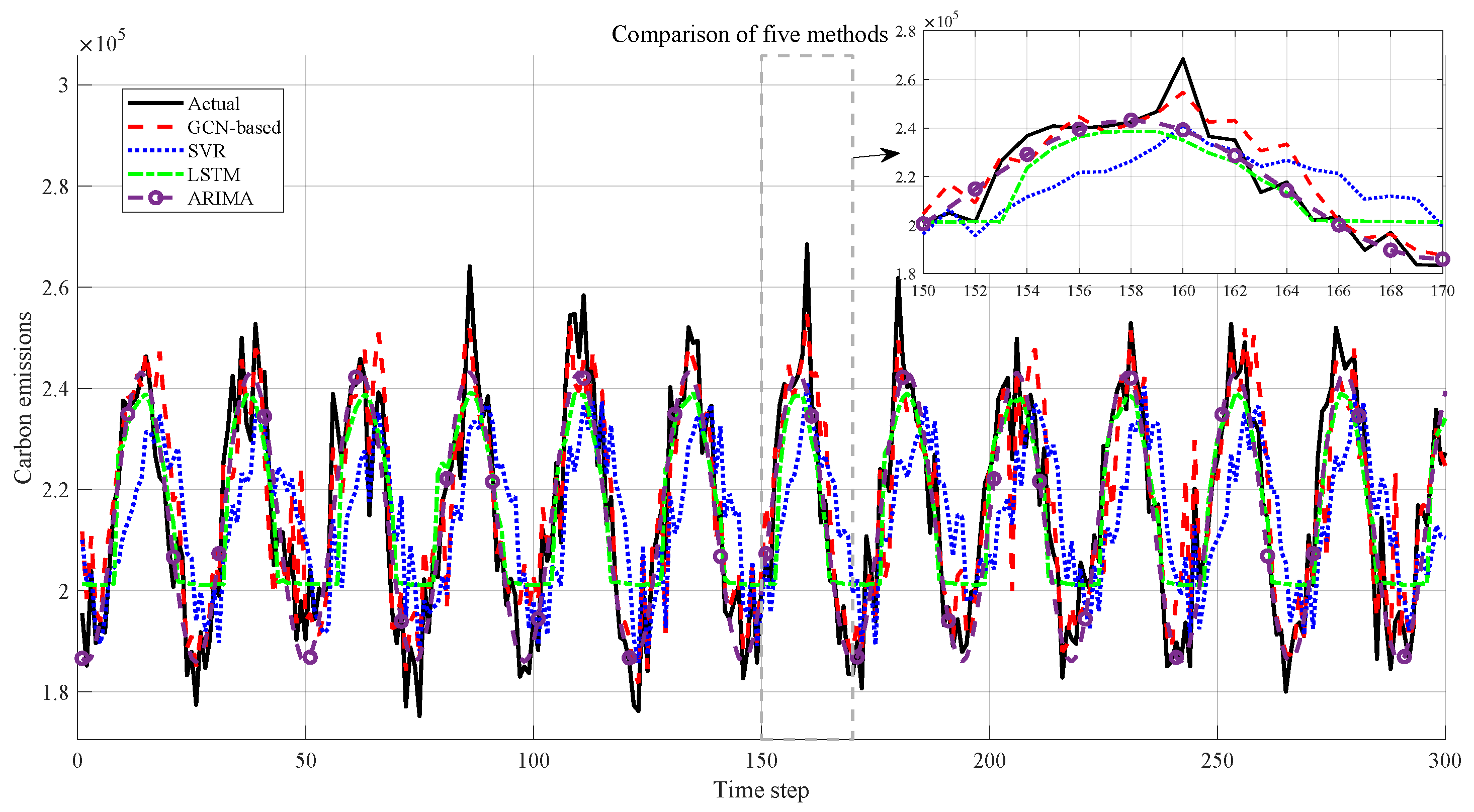
| Node | Average Power Output (MW) |
|---|---|
| 1 | 232.14 |
| 2 | 37.76 |
| 3 | 1.99 |
| 6 | 2.07 |
| 8 | 2.10 |
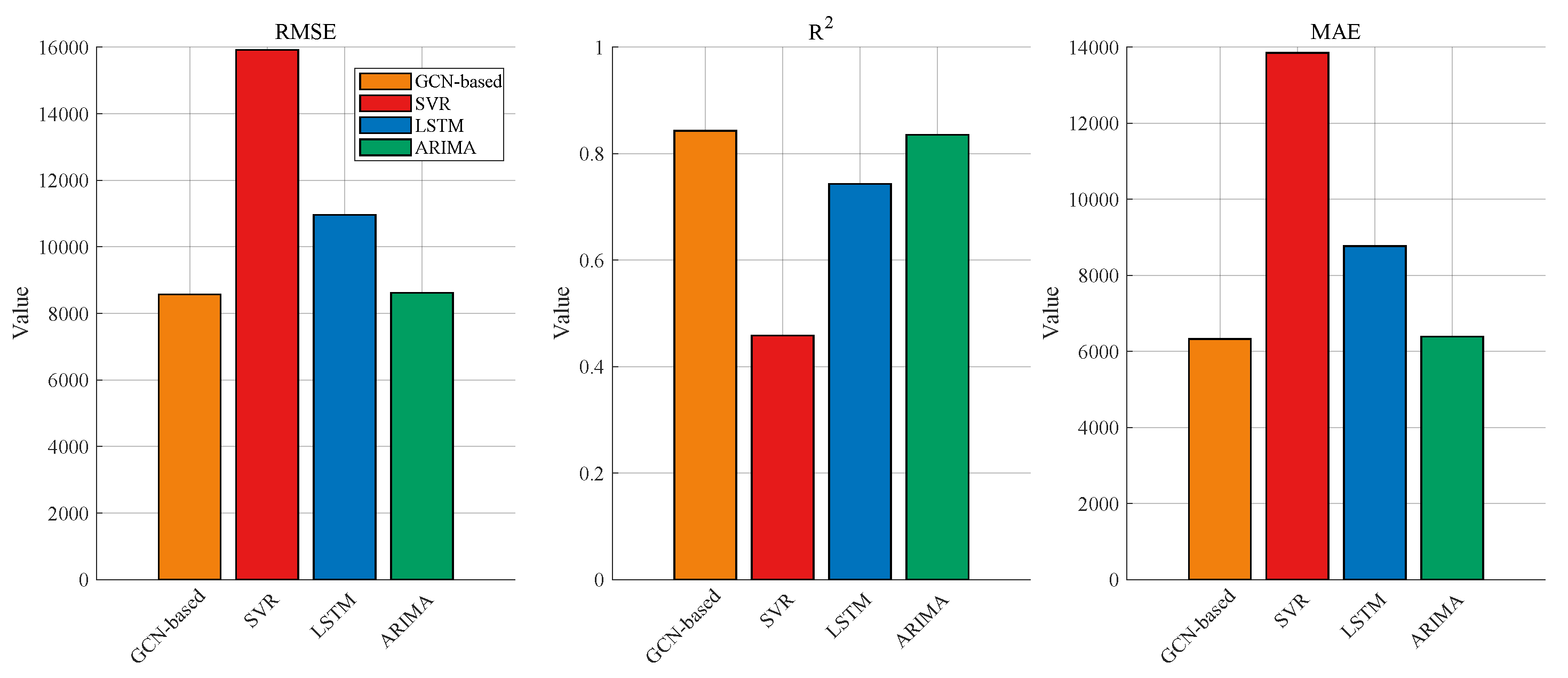
| Model | RMSE (kgCO2) | R2 | MAE (kgCO2) |
|---|---|---|---|
| GCN-based | 8566.9159 | 0.8431 | 6326.2168 |
| SVR | 15,918.2416 | 0.4584 | 13,854.6673 |
| LSTM | 10,963.1422 | 0.7431 | 8769.0145 |
| ARIMA | 8618.3974 | 0.8356 | 6390.3763 |
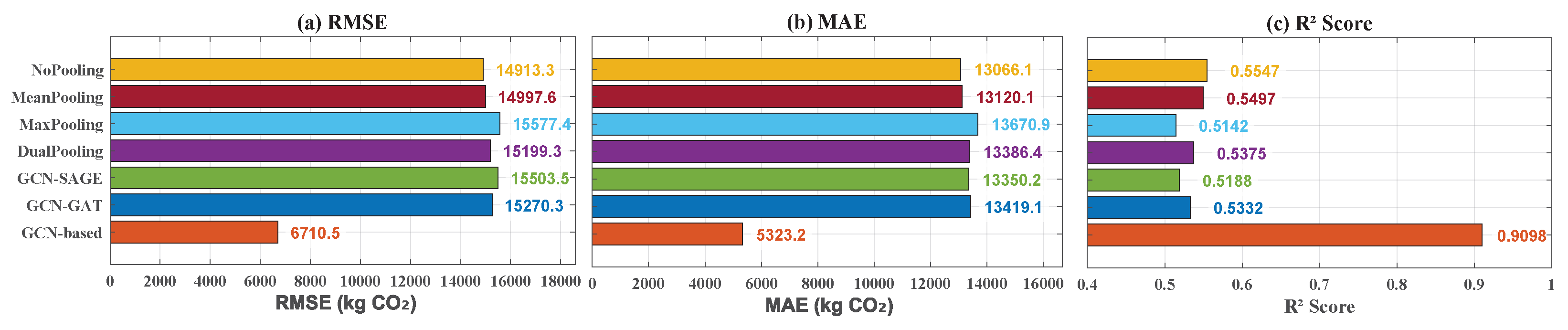
| Model | Pooling Strategy | TCN Layer | GCN Layer |
|---|---|---|---|
| GCN-based | Dual Pooling | TCN | GCN |
| GCN-GAT | Dual Pooling | No | GAT |
| GCN-SAGE | Dual Pooling | No | SAGE |
| DualPooling | Dual Pooling | No | GCN |
| MaxPooling | Max Pooling | No | GCN |
| MeanPooling | Mean Pooling | No | GCN |
| NoPooling | No Pooling | No | GCN |
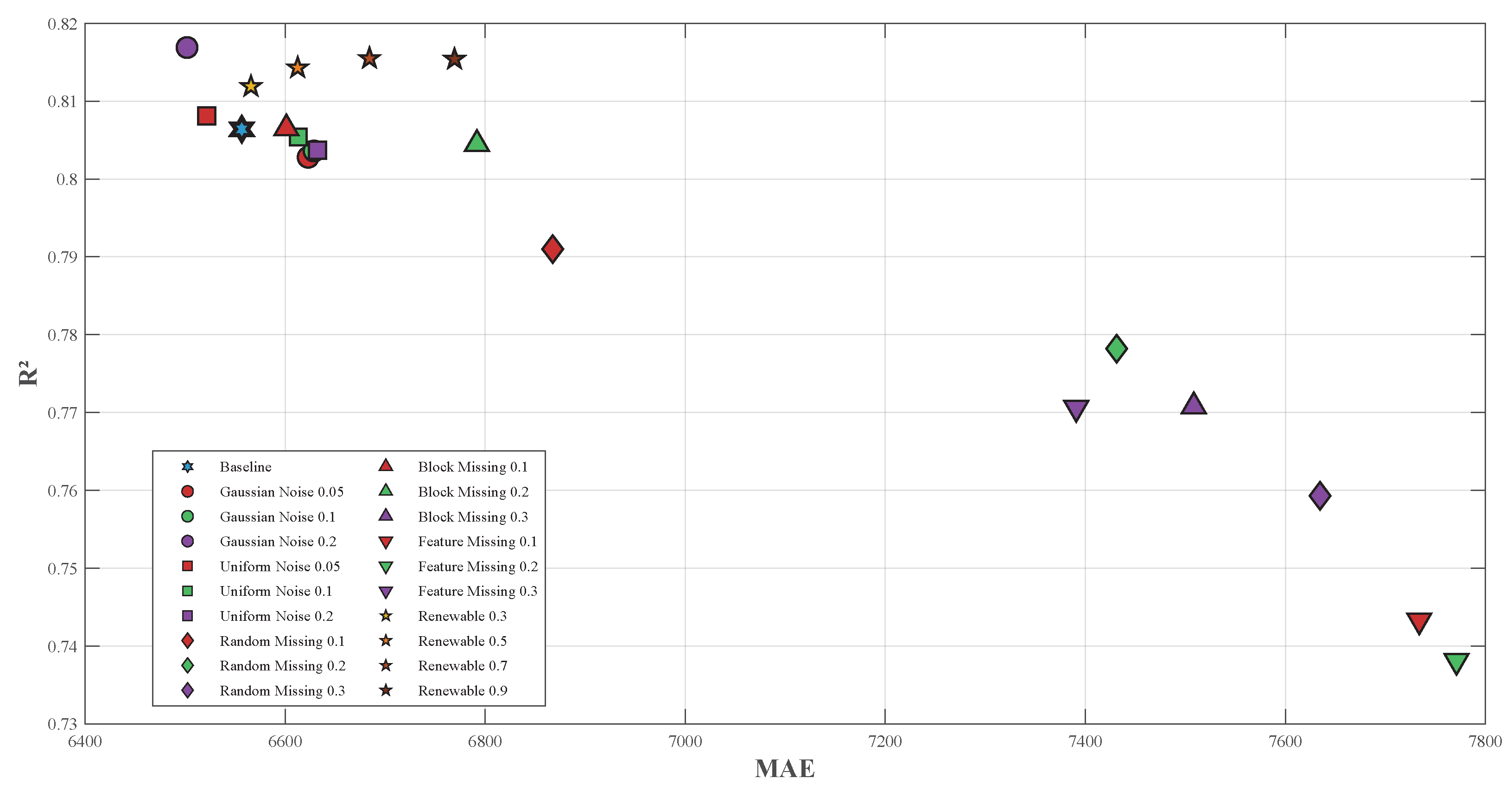
| Model | RMSE (kgCO2) | MAE (kgCO2) | R2 |
|---|---|---|---|
| Baseline | 9605.01 | 6556.59 | 0.8064 |
| Gaussian Noise 0.05 | 9693.92 | 6622.94 | 0.8028 |
| Gaussian Noise 0.1 | 9674.88 | 6628.84 | 0.8036 |
| Gaussian Noise 0.2 | 9340.27 | 6501.82 | 0.8169 |
| Uniform Noise 0.05 | 9561.43 | 6521.51 | 0.8081 |
| Uniform Noise 0.1 | 9629.72 | 6613.13 | 0.8054 |
| Uniform Noise 0.2 | 9672.01 | 6632.33 | 0.8037 |
| Random Missing 0.1 | 9978.91 | 6867.45 | 0.7910 |
| Random Missing 0.2 | 10,279.39 | 7431.31 | 0.7782 |
| Random Missing 0.3 | 10,708.84 | 7634.64 | 0.7593 |
| Block Missing 0.1 | 9602.47 | 6601.19 | 0.8065 |
| Block Missing 0.2 | 9664.98 | 6791.65 | 0.8040 |
| Block Missing 0.3 | 10,450.40 | 7508.43 | 0.7708 |
| Feature Missing 0.1 | 11,060.08 | 7733.86 | 0.7433 |
| Feature Missing 0.2 | 11,170.17 | 7771.10 | 0.7381 |
| Feature Missing 0.3 | 10,454.12 | 7390.90 | 0.7706 |
| Renewable 0.3 | 9470.38 | 6565.78 | 0.8119 |
| Renewable 0.5 | 9413.37 | 6612.50 | 0.8143 |
| Renewable 0.7 | 9385.58 | 6684.25 | 0.8155 |
| Renewable 0.9 | 9389.30 | 6769.28 | 0.8154 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Q.; Chen, J.; Jia, Q.; Sun, C.; Chen, X.; Chen, H. Predicting Real-Time Carbon Emissions for Power Grids Using Graph Convolutional Networks. Machines 2025, 13, 1061. https://doi.org/10.3390/machines13111061
Zhao Q, Chen J, Jia Q, Sun C, Chen X, Chen H. Predicting Real-Time Carbon Emissions for Power Grids Using Graph Convolutional Networks. Machines. 2025; 13(11):1061. https://doi.org/10.3390/machines13111061
Chicago/Turabian StyleZhao, Qian, Jianhua Chen, Qianwei Jia, Cong Sun, Xi Chen, and Hongtian Chen. 2025. "Predicting Real-Time Carbon Emissions for Power Grids Using Graph Convolutional Networks" Machines 13, no. 11: 1061. https://doi.org/10.3390/machines13111061
APA StyleZhao, Q., Chen, J., Jia, Q., Sun, C., Chen, X., & Chen, H. (2025). Predicting Real-Time Carbon Emissions for Power Grids Using Graph Convolutional Networks. Machines, 13(11), 1061. https://doi.org/10.3390/machines13111061







