Mechanism Design of Lower-Limb Rehabilitation Robot Based on Chord Angle Descriptor Method
Abstract
1. Introduction
- Treadmill-based Gait TrainersThese systems often integrate a body-weight support system with a robotic exoskeleton on a treadmill. The most prominent example is the Lokomat (Hocoma, Switzerland) [1], a driven gait orthosis that guides the patient’s legs on a predefined physiological walking path. Its linkage lengths are adjustable to accommodate different patient anthropometries. While highly effective for gait pattern training, such systems are typically large, expensive, and confine training to a fixed location on a treadmill, lacking overground walking transfer.
- Overground ExoskeletonsDevices like LOPES (University of Twente, Netherlands) [2,3] are lightweight, wearable exoskeletons designed for overground walking assistance. LOPES employs compliant actuators to enable a more natural gait and provide task-specific training. However, the accuracy of torque and position measurements for precise dynamic analysis can be a challenge, and the control system complexity increases with the number of degrees of freedom.
- End-effector and Stationary Motion TrainersThis category includes devices where the patient’s limb interacts with a robot at a single point (the end-effector), such as the footplate. The Rutgers Ankle (University of Rutgers, USA) [4,5] is a notable example, using a Stewart platform to provide resistance and assistance across the ankle’s range of motion. While compact and capable, parallel manipulators like the Stewart platform can have complex control issues and limited workspace. Other research has focused on stationary linkage-based trainers, such as the single-DOF six-bar mechanism for sit-to-stand training [6], which prioritize control simplicity and cost-effectiveness for specific motions.
- Ankle/Foot-specific Rehabilitation DevicesSignificant research has targeted the ankle joint due to its complexity. Devices range from redundant parallel mechanisms [7] to cable-driven systems [8]. While these can offer high torque and precise control within a specific workspace, challenges remain, including cable sag, platform stiffness management, and ensuring alignment with the patient’s natural ankle axis to avoid discomfort.
- A novel trajectory synthesis method for rehabilitation robotics: We introduce a planar trajectory synthesis method based on the chord angle descriptor. This method leverages the descriptor’s invariance to rotation, translation, and scaling, allowing for the direct extraction of trajectory shape characteristics independent of the mechanism’s installation pose or size. This innovation eliminates the need for trajectory normalization and interval design parameters, thereby resolving the issues of large computational load, low retrieval efficiency, and substantial data storage in open-loop trajectory synthesis for rehabilitation robots.
- A hybrid dynamic modeling framework for gear-linkage mechanisms: We develop a novel dynamic modeling approach that integrates finite element analysis, Fourier series, and Lagrangian dynamics. This framework explicitly incorporates the time-varying gear mesh stiffness—a critical factor often neglected in traditional models—through a feature decomposition process. It successfully bridges the gap between the prohibitive computational complexity of full-system FEM models and the oversimplification of traditional models, achieving high accuracy with a minimal number of degrees of freedom. We present the complete design and stability analysis of a single-degree-of-freedom gear-five-bar mechanism, offering a theoretical and practical solution for clinical rehabilitation.
2. Methods and Experiments
2.1. Trajectory Acquisition of Lower-Limb Rehabilitation Motion
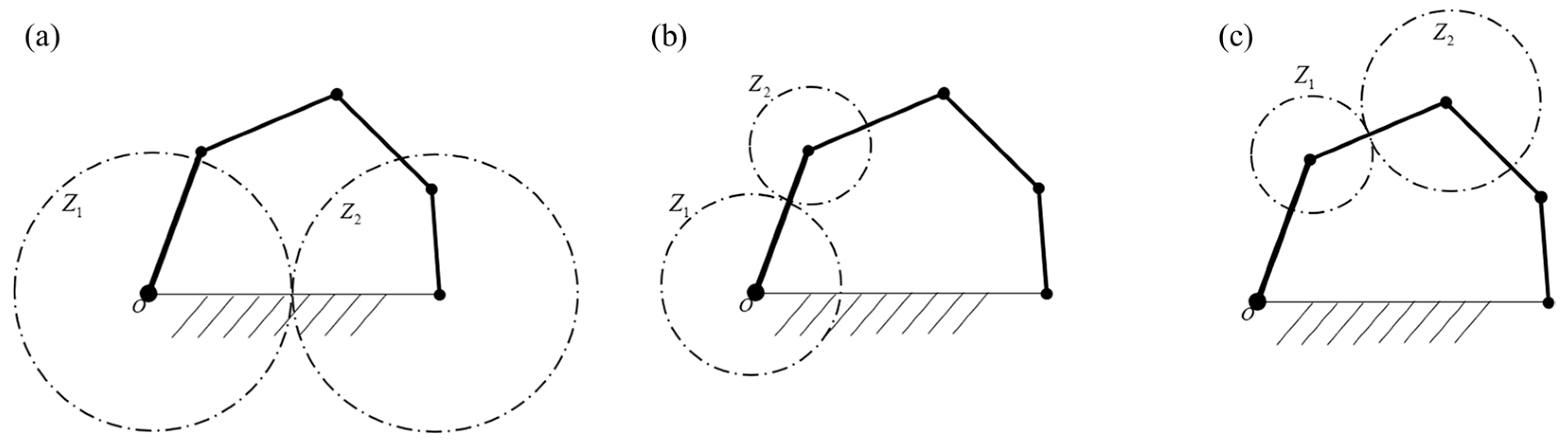
2.2. Method for Chord Angle Descriptor
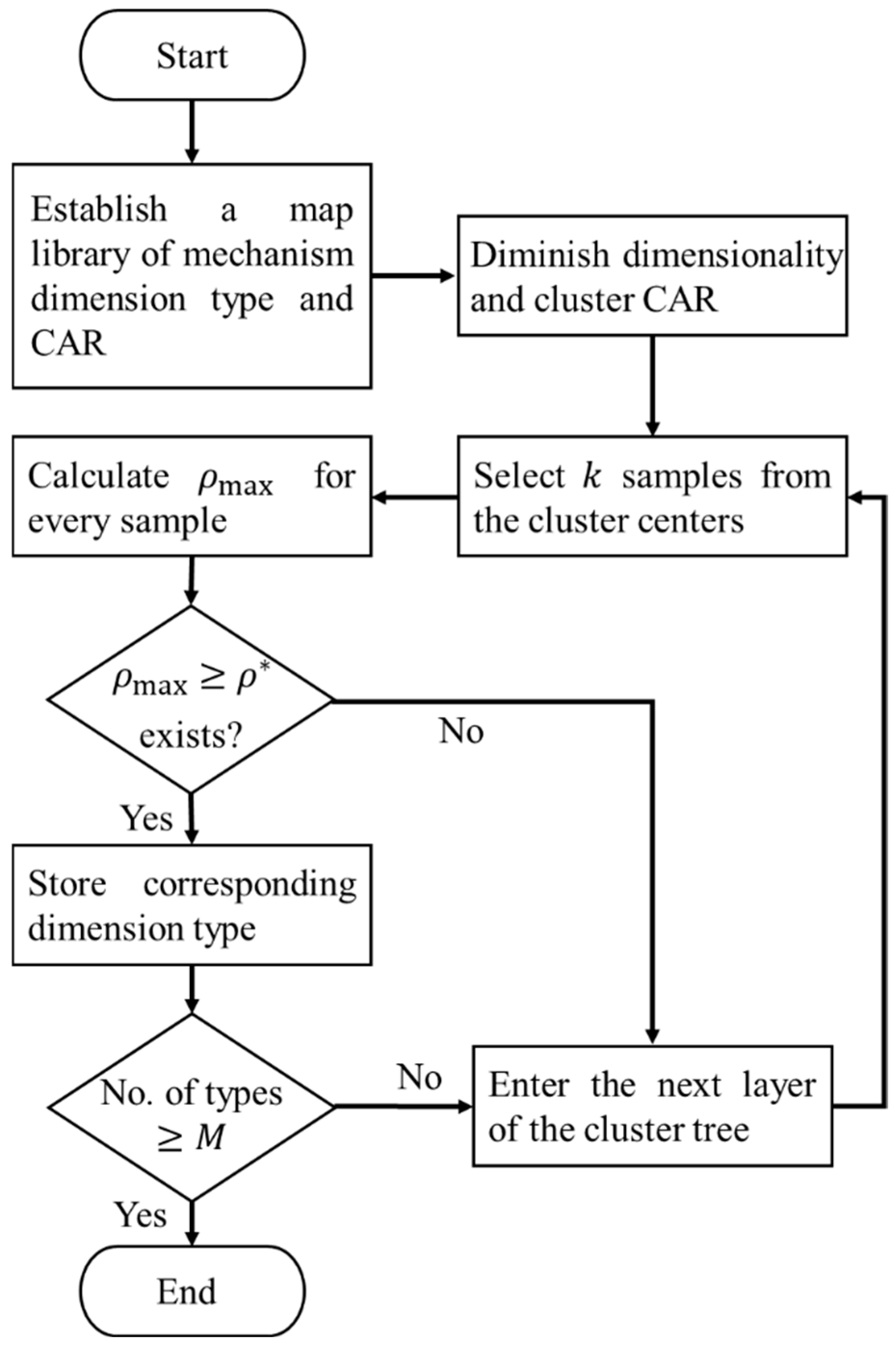
2.3. Trajectory Synthesis Based on the CAR Method
- Compute the CAR matrix for the mechanism dimension type and establish the graph library.
- Given the target value and the number of mechanisms , select samples near the cluster centers. Calculate their similarity to the target trajectory’s CAR usingsignifies the submatrix of the string angle descriptor matrix, whereas and represent the averages of the total sum of all elements in their respective matrices, while denotes the variance. The range of is [0, 1], a value approaching 1 indicates a greater similarity between the target trajectory’s form and the contour segment shape of that component of the mechanism trajectory, while a value nearing 0 signifies reduced similarity.
- Ascertain the existence of a contour segment that meets the condition . If available, use this contour segment as the trajectory matching outcome and record its associated dimensional parameters as mechanism design parameters. If not present, advance to the subsequent level of the clustering hierarchy.
- Repeat steps (3) and (4) until matching mechanism dimension types are retrieved from the library.
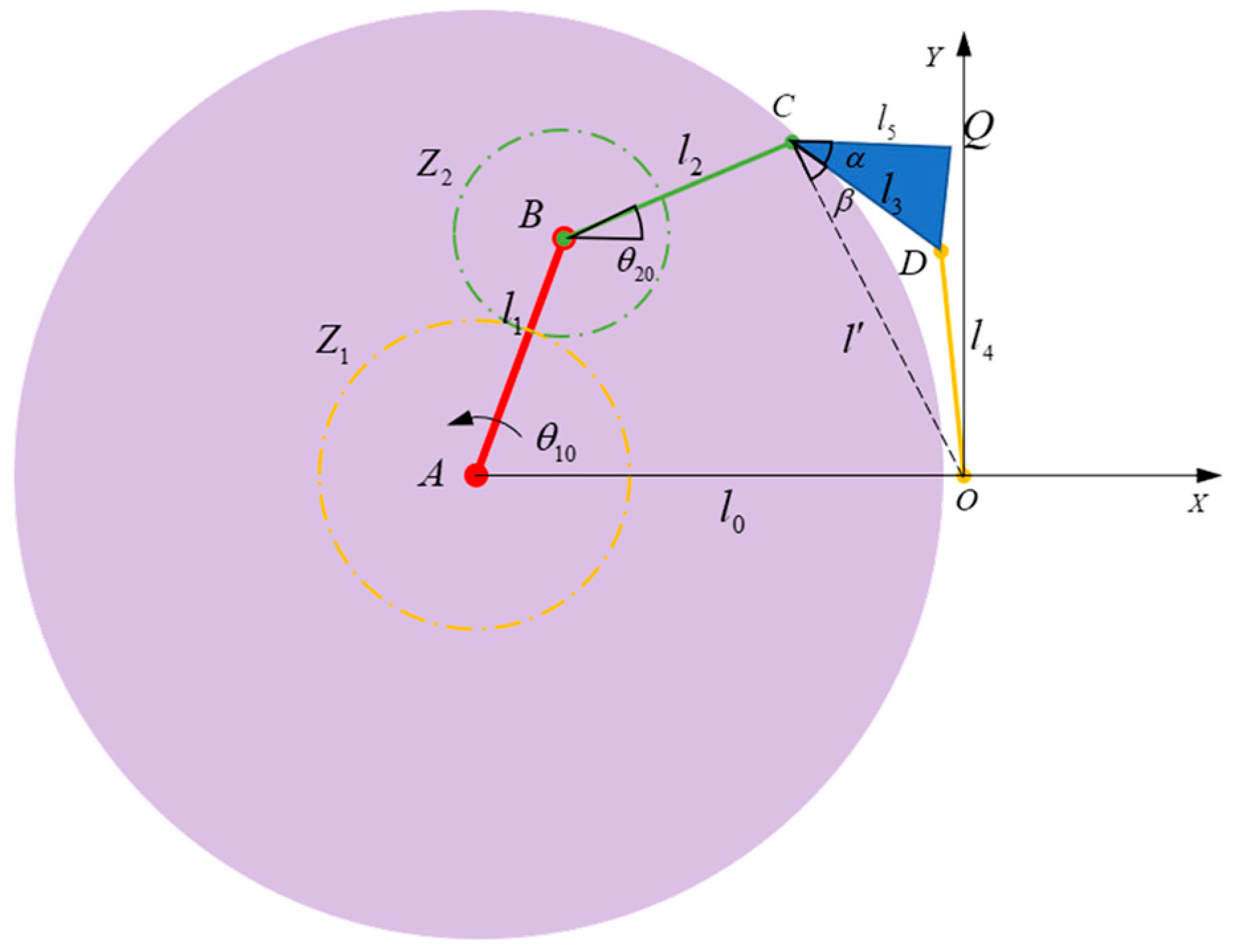
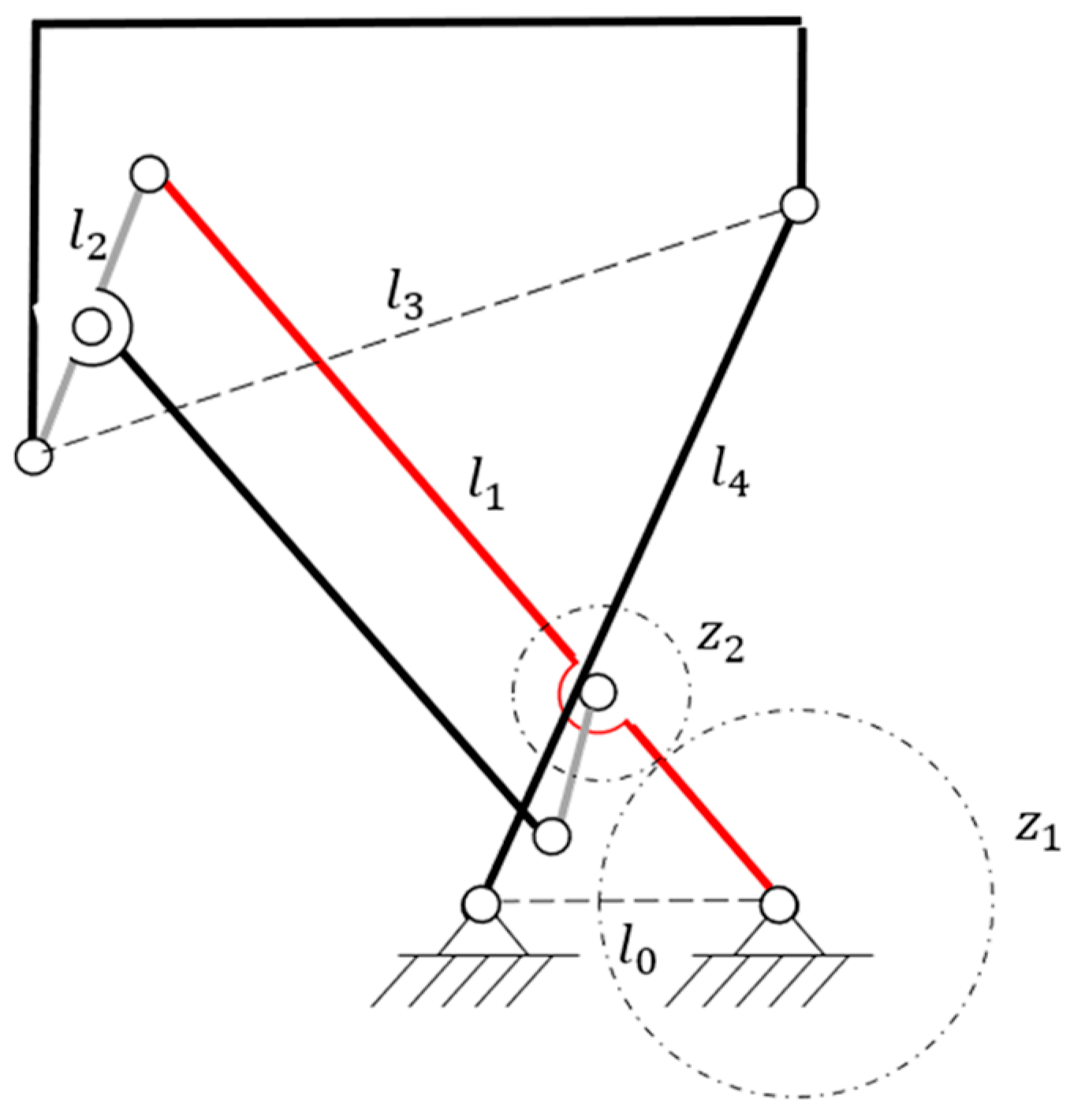
2.4. Design of Gear-Five-Bar Mechanism
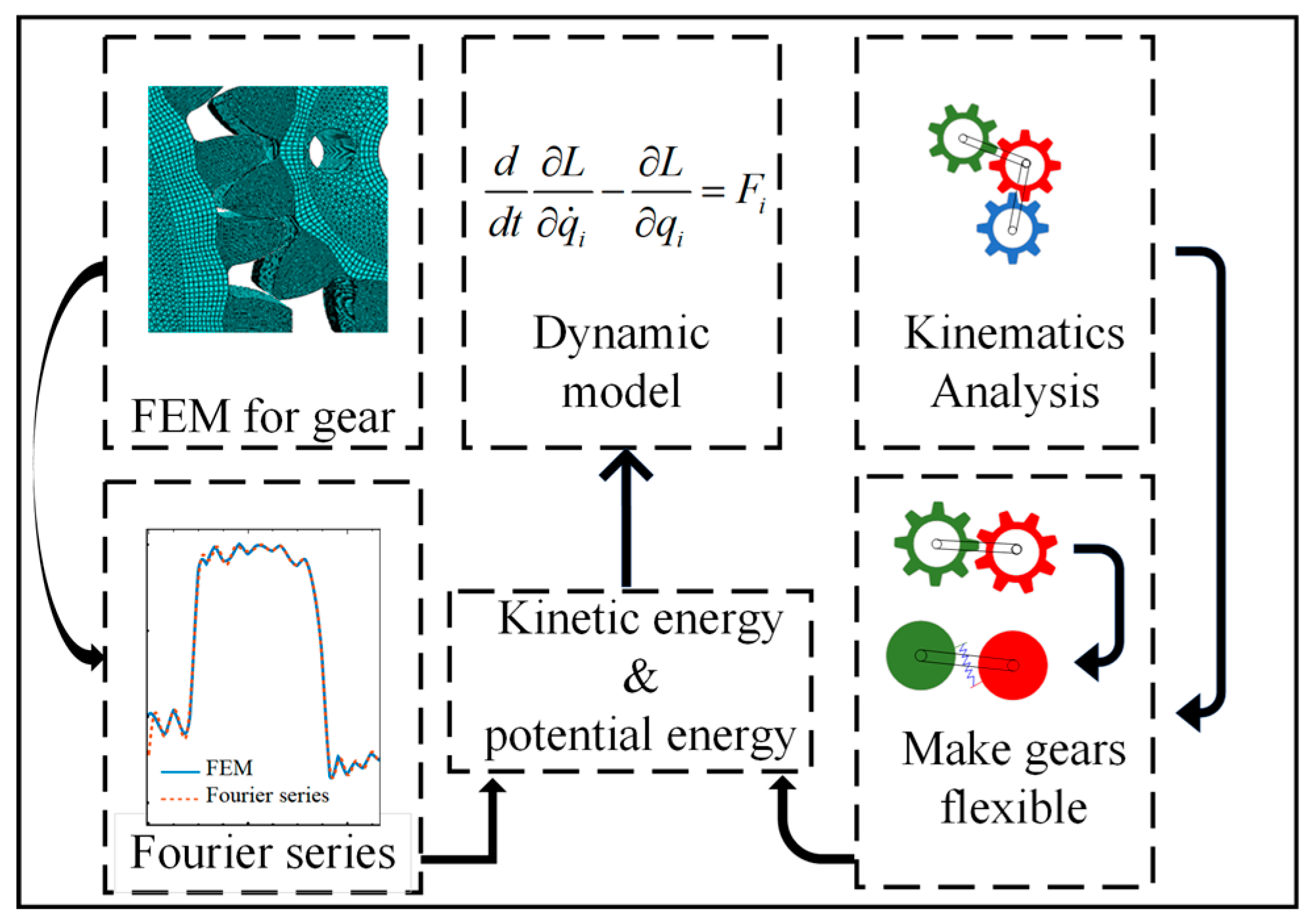
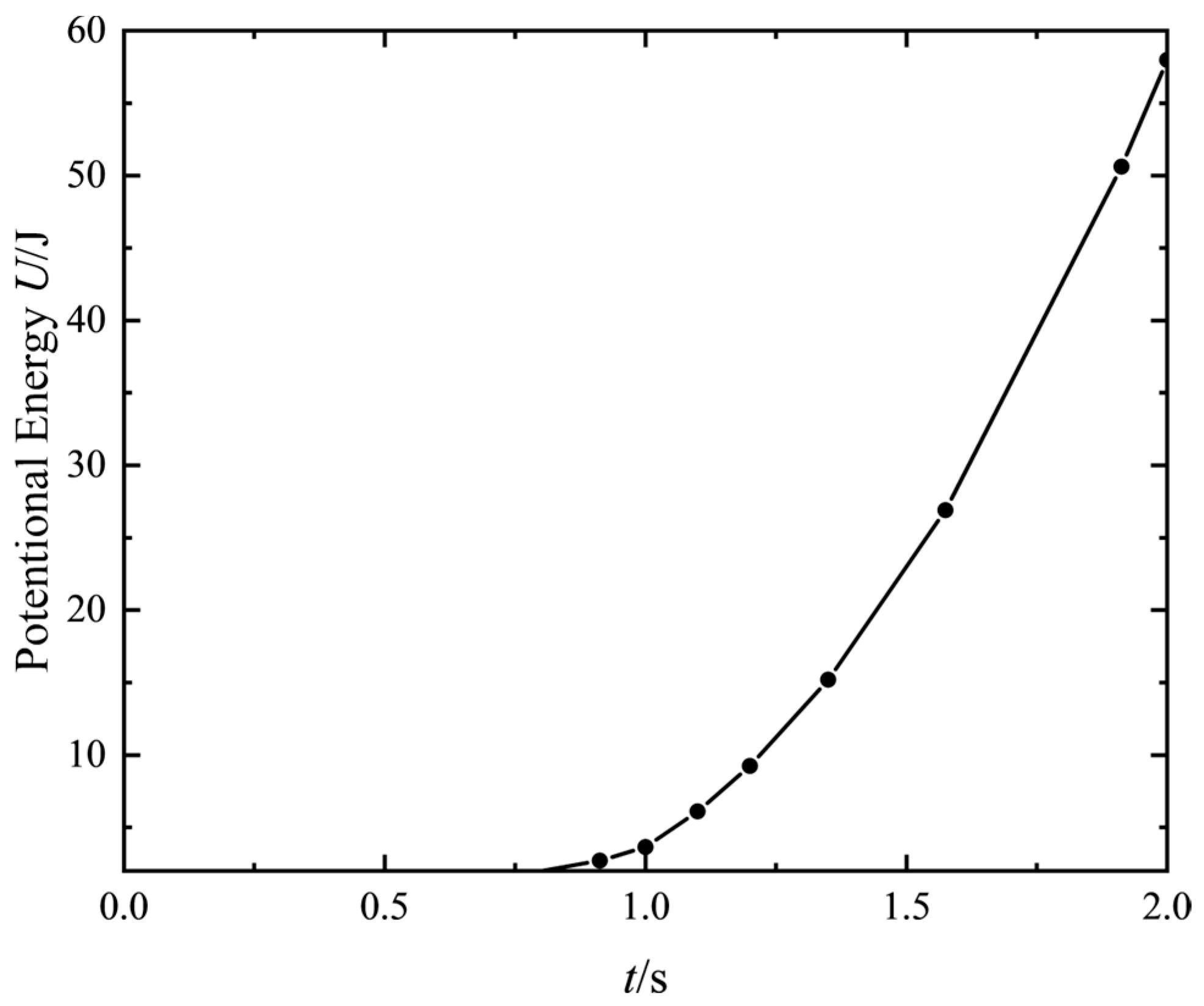
2.5. Calculation of Time-Varying Mesh Stiffness via Potential Energy Method
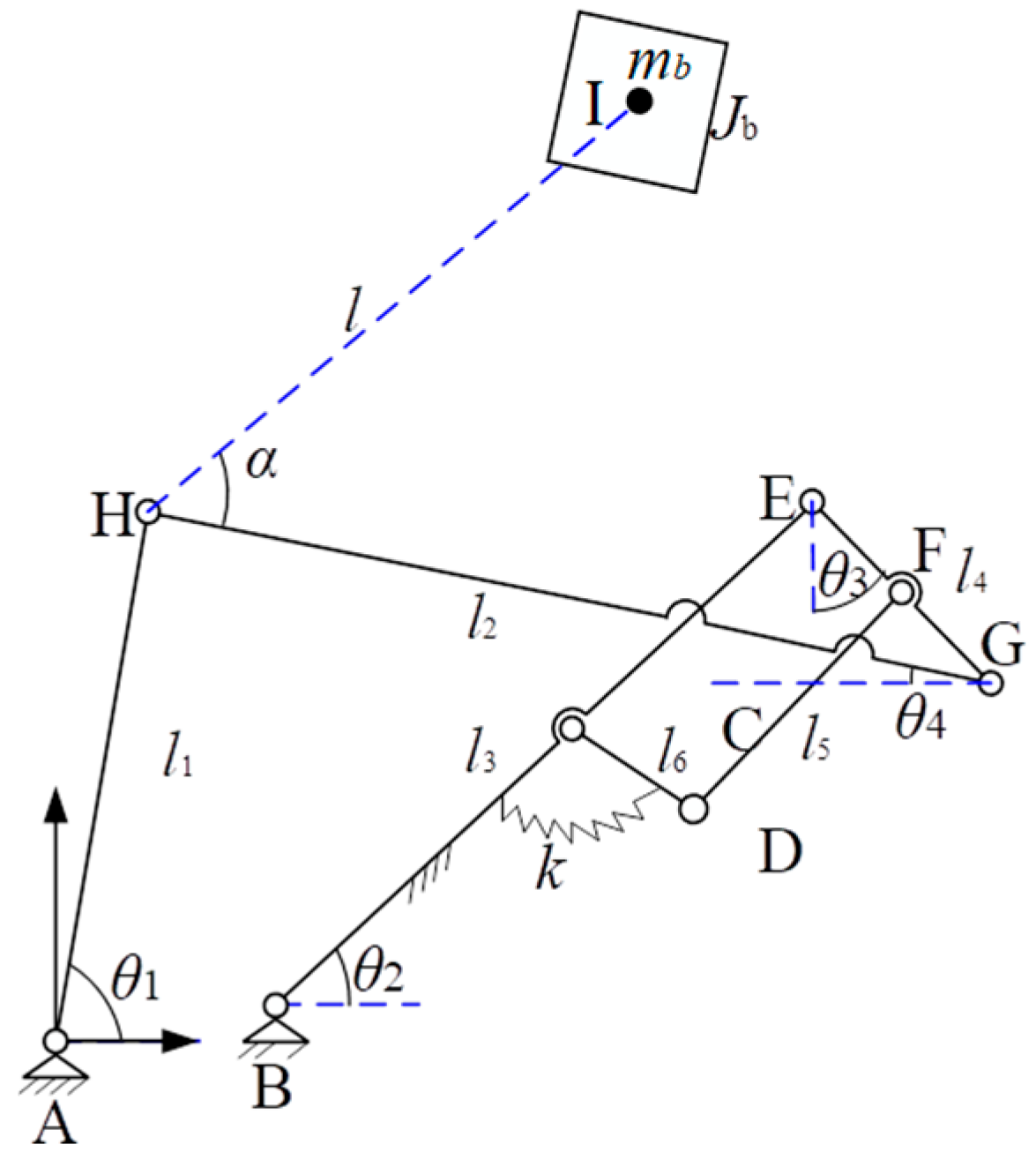
2.6. Dynamic Analysis of Gear-Linkage Mechanisms Considering Gear Elasticity
3. Results and Discussion
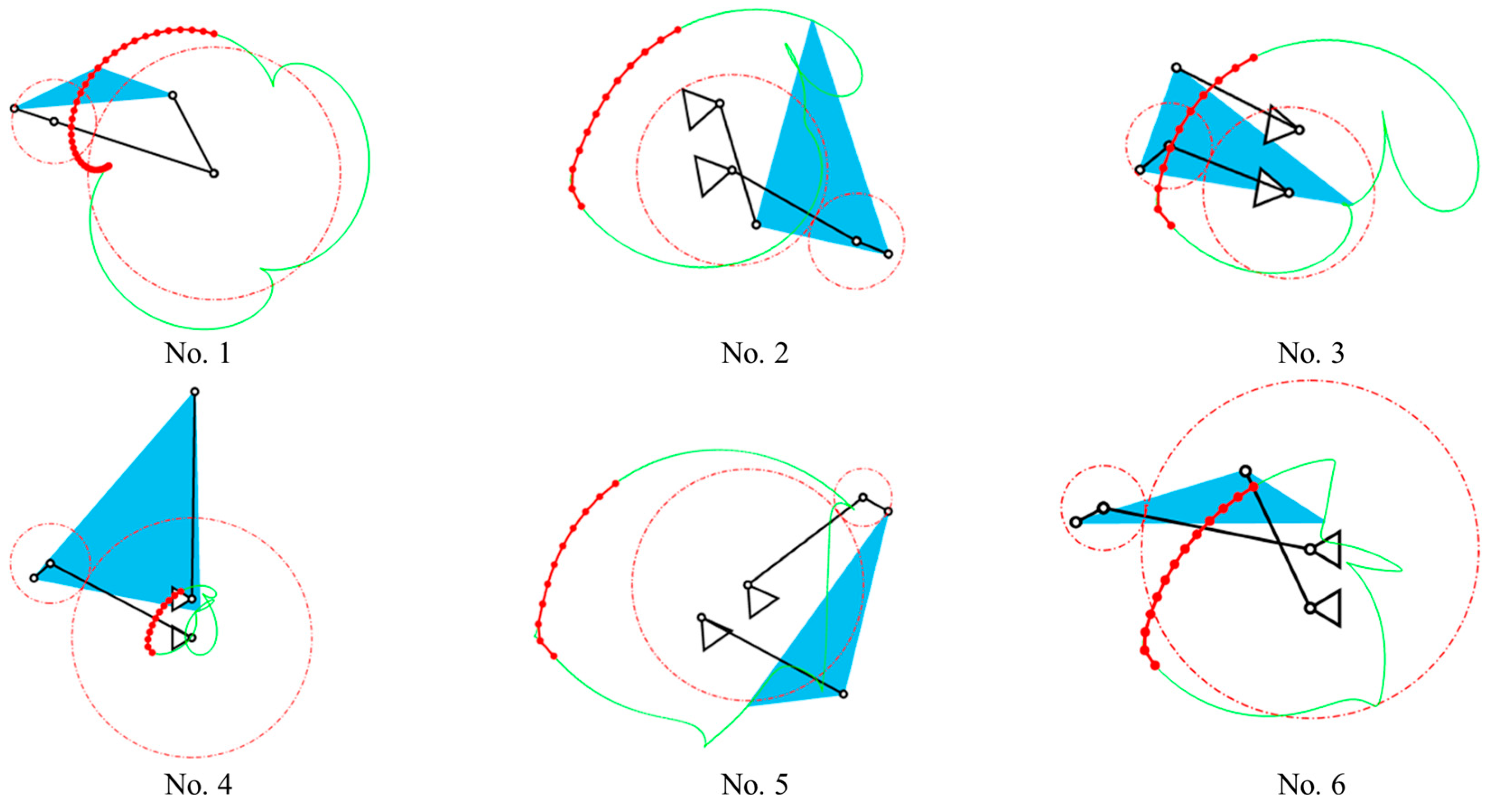
3.1. Trajectory Synthesis
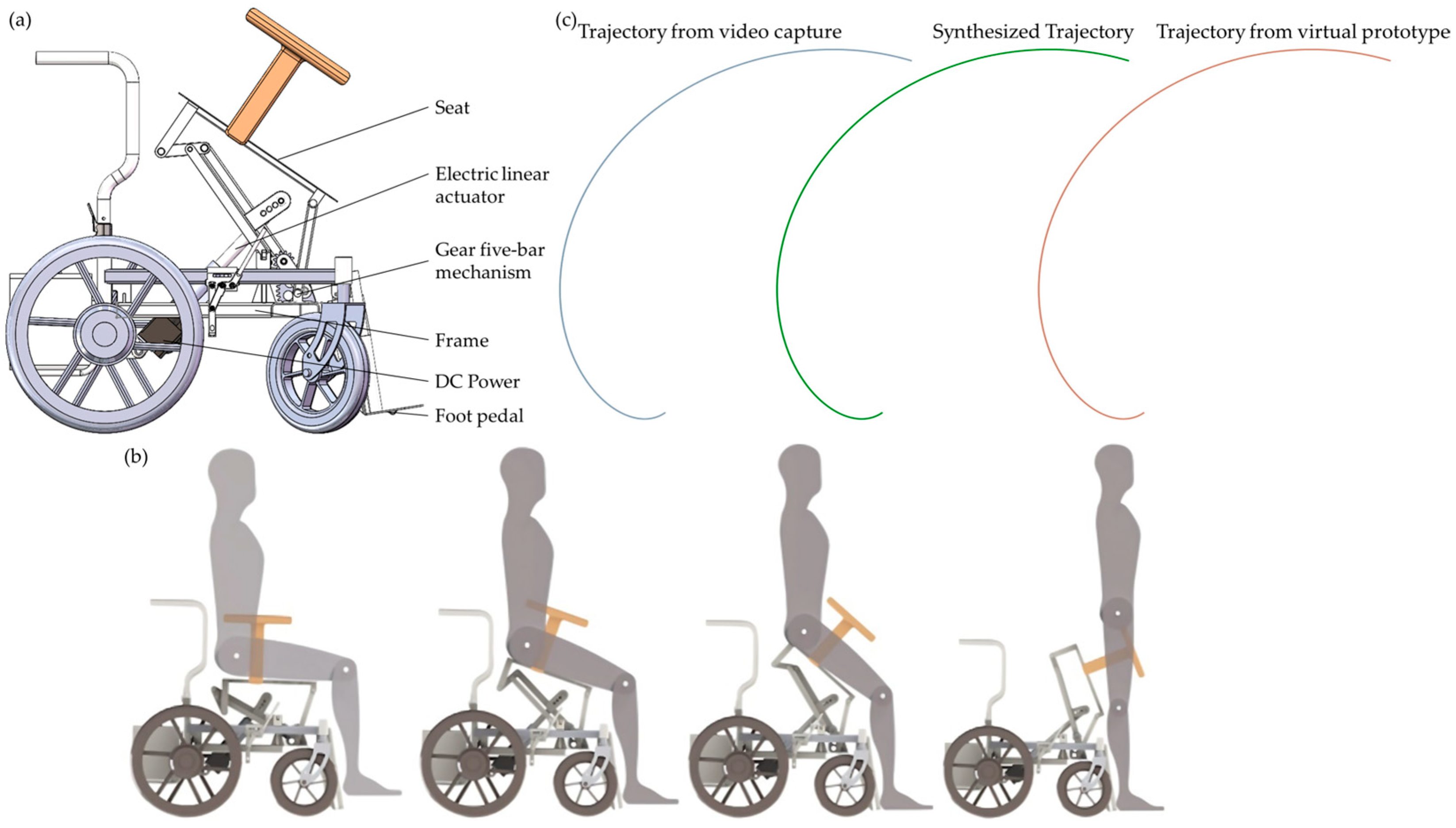
3.2. Mechanical Design of Lower-Limb Rehabilitation Robot
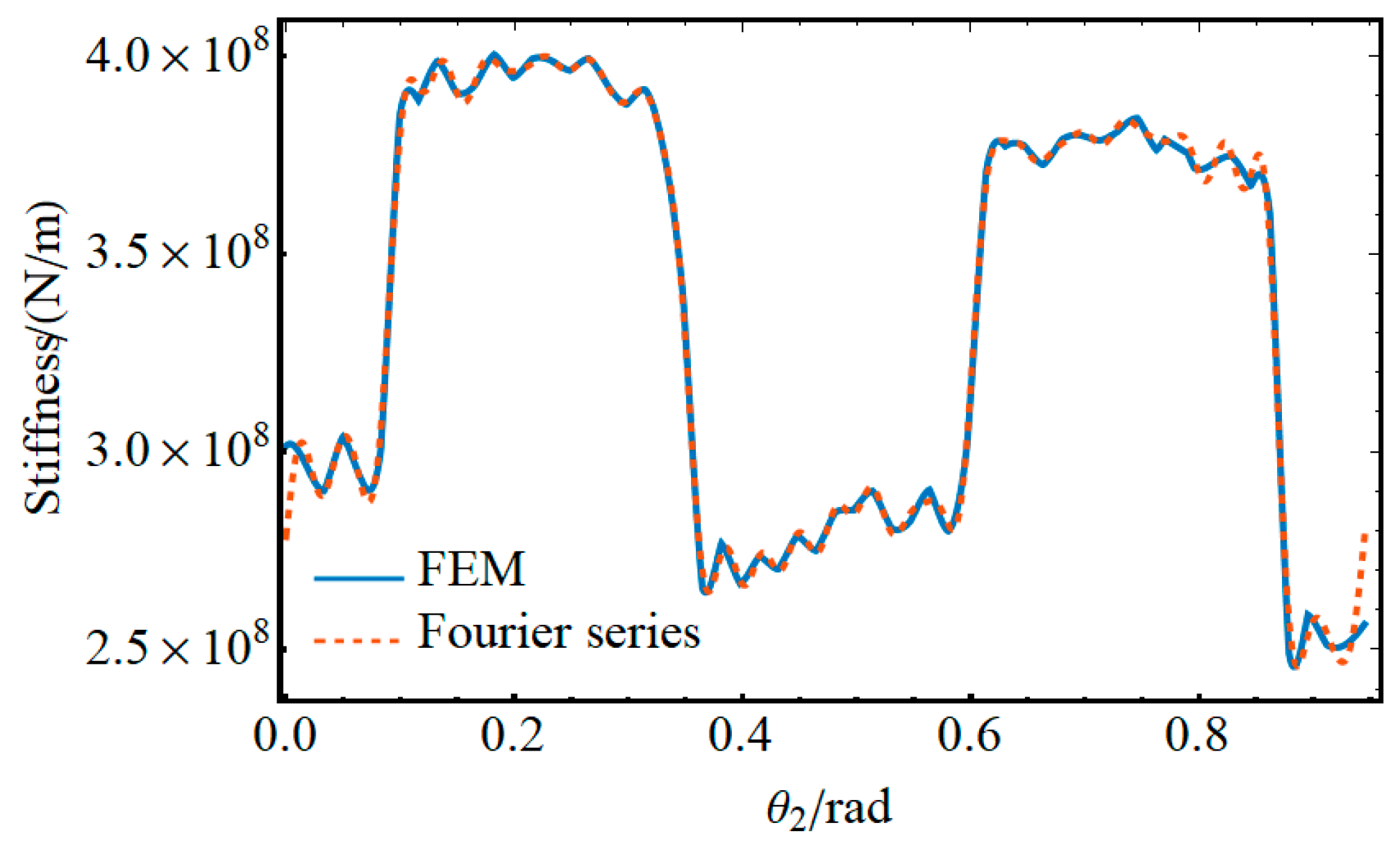
3.3. Evaluation of Time-Varying Mesh Stiffness
3.4. Dynamic Model of the Lower-Limb Rehabilitation Robot Mechanism System
3.5. Stability Analysis of Lower-Limb Rehabilitation Robot Mechanisms Considering Gear Flexibility
3.6. Development of Virtual and Physical Prototype
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Riener, R.; Lünenburger, L.; Maier, I.C.; Colombo, G.; Dietz, V. Locomotor Training in Subjects with Sensori-Motor Deficits: An Overview of the Robotic Gait Orthosis Lokomat. J. Healthc. Eng. 2010, 1, 517674. [Google Scholar] [CrossRef]
- Meuleman, J.; van Asseldonk, E.; van Oort, G.; Rietman, H.; van der Kooij, H. LOPES II—Design and Evaluation of an Admittance Controlled Gait Training Robot with Shadow-Leg Approach. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 352–363. [Google Scholar] [CrossRef]
- Koopman, B.; van Asseldonk, E.H.F.; van der Kooij, H. Estimation of Human Hip and Knee Multi-Joint Dynamics Using the LOPES Gait Trainer. IEEE Trans. Robot. 2016, 32, 920–932. [Google Scholar] [CrossRef]
- Girone, M.J.; Burdea, G.C.; Bouzit, M. The “Rutgers Ankle” Orthopedic Rehabilitation Interface; American Society of Mechanical Engineers: New York, NY, USA, 1999. [Google Scholar]
- Yoon, J.; Ryu, J.; Burdea, G.; Boian, R. Control of the Rutgers Ankle Rehabilitation Interface. In Proceedings of the ASME 2002 International Mechanical Engineering Congress and Exposition, New Orleans, LA, USA, 17–22 November 2002. [Google Scholar]
- Purwar, A.; Galeotafiore, T.; Miles, J.; Renert, J. Portable Six-Bar Apparatus for Lifting, Lowering and Self-Propelled Transit. U.S. Patent No. 8,468,622, 25 June 2013. [Google Scholar]
- Saglia, J.A.; Tsagarakis, N.G.; Dai, J.S.; Caldwell, D.G. A High Performance 2-Dof over-Actuated Parallel Mechanism for Ankle Rehabilitation. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 2180–2186. [Google Scholar]
- Wang, H.; Kinugawa, J.; Kosuge, K. Exact Kinematic Modeling and Identification of Reconfigurable Cable-Driven Robots With Dual-Pulley Cable Guiding Mechanisms. IEEE/ASME Trans. Mechatron. 2019, 24, 774–784. [Google Scholar] [CrossRef]
- Pisla, D.; Nadas, I.; Tucan, P.; Albert, S.; Carbone, G.; Antal, T.; Banica, A.; Gherman, B. Development of a Control System and Functional Validation of a Parallel Robot for Lower Limb Rehabilitation. Actuators 2021, 10, 277. [Google Scholar] [CrossRef]
- Vaida, C.; Birlescu, I.; Pisla, A.; Ulinici, I.-M.; Tarnita, D.; Carbone, G.; Pisla, D. Systematic Design of a Parallel Robotic System for Lower Limb Rehabilitation. IEEE Access 2020, 8, 34522–34537. [Google Scholar] [CrossRef]
- Al-Smadi, Y.M.; Russell, K.; Sodhi, R.S. Geared Five-Bar Path Generation with Structural Constraints. Inverse Probl. Sci. Eng. 2009, 17, 1059–1072. [Google Scholar] [CrossRef]
- Sun, Y.; Ge, W.; Zheng, J.; Dong, D. Design and Evaluation of a Prosthetic Knee Joint Using the Geared Five-Bar Mechanism. IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 23, 1031–1038. [Google Scholar] [CrossRef]
- Xu, G.; Fang, H.; Song, Y.; Du, W.; Wang, N. Performance Improvement of a Geared Five-Bar Transplanting Mechanism for Salvia Miltiorrhiza by Orthogonal Design Based on an Interactive Human–Computer Auxiliary Interface. Sustainability 2023, 15, 2219. [Google Scholar] [CrossRef]
- Sun, Y. Design Optimization and Actuation Control of a Prosthetic Knee Joint Using the Geared Five-Bar Mechanism. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2018. [Google Scholar]
- Sun, Y.; Ge, W.; Zheng, J.; Dong, D.; Zhao, D. Optimal Design of a Geared Five-Bar Prosthetic Knee Considering Motion Interference. In Recent Developments in Mechatronics and Intelligent Robotics; Deng, K., Yu, Z., Patnaik, S., Wang, J., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 828–837. [Google Scholar]
- Yu, C.; Ye, J.; Jia, J.; Zhao, X.; Chen, Z.; Chen, J. Design, Synthesis, and Experiment of Foot-Driven Lower Limb Rehabilitation Mechanisms. J. Mech. Robot. 2021, 14, 4051788. [Google Scholar] [CrossRef]
- Li, X.; Lv, H.; Zhao, P.; Lu, Q. A Fourier Approach to Kinematic Acquisition of Geometric Constraints of Planar Motion for Practical Mechanism Design. J. Mech. Des. 2022, 144, 4055378. [Google Scholar] [CrossRef]
- Kukla, M.; Wieczorek, B.; Warguła, Ł.; Rybarczyk, D.; Górecki, J. Manual Wheelchair Equipped with a Planetary Gear-Research Methodology and Preliminary Results. Appl. Sci. 2022, 12, 7737. [Google Scholar] [CrossRef]
- Kong, X.; Hu, Z.; Tang, J.; Chen, S.; Wang, Z. Effects of Gear Flexibility on the Dynamic Characteristics of Spur and Helical Gear System. Mech. Syst. Signal Process. 2023, 184, 109691. [Google Scholar] [CrossRef]
- Chen, Z.; Shao, Y. Dynamic Simulation of Spur Gear with Tooth Root Crack Propagating along Tooth Width and Crack Depth. Eng. Fail. Anal. 2011, 18, 2149–2164. [Google Scholar] [CrossRef]
- Ma, H.; Zeng, J.; Feng, R.; Pang, X.; Wen, B. An Improved Analytical Method for Mesh Stiffness Calculation of Spur Gears with Tip Relief. Mech. Mach. Theory 2016, 98, 64–80. [Google Scholar] [CrossRef]
- Ma, H.; Song, R.; Pang, X.; Wen, B. Time-Varying Mesh Stiffness Calculation of Cracked Spur Gears. Eng. Fail. Anal. 2014, 44, 179–194. [Google Scholar] [CrossRef]
- Saxena, A.; Parey, A.; Chouksey, M. Effect of Shaft Misalignment and Friction Force on Time Varying Mesh Stiffness of Spur Gear Pair. Eng. Fail. Anal. 2015, 49, 79–91. [Google Scholar] [CrossRef]
- Xie, C.; Hua, L.; Lan, J.; Han, X.; Wan, X.; Xiong, X. Improved Analytical Models for Mesh Stiffness and Load Sharing Ratio of Spur Gears Considering Structure Coupling Effect. Mech. Syst. Signal Process. 2018, 111, 331–347. [Google Scholar] [CrossRef]
- Wang, Y.; Li, K.; Qiao, B.; Shen, Z.; Chen, X. Theoretical Investigation of Mesh Relationship and Mesh Stiffness of Internal Spur Gears with Tooth Wear. Appl. Sci. 2023, 13, 2022. [Google Scholar] [CrossRef]
- Yang, J.; Lin, T.; He, Z.; Chen, M. Novel Calculation Method for Dynamic Excitation of Modified Double-Helical Gear Transmission. Mech. Mach. Theory 2022, 167, 104467. [Google Scholar] [CrossRef]
- Chen, K.; Huangfu, Y.; Ma, H.; Xu, Z.; Li, X.; Wen, B. Calculation of Mesh Stiffness of Spur Gears Considering Complex Foundation Types and Crack Propagation Paths. Mech. Syst. Signal Process. 2019, 130, 273–292. [Google Scholar] [CrossRef]
- Chen, K.; Ma, H.; Che, L.; Li, Z.; Wen, B. Comparison of Meshing Characteristics of Helical Gears with Spalling Fault Using Analytical and Finite-Element Methods. Mech. Syst. Signal Process. 2019, 121, 279–298. [Google Scholar] [CrossRef]
- He, Z.; Hu, Y.; Zheng, X.; Yu, Y. A Calculation Method for Tooth Wear Depth Based on the Finite Element Method That Considers the Dynamic Mesh Force. Machines 2022, 10, 69. [Google Scholar] [CrossRef]
- Liang, X.; Zhang, H.; Zuo, M.J.; Qin, Y. Three New Models for Evaluation of Standard Involute Spur Gear Mesh Stiffness. Mech. Syst. Signal Process. 2018, 101, 424–434. [Google Scholar] [CrossRef]
- Ma, H.; Pang, X.; Zeng, J.; Wang, Q.; Wen, B. Effects of Gear Crack Propagation Paths on Vibration Responses of the Perforated Gear System. Mech. Syst. Signal Process. 2015, 62–63, 113–128. [Google Scholar] [CrossRef]
- Mohammed, O.D.; Rantatalo, M. Gear Fault Models and Dynamics-Based Modelling for Gear Fault Detection—A Review. Eng. Fail. Anal. 2020, 117, 104798. [Google Scholar] [CrossRef]
- Natali, C.; Battarra, M.; Dalpiaz, G.; Mucchi, E. A Critical Review on FE-Based Methods for Mesh Stiffness Estimation in Spur Gears. Mech. Mach. Theory 2021, 161, 104319. [Google Scholar] [CrossRef]
- Pehlivanoglu, Y.; Aydogan, M.O.; Sabuncuoglu, B. Mesh Stiffness of Micro-Spur Gears by Finite Element Formulations Based on Modified Couple Stress Theory. Microsyst. Technol. 2020, 26, 3829–3838. [Google Scholar] [CrossRef]
- Shen, Z.; Yang, L.; Qiao, B.; Luo, W.; Chen, X.; Yan, R. Mesh Relationship Modeling and Dynamic Characteristic Analysis of External Spur Gears with Gear Wear. Front. Mech. Eng. 2022, 17, 9. [Google Scholar] [CrossRef]
- Chen, P.; Dong, D.; Lv, H.; Zhu, L. A User Motion Data Acquisition and Processing Method for the Design of Rehabilitation Robot with Few Degrees-of-Freedom. ASME J. Med. Diagn. 2020, 3, 4046320. [Google Scholar] [CrossRef]
- Wei, W.; Shu, X.; Chen, P.; Li, X. A Chord-Angle-Based Approach with Expandable Solution Space to 1-Degree-of-Freedom (DOF) Rehabilitation Mechanism Synthesis. Mech. Sci. 2022, 13, 341–352. [Google Scholar] [CrossRef]
- Donoser, M.; Riemenschneider, H.; Bischof, H. Efficient Partial Shape Matching of Outer Contours. In Proceedings of the Computer Vision—ACCV 2009, Xi’an, China, 23–27 September 2009; Zha, H., Taniguchi, R., Maybank, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 281–292. [Google Scholar]
- Wang, J. Geometric Structure of High-Dimensional Data. In Geometric Structure of High-Dimensional Data and Dimensionality Reduction; Wang, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 51–77. ISBN 978-3-642-27497-8. [Google Scholar]
- Nielsen, F. Hierarchical Clustering. In Introduction to HPC with MPI for Data Science; Nielsen, F., Ed.; Springer International Publishing: Cham, Switzerland, 2016; pp. 195–211. ISBN 978-3-319-21903-5. [Google Scholar]
- Flek, J.; Dub, M.; Kolář, J.; Lopot, F.; Petr, K. Determination of Mesh Stiffness of Gear—Analytical Approach vs. FEM Analysis. Appl. Sci. 2021, 11, 4960. [Google Scholar] [CrossRef]










| Device (Source) | Type | DOF (per Leg) | Adaptability /Customizability | Key Limitations |
|---|---|---|---|---|
| Lokomat [1] | Treadmill-based Exoskeleton | 2 (hip, knee) | Link length adjustment | Very high cost, large footprint, limited to treadmill walking |
| LOPES [2,3] | Overground Exoskeleton | 3 (2 hips, 1 knee) | - | Complex control, accuracy challenges in measurement |
| Rutgers Ankle [4,5] | End-effector (Ankle) | 6 (on ankle) | - | Complex control, limited workspace |
| Single-DOF 6 bar [6] | Stationary Trainer | 1 (system) | Fixed design for a specific trajectory | Limited to a single, fixed trajectory |
| 2-DOF Ankle Robot [7] | Stationary (Ankle) | 2 (on ankle) | - | High stiffness, challenging direction control |
| RECOVER [9,10] | Stationary Exoskeleton | 2 (hip, knee) | Adjustable link lengths and joint axes | Primarily focused on seated training |
| Proposed Robot | Stationary Trainer | 1 (system) | Modular links and Re-synthesizable kinematics | Limited to planar sit-to-stand motion |
| No. | (mm) | (mm) | (mm) | (mm) | (mm) | (rad) | (rad) | (rad) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 362 | 90 | 341.8 | 190 | 200 | 0.3693 | 3 | 0.3142 | 0.3142 | 0.9999 |
| 2 | 2.1096 | 0.5079 | 1.9956 | 1.8655 | 3.6134 | −1.0374 | 2 | 2.2711 | 2.1379 | 0.9991 |
| 3 | 2.0173 | 0.5929 | 1.7049 | 2.1608 | 3.3707 | −1.3893 | 2 | −1.3626 | −2.4269 | 0.9988 |
| 4 | 4.1251 | 0.5686 | 6.3604 | 5.3590 | 4.3497 | −1.0539 | 3 | −1.0868 | −2.3058 | 0.9985 |
| 5 | 2.5562 | 0.5099 | 3.3261 | 2.8518 | 4.2343 | −0.3848 | 4 | 3.1042 | −2.0287 | 0.9981 |
| 6 | 3.5944 | 0.5301 | 3.0195 | 2.5803 | 4.2276 | −0.2896 | 4 | 1.7681 | 1.0926 | 0.9981 |
| Parameter | Pinion | Gear Wheel |
|---|---|---|
| Normal Module | 3 | 3 |
| End Module | 3 | 3 |
| Number of teeth | 12 | 38 |
| Normal pressure angle | 20° | 20° |
| Helix angle | 0° | 0° |
| Addendum coefficient | 1 | 1 |
| Addendum modification coefficient | 0.47 | −0.47 |
| Precision grade | 7 | 7 |
| Common normal length | 14.753 | 31.63 |
| Common normal tooth span number | 2 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, L.; Wei, W.; Li, L.; Gong, S. Mechanism Design of Lower-Limb Rehabilitation Robot Based on Chord Angle Descriptor Method. Machines 2025, 13, 1059. https://doi.org/10.3390/machines13111059
Zhu L, Wei W, Li L, Gong S. Mechanism Design of Lower-Limb Rehabilitation Robot Based on Chord Angle Descriptor Method. Machines. 2025; 13(11):1059. https://doi.org/10.3390/machines13111059
Chicago/Turabian StyleZhu, Liuxian, Wei Wei, Li Li, and Shan Gong. 2025. "Mechanism Design of Lower-Limb Rehabilitation Robot Based on Chord Angle Descriptor Method" Machines 13, no. 11: 1059. https://doi.org/10.3390/machines13111059
APA StyleZhu, L., Wei, W., Li, L., & Gong, S. (2025). Mechanism Design of Lower-Limb Rehabilitation Robot Based on Chord Angle Descriptor Method. Machines, 13(11), 1059. https://doi.org/10.3390/machines13111059





