Literature Review on Fault Mechanism Analysis and Diagnosis Methods for Main Pump Systems
Abstract
1. Introduction
2. Main Pump Systems and Analysis of Typical Failure Mechanisms
2.1. Analysis of Structural Composition and Functions of the Main Pump
2.2. Analysis of Typical Failure Mechanism
2.2.1. Failure Mechanism of Bearing System
- Rolling bearing failure: Rolling bearing failure primarily manifests as pitting, spalling, and cage fracture, primarily caused by contact fatigue under alternating stress [37,38]. The underlying mechanisms are as follows: Lei et al. [39,40] confirmed that cooling water intrusion into lubricants leads to oil film rupture, causing direct metal-to-metal wear; the generated wear particles further exacerbate surface spalling. Under elevated temperatures (>120 °C), bearing steel underwent annealing-induced softening, with a 20–30% decrease in hardness, thereby accelerating fatigue crack propagation. Chen et al. [41] developed a nonlinear dynamic model that revealed the sensitivity of whirl trajectory to slip: a 15% increase in the amplitude in the X-direction resulted in more than a 40% increase in the roller-raceway slip ratio. This whirl effect leads to oscillations of the minimum oil film thickness and micropitting under boundary lubrication conditions. Li et al. [42] further reported that the coupling of centrifugal force and gyroscopic moment triggered atypical spalling of aeroengine main shaft bearings under high-speed, light-load conditions. This spalling was characterized by axially distributed fish-scale cracks, distinct from the radial spalling typical of traditional Hertzian contact fatigue. Patil et al. [43] established a theoretical model that quantified the relationship between pitting size and harmonic components of the vibration spectrum, although multi-defect coupling was not taken into account. Cao et al. [26] extended the model and demonstrated through a five-degree-of-freedom rotor-bearing system simulation that multi-point damage can excite a 2–5 kHz high-frequency resonance band. However, the requirement of preset defect locations limited its engineering applicability. Recent research has focused on the optimization of fatigue life models and slip dynamics. Zhai et al. [44] proposed a performance degradation assessment model based on cluster migration distance, enabling early fatigue failure warning through vibration signal feature extraction. Xia et al. [45] combined machine learning algorithms, such as SVM and cluster analysis, to improve fault classification accuracy; however, reliance on high-quality labeled data constrains its engineering generalization ability. Lee et al. [46] verified that insufficient lubrication and misalignment are the primary causes of overheating failure and verified that abnormal temperature rises can be monitored in real time using infrared thermal imaging.
- Failure mechanism of sliding bearing: The failure mechanisms of sliding bearings, which rely on hydrodynamic lubrication to form a load-bearing oil film, primarily include oil film rupture, vortex instability, and material adhesion [47,48,49]. Wang et al. [50] identified rotor eccentricity as a factor causing uneven lubricant flow, which in turn induces half-speed whirl and self-excited vibration. Antunović et al. [51] reported that solid particles embedded in the babbitt bushing can initiate scratching and plastic deformation. McKee et al. [52] demonstrated that local overheating softens the bearing alloy, leading to micro-welding with the journal. Recent research has further advanced the understanding of wear mechanisms, abrasive wear thermal runaway, and eddy instability. Traditional theory predicts a vortex frequency at half the power frequency; however, Wang et al. [50], using CFD simulation, found that turbulence in water-lubricated bearings at 15.4 MPa reduces the frequency to 0.48 times the power frequency, attributing the discrepancy to previously neglected fluid inertia effects. König et al. [53] demonstrated through acoustic emission signal analysis that particles larger than 5 μm can penetrate the oil film and embed into the soft liner, with embedding depth increasing under higher loads. This particle embedding can elevate the wear rate by 300%. Wang et al. [50] attributed wear primarily to fluid inertia forces, while Chen et al. [41] argued that the flexible deformation of the bearing housing plays a more predominant role. Current microscopic models address a single adhesion mechanism but fail to predict macroscopic lifetimes, whereas phenomenological models like the Archard equation rely heavily on empirical coefficients and therefore lack universality [53,54].
- Failure mechanism of mating interface: The failure of mating interfaces primarily manifests as interference-fit loosening, fretting wear, and interfacial debonding, typically caused by preload imbalance [55]. These failures can significantly reduce structural stiffness, trigger abnormal vibrations, and accelerate fatigue crack propagation. Li et al. [56] confirmed through residual stress analysis that concentrated interfacial shear stress during thermal cycling is the dominant cause of package module cracking. Needleman’s [57] continuum model identified two debonding modes: ductile matrix and brittle interface. Dong et al. [58] showed through simulations that wear at the interference-fit edge of a hollow shaft was 150% greater than that of a solid shaft, due to uneven contact stress distribution resulting from the lower stiffness of the hollow structure. Additionally, wear depth predicted by the Archard equation indicated a shift in the crack initiation site from the fit edge to the interior, leading to a 40% reduction in the fatigue life for hollow shafts compared with solid ones. Recent studies on molecular and medium dynamics have focused on understanding the mechanisms of interface failure. Zhou et al. [59] argued that atomic bond fracture energy is the dominant factor, whereas Needleman [57] maintained that stress triaxiality T is the key parameter. The core challenge remains the absence of cross-scale correlation models, hindering the integration of micro-parameters into engineering criteria. Nonetheless, consensus exists that debonding is governed by intrinsic strength and stress state, fretting wear results from the interaction of kinematics and material response, preload must be dynamically aligned with interference, and insights from molecular dynamics regarding bond fracture should be incorporated into continuum-scale models.
2.2.2. Failure Mechanism of Sealing System
- Mechanical seal failure: The mechanical seal is a critical component that forms a dynamic seal through contact between the rotating and stationary ring faces. Its failure primarily manifests as end-face wear, thermal cracking, and auxiliary system malfunction [63,64]. The predominant cause is dry running, where insufficient lubrication leads to a sudden increase in frictional heat at the sealing surfaces, resulting in thermoelastic instability, surface deformation, and the initiation of microcracks [52,61]. Shaft vibration further exacerbates the misalignment of the sealing surfaces, leading to localized contact stresses that exceed the material’s yield limit and accelerate fatigue failure [46,65]. Antunović et al. [51] and Chittora [61] reported that the leakage from seal face clearances originates from the transmission of bearing vibration to the seal assemblies. Additionally, long-term operation can generate microcracks in sealing materials due to cyclic fatigue stress, leading to grease loss and a reduction in interface compression force, as observed by Berezhansky et al. [33]. Seal performance is particularly vulnerable under extreme conditions compared with conventional conditions. Lee et al. [46] demonstrated that during low-temperature start-up, the increased viscosity of sealing grease can result in dry friction at the seal interface, raising the wear rate by 40% compared with standard operating conditions.
- Packing seal failure mechanism: The sealing performance of packed glands relies on the axial compression force to induce radial expansion of the soft packing material, thereby filling the gap between the shaft and sleeve. However, the failure of such seals is often attributed to a combination of packing wear, thermal hardening, and stress relaxation [66]. Continuous friction between the packing and sleeve causes progressive material wear, enlarging the clearance and ultimately leading to leakage. Microscopic analysis by Bistriceanu et al. [65] revealed that aramid fiber packing subjected to cyclic loading experienced fiber fracture, resulting in a 12% reduction in sealing pressure. Furthermore, high-temperature conditions promote thermal hardening of the filler resin matrix, reducing its elastic deformability. Makay et al. [67] reported a 40% decrease in compression resilience in braided fillers above 120 °C, whereas metal foil fillers exhibited high-temperature resistance but caused increased journal wear. Additionally, relaxation of the bolt preload can cause uneven gland pressure, thereby inducing medium leakage along preferential paths within the packing layer. The nuclear main pump experiences thermal shock during a loss-of-coolant accident. Azarm et al. [68] demonstrated through a probabilistic model that vulcanized rubber hardens when the seal ring material’s temperature gradient exceeds 200 °C/min, tripling the probability of elastic failure compared with normal conditions. Under high-pressure scenarios, Taylor [69] found that the Octagonal Gasket Flange relaxes due to the bolt temperature hysteresis, reducing the sealing compression force by 15–20%. Additionally, extreme pressure fluctuations expand the plastic deformation area of the gasket.
2.2.3. Failure Mechanism of Hydraulic Components
- Impeller damage: The impeller’s high-speed rotation propels the fluid, with its structural integrity crucial for maintaining head and efficiency. Common failures include blade fracture, cavitation, and wear. Bennekom et al. [75,76] identified casting defects as the primary cause of blade fractures. Zaman et al. [77] attributed cavitation mainly to bubble collapse in low-pressure regions impacting the blade surface. Zhou et al. [78] demonstrated that cavitation leads to impeller surface erosion and induces high-frequency impact vibrations, as revealed by vibration signal analysis. Numerical simulations by Gong et al. [79] indicated that the distribution of low-pressure regions is directly related to the geometry of the impeller inlet. Wang et al. [80] observed that during temperature transients, the cavitation erosion rate of PWR main pumps increases significantly, elevating the risk of seal failure. Tao and Li [81,82] highlighted that off-design operations, such as low load, can easily trigger flow separation and secondary flows, exacerbating hydraulic losses. For instance, under low-flow conditions, centrifugal pump outlet flow exhibits marked asymmetry, leading to head drop and the formation of a hump characteristic. Concurrently, Przybyla et al. [83] demonstrated that leading-edge wear results from foreign body impact or erosion by solid–liquid two-phase flow, as evidenced by aviation compressor impeller notch analysis. A central debate concerns the universality of cavitation prediction models. Wu et al. [84] argued that existing models lack adaptability to multiphase flow conditions and fail to capture the microscopic fatigue characteristics of materials.
- Guide vane failure: Guide vanes are essential fluid machinery components, serving to rectify flow and reduce vortex losses. The adjustment of their opening significantly affects pump efficiency and stability. Common issues associated with guide vanes include wear, deformation, and flow-induced vibration [85,86]. Wear is primarily caused by particle-laden fluid scouring [87], while deformation mainly results from fatigue accumulation [50] under high-frequency eddy loading. Visual experiments conducted by Song et al. [87] demonstrated that the wear rate of guide vanes increased with greater opening, and the maximum wear area is located on the blade pressure surface, showing a positive correlation with fluid sediment concentration. Wang et al. [50] highlighted that high-frequency whirl in water-lubricated guide bearings can be transmitted to the guide vanes, inducing resonance and accelerating structural fatigue. Two-dimensional holography has demonstrated that the vertical rotation axis of a vertical Reactor Coolant Pump is lubricated by high-pressure water, which can lead to water film whirl faults. The characteristic frequency of this whirl is 0.48 times the power frequency, and the whirl amplitude can exceed 50%. Under normal conditions, the water film vortex can be suppressed by damping forces [88,89], but in extreme environments, the coupling of random fluid disturbance forces with the system’s natural frequency can readily induce resonance instability [89,90,91].
- Wear of the mouth ring: Wear leads to increased clearance, diminishing efficiency and amplifying vibration [92]. Primary causes of wear include material mismatch in friction pairs and particle invasion [84]. Wu et al. [84,93] demonstrated via experiments and simulations that increasing front ring wear clearance from 0.2 mm to 0.5 mm results in a 12% decrease in pump head and a 150% increase in vibration velocity. DEM–CFD coupling simulations indicated a significant rise in flow field turbulence post-wear. Li et al. [94] noted that the uneven distribution of the self-lubricating phase in 1Cr13 MoS steel rings causes abrupt local friction coefficient changes, accelerating wear. Bonet-Jara et al. [95] developed a dynamic model of end-ring wear, employing the Runge-Kutta method to solve the rotor circuit equation, enabling real-time simulation of wear resistance changes for the first time. They observed that clearance enlargement exponentially decreases efficiency while linearly increasing vibration. Front ring wear reduces lift, whereas rear ring wear exacerbates vibration. Controversies exist in material selection: high-hardness alloys resist wear but are susceptible to stress corrosion cracking, while self-lubricating composites are expensive and last under 10,000 h [44,96]. Maintenance priorities also vary; for instance, FMEA analysis ranks ring wear as low risk, yet experimental evidence indicates it can lead to interlocking bearing failures [97,98].
2.2.4. Rotor Dynamic Fault
- Critical speed: The natural frequency of the rotor system and its rotation frequency can coincide at a specific speed, leading to resonance upon even minor excitation and resulting in a surge in amplitude [104,105]. The classical theory developed by Jeffcott [100] elucidates the abrupt changes in amplitude exhibited by rotors near the critical speed. The Jeffcott rotor model is a single-disk symmetric rotor, and its motion can be described by the following differential equations:where is the rotor mass, is the damping coefficient, is the bearing stiffness, is the mass eccentricity, and ω is the rotational angular velocity. The solution shows that resonance occurs when , and at the critical speed, the theoretical amplitude approaches infinity. Over the past decade, research has focused on the correction of complex boundary conditions. Furthermore, Zhang [106] demonstrated through a multi-field coupling model that thermal expansion of materials under high-temperature and high-pressure conditions can reduce the critical speed, while nonlinear variations in bearing stiffness can broaden the critical speed range. Comparative findings by Pennacchi et al. [107] focused on experimental validation, capturing bifurcation phenomena of axis trajectories through high-speed cameras. In contrast, research [106] preferred finite element method (FEM) simulations, which are computationally efficient but neglect turbulence effects. Controversies remain regarding damping quantification. The Muszynska model [108] assumed linear damping, whereas Wilkening [3], based on the case of nuclear power main pumps, demonstrated that fluid damping exhibits strong velocity dependence, necessitating the introduction of a nonlinear term correction. The limitation of current models lies in their inability to accurately characterize the transient over-critical process, along with the neglect of material creep effect under high-temperature environments, as highlighted in the separation margin design criterion [97,106] of the international standard API 610 [109]. Accurate prediction of critical velocity requires consideration of geometric nonlinearity, sealing effects, and thermal deformation, but the computational cost of high-fidelity models restricts real-time application.
- Unbalance response: Rotor mass eccentricity is a common source of excitation, and the corresponding response amplitude increases nonlinearly with rotational speed [110]. Lee et al. [111] demonstrated through a rotor–ball bearing system model that angular misalignment amplifies the unbalanced force, leading to a degeneration of the axis trajectory from an ellipse to a straight line. Recent progress in the field is reflected in the analysis of multi-fault coupling. Wang et al. [112] established a rotor model for a turbocharger, revealing that when imbalance and friction are coupled, the spectrum is dominated by the first-order harmonic (1×, corresponding to the rotation frequency), and the axis track exhibits a “0” pattern. Conversely, if the superposition is not centered, second-order harmonics (2×) are excited, and the track distortion resembles an “8” pattern. Methodologically, there are significant differences among approaches. The lumped parameter method employed by Lee et al. [111] is computationally straightforward but limited in accuracy, while the method by Marscher et al. [97] extracts parameters from field vibration data, which is more representative of engineering practice but constrained by sensor layout. Active balancing devices offer superior efficiency compared to passive dampers, though they require precise installation. While laser dynamic balancing is cost-effective, it has a dynamic error margin of ±15% [112]. Ma et al. [113] introduced a flexible coupling–rotor system model that first quantifies the fluid inertia effect due to misalignment, yet it fails to address force transfer lag in multiphase flow media. Typically, unbalance diagnosis relies on vibration signals; however, the enclosed structure of the main pump restricts sensor placement, and fluid noise often masks power-frequency components, complicating accurate fault detection.
- Fluid-induced instability: Fluid-induced instability is primarily characterized by self-excited vibrations resulting from the interaction between fluid excitation forces and rotor motion, often manifesting as half-frequency whirl or whip. This phenomenon arises from a positive feedback loop caused by the phase difference between the fluid dynamic pressure field and rotor displacement. Instability occurs when high-pressure fluid generates an asymmetric pressure distribution within the bearing clearance or impeller seal, aligning the resultant force with the rotor’s whirl direction [114,115]. Wang et al. [50] demonstrated, in the context of a nuclear main pump, that a 15.4 MPa high-pressure water flow induces a radial pressure gradient in the bearing gap. Changes in vortex displacement alter the clearance geometry, causing the fluid dynamic pressure field to amplify vortex amplitude, thus perpetuating a cycle of self-excited vibration. This effect is particularly pronounced in water-lubricated bearings, where water’s low viscosity results in insufficient damping and ability to suppress the accumulation of eddy energy. Additionally, research has increasingly examined turbulence nonlinearity and the instability threshold. The classical half-speed vortex theory, which assumes a constant vortex ratio of 0.5, is notably weakened by turbulence effects. Zhai et al. [116] demonstrated via vertical rotor tests that turbulence in slotted bearings reduces the swirl ratio to 0.42–0.48, consistent with the 0.48 frequency-doubling characteristic measured in nuclear main pumps. This occurs because turbulence increases the fluid’s equivalent mass, thereby altering the system’s natural frequency. Additionally, Pennacchi et al. [107] found that misalignment decreases the instability threshold by 30% due to exacerbated pressure field inhomogeneities from geometric deviations. A central debate in fluid-induced instability concerns fluid excitation forces: the traditional Reynolds equation neglects inertia forces, leading to significant errors at high speeds [3]. In contrast, the CFD full model by Gao et al. [117] offers high accuracy but requires over 100 times the computational resources of the simplified model, severely limiting its applicability for real-time monitoring.
3. Fault Diagnosis Methods for Main Pump Systems
3.1. Methods Based on Signal Processing
3.1.1. Time–Frequency Domain Analysis Techniques
3.1.2. Signal Decomposition and Reconstruction Methods
3.1.3. Nonlinear Signal Processing Methods
3.1.4. Physical Feature Demodulation Method
3.1.5. Special Consideration for Signal Processing Methods in the Fault Diagnosis of Main Pumps
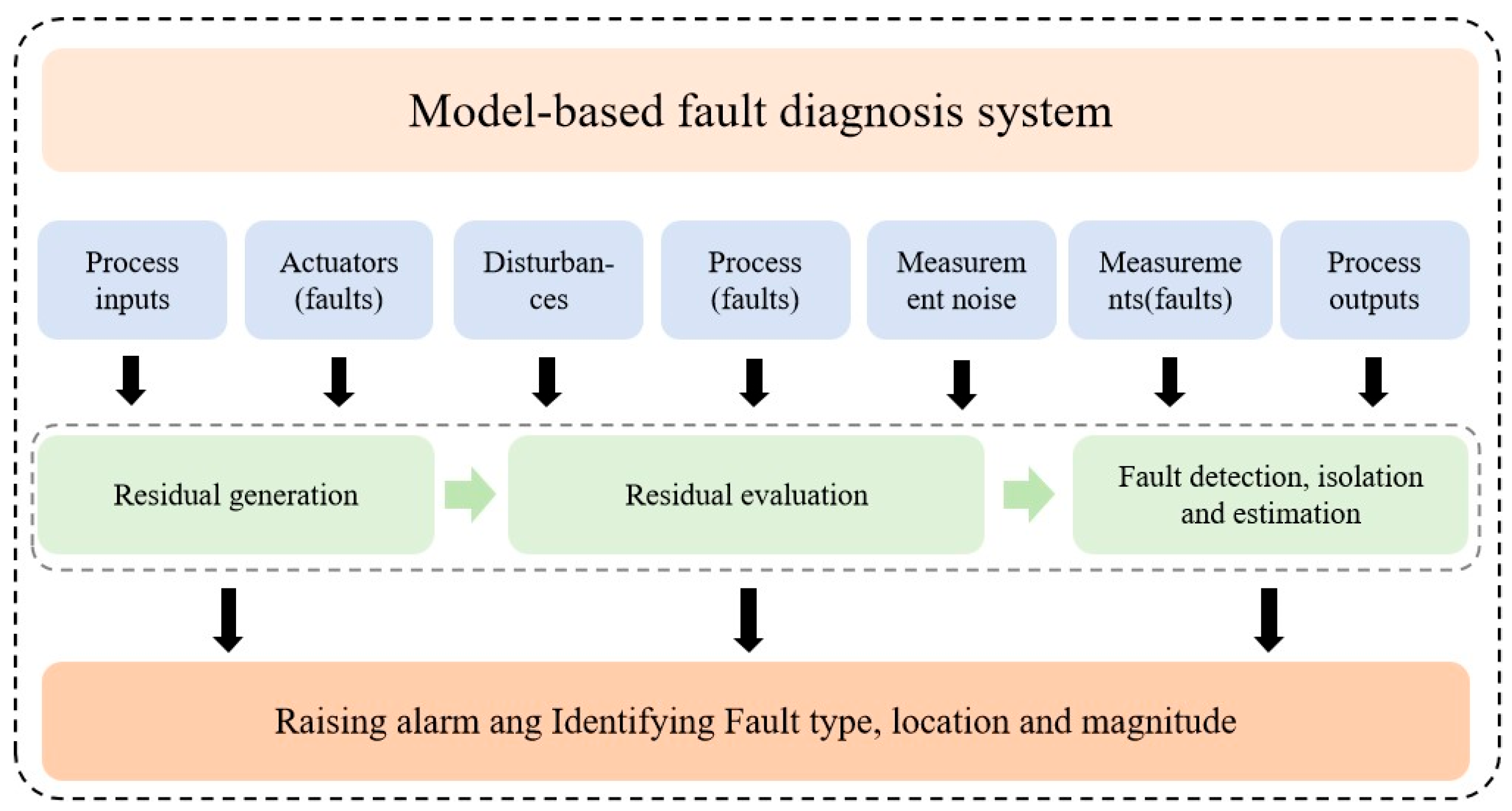
3.2. Model-Based Approach
3.2.1. Fault Diagnosis Methods Based on Physical Models
3.2.2. Model Methods Based on Signal Processing and Feature Extraction
3.2.3. Model Comparison Methods Based on Analytical Redundancy
3.2.4. Special Consideration for Model Methods in the Fault Diagnosis of Main Pumps
3.3. Data-Driven Approach
3.3.1. Traditional Machine Learning Intelligent Diagnosis Methods
3.3.2. Deep Learning-Based Intelligent Diagnosis Method
3.3.3. Transfer Learning-Based Intelligent Diagnosis Method
3.3.4. Special Considerations for Data-Driven Methods in Main Pump Fault Diagnosis
3.4. Fusion-Based Approach
3.4.1. Data Level Fusion
3.4.2. Feature-Level Fusion
3.4.3. Decision-Level Fusion
3.4.4. Special Consideration for Fusion Methods in the Fault Diagnosis of Main Pumps
3.5. Diagnostic Methods
4. Analysis of the Development of Fault Diagnosis Methods for Main Pumps
5. Core Challenges and Future Research Directions
5.1. Core Challenge 1: Failure Mechanism Coupling and Evolution Law Under Extreme Working Conditions Are Unclear
5.2. Core Challenge 2: Insufficient Generalization and Reliability of Diagnostic Models in Complex Environments
5.3. Core Challenge 3: Leap from Fault Diagnosis to Predictive Maintenance and Proactive Health Management
6. Conclusions
6.1. Study Summary
6.2. Comparison with Existing Reviews and Innovation
6.3. Future Expectations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhu, Q.; Zhu, L.; Wang, Z. Hybrid Triboelectric-Piezoelectric Nanogenerator Assisted Intelligent Condition Monitoring for Aero-Engine Pipeline System. Chem. Eng. J. 2025, 519, 165121. [Google Scholar] [CrossRef]
- Cao, J.; Lin, Y.; Fu, X. Self-Powered Overspeed Wake-Up Alarm System Based on Triboelectric Nanogenerators for Intelligent Transportation. Nano Energy 2023, 107, 108150. [Google Scholar] [CrossRef]
- Wilkening, J. Practical Error Estimates for Reynolds’ Lubrication Approximation and Its Higher Order Corrections. SIAM J. Math. Anal. 2009, 41, 588–630. [Google Scholar] [CrossRef]
- Yang, Y.; Ding, L.; Xiao, H.; Fang, G.; Li, J. Current Status and Applications for Hydraulic Pump Fault Diagnosis: A Review. Sensors 2022, 22, 9714. [Google Scholar] [CrossRef]
- Makay, E. Centrifugal Pump Hydraulic Instability. Final Report; Energy Research and Consultants Corp.: Morrisville, PA, USA, 1980. [Google Scholar]
- Zhu, Y.; Wu, Q.; Tang, S.; Khoo, B.C.; Chang, Z. Intelligent Fault Diagnosis Methods for Hydraulic Piston Pumps: A Review. J. Mar. Sci. Eng. 2023, 11, 1609. [Google Scholar] [CrossRef]
- Dai, J.; Tang, J.; Huang, S.; Wang, Y. Signal-Based Intelligent Hydraulic Fault Diagnosis Methods: Review and Prospects. Chin. J. Mech. Eng. 2019, 32, 75. [Google Scholar] [CrossRef]
- Zhao, X. Data-Driven Fault Detection, Isolation and Identification of Rotating Machinery: With Applications to Pumps and Gearboxes. Ph.D. Thesis, University of Alberta, Edmonton, AB, Canada, 2012. [Google Scholar]
- Liu, X.; Mou, J.; Xu, X.; Qiu, Z.; Dong, B. A Review of Pump Cavitation Fault Detection Methods Based on Different Signals. Processes 2023, 11, 2007. [Google Scholar] [CrossRef]
- Hassan, I.U.; Panduru, K.; Walsh, J. Review of Data Processing Methods Used in Predictive Maintenance for Next Generation Heavy Machinery. Data 2024, 9, 69. [Google Scholar] [CrossRef]
- Ahmed, A.; Wang, X.; Yang, M. Biocompatible Materials of Pulsatile and Rotary Blood Pumps: A Brief Review. Rev. Adv. Mater. Sci. 2020, 59, 322–339. [Google Scholar] [CrossRef]
- Trivedi, V.; Singh, V. A Comprehensive Review on Development of Solar Pump Operated by PV Module. Renew. Sustain. Energy Rev. 2024, 11, 1964–1989. [Google Scholar] [CrossRef]
- Davies, N. Novel, Induced Flow, Centrifugal Water Pump System for Off Grid Application. Ph.D. Thesis, University of Liverpool, Liverpool, UK, 2015. [Google Scholar]
- Wieczorek, U.; Ivantysynova, M. Computer Aided Optimization of Bearing and Sealing Gaps in Hydrostatic Machines—The Simulation Tool CASPAR. Int. J. Fluid Power 2002, 3, 7–20. [Google Scholar] [CrossRef]
- Ivantysynova, M.; Baker, J. Power Loss in the Lubricating Gap Between Cylinder Block and Valve Plate of Swash Plate Type Axial Piston Machines. Int. J. Fluid Power 2009, 10, 29–43. [Google Scholar] [CrossRef]
- Ivantysynova, M.; Lasaar, R. An Investigation into Micro- and Macrogeometric Design of Piston/Cylinder Assembly of Swash Plate Machines. Int. J. Fluid Power 2004, 5, 23–36. [Google Scholar] [CrossRef]
- Zhang, C.; Zhu, C.; Meng, B.; Li, S. Challenges and Solutions for High-Speed Aviation Piston Pumps: A Review. Aerospace 2021, 8, 392. [Google Scholar] [CrossRef]
- Yang, S.; Li, P.; Tao, R.; Zhang, F.; Xiao, R.; Liu, W.; Wang, F. Investigate the Full Characteristic of a Centrifugal Pump-as-Turbine (PAT) in Turbine and Reverse Pump Modes. Eng. Appl. Comput. Fluid Mech. 2023, 17, 2246527. [Google Scholar] [CrossRef]
- Chen, J.; Shi, W.; Zhang, D. Influence of Blade Inlet Angle on the Performance of a Single Blade Centrifugal Pump. Eng. Appl. Comput. Fluid Mech. 2021, 15, 462–475. [Google Scholar] [CrossRef]
- Sakran, H.K.; Abdul Aziz, M.S.; Abdullah, M.Z.; Khor, C.Y. Effects of Blade Number on the Centrifugal Pump Performance: A Review. Arab. J. Sci. Eng. 2022, 47, 7945–7961. [Google Scholar] [CrossRef]
- Lugovaja, I.S. Investigation of the Centrifugal Pump’s Cavitation Characteristics under Various Operating Conditions. Sci. Tech. 2019, 18, 422–426. [Google Scholar]
- Wang, X.; Feng, Y.Q.; Hung, T.C.; He, Z.X.; Lin, C.H.; Sultan, M. Investigating the System Behaviors of a 10 kW Organic Rankine Cycle (ORC) Prototype Using Plunger Pump and Centrifugal Pump. Energies 2020, 13, 1141. [Google Scholar] [CrossRef]
- Wu, D.; Ren, Y.; Mou, J.; Gu, Y.; Jiang, L. Unsteady Flow and Structural Behaviors of Centrifugal Pump Under Cavitation Conditions. Chin. J. Mech. Eng. 2019, 32, 17. [Google Scholar] [CrossRef]
- Zhou, F.M.; Xu, S.L.; Wang, X.L.; Sun, T.; Wang, W. High Efficiency Hydraulic Model Development of CAP1400 Canned Nuclear Reactor Coolant Pump. J. Mech. Eng. 2018, 54, 176–183. [Google Scholar] [CrossRef]
- Li, Y.; Xu, M.; Wei, Y.; Huang, W. Bearing Fault Diagnosis Based on Adaptive Multiscale Fuzzy Entropy and Support Vector Machine. J. Vibroeng. 2015, 17, 1188–1202. [Google Scholar]
- Cao, H.R.; Jing, X.; Su, S.M.; Chen, X.F. Dynamic Modeling and Vibration Analysis for Inter-Shaft Bearing Fault. J. Mech. Eng. 2020, 56, 89–99. [Google Scholar]
- Hsieh, N.K.; Lin, W.Y.; Young, H.T. High-Speed Spindle Fault Diagnosis with the Empirical Mode Decomposition and Multiscale Entropy Method. Entropy 2015, 17, 2170–2183. [Google Scholar] [CrossRef]
- Li, R.; Liu, J.; Ding, X.; Liu, Q. Study on the Influence of Flow Distribution Structure of Piston Pump on the Output of Pulsation Pump. Processes 2022, 10, 1077. [Google Scholar] [CrossRef]
- Cho, I.S.; Jung, J. A Study on the Pressure Ripple Characteristics in a Bent-Axis Type Oil Hydraulic Piston Pump. J. Mech. Sci. Technol. 2013, 27, 3713–3719. [Google Scholar] [CrossRef]
- Wang, Y.C.; Tan, L.; Cao, S.L.; Zhu, B.S. Characteristics of Transient Flow and Pressure Fluctuation in Impeller for Centrifugal Pump. J. Mech. Eng. 2014, 50, 163–169. [Google Scholar] [CrossRef]
- Barrio, R.; Parrondo, J.; Blanco, E. Numerical Analysis of the Unsteady Flow in the Near-Tongue Region in a Volute-Type Centrifugal Pump for Different Operating Points. Comput. Fluids 2010, 39, 859–870. [Google Scholar] [CrossRef]
- Greene, R.H.; Casada, D.A.; Ayers, C.W. Detection of Pump Degradation; Nuclear Regulatory Commission: Washington, DC, USA, 1995. [Google Scholar]
- Berezhansky, N.; Zaplatyn, A.; Karymov, R. Development of Bearing Beam and Seal System for Main Pumps. In Proceedings of the International Conference on Industrial Engineering, Moscow, Russia, 15–18 May 2018; Springer: Cham, Switzerland, 2018; pp. 1063–1069. [Google Scholar]
- Fausing Olesen, J.; Shaker, H.R. Predictive Maintenance for Pump Systems and Thermal Power Plants: State-of-the-Art Review, Trends and Challenges. Sensors 2020, 20, 2425. [Google Scholar] [CrossRef] [PubMed]
- Bakhri, S.; Ertugrul, N.; Soong, W.L. The Methods of Condition Monitoring for Circulator of HTGR. J. Phys. Conf. Ser. 2019, 1198, 022054. [Google Scholar] [CrossRef]
- Lannoo, J.; Vanoost, D.; Peuteman, J.; Debruyne, S.; De Gersem, H.; Pissoort, D. Improved Air Gap Permeance Model to Characterise the Transient Behaviour of Electrical Machines Using Magnetic Equivalent Circuit Method. Int. J. Numer. Model. 2020, 33, e2749. [Google Scholar] [CrossRef]
- Tandon, N.; Choudhury, A. A Review of Vibration and Acoustic Measurement Methods for the Detection of Defects in Rolling Element Bearings. Tribol. Int. 1999, 32, 469–480. [Google Scholar] [CrossRef]
- Moyar, G.J.; Morrow, J. Surface Failure of Bearings and Other Rolling Elements. Bull. Univ. Ill. Eng. Exp. Stn. 1964, 468. [Google Scholar]
- Lei, Y.; Lin, J.; He, Z.; Zuo, M.J. A Review on Empirical Mode Decomposition in Fault Diagnosis of Rotating Machinery. Mech. Syst. Signal Process. 2013, 35, 108–126. [Google Scholar] [CrossRef]
- Shi, X. TEHL Analysis of Aero-Engine Mainshaft Roller Bearing Based on Quasi-Dynamics. J. Mech. Eng. 2016, 52, 86–92. [Google Scholar] [CrossRef]
- Chen, W.; Li, J.N.; Zhang, L.B.; Wang, P.Y. Skidding Analysis of High Speed Rolling Bearing Considering Whirling of Bearing. J. Mech. Eng. 2013, 49, 38–43. [Google Scholar] [CrossRef]
- Li, Y.F.; Mo, J.Y.; Zeng, J.H.; Xu, T.; Xu, S.D. Design and Dynamic Characteristics Analysis of a Novel Cageless Ball Bearing with Pure Rolling. J. Mech. Eng. 2023, 59, 256–269. [Google Scholar]
- Patil, M.S.; Mathew, J.; Rajendrakumar, P.K.; Desai, S. A Theoretical Model to Predict the Effect of Localized Defect on Vibrations Associated with Ball Bearing. Int. J. Mech. Sci. 2010, 52, 1193–1201. [Google Scholar] [CrossRef]
- Zhai, Z.; Zhu, Z.; Xu, Y.; Zhao, X.; Liu, F.; Feng, Z. Cluster Migration Distance for Performance Degradation Assessment of Water Pump Bearings. Sensors 2022, 22, 6809. [Google Scholar] [CrossRef] [PubMed]
- Xia, Y.; Guo, X.J.; Su, E.; Kong, L. Research on Bearing Fault Diagnosis Technology Based on Machine Learning. Int. J. Ind. Optim. 2024, 5, 45–59. [Google Scholar] [CrossRef]
- Lee, J.J.; Kim, Y.; Lee, T.; Kim, M.S.; Kim, J.H.; Tak, H.J.; Park, J.W.; Oh, D. Investigation of Failure Causes of Oil Pump Based on Operating Conditions. Appl. Sci. 2023, 13, 4308. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. An Average Flow Model for Determining Effects of Three-Dimensional Roughness on Partial Hydrodynamic Lubrication. J. Tribol. 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Ishii, N.; Oku, T.; Anami, K.; Knisely, C.W.; Sawai, K.; Morimoto, T.; Iida, N. Experimental Study of the Lubrication Mechanism for Thrust Slide Bearings in Scroll Compressors. HVAC&R Res. 2008, 14, 453–465. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, M.; Qin, D.; Yan, Z. Performance of High-Speed Hydrodynamic Sliding Bearings with Lubricating Oils Combining Laminar and Turbulent Flows. Adv. Mech. Eng. 2020, 12, 1687814020933389. [Google Scholar] [CrossRef]
- Wang, X.F.; Hong, Y.C.; Qiu, D.M. Fault Diagnosis and Mechanism Study of Water-Film Whirl in Vertical Reactor Coolant Pumps. J. Mech. Eng. 2020, 56, 89–95. [Google Scholar]
- Antunović, R.; Šiniković, G.; Vučetić, N. Diagnostics and Failure of Plain Bearings. IETI Trans. Eng. Res. Pract. 2018, 2, 9–18. [Google Scholar]
- McKee, K.K.; Forbes, G.; Mazhar, I.; Entwistle, R.; Howard, I. A Review of Major Centrifugal Pump Failure Modes with Application to the Water Supply and Sewerage Industries. In Proceedings of the ICOMS Asset Management Conference, Gold Coast, Australia, 16–19 May 2011. [Google Scholar]
- König, F.; Jacobs, G.; Stratmann, A.; Cornel, D. Fault Detection for Sliding Bearings Using Acoustic Emission Signals and Machine Learning Methods. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1097, 012013. [Google Scholar] [CrossRef]
- West, O.H.; Dahl, K.V.; Christiansen, T.L.; Somers, M.A. Failure Analysis and Thermochemical Surface Engineering of Bearings for Wind Turbine Drivetrains. In Proceedings of the 2nd International Conference on Energy and the Future of Heat Treatment and Surface Engineering, Beijing, China, 11–13 October 2014; pp. 361–365. [Google Scholar]
- Li, J.; Lai, X.; Zou, P.; Guo, W.; Tang, C. Effect of Imbalanced Interface Pre-Tightening Force on the Bearing Behavior of Carbon Fiber Reinforced Polymer Interference-Fit Lap Joint. Adv. Mech. Eng. 2021, 13, 16878140211012540. [Google Scholar] [CrossRef]
- Li, Y.Z.; He, E.M.; Chen, P.X.; Yi, M.H. Cracking Mechanism Analysis and Experimental Verification of Encapsulated Module Under High Low Temperature Cycle Considering Residual Stress. J. Northwest. Polytech. Univ. 2023, 41, 447–454. [Google Scholar] [CrossRef]
- Needleman, A. A Continuum Model for Void Nucleation by Inclusion Debonding. J. Appl. Mech. 1987, 54, 525–531. [Google Scholar] [CrossRef]
- Dong, Y.H.; Lu, L.T.; Li, X.X.; Zhao, H.; Chen, H.; Ceng, D.F. Simulation Analysis of Fretting Wear and Fatigue of Press-Fitted Structure of Hollow Axle and Solid Axle. J. Mech. Eng. 2022, 58, 161–169. [Google Scholar]
- Zhou, Y.; Ye, T.; Ma, L.; Lu, Z.; Yang, Z.; Liu, S. Investigation on Cf/PyC Interfacial Properties of C/C Composites by the Molecular Dynamics Simulation Method. Materials 2019, 12, 679. [Google Scholar] [CrossRef] [PubMed]
- Ruger, C.J.; Luckas, W.J., Jr. Technical Findings Related to Generic Issue 23: Reactor Coolant Pump Seal Failure; Nuclear Regulatory Commission: Washington, DC, USA, 1989. [Google Scholar]
- Chittora, S.M. Monitoring of Mechanical Seals in Process Pumps. Master’s Thesis, University of Texas at Austin, Austin, TX, USA, 2018. [Google Scholar]
- Zainal, M.Z.; Yunus, M.Y.; Azizan, A.S.; Ismail, N.A. The Effect of Size and Material of Packing Seal and Pump Flow Rate to Leakage Rate at Stuffing Box of Centrifugal Pump. Int. J. Eng. Technol. Sci. 2019, 6, 101–114. [Google Scholar] [CrossRef]
- Hu, S.T.; Huang, W.F.; Shi, X.; Peng, Z.K.; Liu, X.F. Review on Mechanical Seals Using a Bi-Gaussian Stratified Surface Theory. J. Mech. Eng. 2019, 55, 91–105. [Google Scholar] [CrossRef]
- Mba, D.; Roberts, T.; Taheri, E.; Roddis, A. Application of Acoustic Emission Technology for Detecting the Onset and Duration of Contact in Liquid Lubricated Mechanical Seals. Insight 2006, 48, 486–487. [Google Scholar] [CrossRef]
- Bistriceanu, D.P.; Pal, S.G.; Ciornei, F.C.; Bujoreanu, C. Study on the Sealing Defects Impact on High Pressure Pump. IOP Conf. Ser. Mater. Sci. Eng. 2020, 997, 012005. [Google Scholar] [CrossRef]
- Tashiro, H.; Yoshida, F. Stress Relaxation of Gland Packings and Its Modeling. JSME Int. J. 1990, 33, 219–223. [Google Scholar] [CrossRef]
- Makay, E.; Szamody, O. Survey of Feed Pump Outages; Final Report; Energy Research and Consultants Corp.: Morrisville, PA, USA, 1978. [Google Scholar]
- Azarm, M.A.; Boccio, J.L.; Mitra, S. Impact of Mechanical- and Maintenance-Induced Failures of Main Reactor Coolant Pump Seals on Plant Safety; Brookhaven National Laboratory: Upton, NY, USA, 1985. [Google Scholar]
- Taylor, R. Relaxation of the Bolted Flange Connection. In Proceedings of the Pressure Vessels and Piping Conference, Virtual, 3 August 2020; American Society of Mechanical Engineers: New York, NY, USA, 2020. V002T02A016. [Google Scholar]
- Wong, K. Computer Model of a Nuclear Reactor Primary Coolant Pump. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1978. [Google Scholar]
- Phillips, R.L.; Jacobs, L.E.; Merati, P. Experimental Determination of the Thermal Characteristics of a Mechanical Seal and Its Operating Environment. Tribol. Trans. 1997, 40, 559–568. [Google Scholar] [CrossRef]
- Fu, Q.; Zhao, Y.; Lu, Y.; Zhao, W.; Zhu, R. An Impeller Optimization Method for the High Specific Speed Mixed-Flow Reactor Coolant Pump Applied to Marine Nuclear Power. J. Mar. Sci. Eng. 2023, 11, 1301. [Google Scholar] [CrossRef]
- Ni, D.; Lu, H.; Huang, S. Experimental Study on PIV Measurement and CFD Investigation of the Internal Flow Characteristics in a Reactor Coolant Pump. Energies 2023, 16, 4345. [Google Scholar] [CrossRef]
- Al-Obaidi, A.R. Influence of Guide Vanes on the Flow Fields and Performance of Axial Pump Under Unsteady Flow Conditions: Numerical Study. J. Mech. Eng. Sci. 2020, 14, 6570–6593. [Google Scholar] [CrossRef]
- Van Bennekom, A.; Berndt, F.; Rassool, M.N. Pump Impeller Failures—A Compendium of Case Studies. Eng. Fail. Anal. 2001, 8, 145–156. [Google Scholar] [CrossRef]
- Wang, G.; Jia, X.; Li, J.; Li, F.; Liu, Z.; Gong, B. Current State and Development of the Research on Solid Particle Erosion and Repair of Turbomachine Blades. In Re-engineering Manufacturing for Sustainability, Proceedings of the 20th CIRP International Conference on Life Cycle Engineering, Singapore, 17–19 April 2013; Springer: Singapore, 2013; pp. 633–638. [Google Scholar]
- Zaman, W.; Ahmad, Z.; Kim, J.M. Fault Diagnosis in Centrifugal Pumps: A Dual-Scalogram Approach with Convolution Autoencoder and Artificial Neural Network. Sensors 2024, 24, 851. [Google Scholar] [CrossRef]
- Zhou, S.; Qin, L.; Yang, Y.; Wei, Z.; Wang, J.; Wang, J.; Ruan, J.; Tang, X.; Wang, X.; Liu, K. A Novel Ensemble Fault Diagnosis Model for Main Circulation Pumps of Converter Valves in VSC-HVDC Transmission Systems. Sensors 2023, 23, 5082. [Google Scholar] [CrossRef]
- Gong, X.; Pei, J.; Wang, W.; Osman, M.K.; Jiang, W.; Zhao, J.; Deng, Q. Nature-Inspired Modified Bat Algorithm for the High-Efficiency Optimization of a Multistage Centrifugal Pump for a Reverse Osmosis Desalination System. J. Mar. Sci. Eng. 2021, 9, 771. [Google Scholar] [CrossRef]
- Wang, X.L.; Wang, P.; Yuan, S.Q.; Zhu, R.S.; Fu, Q. Analysis on Transient Hydrodynamic Characteristics of Cavitation Process for Reactor Coolant Pump. At. Energy Sci. Technol. 2014, 48, 1421–1427. [Google Scholar]
- Tao, R.; Xiao, R.; Yang, W.; Liu, W. Hump Characteristic of Reversible Pump-Turbine in Pump Mode. J. Drain. Irrig. Mach. Eng. 2014, 32, 927–930. [Google Scholar]
- Li, D.Y.; Gong, R.Z.; Wang, H.J.; Fu, W.W.; Wei, X.Z.; Liu, Z.S. Fluid Flow Analysis of Droop Phenomena in Pump Mode for a Given Guide Vane Setting of a Pump-Turbine Model. J. Zhejiang Univ.-Sci. A 2015, 16, 851–863. [Google Scholar] [CrossRef]
- Przybyła, B.; Zapałowicz, Z. Uszkodzenia Sprężarki Odśrodkowej Silnika Lotniczego P&W 206 b2 Spowodowane Zassaniem Ciał Obcych. Adv. Mech. Mater. Eng. 2016, 33, 141–152. [Google Scholar]
- Wu, X.F.; Du, X.L.; Tan, M.G.; Liu, H.L. Advances in Mechanical Engineering. Adv. Mech. Eng. 2021, 13, 1687814021998115. [Google Scholar]
- Son, Y.J.; Kim, Y.I.; Yang, H.M.; Lee, K.Y.; Yoon, J.Y.; Choi, Y.S. Numerical Study on the Hydrodynamic Performance and Internal Flow of an Axial-Flow Pump with Various Inlet Flow Angles. Sci. Rep. 2023, 13, 22303. [Google Scholar] [CrossRef]
- Zhang, J.F.; Xiao, Y.J.; Jin, S.B.; Cai, H.K.; Song, H.Q. Effect of Guide Vane Openings and Different Flow Rates on Characteristics in Pump Mode of Pump-Turbine with Splitter Blades. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1081, 012016. [Google Scholar] [CrossRef]
- Song, X.; Zhou, X.; Song, H.; Deng, J.; Wang, Z. Study on the Effect of the Guide Vane Opening on the Band Clearance Sediment Erosion in a Francis Turbine. J. Mar. Sci. Eng. 2022, 10, 1396. [Google Scholar] [CrossRef]
- Ni, W.; Yang, W.; Ma, Y.; Kang, Z. An Experimental Investigation of Modal Control and Suppression Mechanism of Particle Damper on Vortex Induced Vibration. Nonlinear Dyn. 2025, 113, 2079–2090. [Google Scholar] [CrossRef]
- Yuan, X.; Qiu, T.; Tian, T. Design and Modelling Methodology for a New Magnetorheological Damper Featuring a Multi-Stage Circumferential Flow Mode. Int. J. Mech. Mater. Des. 2022, 18, 785–806. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, X.Q.; Xie, W.C.; So, R.M.C. Flow-Induced Instability Under Bounded Noise Excitation in Cross-Flow. J. Sound Vib. 2008, 312, 476–495. [Google Scholar] [CrossRef]
- Nishida, S.; Kawakami, R.; Hirota, K.; Morita, H.; Kondo, Y.; Utsumi, S. Unsteady Fluid Force and Random Excitation Force Measurement of Triangular Array Tube Bundle in Steam-Water Two Phase Flow. In Proceedings of the Pressure Vessels and Piping Conference, San Antonio, TX, USA, 14–18 July 2019; American Society of Mechanical Engineers: New York, NY, USA, 2019. V004T04A010. [Google Scholar]
- Emzain, Z.F.; Wardhana, Z.G.; Adiwidodo, S.; Rosady, S.D.; Prasetyo, P.; Nova, M.A. Implementation of Failure Mode and Effect Analysis (FMEA) for Centrifugal Pump Maintenance in Water Supply Distribution System. J. Polimesin 2024, 22, 295–298. [Google Scholar] [CrossRef]
- Li, Y.W.; Guo, Z.M.; Shaojun, L.; Hu, X.Z. Flow Field and Particle Flow of Two-Stage Deep-Sea Lifting Pump Based on DEM-CFD. Front. Energy Res. 2022, 10, 884571. [Google Scholar] [CrossRef]
- Li, S.; Che, Y.; Song, J.; Li, C.; Shu, Y.; He, J.; Yang, B. Study on Hardness, Microstructure, Distribution of the Self-Lubricating Phase, Friction and Wear Property of 1Cr13MoS After Heat Treatment. Materials 2019, 12, 3171. [Google Scholar] [CrossRef]
- Bonet-Jara, J.; Morinigo-Sotelo, D.; Duque-Perez, O.; Serrano-Iribarnegaray, L.; Pons-Llinares, J. End-Ring Wear in Deep-Well Submersible Motor Pumps. IEEE Trans. Ind. Appl. 2022, 58, 4522–4531. [Google Scholar] [CrossRef]
- Kumar, A.N.; Murray, P. Stress-Corrosion Cracking of Reactor Feed Pump Wear Rings. J. Fail. Anal. Prev. 2006, 6, 83–89. [Google Scholar] [CrossRef]
- Marscher, W.D.; Campbell, J.S. Methods of Investigation and Solution of Stress, Vibration, and Noise Problems in Pumps. In Proceedings of the 15th International Pump Users Symposium, Houston, TX, USA, 2–5 March 1998. [Google Scholar]
- Zhang, X.; Wei, R.; Wu, Z.; Dong, L.; Liu, H. Risk Assessment and Reliability Analysis of Oil Pump Unit Based on DS Evidence Theory. Energies 2023, 16, 4887. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Jeffcott, H.H. The Lateral Vibration of Loaded Shafts in the Neighbourhood of a Whirling Speed—The Effect of Want of Balance. Philos. Mag. 1919, 37, 304–314. [Google Scholar] [CrossRef]
- Nicholas, J.C.; Barrett, L.E. The Effect of Bearing Support Flexibility on Critical Speed Prediction. ASLE Trans. 1986, 29, 329–338. [Google Scholar] [CrossRef]
- Orcutt, F.K.; Arwas, E.B. An Investigation of Rotor-Bearing Dynamics with Flexible Rotors and Turbulent-Flow Journal Bearings. Part I. Analysis, Design and Fabrication of the Test Apparatus (Report No. NYO-3363-3; MTI-65TR12); U.S. Atomic Energy Commission Contract AT(30-1)-3363; Mechanical Technology Incorporated: Latham, NY, USA, 1965. [Google Scholar]
- Brennen, C.E.; Acosta, A.J. Fluid-Induced Rotordynamic Forces and Instabilities. Struct. Control Health Monit. 2006, 13, 10–26. [Google Scholar] [CrossRef]
- Childs, D. Turbomachinery Rotordynamics: Phenomena, Modeling, and Analysis; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Živković, V.B.; Grković, V.R.; Kljajić, M.V. The Instigating Factors Behind the Occurrence of Vibration in Steam Turbines: A Review Analysis. Therm. Sci. 2024, 28, 4451–4471. [Google Scholar] [CrossRef]
- Zhang, H. Model Development and Stability Analysis for a Turbocharger Rotor System Under Multi-Field Coupled Forces. Ph.D. Thesis, University of Huddersfield, Huddersfield, UK, 2021. [Google Scholar]
- Pennacchi, P.; Vania, A.; Chatterton, S. Nonlinear Effects Caused by Coupling Misalignment in Rotors Equipped with Journal Bearings. Mech. Syst. Signal Process. 2012, 30, 306–322. [Google Scholar] [CrossRef]
- Wang, R.; Wang, Y.; Cao, X.; Yang, S.; Guo, X. Nonlinear Analysis of Rotor-Bearing-Seal System with Varying Parameters Muszynska Model Based on CFD and RBF. Machines 2022, 10, 1238. [Google Scholar] [CrossRef]
- Jones, R.L.; Korkowski, F.J.; Cooper, J. Highlights of Draft API 610 12th Edition. In Proceedings of the 45th Turbomachinery & 32nd Pump Symposia, Houston, TX, USA, 11–15 September 2016. [Google Scholar] [CrossRef]
- Tiwari, M.; Gupta, K.; Prakash, O. Effect of Radial Internal Clearance of a Ball bearing on the Dynamics of a Balanced Horizontal Rotor. J. Sound Vib. 2000, 238, 723–756. [Google Scholar] [CrossRef]
- Lee, Y.S.; Lee, C.W. Modelling and Vibration Analysis of Misaligned Rotor-Ball Bearing Systems. J. Sound Vib. 1999, 224, 17–32. [Google Scholar] [CrossRef]
- Wang, J.; Wen, H.; Qian, H.; Guo, J.; Zhu, J.; Dong, J.; Shen, H. Typical Fault Modeling and Vibration Characteristics of the Turbocharger Rotor System. Machines 2023, 11, 311. [Google Scholar] [CrossRef]
- Ma, H.; Wang, X.; Niu, H.; Wen, B. Oil-Film Instability Simulation in an Overhung Rotor System with Flexible Coupling Misalignment. Arch. Appl. Mech. 2015, 85, 893–907. [Google Scholar] [CrossRef]
- Wu, Y.; Li, S.; Liu, S.; Dou, H.S.; Qian, Z. Vibration of Hydraulic Machinery; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar]
- Williamson, C.H.; Govardhan, R. Vortex-Induced Vibrations. Annu. Rev. Fluid Mech. 2004, 36, 413–455. [Google Scholar] [CrossRef]
- Zhai, L.; Luo, Y.; Wang, Z.; Kitauchi, S.; Miyagawa, K. Nonlinear Vibration Induced by the Water-Film Whirl and Whip in a Sliding Bearing Rotor System. Chin. J. Mech. Eng. 2016, 29, 260–270. [Google Scholar] [CrossRef]
- Gao, G.Y.; Yin, Z.W.; Jiang, D.; Zhang, X.L. CFD Analysis of Load-Carrying Capacity of Hydrodynamic Lubrication on a Water-Lubricated Journal Bearing. Ind. Lubr. Tribol. 2015, 67, 30–37. [Google Scholar]
- Nakamura, T.; Fujikawa, R.; Matsushita, M. Reconstruction of Grand Design for Fatigue Evaluation Based on Fatigue Failure Analysis of Japanese NPPs. E-J. Adv. Maint. 2015, 7, 66–73. [Google Scholar]
- Sayed-Mouchaweh, M. Introduction to the Diagnosis of Discrete Event Systems. In Discrete Event Systems: Diagnosis and Diagnosability; Springer: New York, NY, USA, 2014; pp. 1–11. [Google Scholar]
- Jardine, A.K.; Lin, D.; Banjevic, D. A Review on Machinery Diagnostics and Prognostics Implementing Condition-Based Maintenance. Mech. Syst. Signal Process. 2006, 20, 1483–1510. [Google Scholar] [CrossRef]
- Engin, Ş.N.; Gülez, K.; Badi, M.N. Advanced Signal Processing Techniques for Fault Diagnostics—A Review. Math. Comput. Appl. 1999, 4, 121–136. [Google Scholar]
- Sun, L.; Bai, H.; Zhao, G.; Wang, X. Review of Diagnosis Technique for Equipment Faults and Its Development Trend. MATEC Web Conf. 2015, 22, 03007. [Google Scholar] [CrossRef]
- Anwarsha, A.; Narendiranath Babu, T. Recent Advancements of Signal Processing and Artificial Intelligence in the Fault Detection of Rolling Element Bearings: A Review. J. Vibroeng. 2022, 24, 1027–1055. [Google Scholar] [CrossRef]
- Romanssini, M.; de Aguirre, P.C.; Compassi-Severo, L.; Girardi, A.G. A Review on Vibration Monitoring Techniques for Predictive Maintenance of Rotating Machinery. Eng 2023, 4, 1797–1817. [Google Scholar] [CrossRef]
- Yu, J. Early Fault Detection for Gear Shaft and Planetary Gear Based on Wavelet and Hidden Markov Modeling. Ph.D. Thesis, University of Massachusetts, Amherst, MA, USA, 2012. [Google Scholar]
- Al Thobiani, F. The Non-Intrusive Detection of Incipient Cavitation in Centrifugal Pumps. Ph.D. Thesis, University of Huddersfield, Huddersfield, UK, 2011. [Google Scholar]
- Chao, Q.; Gao, H.; Tao, J.; Wang, Y.; Zhou, J.; Liu, C. Adaptive Decision-Level Fusion Strategy for the Fault Diagnosis of Axial Piston Pumps Using Multiple Channels of Vibrationsignals. Sci. China Technol. Sci. 2022, 65, 470–480. [Google Scholar] [CrossRef]
- Kamiel, B.; McKee, K.; Entwistle, R.; Mazhar, I.; Howard, I. Multi Fault Diagnosis of the Centrifugal Pump Using the Wavelet Transform and Principal Component Analysis. In Proceedings of the 9th IFToMM International Conference on Rotor Dynamics, Milan, Italy, 26–29 May 2015; Springer: Cham, Switzerland, 2015; pp. 555–566. [Google Scholar]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Z.; Ma, J.; Yuan, H. Fault Diagnosis for Hydraulic Pump Based on EEMD-KPCA and LVQ. Vibroeng. Procedia 2014, 4, 188–193. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proc. R. Soc. Lond. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Liu, S.; Liu, X. Fault Diagnosis of Pump Valve Spring Based on Improved Singularity Analysis. J. Vibroeng. 2014, 16, 704–712. [Google Scholar]
- Du, J.; Wang, S.; Zhang, H. Layered Clustering Multi-Fault Diagnosis for Hydraulic Piston Pump. Mech. Syst. Signal Process. 2013, 36, 487–504. [Google Scholar] [CrossRef]
- Lan, Y.; Hu, J.; Huang, J.; Niu, L.; Zeng, X.; Xiong, X.; Wu, B. Fault Diagnosis on Slipper Abrasion of Axial Piston Pump Based on Extreme Learning Machine. Measurement 2018, 124, 378–385. [Google Scholar] [CrossRef]
- Miao, Y.; Jiang, Y.; Huang, J.; Zhang, X.; Han, L. Application of Fault Diagnosis of Seawater Hydraulic Pump Based on Transfer Learning. Shock Vib. 2020, 2020, 9630986. [Google Scholar] [CrossRef]
- Yang, W.; Peng, Z.; Wei, K.; Shi, P.; Tian, W. Superiorities of Variational Mode Decomposition Over Empirical Mode Decomposition Particularly in Time–Frequency Feature Extraction and Wind Turbine Condition Monitoring. IET Renew. Power Gener. 2017, 11, 443–452. [Google Scholar] [CrossRef]
- Benosman, M. A Survey of Some Recent Results on Nonlinear Fault Tolerant Control. Math. Probl. Eng. 2010, 2010, 586169. [Google Scholar] [CrossRef]
- Dai, L.; Han, L. Characteristics Diagnosis of Nonlinear Dynamical Systems. In Dynamical Systems and Methods; Springer: New York, NY, USA, 2011; pp. 85–103. [Google Scholar]
- Swelam, M.; Kotb, A.; Abdulaziz, A.M. Acoustic Diagnosis of Cavitation for Centrifugal Pumps of Different Materials. Eng. Res. J. 2019, 164, 214–228. [Google Scholar] [CrossRef]
- Čdina, M. Detection of Cavitation Phenomenon in a Centrifugal Pump Using Audible Sound. Mech. Syst. Signal Process. 2003, 17, 1335–1347. [Google Scholar] [CrossRef]
- Jiang, W.; Zheng, Z.; Zhu, Y.; Li, Y. Demodulation for Hydraulic Pump Fault Signals Based on Local Mean Decomposition and Improved Adaptive Multiscale Morphology Analysis. Mech. Syst. Signal Process. 2015, 58, 179–205. [Google Scholar] [CrossRef]
- Wang, S.; Yuan, Z.; Yang, G. Study on Fault Diagnosis of Data Fusion in Hydraulic Pump. China Mech. Eng. 2005, 16, 327–331. [Google Scholar]
- Xue, H.; Li, Z.; Wang, H.; Chen, P. Intelligent Diagnosis Method for Centrifugal Pump System Using Vibration Signal and Support Vector Machine. Shock Vib. 2014, 2014, 407570. [Google Scholar] [CrossRef]
- Pei, S.Y.; Niu, H.J.; Hong, J. Lubrication Characteristics of Hybrid Bearing in Sodium-Cooled Fast Reactor. J. Mech. Eng. 2020, 56, 29–37. [Google Scholar]
- Randall, R.B.; Antoni, J. Rolling Element Bearing Diagnostics—A Tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Adams, D.A. Improved CBM of Top Drives Using Advanced Sensors and Novel Analysis Techniques. Ph.D. Thesis, University of Texas at Austin, Austin, TX, USA, 2015. [Google Scholar]
- Leite, V.C.; da Silva, J.G.; Torres, G.L.; Veloso, G.F.; da Silva, L.E.; Bonaldi, E.L.; de Oliveira, L.E. Bearing Fault Detection in Induction Machine Using Squared Envelope Analysis of Stator Current. Bearing Technol. 2017. [Google Scholar] [CrossRef]
- Ho, D.; Randall, R.B. Optimisation of Bearing Diagnostic Techniques Using Simulated and Actual Bearing Fault Signals. Mech. Syst. Signal Process. 2000, 14, 763–788. [Google Scholar] [CrossRef]
- Cui, L.L.; Wang, X.; Wang, H.Q.; Xu, Y.G.; Zhang, J.Y. Feature Extraction of Bearing Fault Based on Improved Switching Kalman Filter. J. Mech. Eng. 2019, 55, 44–51. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Y.; Deng, W. Fault Diagnosis for Rolling Bearings Using Optimized Variational Mode Decomposition and Resonance Demodulation. Entropy 2020, 22, 739. [Google Scholar] [CrossRef]
- Han, S.; Niu, P.; Luo, S.; Li, Y.; Zhen, D.; Feng, G.; Sun, S. A Novel Deep Convolutional Neural Network Combining Global Feature Extraction and Detailed Feature Extraction for Bearing Compound Fault Diagnosis. Sensors 2023, 23, 8060. [Google Scholar] [CrossRef] [PubMed]
- Qi, R.; Zhang, J.; Spencer, K. A Review on Data-Driven Condition Monitoring of Industrial Equipment. Algorithms 2022, 16, 9. [Google Scholar] [CrossRef]
- Ye, C.; Tang, Y.; An, D.; Wang, F.; Zheng, Y.; Van Esch, B.P.M. Investigation on Stall Characteristics of Marine Centrifugal Pump Considering Transition Effect. Ocean Eng. 2023, 280, 114823. [Google Scholar] [CrossRef]
- Ye, S.G.; Zhang, J.H.; Xu, B. Noise Reduction of an Axial Piston Pump by Valve Plate Optimization. Chin. J. Mech. Eng. 2018, 31, 57. [Google Scholar] [CrossRef]
- Jin, Z.Z. Research on Fault Diagnosis Method of Bearing Based on Parameter Optimization VMD and Improved DBN. J. Vibroeng. 2023, 25, 1068–1082. [Google Scholar]
- Venkat, V. A Review of Process Fault Detection and Diagnosis Part I, II, III. Comput. Chem. Eng. 2003, 27, 293–346. [Google Scholar]
- Fusel, D.; Isermann, R. Model-Based Fault Detection and Diagnosis Part A: Methods. In Proceedings of the International Conference on Probability, Safety, Assessment, and Management, New York, NY, USA, 13–18 September 1998. [Google Scholar]
- Nordmann, R.; Aenis, M. Fault Diagnosis in a Centrifugal Pump Using Active Magnetic Bearings. Int. J. Rotating Mach. 2004, 10, 183–191. [Google Scholar] [CrossRef]
- Xi, A.; Mo, Y.; Zhang, L. Research Status of Fault Diagnosis of Large and Medium-Sized Vertical Water Pump Units. In Proceedings of the 10th IIAE International Conference on Industrial Application Engineering, Matsue, Japan, 26–30 March 2022; pp. 191–194. [Google Scholar] [CrossRef]
- Willersrud, A. Model-Based Diagnosis of Drilling Incidents. Ph.D. Dissertation, Norwegian University of Science and Technology, Trondheim, Norway, 2015. [Google Scholar]
- Gertler, J. Fault Detection and Diagnosis in Engineering Systems; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Łatas, W.; Stojek, J. Dynamic Model of Axial Piston Swash-Plate Pump for Diagnostics of Wear in Elements. Arch. Mech. Eng. 2011, 58, 135–155. [Google Scholar] [CrossRef]
- Gnepper, O.; Hitzer, H.; Enge-Rosenblatt, O. Predictive Diagnosis in Axial Piston Pumps: A Study for High Frequency Condition Indicators Under Variable Operating Conditions. Int. J. Progn. Health Manag. 2023, 14, 3393. [Google Scholar] [CrossRef]
- Tang, H.; Fu, Z.; Huang, Y. A Fault Diagnosis Method for Loose Slipper Failure of Piston Pump in Construction Machinery Under Changing Load. Appl. Acoust. 2021, 172, 107634. [Google Scholar] [CrossRef]
- Harris, R.M.; Edge, K.A.; Tilley, D.G. Predicting the Behavior of Slipper Pads in Swashplate-Type Axial Piston Pumps. J. Dyn. Syst. Meas. Control 1996, 118, 41–47. [Google Scholar] [CrossRef]
- Jiang, W.L.; Zhang, P.Y.; Li, M.; Zhang, S.Q. Axial Piston Pump Fault Diagnosis Method Based on Symmetrical Polar Coordinate Image and Fuzzy C-Means Clustering Algorithm. Shock Vib. 2021, 2021, 6681751. [Google Scholar] [CrossRef]
- Litak, G.; Margielewicz, J.; Gąska, D.; Yurchenko, D.; Dąbek, K. Dynamic Response of the Spherical Pendulum Subjected to Horizontal Lissajous Excitation. Nonlinear Dyn. 2020, 102, 2125–2142. [Google Scholar] [CrossRef]
- Guo, Q.; Li, Y. Early Fault Diagnosis of Rolling Bearing Based on Lyapunov Exponent. J. Vib. Eng. 2019, 32, 296–303. [Google Scholar]
- Ma, Z.H.; Wang, S.; Shi, J. Fault Diagnosis of an Intelligent Hydraulic Pump Based on a Nonlinear Unknown Input Observer. Chin. J. Aeronaut. 2018, 31, 185–194. [Google Scholar] [CrossRef]
- Zhou, C.; Jia, Y.; Bai, H. Sliding Dispersion Entropy-Based Fault State Detection for Diaphragm Pump Parts. Coatings 2021, 11, 1536. [Google Scholar] [CrossRef]
- Yan, X.; Sun, Z.; Zhao, J.; Shi, Z.; Zhang, C.A. Fault Diagnosis of Rotating Machinery Equipped with Multiple Sensors Using Space-Time Fragments. J. Sound Vib. 2019, 456, 49–64. [Google Scholar] [CrossRef]
- Wang, W.; Li, Y.; Song, Y. Fault Diagnosis Method of Hydraulic System Based on Multi-Source Information Fusion and Fractal Dimension. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 561. [Google Scholar] [CrossRef]
- Chen, L.; Hu, J.M.; Li, H.M. Application of EMD-AR and MTS for Hydraulic Pump Fault Diagnosis. J. Vibroeng. 2013, 15, 761–772. [Google Scholar]
- Ramasso, E. Contribution of Belief Functions to Hidden Markov Models with an Application to Fault Diagnosis. In Proceedings of the IEEE International Workshop on Machine Learning for Signal Processing, Grenoble, France, 1–4 September 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1–6. [Google Scholar]
- Jia, Y.; Xu, M.; Wang, R. Symbolic Important Point Perceptually and Hidden Markov Model Based Hydraulic Pump Fault Diagnosis Method. Sensors 2018, 18, 4460. [Google Scholar] [CrossRef]
- Marzat, J.; Piet-Lahanier, H.; Damongeot, F.; Walter, E. Model-Based Fault Diagnosis for Aerospace Systems: A Survey. Proc. Inst. Mech. Eng. Part G 2012, 226, 1329–1360. [Google Scholar] [CrossRef]
- Farza, M.; Triki, M.; M’Saad, M.; Dahhou, B. Unknown Inputs Observers for a Class of Nonlinear Systems. In Proceedings of the 10th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering, Sousse, Tunisia, 20–22 December 2009. [Google Scholar]
- Bento, A.; Oliveira, L.; Leite, V.J. Estimaçao de Falhas com Observadores de Entrada Desconhecida and Modelagem Fuzzy Granular. In Proceedings of the Simpósio Brasileiro de Automação Inteligente, Virtual, 20–22 October 2021. [Google Scholar]
- Zhou, Z.; Ma, Z.; Jiang, Y.; Peng, M. Fault Diagnosis Using Bond Graphs in an Expert System. Energies 2022, 15, 5703. [Google Scholar] [CrossRef]
- Sun, Y.; Zuo, Z.; Liu, S. Distribution of Pressure Fluctuations in a Prototype Pump Turbine at Pump Mode. Adv. Mech. Eng. 2014, 6, 923937. [Google Scholar] [CrossRef]
- De Castro, H.F.; Cavalca, K.L.; Nordmann, R. Whirl and Whip Instabilities in Rotor-Bearing System Considering a Nonlinear Force Model. J. Sound Vib. 2008, 317, 273–293. [Google Scholar] [CrossRef]
- Ren, L.; Xu, Z.Y.; Yan, X.Q. Single-Sensor Incipient Fault Detection. IEEE Sens. J. 2010, 11, 2102–2107. [Google Scholar] [CrossRef]
- Li, B.; Chow, M.Y.; Tipsuwan, Y.; Hung, J.C. Neural-Network-Based Motor Rolling Bearing Fault Diagnosis. IEEE Trans. Ind. Electron. 2002, 47, 1060–1069. [Google Scholar] [CrossRef]
- Konieczny, J.; Łatas, W.; Stojek, J. Application of Analysis of Variance to Determine Important Features of Signals for Diagnostic Classifiers of Displacement Pumps. Sci. Rep. 2024, 14, 6098. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.Y.; Zhong, Q.; Huang, R.Y.; Liao, Y.X.; Li, J.P.; Li, W.H. Intelligent Fault Diagnosis for Machinery Based on Enhanced Transfer Convolutional Neural Network. J. Mech. Eng. 2021, 57, 96–105. [Google Scholar]
- Zheng, H.L.; Wang, R.X.; Yang, Y.T.; Yin, J.C.; Xu, M.Q. An Empirical Analysis about the Generalization Performance of Data-Driven Fault Diagnosis Methods. J. Mech. Eng. 2020, 56, 102. [Google Scholar]
- Widodo, A.; Yang, B.S. Support Vector Machine in Machine Condition Monitoring and Fault Diagnosis. Mech. Syst. Signal Process. 2007, 21, 2560–2574. [Google Scholar] [CrossRef]
- Czarnecki, W.M.; Tabor, J. Extreme Entropy Machines: Robust Information Theoretic Classification. Pattern Anal. Appl. 2017, 20, 383–400. [Google Scholar] [CrossRef]
- Li, J.; Shao, J. A Fault Diagnosis Method Based on the Support Vector Machine in Rod Pumping Systems. J. Pet. Sci. Eng. 2021, 207, 109123. [Google Scholar] [CrossRef]
- Yu, C.; Yan, H.; Zhang, X.; Ye, H. A Multi-Model Diagnosis Method for Slowly Varying Faults of Plunger Pump. J. Mar. Sci. Eng. 2022, 10, 1968. [Google Scholar] [CrossRef]
- Jiang, W.; Li, Z.; Li, J.; Zhu, Y.; Zhang, P. Study on a Fault Identification Method of the Hydraulic Pump Based on a Combination of Voiceprint Characteristics and Extreme Learning Machine. Processes 2019, 7, 894. [Google Scholar] [CrossRef]
- Chen, Y.B.; Cui, H.S.; Huang, C.W.; Hsu, W.T. Improving Transmission Line Fault Diagnosis Based on EEMD and Power Spectral Entropy. Entropy 2024, 26, 806. [Google Scholar] [CrossRef]
- Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial Intelligence for Fault Diagnosis of Rotating Machinery: A Review. Mech. Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- Lei, Y.; Yang, B.; Jiang, X.; Jia, F.; Li, N.; Nandi, A.K. Applications of Machine Learning to Machine Fault Diagnosis: A Review and Roadmap. Mech. Syst. Signal Process. 2020, 138, 106587. [Google Scholar] [CrossRef]
- Jiang, H.K. Deep Learning Theory with Application in Intelligent Fault Diagnosis of Aircraft. J. Mech. Eng. 2019, 55, 27. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.; Gao, L.; Zhang, Y. A New Convolutional Neural Network-Based Data-Driven Fault Diagnosis Method. IEEE Trans. Ind. Electron. 2017, 65, 5990–5998. [Google Scholar] [CrossRef]
- Tang, S.; Zhu, Y.; Yuan, S.; Li, G. Intelligent Diagnosis Towards Hydraulic Axial Piston Pump Using a Novel Integrated CNN Model. Sensors 2020, 20, 7152. [Google Scholar] [CrossRef]
- Tang, S.; Yuan, S.; Zhu, Y.; Li, G. An Integrated Deep Learning Method Towards Fault Diagnosis of Hydraulic Axial Piston Pump. Sensors 2020, 20, 6576. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhou, T.; Tang, S.; Yuan, S. A Data-Driven Diagnosis Scheme Based on Deep Learning Toward Fault Identification of the Hydraulic Piston Pump. J. Mar. Sci. Eng. 2023, 11, 1273. [Google Scholar] [CrossRef]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to Forget: Continual Prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef]
- Zhao, Q.; Cheng, G.; Han, X.; Liang, D.; Wang, X. Fault Diagnosis of Main Pump in Converter Station Based on Deep Neural Network. Symmetry 2021, 13, 1284. [Google Scholar] [CrossRef]
- Zhang, Z.; Tang, A.; Zhang, T. A Transfer-Based Convolutional Neural Network Model with Multi-Signal Fusion and Hyperparameter Optimization for Pump Fault Diagnosis. Sensors 2023, 23, 8207. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Jiang, Q.; Shen, Y.; Qian, C.; Xu, F.; Zhu, Q. Application of Recurrent Neural Network to Mechanical Fault Diagnosis: A Review. J. Mech. Sci. Technol. 2022, 36, 527–542. [Google Scholar] [CrossRef]
- Chen, H.; Luo, H.; Huang, B.; Jiang, B.; Kaynak, O. Transfer Learning-Motivated Intelligent Fault Diagnosis Designs: A Survey, Insights, and Perspectives. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 2969–2983. [Google Scholar] [CrossRef] [PubMed]
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2009, 22, 1345–1359. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, X.; Cao, G. Multi-Source Tri-Training Transfer Learning. IEICE Trans. Inf. Syst. 2014, 97, 1668–1672. [Google Scholar] [CrossRef]
- Cody, T.; Beling, P.A. A Systems Theory of Transfer Learning. IEEE Syst. J. 2023, 17, 26–37. [Google Scholar] [CrossRef]
- Yang, B.; Lei, Y.; Jia, F.; Xing, S. An Intelligent Fault Diagnosis Approach Based on Transfer Learning from Laboratory Bearings to Locomotive Bearings. Mech. Syst. Signal Process. 2019, 122, 692–706. [Google Scholar] [CrossRef]
- Zhang, P.; Jiang, W.; Zheng, Y.; Zhang, S.; Zhang, S.; Liu, S. Hydraulic-Pump Fault-Diagnosis Method Based on Mean Spectrogram Bar Graph of Voiceprint and ResNet-50 Model Transfer. J. Mar. Sci. Eng. 2023, 11, 1678. [Google Scholar] [CrossRef]
- Xiang, J.W. Numerical Simulation Driving Generative Adversarial Networks in Association with the Artificial Intelligence Diagnostic Principle to Detect Mechanical Faults. Sci. Sin. Technol. 2021, 51, 341–355. [Google Scholar] [CrossRef]
- Wang, C.; Chen, L.; Zhang, Y.; Zhang, L.; Tan, T. A Novel Cross-Sensor Transfer Diagnosis Method with Local Attention Mechanism: Applied in a Reciprocating Pump. Sensors 2023, 23, 7432. [Google Scholar] [CrossRef]
- Cai, W.; Zhang, Q.; Cui, J. A Novel Fault Diagnosis Method for Denoising Autoencoder Assisted by Digital Twin. Comput. Intell. Neurosci. 2022, 2022, 5077134. [Google Scholar] [CrossRef] [PubMed]
- Yang, P.; Chen, J.; Wu, L.; Li, S. Fault Identification of Electric Submersible Pumps Based on Unsupervised and Multi-Source Transfer Learning Integration. Sustainability 2022, 14, 9870. [Google Scholar] [CrossRef]
- Wassenaar, J.M. A Framework and Implementation of Data-Driven Maintenance Modeling. Master’s Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 31 August 2019. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why Should I Trust You?” Explaining the Predictions of Any Classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar]
- Shuvo, M.M.H.; Islam, S.K.; Cheng, J. Efficient Acceleration of Deep Learning Inference on Resource-Constrained Edge Devices: A Review. Proc. IEEE 2022, 111, 42–91. [Google Scholar] [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A Survey of Fault Diagnosis and Fault-Tolerant Techniques—Part I: Fault Diagnosis with Model-Based and Signal-Based Approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef]
- Tang, H.; Wang, Z.; Wu, Y. A Multi-Fault Diagnosis Method for Piston Pump in Construction Machinery Based on Information Fusion and PSO-SVM. J. Vibroeng. 2019, 21, 1904–1916. [Google Scholar] [CrossRef]
- Pei, M.; Li, H.; Yu, H. A Novel Three-Stage Feature Fusion Methodology and Its Application in Degradation State Identification for Hydraulic Pump. Meas. Sci. Rev. 2021, 21, 123–135. [Google Scholar] [CrossRef]
- Xu, X.B.; Zheng, J.; Xu, D.L.; Yang, J.B. Information Fusion Method for Fault Diagnosis Based on Evidential Reasoning Rule. J. Control Theory Appl. 2015, 32, 1170–1182. [Google Scholar]
- Chun-Li, X.; Hong, X.; Yong-Kuo, L. Application of Data Fusion Method to Fault Diagnosis of Nuclear Power Plant. J. Mar. Sci. Appl. 2005, 4, 30–33. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, G.; Wang, R.; Tang, S.; Su, H.; Cao, K. Intelligent Fault Diagnosis of Hydraulic Piston Pump Based on Wavelet Analysis and Improved AlexNet. Sensors 2021, 21, 549. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, K. Fault Diagnosis of Submersible Motor on Offshore Platform Based on Multi-Signal Fusion. Energies 2022, 15, 756. [Google Scholar] [CrossRef]
- Yan, J.; Zhu, H.; Yang, X.; Cao, Y.; Shao, L. Research on Fault Diagnosis of Hydraulic Pump Using Convolutional Neural Network. J. Vibroeng. 2016, 18, 5141–5152. [Google Scholar] [CrossRef]
- Ali, M.M.; Gaikwad, A.T. Multimodal Biometrics Enhancement Recognition System Based on Fusion of Fingerprint and Palmprint: A Review. Glob. J. Comput. Sci. Technol. 2016, 16, 13–26. [Google Scholar]
- Wang, Y.; Lohmann, B. Multisensor Image Fusion: Concept, Method and Applications; Technical Report; University of Bremen: Bremen, Germany, 2000; Available online: https://www.epc.ed.tum.de/fileadmin/w00cgc/rt/publikationen/forschungsberichte/FB_2000_Lohmann_techrepwang.pdf (accessed on 5 December 2000).
- Kannan, V.; Zhang, T.; Li, H. A Review of the Intelligent Condition Monitoring of Rolling Element Bearings. Machines 2024, 12, 484. [Google Scholar] [CrossRef]
- Zhang, P.; Hu, W.; Cao, W.; Chen, L.; Wu, M. Multi-Fault Diagnosis and Fault Degree Identification in Hydraulic Systems Based on Fully Convolutional Networks and Deep Feature Fusion. Neural Comput. Appl. 2024, 36, 9125–9140. [Google Scholar] [CrossRef]
- Yu, H.; Li, H.; Li, Y. Vibration Signal Fusion Using Improved Empirical Wavelet Transform and Variance Contribution Rate for Weak Fault Detection of Hydraulic Pump. ISA Trans. 2020, 107, 385–401. [Google Scholar] [CrossRef] [PubMed]
- Lou, C.; Atoui, M.A.; Li, X. Recent Deep Learning Models for Diagnosis and Health Monitoring: A Review of Research Works and Future Challenges. Trans. Inst. Meas. Control 2024, 46, 2833–2870. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, Z.; Li, K.; Si, C.; Li, L. Survey on Advanced Equipment Fault Diagnosis and Warning Based on Big Data Technique. J. Phys. Conf. Ser. 2020, 1549, 042134. [Google Scholar] [CrossRef]
- Kamarzarrin, M.; Refan, M.H.; Amiri, P.; Dameshghi, A. Fault Diagnosis of Wind Turbine Double-Fed Induction Generator Based on Multi-Level Fusion and Measurement of Back-to-Back Converter Current Signal. Iran. J. Electr. Electron. Eng. 2022, 18, 26–34. [Google Scholar]
- Chen, Z.; Li, W. Multisensor Feature Fusion for Bearing Fault Diagnosis Using Sparse Autoencoder and Deep Belief Network. IEEE Trans. Instrum. Meas. 2017, 66, 1693–1702. [Google Scholar] [CrossRef]
- Jiang, D.; Wang, Z. Research on Mechanical Equipment Fault Diagnosis Method Based on Deep Learning and Information Fusion. Sensors 2023, 23, 6999. [Google Scholar] [CrossRef] [PubMed]




| Component Category | Specific Component | Fault Causes | Impact | Severity Level |
|---|---|---|---|---|
| Bearing System | Rolling Bearings | Lubrication contamination (water/particles in oil), overheating (improper oil level/poor oil quality), misalignment, and fatigue wear. | Increased vibration, elevated noise levels, and temperature rise, leading to shaft damage or seizure. | High |
| Plain Bearings | Oil whirl, journal/bearing friction, and insufficient lubrication. | Oil film failure and direct metal contact, causing high temperature and vibration. | High | |
| Fitted Interfaces | Shaft wear (corrosion/imbalance) and installation stress. | Increased clearance, exacerbating vibration and seal failure. | Medium | |
| Sealing System | Mechanical Seals | Dry running, vibration, seal face wear, shaft vibration, and insufficient lubrication. | Medium leakage (e.g., glue solution), flushing phenomena, and pressure/flow reduction. | High |
| Packed Seals | Vibration, foreign material blockage, and wear. | Reduced rotational speed, increased leakage, and decreased pump efficiency. | Medium | |
| Hydraulic Components | Impeller | Cavitation (inlet pressure < saturation vapor pressure), wear (impurities/prolonged operation), blockage, and reverse installation. | Efficiency reduction, increased vibration/noise, unstable flow, and blade fracture. | High |
| Guide Vanes | Wear and corrosion. | Hydraulic imbalance and flow channel blockage, exacerbating vibration. | Medium | |
| Wear Rings | Improper clearance (misalignment/wear) and dirty medium. | Increased internal leakage and reduced volumetric efficiency. | Medium | |
| Rotor Dynamics | Critical Speed | Rotor resonance (design defects/deposits) and loose baseplate. | Sudden increase in amplitude, causing bearing/seal damage. | High |
| Unbalance Response | Impeller imbalance, shaft bending, coupling wear, and piping stress. | Periodic vibration, inducing mechanical fatigue and component loosening. | High | |
| Fluid-Induced Instability | Cavitation, vortex shedding, and hydraulic excitation. | Low-frequency vibration and flow pulsation, potentially triggering structural resonance. | Medium |
| Fusion Level | Description | Advantages | Disadvantages | Typical Methods | Applicable Scenarios |
|---|---|---|---|---|---|
| Data-level Fusion | Direct alignment, filtering, and fusion of raw sensor data. | Minimal information loss and theoretically highest accuracy. | Large data volume and high computational cost; requires precise sensor synchronization; sensitive to noise. | Wavelet transform and CNN directly processing multi-source signals. | Offline precision analysis and in-depth study of failure mechanisms. |
| Feature-level Fusion | First extracts features from each sensor signal, and then fuses the feature vectors. | Significantly compresses data volume; retains key information; high flexibility and strong robustness. | Quality of feature extraction directly affects the final result; complex fusion algorithm selection. | Feature concatenation, weighted fusion, and principal component analysis (PCA). | Most commonly used in online real-time or quasi-real-time diagnostic systems. |
| Decision-level Fusion | Each sensor or method first independently performs preliminary diagnosis, and then fuses the multiple diagnostic results. | Best fault tolerance; modular design and easy to expand; friendly to asynchronous sensors. | Maximum information loss; relies on the preliminary diagnosis performance of each sub-module. | Voting methods, D-S evidence theory, and Bayesian inference. | High reliability requirements, fault-tolerant control, and distributed monitoring systems. |
| Comparison Dimension | Signal Processing Methods | Model-Driven Methods | Data-Driven Methods | Information Fusion Methods |
|---|---|---|---|---|
| Core Principle | Direct feature extraction from signals (vibration and pressure) | Residual-based diagnosis using system | ML-based learning of fault-state mappings from historical data | Integration of multi-sensor/multi-method information |
| Optimal Scenario | Periodic impact faults in rotating components | Parametric faults (sensors, actuators, and leaks) | Complex systems with ample data but no precise models | High-reliability systems with unreliable single sources |
| Main Advantage | Clear physical interpretation; minimal fault data needed | Strong explainability; reasoning and early warning capabilities | Powerful feature extraction; high accuracy for complex faults | Enhanced accuracy and robustness; good fault tolerance |
| Main Limitation | Expert-dependent; low intelligence; insensitive to unknown faults | Complex modeling; sensitive to parameter variations | Data quality/quantity dependent; “black box” models | Complex implementation; high computational/communication costs |
| Diagnostic Paradigm | Signal Processing | |||
|---|---|---|---|---|
| Specific Methods | Time–domain analysis. | Signal decomposition and reconstruction. | Nonlinear signal processing. | Physical feature extraction. |
| Advantages | Simultaneously captures time-frequency characteristics; suitable for non-stationary signal analysis. | Can separate fault feature components; effectively suppresses background noise. | Can reveal nonlinear characteristics of systems; detects weak nonlinear faults. | Directly extracts physical fault features (e.g., characteristic frequencies); strong engineering interpretability. |
| Disadvantages | Basis function selection depends on experience; requires parameter tuning. | Endpoint effects exist; high computational complexity. | Parameter optimization is difficult; requires high sampling rate data support. | Relies on prior knowledge for demodulation strategy design; insensitive to compound faults. |
| Signal Type | Vibration and noise. | Vibration and pressure. | Vibration and pressure. | Vibration. |
| Real-time Capability | Medium. | Medium. | Medium. | High. |
| Typical Applicable Faults | Bearing pitting, gear tooth breakage, and cavitation | Early bearing wear, pulley loosening, and valve plate failure | Rotor wear, misalignment, and nonlinear damage | Bearing spalling, ball damage, and gear local defects |
| Application Scenarios | Transient fault diagnosis in rotating machinery. | Early weak fault extraction in strong noise environments. | Fault diagnosis in complex dynamic systems. | Quantitative diagnosis of characteristic faults in rotating components like bearings/gears. |
| Diagnostic Paradigm | Model-Driven | ||
|---|---|---|---|
| Specific Methods | Physical Model. | Signal Processing and Feature Extraction Model. | Analytical Redundancy Model Comparison. |
| Advantages | Provides accurate and precise diagnostic estimates; strong fault isolation capability. | Improves diagnostic robustness; can handle certain noise and instability. | Robust to unknown disturbances; suitable for real-time systems with fast fault detection. |
| Disadvantages | High model complexity; not easily adaptable to system changes or new fault types. | Complex model training; improper feature selection may cause overfitting. | Model errors may cause false alarms; not suitable for strongly nonlinear or time-varying systems. |
| Signal Type | Pressure, flow, and speed. | Vibration and pressure. | Pressure, flow, and temperature. |
| Real-time Capability | High. | Medium. | High. |
| Typical Applicable Faults | System leakage, efficiency decline, and parametric faults. | Pulley wear, plunger sticking, and performance degradation. | Sensor faults, actuator faults, and control anomalies. |
| Application Scenarios | Efficiency decline or leakage fault diagnosis in hydraulic systems, suitable for internal system mechanisms. | Fault classification and early warning, suitable for nonlinear systems. | Detection of sensor faults or control system abnormalities, suitable for linear time-invariant systems. |
| Diagnostic Paradigm | Data-Driven | ||
|---|---|---|---|
| Specific Methods | Traditional machine learning. | Deep learning. | Transfer learning. |
| Advantages | Simple architecture, high classification performance, and strong noise immunity; can handle multivariate data. | Automatically extracts features, avoiding manual interference; excellent capability for processing high-dimensional data. | Can adapt to new scenarios or small data, reducing training requirements and data dependency. |
| Disadvantages | High computational complexity, requires large training data; parameter selection is ambiguous; decision process is opaque. | “Black box” nature leads to unclear decisions; long training time; stability affected by gradient issues. | Transfer effect depends on similarity between source and target; accuracy may be unstable in new environments. |
| Signal Type | Vibration and feature values. | Vibration images, time-series signals, and multi-source data. | Vibration, images, and multi-source. |
| Real-time Capability | High. | Low (training)/Medium (application). | Medium. |
| Typical Applicable Faults | Bearing wear, misalignment, and impeller imbalance. | Compound faults, deep-seated faults, and unknown faults. | Cross-condition faults and small-sample faults. |
| Application Scenarios | Fan fault diagnosis in ventilation systems, suitable for situations with labeled historical data. | End-to-end intelligent diagnosis and prediction in industrial systems, suitable for big data scenarios. | Cross-condition diagnosis in industrial systems, solving small-sample and zero-shot problems. |
| Diagnostic Paradigm | Information Fusion | ||
|---|---|---|---|
| Specific Methods | Data-level fusion. | Feature-level fusion. | Decision-level fusion. |
| Advantages | Fuses raw data, complete information retention, and theoretically highest accuracy. | Reduces data dimensionality; strong robustness, can handle partial information loss. | Highest fault tolerance, can handle uncertainty; friendly to asynchronous sensors. |
| Disadvantages | Large data volume and complex processing; susceptible to noise and synchronization issues; high computational overhead. | Improper feature extraction may cause information loss; complex fusion algorithm selection. | Maximum information loss; decision delay may affect real-time performance. |
| Signal Type | Multi-source heterogeneous (Vibration + Pressure + Current). | Multi-source features. | Multi-source decisions. |
| Real-time Capability | Low. | Medium. | High. |
| Typical Applicable Faults | Multiple faults. | Compound faults. | System faults. |
| Application Scenarios | Offline precision analysis and in-depth study of failure mechanisms. | Most commonly used in online monitoring and diagnostic systems, balancing performance and efficiency. | Final decision-making in high-reliability requirements and fault-tolerant control systems. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, W.; Ma, S.; Zou, Z.; Fu, B.; Ma, J.; Liu, J.; Zhang, Q. Literature Review on Fault Mechanism Analysis and Diagnosis Methods for Main Pump Systems. Machines 2025, 13, 1000. https://doi.org/10.3390/machines13111000
Ma W, Ma S, Zou Z, Fu B, Ma J, Liu J, Zhang Q. Literature Review on Fault Mechanism Analysis and Diagnosis Methods for Main Pump Systems. Machines. 2025; 13(11):1000. https://doi.org/10.3390/machines13111000
Chicago/Turabian StyleMa, Wensheng, Shoutao Ma, Zheng Zou, Benyuan Fu, Jinghua Ma, Junjiang Liu, and Qi Zhang. 2025. "Literature Review on Fault Mechanism Analysis and Diagnosis Methods for Main Pump Systems" Machines 13, no. 11: 1000. https://doi.org/10.3390/machines13111000
APA StyleMa, W., Ma, S., Zou, Z., Fu, B., Ma, J., Liu, J., & Zhang, Q. (2025). Literature Review on Fault Mechanism Analysis and Diagnosis Methods for Main Pump Systems. Machines, 13(11), 1000. https://doi.org/10.3390/machines13111000







