Prediction of Cutting Parameters in Band Sawing Using a Gradient Boosting-Based Machine Learning Approach

Abstract

This study presents a gradient boosting-based machine learning (ML) approach developed to predict cutting speed and feed rate in band sawing operations. The model was built using a dataset of 1701 experimental samples from three industrially common material types: AISI 304, CK45, and AISI 4140. Each sample was defined by key process parameters, namely, material type, a hardness range of 15–44 HRC, and a diameter range of 100–500 mm, with cutting speed and feed rate as target variables. Five ML models were examined and compared in this study, including linear regression (LR), support vector regression (SVR), random forest regression (RFR), least squares boosting (LSBoost), and extreme gradient boosting (XGBoost). Model training and validation were carried out using five-fold cross-validation. The results show that the XGBoost model offers the highest accuracy. For cutting speed estimation, the performance values of XGBoost are an RMSE of 0.213, an MAE of 0.140, an R² of 0.999, and an MAPE of 0.407%; and for feed rate estimation, an RMSE of 0.259, an MAE of 0.169, an R² of 0.999, and a MAPE of 1.14%. These results indicate that gradient-based ensemble methods capture the nonlinear behavior of cutting parameters more effectively than linear or kernel-driven techniques, providing a practical and robust approach for data-driven optimization in intelligent manufacturing.

1. Introduction

Band saw machines are a fundamental tool in modern manufacturing, capable of cutting a wide range of materials, including metals and composites [1]. Their precision cuts, high production speeds, and energy-efficient operation capabilities make them particularly valuable in the metalworking and machining industries [2]. However, the cutting performance of band saw machines is significantly influenced by a set of critical parameters such as cutting speed, feed rate, blade characteristics, material type, hardness, and diameter [3]. These parameters directly affect results such as cutting force [4], tool life [5], and surface quality [6], which are critical to maintaining operational efficiency and product quality.

The selection and optimization of these cutting parameters have traditionally been based on manual adjustments, which often lead to inconsistencies, especially when dealing with variable material conditions [7]. For example, hard materials such as high-carbon steels typically require lower cutting speeds to reduce tool wear and ensure dimensional accuracy. In contrast, soft materials, such as aluminum alloys, benefit from higher speeds for higher productivity [8,9]. Similarly, feed rate is decisive in material removal efficiency and mechanical load on the cutting tool. Incorrect parameter settings can lead to increased energy consumption, shortened cutting tool life, and the deterioration of surface integrity, including increased roughness, micro-cracks, residual stresses, microstructural alterations, and hardness variations [10]. These issues underscore the critical importance of accurate parameter estimation. Ultimately, a comprehensive understanding of material properties equips manufacturers to make informed decisions regarding tool specifications, leading to improved operational outputs and sustainability in band sawing practices.

Despite their widespread industrial use, research on optimizing cutting parameters for band saw machines remains limited compared to other machining processes, such as turning and milling [11,12,13]. While existing studies often focus on analytical methods or finite element modeling [14,15], these approaches are either computationally expensive or poorly adapted to real-time operational variability. Recent advances in data-driven approaches such as machine learning (ML) and regression-based prediction models offer promising solutions to overcome these challenges [16,17,18]. These methods present a compelling alternative, offering enhanced predictive accuracy and the generalization capacity across diverse material-process combinations.

To overcome these limitations, this study presents a gradient boosting (GB)-based ML framework that reliably predicts critical band sawing parameters—namely, cutting speed and feed rate. The model uses easily accessible material properties such as type, hardness, and diameter. To evaluate this framework, the performance of the XGBoost and LSBoost models, which represent the GB family, was analyzed comparatively with kernel-based support vector regression (SVR), bagging-based random forest regression (RFR), and linear regression (LR) models as the baseline. This comparative structure is designed to identify the best performer and elucidate the relative strengths of different algorithmic strategies for capturing complex and nonlinear relationships underlying the process. All models were trained and optimized using a specialized dataset of three significant materials (AISI 304, CK45, and AISI 4140) through a nested cross-validation (CV) scheme. The findings demonstrate the strong potential of GB-based ML approaches for modeling the complex, nonlinear relationships between material characteristics and optimal cutting parameters, especially when compared to linear, bagging-based, and kernel-based methods. This study aims to provide valuable insights for integrating intelligent parameter recommendation systems in practical manufacturing environments. Consequently, this approach has the potential to contribute to improved decision making and operational sustainability.

2. Related Works

In recent years, the accurate estimation and optimization of cutting parameters have gained significant attention in machining processes. Although many studies have investigated turning, milling, and drilling operations, research focusing on band sawing machines remains relatively limited. The studies reviewed in this section are grouped as (i) ML-based predictive modeling, (ii) cutting force and tool wear prediction, and (iii) optimization of cutting performance parameters using hybrid and analytical methods.

Saglam et al. [19] combined the Taguchi method with an artificial neural network (ANN) to predict tooth wear in band saw blades. The model was trained with process parameters such as cutting speed, feed rate, cutting length, and material hardness. The study demonstrated the efficacy of the ANN model, trained using a backpropagation algorithm, in accurately estimating tooth wear. Li et al. [17] proposed a deep learning framework based on convolutional neural networks (CNNs) to optimize cutting parameters and minimize tool wear in band sawing processes. Their model effectively captured the nonlinear interactions between input variables and tool life, showcasing the potential of CNNs for predictive modeling in sawing operations. Makhfi et al. [16] explored several ML models, including Gaussian process regression (GPR) and decision tree regression, to predict cutting forces during the turning of AISI 52100 steel. GPR outperformed other models’ accuracy, with strong potential for managing heat generation and tool wear. Khrouf et al. [20] studied the turning of EN AW-1350 aluminum alloy and compared six regression models. XGBoost achieved the highest predictive accuracy (R² = 1.000), indicating its robustness for estimating surface roughness and optimizing cutting parameters.

Chuchala et al. [21] analyzed the cutting forces in band sawing of pine and beech wood subjected to different drying methods. Using the Atkins model, the authors emphasized the influence of material-specific properties such as fracture toughness and shear yield stress on cutting demands. Jurkovic et al. [22] compared SVR, polynomial regression, and ANN models for predicting surface roughness, cutting force, and tool life in high-speed turning. The results showed that polynomial regression was superior in estimating surface roughness and cutting force, while ANN was more effective for tool life prediction. Bhuiyan et al. [23] applied response surface methodology (RSM) and genetic algorithms (GAs) to optimize cutting speed, feed rate, and depth of cut in the turning of AISI 1040 steel. The study achieved a 99.66% prediction accuracy for cutting force while significantly reducing energy consumption.

Tayisepi et al. [24] developed an integrated energy use optimization and cutting parameter prediction tool model for optimizing energy consumption and cutting parameters in CNC lathes. The system, built using MATLAB’s GA platform and a Visual Basic application, reported up to a 30% reduction in energy usage while improving machining performance. Kuntoğlu et al. [25] conducted a multi-objective optimization study on AISI 5140 steel turning using quadratic regression and RSM. The analysis revealed that feed rate was the dominant factor affecting surface roughness and axial vibrations, while the cutting edge angle and cutting speed influenced radial and tangential vibrations, respectively. Similarly, Camposeco-Negrete [26] employed the RSM and desirability analysis to optimize cutting speed, feed rate, and depth of cut in the rough turning of AISI 6061 T6 aluminum. That study aimed to simultaneously minimize specific energy consumption and surface roughness. Experimental results showed that a feed rate of 0.14 mm/rev, a depth of cut of 2.30 mm, and a cutting speed of 434 m/min yielded the best trade-off between energy efficiency and surface quality.

These studies highlight the increasing significance of ML and data-driven approaches in machining. Although there is extensive literature on turning and milling operations, systematic and parametric estimation studies for band sawing have not yet been conducted sufficiently. To address this, the present study aims to develop prediction models based on material properties that can directly and accurately estimate band saw cutting parameters.

3. Materials and Methods

3.1. Dataset Description

The dataset used in this study was generated using a web-based parametric recommendation interface developed by WIKUS-Sägenfabrik (Spangenberg, Germany), a manufacturer specializing in industrial saw cutting tools. This platform allows users to input material type, hardness level, and diameter, and it provides recommended values for cutting speed (m/min) and feed rate (mm/min). In addition to the toolmaker-provided recommendations, the dataset was refined and validated through cutting trials and parameter optimization studies conducted by BEKAMAK (Bursa, Türkiye), a certified R&D center and manufacturer specializing in band sawing technologies. This integration ensured that the final dataset reflects expert-driven recommendations and experimentally verified field data obtained under real-world production conditions.

In total, 1701 samples were compiled, each representing a unique material type, hardness level, and diameter combination. These parameters are known to affect cutting dynamics in band sawing operations significantly. The workpieces modeled in this study were solid cylindrical bars, and the material diameter was used as the primary geometric parameter. The dataset included three commonly used industrial materials: AISI 304, CK45, and AISI 4140. These materials were selected due to their widespread industrial use and distinct metallurgical and mechanical properties, enabling comprehensive analysis across a wide range of machinability and hardness characteristics. The dataset was balanced across material categories, with each of the three material types represented by 567 samples, ensuring equal distribution and avoiding model bias toward any specific material class.

The two continuous target variables to be predicted were cutting speed (S) and feed rate (F). Material hardness values were provided in the Rockwell C hardness scale (HRC) and ranged from 15 to 44 HRC. Based on hardness conversion standards [27], specimens with hardness values below 20 HRC were classified as annealed. The remaining specimens, with hardness levels of 27, 32, 35, 38, 41, and 44 HRC, were considered unannealed and represent varying degrees of cold-working or heat treatment. Material diameters varied uniformly between 100 and 500 mm, in increments of 5 mm, offering a broad and balanced basis for analyzing the effect of geometry on cutting performance.

3.2. Experimental Setup and Measurement System

The tests were performed using a BEKAMAK BMSO 570 XS model (Bursa, Türkiye). The machine setup used in the experiments is shown in Figure 1. The main electrical and mechanical specifications of the machine are summarized in

Table 1. Specifications of the band sawing machine used in the experiments.

Specification	Value	Unit
Main drive motor	15	kW
Hydraulic motor	2.2	kW
Feeder servo motor	2	kW
Head servo motor	1.5	kW
Blade speed range	15–150	m/min
Blade dimension	7400 × 54 × 1.6	mm
Cutting capacity (round material)	570	mm
Cutting capacity (rectangular material)	600 × 570	mm
Cutting capacity (square material)	570 × 570	mm
Working height	805	mm
Machine weight	5900	kg
Coolant pump	0.12	kW
Chip conveyor	0.25	kW
Dimensions (L × W × H)	3540 × 2190 × 2700	mm

. The cutting capacity covers circular bars up to 570 mm in diameter.

During the validation trials, cutting speed and feed rate data were acquired directly from the drive system of the band sawing machine using industrial communication (Modbus TCP/IP). The rotational speed of the main drive motor was read from the inverter feedback and converted into the corresponding cutting speed within the programmable logic controller (PLC) using a predefined gear ratio. Similarly, the speed of the head servo motor, which drives the feed motion through a lead screw mechanism, was converted into the actual feed rate by applying the respective lead screw pitch constant. An OMRON NJ101-1000 PLC (Kyoto, Japan) was the central data acquisition, synchronization, and logging unit. The controller performed these operations using an Ethernet interface using the continuous data trace function of Sysmac Studio v1.52. The recorded data were stored in the .csv format and processed for validation and analysis.

3.3. Regression Models

In this study, an ML framework based on the GB approach was adopted to predict two important operational parameters, cutting speed and feed rate, associated with the band sawing process. Focusing on GB ensemble models such as LSBoost and XGBoost, this approach is designed to allow the performance of these methods to be compared with kernel-based SVR, bagging-based RFR, and linear baseline model LR. Therefore, the performance of GB models was evaluated according to their internal metrics and compared with other models that employ different algorithmic approaches. In this context, LR was included in the model as a baseline. LR establishes a reference point that illustrates the linearity of the problem. The performance of more complex models is evaluated based on how much they exceed this baseline. As a competitor to GB, RFR offers a strong alternative ensemble method. RFR’s performance reveals the relative effectiveness of a sequential error-correction approach (boosting) for a dataset compared to a parallel tree-building and averaging approach (bagging). Furthermore, SVR, which adopts a fundamentally different strategy for modeling nonlinear relationships, was also included in the comparison. It allows testing the effectiveness of modeling data in high-dimensional space using kernel methods instead of the rule-based approach of tree-based methods. Consequently, the models used in the study were selected to form a systematic comparison structure that tests the performance of GB from different perspectives. The prominence of GB-based methods, namely LSBoost and XGBoost, within this framework stems from their high predictive accuracy and well-established reliability in the literature [28,29,30].

3.3.1. Linear Regression

LR is a classical method in regression analysis that models the relationship between a dependent variable and one or more independent variables through a linear function [31]. It is frequently applied in predictive modeling to estimate continuous target values based on explanatory variables [32]. The prediction function can be expressed as Equation (1):

$$\widehat{y}={\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b$$

(1)

where x ∈ ℝ^d represents the input feature vector, w ∈ ℝ^d denotes the vector of model coefficients, and b is the bias term. The parameters are estimated by minimizing the sum of squared differences between the predicted and actual target values, typically using the ordinary least squares method. Despite its simplicity and interpretability, LR may perform poorly when the underlying relationship between inputs and outputs is nonlinear or when interactions among variables are not explicitly modeled [31].

3.3.2. Support Vector Regression

SVR is a kernel-based supervised learning algorithm that aims to construct a regression function within a specified margin of tolerance ε from the true target values, while maintaining model simplicity [33]. The approach seeks a balance between model complexity and prediction accuracy by employing a sparse representation of the training data in the form of support vectors [34]. The SVR model predicts the output using Equation (2):

$$\widehat{y}=\sum _{i=1}^n\left({\alpha }_i-{\alpha }_i^{*}\right)K({\mathbf{x}}_i,\mathbf{x})+b$$

(2)

where α_i and α_i* are Lagrange multipliers obtained by solving a convex optimization problem, x_i denotes the training samples, x is the input vector, and K(.,.) represents a kernel function allowing nonlinear input space mapping. The most commonly used kernel in SVR is the radial basis function (RBF), which enables the model to capture complex, nonlinear relationships [35]. The hyperparameters C, ε, and kernel parameters must be carefully tuned to optimize the model’s generalization performance [36].

3.3.3. Least Squares Boosting

LSBoost is a powerful ensemble learning algorithm that builds a strong regression model by sequentially combining multiple weak learners, typically decision trees [37]. At each iteration, LSBoost fits a new model to the residual errors of the previous model, aiming to minimize the squared loss between predicted and actual target values. This iterative process allows the ensemble to progressively correct its mistakes, improving overall prediction accuracy [38].

Given a training dataset ${\left\{\left({\mathbf{x}}_i,y_i\right)\right\}}_{i=1}^n$, the final LSBoost model after M iterations is expressed as Equation (3):

$$\widehat{y}(\mathbf{x})=\sum _{m=1}^M{\eta \alpha }_m{h}_m\left(\mathbf{x}\right)$$

(3)

where h_m(x) represents the prediction of the m-th weak learner, typically a shallow decision tree. The term α_m indicates the weight assigned to each weak learner based on performance. At the same time, η is the learning rate (also referred to as the shrinkage factor), which controls the contribution of each learner to the final ensemble prediction. The objective is to minimize the squared error loss (Equation (4)):

$$\mathcal{L}=\sum _{i=1}^n{(y_i-\widehat{y}({\mathbf{x}}_{\mathit{i}}\left)\right)}^2$$

(4)

LSBoost is particularly effective in capturing complex, nonlinear relationships in data while maintaining robustness to overfitting when appropriately regularized [39].

3.3.4. Extreme Gradient Boosting

XGBoost is an advanced gradient boosting framework that extends traditional boosting techniques by incorporating regularization and second-order optimization to improve accuracy and generalization [40]. It constructs an ensemble of regression trees in an additive fashion, where each new tree is trained to minimize a regularized loss function that accounts for the model’s complexity [41].

Given a dataset ${\left\{\left({\mathit{x}}_i,y_i\right)\right\}}_{i=1}^n$, the prediction at iteration t is computed as Equation (5):

$${\widehat{y}}_i^{\left(t\right)}={\widehat{y}}_i^{(t-1)}+f_t\left({\mathbf{x}}_{\mathit{i}}\right)$$

(5)

where f_t denotes the regression tree fitted at iteration t. The overall objective function optimized at each iteration is defined as Equation (6):

$${\mathcal{L}}^{\left(t\right)}=\sum _{i=1}^{n}l\left(y_i-{\widehat{y}}_i^{\left(t\right)}\right)+\sum _{t=1}^T\mathsf{\Omega }\left(f_t\right)$$

(6)

where l is a convex loss function (e.g., squared error), and Ω(f_t) is a regularization term defined as:

$$\mathsf{\Omega }\left(f_t\right)=\gamma T+{\displaystyle \frac{1}{2}}\lambda \sum _{j=1}^T{w}_j^2$$

(7)

where T is the number of leaves in the tree, w_j are the leaf weights, γ controls model complexity, and λ is a regularization parameter. These enhancements make XGBoost highly effective in handling noisy datasets and improving generalization [42].

3.3.5. Random Forest Regression

RFR is an ensemble learning method based on decision trees; it aims to improve predictive performance by aggregating the outputs of multiple uncorrelated trees [43]. Unlike boosting methods that build trees sequentially, RFR constructs each decision tree independently using a randomly sampled subset of the training data and features, a process known as bootstrap aggregation or bagging [44]. This randomness introduces diversity among trees and helps reduce overfitting while maintaining high prediction accuracy [45].

The prediction of a RFR model with M individual regression trees ${\left\{\left(h_m\left(x\right)\right)\right\}}_{m=1}^M$ is computed as the average of their outputs (Equation (8)):

$$\widehat{y}(\mathbf{x})={\displaystyle \frac{1}{M}}\sum _{m=1}^M{h}_m\left(\mathbf{x}\right)$$

(8)

where h_m(x) represents the prediction from the mth tree for input x, and M is the total number of trees in the forest. Randomized feature selection and bagging make RFR robust to noise and effective for modeling complex nonlinear relationships, particularly in high-dimensional data [46].

While the LR model relies on an analytical solution and does not require hyperparameter tuning, the remaining models (SVR, LSBoost, XGBoost, and RFR) were subjected to a tuning procedure to optimize their predictive performance. Details regarding the hyperparameter selection strategy are provided in Section 3.4.

3.4. Model Training and Hyperparameter Tuning

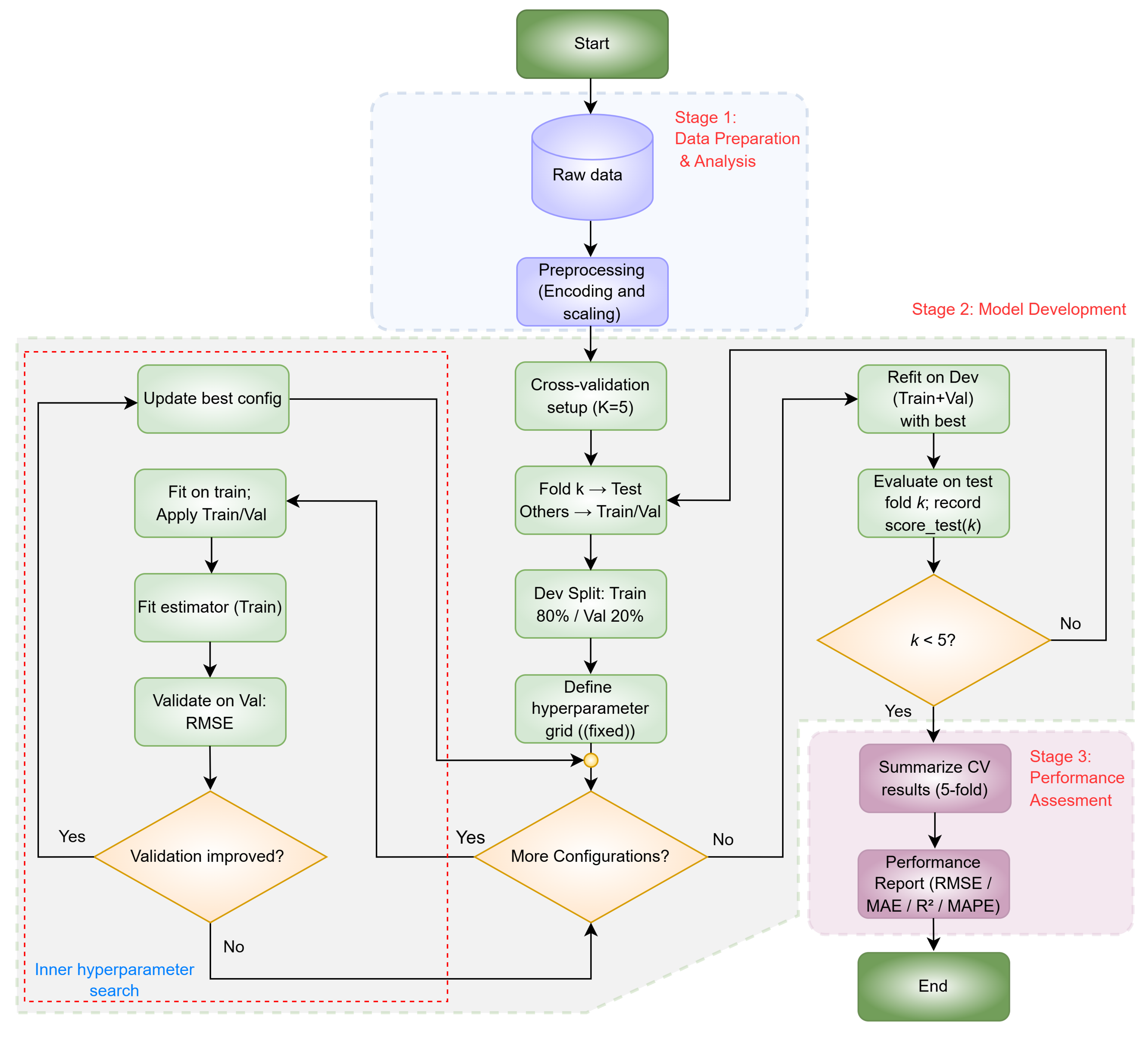
This section covers the most critical stages that shape final predictive performance and provides a systematic evaluation of the generalization capabilities of the investigated models. This evaluation was conducted based on a modeling system founded on nested CV. This framework follows the comprehensive workflow illustrated in Figure 2, which progresses through three main stages: data preparation, model development, and performance evaluation.

This approach’s foundation is an ML strategy based on the GB algorithm, which stands out because it effectively captures complex nonlinear relationships. To objectively test this potential, the performance of LSBoost and XGBoost models was compared with kernel-based SVR, bagging-based RFR, and the linear baseline model LR, which have different algorithmic foundations. In this comprehensive architecture, summarized in Figure 2 and including hyperparameter optimization, the optimization step was excluded for the LR model, while the same methodological consistency was maintained for all other models. Through the comprehensive hyperparameter tuning conducted within the nested CV structure, all models included in the comparison were evaluated using the most appropriate hyperparameter settings optimized for each model’s architecture, thus enabling a fair, unbiased, and comparable performance analysis.

3.4.1. Stage 1: Data Preparation and Analysis

The process begins with acquiring raw data originating from band sawing operations, as outlined in Section 3.1. This dataset contains both categorical and numerical input variables. During this initial stage, categorical inputs, particularly the material type, are converted into binary vector representations through one-hot encoding. For example, the material classes AISI 304, CK45, and AISI 4140 are encoded respectively as [1 0 0], [0 1 0], and [0 0 1]. This transformation prevents the model from inferring any unintended ordinal relationship between distinct material categories.

In parallel, continuous variables such as material diameter and hardness value are subjected to scaling to align all numeric features within a comparable range. This step enhances numerical stability, prevents features with larger magnitudes from dominating the training process, and accelerates the convergence of the optimization algorithms used during model fitting. Overall, this stage establishes a standardized and model-compatible dataset structure, thereby enabling the development of robust and generalizable prediction models in subsequent stages.

3.4.2. Stage 2: Model Development

Following the preprocessing stage, the prepared dataset was used to develop regression models to predict cutting speed and feed rate. In this study, the selected regression models (SVR, RFR, LSBoost, and XGBoost) were tuned and evaluated according to the flowchart shown in Figure 2, which includes hyperparameter optimization and model training stages. In addition, the LR model is used as a baseline. It shows potential non-linear relationships between the input variables and the target outputs. The model development steps shown in the flowchart are explained in detail below:

The model development stage is designed to systematically select the best-performing configuration and obtain an unbiased generalization performance estimate. The process consists of two main components: an inner search for hyperparameter selection and an outer k-fold CV for evaluating model generalization.

First, the data were partitioned with a fixed random seed into K = 5 folds, and the fold assignments were held fixed throughout all experiments. In each outer iteration (k = 1,…,5), the development set (Dev) was defined by the union of all folds other than the k-th (test) fold, while the k-th fold was held out exclusively for testing. For hyperparameter optimization within that iteration, Dev was randomly split into 80% training (Train) and 20% validation (Val). A predefined, fixed hyperparameter grid was then searched exhaustively. For each candidate configuration, all preprocessing transforms fit on the train set (Train) and were then applied to transform the training and validation sets to avoid data leakage. The model was then trained on the preprocessed training set and evaluated on the preprocessed validation set. For each candidate configuration in the inner hyperparameter search, the preprocessing pipeline defined in Stage 1 was fit using only the training subset of the current outer iteration’s Dev set and then applied to both the training and validation subsets to prevent data leakage. The estimator was subsequently trained on the preprocessed training subset and evaluated on the preprocessed validation subset. After the best configuration had been identified, the same preprocessing pipeline was refit on the development set, the union of the training and validation subsets (Train + Val), and applied to the held-out test fold (Test) before computing the final performance metrics. During the inner hyperparameter search, the root mean square error (RMSE) served as the optimization objective. Because LR has no tunable hyperparameters, the inner grid-search loop was omitted for LR; however, the outer cross-validation and the leakage-free preprocessing strategy were applied uniformly to all models, including LR.

After the hyperparameter optimization on the Dev set of the current outer iteration, a refit on the Dev set was performed: the training and the validation subsets (Train and Val) were merged to form the Dev set; the preprocessing pipeline was refit on this Dev set; and the estimator was retrained on the Dev set using the previously selected best configuration (best_config), without further hyperparameter tuning. The held-out test fold (Test) was then transformed using the preprocessing pipeline fit on the Dev set, predictions were generated, and RMSE, mean absolute error (MAE), coefficient of determination (R²), and mean absolute percentage error (MAPE) were computed and stored as the test score for iteration k (score_test(k)). This procedure was repeated for all outer iterations (k = 1,…,5). This two-layer design enabled a consistent assessment of model performance across distinct data subsets.

In summary, optimizing hyperparameters on an inner validation split and estimating final performance using a stringent outer CV improved the robustness and reliability of the reported results. All steps were executed separately for the cutting speed and feed rate targets under the same methodological framework. The optimal hyperparameter sets determined for each ML model are summarized in

Table 2. Optimal hyperparameters for each regression model.

Model	Hyperparameter	Optimal Values
SVR	Kernel	RBF
	C	4000
	ε	0.3
LSBoost	Number of estimators	450
	Learning rate	0.15
	Max depth	4
RFR	Number of trees	160
	Min samples split	2
	Max depth	13
	Max features	sqrt
XGBoost	Number of estimators	320
	Learning rate	0.3
	Max depth	4
	Gamma (γ)	0
	Regularization (λ)	1

.

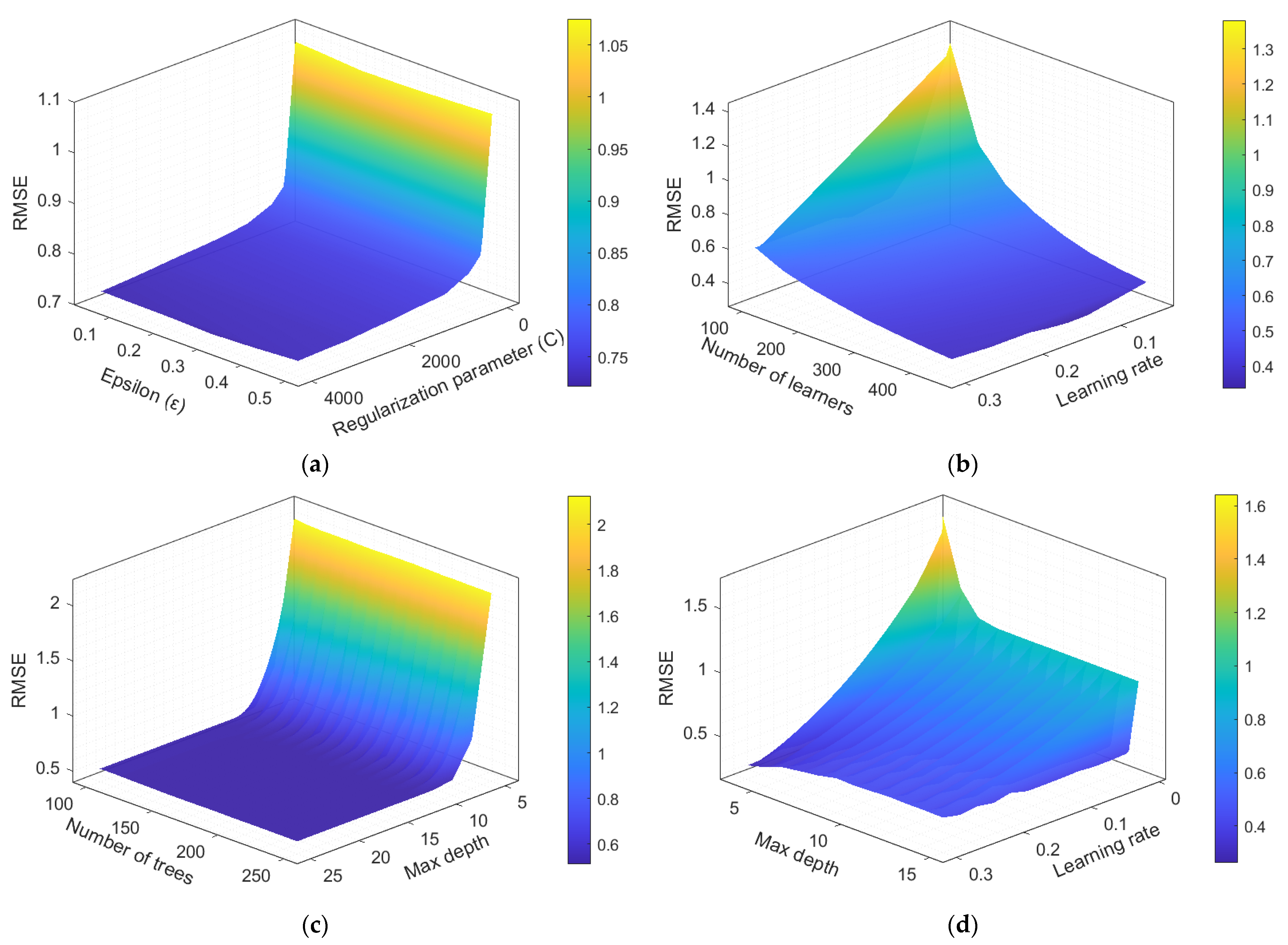
To provide further insight into the hyperparameter space and model sensitivity, Figure 3 presents 3D response surfaces of the validation performance (e.g., RMSE) over selected hyperparameter pairs. These plots clarify how specific settings influence the inner-search validation scores and, by extension, guide model selection. Within each outer cross-validation iteration, once the optimal hyperparameters were identified, the estimator was refit on the development set, the union of the training and validation subsets, and then evaluated on the held-out test fold.

3.4.3. Stage 3: Performance Assessment

In the final stage, the test results obtained from each iteration of outer CV were combined to summarize and report the final model performance. For each fold, the RMSE, MAE, R², and MAPE values were computed; their arithmetic means across the five folds are reported as the final performance metrics. This cross-fold design allows for the evaluation of the consistency of performance across different subsets of the data. The evaluation was conducted separately for each target variable (cutting speed and feed rate) within the same methodological framework. The mathematical definitions of the relevant metrics are given in Equations (9)–(12):

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}\sum _{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}$$

(9)

$$MAE={\displaystyle \frac{1}{n}}\sum _{i=1}^n\left|y_i-{\widehat{y}}_i\right|$$

(10)

$$MAPE={\displaystyle \frac{100}{n}}{\displaystyle \sum _{i=1}^n}\left|{\displaystyle \frac{y_i-{\widehat{y}}_i}{y_i}}\right|$$

(11)

$$R^2=1-{\displaystyle \frac{\sum _{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}{\sum _{i=1}^n{\left(y_i-\overline{y}\right)}^2}}$$

(12)

where y_i represents the actual cutting speed or feed rate of the i-th sample, ${\widehat{y}}_i$ denotes the corresponding predicted values, and n is the total number of samples. $\overline{y}$ refers to the mean of the actual values across all samples.

RMSE quantifies the standard deviation of prediction errors, reflecting how closely the predicted values align with the actual observations. Lower RMSE indicates better predictive precision, with values approaching zero denoting higher model accuracy [47]. MAE measures the average magnitude of prediction errors, regardless of their direction. Unlike RMSE, it does not disproportionately penalize larger errors, making it a robust and interpretable indicator of overall prediction bias. Lower MAE values indicate enhanced predictive performance [48]. R² ranges from 0 to 1, where higher values signify that a greater proportion of the variance in the observed data is captured by the model’s predictions, thereby indicating stronger predictive capability [48]. MAPE captures the average percentage deviation between predicted and actual values, offering an interpretable metric for assessing model accuracy. Smaller MAPE values indicate greater predictive precision and reliability, with zero representing a perfect prediction [47,49]. In general, MAPE values can be interpreted using the following thresholds: values less than or equal to 10% indicate high prediction accuracy, values between 10% and 20% suggest good predictive performance, values between 20% and 50% reflect reasonable accuracy, while values exceeding 50% are considered indicative of poor model reliability [50,51].

4. Results and Discussions

4.1. Data Overview and Descriptive Statistics

The dataset generation process, structure, and variable definitions are explained in detail in Section 3.1. This section focuses on presenting the statistical properties of the input features and exploring their relationships with the target variables. The input features, material type, hardness (HRC), and diameter (mm), were used to predict cutting speed and feed rate in band sawing operations. Summary statistics for the continuous features are provided in

Table 3. Descriptive statistics of the input features used in the study.

Feature	Unit	Min	Max	Mean	Standard Deviation
Material hardness	HRC	15	44	33.14	9.06
Material diameter	mm	100	500	300	116.93

, while 3D scatter plots in Figure 4 illustrate the combined effects of material properties and geometry on machining behavior.

As shown in Table 3, the hardness values range from 15 to 44 HRC, with a mean of 33.14 and a standard deviation of 9.06. Material diameters span from 100 mm to 500 mm, with a mean of 300 mm and a standard deviation of 116.93 mm, reflecting a well-distributed range of geometries.

As visualized in Figure 4, the 3D scatter plots provide insight into the relationships between the selected input parameters and the target output variables. Figure 4a shows a clear inverse relationship between material hardness and cutting speed across all material types. This finding is consistent with the well-established machining principle that increased hardness typically leads to reduced machinability, necessitating lower cutting speeds. Moreover, for a fixed hardness value, an increase in diameter correlates with a modest reduction in cutting speed, indicating the influence of cross-sectional area on cutting performance. Among the three materials, CK45 and AISI 4140 generally exhibit higher cutting speeds than AISI 304, likely due to differences in their metallurgical structure and thermal properties. Similarly, Figure 4b demonstrates that material hardness also negatively affects feed rate. Higher hardness levels consistently result in lower feed rates. However, the effect of diameter is more pronounced in feed rate behavior than in cutting speed. In particular, CK45 and AISI 4140 exhibit a sharper decline in feed rate as diameter increases, reflecting the adaptive toolpath and feed rate adjustments commonly made during machining to maintain process stability and extend tool life.

These visualizations confirm that all three input variables substantially impact the output responses. Their inclusion in the regression modeling framework is therefore well justified. Additionally, the observed trends reveal the non-linear and material-dependent nature of the relationships, further emphasizing the necessity for robust and flexible predictive models.

4.2. Cutting Speed Prediction

In the first stage of the study, regression models were developed to predict the cutting speed of band saw operations based on three input features: material type, material hardness (HRC), and material diameter (mm). Cutting speed (m/min) was used as the dependent variable (output). Five regression algorithms were implemented and evaluated comparatively: LR, SVR, LSBoost, RFR, and XGBoost. To ensure a fair and statistically reliable performance comparison, all models were trained and validated using the same set of input features within a consistent five-fold CV scheme.

Table 4. Performance metrics of different regression models for cutting speed prediction.

Model	Mean RMSE	Mean MAE	Mean R2	Mean MAPE (%)
LR	4.640	3.743	0.888	10.57
SVR	0.631	0.483	0.991	1.251
LSBoost	0.439	0.337	0.995	1.043
RFR	0.402	0.195	0.996	0.486
XGBoost	0.213	0.140	0.999	0.407

summarizes each regression model’s average performance metrics obtained from five-fold CV. The reported RMSE, MAE, R², and MAPE values represent the mean scores computed across the five validation folds. Among the tested models, XGBoost outperformed the others in all evaluation metrics, achieving the lowest mean RMSE (0.213), MAE (0.140), and MAPE (0.407%), while maintaining an exceptionally high R² score (0.999). This indicates the model’s strong predictive capability and generalization across different hardness levels and material geometries.

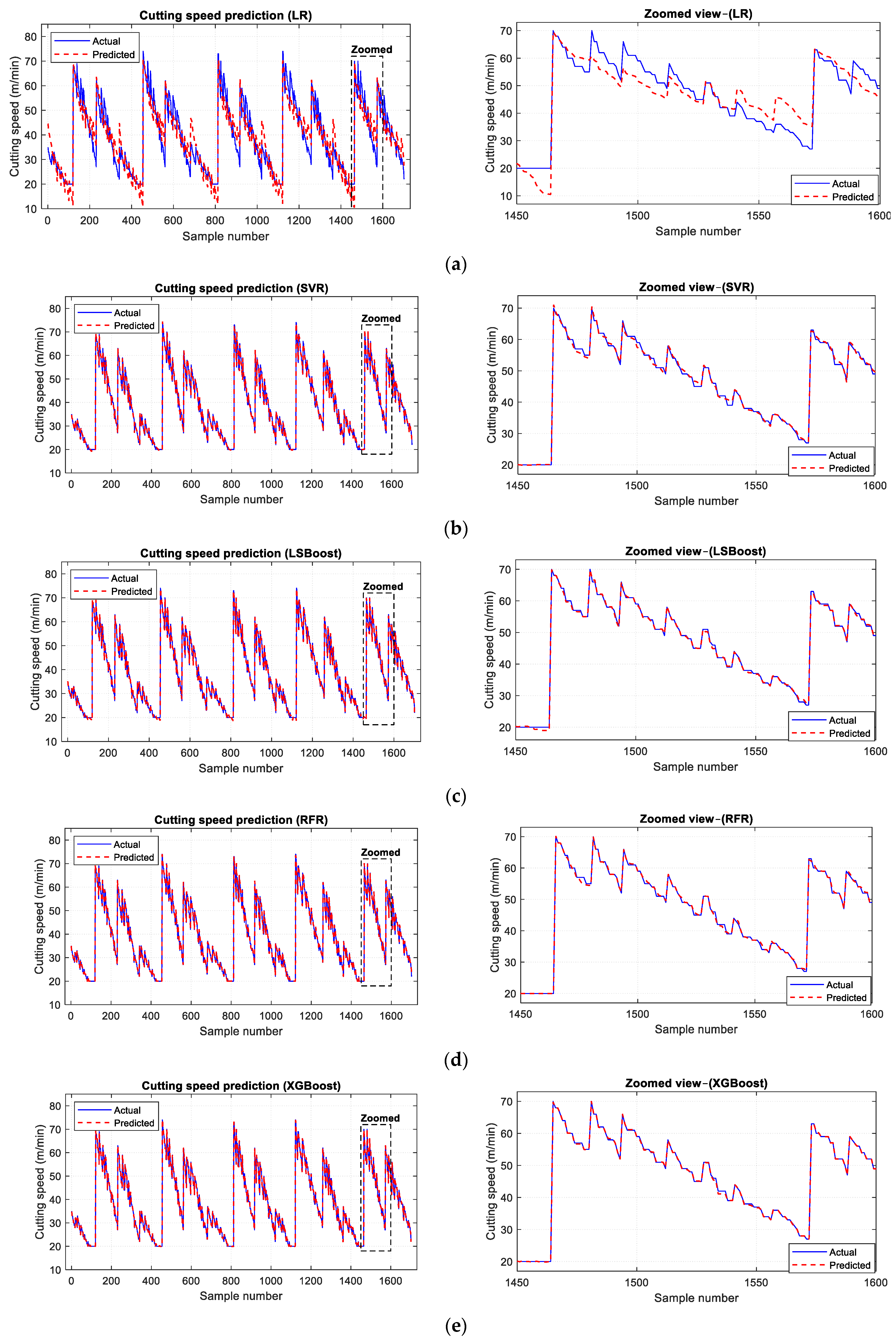
Figure 5 compares the actual and predicted cutting speed values of five regression models. Each subplot presents the full-range prediction performance over the entire sample set, highlighting a selected zoomed-in region to visualize local deviations better. The close overlap between the actual and predicted cutting speeds over the sample range demonstrates the model’s high prediction accuracy and consistency. Among the evaluated models, the GB-based methods (LSBoost and XGBoost) demonstrate superior agreement with the cutting speed trends compared to linear and kernel-based approaches. In particular, Figure 5e shows that the XGBoost model provides the closest match between the actual and predicted cutting speed values, particularly within the zoomed-in region, highlighting its superior prediction accuracy among the tested models.

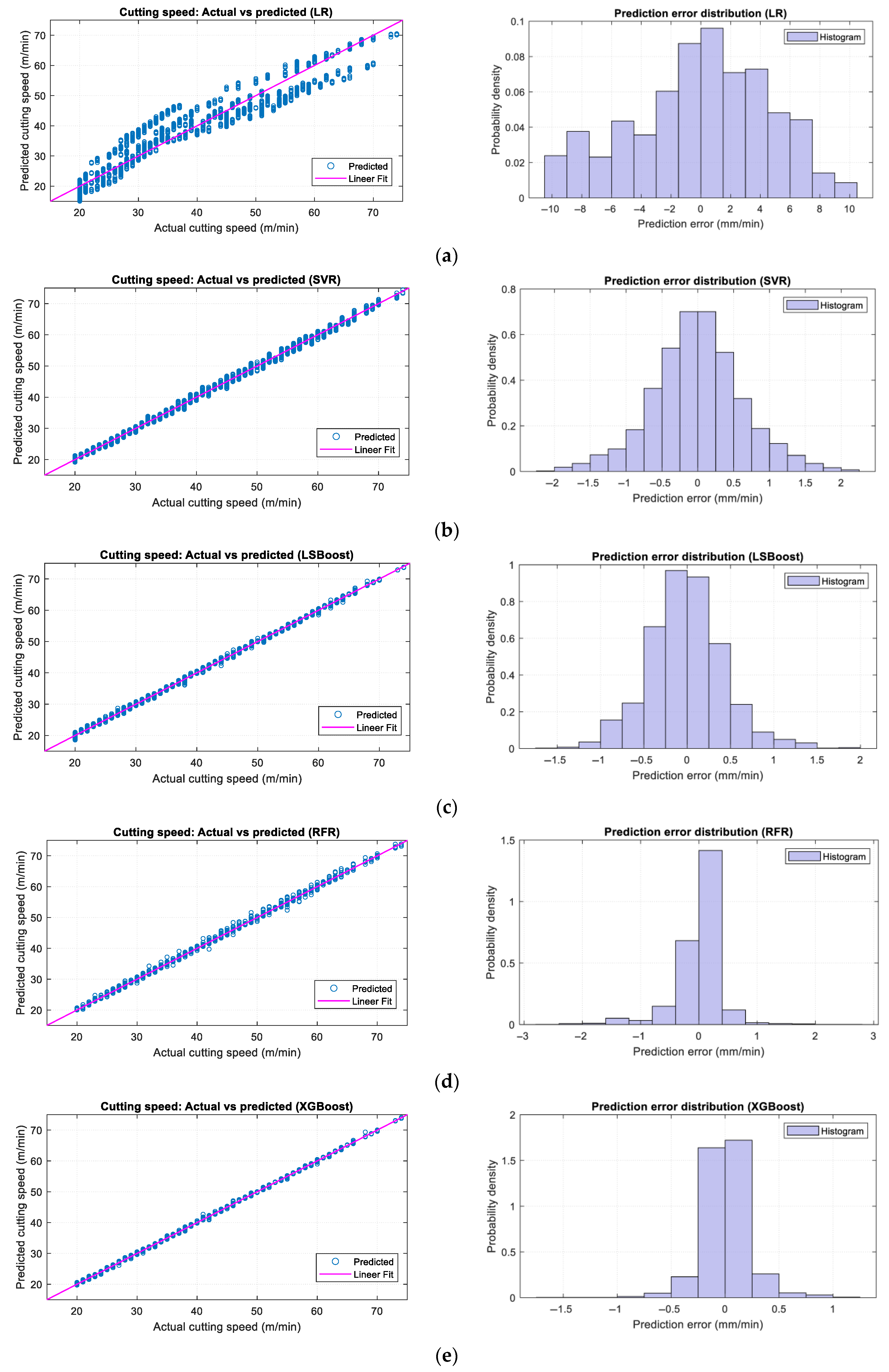
Figure 6 presents a comparative evaluation of five regression models for cutting speed prediction, using parity plots and the corresponding prediction error distributions. Among these models, GB-based approaches, particularly LSBoost and XGBoost, exhibit strong alignment with the ideal diagonal line, indicating high prediction accuracy. The associated error histograms are sharply peaked and centered around zero, suggesting low bias and minimal variance. By contrast, Figure 6a demonstrates that the LR model shows considerable deviations from the reference line, especially in the mid and upper cutting speed ranges. This behavior highlights the absence of a strictly linear relationship between the input features and cutting speed. The corresponding error histogram further supports this observation, revealing a broader and more dispersed error distribution, approximately from −10 to +10 m/min, reflecting greater prediction variability and reduced overall accuracy. The most accurate results are obtained with the XGBoost model, as depicted in Figure 6e. Its parity plot closely aligns with the ideal diagonal, and its error distribution is notably narrow. The prediction errors for XGBoost are predominantly contained within a tight range of approximately −1.5 to +1 m/min, indicating high precision and consistent predictive performance.

4.3. Feed Rate Prediction

In the second stage of the study, regression models were developed to predict the feed rate of band sawing operations based on the same three input features. The target variable in this stage was the feed rate, expressed in millimeters per minute. The same five regression algorithms were employed to ensure consistency with the cutting speed analysis. All models were trained and evaluated using a five-fold CV strategy to obtain statistically robust performance metrics.

Table 5. Performance metrics of different regression models for feed rate prediction.

Model	Mean RMSE	Mean MAE	Mean R2	Mean MAPE (%)
LR	5.299	3.766	0.799	34.271
SVR	0.804	0.526	0.988	2.928
LSBoost	0.489	0.356	0.994	2.703
RFR	0.623	0.365	0.991	1.992
XGBoost	0.259	0.169	0.999	1.140

presents the average performance metrics obtained from five-fold CV for each regression model in the feed rate prediction. Like the cutting speed analysis, the XGBoost model outperformed all other methods across all evaluation criteria. Specifically, XGBoost achieved the lowest mean RMSE (0.259), MAE (0.169), and MAPE (1.14%), along with the highest R² score of 0.999, indicating a high level of prediction accuracy and generalization. In contrast, the LR model yielded the weakest results, with the highest RMSE (5.299), MAE (3.766), and MAPE (34.271%), and a notably lower R² value of 0.799, which points to its limited capacity in capturing the underlying nonlinearities of the problem.

Figure 5. Comparison of the actual and predicted cutting speed for each regression model and the corresponding zoomed-in view: (a) LR; (b) SVR; (c) LSBoost; (d) RFR; (e) XGBoost.

Figure 5. Comparison of the actual and predicted cutting speed for each regression model and the corresponding zoomed-in view: (a) LR; (b) SVR; (c) LSBoost; (d) RFR; (e) XGBoost.

Figure 6. Parity plots and prediction error distributions for each regression model in cutting speed prediction: (a) LR; (b) SVR; (c) LSBoost; (d) RFR; (e) XGBoost.

Figure 6. Parity plots and prediction error distributions for each regression model in cutting speed prediction: (a) LR; (b) SVR; (c) LSBoost; (d) RFR; (e) XGBoost.

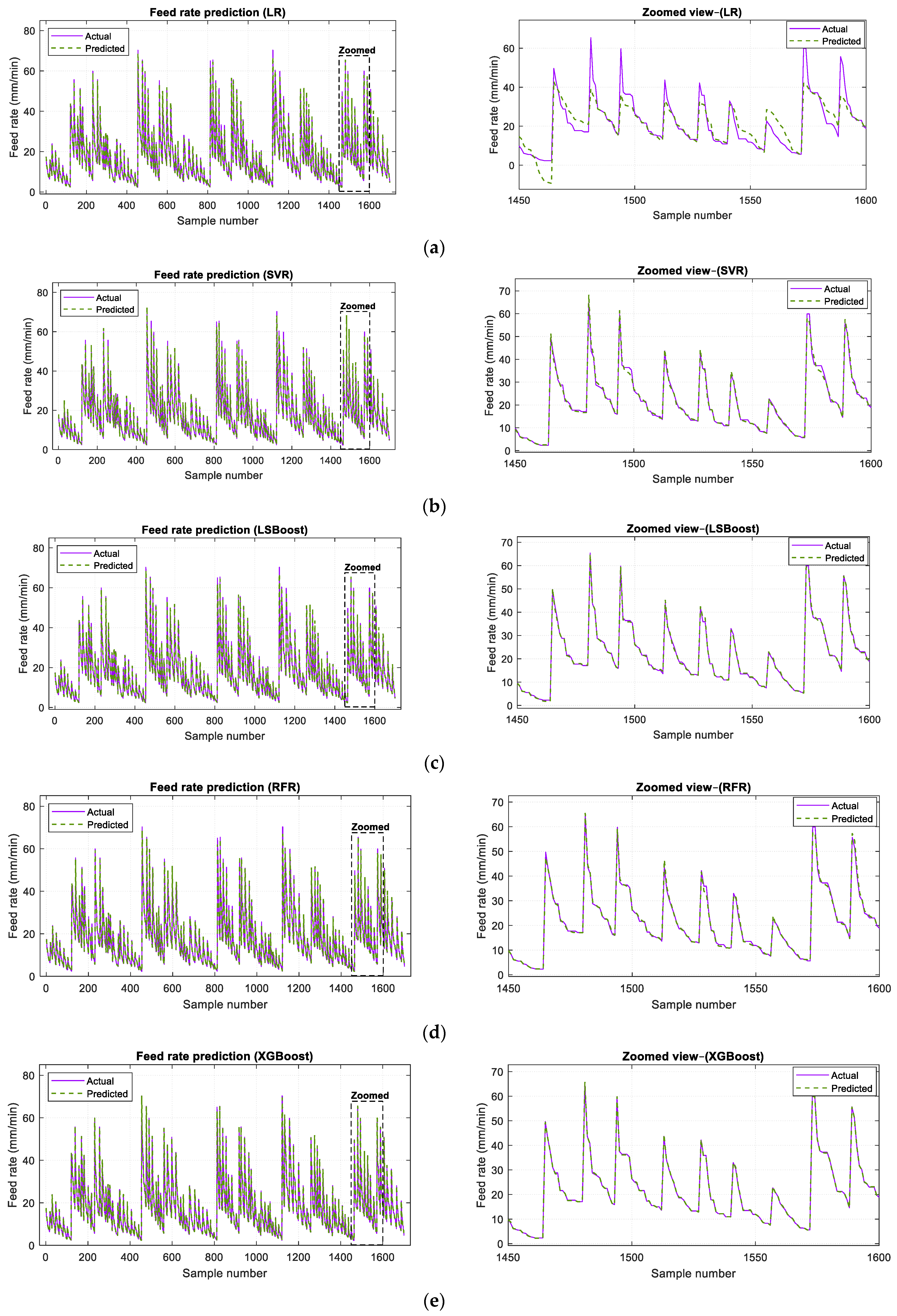
Figure 7 compares actual and predicted values from five different regression models. Each sub-figure shows the overall prediction performance across the entire dataset, with a zoomed-in view highlighting local deviations for detailed evaluation. Similarly, the LSBoost, RFR, and XGBoost approaches strongly agree with the actual feed rate values than the linear and kernel-based alternatives. In particular, Figure 7e shows that the XGBoost model provides the closest match between predicted and actual values, especially within the zoomed region, highlighting its superior performance and robustness in feed rate prediction.

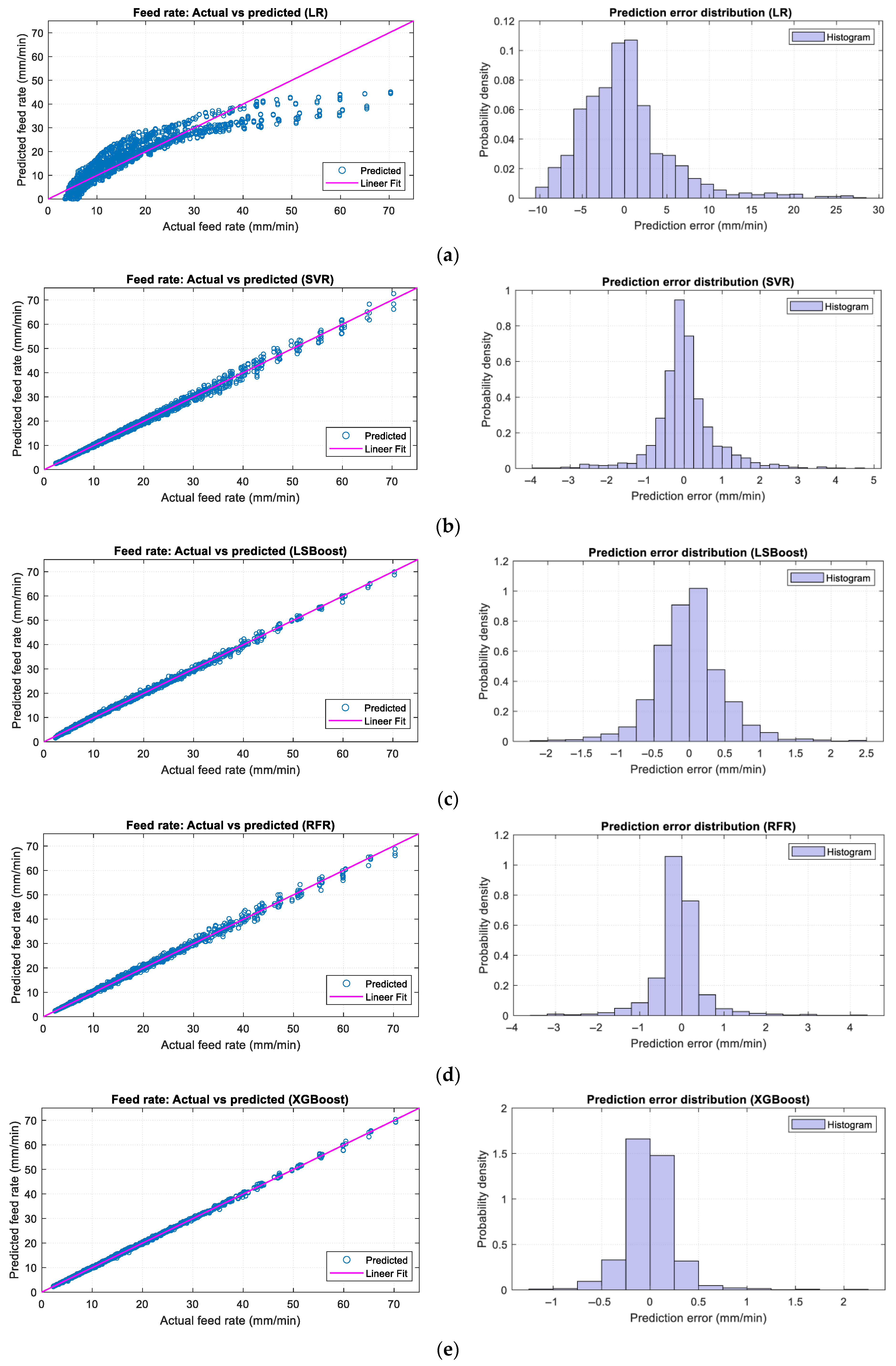
Figure 8 compares the five regression models applied to feed rate prediction, using parity plots alongside their respective error distributions. GB-based models (LSBoost and XGBoost) strongly cluster predicted values around the ideal diagonal, indicating robust predictive performance. Their narrow and symmetrical error histograms further support this visual trend, which suggests low deviation and consistent model behavior across the dataset. In contrast, Figure 8a reveals that the LR model struggles to capture the nonlinear relationship between the input features and feed rate, as evidenced by significant deviations from the reference line. Its associated error histogram displays a broader and more uneven distribution, reflecting higher variability and lower prediction reliability. Among all models, the XGBoost algorithm again demonstrates the best performance, as shown in Figure 8e. Its parity plot reveals a nearly perfect alignment between predicted and actual feed rate values, while its error distribution remains tightly concentrated around zero. Notably, most of the prediction errors for XGBoost lie within a narrow interval of approximately −1 to +1.5 mm/min, highlighting its high accuracy and excellent generalization capability in feed rate estimation.

4.4. Discussion

In this study, the performance of five different ML models was systematically evaluated to predict cutting parameters in the band sawing process. The primary objective in model selection was to systematically compare the effectiveness of different learning strategies on this unique problem.

Evaluation results showed that the LR model’s prediction performance was significantly lower than that of other models. This result confirms that the relationship between the input material properties and the output cutting parameters is inherently nonlinear and complex. The principal value of LR is to clarify this critical fact about the nature of the problem and to support the need for more advanced modeling techniques with concrete data.

Despite its capacity to model non-linear relationships, the SVR model exhibited poorer performance than tree- and GB-based ensemble methods. This result suggests that decision boundaries based on tree structures are more effective than those based on kernel functions for the current problem. The interpretability advantage offered by tree models is also expected to provide significant added value in practical applications.

The generally successful results of ensemble methods reaffirm the power of these techniques in complex engineering problems. RFR demonstrated extremely stable and reliable performance, a typical feature of the bagging method. However, GB algorithms (LSBoost and XGBoost) were more successful in the final performance comparison. It was observed that XGBoost, in particular, achieved the lowest error values and the highest explanatory power in both cutting speed and feed rate predictions, thanks to its advanced regularization techniques and efficient learning mechanism. These findings indicate that XGBoost is the most suitable algorithm for the prediction problems under consideration.

Figure 7. Comparison of the actual and predicted feed rates for each regression model and the corresponding zoomed-in view: (a) LR; (b) SVR; (c) LSBoost; (d) RFR; (e) XGBoost.

Figure 7. Comparison of the actual and predicted feed rates for each regression model and the corresponding zoomed-in view: (a) LR; (b) SVR; (c) LSBoost; (d) RFR; (e) XGBoost.

Figure 8. Parity plots and prediction error distributions for each regression model in feed rate prediction: (a) LR; (b) SVR; (c) LSBoost; (d) RFR; (e) XGBoost.

Figure 8. Parity plots and prediction error distributions for each regression model in feed rate prediction: (a) LR; (b) SVR; (c) LSBoost; (d) RFR; (e) XGBoost.

The methodological approach adopted in the study is also critical for the reliability of the results. The size of the dataset used (n = 1701) provided sufficient training opportunities for the selected GB-based models while keeping the risk of overfitting at a manageable level. Combined with nested CV and comprehensive hyperparameter optimization, this approach increased statistical robustness in model evaluation and strengthened the generalizability of the results.

The most notable practical aspect of the findings is that the developed models can produce highly accurate predictions using only basic and readily available information such as material type, hardness, and diameter. Without complex experiments or detailed physical modeling, a simple software interface integrating a model such as XGBoost can provide real-time recommendations for cutting parameters in production environments. This situation promises concrete benefits such as extending blade life, improving energy efficiency, reducing overall operational costs, and supporting operator decision-making processes. Therefore, this study provides an applicable infrastructure for integrating data-driven decision support systems into production processes.

In conclusion, the multi-model framework established in this research conclusively demonstrates the superiority of GB, specifically the XGBoost algorithm, for predicting band sawing parameters. The systematic comparison approach guiding model selection is expected to provide valuable contributions to academic literature and industrial applications.

5. Conclusions

This study compares five regression-based ML algorithms for predicting cutting speed and feed rate in band sawing operations using material-related input features. The predictive models were trained and validated using a dataset of 1701 samples across three industrially relevant materials, namely AISI 304, CK45, and AISI 4140, characterized by their hardness and diameter. The regression algorithms evaluated include LR, SVR, LSBoost, RFR, and XGBoost, all implemented under a consistent five-fold cross-validation framework.

The significant findings of this research can be summarized as follows:

• Among all tested algorithms, the XGBoost model demonstrated superior predictive performance for cutting speed and feed rate. For cutting speed prediction, it achieved an RMSE of 0.213, an MAE of 0.140, an R² of 0.999, and an MAPE of 0.407%. Similarly, for feed rate prediction, it yielded an RMSE of 0.259, an MAE of 0.169, an R² of 0.999, and an MAPE of 1.140%.
• The success of GB methods was particularly pronounced; the XGBoost algorithm demonstrated superior performance, even against its peer LSBoost. Its advanced regularization and sequential learning mechanism enabled it to capture the complex, nonlinear relationships between material properties and cutting parameters more accurately than linear (LR), bagging-based (RFR), and kernel-based (SVR) alternatives.
• Hyperparameter optimization results were visualized through 3D response surfaces, offering clear insights into parameter sensitivity and performance trends, while parity plots and error histograms provided additional evidence of each model’s robustness.

While the present study offers valuable insights into the prediction of cutting parameters in band sawing operations, certain limitations suggest future improvement opportunities. The predictive models were constructed based on a dataset involving only three material types: AISI 304, CK45, and AISI 4140. Expanding the dataset to include various alloys or composite materials could significantly improve the model’s generalization capacity and broaden its industrial relevance. In addition, the geometrical representation of the workpieces was limited to solid cylindrical bars. Future studies may consider incorporating other geometries, such as hollow profiles, rectangular cross-sections, or irregular forms, to evaluate the robustness of the proposed approach across diverse machining contexts.

Another important consideration is that the ML models were developed and validated in an offline computational environment. For broader applicability, future research could explore deploying these models into embedded systems or predictive maintenance frameworks to support real-time process optimization in manufacturing settings. Including sensor-based information, such as vibration signals, temperature measurements, or current flow data, may also enable the creation of intelligent control mechanisms capable of responding dynamically to changes in operating conditions. Furthermore, incorporating adaptive learning techniques and continuous model updates could enhance the responsiveness and long-term reliability of the predictive system.