Estimation of Railway Track Vertical Alignment Using Instrumented Wheelsets and Contact Force Recordings †
Abstract
1. Introduction
2. State-of-the-Art Review of Equipment and Methods for Railway Condition Monitoring
3. Review of Models and Methods for On-Board Railway Condition Monitoring
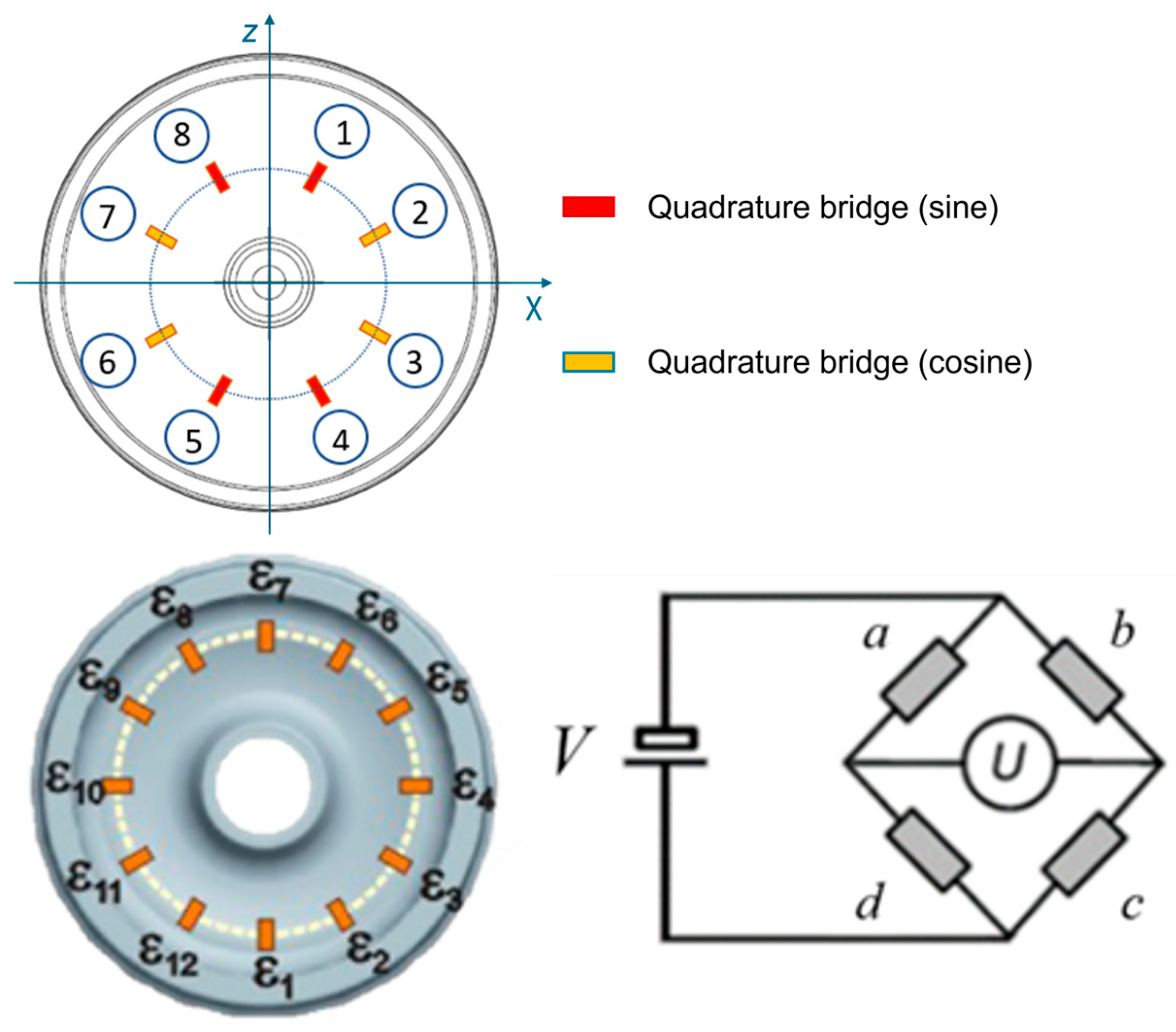
4. Instrumented Wheelsets and Data Acquisition
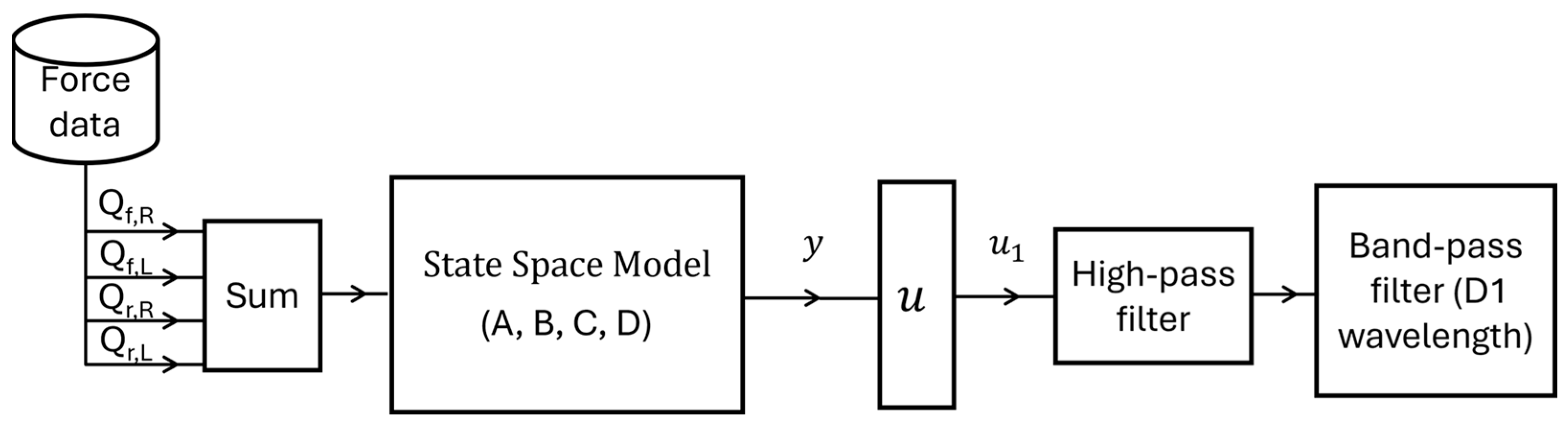
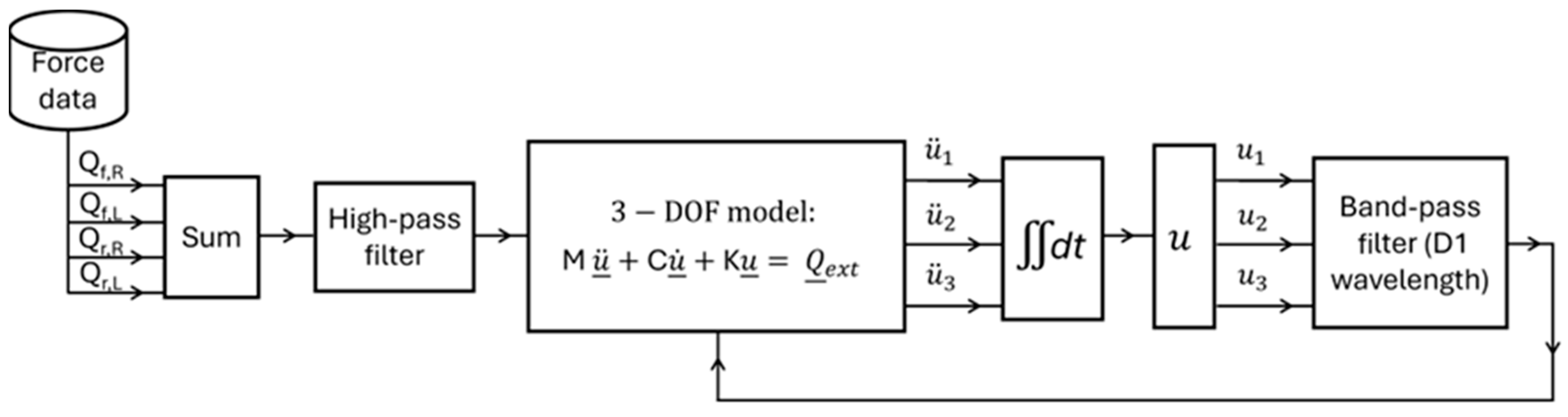
Model Description and Simulation Methods
- Unavoidable offsets in force measurements are removed by the high-pass filter (see Figure 5).
- Gain errors on measured forces are small. Their near influence is almost negligible.
- High-frequency errors introduced by noise and bandwidth limits of the measurement system are rejected by the bandpass filter (see Figure 5) and by the intrinsic nature of the 3-DOF model implemented by the estimator (a double stage integration associated with additional poles at few Hertz).
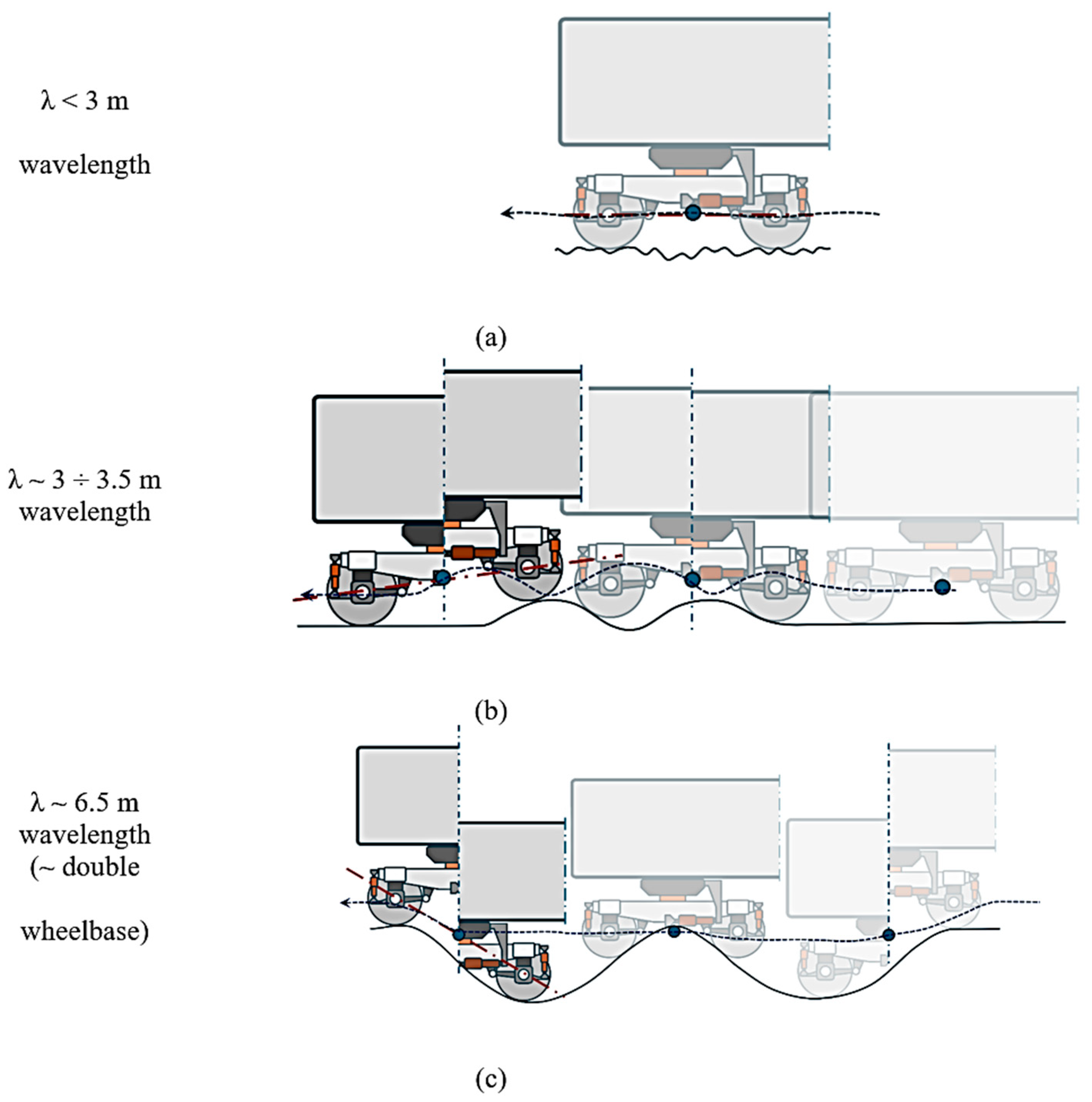
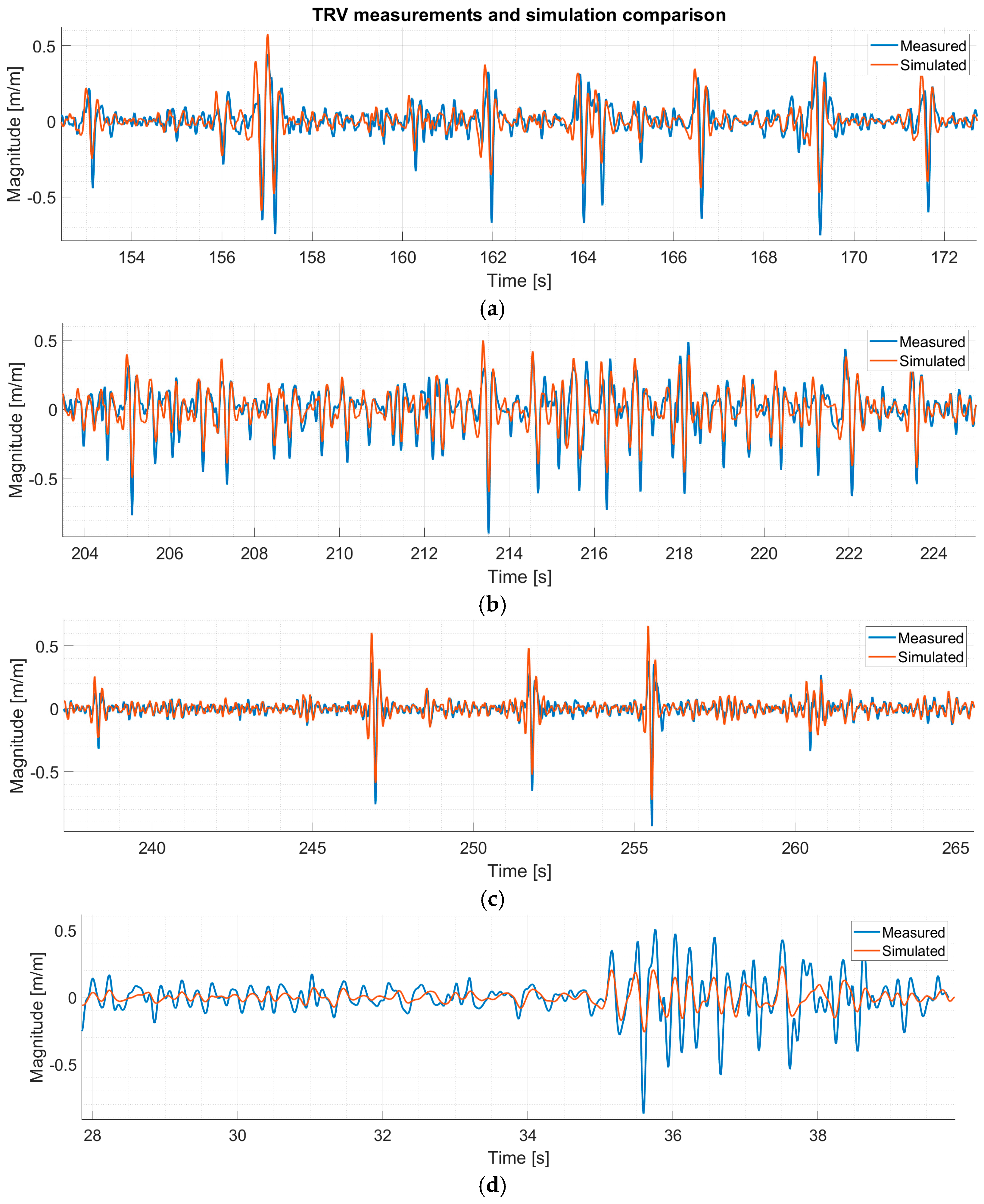
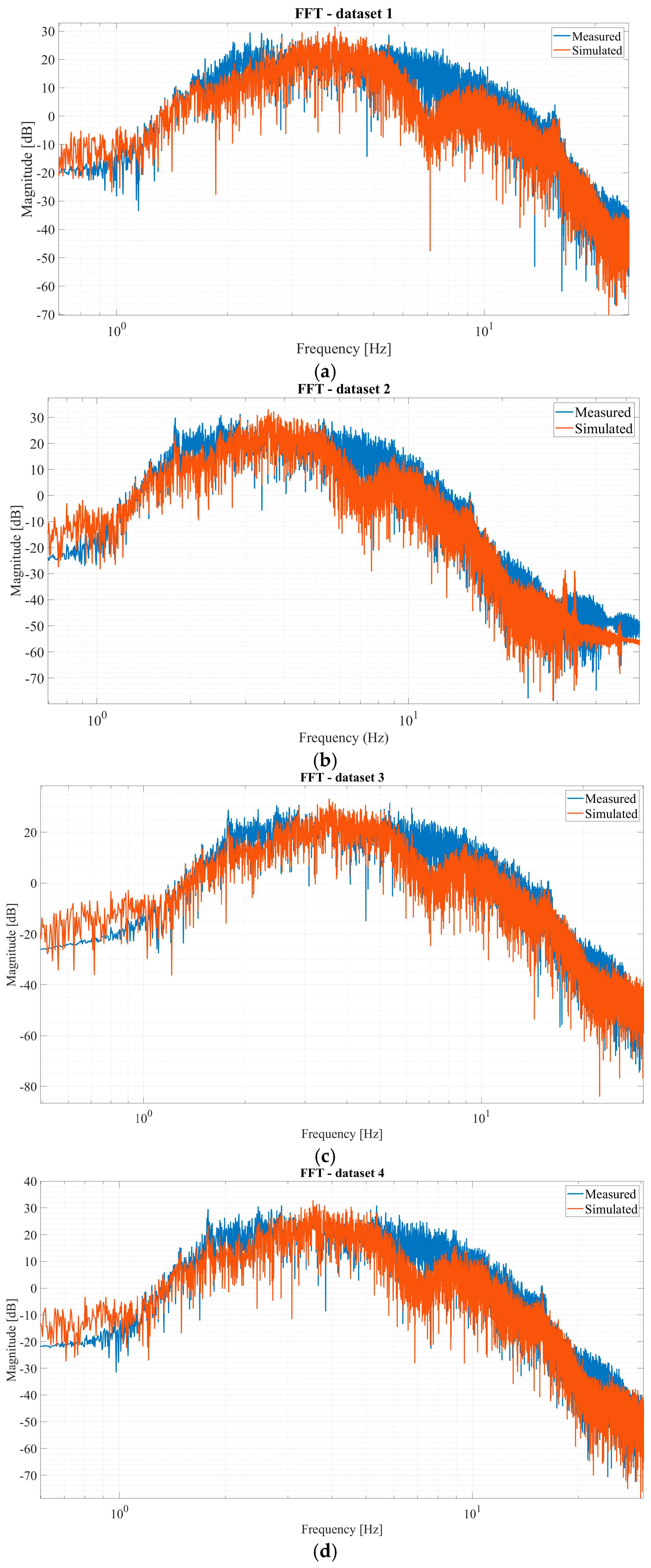
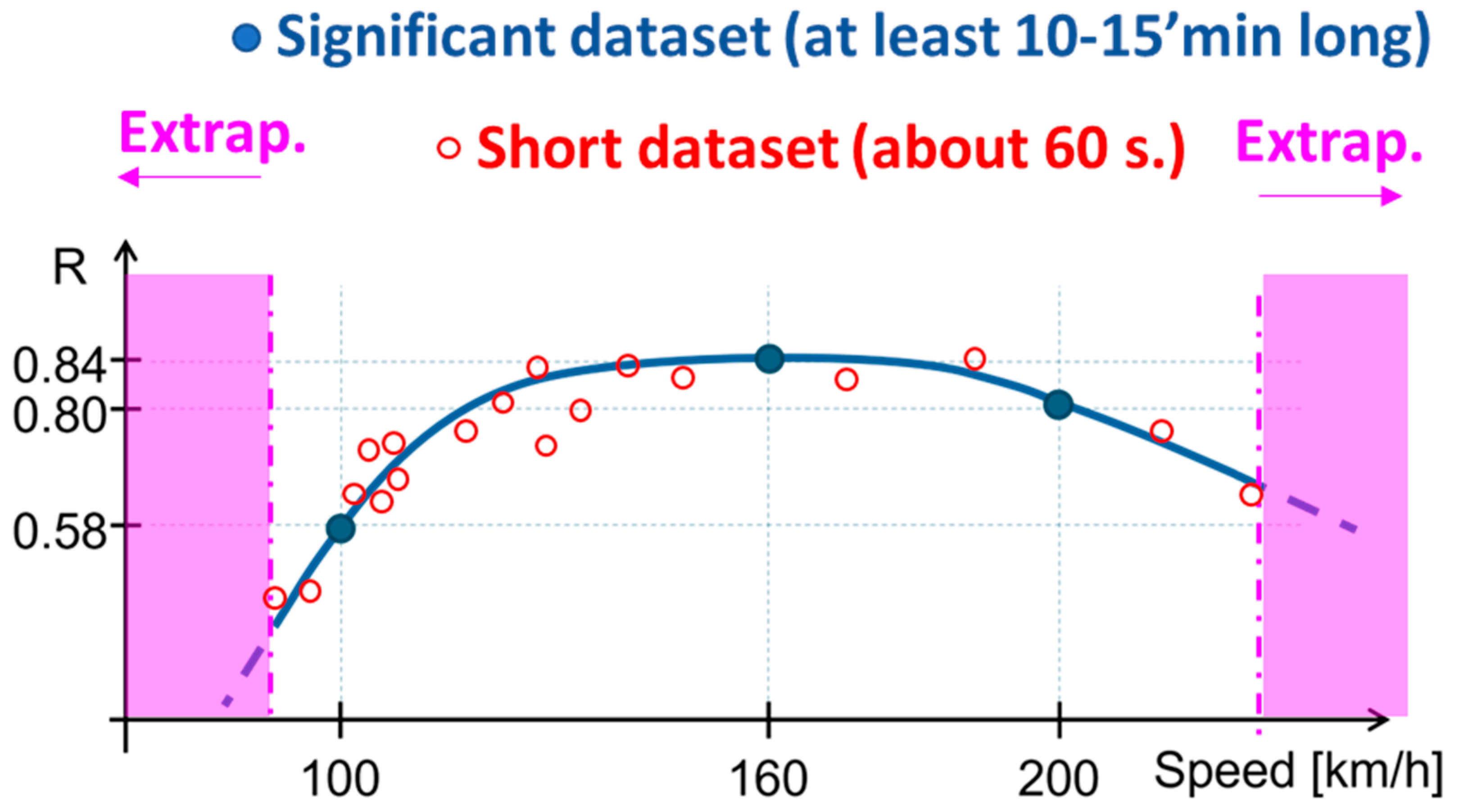
5. Results and Discussion
6. Error Analysis
7. Conclusions and Future Developments
- Calibrate model parameters when uncertain or partially known
- Self-calibration and optimal filtering with respect of speed, line conditions on other external disturbances
- Data fusion with additional measurements from inertial or optical sensors further improving measurement precision and reliability.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| TRV | Track Recording Vehicle |
| DOF | Degree of Freedom |
| MDOF | Multi Degree of Freedom |
| TG | Track Geometry |
| FFT | Fast Fourier Transform |
| FE | Finite Element |
| IWS | Instrumented Wheelsets |
| BP | Band-Pass |
| HPF | High-Pass Filter |
| VKF | Vold–Kalman Filtering |
Appendix A
Linear State Space Representation of the Half-a-Coach Vehicle Model
References
- European Commission. EU Transport in Figures: Statistical Pocketbook 2024; Mobility and Transport, Publications Office of the European Union: Luxembourg, 2024; ISBN 978-92-68-19812-4. [Google Scholar] [CrossRef]
- Ward, C.P.; Weston, P.F.; Stewart, E.J.C.; Li, H.; Goodman, C.J.; Roberts, C. Condition Monitoring Opportunities Using Vehicle-Based Sensors. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2011, 225, 202–218. [Google Scholar] [CrossRef]
- CIFI. La Diagnostica Mobile e le Misure per la Certificazione. Webinar, 31 January 2022. Available online: https://www.cifi.it/UplDocumenti/Roma31012022/Presentazione%20Bonafe_Palmiotto%20CIFI%202022-01-31.pdf (accessed on 7 January 2025).
- MERMEC Group. I Rotabili di RFI—Il Treno Archimede. Available online: https://www.mermecgroup.com/press-room/media-coverage/420/i-rotabili-di-rfi-il-treno-archimede.php (accessed on 7 January 2025).
- Gomez, E.; Giménez, J.G.; Alonso, A. Method for the Reduction of Measurement Errors Associated to the Wheel Rotation in Railway Dynamometric Wheelsets. Mech. Syst. Signal Process. 2011, 25, 3062–3077. [Google Scholar] [CrossRef]
- Nielsen, J.C.O. High-Frequency Vertical Wheel–Rail Contact Forces—Validation of a Prediction Model by Field Testing. Wear 2008, 265, 1465–1471. [Google Scholar] [CrossRef]
- Ronasi, H.; Johansson, H.; Larsson, F. Identification of Wheel–Rail Contact Forces Based on Strain Measurements, an Inverse Scheme and a Finite-Element Model of the Wheel. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2014, 228, 343–354. [Google Scholar] [CrossRef]
- Bellacci, G.; Entezami, M.; Weston, P.; Baldanzini, N.; Pugi, L. Evaluating the Feasibility of Estimating Rail Longitudinal Level Through Double Integration of Vertical Contact Forces. Mech. Mach. Sci. 2025, 180, 607–614. [Google Scholar] [CrossRef]
- EN 13848-1:2019; Railway Applications—Track—Track Geometry Quality—Part 1: Characterization of Track Geometry. European Committee for Standardization (CEN): Brussels, Belgium, 2019.
- EN 14363:2022; Railway Applications—Testing and Simulation for the Acceptance of Running Characteristics of Railway Vehicles—Running Behaviour and Stationary Tests. European Committee for Standardization (CEN): Brussels, Belgium, 2022.
- Thong, Y.K.; Woolfson, M.S.; Crowe, J.A.; Hayes-Gill, B.R. Numerical Double Integration of Acceleration Measurements in Noise. Measurement 2004, 36, 73–92. [Google Scholar] [CrossRef]
- Lewis, R.B.; Richards, A.N. A Compensated Accelerometer for the Measurement of Railway Track Crosslevel. IEEE Trans. Veh. Technol. 1988, 37, 174–178. [Google Scholar] [CrossRef]
- Weston, P.F.; Ling, C.S.; Goodman, C.J.; Roberts, C.; Li, H.; Goodall, R.M. Monitoring Vertical Track Irregularity from In-Service Railway Vehicles. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2007, 221, 75–88. [Google Scholar] [CrossRef]
- Weston, P.F.; Ling, C.S.; Goodman, C.J.; Roberts, C.; Li, H.; Goodall, R.M. Monitoring Lateral Track Irregularity from In-Service Railway Vehicles. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2007, 221, 89–100. [Google Scholar] [CrossRef]
- Zschiesche, K.; Reiterer, A. Optical Measurement System for Monitoring Railway Infrastructure—A Review. Appl. Sci. 2024, 14, 8801. [Google Scholar] [CrossRef]
- Soilán, M.; Sánchez-Rodríguez, A.; del Río-Barral, P.; Pérez-Collazo, C.; Lorenzo, H.; Arias, P. Review of Laser Scanning Technologies and Their Applications for Road and Railway Infrastructure Monitoring. Infrastructures 2019, 4, 58. [Google Scholar] [CrossRef]
- CIFI. CIFI Documents and Webinars. Available online: https://www.cifi.it/UplDocumenti/WebinarCIFI23112020-Dalla%20manutenzione%20ciclica%20alla%20predittiva.pdf (accessed on 7 January 2025).
- Rosano, G.; Massini, D.; Bocciolini, L.; Zappacosta, C.; Di Gialleonardo, E.; Somaschini, C.; La Paglia, I.; Pugi, L. Diagnostics of the Railway Track—Possibility of Development through the Measurement of Accelerations and Contact Forces. Ing. Ferrov. 2024, 79, 81–102. [Google Scholar] [CrossRef]
- Bellacci, G.; Pugi, L.; Baldanzini, N. Validation of a Wheelset Finite Element Model for Static Structural Analysis and Inverse Force Identification. In Latest Advancements in Mechanical Engineering; ISIEA 2024. Lecture Notes in Networks and Systems; Concli, F., Maccioni, L., Vidoni, R., Matt, D.T., Eds.; Springer: Cham, Switzerland, 2024; Volume 1124, pp. 236–244. [Google Scholar] [CrossRef]
- Ronasi, H.; Nielsen, J.C.O. Inverse Identification of Wheel–Rail Contact Forces Based on Observation of Wheel Disc Strains: An Evaluation of Three Numerical Algorithms. Veh. Syst. Dyn. 2012, 51, 74–90. [Google Scholar] [CrossRef]
- Bracciali, A.; Cavaliere, F.; Macherelli, M. Review of Instrumented Wheelset Technology and Applications. In Proceedings of the Second International Conference on Railway Technology: Research, Development and Maintenance; Pombo, J., Ed.; Civil-Comp Press: Stirlingshire, UK, 2014. [Google Scholar]
- Bellacci, G.; Neri, F.; Pugi, L.; Giachetti, A.; Barlacchi, E.; Baldanzini, N. Preliminary Frequency Response Analysis of a Contact Force Measurement System for Rail Applications. In Applications in Electronics Pervading Industry, Environment and Society; ApplePies 2023; Bellotti, F., Grammatikakis, M.D., Mansour, A., Roch, M.R., Seepold, R., Solanas, A., Berta, R., Eds.; Lecture Notes in Electrical Engineering, Volume 1110; Springer: Cham, Switzerland, 2024; pp. 240–247. [Google Scholar] [CrossRef]
- Italcertifer. Estensimetria, Sale e Pantografi Strumentati. Available online: https://www.italcertifer.com/it/laboratori/estensimetria--sale-e-pantografi-strumentati-.html (accessed on 7 January 2025).
- Iwnicki, S.; Spiryagin, M.; Cole, C.; McSweeney, T. Handbook of Railway Vehicle Dynamics, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar] [CrossRef]
- Abeidi, A.S.; Bosso, N.; Gugliotta, A.; Somà, A. Numerical Simulation of Wear in Railway Wheel Profiles. In Proceedings of the ASME 8th Biennial Conference on Engineering Systems Design and Analysis (ESDA 2006), Torino, Italy, 4–7 July 2006; Volume 3: Dynamic Systems and Controls, Symposium on Design and Analysis of Advanced Structures, and Tribology. ASME: Torino, Italy, 2006; pp. 963–977. [Google Scholar] [CrossRef]
- Bosso, N.; Magelli, M.; Zampieri, N. Simulation of Wheel and Rail Profile Wear: A Review of Numerical Models. Railw. Eng. Sci. 2022, 30, 403–436. [Google Scholar] [CrossRef]
- Logozzo, S.; Valigi, M.C. Green Tribology: Wear Evaluation Methods for Sustainability Purposes. Int. J. Mech. Control. 2022, 23, 23–34. [Google Scholar]
- Logozzo, S.; Valigi, M.C. Wear Assessment and Reduction for Sustainability: Some Applications. In Mechanisms and Machine Science; Springer: Cham, Switzerland, 2022; Volume 108, pp. 395–402. [Google Scholar] [CrossRef]
- EN 13848-2:2020; Railway Applications—Track—Track Geometry Quality—Part 2: Measuring Systems—Track Recording Vehicles. European Committee for Standardization (CEN): Brussels, Belgium, 2020.
- Hernández, W. Improving the Responses of Several Accelerometers Used in a Car Under Performance Tests by Using Kalman Filtering. Sensors 2001, 1, 38–52. [Google Scholar] [CrossRef]
- Sun, Y.Q.; Dhanasekar, M. A Dynamic Model for the Vertical Interaction of the Rail Track and Wagon System. Int. J. Solids Struct. 2002, 39, 1337–1359. [Google Scholar] [CrossRef]
- Zhai, W.; Cai, Z. Dynamic Interaction between a Lumped Mass Vehicle and a Discretely Supported Continuous Rail Track. Comput. Struct. 1997, 63, 987–997. [Google Scholar] [CrossRef]
- Kawasaki, J.; Youcef-Toumi, K. Estimation of Rail Irregularities. In Proceedings of the 2002 American Control Conference, Anchorage, AK, USA, 8–10 May 2002. [Google Scholar]
- Mori, H.; Tsunashima, H.; Kojima, T.; Matsumoto, A.; Mizuma, T. Condition Monitoring of Railway Track Using In-Service Vehicle. J. Mech. Syst. Transp. Logist. 2012, 3, 154–165. [Google Scholar] [CrossRef]
- Odashima, M.; Azami, S.; Naganuma, Y.; Mori, H. Track Geometry Estimation of a Conventional Railway from Car-Body Acceleration Measurement. Mech. Eng. J. 2017, 4, 16–00498. [Google Scholar] [CrossRef]
- Alfi, S.; Bruni, S. Estimation of Long Wavelength Track Irregularity from Onboard Measurement. In Proceedings of the 4th IET International Conference on Railway Condition Monitoring (RCM 2008), London, UK, 18–20 June 2008; pp. 1–6. [Google Scholar] [CrossRef]
- Miwa, M.; Kawasaki, Y.; Yoshimura, A. Influence of Vehicle Unsprung-Mass on Dynamic Wheel Load. In Computers in Railways XI—Computer System Design and Operation in the Railway and Other Transit Systems; Allan, J., Arias, E., Brebbia, C.A., Goodman, C., Rumsey, A.F., Sciutto, G., Tomii, N., Eds.; WIT Press: Southampton, UK, 2008; Volume 103, pp. 715–724. [Google Scholar]
- Tsunashima, H. Condition Monitoring of Railway Tracks from Car-Body Vibration Using a Machine Learning Technique. Appl. Sci. 2019, 9, 2734. [Google Scholar] [CrossRef]
- La Paglia, I.; Di Gialleonardo, E.; Facchinetti, A.; Carnevale, M.; Corradi, R. Acceleration-based condition monitoring of track longitudinal level using multiple regression models. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2024, 238, 479–488. [Google Scholar] [CrossRef]
- De Rosa, A.; Kulkarni, R.; Qazizadeh, A.; Berg, M.; Di Gialleonardo, E.; Facchinetti, A.; Bruni, S. Monitoring of Lateral and Cross Level Track Geometry Irregularities through Onboard Vehicle Dynamics Measurements Using Machine Learning Classification Algorithms. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2021, 235, 107–120. [Google Scholar] [CrossRef]
- Ghiasi, R.; Khan, A.M.; Sorrentino, D.; Diaine, C.; Malekjafarian, A. An Unsupervised Anomaly Detection Framework for Onboard Monitoring of Railway Track Geometrical Defects Using One-Class Support Vector Machine. Eng. Appl. Artif. Intell. 2024, 133, 108167. [Google Scholar] [CrossRef]
- Gullers, P.; Dreik, P.; Nielsen, J.C.O.; Ekberg, A.; Andersson, L. Track Condition Analyser: Identification of Rail Rolling Surface Defects Likely to Generate Fatigue Damage in Wheels Using Instrumented Wheelset Measurements. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2011, 225, 1–13. [Google Scholar] [CrossRef]
- Diana, G.; Resta, F.; Braghin, F.; Bocciolone, M.; Di Gialleonardo, E.; Crosio, P. Methodology for the Calibration of Dynamometric Wheelsets for the Measurement of the Wheel–Rail Contact Forces. Ing. Ferrov. 2012, 67, 9–21. [Google Scholar]
- Velletrani, F.; Licciardello, R.; Bruner, M. Intelligent Wheelsets for the Trains of the Future: The Role of In-Service Wheel–Rail Force Measurement. Ing. Ferrov. 2020, 75, 701–725. [Google Scholar]
- Evans, J.R. The Modelling of Railway Passenger Vehicles. Veh. Syst. Dyn. 2007, 20, 144–156. [Google Scholar] [CrossRef]
- Wong, J.Y. Theory of Ground Vehicles, 3rd ed.; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Dragoș, S.; Madalina, D.; Mihai, L. The Geometric Filtering Effect on Ride Comfort of the Railway Vehicles. UPB Sci. Bull. Ser. D Mech. Eng. 2021, 83, 137–154. [Google Scholar]
- Yeo, G.J.; Weston, P.F.; Roberts, C. The Utility of Continual Monitoring of Track Geometry from an In-Service Vehicle. In Proceedings of the 6th IET Conference on Railway Condition Monitoring (RCM 2014), Birmingham, UK, 17–20 November 2014; pp. 1–6. [Google Scholar]
- Hoelzl, C.; Dertimanis, V.; Ancu, L.; Kollros, A.; Chatzi, E. Vold–Kalman Filter Order Tracking of Axle Box Accelerations for Track Stiffness Assessment. Mech. Syst. Signal Process. 2023, 204, 110817. [Google Scholar] [CrossRef]
- Pieringer, A.; Kropp, W. Model-Based Estimation of Rail Roughness from Axle Box Acceleration. Appl. Acoust. 2022, 193, 108760. [Google Scholar] [CrossRef]
- Howell, D.C. Statistical Methods for Psychology, 7th ed.; Wadsworth, Cengage Learning: Belmont, CA, USA, 2009. [Google Scholar]
- OpenRailwayMap. Available online: https://www.openrailwaymap.org/ (accessed on 7 January 2025).
- Locorotondo, E.; Lutzemberger, G.; Pugi, L. State-of-charge estimation based on model-adaptive Kalman filters. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2021, 235, 1272–1286. [Google Scholar] [CrossRef]



| Range | Wavelength Value | Unit |
|---|---|---|
| D0 | 1 < λ ≤ 5 | [m] |
| D1 | 3 < λ ≤ 25 | [m] |
| D2 | 25 < λ ≤ 70 | [m] |
| D3 | 70 < λ ≤ 150 (200) | [m] |
| Parameter | Value | Unit |
|---|---|---|
| mweq | 2300 | [kg] |
| mb | 2180 | [kg] |
| mc | 19,000 | [kg] |
| k1eq | 2.0 × 106 | [N/m] |
| k2eq | 2.16 × 106 | [N/m] |
| c1eq | 64.9 × 103 | [kNs/m] |
| c2eq | 38.2 × 103 | [kNs/m] |
| Name | Train Speed and Tolerance [km/h] | Track Type | Length [km] (Duration [s]) |
|---|---|---|---|
| Dataset 1 (calibration) | 160 ± 5 | Mixed 1 | 29.4 (661) |
| Dataset 2 (validation) | 160 ± 5 | Mixed 2 | 30.5 (686) |
| Dataset 3 (validation) | 200 ± 5 | Mixed 3 | 33.5 (603) |
| Dataset 4 (validation) | 100 ± 5 | Mixed 4 | 13.2 (488) |
| Property | Dataset 1: 160 km/h | Dataset 2: 160 km/h | Dataset 3: 200 km/h | Dataset 4: 100 km/h |
|---|---|---|---|---|
| Residuals [mm] | 0.323 | 0.323 | 0.282 | 0.588 |
| RMSE [mm] | 0.578 | 0.705 | 0.497 | 0.994 |
| R | 0.827 | 0.843 | 0.798 | 0.579 |
| R2 | 0.684 | 0.711 | 0.636 | 0.336 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bellacci, G.; Entezami, M.; Weston, P.F.; Pugi, L. Estimation of Railway Track Vertical Alignment Using Instrumented Wheelsets and Contact Force Recordings. Machines 2025, 13, 963. https://doi.org/10.3390/machines13100963
Bellacci G, Entezami M, Weston PF, Pugi L. Estimation of Railway Track Vertical Alignment Using Instrumented Wheelsets and Contact Force Recordings. Machines. 2025; 13(10):963. https://doi.org/10.3390/machines13100963
Chicago/Turabian StyleBellacci, Giovanni, Mani Entezami, Paul Francis Weston, and Luca Pugi. 2025. "Estimation of Railway Track Vertical Alignment Using Instrumented Wheelsets and Contact Force Recordings" Machines 13, no. 10: 963. https://doi.org/10.3390/machines13100963
APA StyleBellacci, G., Entezami, M., Weston, P. F., & Pugi, L. (2025). Estimation of Railway Track Vertical Alignment Using Instrumented Wheelsets and Contact Force Recordings. Machines, 13(10), 963. https://doi.org/10.3390/machines13100963







