Phase-Aware Complex-Spectrogram Autoencoder for Vibration Preprocessing: Fault-Component Separation via Input-Phasor Orthogonality Regularization
Abstract
1. Introduction
1.1. Research Background
1.2. Related Work
1.3. Research Objectives
2. Materials and Methods
2.1. Data Sources and Experimental Setup
2.2. Signal Aggregation and Segmentation
2.3. Phase-Aware Complex Spectrogram Autoencoder
2.3.1. Problem Statement and Notation
2.3.2. Phase-Orthogonality Regularization
2.3.3. Training Objective
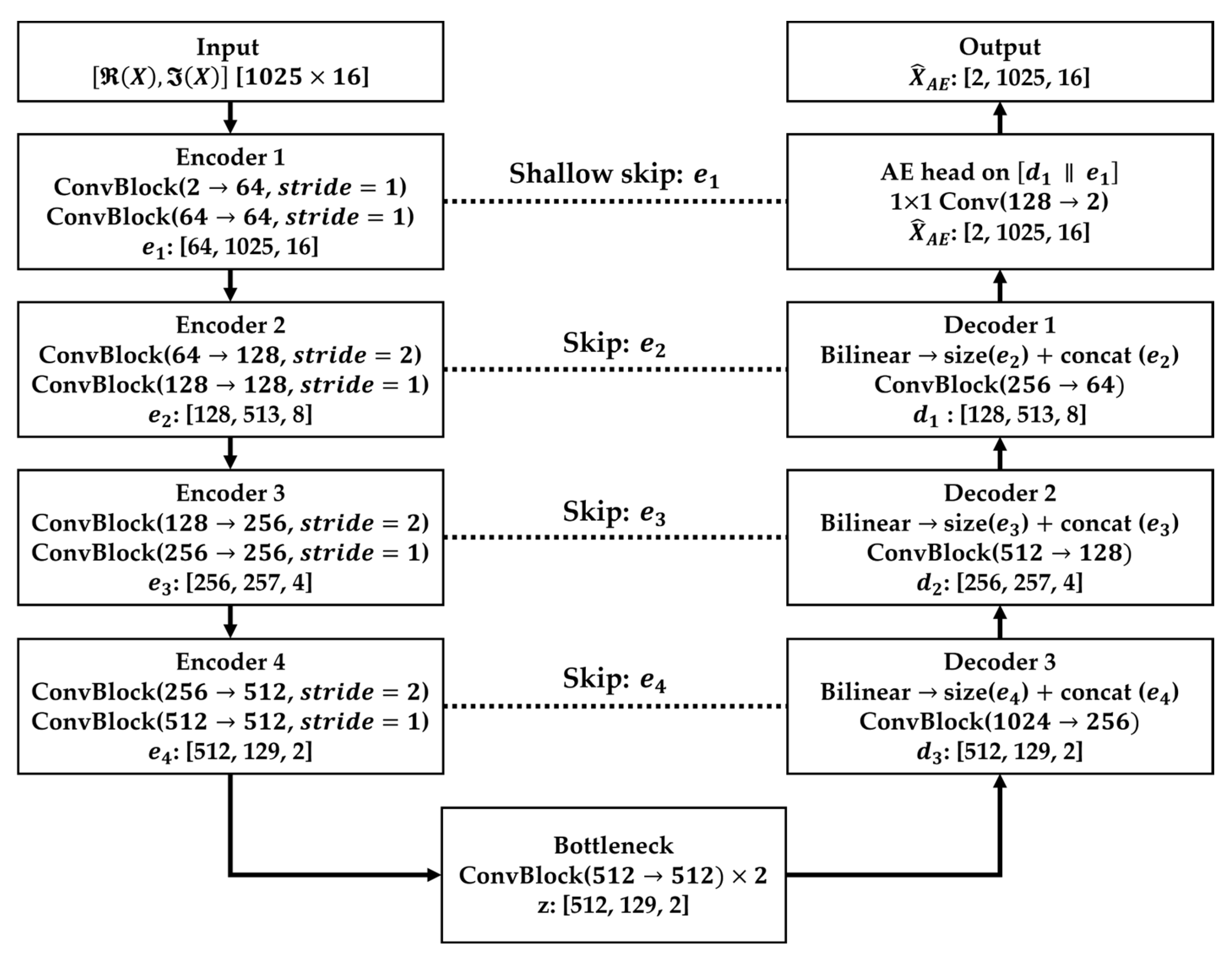
2.4. Model Architecture and Implementation
2.4.1. U-Net-Based Autoencoder (Normal Extractor)
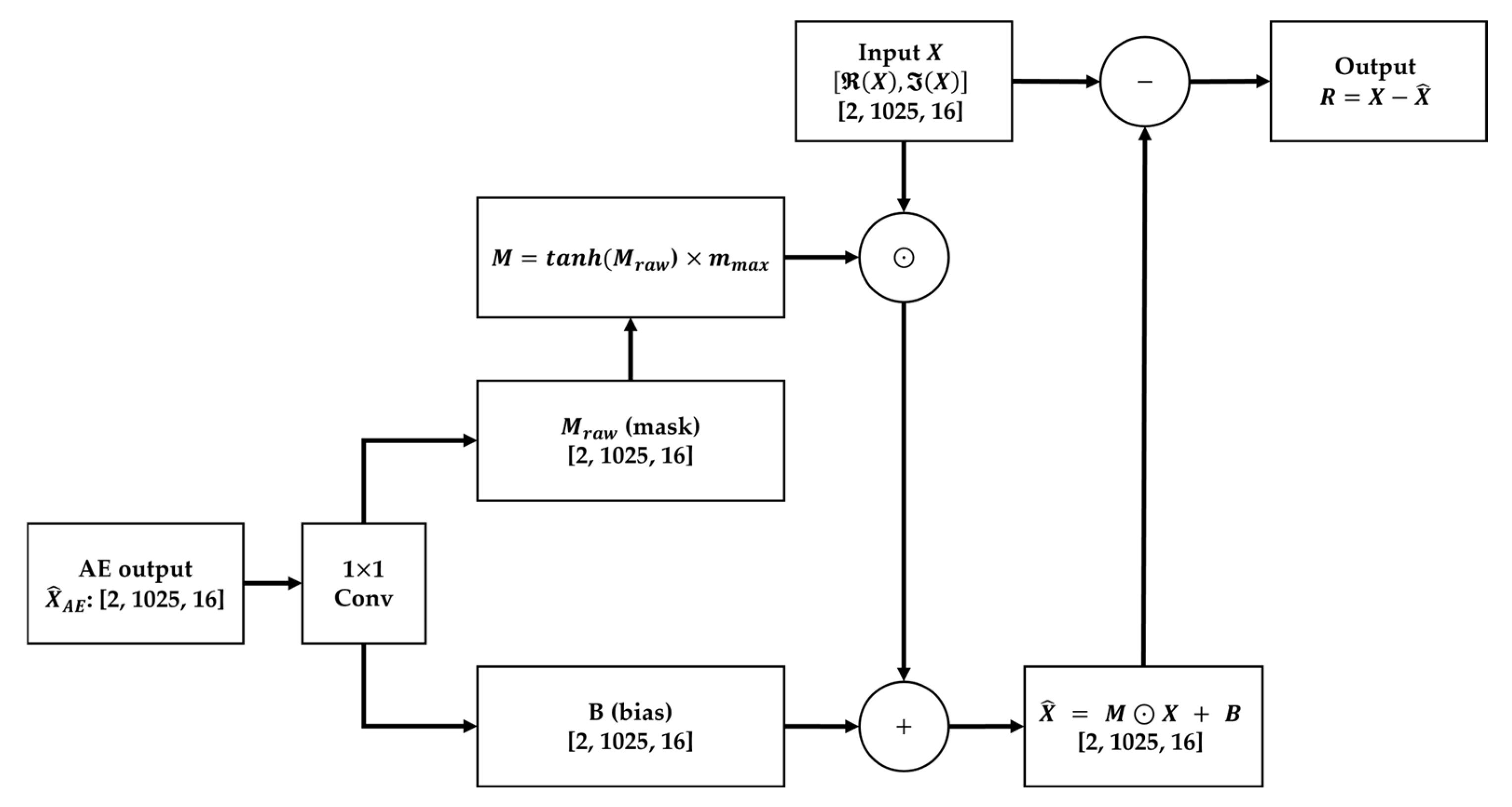
2.4.2. Mask-Bias Head
2.4.3. Training and Inference
2.5. Residual Features for Decision
2.6. Evaluation Protocol and Metrics
3. Results
3.1. Misalignment
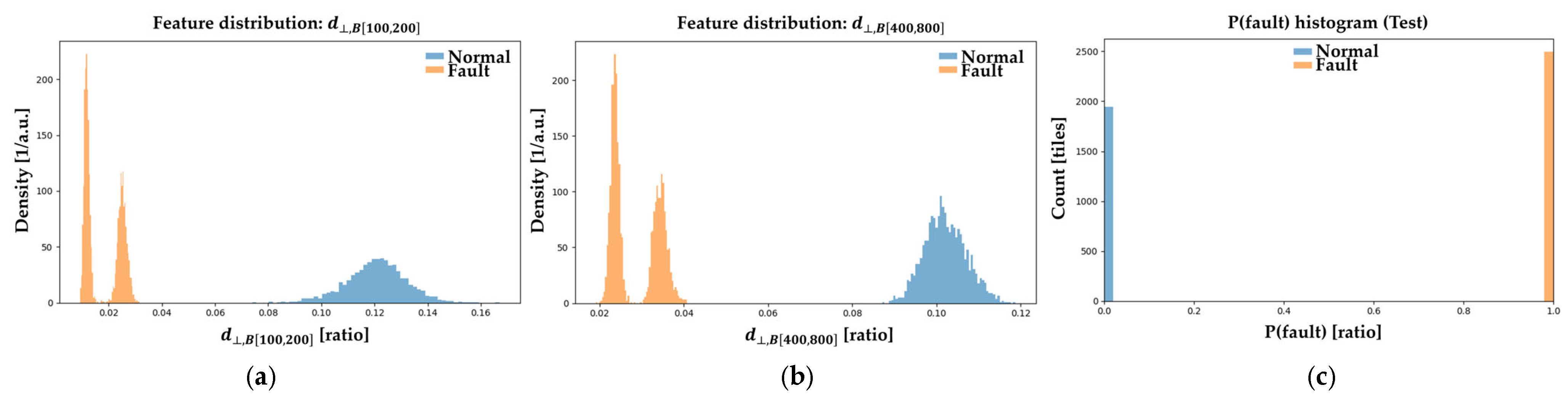
3.1.1. Data Preprocessing Results
3.1.2. Feature Selection & Classification Results
3.2. Bearing Fault—Lubricant-Removed
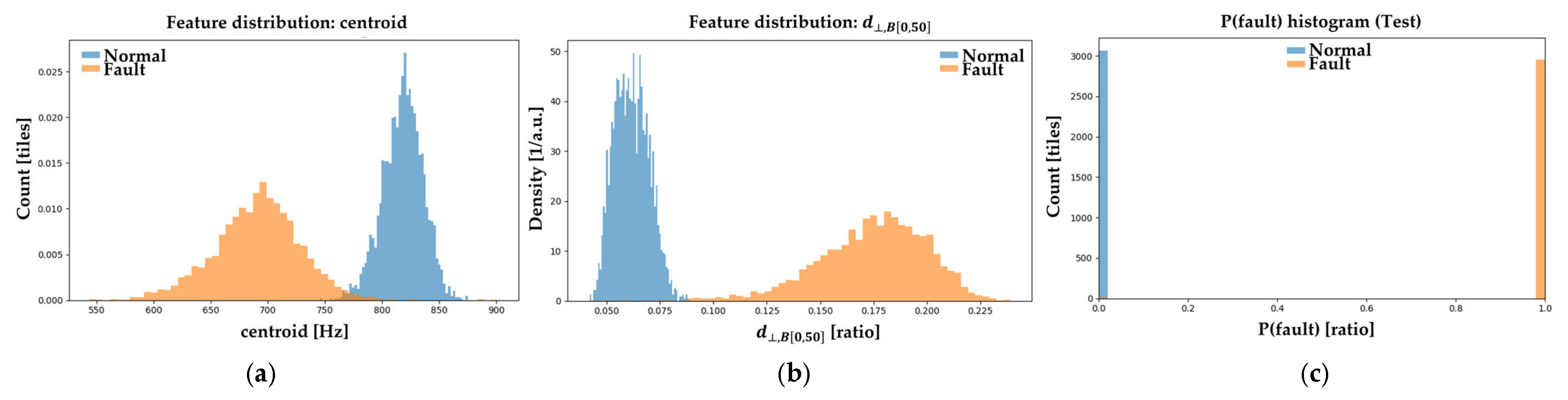
3.2.1. Data Preprocessing Results
3.2.2. Feature Selection & Classification Results
3.3. Belt Looseness
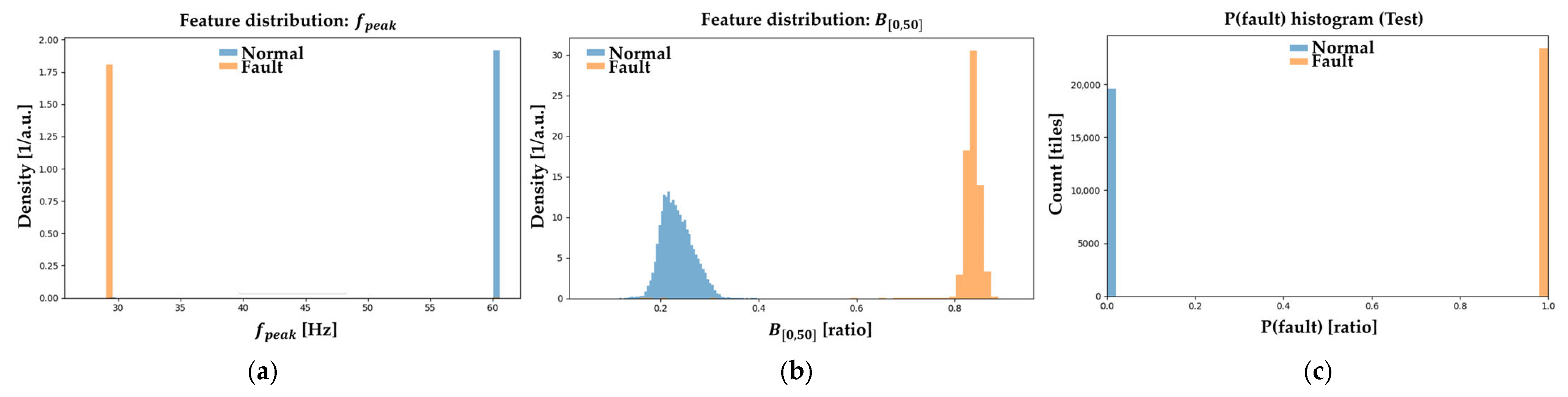
3.3.1. Data Preprocessing Results
3.3.2. Feature Selection & Classification Results
3.4. Unbalance
3.4.1. Data Preprocessing Results
3.4.2. Feature Selection & Classification Results
4. Discussion
4.1. Overall Discriminative Performance (ROC-AUC)
4.2. Threshold-Dependent Metrics (F1-Score, Confusion Matrix) and Error Characteristics
4.3. Calibration Quality and Drift
4.4. Accuracy, Balanced Accuracy, and Overall Weighted Summary
4.5. Spectrum-Level Preprocessing Effects (Normal vs. Fault Frequency Bands)
4.6. Generalization Performance and Statistical Significance (LOFO, Permutation, Null)
4.7. Overfitting Monitoring Results
4.8. Performance Comparison with Baselines
4.9. Consistency with Prior Work and Distinctive Contributions
4.10. Ablation Study
4.11. Limitations and Threats to Validity
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

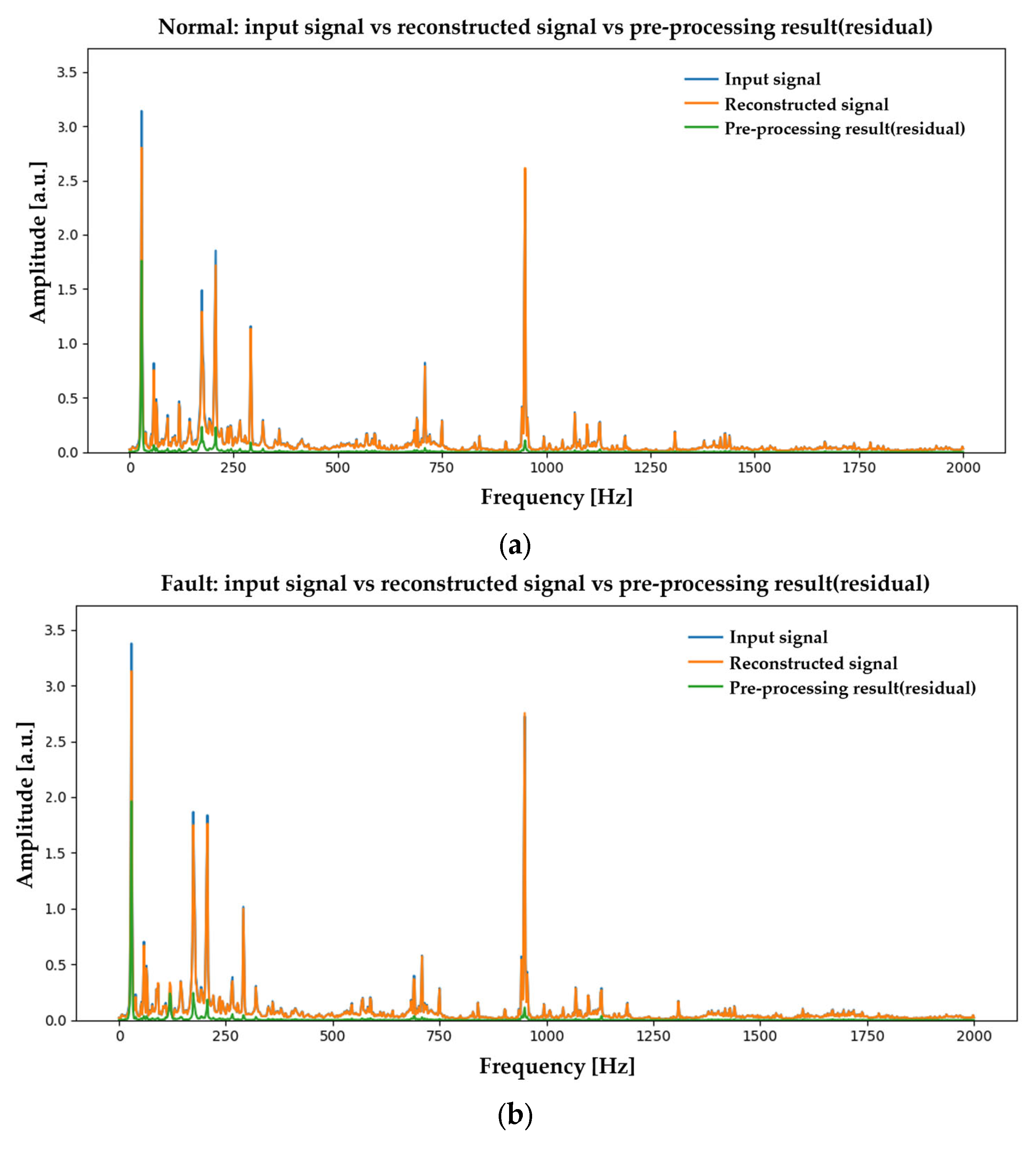
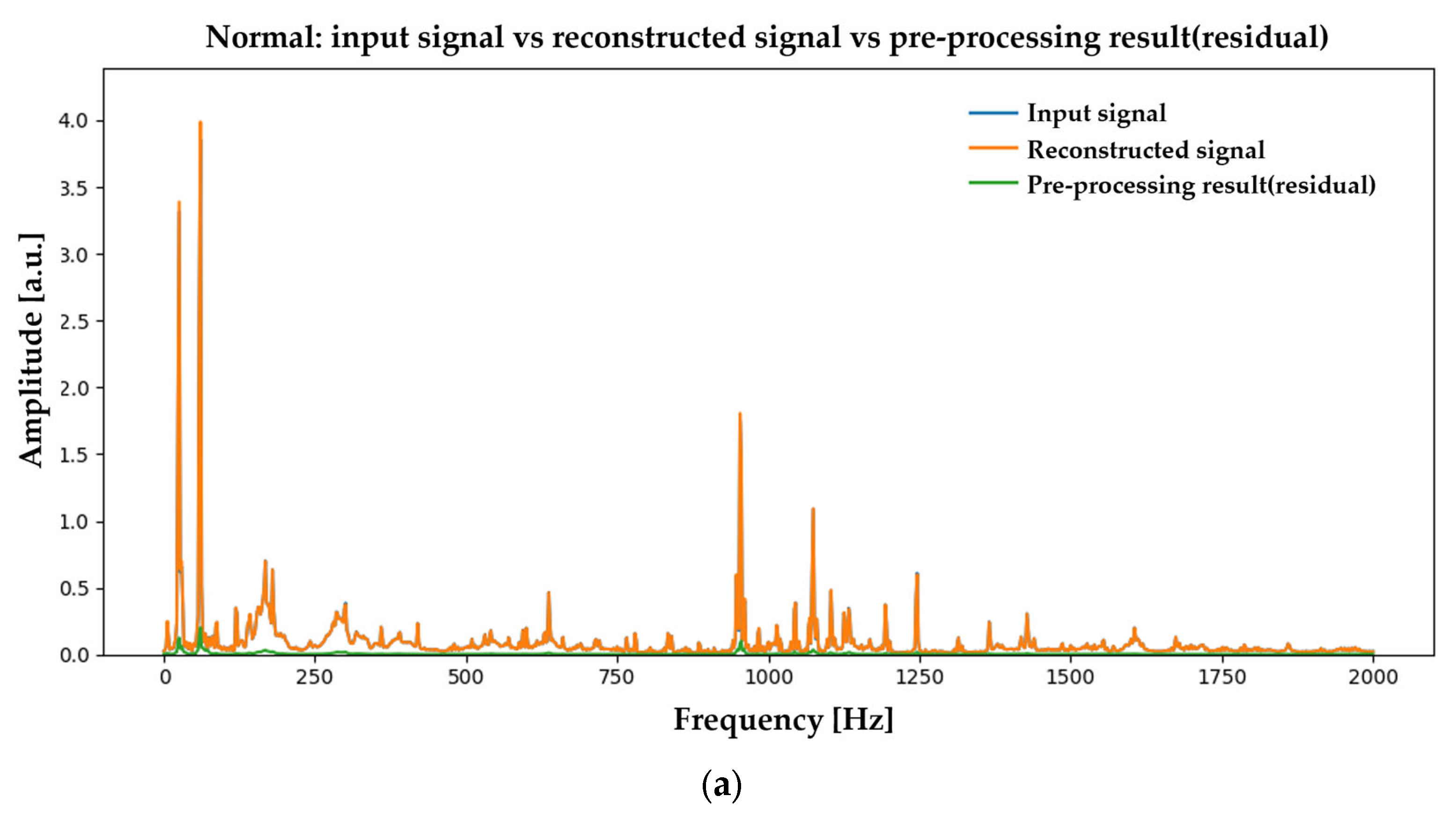
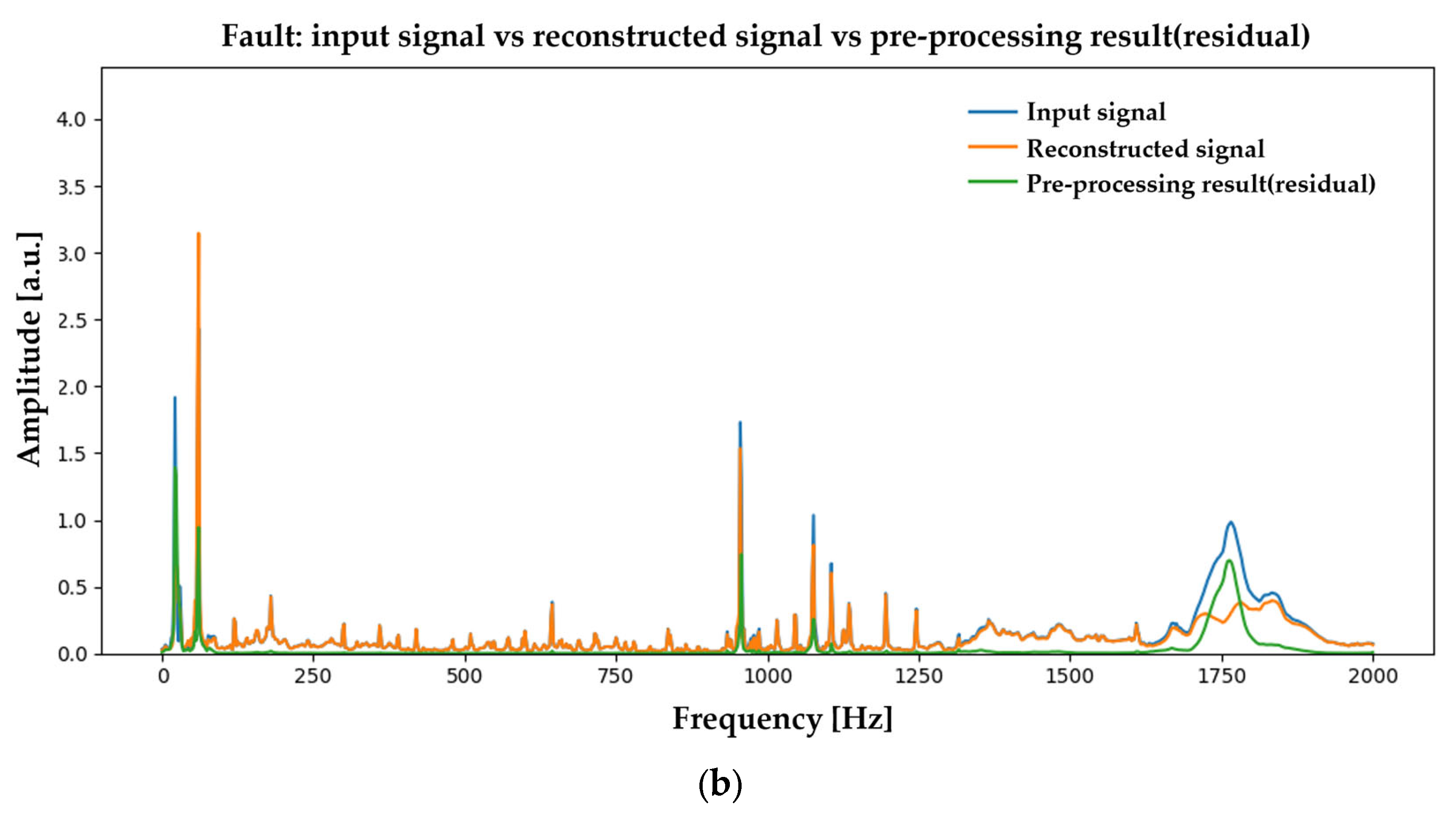
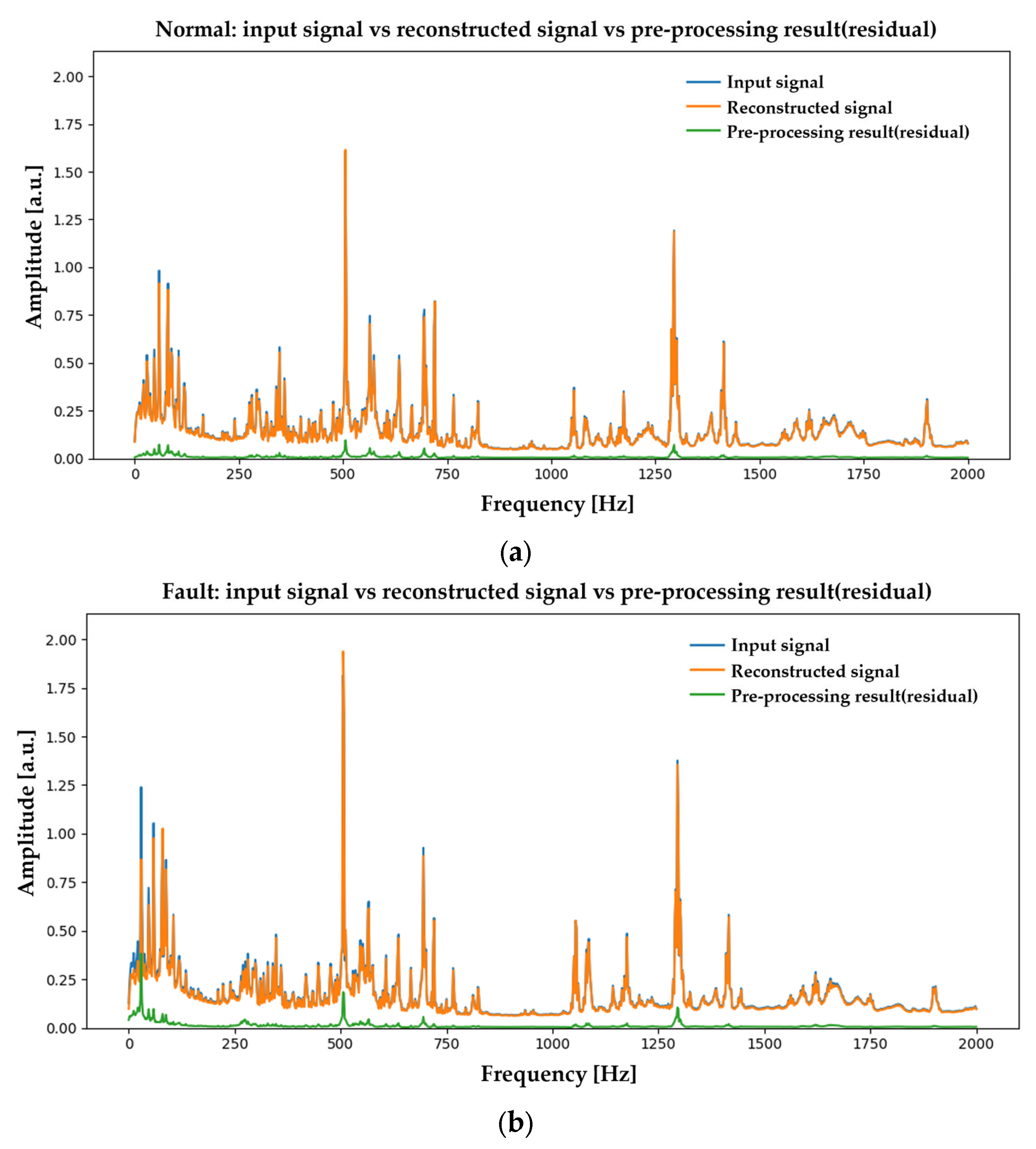

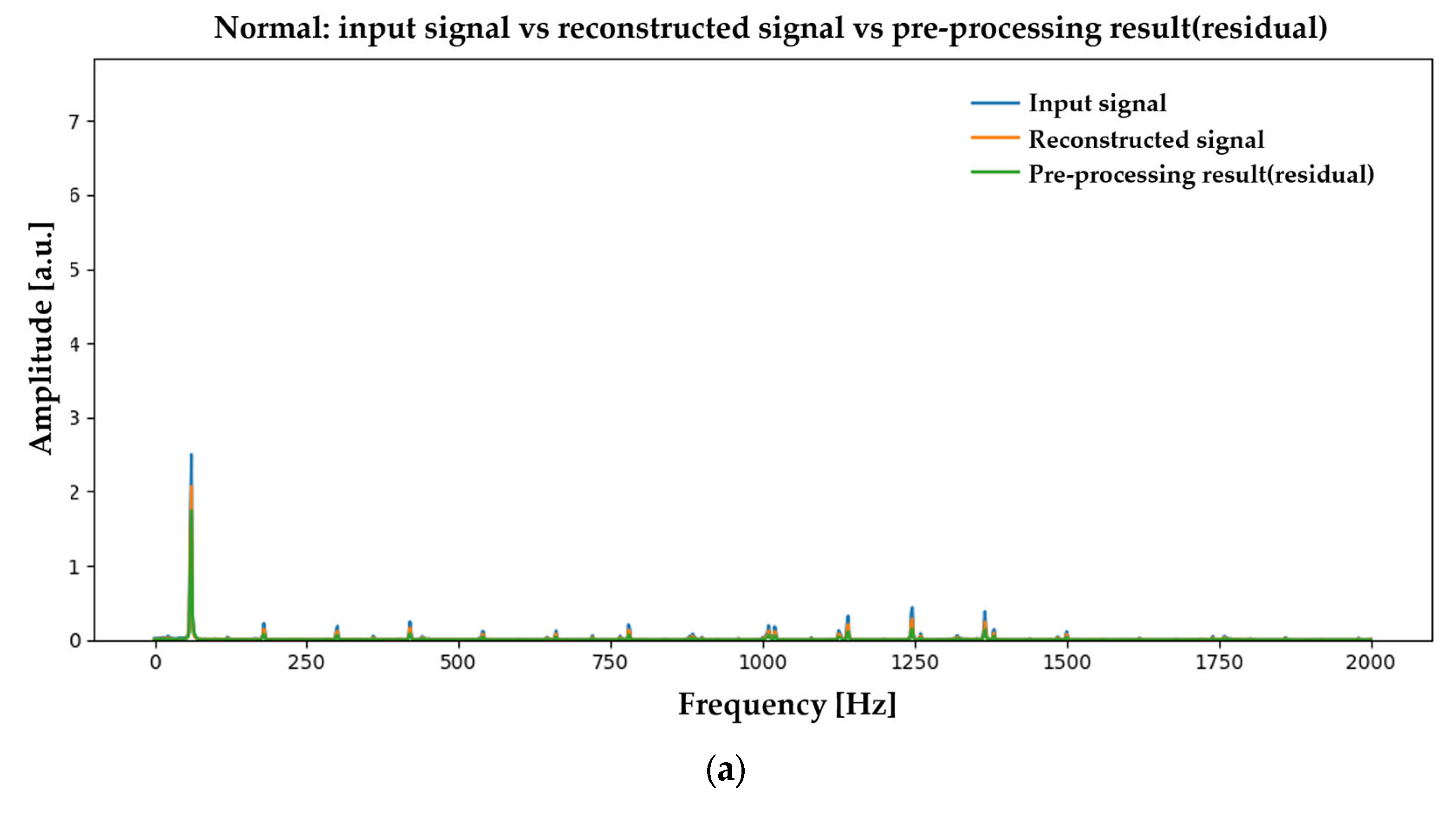
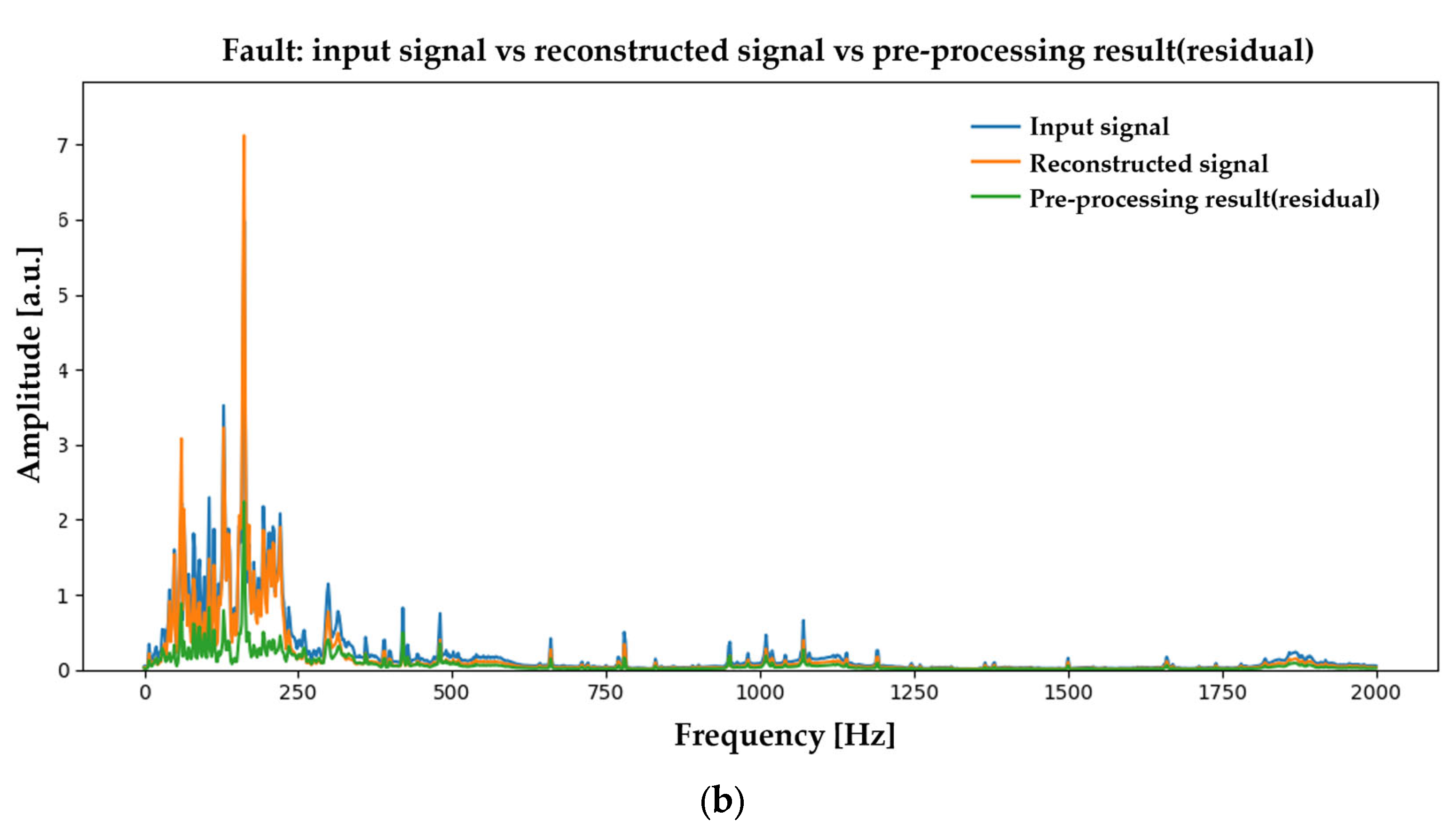

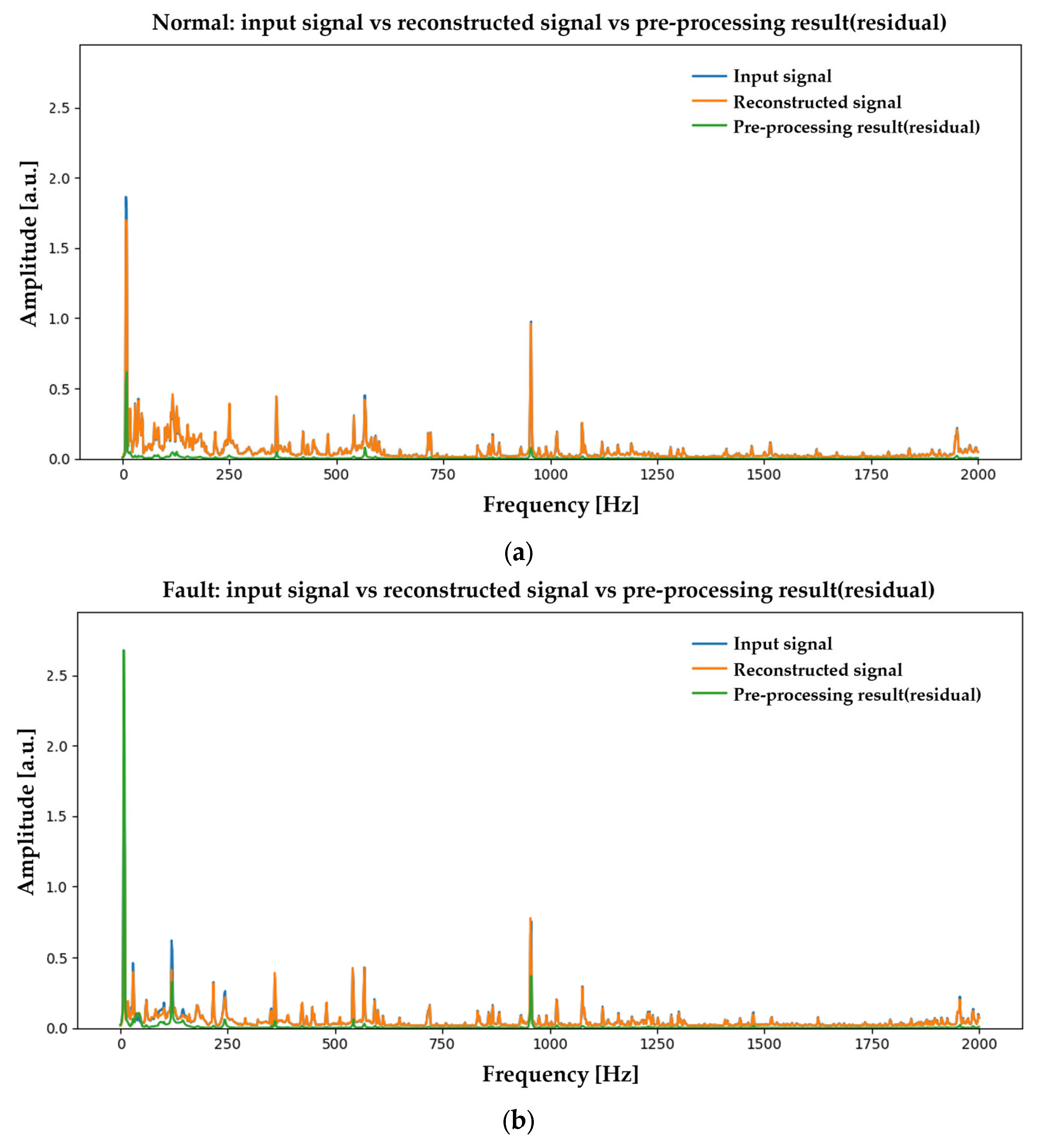
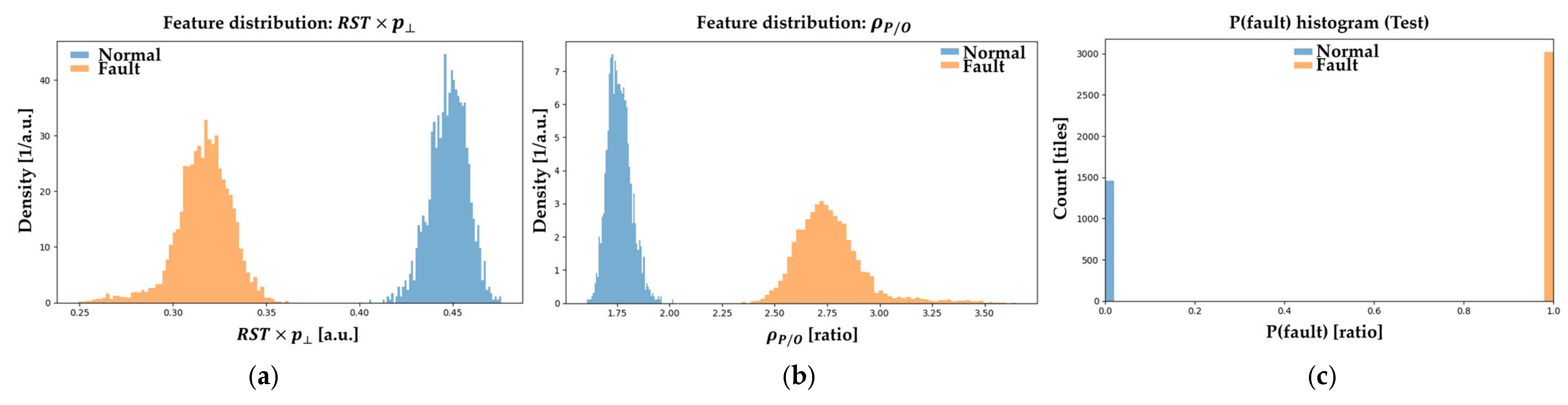
Appendix B




References
- Tavner, P.J. Review of condition monitoring of rotating electrical machines. IET Electr. Power Appl. 2008, 2, 215–247. [Google Scholar] [CrossRef]
- Gangsar, P.; Tiwari, R. Signal based condition monitoring techniques for fault detection and diagnosis of induction motors: A state-of-the-art review. Mech. Syst. Signal Process. 2020, 144, 106908. [Google Scholar] [CrossRef]
- Kim, S.; An, D.; Choi, J.-H. Diagnostics 101: A Tutorial for Fault Diagnostics of Rolling Element Bearing Using Envelope Analysis in MATLAB. Appl. Sci. 2020, 10, 7302. [Google Scholar] [CrossRef]
- Wang, Y.; Xiang, J.; Markert, R.; Liang, M. Spectral kurtosis for fault detection, diagnosis and prognostics of rotating machines: A review with applications. Mech. Syst. Signal Process. 2016, 66–67, 679–698. [Google Scholar] [CrossRef]
- Antoni, J. Fast computation of the kurtogram for the detection of transient faults. Mech. Syst. Signal Process. 2007, 21, 108–124. [Google Scholar] [CrossRef]
- Peeters, C.; Guillaume, P.; Helsen, J. A Comparison of Cepstral Editing Methods as Signal Pre-Processing Techniques for Vibration-Based Bearing Fault Detection. Mech. Syst. Signal Process. 2017, 91, 354–381. [Google Scholar] [CrossRef]
- Kiakojouri, A.; Lu, Z.; Mirring, P.; Powrie, H.; Wang, L. A Novel Hybrid Technique Combining Improved Cepstrum Pre-Whitening and High-Pass Filtering for Effective Bearing Fault Diagnosis Using Vibration Data. Sensors 2023, 23, 9048. [Google Scholar] [CrossRef]
- Chen, J.; Li, Z.; Pan, J.; Chen, G.; Zi, Y.; Yuan, J.; Chen, B.; He, Z. Wavelet transform based on inner product in fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2016, 70–71, 1–35. [Google Scholar] [CrossRef]
- Li, H.; Liu, T.; Wu, X.; Chen, Q. Application of EEMD and Improved Frequency Band Entropy in Bearing Fault Feature Extraction. ISA Trans. 2019, 88, 170–185. [Google Scholar] [CrossRef]
- Jia, Y.; Li, G.; Dong, X.; He, K. A novel denoising method for vibration signal of hob spindle based on EEMD and grey theory. Measurement 2021, 169, 108490. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, R. Role of signal processing, modeling and decision making in the diagnosis of rolling element bearing defect: A review. J. Nondestruct. Eval. 2019, 38, 5. [Google Scholar] [CrossRef]
- Wei, Y.; Li, Y.; Xu, M.; Huang, W. A review of early fault diagnosis approaches and their applications in rotating machinery. Entropy 2019, 21, 409. [Google Scholar] [CrossRef] [PubMed]
- Park, H.J.; Sim, J.; Jang, J.; Jang, K.-H.; Seol, J.-W.; Kwon, J.-Y.; Choi, J.-H. Study on Fault Severity Diagnosis of Planetary Gearbox in Unmanned Aerial Vehicle using Artificial Neural Network. J. Appl. Reliab. 2021, 21, 329–340. [Google Scholar] [CrossRef]
- Verstraete, D.; Ferrada, A.; Droguett, E.L.; Meruane, V.; Modarres, M. Deep Learning Enabled Fault Diagnosis Using Time-Frequency Image Analysis of Rolling Element Bearings. Shock Vib. 2017, 2017, 5067651. [Google Scholar] [CrossRef]
- Jiang, G.; He, H.; Xie, P.; Tang, Y. Stacked multilevel-denoising autoencoders: A new representation learning approach for wind turbine gearbox fault diagnosis. IEEE Trans. Instrum. Meas. 2017, 66, 2391–2402. [Google Scholar] [CrossRef]
- Pandey, A.; Wang, D.L. Exploring deep complex networks for complex spectrogram enhancement. In Proceedings of the ICASSP 2019—2019 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019. [Google Scholar] [CrossRef]
- Sung, S.-H.; Hong, S.; Choi, H.-R.; Park, D.-M.; Kim, S. Enhancing Fault Diagnosis in iot Sensor Data through Advanced Preprocessing Techniques. Electronics 2024, 13, 3289. [Google Scholar] [CrossRef]
- Seo, J.; Park, J.; Yoo, J.; Park, H. Anomaly Detection System in Mechanical Facility Equipment: Using Long Short-Term Memory Variational Autoencoder. J. Korean Soc. Qual. Manag. 2021, 49, 581–594. [Google Scholar] [CrossRef]
- An, D.; Shin, J.; Lee, S. A Lightweight Deep Learning Model based on Image Encoding for Failure Classification of Motor Mechanical Facilities. J. Inst. Electron. Inf. Eng. 2022, 59, 57–63. [Google Scholar] [CrossRef]
- Lee, S.; Ko, S.; Lee, S. Fault Classification Model Based on Deep Learning Using Vibration Data of Mechanical Equipment. J. Korean Inst. Next Gener. Comput. 2022, 18, 36–46. [Google Scholar] [CrossRef]
- Sim, Y.; Choi, J.; Kim, B.; Im, S. Outlier Detection Based on Multivariate Kernel Density Estimation in Induction Motors. In Proceedings of the 2nd Korea Artificial Intelligence Conference (Korea AI Conf.), Jeju, Republic of Korea, 29 September–1 October 2021; pp. 337–338. [Google Scholar]
- Li, X.; Xiao, S.; Zhang, F.; Huang, J.; Xie, Z.; Kong, X. A fault diagnosis method with AT-ICNN based on a hybrid attention mechanism and improved convolutional layers. Appl. Acoust. 2024, 225, 110191. [Google Scholar] [CrossRef]
- Hua, L.; Qiang, Y.; Gu, J.; Chen, L.; Zhang, X.; Zhu, H. Mechanical Fault Diagnosis Using Color Image Recognition of Vibration Spectrogram Based on Quaternion Invariant Moments. Math. Probl. Eng. 2015, 2015, 1–11. [Google Scholar] [CrossRef]
- Hu, Y.; Liu, Y.; Lv, S.; Xing, M.; Zhang, S.; Fu, Y.; Wu, J.; Zhang, B.; Xie, L. DCCRN: Deep Complex Convolution Recurrent Network for Phase-Aware Speech Enhancement. In Proceedings of the Interspeech 2020, Shanghai, China, 25–29 October 2020. [Google Scholar] [CrossRef]

| Case | Power (kW) | Failure Mode | Target Equipment | Name | RPM |
|---|---|---|---|---|---|
| 1 | 2.2 | Misalignment (shaft misaligned by +5 mm/+4 mm) | Blower | L-DSF-01 | 1730 |
| 2 | 2.2 | Bearing fault (lubricant-removed from bearing) | Blower A | L-SF-04 | 1760 |
| 3 | 2.2 | Belt looseness (belt removed, motor shifted 5 mm) | Blower | R-SF-03 | 1760 |
| 4 | 3.7 | Unbalance (added rotor imbalance weight) | Air Handling Unit A | L-PAC-01 | 1750 |
| 5 | 3.7 | Bearing fault (lubricant-removed from bearing) | Blower A | L-EF-02 | 1755 |
| 6 | 5.5 | Misalignment (shaft misaligned by +5 mm/+4 mm) | Blower | R-SF-01 | 1765 |
| 7 | 5.5 | Unbalance (added rotor imbalance weight) | Air Handling Unit B | R-CAHU-01R | 1760 |
| 8 | 5.5 | Belt looseness (belt removed, motor shifted 5 mm) | Blower | L-SF-01 | 1765 |
| Case | Failure Mode | Power /RPM | Files (N/F) | Samples (N/F) | STFT Frames T (N/F) | Patches (N/F) | Validation Speed (it/s, N/F) |
|---|---|---|---|---|---|---|---|
| 1 | Misalignment | 2.2 kW /1730 | 998 /2066 | 11,976,000/24,792,000 | 11,694 /24,209 | 1460 /3025 | 2.89 /2.87 |
| 2 | Bearing fault | 2.2 kW /1760 | 838 /2397 | 10,056,000/28,764,000 | 9819 /28,088 | 1226 /3510 | 3.37 /2.91 |
| 3 | Belt looseness | 2.2 kW /1760 | 1329 /1707 | 15,948,000/20,484,000 | 15,573 /20,002 | 1945 /2499 | 9.28 /9.63 |
| 4 | Unbalance | 3.7 kW /1750 | 2095 /2027 | 25,140,000/24,324,000 | 24,549 /23,752 | 3067 /2968 | 10.21 /10.61 |
| 5 | Bearing fault | 3.7 kW /1755 | 1011 /2171 | 12,132,000/26,052,000 | 11,846 /25,440 | 1479 /3179 | 9.14 /9.44 |
| 6 | Misalignment | 5.5 kW /1765 | 12,089 /16,000 | 145,068,000/192,000,000 | 141,666/187,499 | 17,707 /23,436 | 9.61 /10.71 |
| 7 | Unbalance | 5.5 kW /1760 | 13,369 /16,000 | 160,428,000/192,000,000 | 156,666/187,499 | 19,582 /23,436 | 8.85 /9.24 |
| 8 | Belt looseness | 5.5 kW /1765 | 13,025 /14,877 | 156,300,000/178,524,000 | 152,635/174,338 | 19,078 /21,791 | 3.03 /3.05 |
| Category | Item | Value/Description |
|---|---|---|
| Input | , hop, window | |
| Patch | T (frames), channels | ] |
| Common block | Conv-BN-GELU | 3, padding = 1 |
| Down/Up | Down/up | Stride-2 Conv/bilinear + Conv |
| U-Net (teacher) | Base_ch, depth | 64, 4-stage encoder–decoder |
| Output (teacher) | Out-ch | ) |
| Affine head (student) | Head-ch | 4ch ) |
| Affine constraints | 1.5 | |
| Optimization | Adamw, early-stop | Validation-MAE, patience = 30, |
| AMP/Hardware | dtype, HW | bf16, A100 40 GB |
| Category | Item | Setting/Method | Notes |
|---|---|---|---|
| Datasplit | Training /Internal validation | Public training set, 70/30 stratified split | Maintain class/case balance |
| Independent test | Public validation set, Entirely used | Prevent information leakage | |
| Cross-validation | LOFO | File-level generalization check | |
| Classification Performance | ROC-AUC | Report with bootstrap 95% CI | Threshold-invariant Performance |
| F1-score | Computed at the optimal threshold | Balances precision and recall | |
| Confusion matrix | Report TP/FP/FN/TN | Identifies error patterns | |
| Calibration | ECE | Expected Calibration Error | Closer to 0 is better |
| Brier score | Mean squared error of Probabilistic predictions | Closer to 0 is better | |
| Generalization /statisticaltests | LOFO file-level accuracy | Accuracy with file-level holdout | Checks split bias |
| Permutation test | Label-shuffle p-value | Rules out chance performance | |
| Null test | Performance against No-information inputs | Detects overfitting/bias | |
| Overfitting Prevention | Regularization | AdamW weight decay (L2) | Weight-level regularization |
| Early stopping | Validation MAE criterion | Prevents overfitting | |
| Normal-region regularizer | Identity preservation on normal segments | Preserves normal patterns | |
| Overfittingdetection (monitoring) | Performance gap | Train-test AUC gap | Generalization drop Indicator |
| Calibration drift | ECE change over training | Over/under-confidence Indicator |
| Case | ROC-AUC (Train/Test) | AUC 95% CI (Bootstrap) | F1-Score | Confusion | ECE (Train/Test) | Brier Score (Train/Test) |
|---|---|---|---|---|---|---|
| 1 | 1.000 /1.000 | 1.000–1.000 | 1.000 | = 1.000 = 0.000 = 0.000 = 1.000 | 0.000 /0.000 | 0.0000/0.0000 |
| 2 | 1.000 /1.000 | 1.000–1.000 | 1.000 | = 1.000 = 0.000 = 0.000 = 1.000 | 0.000 /0.000 | 0.0001/0.0000 |
| 3 | 1.000 /0.999 | 0.999–1.000 | 1.000 | = 0.999 = 0.001 = 0.000 = 1.000 | 0.000 /0.000 | 0.0001/0.0004 |
| 4 | 1.000 /1.000 | 1.000–1.000 | 0.997 | = 1.000 = 0.000 = 0.006 = 0.994 | 0.000 /0.003 | 0.0001/0.0031 |
| 5 | 0.998 /1.000 | 1.000–1.000 | 0.996 | = 0.997 = 0.003 = 0.007 = 0.963 | 0.016 /0.005 | 0.0172/0.0039 |
| 6 | 1.000 /1.000 | 1.000–1.000 | 1.000 | = 1.000 = 0.000 = 0.000 = 1.000 | 0.000 /0.000 | 0.0001/0.0001 |
| 7 | 1.000 /1.000 | 0.999–1.000 | 1.000 | = 1.000 = 0.000 = 0.000 = 1.000 | 0.000 /0.000 | 0.0002/0.0002 |
| 8 | 1.000 /1.000 | 1.000–1.000 | 1.000 | = 1.000 = 0.000 = 0.000 = 1.000 | 0.000 /0.000 | 0.0000/0.0000 |
| Case | Acc (%) | Balanced Acc (%) | FP (N→F) | FN (F→N) | Number of Test Patches |
|---|---|---|---|---|---|
| 1 | 100.0 | 100.0 | 0 | 0 | 4485 |
| 2 | 100.0 | 100.0 | 0 | 0 | 4736 |
| 3 | 100.0 | 100.0 | 2 | 0 | 4444 |
| 4 | 99.7 | 99.7 | 0 | 18 | 6035 |
| 5 | 99.4 | 99.5 | 4 | 22 | 4658 |
| 6 | 100.0 | 100.000 | 0 | 0 | 41,143 |
| 7 | 100.0 | 100.000 | 0 | 0 | 43,018 |
| 8 | 100.0 | 100.000 | 0 | 0 | 40,869 |
| Case | LOFO | Permutation Test (p, R = 2000) | Null Test (p, R = 500) |
|---|---|---|---|
| 1 | 1.000 | <0.0005 | <0.002 |
| 2 | 1.000 | <0.0005 | <0.002 |
| 3 | 1.000 | <0.0005 | <0.002 |
| 4 | 1.000 | <0.0005 | <0.002 |
| 5 | 0.994 | <0.0005 | <0.002 |
| 6 | 1.000 | <0.0005 | <0.002 |
| 7 | 1.000 | <0.0005 | <0.002 |
| 8 | 1.000 | <0.0005 | <0.002 |
| Case | Performance Gap ) | Calibration Drift |
|---|---|---|
| 1 | 0.000 | 0.000 |
| 2 | 0.000 | 0.000 |
| 3 | −0.001 | 0.000 |
| 4 | 0.000 | +0.003 |
| 5 | +0.002 | −0.011 |
| 6 | 0.000 | 0.000 |
| 7 | 0.000 | 0.000 |
| 8 | 0.000 | 0.000 |
| Case | Proposed Full (ROC-AUC/F1-Score) | NB (ROC-AUC/F1-Score) | Logit (ROC-AUC/F1-Score) | SVM (ROC-AUC/F1-Score) | BP-Logit (ROC-AUC/F1-Score) |
|---|---|---|---|---|---|
| 1 | 1.000000/1.000000 | 1.000000/1.00000 | 1.000000/1.00000 | 1.000000/0.99278 | 0.049978/0.00000 |
| 2 | 1.000000/1.000000 | 0.963850/0.85090 | 0.964972/0.85132 | 0.964972/0.85132 | 0.626469/0.85132 |
| 3 | 0.999486/0.999600 | 0.970200/0.71986 | 0.452837/0.71968 | 0.824507/0.71986 | 0.080720/0.00000 |
| 4 | 1.000000/0.996789 | 0.998864/0.99899 | 1.000000/0.99983 | 1.000000/0.99748 | 0.997184/0.65934 |
| 5 | 0.999971/0.998111 | 0.000237/0.00000 | 1.000000/0.83232 | 1.000000/0.96230 | 0.004541/0.12746 |
| 6 | 0.999887/0.999893 | 0.999944/0.99998 | 1.000000/1.00000 | 1.000000/0.99979 | 1.000000/0.72581 |
| 7 | 0.999744/0.999829 | 1.000000/1.00000 | 1.000000/1.00000 | 0.999515/0.92381 | 0.999924/0.70533 |
| 8 | 1.000000/1.000000 | 1.000000/1.00000 | 1.000000/1.00000 | 1.000000/0.99662 | 1.000000/0.75814 |
| No. | Study | Sensor | Task | Method (Traditional/DL) | Reported Test Metric(s) |
|---|---|---|---|---|---|
| 1 | This Paper | Vibration | Binary (normal vs. fault) | Complex-spectrogram AE + phase-orthogonality regularization. 2 residual features + simple classifier | ROC-AUC 0.998–1.000 F1-score 0.983–1.000 LOFO 0.980–1.000 ECE 0.000–0.023 Brier 0.0000–0.0228 |
| 2 | [17] | Vibration/Current | Binary (per-fault) | Preprocessing (noise reduction & spectrum augmentation) + LR/KNN/SVM/RF/LGBM | After preprocessing F1-score ≈ 0.999–1.000 (tree models) Without preprocessing Acc 52.8–96.7% |
| 3 | [18] | Vibration/Current | Anomaly detection | LSTM-VAE (unsupervised) vs. IF/OC-SVM/AE | Accuracy > 97% (two scenarios) |
| 4 | [19] | Current | Multi/Binary | Time-series → image (GASF/GADF/MTF/RP) + CNN | Bearing F1-score 0.999/Acc 0.998 Rotor F1-score 0.996 Belt F1-score 0.990 Misalignment F1-score 0.948 |
| 5 | [20] | Vibration | Multi | 13 DL time-series classifiers compared | CNN variants reported near-100% Acc/Prec/Rec/F1-score (abstract level) |
| 6 | [21] | Current | Anomaly detection | FFT/THD features + MKDE (non-parametric density) | = 5974) |
| Case | Proposed Full (ROC-AUC/F1-Score/ECE) | No-Ortho-Feats (ROC-AUC/F1-Score/ECE) | M = I (No-Mask) (ROC-AUC/F1-Score/ECE) | B = 0 (No-Bias) (ROC-AUC/F1-Score/ECE) | Phase-Random (ROC-AUC/F1-Score/ECE) | (ROC-AUC/F1-Score/ECE) |
|---|---|---|---|---|---|---|
| 1 | 1.000000/1.000000/ | 1.000000/1.000000/ | 1.000000/0.999835/ | 1.000000/1.000000/ | 1.000000/1.000000/ | 1.000000/0.999174/ |
| 2 | 1.000000/1.000000/ | 0.999928/0.998006/ | 1.000000/1.000000/ 1.00 | 1.000000/1.000000/ 1.00 | 1.000000/1.000000/ | 1.000000/1.000000/ |
| 3 | 0.999486/0.999600/ | 0.998972/0.999600/ | 1.000000/0.999800/ | 0.998972/0.999400/ | 0.999486/0.999600/ | 0.998458/0.999400/ |
| 4 | 1.000000/0.996789/ | 1.000000/0.998650/ | 0.997934/0.768465/ | 0.999921/0.997128/ | 1.000000/0.996958/ | 1.000000/1.000000/ |
| 5 | 0.999971/0.998111/ | 0.999995/0.999528/ | 0.887223/0.864343/ | 0.999995/0.998109/ | 0.999984/0.996845/ | 0.983043/0.954070/ |
| 6 | 0.999887/0.999893/ | 0.999944/0.999957/ | 0.999887/0.999893/ | 0.999944/0.999957/ | 0.999887/0.999893/ | 0.999887/0.999851/ |
| 7 | 0.999744/0.999829/ | 0.999584/0.999723/ | 0.999995/0.999872/ | 0.999744/0.999829/ | 0.999460/0.999274/ | 0.999900/0.999637/ |
| 8 | 1.000000/1.000000/ | 1.000000/1.000000/ | 1.000000/0.999977/ | 1.000000/0.999908/ | 0.999991/0.999242/ | 0.999947/0.999862/ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoo, S.-y.; Lee, Y.-n.; Lee, J.-c.; Hwang, S.-y.; Lee, J.-y.; Lee, S.-s. Phase-Aware Complex-Spectrogram Autoencoder for Vibration Preprocessing: Fault-Component Separation via Input-Phasor Orthogonality Regularization. Machines 2025, 13, 945. https://doi.org/10.3390/machines13100945
Yoo S-y, Lee Y-n, Lee J-c, Hwang S-y, Lee J-y, Lee S-s. Phase-Aware Complex-Spectrogram Autoencoder for Vibration Preprocessing: Fault-Component Separation via Input-Phasor Orthogonality Regularization. Machines. 2025; 13(10):945. https://doi.org/10.3390/machines13100945
Chicago/Turabian StyleYoo, Seung-yeol, Ye-na Lee, Jae-chul Lee, Se-yun Hwang, Jae-yun Lee, and Soon-sup Lee. 2025. "Phase-Aware Complex-Spectrogram Autoencoder for Vibration Preprocessing: Fault-Component Separation via Input-Phasor Orthogonality Regularization" Machines 13, no. 10: 945. https://doi.org/10.3390/machines13100945
APA StyleYoo, S.-y., Lee, Y.-n., Lee, J.-c., Hwang, S.-y., Lee, J.-y., & Lee, S.-s. (2025). Phase-Aware Complex-Spectrogram Autoencoder for Vibration Preprocessing: Fault-Component Separation via Input-Phasor Orthogonality Regularization. Machines, 13(10), 945. https://doi.org/10.3390/machines13100945








