Encoding Multivariate Time Series of Gas Turbine Data as Images to Improve Fault Detection Reliability
Abstract
1. Introduction
2. Literature Survey
2.1. Related Work
2.1.1. GT Diagnostics by Means of ML Models
2.1.2. Encoding Time Series as Images
2.1.3. CNN Visualization Techniques
2.2. Knowledge Gap and Novelty of This Study
- The development of a comprehensive methodology, which includes (i) transformation of time series into images, (ii) Convolutional Neural Network models, and (iii) classification criterion, in order to provide significant quantitative advantages to improve the accuracy and robustness of the fault diagnosis process. Such an architectural innovation (GASF/MTF and CNN) coupled with a pioneering application to GT diagnostics and a subtle type of fault (random spikes) represents the key novel contribution that this study provides.
- The exploitation and comparison of two different approaches for image encoding, namely, GASF and MTF.
- The analysis of a hard-to-detect type of fault, represented by a random series of spikes of different magnitudes and frequencies of occurrence. Because of its random nature, such a fault cannot be detected by applying standard data-driven approaches, as demonstrated in this paper. Both magnitude and frequency are varied in agreement with spikes encountered in industry practice to highlight the respective minimum value that makes such fault detectable. Moreover, the faults are artificially implanted in different combinations of the available measurable parameters to infer rules of thumb that account for both methodology capability and fault detectability. In fact, such random and isolated anomalies may be masked by measurement noise, especially in the case of low magnitude (in fact, in our paper, we also consider 1% maximum magnitude).
- The comparison of a state-of-the-art baseline approach for analyzing time series data, namely a Temporal Convolution Network (TCN), and the employment of two different CNNs with a remarkably different number of learnable parameters in order to prove that the methodology presented in this paper is clearly preferable in terms of accuracy.
- The application of the most up-to-date techniques aimed at the interpretability of CNN predictions, providing insights into the detected fault patterns and contributing to the overall trustworthiness of the whole diagnostic system.
3. Methodology
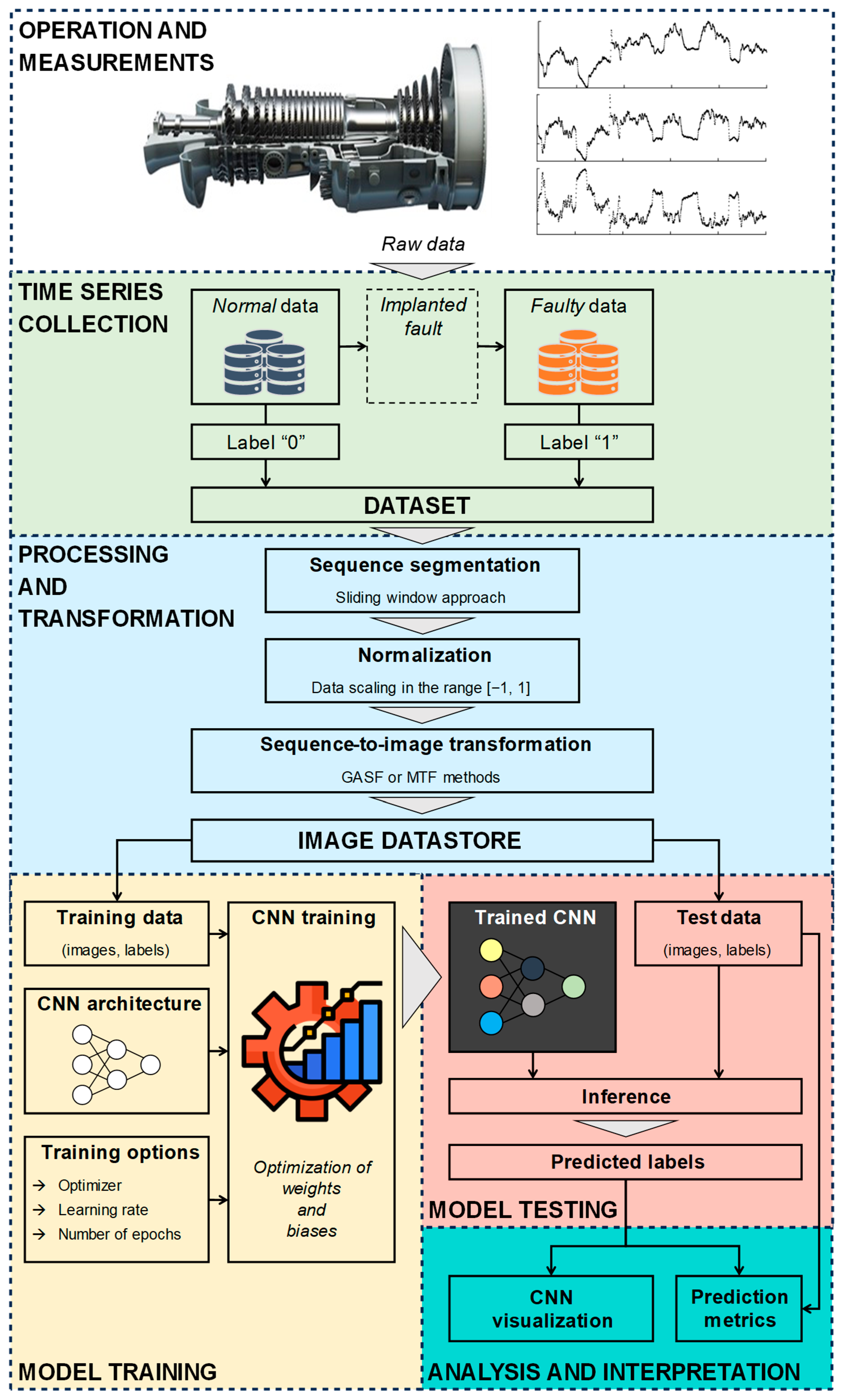
3.1. Rationale and Overview
3.2. Processing and Sequence-to-Image Transformation
3.2.1. Gramian Angular Summation Field
3.2.2. Markov Transition Field
- (i)
- Split the rescaled time series into Q quantile bins. Each bin must include the same number of data points of .
- (ii)
- Each data point, n, is assigned to the corresponding bin qj (j ∈ [1, Q]).
- (iii)
- Markov transition probability, pij, with which a data point in quantile qi is followed by a data point in quantile qj, is calculated. The sum of all probabilities makes one.
- (iv)
- Calculate ymn = pij | m ∈ qi, n ∈ qj.
3.3. Convolutional Neural Networks
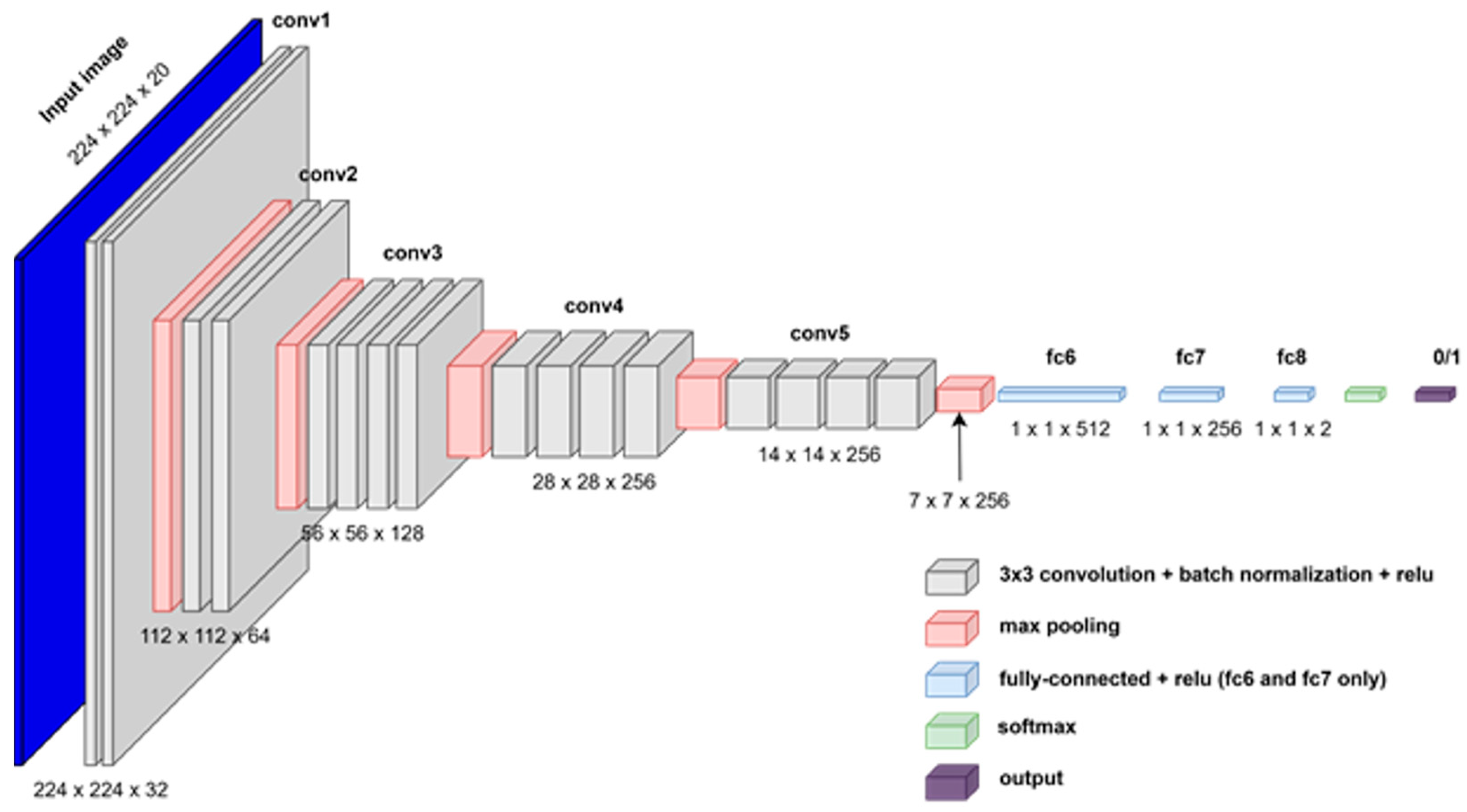
3.3.1. VGG-19 Architecture
3.3.2. SqueezeNet Architecture
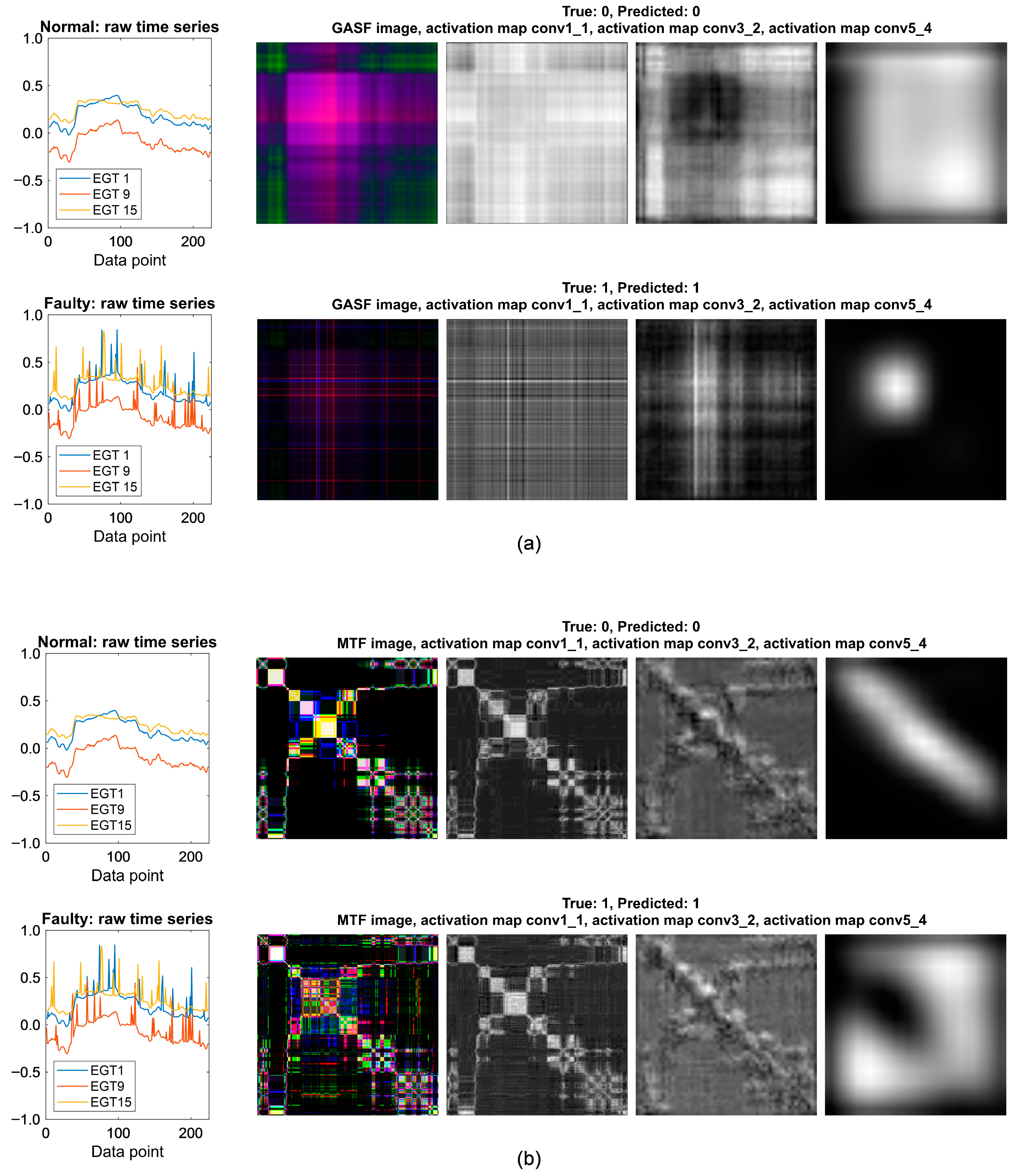
3.4. Visualization Techniques
- Activation map (AM) shows (for example, by means of a gray-scale image) the output feature map of a CNN layer during the forward pass. It can be applied to any layers of the network. The returned activation map (i.e., a square matrix for convolutional layers or a feature vector for fully connected layers) has a reduced size with respect to the input image, i.e., the activation map has lower resolution than the input image. In particular, the deeper the considered layer, the lower the resolution of the activation map. Thus, an upscaling method is required to obtain an activation map of the same size as the input image.
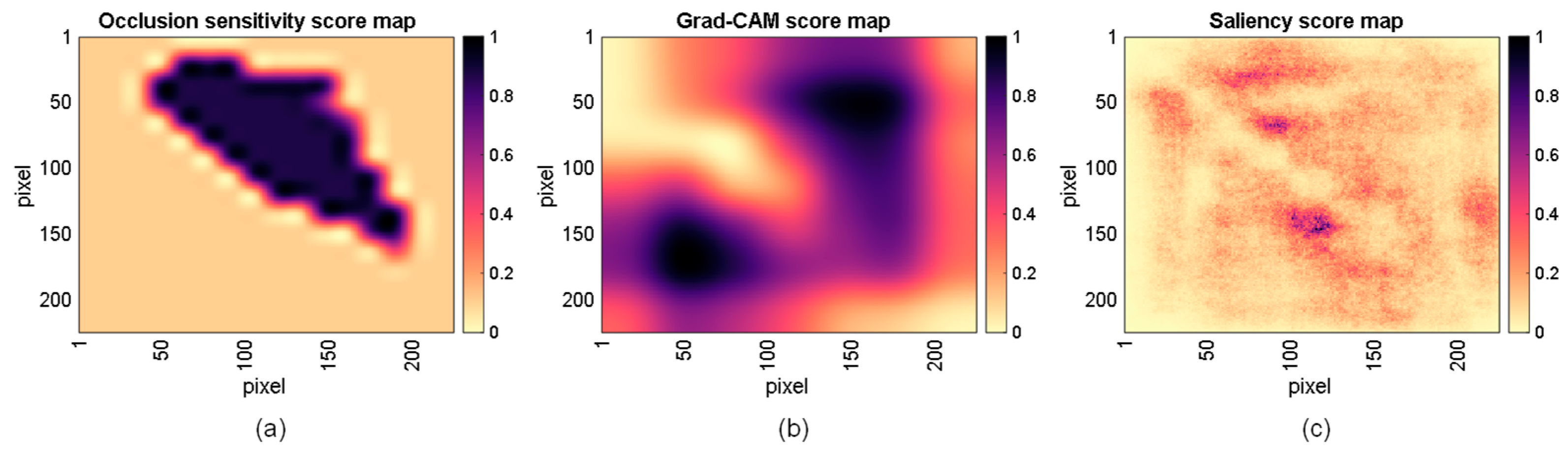
- Occlusion sensitivity (OS) measures CNN sensitivity to perturbations in the input image. The method perturbs areas of the input images by replacing it with an occluding mask. As the mask moves across the image, the technique measures the change in the probability score for a given class. The change in activation score is estimated by comparing it to the score without occlusion. Thus, occlusion sensitivity highlights the parts of the image that are most important for a given classification task. This technique requires the fine-tuning of three hyperparameters, i.e., size mask, stride, and mask value. In particular, the size of the returned score map depends on mask size and stride and a resize of the score map is required to obtain the same size as the input image. The map returned by occlusion sensitivity can be visualized by means of a heat map.
- Gradient-weighted class activation mapping (Grad-CAM) computes the gradient of the classification score with respect to a feature map learnt by CNN. Once again, the goal is the identification of the parts of an image that are most important for the classification task. The portions of an observation with a large value of the Grad-CAM map are those that most impact the CNN score for that class. The gradients of the classification score can be computed with respect to any convolutional layer in the CNN. In this work, we apply the Grad-CAM to the feature map of the ReLU layer after the last convolutional layer in the CNN (namely “relu5_4”). As observed for the AM technique, the size of the returned map depends on the selected layer and an upsampling method is usually required to obtain a score map of the same size as the input image.
- A gradient-based saliency map (Grad-SM) provides a pixel-resolution map showing the pixels that are most important. This method computes the gradient of the class score with respect to the input pixels. Intuitively, the map highlights the pixels that mostly affect the class score if it was changed. This technique produces a map of the same size as the input image. Therefore, Grad-SM images have a high resolution, but they tend to be much more affected by noise than score maps obtained by means of OS or Grad-CAM techniques.
4. Case Study
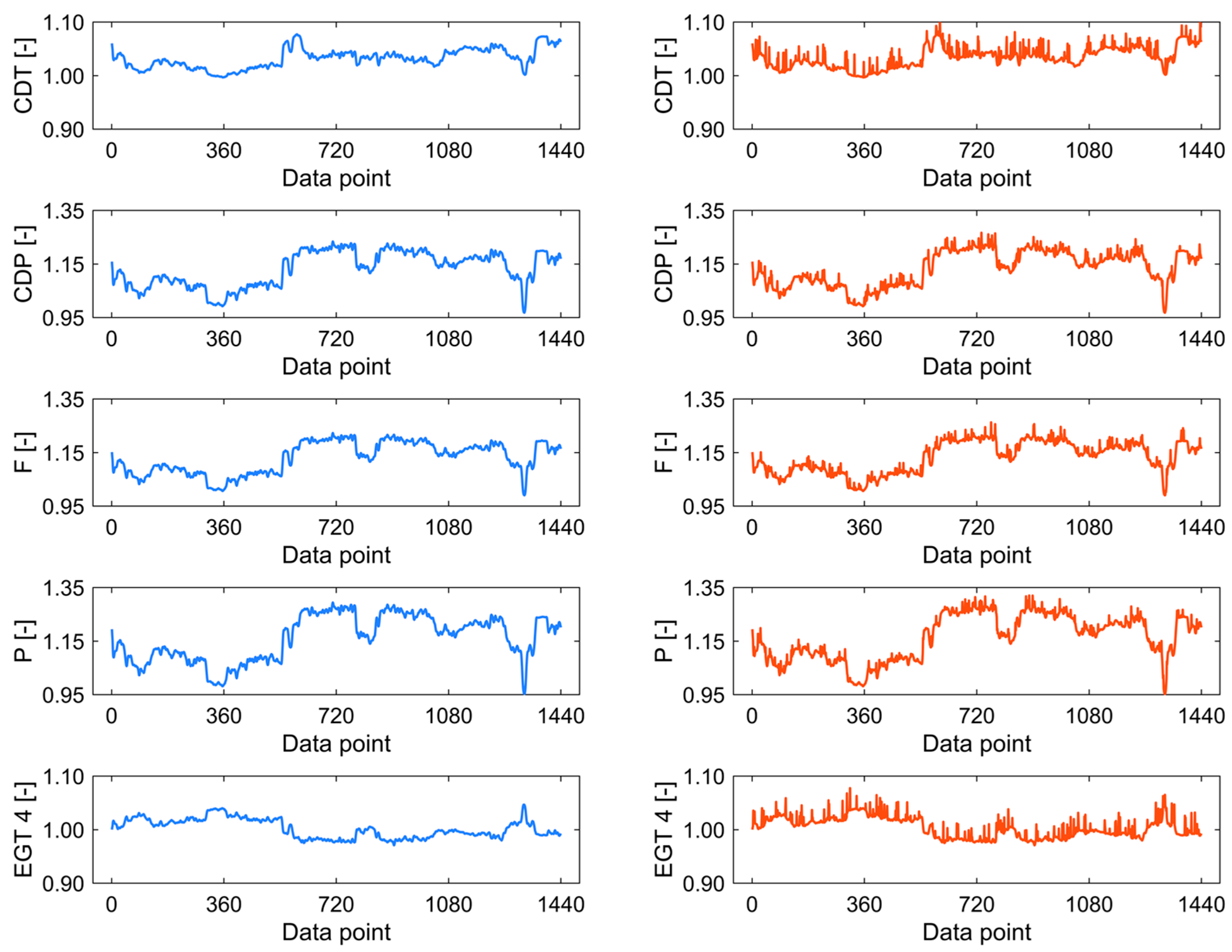
4.1. Normal Data
4.2. Implanted Fault
4.3. Training and Testing
4.4. Analyses
4.4.1. Prediction Models
- TCN: Temporal Convolutional Network fed with raw time series;
- SqueezeNet-GASF: SqueezeNet neural network fed with images obtained by means of GASF transformation;
- VGG19-GASF: VGG-19 neural network fed with images obtained by means of GASF transformation;
- SqueezeNet-MTF: SqueezeNet neural network fed with images obtained by means of MTF transformation;
- VGG19-MTF: VGG-19 neural network fed with images obtained by means of MTF transformation.
4.4.2. Fault Scenarios
- (i)
- Scenario 1: spikes are implanted in CDT and CDP variables at the same time stamps.
- (ii)
- Scenario 2: spikes are implanted in CDT, CDP, F, and P variables at the same time stamps.
- (iii)
- Scenario 3: spikes are implanted in all EGTs at the same time stamps.
- (iv)
- Scenario 4: spikes are implanted at the same time stamps in the following variables:
- -
- CDT and CDP;
- -
- CDT, CDP, F, and P;
- -
- all EGTs.
- (v)
- Scenario 5: spikes are implanted in the same combinations of variables as scenario 4, but at different time stamps across variables.
- (vi)
- Scenario 6: spikes are implanted in six different subsets of variables (s1 through s6), as follows:
- -
- s1: CDT and CDP;
- -
- s2: CDT, CDP, F, and P;
- -
- s3: CDT, CDP, and 2 EGTs;
- -
- s4: CDT, CDP, F, P, and 4 EGTs;
- -
- s5: 8 (out of 16) EGTs;
- -
- s6: 16 (all) EGTs.
4.4.3. Fault Parameters
4.5. Prediction Reliability Assessment
5. Results and Discussion
5.1. Prediction Model Performance
- VGG-19 and SqueezeNet architectures, fed with either GASF or MTF image data, almost always achieve significantly higher classification accuracy than TCN models fed with raw time series data, thus proving that the considered type of fault, i.e., a series of random and unrelated spikes of varying magnitude and frequency, can be more effectively detected by employing a 2D representation thanks to 2D convolutions. In fact, TCN models, as well as LSTM and GRU networks, are not able to grasp the temporal pattern embedded in the faulty data, which are affected by isolated and random spikes.
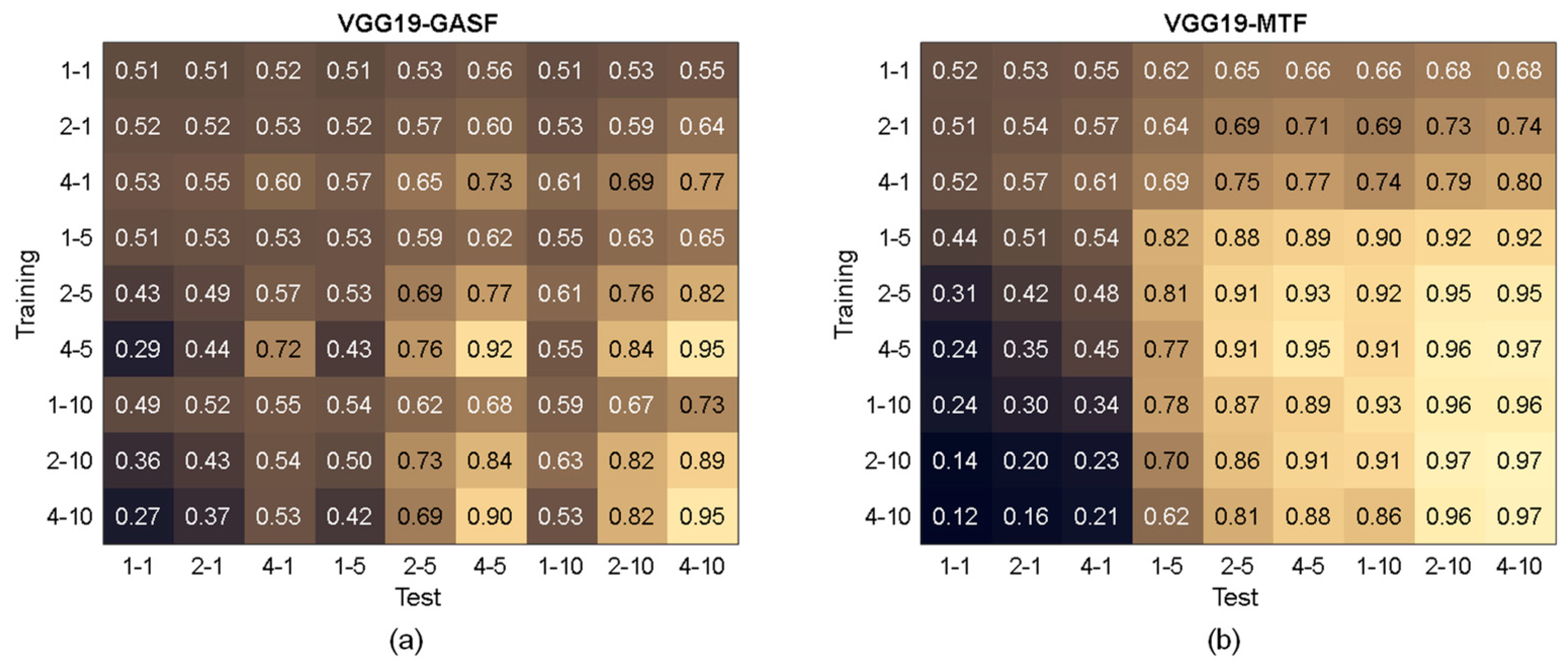
- VGG-19-MTF outperforms SqueezeNet-MTF by at least 10% on average in scenario 6, but requires higher computational time (1.8× for training and 1.25× for inference).
- The MTF method is more robust and allows for higher accuracy than the GASF method. In particular, CNN models trained by means of MTF images are less affected by spike magnitude and number of faulty input variables (i.e., channels of the image). However, it has to be highlighted that the MTF method itself requires Φ ≥ 1%, i.e., a sufficient numerosity of spikes over time.
- Models trained on more heterogeneous datasets (scenarios 4 through 6) achieve slightly lower accuracy values, but are more general than models trained on a specific pattern of fault occurrence (scenarios 1 through 3).
- The F1-score of VGG19-MTF is higher than 0.9 in 21 out of 81 tests, while VGG19-GASF achieves F1-score values higher than 0.9 only in 3 out of 81 tests.
- If Δ and/or Φ values considered for model testing are increased with respect to the values implanted in the data used for training, the F1-score of the VGG-19-MTF almost always increases (from 3% to 20%) with respect to the value achieved in the test with Δ and Φ values equal to those employed for training; instead, for VGG19-GASF, this outcome is verified only if both Δ and Φ increase with respect to the values used for training.
- If Δ and/or Φ values considered for testing are lower than the ones used for training, the F1-score of VGG19-MTF always decreases, as expected. In particular, the higher the fault severity in the training data, the higher the drop of the F1-score by decreasing fault severity during testing. However, VGG19-MTF models trained with high Δ and/or Φ have the lowest drop of F1-score (less than 4%) if fault severity is only slightly decreased during testing.
- If Δ and/or Φ values in the test data are lower than the corresponding values in the training data, the drop in the F1-score of VGG19-MTF is usually lower than that of VGG19-GASF. For example, if Δ is halved with respect to the training value, the decrease in the F1-score of VGG19-GASF is at least 25%, while that of the VGG19-MTF is negligible. On the other hand, if Φ is halved with respect to training, the F1-score of VGG19- MTF drops more (about 15–20%) than that of VGG19- GASF.
5.2. Computational Complexity, Storage Requirements, and Computational Time
5.3. CNN Visualization
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Symbols | |
| Acc | accuracy |
| C | number of channels |
| CDP | compressor discharge pressure |
| CDT | compressor discharge temperature |
| dataset | |
| EGT | exhaust gas temperature |
| F | fuel mass flow rate |
| set of faulty instances | |
| fn | number of false negatives |
| fp | number of false positives |
| h | image height |
| F1-score | F1-score |
| I | multichannel 2D image |
| K | number of folds |
| set of spike locations | |
| L | time series length |
| N | number of implanted spikes |
| p | Markov transition probability |
| P | power output variable |
| Prec | precision |
| q | quantile |
| Rec | recall |
| s | subset of faulty input variables |
| set of normal instances | |
| tn | number of true negatives |
| tp | number of true positives |
| w | image size |
| x | data point |
| x | 1D time series |
| rescaled 1D time series | |
| x* | faulty data point |
| X | multivariate time series |
| y | image pixel |
| Y | 2D image |
| Greek letters | |
| α | random coefficient |
| δ | fault magnitude |
| Δ | relative spike magnitude |
| Φ | relative numerosity of implanted spikes |
| Subscripts and superscripts | |
| i, j | quantile counter |
| max | maximum value |
| min | minimum value |
| m, n | pixel counter |
| test | test |
| train | training |
| Acronyms | |
| AI | Artificial Intelligence |
| AM | Activation Map |
| CNN | Convolutional Neural Network |
| DL | Deep Learning |
| FC | Fully connected |
| GASF | Gramian Angular Summation Field |
| Grad-CAM | Gradient-based Class Activation Mapping |
| Grad-SM | Gradient-based Saliency Map |
| GRU | Gated Recurrent Unit network |
| GT | Gas Turbine |
| LSTM | Long Short-Term Memory network |
| ML | Machine Learning |
| MTF | Markov Transition Field |
| MTS | Multivariate Time Series |
| OS | Occlusion Sensitivity |
| TCN | Temporal Convolutional Network |
Appendix A


| Fault Parameters | Subset, s# | |||||
|---|---|---|---|---|---|---|
| Δ-Φ [%-%] | 1 | 2 | 3 | 4 | 5 | 6 |
| 1-1 | 0.619 | 0.614 | 0.429 | 0.586 | 0.577 | 0.432 |
| 2-1 | 0.569 | 0.606 | 0.438 | 0.543 | 0.621 | 0.392 |
| 4-1 | 0.578 | 0.581 | 0.431 | 0.549 | 0.594 | 0.461 |
| 1-5 | 0.657 | 0.583 | 0.464 | 0.562 | 0.552 | 0.423 |
| 2-5 | 0.619 | 0.544 | 0.457 | 0.586 | 0.555 | 0.396 |
| 4-5 | 0.576 | 0.628 | 0.421 | 0.545 | 0.572 | 0.376 |
| 1-10 | 0.581 | 0.551 | 0.456 | 0.534 | 0.556 | 0.374 |
| 2-10 | 0.603 | 0.593 | 0.505 | 0.529 | 0.579 | 0.446 |
| 4-10 | 0.605 | 0.588 | 0.485 | 0.598 | 0.728 | 0.558 |
| Fault Parameters | Subset, s# | |||||
|---|---|---|---|---|---|---|
| Δ-Φ [%-%] | 1 | 2 | 3 | 4 | 5 | 6 |
| 1-1 | 0.544 | 0.596 | 0.473 | 0.525 | 0.582 | 0.428 |
| 2-1 | 0.645 | 0.577 | 0.470 | 0.595 | 0.589 | 0.391 |
| 4-1 | 0.446 | 0.399 | 0.514 | 0.642 | 0.706 | 0.638 |
| 1-5 | 0.564 | 0.594 | 0.540 | 0.590 | 0.624 | 0.387 |
| 2-5 | 0.442 | 0.428 | 0.500 | 0.642 | 0.790 | 0.706 |
| 4-5 | 0.555 | 0.533 | 0.784 | 0.957 | 0.948 | 0.962 |
| 1-10 | 0.471 | 0.485 | 0.475 | 0.556 | 0.638 | 0.482 |
| 2-10 | 0.417 | 0.438 | 0.653 | 0.862 | 0.904 | 0.919 |
| 4-10 | 0.672 | 0.687 | 0.923 | 0.977 | 0.983 | 0.964 |
| Fault Parameters | Subset, s# | |||||
|---|---|---|---|---|---|---|
| Δ-Φ [%-%] | 1 | 2 | 3 | 4 | 5 | 6 |
| 1-1 | 0.586 | 0.525 | 0.503 | 0.533 | 0.594 | 0.334 |
| 2-1 | 0.571 | 0.556 | 0.514 | 0.561 | 0.603 | 0.389 |
| 4-1 | 0.530 | 0.534 | 0.504 | 0.699 | 0.675 | 0.736 |
| 1-5 | 0.556 | 0.555 | 0.562 | 0.583 | 0.616 | 0.425 |
| 2-5 | 0.478 | 0.510 | 0.631 | 0.823 | 0.850 | 0.885 |
| 4-5 | 0.798 | 0.843 | 0.936 | 0.986 | 0.970 | 0.997 |
| 1-10 | 0.504 | 0.559 | 0.534 | 0.622 | 0.741 | 0.666 |
| 2-10 | 0.537 | 0.703 | 0.845 | 0.964 | 0.924 | 0.988 |
| 4-10 | 0.855 | 0.908 | 0.957 | 1.000 | 1.000 | 1.000 |
| Fault Parameters | Subset, s# | |||||
|---|---|---|---|---|---|---|
| Δ-Φ [%-%] | 1 | 2 | 3 | 4 | 5 | 6 |
| 1-1 | 0.500 | 0.533 | 0.488 | 0.485 | 0.453 | 0.509 |
| 2-1 | 0.530 | 0.502 | 0.473 | 0.492 | 0.470 | 0.535 |
| 4-1 | 0.443 | 0.514 | 0.500 | 0.572 | 0.518 | 0.627 |
| 1-5 | 0.544 | 0.552 | 0.581 | 0.658 | 0.533 | 0.694 |
| 2-5 | 0.671 | 0.664 | 0.748 | 0.849 | 0.643 | 0.861 |
| 4-5 | 0.766 | 0.768 | 0.839 | 0.927 | 0.711 | 0.920 |
| 1-10 | 0.741 | 0.713 | 0.805 | 0.874 | 0.562 | 0.884 |
| 2-10 | 0.901 | 0.827 | 0.930 | 0.948 | 0.653 | 0.967 |
| 4-10 | 0.945 | 0.884 | 0.951 | 0.968 | 0.694 | 0.989 |
| Fault Parameters | Subset, s# | |||||
|---|---|---|---|---|---|---|
| Δ-Φ [%-%] | 1 | 2 | 3 | 4 | 5 | 6 |
| 1-1 | 0.483 | 0.524 | 0.462 | 0.516 | 0.470 | 0.599 |
| 2-1 | 0.509 | 0.470 | 0.474 | 0.562 | 0.500 | 0.684 |
| 4-1 | 0.522 | 0.538 | 0.553 | 0.659 | 0.594 | 0.777 |
| 1-5 | 0.740 | 0.736 | 0.803 | 0.891 | 0.695 | 0.979 |
| 2-5 | 0.820 | 0.836 | 0.922 | 0.974 | 0.790 | 0.997 |
| 4-5 | 0.895 | 0.925 | 0.958 | 0.990 | 0.842 | 0.998 |
| 1-10 | 0.915 | 0.900 | 0.961 | 0.981 | 0.730 | 0.989 |
| 2-10 | 0.960 | 0.971 | 0.988 | 0.998 | 0.851 | 0.997 |
| 4-10 | 0.965 | 0.981 | 0.988 | 0.997 | 0.870 | 0.997 |
References
- Moghaddass, R.; Sheng, S. An anomaly detection framework for dynamic systems using a Bayesian hierarchical framework. Appl. Energy 2019, 240, 561–582. [Google Scholar] [CrossRef]
- Zio, E. Prognostics and Health Management (PHM): Where are we and where do we (need to) go in theory and practice. Reliab. Eng. Syst. Saf. 2022, 218, 108119. [Google Scholar] [CrossRef]
- Huang, C.; Bu, S.; Lee, H.H.; Chan, C.H.; Kong, S.W.; Yung, W.K.C. Prognostics and health management for predictive maintenance: A review. J. Manuf. Syst. 2024, 75, 78–101. [Google Scholar] [CrossRef]
- Surucu, O.; Gadsden, S.A.; Yawney, J. Condition Monitoring using Machine Learning: A Review of Theory, Applications, and Recent Advances. Expert Syst. Appl. 2023, 221, 119738. [Google Scholar] [CrossRef]
- Manservigi, L.; Venturini, M.; Ceschini, G.F.; Bechini, G.; Losi, E. Development and Validation of a General and Robust Methodology for the Detection and Classification of Gas Turbine Sensor Faults. J. Eng. Gas Turbines Power 2020, 142, 021009. [Google Scholar] [CrossRef]
- Zendehboudi, S.; Rezaei, N.; Lohi, A. Applications of hybrid models in chemical, petroleum, and energy systems: A systematic review. Appl. Energy 2018, 228, 2539–2566. [Google Scholar] [CrossRef]
- Prince, S.J.D. Understanding Deep Learning; The MIT Press: Cambridge, MA, USA, 2024; Available online: http://udlbook.com (accessed on 13 December 2024).
- Guo, J.; Yang, Y.; Li, H.; Wang, J.; Tang, A.; Shan, D.; Huang, B. A hybrid deep learning model towards fault diagnosis of drilling pump. Appl. Energy 2024, 372, 123773. [Google Scholar] [CrossRef]
- Marugána, A.P.; García Márquez, F.P.; Pinar Perez, J.M.; Ruiz-Hernández, D. A survey of artificial neural network in wind energy systems. Appl. Energy 2018, 228, 1822–1836. [Google Scholar] [CrossRef]
- Ko, J.U.; Na, K.; Oh, J.; Kim, J.; Youn, B.D. A new auto-encoder-based dynamic threshold to reduce false alarm rate for anomaly detection of steam turbines. Expert Syst. Appl. 2022, 189, 116094. [Google Scholar] [CrossRef]
- Hu, R.L.; Granderson, J.; Auslander, D.M.; Agogino, A. Design of machine learning models with domain experts for automated sensor selection for energy fault detection. Appl. Energy 2019, 235, 117–128. [Google Scholar] [CrossRef]
- Qin, Z.; Yu, F.; Liu, C.; Chen, X. How Convolutional Neural Networks See the World|A Survey of Convolutional Neural Network Visualization Methods. Math. Found. Comput. 2018, 1, 149–180. [Google Scholar] [CrossRef]
- Barra, S.; Carta, S.; Corriga, A.; Podda, A.S.; Reforgiato, D. Deep Learning and Time Series-to-Image Encoding for Financial Forecasting. IEEE/CAA J. Autom. Sin. 2020, 7, 683–692. [Google Scholar]
- Hyun, Y.; Yoo, Y.; Kim, Y.; Lee, T.; Kim, W. Encoding Time Series as Images for Anomaly Detection in Manufacturing Processes Using Convolutional Neural Networks and Grad-CAM. Int. J. Precis. Eng. Manuf. 2024, 25, 2583–2598. [Google Scholar] [CrossRef]
- Yang, J.; Sun, Y.; Chen, Y.; Mao, M.; Bai, L.; Zhang, S. Time series-to-image encoding for saturation line prediction using channel and spatial-wise attention network. Expert Syst. Appl. 2024, 237, 121440. [Google Scholar] [CrossRef]
- Simonyan, K.; Vedaldi, A.; Zisserman, A. Deep Inside Convolutional Networks: Visualising Image Classification Models and Saliency Maps. In Proceedings of the 2nd International Conference on Learning Representations, ICLR 2014, Banff, AB, Canada, 14–16 April 2014; 1312. [Google Scholar] [CrossRef]
- Mathioudakis, K.; Alexiou, A.; Aretakis, N.; Romesis, C. Signatures of Compressor and Turbine Faults in Gas Turbine Performance Diagnostics: A Review. Energies 2024, 17, 3409. [Google Scholar] [CrossRef]
- Brahimi, L.; Hadroug, N.; Iratni, A.; Hafaif, A.; Colak, I. Advancing predictive maintenance for gas turbines: An intelligent monitoring approach with ANFIS, LSTM, and reliability analysis. Comput. Ind. Eng. 2024, 191, 110094. [Google Scholar] [CrossRef]
- Arena s Florian, E.; Sgarbossa, F.; Sølvsberg, E.; Zennaro, I. A conceptual framework for machine learning algorithm selection for predictive maintenance. Eng. Appl. Artif. Intell. 2024, 133, 108340. [Google Scholar] [CrossRef]
- Rivas, A.; Delipei, G.K.; Davis, I.; Bhongale, S.; Yang, J.; Hou, J. A component diagnostic and prognostic framework for pump bearings based on deep learning with data augmentation. Reliab. Eng. Syst. Saf. 2024, 247, 110121. [Google Scholar] [CrossRef]
- Abed, A.I.; Ping, L.W. Implementing data mining techniques for gas-turbine (GT) health tracking and life management: The bibliographic perspective. Expert Syst. Appl. 2024, 252, 124077. [Google Scholar] [CrossRef]
- Bai, M.; Yang, X.; Liu, J.; Liu, J.; Yu, D. Convolutional neural network-based deep transfer learning for fault detection of gas turbine combustion chambers. Appl. Energy 2021, 302, 117509. [Google Scholar] [CrossRef]
- Irani, F.N.; Soleimani, M.; Yadegar, M.; Meskin, N. Deep transfer learning strategy in intelligent fault diagnosis of gas turbines based on the Koopman operator. Appl. Energy 2024, 365, 123256. [Google Scholar] [CrossRef]
- Sun, J.; Yan, Z.; Han, Y.; Zhu, X.; Yang, C. Deep learning framework for gas turbine performance digital twin and degradation prognostics from airline operator perspective. Reliab. Eng. Syst. Saf. 2023, 238, 109404. [Google Scholar] [CrossRef]
- Bettocchi, R.; Pinelli, M.; Spina, P.R.; Venturini, M. Artificial Intelligence for the Diagnostics of Gas Turbines. Part I: Neural Network Approach. ASME J. Eng. Gas Turbines Power 2007, 129, 711–719. [Google Scholar] [CrossRef]
- Losi, E.; Venturini, M.; Manservigi, L.; Bechini, G. Ensemble Learning Approach to the Prediction of Gas Turbine Trip. J. Eng. Gas Turbines Power 2023, 145, 021009. [Google Scholar] [CrossRef]
- Losi, E.; Venturini, M.; Manservigi, L.; Bechini, G. Methodology to Monitor Early Warnings Before Gas Turbine Trip. J. Eng. Gas Turbines Power 2024, 146, 051005. [Google Scholar] [CrossRef]
- Wen, Y.; Rahman Md, F.; Xu, H.; Tseng, T.-L.B. Recent advances and trends of predictive maintenance from data-driven machine prognostics perspective. Measurement 2022, 187, 110276. [Google Scholar] [CrossRef]
- Li, Q.; Tang, Y.; Chu, L. Generative adversarial networks for prognostic and health management of industrial systems: A review. Expert Syst. Appl. 2024, 253, 124341. [Google Scholar] [CrossRef]
- Losi, E.; Manservigi, L.; Spina, P.R.; Venturini, M. Data-driven Generative Model Aimed to Create Synthetic Data for the Long-Term Forecast of Gas Turbine Operation. In Proceedings of the ASME Turbo Expo 2024: Turbomachinery Technical Conference and Exposition, London, UK, 24–28 June 2024. ASME Paper GT2024-122162. [Google Scholar]
- Sok, R.; Jeyamoorthy, A.; Kusaka, J. Novel virtual sensors development based on machine learning combined with convolutional neural-network image processing-translation for feedback control systems of internal combustion engines. Appl. Energy 2024, 365, 123224. [Google Scholar] [CrossRef]
- Thiel, M.; Romano, M.C.; Kurths, J. How much information is contained in a recurrence plot? Phys. Lett. A 2004, 330, 343–349. [Google Scholar] [CrossRef]
- McGuire, G.; Azar, N.B.; Shelhamer, M. Recurrence matrices and the preservation of dynamical properties. Phys. Lett. A 1997, 237, 41–43. [Google Scholar] [CrossRef]
- Łuczak, D. Machine Fault Diagnosis through Vibration Analysis: Time Series Conversion to Grayscale and RGB Images for Recognition via Convolutional Neural Networks. Energies 2024, 17, 1998. [Google Scholar] [CrossRef]
- Wang, Z.; Oates, T. Encoding Time Series as Images for Visual Inspection and Classification Using Tiled Convolutional Neural Networks. In Proceedings of the AAAI-15 (Twenty-Ninth Conference on Artificial Intelligence), Austin, TX, USA, 25–30 January 2015. [Google Scholar]
- Wang, Z.; Oates, T. Imaging Time-Series to Improve Classification and Imputation. In Proceedings of the IJCAI’15: 24th International Conference on Artificial Intelligence, Buenos Aires, Argentina, 25–31 July 2015. [Google Scholar] [CrossRef]
- Xu, H.; Li, J.; Yuan, H.; Liu, Q.; Fan, S.; Li, T.; Sun, X. Human Activity Recognition Based on Gramian Angular Field and Deep Convolutional Neural Network. IEEE Access 2020, 8, 199393–199405. [Google Scholar] [CrossRef]
- Jiang, W.; Zhang, D.; Ling, L.; Lin, R. Time Series Classification Based on Image Transformation Using Feature Fusion Strategy. Neural Process. Lett. 2022, 54, 3727–3748. [Google Scholar] [CrossRef]
- Sayed, A.N.; Himeur, Y.; Bensaali, F. From time-series to 2D images for building occupancy prediction using deep transfer learning. Eng. Appl. Artif. Intell. 2023, 119, 105786. [Google Scholar] [CrossRef]
- Li, X.; Zhang, J.; Xiao, B.; Zeng, Y.; Lv, S.; Qian, J.; Du, Z. Fault Diagnosis of Hydropower Units Based on Gramian Angular Summation Field and Parallel CNN. Energies 2024, 17, 3084. [Google Scholar] [CrossRef]
- Zeiler, M.D.; Fergus, R. Visualizing and Understanding Convolutional Networks. In Computer Vision—ECCV 2014. ECCV 2014. Lecture Notes in Computer Science; Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; Springer: Cham, Switzerland, 2014; Volume 8689. [Google Scholar] [CrossRef]
- Bach, S.; Binder, A.; Montavon, G.; Klauschen, F.; Müller, K.-R.; Samek, W. On Pixel-Wise Explanations for Non-Linear Classifier Decisions by Layer-Wise Relevance Propagation. PLoS ONE 2015, 10, e0130140. [Google Scholar] [CrossRef]
- Yosinski, J.; Clune, J.; Nguyen, A.; Fuchs, T.; Lipson, H. Understanding Neural Networks Through Deep Visualization. In Proceedings of the 31st International Conference on Machine Learning, Lille, France, 6–11 July 2015; 1506. [Google Scholar] [CrossRef]
- Yu, W.; Yang, K.; Bai, Y.; Rui, Y.; Yao, H. Visualizing and Comparing Convolutional Neural Networks. In Proceedings of the ICLR 2015 Conference, San Diego, CA, USA, 7–9 May 2015; 1412. [Google Scholar] [CrossRef]
- Zhou, B.; Khosla, A.; Lapedriza, A.; Oliva, A.; Torralba, A. Learning Deep Features for Discriminative Localization. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016. [Google Scholar]
- Samek, W.; Wiegand, T.; Muller, K.-R. Explainable Artificial Intelligence: Understanding, Visualizing and Interpreting Deep Learning Models. arXiv 2017, arXiv:1708.08296v1. [Google Scholar] [CrossRef]
- Liu, L.; Wang, Z. Encoding Temporal Markov Dynamics in Graph for Visualizing and Mining Time Series, AAAI 2018 workshop. arXiv 2018, arXiv:1610.07273. [Google Scholar] [CrossRef]
- Montavon, G.; Binder, A.; Lapuschkin, S.; Samek, W.; Müller, K.R. Layer-Wise Relevance Propagation: An Overview. In Explainable AI: Interpreting, Explaining and Visualizing Deep Learning; Lecture Notes in Computer Science; Samek, W., Montavon, G., Vedaldi, A., Hansen, L., Müller, K.R., Eds.; Springer: Cham, Switzerland, 2019; Volume 11700. [Google Scholar] [CrossRef]
- Iwana, B.K.; Kuroki, R.; Uchida, S. Explaining Convolutional Neural Networks using Softmax Gradient Layer-wise Relevance Propagation. arXiv 2019, arXiv:1908.04351v3. [Google Scholar] [CrossRef]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual Explanations from Deep Networks via Gradient-Based Localization. Int. J. Comput. Vis. 2020, 128, 336–359. [Google Scholar] [CrossRef]
- Ruan, Y.; Zheng, M.; Qian, F.; Meng, H.; Yao, J.; Xu, T.; Pei, D. Fault detection and diagnosis of energy system based on deep learning image recognition model under the condition of imbalanced samples. Appl. Therm. Eng. 2024, 238, 122051. [Google Scholar] [CrossRef]
- Płuciennik, P.; Jaśkiewicz, M.; Liśkiewicz, G. Classification of Compressors Stability Using an Image Recognition Machine Learning Model. In Proceedings of the ASME Turbo Expo 2025: Turbomachinery Technical Conference and Exposition, Memphis, TN, USA, 16–20 June 2025. ASME Paper GT2025-154137. [Google Scholar]
- Losi, E.; Venturini, M.; Manservigi, L.; Bechini, G. Gas Turbine Diagnostics by Means of Convolutional Neural Networks Fed With Time Series Data Encoded as Images. ASME J. Eng. Gas Turbines Power 2025, 1–25. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Iandola, F.N.; Han, S.; Moskewicz, M.W.; Ashraf, K.; Dally, W.J.; Keutzer, K. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <0.5 MB model size. In Proceedings of the 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, 24–26 April 2017. [Google Scholar]
- Iandola, F.N. SqueezeNet. Available online: https://github.com/forresti/SqueezeNet/tree/master/SqueezeNet_v1.1 (accessed on 13 December 2024).
- Lo, C.; Lynch, J.P.; Liu, M. Distributed Model-Based Nonlinear Sensor Fault Diagnosis in Wireless Sensor Networks. Mech. Syst. Signal Process. 2016, 66–67, 470–484. [Google Scholar] [CrossRef]
- Muhammed, T.; Shaikh, R.A. An Analysis of Fault Detection Strategies in Wireless Sensor Networks. J. Netw. Comput. Appl. 2017, 78, 267–287. [Google Scholar] [CrossRef]
- Jombo, G.; Zhang, Y.; Griffiths, J.D. Automated Gas Turbine Sensor Fault Diagnostics. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition, Oslo, Norway, 11–15 June 2018. ASME Paper No. GT2018-75229. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations (ICLR), 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]




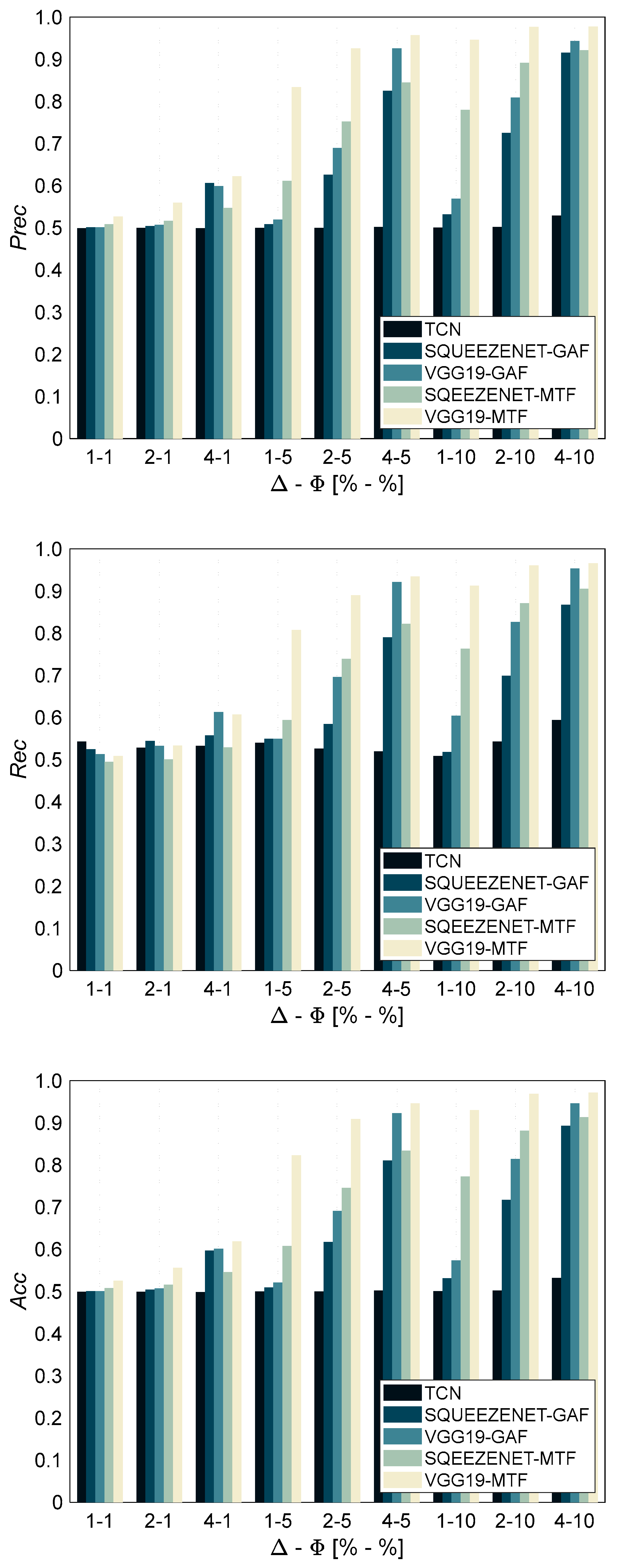

| Fault Parameters | Prediction Model | ||||
|---|---|---|---|---|---|
| Δ-Φ [%-%] | TCN | SqueezeNet-GASF | VGG19-GASF | SqueezeNet-MTF | VGG19-MTF |
| 1-1 | 0.500 | 0.500 | 0.500 | 0.501 | 0.513 |
| 2-1 | 0.500 | 0.500 | 0.501 | 0.507 | 0.516 |
| 4-1 | 0.500 | 0.502 | 0.502 | 0.515 | 0.541 |
| 1-5 | 0.500 | 0.501 | 0.502 | 0.679 | 0.848 |
| 2-5 | 0.500 | 0.510 | 0.511 | 0.809 | 0.897 |
| 4-5 | 0.502 | 0.609 | 0.666 | 0.897 | 0.951 |
| 1-10 | 0.500 | 0.502 | 0.506 | 0.921 | 0.973 |
| 2-10 | 0.501 | 0.573 | 0.642 | 0.971 | 0.988 |
| 4-10 | 0.505 | 0.746 | 0.856 | 0.983 | 0.990 |
| Fault Parameters | Prediction Model | ||||
|---|---|---|---|---|---|
| Δ-Φ [%-%] | TCN | SqueezeNet-GASF | VGG19-GASF | SqueezeNet-MTF | VGG19-MTF |
| 1-1 | 0.500 | 0.500 | 0.500 | 0.505 | 0.514 |
| 2-1 | 0.500 | 0.500 | 0.500 | 0.508 | 0.526 |
| 4-1 | 0.500 | 0.504 | 0.503 | 0.524 | 0.565 |
| 1-5 | 0.500 | 0.501 | 0.502 | 0.695 | 0.845 |
| 2-5 | 0.500 | 0.514 | 0.530 | 0.822 | 0.931 |
| 4-5 | 0.500 | 0.662 | 0.770 | 0.889 | 0.963 |
| 1-10 | 0.500 | 0.505 | 0.507 | 0.919 | 0.973 |
| 2-10 | 0.501 | 0.573 | 0.671 | 0.970 | 0.989 |
| 4-10 | 0.502 | 0.778 | 0.879 | 0.975 | 0.992 |
| Fault Parameters | Prediction Model | ||||
|---|---|---|---|---|---|
| Δ-Φ [%-%] | TCN | SqueezeNet-GASF | VGG19-GASF | SqueezeNet-MTF | VGG19-MTF |
| 1-1 | 0.500 | 0.505 | 0.503 | 0.525 | 0.620 |
| 2-1 | 0.500 | 0.604 | 0.567 | 0.589 | 0.770 |
| 4-1 | 0.504 | 0.928 | 0.985 | 0.657 | 0.850 |
| 1-5 | 0.501 | 0.685 | 0.767 | 0.882 | 0.960 |
| 2-5 | 0.718 | 0.956 | 0.986 | 0.958 | 0.990 |
| 4-5 | 0.997 | 0.992 | 0.999 | 0.980 | 0.990 |
| 1-10 | 0.506 | 0.885 | 0.958 | 0.971 | 0.980 |
| 2-10 | 0.976 | 0.987 | 0.992 | 0.990 | 0.990 |
| 4-10 | 1.000 | 0.998 | 0.996 | 0.990 | 1.000 |
| Fault Parameters | Prediction Model | ||||
|---|---|---|---|---|---|
| Δ-Φ [%-%] | TCN | SqueezeNet-GASF | VGG19-GASF | SqueezeNet-MTF | VGG19-MTF |
| 1-1 | 0.500 | 0.501 | 0.501 | 0.504 | 0.517 |
| 2-1 | 0.500 | 0.508 | 0.504 | 0.509 | 0.522 |
| 4-1 | 0.501 | 0.562 | 0.575 | 0.512 | 0.540 |
| 1-5 | 0.500 | 0.512 | 0.516 | 0.577 | 0.784 |
| 2-5 | 0.501 | 0.581 | 0.653 | 0.664 | 0.894 |
| 4-5 | 0.560 | 0.798 | 0.903 | 0.769 | 0.937 |
| 1-10 | 0.501 | 0.529 | 0.556 | 0.766 | 0.931 |
| 2-10 | 0.512 | 0.703 | 0.813 | 0.889 | 0.971 |
| 4-10 | 0.607 | 0.871 | 0.949 | 0.924 | 0.979 |
| Fault Parameters | Prediction Model | ||||
|---|---|---|---|---|---|
| Δ-Φ [%-%] | TCN | SqueezeNet-GASF | VGG19-GASF | SqueezeNet-MTF | VGG19-MTF |
| 1-1 | 0.500 | 0.501 | 0.501 | 0.507 | 0.525 |
| 2-1 | 0.500 | 0.503 | 0.511 | 0.513 | 0.559 |
| 4-1 | 0.500 | 0.551 | 0.557 | 0.533 | 0.603 |
| 1-5 | 0.500 | 0.507 | 0.516 | 0.621 | 0.837 |
| 2-5 | 0.502 | 0.555 | 0.626 | 0.759 | 0.920 |
| 4-5 | 0.507 | 0.772 | 0.921 | 0.850 | 0.961 |
| 1-10 | 0.500 | 0.518 | 0.548 | 0.820 | 0.957 |
| 2-10 | 0.506 | 0.652 | 0.783 | 0.915 | 0.980 |
| 4-10 | 0.550 | 0.867 | 0.957 | 0.950 | 0.985 |
| Fault Parameters | Prediction Model | ||||
|---|---|---|---|---|---|
| Δ-Φ [%-%] | TCN | SqueezeNet-GASF | VGG19-GASF | SqueezeNet-MTF | VGG19-MTF |
| 1-1 | 0.500 | 0.501 | 0.501 | 0.509 | 0.525 |
| 2-1 | 0.500 | 0.505 | 0.508 | 0.517 | 0.556 |
| 4-1 | 0.499 | 0.597 | 0.601 | 0.546 | 0.619 |
| 1-5 | 0.500 | 0.510 | 0.521 | 0.608 | 0.823 |
| 2-5 | 0.500 | 0.617 | 0.691 | 0.745 | 0.909 |
| 4-5 | 0.503 | 0.811 | 0.923 | 0.834 | 0.946 |
| 1-10 | 0.501 | 0.531 | 0.574 | 0.773 | 0.930 |
| 2-10 | 0.503 | 0.717 | 0.814 | 0.882 | 0.969 |
| 4-10 | 0.532 | 0.893 | 0.946 | 0.914 | 0.972 |
| Method | Computational Complexity | Optimization Strategy | Storage Requirement | Store Precision | Size (MB) |
|---|---|---|---|---|---|
| GASF | O(w2) | Store only the upper triangular part | O(w2/2) | int16 (2 bytes) | 4 |
| MTF | O(w) | Store the entire MTM matrix | O(Q2) | float32 (4 bytes) | 0.005 |
| Model | Training Time [Hours] | Inference Time [Hours] |
|---|---|---|
| VGG19-MTF | 0.625 ± 0.017 | 0.013 ± 0.002 |
| VGG19-GASF | 0.631 ± 0.038 | 0.023 ± 0.002 |
| SqueezeNet-MTF | 0.328 ± 0.002 | 0.010 ± 0.002 |
| SqueezeNet-GASF | 0.410 ± 0.003 | 0.023 ± 0.003 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Losi, E.; Venturini, M.; Manservigi, L.; Bechini, G. Encoding Multivariate Time Series of Gas Turbine Data as Images to Improve Fault Detection Reliability. Machines 2025, 13, 943. https://doi.org/10.3390/machines13100943
Losi E, Venturini M, Manservigi L, Bechini G. Encoding Multivariate Time Series of Gas Turbine Data as Images to Improve Fault Detection Reliability. Machines. 2025; 13(10):943. https://doi.org/10.3390/machines13100943
Chicago/Turabian StyleLosi, Enzo, Mauro Venturini, Lucrezia Manservigi, and Giovanni Bechini. 2025. "Encoding Multivariate Time Series of Gas Turbine Data as Images to Improve Fault Detection Reliability" Machines 13, no. 10: 943. https://doi.org/10.3390/machines13100943
APA StyleLosi, E., Venturini, M., Manservigi, L., & Bechini, G. (2025). Encoding Multivariate Time Series of Gas Turbine Data as Images to Improve Fault Detection Reliability. Machines, 13(10), 943. https://doi.org/10.3390/machines13100943






