Research and Mechanism Design Analysis of Devices Based on Human Upper Limb Stretching

Abstract

The upper limb stretching device plays a key role in enhancing physical function. Current commercial upper limb stretching devices often suffer from limited functionality and are poorly aligned with the biomechanics of the human arm. To address these limitations, this paper presents the design of an ergonomic device for upper limb stretching. Firstly, the development of a regression model for the upper limb force test was carried out through the Box–Behnken Design (BBD) response surface methodology. Secondly, the Denavit-Hartenberg (D-H) method was adopted for the kinematic analysis of the human upper limb stretching mechanism. Subsequently, a kinematic model was established by coupling the data from Creo Parametric and ADAMS models. The kinematic characteristics were then investigated throughout the entire range of motion, yielding the corresponding kinematic parameter curves. Next, the finite element method was employed within ABAQUS to model the upper limb stretching mechanism, to allow for a detailed strength analysis of its key components. Finally, a prototype was manufactured and tested through upper limb stretching experiments to validate its performance. The results demonstrate that the designed stretching mechanism achieved the desired range of motion, with its angular velocity and angular acceleration exhibiting smooth variations. The maximum stress observed is 195.2 MPa, which meets the design requirements. This study provides a valuable reference for the development of future human stretching devices.

1. Introduction

Data from the World Health Organization (WHO) indicates that physical overexertion claims as many as two million lives annually worldwide [1]. Using mechanical devices for stretching is one of the effective ways to relieve mental or physical fatigue in individuals [2,3,4,5]. A growing number of researchers are directing their efforts toward the development of devices for stretching human muscles and skeletons to alleviate physical fatigue.

Substantial research has been conducted on the kinematic characteristics of devices designed for human body stretching. Among these, continuous technological advancements have driven significant progress in the design, performance, and applications of upper limb devices. In 1992, Neville Hogan et al. developed the MIT-Manus rehabilitation robot [6]. The system employs a two-degree-of-freedom (2-DOF) linkage mechanism. Its end-effector drives the patient’s upper limb to perform targeted motion training for shoulder and elbow joints within a two-dimensional plane. MIME, an upper limb rehabilitation device developed at Stanford University in the 1990s. It adds a movable arm brace in front of the robotic arm, and the patient’s hand and wrist joints are immobilized by the brace and move with the movement of the end of the robotic arm [7,8]. In comparison with the existing equipment, the design presented in this study offers a significant advantage in size, resulting in greater portability, without compromising functional performance. The RUPERT upper limb rehabilitation exoskeleton was designed by Arizona State University in the United States. It has five degrees of freedom and can achieve most of the movements of the shoulder, elbow and wrist joints of the upper limb [9]. This apparatus employs pneumatic artificial muscles (PAMs) for actuation, featuring compact dimensions, lightweight construction, enhanced ergonomic compatibility, and user-friendly operation. The wearable variable-stiffness upper limb motion device was developed at Kagawa University (Japan). Incorporating five passive degrees of freedom and one variable stiffness actuator [10,11], the system autonomously regulates joint drive torque magnitude. A research team from Tsinghua University developed a two-degree-of-freedom (2-DOF) upper limb motion device. This system achieves planar 2-DOF training motions through linkage-based immobilization of the human upper limb [12,13]. Huazhong University of Science and Technology (HUST) developed an upper limb exoskeletal device with three degrees of freedom (3-DOF) motion capability in 2016 [14]. This device adopts pneumatic artificial muscles as the core driving component and has developed a dedicated control architecture accordingly [15]. Through triaxial cooperative actuation of shoulder flexion-extension, internal–external rotation, and elbow flexion–extension, the system achieves coordinated multi-joint movements during rehabilitation training. The aforementioned devices are characterized by high costs and require operation by specialized personnel. However, the present design prioritizes a simplified user interface and safety, achieving lower manufacturing costs and resulting in a significant cost-effectiveness advantage.

Although there has been considerable worldwide research into the design, manufacturing, and analysis of assistive devices, limitations in functionality and kinematic mismatches with human biomechanics persist in current systems. Through investigating stretch kinematics of the upper limbs, this study employs response surface methodology to analyze force variations during stretching under multifactorial conditions. An ergonomic tensile mechanism tailored to the biomechanical requirements of the upper limbs has been designed. Subsequent 3D modeling and kinematic analysis establish the theoretical foundation for developing human-centered stretching devices.

2. Methods

2.1. Mechanism Prototype Design

2.1.1. Requirements Analysis for an Upper Limb Stretching Mechanisms

(1)

Functional Requirements for Mechanisms

Analysis of upper limb stretching methods indicates that the stretching mechanism should be capable of multi-degree-of-freedom motion at the human shoulder joint, including flexion-extension and abduction-adduction movements. The operational range of the upper limb stretching mechanism was designed based on the shoulder joint’s range of motion. In designing the mechanism, stretching efficacy was also considered, as shown in Figure 1.

(2)

Dimensional Requirements for Mechanisms

The human-body stretching mechanism must ensure proper functioning while accommodating dimensional constraints. To achieve a stretching effect on the human upper limbs while ensuring comfort, the design of the stretching mechanism must adapt to the physical characteristics of different user groups defined by age and gender. The dimensional design of the upper limb stretching mechanisms was based on the anthropometric sitting measurements [16] and ergonomic principles. The resulting designs are shown in Figure 2 and

Table 1. Upper Limb Dimensions of Adults.

Test Item (mm) and Percentile (%)	Male (18–70 Years Old)					Female (18–70 Years Old)
	5	10	50	90	95	5	10	50	90	95
Forward Reach Length	760	774	822	873	888	693	709	755	805	820
Functional Forward Reach	654	667	710	758	774	595	609	653	700	715
Seated Overhead Reach Height	1242	1267	1348	1432	1456	1137	1159	1234	1307	1329

.

The design reference adopted the central range covering the 10th to 90th percentiles of the seated anthropometric dimensions. The extreme 5th and 95th percentile groups were excluded to accommodate the majority population. The upper limb extension mechanism must accommodate motion requirements for the target user population. Given significant anthropometric variations in key upper limb dimensions, the mechanism requires an adjustable range to ensure ergonomic functionality. The design bounds for the upper limb extension mechanism were derived from a synthesis of primary anthropometric dimensions of adult males and females. The maximum value defined the upper limit, while the minimum value established the lower limit. This defined the dimensional operating envelope.

2.1.2. Configuration Design of the Upper Limb Extension Mechanism

Analysis of the mechanism and requirements for human upper limb stretching movements determined the intended motions for the stretching mechanism: arm abduction/adduction in the coronal plane and arm flexion/extension in the sagittal plane. Therefore, the mechanism requires two independent actuators: one for arm raising and another for arm opening. The upper limb stretching mechanism that had been presented in this paper was electrically driven. Figure 3 shows a schematic diagram illustrating its working principle.

The upper limb stretching mechanism consisted of two distinct sections: the arm-raising section and the arm-opening section. The initial state of the mechanism is shown in Figure 3a,c. The arm-opening actuator divided the arm assembly into a forearm segment and an upper arm segment. The arm-raising actuator was mounted to the rear end of the upper arm segment, and the arm-opening actuator was mounted to the rear end of the forearm segment. The upper arm and forearm segments were rigidly joined, retaining only rotational degrees of freedom in the coronal plane. An adjustable rod was included at the distal end of the forearm segment to accommodate the upper limb stretching requirements of most individuals. The lifting motion was achieved by the arm-raising actuator driving the upper arm segment. This motion propagated to the forearm segment, resulting in the lifting and lowering action of the entire upper limb assembly. During the lifting and lowering motion of the upper limb stretching mechanism in the sagittal plane, the arm-opening actuator controlled the forearm segment to perform opening-closing motion in the coronal plane. This combined action thus enabled effective stretching of the human upper limb. Figure 3b,d depict the lifted state and opened state of the mechanism, respectively.

2.2. Kinematic Analysis of an Upper Limb Stretching Mechanism

The establishment of a kinematic model was fundamental to analyzing the motion performance of the upper limb stretching mechanism. The upper-limb stretching mechanism designed in this study comprises two independent degrees of freedom: arm abduction/adduction in the coronal plane and arm elevation/depression in the sagittal plane. Therefore, the mechanism can be considered as a serial chain of two revolute joints and connecting links.

Based on the D-H parameter method, the pose relationships and kinematic models of the components of the human upper limb stretching mechanisms were established [17]. D-H coordinate frames for all components of the human upper limb stretching mechanisms are shown in Figure 4. There, L₁ represents the distance from the rotation center of the arm lifting mechanism to the rotation center of the arm opening mechanism, and L₂ denotes the distance from the rotation center of the arm opening mechanism to the endpoint of the arm.

The D-H parameters of the mechanism, which are defined according to the coordinate frames shown in Figure 4, are listed in

Table 2. Parameters of upper limb stretching mechanism D-H.

$\mathit{i}$	${\mathit{\alpha }}_{\mathit{i}-1}$	${\mathit{a}}_{\mathit{i}-1}$	${\mathit{d}}_{\mathit{i}}$	${\mathit{\theta }}_{\mathit{i}}$
1	0	0	0	${\theta }_1$
2	90°	$L_1$	0	${\theta }_2$

[18]. It can be concluded that the stretching motion of the human upper limb involves rotation around the joints without translation; therefore, the joint distance ‘d’ is 0.

(1)

Forward Kinematics Analysis

For the forward kinematics of the upper limb stretching mechanism, the coordinate transformation between adjacent links can be described using homogeneous transformation matrices. Based on the D-H coordinate system and its parameters, the individual transformation matrices are derived.

$${\mathit{T}}_{\mathbf{1}}=\left[\begin{array}{cccc}c{\theta }_1& -s{\theta }_1& 0& 0\\ s{\theta }_1& c{\theta }_1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$

(1)

$${\mathit{T}}_{\mathbf{2}}=\left[\begin{array}{cccc}c{\theta }_2& -s{\theta }_2& 0& L_1\\ 0& 0& -1& 0\\ s{\theta }_2& c{\theta }_2& 0& 0\\ 0& 0& 0& 1\end{array}\right]$$

(2)

Multiplying the above transformation matrices yields Matrix (3):

$$\mathit{T}={\mathit{T}}_{\mathbf{1}}{\mathit{T}}_{\mathbf{2}}=\left[\begin{array}{cccc}c{\theta }_{1}c{\theta }_2& -c{\theta }_{1}s{\theta }_2& s{\theta }_1& L_1\cdot c{\theta }_1\\ s{\theta }_{1}c{\theta }_2& -s{\theta }_{1}s{\theta }_2& -c{\theta }_1& L_1\cdot s{\theta }_1\\ s{\theta }_2& c{\theta }_2& 0& 0\\ 0& 0& 0& 1\end{array}\right]$$

(3)

The end-effector pose can be obtained by applying a translation of distance L₂ from the rotation center of the arm opening mechanism to the endpoint of the arm.

$${\mathit{T}}_{\mathit{f}\mathit{i}\mathit{n}\mathit{a}\mathit{l}}=\left[\begin{array}{cccc}\cos {\theta }_1\cos {\theta }_2& -\cos {\theta }_1\sin {\theta }_2& \sin {\theta }_1& L_1\cos {\theta }_1+L_2\cos {\theta }_1\cos {\theta }_2\\ \sin {\theta }_1\cos {\theta }_2& -\sin {\theta }_1\sin {\theta }_2& -\cos {\theta }_1& L_1\sin {\theta }_1+L_2\sin {\theta }_1\cos {\theta }_2\\ \sin {\theta }_2& \cos {\theta }_2& 0& L_2\sin {\theta }_2\\ 0& 0& 0& 1\end{array}\right]$$

(4)

Substituting the known parameters, including joint angles and link lengths, into the transformation matrices allows the end-effector position of the upper limb stretching mechanism to be determined.

(2)

Inverse Kinematics Analysis

Given the end-effector position and orientation, the joint rotation angles can be determined. The position equations can be derived from the fourth column of the ${\mathit{T}}_{\mathit{f}\mathit{i}\mathit{n}\mathit{a}\mathit{l}}$ matrix.

$$\left\{\begin{array}{l}x=L_{1}cos{\theta }_1+L_{2}cos{\theta }_{1}cos{\theta }_2\\ y=L_{1}sin{\theta }_1+L_{2}sin{\theta }_{1}cos{\theta }_2\\ z=L_{2}sin{\theta }_2\end{array}\right.$$

(5)

From Equation (5), we obtain:

$${\theta }_2=\mathrm{atan}2\left(z,{\displaystyle \frac{x^2+y^2-L_1^2}{2L_1}}\right)$$

(6)

$${\theta }_1=\mathrm{atan}2\left(y,x\right)$$

(7)

(3)

Velocity Analysis

The velocity equations are obtained by differentiating the position equations with respect to time. Let ${\dot{\theta }}_1$ and ${\dot{\theta }}_2$ represent the angular velocities of joint 1 and joint 2, respectively.

Differentiating with respect to x, y, and z, respectively, yields Equation (8):

$$\left\{\begin{array}{l}\dot{x}=-\left(L_1+L_2\cos {\theta }_2\right)\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_1{\dot{\theta }}_1-L_2\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_1\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_2{\dot{\theta }}_2\\ \dot{y}=\left(L_1+L_2\cos {\theta }_2\right)\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_1{\dot{\theta }}_1-L_2\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_1\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_2{\dot{\theta }}_2\\ \dot{z}=L_2\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_2{\dot{\theta }}_2\end{array}\right.$$

(8)

The velocity relationship can be described by the Jacobian matrix J:

$$\left[\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{z}\end{array}\right]=\mathit{J}\left[\begin{array}{c}{\dot{\theta }}_1\\ {\dot{\theta }}_2\end{array}\right]$$

(9)

where the Jacobian matrix J is given by Equation (10):

$$\mathit{J}=\left[\begin{array}{cc}-\left(L_1+L_2\cos {\theta }_2\right)\sin {\theta }_1& -L_2\cos {\theta }_1\sin {\theta }_2\\ \left(L_1+L_2\cos {\theta }_2\right)\cos {\theta }_1& -L_2\sin {\theta }_1\sin {\theta }_2\\ 0& L_2\cos {\theta }_2\end{array}\right]$$

(10)

In the kinematic analysis of the upper limb stretching mechanism, the range of ${\theta }_1$ and ${\theta }_2$ was set to $\left[0,{\displaystyle \frac{2\pi }{3}}\right]$. This made it possible to clearly define the mapping relationship between the joint angles and the end-effector pose. The resulting Jacobian matrix serves as a key parameter for characterizing the motion properties of the mechanism. It further enables motion control of the stretching device, thereby providing a theoretical foundation for research on upper limb stretching mechanisms.

2.2.1. Kinematic Simulation of Human-Body Upper Limb Stretching Mechanisms Based on ADAMS

Coupling was performed between the 3D model data and the ADAMS model data. To ensure stable solution processing, the mechanism underwent rational simplification while preserving the primary motion assemblies of the stretching mechanism. Material properties for all mechanism components are defined in ADAMS 2017 simulation software as follows: material type “steel”, density 7.801 × 10³ kg/m³, elastic modulus 2.07 × 10¹¹ Pa, and Poisson’s ratio 0.29 [19]; Based on practical engineering constraints corresponding kinematic pairs were established for all components and articulation points within each mechanism model.

After simplifying the model of the upper limb stretching mechanism, the refined model was subsequently imported into the ADAMS simulation environment. The upper limb stretching mechanism designed in this study comprises a limb-spreading module and a limb-lifting module. Given the bilateral symmetry of the mechanism, the analysis focuses exclusively on the left-side assembly. The motion simulation model of the mechanism is shown in Figure 5. To achieve stretching motions of the human upper limb, including abduction-adduction in the frontal plane and elevation-depression in the sagittal plane, two independent drives are required. Based on the range of motion during upper limb stretching, the motor drive function is defined by a step function. Specifically, the drive function for arm extension is step (time, 0, 0, 10, 120 d) + step (time, 10, 0, 20, −120 d). The motor drive function for arm elevation is step (time, 0, 0, 10, 120 d) + step (time, 10, 0, 20, −120 d). To facilitate observation of the upper limb stretching mechanism’s motion characteristics, the simulation duration was set to 80 s with 1000 steps. This configuration executes the drive function over four complete cycles, during which the mechanism undergoes four repetitions of both extension-flexion and elevation-lowering motions.

2.2.2. Strength Analysis of Upper Limb Stretching Devices Based on ABAQUS

This study performed finite element analysis in ABAQUS on both the upper limb stretching mechanisms to verify the strength and stiffness of the primary load-bearing components during motion.

The main structural model of the upper limb stretching mechanism was imported into Abaqus for simulation analysis. Material selection specified Grade 45 steel, with structural connections adjusted for operational conditions. A 100 N downward rotating force was applied at the interface between the telescoping rod and handle assembly to simulate upper limb loading during stretching. The upper limb simulation model is shown in Figure 6.

2.3. Experiments

2.3.1. Test of Upper Limb Stretching Motions

The test participant was seated in a designated chair. During experimental procedures, the arm was immobilized using non-elastic straps secured to a rigid plate, which was firmly fixed to the distal forearm region to prevent elbow flexion during upper limb stretching and ensure measurement accuracy. A digital force gauge was mounted on the ventral surface of the distal forearm. The test operator grasped the force gauge to elevate and abduct the participant’s arm while maintaining perpendicular alignment between the gauge and limb. Simultaneously, an assistant recorded angular displacement using a digital goniometer and documented tensile force data. A cohort of twenty volunteers took part in the research. The participant group (n = 20) was an average age of 27.6 years old (±9.02 SD) and comprised healthy individuals [20]. To ensure data reliability, each experimental condition was tested 3–5 times. These repeated measurements were carried out at different times of day, including early morning, around noon, and before and after physical exercise. To secure reliable and unbiased data, a rest period of 15–30 min was incorporated between consecutive measurement sessions. The corresponding results are shown in Figure 7 and Figure 8.

As a mathematical–statistical approach, Response Surface Methodology is widely applied to efficiently pinpoint the optimal set of experimental conditions in the presence of multiple factors. It offers advantages of high-predictive accuracy, reduced experimental runs, and cost-effectiveness [21]. This study employed the Box–Behnken Design (BBD) methodology. A series of separate three-factor, three-level response surface regression models were developed, incorporating human height (A), body weight (B), upper limb elevation angle (E), and arm abduction angle (H) as independent variables. These models were used to analyze the load characteristics during upper limb stretching under multifactorial conditions. The experimental factors and levels are detailed in

Table 3. Experimental factors and levels for the upper limb elevation test.

Factors	Levels
	−1	0	1
Height/cm	170	175	180
Weight/kg	70	80	90
Angle/deg	30	75	120

and

Table 4. Experimental factors and levels for the upper limb abduction test.

Factors	Levels
	−1	0	1
Height/cm	170	175	180
Weight/kg	70	80	90
Angle/deg	0	15	30

.

2.3.2. Prototype Bench Testing

Based on kinematic and strength analyses of the upper limb stretching mechanism, a physical prototype was fabricated according to the structural model of the device and subsequently tested. The experimental prototype is shown in Figure 9.

As shown in Figure 10, the performance of the upper limb stretching device was evaluated through experimental testing. The test protocol consisted of two different types of exercises: upper limb abduction stretching and upper limb elevation stretching. The experimental procedure was as follows: the participant sat on the test apparatus, firmly gripping the handles with their arms. An assistant operated the device controls for starting and stopping, while the experimenter conducted the upper limb stretching tests. The original cohort of 20 participants was maintained for the experimental validation of the device prototype. All participants were in good health with a mean age of 27.6 years (SD = 9.02), each engaging in 3–5 prototype testing sessions.

Participants were surveyed using a 5-point Likert scale [22]. The rating scale options for user feedback are listed in

Table 5. User Feedback Rating Options.

Evaluative Dimension	Level 1	Level 2	Level 3	Level 4	Level 5
(1) Stretching comfort	Very uncomfortable	Uncomfortable	Neutral	Comfortable	Very comfortable
(2) Stretching effectiveness	Minimal effect	Slight effect	Moderate effect	Marked effect	Very marked effect
(3) Stability	Highly unstable (severe vibrations)	Unstable (noticeable vibrations)	Moderate (occasional minor vibrations)	Stable (essentially vibration-free)	Very stable (no vibrations)

.

3. Results and Discussion

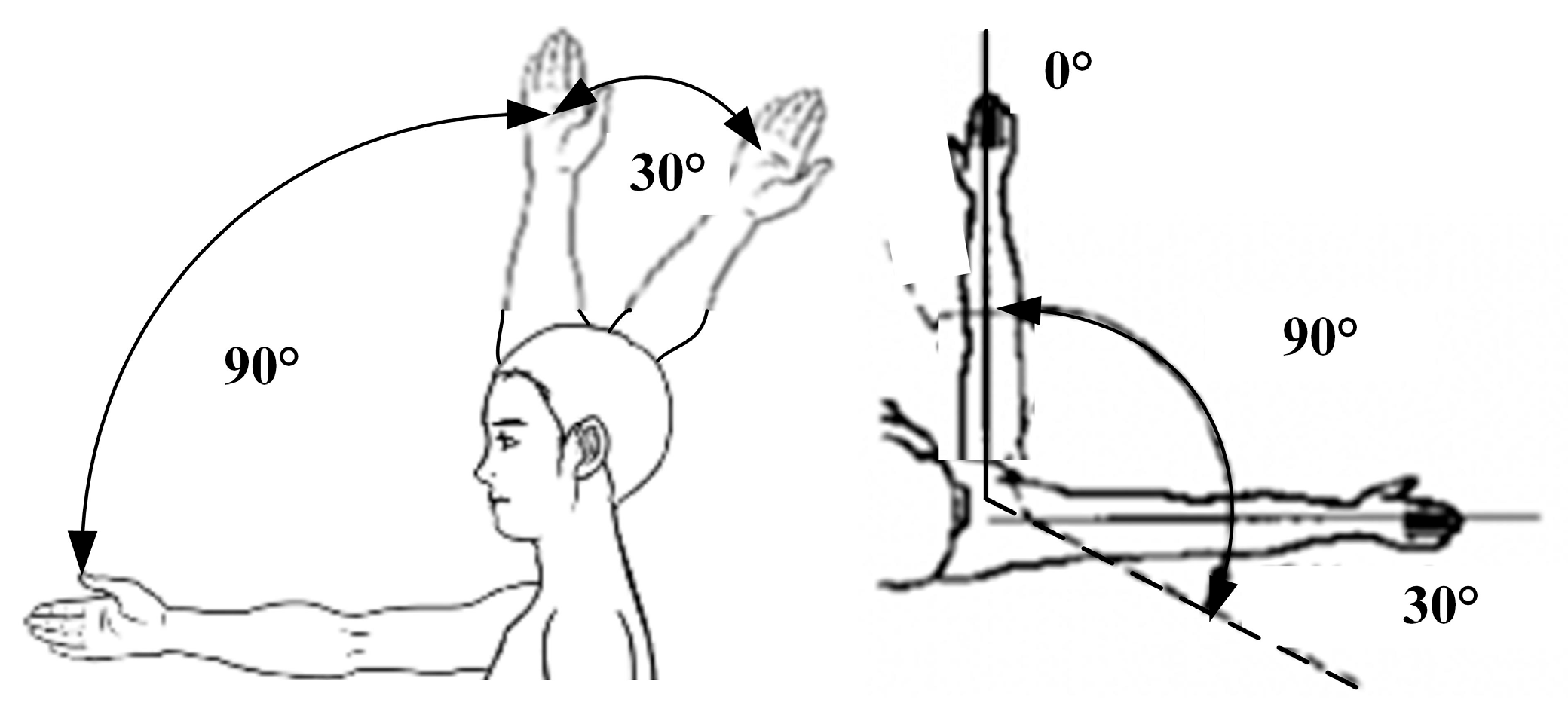
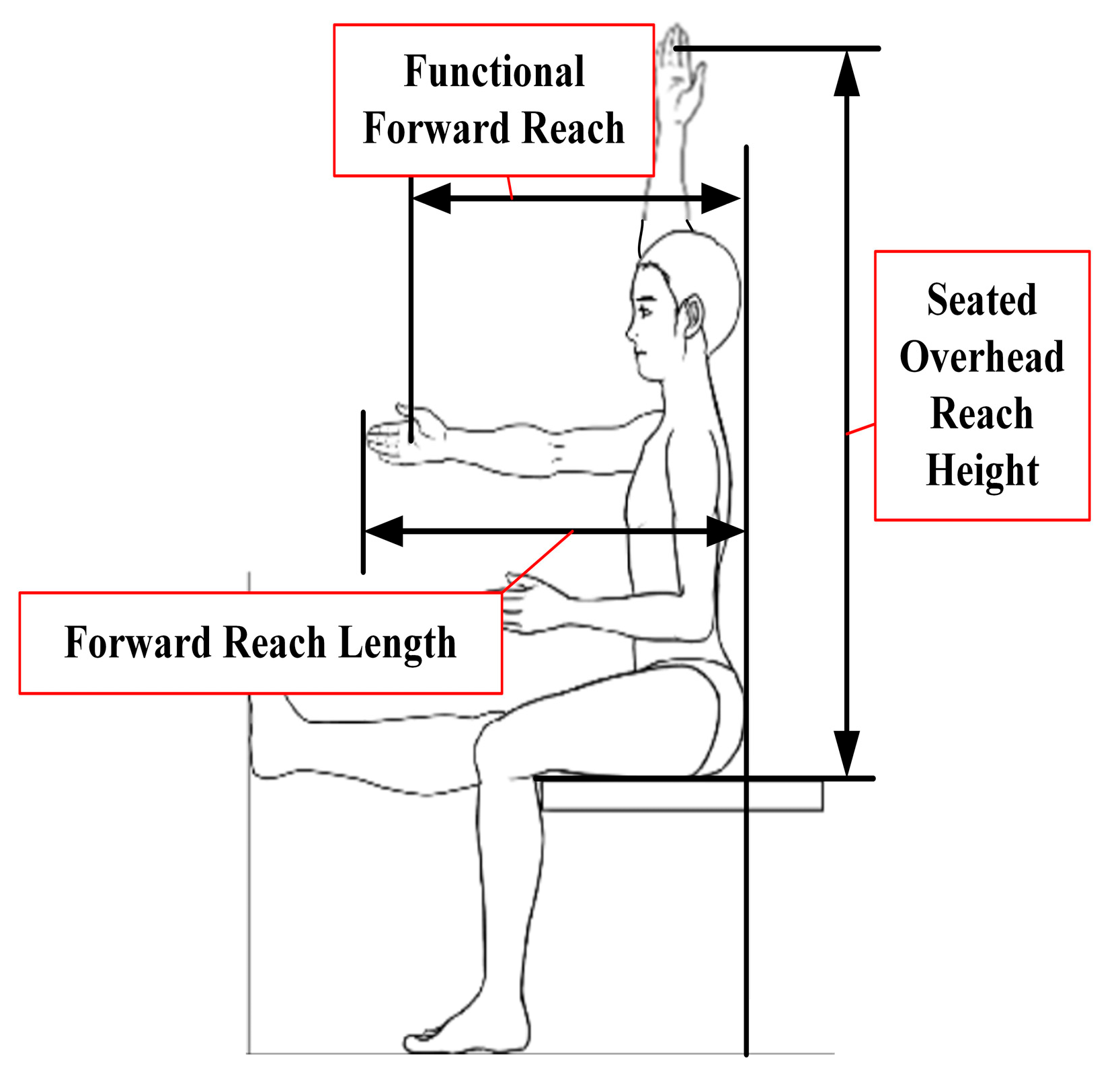
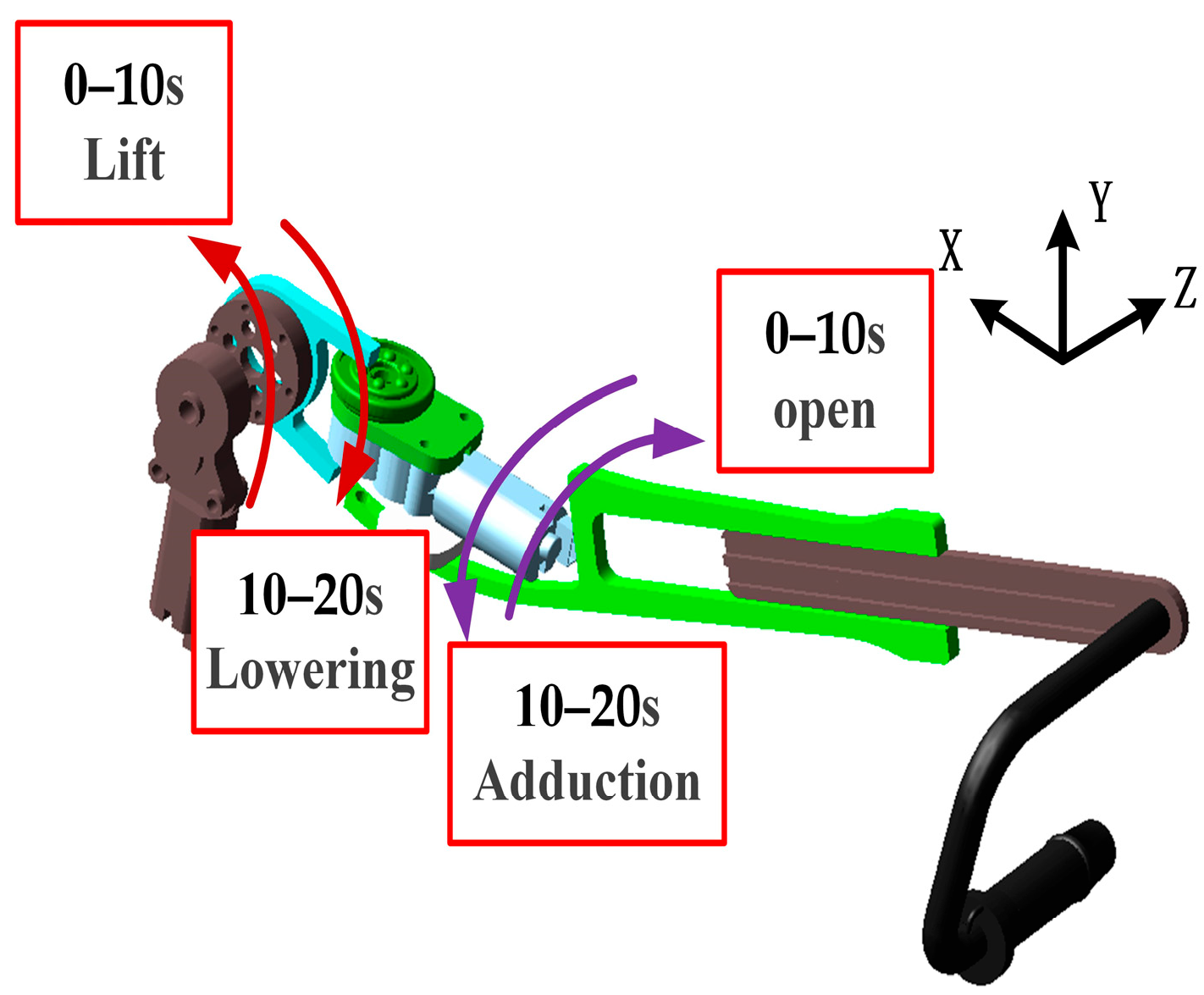
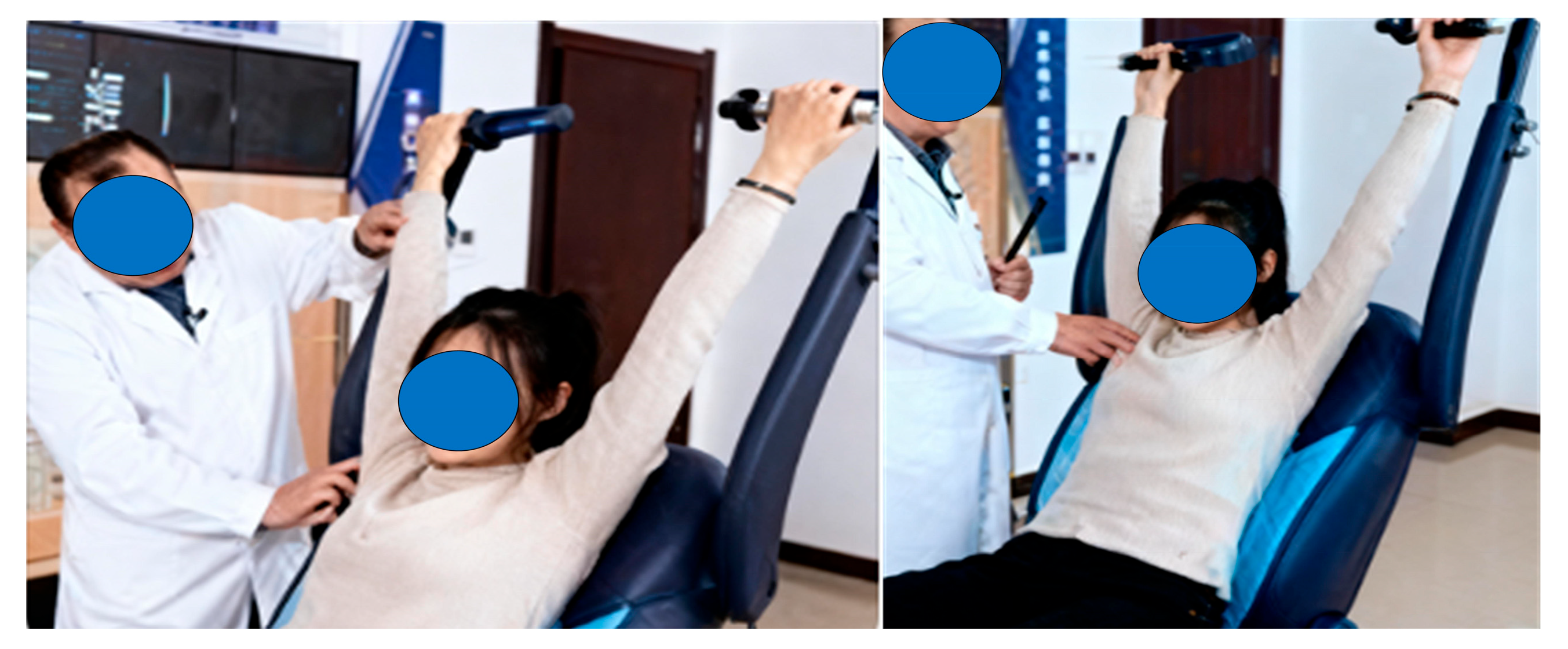
3.1. Analysis of Upper Limb Stretching Testing Results

The results of the upper limb elevation test and upper limb abduction test are listed in

Table 6. Results of the Upper Limb Elevation Test.

Serial Number	Height/cm	Weight/kg	Angle/deg	Avg F/N
1	170	80	120	30.23
2	175	80	75	25.05
3	175	80	75	21.85
4	175	70	30	15.15
5	170	80	30	15.15
6	180	70	75	26.20
7	175	90	120	33.50
8	180	80	120	39.30
9	170	70	75	17.26
10	175	90	30	30.50
11	180	90	75	35.20
12	180	80	30	29.90
13	175	80	75	22.10
14	175	70	120	20.95
15	170	90	75	21.35

and

Table 7. Upper Limb Abduction Test Results.

Serial Number	Height/cm	Weight/kg	Angle/deg	Avg F/N
1	180	80	30	36.25
2	175	90	0	15.79
3	175	70	0	13.35
4	170	90	15	20.15
5	180	70	15	23.13
6	175	80	15	23.32
7	175	90	30	33.25
8	170	80	30	27.32
9	175	80	15	24.32
10	175	70	30	25.95
11	170	70	15	14.53
12	175	80	15	21.23
13	180	80	0	15.23
14	170	80	0	11.40
15	180	90	15	25.32

, respectively. During testing, the tensile force was recorded as F.

Based on the data in the table, we could calculate the 95% confidence intervals for the total average force under all experimental conditions of upper limb elevation and upper limb abduction. According to the average values of the experimental runs, the total average force for upper limb elevation was 25.58 Newtons (95% confidence interval: 21.50 to 29.66 Newtons), and the total average force for upper limb abduction was 22.04 Newtons (95% confidence interval: 18.50 to 26.04 Newtons). This clearly demonstrated the precision of our overall measurements. Given the repeated—measures nature of the experimental design, we used the Intraclass Correlation Coefficient (ICC) to assess the consistency and stability of the measurement method. The specific results are as follows: the ICC for upper limb elevation was approximately 0.9996, and that for upper limb abduction was approximately 0.9999. This indicates that the differences among different samples were far greater than the measurement errors, and the measurement results showed extremely high consistency.

Significance testing was conducted on the linear, second-order, and third-order models. The model significance tests, fit statistics, and correlation analyses were subsequently benchmarked against each other. This comparative analysis identified the second-order model as the optimal choice for this experimental study. Using body height A, body weight B, upper limb elevation angle E and abduction angle H as independent variables, the regression model equations obtained via Design-Expert 13.0 software [23] are presented in Equations (11) and (12). The Analysis of Variance (ANOVA) results for the regression models are listed in

Table 8. ANOVA for the Upper Limb Elevation Regression Model.

Source	Sum of Squares	Mean Square	F-Value	p-Value	η2p	Distinctiveness
Model	696.19	77.35	5.99	0.0315	0.923	significant
A-height	271.56	271.56	21.01	0.0059	0.823
B-weight	210.02	210.02	16.25	0.0100	0.783
E-angle	138.44	138.44	10.71	0.0221	0.740
AB	6.03	6.03	0.4664	0.5250
AE	8.07	8.07	0.6241	0.4653
BE	1.96	1.96	0.1517	0.7130
A2	29.18	29.18	2.26	0.1932
B2	2.42	2.42	0.1869	0.6835
E2	29.65	29.65	2.29	0.1903
Lack of Fit	58.28	19.43	6.13	0.1434		not significant

and

Table 9. ANOVA for the Upper Limb Abduction Regression Model.

Source	Sum of Squares	Mean Square	F-Value	p-Value	η2p	Distinctiveness
Model	712.85	79.21	34.49	0.0006	0.991	significant
A-height	87.98	87.98	38.31	0.0016	0.931
B-weight	38.50	38.50	16.77	0.0094	0.855
H-angle	561.13	561.13	244.35	<0.0001	0.989
AB	2.94	2.94	1.28	0.3091
AH	6.50	6.50	2.83	0.1532
BH	5.90	5.90	2.57	0.1697
A2	2.70	2.70	1.17	0.3280
B2	6.43	6.43	2.80	0.1551
H2	0.7408	0.7408	0.3226	0.5946
Lack of Fit	6.51	2.17	0.8729	0.5731		not significant

.

$$\begin{array}{ll}F& =3422.58403-39.68292A-2.37321B+1.1143E+0.02455AB\\ & -0.006311AE-0.001556BE+0.11245A^2-0.008088B^2+0.001399E^2\end{array}$$

(11)

$$\begin{array}{ll}F& =-1435.66208+13.74442A+5.21046B-3.12439H-0.01715AB\\ & +0.017AH+0.0081BH-0.034183A^2-0.13196B^2+0.001991H^2\end{array}$$

(12)

As shown in Table 8, the model yields p = 0.0315 (<0.05), demonstrating statistically significant regression model fitting, which indicates good agreement between the regression model and experimental testing. Comparison of the p-values and F-values in the table reveals the relative influence of each factor on the model. Height exhibits a highly significant effect on upper limb elevation force (p < 0.01), while body weight and elevation angle show significant effects (p < 0.05). The ANOVA revealed that height had a statistically significant and very large effect on the output force (F-value = 21.01, p = 0.0059, η²_p = 0.823). The significance ranking of factors affecting force magnitude is A > B > E > AE > AB > BE. Response surface and contour plots depicting the force during upper limb elevation were generated from the regression model equation. The interaction effects of factors on force magnitude were analyzed, as shown in Figure 11.

As shown in Table 9, the model yields p = 0.0006 (<0.01), demonstrating a highly significant regression model fit, which confirms excellent agreement between the regression model and experimental testing. Based on the p-values and F-values, the influence magnitude of each factor on the model was determined. The abduction angle exhibited a highly significant effect (p < 0.01) on upper limb abduction force, while height and body weight showed significant effects (p < 0.05). The ANOVA revealed that angle had a statistically significant and very large effect on the output force (F-value = 244.35, p < 0.0001, η²_p = 0.989). The significance ranking of factors affecting force magnitude is H > A > B > AH > BH > AB. Response surface and contour plots of the arm expansion force were constructed from the regression model equation. These graphical representations were then employed to analyze the factor interaction effects, shown in Figure 12.

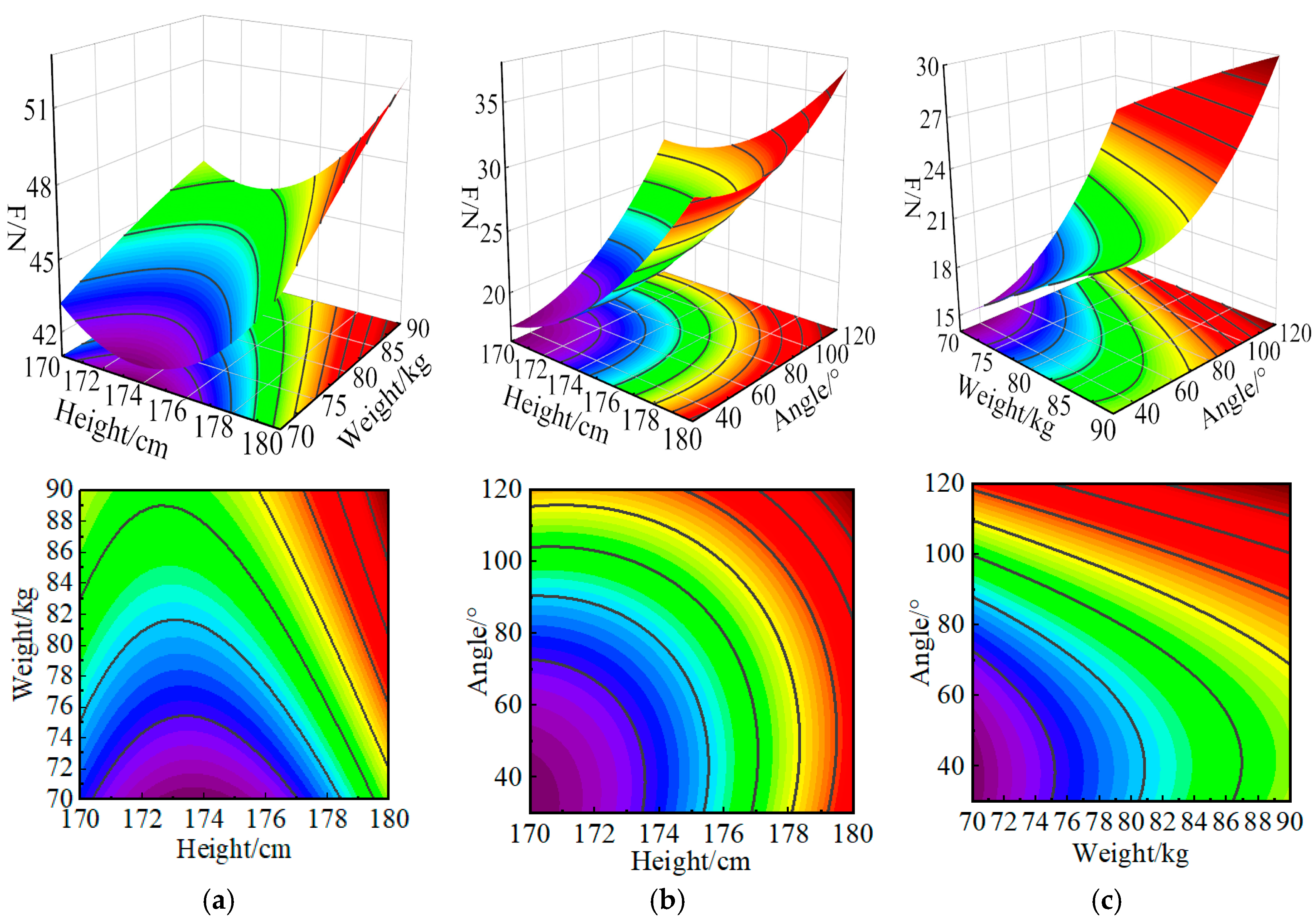
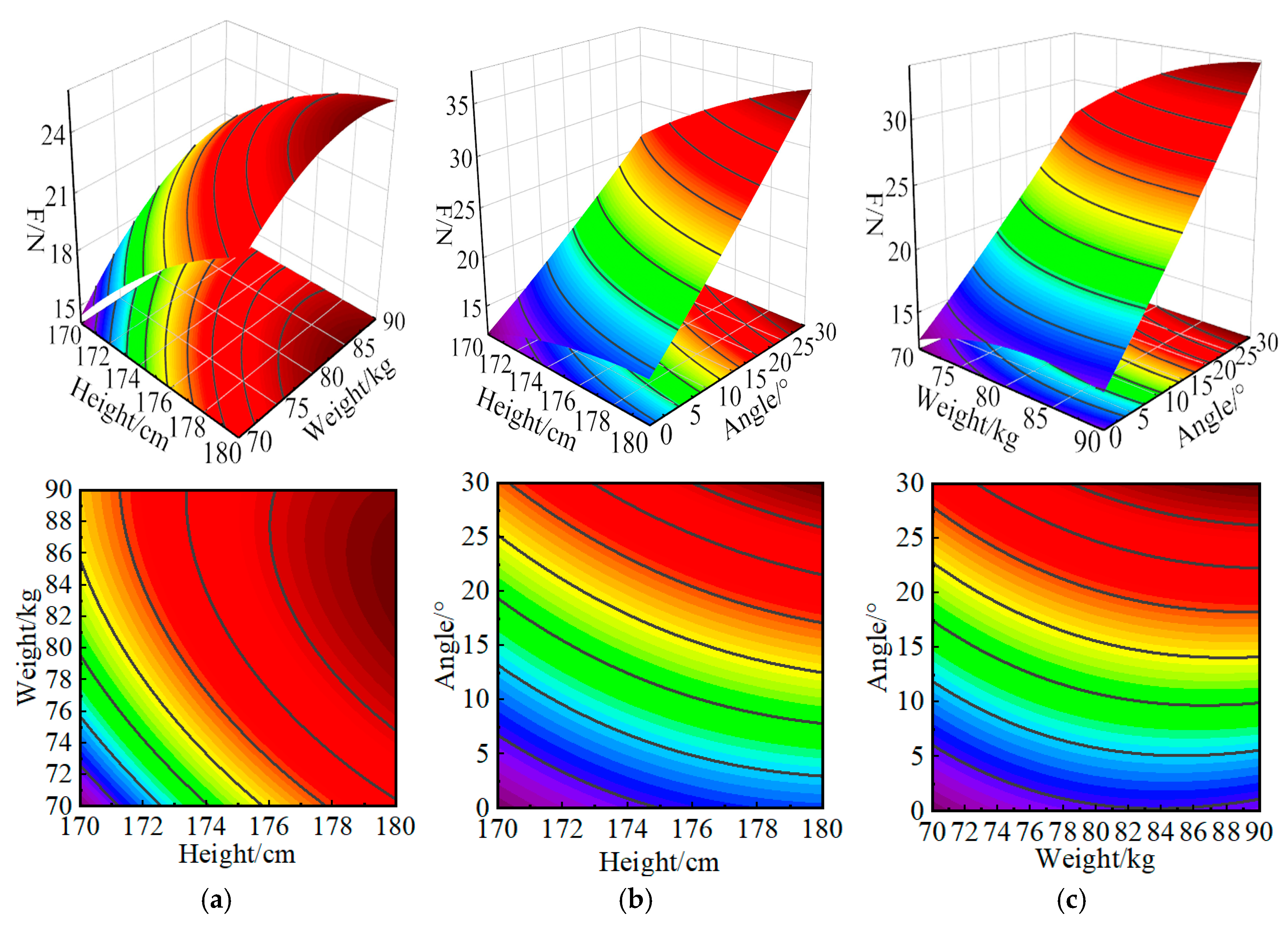
As shown in Figure 11a, the force during upper limb elevation increases with greater height and body weight. The steeper slope of the height curve signifies its greater influence on the force, while the steep gradient and dense contour lines of the response surface reveal a pronounced interaction between height and weight on the elevation force. As shown in Figure 11b, the force during upper limb elevation increases with greater height and larger elevation angles. The height curve exhibits a steeper slope than the angle curve, suggesting that height exerts a more significant influence on the force. The steep gradient and dense contour lines of the response surface demonstrate a pronounced interaction effect between height and elevation angle on the force. As shown in Figure 11c, the force during upper limb elevation increases with greater body weight and larger elevation angles. In contrast to the angle curve, the steeper slope of the body weight curve identifies it as the more dominant factor. Furthermore, the steep gradient and dense contour lines of the response surface collectively point to a strong interactive effect between body weight and elevation angle on the force.

As shown in Figure 12a, the force during upper limb abduction rises with increasing height and body weight. The steeper slope of the height curve demonstrates that height has a stronger effect on the force than weight. The steep gradient and dense contour lines of the response surface demonstrate a pronounced interaction effect between height and body weight on the abduction force. As shown in Figure 12b, the force during upper limb abduction increases with greater height and larger abduction angles. The steeper slope of the abduction angle curve compared to the height curve signifies its greater influence on the force; the response surface’s steep gradient and dense contour lines further demonstrate a pronounced interaction between these two factors on the abduction force. As shown in Figure 12c, the force during upper limb abduction increases with greater body weight and larger abduction angles. A comparative analysis of the slopes reveals that the abduction angle has a greater influence on the force than body weight, as evidenced by its steeper curve. The steep gradient and dense contour lines of the response surface demonstrate a pronounced interaction effect between body weight and abduction angle on the abduction force.

3.2. ADAMS-Based Motion Simulation Results for the Upper Limb Stretching Device

Simulation results for the upper limb abduction and elevation stretching mechanisms are shown in Figure 13 and Figure 14.

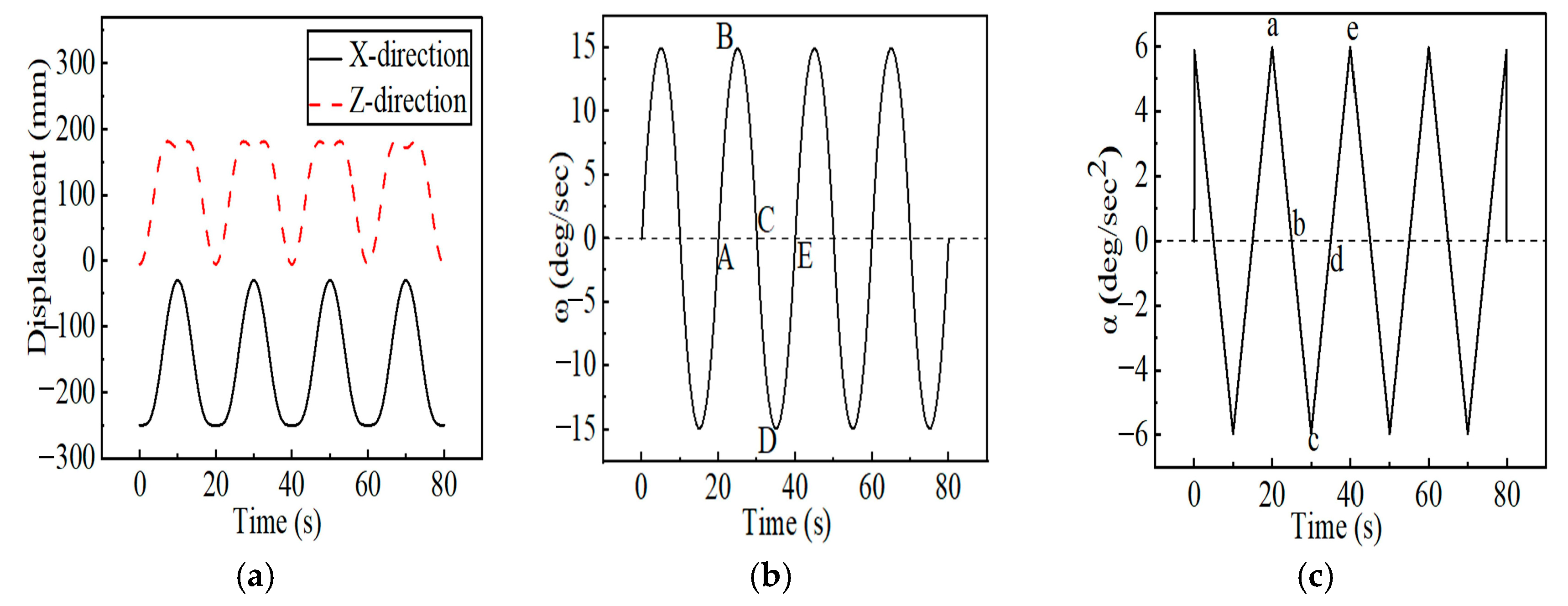
As shown in Figure 13a, the discrepancies between displacement peaks and initial values at the mechanism’s centroid are approximately 219.99 mm in the X-direction and 186.44 mm in the Z-direction. These results demonstrate that the positioning performance of the upper limb abduction stretching mechanism satisfies the design requirements. Figure 13b displays the angular velocity variation at points A-E during a full abduction-adduction cycle in the frontal plane of the mechanism, with a peak angular velocity of approximately 14.92 deg/s. Figure 13c illustrates the angular acceleration variation at points A-E during a complete abduction-adduction cycle of the mechanism, with a peak angular acceleration of approximately 5.97 deg/s². The motion curves of the upper limb abduction mechanism exhibit smooth variations without abrupt changes, demonstrating good kinematic performance and compliance with design requirements.

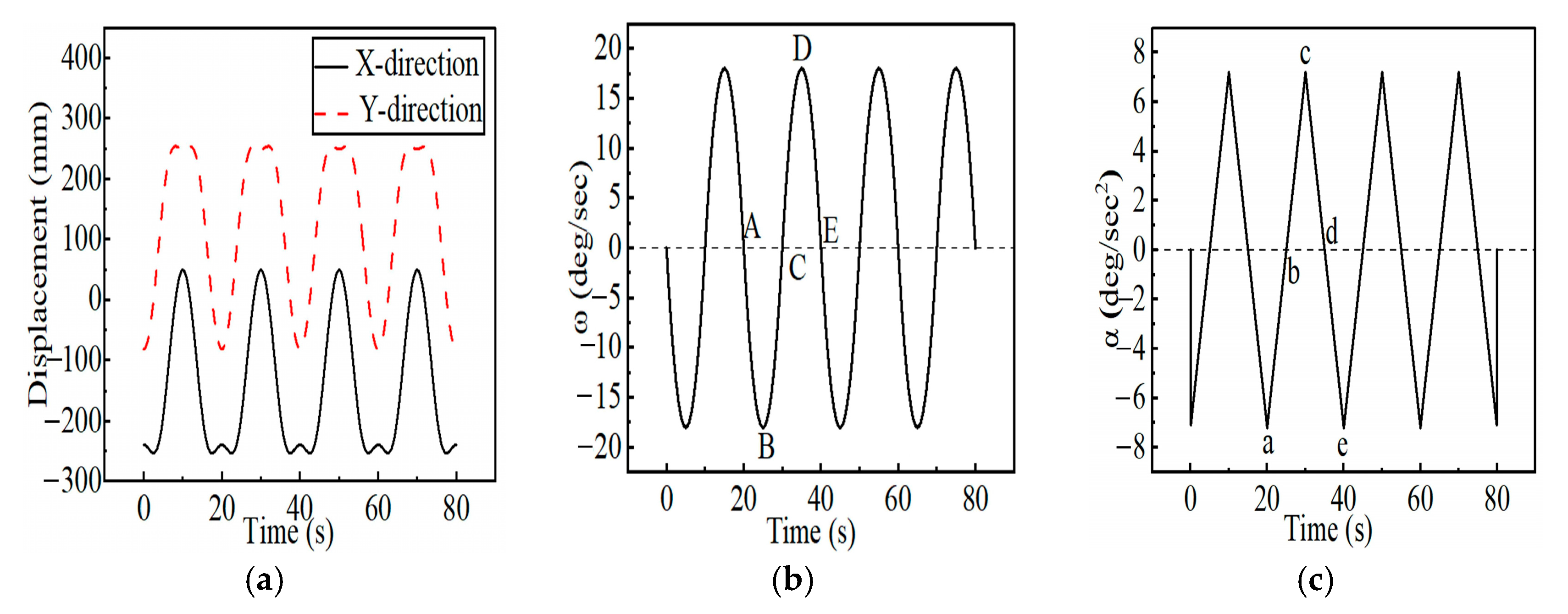
As shown in Figure 14a, the discrepancies between displacement peaks and initial values at the mechanism’s centroid are approximately 288.91 mm in the X-direction and 334.82 mm in the Y-direction. These results demonstrate that the positioning performance of the upper limb elevation stretching mechanism satisfies its design requirements. As shown in Figure 14b, angular velocity variation at points A-E during a complete elevation-lowering cycle in the sagittal plane of the mechanism is presented, with a peak angular velocity of approximately 17.99 deg/s. Figure 14c illustrates angular acceleration variation at points A-E during a complete elevation-lowering cycle in the mechanism’s sagittal plane, with a peak angular acceleration of approximately 7.08 deg/s². The motion curves of the upper limb elevation mechanism exhibit smooth variations without abrupt changes, demonstrating satisfactory kinematic performance and compliance with design requirements.

3.3. ABAQUS-Based Strength Analysis Results for Upper Limb Stretching Mechanisms

As shown in Figure 15 for the upper limb stretching mechanism, the von Mises stress contour plot and strain contour plot demonstrate a maximum stress of 195.2 MPa and maximum strain of 9.246 × 10⁻⁴ mm under this loading condition. According to the GB/T 699-2015 standard [24], W45 steel has a tensile strength of 600 MPa and a yield strength of 355 MPa. The maximum stress in the upper limb stretching mechanism is lower than the yield strength of 45 steel, demonstrating that its strength and stiffness comply with design requirements.

Verification of Simulation Results

To ensure the accuracy of the simulation results, this study conducted systematic validation through experimental testing. A physical prototype, identical to the simulation model in both dimensions and materials, was fabricated and tested under the same working conditions. A downward load of 100 N was applied to the front end of the telescopic rod. The strain at key locations was measured using strain gauges and then converted into stress values. The experimentally measured maximum stress was 190.5 MPa, which shows a relative error of 2.47% compared to the simulation result (195.2 MPa), indicating good agreement.

3.4. Prototype Testing Results

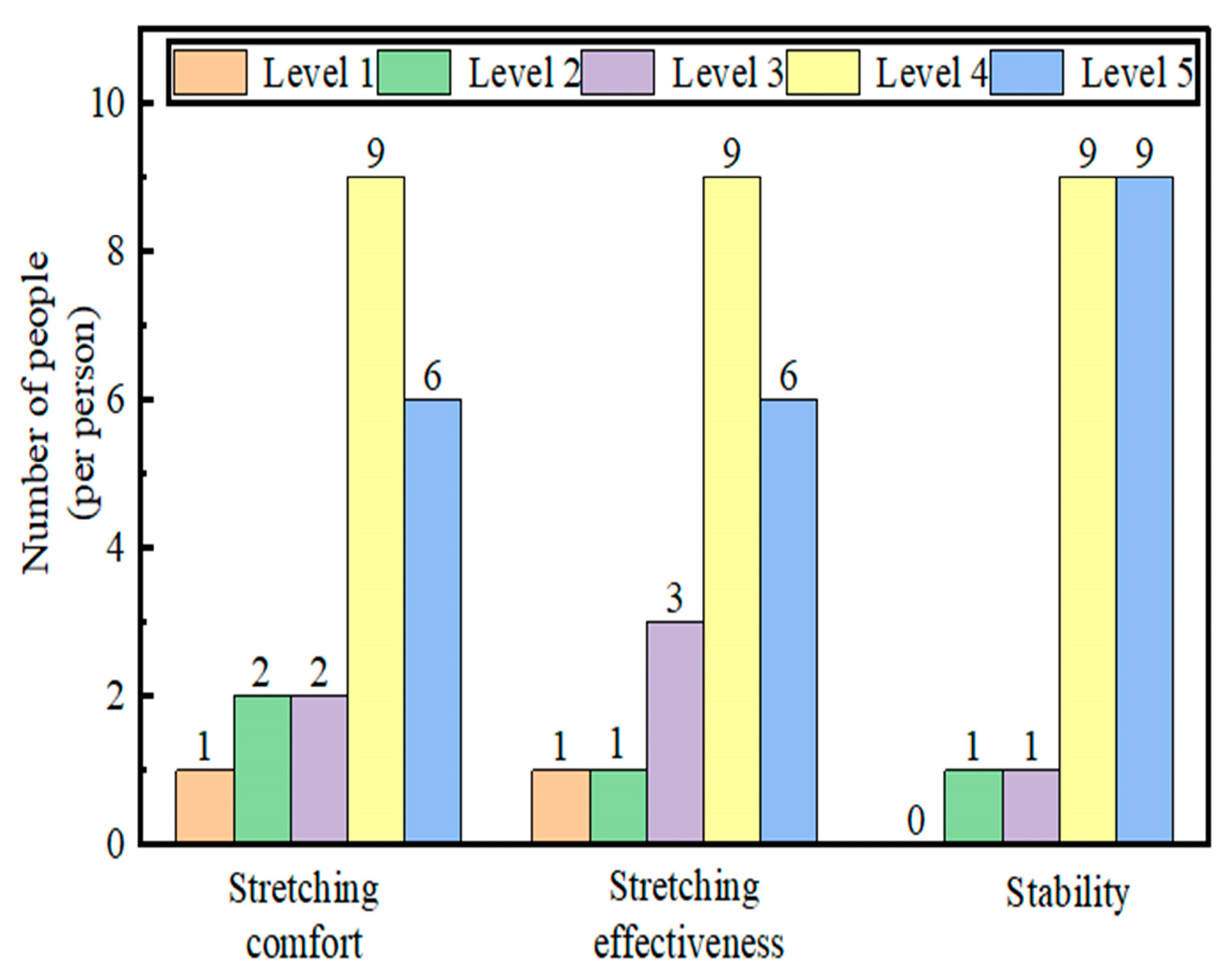
Following prototype testing, the evaluation data were processed. The experimental findings demonstrate that the upper limb stretching device successfully meets the design specifications. The subjective ratings from participants regarding the stretching comfort, muscle stretching effectiveness, and stability of the upper limbs stretching device are shown in Figure 16.

The comfort ratings were concentrated at the highest levels, with 15 participants choosing either level 4 “Comfortable” or level 5 “Very Comfortable”. This result indicated a high level of comfort provided by the upper limbs stretching device during the stretching process. Five participants assigned lower ratings, which they attributed to a more pronounced sensation of muscle stretching during the process, resulting in discomfort. With regard to muscle stretching effectiveness, only one participant reported feeling “Minimal effect”. Combined with the comfort assessment, the stretching device for the upper limbs demonstrated effective stretching performance. In terms of stability, level 1 “severe vibrations” was not selected by any participant, whereas levels 4 and 5 were chosen by a total of 18 individuals. Therefore, the stretching device for the upper limbs exhibited good stability and posed no safety concerns during stretching exercises. In summary, the usability evaluation of the stretching device yielded positive results, which confirmed the feasibility of its design.

4. Conclusions

A device for upper limb stretching was designed based on an analysis of force changes during the stretching process. This work was accompanied by an examination of the factors influencing upper limb stretching. Experimental validation demonstrated the feasibility of the device.

(1)

The experimental results on force variation during human upper limb stretching, based on the Box–Behnken Design (BBD) response surface methodology, revealed that height had the most significant effect on the lifting motion, while the opening angle was the primary influencing factor for the abduction motion. These findings provide guidance for the design and modeling of a human upper limb stretching mechanism.

(2)

The upper limb stretching mechanism was modeled in CREO. Kinematic analysis and calculations performed on the model enabled the derivation of its position and angular velocity equations. Simulations conducted in ADAMS demonstrate that the mechanism produces a smooth stretching motion, and its kinematic trajectory matches the practical needs of upper limb extension.

(3)

Finite element analysis was conducted in ABAQUS based on experimental force data from upper limb stretching to evaluate the strength of key components. The analysis revealed a maximum stress of 195.2 MPa in the connecting rod, which is below the material’s strength limit, confirming that the mechanism satisfies the design specifications.

(4)

The device prototype was constructed and its performance was verified by means of upper limb stretching testing. The outcomes indicated that the device satisfied the design requirements.

Future work will focus on structural refinement of the stretching device and a deeper mechanical analysis, particularly of the connecting pins. Whereas the current study did not establish a definitive control strategy, developing an effective control method will be a primary objective to enhance stretching performance.