Research on Fractional-Order Sliding Mode Control of Fractional-Order Permanent Magnet Direct-Drive Wind Power System
Abstract
1. Introduction
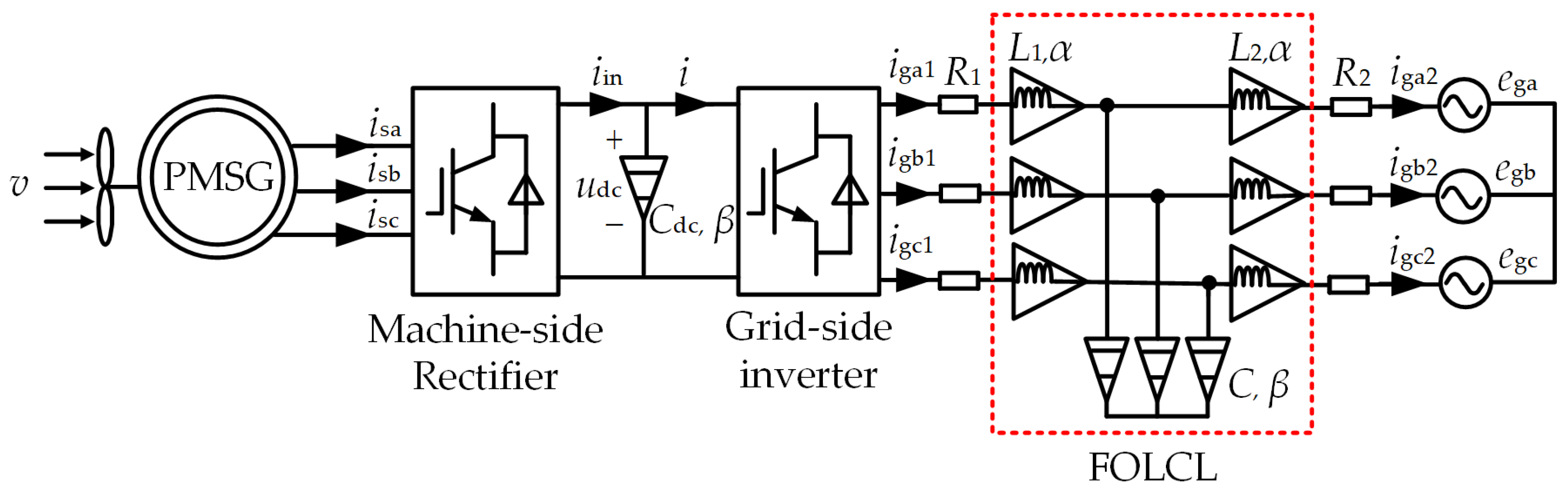
2. Fractional-Order Permanent Magnet Direct-Drive Wind Power System Model
2.1. Wind Turbine Model
2.2. Permanent Magnet Direct-Drive Synchronous Generator Model
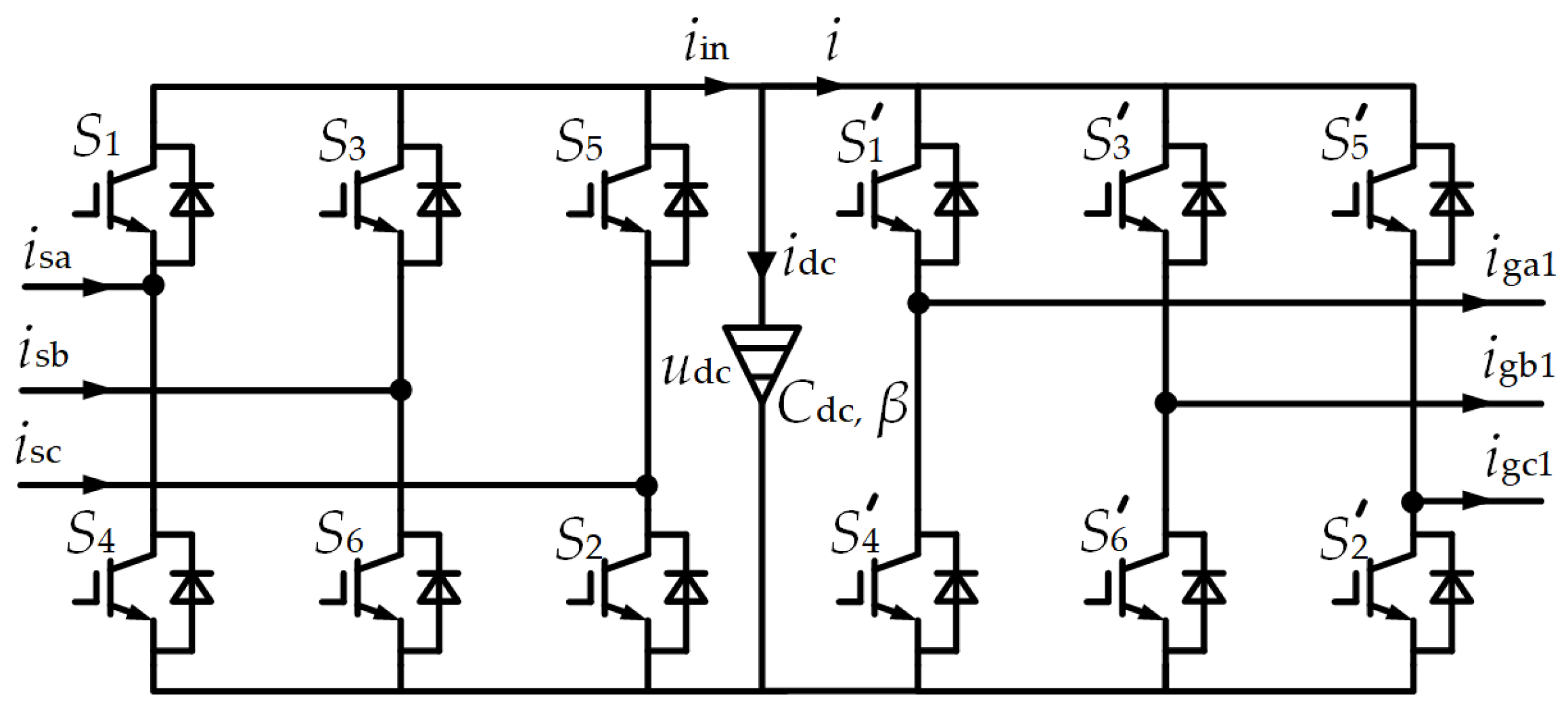
2.3. Fractional-Order Back-to-Back Converter Model
2.4. Fractional-Order Grid-Connected Filter Model
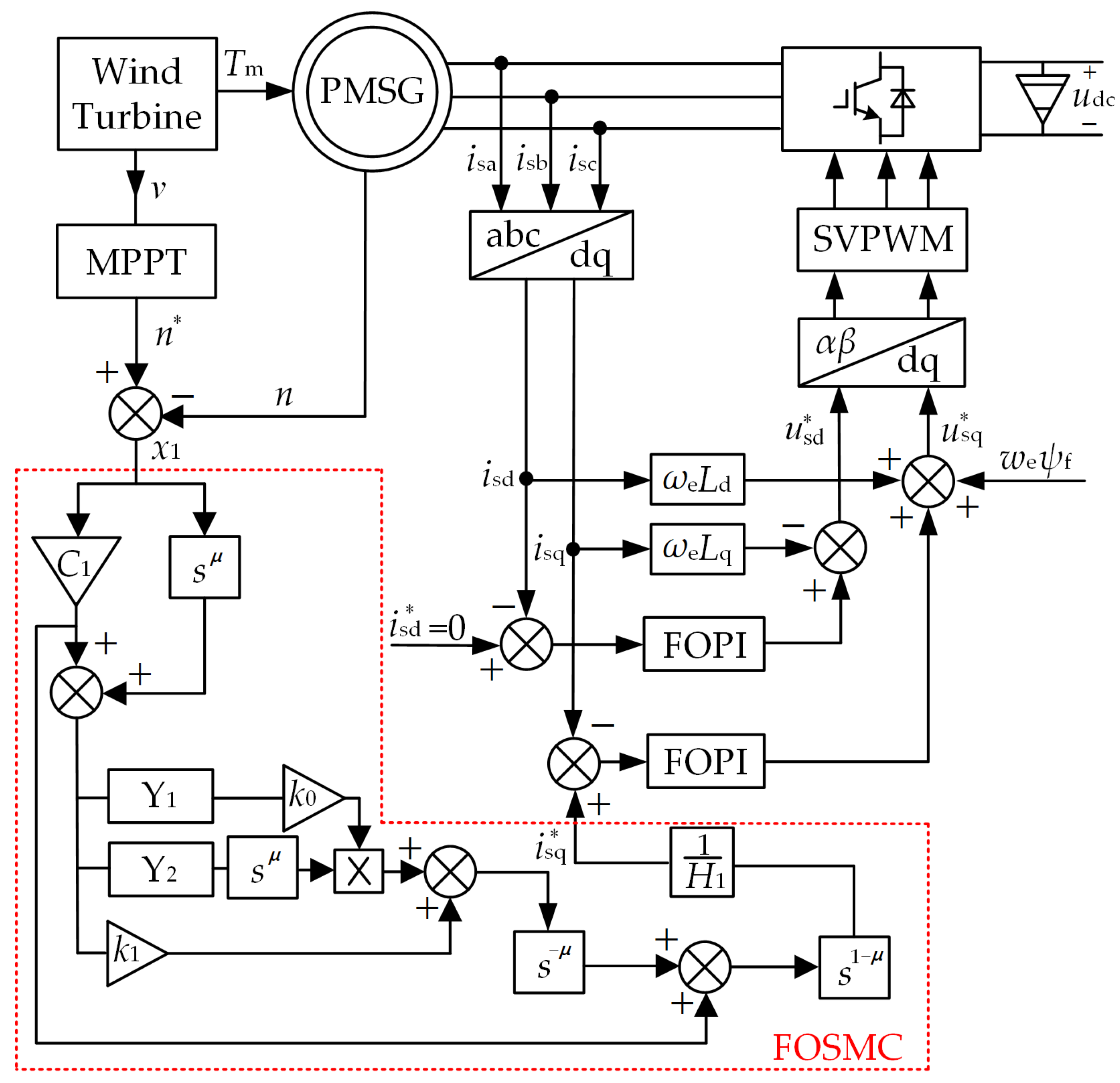
3. Fractional-Order Control Design
3.1. Machine-Side Rectifier Fractional-Order Control
3.1.1. FOPI Current Inner-Loop Control with dq-Axis Decoupling
3.1.2. FOSM Speed Outer-Loop Control
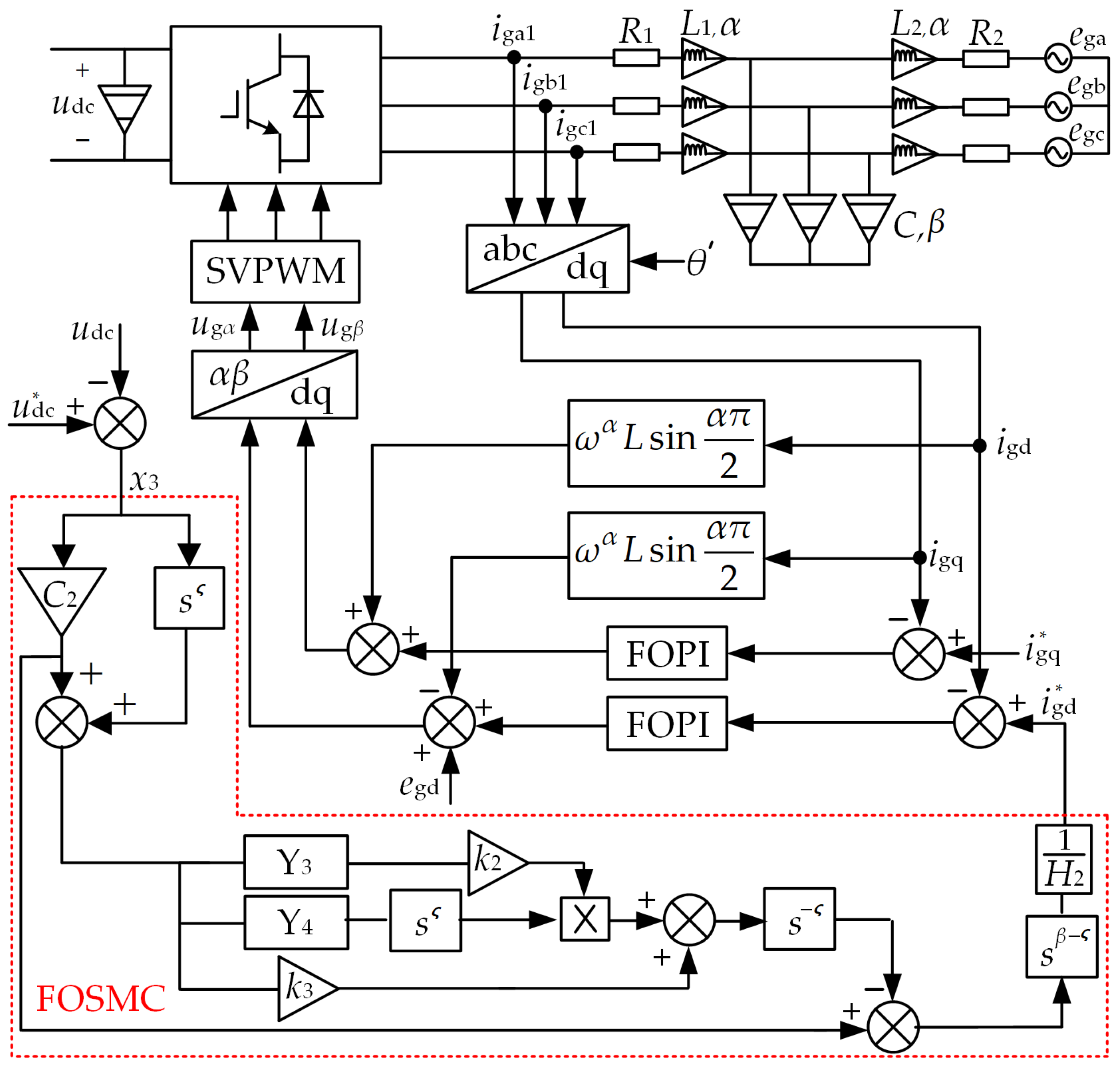
3.2. Grid-Side Inverter Fractional-Order Control
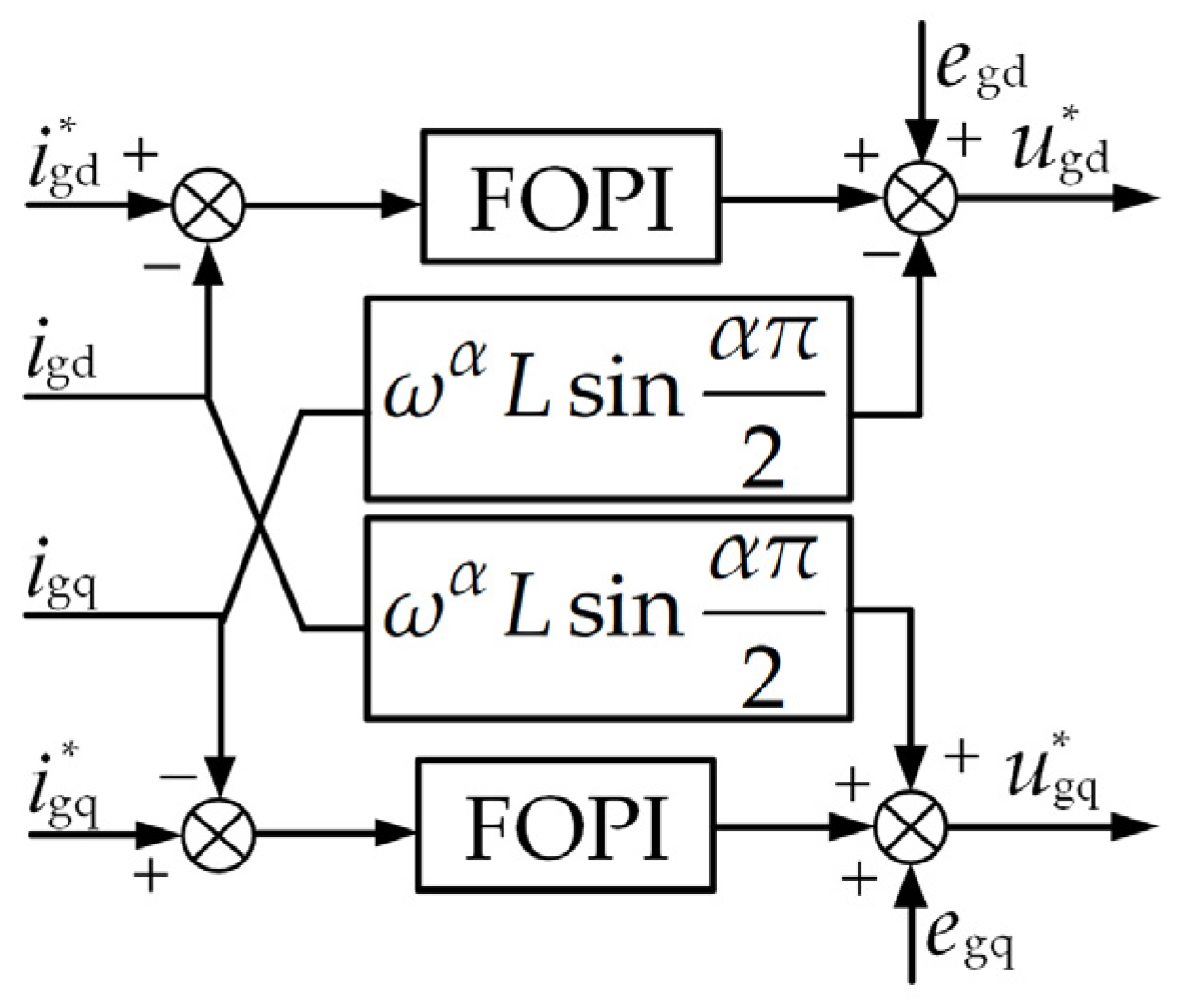
3.2.1. FOPI Current Inner-Loop Control with dq-Axis Decoupling
3.2.2. Fractional-Order Sliding-Mode Voltage Outer-Loop Control
4. Simulation Analysis
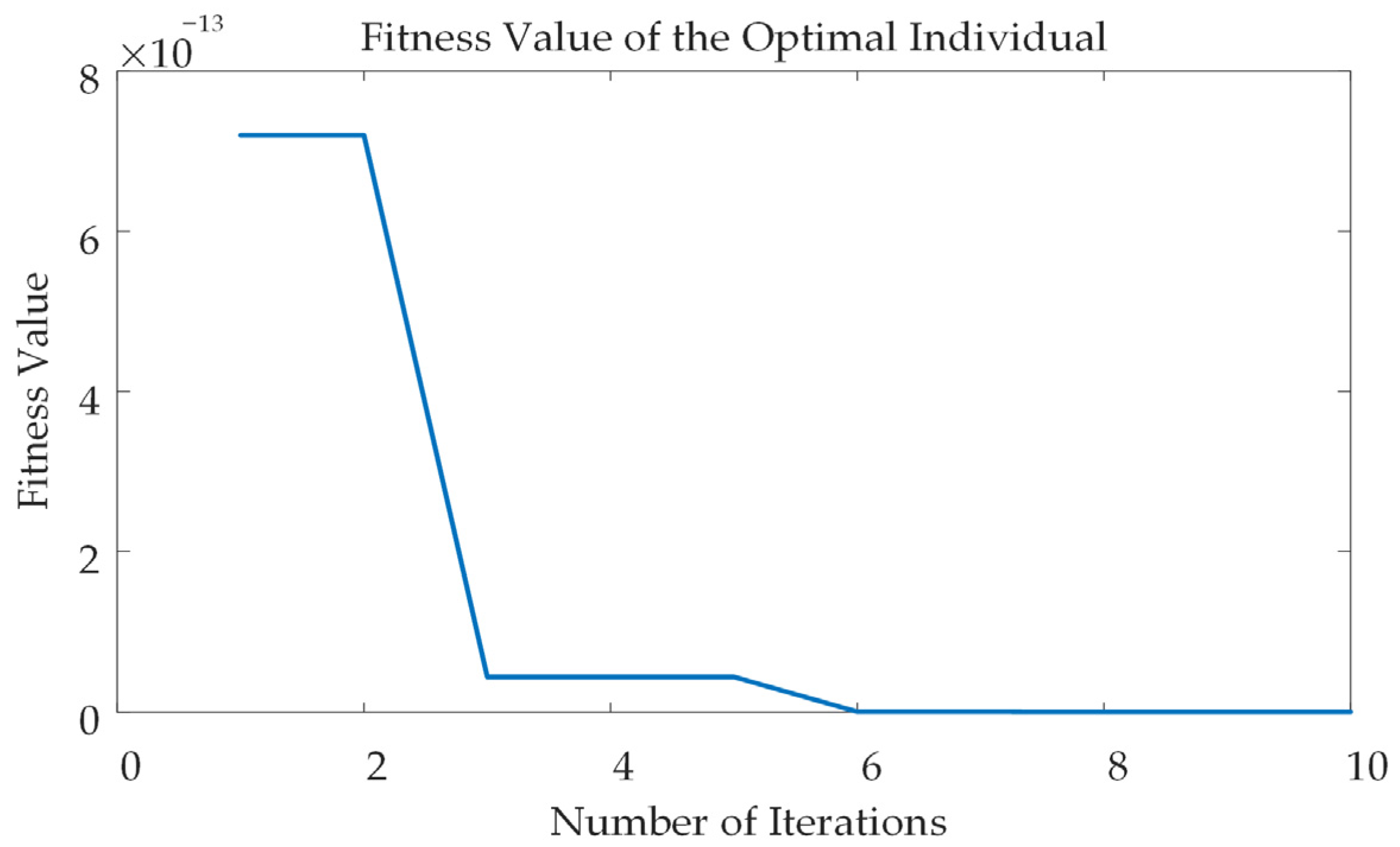
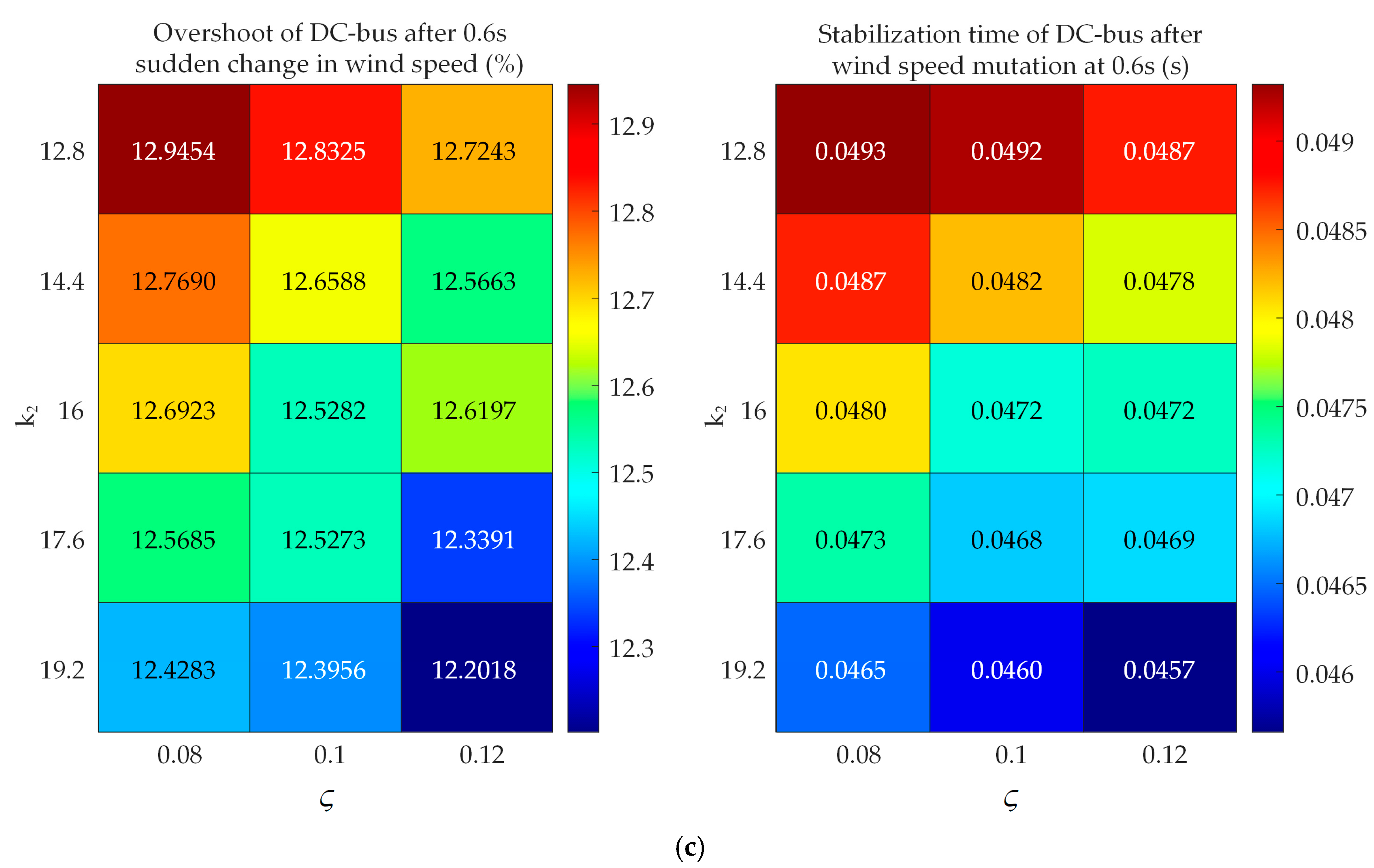
4.1. Control Parameter Design
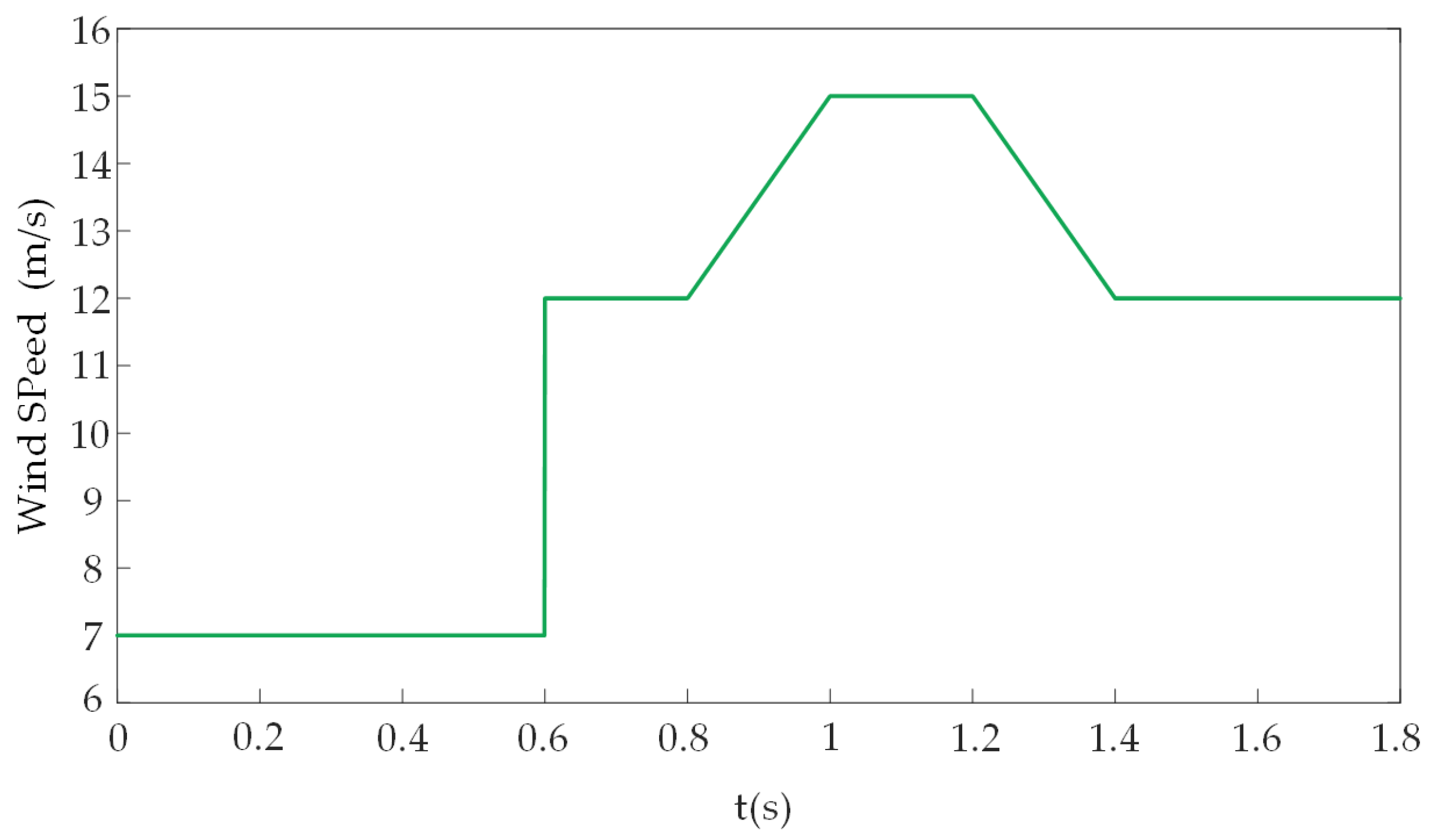
4.2. Simulation Analysis Under Changing Wind Speeds
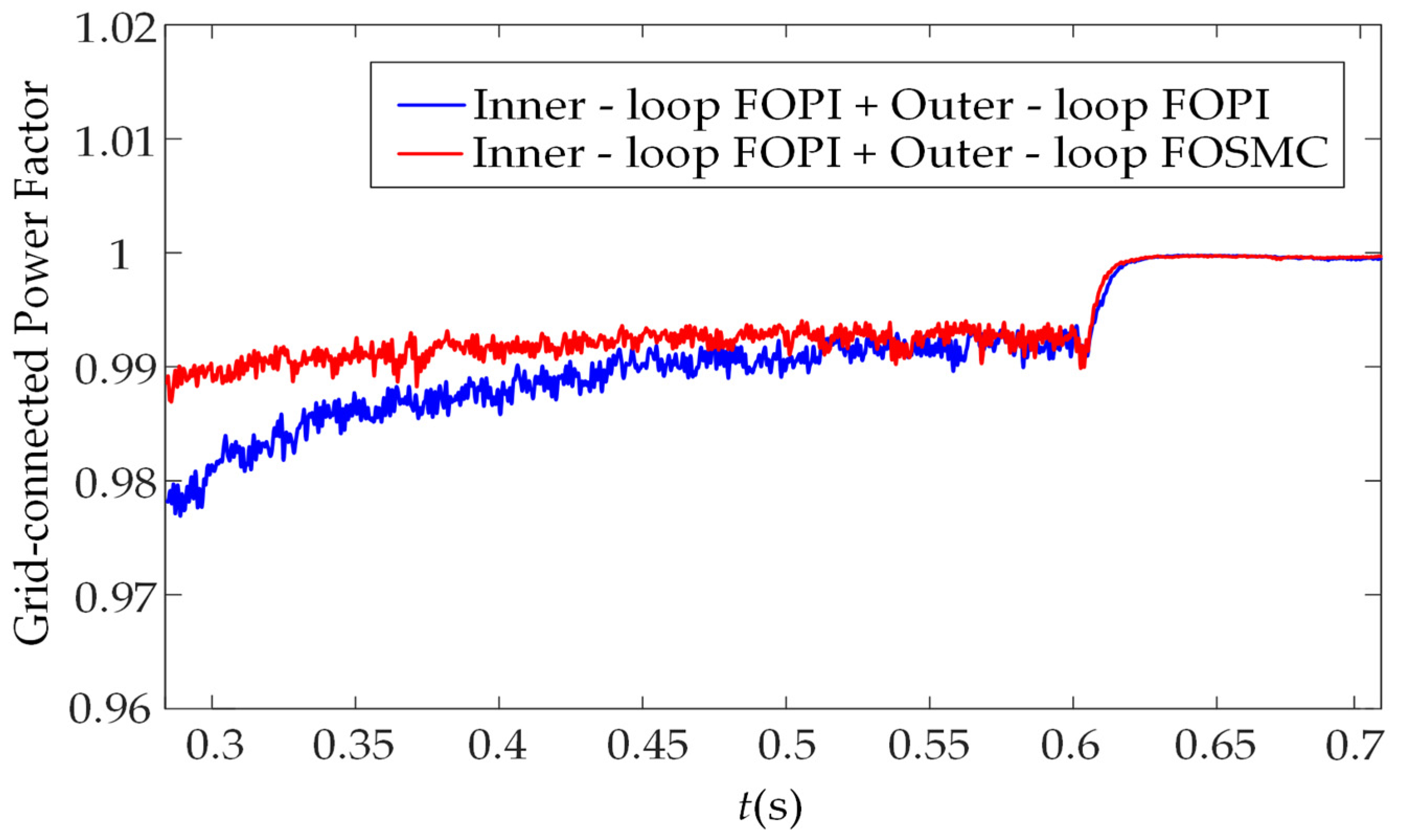
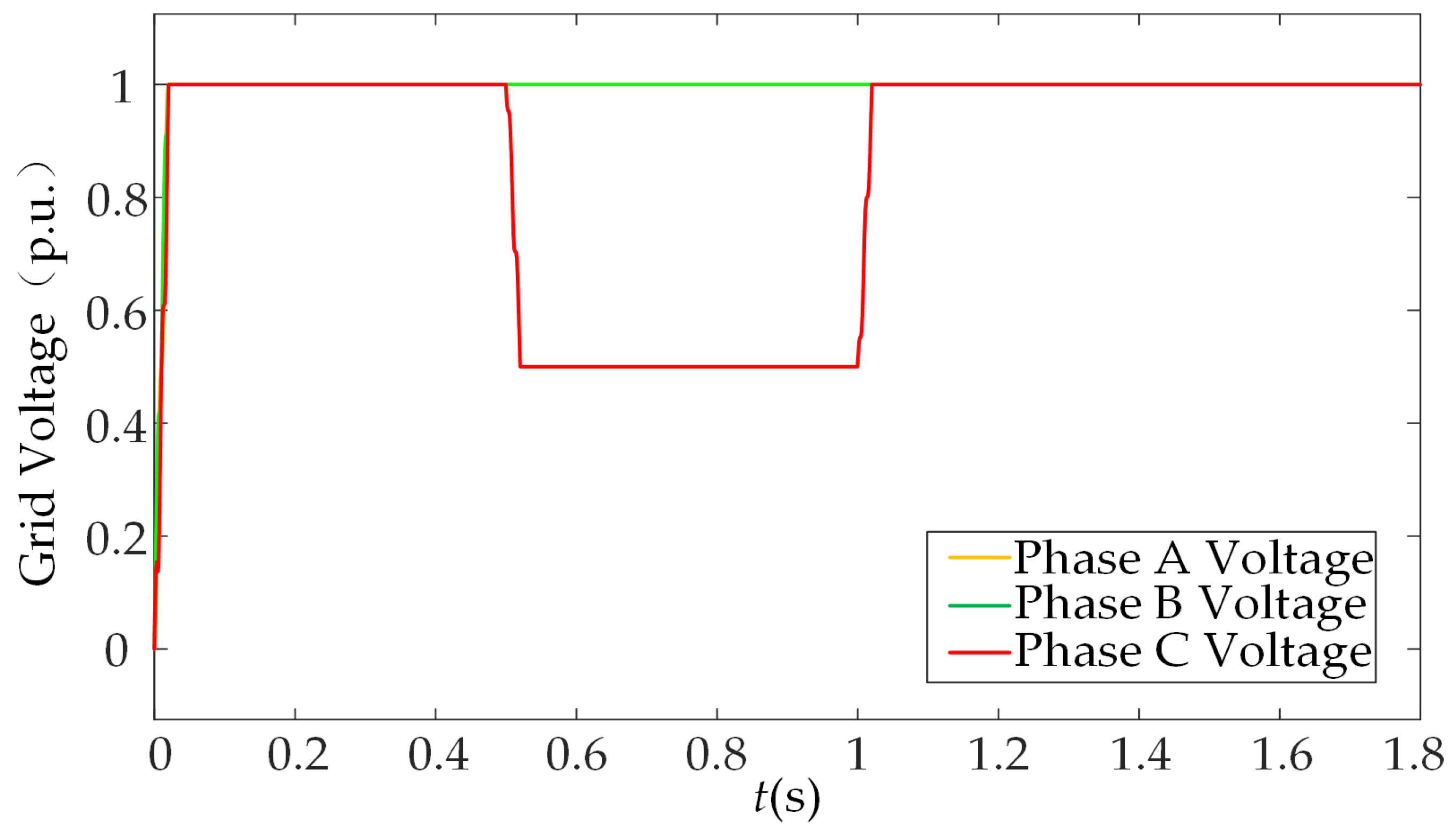
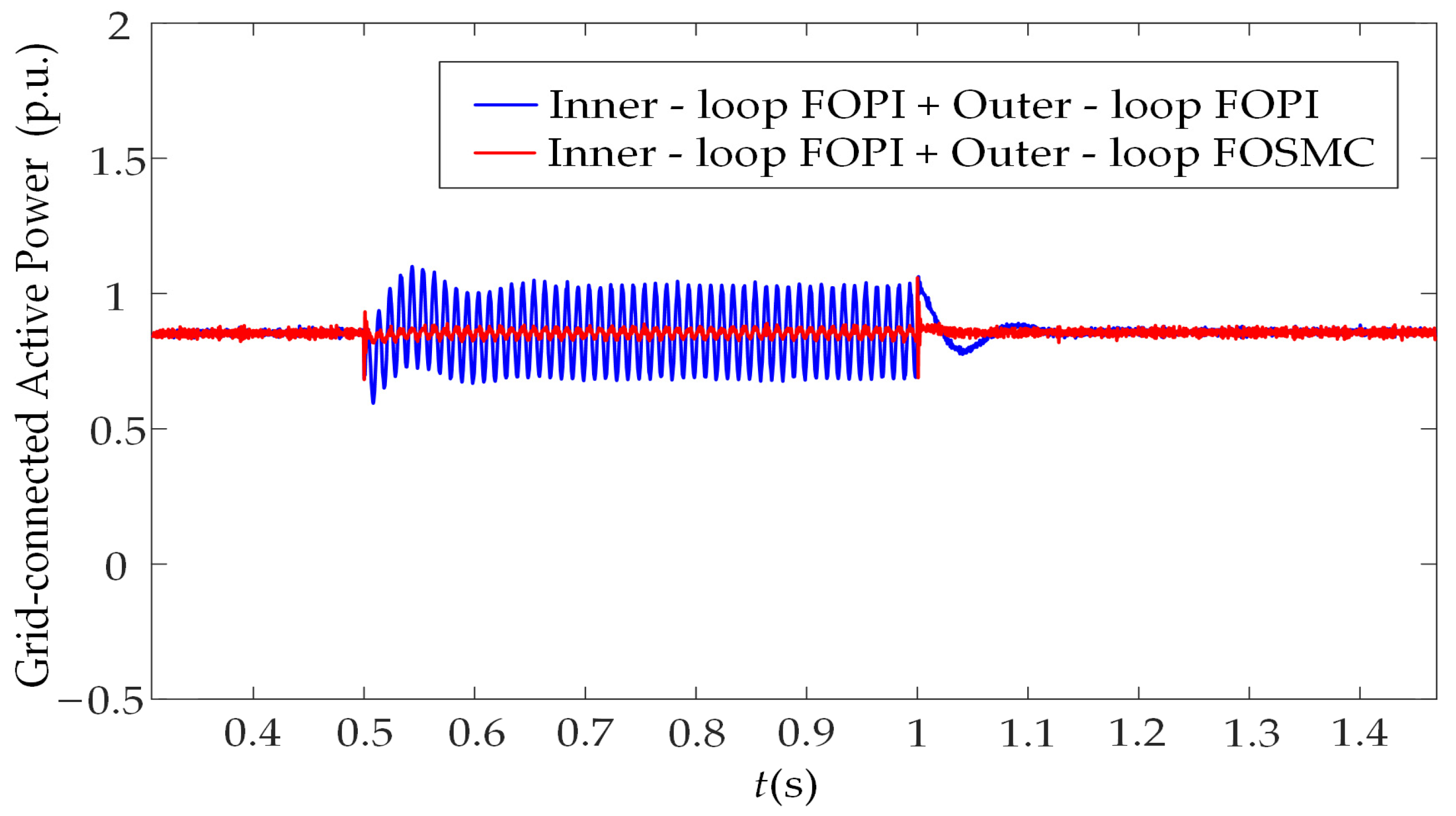
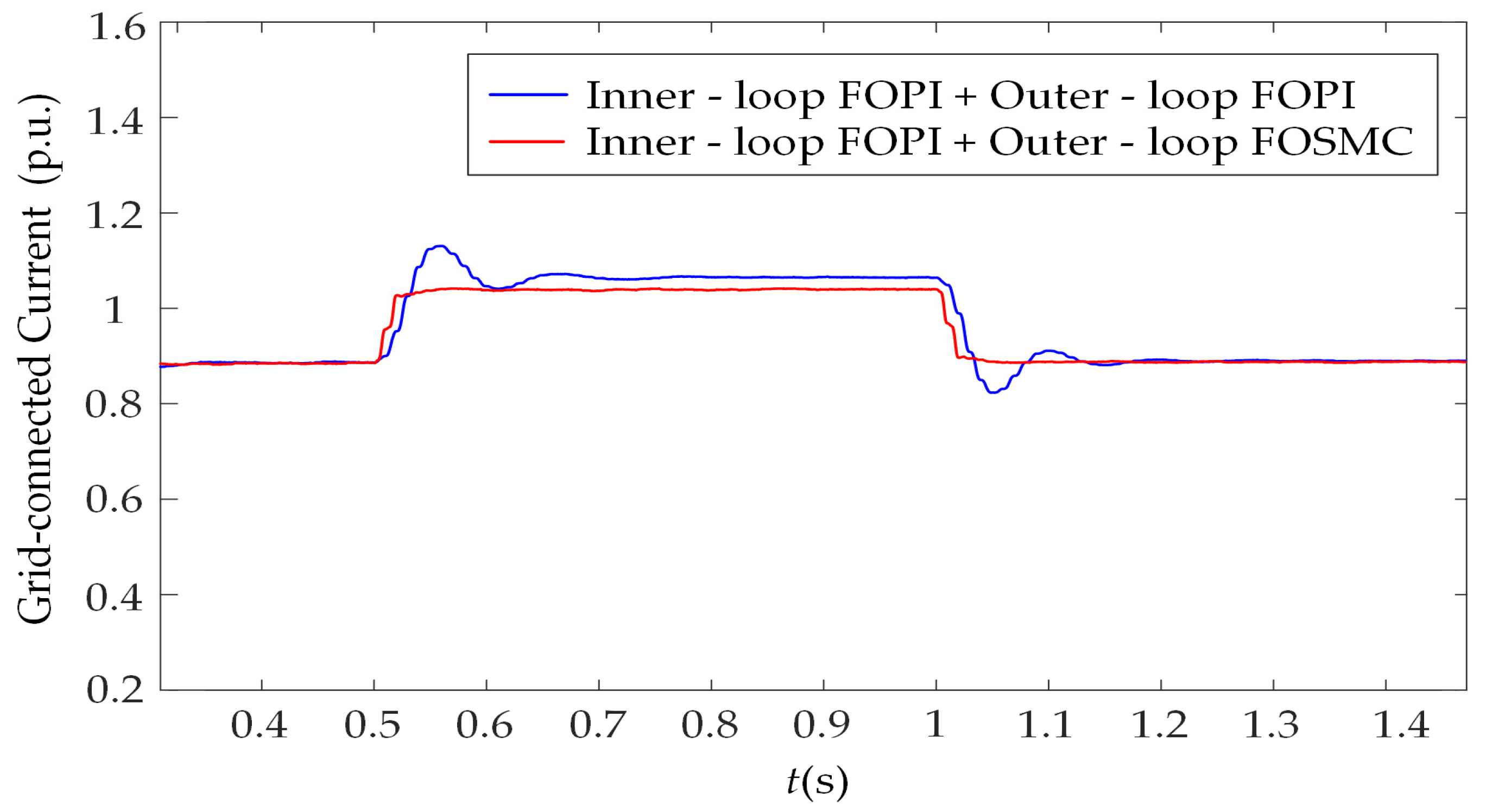
4.3. Simulation Analysis Under Asymmetric Grid Faults
4.4. Robustness Test of the FOSM Controller
5. Conclusions
- (1)
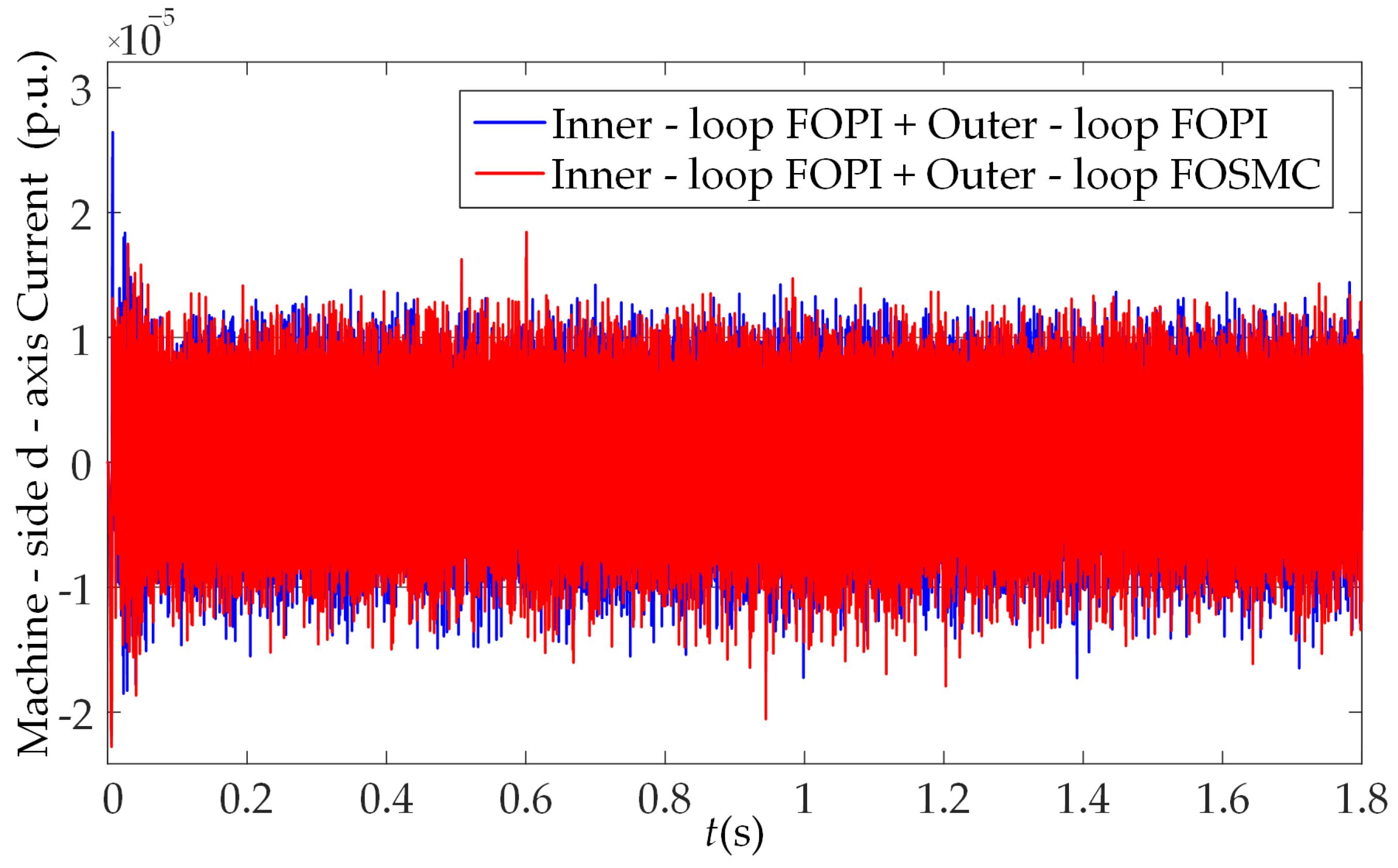
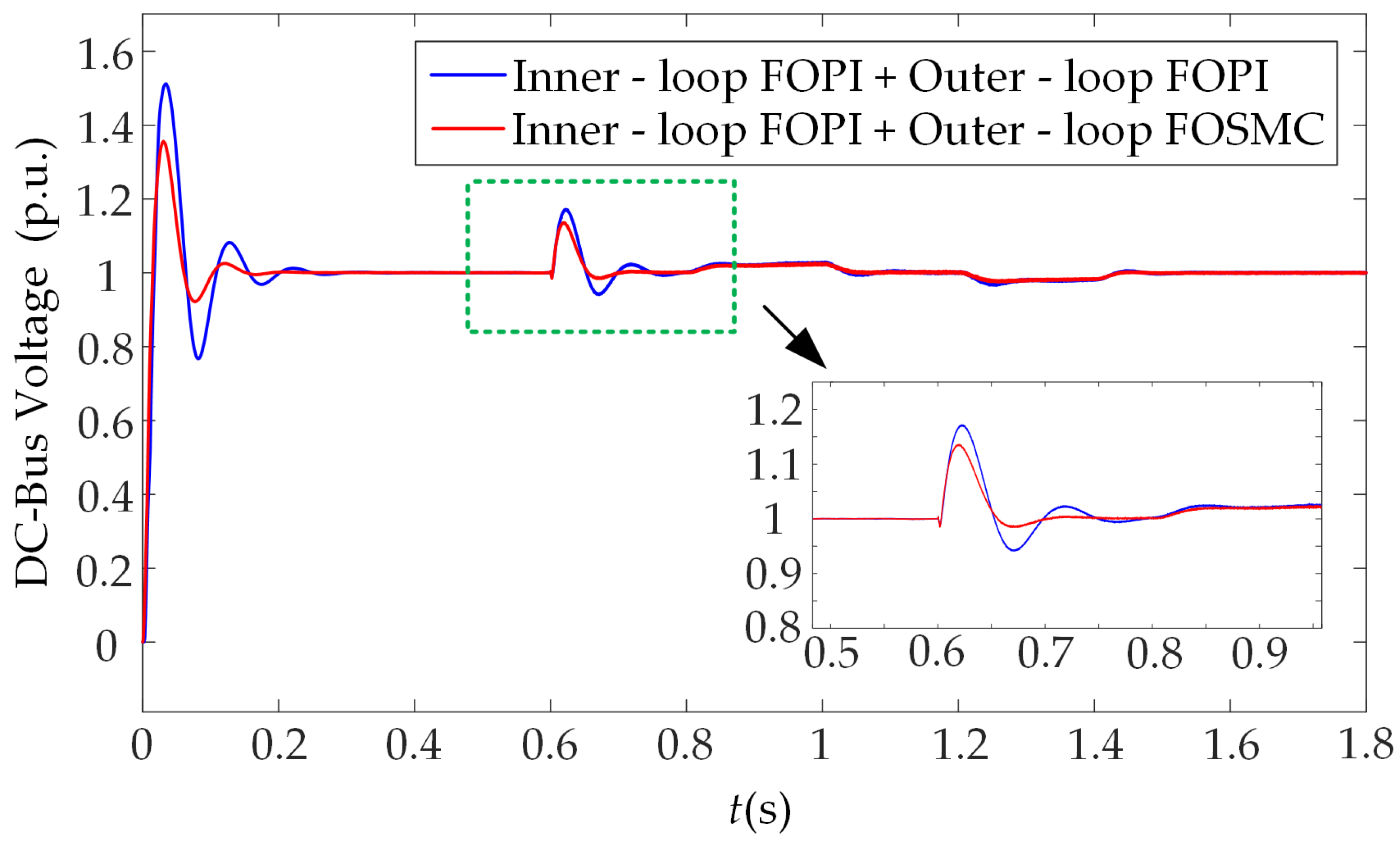
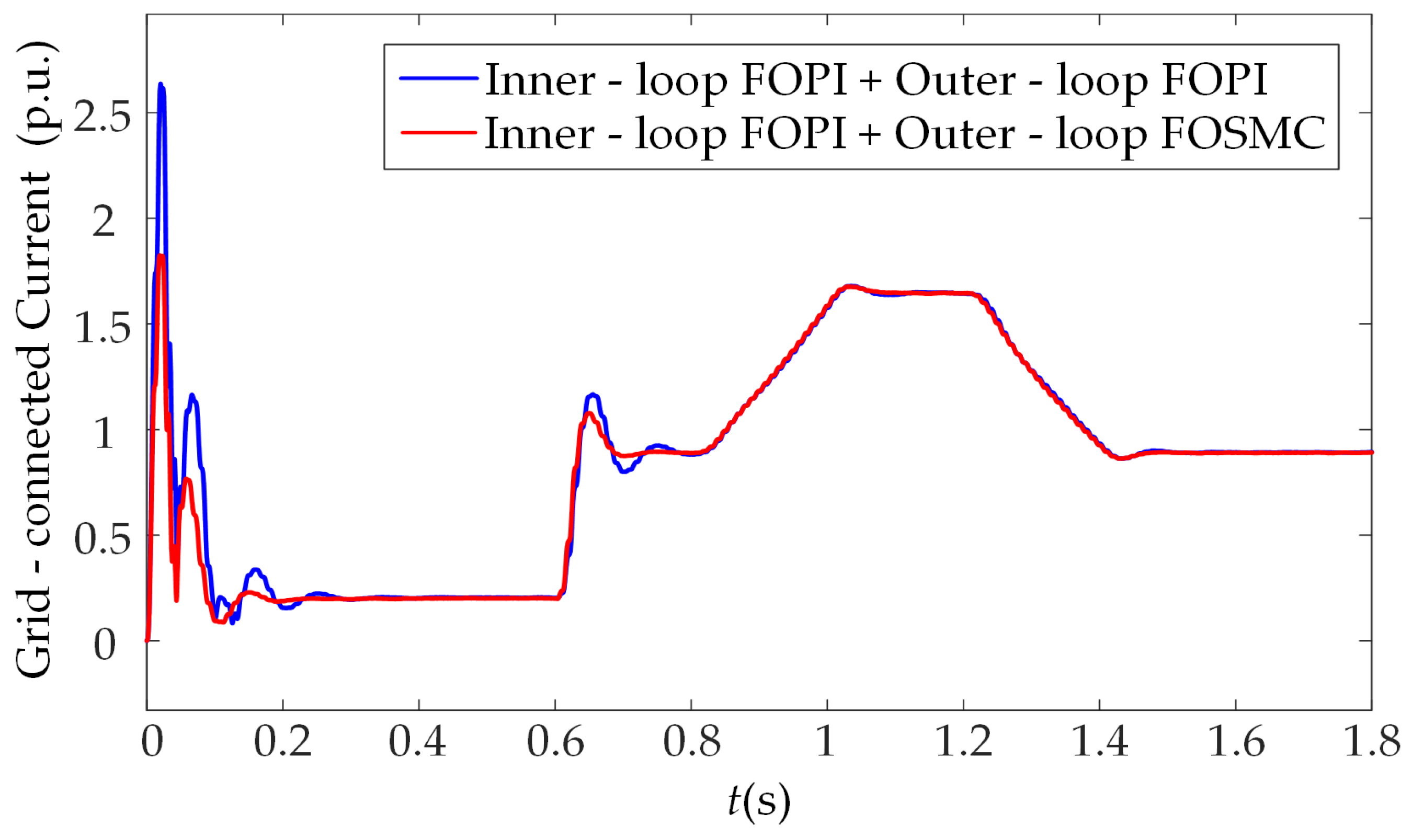
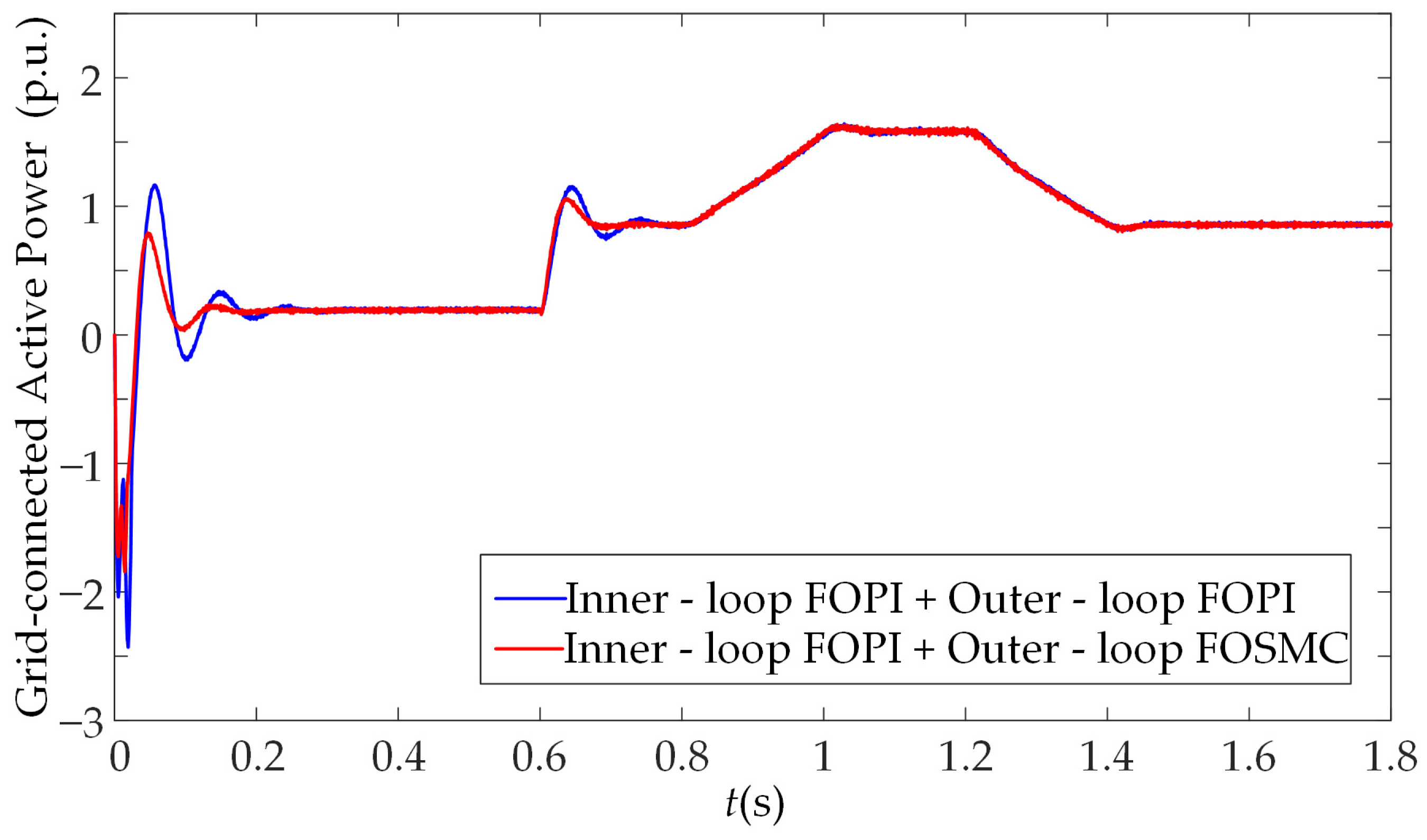
- Compared with the traditional FOPI outer-loop control, the FOSM outer-loop control demonstrates superior dynamic and static performance. In the presence of disturbances such as sudden wind speed fluctuations and grid voltage faults, FOSMC not only achieves lower overshoot and faster response speed but also exhibits notable superiority in terms of steady-state accuracy and anti-interference ability, thus providing a more dependable control support for the efficient grid integration of permanent magnet direct-drive wind power systems.
- (2)
- When both the speed outer-loop and the voltage outer-loop employ FOSMC, the system’s performance improvement under different disturbance scenarios exhibits distinct focus areas. Applying FOSMC in the speed outer-loop can enhance the dynamic regulation capability for the d-axis current and speed; adopting FOSMC in the voltage outer-loop can significantly improve the stability of the DC-bus voltage, as well as the control accuracy of grid-connected current and power. Meanwhile, under complex operating conditions such as grid voltage faults, the robustness advantage of FOSMC can effectively suppress system fluctuations and facilitate faster system recovery.
- (1)
- The permanent magnet direct-drive generator studied in this paper is an integer-order model, and this research focuses on the basic effectiveness verification of the FOSMC strategy in the fractional-order permanent magnet direct-drive wind power grid-connected system. Therefore, in simulation modeling, only some delay links of the system (such as pulse width modulation delay and communication transmission delay) are taken into account, with the focus on verifying the control performance of the control strategy under wind speed variation and grid voltage faults. This study does not consider noise and quantization effects for the time being and does not extend to the influence of nonlinear disturbances in engineering scenarios.
- (2)
- This study focuses on the working conditions of wind speed changes and single-phase grid voltage sags, without considering more complex composite fault conditions, such as “wind speed change + grid fault”. The control performance under multiple external disturbance conditions has not been verified, and there is a certain limitation in the coverage of working conditions.
- (3)
- The selection of relevant parameters for FOSMC is optimized according to the working conditions set in this study, and the adaptive matching between working condition parameters and control parameters has not been achieved. When the working condition range is beyond the scope of this study, the parameters need to be re-tuned, resulting in a lack of cross-working condition universality.
- (1)
- The proposed FOSMC can achieve smooth power output by quickly adjusting the electromagnetic torque above the rated wind speed. However, in the low-wind-speed range, due to the small output torque of the permanent magnet synchronous generator, the chattering suppression effect of FOSMC will weaken as the signal-to-noise ratio of the torque signal decreases, and there are certain limitations.
- (2)
- The algorithm proposed in this paper can suppress torque ripple by virtue of the fast convergence characteristic of FOSM when the single-phase voltage sag is 50%. But when the voltage sag is deep, the switching gain of the fractional-order sliding mode surface needs to be greatly increased to maintain control stability. At this time, the chattering phenomenon of the algorithm will be significantly aggravated, and its applicability in deep sag scenarios is limited.
- (1)
- For the permanent magnet synchronous generator in the fractional-order permanent magnet direct-drive wind power system investigated in this paper—currently modeled using an integer-order mathematical framework—it is necessary to conduct in-depth studies on its fractional-order mathematical model.
- (2)
- This paper employs FOPI control for the inner-loop control of back-to-back converters. In subsequent work, FOSMC can be applied to the inner-loop control for comparative analysis. Additionally, based on (1), FOSMC can be used for full-system control and then compared and analyzed in detail with other fractional-order control strategies.
- (3)
- Noise and quantization effects play a crucial role in practical system performance. In future work, we will introduce noise to analyze its impact on the control accuracy of FOSMC; explore the coupling mechanism between quantization effects and the dynamic characteristics of fractional-order capacitors; and verify the anti-disturbance capability of the proposed control strategy when such disturbances are considered through comparative simulations, thereby further enhancing the engineering applicability of the method.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Loop | Parameter | Parameter Boundaries | Stopping Criteria |
|---|---|---|---|
| FOPI current loop | kp | [0, 100] | 10−6 |
| ki | [800, 1200] | ||
| η | [0, 1] | ||
| FOPI speed loop | kp′ | [0, 100] | 10−6 |
| ki′ | [2800, 3500] | ||
| η′ | [0, 1] | ||
| FOSMC speed loop | μ | [0, 1] | 10−14 |
| σ | [0, 1] | ||
| k0 | [0, 100] | ||
| k1 | [0, 100] |
| Loop | Parameter | Parameter Boundaries | Stopping Criteria |
|---|---|---|---|
| FOPI current loop | kp0 | [0, 100] | 10−6 |
| ki0 | [800, 1200] | ||
| η0 | [0, 1] | ||
| FOPI voltage loop | kp0′ | [0, 10] | 10−6 |
| ki0′ | [0, 100] | ||
| η0′ | [0, 1] | ||
| FOSMC voltage loop | ς | [0, 1] | 10−14 |
| τ | [0, 1] | ||
| k2 | [0, 50] | ||
| k3 | [50, 150] |

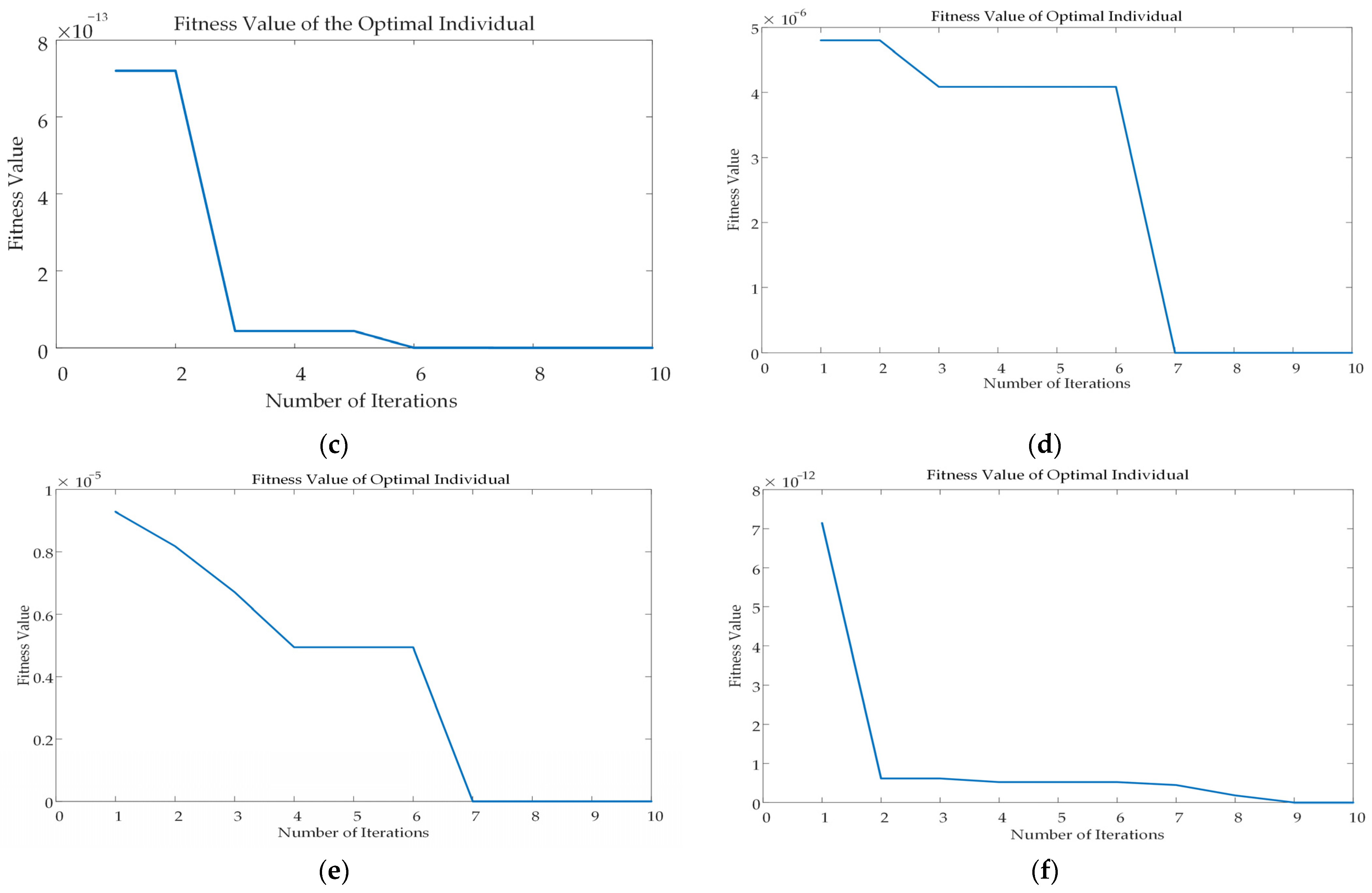
References
- Ma, X.; Li, M.; Li, W.; Liu, Y. Overview of offshore wind power technologies. Sustainability 2025, 17, 596. [Google Scholar] [CrossRef]
- Mossa, M.A.; Mohamed, R.A.; Al-Sumaiti, A.S. Performance Enhancement of a Grid Connected Wind Turbine Based PMSG Using Effective Predictive Control Algorithm. IEEE Access 2025, 13, 64160–64185. [Google Scholar] [CrossRef]
- Rausell, E.; Arnaltes, S.; Rodríguez, J.L.; Lafoz, M.; Navarro, G. Control of wind energy conversion systems with permanent magnet synchronous generator for isolated green hydrogen production. Int. J. Hydrogen Energy 2025, 107, 241–251. [Google Scholar] [CrossRef]
- Liu, D.; Han, J.; Chen, G.; Cheng, Y.; Liang, X.; Song, C. Fuzzy self-tuning fractional order PD permanent magnet synchronous motor speed control based on torque compensation. Sci. Rep. 2025, 15, 2141. [Google Scholar] [CrossRef]
- Zhang, B.; Shu, X. Fractional-Order Electrical Circuit Theory; Springer: Singapore, 2022. [Google Scholar]
- Zhang, L.; Kartci, A.; Elwakil, A.; Bagci, H.; Salama, K.N. Fractional-order inductor: Design, simulation, and implementation. IEEE Access 2021, 9, 73695–73702. [Google Scholar] [CrossRef]
- Mijat, N.; Jurisic, D.; Moschytz, G.S. Analog modeling of fractional-order elements: A classical circuit theory approach. IEEE Access 2021, 9, 110309–110331. [Google Scholar] [CrossRef]
- Zheng, Z.; Ma, F.J.; Wei, Y.F. Fractional-order modeling and simulation analysis of single-phase PWM rectifier. J. Syst. Simul. 2017, 29, 784. [Google Scholar]
- Li, X.C.; Hou, L.L.; Luo, X.L.; Xu, J.H. Fractional-order modeling and controller design of three-phase inverter grid-connected system. Acta Energiae Solaris Sin. 2023, 44, 415–424. [Google Scholar]
- Li, X.C.; Luo, X.L.; Hou, L.L.; Xu, J.H. Grid-side control research of wind power generation based on fractional-order LCL filter. Acta Energiae Solaris Sin. 2022, 43, 383–391. [Google Scholar]
- Aarif, M.; Joshi, D.; Jangid, R.; Sharma, S.S. Grid Power Smoothing Management for Direct-Drive PMSG Variable-Speed Wind Energy Conversion System with Multilevel Converter. In ICT Infrastructure and Computing: Proceedings of ICT4SD 2022; Springer Nature Singapore: Singapore, 2022; pp. 19–28. [Google Scholar]
- Yu, J.; Ouyang, J.; Zhang, A.; Chen, J. Modeling of dynamic control error and emergency frequency control for direct-drive PMSG-based wind turbine under grid fault. IEEE Trans. Sustain. Energy 2024, 15, 1690–1702. [Google Scholar] [CrossRef]
- Vu, N.T.T.; Nguyen, H.D.; Nguyen, A.T. Reinforcement learning-based adaptive optimal fuzzy MPPT control for variable speed wind turbine. IEEE Access 2022, 10, 95771–95780. [Google Scholar] [CrossRef]
- Bu, W.; Guo, S.; Fan, Z.; Li, J. Improved Adaptive PI-like Fuzzy Control Strategy of Permanent Magnet Synchronous Motor. Energies 2025, 18, 362. [Google Scholar] [CrossRef]
- Pathak, D.; Bhati, S.; Gaur, P. Fractional-order nonlinear PID controller based maximum power extraction method for a direct-driven wind energy system. Int. Trans. Electr. Energy Syst. 2020, 30, e12641. [Google Scholar] [CrossRef]
- Pathak, D.; Gaur, P. Output power control of wind energy system by tip speed ratio control using fractional PI β D α controller. Int. J. Inf. Technol. 2021, 13, 299–305. [Google Scholar]
- Benbouhenni, H.; Bizon, N.; Colak, I.; Thounthong, P.; Takorabet, N. Application of fractional-order PI controllers and neuro-fuzzy PWM technique to multi-rotor wind turbine systems. Electronics 2022, 11, 1340. [Google Scholar] [CrossRef]
- Feyzi, M.; Roozbehani, S.; Ghaseminejad Liasi, S.; Kordkandi, R.D. Real-Time Fault Ride Through Capability Improvement of PMSG-Wind Turbine Based on Robust Fractional Order Sliding Mode Control. Optim. Control. Appl. Methods 2025, 46, 859–874. [Google Scholar] [CrossRef]
- Ferhat, N.; Aounallah, T.; Essounbouli, N.; Hamzaoui, A.; Bouchafaa, F. Fractional Adaptive Fuzzy Sliding Mode Control Algorithm for Permanent Magnet Synchronous Generators. In Proceedings of the 2021 International Conference on Control, Automation and Diagnosis (ICCAD), Grenoble, France, 3–5 November 2021; IEEE: Washington, DC, USA, 2021; pp. 1–6. [Google Scholar]
- Qu, X.; Zhang, S.; Peng, C. Model-Free Adaptive Fast Integral Terminal Sliding Mode Control for Permanent Magnet Synchronous Motor with Position Error Constraint. World Electr. Veh. J. 2025, 16, 341. [Google Scholar] [CrossRef]
- Wu, Z.; Zhuang, J.; Liu, B.; Yang, P. Control method for permanent magnet synchronous motor based on fractional active disturbance rejection. Trans. Inst. Meas. Control. 2023, 45, 2352–2363. [Google Scholar] [CrossRef]
- Wang, W. Simulation Study on Permanent Magnet Direct-Drive Motor Based on Fractional-Order PID Control. Electr. Meas. Instrum. 2016, 53 (Suppl. 1), 223–226. [Google Scholar]
- Gao, P.; Zhang, G.; Lv, X. Model-free hybrid control with intelligent proportional integral and super-twisting sliding mode control of PMSM drives. Electronics 2020, 9, 1427. [Google Scholar] [CrossRef]
- Zaihidee, F.M.; Mekhilef, S.; Mubin, M. Application of fractional order sliding mode control for speed control of permanent magnet synchronous motor. IEEE Access 2019, 7, 101765–101774. [Google Scholar] [CrossRef]
- Ahmed, T.; Waqar, A.; Elavarasan, R.M.; Imtiaz, J.; Premkumar, M.; Subramaniam, U. Analysis of fractional order sliding mode control in a D-STATCOM integrated power distribution system. IEEE Access 2021, 9, 70337–70352. [Google Scholar] [CrossRef]
- Jiang, L.J.; Wang, X.Y.; Su, J.; Zhang, Z.T. Fuzzy Fractional-Order Control for Maximum Power Point Tracking of Permanent Magnet Synchronous Wind Power Generation System. Mod. Electr. Power 2024, 41, 230–239. [Google Scholar]
- Prajzendanc, P.; Kreischer, C. A Review of New Technologies in the Design and Application of Wind Turbine Generators. Energies 2025, 18, 4082. [Google Scholar] [CrossRef]
- Lin, L.; He, Y.; Zhou, J.H.; Chen, H.Z.; Liu, Y.L.; Chen, H.W. Modeling and Simulation of Direct-Drive Permanent Magnet Synchronous Wind Turbine Generator-Side System. Electr. Drive 2020, 50, 73–76. [Google Scholar]
- Zhang, M.; He, G.Q.; Zhao, H.X.; Zhang, K.S. Modeling and Simulation of Direct-Drive Permanent Magnet Synchronous Wind Turbine Units. Electr. Power 2008, 41, 79–84. [Google Scholar]
- Xu, J.; Tang, S.; He, G.; Gong, Z.; Lin, G.; Liu, J. Modeling and Control Research of Fractional-Order Cascaded H-Bridge Multilevel STATCOM. Fractal Fract. 2024, 8, 392. [Google Scholar] [CrossRef]
- Wang, H.B.; Zhou, B.; Fang, S.C. Sliding Mode Control of Permanent Magnet Synchronous Motor Speed Regulation System. Trans. China Electrotech. Soc. 2009, 24, 71–77. [Google Scholar]
- Abdolrasol, M.G.M.; Hannan, M.A.; Hussain, S.M.S.; Ustun, T.S. Optimal PI controller based PSO optimization for PV inverter using SPWM techniques. Energy Rep. 2022, 8, 1003–1011. [Google Scholar] [CrossRef]
- Wang, X.; Guo, W.; Wei, M. Parameter Tuning of Fractional-Order PID Sliding Mode Control Based on Particle Swarm Optimization. Meas. Control. Technol. 2017, 36, 63–66. [Google Scholar]






| Parameter | Value |
|---|---|
| udc | 850 V |
| α | 0.85 |
| β | 0.95 |
| L1 | 0.72 mH/s1−α |
| L2 | 0.72 mH/s1−α |
| Cdc | 0.01 F/s1−β |
| C | 0.001 F/s1−β |
| p | 10 |
| J | 5 kg·m2 |
| Rs | 0.045 Ω |
| ψf | 1.832 Wb |
| Lsd, Lsq | 0.755 mH/s1−α |
| Loop | Parameter | Value |
|---|---|---|
| FOPI current loop | kp | 50 |
| ki | 1000 | |
| η | 0.8 | |
| FOPI speed loop | kp′ | 20 |
| ki′ | 3000 | |
| η′ | 0.9 | |
| FOSMC speed loop | μ | 0.976 |
| σ | 0.142 | |
| k0 | 63 | |
| k1 | 59 |
| Loop | Parameter | Value |
|---|---|---|
| FOPI current loop | kp0 | 80 |
| ki0 | 1000 | |
| η0 | 0.78 | |
| FOPI voltage loop | kp0′ | 0.5 |
| ki0′ | 60 | |
| η0′ | 0.95 | |
| FOSMC voltage loop | ς | 0.1 |
| τ | 0.869 | |
| k2 | 16 | |
| k3 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Lan, Y.; Wang, C.; Liu, B.; Li, Y.; Xie, Y. Research on Fractional-Order Sliding Mode Control of Fractional-Order Permanent Magnet Direct-Drive Wind Power System. Machines 2025, 13, 928. https://doi.org/10.3390/machines13100928
Xu J, Lan Y, Wang C, Liu B, Li Y, Xie Y. Research on Fractional-Order Sliding Mode Control of Fractional-Order Permanent Magnet Direct-Drive Wind Power System. Machines. 2025; 13(10):928. https://doi.org/10.3390/machines13100928
Chicago/Turabian StyleXu, Junhua, Yue Lan, Chunwei Wang, Bin Liu, Yingheng Li, and Yongzeng Xie. 2025. "Research on Fractional-Order Sliding Mode Control of Fractional-Order Permanent Magnet Direct-Drive Wind Power System" Machines 13, no. 10: 928. https://doi.org/10.3390/machines13100928
APA StyleXu, J., Lan, Y., Wang, C., Liu, B., Li, Y., & Xie, Y. (2025). Research on Fractional-Order Sliding Mode Control of Fractional-Order Permanent Magnet Direct-Drive Wind Power System. Machines, 13(10), 928. https://doi.org/10.3390/machines13100928






