Comparative Study of TriVariant and Delta Three-Degree-of-Freedom Parallel Mechanisms for Aerial Manipulation
Abstract
1. Introduction
2. Kinematics of the TriVariant
2.1. Forward Kinematics
2.2. Inverse Kinematics
2.3. Jacobian Matrix
3. Kinematics of the Delta Robot
3.1. Forward Kinematics
3.2. Inverse Kinematics
3.3. Jacobian Matrix
4. Performance Comparison of the TriVariant and the Delta Robot
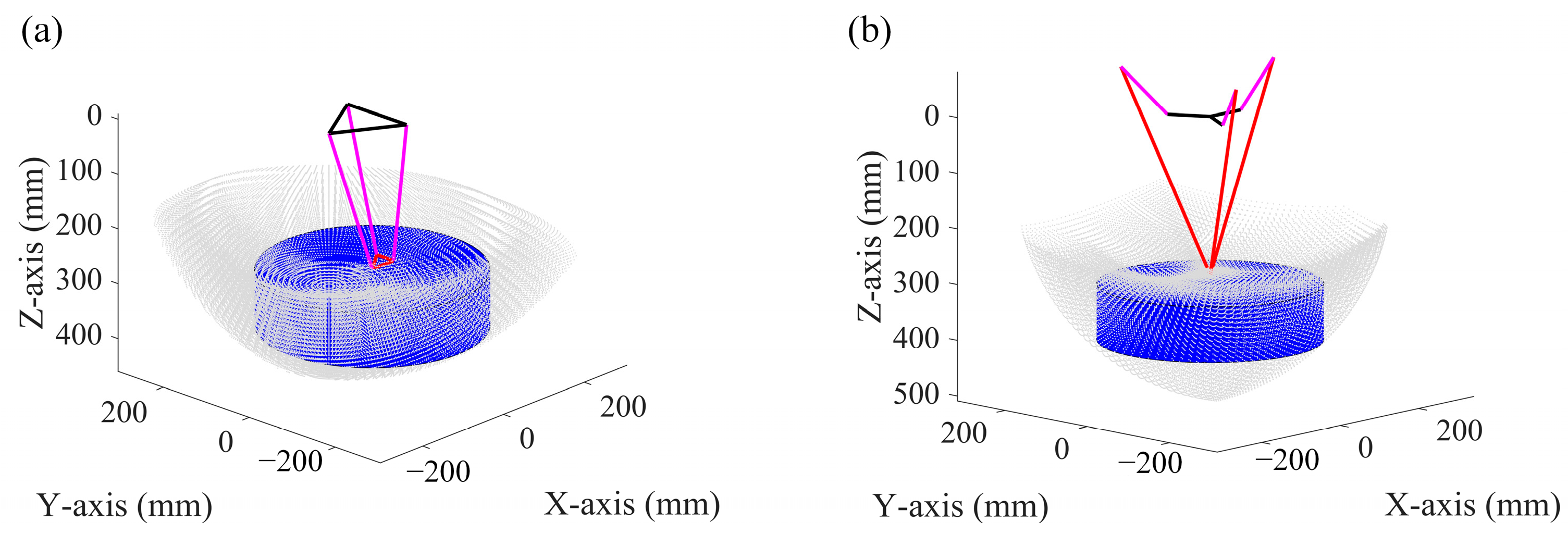
4.1. Dimension
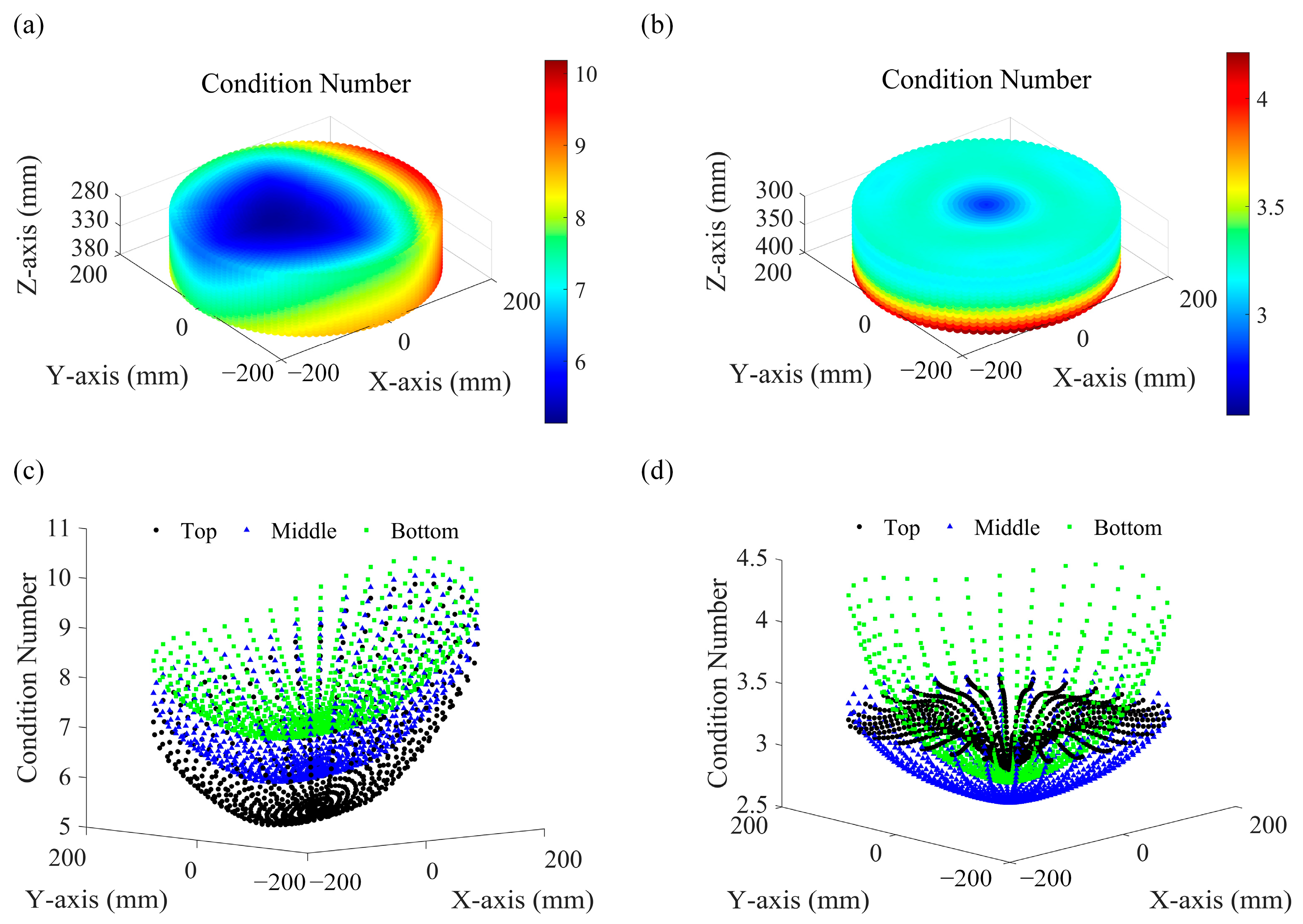
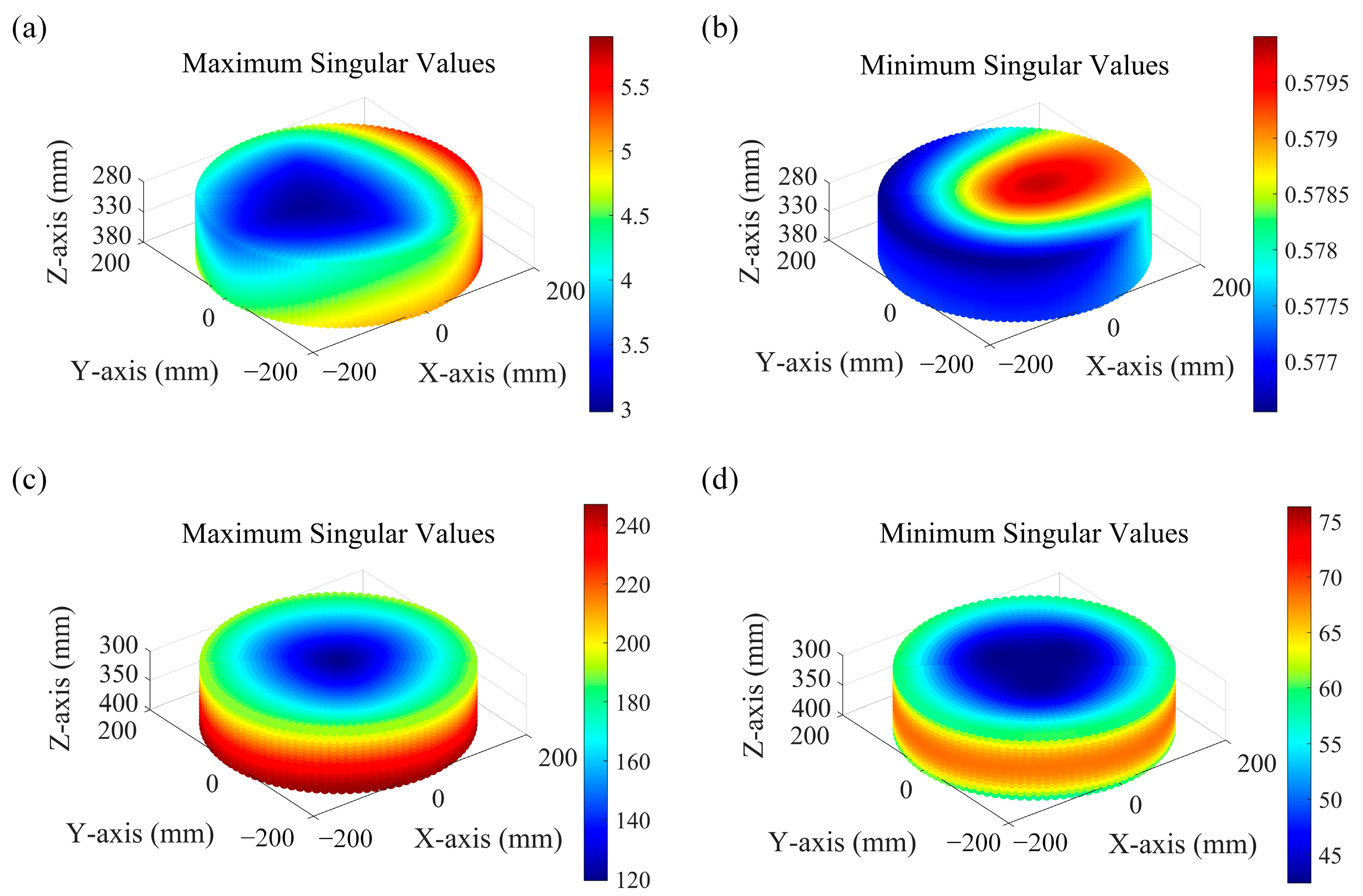
4.2. Dexterity
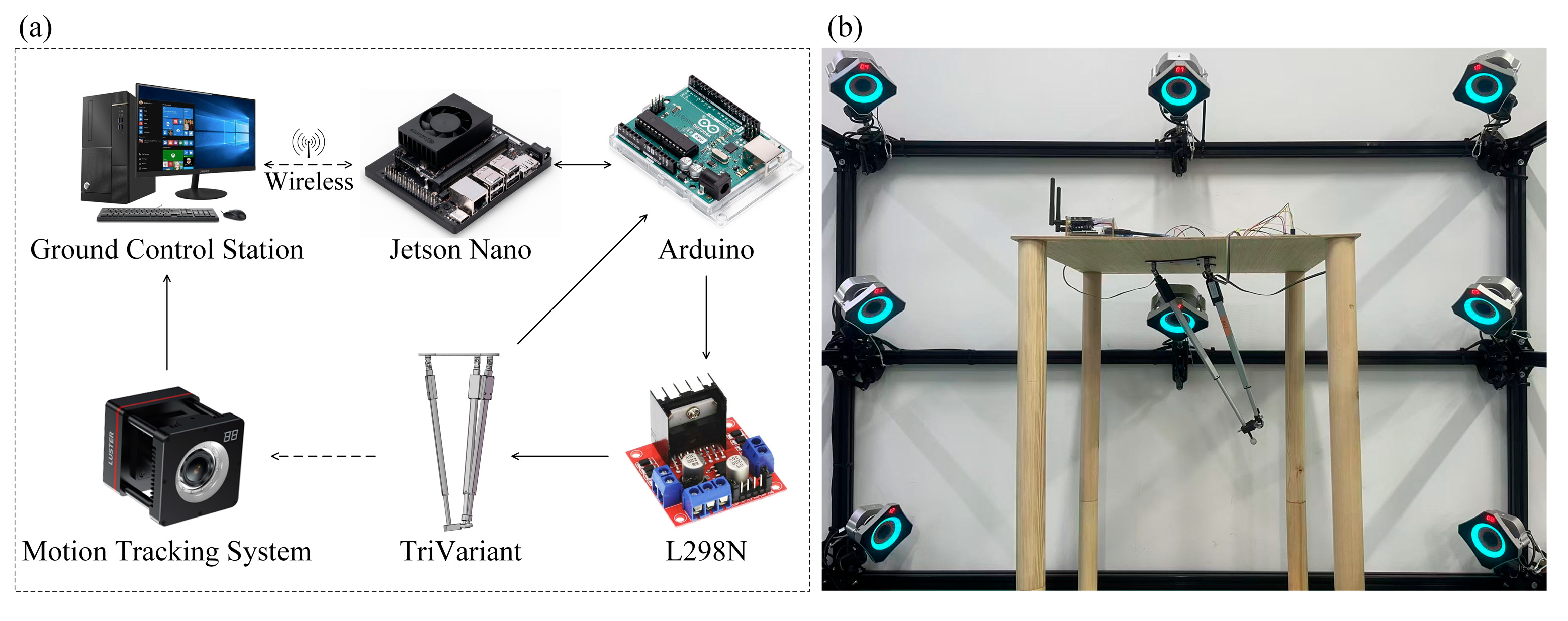
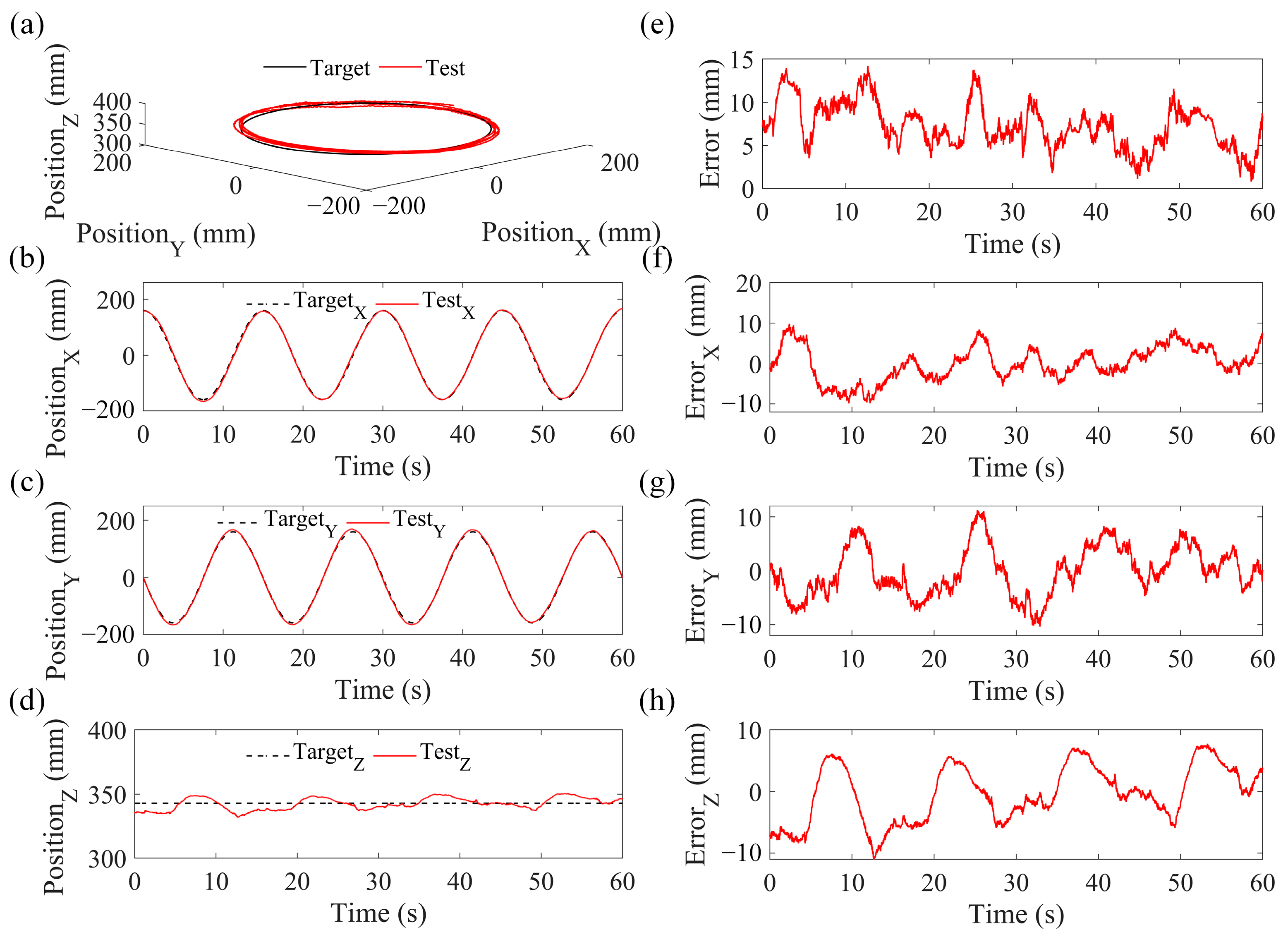
5. Trajectory Tracking Experiments of the TriVariant
6. Discussions
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Meng, X.; He, Y.; Han, J. Survey on aerial manipulator: System, modeling, and control. Robotica 2020, 38, 1288–1317. [Google Scholar] [CrossRef]
- Ahmed, F.; Mohanta, J.; Keshari, A.; Yadav, P.S. Recent advances in unmanned aerial vehicles: A review. Arab. J. Sci. Eng. 2022, 47, 7963–7984. [Google Scholar] [CrossRef] [PubMed]
- Ladig, R.; Paul, H.; Miyazaki, R.; Shimonomura, K. Aerial manipulation using multirotor UAV: A review from the aspect of operating space and force. J. Robot. Mechatron. 2021, 33, 196–204. [Google Scholar] [CrossRef]
- Xilun, D.; Pin, G.; Kun, X.; Yushu, Y. A review of aerial manipulation of small-scale rotorcraft unmanned robotic systems. Chin. J. Aeronaut. 2019, 32, 200–214. [Google Scholar] [CrossRef]
- Bodie, K.; Brunner, M.; Pantic, M.; Walser, S.; Pfändler, P.; Angst, U.; Siegwart, R.; Nieto, J. Active interaction force control for contact-based inspection with a fully actuated aerial vehicle. Trans. Robot. 2020, 37, 709–722. [Google Scholar] [CrossRef]
- Brunner, M.; Rizzi, G.; Studiger, M.; Siegwart, R.; Tognon, M. A planning-and-control framework for aerial manipulation of articulated objects. IEEE Robot. Autom. Lett. 2022, 7, 10689–10696. [Google Scholar] [CrossRef]
- Kim, S.-J.; Lee, D.-Y.; Jung, G.-P.; Cho, K.-J. An origami-inspired, self-locking robotic arm that can be folded flat. Sci. Robot. 2018, 3, eaar2915. [Google Scholar] [CrossRef]
- Bartelds, T.; Capra, A.; Hamaza, S.; Stramigioli, S.; Fumagalli, M. Compliant aerial manipulators: Toward a new generation of aerial robotic workers. IEEE Robot. Autom. Lett. 2016, 1, 477–483. [Google Scholar] [CrossRef]
- Xu, M.; Hu, A.; Wang, H. Image-based visual impedance force control for contact aerial manipulation. IEEE Trans. Autom. Sci. Eng. 2022, 20, 518–527. [Google Scholar] [CrossRef]
- Zhong, H.; Miao, Z.; Wang, Y.; Mao, J.; Li, L.; Zhang, H.; Chen, Y.; Fierro, R. A practical visual servo control for aerial manipulation using a spherical projection model. IEEE Trans. Ind. Electron. 2019, 67, 10564–10574. [Google Scholar] [CrossRef]
- Emami, S.A.; Banazadeh, A. Simultaneous trajectory tracking and aerial manipulation using a multi-stage model predictive control. Aerosp. Sci. Technol. 2021, 112, 106573. [Google Scholar] [CrossRef]
- Imanberdiyev, N.; Sood, S.; Kircali, D.; Kayacan, E. Design, development and experimental validation of a lightweight dual-arm aerial manipulator with a COG balancing mechanism. Mechatronics 2022, 82, 102719. [Google Scholar] [CrossRef]
- Cacace, J.; Orozco-Soto, S.M.; Suarez, A.; Caballero, A.; Orsag, M.; Bogdan, S.; Vasiljevic, G.; Ebeid, E.; Rodriguez, J.A.A.; Ollero, A. Safe local aerial manipulation for the installation of devices on power lines: Aerial-core first year results and designs. Appl. Sci. 2021, 11, 6220. [Google Scholar] [CrossRef]
- Peng, R.; Wang, Y.; Lu, M.; Lu, P. A dexterous and compliant aerial continuum manipulator for cluttered and constrained environments. Nat. Commun. 2025, 16, 889. [Google Scholar] [CrossRef] [PubMed]
- Uthayasooriyan, A.; Vanegas, F.; Jalali, A.; Digumarti, K.M.; Janabi-Sharifi, F.; Gonzalez, F. Tendon-Driven Continuum Robots for Aerial Manipulation—A Survey of Fabrication Methods. Drones 2024, 8, 269. [Google Scholar] [CrossRef]
- Guo, X.; Tang, W.; Qin, K.; Zhong, Y.; Xu, H.; Qu, Y.; Li, Z.; Sheng, Q.; Gao, Y.; Yang, H. Powerful UAV manipulation via bioinspired self-adaptive soft self-contained gripper. Sci. Adv. 2024, 10, eadn6642. [Google Scholar] [CrossRef]
- Wang, Z.; Freris, N.M.; Wei, X. SpiRobs: Logarithmic spiral-shaped robots for versatile grasping across scales. Device 2024, 3, 100646. [Google Scholar] [CrossRef]
- Carbone, G.; Ceccarelli, M.; Oliveira, P.; Saramago, S.F.; Carvalho, J.C.M. An optimum path planning for Cassino parallel manipulator by using inverse dynamics. Robotica 2008, 26, 229–239. [Google Scholar] [CrossRef]
- Gan, D.; Liao, Q.; Dai, J.S.; Wei, S. Design and kinematics analysis of a new 3CCC parallel mechanism. Robotica 2010, 28, 1065–1072. [Google Scholar] [CrossRef]
- Bodie, K.; Brunner, M.; Allenspach, M. Omnidirectional Tilt-Rotor Flying Robots for Aerial Physical Interaction: Modelling, Control, Design and Experiments; Springer Nature: Cham, Switzerland, 2023; Volume 157. [Google Scholar]
- Zhang, K.; Chermprayong, P.; Xiao, F.; Tzoumanikas, D.; Dams, B.; Kay, S.; Kocer, B.B.; Burns, A.; Orr, L.; Alhinai, T. Aerial additive manufacturing with multiple autonomous robots. Nature 2022, 609, 709–717. [Google Scholar] [CrossRef]
- Cao, H.; Li, Y.; Liu, C.; Zhao, S. ESO-based robust and high-precision tracking control for aerial manipulation. IEEE Trans. Autom. Sci. Eng. 2023, 21, 2139–2155. [Google Scholar] [CrossRef]
- Bodie, K.; Tognon, M.; Siegwart, R. Dynamic end effector tracking with an omnidirectional parallel aerial manipulator. IEEE Robot. Autom. Lett. 2021, 6, 8165–8172. [Google Scholar] [CrossRef]
- Pierrot, F.; Reynaud, C.; Fournier, A. DELTA: A simple and efficient parallel robot. Robotica 1990, 8, 105–109. [Google Scholar] [CrossRef]
- Yang, X.; Feng, Z.; Liu, C.; Ren, X. A Geometric Method for Kinematics of Delta Robot and Its Path Tracking Control. In Proceedings of the 2014 14th International Conference on Control, Automation and Systems (ICCAS), Seoul, Republic of Korea, 22–25 October 2014; pp. 509–514. [Google Scholar]
- Dastjerdi, A.H.; Sheikhi, M.M.; Masouleh, M.T. A complete analytical solution for the dimensional synthesis of 3-DOF delta parallel robot for a prescribed workspace. Mech. Mach. Theory 2020, 153, 103991. [Google Scholar] [CrossRef]
- Brinker, J.; Corves, B.; Takeda, Y. Kinematic performance evaluation of high-speed Delta parallel robots based on motion/force transmission indices. Mech. Mach. Theory 2018, 125, 111–125. [Google Scholar] [CrossRef]
- Keemink, A.Q.; Fumagalli, M.; Stramigioli, S.; Carloni, R. Mechanical design of a manipulation system for unmanned aerial vehicles. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 3147–3152. [Google Scholar]
- Fumagalli, M.; Naldi, R.; Macchelli, A.; Carloni, R.; Stramigioli, S.; Marconi, L. Modeling and control of a flying robot for contact inspection. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Portugal, 7–12 October 2012; pp. 3532–3537. [Google Scholar]
- Scholten, J.L.; Fumagalli, M.; Stramigioli, S.; Carloni, R. Interaction control of an UAV endowed with a manipulator. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 4910–4915. [Google Scholar]
- Fumagalli, M.; Naldi, R.; Macchelli, A.; Forte, F.; Keemink, A.Q.; Stramigioli, S.; Carloni, R.; Marconi, L. Developing an aerial manipulator prototype: Physical interaction with the environment. IEEE Robot. Autom. Mag. 2014, 21, 41–50. [Google Scholar] [CrossRef]
- Danko, T.W.; Chaney, K.P.; Oh, P.Y. A parallel manipulator for mobile manipulating UAVs. In Proceedings of the 2015 IEEE International Conference on Technologies for Practical Robot Applications (TePRA), Boston, MA, USA, 11–12 May 2015; pp. 1–6. [Google Scholar]
- Zhang, K.; Hao, G.; Pakrashi, V.; Murphy, J.; Long, P. Design of a 6-DOF Aerial Hybrid Cable-Driven Parallel Manipulator. In Proceedings of the 2024 20th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications (MESA), Genova, Italy, 2–4 September 2024; pp. 1–8. [Google Scholar]
- Russo, M.; Zhang, D.; Liu, X.-J.; Xie, Z. A review of parallel kinematic machine tools: Design, modeling, and applications. Int. J. Mach. Tools Manuf. 2024, 196, 104118. [Google Scholar] [CrossRef]
- Huang, T.; Li, M.; Zhao, X.; Mei, J.; Chetwynd, D.G.; Hu, S.J. Conceptual design and dimensional synthesis for a 3-DOF module of the TriVariant-a novel 5-DOF reconfigurable hybrid robot. Trans. Robot. 2005, 21, 449–456. [Google Scholar] [CrossRef]
- Li, M.; Huang, T.; Mei, J.; Zhao, X.; Chetwynd, D.G.; Hu, S.J. Dynamic formulation and performance comparison of the 3-DOF modules of two reconfigurable PKM—The tricept and the trivariant. J. Mech. Des. 2005, 127, 1129–1136. [Google Scholar] [CrossRef]
- Li, M.; Huang, T.; Chetwynd, D.G.; Hu, S.J. Forward position analysis of the 3-DOF module of the TriVariant: A 5-DOF reconfigurable hybrid robot. J. Mech. Des. 2006, 128, 319–322. [Google Scholar] [CrossRef]
- Zargarbashi, S.; Khan, W.; Angeles, J. The Jacobian condition number as a dexterity index in 6R machining robots. Robot. Comput.-Integr. Manuf. 2012, 28, 694–699. [Google Scholar] [CrossRef]
- Pond, G.; Carretero, J.A. Quantitative dexterous workspace comparison of parallel manipulators. Mech. Mach. Theory 2007, 42, 1388–1400. [Google Scholar] [CrossRef]
- Murray, R.M.; Li, Z.; Sastry, S.S. A Mathematical Introduction to Robotic Manipulation; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Liu, H.; Huang, T.; Chetwynd, D.G.; Kecskeméthy, A. Stiffness modeling of parallel mechanisms at limb and joint/link levels. Trans. Robot. 2017, 33, 734–741. [Google Scholar] [CrossRef]
- Xie, F.; Liu, X.-J.; Zhou, Y. Optimization of a redundantly actuated parallel kinematic mechanism for a 5-degree-of-freedom hybrid machine tool. Proc. Inst. Mech. Eng. Part B J. Eng. Manufact. 2014, 228, 1630–1641. [Google Scholar] [CrossRef]
- Abadi, B.N.R.; Farid, M.; Mahzoon, M. Redundancy resolution and control of a novel spatial parallel mechanism with kinematic redundancy. Mech. Mach. Theory 2019, 133, 112–126. [Google Scholar] [CrossRef]
- Nouri Rahmat Abadi, B.; Mahzoon, M.; Farid, M. Singularity-free trajectory planning of a 3-RP RR planar kinematically redundant parallel mechanism for minimum actuating effort. Iran. J. Sci. Technol. Trans. Mech. Eng. 2019, 43, 739–751. [Google Scholar] [CrossRef]
- Nouri Rahmat Abadi, B.; Carretero, J.A. Modeling and real-time motion planning of a class of kinematically redundant parallel mechanisms with reconfigurable platform. J. Mech. Robot. 2023, 15, 021004. [Google Scholar] [CrossRef]
- Mirnajafizadeh, S.; Shafei, A. A Unified Framework for Dynamic Analysis and Path Tracking Control of Multi—Rotor Aerial Manipulators. Int. J. Mech. Syst. Dyn. 2025. [Google Scholar] [CrossRef]

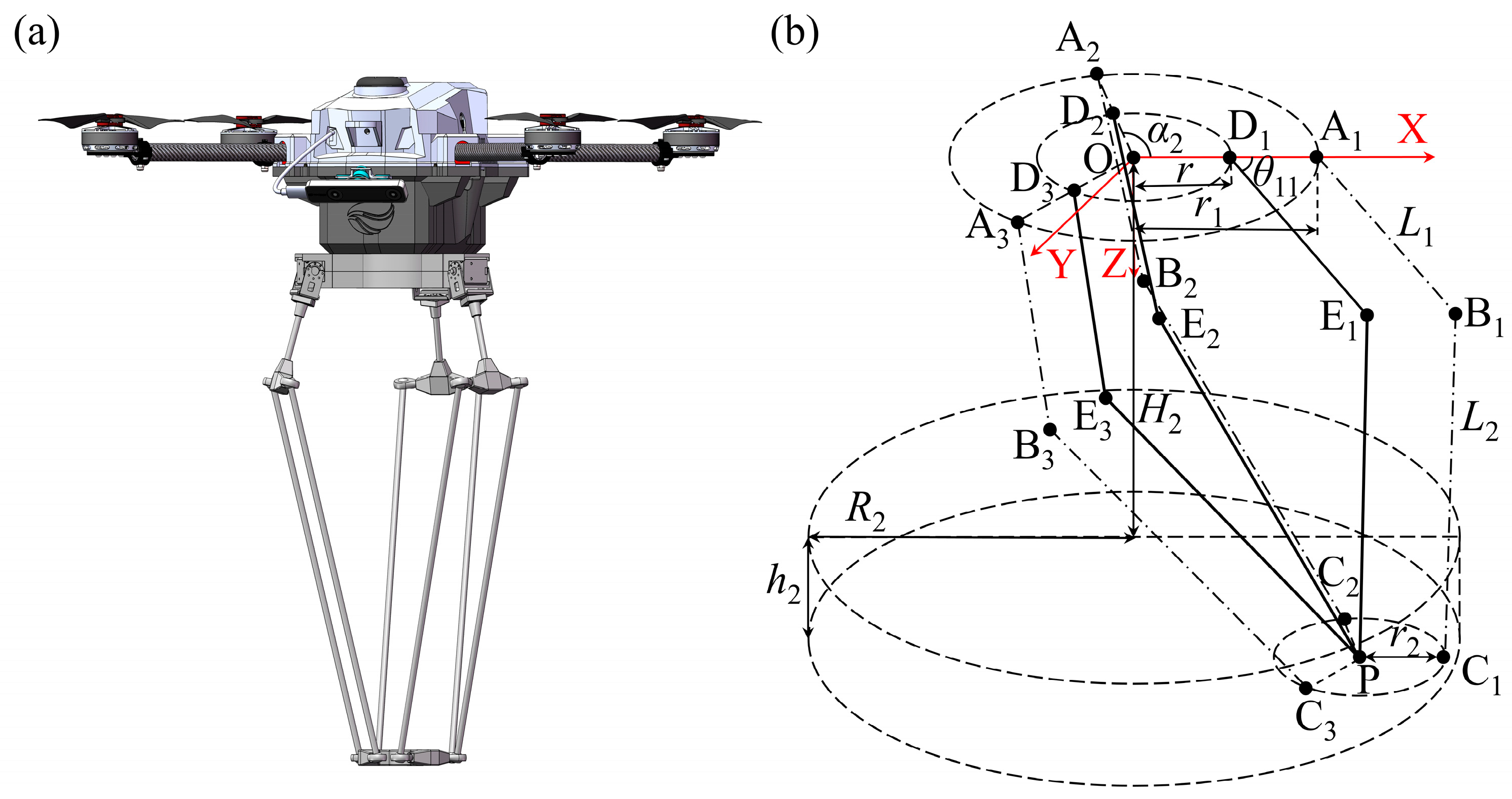


| TriVariant | R1 | h1 | H1 | e | a | b | q3min | q3max | q1min/q2min | q1max/q2max |
| 200 | 100 | 279 | 107.5 | 39 | 137.5 | 279 | 488 | 262 | 458 | |
| Delta | R2 | h2 | H2 | L1 | L2 | r1 | r2 | |||
| 200 | 100 | 300 | 117.5 | 400 | 100 | 22.5 |
| σ | |||||
|---|---|---|---|---|---|
| TriVariant | 6.935 | 0.954 | 5.144 | 10.179 | [0.577, 5.886] |
| Delta robot | 2.952 | 0.296 | 2.533 | 4.213 | [42.503, 247.027] |
| Direction | X | Y | Z | 3D |
|---|---|---|---|---|
| MAE (mm) | 3.437 | 3.736 | 3.909 | 7.719 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Z.; Lin, Y.; Zhang, Y.; Ling, M.; Liu, C. Comparative Study of TriVariant and Delta Three-Degree-of-Freedom Parallel Mechanisms for Aerial Manipulation. Machines 2025, 13, 926. https://doi.org/10.3390/machines13100926
Jiang Z, Lin Y, Zhang Y, Ling M, Liu C. Comparative Study of TriVariant and Delta Three-Degree-of-Freedom Parallel Mechanisms for Aerial Manipulation. Machines. 2025; 13(10):926. https://doi.org/10.3390/machines13100926
Chicago/Turabian StyleJiang, Zhujin, Yihao Lin, Yueyuan Zhang, Mingxiang Ling, and Chao Liu. 2025. "Comparative Study of TriVariant and Delta Three-Degree-of-Freedom Parallel Mechanisms for Aerial Manipulation" Machines 13, no. 10: 926. https://doi.org/10.3390/machines13100926
APA StyleJiang, Z., Lin, Y., Zhang, Y., Ling, M., & Liu, C. (2025). Comparative Study of TriVariant and Delta Three-Degree-of-Freedom Parallel Mechanisms for Aerial Manipulation. Machines, 13(10), 926. https://doi.org/10.3390/machines13100926







