Field Measurement and Characteristics Analysis of Transverse Load of High-Speed Train Bogie Frame
Abstract
1. Introduction
2. Transverse Load Calibration and Measurement
2.1. Transverse Load Description
2.2. Load Channels Calibration
2.3. Track Test
3. Typical Operating Condition Identification
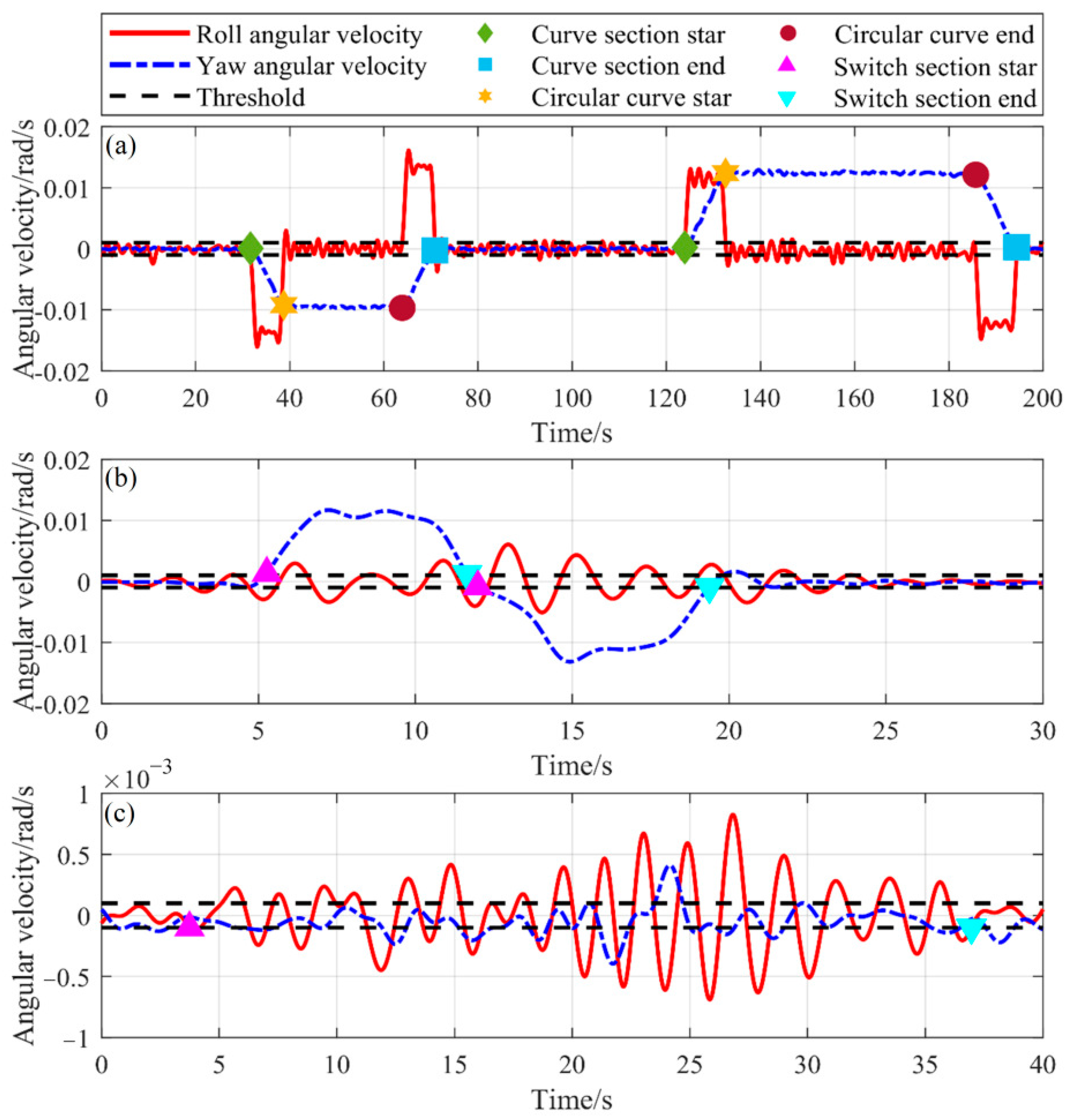
3.1. Time-Domain Characteristics of Gyroscope Signal
- (1)
- The radius decreases gradually from infinite (corresponding to the straight section) to the radius R of the circular curve (or increases from R to infinite);
- (2)
- The gauge widening of the inner rail gradually increases from zero to the full widening value on the circular curve (or gradually decreases from the full circular curve widening value back to zero);
- (3)
- The outer rail superelevation increases gradually from zero on the straight section to the superelevation value at the circular curve (or decreases from the curve’s superelevation to zero).
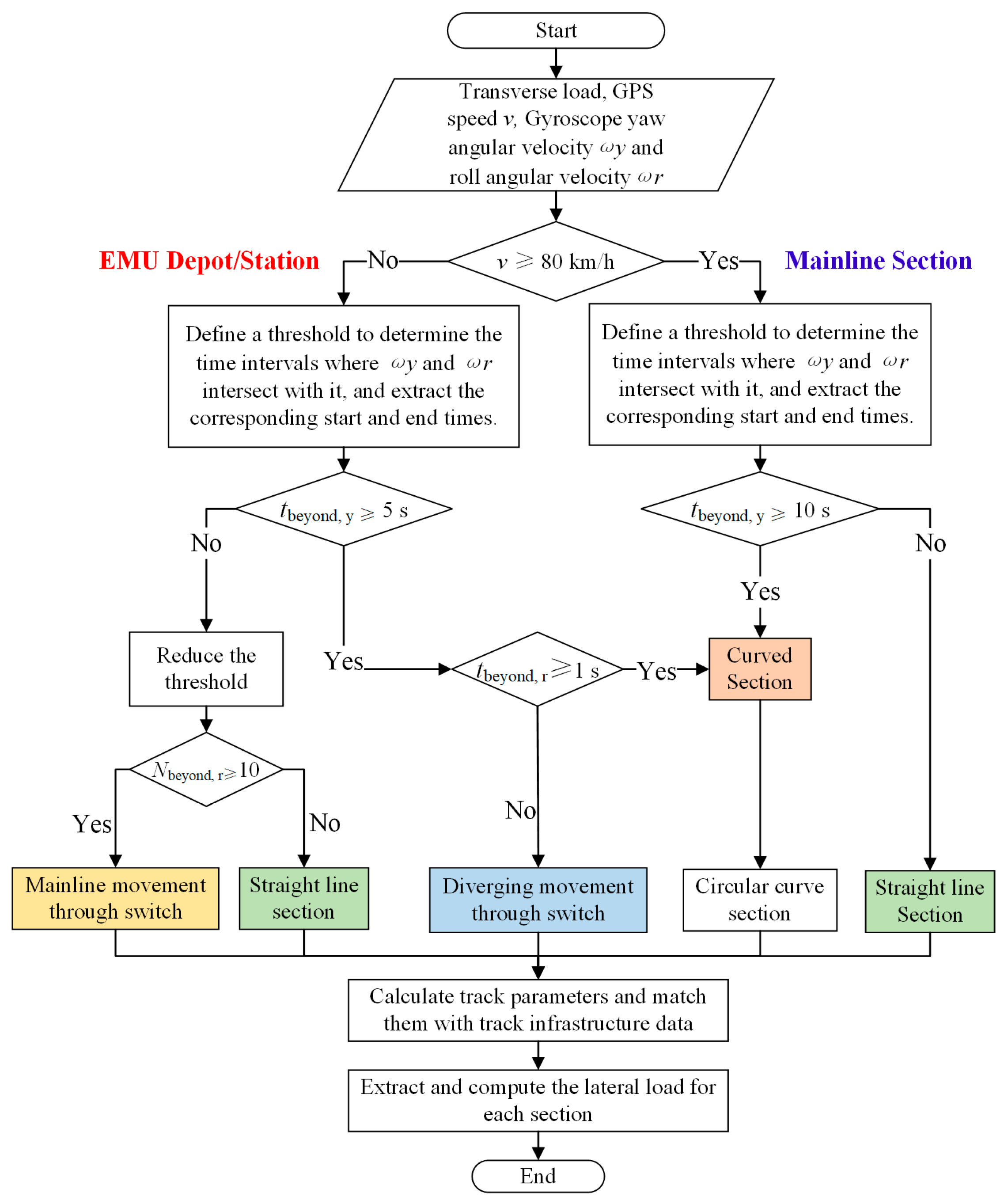
3.2. Condition Identification Method
- (1)
- According to the diverging movement operating speed (80 km/h) of the single switch connecting the mainline section and arrival–departure tracks, the input signals are divided into two segments: those corresponding to the mainline sections, stations, and high-speed train depots;
- (2)
- By setting appropriate upper and lower threshold values (±1 × 10−3 rad/s) for the mainline gyroscope signal, the start and end moments of the switch sections are determined when the gyroscope signal intersects the thresholds. The type of track sections (curve-line or straight-line) is determined based on the duration tbeyond,y, for which the yaw angular velocity signal exceeds the defined threshold range. The start and end times, as well as the number of such sections, are recorded accordingly. Within a curve-line section, the first and last moments at which the roll angular velocity signal intersects the threshold are identified as the start and end times of the circular curve-line section;
- (3)
- A similar procedure is applied to the gyroscope signals within the station. The existence of a transition curve is determined based on tbeyond,y, and the durations for which the first and last roll angular velocity signal exceed the threshold within a curve-line section (tbeyond1,r and tbeyond2,r, respectively). This allows for distinguishing between a regular curve-line section and a diverging movement section. The start and end times of each curve-line section and diverging movement section, along with the total number of occurrences, are recorded accordingly;
- (4)
- If tbeyond,y does not meet the required duration threshold, the upper and lower threshold range is reduced (set to ± 1 × 10−4 rad/s). Then, based on the number of consecutive peak and trough values of the roll angular velocity signal that exceed the threshold, the section is classified as a straight-line section or a straight movement section. The start and the end time of each segment, along with their counts, are recorded accordingly;
- (5)
- The corresponding track parameters are calculated according to the starting and ending time of each section, including the start position of the sections. The length of the section l and the radius of the curve R (for curve-line sections and diverging movement sections) are calculated by Equation (1).where v is the train operating speed, and ωy is the gyroscope yaw angular velocity. To reduce the calculation error, v and ωy are averaged separately in the curve-line section and the switch section, respectively;
- (6)
- By aligning the calculated track parameters with track maintenance data, more comprehensive track information, such as the superelevation of curves, can be retrieved.
3.3. Working Condition Recognition Accuracy
4. Dynamic Response Characteristics of Transverse Load
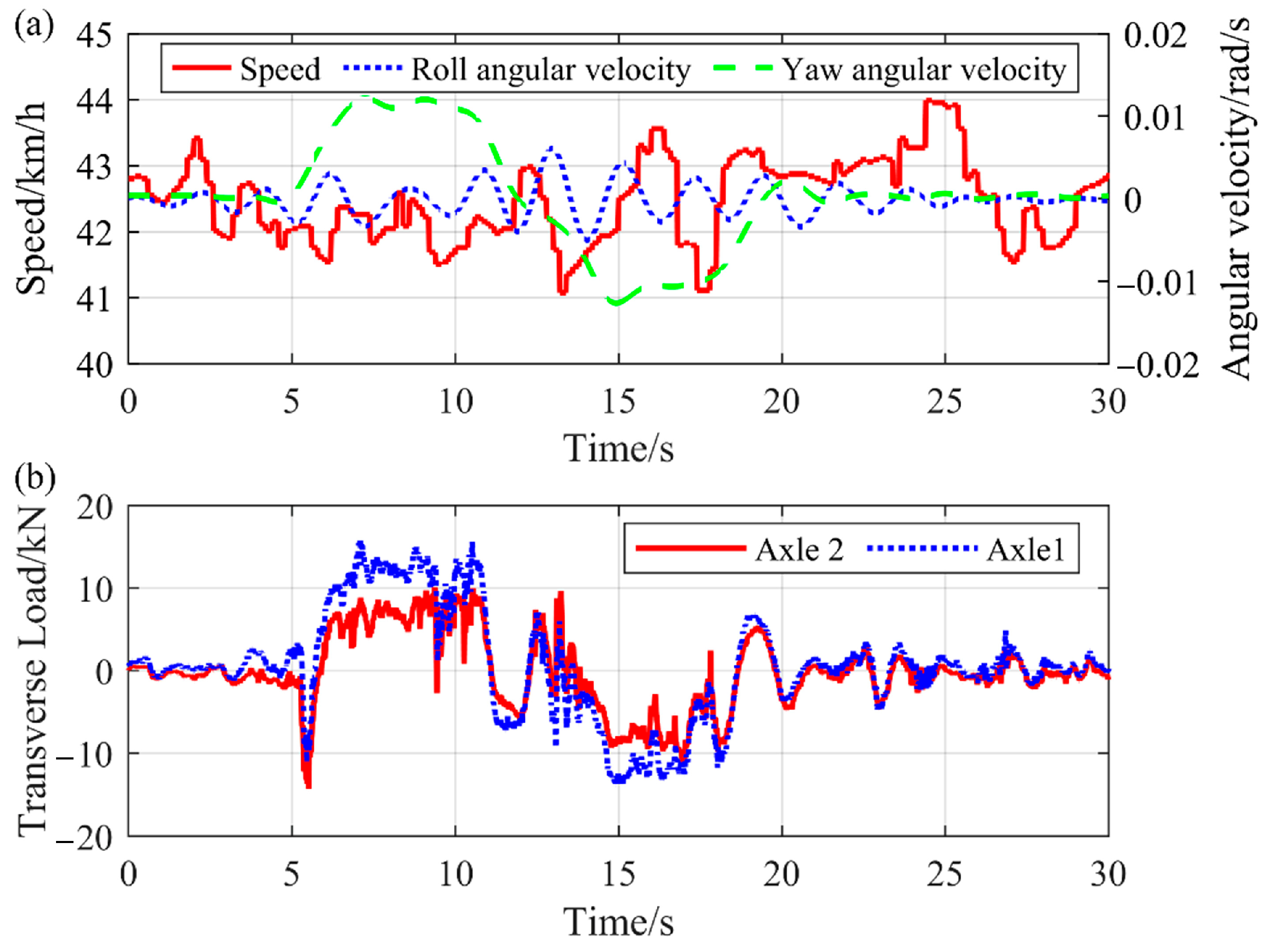
4.1. Curve-Line Operating Condition
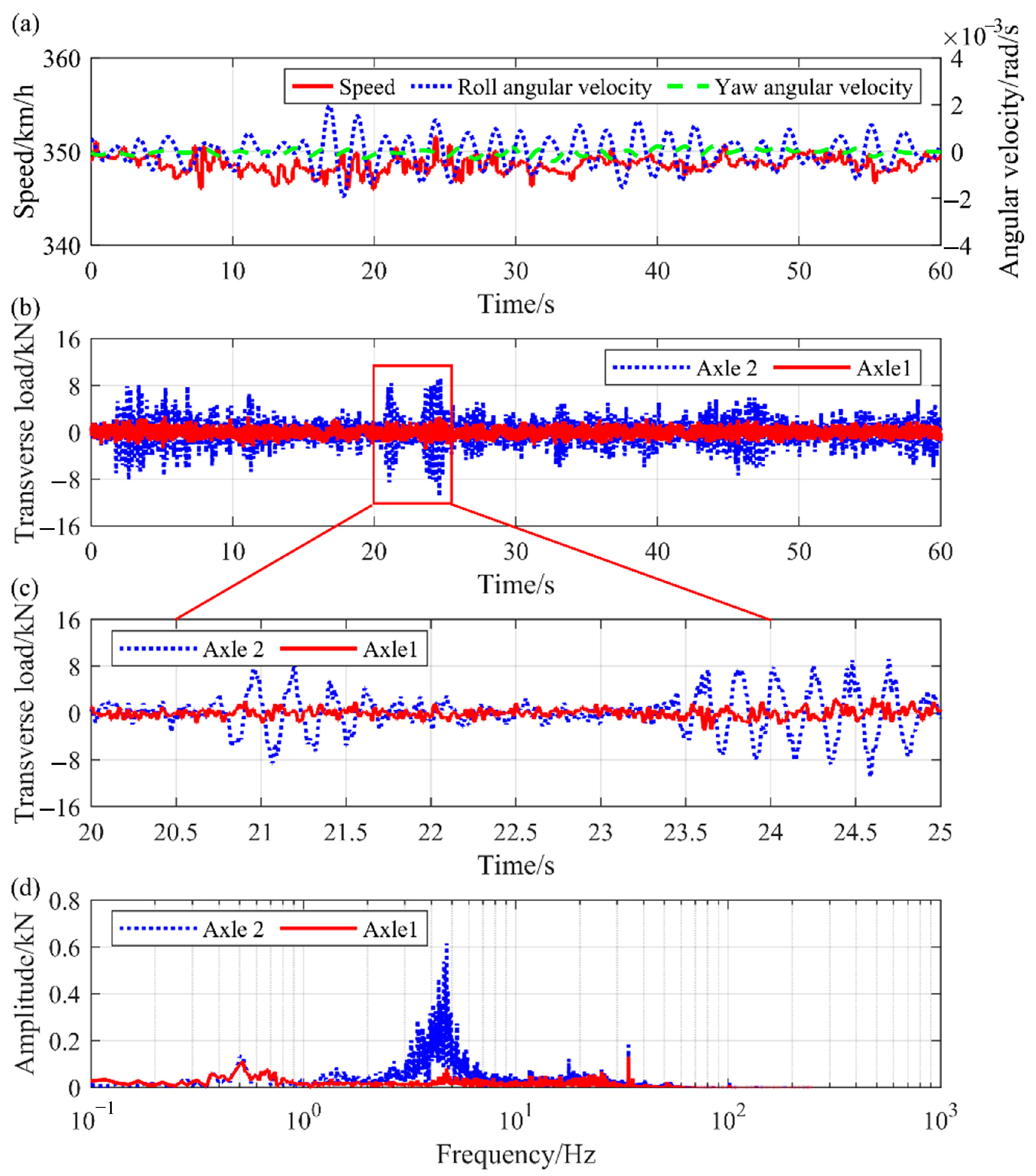
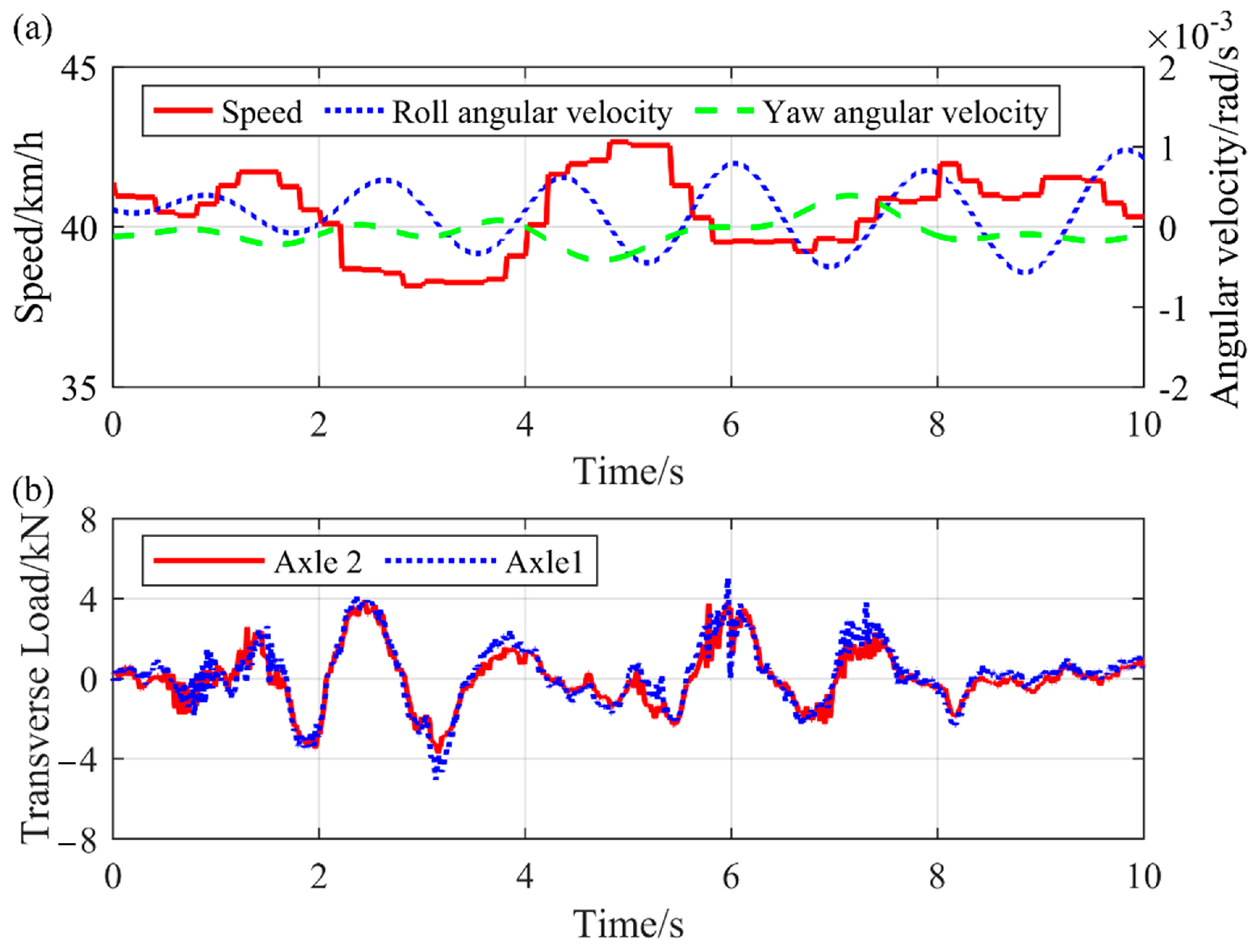
4.2. Straight-Line Operating Condition
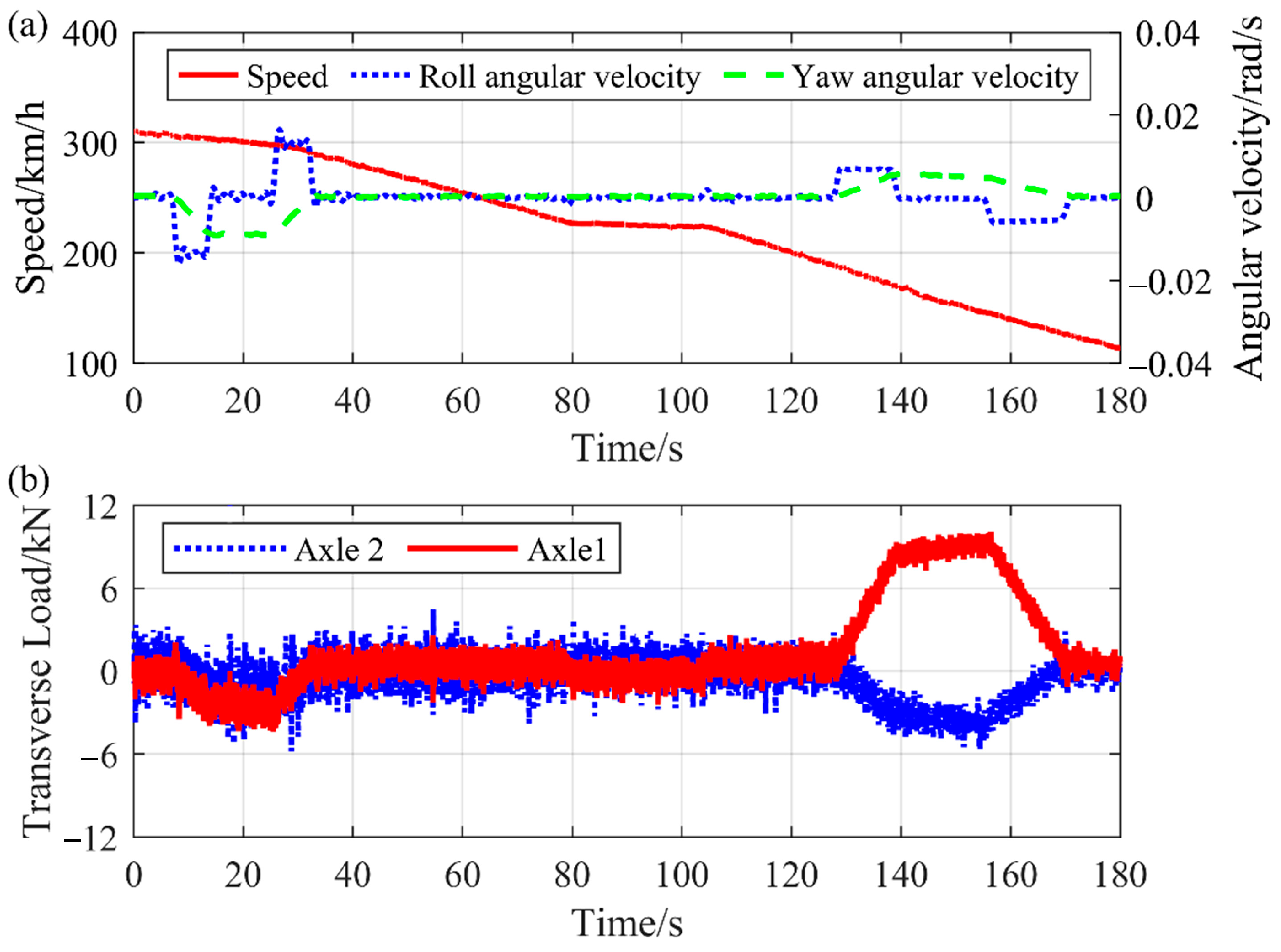
4.3. Switch Operating Condition
5. Statistical Characteristics of Transverse Load
5.1. Different Track Conditions
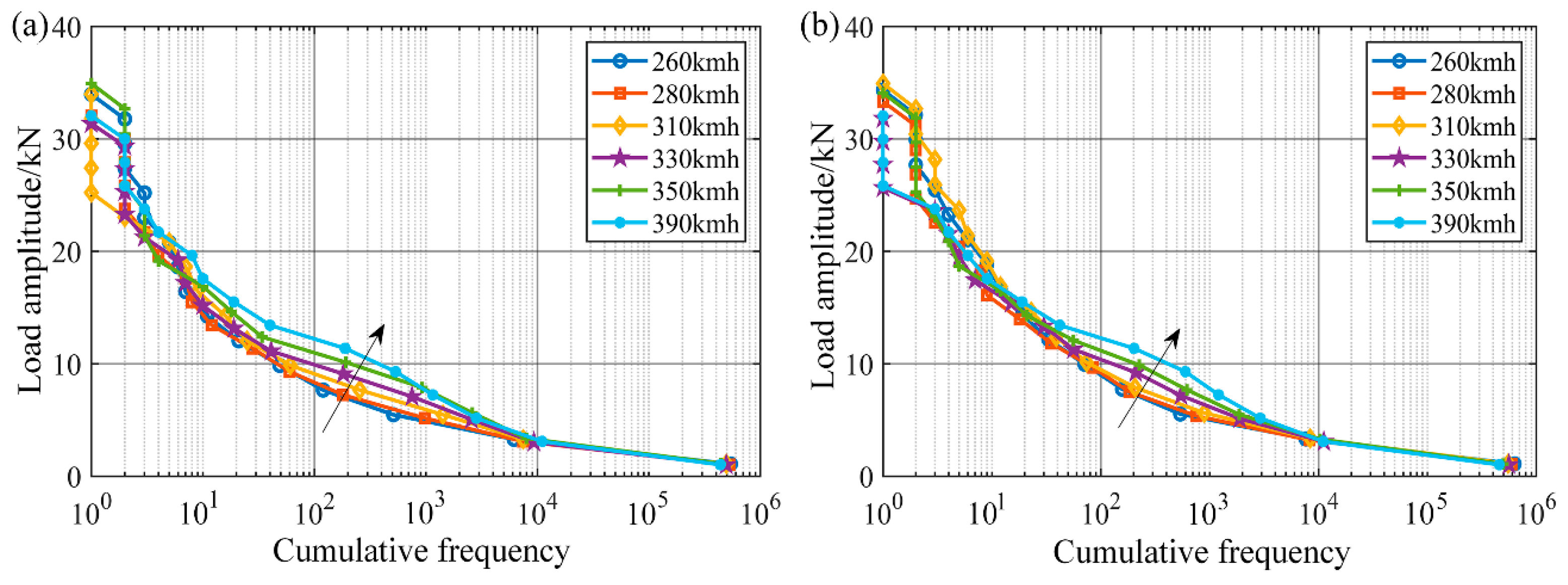
5.2. Different Speed Level
5.3. Different Curve Superelevation
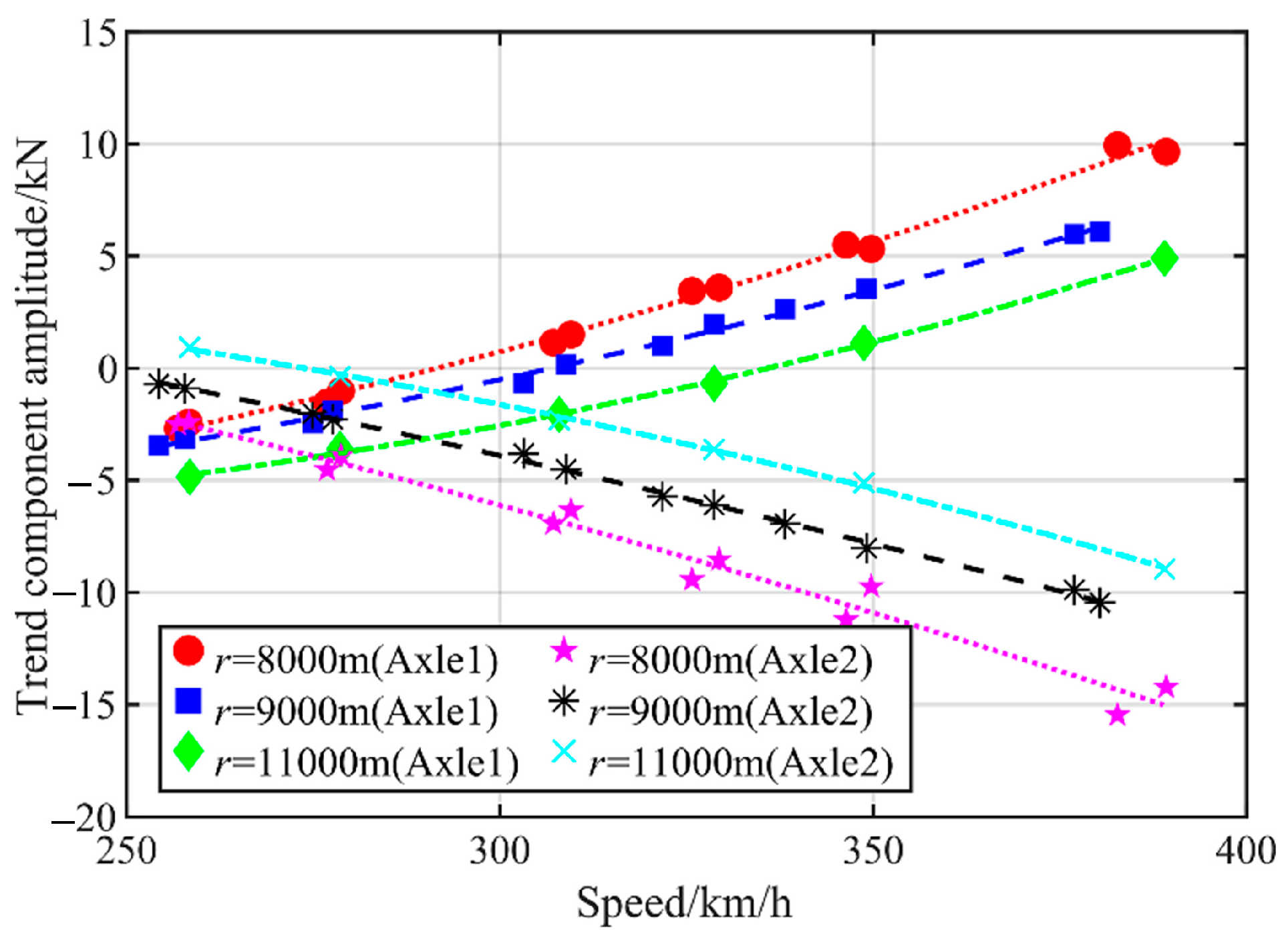
5.4. Different Curve Radius
5.5. Transverse Load Spectrum
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- EN 13749:2011(E); Railway Applications—Wheelsets and Bogies—Method of Specifying the Structural Requirements of Bogie Frames. European Committee for Standardization: Brussels, Belgium, 2011; pp. 19–50.
- UIC 615-4; Tractive Units Bogies and Running Gear Bogie Frame Structure Strength Tests. International Union of Railways: Paris, France, 2003; pp. 2–12.
- JIS E 4207:2004(E); Truck Frames for Railway Rolling Stock-General Rules for Design. Japanese Standards Association: Tokyo, Japan, 2004; pp. 4–5.
- Wang, B.; Li, Q.; Ren, Z.; Sun, S. Improving the fatigue reliability of metro vehicle bogie frame based on load spectrum. Int. J. Fatigue 2020, 132, 105389. [Google Scholar] [CrossRef]
- Ji, C.; Sun, S.; Li, Q.; Ren, Z.; Yang, G. Realistic fatigue damage assessment of a high-speed train bogie frame by damage consistency load spectra based on measured field load. Measurement 2020, 166, 108164. [Google Scholar] [CrossRef]
- Wang, B.; Sun, S.; Li, Q.; Tang, Q. Research on the Improvement of Speed Increased Passenger Car Bogie Frame Reliablility Based on Load Spectrum. J. China Railw. Soc. 2019, 41, 23–30. [Google Scholar] [CrossRef]
- Ma, X. Research on Some Issues of Dynamic Load Location Identification in Time Domain. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2012. [Google Scholar]
- Ren, Z.; Sun, S.; Li, Q.; Liu, Z. Experimental studies of load characteristics of bogie frames for 350 km/h EMUs. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2012, 226, 216–227. [Google Scholar] [CrossRef]
- Ren, Z.; Cao, J.; Li, Y.; Wang, B.; Wei, X. The load characteristics of the bogieframe of high-speed EMU. Eng. Mech. 2021, 38, 242–256. [Google Scholar]
- Ren, Z.; Zhao, Y.; Li, Y.; Wang, B.; Wang, Y. Loads and Damage Characteristics of the Traction and Brake Devices of Bogie of High Speed EMU. J. Mech. Eng. 2022, 58, 151–158. [Google Scholar]
- Ren, Z.; Sun, S.; Li, Q. Axle Spring Load Test and Dynamic Characteristics Analysis of High Speed EMU. J. Mech. Eng. 2010, 46, 109–115. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, S.; Yang, G.; Li, G. Load Characteristics and Fatigue Damage Assessment of High Speed Train Bogie Frame. J. Mech. Eng. 2020, 56, 163–171. [Google Scholar]
- Ji, C.; Sun, S.; Yang, G.; Meng, Q. Study on Torsional Load Characteristics of High-speed Train Bogie Frame. J. Mech. Eng. 2021, 57, 147–157. [Google Scholar]
- Gao, Y. Study on Load Characteristics of Bogie Frame in Alpine EMU. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2017. [Google Scholar]
- Wu, Y.; Ren, Z. Fatigue Damage Assessment of a Metro Vehicle Bogie Frame Based on Measured Field Load. Machines 2025, 13, 306. [Google Scholar] [CrossRef]
- Li, J.; Ren, Z.; Wu, Y.; Rui, A. Fatigue damage assessment of high-speed train bogie frame load spectra based on phase reconstruction. Eng. Fail. Anal. 2024, 159, 108008. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, X.; Zheng, Y.; Liu, Y.; Jin, X.; Zhou, J.; Chi, M.; Wen, Z. Study on vibration fatigue of lifeguard in a metro bogie and methodology for damage estimation based on the measured acceleration. J. Vib. Control 2024. [Google Scholar] [CrossRef]
- Wu, X.; Gao, A.; Wen, Z.; Wu, S.; He, S.; Chi, M.; Liang, S. Online estimation of fatigue damage of railway bogie frame based on axle box accelerations. Veh. Syst. Dyn. 2023, 61, 286–308. [Google Scholar] [CrossRef]
- Tao, G.; Liu, Z.; Ji, C.; Yang, G. Establishment and Analysis of Load Spectrum for Bogie Frame of High-Speed Train at 400 km/h Speed Level. Machines 2024, 12, 382. [Google Scholar] [CrossRef]
- Zhang, Z. Study on Load Spectrum of 400 km/h EMU Bogie Frame. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2018. [Google Scholar]
- Su, F. Research on Load and Dynamic Stress Tracking Period of Bogie Frame of High-Speed EMU. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2023. [Google Scholar] [CrossRef]
- Qiao, S. Research on High-Speed Train Working Condition Recognition Based on Multi-Scale Entropy of Frame Load Signal. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2021. [Google Scholar]
- Zhang, Y. Study on Fatigue Damage of High-Speed EMU Frame Based on Working Condition Identify. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2019. [Google Scholar]
- Chen, D.; Sun, S.; Li, Q.; Lin, F.; Xiao, Q. Development of the Railway Working Condition Recognition Software. J. Mech. Eng. 2019, 55, 176–184. [Google Scholar]
- Chen, D. Study on Establishment of Standardized Load Spectrum on Bogie Frames of High-Speed Trains. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2018. [Google Scholar]
- Rao, Q. Research on Condition Recognition of High Speed Train Bogie Based on Multi-View Clustering Ensemble. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2018. [Google Scholar]
- Guo, C. Research on Condition Recognition of High Speed Train Based on Deep Learing and Classification Ensemble. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2017. [Google Scholar]
- Zou, H. Load Spectrum Study on Intercity EMU Bogie Frame. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2016. [Google Scholar]
- Wang, M. Study on Characteristics and Applications of On-track Load of Welded Bogie Frame. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2016. [Google Scholar]
- Hou, J.; Yi, Y. Design of railway transition curve. Theor. Res. 2012, 10, 27–28. [Google Scholar]
- Bao, K. Simulation Study on Dynamic Performance of Transition Curve Parameters of High-Speed Railway. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2012. [Google Scholar]
- TB 10621-2014; Code for Design of High Speed Railway. National Railway Administration of the People’s Republic of China: Beijing, China, 2014; pp. 17–22.
- Sun, L.; Cui, S.; Yan, Z.; Liang, C.; Yu, H. Study on Adaptability of Curve Superelevation with Speed of Beijing-Shanghai High Speed Railway Being Increased to 400 km/h. J. China Railw. Soc. 2021, 61, 96–99. [Google Scholar]
- Hu, H. Study on the Allowable Cant Deficiency Value for the Curve Section of High Speed Railway. China Railw. 2019, 32–40. [Google Scholar]






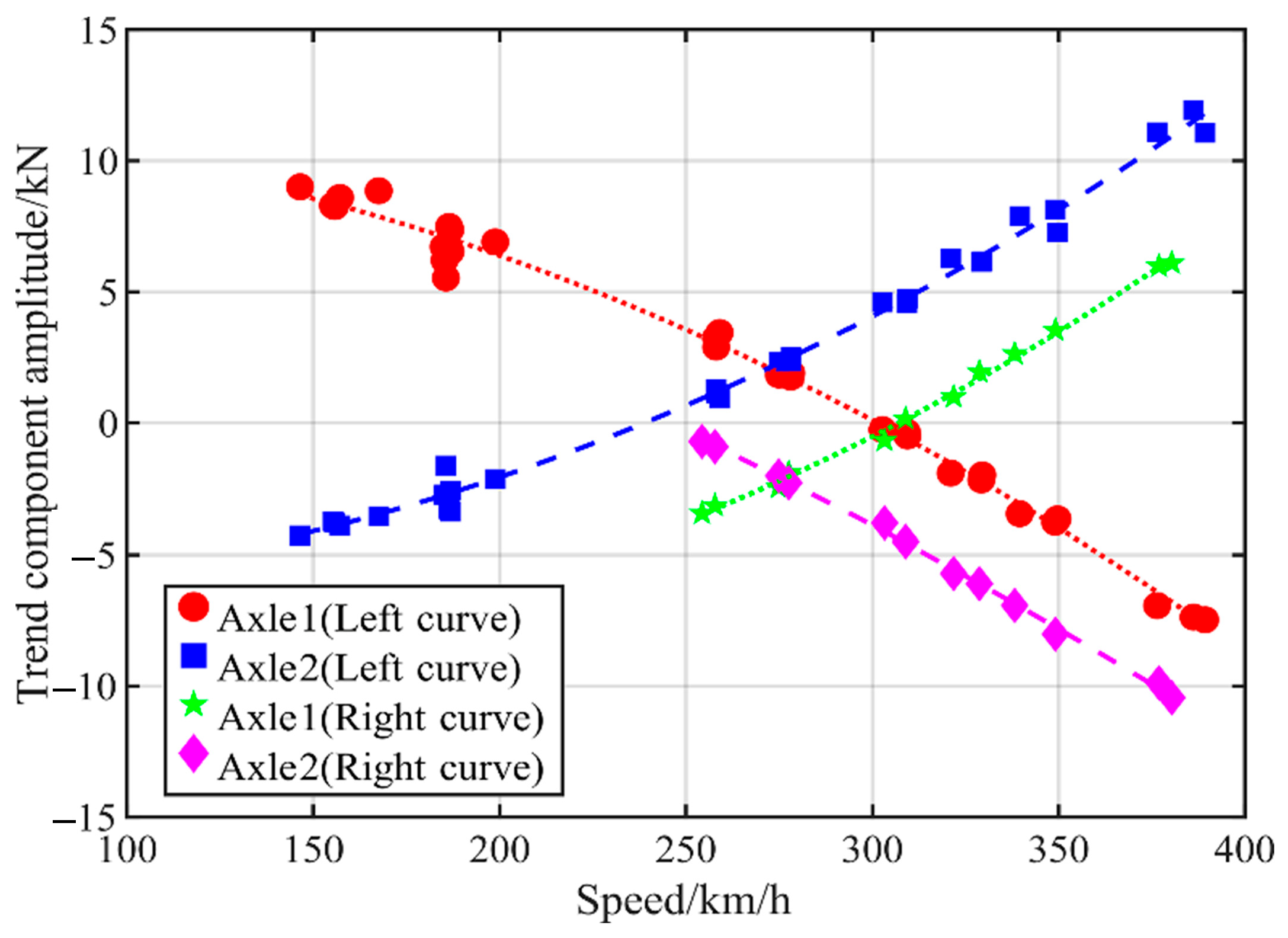

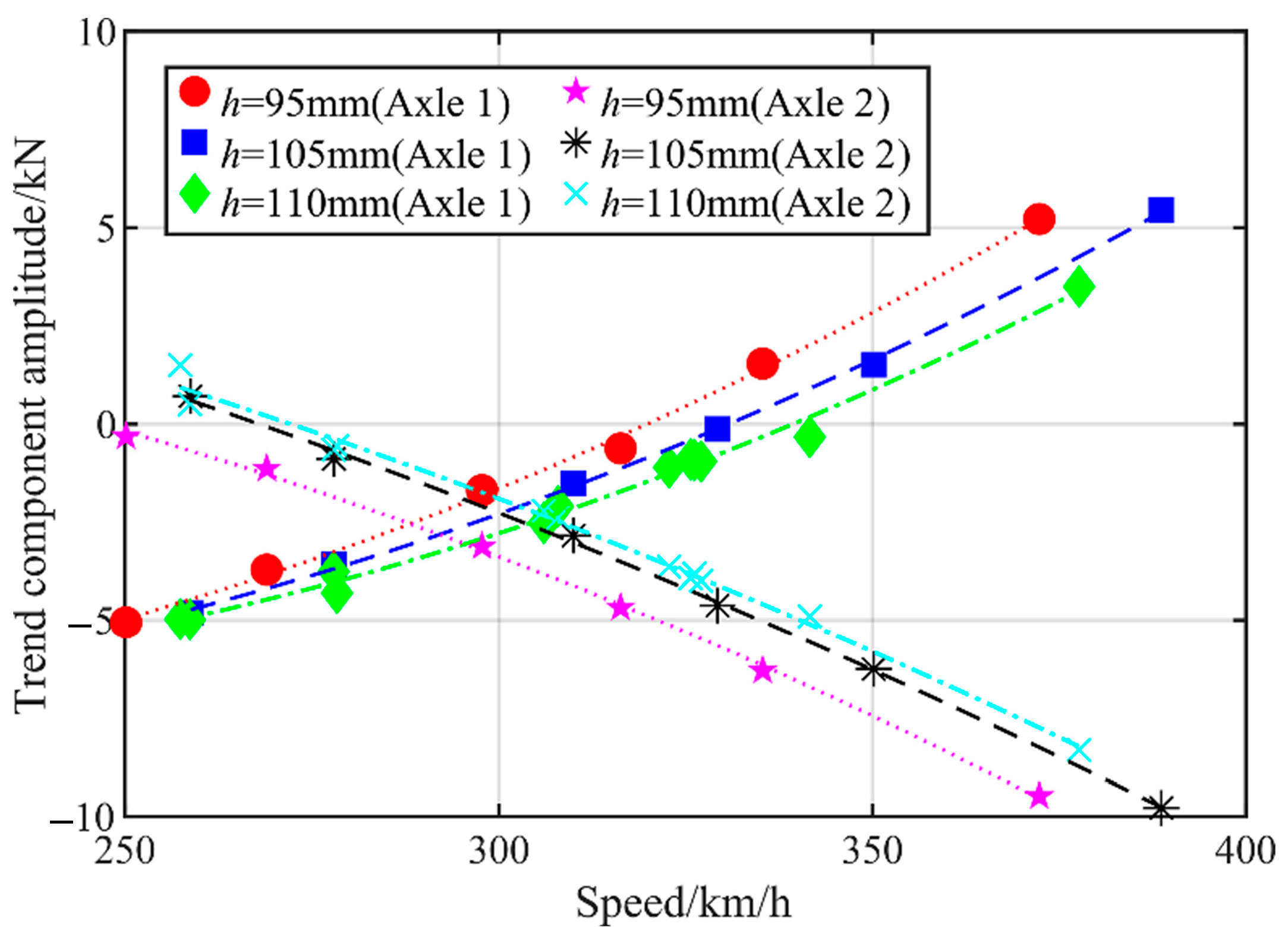
| Curve Type | Axle | a | b | c | R2 |
|---|---|---|---|---|---|
| Left curve | 1 | −1.28 × 10−4 | 1.46 × 10−3 | 11.23 | 0.9919 |
| 2 | 1.34 × 10−4 | −5.89 × 10−3 | −6.25 | 0.9935 | |
| Right curve | 1 | 1.53 × 10−4 | −1.98 × 10−2 | −8.36 | 0.9965 |
| 2 | −7.48 × 10−5 | −3.01 × 10−2 | 11.87 | 0.9977 |
| Superelevation | Axle | a | b | c | R2 |
|---|---|---|---|---|---|
| h = 95 mm | 1 | 2.31 × 10−4 | −6.03× 10−2 | −4.32 | 0.9977 |
| 2 | −1.73 × 10−4 | 3.14 × 10−2 | 2.81 | 0.9987 | |
| h = 105 mm | 1 | 2.11 × 10−4 | −5.89 × 10−2 | −3.64 | 0.9993 |
| 2 | −1.16 × 10−4 | −4.87 × 10−3 | 9.62 | 0.9987 | |
| h = 110 mm | 1 | 2.29 × 10−4 | −7.59 × 10−2 | −0.64 | 0.9915 |
| 2 | −1.25 × 10−4 | 2.89 × 10−3 | 8.43 | 0.9919 |
| Curve Radius | Axle | a | b | c | R2 |
|---|---|---|---|---|---|
| r = 8000 m | 1 | 1.90 × 10−04 | −2.55 × 10−2 | −8.74 | 0.9950 |
| 2 | −1.08 × 10−4 | −2.55 × 10−2 | 11.29 | 0.9733 | |
| r = 9000 m | 1 | 1.53 × 10−4 | −1.98 × 10−2 | −8.36 | 0.9965 |
| 2 | −7.48 × 10−5 | −7.48 × 10−2 | 11.87 | 0.9977 | |
| r = 11,000 m | 1 | 2.36 × 10−4 | −7.88 × 10−2 | −0.14 | 0.9990 |
| 2 | −1.72 × 10−4 | 3.70 × 10−2 | 2.78 | 0.9989 |
| Speed Level (km/h) | Axle 1 | Axle 2 | ||||
|---|---|---|---|---|---|---|
| ν | H0 | Smax | ν | H0 | Smax | |
| 260 | 0.3674 | 13.2 | 35.1 | 0.3725 | 13.4 | 35.5 |
| 280 | 0.3852 | 13.2 | 33.1 | 0.3908 | 13.3 | 34.4 |
| 310 | 0.3904 | 13.1 | 35.1 | 0.4060 | 13.2 | 36.1 |
| 330 | 0.4267 | 13.1 | 32.4 | 0.4268 | 13.2 | 32.8 |
| 350 | 0.4318 | 13.0 | 36.1 | 0.4347 | 13.1 | 35.2 |
| 390 | 0.4968 | 13.0 | 33.1 | 0.4910 | 13.0 | 33.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, C.; Gao, Y.; Liu, Z.; Yang, G. Field Measurement and Characteristics Analysis of Transverse Load of High-Speed Train Bogie Frame. Machines 2025, 13, 905. https://doi.org/10.3390/machines13100905
Ji C, Gao Y, Liu Z, Yang G. Field Measurement and Characteristics Analysis of Transverse Load of High-Speed Train Bogie Frame. Machines. 2025; 13(10):905. https://doi.org/10.3390/machines13100905
Chicago/Turabian StyleJi, Chengxiang, Yuhe Gao, Zhiming Liu, and Guangxue Yang. 2025. "Field Measurement and Characteristics Analysis of Transverse Load of High-Speed Train Bogie Frame" Machines 13, no. 10: 905. https://doi.org/10.3390/machines13100905
APA StyleJi, C., Gao, Y., Liu, Z., & Yang, G. (2025). Field Measurement and Characteristics Analysis of Transverse Load of High-Speed Train Bogie Frame. Machines, 13(10), 905. https://doi.org/10.3390/machines13100905





