FRMA: Four-Phase Rapid Motor Adaptation Framework
Abstract
1. Introduction
- Full-State Pretraining: A base policy is first trained using full access to the ground-truth system state. This policy captures essential control behaviors without concern for observability constraints, providing a strong performance ceiling and serving as a foundation for subsequent learning stages.
- Auxiliary Hidden-State Prediction: An auxiliary network is trained to predict the initial hidden and cell states of the recurrent encoder (LSTM) from recent observation–action sequences. These predicted states initialize the LSTM memory, enabling immediate inference of latent dynamics, even in partially observable conditions.
- Aligned Latent Representation Learning: A recurrent encoder is trained to map sequences of partial observations and actions to latent states that are aligned with those learned during full-state training. This phase bridges the gap between limited observations and the underlying full latent states, ensuring that the encoder produces informative representations for policy execution.
- Latent-State Policy Fine-Tuning: Finally, the policy is fine-tuned using only the estimated latent encoding , allowing it to operate under realistic partially observable conditions. This phase ensures that the agent can perform fast, reliable control without requiring full-state information at deployment.
- High-Frequency, Single-Step Adaptation: During training, FRMA leverages multi-step sequence regression to learn latent-state inference. At deployment, it switches to single-step LSTM updates, continuously updating the hidden and cell states at each timestep. This allows the latent encoding to be refreshed at high frequency, enabling rapid and precise control.
- Extended Temporal Coverage: By propagating the LSTM’s hidden and cell states across timesteps, FRMA avoids fixed-horizon limitations (e.g., 50-step windows). It effectively captures long-term temporal dependencies without the computational burden of long input sequences, reducing GPU memory usage and accelerating both training and inference.
- Policy-Invariant Latent Representation: Observation–action histories contain both environmental dynamics and policy-dependent information. FRMA uses supervised learning to ensure that the LSTM hidden and cell states primarily encode environment dynamics, effectively minimizing the influence of the sampling policy . This design enhances generalization and robustness when the policy changes or under different deployment conditions.
2. Related Work
2.1. Artificial Neural Networks
2.2. Classical Control Methods
2.3. Reinforcement Learning
2.4. Observation–Action Sequence-Based Reinforcement Learning
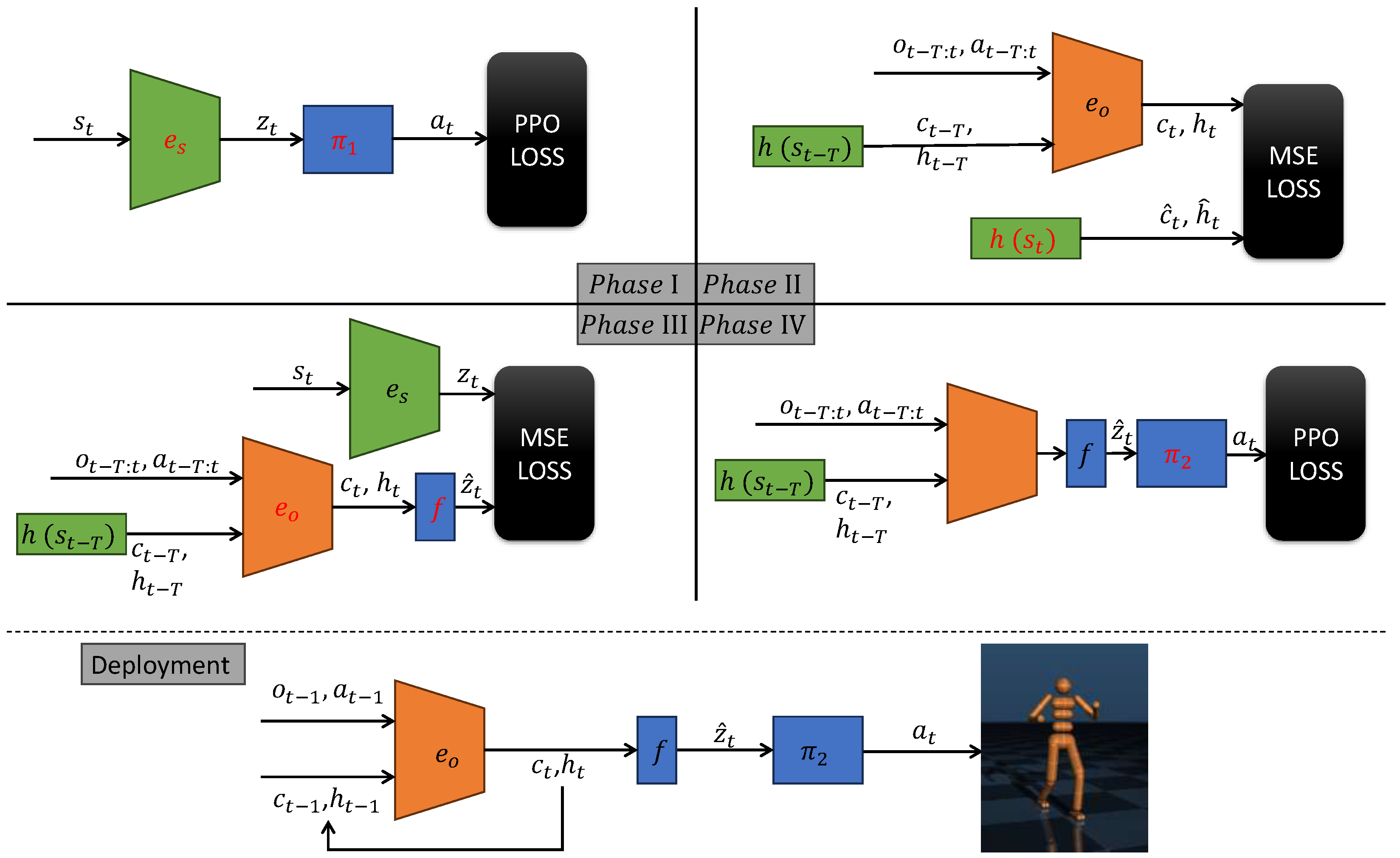
3. FRMA Details
3.1. Phase I: Full-State Policy Learning
3.2. Phase II: Supervised Training of Hidden Network
3.3. Phase III: Learning Latent Representations from Partial Observations
3.4. Phase IV: Policy Fine-Tuning on Estimated Latent States
3.5. Training Procedure
- Phase I: Full-State Policy Learning. For train_step iterations, sample batch_size state–action–reward transitions from full-state rollouts. The state encoder and the base policy are jointly optimized using Proximal Policy Optimization (PPO) under full observability. This phase establishes a high-quality latent state representation and a competent control policy, providing a strong foundation for subsequent modules.
- Phase II & III: Hidden-Network Pretraining and Joint LSTM–Mapping Training. These two phases are interleaved within each iteration to maintain a balanced learning pace between the hidden state predictor and the observation-based latent inference pipeline . For train_step iterations:
- Sample 5 independent batches to update via the hidden-state MSE loss , using full-state trajectories as supervision.
- Sample 1 fresh, non-overlapping batch to jointly optimize and by minimizing the mapping loss , which aligns the predicted latent with the ground-truth latent from Phase I.
This strict batch independence is critical: is trained on , whereas relies on . Sharing identical samples would bias toward the short-horizon regime, degrading its generalization to long-term dependencies. - Phase IV: Policy Fine-Tuning. For train_step iterations, sample batch_size trajectories of estimated latent states from the Phase III pipeline. The policy , initialized from , is fine-tuned using PPO to adapt to the noisy and potentially biased distribution of . This step completes the transition from privileged, full-state decision-making to deployable, observation-driven control.
3.6. Deployment
- Receives the latest observation and executed action from the previous step.
- Updates the LSTM memory via a single forward step:
- Computes the current latent state estimate through the feature extraction network:
- Feeds into the fine-tuned policy to determine the next action:
- Zero-initialization. Used here for fair comparison; FRMA inherently supports hot-start initialization via when privileged or learned initial state information is available.
- Policy optimization. Phase IV uses on-policy PPO for stability in MuJoCo, but FRMA is compatible with off-policy methods such as SAC for enhanced generalization.
- Full-state supervision during training. Ground-truth state information shapes the encoder only; deployment relies solely on partial observations. When a simulator is unavailable, FRMA can use data-driven environment models or other reconstruction methods to provide training supervision.
- Staged training. The multi-phase schedule decouples encoder learning from policy learning to improve stability and fairness; end-to-end training remains feasible within the same framework.
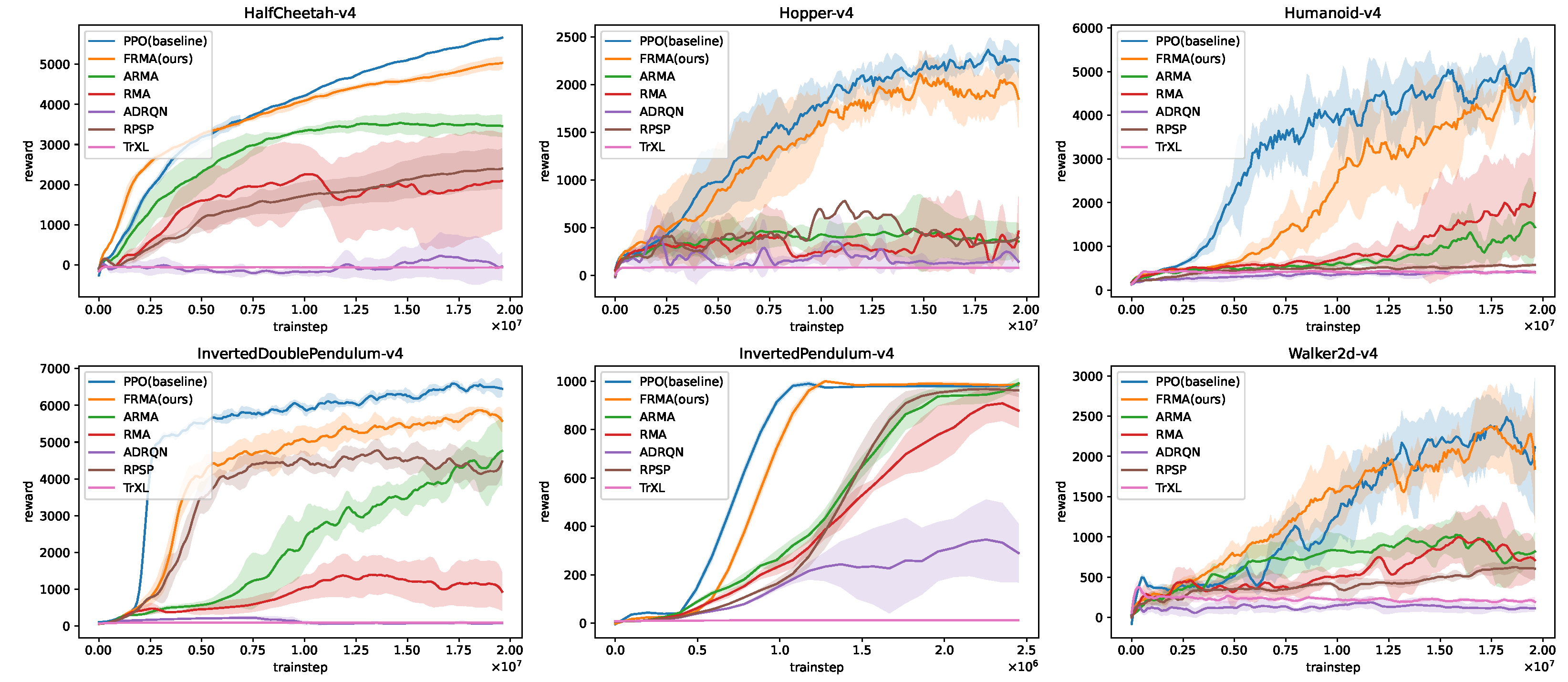
4. Experiments
- FullState (baseline) [28]: A PPO agent trained with full-state access, representing an upper bound on achievable performance.
- FRMA (ours): The proposed Four-phase Rapid Motor Adaptation framework, designed for learning in partially observable environments.
- ARMA [30]: An extension of RMA that fine-tunes the base policy using full-state supervision after adaptation.
- RMA [10]: Rapid Motor Adaptation with a fixed-length encoder over recent observation–action sequences.
- ADRQN [33]: An adaptation of Deep Recurrent Q-Networks employing LSTM encoders to process partial observation–action histories.
- RPSP [34]: A recurrent predictive state policy method that explicitly models predictive latent states for control.
- TrXL [37]: A Transformer-XL-based agent using multi-head attention to encode long-term dependencies in observation–action sequences.
- standard evaluation without perturbations,
- observation corrupted by Gaussian noise,
- observation dropouts with a fixed probability,
- action corrupted by Gaussian noise,
- action dropouts with a fixed probability.
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. FRMA Pseudocode
| Algorithm A1 FRMA Training Procedure |
| 1: Initialize networks: , , , , , and 2: Phase I: Full-State Policy Learning Freeze , , , and 3: for i = 1 to train_step do 4: Train and with PPO using full-state input 5: end for 6: 7: Phase II & III Freeze and 8: for i = 1 to train_step do 9: Phase II: LSTM Memory Pretraining 10: Initialize memory: 11: Update memory: 12: Estimate LSTM memory: 13: Compute MSE loss: 14: Train to predict from (e.g., for 5 steps) 15: 16: Phase III: Latent Encoding Reconstruction 17: Estimate latent encoding: 18: Compute MSE loss: 19: Update and 20: end for 21: 22: Phase IV: Secondary Policy Fine-Tuning Initialize secondary policy: 23: for i = 1 to train_step do 24: Train with PPO using 25: end for |
| Algorithm A2 FRMA Online Deployment |
|
Appendix B. Network Architectures of Compared Methods
| Method | Encoder | Policy Network |
|---|---|---|
| PPO (FullState) | ||
| FRMA (ours) | ||
| ARMA | ||
| RMA | ||
| ADRQN | ||
| RPSP | ||
| TrXL |
| Hyperparameter | Value |
|---|---|
| Learning rate (actor/critic) | |
| PPO clip range | 0.2 |
| Discount factor | 0.99 |
| GAE | 0.95 |
| Batch size per update | 8192 transition |
| Training steps per phase | 100 |
| Optimizer | Adam |
| Entropy coefficient | 0.01 |
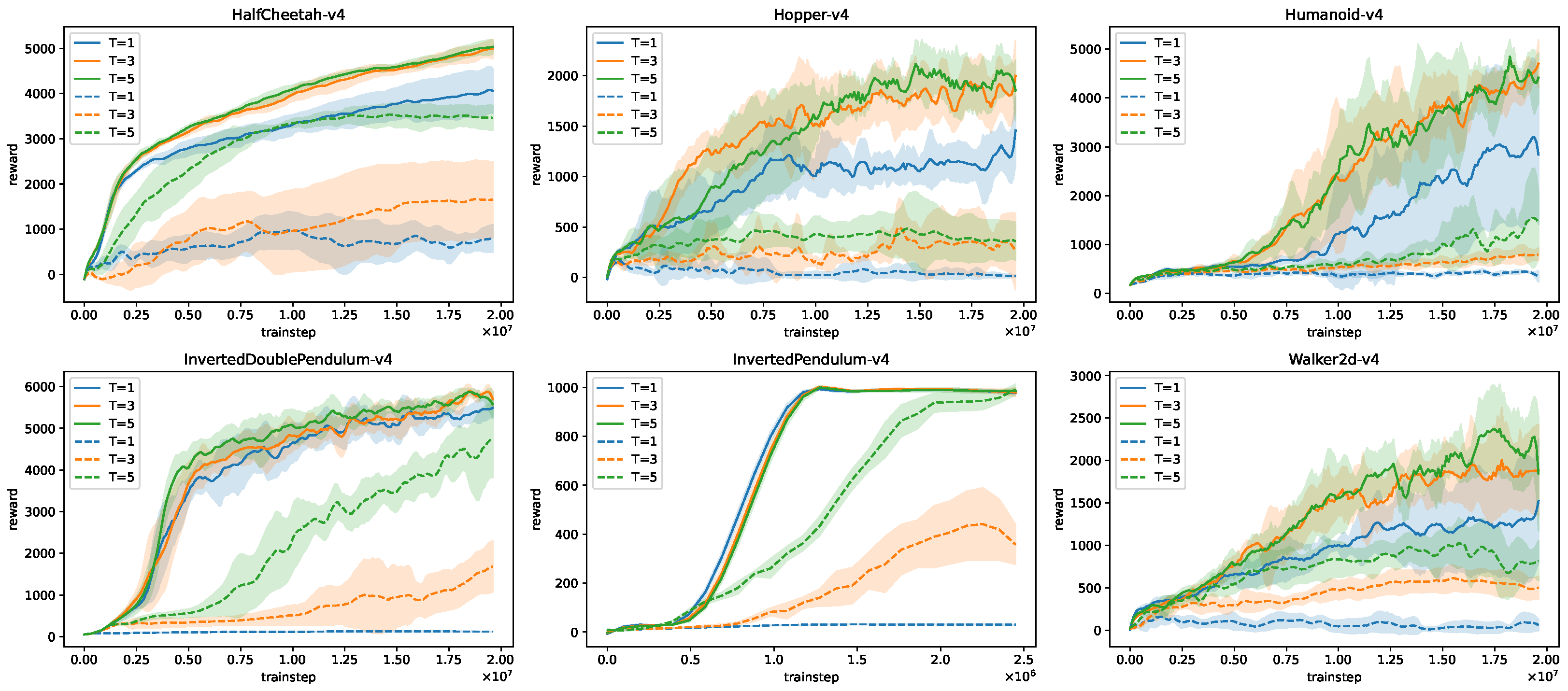
Appendix C. State Inference from Observation–Action Sequences
Appendix D. Hidden-Network h
Appendix E. Additional Experimental Results
| Algorithm | InvertedPendulum-v4 | Hopper-v4 | HalfCheetah-v4 | Walker2d-v4 | InvertedDoublePendulum-v4 | Humanoid-v4 |
|---|---|---|---|---|---|---|
| FullState (baseline) | 993.4, 4.5 | 2203.9, 407.7 | 5747.1, 123.2 | 2129.0, 731.4 | 6357.6, 235.7 | 4620.9, 1257.2 |
| FRMA (ours) | 988.1, 10.4 | 1966.1, 210.0 | 5050.0, 138.3 | 2638.0, 465.8 | 5724.1, 323.6 | 4584.9, 987.5 |
| ARMA | 976.4, 12.8 | 348.7, 188.5 | 3463.7, 315.7 | 777.6, 160.0 | 4642.3, 443.4 | 1460.2, 953.5 |
| RMA | 930.4, 46.2 | 383.3, 385.3 | 2172.5, 1350.8 | 826.1, 349.0 | 959.9, 632.7 | 1920.2, 1410.3 |
| ADRQN | 449.1, 407.9 | 145.6, 43.8 | −24.1, 491.2 | 108.4, 44.9 | 75.1, 25.0 | 415.6, 42.7 |
| RPSP | 920.3, 79.4 | 485.9, 131.1 | 2358.1, 552.7 | 618.5, 200.8 | 4211.9, 404.1 | 572.1, 39.4 |
| TrXL | 12.7, 0.1 | 83.6, 1.3 | −93.1, 6.7 | 174.3, 87.9 | 84.3, 1.3 | 441.4, 29.9 |
| Algorithm | InvertedPendulum-v4 | Hopper-v4 | HalfCheetah-v4 | Walker2d-v4 | InvertedDoublePendulum-v4 | Humanoid-v4 |
|---|---|---|---|---|---|---|
| FullState (baseline) | 975.5, 10.0 | 890.4, 147.8 | 4826.7, 52.9 | 1164.8, 449.1 | 3364.5, 383.1 | 4282.4, 1309.1 |
| FRMA (ours) | 980.8, 16.7 | 1119.5, 243.3 | 4179.3, 145.9 | 2063.0, 432.6 | 4336.2, 296.5 | 3177.9, 691.4 |
| ARMA | 972.2, 13.3 | 310.9, 145.2 | 2982.5, 297.1 | 582.5, 89.5 | 2869.2, 447.3 | 1300.8, 776.3 |
| RMA | 811.8, 110.6 | 359.2, 378.4 | 1850.3, 1166.6 | 709.6, 282.4 | 516.7, 134.0 | 1537.7, 987.4 |
| ADRQN | 433.6, 393.2 | 144.0, 42.1 | −88.1, 351.3 | 103.4, 47.6 | 75.0, 24.8 | 416.8, 42.0 |
| RPSP | 895.3, 72.0 | 356.5, 95.7 | 2087.8, 517.0 | 378.4, 71.2 | 790.5, 203.3 | 556.0, 22.3 |
| TrXL | 12.7, 0.1 | 84.8, 1.6 | −96.8, 5.9 | 173.4, 87.2 | 84.3, 1.0 | 441.0, 29.0 |
| Algorithm | InvertedPendulum-v4 | Hopper-v4 | HalfCheetah-v4 | Walker2d-v4 | InvertedDoublePendulum-v4 | Humanoid-v4 |
|---|---|---|---|---|---|---|
| FullState (baseline) | 880.9, 35.5 | 556.4, 35.2 | 4201.3, 140.2 | 521.0, 44.5 | 1788.4, 123.6 | 1855.3, 834.4 |
| FRMA (ours) | 918.3, 56.8 | 688.9, 171.9 | 3819.4, 153.7 | 980.9, 148.5 | 362.9, 17.9 | 1425.2, 391.4 |
| ARMA | 674.3, 90.5 | 227.3, 52.3 | 2129.7, 158.1 | 337.1, 37.7 | 351.6, 69.6 | 955.8, 316.5 |
| RMA | 331.0, 80.7 | 241.5, 185.6 | 1638.0, 993.0 | 550.7, 258.5 | 241.1, 36.0 | 1018.6, 390.7 |
| ADRQN | 237.0, 179.2 | 139.3, 39.1 | −164.9, 164.8 | 84.2, 43.5 | 73.7, 22.8 | 409.1, 45.2 |
| RPSP | 729.8, 164.5 | 250.0, 82.2 | 1542.8, 565.2 | 225.5, 83.2 | 313.0, 33.9 | 511.9, 36.6 |
| TrXL | 12.7, 0.1 | 84.2, 2.5 | −93.4, 6.4 | 173.1, 86.2 | 84.4, 1.0 | 439.1, 28.0 |
| Algorithm | InvertedPendulum-v4 | Hopper-v4 | HalfCheetah-v4 | Walker2d-v4 | InvertedDoublePendulum-v4 | Humanoid-v4 |
|---|---|---|---|---|---|---|
| FullState (baseline) | 971.8, 11.7 | 1635.4, 370.1 | 5356.4, 129.1 | 1853.0, 761.7 | 5953.8, 263.9 | 4297.1, 1262.0 |
| FRMA (ours) | 981.4, 10.2 | 1513.1, 248.5 | 4780.8, 148.6 | 2517.6, 479.6 | 5312.6, 283.8 | 4264.1, 1084.6 |
| ARMA | 980.9, 2.5 | 342.3, 183.7 | 3266.7, 270.6 | 763.2, 174.3 | 4344.0, 741.4 | 1435.0, 920.9 |
| RMA | 908.7, 47.6 | 383.3, 388.9 | 2065.3, 1312.2 | 830.2, 355.6 | 708.3, 270.8 | 1816.5, 1293.6 |
| ADRQN | 444.4, 405.1 | 144.7, 42.9 | −71.2, 391.8 | 105.7, 41.2 | 75.0, 24.9 | 416.9, 41.8 |
| RPSP | 897.3, 82.7 | 475.0, 132.0 | 2262.4, 514.5 | 616.9, 200.5 | 3718.2, 435.9 | 569.5, 31.3 |
| TrXL | 12.7, 0.1 | 84.0, 2.1 | −94.9, 3.3 | 171.6, 86.8 | 84.4, 1.2 | 437.7, 30.4 |
| Algorithm | InvertedPendulum-v4 | Hopper-v4 | HalfCheetah-v4 | Walker2d-v4 | InvertedDoublePendulum-v4 | Humanoid-v4 |
|---|---|---|---|---|---|---|
| FullState (baseline) | 954.9, 19.5 | 864.9, 94.6 | 4377.6, 99.5 | 906.7, 246.1 | 3193.4, 198.7 | 2307.3, 1066.3 |
| FRMA (ours) | 956.2, 22.5 | 854.1, 163.1 | 4011.9, 84.2 | 1987.1, 306.1 | 2667.4, 175.9 | 2019.9, 654.8 |
| ARMA | 937.9, 14.6 | 282.4, 131.1 | 2579.1, 301.5 | 688.5, 186.5 | 2288.1, 519.8 | 1139.6, 579.6 |
| RMA | 843.1, 81.4 | 379.3, 385.9 | 1686.4, 1070.0 | 749.6, 289.5 | 416.2, 71.8 | 1222.8, 633.6 |
| ADRQN | 359.7, 308.5 | 142.9, 40.0 | −153.8, 120.9 | 92.7, 37.4 | 75.2, 23.6 | 417.4, 43.0 |
| RPSP | 817.3, 88.9 | 420.0, 107.0 | 1917.8, 456.1 | 524.1, 123.6 | 1016.0, 120.9 | 559.1, 29.2 |
| TrXL | 13.0, 0.1 | 85.6, 1.4 | −103.4, 13.4 | 185.3, 80.7 | 84.6, 0.9 | 429.2, 32.0 |
References
- Subramanian, A.; Chitlangia, S.; Baths, V. Reinforcement learning and its connections with neuroscience and psychology. Neural Netw. 2022, 145, 271–287. [Google Scholar] [CrossRef]
- Jensen, K.T. An introduction to reinforcement learning for neuroscience. arXiv 2023, arXiv:2311.07315. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
- Gu, S.; Holly, E.; Lillicrap, T.; Levine, S. Deep reinforcement learning for robotic manipulation with asynchronous off-policy updates. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 3389–3396. [Google Scholar]
- Tracey, B.D.; Michi, A.; Chervonyi, Y.; Davies, I.; Paduraru, C.; Lazic, N.; Felici, F.; Ewalds, T.; Donner, C.; Galperti, C.; et al. Towards practical reinforcement learning for tokamak magnetic control. Fusion Eng. Des. 2024, 200, 114161. [Google Scholar] [CrossRef]
- Mohan, A.; Zhang, A.; Lindauer, M. Structure in deep reinforcement learning: A survey and open problems. J. Artif. Intell. Res. 2024, 79, 1167–1236. [Google Scholar] [CrossRef]
- Shakya, A.K.; Pillai, G.; Chakrabarty, S. Reinforcement learning algorithms: A brief survey. Expert Syst. Appl. 2023, 231, 120495. [Google Scholar] [CrossRef]
- Kurniawati, H. Partially observable markov decision processes and robotics. Annu. Rev. Control Robot. Auton. Syst. 2022, 5, 253–277. [Google Scholar] [CrossRef]
- Hauskrecht, M. Value-function approximations for partially observable Markov decision processes. J. Artif. Intell. Res. 2000, 13, 33–94. [Google Scholar] [CrossRef]
- Kumar, A.; Fu, Z.; Pathak, D.; Malik, J. RMA: Rapid Motor Adaptation for Legged Robots. arXiv 2021, arXiv:2107.04034. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 2002, 86, 2278–2324. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Dey, R.; Salem, F.M. Gate-variants of gated recurrent unit (GRU) neural networks. In Proceedings of the 2017 IEEE 60th International Midwest Symposium on Circuits and Systems (MWSCAS), Boston, MA, USA, 6–9 August 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1597–1600. [Google Scholar]
- Graves, A.; Mohamed, A.r.; Hinton, G. Speech recognition with deep recurrent neural networks. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 6645–6649. [Google Scholar]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. Advances in Neural Information Processing Systems 2014, 27, 3104–3112. [Google Scholar]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Yang, G.; Yao, J. Multilayer neurocontrol of high-order uncertain nonlinear systems with active disturbance rejection. Int. J. Robust Nonlinear Control 2024, 34, 2972–2987. [Google Scholar] [CrossRef]
- Bidikli, B.; Tatlicioglu, E.; Bayrak, A.; Zergeroglu, E. A new robust ‘integral of sign of error’feedback controller with adaptive compensation gain. In Proceedings of the 52nd IEEE Conference on Decision and Control, Firenze, Italy, 10–13 December 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 3782–3787. [Google Scholar]
- Hfaiedh, A.; Chemori, A.; Abdelkrim, A. Observer-based robust integral of the sign of the error control of class I of underactuated mechanical systems: Theory and real-time experiments. Trans. Inst. Meas. Control 2022, 44, 339–352. [Google Scholar] [CrossRef]
- Michalski, J.; Mrotek, M.; Retinger, M.; Kozierski, P. Adaptive active disturbance rejection control with recursive parameter identification. Electronics 2024, 13, 3114. [Google Scholar] [CrossRef]
- Ting, J.; Basyal, S.; Allen, B.C. Robust control of a nonsmooth or switched control affine uncertain nonlinear system using a novel rise-inspired approach. In Proceedings of the 2023 American Control Conference (ACC), San Diego, CA, USA, 31 May–2 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 4253–4257. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, UK, 1998; Volume 1. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing atari with deep reinforcement learning. arXiv 2013, arXiv:1312.5602. [Google Scholar] [CrossRef]
- Williams, R.J. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Mach. Learn. 1992, 8, 229–256. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proceedings of the International Conference on Machine Learning (PMLR), Stockholm, Sweden, 10–15 July 2018; pp. 1861–1870. [Google Scholar]
- Kumar, A.; Li, Z.; Zeng, J.; Pathak, D.; Sreenath, K.; Malik, J. Adapting Rapid Motor Adaptation for Bipedal Robots. arXiv 2022, arXiv:2205.15299. [Google Scholar]
- Liang, Y.; Ellis, K.; Henriques, J. Rapid motor adaptation for robotic manipulator arms. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 17–18 June 2024; pp. 16404–16413. [Google Scholar]
- Hausknecht, M.J.; Stone, P. Deep Recurrent Q-Learning for Partially Observable MDPs. In Proceedings of the AAAI Fall Symposia, Arlington, VA, USA, 12–14 November 2015; Volume 45, p. 141. [Google Scholar]
- Zhu, P.; Li, X.; Poupart, P.; Miao, G. On improving deep reinforcement learning for pomdps. arXiv 2017, arXiv:1704.07978. [Google Scholar]
- Hefny, A.; Marinho, Z.; Sun, W.; Srinivasa, S.; Gordon, G. Recurrent predictive state policy networks. In Proceedings of the International Conference on Machine Learning (PMLR), Stockholm, Sweden, 10–15 July 2018; pp. 1949–1958. [Google Scholar]
- Zumsteg, O.; Graf, N.; Haeusler, A.; Kirchgessner, N.; Storni, N.; Roth, L.; Hund, A. Deep Supervised LSTM for 3D morphology estimation from Multi-View RGB Images of Wheat Spikes. arXiv 2025, arXiv:2506.18060. [Google Scholar] [CrossRef]
- Todorov, E.; Erez, T.; Tassa, Y. MuJoCo: A physics engine for model-based control. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Algarve, Portugal, 7–12 October 2012; pp. 5026–5033. [Google Scholar] [CrossRef]
- Parisotto, E.; Song, H.F.; Rae, J.W.; Pascanu, R.; Hadsell, R. Stabilizing Transformers for Reinforcement Learning. arXiv 2019, arXiv:1910.06764. [Google Scholar] [CrossRef]
- Dini, P.; Basso, G.; Saponara, S.; Chakraborty, S.; Hegazy, O. Real-Time AMPC for Loss Reduction in 48 V Six-Phase Synchronous Motor Drives. IET Power Electron. 2025, 18, e70072. [Google Scholar] [CrossRef]
- Dini, P.; Basso, G.; Saponara, S.; Romano, C. Real-time monitoring and ageing detection algorithm design with application on SiC-based automotive power drive system. IET Power Electron. 2024, 17, 690–710. [Google Scholar] [CrossRef]
- Dini, P.; Paolini, D.; Saponara, S.; Minossi, M. Leaveraging digital twin & artificial intelligence in consumption forecasting system for sustainable luxury yacht. IEEE Access 2024, 12, 160700–160714. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Graves, A. Generating sequences with recurrent neural networks. arXiv 2013, arXiv:1308.0850. [Google Scholar]

| Symbol | Description |
|---|---|
| Observation at time step t | |
| State at time step t | |
| Action at time step t | |
| Observation sequence from time to t: | |
| Action sequence from time to t: | |
| Latent state encoding: | |
| LSTM hidden and cell states at time t | |
| Primary and secondary policy networks: | |
| State encoder: | |
| LSTM-based encoder: | |
| Hidden network: | |
| Mapping network: | |
| T | Length of observation–action history used by LSTM |
| d | LSTM hidden size |
| k | Dimension of latent state encoding |
| Environment | State Dim. | Action Dim. | Observation Dim. |
|---|---|---|---|
| InvertedPendulum-v4 | 4 | 1 | 2 |
| HalfCheetah-v4 | 17 | 6 | 2 |
| Walker2d-v4 | 17 | 6 | 10 |
| InvertedDoublePendulum-v4 | 9 | 1 | 5 |
| Hopper-v4 | 11 | 3 | 5 |
| Humanoid-v4 | 348 | 17 | 25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Lu, C.; Wu, H.; Hu, B.; Li, X.; Li, Z.; Guo, X. FRMA: Four-Phase Rapid Motor Adaptation Framework. Machines 2025, 13, 885. https://doi.org/10.3390/machines13100885
Liu X, Lu C, Wu H, Hu B, Li X, Li Z, Guo X. FRMA: Four-Phase Rapid Motor Adaptation Framework. Machines. 2025; 13(10):885. https://doi.org/10.3390/machines13100885
Chicago/Turabian StyleLiu, Xiangbei, Chang Lu, Hui Wu, Bo Hu, Xutong Li, Zongyuan Li, and Xian Guo. 2025. "FRMA: Four-Phase Rapid Motor Adaptation Framework" Machines 13, no. 10: 885. https://doi.org/10.3390/machines13100885
APA StyleLiu, X., Lu, C., Wu, H., Hu, B., Li, X., Li, Z., & Guo, X. (2025). FRMA: Four-Phase Rapid Motor Adaptation Framework. Machines, 13(10), 885. https://doi.org/10.3390/machines13100885






