Abstract
The article deals with the properties of fault detection filters when applying their structure to a class of linear, continuous-time systems, with dynamics being specified by the system matrix of the ostensible Metzler structure. The proposed solution is reduced to the use of diagonal stabilization in the synthesis of the state observer and uses the decomposition of the ostensible Metzler matrix. The approach creates a unified framework that covers the compactness of parametric constraints on Metzler matrices and their quadratic stability. Due to the complexity of such constraints, the design conditions are formulated using sharp linear matrix inequalities. For potential application in network control structures, the problem is formulated and solved for linear discrete-time ostensible positive systems. Finally, a linearized model of the B747-100/200 aircraft is used to validate the proposed method. The numerical solution and simulation results show that the proposed approach provides superior sensitivity of the fault detection filter in detecting faults, compared to synthesis methods that do not guarantee the positivity of the filter gain.
1. Introduction
Given the complexity of control design tasks, it is necessary to respect not only the boundaries of system quantities, but also the limitations of system parameters and the balance of conflicting goals. Such a class of systems includes positive systems [1,2], with hard parametric constraints on the elements of the dynamics matrix of Metzler systems [3], where most of the procedures that are valid for linear systems [4,5,6] cannot be used due to the requirement of their diagonal stabilization [7]. In these applications, significant simplifications can be achieved by exploiting the principle of diagonal parameterization of the strictly Metzler matrix [8], combining the quadratic Lyapunov function with the definition of constraints in the form of linear matrix inequalities (LMI). If the description of the system dynamics does not have a strictly Metzler matrix structure (ostensible Metzler systems), or if the positivity of the input matrix parameters varies depending on the operating environment [9], there is a risk of reduction or loss of the positive properties of the system.
System faults are dangerous for practical systems; because they can drastically change the behavior of the system, it is necessary to design control structures to correct the behavior of the system at least within the range of acceptable degradation. Fault-tolerant control (FTC) schemes provide procedures that improve system tolerance to certain classes of faults [10,11]. The motivation comes from the fact that the most common model-based fault detection approaches use state observers to construct residual fault signals [12,13,14]. In standard control structures of multi-agent systems, controller faults can be transmitted to neighboring agents; thus, a single fault in one agent can cause a cascade of subsequent faults. The principle of early detection of small loss of actuator gain characterizes new trends in FTC. It should be noted that the principles presented in [15,16,17] cannot be used to directly solve the problem of detecting faults in ostensible Metzler systems because they do not support the constraints defined by the ostensible structure of Metzler matrices.
Another interesting class is linear positive switched systems, consisting of a set of linear strictly positive subsystems, where the active subsystem is defined by a switching signal [18]. Their mathematical models for diagnostic purposes are usually given via discrete-time representation and the synthesis is linked to the linear programming technique [19,20], which implies stability conditions using a linear co-positive Lyapunov functional [21,22]. These results can only be marginally used for non-switching positive systems as a special case because they are limited in estimating the constrained and distributed states [23,24]. The same difficulties in FDF design and fault detection in positive complex network structures can be noted in [25,26,27,28] and in stochastic linear dynamical systems, such as positive Markov jump systems, whose structures or parameters may change probabilistically at a certain transition [29,30,31].
This paper deals with the design of a fault detection filter (FDF) for ostensible linear Metzler systems. New conditions for the stability of the FDF based on the system state observer are formulated using a set of LMIs, taking into account the norm of the FDF transfer function matrix. Given the necessity of diagonal stabilization of the state observer, the proposed approach uses a suitable form of decomposition of the ostensible Metzler matrix and defines parametric constraints for the one of the separated matrices that is strictly Metzler. The FDF scheme is based on the Luenberger observer, which generates residuals with high sensitivity to small losses in the actuator gain, which is guaranteed by the dynamic properties of the strictly Metzler part of the observer state dynamics. Considering applications in network control structures, the problems are also reformulated and solved in the context of linear discrete-time ostensible positive systems. The parameterized matrices of this form of FDFs are constructed by solving the corresponding set of LMIs; the Lyapunov method forms the basis of stability analyses under the required positivity and synthesis conditions with given parameter bounds. A linearized model of the B747-100/200 aircraft is used to illustrate the proposed procedure and present its properties. Considering stability in the presence of actuator gain loss, the FDF is designed as a quadratic stable observer with ostensible Metzler dynamics. The most likely extension of the presented approach appears to be the area of fault detection of systems, whose mathematical models have the characteristics of structures that temporarily overlap with those of the structures of linear ostensible Metzler systems.
The paper is organized in the following order. Following the properties of linear strictly positive systems presented in Section 2, the parametric bounds and representation approaches for linear, continuous-time ostensible Metzler systems and linear, discrete-time ostensible positive systems are given in Section 3. The application of the FDF design principle to these classes of systems is given in Section 4. To illustrate the proposed digital implementation of FDFs, essential results are demonstrated on an example in Section 4 and concluding remarks are given in Section 6.
For convenience, the notations used in this document reflect common convention: , denote the transpose of the vector x, and the matrix X, respectively; denotes the (block) diagonal matrix; for a square symmetric matrix, denotes its negative definiteness; denotes the n-th order identity matrix; and denote the inverse matrix and the eigenvalue spectrum of a square matrix X; the maximal positive real part of the eigenvalue spectrum of X is denoted by ; denotes a vector whose elements are all 1; for a real matrix, means that its components are non-negative; () denotes the set of (non-negative) real numbers; () refers to the set of (non-negative) real matrices; () denotes the set of strictly (ostensible) Metzler matrices.
2. Consequences of Internal System Positivity
This section deals with internally positive linear, time-invariant systems described by state–space realizations for and
where , are non-negative, , are non-negative and with a suitably chosen sampling period
If is strictly Metzler, all its diagonal elements are negative and its off-diagonal elements are strictly positive, then is strictly positive (all its elements are strictly positive) [32], i.e., their elements have parametric bounds
and according to (3) these matrix parameterizations imply:
Lemma 1
(Parameterization of , [33]). For , , the following statements hold equivalently
for the notations
where is the circulant form of a permutation matrix [34].
The following remark is a slightly generalized characterization of the parametric representation of the boundaries of positive systems.
Remark 1.
If the matrix is represented in the equivalent rhombic forms
then, in the sense of (5), the diagonal matrices are defined by the diagonals (6 (i)), (6 (ii)) such that for ,
As a result, the structural constraints (3) of the Metzler matrix can be equivalently formalized as
ad the structural constraints (3) of the strictly positive matrix can be formalized as
Moreover, for example with , the following holds
and these circular shift operations do not change the existing definiteness of diagonal matrices. Analogously, these procedures can be applied to (8) and (9) using , in constructions with multiple circular shifts.
The defined constructions of positivity constraints reflect the dual formulation of the state control design conditions and the system state estimation conditions, necessary with respect to the parameterization of system dynamics matrices in positive systems. Diagonal formulations follow from the restriction that positive systems are only diagonally stabilized [35].
Theorem 1
([36]). In limiting the positivity of Luenberger state observers on
with (c) , , or (d) , , , diagonal parameterization is prescribed using the diagonal matrices , , , and diagonal parameterization is prescribed using the diagonal matrices , , , constructed so that
and the observer system matrices , are
The parameterization defined in this way does not guarantee that the strictly Metzler matrix is Hurwitz, or that the strictly positive matrix is Schur. In the Lyapunov sense, these matrices must still have a solution for a positive definite diagonal matrix .
Regarding the control design task, the dual parameterization process is obvious, where the duality of positive parameterization yields.
3. Ostensible System Characterization
Let the matrix in the system (1) be an ostensible Metzler matrix. Then, since is not strictly Metzler, the autonomous part of the system is not internally positive.
Definition 1.
A matrix is ostensible Metzler if there is at least one negative off-diagonal element in the structure A while the number of positive off-diagonal elements of A is predominant and all diagonal elements of the matrix A are negative.
Theorem 2
([37]). If for U is prescribed in the form
with , , , then the eigenvectors U and V are identical and
where are the eigenvalues of V and are the eigenvalues of U.
By exploiting the above property, the compatibility of the parametric bounds of the ostensible Metzler matrix can be achieved by using the constructive separation
where is strictly Metzler and is element-wise negative and Hurwitz. This concept transforms the synthesis task for ostensible Metzler systems into the synthesis task for strictly Metzler systems, parameterizing by its rhombic diagonals.
Lemma 2
([38]). For ostensible Metzler there exists a strictly Metzler and an element-wise negative and Hurwitz satisfying (17) with relation to positive scalars only if
The parameterization defined in this way does not guarantee that the desired ostensible Metzler matrix is Hurwitz. In the Lyapunov sense, this matrix must still have a solution for a positive definite diagonal matrix .
Corollary 1.
When working with from (1), it is necessary to define ostensible positivity constraints for and obtain a strictly positive matrix and a strictly negative and Schur matrix . If a solution satisfying Lemma 2 is known for the parameters of a continuous-time system from (1), the simplest way is to use the definite relations for the conversion of the system description and calculate the parameters according to the relations (2) as follows:
where is a suitably chosen sampling period.
Subsequently, the structural constraints will be automatically satisfied.
The parameterization defined in this way does not guarantee that the ostensible positive matrix is Schur.
In the Lyapunov sense, this matrix must still have a solution for a positive definite diagonal matrix .
To complete the above procedures, it is necessary to find J, H such that is ostensible Metzler and Hurwitz and is ostensible positive and Schur.
4. Design of Fault Detection Filters
Let the description of the faulty state of the system be extended
where , the cores of FDFs are state observers
Using the estimation errors , , then from (26), (27) follows
with , and respecting principle of constructive separation (17), then
where must be strictly Metzler and Hurwitz, is element-wise negative and Hurwitz, must be strictly positive and Schur and is element-wise negative and Schur.
By defining the form of the residual weighting depending on the observer error innovation, the additive fault detection filters are defined as
where the weight matrix is a positive definite diagonal matrix.
Using (30), it is possible to derive design conditions for FDF parameters considering only a pair of parameters or .
Theorem 3.
(30) is stable with ostensible Metzler and Hurwitz matrix if for a strictly Metzler matrix and non-negative , there exist positive definite diagonal matrices , and a positive scalar such that for and the following set of LMIs is feasible:
When the above conditions hold, the strictly positive observer gain matrix is computed as
Hereafter, ∗ is a symmetric entry in a symmetric matrix.
Proof.
For a positive definite diagonal matrix , and an upper bound on the norm , of the disturbance transfer function matrix the Lyapunov function has the form
and under this assumption, it must hold
If is not considered when substituting (30) into (36), then
and the redefinition with respect to means that (37) prescribes a solution in bilinear form
which, using the Schur complement property, can be linearized as
The basic idea is to construct a residual signal that remains at zero (or below a certain threshold) before the occurrence of a fault and reaches a non-zero value higher than a given threshold at the onset of the fault, allowing the fault to be detected.
Theorem 4.
(30) is stable with ostensible positive and Schur matrix if for a strictly positive matrix and non-negative , there exist positive definite diagonal matrices , and a positive scalar such that for and the following set of LMIs is feasible:
When the above conditions hold, the strictly positive observer gain matrix is computed as
Proof.
For a positive definite diagonal matrix , and an upper bound on the norm , of the disturbance transfer function matrix, the Lyapunov function has the form
and under these assumptions the forward difference of Lyapunov function at the time instant i must satisfy
When substituting (30) into (49) not considering then
and the redefinition with respect to means that (50) prescribes a solution
Consequently,
which, using the Schur complement property, can be written as
Analogously to (43), pre-multiplying the left-hand side by P and post-multiplying the right-hand side by then (14d) for and any gives
and (55), (56) give the inequalities in (45).
Based on the potential tuning optimization of the parameter , this also allows for a relatively simple way of determining the detection threshold. This concludes the proof. □
Corollary 2.
For the design of a continuous-time Luenberger observer with ostensible Metzler and Hurwitz matrix in a disturbance-free environment () or the design of a discrete-time Luenberger observer with ostensible positive and Schur matrix from Theorems 3 and 4, it follows:
where strictly positive gain matrices J, H are calculated as defined.
Remark 2.
In the presented paradigm of continuous-time residual filter design, matrix inequalities (32) express parametric constraints imposed in the design on a strictly Metzler matrix , (33) prescribes the asymptotic stability of the observer, and diagonal matrix variables in (31) reflect the principle of diagonal stabilization.
Analogously, in the design of a discrete-time residual filter, the matrix inequalities (45) express the parametric constraints given in the design for a strictly positive matrix , (46) prescribes the asymptotic stability of the observer, and the diagonal matrix variables in (44) reflect the principle of diagonal stabilization.
In both cases, the diagonal weight matrix is optimized with respect to the norm of the input disturbance transfer function matrix.
The threshold computation for additive fault detection and isolation can be solved as an optimization problem by [39].
5. Illustrative Example
To illustrate the effectiveness of the approach, an apparent Metzler linear system (1) is used for the stable linearized B747-100/200 aircraft model [40] with nominal and derived model matrices given by
Choosing = 0.005
and for the resulting with the prescribed D-parameter of the D-stability region the value of the tuning parameter will be , which implies the strictly negative and Hurwitz matrix ,
and the unstable diagonally corrupted Metzler matrix ,
which solves the required separation of the matrix A.
Since parameterization is necessary to address the consistency of design constraints, manipulation according to (5), (12) yields:
and solving the set of inequalities within (31)–(33) gives
The corresponding strictly positive observer gain is determined as
and the desired fault detection filter is obtained with the parameterized matrices as follows:
prescribing a strictly Metzler and Hurwitz matrix and an ostensible Matzler and Hurwitz matrix . while the residual gain is optimized as
Note that the positions of the negative off-diagonal elements in are preserved and the elements of the third columns in remain the same due to the specified structure of the matrix C.
All the results are obtained by SeDuMi package [41], implemented in Matlab R2018a.
As expected, a stable strictly Metzler part of the observer is designed which produces asymptotical observer state responses and aperiodically reacted actuator fault residuals.
For the simulation phase, the control law rule for is as
with gains K [15], W and desired output w of the form
and setting the initial conditions .
The simulations results are presented in Figure 1 and Figure 2, where Figure 2 shows the evolution of the residual signals generated by the residual disturbance filter in response to a step loss of gain of the second actuator , starting its operation at time . It is clear from Figure 1 that such a small change in gain is practically not reflected in the time expressions of the state variables and their estimated values. The cases of loss of gain of other actuators are manifested analogously.
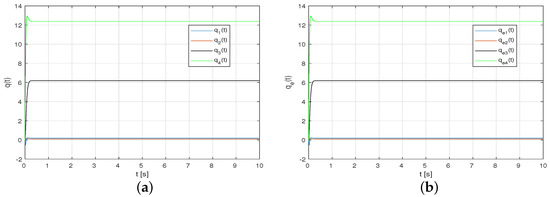
Figure 1.
System state (a) and estimation of system state (b) in fault mode starting at time t = 6 s.
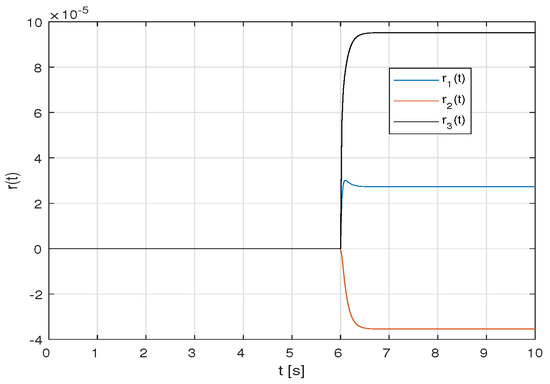
Figure 2.
Fault residual filter response in fault mode starting at time t = 6 s.
In the discrete-time model, the matrix parameters are rewritten into expressions corresponding to (25), with the guarantee of preserving all parametric constraints, such that, with s
Analogously, by constructing the required diagonal parameterization and solving LMIs according to Theorem 4
and with the strictly positive observer gain, it is
when constructing for
Simulations with the discrete-time model structure show no significant change in terms of the residual signals presented in the figures of this section and confirm the effectiveness of this scheme as well.
The properties of the state estimator remain valid even in the case of the lossless actuator gain regime, which is characterized by zero values of the FDF outputs.
6. Conclusions
The article generalizes a design framework for constructing FDFs for linear, continuous-time ostensible Mezler systems and for linear, discrete-time ostensible positive systems. The LMIs-based design, which takes into account the parametric constraints and quadratic stability of the state-based observer FDF, exploits the ostensible matrix separation of the system dynamics to apply the diagonal stabilization principle for strictly Metzler systems. Such a philosophy means constructing a set of LMIs based on diagonal matrix variables only for a separated strictly Metzler dynamics matrix such that their fulfillment guarantees a separated state observer dynamics in the form of a strictly Metzler and Hurwitz matrix, while the remaining part of the observer dynamics is determined by a strictly negative and Hurwitz matrix. For potential use in the diagnosis of ostensible positive systems in network structures and distributed systems, the observer design problem for fault detection is defined and solved for linear ostensible positive systems with discrete-time state models. For the FDF design problem for these classes of models, conditions for the existence of such an FDF are established, where the required FDF parameter matrices can be easily determined from the solution of the matrix variables of the set of LMIs.
Using the example of a linearized model of the B747-100/200 aircraft, it is shown that the FDF with such a defined parameter design is able to detect relatively small gain losses of the actuators of the linear ostensible Metzler system, while all the aforementioned design constraints are mutually conditional.
Special cases of these problems may arise in various contexts related to actuator failure detection in the class of distributed multi-agent systems based on ostensible Metzler agents or in actuator failure detection in unmanned aerial vehicles (UAVs) because they are modeled by temporally overlapping forms with ostensible Metzler structures. All of these problems are currently being addressed by the authors.
Author Contributions
A.F. developed and implemented the principles of observer parameter synthesis and their numerical validation. D.K. solved the projection of system positivity and parametric constraints into LMIs sets. All authors have read and agreed to the published version of the manuscript.
Funding
The research covering the work area presented in this paper was not supported by any grant.
Data Availability Statement
No new data were created for this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| LMI | linear matrix inequality |
| MIMO | multiple-input multiple-output |
| FDF | fault detection filter |
| SeDuMi | self dual minimization |
Notations
The following basic notations are used in this manuscript:
| , , , , | state, input, output and fault variable vectors |
| A, B, C, M, , , F, G, N, , | system matrix parameters |
| , , , , J, H | observer’s system matrices, observer gains |
| Q, , R, P, , , | LMI variables |
All other notations are defined in the given context fluently.
References
- Haddad, W.M.; Chellaboina, V.; Hui, Q. Nonnegative and Compartmental Dynamical Systems; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Shen, J. Analysis and Synthesis of Dynamic Systems with Positive Characteristics; Springer Nature: Singapore, 2017. [Google Scholar]
- Arrow, K.J. The genesis of dynamic systems governed by Metzler matrices. In Mathematical Economics and Game Theory; Henn, R., Moeschlin, O., Eds.; Springer: Berlin/Heidelberg, Germany, 1977; pp. 629–644. [Google Scholar]
- Franklin, G.F.; Powel, D.; Emami-Naeini, A.F. Feedback Control of Dynamic Systems; Pearson: London, UK, 2021. [Google Scholar]
- Cassel, K.W. Matrix, Numerical, and Optimization Methods in Science and Engineering; Cambridge University Press: New York, NY, USA, 2021. [Google Scholar]
- Wang, Z.; Wang, Y.; Ji, Z. Filter Design for System Modeling, State Estimation and Fault Diagnosis; CRC Press: Boca Raton, FL, USA, 2023. [Google Scholar]
- Barker, G.P.; Berman, A.; Plemmons, R.J. Positive diagonal solutions to the Lyapunov equations. Linear Multilinear Algebra 1978, 5, 249–256. [Google Scholar] [CrossRef]
- Krokavec, D.; Filasová, A. LMI based principles in strictly Metzlerian systems control design. Math. Probl. Eng. 2018, 2018, 9590253. [Google Scholar] [CrossRef]
- Kwon, W.H.; Kim, P.S.; Park, P.G. A receding horizon Kalman FIR filter for linear continuous-time systems. IEEE Trans. Autom. Control 1999, 44, 2115–2120. [Google Scholar] [CrossRef]
- Zhang, K.; Jiang, B.; Shi, P. Observer-based Fault Estimation and Accomodation for Dynamic Systems; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Lan, J.; Patton, R. Robust Integration of Model-Based Fault Estimation and Fault-Tolerant Control; Springer Nature: Cham, Switzerland, 2021. [Google Scholar]
- Chen, W.; Chowdhury, F.; Djuric, A.; Yeh, C.P. Robust fault detection of turbofan engines subject to adaptive controllers via a total measurable fault information residual (ToMFIR) technique. ISA Trans. 2014, 53, 1383–1388. [Google Scholar] [CrossRef]
- Ren, X.L. Observer design for actuator failure of a quadrotor. IEEE Access 2020, 8, 152742–152750. [Google Scholar] [CrossRef]
- Hu, Q.; Li, B.; Xiao, B.; Zhang, Y. Control Allocation for Spacecraft Under Actuator Faults; Springer Nature: Singapore, 2021. [Google Scholar]
- Wang, X.; Yang, G.H. Distributed reliable H∞ consensus control for a class of multi-agent systems under switching networks. A topology-based average dwell time approach. Int. J. Robust Nonlinear Control 2016, 26, 2767–2787. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Yang, G.H. Distributed fault detection and isolation for multi-agent systems. An interval observer approach. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 2220–2230. [Google Scholar] [CrossRef]
- Xiao, S.; Dong, J. Distributed fault-tolerant containment control for nonlinear multi-agent systems under directed network topology via hierarchical approach. IEEE/CAA J. Autom. Sin. 2021, 8, 806–816. [Google Scholar] [CrossRef]
- Du, D.; Xu, S.; Cocquempot, V. Observer-Based Fault Diagnosis and Fault Tolerant Control for Switched Systems; Springer Nature: Singapore, 2021. [Google Scholar]
- Ait Rami, M.; Tadeo, F. Linear programming approach to impose positiveness in closed-loop and estimated states. In Proceedings of the 17th International Symposium on Mathematical Theory of Networks and Systems, Kyoto, Japan, 24–28 July 2006; pp. 2470–2477. [Google Scholar]
- Sierksma, G.; Zwols, Y. Linear and Integer Optimization: Theory and Practice; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Li, S.; Xiang, Z.; Reza Karimi, H. Mixed L_/L1 fault detection observer design for positive switched systems with time-varying delay via delta operator approach. Int. J. Control Autom. Syst. 2014, 12, 709–721. [Google Scholar] [CrossRef]
- Xiang, M.; Xiang, Z. Robust fault detection for switched positive linear systems with time-varying delays. ISA Trans. 2014, 53, 10–16. [Google Scholar] [CrossRef]
- Han, W.; Trentelman, H.L.; Xu, B. Distributed H_/L∞ fault detection observer design for linear systems. IFAC-PapersOnLine 2020, 53, 688–693. [Google Scholar] [CrossRef]
- Wang, L.; Morse, A.S. A distributed observer for a time-invariant linear system. IEEE Trans. Autom. Control 2018, 63, 2123–2130. [Google Scholar] [CrossRef]
- He, X.; Wang, Z.; Ji, Y.D.; Ji, Y.D.; Zhou, D.H. Robust fault detection for networked systems with distributed sensors. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 166–177. [Google Scholar] [CrossRef]
- Shen, J.; Liu, J.R.; Cui, Y. An exact characterization of the L_/L1 index of positive systems and its application to fault detection filter design. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 3262–3266. [Google Scholar]
- Ju, Y.; Tian, X.; Liu, H.; Ma, L. Fault detection of networked dynamical systems. A survey of trends and techniques. Int. J. Syst. Sci. 2021, 52, 3390–3409. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, J.; Xing, W.; Wu, Y.; Teng, S. Event-triggered observation and control of positive complex networks using linear programming. In Proceedings of the 39th Youth Academic Annual Conference of Chinese Association of Automation, Dalian, China, 7–9 June 2024; pp. 428–433. [Google Scholar]
- Jiang, J.; Shen, J. L_/L1 filter-based fault detection for positive Markov jump linear systems with time delay. IEEE Access 2019, 7, 17727–117739. [Google Scholar]
- Xiao, S.; Zhang, Y.; Zhang, B. Event-triggered networked fault detection for positive Markovian systems. Signal Process. 2019, 157, 161–169. [Google Scholar] [CrossRef]
- Zhang, J.; Du, B.; Zhang, S.; Ding, S. A double sensitive fault detection filter for positive Markovian jump systems with a hybrid event-triggered mechanism. IEEE/CAA J. Autom. Sinica 2024, 11, 2298–2315. [Google Scholar] [CrossRef]
- Berman, A.; Neumann, M.; Stern, R. Nonnegative Matrices in Dynamic Systems; John Wiley & Sons: New York, NY, USA, 1989. [Google Scholar]
- Krokavec, D. Ostensible Metzler linear uncertain systems. Goals, LMI synthesis, constraints and quadratic stability. WSEAS Trans. Syst. Control 2023, 18, 255–262. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: New York, NY, USA, 2013. [Google Scholar]
- Berman, A.; Hershkowitz, D. Matrix diagonal stability and its implications. SIAM J. Discret. Math. 1983, 4, 377–382. [Google Scholar] [CrossRef]
- Krokavec, D.; Filasova, A. State control design of ostensible Metzler linear systems with unsigned input parameters. Designs 2024, 8, 54. [Google Scholar] [CrossRef]
- Shores, T.S. Applied Linear Algebra and Matrix Analysis; Springer: New York, NY, USA, 2007. [Google Scholar]
- Krokavec, D.; Filasova, A. Performances of additive fault detection in linear ostensible Metzler systems. In Proceedings of the 8th International Conference on Control, Automation and Diagnosis ICCAD 2024, Paris, France, 15–17 May 2024; pp. 1–6. [Google Scholar]
- Ding, S. Model-Based Fault Diagnosis Techniques; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Hao, L.Y.; Yang, G.H. Fault-tolerant control via sliding-mode output feedback for uncertain linear systems with quantisation. IET Control Theory Appl. 2013, 7, 1992–2006. [Google Scholar] [CrossRef]
- Peaucelle, D.; Henrion, D.; Labit, Y.; Taitz, K. User’s Guide for SeDuMi Interface; LAAS-CNRS: Toulouse, France, 2002. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).