Calculation Model for Multi-Roller Load Distribution of Planetary Threaded Roller Bearings Considering Machining Errors
Abstract
1. Introduction
2. Model
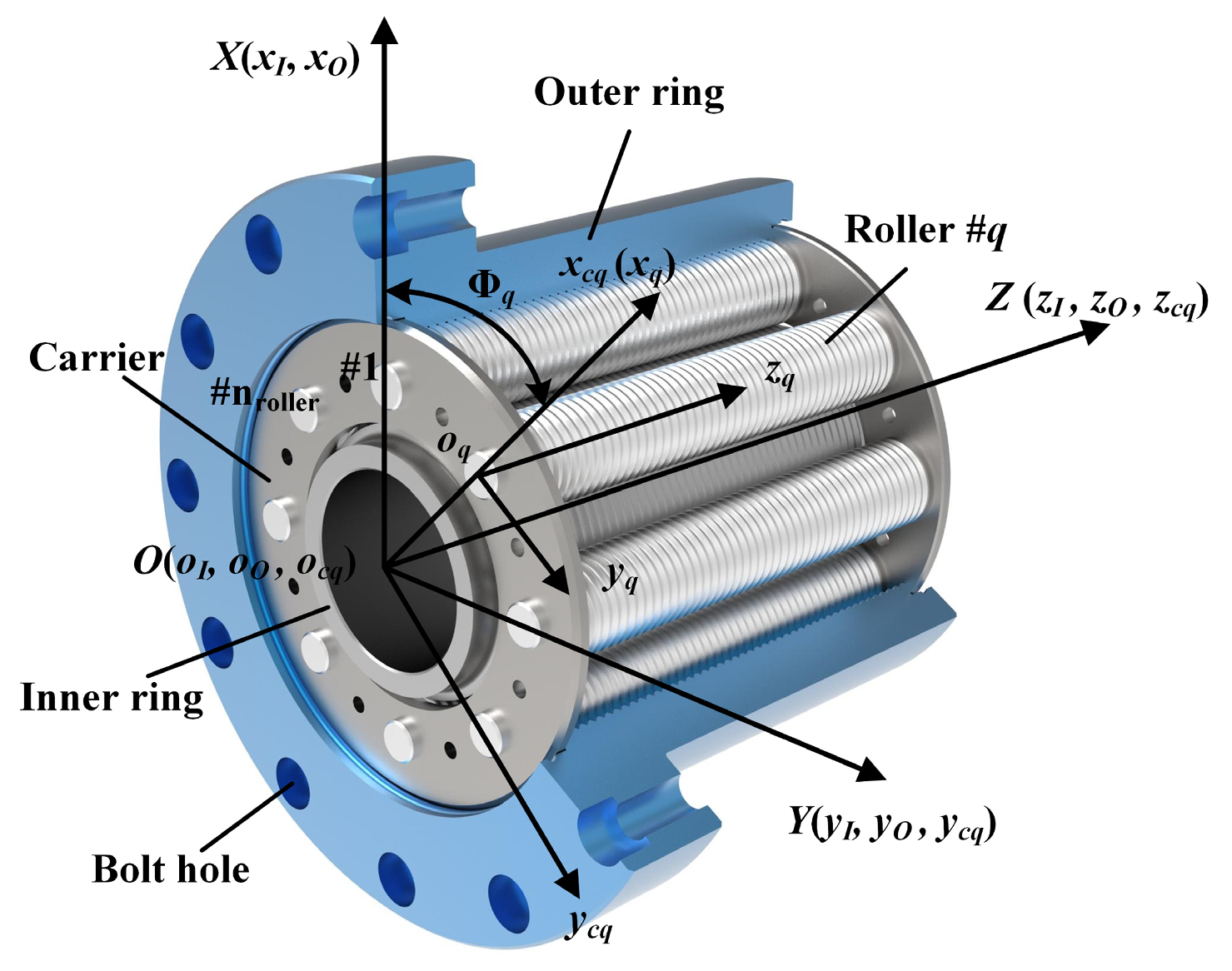
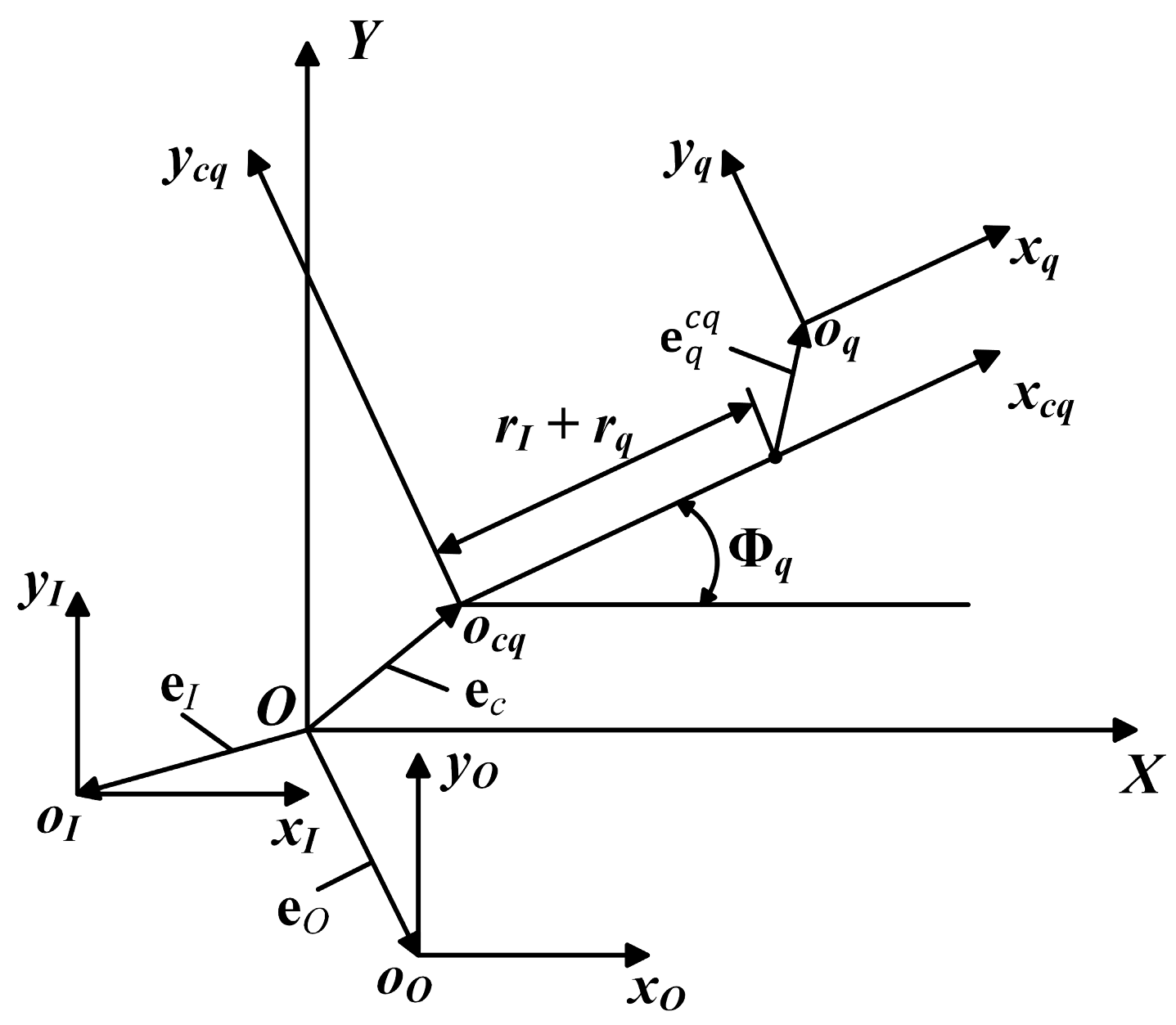
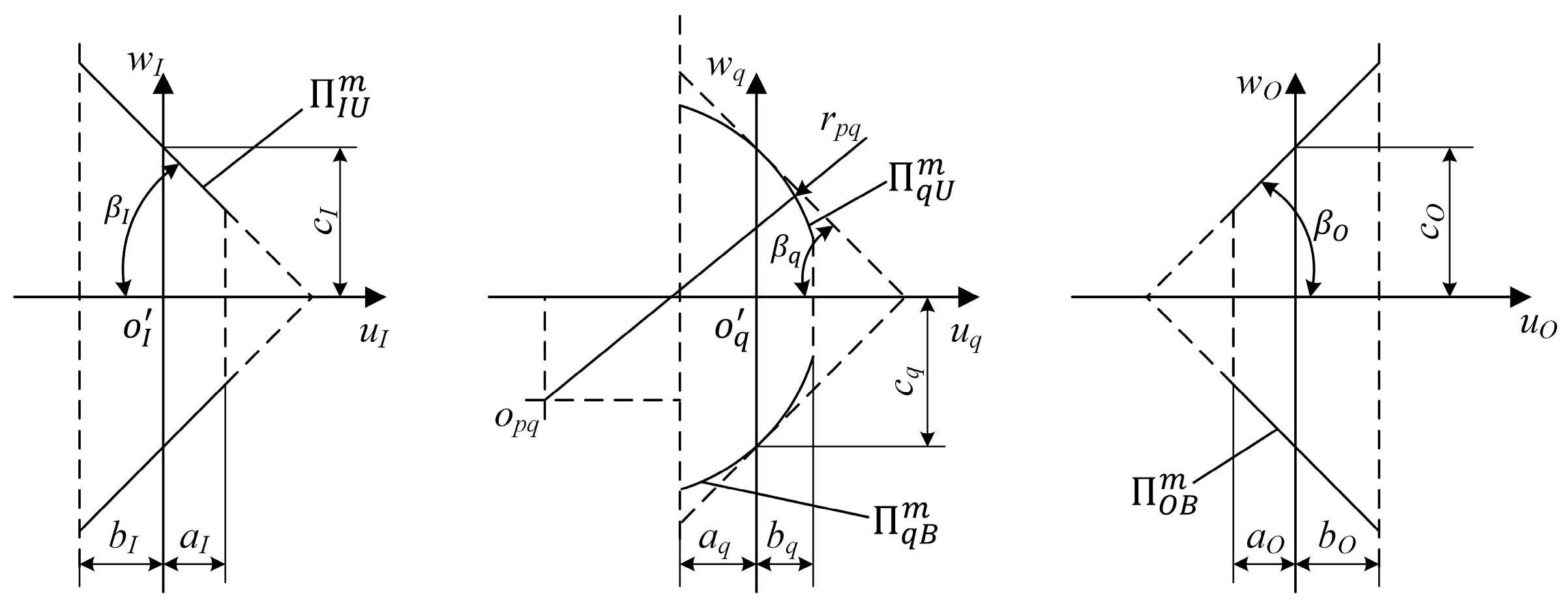
2.1. Establishing the Coordinate Systems for PTRB
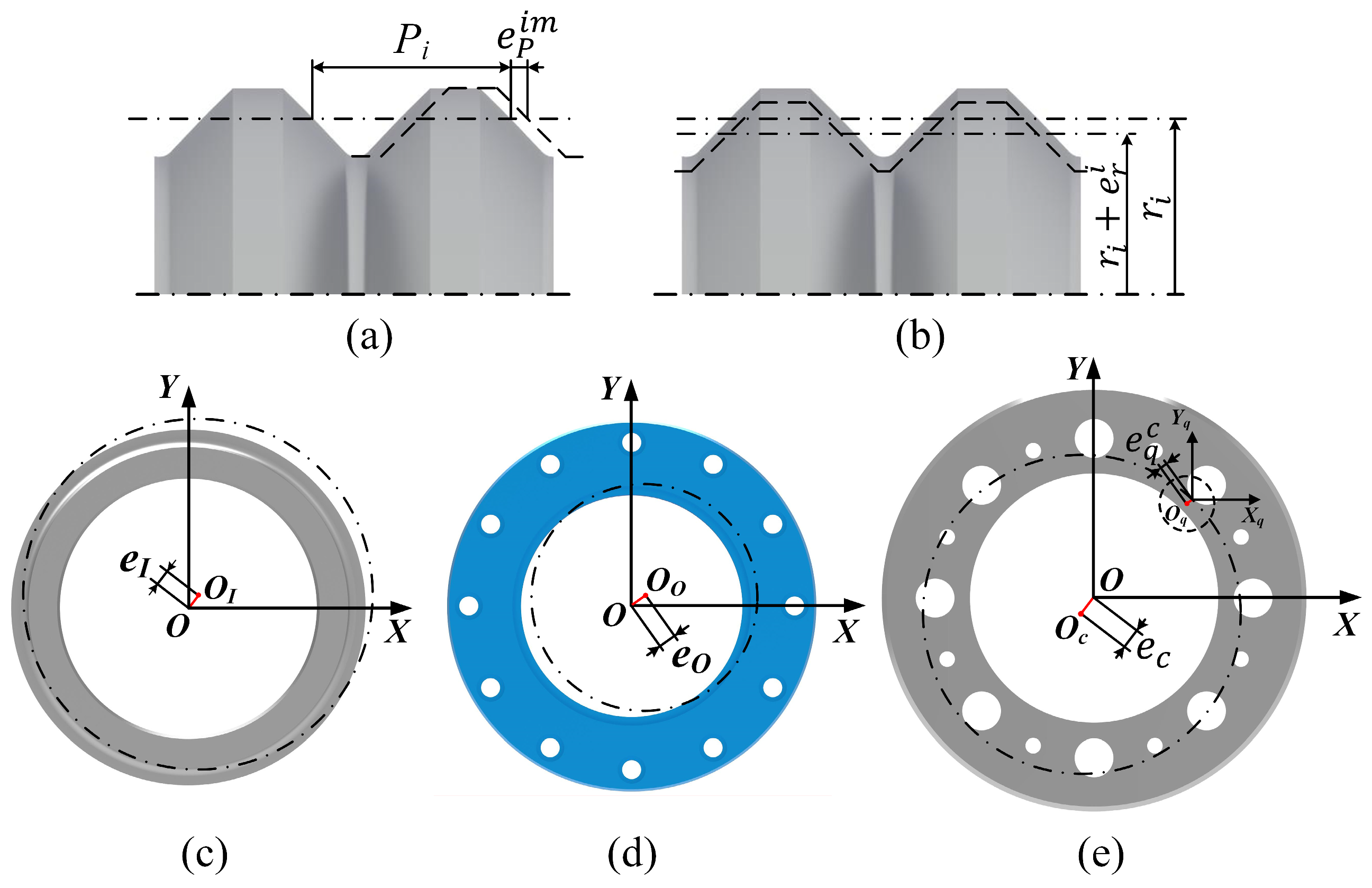
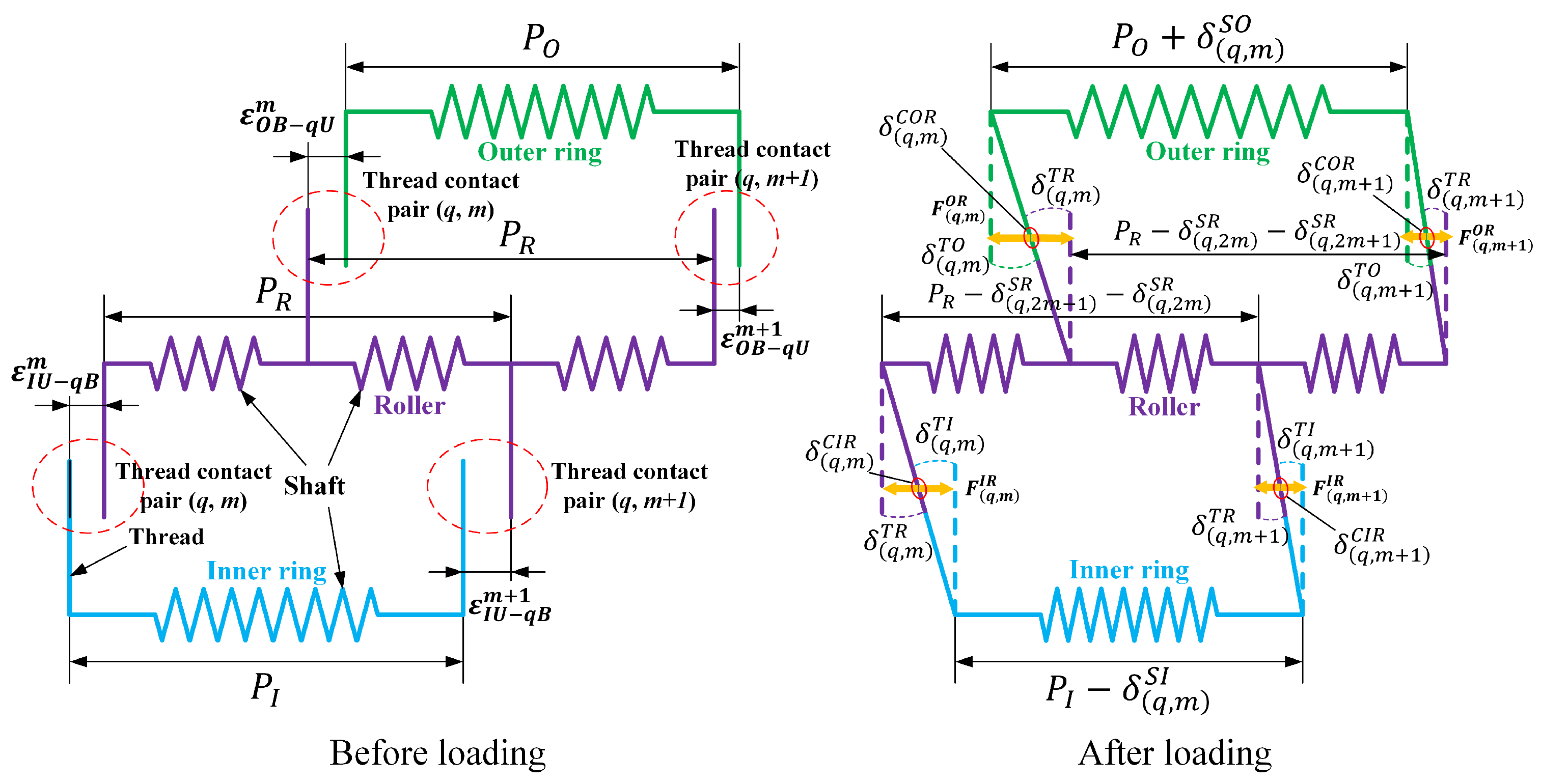
2.2. PTRB Axial Clearance Model Considering Manufacturing Errors
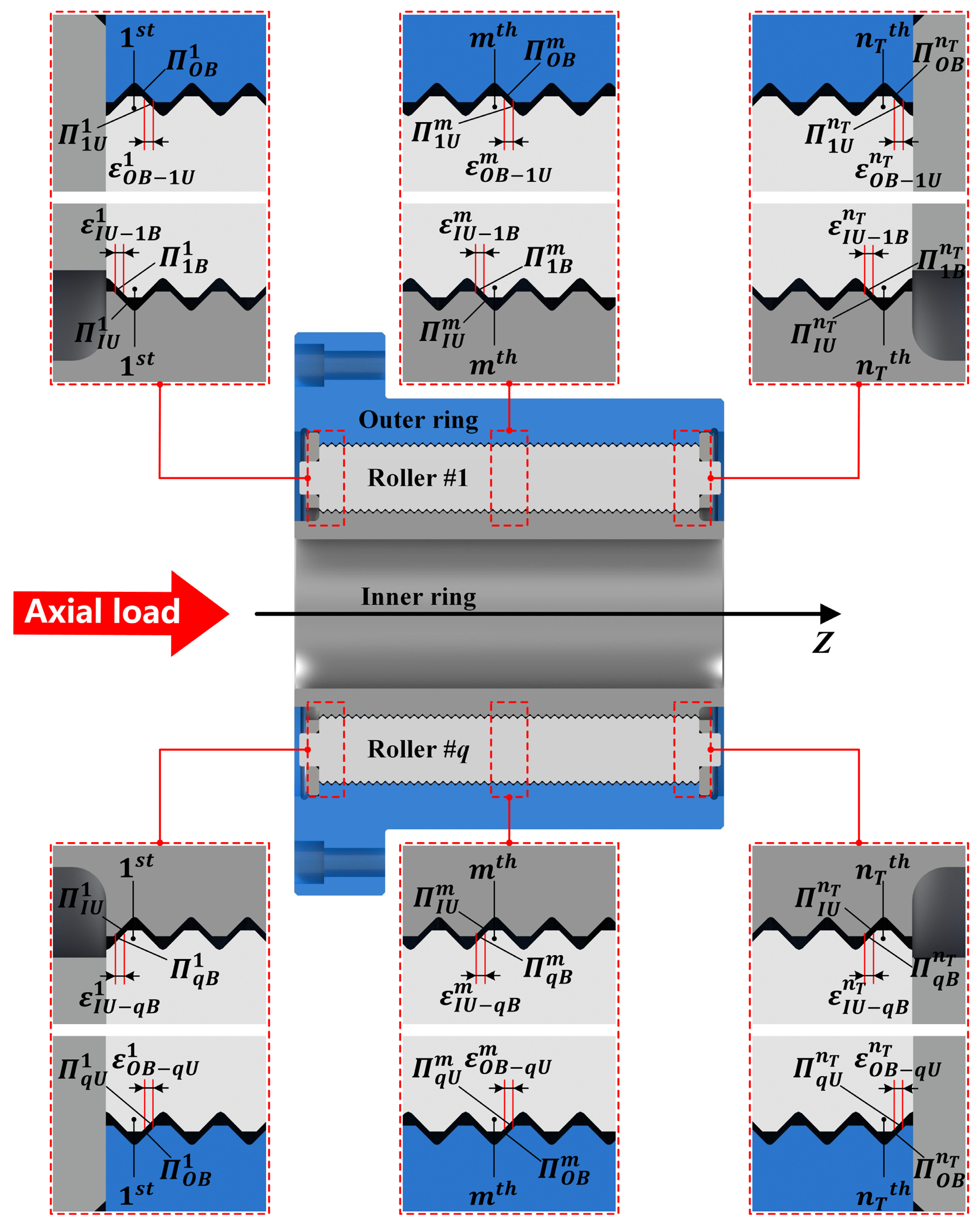
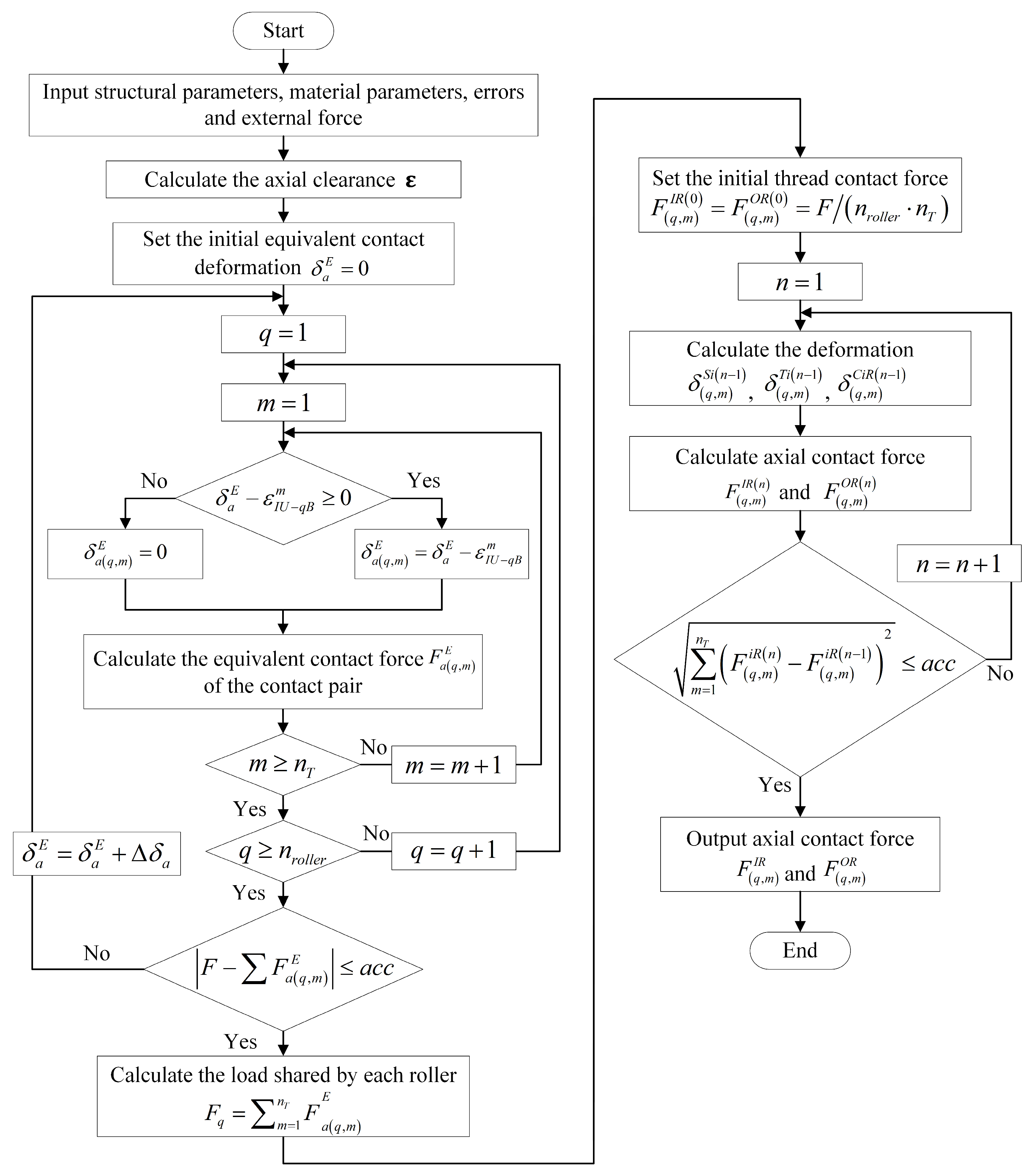
2.3. Equivalent Contact Force and Contact Deformation
- The equivalent contact deformation is set to zero. A step size for contact deformation iteration is introduced, and appropriate calculation precision is established. In this study, an iteration step size of mm and a calculation accuracy of are used in MATLAB 2021b to ensure result convergence while maintaining a reasonable balance between calculation speed and acceptable accuracy.
- The equivalent contact deformation is computed by considering the machining error. Machining error causes variations in the axial clearance of meshing thread teeth, resulting in different contact conditions among the threads. Therefore, determining whether thread teeth are in contact based on the following conditions is essential (the inner ring-roller side is taken as an example; the same rules apply to the outer ring-roller side):
- If , the preset equivalent contact deformation is insufficient to eliminate the axial clearance between the m-th thread tooth of the q-th roller. In other words, the two corresponding thread teeth have not yet made contact, and the thread tooth is in a non-contact state. The equivalent contact deformation of the corresponding thread tooth is .
- If , the axial clearance between the m-th thread tooth of the q-th roller is fully eliminated, resulting in contact. The thread tooth is now in contact mode, and its equivalent contact deformation is .
- The equivalent axial contact force is calculated. It can be calculated by the following formula [8]:
- 4.
- A check is performed to see whether the calculation precision has been met.
- If , the calculation precision is satisfied. The equivalent contact force is output as the corresponding thread tooth’s equivalent contact load.
- If , the precision is not satisfied. In this case, the equivalent contact deformation is updated by adding the iteration step size. The updated equivalent deformation is returned for recalculation in steps 2 and 3. This process is repeated until the result satisfies the calculation precision.
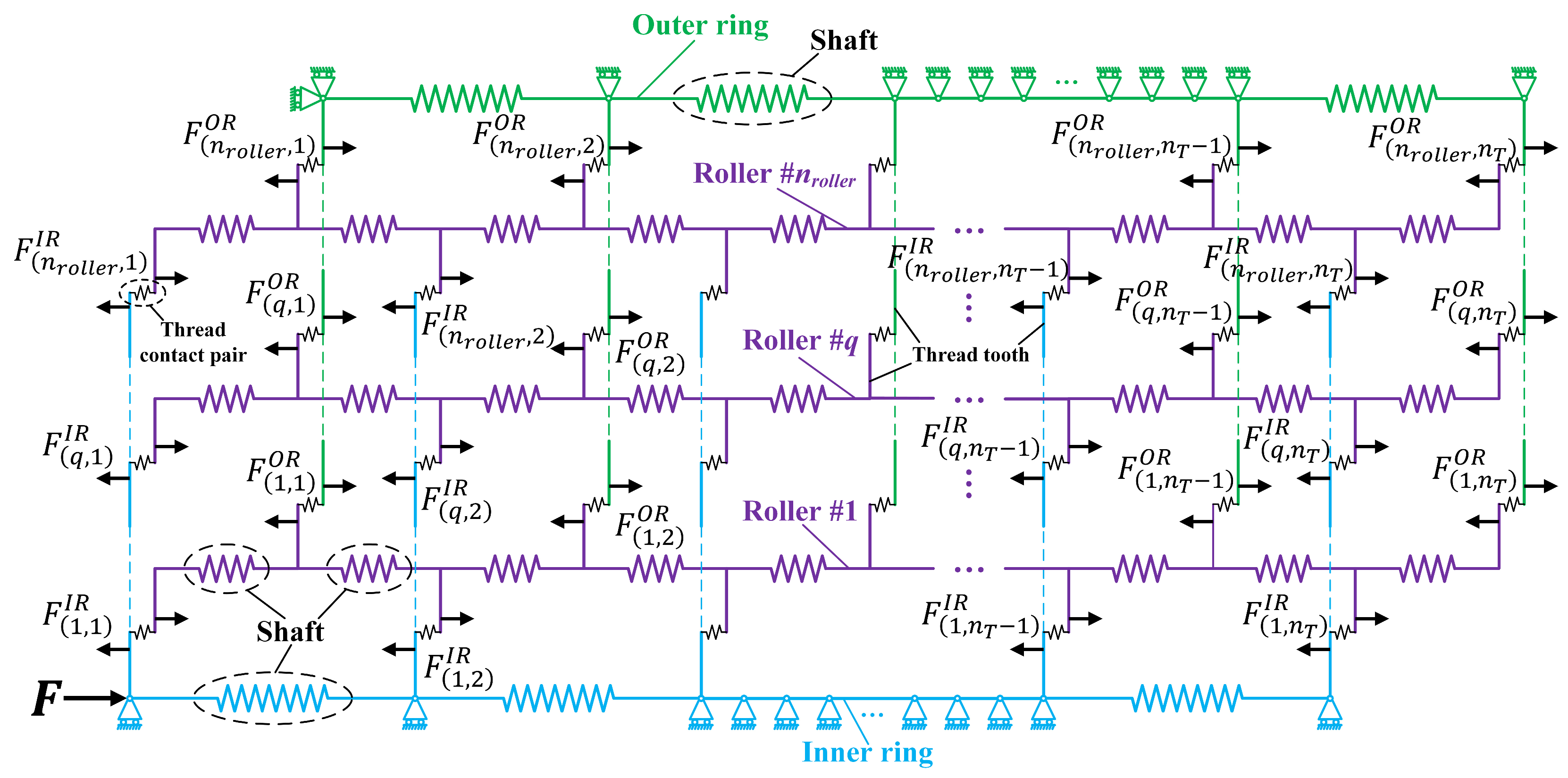
2.4. Calculation Model for PTRB Contact Load Distribution
- The external axial load is assumed to be uniformly distributed among all thread teeth, with the initial contact load on each thread tooth being .
- The initial contact load is substituted into nonlinear equations to solve for the updated contact load and obtain the updated contact stiffness of the thread teeth.
- The contact load for all thread tooth contact pairs is determined through iterative calculations, meeting the preset precision.
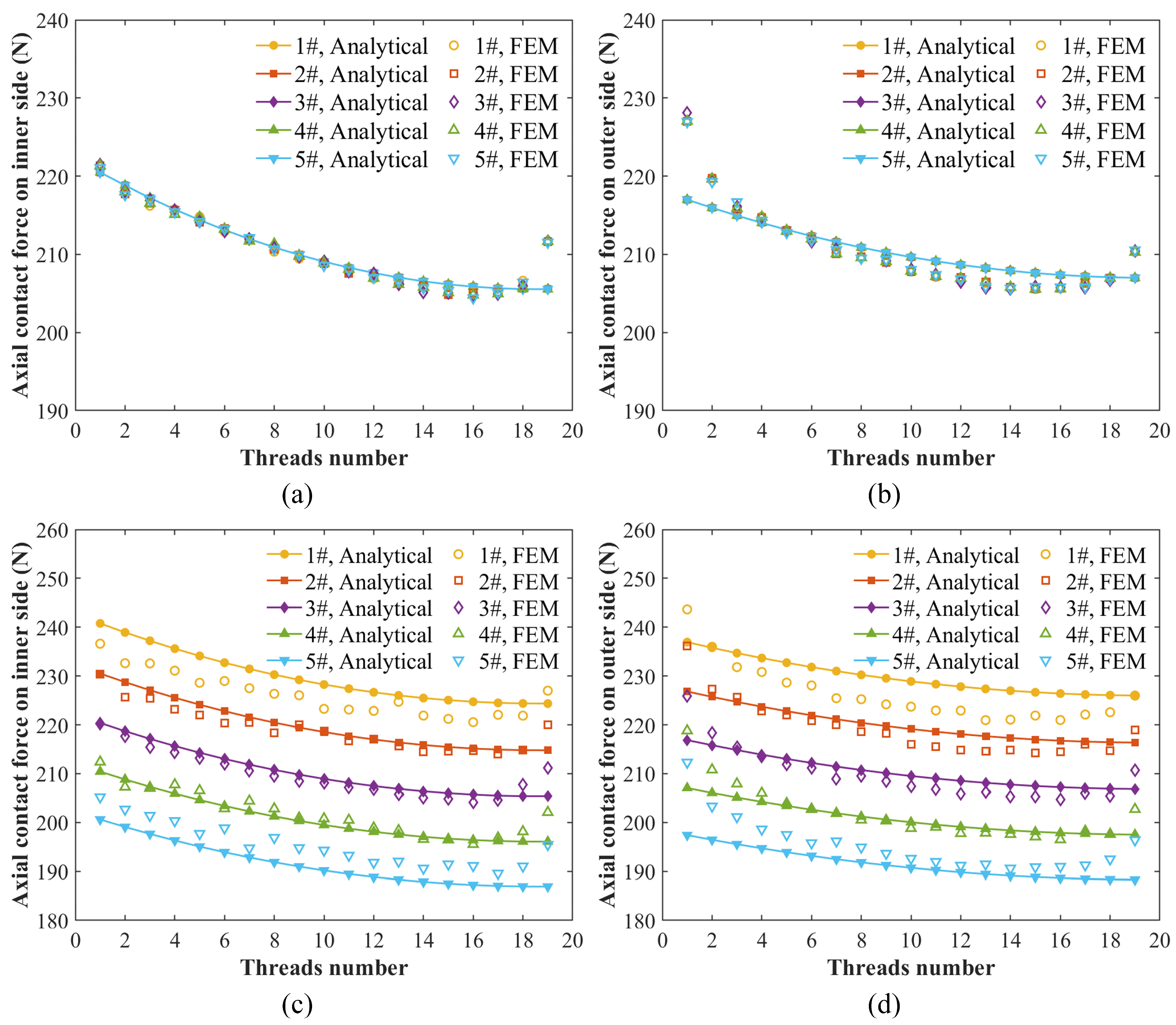
3. Model Validation
4. Results and Discussion
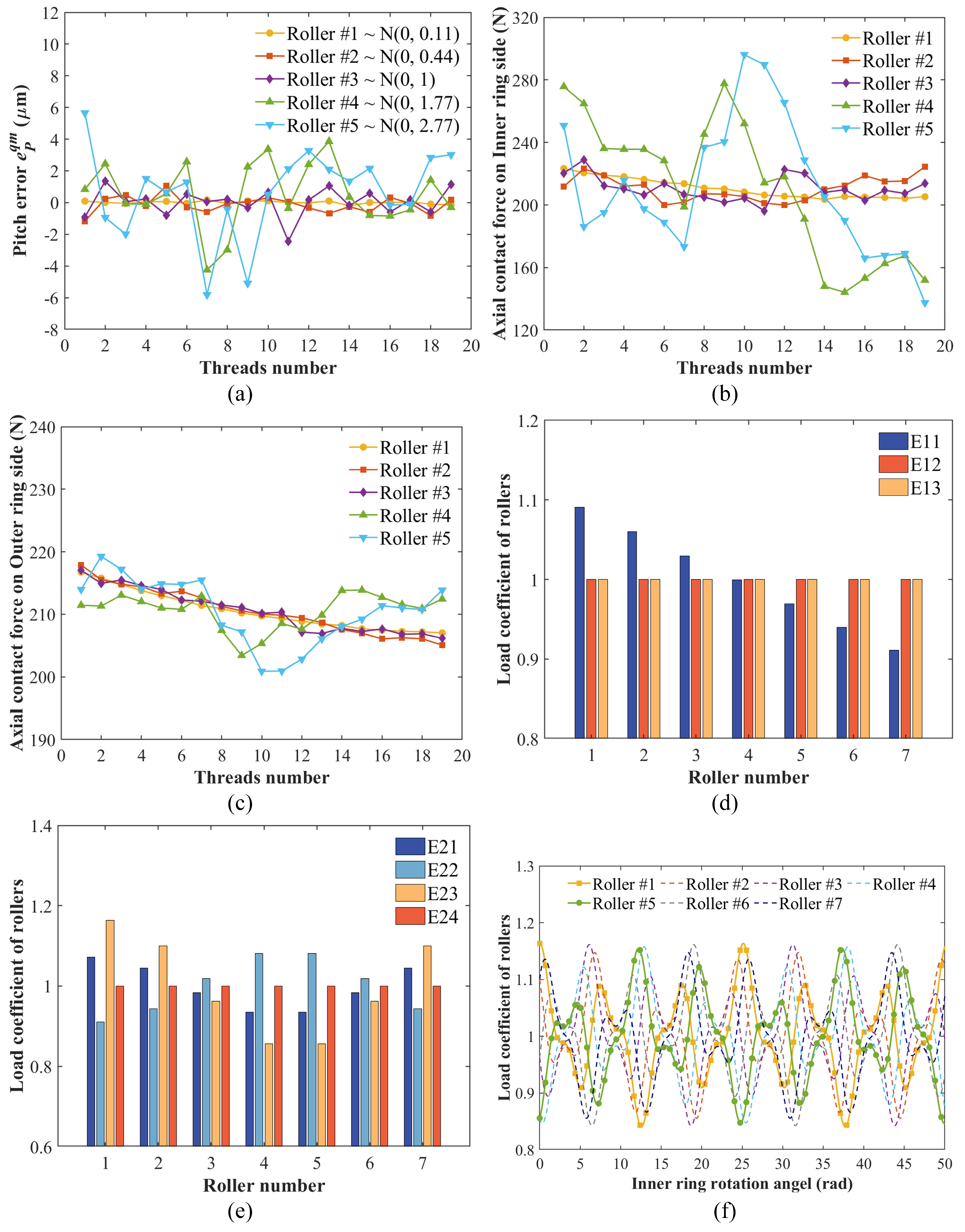
4.1. Influence of Thread Pitch Error
4.2. Influence of Nominal Diameter Error
4.3. Influence of Axis Misalignment Error
5. Conclusions
- The proposed computational model can quickly and accurately calculate the LDC among PTRB rollers and threaded teeth while considering multiple manufacturing errors. The calculation results show a less than 10% deviation compared to the finite element simulation results.
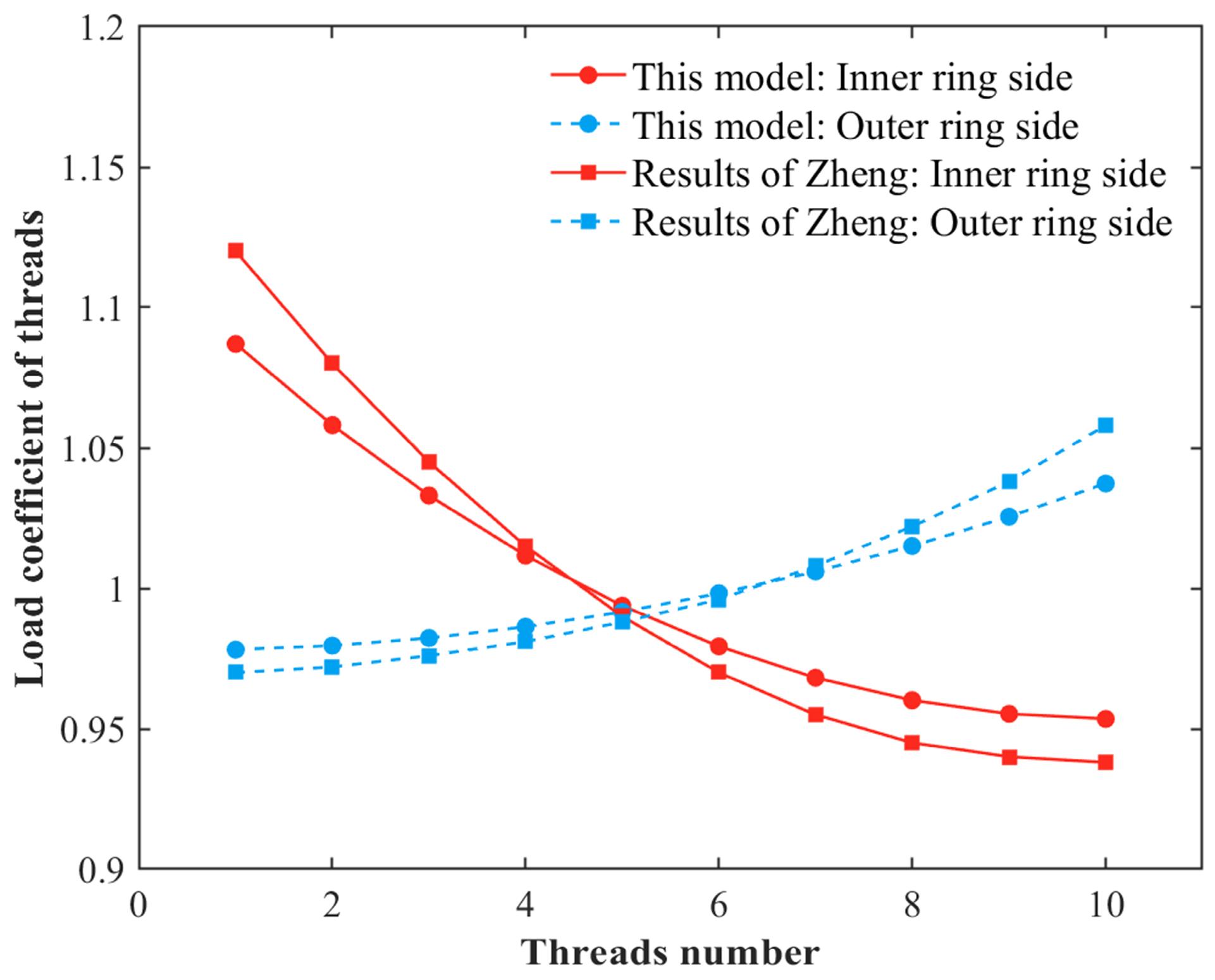
- Even though pitch errors may not significantly affect the LDC among rollers, they can cause uneven LDC among threaded teeth. Higher manufacturing precision can reduce pitch errors and improve LDC among threaded teeth. Additionally, the load variation on the inner ring-roller side is more pronounced than on the outer ring-roller side under the same pitch error conditions.
- Nominal diameter errors of the inner and outer rings do not affect the LDC among rollers. However, different nominal diameter errors among rollers cause load redistribution. Rollers with smaller negative nominal diameter errors bear greater loads, making them more prone to wear. Therefore, selecting rollers with consistent nominal diameters during assembly can improve the service life of PTRB.
- Compared to nominal diameter errors, the inner and outer ring axial errors result in a more uneven LDC among rollers. The load on the most heavily loaded roller in this study’s PTRB was approximately 1.36 times that of the least loaded roller. Additionally, PTRBs with axial errors exhibited complex load distribution in practical applications. The LDC of each roller periodically fluctuates with the inner ring’s rotation. Therefore, attention should be paid to PTRB axial errors during design and manufacturing processes.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Meng, F.N.; Wang, L.J.; Li, H.; Du, W.L.; Gong, X.Y.; Wu, C.J.; Luo, S.Q. Reliability evaluation of rolling bearings based on generative adversarial network sample enhancement and maximum entropy method. Sci. Rep. 2024, 14, 31185. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Q.; Liu, Y.H.; Du, W.T.; Jiang, L.B.; Yu, W.N. Dynamic characteristic analysis of a gear-rotor-bearing coupling system considering bearing fit. Nonlinear Dyn. 2024, 113, 2131–2154. [Google Scholar] [CrossRef]
- Zheng, S.C.; Fu, Y.L.; Wang, D.Y.; Liu, Z.Y.; Pan, J.L.; Chen, J. Effect of structural parameters and load states on PTRB’s load distribution. Adv. Mech. Eng. 2023, 15, 16878132231161004. [Google Scholar] [CrossRef]
- Du, Z.; Zhang, X.L.; Tao, T. Study of the dynamic characteristics of ball screw with a load disturbance. Math. Probl. Eng. 2016, 2016, 8208241. [Google Scholar] [CrossRef]
- Zhen, N.; An, Q. Analysis of stress and fatigue life of ball screw with considering the dimension errors of balls. Int. J. Mech. Sci. 2018, 137, 68–76. [Google Scholar] [CrossRef]
- Wei, C.C.; Lai, R.S. Kinematical analyses and transmission efficiency of a preloaded ball screw operating at high rotational speeds. Mech. Mach. Theory 2011, 46, 880–898. [Google Scholar] [CrossRef]
- Zhou, H.X.; Zhou, C.G.; Ou, Y.; Chen, Z.T. Recalculation of the basic static load of ball screws. Adv. Mech. Eng. 2019, 11, 168781401986269. [Google Scholar] [CrossRef]
- Du, X.; Chen, B.K.; Zheng, Z.D. Investigation on mechanical behavior of planetary roller screw mechanism with the effects of external loads and machining errors. Tribol. Int. 2021, 154, 106689. [Google Scholar] [CrossRef]
- Hu, R.; Wei, P.T.; Liu, H.J.; Du, X.S.; Zhou, P.L.; Zhu, C.C. Investigation on load distribution among rollers of planetary roller screw mechanism considering machining errors: Analytical calculation and machine learning approach. Mech. Mach. Theory 2023, 185, 105322. [Google Scholar] [CrossRef]
- Liu, J. A dynamic modelling method of a rotor-roller bearing-housing system with a localized fault including the additional excitation zone. J. Sound Vib. 2020, 469, 115144. [Google Scholar] [CrossRef]
- Ryś, J.; Lisowski, F. The computational model of the load distribution between elements in a planetary roller screw. J. Theor. Appl. Mech. 2014, 52, 699–705. [Google Scholar]
- Abevi, F.; Daidie, A.; Chaussumier, M.; Sartor, M. Static load distribution and axial stiffness in a planetary roller screw mechanism. J. Mech. Des. 2016, 138, 012301. [Google Scholar] [CrossRef]
- Jones, M.H.; Velinsky, S.A. Stiffness of the roller screw mechanism by the direct method. Mech. Based Des. Struct. Mach. 2014, 42, 17–34. [Google Scholar] [CrossRef]
- Zhang, W.J.; Liu, G.; Tong, R.T.; Ma, S.J. Load distribution of planetary roller screw mechanism and its improvement approach. Proc. Inst. Mech. Eng. C J. Mec. Eng. Sci. 2016, 230, 3304–3318. [Google Scholar] [CrossRef]
- Zhang, W.J.; Liu, G.; Ma, S.J.; Tong, R.T. Load distribution over threads of planetary roller screw mechanism with pitch deviation. Proc. Inst. Mech. Eng. C J. Mec. Eng. Sci. 2019, 233, 4653–4666. [Google Scholar] [CrossRef]
- Fu, X.J.; Li, X.; Ma, S.J.; Gerada, D.; Liu, G.; Gerada, C. A multi-roller static model of the planetary roller screw mechanism considering load sharing. Tribol. Int. 2022, 173, 107648. [Google Scholar] [CrossRef]
- Zheng, S.C.; Fu, Y.L.; Wang, D.Y.; Pan, J.L.; Liu, Z.Y.; Chen, J. Characteristics analysis and optimization of the structural parameters of PTRB. Machines 2022, 10, 1051. [Google Scholar] [CrossRef]
- Ni, J.N.; Yin, J.H.; Li, D.D.; Liu, J.Q.; Xie, Z.J. Modeling of contact load distribution of planetary threaded roller bearing based on deformation coordination. Mech. Based Des. Struct. Mach. 2021, 51, 5856–5877. [Google Scholar] [CrossRef]
- Xie, Z.J.; Wang, Y.; Zhan, H.; Xie, W.J.; Deng, J.X.; Yu, D.; Yin, J.H. Calculation model of contact load and axial stiffness of planetary thread roller bearing based on direct stiffness method. Adv. Theory Simul. 2023, 6, 2300126. [Google Scholar] [CrossRef]
- Zheng, S.C.; Fu, Y.L.; Pan, J.L.; Li, L.J.; Wang, D.Y. An in-depth study on load distribution characteristics of the planetary threaded roller bearing. Math. Probl. Eng. 2020, 2020, 9593051. [Google Scholar] [CrossRef]
- Qiao, G.; Liu, G.; Shi, Z.H.; Wang, Y.W.; Ma, S.J.; Lim, T.C. A review of electromechanical actuators for More/All Electric aircraft systems. Proc. Inst. Mech. Eng. C J. Mec. Eng. Sci. 2018, 232, 4128–4151. [Google Scholar] [CrossRef]
- Sandu, S.; Biboulet, N.; Nelias, D.; Abevi, F. An efficient method for analyzing the roller screw thread geometry. Mech. Mach. Theory 2018, 126, 243–264. [Google Scholar] [CrossRef]
- Litvin, F.L.; Fuentes, A. Gear Geometry and Applied Theory; Cambridge University Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Fu, X.J.; Liu, G.; Ma, S.J.; Tong, R.T.; Lim, T.C. A comprehensive contact analysis of planetary roller screw mechanism. J. Mech. Des. 2017, 139, 012302. [Google Scholar] [CrossRef]
- Yamamoto, S. Theory and Calculation of Screw Thread Connection; Shanghai Scientific and Technical Press: Shanghai, China, 1984. [Google Scholar]
- Ma, S.J.; Wu, L.P.; Liu, G.; Fu, X.J. Local contact characteristics of threaded surfaces in a planetary roller screw mechanism. Mech. Based Des. Struct. Mach. 2019, 48, 1–26. [Google Scholar] [CrossRef]
- Yao, Q.; Zhang, M.C.; Liu, G.; Ma, S.J. Multi-objective optimization of planetary roller screw mechanism based on improved mathematical modelling. Tribol. Int. 2021, 161, 107095. [Google Scholar] [CrossRef]
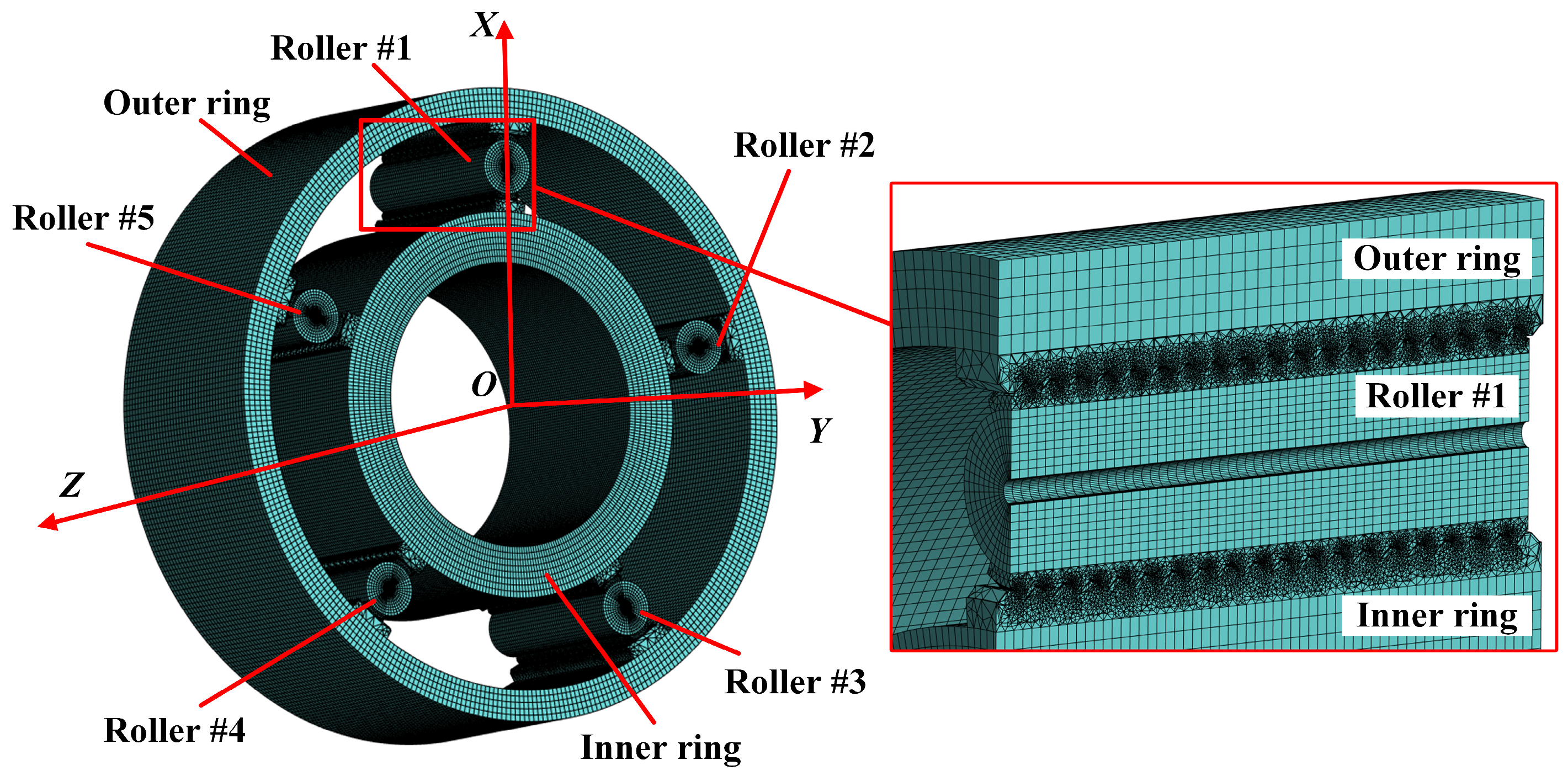
| Parameters | Symbols | Inner Ring | Roller | Outer Ring |
|---|---|---|---|---|
| Nominal diameter | /mm | 189 | 31.5 | 252 |
| Major diameter | /mm | 190.25 | 32.75 | 253.75 |
| Minor diameter | /mm | 187.25 | 29.75 | 250.75 |
| Pitch | /mm | 5 | 5 | 5 |
| Flank angel | /mm | 45 | 45 | 45 |
| Outer ring external diameter | /mm | ― | ― | 292 |
| Inner ring internal diameter | /mm | 131 | ― | ― |
| Roller profile radius | /mm | ― | 22.274 | ― |
| Number of rollers | ― | 11 | ― | |
| Number of threads | 19 | 19 | 19 |
| No. | Nominal Diameter Error (μm) |
|---|---|
| E11 | = [−10, −15, −20, −25, −30, −40] |
| E12 | = −20 |
| E13 | = 20 |
| No. | Eccentricity Error of Inner Ring | Eccentricity Error of Outer Ring |
|---|---|---|
| E21 | = [12 μm, 0, 0] | = [0, 0, 0] |
| E22 | = [0, 0, 0] | = [15 μm, 0, 0] |
| E23 | = [12 μm, 0, 0] | = [−15 μm, 0, 0] |
| E24 | = [12 μm, 0, 0] | = [12 μm, 0, 0] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Z.; Li, M.; Hou, Y.; Wang, Z.; Zhang, K. Calculation Model for Multi-Roller Load Distribution of Planetary Threaded Roller Bearings Considering Machining Errors. Machines 2025, 13, 26. https://doi.org/10.3390/machines13010026
Xie Z, Li M, Hou Y, Wang Z, Zhang K. Calculation Model for Multi-Roller Load Distribution of Planetary Threaded Roller Bearings Considering Machining Errors. Machines. 2025; 13(1):26. https://doi.org/10.3390/machines13010026
Chicago/Turabian StyleXie, Zhijie, Mingyang Li, Yicheng Hou, Zhiwei Wang, and Kailiang Zhang. 2025. "Calculation Model for Multi-Roller Load Distribution of Planetary Threaded Roller Bearings Considering Machining Errors" Machines 13, no. 1: 26. https://doi.org/10.3390/machines13010026
APA StyleXie, Z., Li, M., Hou, Y., Wang, Z., & Zhang, K. (2025). Calculation Model for Multi-Roller Load Distribution of Planetary Threaded Roller Bearings Considering Machining Errors. Machines, 13(1), 26. https://doi.org/10.3390/machines13010026







