Fast Load Distribution Calculation for Cylindrical Gears with Non-Involute Tooth Profiles
Abstract
1. Introduction and State of the Art
2. Methods
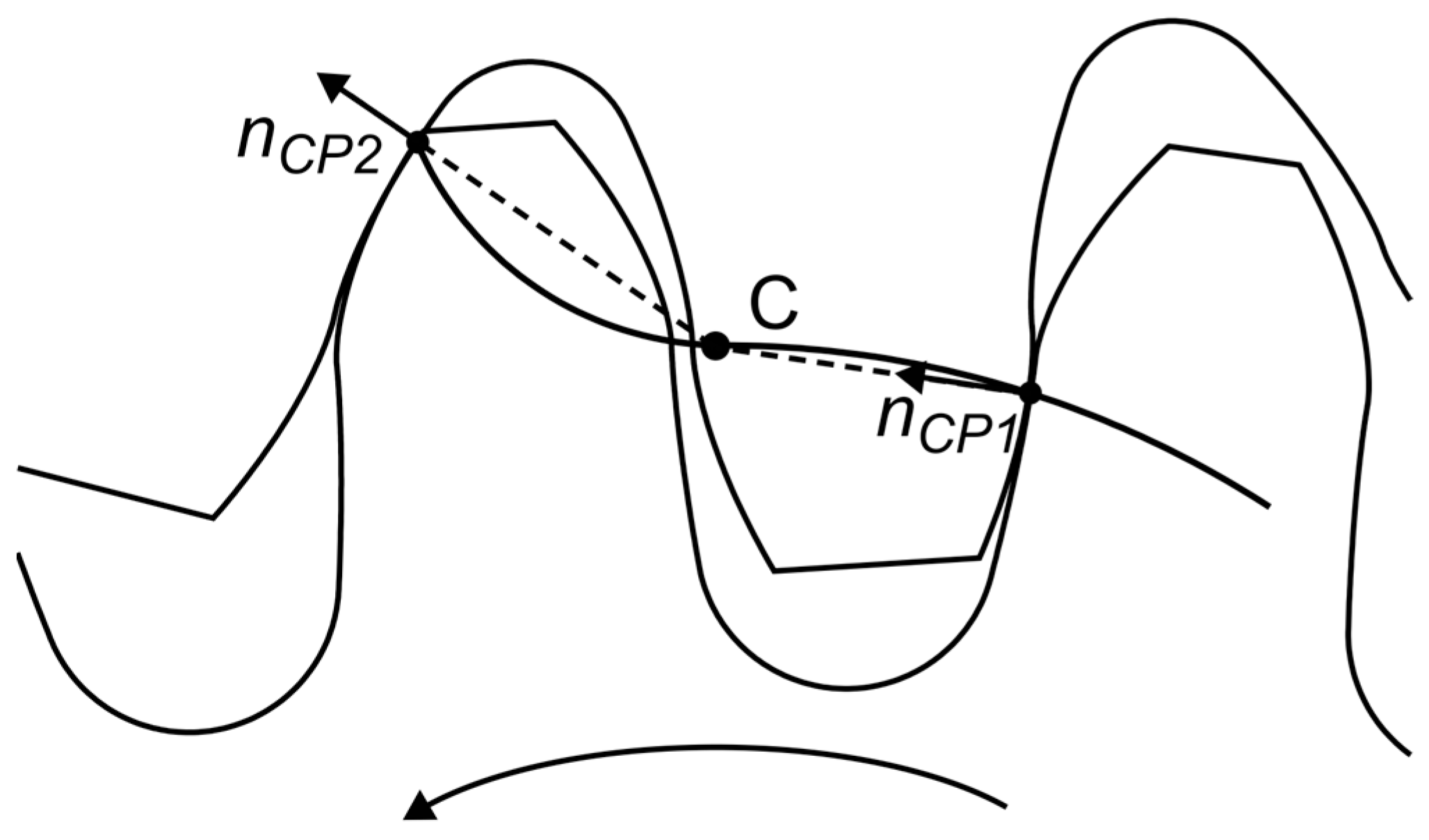
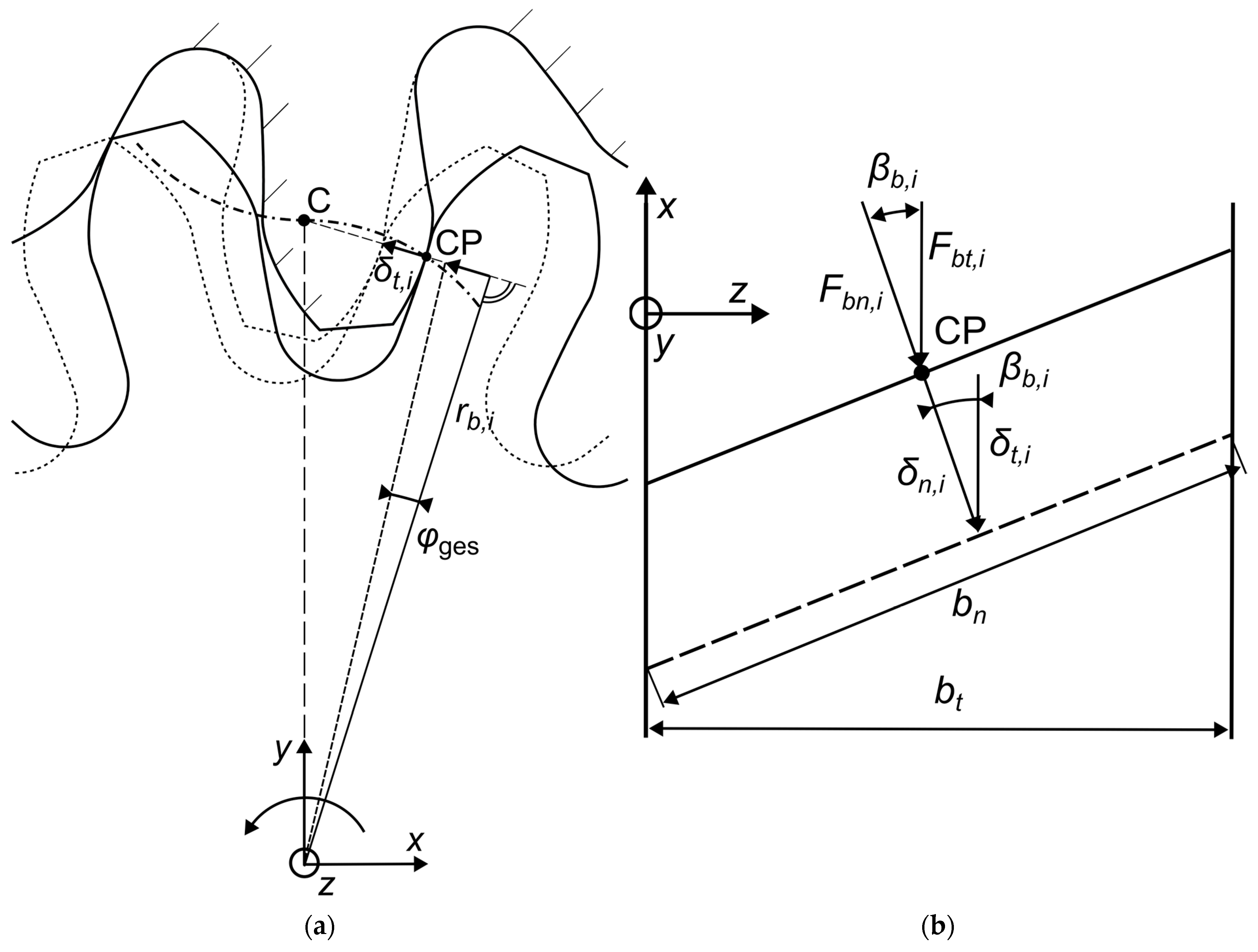
2.1. Generalized Analytical Load Distribution Calculation
2.2. Planar Normal Cross-Section of the Tooth Profile for the Analytical Tooth Stiffness Calculation
3. Results and Discussion
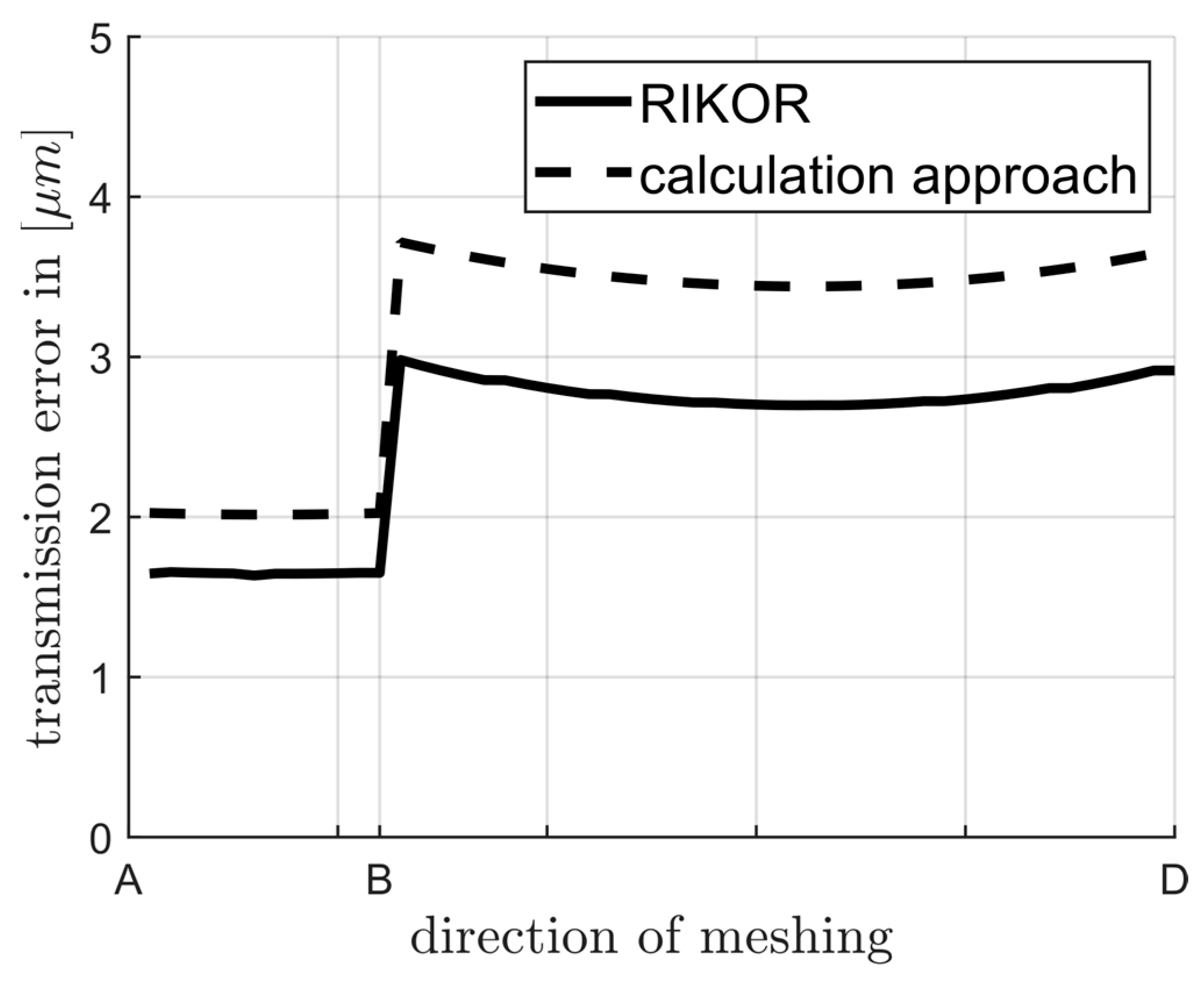
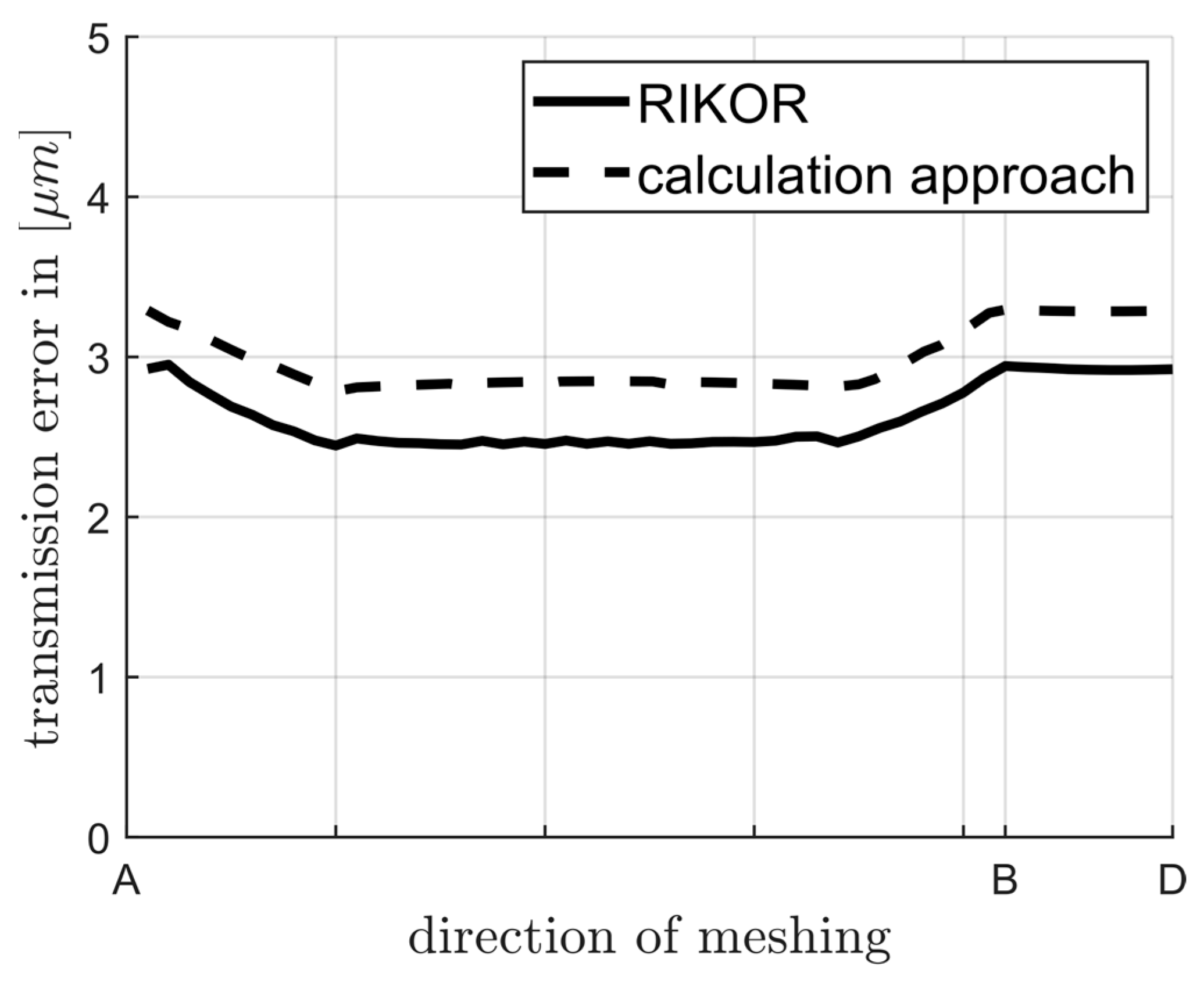
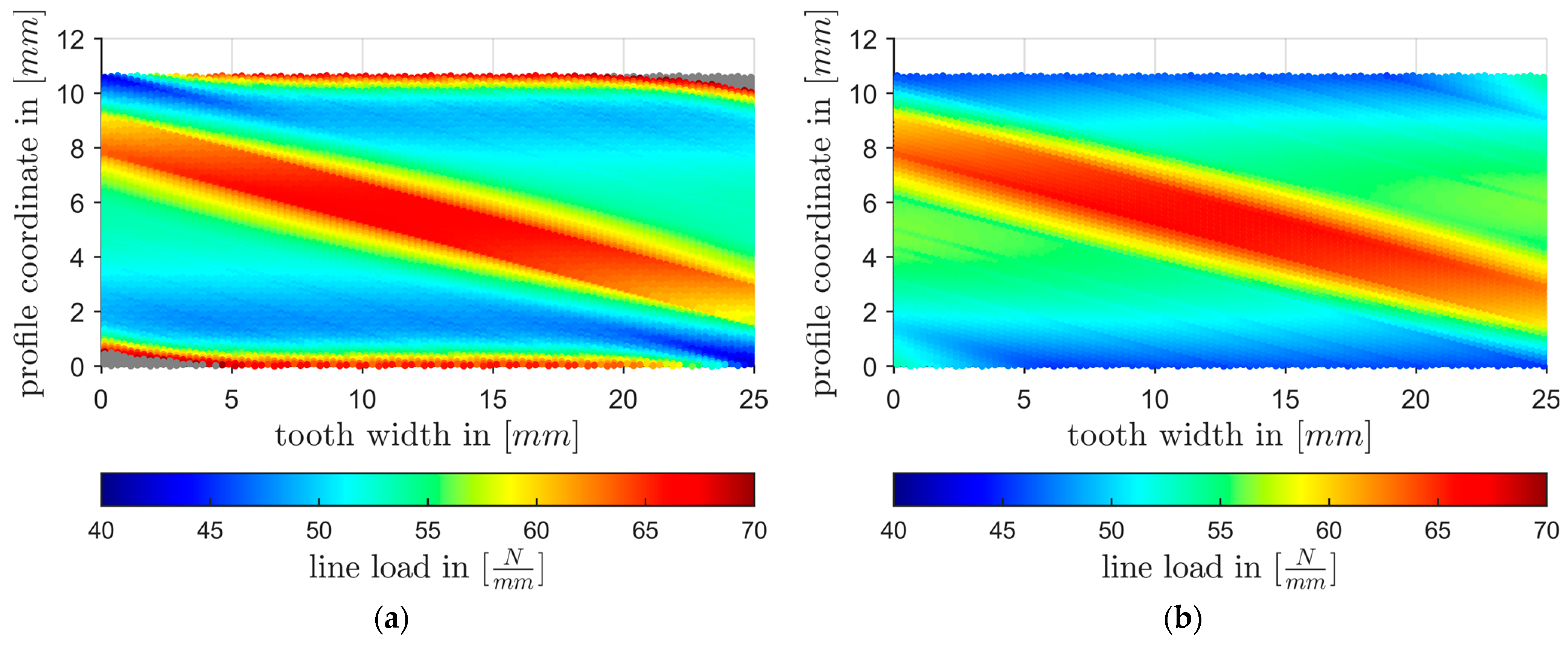
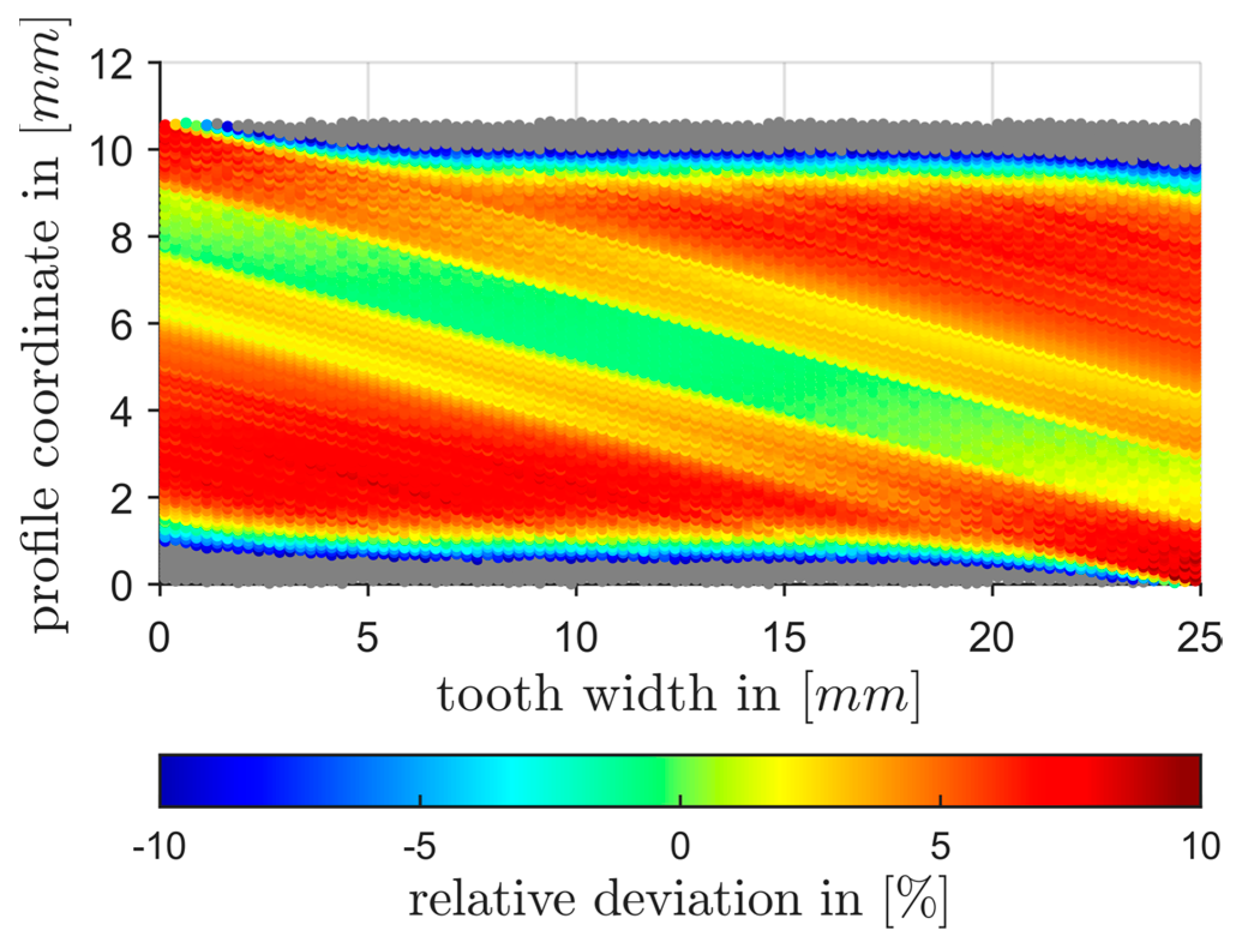
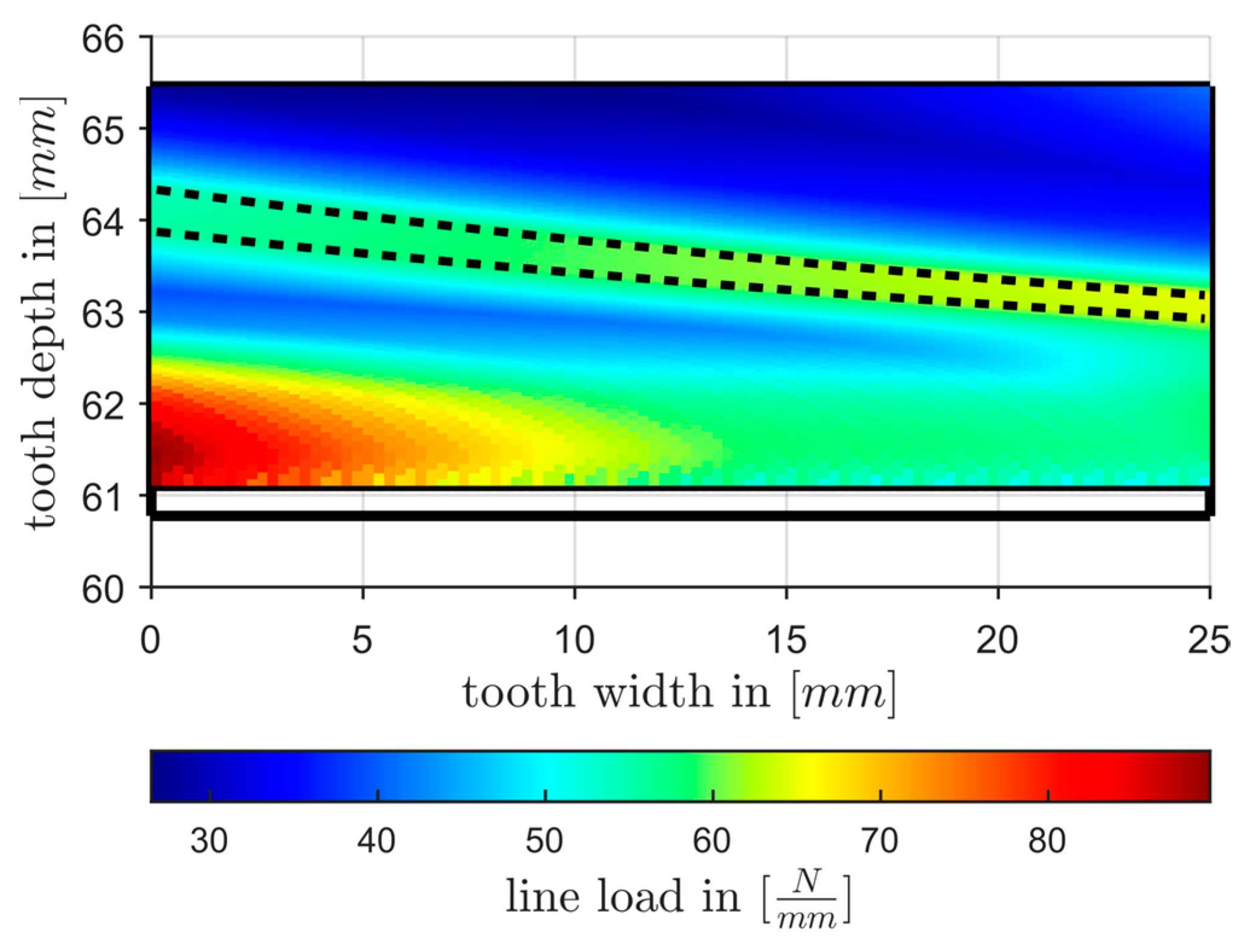
3.1. Comparative Calculation with RIKOR
3.1.1. Comparison for an Exemplary Spur Gear (Gearing No. 1)
3.1.2. Comparison for an Exemplary Helix Gear (Gearing No. 2)
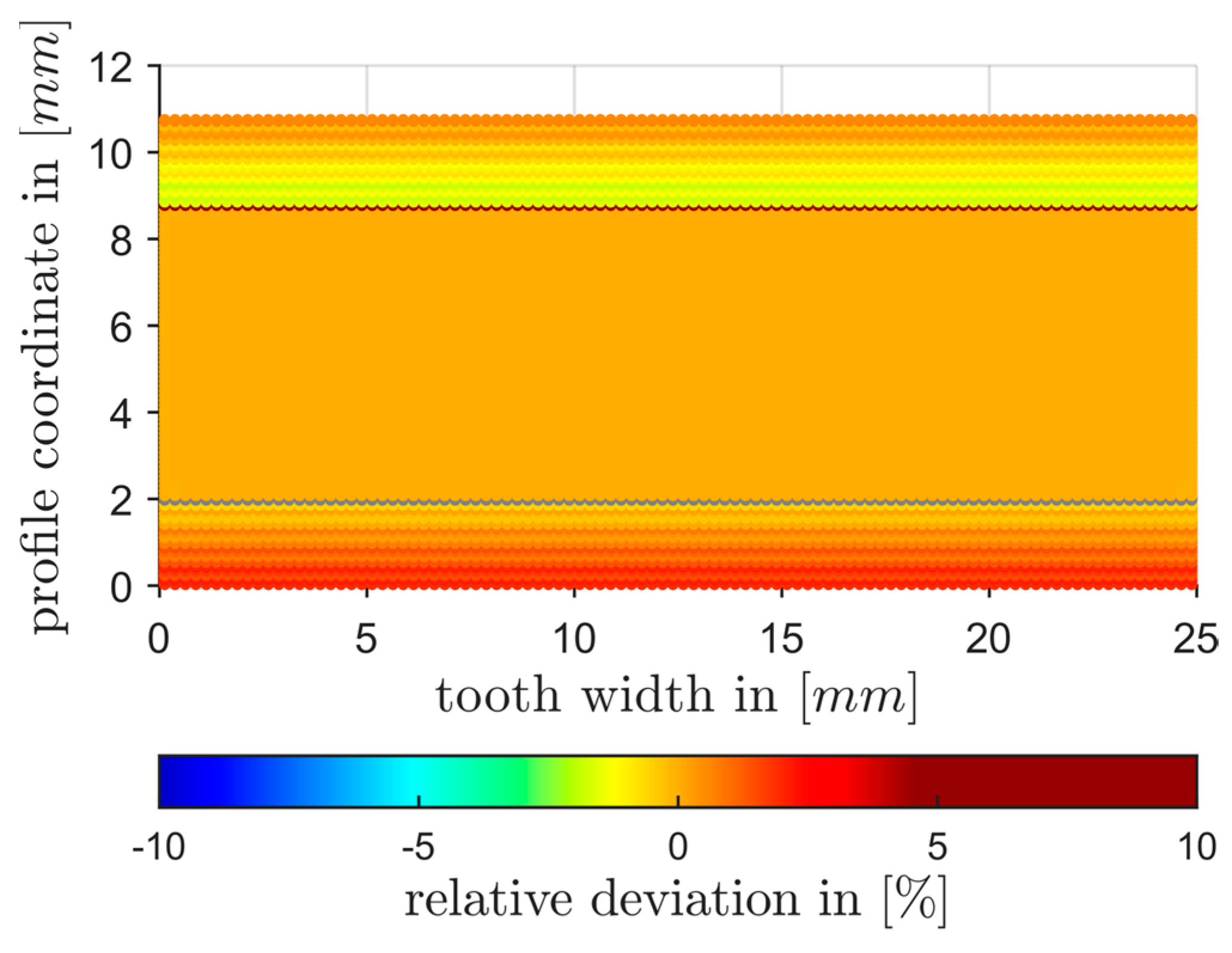
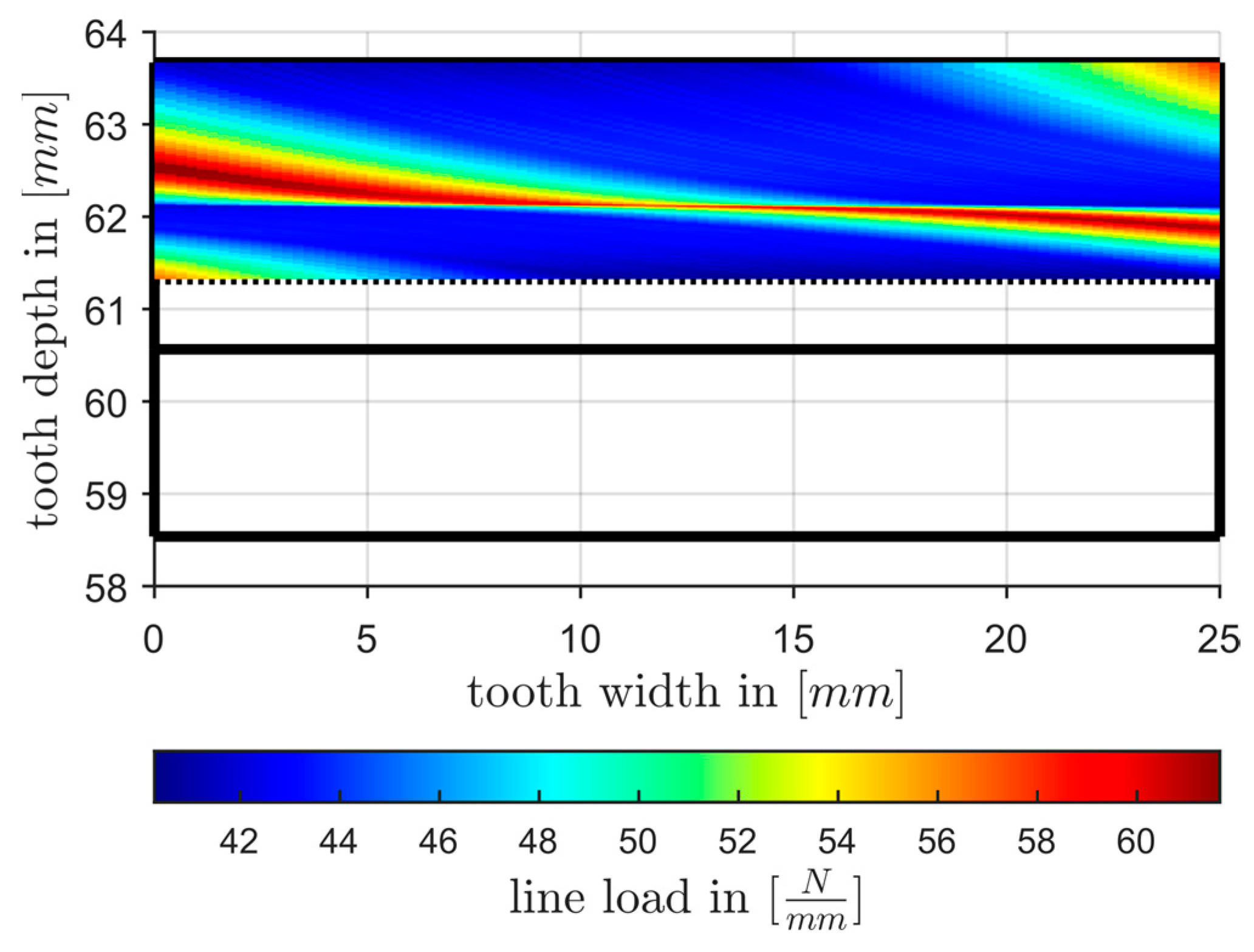
3.2. Application of the Presented Calculation Approach to Non-Involute Tooth Profiles
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | |||||
| A | Starting point of meshing | Center distance | B | Starting point of single-flank engagement | |
| Face width | C | Pitch point | CP | Contact point | |
| Stiffness | Tip clearance factor | D | Ending point of single-flank engagement | ||
| Diameter | Young’s modulus | Force on a finite gear slice | |||
| Normal module | Normal vector | Line load | |||
| Radius | Arc radius factor | Tooth thickness | |||
| Tooth thickness factor | Torque | Profile shift coefficient, X-coordinate | |||
| Y-coordinate | Number of teeth, Z-coordinate | ||||
| Greek symbols | |||||
| Pressure angle | Helix angle | Relative deviation | |||
| Local deflection at a point on the tooth flank | Local flank modification in the normal direction at a point on the tooth flank | Pitch circle of the hypocycloid | |||
| Pitch circle of the epicycloid | Total deflection in the plane of action | Total contact ratio | |||
| Trochoid ratio | Poisson’s ratio | Starting angle of arc profile | |||
| Ending angle of arc profile | Transmission error | Backlash angle | |||
| Indices | |||||
| Pinion gear | Mating gear | Base circle | |||
| Contact point | Calculation approach | Active tip | |||
| Active root | Normal | RIKOR | |||
| Transverse | Y-cylinder | ||||
References
- ISO 6336-1:2019-11; Calculation of Load Capacity of Spur and Helical Gears—Part 1: Basic Principles, Introduction and General Influence Factors. ISO: Geneva, Switzerland, 2019.
- Weber, C.; Banaschek, K. Formänderung und Profilrücknahme bei Gerad- und Schrägverzahnten Rädern; Schriftreihe Antriebstechnik vol. 11; Vieweg-Verlag: Braunschweig, Germany, 1953. [Google Scholar]
- Geiser, H.; Schinagl, S. Messung der Zahnsteifigkeit eines geradverzahnten Stirnrades und Vergleich mit FEM und Berechnungen nach Weber/Banaschek. FZG Bericht 1996, Nr. 2064, 1–52. [Google Scholar]
- Lutz, M. Methoden zur rechnerischen Ermittlung und Optimierung von Tragbildern an Schneckengetrieben. Ph.D. Dissertation, Technical University of Munich, Munich, Germany, 2000. [Google Scholar]
- Hochrein, J.-F.; Otto, M.; Stahl, K. Fast tooth deflection calculation method and its validation. Forsch. Im Ingenieurwesen 2022, 86, 854–859. [Google Scholar] [CrossRef]
- DIN 3990-1:1987-12; Tragfähigkeitsberechnung von Stirnrädern—Einführung und allgemeine Einflußfaktoren. DIN: Berlin, Germany, 1987.
- Niemann, G.; Winter, H. Maschinenelemente: Band 2: Getriebe allgemein, Zahnradgetriebe—Grundlagen, Stirnradgetriebe, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2003; ISBN 978-3-662-11874-0. [Google Scholar]
- Schmidt, G. Berechnung der Wälzpressung Schrägverzahnter Stirnräder unter Berücksichtigung der Lastverteilung. Ph.D. Dissertation, Technical University of Munich, Munich, Germany, 1972. [Google Scholar]
- Kunert, J.; Trempler, U.; Wikidal, F.; Senf, M.; Oster, P.; Linke, H.; Höhn, B.-R. FVA-Nr. 224/I+II—Heft 458—Lastverteilungsmessung: Weiterentwicklung der Grundlagen zur Ermittlung der Lastaufteilung und Lastverteilung bei Außenverzahnten Gerad- und Schrägstirnrädern durch Verformungs- und Spannungsmessung; Forschungsvereinigung Antriebstechnik e.V.: Frankfurt, Germany, 1995. [Google Scholar]
- Schaefer, S. Verformungen und Spannungen von Kegelradverzahnungen Effizient Berechnet. Ph.D. Dissertation, Technische Universität Dresden, Dresden, Germany, 2018. [Google Scholar]
- Wu, S.-H.; Tsai, S.-J. Contact stress analysis of skew conical involute gear drives in approximate line contact. Mech. Mach. Theory 2009, 9, 1658–1676. [Google Scholar] [CrossRef]
- Marafona, J.D.; Marques, P.M.; Martins, R.C.; Seabra, J.H. Mesh stiffness models for cylindrical gears: A detailed review. Mech. Mach. Theory 2021, 166, 104472. [Google Scholar] [CrossRef]
- Natali, C.; Battarra, M.; Dalpiaz, G.; Mucchi, E. A critical review on FE-based methods for mesh stiffness estimation in spur gears. Mech. Mach. Theory 2021, 161, 104319. [Google Scholar] [CrossRef]
- Placzek, T. Lastverteilung und Flankenkorrektur in Gerad- und Schrägverzahnten Stirnradstufen. Ph.D. Dissertation, Technical University of Munich, Munich, Germany, 1988. [Google Scholar]
- Winter, H.; Placzek, T. Load Distribution and Topological Flank Modification of Helical and Double Helical Gears. Eur. J. 1991, 36, 171–176. [Google Scholar]
- Weinberger, U.; Otto, M.K.; Stahl, K. Closed-Form Calculation of Lead Flank Modification Proposal for Spur and Helical Gear Stages. J. Mech. Des. 2020, 142, 031106. [Google Scholar] [CrossRef]
- Daffner, M. Validierung von Verformungsberechnungen im System Zahnrad-Welle-Lager-Gehäuse. Ph.D. Dissertation, Technical University of Munich, Munich, Germany, 2017. [Google Scholar]
- Gu, L.; Xu, J.; Luo, S. The Design of New Cycloid Gear with Variable Cross Section and the Research of End Milling in Five-Axis Machine Tool. Manuf. Technol. 2016, 3, 497–502. [Google Scholar] [CrossRef]
- Baciu, I.; Vasilescu, A.-G.; Avram, M.; Gramescu, B.; Constantin, V.; Moraru, E. A Review of Additive Technologies Applied to Gear Transmission. In Innovations in Mechanical Engineering III. icieng 2024; Machado, J., Soares, F., Trojanowska, J., Ottaviano, E., Valášek, P., Reddy, D.M., Perondi, E.A., Basova, Y., Eds.; Springer Nature: Cham, Switzerland, 2024; pp. 44–55. ISBN 978-3-031-62684-5. [Google Scholar]
- Johann, A.; Scheurle, J. On the generation of conjugate flanks for arbitrary gear geometries. GAMM 2009, 1, 61–79. [Google Scholar] [CrossRef]
- Römhild, I.; Linke, H. FVA-Nr. T 492—Heft 436—Sonderprofile: Evolventische und Nichtevolventische Sonderverzahnungen -Studie-; Forschungsvereinigung Antriebstechnik e.V.: Frankfurt, Germany, 1994. [Google Scholar]
- Lehmann, M. Die Beschreibung der Zykloiden, ihrer Äquidistanten und Hüllkurven: Unter besonderer Berücksichtigung der Planeten-Getriebe mit Zykloiden-Kurvenscheiben. Habilitation Thesis, Technical University of Munich, Munich, Germany, 1981. [Google Scholar]
- Landler, S.; Trübswetter, M.; Otto, M.; Stahl, K. Parameter based definition of ecentric cycloid gearings. Forsch. Im Ingenieurwesen 2023, 87, 807–819. [Google Scholar] [CrossRef]
- Kazakyavichyus, S.M.; Stanovskoy, V.V.; Remneva, T.A.; Kuznetsov, V.M.; Bubenchikov, A.M.; Shcherbakov, N.R. Performance of eccentric-cycloid engagement with change in the interaxial distance: Modification of tooth configuration. Russ. Eng. Res. 2011, 3, 197–199. [Google Scholar] [CrossRef]
- Li, X.; Li, C.; Chen, B.; Liang, D. Design and investigation of a cycloid helical gear drive. J. Mech. Sci. Technol. 2017, 9, 4329–4336. [Google Scholar] [CrossRef]
- Batsch, M.; Wydrzyński, D.; Przeszłowski, Ł. Tooth Contact Analysis of Cylindrical Gears with an Unconventional Tooth Profile. Adv. Sci. Technol. Res. J. 2022, 4, 119–129. [Google Scholar] [CrossRef]
- Bubenchikov, A.M.; Kazakavitschyus, S.M.; Shcherbakov, N.R. Mathematical simulation of a profile cutter as a surface of revolution. IOP Conf. Ser. Mater. Sci. Eng. 2016, 124, 12095. [Google Scholar] [CrossRef]
- Batsch, M. Rapid Prototyping and Tooth Contact Analysis of Eccentric Cycloid Gear Mesh. J. KONBiN 2019, 1, 369–382. [Google Scholar] [CrossRef]
- Linke, H.; Börner, J.; Heß, R. Cylindrical Gears: Calculation—Materials—Manufacturing, 1st ed.; Carl Hanser Verlag: Munich, Germany, 2016; ISBN 978-1-56990-489-3. [Google Scholar]
- DIN ISO 21771:2014-08; Zahnräder—Zylinderräder und Zylinderradpaare mit Evolventenverzahnung—Begriffe und Geometrie. DIN: Berlin, Germany, 2014.
- Otto, M. Lastverteilung und Zahnradtragfähigkeit von schrägverzahnten Stirnrädern. Ph.D. Dissertation, Technical University of Munich, Munich, Germany, 2009. [Google Scholar]


| 1 | |||||||||||||
| 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fetzer, K.; Landler, S.; Berger, J.-F.; Otto, M.; Stahl, K. Fast Load Distribution Calculation for Cylindrical Gears with Non-Involute Tooth Profiles. Machines 2025, 13, 22. https://doi.org/10.3390/machines13010022
Fetzer K, Landler S, Berger J-F, Otto M, Stahl K. Fast Load Distribution Calculation for Cylindrical Gears with Non-Involute Tooth Profiles. Machines. 2025; 13(1):22. https://doi.org/10.3390/machines13010022
Chicago/Turabian StyleFetzer, Karsten, Stefan Landler, Jonas-Frederick Berger, Michael Otto, and Karsten Stahl. 2025. "Fast Load Distribution Calculation for Cylindrical Gears with Non-Involute Tooth Profiles" Machines 13, no. 1: 22. https://doi.org/10.3390/machines13010022
APA StyleFetzer, K., Landler, S., Berger, J.-F., Otto, M., & Stahl, K. (2025). Fast Load Distribution Calculation for Cylindrical Gears with Non-Involute Tooth Profiles. Machines, 13(1), 22. https://doi.org/10.3390/machines13010022







