Thermal–Electrical–Mechanical Coupled Finite Element Models for Battery Electric Vehicle
Abstract
1. Introduction
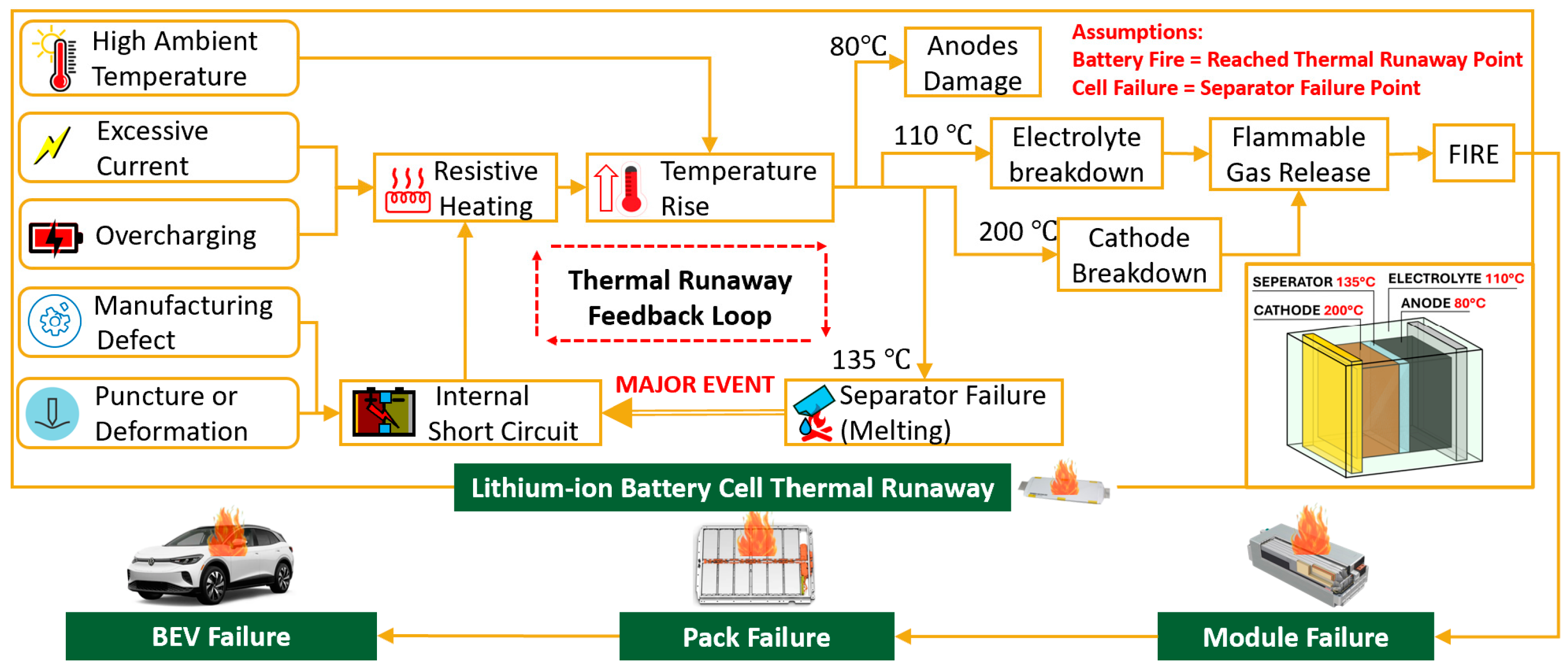
1.1. Lithium-Ion Battery Thermal Runaway Process
1.2. Selection of Battery Simulation Techniques
1.3. Full Vehicle Finite Element Models for Crash Analysis
2. Methodology and Results
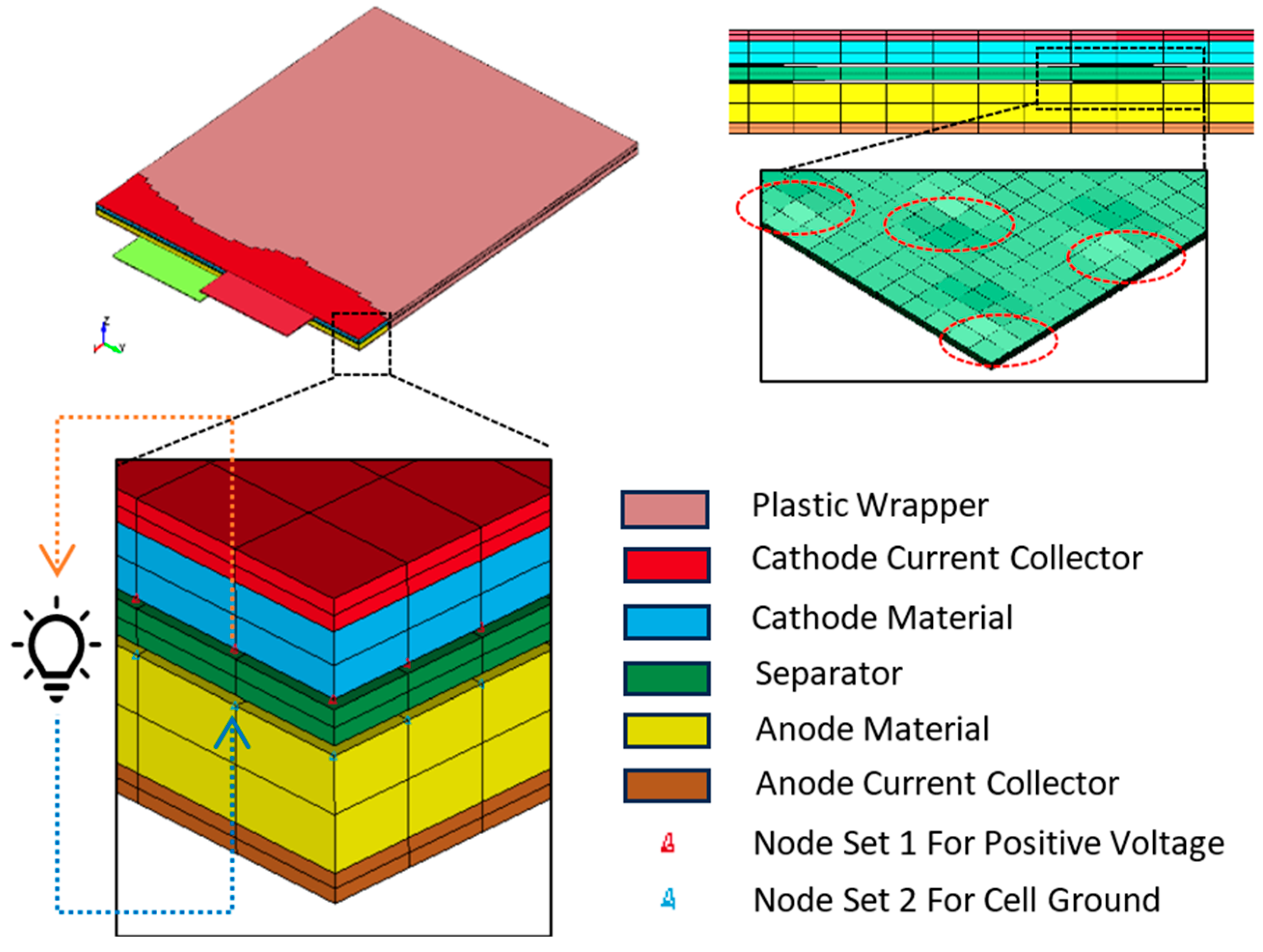
- A. Single-Cell Model
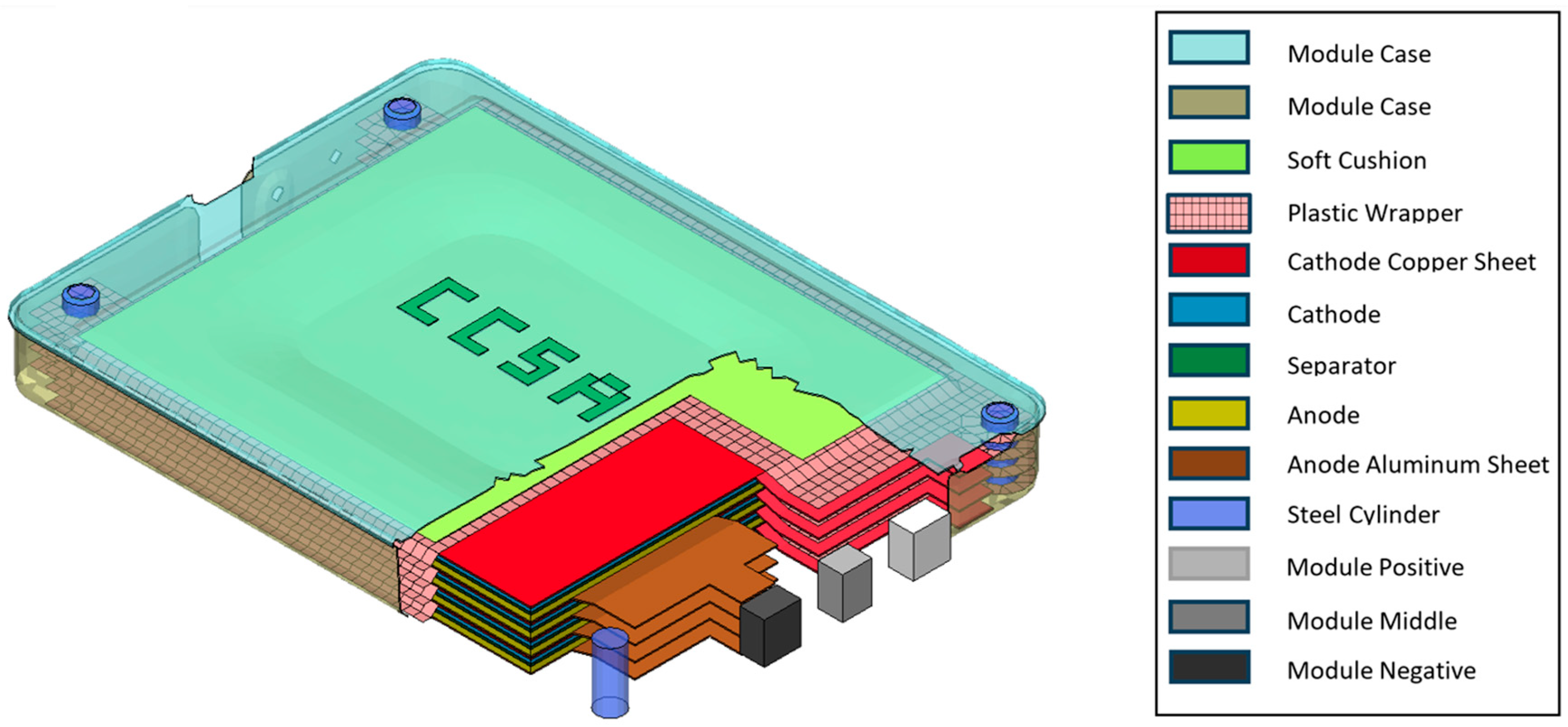
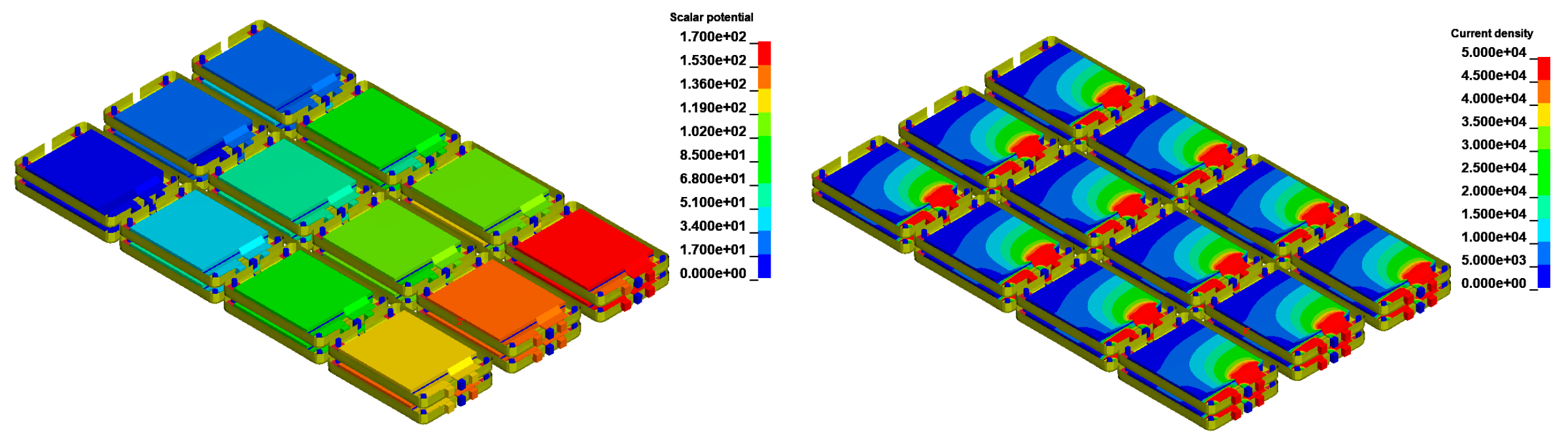
- B. Battery Module Models
- (1)
- Electric Verification
- (2)
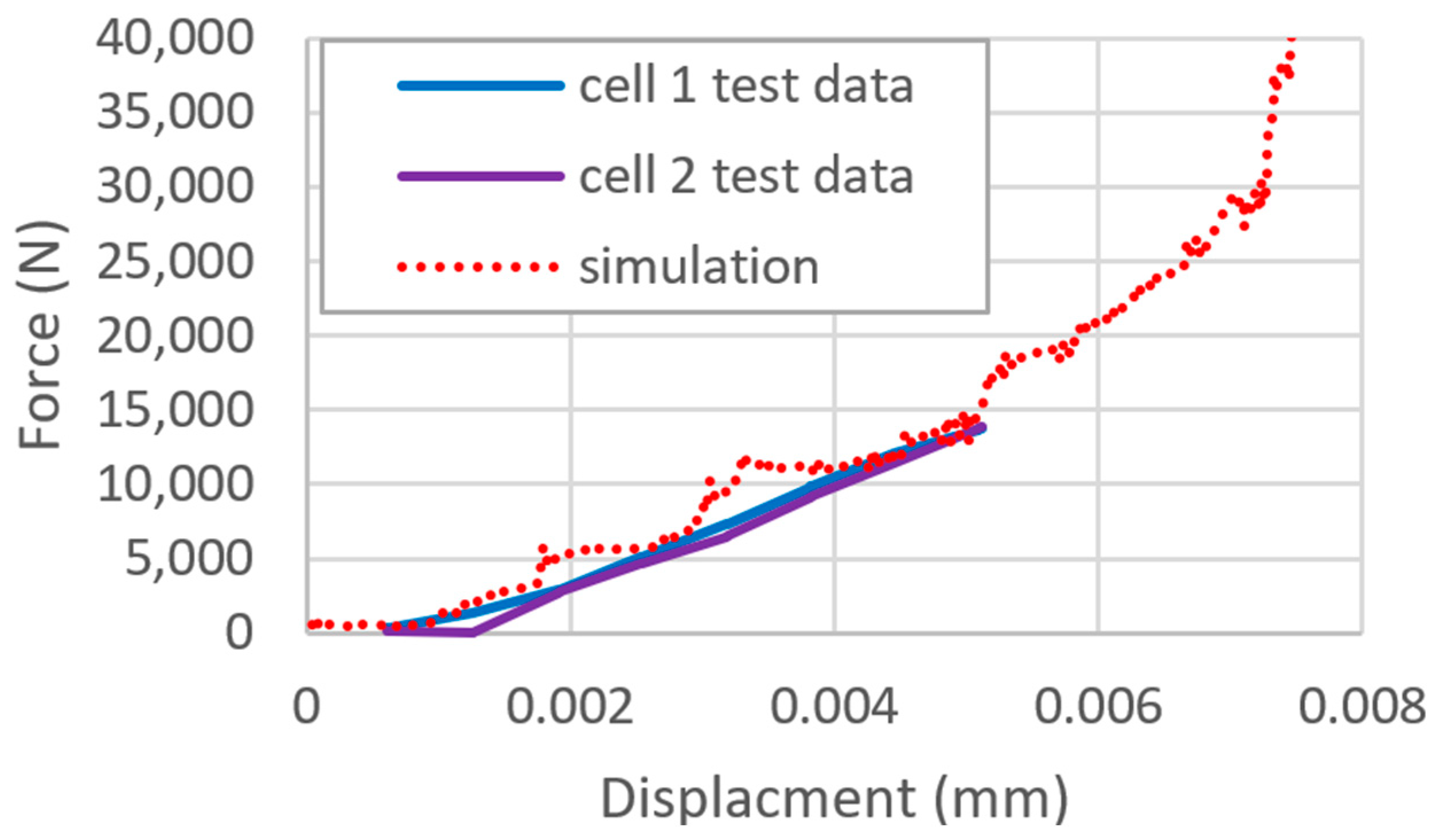
- Mechanical Verification
- (3)
- Thermal Verification
- (4)
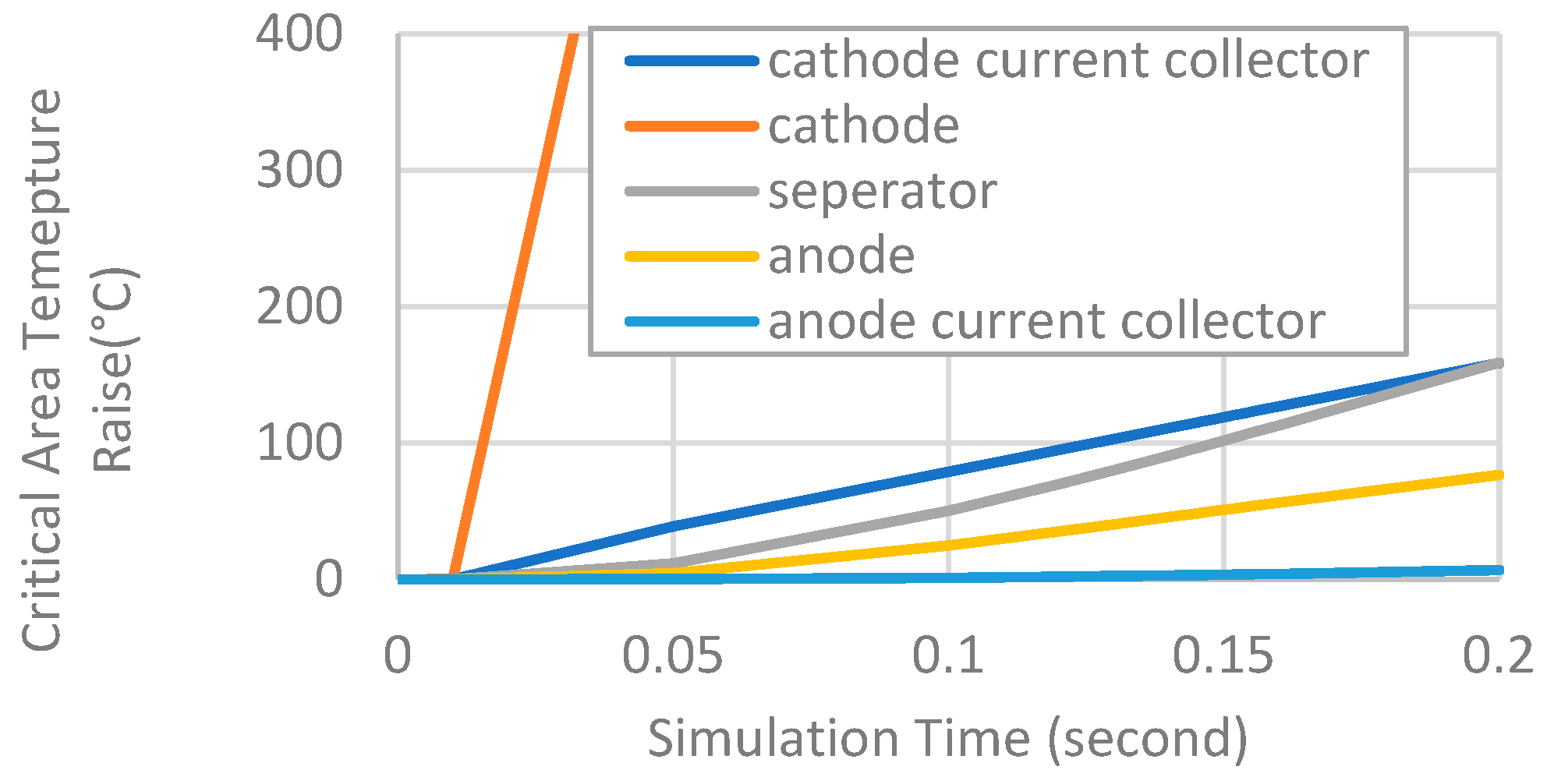
- Thermal–Mechanical–Electrical Verification
- (5)
- Coarse Battery Module Model
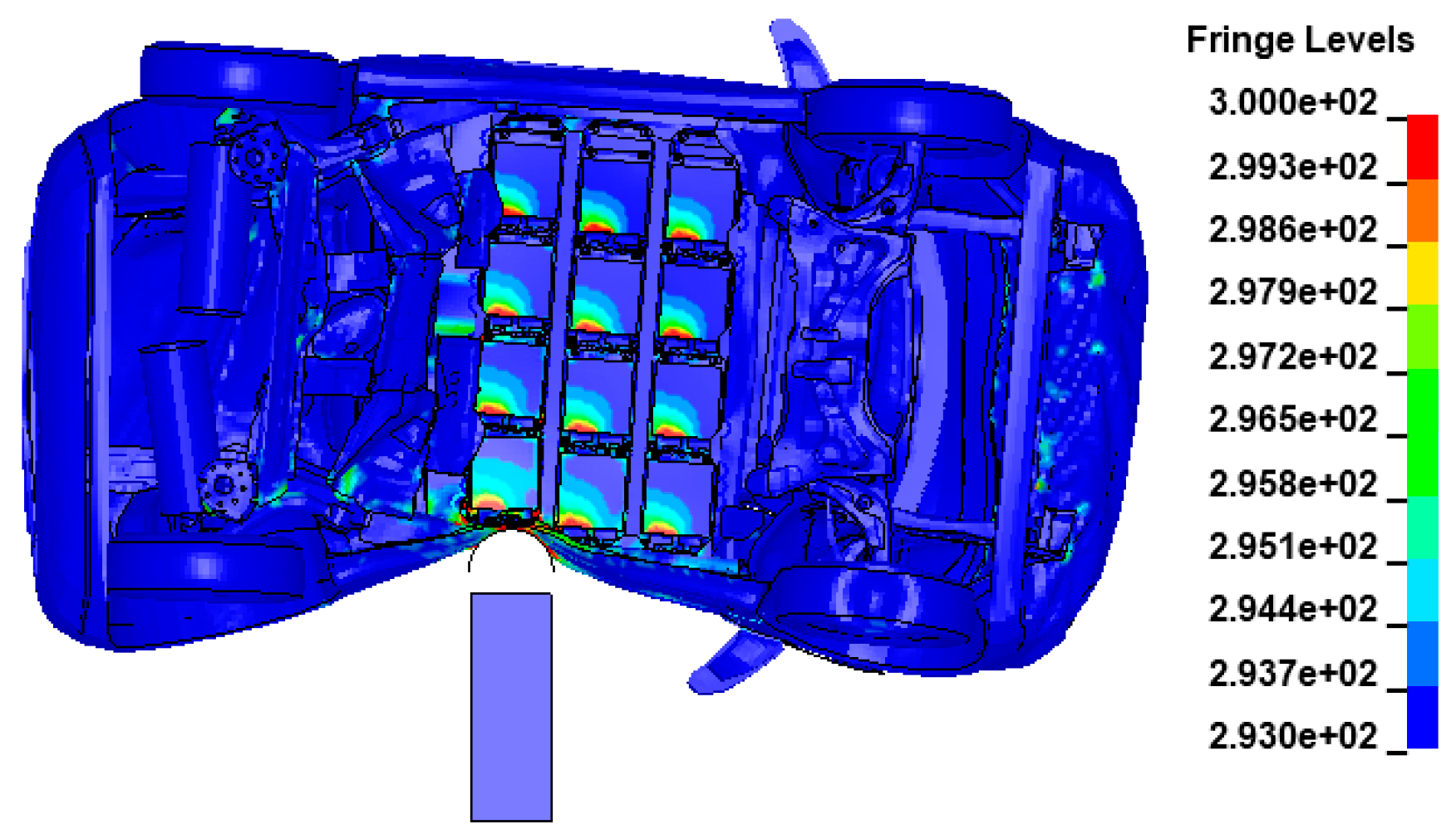
- C. Battery Electric Vehicle with 24 Active Cells
- (1)
- BEV in Normal Usage and External Short Circuit
- (2)
- BEV in FMVSS Pole Impact (20 mph impact speed):
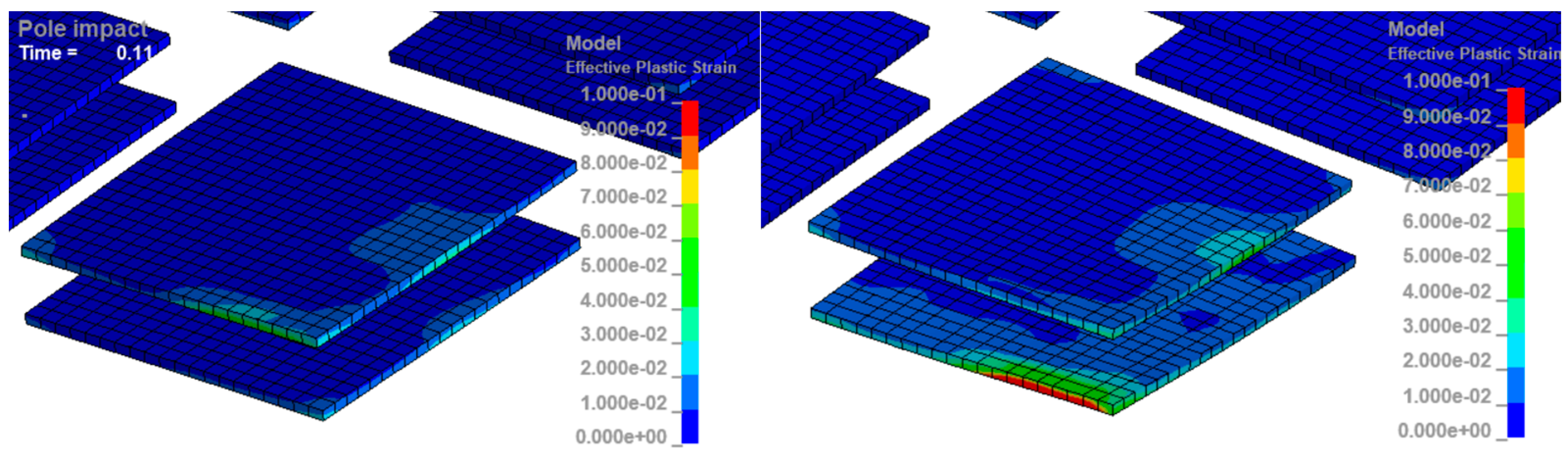
- (3)
- BEV in Pole Impact with 25 mph impact speed:
- (4)
- BEV Pole Impact with 30 mph impact speed:
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Czerwinski, F. Current Trends in Automotive Lightweighting Strategies and Materials. Materials 2021, 14, 6631. [Google Scholar] [CrossRef]
- Sanguesa, J.A.; Torres-Sanz, V.; Garrido, P.; Martinez, F.J.; Marquez-Barja, J.M. A Review on Electric Vehicles: Technologies and Challenges. Smart Cities 2021, 4, 372–404. [Google Scholar] [CrossRef]
- Arbelaez, R. As Heavy EVs Proliferate, Their Weight May Be a Drag on Safety. Available online: https://www.iihs.org/news/detail/as-heavy-evs-proliferate-their-weight-may-be-a-drag-on-safety (accessed on 6 June 2023).
- Susilawati, S.; Wong, W.J.; Pang, Z.J. Safety Effectiveness of Autonomous Vehicles and Connected Autonomous Vehicles in Reducing Pedestrian Crashes. Transp. Res. Rec. 2023, 2677, 1605–1618. [Google Scholar] [CrossRef]
- Parekh, D.; Poddar, N.; Rajpurkar, A.; Chahal, M.; Kumar, N.; Joshi, G.P.; Cho, W. A Review on Autonomous Vehicles: Progress, Methods and Challenges. Electronics 2022, 11, 2162. [Google Scholar] [CrossRef]
- Arango, J.F.; Bergasa, L.M.; Revenga, P.A.; Barea, R.; López-Guillén, E.; Gómez-Huélamo, C.; Araluce, J.; Gutiérrez, R. Drive-By-Wire Development Process Based on ROS for an Autonomous Electric Vehicle. Sensors 2020, 20, 6121. [Google Scholar] [CrossRef]
- Liang, J.; Feng, J.; Fang, Z.; Lu, Y.; Yin, G.; Mao, X.; Wu, J.; Wang, F. An Energy-Oriented Torque-Vector Control Framework for Distributed Drive Electric Vehicles. IEEE Trans. Transp. Electrif. 2023, 9, 4014–4031. [Google Scholar] [CrossRef]
- Abdelkader, G.; Elgazzar, K.; Khamis, A. Connected Vehicles: Technology Review, State of the Art, Challenges and Opportunities. Sensors 2021, 21, 7712. [Google Scholar] [CrossRef]
- Liang, J.; Wang, F.; Feng, J.; Zhao, M.; Fang, R.; Pi, D.; Yin, G. A Hierarchical Control of Independently Driven Electric Vehicles Considering Handling Stability and Energy Conservation. IEEE Trans. Intell. Veh. 2024, 9, 738–751. [Google Scholar] [CrossRef]
- Dorsz, A.; Lewandowski, M. Analysis of Fire Hazards Associated with the Operation of Electric Vehicles in Enclosed Structures. Energies 2022, 15, 11. [Google Scholar] [CrossRef]
- Valdes-Dapena, P. Latest Tesla Fire Caused by Running over a Metal Object. Available online: https://money.cnn.com/2013/11/08/autos/tesla-fire-details/index.html (accessed on 6 June 2023).
- Sun, P.; Bisschop, R.; Niu, H.; Huang, X. A Review of Battery Fires in Electric Vehicles. Fire Technol. 2020, 56, 1361–1410. [Google Scholar] [CrossRef]
- Kia Recall 23V218000: High Voltage Battery Pack Short Circuits Causing Fire Hazard. Available online: https://repairpal.com/recall/23V218000 (accessed on 7 June 2023).
- Larsson, F.; Andersson, P.; Blomqvist, P.; Mellander, B.-E. Toxic Fluoride Gas Emissions from Lithium-Ion Battery Fires. Sci. Rep. 2017, 7, 10018. [Google Scholar] [CrossRef] [PubMed]
- Hynynen, J.; Quant, M.; Pramanik, R.; Olofsson, A.; Li, Y.Z.; Arvidson, M.; Andersson, P. Electric Vehicle Fire Safety in Enclosed Spaces; RISE Research Institutes of Sweden: Gothenburg, Sweden, 2023. [Google Scholar]
- Tessin–Tesla En Feu Sur L’A2: La Batterie Serait En Cause|24 Heures. Available online: https://www.24heures.ch/tesla-en-feu-sur-l-a2-la-batterie-serait-en-cause-373966884791 (accessed on 6 June 2023).
- Gastelu, G. NTSB: Tesla Was Going 116 Mph at Time of Fatal Florida Accident, Battery Pack Reignited Twice Afterwards. Available online: https://www.foxnews.com/auto/ntsb-tesla-was-going-116-mph-at-time-of-fatal-florida-accident-battery-pack-reignited-twice-afterwards (accessed on 6 June 2023).
- NTSB to Investigate Fiery Tesla Crash in Coral Gables That Killed 2. Available online: https://wsvn.com/news/local/miami-dade/ntsb-to-investigate-fiery-tesla-crash-in-coral-gables-that-killed-2/ (accessed on 6 June 2023).
- Sacramento Metro Fire District on Instagram on Instagram. Available online: https://www.instagram.com/reel/CewdngRAWNQ/ (accessed on 31 July 2024).
- National Transportation Safety Board. Safety Risks to Emergency Responders from Lithium-Ion Battery Fires in Electric Vehicles; National Transportation Safety Board. 2020. Available online: https://www.ntsb.gov/safety/safety-studies/Documents/SR2001.pdf (accessed on 11 August 2024).
- Mauger, A.; Julien, C.M. Critical Review on Lithium-Ion Batteries: Are They Safe? Sustainable? Ionics 2017, 23, 1933–1947. [Google Scholar] [CrossRef]
- Si, R.; Liu, D.; Xue, S. Experimental Study on Fire and Explosion Suppression of Self-Ignition of Lithium Ion Battery. Procedia Eng. 2018, 211, 629–634. [Google Scholar] [CrossRef]
- GWL Dangerous vs. Safe Batteries, Explosion and Fire Test! Available online: https://www.youtube.com/watch?v=Qzt9RZ0FQyM (accessed on 14 July 2023).
- Zhu, L.; Xia, Y.; Liu, Y.; Ge, Y.; Wang, L.; Zhang, L. Extending a Homogenized Model for Characterizing Multidirectional Jellyroll Failure in Prismatic Lithium-Ion Batteries. Energies 2021, 14, 3444. [Google Scholar] [CrossRef]
- Werling, T.; Sprenger, M.; Ellersdorfer, C.; Sinz, W. Experimental and Numerical Investigation of the Behavior of Automotive Battery Busbars under Varying Mechanical Loads. Energies 2020, 13, 6572. [Google Scholar] [CrossRef]
- Kalnaus, S.; Wang, H.; Simunovic, S.; Kumar, A.; Gorti, S.B.; Allu, S.; Turner, J.A. Crashworthiness Models for Automotive Batteries. Crashworthiness Models for Automotive Batteries A Report on the Department of Energy Project 2088-A031-15 for the National Highway Traffic Safety Administration (NHTSA), an Agency of the U.S. Department of Transportation; Oak Ridge National Lab. (ORNL): Oak Ridge, TN, USA, 2018. [CrossRef]
- Gu, W.B.; Wang, C.Y. Thermal-Electrochemical Modeling of Battery Systems. J. Electrochem. Soc. 2000, 147, 2910. [Google Scholar] [CrossRef]
- Li, Q.; Zhu, L.; Ruan, H. Electromagnetic–Thermo–Mechanical Coupling Behavior of Cu/Si Layered Thin Plate Under Pulsed Magnetic Field. Acta Mech. Solida Sin. 2022, 35, 90–100. [Google Scholar] [CrossRef]
- Bateau-Meyer, S.; L’Eplattenier, P.; Deng, J.; Zhu, M.; Bae, C. Randles Circuit Parameters Set Up for Battery Simulations in LS-DYNA®. In Proceedings of the 15th International LS-DYNA® Users Conference, LSTC, Dearborn, MI, USA, 10–14 June 2018; p. 15. [Google Scholar]
- L’Eplattenier, P.; Çaldichoury, I.; Marcicki, J.; Bartlett, A.; Yang, X.G.; Mejia, V.; Zhu, M.; Chen, Y. A Distributed Randle Circuit Model for Battery Abuse Simulations Using LS-DYNA®. In Proceedings of the 14th International LS-DYNA Users Conference, Detroit, MI, USA, 12 June 2016; p. 18. [Google Scholar]
- Keshavarzi, M.; Derakhshan, M.; Gilaki, M.; L’Eplattenier, P.; Caldichoury, I.; Soudbakhsh, D.; Sahraei, E. Coupled Electrochemical-Mechanical Modeling of Lithium-Ion Batteries Using Distributed Randle Circuit Model. In Proceedings of the 2021 International Conference on Electrical, Computer and Energy Technologies (ICECET), Cape Town, South Africa, 9–10 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, L.; Ling, C.; Kan, C.-D.; Yang, C. A Coupled Thermal–Electrical–Mechanical Analysis for Lithium-Ion Battery. J. Micromechanics Mol. Phys. 2022, 07, 61–70. [Google Scholar] [CrossRef]
- Zhao, R.; Liu, J.; Gu, J. The Effects of Electrode Thickness on the Electrochemical and Thermal Characteristics of Lithium Ion Battery. Appl. Energy 2015, 139, 220–229. [Google Scholar] [CrossRef]
- Jiang, W.; Zhou, Q.; Lu, F.; Chen, Y.; Ma, Z. A Thermal-Electrochemical-Mechanical Coupled Model Based on Non-Equilibrium Thermodynamics of Li-Ion Batteries. J. Energy Storage 2022, 55, 105655. [Google Scholar] [CrossRef]
- Zhang, X.; Chumakov, S.; Li, X.; Klinsmann, M.; Kim, S.U.; Linder, C.; Christensen, J. An Electro-Chemo-Thermo-Mechanical Coupled Three-Dimensional Computational Framework for Lithium-Ion Batteries. J. Electrochem. Soc. 2020, 167, 160542. [Google Scholar] [CrossRef]
- Im, K.; Lim, J.; Lee, K.-J.; Zhang, Z.-C.; Cook, G., Jr. Electrochemical-Thermal-Mechanical Coupling of Lithium-Ion Battery Model in LS-DYNA. In Proceedings of the 16th International LS-DYNA Users Conference, Virtual Event, 10 June 2020. [Google Scholar]
- Kim, S.; Wee, J.; Peters, K.; Huang, H.-Y.S. Multiphysics Coupling in Lithium-Ion Batteries with Reconstructed Porous Microstructures. J. Phys. Chem. C 2018, 122, 5280–5290. [Google Scholar] [CrossRef]
- Fill, A.; Bubeck, L.; Knauer, D.; Hemmerling, J.; Birke, K.P. Multi-Dimensional Model for Electrical, Thermal and Mechanical Simulation of a Lithium-Ion Cell. In Proceedings of the NEIS 2022; Conference on Sustainable Energy Supply and Energy Storage Systems, Hamburg, Germany, 26 September 2022; pp. 1–8. [Google Scholar]
- Kumar, P.; Rankin, G.; Pattipati, K.R.; Balasingam, B. Model-Based Approach to Long Term Prediction of Battery Surface Temperature. IEEE J. Emerg. Sel. Top. Ind. Electron. 2023, 4, 389–399. [Google Scholar] [CrossRef]
- Sevgi, L. Electromagnetic Modeling and Simulation; The IEEE Press Series on Electromagnetic Wave Theory; IEEE Press: Piscataway, NJ, USA, 2014; ISBN 978-1-118-71618-2. [Google Scholar]
- L’Eplattenier, P.; Cook, G.; Ashcraft, C.; Burger, M.; Imbert, J.; Worswick, M. Introduction of an Electromagnetism Module in LS-DYNA for Coupled Mechanical-Thermal-Electromagnetic Simulations. Met. Form. 2009, 8, 351–358. [Google Scholar]
- L’Eplattenier, P.; Çaldichoury, I.; Anton, J. LS-DYNA® R7: Update on the Electromagnetism Module (EM). In Proceedings of the 9th European LS-DYNA Conference, Manchester, UK, 2–4 June 2013. [Google Scholar]
- Biro, O.; Preis, K. On the Use of the Magnetic Vector Potential in the Finite-Element Analysis of Three-Dimensional Eddy Currents. IEEE Trans. Magn. 1989, 25, 3145–3159. [Google Scholar] [CrossRef]
- Chen, Y.; Kang, Y.; Zhao, Y.; Wang, L.; Liu, J.; Li, Y.; Liang, Z.; He, X.; Li, X.; Tavajohi, N.; et al. A Review of Lithium-Ion Battery Safety Concerns: The Issues, Strategies, and Testing Standards. J. Energy Chem. 2021, 59, 83–99. [Google Scholar] [CrossRef]
- Kisters, T.; Sahraei, E.; Wierzbicki, T. Dynamic Impact Tests on Lithium-Ion Cells. Int. J. Impact Eng. 2017, 108, 205–216. [Google Scholar] [CrossRef]
- Blomgren, G.E. The Development and Future of Lithium Ion Batteries. J. Electrochem. Soc. 2016, 164, A5019. [Google Scholar] [CrossRef]
- Zhang, X.; Sahraei, E.; Wang, K. Deformation and Failure Characteristics of Four Types of Lithium-Ion Battery Separators. J. Power Sources 2016, 327, 693–701. [Google Scholar] [CrossRef]
- Sahraei, E.; Hill, R.; Wierzbicki, T. Calibration and Finite Element Simulation of Pouch Lithium-Ion Batteries for Mechanical Integrity. J. Power Sources 2012, 201, 307–321. [Google Scholar] [CrossRef]
- Time Step Size. Available online: https://www.dynasupport.com/tutorial/ls-dyna-users-guide/time-step-size (accessed on 19 July 2023).
- Morgan, R.M.; Cui, C.; Digges, K.H.; Cao, L.; Kan, C.-D. (Steve) Impact and Injury Patterns in Between-Rails Frontal Crashes of Vehicles with Good Ratings for Frontal Crash Protection. Ann. Adv. Automot. Med. Annu. Sci. Conf. 2012, 56, 255–265. [Google Scholar]
- Kan, C.-D.; Marzougui, D.; Bahouth, G.T.; Bedewi, N.E. Crashworthiness Evaluation Using Integrated Vehicle and Occupant Finite Element Models. Int. J. Crashworthiness 2001, 6, 387–398. [Google Scholar] [CrossRef]
- Reichert, R.; Mohan, P.; Marzougui, D.; Kan, C.-D.; Brown, D. Validation of a Toyota Camry Finite Element Model for Multiple Impact Configurations; SAE International: Warrendale, PA, USA, 2016. [Google Scholar]
- Eskandarian, A.; Marzougui, D.; Bedewi, N.E. Finite Element Model and Validation of a Surrogate Crash Test Vehicle for Impacts with Roadside Objects. Int. J. Crashworthiness 1997, 2, 239–258. [Google Scholar] [CrossRef]
- Simulation Vehicle Models|NHTSA. Available online: https://www.nhtsa.gov/crash-simulation-vehicle-models (accessed on 11 August 2024).
- Center for Collision Safety and Analysis–Finite Element Models. Available online: https://www.ccsa.gmu.edu/models/ (accessed on 18 July 2023).
- Powers, R.; Boodlal, K.; Durkos, J.; Boodlal, L.; Marzougui, D.; Kan, C.D.; Opiela, K.; Tahan, F. Roadside Barrier Designs near Bridge Rail Ends with Restricted Rights-of-Way: A Guide; Transportation Research Board: Washington, DC, USA, 2022; ISBN 978-0-309-68750-8. [Google Scholar]
- Marzougui, D.; Kan, C.-D.; Mahadevaiah, U.; Tahan, F.; Story, C.; Dolci, S.; Moreno, A.; Opiela, K.S.; Powers, R. Evaluating the Performance of Longitudinal Barriers on Curved, Superelevated Roadway Sections; Transportation Research Board: Washington, DC, USA, 2019; ISBN 978-0-309-48578-4. [Google Scholar]
- Center for Collision Safety and Analysis–2010 Toyota Yaris. Available online: https://www.ccsa.gmu.edu/models/2010-toyota-yaris/ (accessed on 19 July 2023).
- 2024 Nissan LEAF|All-Electric Vehicle. Available online: https://www.nissanusa.com/vehicles/electric-cars/leaf.html (accessed on 19 July 2023).
- Online Circuit Simulator & Schematic Editor. Available online: https://www.circuitlab.com/ (accessed on 4 February 2021).
- Kalnaus, S.; Kumar, A.; Lebrun-Grandie, D.T.; Simunovic, S.; Slattery, S.R.; Turner, J.A.; Wang, H.; Allu, S.; Gorti, S.B.; Turcksin, B.R. Crashworthiness Models for Automotive Batteries-Report on Project 2088-A031-15 for DOT/NHTSA; Oak Ridge National Lab. (ORNL): Oak Ridge, TN, USA, 2016. [CrossRef]
- Livermore Software Technology LS-DYNA Manual Volume III Multiphysics. Available online: https://lsdyna.ansys.com/manuals/ (accessed on 11 August 2024).
- Air-Thermal Conductivity vs. Temperature and Pressure. Available online: https://www.engineeringtoolbox.com/air-properties-viscosity-conductivity-heat-capacity-d_1509.html (accessed on 21 July 2023).
- Water-Thermal Conductivity vs. Temperature. Available online: https://www.engineeringtoolbox.com/water-liquid-gas-thermal-conductivity-temperature-pressure-d_2012.html (accessed on 21 July 2023).
- Ahmeid, M.; Muhammad, M.; Lambert, S.; Attidekou, P.S.; Milojevic, Z. A Rapid Capacity Evaluation of Retired Electric Vehicle Battery Modules Using Partial Discharge Test. J. Energy Storage 2022, 50, 104562. [Google Scholar] [CrossRef]
- Braco, E.; San Martín, I.; Sanchis, P.; Ursúa, A. Fast Capacity and Internal Resistance Estimation Method for Second-Life Batteries from Electric Vehicles. Appl. Energy 2023, 329, 120235. [Google Scholar] [CrossRef]
- Bao, Y.; Gong, Y. Li-Ion Battery Charge Transfer Stability Studies with Direct Current Impedance Spectroscopy. Energy Rep. 2023, 9, 34–41. [Google Scholar] [CrossRef]
- Turner, J.A.; Kalnaus, S.; Wang, H.; Simunovic, S.; Kumar, A.; Gorti, S.; Allu, S. Crashworthiness Models for Automotive Batteries. A Report on the Department of Energy Project 2088-A031-15 for the National Highway Traffic Safety Administration. 2019. Available online: https://rosap.ntl.bts.gov/view/dot/41005 (accessed on 11 August 2024).
- Nigel 2010 Nissan Leaf. Available online: https://www.batterydesign.net/2010-nissan-leaf/ (accessed on 2 November 2023).
- Jones, J. Laboratory Test Procedure for FMVSS No. 214, Dynamic Side Impact Protection Rigid Pole Side Impact Test Requirements; TP-214P-01; Enforcement Office of Vehicle Safety Compliance, Department of Transportation: Washington, DC, USA, 2012.





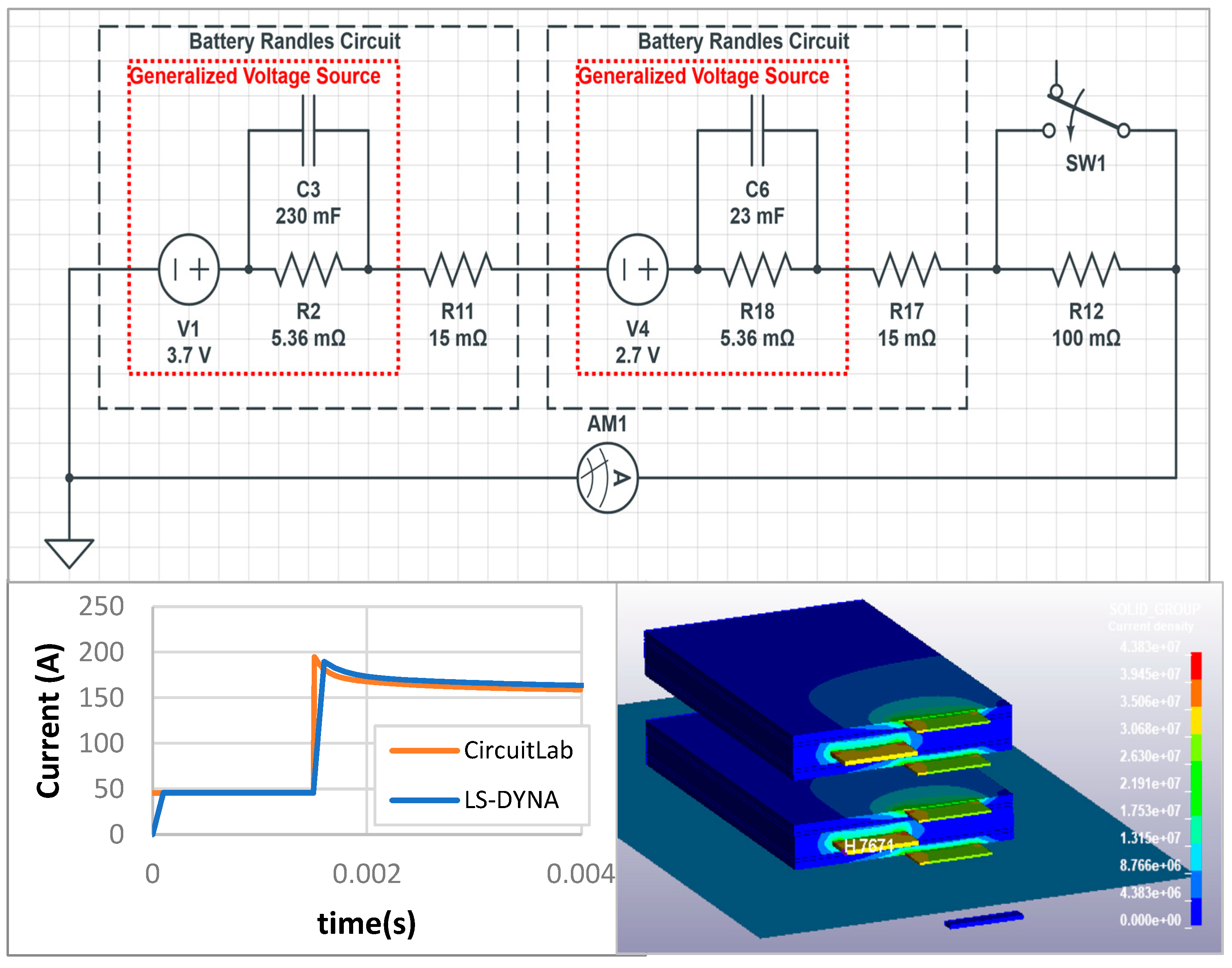
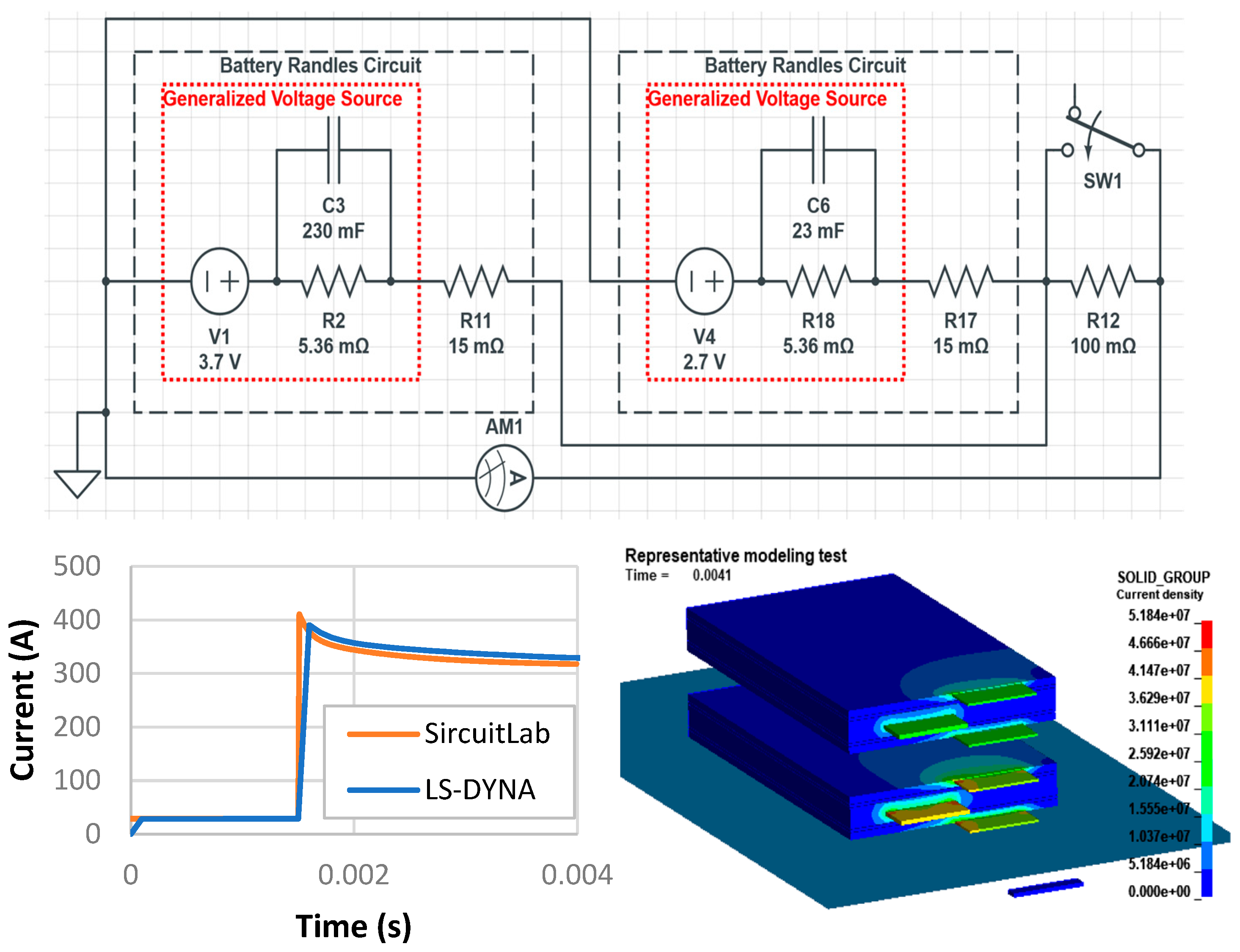
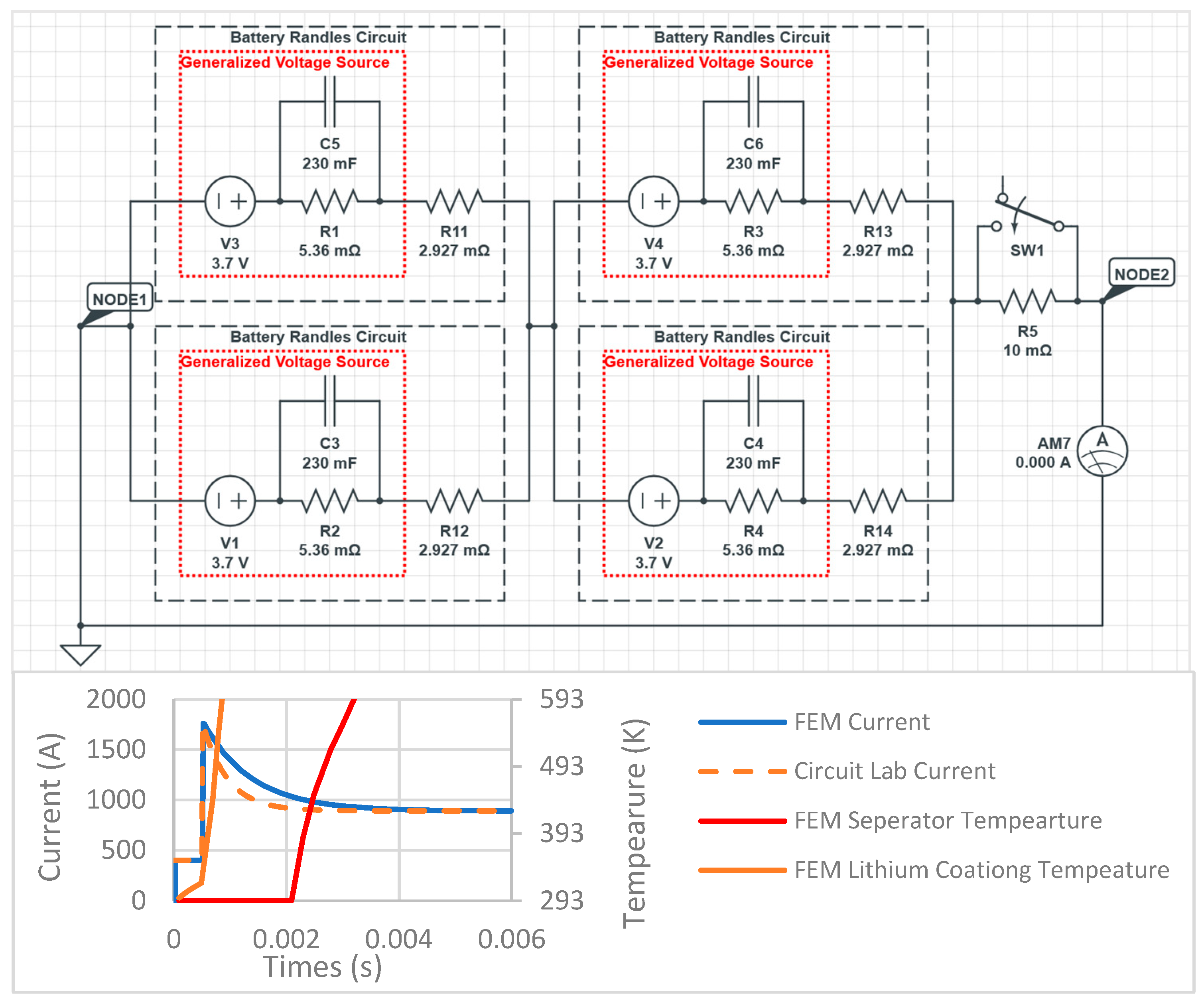

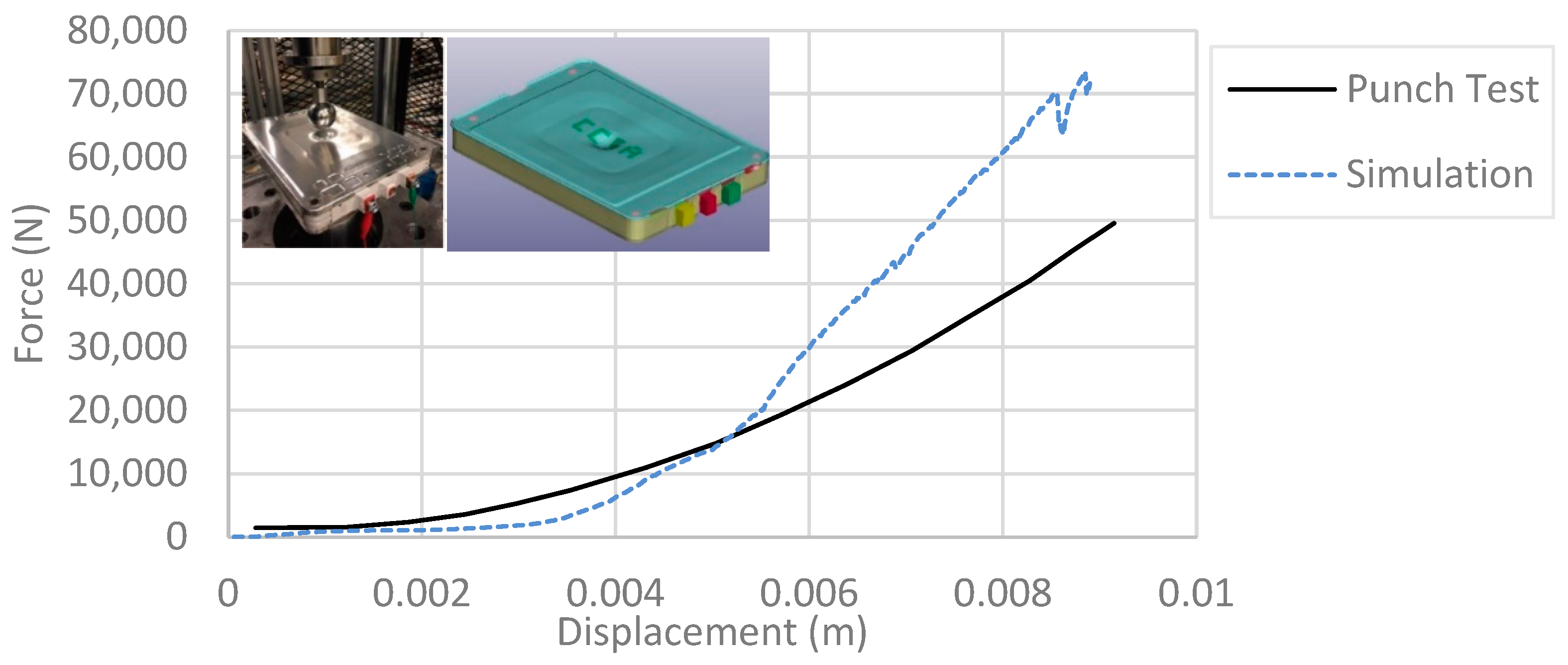













| AC Impedance at 1 kHz | DC Internal Resistance | |
|---|---|---|
| “CHI660E” Test Data | 5.61 mΩ | 6.46 mΩ |
| “YR1035+” Test Data | 4.89 mΩ | N/A |
| Literature [66] | 1.08–2.06 mΩ | 2–6 mΩ |
| LS-DYNA Simulation | N/A | 2.927 mΩ |
| Immediate Thermal Runaway | Risk of Thermal Runaway with Continued Use | Cell Leakage | |
|---|---|---|---|
| 20 mph | No | No | No |
| 25 mph | No | Yes | No |
| 30 mph | Yes | N/A | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ling, C.; Wang, L.; Kan, C.-D.; Yang, C. Thermal–Electrical–Mechanical Coupled Finite Element Models for Battery Electric Vehicle. Machines 2024, 12, 596. https://doi.org/10.3390/machines12090596
Ling C, Wang L, Kan C-D, Yang C. Thermal–Electrical–Mechanical Coupled Finite Element Models for Battery Electric Vehicle. Machines. 2024; 12(9):596. https://doi.org/10.3390/machines12090596
Chicago/Turabian StyleLing, Chenxi, Leyu Wang, Cing-Dao Kan, and Chi Yang. 2024. "Thermal–Electrical–Mechanical Coupled Finite Element Models for Battery Electric Vehicle" Machines 12, no. 9: 596. https://doi.org/10.3390/machines12090596
APA StyleLing, C., Wang, L., Kan, C.-D., & Yang, C. (2024). Thermal–Electrical–Mechanical Coupled Finite Element Models for Battery Electric Vehicle. Machines, 12(9), 596. https://doi.org/10.3390/machines12090596






