An Advanced Technique for the Detection of Pathological Gaits from Electromyography Signals: A Comprehensive Approach
Abstract
1. Introduction
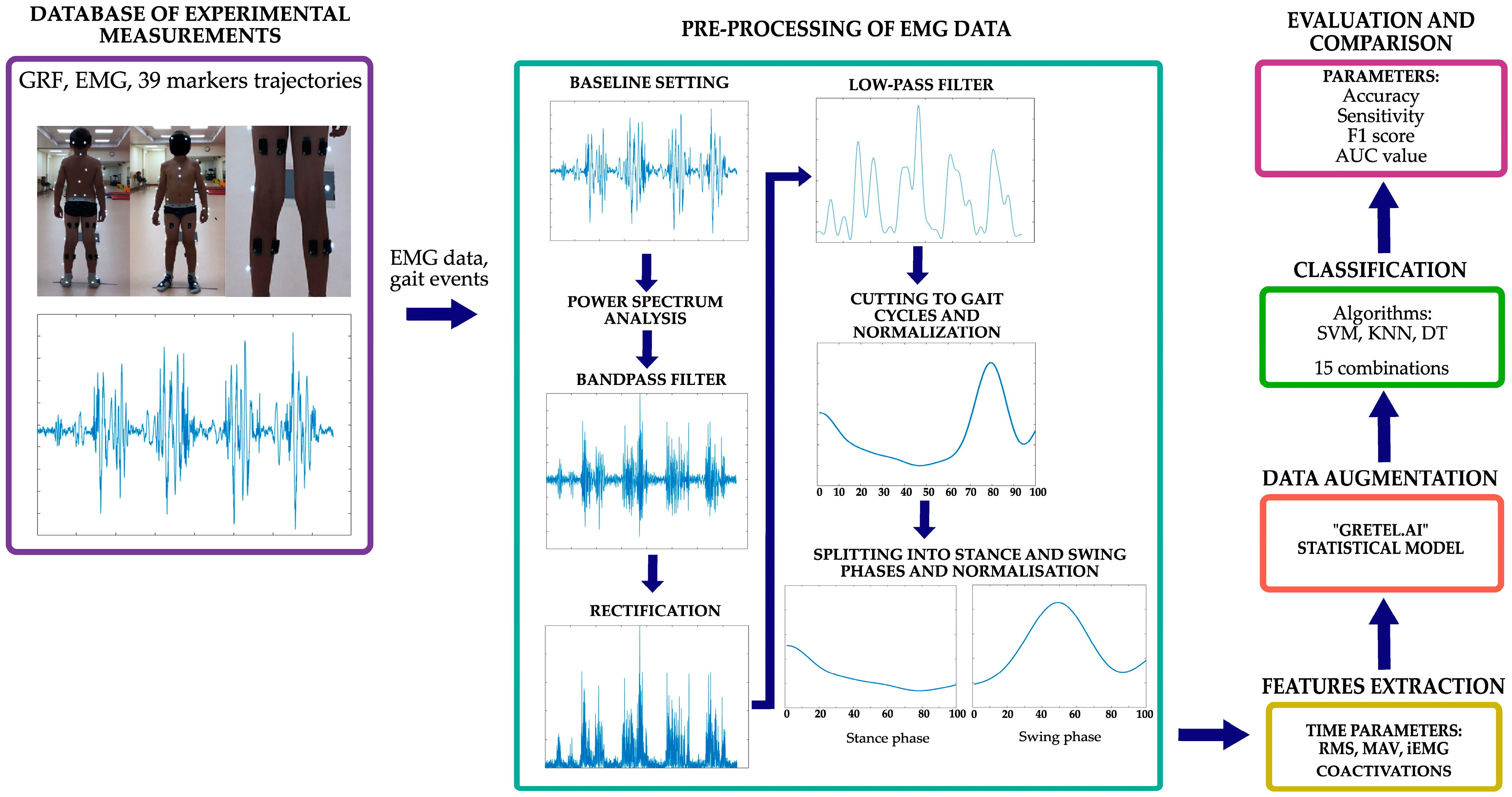
2. Materials and Methods
2.1. Participant and Dataset Descriptions
2.2. Study Protocol
2.2.1. EMG Data Pre-Processing
- EMG data baseline determination.
- Filtering with a second-order Butterworth bandpass filter with the lowest (30 Hz) and the highest (500 Hz) cut-off frequency limits being based on the results of a signal power spectrum analysis.
- Full-wave rectification, i.e., the EMG signal is converted from a bipolar to a unipolar form, which facilitates further analysis by removing negative values, and equalization.
- Filtering with a low-pass 5th-order zero-phase Butterworth filter with a cut-off frequency of 6 Hz.
- Signal cutting to gait cycles from heel contact to heel contact based on the camera system and force plate data and performing normalization at a 0–100% gait cycle.
- For the calculations of coactivations, the gait cycle was divided into stance and swing phases in a 60:40 ratio. Then, the signal was again normalized by duration, i.e., 100% of the stance and 100% of the swing phase, and by RMS, i.e., the EMG signal was then normalized by dividing each data point by the RMS value.
2.2.2. Feature Extraction of EMG Signals
2.2.3. Data Augmentation
- A larger amount of data requires more computer resources, capabilities, and time.
- When synthesizing a larger amount of data, there is a risk that the deviation from the real measured data will be greater, so the goal is to keep as much real data in the set as possible.
2.2.4. Classification
- Dataset preparation: The entire dataset is processed and divided into training, validation, and testing sets. The sets are divided into 80%, 10%, and 10% parts, respectively.
- The data are prepared for validation using a k-fold cross-validation. A value of k = 10 was chosen, knowing that higher values are recommended when the dataset is larger. The cross-validation used a stratified distribution of the data to ensure that each validation stratum contained equal amounts of data from both classes, thus achieving more reliable results.
- Finding the best parameters: For the SVM algorithm, it is important to choose the best combination of the C parameter and kernel scale (S) by testing the algorithm with different combinations of these parameters. The C parameter is a regularization parameter that controls the trade-off between low training data errors and reduces the model complexity to avoid overfitting. The S parameter affects the width of the Gaussian function used in the kernel. A smaller scale results in a narrower kernel, making the decision boundary more complex, while a larger scale results in a smoother decision boundary. The SVM algorithm was tested with the following values: C = {0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30} and S = {0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30}. Different kernel functions were also tested with all values: Gaussian, quadratic, and cubic.
- For the KNN algorithm, it is important to choose the K parameter correctly, so the following values were tested in this work: K = {1, 2, 3, 4, …., 15}. Two different methods of measuring the distance between neighbors (distance metric) were tested: cosine and L1. We randomly selected one of the tied classes.
- Two parameters are important for the DT algorithm—the maximum number of splits (P) and the split criterion. The following P values were tested in this study: {2, 4, 8, 16, 32, 64}. All values were tested based on two-split criteria—the Gini index and maximum variance reduction (MVR). The Gini index quantifies how often a randomly chosen element from the set would be incorrectly labeled if it were randomly labeled according to the distribution of labels in the node. And MVR is a criterion used to split nodes in decision trees, and it chooses the split to create the most homogeneous nodes possible. The Gini index was employed as the splitting criterion in our decision tree model, specifically utilizing the CART (Classification and Regression Trees) algorithm.
2.2.5. Methods of Evaluation and Comparison of Results
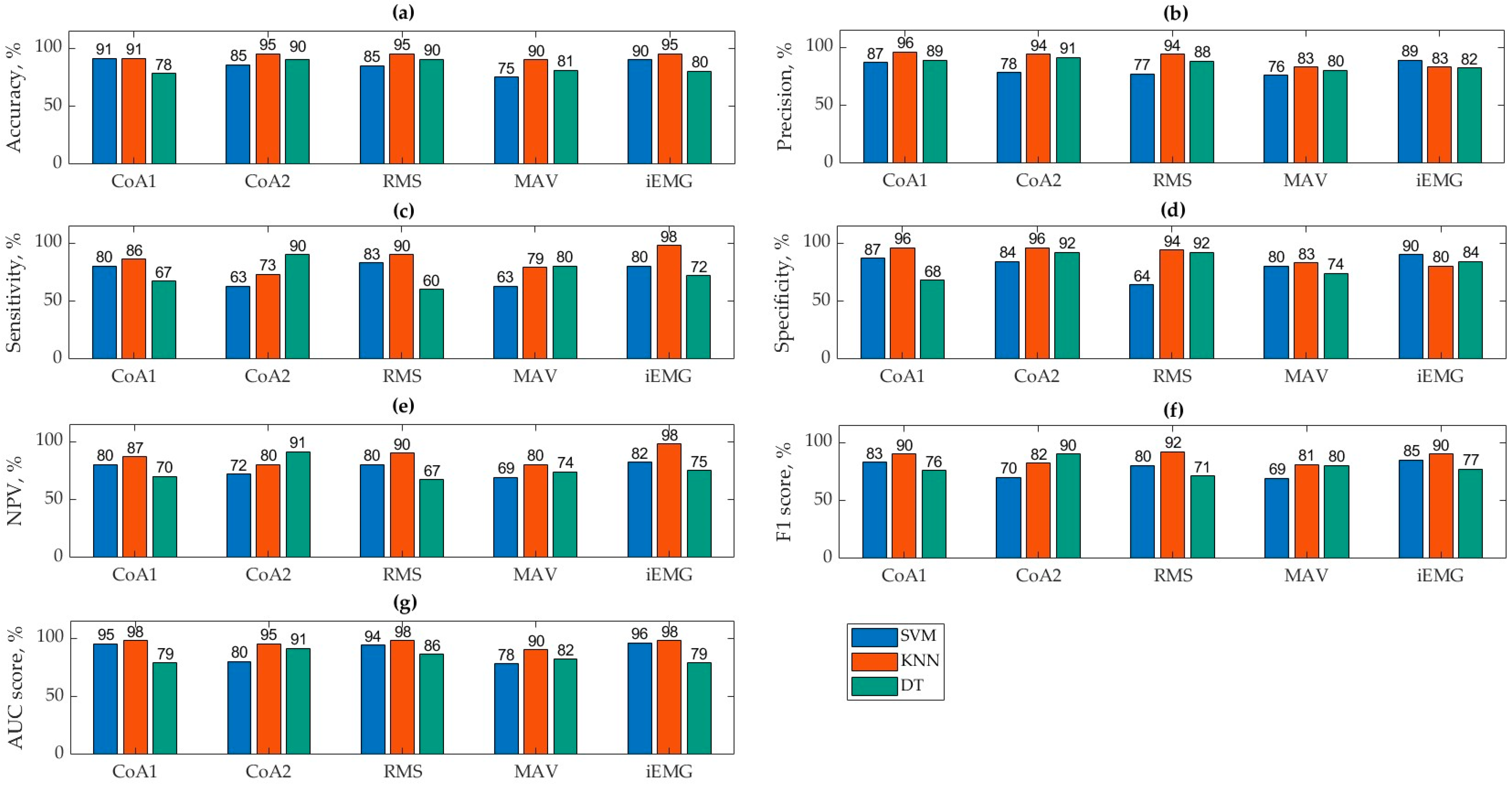
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guo, Y.; Gravina, R.; Gu, X.; Fortino, G.; Yang, G.-Z. EMG-based Abnormal Gait Detection and Recognition. In Proceedings of the 2020 IEEE International Conference on Human-Machine Systems, ICHMS 2020, Rome, Italy, 7–9 September 2020. [Google Scholar] [CrossRef]
- Smith, S.; Rush, J.; Glaviano, N.R.; Murray, A.; Bazett-Jones, D.; Bouillon, L.; Blalckburn, T.; Norte, G. Sex influences the relationship between hamstrings-to-quadriceps strength imbalance and co-activation during walking gait. Gait Posture 2021, 88, 138–145. [Google Scholar] [CrossRef] [PubMed]
- Akl, A.R.; Conceição, F.; Richards, J. An exploration of muscle co-activation during different walking speeds and the association with lower limb joint stiffness. J. Biomech. 2023, 157, 111715. [Google Scholar] [CrossRef] [PubMed]
- Ippersiel, P.; Dussault-Picard, C.; Mohammadyari, S.G.; De Carvalho, G.B.; Chandran, V.D.; Pal, S.; Dixon, P.C. Muscle coactivation during gait in children with and without cerebral palsy. Gait Posture 2024, 108, 110–116. [Google Scholar] [CrossRef]
- Gharehbolagh, S.M.; Dussault-Picard, C.; Arvisais, D.; Dixon, P.C. Muscle co-contraction and co-activation in cerebral palsy during gait: A scoping review. Gait Posture 2023, 105, 6–16. [Google Scholar] [CrossRef] [PubMed]
- Agostini, V.; Ghislieri, M.; Rosati, S.; Balestra, G.; Knaflitz, M. Surface Electromyography Applied to Gait Analysis: How to Improve Its Impact in Clinics? Front. Neurol. 2020, 11, 561815. [Google Scholar] [CrossRef]
- Reeves, J.; Starbuck, C.; Nester, C. EMG gait data from indwelling electrodes is attenuated over time and changes independent of any experimental effect. J. Electromyogr. Kinesiol. 2020, 54, 102461. [Google Scholar] [CrossRef]
- Schlink, B.R.; Nordin, A.D.; Ferris, D.P. Comparison of signal processing methods for reducing motion artifacts in high-density electromyography during human locomotion. IEEE Open J. Eng. Med. Biol. 2020, 1, 156–185. [Google Scholar] [CrossRef]
- Gao, S.; Gong, J.; Chen, B.; Zhang, B.; Luo, F.; Yerabakan, M.O.; Pan, Y.; Hu, B. Use of Advanced Materials and Artificial Intelligence in Electromyography Signal Detection and Interpretation. Adv. Intell. Syst. 2022, 4, 2200063. [Google Scholar] [CrossRef]
- Park, H.; Han, S.; Sung, J.; Hwang, S.; Youn, I.; Kim, S.-J. Classification of gait phases based on a machine learning approach using muscle synergy. Front. Hum. Neurosci. 2023, 17, 1201935. [Google Scholar] [CrossRef]
- Qin, P.; Shi, X. Evaluation of Feature Extraction and Classification for Lower Limb Motion Based on sEMG Signal. Entropy 2020, 22, 852. [Google Scholar] [CrossRef]
- Yao, T.; Gao, F.; Zhang, Q.; Ma, Y. Multi-feature gait recognition with DNN based on sEMG signals. Math. Biosci. Eng. 2021, 18, 3521–3542. [Google Scholar] [CrossRef] [PubMed]
- Gagnat, Y.; Brændvik, S.M.; Roeleveld, K. Surface Electromyography Normalization Affects the Interpretation of Muscle Activity and Coactivation in Children with Cerebral Palsy during Walking. Front. Neurol. 2020, 11, 202. [Google Scholar] [CrossRef] [PubMed]
- Martinek, R.; Ladrova, M.; Sidikova, M.; Jaros, R.; Behbehani, K.; Kahankova, R.; Kawala-Sterniuk, A. Advanced Bioelectrical Signal Processing Methods: Past, Present, and Future Approach—Part III: Other Biosignals. Sensors 2021, 21, 6064. [Google Scholar] [CrossRef]
- Nadzri, A.A.B.A.; Ahmad, S.A.; Marhaban, M.H.; Jaafar, H. Characterization of surface electromyography using time domain features for determining hand motion and stages of contraction. Australas. Phys. Eng. Sci. Med. 2014, 37, 133–137. [Google Scholar] [CrossRef]
- Daunoraviciene, K.; Ziziene, J.; Pauk, J.; Juskeniene, G.; Raistenskis, J. EMG Based Analysis of Gait Symmetry in Healthy Children. Sensors 2021, 21, 5983. [Google Scholar] [CrossRef]
- Fricke, C.; Alizadeh, J.; Zakhary, N.; Woost, T.B.; Bogdan, M.; Classen, J. Evaluation of Three Machine Learning Algorithms for the Automatic Classification of EMG Patterns in Gait Disorders. Front. Neurol. 2021, 12, 666458. [Google Scholar] [CrossRef] [PubMed]
- Al-Angari, H.M.; Kanitz, G.; Tarantino, S.; Cipriani, C. Distance and mutual information methods for EMG feature and channel subset selection for classification of hand movements. Biomed. Signal. Process. Control 2016, 27, 24–31. [Google Scholar] [CrossRef]
- Go, S.A.; Coleman-Wood, K.; Kaufman, K.R. Frequency analysis of lower extremity electromyography signals for the quantitative diagnosis of dystonia. J. Electromyogr. Kinesiol. 2014, 24, 31. [Google Scholar] [CrossRef]
- De Luca, C.J. Surface electromyography: Detection and recording. DelSys Inc. 2002, 10, 1–10. [Google Scholar]
- De Luca, C.J.; Donald Gilmore, L.; Kuznetsov, M.; Roy, S.H. Filtering the surface EMG signal: Movement artifact and baseline noise contamination. J. Biomech. 2010, 43, 1573–1579. [Google Scholar] [CrossRef]
- Amrutha, N.; Arul, V.H. A Review on Noises in EMG Signal and its Removal. Int. J. Sci. Res. Publ. 2017, 7, 5. [Google Scholar]
- Van Boxtel, A. Optimal signal bandwidth for the recording of surface EMG activity of facial, jaw, oral, and neck muscles. Psychophysiology 2001, 38, 22–34. [Google Scholar] [CrossRef]
- Merletti, R. Standards for Reporting EMG Data. Italy. 1999. Available online: https://people.stfx.ca/smackenz/courses/HK474/Labs/EMG%20Lab/isek_emg-standards.pdf (accessed on 12 June 2024).
- Nazmi, N.; Rahman, M.A.A.; Yamamoto, S.-I.; Ahmad, S.A.; Zamzuri, H.; Mazlan, S.A. A Review of Classification Techniques of EMG Signals during Isotonic and Isometric Contractions. Sensors 2016, 16, 1304. [Google Scholar] [CrossRef]
- Kamruzzaman, J.; Begg, R.K. Support Vector Machines and Other Pattern Recognition Approaches to the Diagnosis of Cerebral Palsy Gait. IEEE Trans. Biomed. Eng. 2006, 53, 2479–2490. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Romijnders, R.; Hansen, C.; Campen, J.V.; Maetzler, W.; Hortobágyi, T.; Lamoth, C.J. The detection of age groups by dynamic gait outcomes using machine learning approaches. Sci. Rep. 2020, 10, 4426. [Google Scholar] [CrossRef]
- Ziegier, J.; Gattringer, H.; Mueller, A. Classification of Gait Phases Based on Bilateral EMG Data Using Support Vector Machines. In Proceedings of the IEEE RAS and EMBS International Conference on Biomedical Robotics and Biomechatronics, Enschede, The Netherlands, 26–29 August 2018; pp. 978–983. [Google Scholar]
- Zhang, Y.; Ma, Y. Application of supervised machine learning algorithms in the classification of sagittal gait patterns of cerebral palsy children with spastic diplegia. Comput. Biol. Med. 2019, 106, 33–39. [Google Scholar] [CrossRef]
- Alaqtash, M.; Sarkodie-Gyan, T.; Yu, H.; Fuentes, O.; Brower, R.; Abdelgawad, A. Automatic classification of pathological gait patterns using ground reaction forces and machine learning algorithms. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 453–457. [Google Scholar]
- Eltanani, S.; Scheper, T.O.; Dawes, H. K-Nearest Neighbor Algorithm: Proposed Solution for Human Gait Data Classification. In Proceedings of the 2021 IEEE Symposium on Computers and Communications (ISCC), Athens, Greece, 5–8 September 2021. [Google Scholar] [CrossRef]
- Naji, A.; Abboud, S.A.; Jumaa, B.A.; Abdullah, M.N. Gait Classification Using Machine Learning for Foot Disseises Diagnosis. Tech. Rom. J. Appl. Sci. Technol. 2022, 4, 37–49. [Google Scholar] [CrossRef]
- Ramírez-Pérez, V.; Guerrero-Díaz-de-León, J.A.; Macías-Díaz, J.E. On the detection of activity patterns in electromyographic signals via decision trees. Evol. Intell. 2024, 17, 577–588. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Y.; Yu, Z.; Huang, X.; Xu, J.; Detng, C. An end-to-end lower limb activity recognition framework based on sEMG data augmentation and enhanced CapsNet. Expert. Syst. Appl. 2023, 227, 120257. [Google Scholar] [CrossRef]
- Zanini, R.A.; Colombini, E.L. Parkinson’s Disease EMG Data Augmentation and Simulation with DCGANs and Style Transfer. Sensors 2020, 20, 2605. [Google Scholar] [CrossRef]
- König, T.; Wagner, F.; Kley, M.; Liebschner, M. Enhanced damage classification accuracy on a transmission by extending existing datasets with generative adversarial networks. Forsch. Im Ingenieurwesen/Eng. Res. 2023, 87, 757–766. [Google Scholar] [CrossRef]
- Coelho, F.; Pinto, M.F.; Melo, A.G.; Ramos, G.S.; Marcato, A.L.M. A novel sEMG data augmentation based on WGAN-GP. Comput. Methods Biomech. Biomed. Eng. 2023, 26, 1008–1017. [Google Scholar] [CrossRef] [PubMed]
- Gross, R.; Leboeuf, F.; Hardouin, J.B.; Perrouin-Verbe, B.; Brochalrd, S.; Rémy-Néris, O. Does muscle coactivation influence joint excursions during gait in children with and without hemiplegic cerebral palsy? Relationship between muscle coactivation and joint kinematics. Clin. Biomech. 2015, 30, 1088–1093. [Google Scholar] [CrossRef] [PubMed]
- Amorim, C.F.; Marson, R.A. Application of Surface Electromyography in the Dynamics of Human Movement. In Computational Intelligence in Electromyography Analysis—A Perspective on Current Applications and Future Challenges; Intech: Cheadle Hulme, UK, 2012. [Google Scholar] [CrossRef][Green Version]
- Gavilanes-Miranda, B.; Gandarias, J.J.G.D.; Garcia, G.A. Comparison by EMG of Running Barefoot and Running Shod. In Computational Intelligence in Electromyography Analysis—A Perspective on Current Applications and Future Challenges; Intech: Cheadle Hulme, UK, 2012. [Google Scholar] [CrossRef][Green Version]
- Zarin Mousavi, S.S.; Mohammadi Zanjireh, M.; Oghbaie, M. Applying computational classification methods to diagnose Congenital Hypothyroidism: A comparative study. Inf. Med. Unlocked 2020, 18, 100281. [Google Scholar] [CrossRef]
- Jason, B. Tour of Evaluation Metrics for Imbalanced Classification—MachineLearningMastery.com. 2021. Available online: https://machinelearningmastery.com/tour-of-e,valuation-metrics-for-imbalanced-classification/ (accessed on 17 June 2024).
- Bird, J.J.; Pritchard, M.; Fratini, A.; Ekart, A.; Faria, D.R. Synthetic Biological Signals Machine-Generated by GPT-2 Improve the Classification of EEG and EMG through Data Augmentation. IEEE Robot. Autom. Lett. 2021, 6, 3498–3504. [Google Scholar] [CrossRef]
- Tsinganos, P.; Cornelis, B.; Cornelis, J.; Jansen, B.; Skodras, A. Data Augmentation of Surface Electromyography for Hand Gesture Recognition. Sensors 2020, 20, 4892. [Google Scholar] [CrossRef]
- Chen, Z.; Qian, Y.; Wang, Y.; Fang, Y. Deep Convolutional Generative Adversarial Network-Based EMG Data Enhancement for Hand Motion Classification. Front. Bioeng. Biotechnol. 2022, 10, 909653. [Google Scholar] [CrossRef]
- Alvarez, I. Explaining the result of a Decision Tree to the End-User. In Proceedings of the ECAI 2004—16th European Conference on Artificial Intelligence, Valencia, Spain, 22–27 August 2004; IOS Press: Amsterdam, The Netherlands; pp. 411–415. [Google Scholar]
- Ijaz, A.; Choi, J. Anomaly Detection of Electromyographic Signals. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 770–779. [Google Scholar] [CrossRef]

| Group | Age, Years | Height, m | Weight, kg |
|---|---|---|---|
| All (n = 22) | 7.64 ± 1.81 | 1.30 ± 0.10 | 27.9 ± 7.05 |
| CO (n = 17) | 7.88 ± 1.97 | 1.31 ± 0.11 | 28.7 ± 7.40 |
| CP (n = 5) | 6.80 ± 0.84 | 1.27 ± 0.08 | 25.2 ± 5.40 |
| Class | Values before Augmentation | Values after Augmentation | Variables per Patient |
|---|---|---|---|
| CO | 100 | 2000 | 10 |
| CP | 100 | 2000 | 10 |
| Parameter | Kernel Function | Kernel Scale | C | Accuracy |
|---|---|---|---|---|
| CoA1 | Cubic | Auto | 1 | 91.30% |
| CoA2 | Gaussian | 30 | 10 | 85.71% |
| RMS | Gaussian | 30 | 10 | 85.00% |
| MAV | Cubic | Auto | 1 | 75.00% |
| iEMG | Cubic | Auto | 1 | 90.00% |
| Parameter | K | Distance Metric | Accuracy |
|---|---|---|---|
| CoA1 | 10 | cosine | 91.30% |
| CoA2 | 10 | cosine | 95.24% |
| RMS | 10 | cosine | 95.00% |
| MAV | 10 | L1 | 90.00% |
| iEMG | 10 | cosine | 94.67% |
| Parameter | P | Split Criterion | Accuracy |
|---|---|---|---|
| CoA1 | 32 | MVR | 78.26% |
| CoA2 | 16 | Gini | 90.48% |
| RMS | 32 | MVR | 90.17% |
| MAV | 8 | MVR | 81.00% |
| iEMG | 4 | Gini | 80.00% |
| Combination | Classifier | Accuracy | Precision | Sensitivity | Specificity | NPV | F1 Score | AUC Score |
|---|---|---|---|---|---|---|---|---|
| CoA1+RMS | SVM | 88.2 | 82.0 | 81.5 | 75.5 | 80.0 | 81.5 | 94.5 |
| KNN | 93.2 | 94.0 | 88.0 | 94.0 | 90.0 | 92.0 | 98.0 | |
| DT | 89.3 | 89.0 | 78.5 | 78.5 | 76.5 | 76.5 | 84.3 | |
| CoA1+MAV | SVM | 83.2 | 81.5 | 71.5 | 83.5 | 74.5 | 76.0 | 86.5 |
| KNN | 90.7 | 89.5 | 82.5 | 89.5 | 85.0 | 86.0 | 94.0 | |
| DT | 84.7 | 83.7 | 78.5 | 76.0 | 74.0 | 79.0 | 85.3 | |
| CoA1+iEMG | SVM | 90.7 | 88.0 | 80.0 | 88.5 | 81.0 | 84.0 | 95.5 |
| KNN | 93.2 | 91.0 | 93.0 | 88.5 | 91.0 | 91.0 | 97.0 | |
| DT | 84.2 | 83.0 | 76.0 | 75.5 | 72.5 | 74.5 | 82.0 | |
| CoA2+RMS | SVM | 85.4 | 77.5 | 73.0 | 74.0 | 76.0 | 75.0 | 87.0 |
| KNN | 95.1 | 94.5 | 92.0 | 92.0 | 92.0 | 93.0 | 97.5 | |
| DT | 90.4 | 91.0 | 90.0 | 92.0 | 91.0 | 90.0 | 90.5 | |
| CoA2+MAV | SVM | 80.4 | 77.0 | 63.0 | 82.0 | 70.5 | 69.5 | 79.0 |
| KNN | 92.6 | 89.0 | 88.0 | 86.0 | 87.0 | 88.0 | 93.0 | |
| DT | 85.8 | 85.5 | 81.0 | 83.0 | 82.5 | 82.5 | 85.5 | |
| CoA2+iEMG | SVM | 87.9 | 83.5 | 71.5 | 87.0 | 77.0 | 77.5 | 90.0 |
| KNN | 95.1 | 90.0 | 95.0 | 92.0 | 93.0 | 92.5 | 98.0 | |
| DT | 85.3 | 85.0 | 79.5 | 81.5 | 79.0 | 78.5 | 82.0 | |
| RMS+MAV | SVM | 80.0 | 76.5 | 73.0 | 72.0 | 74.5 | 73.5 | 81.0 |
| KNN | 92.5 | 88.5 | 90.0 | 88.5 | 89.0 | 88.5 | 94.0 | |
| DT | 85.6 | 84.0 | 70.0 | 83.0 | 70.5 | 71.0 | 83.5 | |
| RMS+iEMG | SVM | 87.5 | 83.0 | 81.5 | 77.0 | 81.0 | 81.0 | 88.5 |
| KNN | 95.0 | 92.5 | 94.0 | 91.0 | 93.0 | 93.0 | 98.0 | |
| DT | 85.1 | 85.0 | 66.0 | 88.0 | 71.0 | 69.0 | 82.0 | |
| CoA1+RMS+MAV | SVM | 83.8 | 80.0 | 75.3 | 77.0 | 76.3 | 76.0 | 85.7 |
| KNN | 92.1 | 90.5 | 86.5 | 87.5 | 88.0 | 88.0 | 92.5 | |
| DT | 86.5 | 85.7 | 76.0 | 78.0 | 70.3 | 78.0 | 85.0 | |
| CoA1+RMS+iEMG | SVM | 88.8 | 84.3 | 81.0 | 80.3 | 80.7 | 82.0 | 90.0 |
| KNN | 93.8 | 91.3 | 92.0 | 91.5 | 92.0 | 92.0 | 96.0 | |
| DT | 86.2 | 86.0 | 74.0 | 81.0 | 70.0 | 71.0 | 85.0 | |
| CoA1+MAV+iEMG | SVM | 85.4 | 84.0 | 74.3 | 85.7 | 77.0 | 80.0 | 89.0 |
| KNN | 92.1 | 89.5 | 88.0 | 87.0 | 88.0 | 88.0 | 92.5 | |
| DT | 83.1 | 83.7 | 73.0 | 75.3 | 73.0 | 73.0 | 83.0 | |
| CoA2+RMS+MAV | SVM | 81.9 | 79.0 | 69.7 | 76.0 | 73.7 | 73.3 | 84.0 |
| KNN | 93.4 | 90.5 | 91.5 | 90.5 | 91.0 | 91.0 | 94.5 | |
| DT | 87.2 | 86.3 | 76.7 | 86.0 | 77.3 | 78.0 | 88.0 | |
| CoA2+RMS+iEMG | SVM | 86.9 | 81.3 | 75.3 | 79.3 | 78.0 | 78.0 | 88.0 |
| KNN | 95.1 | 92.5 | 93.0 | 92.5 | 93.0 | 93.0 | 98.0 | |
| DT | 86.9 | 87.0 | 74.0 | 89.3 | 77.7 | 75.0 | 87.0 | |
| CoA2+MAV+iEMG | SVM | 83.6 | 81.0 | 68.7 | 84.7 | 74.3 | 75.0 | 85.0 |
| KNN | 93.4 | 90.0 | 91.0 | 90.0 | 90.5 | 90.5 | 95.0 | |
| DT | 83.8 | 83.5 | 80.7 | 83.3 | 80.0 | 80.0 | 85.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lenkevitciute, K.; Ziziene, J.; Daunoraviciene, K. An Advanced Technique for the Detection of Pathological Gaits from Electromyography Signals: A Comprehensive Approach. Machines 2024, 12, 581. https://doi.org/10.3390/machines12080581
Lenkevitciute K, Ziziene J, Daunoraviciene K. An Advanced Technique for the Detection of Pathological Gaits from Electromyography Signals: A Comprehensive Approach. Machines. 2024; 12(8):581. https://doi.org/10.3390/machines12080581
Chicago/Turabian StyleLenkevitciute, Karina, Jurgita Ziziene, and Kristina Daunoraviciene. 2024. "An Advanced Technique for the Detection of Pathological Gaits from Electromyography Signals: A Comprehensive Approach" Machines 12, no. 8: 581. https://doi.org/10.3390/machines12080581
APA StyleLenkevitciute, K., Ziziene, J., & Daunoraviciene, K. (2024). An Advanced Technique for the Detection of Pathological Gaits from Electromyography Signals: A Comprehensive Approach. Machines, 12(8), 581. https://doi.org/10.3390/machines12080581







