1. Introduction
The axle box bearing is one of the important components of high-speed train bogies [
1], and its operating state is crucial to the safety of the train. The type of axle box bearing is mostly a rolling bearing. With an increase in operation time, pitting and peeling may form between the contact surfaces of various components inside the bearing. With the relative rotation between components, repetitive pulse impacts are generated. In an ideal situation, these pulse impacts are periodic, but in an actual situation, some additional impacts and disturbances are often pseudo-cyclostationary, such as the vibration impact between train wheels and rails and the randomness of relative sliding between bearing components, which increase the uncertainty of vibration changes, reduce the signal-to-noise ratio (SNR) of the signal [
2], and lead the vibration acceleration change in the bearing to be pseudo-cyclostationary. It is often difficult to extract characteristic frequencies directly by Fourier transform [
3]. Therefore, it is necessary to carry out research on the signal model and signal processing method of bearings and reduce the interference of irrelevant signals through various methods, improve the proportion of periodic impact components in the signal, and make it easier to extract the fault frequency of bearings.
The signal processing methods of bearings can be divided into time-domain, frequency-domain, and joint time–frequency-domain methods. Some scholars have established time-domain signal characteristic indicators, such as the sparsity impact measure index (SIMI) [
4], multiscale symbolic dynamic entropy (MSDE) [
5], and some representative statistical metrics in the time domain [
6]. In the study of frequency-domain signal processing methods, there are also novel methods, such as the amplitude modulation bispectrum [
7] and product envelope spectrum optimization-gram [
8]. Some joint time–frequency-domain methods, such as the time–frequency spectral amplitude modulation method [
9] and the novel time–frequency modulation bispectrum [
10], have also achieved good results in bearing fault diagnosis. Some researchers have also studied signal denoising decomposition algorithms, such as adaptive mode decomposition, the improved morphological filtering algorithm, the blind deconvolution algorithm, etc., which provide novel and effective solutions for the research of the bearing fault diagnosis method, and also lay a solution foundation for the proposed fault diagnosis method in this paper.
With the development of bearing monitoring technology and the improvement of safety monitoring requirements for mechanical systems, the fault diagnosis method based on a single signal has gradually developed into multi-signal fault diagnosis methods and research on bearing fault diagnosis based on multi-signal fusion has also increased. During actual operation, the axle box bearing is subjected to vibration and impact from multiple directions, including lateral, longitudinal, and vertical directions between the wheel and rail, resulting in complex spatial curves for the motion trajectories of the internal components of the bearing. The vibration acceleration of the bearing is not a single-direction signal, which needs to be decomposed in a three-dimensional coordinate system to completely represent the vibration condition of the bearing. Therefore, the bearing signal collected by the triaxial accelerometer is more comprehensive, and how to reasonably use the fusion of three-dimensional vibration acceleration signals and other multivariate signals to improve the accuracy of bearing fault diagnosis has become a research hotspot [
11]. Multi-signal data fusion can be divided into data-level, feature-level, and decision-level fusion [
12]. The fusion based on the data level focuses more on the physical attributes of the signal itself and the external interference to the signal can be reduced by the weighting, linear combination, the Kalman filter [
13] and other methods. The fusion of the feature level pays more attention to the extraction of signal features [
14], which can be obtained from different physical data through continuous dimension reduction and fusion. The fusion of the decision level focuses on the role of probability in multi-decision fusion, such as the use of the Dempster–Shafer (DS) information fusion theory [
15] and generalized methods [
16] in fusion.
In the processing of multi-dimensional signals, such as three-dimensional vibration acceleration [
17], various multi-dimensional signal analysis methods have been widely used in bearing fault diagnosis, such as bivariate empirical mode decomposition (BEMD) [
18], trivariate empirical mode decomposition (TEMD) [
19], multivariate empirical mode decomposition (MEMD) [
20], noise assisted multivariate empirical mode decomposition (NA-MEMD) [
21], multivariate variational mode decomposition (MVMD) [
22], multivariate complex modulation model decomposition (MCMMD) [
23], multivariate local characteristic-scale decomposition (MLCD) [
24], and other methods. These types of decomposition methods can achieve synchronous correlation analysis of multi-signals, map the signal to the multi-dimensional space hypersphere direction vector, obtain the envelope lines in various directions, and then perform feature extraction. They integrate the fusion of the data level and the feature level and play a role in promoting the research into using multivariate signals for fault diagnosis. However, this type of method often takes a long time in obtaining ideal computational results. Principal component analysis (PCA) is a commonly used method for fast data dimension reduction, and it is also used in signal fusion [
25]. Shahdoosti et al. [
26] proposed an optimal filter using the PCA fusion method for image fusion, which improved the quality of the image. Mochammad et al. [
27] used PCA to fuse the characteristics of bearings in multiple time windows and established a standard for detecting the degradation performance of bearings. Bashir et al. [
28] used stationary wavelet transform (SWT) and PCA to fuse image input by multiple sensors, and the results showed that PCA had a better effect on image inputs with different brightness levels.
PCA is mostly used for image fusion and feature dimensionality reduction in neural networks and is rarely used in data-level fusion algorithms. Therefore, PCA is used to fuse multi-dimensional data in the data level in this paper, the filter bank is used to filter the fused signal to highlight the periodic pulse impact component, and the fault frequency of the signal is extracted by demodulation.
The remaining sections are as follows.
Section 2 introduces the signal processing methods used in this paper and proposes improved average kurtosis and a dimensionless characteristic index for selecting the optimal signal.
Section 3 is the simulation signal analysis of the simulation signal to verify the effectiveness of PCA fusion and the effectiveness of the proposed method process for the simulation signal with the inclusion of prior knowledge.
Section 4 is the experimental signal analysis, and the fault diagnosis method is verified by four fault-bearing cases experimental signals collected by an axle box bearing test rig.
Section 5 presents the conclusions of this paper.
2. Theoretical Background and the Proposed Method
Bearings often produce vibrations in multiple directions during operation. The vibration data are highly nonlinear and often contain strong noise [
29]. In order to comprehensively and accurately evaluate the operating state of bearings, a method for bearing fault diagnosis by comprehensively using a three-directional vibration acceleration signal is proposed in this paper.
2.1. PCA Data Fusion Denoising Method
In statistics, PCA is a technique to simplify data sets by using linear transformations to represent the original high-dimensional data with new coordinate coefficients, arranged in order of data variance size and dimensionality reduction [
30]. The purpose of PCA is to find a new set of orthogonal bases that maximize the distance between data after projecting multi-dimensional signals onto the plane formed by the orthogonal bases; the similarity between the multi-dimensional signals is maintained as much as possible, and the components with weak correlation are gradually removed. The maximum amount of original information is preserved with the least number of dimensions.
In signal processing and analysis, the signal containing periodic impulses often has a relatively large variance, while interference noise has a small variance. In order to make the signal obtain a higher SNR and reduce the interference of noise, the PCA dimension reduction method can be used to extract a new signal with a large variance as the optimized signal to achieve the purpose of noise reduction.
The PCA algorithm is illustrated with the example of reducing a two-dimensional array to a one-dimensional array.
The two-dimensional array
X is as follows:
To simplify the calculation of variance in subsequent processes, each dimension of X can be removed from the mean value to make the mean of each dimension equal to 0.
It is hard for a two-dimensional array to contain all the data points on a straight line, and the two-dimensional coordinate system always has its own orthonormal basis. The data points can be described as linear combinations of orthonormal bases in the coordinate system. The variance of the projection of matrix
X onto the orthogonal basis
u1 is as follows:
where
xi is the
i-th column vector in matrix
X,
xi = [
x1,i x2,i]
T. Since
n and
XXT are constants, the above equation can be simplified as follows:
According to the concept of PCA, the
u1 corresponding to the maximum
Var1 needs to be solved. The constrained problem can be solved according to the Lagrange operator [
31]:
The extremal function is constructed as follows:
When
, the above equation can be simplified as follows:
Therefore, the key step in the process of solving PCA dimensionality reduction fusion is to solve the eigenvalues and eigenvectors of
Q [
32], where
Q is the covariance matrix of matrix
X. The eigenvalues of the covariance matrix are sorted from large to small, and the corresponding number of eigenvalues can be selected for dimensionality reduction and fusion of the corresponding dimensions, and then the signal with higher SNR is obtained.
PCA, as a powerful data dimensionality reduction method, is able to transform multiple variables in the original data into a few principal components by linear transformations that are able to retain most of the information of the original data while removing noise. PCA achieves dimensionality reduction in the data by finding the directions of maximum variance in the data, using these directions as principal components. Therefore, the benchmark of the maximum variance direction will also be used as the benchmark of the subsequent signal dimension reduction fusion in this paper, so that the most relevant part of the signals can be retained.
2.2. Bandpass Filter Bank Signal Denoising Method
The collected signals are often accompanied by strong random pulse interference. The signal processing method, based on spectral kurtosis [
33], is a relatively effective method for filtering and noise reduction, which is the process of signal filtering from different bandpass filters and selecting the signal corresponding to the optimal kurtosis value. In the case of complex signals, due to the sensitivity of kurtosis to single pulse impulses, the optimal bandwidth selected may likely lose information due to the extremely short bandwidth. Consequently, based on the processing method of spectrum kurtosis, an improved kurtosis index is adopted to avoid the interference of the single pulse impact component on the results in this section. In parallel, a more reasonable filter bank is established through the subsection processing of the whole frequency band, and the bandpass filtering of the signal is measured adaptively to extract the characteristic information.
2.2.1. FIR Bandpass Filter Bank
The filters of the filter bank are Finite Impulse Response (FIR) filters [
34]. In order to balance the time resolution and frequency resolution of the signal after spectrum segmentation, the number of filters in the filter bank is determined according to the length of the original signal as shown in the following equation:
where
M is the number of frequency domain segments,
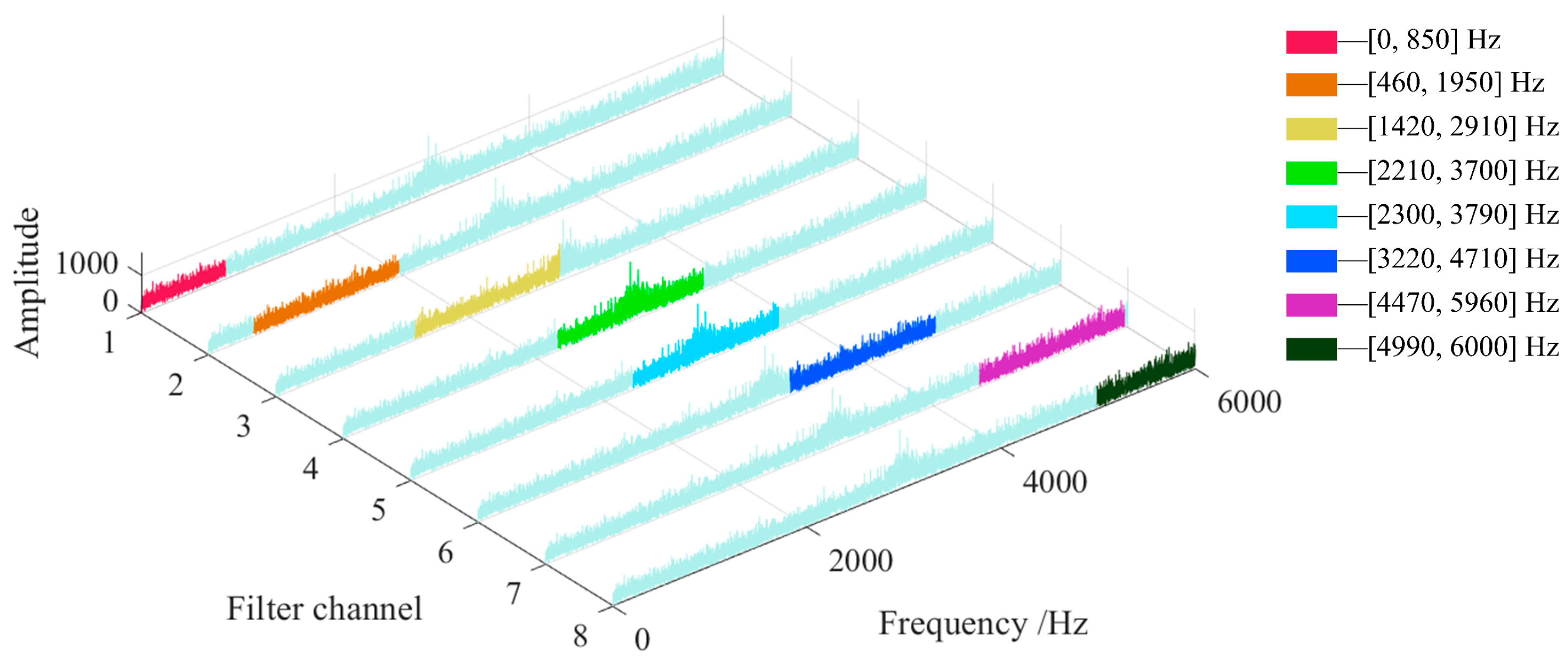
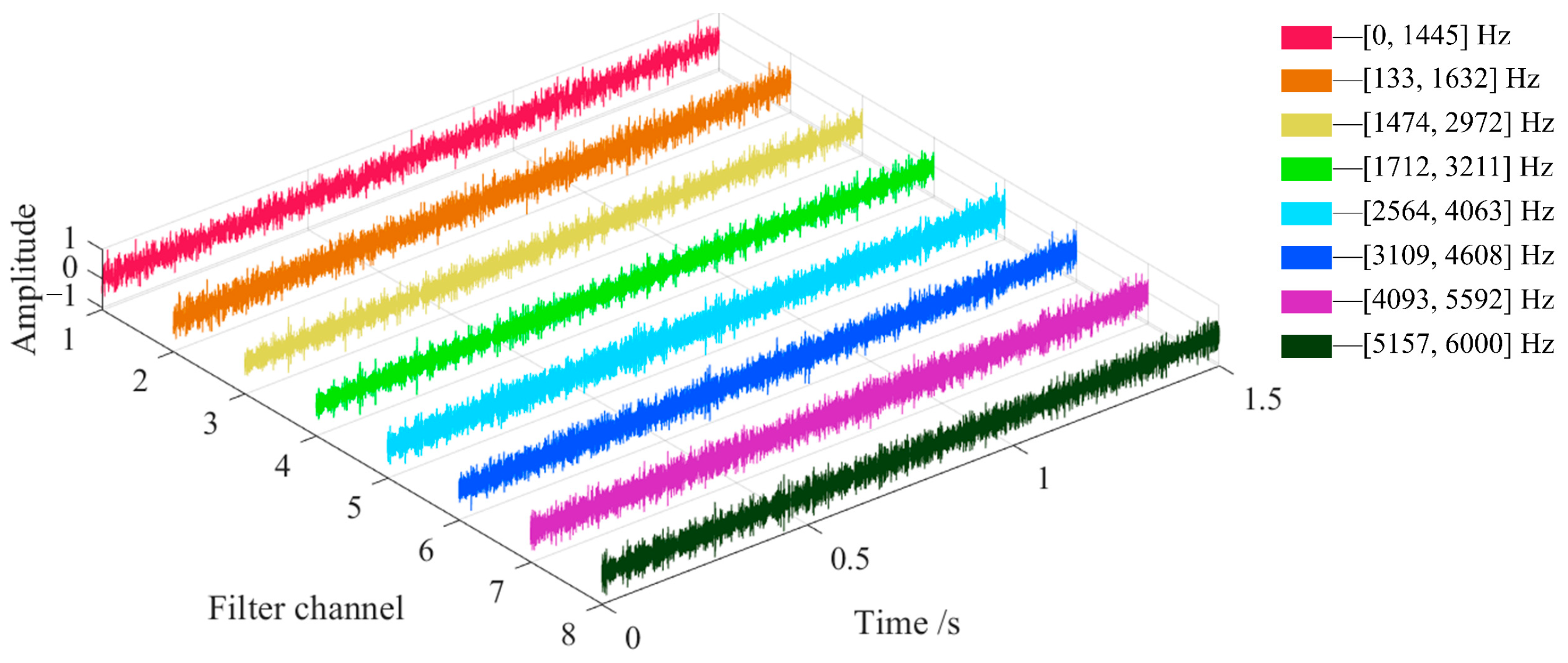
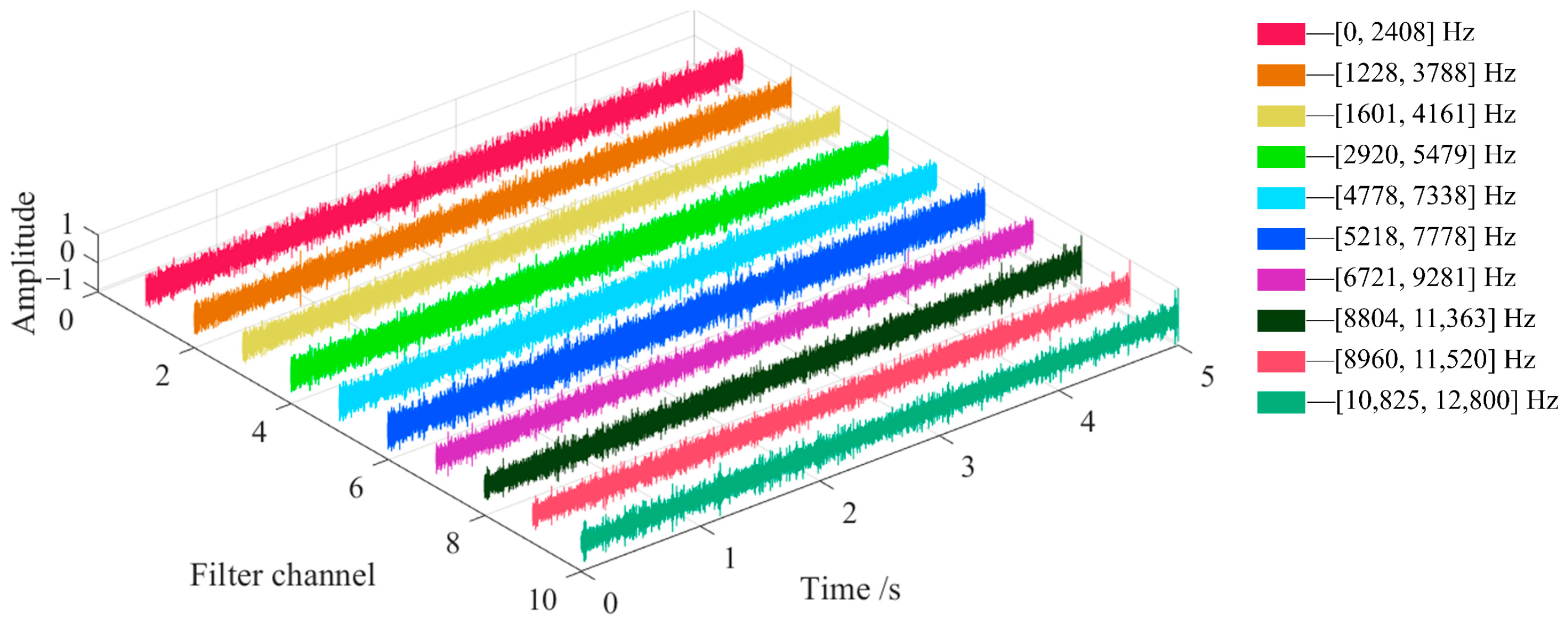
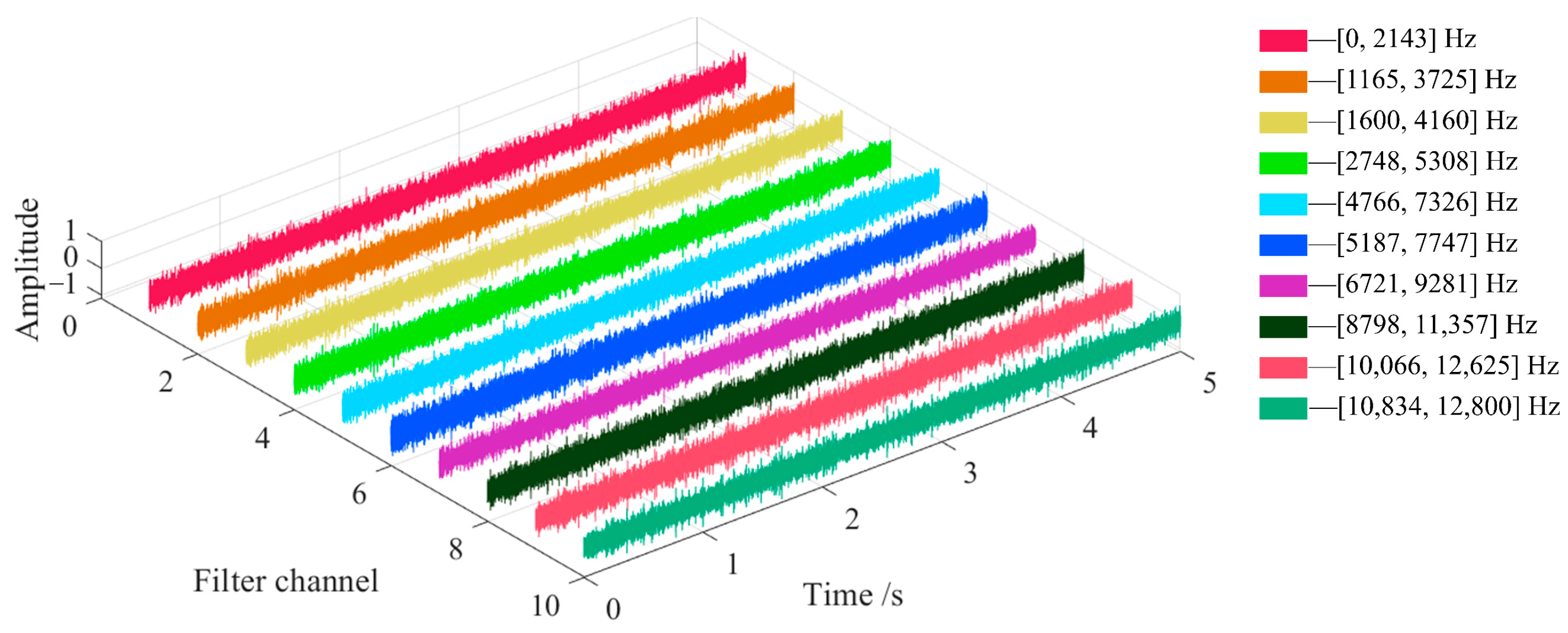
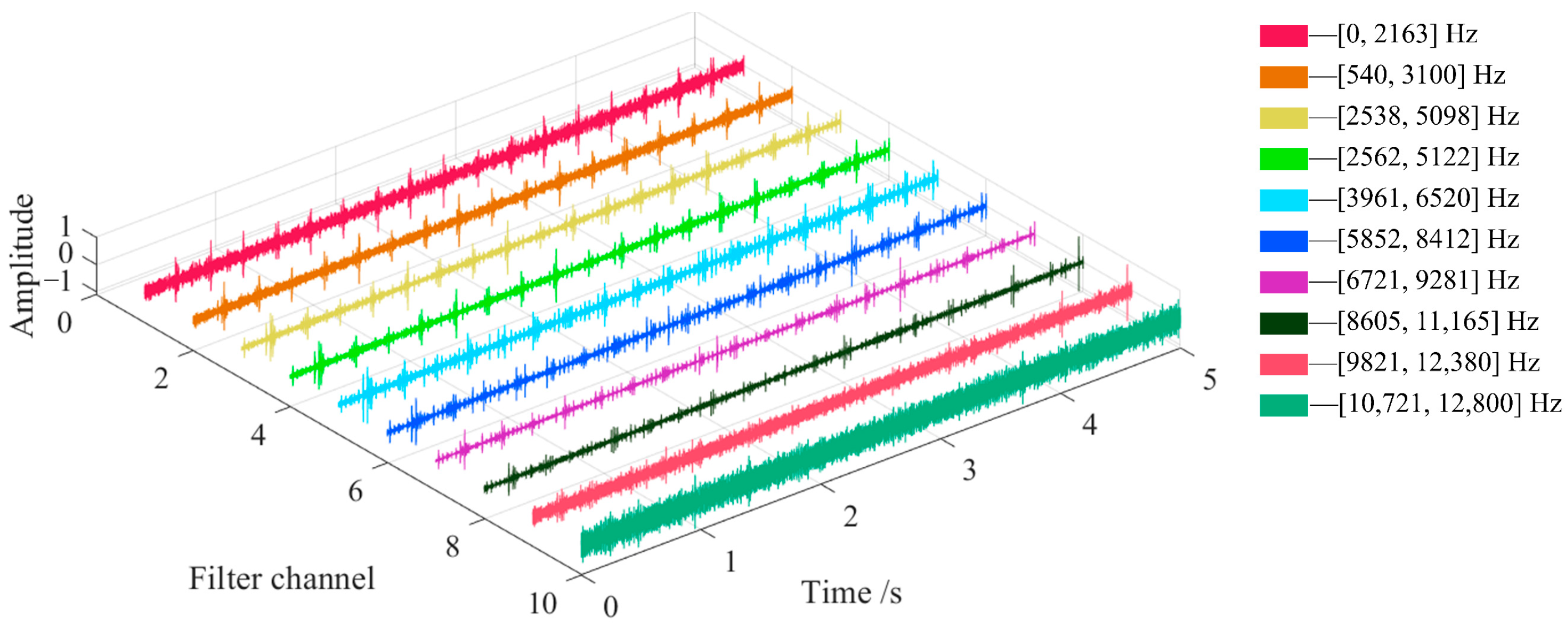
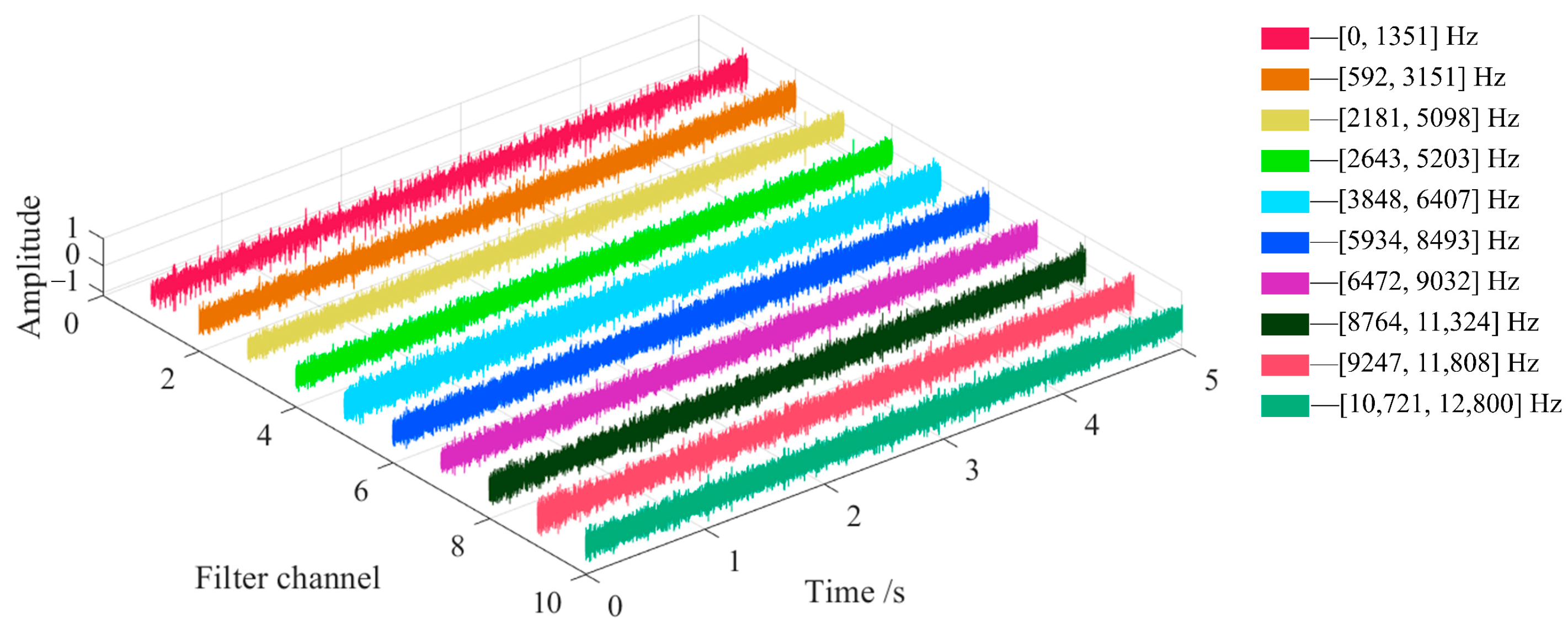
N is the number of original discrete signal sample points, and the calculation result is rounded down. If there is a discrete sequence of 18,000 sample points and the data sampling frequency is 12,000 Hz, the signal frequency spectrum can be divided into 8 components within the frequency range of 0–6000 Hz, and the frequency corresponding to the maximum amplitude in each component is taken as the center frequency of the bandpass filter. In order to cover the entire frequency range, the bandwidth length is twice the length of the frequency component, and the filter window function is selected as the Blackman window. The decomposition of the frequency bandwidth occupied by the individual bandpass filters of the signal in the frequency domain is shown in
Figure 1.
In
Figure 1, it can be seen that the lower-cut-off frequency and upper-cut-off frequency of each filtering channel are different, and the upper-cut-off frequency of the previous channel is larger than the upper-cut-off frequency of the next channel. After determining the center frequency, bandwidth and window function type of each filter, the filtered signal corresponding to different order filter coefficients can be calculated, and the optimal filtered signal under the filter can be selected as the output result. The different bandpass filters are arranged in order of increasing center frequency to form a multi-channel bandpass filter bank of the signal. The amplitude of the filtered signal of each bandpass filter is linearly scaled to the interval of [−1, 1], and the results are combined to form the final output of the FIR bandpass filter bank.
2.2.2. Improved Average Kurtosis
In order to avoid the interference of monopulse impact in the signal, a characteristic index named improved average kurtosis is proposed, as shown in Equation (8):
where KT
final is the improved average kurtosis,
K is the vector composed of the kurtosis of each component after dividing the original time-domain signal into
z consecutive components,
Kmin is the minimum value in
K, and
Kmax is the maximum value in
K.
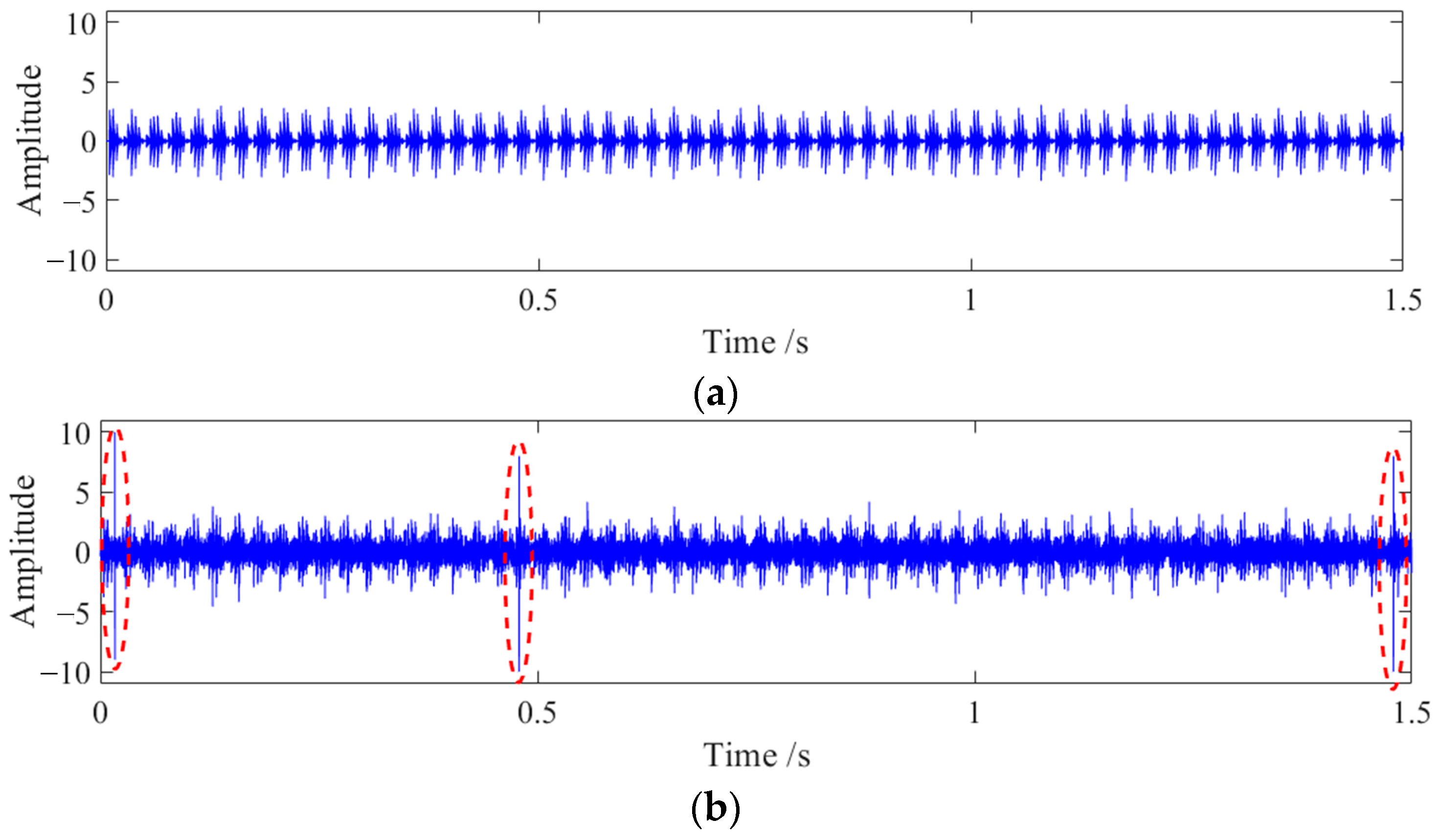
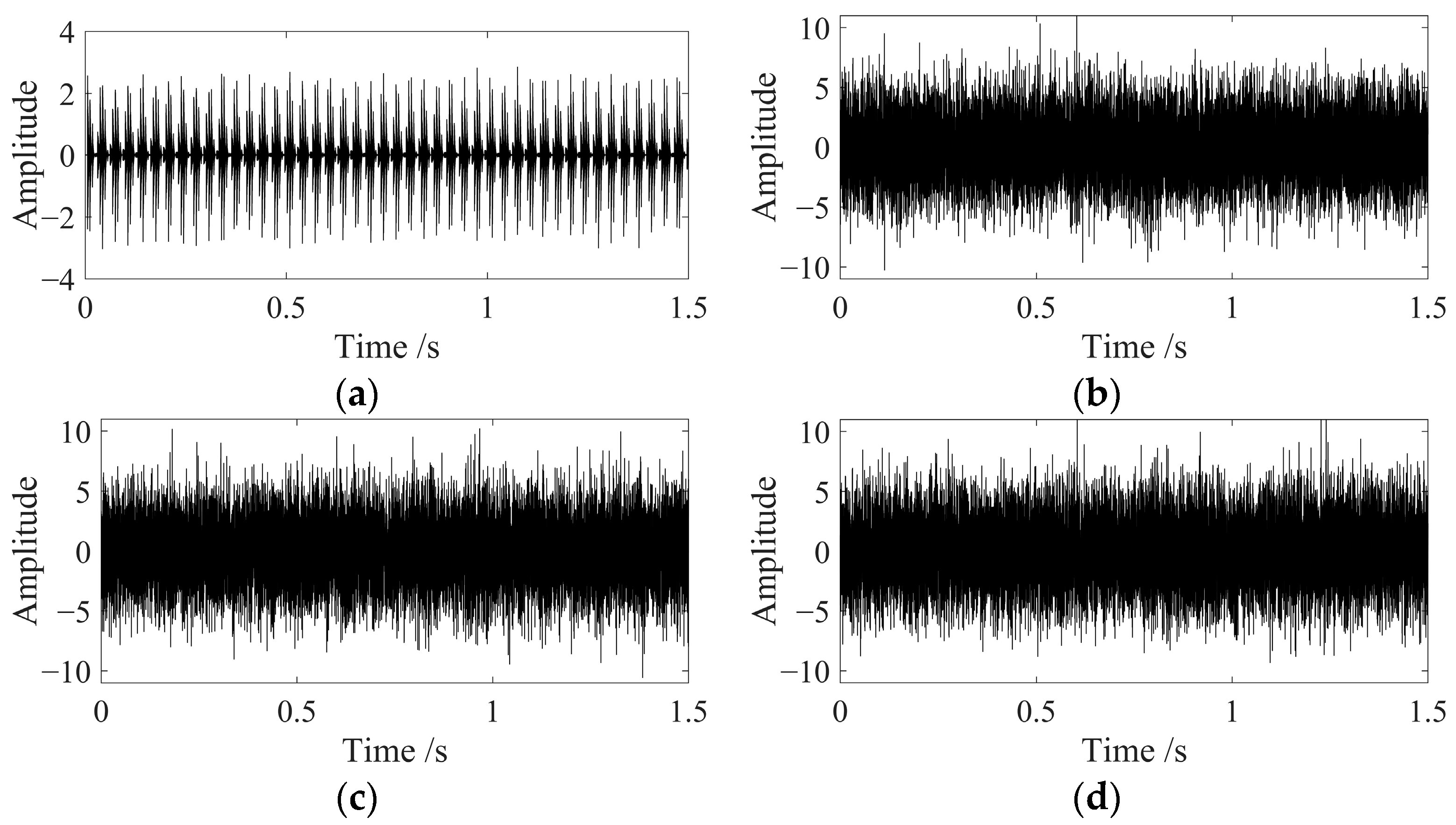
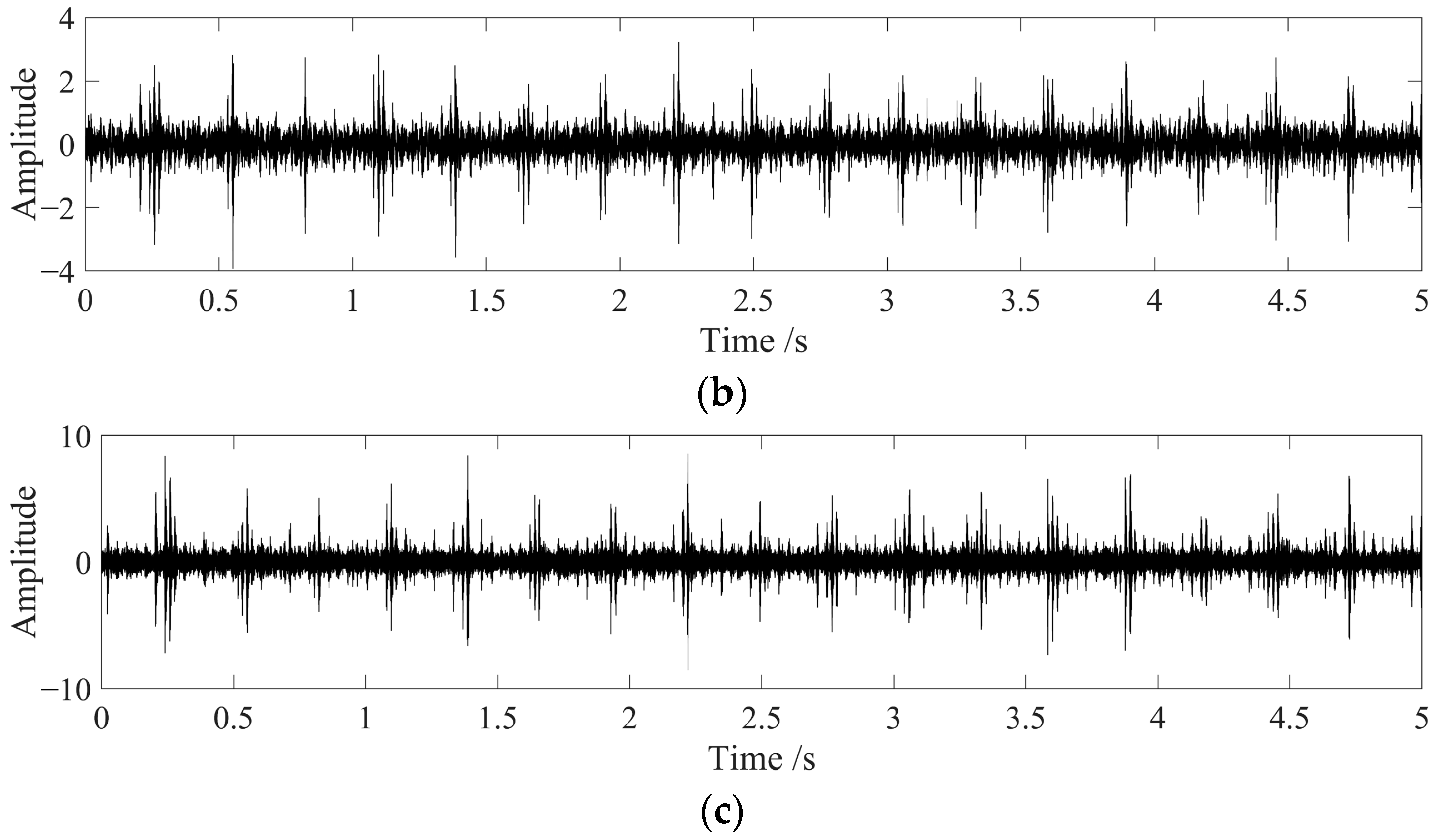
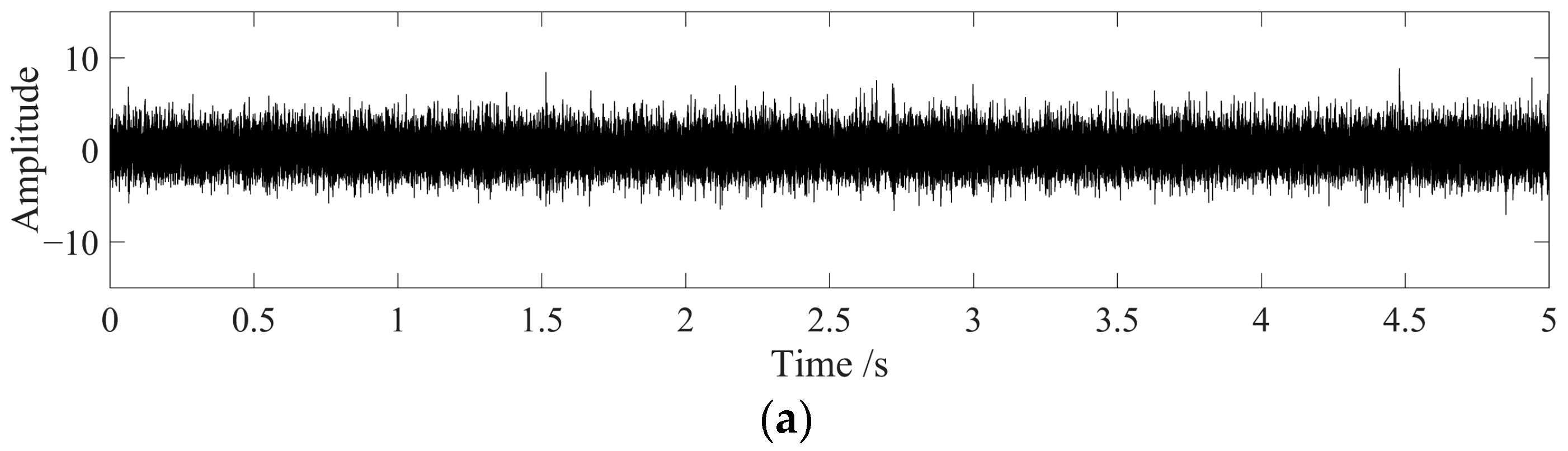
If there are a few single pulse impact components with large amplitude in the signal, these will have a significant impact on the calculation of the signal kurtosis, causing an abnormal increase in the kurtosis and affecting the judgment of the overall change in the signal. During the iterative filtering process of the signal, it is easy to cause an abnormal increase in the amplitude near the endpoint due to the continuous accumulation of endpoint values. If the kurtosis is used to select the optimal filtered signal, it is easy to produce a judgment with large errors. Two sets of signals are shown in
Figure 2.
The signal in
Figure 2a is a periodic amplitude-modulated signal without noise, while the signal in
Figure 2b is a combination of the signal in
Figure 2a with −5 dB of white Gaussian noise, and also contains three large amplitude monopulse signals. The kurtosis of the signals in (a) and (b) are calculated, and signals are divided into 10 components to calculate the improved average kurtosis KT
final. The kurtosis of the signal in (a) is 6.5997, and the KT
final is 5.2971. The kurtosis of the signal in (b) is 7.6692, and the KT
final is 1.8780. If the maximum kurtosis selection method is used, it will be judged that the quality of the signal in (b) is better than that in (a), which is inconsistent with the actual situation. Using the characteristic index proposed in this section can exclude the influence of monopulse impact and improve the reliability of judgment results.
By iterating the filters of different orders continuously, the filtered signal with the largest KT
final among the filtered results of different orders is selected as the optimal filtered result of the bandpass filter, and the final output result of the FIR bandpass filter bank in
Section 2.2.1 is obtained.
2.3. Analytic Energy Operator Demodulation Method
When the signal components are complex, there are often resonance frequency bands of the mechanical signal acquisition system with large energy levels in practice; it is difficult to find the characteristic frequency of the signal in the spectrum directly using Fourier transform. Consequently, the signal demodulation method is often used to remove the interference of the system itself and the influence of high-frequency resonance bands, and improve the accuracy of fault frequency extraction [
35].
The concept of AEO is developed from the analytic signal, which combines the time domain representation of the signal with the corresponding Hilbert transform representation to form the AEO of the signal [
36,
37].
For a real-valued modulated signal
, the signal obtained by Hilbert transformation is
, and they can constitute an analytic signal, as shown in Equation (9):
The instantaneous amplitude and phase of the analytic signal
are as follows:
The instantaneous frequency can be obtained by differentiating the instantaneous phase as follows:
If
is taken as the quantity to be calculated, it can represent the signal amplitude demodulation and frequency demodulation components, and so it is defined as follows:
where
is the AEO, which can be used as the demodulation form of the original time domain signal to further extract the characteristic components of the signal.
2.4. Optimal Demodulation Component Selection Method
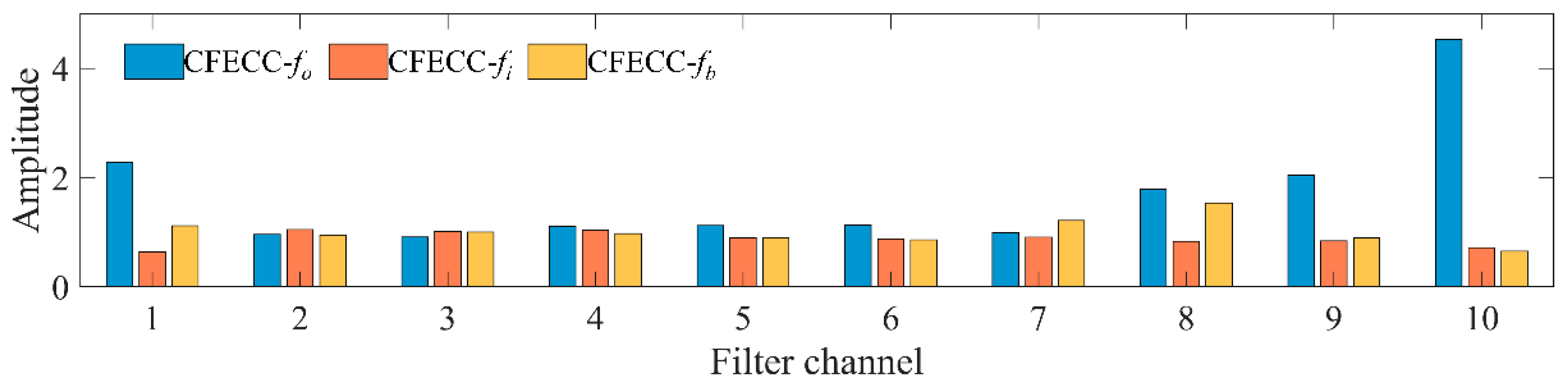
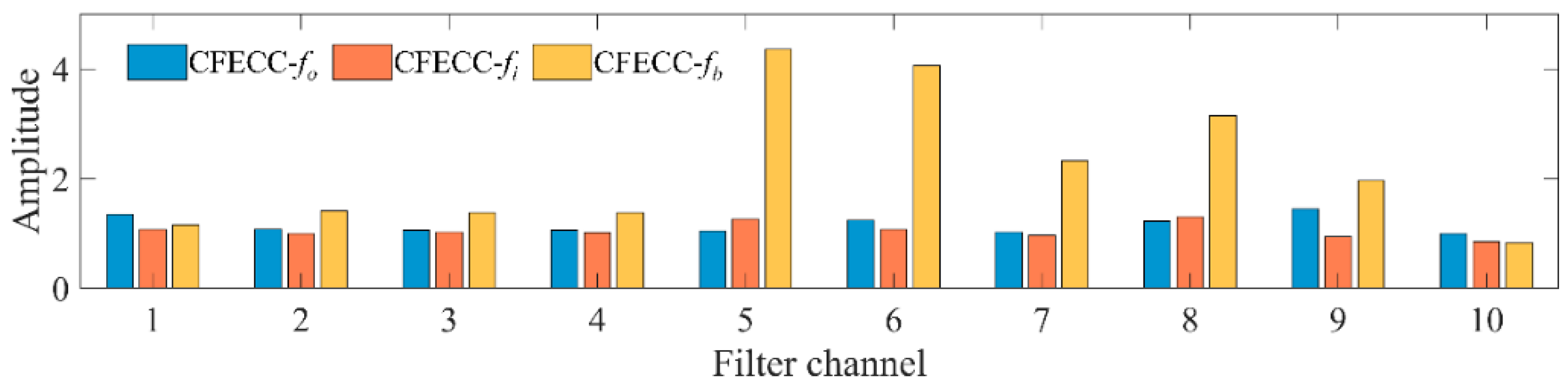
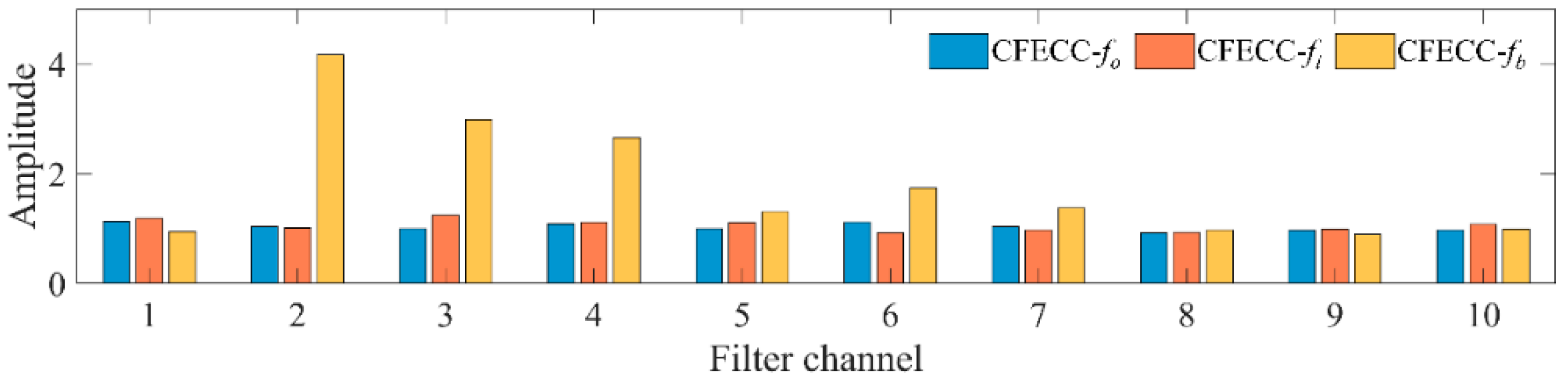
AEO demodulation is performed on the final output result of the FIR bandpass filter bank. The characteristic information in different demodulation spectrums is also different, and it is necessary to find the optimal result from multiple spectrums to extract more obvious fault characteristic frequency components as far as possible. Some characteristic indices can be used to describe the obviousness of the characteristic frequency in the spectrum, such as the characteristic frequency intensity coefficient (CFIC) [
38,
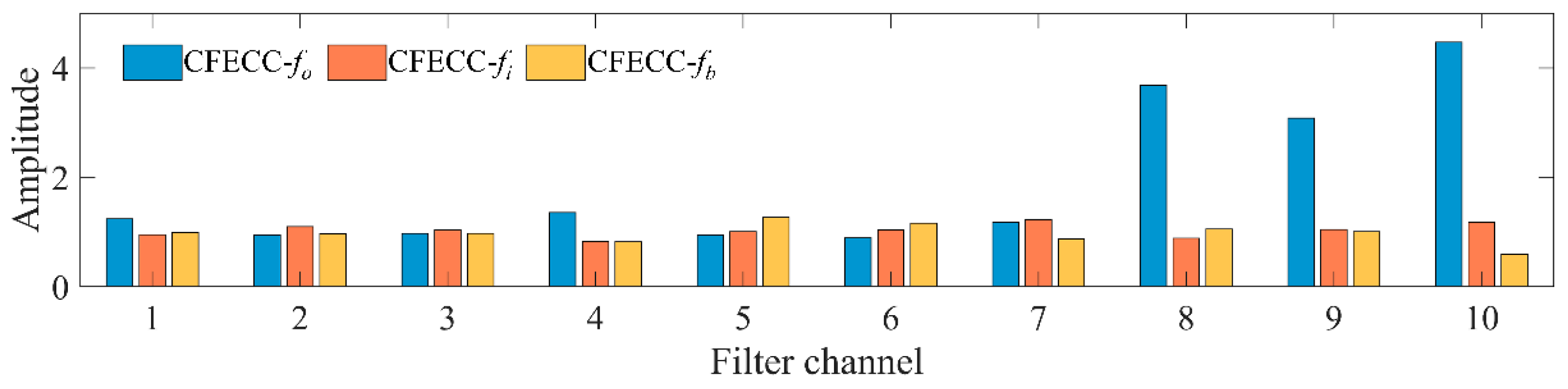
39]. In order to describe the energy prominence ability of characteristic frequencies in the spectrum within a small local frequency band, a dimensionless characteristic index called the characteristic frequency energy concentration coefficient (CFECC) is proposed for the optimal demodulation spectrum selection in this paper, as shown in Equation (14).
where
P is the selectable harmonic order of the fault characteristic frequency,
is the maximum amplitude energy in the demodulated spectrum interval
,
is the sum of each frequency amplitude energy in the corresponding interval,
L is the number of discretized frequency points of the spectrum in this interval,
fc is a fault characteristic frequency,
r is the characteristic frequency relative error range, and CFECC is the dimensionless characteristic index. By calculating the CFECC, the ratio of the amplitude energy of the fault characteristic frequency
fc and the harmonics at the first
P order in the relative error interval to the amplitude energy of the left and right adjacent intervals of the same length can be determined. The larger the CFECC is, the more concentrated the energy is in the error interval containing the characteristic frequency, and the spectrum characteristic frequency has a better representation.
2.5. Calculation of Bearing Fault Characteristic Frequency
When there is local damage in a component of the axle box bearing, the contact of other components at the damage point will produce the corresponding periodic impulse impact excitation. The excitation is different from the vibration of the normal bearing, and its duration is very short, but it has a very wide spectrum range. Different components will produce different impact cycles due to their different motion modes. Therefore, fault defects at different locations will generate different impact frequencies. These frequencies can reflect most of the faults of the bearing, so they can be regarded as the fault characteristic frequencies of the bearing [
40]. Considering the geometrical structure and rotational velocity of the bearing, the fault characteristic frequency of each bearing component can be calculated.
When the outer ring is fixed, the fault characteristic frequency of the bearing outer ring
can be calculated by Equation (15).
The fault characteristic frequency of the bearing inner ring
can be calculated by Equation (16).
The fault characteristic frequency of the bearing rolling element
can be calculated by Equation (17).
The fault characteristic frequency of the bearing cage
can be calculated by Equation (18).
In Equations (15)–(18), r is the rotational velocity of the rolling bearing, n is the number of rolling elements of the bearing; d is the diameter of the rolling element, D is the diameter of the pitch circle of the rolling bearing, and α is the contact angle of the rolling element.
By substituting the geometric parameters of the axle bearing into the fault characteristic frequency calculation equation, the fault frequency of each part of the bearing can be calculated [
41].
2.6. The Framework of the Proposed Fault Diagnosis Method
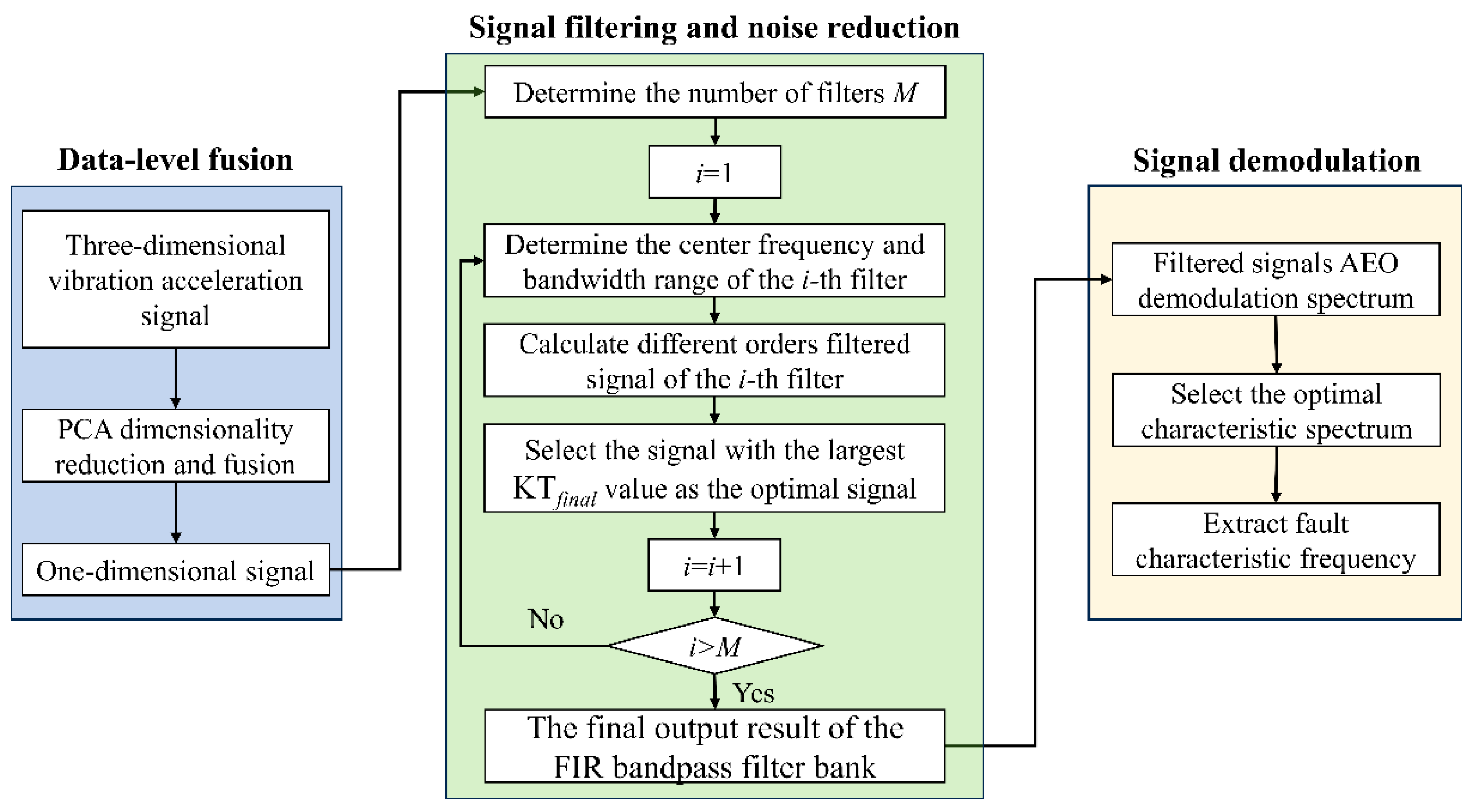
According to the above analysis and introduction, a fault diagnosis method based on PCA data fusion and bandpass filter bank signal decomposition is proposed to extract the fault characteristic frequency from bearing three-dimensional vibration acceleration signals in this paper. The framework of the method is shown in
Figure 3.
The specific process of the fault diagnosis method is as follows.
Step 1: Firstly, according to the PCA dimension reduction rule, the three-dimensional vibration acceleration signals of the bearing fuse into a one-dimensional signal.
Step 2: According to the length of the signal, determine the number of filters, the center frequency, and the bandwidth, filter the signal by the multi-channel bandpass filter bank, and solve the optimal filtering result under each filter iteratively.
Step 3: Linearly scale the amplitude of the signal from each bandpass filter to the interval [−1, 1] and form the filter bank final output result.
Step 4: Perform AEO demodulation on each filter component, solve the corresponding demodulated spectrum, calculate the CFECC of different characteristic frequencies in each spectrum, and select the characteristic frequency corresponding to the maximum value as the fault frequency and the corresponding demodulation spectrum as the final optimal demodulation spectrum.
5. Discussions
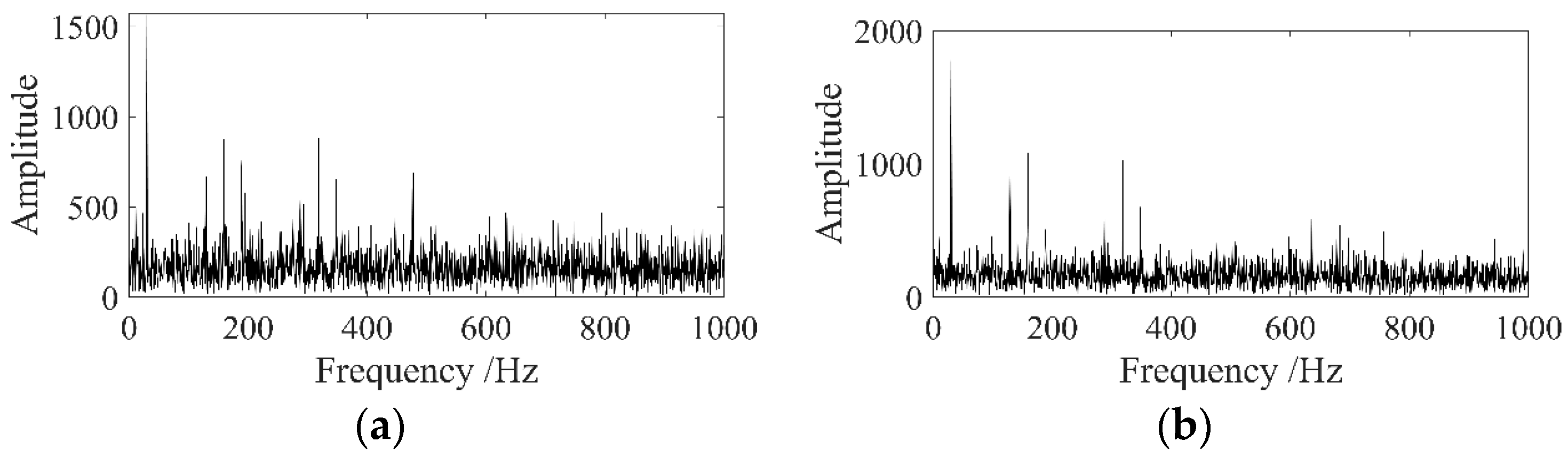
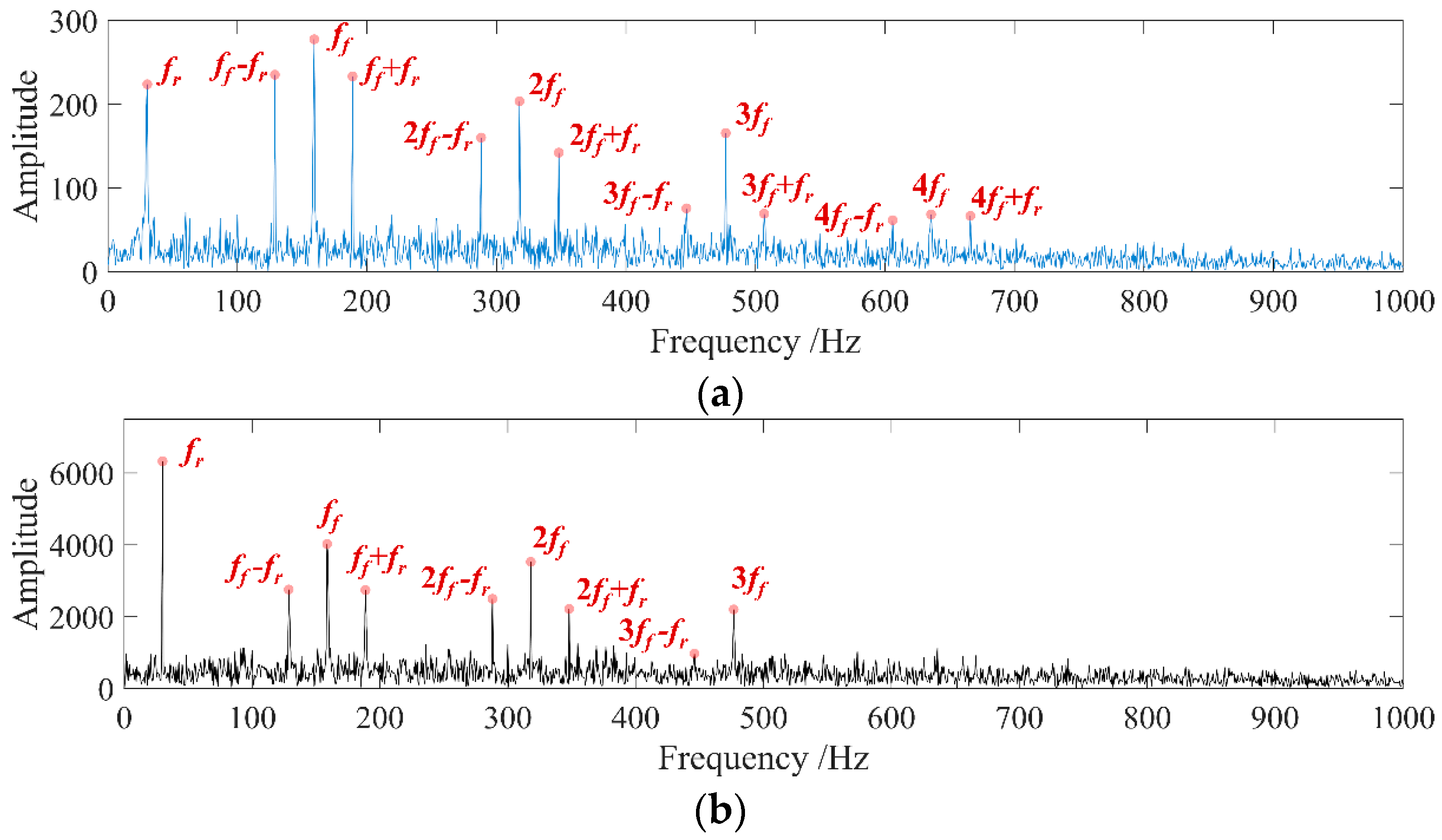
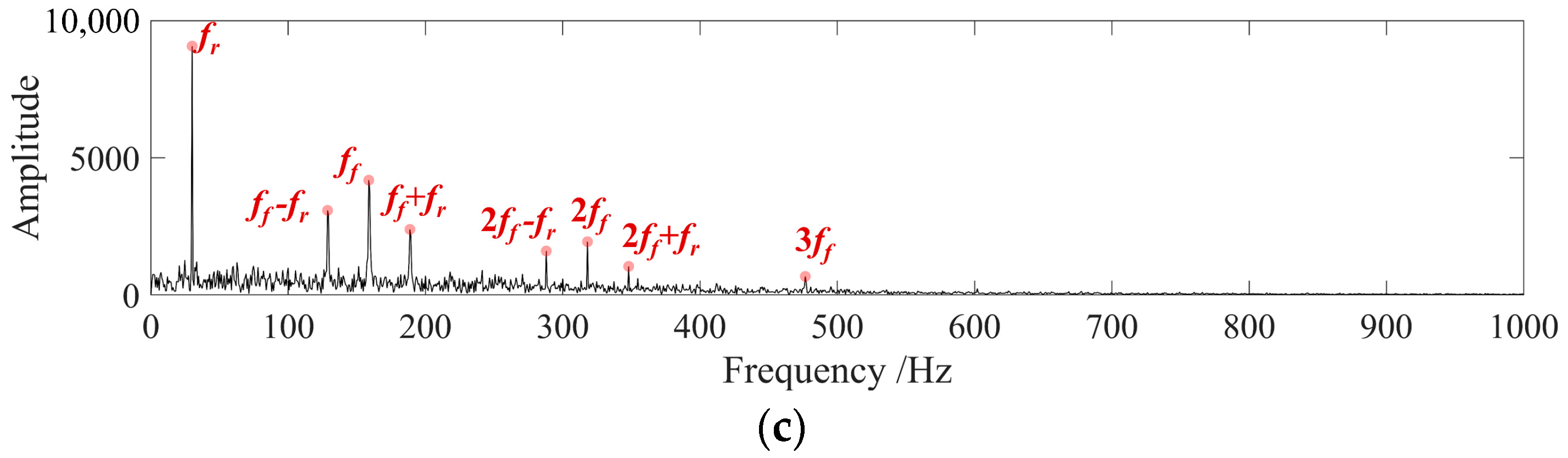
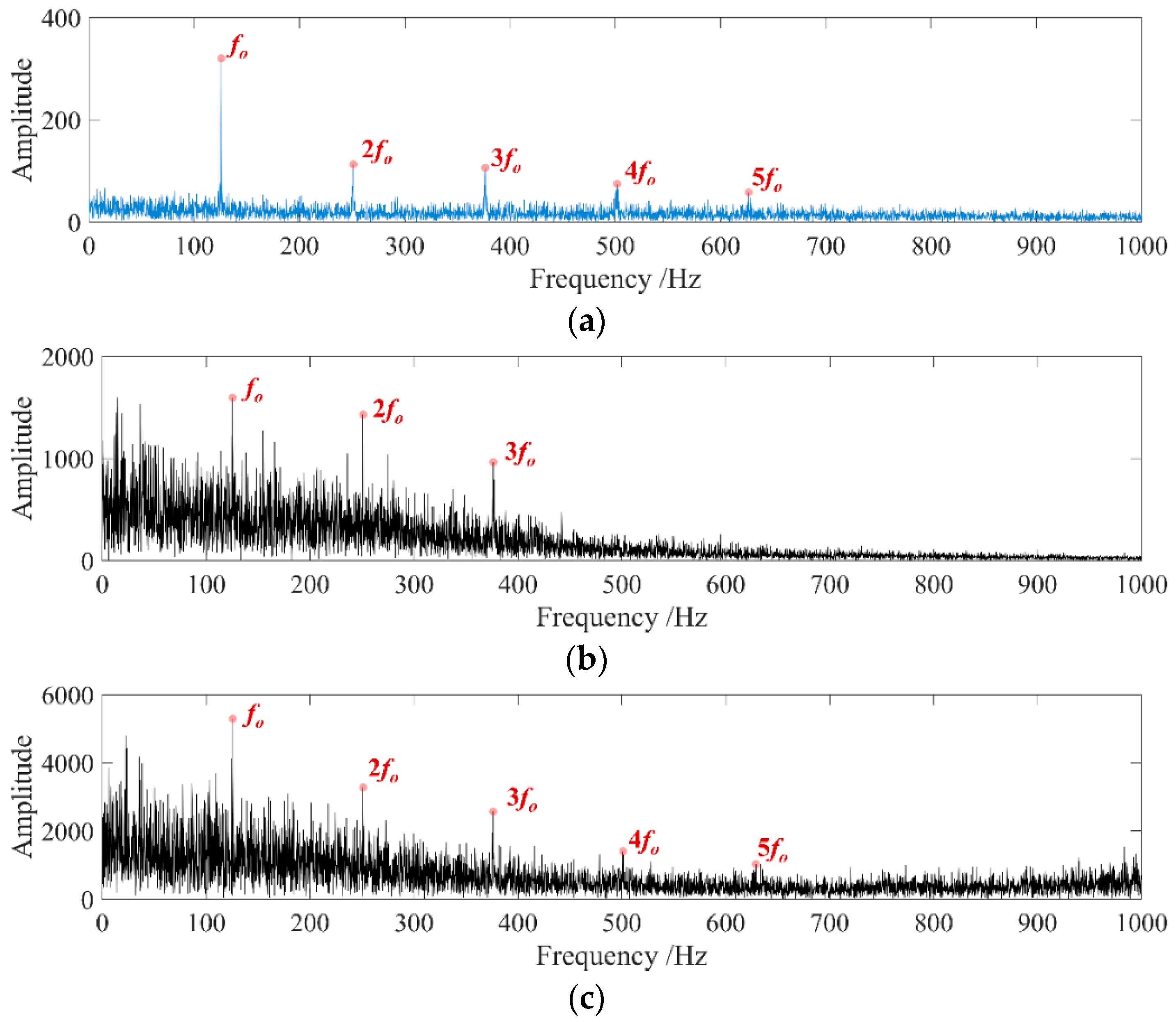
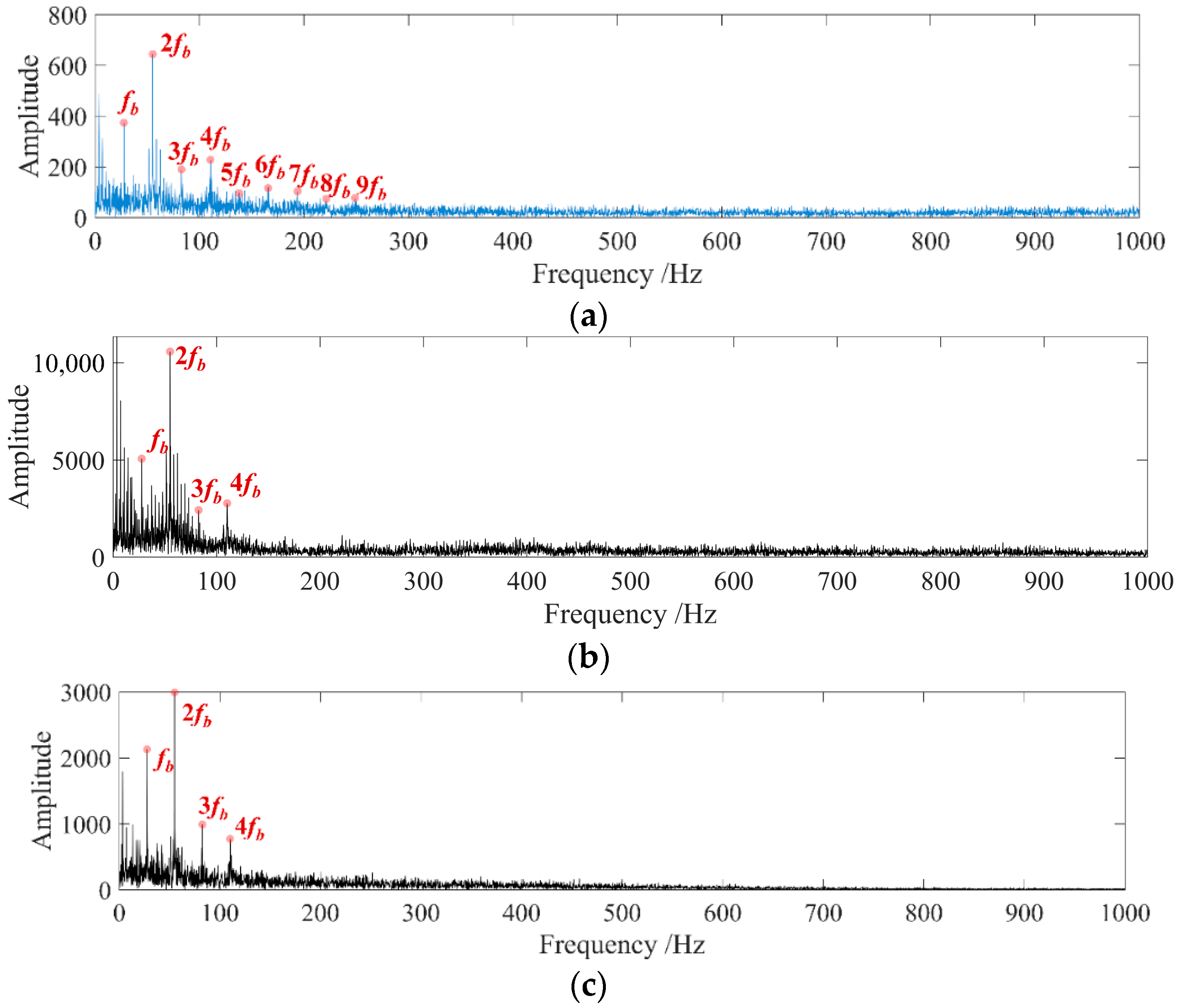
The core of the fault diagnosis method proposed in this paper is bandpass filtering, and the optimal filtering signal is determined by the selection of the AEO demodulation spectrum of the filtering signal. In the simulation signal analysis, a periodic impact signal with a definite frequency was established, and the proportion of the periodic impact component in the signal was weakened by adding noise, which could make the simulation signal closer to the actual signal, and also could verify the superiority of the fault diagnosis method. The noise interference could be clearly seen in
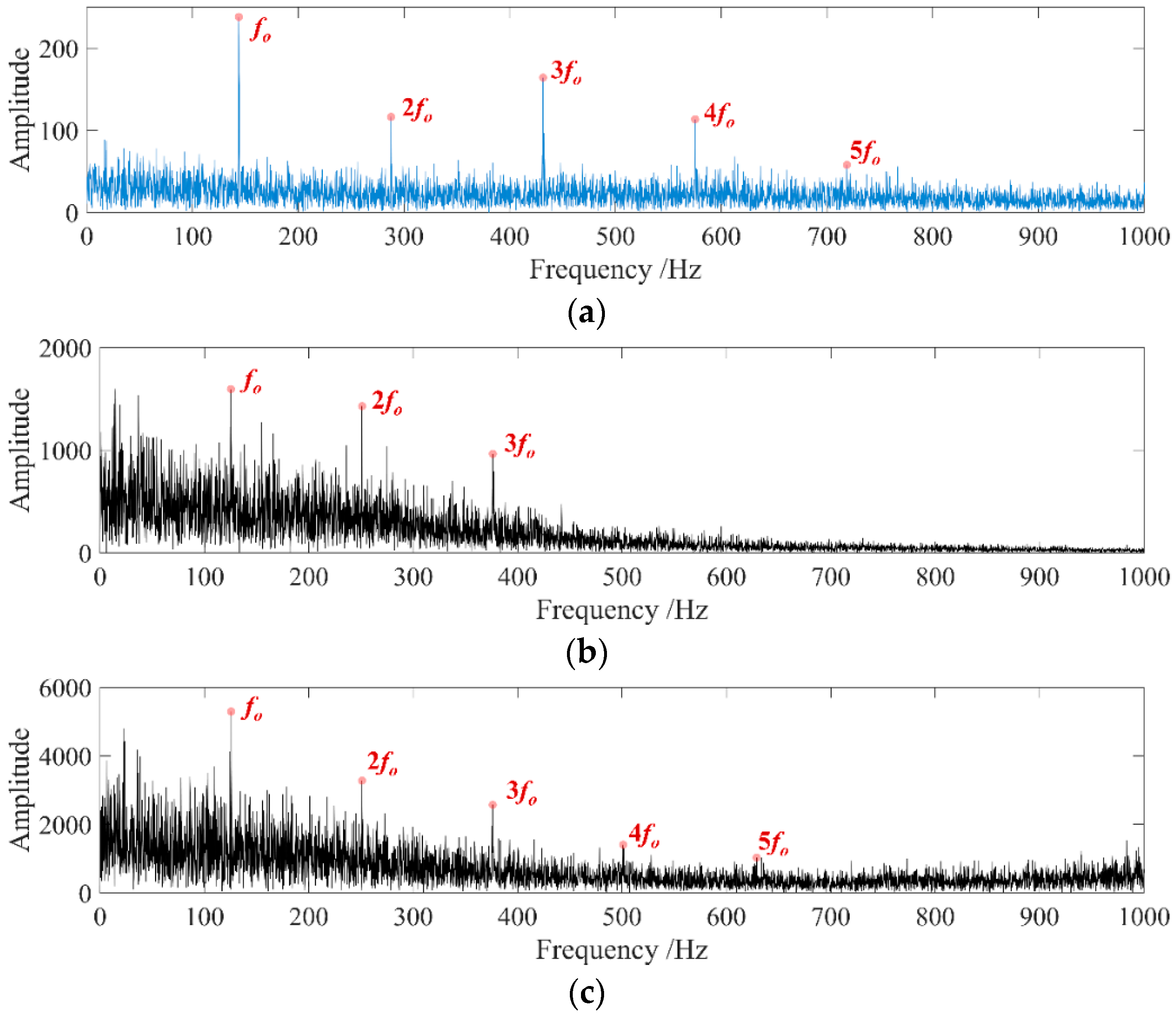
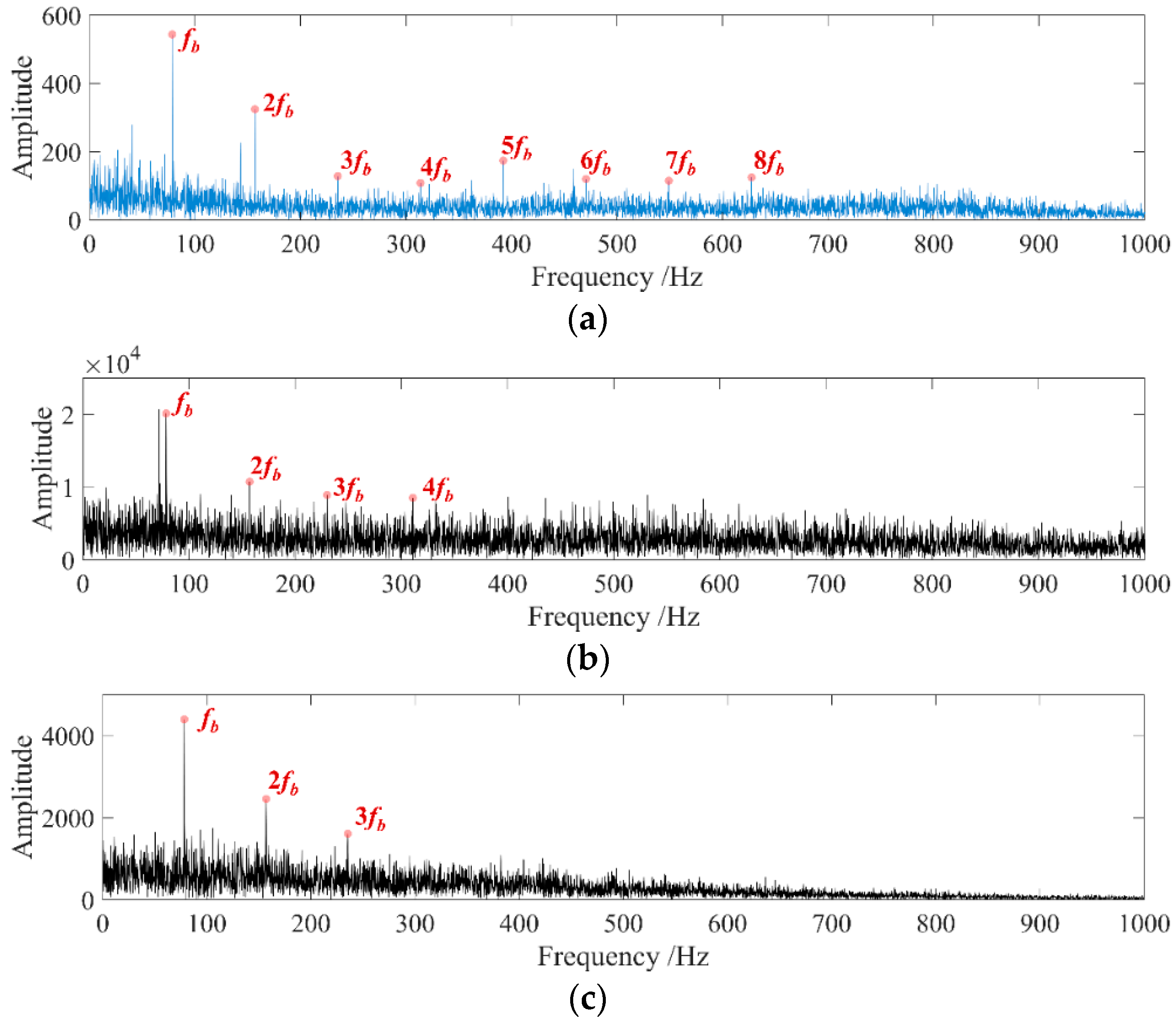
Figure 6b–d, while the periodic shocks were masked. After using the proposed fault diagnosis method to process the signal step by step, a more obvious characteristic frequency appeared in the spectrum as shown in
Figure 8, which was the same as the preset 159 Hz. It could be considered that the proposed method accurately extracted the periodic impact characteristics in the signal. Compared with the spectrum obtained by the NAMEMD–Hilbert and MVMD–Hilbert method, the final spectrum obtained in this paper had more obvious impact spectrum peaks.
The vibration response characteristics after bearing fault impact were considered in the establishment of the simulation signal, and the frequency of 159 Hz was also within the main fault characteristic frequency range in the bearing experiment. If there is strong noise interference in the experimental environment, the characteristic information can still be extracted by the proposed method. The accuracy of the simulation signal analysis results lays a good foundation for subsequent experimental signal analysis. Through the verification of the feasibility of the proposed method, it is proven that the proposed method can be used to identify the bearing fault impact in the actual operation.
In the experimental signal analysis, the bearing signals under different working conditions were also inconsistent, such as the signals under four different working conditions in Case1–Case4. The periodic impact in the fault signal of the bearing rolling element at a low rotational velocity was more obvious, but there was also more interference from the bearing rotational frequency in the spectrum, which may affect the judgment of the bearing health state. Although the method proposed in this paper can extract the fault characteristic frequency of the bearing, the result will also be interfered with by the bearing rotational frequency. In subsequent research, how to avoid the interference of rotational frequency conversion on the diagnosis results must be considered.
6. Conclusions
In this paper, a bearing fault diagnosis method based on PCA data dimension reduction fusion, multi-channel bandpass filter bank filtering, and AEO demodulation is proposed. Through the proposed CFECC value, the fault characteristic frequency of a signal can be determined and the spectrum with the most obvious harmonic performance is selected as the optimal demodulation spectrum. The effectiveness of the proposed method is proved by simulation signals and experimental signals, and it has good extraction effects on the characteristic frequencies of multi-fault type bearings at different speed levels. The main innovations and conclusions of this paper are as follows.
(1) The PCA is used for data dimension reduction and fusion. The effect of PCA on data noise reduction in data dimensionality reduction and fusion is proven by simulation signals, and it is easier to extract the characteristic frequency of the fusion signal.
(2) An improved average kurtosis index KTfinal is proposed, which can effectively avoid the interference of monopulse impact on signal characteristics. Based on the KTfinal, the selection criteria of optimal filtered signals for each channel under a multi-channel bandpass filter bank are determined.
(3) The AEO is used to demodulate the filtered signal to find the fault characteristic frequency, and the spectrum characteristic index CFECC parameter is proposed. The CFECC can be used to calculate the local energy prominence ability of different characteristic frequencies and their harmonics in the spectrum, which is beneficial for determining the type of fault and selecting the demodulation spectrum containing the characteristic frequency and its harmonic component prominence to achieve a better fault diagnosis effect.
The method proposed in this paper provides a new solution for the comprehensive use of bearing three-direction vibration acceleration signals, which can improve the accuracy of bearing fault diagnosis. Meanwhile, it also has good application value for the research of multi-signal fault diagnosis methods for other rotating machinery components. More research is still needed in signal noise reduction.