Abstract
The NVH (Noise, Vibration, and Harshness) characteristics of micro-motors used in vehicles directly affect the comfort of drivers and passengers. However, various factors influence the motor’s structural parameters, leading to uncertainties in its NVH performance. To improve the motor’s NVH characteristics, we propose a method for optimizing the structural parameters of automotive micro-motors under uncertain conditions. This method uses the motor’s maximum magnetic flux as a constraint and aims to reduce vibration at the commutation frequency. Firstly, we introduce the Pareto ellipsoid parameter method, which converts the uncertainty problem into a deterministic one, enabling the use of traditional optimization methods. To increase efficiency and reduce computational cost, we employed a data-driven method that uses the one-dimensional Inception module as the foundational model, replacing both numerical models and physical experiments. Simultaneously, the module’s underlying architecture was improved, increasing the surrogate model’s accuracy. Additionally, we propose an improved NSGA-III (Non-dominated Sorting Genetic Algorithm III) method that utilizes adaptive reference point updating, dividing the optimization process into exploration and refinement phases based on population matching error. Comparative experiments with traditional models demonstrate that this method enhances the overall quality of the solution set, effectively addresses parameter uncertainties in practical engineering scenarios, and significantly improves the vibration characteristics of the motor.
1. Introduction
In recent years, with increasing environmental awareness and technological advancements, the nationwide electrification of automobiles is accelerating. However, due to the absence of the masking effect provided by traditional internal combustion engines, the issue of micro-motor vibrations in electric vehicles become more prominent, directly affecting the comfort of passengers and drivers [1]. Existing vibration optimization methods mainly rely on physical experiments and numerical models, which not only require professional engineers to operate but also fail to fully explore the optimization space, leading to inefficiencies [2]. Furthermore, the structural parameters are influenced by the precision of manufacturing equipment, factors that are often difficult to consider comprehensively during optimization. Therefore, optimizing the NVH performance of automotive micro-motors under parameter uncertainty is both necessary and important.
In the optimization process of micro-motor NVH characteristics, the primary focus is on electromagnetic forces [3,4]. During operation, the motor experiences Lorentz forces and Ampere forces acting on the ferromagnetic components inside the motor, leading to the generation of unbalanced electromagnetic forces. These forces serve as excitation sources, causing vibrations in the motor’s stator structure [5]. Traditional methods for analyzing and optimizing the NVH of automotive micro-motors typically involve numerical models, mathematical models, and physical experiments. Consequently, many researchers have established mathematical models of motor electromagnetic forces to calculate the impact of periodic electromagnetic forces on vibration [6,7,8]. Jie Xu [9] reduced the cogging torque pulsation between the stator and rotor by changing the angle of the motor’s rotor. Other researchers have proposed novel stator and rotor structures to reduce motor vibrations. For instance, Omer Gundogmus [10] proposed placing rectangular windows in both rotor poles and stator poles to reduce the vibration and noise of switched reluctance motors. Some researchers have proposed adjusting the motor current, frequency, phase, and other related parameters through controllers to reduce radiated vibrations [11,12]. However, this method requires real-time monitoring by relevant sensors. Due to its complexity, cost, and maintenance requirements, it is challenging to widely apply this approach to automotive micro-motors.
Compared to the aforementioned methods, optimizing NVH performance by adjusting the structural parameters of the motor itself offers natural advantages. In the motor design process, achieving an optimal combination of parameters is crucial. However, traditional methods such as Design of Experiments (DOE), Taguchi experiments, and expert judgment often fail to thoroughly explore the entire optimization space [13,14]. Moreover, traditional experimental or simulation model approaches still face significant challenges associated with high computational complexity and inefficiency. These factors make it difficult to find high-quality solutions set in multi-objective optimization. In recent years, with the advancement of data-driven algorithms, data-driven methods have gradually replaced traditional methods, significantly reducing computational load [15,16]. For example, Haibo Huang [17] proposed a data-driven genetic algorithm and TOPSIS algorithm based on deep learning for multi-objective optimization of processing parameters. Pengcheng Wu [18] introduced a similar approach for optimizing processing parameters. Song Chi [19] comprehensively discussed three methods to reduce motor vibration and noise, including pole-slot combinations, slot width, and pole arc coefficient. Feng Liu [20] proposed an improved optimization model that considers the interaction of multiple variables in the motor. Despite significant advancements in optimizing motor NVH characteristics using data-driven methods, several issues still require further exploration.
In practical applications, the impact of uncertainty on outcomes cannot be overlooked. The optimization process itself faces significant computational demands [21], and the presence of uncertainty further increases this burden. Therefore, further research on uncertainty is necessary. To address parameter uncertainty in the optimization process, numerous theories and methods have been developed, including probability theory, evidence theory, fuzzy set theory, possibility theory, interval analysis, info-gap decision theory, and hybrid methods [22]. Early methods for optimizing under uncertainty primarily employed probabilistic and stochastic optimization to enhance system robustness. Bernardo [23] embedded the Taguchi method into stochastic optimization formulas, utilizing efficient volume techniques to calculate the expected objective function value, thereby determining optimal design and robust operation strategies. Romero VJ [24] advanced design improvements through ordinal optimization, focusing on relative ranking rather than precise quantification. Hao YD [25] introduced truncated normal distribution and Monte Carlo processes for the first time in the analysis and optimization of the torsional vibration model of the transmission system and rear axle coupling. Gray A [26] carried out reliability analysis and optimization by fusing mixed uncertainty features and integrating data into design decisions. D. W. Coit [27] addressed the uncertainty in component reliability estimates, providing optimal trade-off solutions through multi-objective optimization. Li, ZS [28,29] proposed robust topology optimization strategies and parallel robust topology optimization methods by quantifying the uncertainties in non-design domain positions and parameters. Beyond probabilistic or specifically parameterized uncertainty design methods, non-probabilistic approaches are also evolving. Yang, C [30] proposed an SPS interval dynamic model based on non-probabilistic theory. Masatoshi Shimoda [31] developed a non-parametric optimization method for robust shape design of solids, shells, and frame structures under uncertain loads. Dilaksan Thillaithevan [32] considered material uncertainties, simulated geometric variations during manufacturing, and designed structures tolerant of micro-scale geometric changes. Haibo Huang [33] presented an improved interval analysis method for optimizing road noise quality in pure electric vehicles. The optimization process under uncertainty is complex and costly, especially when dealing with high-dimensional problems and large-scale data. However, the emergence of data-driven methods offers new solutions to these challenges.
Through the above analysis, we identified two main deficiencies in traditional optimization methods for the vibration response of automotive micro-motors: (1) Due to the complexity and high cost of traditional optimization methods, we are hindered from fully exploring the optimization space, resulting in low optimization efficiency. (2) The structural parameters of micro-motors are often constrained by the precision of manufacturing equipment. Additionally, optimization problems involving uncertainties further increase the complexity of optimization. This makes it even more difficult for traditional optimization processes to consider these uncertainty factors, leading to suboptimal results in practical applications. Therefore, it is crucial to consider these factors during the optimization process. These factors restrict the optimization effectiveness of the vibration characteristics of automotive micro-motors, impeding the development of more efficient and lower-vibration motor designs.
To address these challenges, this study proposes a Pareto ellipsoid parameter method to transform the uncertainty problem in micro-motors into a deterministic problem, thus enabling the use of traditional optimization models to optimize the vibration response of micro-motors. This method allows for a more comprehensive exploration of the optimization space, significantly improves optimization efficiency, and provides practical technical support for the development of the electric vehicle industry.
The remainder of this paper is organized as follows: Section 2 introduces the proposed method, including the Pareto ellipsoid parameter method for handling uncertainty issues and optimizing the Inception module in the surrogate model to enhance its feature extraction capability and overall performance. Additionally, the reference point optimization method of NSGA-III is adjusted to improve the quality and diversity of the Pareto front solution set. Section 3 details the experimental and dataset construction process. Section 4 outlines the construction process of the prediction and optimization models, along with a comparison and discussion of different models. Finally, Section 5 presents the conclusions.
2. Pareto Elliptic and Optimization Approaches for Uncertainty
The overall framework for optimizing the vibration response of automotive micro-motors is illustrated in Figure 1. This framework consists of four main parts: data collection and preprocessing, study of the motor vibration surrogate model based on the inception module, motor vibration optimization using NSGA-III with adaptive reference point adjustment, and discussion of the optimization results.
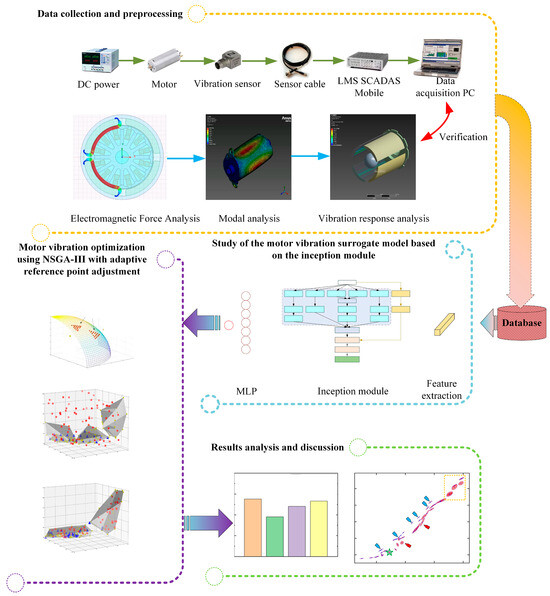
Figure 1.
Overall framework for optimizing the vibration response of automotive micro-motors.
Step 1: Conduct micro-motor vibration experiments in a semi-anechoic chamber and perform benchmark analysis through simulations and experiments. Apply the Fast Fourier Transform (FFT) [34] to the collected time-domain data to convert it into frequency-domain data.
Step 2: Based on the data collected in Step 1, establish a surrogate model for the vibration response of automotive micro-motors using an optimized Inception module, and adjust the model’s hyperparameters to ensure it meets accuracy requirements.
Step 3: Utilize the developed surrogate model to establish an NSGA-III optimization model with adaptive reference point adjustment for the vibration response of micro-motors, in order to calculate the optimal combination of design parameters.
Step 4: Select design parameter combinations that meet the requirements from the Pareto front solution set, analyze their vibration response characteristics, and evaluate their performance within the objective feasible region.
2.1. Pareto Elliptic Parameter Methods for Dealing with Uncertainty
The traditional multi-objective optimization problem can be formulated as follows:
where represents the objective function vector, containing objective values. “s.t.” stands for “subject to.” It indicates the constraints that the solution must satisfy. and denote the inequality constraints and equality constraints, respectively, with inequality constraints and equality constraints. is the vector of decision variables, containing decision variables. represents what needs to be determined in the optimization process. The models for , , and are constructed using simulation models, approximations, and physical experimental tests.
If involves uncertainty, meaning it contains an uncertainty interval denoted by , then the optimization model considering the uncertain decision variables can be expressed as follows:
where is a random variable or belongs to a known uncertainty set . The objective function and constraints must hold for all possible values of . In the optimization process, the uncertainty in parameters is propagated through the model equations. This means seeking solutions that satisfy constraints and optimize objectives under uncertain conditions to the greatest extent possible. Traditional optimization methods are usually based on deterministic processes and struggle to effectively handle uncertainty. To address the issue of uncertainty in decision variables, the Pareto ellipsoid parameter method can be introduced to adjust the optimization objectives under uncertainty, enabling traditional models to deal with uncertainty.
In the manufacturing process of automotive micro-motors, it is often challenging to accurately determine the specific probability distributions of uncertainties. Therefore, Monte Carlo simulation [35] is employed to address these uncertainties in optimization parameters. By generating and analyzing a large number of random samples, Monte Carlo simulation can effectively estimate and manage uncertainties, even in the absence of explicit probability distributions. Using the Monte Carlo method to simulate the range of uncertainty intervals involves generating uncertainty sample points. The optimization objective values and constraint values for all points are obtained from the computational models of , , and , forming a vector of function values for the uncertainty interval with dimensions . The mean vector can be expressed as follows:
After decentering the function value vector through , its covariance matrix can be expressed as follows:
Performing eigenvalue decomposition on yields eigenvalues and eigenvectors . This process can be represented as follows:
where is the eigenvector matrix, is the diagonal matrix, is the diagonal element of the diagonal matrix, and is the column vector of the eigenvector matrix. The corresponding chi-square distribution critical value is calculated from the predetermined confidence level :
Therefore, the above process can be summarized as follows:
Using the above process, we obtain the eigenvalues and eigenvectors corresponding to the function value vector , as well as the critical value corresponding to the distribution of . Subsequently, the width and height of the Pareto ellipsoid can be calculated using , and the angle can be determined using the eigenvectors and the arctangent function. The problem caused by uncertainty can thus be represented by the specific area of the Pareto ellipsoid or its area projection onto the objective or constraints. Through this process, we transform the parameter uncertainty issue in optimizing automotive micro-motors into a deterministic problem, allowing the use of traditional methods to optimize its vibration response. However, propagating parameter uncertainty via numerical models and experimental tests during the optimization process is computationally expensive. To address this issue, we use a data-driven method to replace the traditional numerical model or physical experimental process. This approach allows the propagation of uncertainty in the optimization function , and constraint functions and , significantly reducing the computational load and meeting the needs of uncertainty optimization. The specific construction method of the data-driven surrogate model will be detailed in Section 2.2.
2.2. Optimization Methods under Parameter Uncertainty
2.2.1. Surrogate Models for Vibration Response
Due to the coupling of multiple physical fields such as electromagnetic, structure, and vibration in motors, their nonlinearity is strong. To overcome this problem, the following improvements are made in the construction process of the data-driven surrogate model in this paper. First, basic features are extracted from the raw data using a feature extraction module. Next, a one-dimensional time-series Inception module [36] is employed to extract deeper and more complex features across multiple scales, with the structure of the Inception module optimized. Specifically, and max pooling and average pooling layers are used to extract significant features and smooth feature maps from different scales, preserving the overall trend of the features. The max pooling layers focus on extracting significant local features, while the average pooling layers retain global information. Combining both allows the network to capture both local and global feature information simultaneously, enhancing the richness of feature representation. Residual connections have been added to the original network architecture of the Inception module. Specifically, the input features are passed through a convolutional layer and standardized before being directly connected to the output features of the Inception module through residual connections. This operation helps mitigate the gradient vanishing problem and improves the model’s training efficiency. Following the Inception module, an attention mechanism is incorporated to adaptively assign appropriate weights to different scale features and positions extracted by multiple branches of the Inception module. The improved Inception module architecture is shown in Figure 2.

Figure 2.
Optimized Inception module architecture.
The features extracted by the Inception module vary in importance at different scales and depths and cannot be treated equally. To better adaptively assign weights to the multi-scale features extracted by the Inception module, we combined channel attention and spatial attention mechanisms [37] to improve the overall performance of the model. The channel attention mechanism identifies the importance of different channels in the feature map, while the spatial attention mechanism captures the significance of different positions within the feature map. The integrated attention mechanism is shown in Figure 3, where the green sections represent the channel attention mechanism and the blue sections represent the spatial attention mechanism. In Figure 3, the blue feature part and the green feature part represent the process of max pooling and average pooling to capture the weights, respectively. The channel attention mechanism performs max pooling and average pooling on the input features along the channel dimension to obtain two different feature maps. These feature maps are then passed through a multi-layer perceptron (MLP) and activated by a sigmoid function to generate weights for each channel. Subsequently, the weights of the Inception feature map are multiplied by these channel weights to obtain the weighted features. The spatial attention mechanism operates similarly to the channel attention mechanism, but pooling operations are performed along the spatial dimension. The color intensity of the features in Figure 3 indicates the magnitude of the weight. This attention mechanism integrates both channel and spatial attention, weighting the importance of features in the channel and spatial dimensions, respectively. By fusing the original features and weighted features through residual connections, more distinctive features are ultimately produced. This combined attention mechanism allows for more precise capture and processing of multi-scale feature information, enhancing the feature extraction capability of the Inception module and the overall performance of the model.
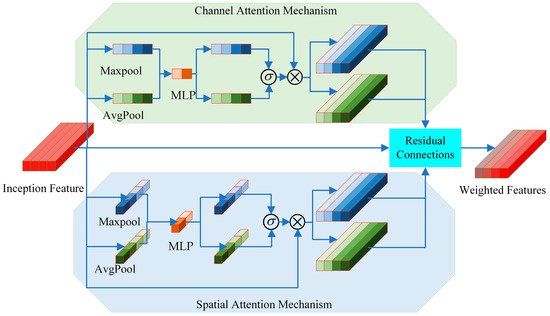
Figure 3.
Architecture of the integrated attention mechanism.
The steps for constructing the surrogate model of the vibration response of automotive micro-motors are as follows:
(1) A parameter combination table is designed using the Latin Hypercube Sampling (LHS) method [38]. Specifically, in the LHS method, five design parameters are stratified for sampling to generate multiple parameter combinations. These five parameters are the pole embrace (denoted as ), pole arc offset (denoted as ), slot wedge maximum width (denoted as ), magnetic tile round corner (denoted as ), and max thickness of magnets (denoted as ). The specific descriptions of each parameter are shown in Figure 4. Subsequently, physical experiments are conducted to obtain the optimization objectives and constraints under different parameter combinations.

Figure 4.
Description of the optimized parameters of the motor.
(2) Using the obtained dataset, a surrogate model for predicting the vibration response of the micro-motor is constructed with the optimized Inception module and attention mechanism.
(3) The hyperparameters of the surrogate model are adjusted to improve its prediction accuracy, ensuring it meets the requirements for subsequent optimization.
2.2.2. Optimization Method for Vibration Response
Compared to the Genetic Algorithm (GA), the NSGA-III is better suited for handling high-dimensional objective optimization problems [39]. It introduces a selection mechanism based on reference points, which helps in finding a more evenly distributed Pareto front solution set, thereby maintaining good performance in high dimensional objective spaces. However, the selection of reference points in NSGA-III is particularly crucial. If the distribution of the reference points is inappropriate, it may lead to some objectives being ignored or unevenly weighted during the optimization process, affecting the algorithm’s performance. Moreover, the reference points in NSGA-III are predefined and cannot be dynamically adjusted according to changes in the population during the optimization process, which limits the guidance of the search process and may result in a decrease in the quality of the solution set. To address this issue, this paper proposes a two-stage update strategy for reference points, namely the population exploration stage and the refinement stage, to improve the model’s search optimization capability. The specifics are as follows:
In the population exploration stage, predefined uniformly distributed reference points are used, and training iterations and optimizations begin. The reference points are sorted based on the shortest distance between the reference points and the population objective values, forming a reference point set :
where is the number of reference points; those better than are retained. The K-means method [40] is used to adaptively divide the population objective values into two blocks. The optimal set of reference points will be saved, and those worse will be discarded. This ensures that the reference point set can always reflect the distribution of the current population and the changes in objective values during the optimization process. Through traversing different cluster numbers and calculating the average score of each cluster number according to the spatial position of the population target value and reference point at this time, the optimal cluster number is found by criterion [41]:
where represents the average distance from a point to all other points within its cluster, while is the average distance from point to all data points in the nearest cluster that it does not belong to. By calculating the overall Silhouette coefficient corresponding to different numbers of clusters , the with the highest is selected as the optimal number of clusters. The K-means method is used to adaptively divide the population objective values into blocks, which are then enclosed by the smallest convex hull. New reference points are uniformly sampled from outside the convex hull, with the number of new reference points matching the number of discarded reference points. Iterative optimization continues with the new reference points. As the population gradually converges, convergence is assessed by the following criterion:
where is a point from the Pareto ellipsoid parameters in the previous iteration, and is the closest value to point in the current iteration. The new matching error is calculated based on these nearest neighbor points. When the matching error remains below a preset threshold for consecutive iterations, the population is considered to have converged. During the first stage, when the population has not yet converged, sampling new reference points outside the convex hull encourages the model to actively explore, avoiding convergence to only a few local optima. The initial process of the second stage is the same as the first stage, but the difference is that after the model converges, additional reference points are sampled from inside the convex hull.
Figure 5 illustrates the update of reference points in two stages. In Figure 5a, the criterion is used adaptively to divide the population and retained reference points into three regions, with points selected outside the convex hull in the first stage. Similarly, Figure 5b shows the adaptive division of the population and retained reference points into two regions, with points selected inside the convex hull in the second stage. The purpose of the second stage is to conduct more detailed searches around the multiple local optima found, thereby further improving the quality of the solution set. Figure 6 shows the naga-iii optimization process for adaptively adjusting the reference point. Overall, this method enhances the diversity of solutions and the performance of global optimization.
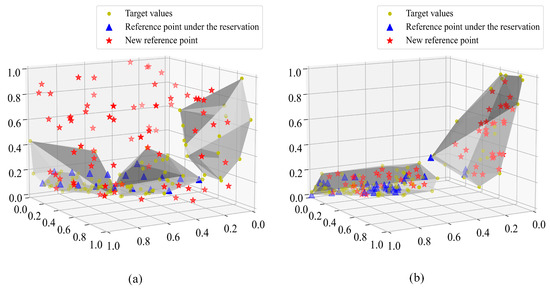
Figure 5.
Reference points for two-stage generation: (a) first stage; (b) second stage.
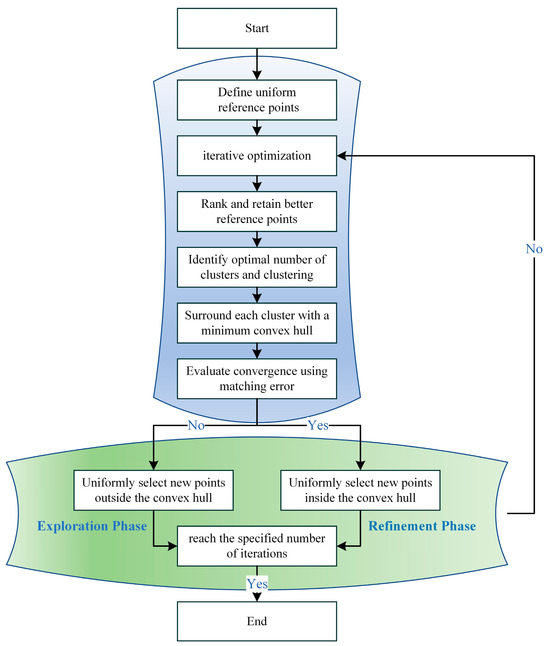
Figure 6.
Adaptive adjustment of reference points in the NAGA-III optimization process.
3. Vehicle Micro-Motor Vibration Response Experiments
In this study, we used a 4-pole 12-slot electric seat motor for the experiment. To minimize external environmental interference, the experiment was conducted in a semi-anechoic chamber. The laboratory temperature was maintained at 25 °C, and the humidity at 50%. A B05Y32 tri-axial accelerometer was used to record the vibration acceleration. Following the Nyquist sampling theorem, the sampling frequency for vibration acceleration was set to 25,600 Hz, enabling the analysis of frequencies up to 12,800 Hz. Data was processed using the Simcenter Testlab 16-channel processing system. The main objective of the experiment was to test the stator vibration response of an automotive micro-motor. First, we employed the LHS method to generate 100 uniformly distributed samples in the parameter space based on the upper and lower limits of the parameters in Table 1 and processed corresponding micro-motor prototypes. Figure 7a shows the experimental motor sample. Figure 7b is a schematic diagram of the motor disassembly. It is required that the motor operates in an unconstrained condition to simulate the free vibration situation of the motor. Fixing the motor could introduce additional constraints, altering the motor’s vibration characteristics and thereby affecting the experimental results. Therefore, during the experiment, the micro-motor was placed in the center of a sponge for operation, and the accelerometer was installed on the surface of the micro-motor stator. It was powered by a DC power supply set to 14V, and data acquisition was conducted using LMS SCADAS Mobile. The data was processed on a PC, with each sample running for 5 s, collecting a total of 100 data samples. Figure 7c shows all the settings for the entire experiment.

Table 1.
Optimization parameters and corresponding optimization space.

Figure 7.
Vibration testing of micro-motors: (a) partial experimental micro-motor; (b) disassembly diagram of micro-motor; (c) overall experimental setup.
Because physical experiments usually require a large amount of materials and equipment, and testing the magnetic flux between the motor stator and rotor is relatively difficult and less accurate, we obtained the dataset of magnetic flux changes over time through simulation. In the simulation, ANSYS and Maxwell were used to calculate the motor’s vibration performance. After ensuring that the simulation results matched the actual vibration response, the magnetic flux data over time for the parameter combination was extracted.
The collected data was analyzed for frequency response using the FFT to obtain the amplitude at the motor’s commutation frequency. Figure 8a shows the motor stator vibration test results. The Figure 8 indicates that the vibration response at the commutation frequency of 600 Hz is significantly higher than at other frequencies, verifying the accuracy of the above analysis. Figure 8b shows the magnetic flux changes over time, indicating that the magnetic flux fluctuates and exhibits a certain level of repeatability. In the optimization process, maximizing the magnetic flux is used as a constraint to ensure that the motor’s vibration response is reduced while achieving the highest possible magnetic flux value.
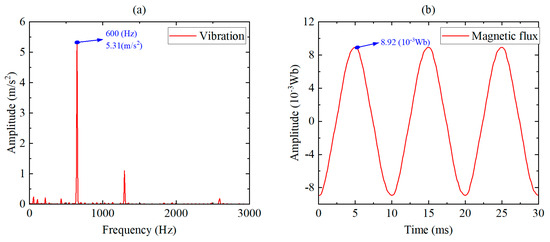
Figure 8.
Micro−motor test results: (a) vibration response; (b) magnetic flux.
4. Optimization of Vibration Response
4.1. Development of Vibration Response Surrogate Model
To verify the effectiveness of the proposed method, we will conduct comparative experiments. The Multilayer Perceptron (MLP), Convolutional Neural Network (CNN), and original approach are chosen as benchmarks, and each model is configured as follows:
MLP: This model includes three hidden layers: the first hidden layer has 64 neurons, the second has 128 neurons, and the third has 64 neurons. The ReLU activation function is used in the first and second layers to enhance non-linear processing capabilities. The features are then passed through an average pooling layer to reduce dimensionality and the complexity of subsequent calculations. Finally, the data is processed through the third layer to produce the final output.
CNN: The first layer of this model has 64 neurons. The second layer is a convolutional layer with 64 filters and a kernel size of 3. The third layer is another convolutional layer with 128 filters and a kernel size of 3. The fourth layer is a fully connected layer with 64 neurons. The ReLU activation function is applied in the first two convolutional layers and the first fully connected layer, with max-pooling layers of size 2 used for dimensionality reduction. Finally, the output of the convolutional layers is flattened into a one-dimensional vector and passed through the fourth fully connected layer to obtain the final prediction result.
Original approach: This method uses the initial Inception module without optimization.
In the experiments, the training and test sets are divided in a 70:30 ratio. Mean Squared Error (MSELoss) is employed as the loss function, Adam is selected as the optimizer, and the number of iterations is set to 3000. To avoid randomness, the experiment is repeated 100 times with the same setup, and the final result is the average of these runs, reported to four decimal places. Additionally, to visually evaluate model performance, common regression metrics including Root Mean Square Error (), Mean Absolute Error (), and Coefficient of Determination () are used to compare the performance of each model. The calculation formulas for each parameter are summarized as follows:
where is the true value, is the predicted value, , and the number of iterations when the model reaches the convergence condition is also considered as an important index in this paper.
Table 2 and Table 3 present the performance of the four models in predicting the motor’s tangential vibration response and maximum magnetic flux, respectively. An analysis of Table 2 shows that, compared to the MLP and CNN, the and significantly decrease after incorporating the Inception module. Specifically, decreases from 0.150 (MLP) and 0.123 (CNN) to 0.106, while decreases from 0.122 (MLP) and 0.104 (CNN) to 0.092. The value increases from 0.933 (MLP) and 0.914 (CNN) to 0.958, indicating higher prediction accuracy, and the number of required iterations also significantly decreases. With the optimized Inception module, the proposed method further reduces from 0.106 to 0.090 and from 0.092 to 0.073. The value increases from 0.958 to 0.981, showing better fitting results. The required number of iterations significantly reduces to 844, demonstrating more efficient convergence. The data in Table 3 show a similar trend to that in Table 2. Adding the Inception module, compared to traditional MLP and CNN methods, results in lower and , higher , and fewer iterations, illustrating the effectiveness of the Inception module in extracting features from multiple scales, thus improving the surrogate model’s accuracy. The proposed method further enhances the original approach, making it the most accurate and efficient among the four evaluated methods. Specifically, the values of the two surrogate models reach up to 0.981 and 0.973, with the fewest iterations. This demonstrates that the optimized Inception module not only surpasses other methods in prediction accuracy but also exhibits superior convergence performance.

Table 2.
Prediction results of maximum magnetic flux for the four models.

Table 3.
Prediction results of tangential vibration response for the four models.
Figure 9 shows the comparison between the predicted and actual values of the motor optimization objective and constraint values. The overall prediction performance of the model is good, with the predicted values closely matching the actual values and no significant deviations. The figure also shows that the tangential vibration and maximum magnetic flux generally exhibit similar trends, indicating that reducing the tangential vibration response inevitably sacrifices some maximum flux. The following conclusions are drawn from the analysis: In some cases, a significant reduction in tangential vibration response can be achieved by sacrificing a small amount of maximum magnetic flux. For example, the black arrows in the figure point to areas where a substantial decrease in tangential vibration is accompanied by only a slight decrease in maximum magnetic flux. Conversely, the green arrows indicate areas where a large sacrifice in maximum magnetic flux results in only a slight improvement in tangential vibration, which is undesirable. This analysis underscores the need for further optimization processes.
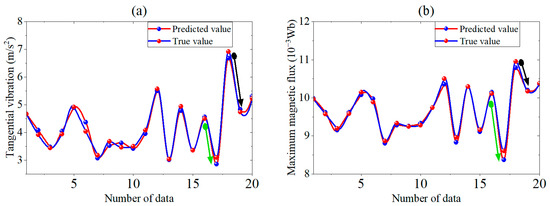
Figure 9.
Comparison of actual and predicted values of tangential vibration and maximum magnetic flux: (a) tangential vibration; (b) maximum magnetic flux.
4.2. Vibration Optimization of Micro-Motor
In the experiment, NSGA-III is used as the base algorithm, and the selection strategy of reference points is adjusted. The evaluation of the optimization results considered five parameters: the optimization objective (motor tangential vibration, denoted as ), the constraints (motor maximum magnetic flux, denoted as ), the area of the Pareto ellipsoid (feasible area of the objective, denoted as ), and the area projections on the optimization objective and the constraints (denoted as and , respectively). The calculation formulas for these parameters are as follows:
where denotes the width of the Pareto ellipsoid, denotes the height of the Pareto ellipsoid, represents the projection of the ellipsoid on the optimization objective, and represents the projection of the ellipsoid on the constraints. represents the counterclockwise rotation angle of the Pareto ellipsoid, and the average values of and , , are obtained using Equation (3). To verify the effectiveness and rationality of the proposed method, it is compared with the initial NSGA-III algorithm. In the optimization process of the NSGA-III algorithm, predefined uniformly distributed reference points are used, and the hyperparameters of the model are kept consistent. The specific settings are as follows: the optimization model’s population size is 100, the crossover probability is 1, the mutation probability is 1, and the number of generations is 200. The parameters and their corresponding design spaces are shown in Table 1. Due to the influence of different manufacturing equipment, the uncertainty of parameters may vary. To fully consider the impact of these uncertainties, three uncertainty parameter scenarios are set, as shown in Table 4. Based on these settings, an optimization model for the tangential vibration uncertainty of micro-motors is established.

Table 4.
Three types of uncertainty intervals of motor design parameters.
Figure 10 illustrates the optimization results of different models under the same parameter settings. In the figure, blue dots represent mean points and red circles represent the Pareto ellipsoids, indicating the feasible region of the objective. Figure 10a shows the results obtained by the NSGA-III method. This method does not consider parameter uncertainty during the optimization process. The Pareto ellipsoid shown is calculated using uncertainty interval 1 and the method described in Section 2.1. Parameter uncertainty has a minor impact on the mean values but directly affects the feasible region of the objective function (including area and angle). This highlights the importance of considering parameter uncertainty during the optimization process to reasonably address its impact. It can be seen that the Pareto front solution set does not follow a smooth curve. In Figure 10a, the part shown by the black dashed rectangle displays a sudden intensification of the solution set variation. In this part, the motor’s tangential vibration decreases sharply, while the maximum magnetic flux changes only slightly. Therefore, the points in the red dashed rectangle are particularly noteworthy because a small sacrifice in magnetic flux can significantly reduce tangential vibration. Additionally, in all the optimization results, the part shown by the yellow dashed rectangle has a large feasible region, making it difficult to find suitable optimization results, and thus, this part of the solution set will not be considered. The part indicated by the blue arrows shows that although these solutions perform poorly in optimization objectives and constraints, their Pareto ellipsoids are smaller, corresponding to smaller feasible regions, indicating higher robustness of these solution sets. Thus, they can also be considered as Pareto front solution sets. In contrast, the part indicated by the red arrows shows that these solution sets perform better in optimization objectives and constraints, but their feasible regions are larger, corresponding to lower robustness of the solution sets, and are generally not considered. The proposed method not only fully considers the optimization objectives and constraints but also identifies front solution sets with high robustness and small feasible regions in the optimization space, as indicated by the blue arrows. These advantages make the proposed method achieve higher solution set quality when dealing with complex multi-objective optimization problems considering the impact of uncertainty.

Figure 10.
Optimization results of different models: (a) initial NSGA−III; (b) optimization results of the proposed method on uncertainty interval 1; (c) optimization results of the proposed method on uncertainty interval 2; (d) optimization results of the proposed method on un-certainty interval.
Figure 11 illustrates the average objective feasible region area for the Pareto front solution sets of different models. As the level of parameter uncertainty increases, the average objective feasible region area of the model’s Pareto front solution sets also increases, as shown in the figure, aligning with practical engineering scenarios. However, when using the initial NSGA-III method for optimization, the calculated average objective feasible region area is still larger than in other cases, even with uncertainty interval 1. This demonstrates that the proposed method achieves higher quality Pareto front solution sets when considering uncertainty. This method can comprehensively account for optimization objectives and constraints and evaluate the impact of parameter uncertainty.

Figure 11.
Average objective feasible region area of the Pareto front solution set for different models.
Figure 12 shows the projections of the feasible region area on the optimization objectives and constraints for various models. Purple dots correspond to the ordinate value indicating the objective feasible region area, and the error bars along the X-axis and Y-axis represent the projections of the objective feasible region area on the maximum magnetic flux and tangential vibration, showing the range of variation for each solution when considering parameter uncertainty. Figure 12a displays the optimization results the optimization results of the initial NSGA-III. Although only the smallest uncertainty interval is used for the calculation, the results of its feasible region area are highly consistent with those of the proposed method using uncertainty interval 3. From the figure, it is evident that the Pareto ellipsoid area of the model improves significantly when considering parameter uncertainty. This demonstrates that the proposed method can enhance the robustness of optimization results when considering parameter uncertainty.

Figure 12.
Objective feasible region of the Pareto front and area projection of the feasible region over the optimization objective and constraints, respectively: (a) initial NSGA−III; (b) optimization results of the proposed method on uncertainty interval 1; (c) optimization results of the proposed method on uncertainty interval 2; (d) optimization results of the proposed method on uncertainty interval.
Considering practical engineering requirements, this paper selects the optimal solutions at different levels of uncertainty, marked with green pentagrams in Figure 10. These are the 7th, 11th, 9th, and 12th solutions from the left, respectively. Table 5 shows the initial state of the micro-motor and the optimization results of the micro-motor structural parameters by different models. Among them, the initial state and the target feasible region parameters of the NSGA-III method are all calculated according to the uncertainty interval 1. The data shows that although the NSGA-III model can find relatively good solution sets, its feasible region of the objective is large due to the lack of consideration of uncertainty factors, resulting in poor robustness of the solution sets, which may cause system instability in practical applications. In contrast, the proposed method achieves significant reductions in the optimized tangential vibration of the micro-motor when considering uncertainty factors. Under the three types of uncertainty, tangential vibration decreases from the initial to , , and , respectively. Meanwhile, the objective feasible region reduces from the initial 7.26 to 1.52, 0.41, and 1.89. Additionally, the uncertainty intervals of the area projections on both axes are significantly reduced. Although the proposed method is slightly higher than the NSGA-III model in terms of vibration response optimization, these fluctuations result from the parameter combinations selected after considering the impact of uncertainty. This proves that the proposed method can effectively optimize objectives while also considering the impact of parameter uncertainty, thus yielding more robust and reliable results in practical applications.

Table 5.
Optimization results of the proposed method and NSGA-III method.
5. Conclusions
In this paper, we address the optimization of the vibration response of automotive micro-motors under parameter uncertainty by proposing a Pareto ellipsoid parameter method, which converts the uncertainty problem into a deterministic optimization problem. To improve optimization efficiency, we optimized the Inception module as the data-driven base algorithm and constructed surrogate models for the motor’s vibration response and maximum magnetic flux. Compared to CNN (with values of 0.914 and 0.937) and MLP (with values of 0.933 and 0.870), the optimized Inception module achieved values of 0.981 and 0.973 for the two models, respectively, demonstrating the effectiveness of the proposed method. Regarding optimization algorithms, we used NSGA-III as the base algorithm and adjusted the principle for selecting reference points, dividing the optimization process into exploration and refinement stages to effectively improve the quality of the solution set. Specifically, the vibration response was reduced from the initial to , , and for the three uncertainty intervals, respectively. The objective feasible region area was reduced from 7.26 to 1.52, 0.41, and 1.89, respectively. Compared to the NSGA-III algorithm (with a feasible objective space area of 2.27), it is evident that the proposed method produces higher quality and more robust Pareto front solution sets when accounting for parameter uncertainty. The proposed Pareto ellipsoid parameter method and NSGA-III reference point selection principle guide the optimization process. By addressing and transforming parameter uncertainty, this method provides a robust and reliable solution for multi-objective optimization.
Author Contributions
Conceptualization, H.H.; methodology, H.H.; formal analysis, D.W. and Y.W.; software, H.H. and D.W.; investigation, H.H. and Y.W.; supervision, J.D. and X.C.; validation, H.H. and W.D.; writing—original draft, H.H.; writing—review and editing, W.D. and Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the Talent Program (Ph.D. Fund) of Chengdu Technological University [grant number 2024RC025], the Natural Science Foundation of Sichuan Province [grant number 2022NSFSC1892], and Fundamental Research Funds for the Central Universities [grant number XJ2021KJZK054].
Data Availability Statement
Data are available from authors on reasonable request.
Conflicts of Interest
Author Deping Wang was employed by the company China FAW Corporation Limited. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Zhao, T.; Ding, W.; Huang, H.; Wu, Y. Adaptive Multi-Feature Fusion for Vehicle Micro-Motor Noise Recognition Considering Auditory Perception. Sound Vib. 2023, 57, 133–153. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, X. Review of design optimization methods for turbomachinery aerodynamics. Prog. Aerosp. Sci. 2017, 93, 1–23. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, H.; Yuan, T.; Ma, L.; Wang, C. Electromagnetic noise analysis and optimization for permanent magnet synchronous motor used on electric vehicles. Eng. Comput. 2021, 38, 699–719. [Google Scholar] [CrossRef]
- Lin, F.; Zuo, S.-G.; Deng, W.-Z.; Wu, S.-L. Reduction of vibration and acoustic noise in permanent magnet synchronous motor by optimizing magnetic forces. J. Sound Vib. 2018, 429, 193–205. [Google Scholar] [CrossRef]
- Islam, M.S.; Islam, R.; Sebastian, T. Noise and vibration characteristics of permanent-magnet synchronous motors using electromagnetic and structural analyses. IEEE Trans. Ind. Appl. 2014, 50, 3214–3222. [Google Scholar] [CrossRef]
- Gajek, J.; Awrejcewicz, J. Mathematical models and nonlinear dynamics of a linear electromagnetic motor. Nonlinear Dyn. 2018, 94, 377–396. [Google Scholar] [CrossRef]
- Nejadpak, A.; Mohammed, O.A. Physics-based modeling of power converters from finite element electromagnetic field computations. IEEE Trans. Magn. 2012, 49, 567–576. [Google Scholar] [CrossRef]
- Wu, Y.-C.; Jian, B.-S. Magnetic field analysis of a coaxial magnetic gear mechanism by two-dimensional equivalent magnetic circuit network method and finite-element method. Appl. Math. Model. 2015, 39, 5746–5758. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, L.; Meng, D.; Su, H. Simulation, Verification and Optimization Design of Electromagnetic Vibration and Noise of Permanent Magnet Synchronous Motor for Vehicle. Energies 2022, 15, 5808. [Google Scholar] [CrossRef]
- Gundogmus, O.; Elamin, M.; Yasa, Y.; Husain, T.; Sozer, Y.; Kutz, J.; Tylenda, J.; Wright, R. Acoustic Noise Mitigation of Switched Reluctance Machines with Windows on Stator and Rotor Poles. IEEE Trans. Ind. Appl. 2020, 56, 3719–3730. [Google Scholar] [CrossRef]
- Hsu, C.-H. Fractional order PID control for reduction of vibration and noise on induction motor. IEEE Trans. Magn. 2019, 55, 6700507. [Google Scholar] [CrossRef]
- Rezig, A.; Boudendouna, W.; Djerdir, A.; N’Diaye, A. Investigation of optimal control for vibration and noise reduction in-wheel switched reluctance motor used in electric vehicle. Math. Comput. Simul. 2020, 167, 267–280. [Google Scholar] [CrossRef]
- Candan, G.; Yazgan, H.R. Genetic algorithm parameter optimisation using Taguchi method for a flexible manufacturing system scheduling problem. Int. J. Prod. Res. 2015, 53, 897–915. [Google Scholar] [CrossRef]
- Viana, F.A.; Simpson, T.W.; Balabanov, V.; Toropov, V. Special section on multidisciplinary design optimization: Metamodeling in multidisciplinary design optimization: How far have we really come? AIAA J. 2014, 52, 670–690. [Google Scholar] [CrossRef]
- Hu, H.; Deng, S.; Yan, W.; He, Y.; Wu, Y. Prediction of Operational Noise Uncertainty in Automotive Micro-Motors Based on Multi-Branch Channel–Spatial Adaptive Weighting Strategy. Electronics 2024, 13, 2553. [Google Scholar] [CrossRef]
- Huang, H.; Huang, X.; Ding, W.; Yang, M.; Yu, X.; Pang, J. Vehicle vibro-acoustical comfort optimization using a multi-objective interval analysis method. Expert Syst. Appl. 2023, 213, 119001. [Google Scholar] [CrossRef]
- Huang, H.; Huang, X.; Ding, W.; Zhang, S.; Pang, J. Optimization of electric vehicle sound package based on LSTM with an adaptive learning rate forest and multiple-level multiple-object method. Mech. Syst. Signal Process. 2023, 187, 109932. [Google Scholar] [CrossRef]
- Wu, P.; He, Y.; Li, Y.; He, J.; Liu, X.; Wang, Y. Multi-objective optimisation of machining process parameters using deep learning-based data-driven genetic algorithm and TOPSIS. J. Manuf. Syst. 2022, 64, 40–52. [Google Scholar] [CrossRef]
- Chi, S.; Yan, J.; Guo, J.; Zhang, Y. Analysis of Mechanical Stress and Vibration Reduction of High-Speed Linear Motors for Electromagnetic Launch System. IEEE Trans. Ind. Appl. 2022, 58, 7226–7240. [Google Scholar] [CrossRef]
- Liu, F.; Wang, X.; Xing, Z.; Ren, J.; Li, X. Analysis and Research on No-Load Air Gap Magnetic Field and System Multiobjective Optimization of Interior PM Motor. IEEE Trans. Ind. Electron. 2022, 69, 10915–10925. [Google Scholar] [CrossRef]
- Mezura-Montes, E.; Coello, C.A.C. Constraint-handling in nature-inspired numerical optimization: Past, present and future. Swarm Evol. Comput. 2011, 1, 173–194. [Google Scholar] [CrossRef]
- Acar, E.; Bayrak, G.; Jung, Y.; Lee, I.; Ramu, P.; Ravichandran, S.S. Modeling, analysis, and optimization under uncertainties: A review. Struct. Multidiscip. Optim. 2021, 64, 2909–2945. [Google Scholar] [CrossRef]
- Bernardo, F.P.; Pistikopoulos, E.N.; Saraiva, P.M. Robustness criteria in process design optimization under uncertainty. Comput. Chem. Eng. 1999, 23, S459–S462. [Google Scholar] [CrossRef]
- Romero, V.J.; Ayon, D.V.; Chen, C.-H. Demonstration of probabilistic ordinal optimization concepts for continuous-variable optimization under uncertainty. Optim. Eng. 2006, 7, 343–365. [Google Scholar] [CrossRef]
- Hao, Y.; He, Z.; Li, G.; Li, E.; Huang, Y. Uncertainty analysis and optimization of automotive driveline torsional vibration with a driveline and rear axle coupled model. Eng. Optim. 2018, 50, 1871–1893. [Google Scholar] [CrossRef]
- Gray, A.; Wimbush, A.; de Angelis, M.; Hristov, P.O.; Calleja, D.; Miralles-Dolz, E.; Rocchetta, R. From inference to design: A comprehensive framework for uncertainty quantification in engineering with limited information. Mech. Syst. Signal Process. 2022, 165, 108210. [Google Scholar] [CrossRef]
- Coit, D.W.; Jin, T.; Wattanapongsakorn, N. System optimization with component reliability estimation uncertainty: A multi-criteria approach. IEEE Trans. Reliab. 2004, 53, 369–380. [Google Scholar] [CrossRef]
- Li, Z.; Wang, L.; Luo, Z. A feature-driven robust topology optimization strategy considering movable non-design domain and complex uncertainty. Comput. Methods Appl. Mech. Eng. 2022, 401, 115658. [Google Scholar] [CrossRef]
- Li, Z.; Wang, L.; Lv, T. Additive manufacturing-oriented concurrent robust topology optimization considering size control. Int. J. Mech. Sci. 2023, 250, 108269. [Google Scholar] [CrossRef]
- Yang, C.; Lu, W.; Xia, Y. Uncertain optimal attitude control for space power satellite based on interval Riccati equation with non-probabilistic time-dependent reliability. Aerosp. Sci. Technol. 2023, 139, 108406. [Google Scholar] [CrossRef]
- Shimoda, M.; Nagano, T.; Shi, J.-X. Non-parametric shape optimization method for robust design of solid, shell, and frame structures considering loading uncertainty. Struct. Multidiscip. Optim. 2018, 59, 1543–1565. [Google Scholar] [CrossRef]
- Thillaithevan, D.; Bruce, P.; Santer, M. Robust multiscale optimization accounting for spatially-varying material uncertainties. Struct. Multidiscip. Optim. 2022, 65, 40. [Google Scholar] [CrossRef]
- Huang, H.; Huang, X.; Ding, W.; Yang, M.; Fan, D.; Pang, J. Uncertainty optimization of pure electric vehicle interior tire/road noise comfort based on data-driven. Mech. Syst. Signal Process. 2022, 165, 108300. [Google Scholar] [CrossRef]
- Duhamel, P.; Vetterli, M. Fast Fourier transforms: A tutorial review and a state of the art. Signal Process. 1990, 19, 259–299. [Google Scholar] [CrossRef]
- Mooney, C.Z. Monte Carlo Simulation; SAGE: Newcastle upon Tyne, UK, 1997. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A. Inception-v4, inception-resnet and the impact of residual connections on learning. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Guo, M.-H.; Xu, T.-X.; Liu, J.-J.; Liu, Z.-N.; Jiang, P.-T.; Mu, T.-J.; Zhang, S.-H.; Martin, R.R.; Cheng, M.-M.; Hu, S.-M. Attention mechanisms in computer vision: A survey. Comput. Vis. Media 2022, 8, 331–368. [Google Scholar] [CrossRef]
- Helton, J.C.; Davis, F.J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems. Reliab. Eng. Syst. Saf. 2003, 81, 23–69. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II. In Proceedings of the Parallel Problem Solving from Nature PPSN VI: 6th International Conference, Paris, France, 18–20 September 2000; pp. 849–858. [Google Scholar]
- Krishna, K.; Murty, M.N. Genetic K-means algorithm. IEEE Trans. Syst. Man Cybern. Part B 1999, 29, 433–439. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).