Abstract
The challenge of effectively managing the formation and recovery of traffic cone robots (TCRs) is addressed by proposing a linear time-varying model predictive control (MPC) strategy. This problem involves coordinating multiple TCR formations within a work area to reach a target location, which is a huge challenge due to the complexity of dynamic coordination. Unlike conventional approaches, our method decomposes the formation control problem into two main components: leader TCR motion planning and follower formation tracking control. The motion planning component involves path and velocity planning to achieve leader trajectory control, which serves as a reference trajectory for the follower. The formation tracking task extends to formation control among multiple robots to achieve the traffic cone robot formation placement and recovery task. To address the TCR input limitation problem, input constraints are considered during the design process of the MPC controllers. The effectiveness and practicality of the proposed control strategy are validated through a series of numerical simulations and physical experiments with TCRs.
1. Introduction
With the destruction and erosion by environmental factors and the constant crushing by traveling vehicles, roads are subject to varying degrees of damage, necessitating regular maintenance to prolong their service life. At present, the predominant approaches in the market for traffic cone placement and collection can be classified as manual placement or the use of collection vehicles [1]. However, manual placement is laborious and time-consuming and poses safety risks. Collection vehicles face issues such as high control costs, complex control systems, and the inability to collect abnormal traffic cones. The challenge of managing the formation and recovery of traffic cone robots (TCRs) involves complex coordination tasks, which are further complicated by dynamic work environments. Effective leader TCR motion planning and follower formation tracking control are crucial for ensuring that TCRs can operate efficiently and maintain desired formations. Among them, The motion planning component involves path and velocity planning to achieve leader trajectory control, which serves as a reference trajectory for the follower. The formation tracking task extends to formation control among multiple robots to achieve the traffic cone robot formation placement and recovery task.
With the rapid development of mobile robot technology, it is widely used in various fields [2,3,4]. Therefore, there has been significant interest in formation design methods, including the virtual structure method [5,6], the behavior-based method [7,8,9], the graph-based method [10,11,12], the artificial potential method [13,14,15], and the leader–follower method [16,17,18]. Among them, in the leader–follower method, one or several TCRs are designated as leaders to set the trajectory or target, while the others are followers. Using the designed formation controller, each follower can track their leader’s movement and maintain the desired formation. Desai first proposed two leader–follower control structures [16], namely, distance–angle control () and distance–distance control (). Moreover, the feedback linearization method is used to design the control law and prove it stable. The control pattern requires a desired distance l and an angle between the follower and leader. In the control pattern, the objective is to maintain the desired distance. Due to its straightforward control mechanism and low computational cost, the leader–follower method has become widely used in practice. To address the formation control problem, this paper proposes a novel formation control scheme for TCRs based on the leader–follower method.
In recent years, based on these two classical leader–follower control structures, many advanced control strategies have been used for formation tracking control, such as sliding mode control [19,20], backstepping control [21], fuzzy systems [22], and model predictive control [23,24]. An innovative two-layer control strategy that combines a kinematic controller based on Lyapunov theory (KCLT) with a dynamic controller based on sliding mode (DCSM) is proposed to address the problem of leader–follower formation tracking control for multiple-wheeled mobile robots (M-WMR) [19]. A novel robust control approach utilizing model predictive control (MPC) is proposed by Wang to address the formation control problem of multi-agent mobile robots, subject to physical constraints and model uncertainty [20]. Chwa et al. [21] design backstepping controllers based on feedback linearization in order to improve formation performance. However, this approach can lead to unrealistic speed jumps when the initial position error is large, which is not practical for formations. In addition, a fuzzy neural network control method with impedance learning is designed for coordinating multi-constrained robots carrying common objects [22]. Xiao et al. [23] develop a nonlinear model predictive control (NMPC) based on neurodynamic optimization for mobile robots. Lin et al. [24] propose a composite control strategy for the formation control of wheeled mobile robots (WMRs) using MPC and adaptive terminal sliding mode control (ATSMC) techniques. MPC is widely used as a popular and effective technique among the above methods. It is an advanced control technique that predicts the future system state behavior by stating the optimal input sequences that minimize the open-loop objective function.
In practical scenarios of formation placement and recovery, TCR systems may need to follow specific trajectories or reach fixed targets. Consequently, TCR systems must not only manage formation behavior but also be capable of path tracking. The path tracking control has been extensively studied in the literature. Viadero-Monasterio et al. [25] propose a multi-input multi-output (MIMO) approach for path tracking control of autonomous vehicles. Their method addresses network-induced delays and incorporates roll dynamics to enhance both driving safety and passenger comfort. An MPC method is employed for path tracking with a focus on rollover stability, using front-wheel steering and external yaw moment as control inputs [26]. An enhanced MPC controller incorporating fuzzy adaptive weight control is proposed to address path tracking in autonomous vehicles. This controller improves tracking accuracy while also considering the vehicle’s dynamic stability during the tracking process [27]. According to the IFAC industry committee [28], MPC ranks fourth in the current industry advanced control influence survey and is expected to be the most popular technique in the future. MPC effectively addresses both formation control and trajectory tracking challenges, making it highly applicable to the placement and recovery of TCRs.
Compared to existing work, this paper proposes an MPC method based on the leader–follower paradigm for TCRs, making three primary contributions. Firstly, for TCRs with incomplete constraints, the proposed linear time-varying MPC ensures locally consistent asymptotic stability, addressing the need for robust formation control under realistic placement and recovery conditions. Secondly, the leader–follower formation model is designed using two relatively “decoupled” steps: the leader TCR’s motion planning and the follower TCRs’ formation controller. This approach simplifies the design process, offering greater flexibility and adaptability to different operational scenarios. Finally, the method provides a practical solution for dynamically integrating TCRs into a formation. By adjusting only the leader TCR’s planning signals, new robots can join the formation without altering the original formation controller, ensuring efficiency and minimal disruption to existing configurations.
The structure of this paper is as follows: In Section 2, the problem formulation and preliminaries are described. Section 3 introduces the proposed formation control design based on the model predictive control. In Section 4, the numerical simulations are presented. Section 5 provides the experimental verification. Finally, Section 6 provides conclusions.
2. Problem Formulation and Preliminaries
2.1. Description of the Formation Working Conditions Problem
Figure 1 illustrates the working condition of TCR formation placement (recovery), which consists of three distinct phases. Phase 1 represents the starting position, which is located in the emergency lane. Phase 2 depicts the TCRs entering the formation placement area, which includes a warning zone, two buffer zones, a working zone, and a termination zone. It is worth noting that the warning zone is the primary placement target in this paper as it is where most safety accidents occur. The remaining areas are placed with normal traffic cones, and a favorable combination of the two allows for the placement of traffic cones as well as the reduction of accidents. Phase 3 describes the formation recovery process where the TCRs return from the placement area to the emergency lane upon receiving a recovery command and await further recovery efforts by crews. In addition, the communication towers shown in the figure serve as GPS signal base stations, which are crucial for providing real-time positional information to the TCRs. These towers enable differential positioning by working in conjunction with the GPS mobile stations equipped on each TCR. This setup ensures accurate tracking and coordination of the TCR formation throughout the placement and recovery process. (Note: In Figure 1, A denotes the warning area; B and D are the buffer areas; C refers to the working area; E is the termination area.)
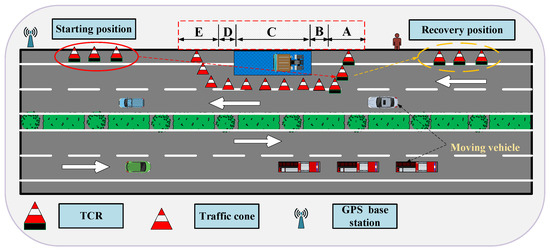
Figure 1.
Working condition schematic of TCRs.
2.2. Kinematic Model of the Traffic Cone Robot
Figure 2 illustrates the configuration of the TCR, which moves along a flat surface. The TCR comprises a front wheel and two back wheels that rotate at different rates to generate linear velocity and angular velocity as control inputs. The two back wheels are denoted by , and the wheel rolling radius is represented by .
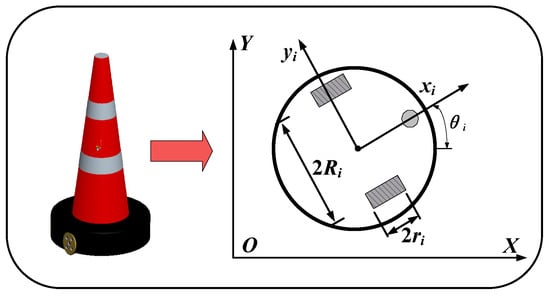
Figure 2.
Diagram of the traffic cone robot.
The kinematic equation of TCR is expressed as
where are the coordinate at the center of mass. As a result of the motor’s hardware limitations, the TCR is subject to the following physical speed constraints.
Considering a TCR moving under pure rolling, the kinematic constraint is
As a result of the motor’s hardware limitations, the TCR is subject to the following physical speed constraints,
where and are the maximum and minimum of , respectively. Similarly, and are the maximum and minimum of , respectively. The linear velocity constraints have been adjusted to permit negative values, allowing for backward movement when necessary. This change reflects a more realistic modeling of the robot’s capabilities. The angular velocity constraints now include negative values, enabling counterclockwise rotations as part of the control strategy.
2.3. Formation Model of Traffic Cone Robots
As shown in Figure 3, is the desired follower TCR position posture, is the actual follower TCR position posture. From the geometric relationship between leader and follower TCRs, we have
where is the leader’s coordinate at the center of mass, is the leader’s heading angle, and and are the desired and actual distances between the follower and the leader, respectively. and are the desired and actual angles between the follower and the leader, respectively.
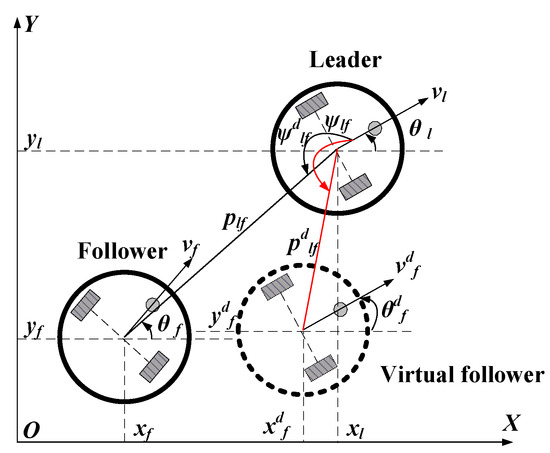
Figure 3.
Formation diagram of traffic cone robots.
By taking the derivative of Equation (12), we obtain
Finally, the TCR formation model is given as follows:
2.4. Description of MPC Design Principles
Suppose a nonlinear mechanical system consists of n state variables and m control inputs, the system dynamics can be described as:
where is the state vector, is the system dynamics function, k represents the discrete time step, and is the control vector.
Next, the error between the system and the reference state vector is given,
By deriving Equation (16), the nonlinear error model of the system is obtained as follows:
Assuming that the model equilibrium point is (0, ) and subjecting it to a Taylor expansion at the equilibrium point, the error model Equation (17) after the expansion is
where W is the higher-order term of the Taylor expansion, and when the higher-order term is neglected, Equation (18) can be reduced to
where and are the Jacobi matrices of at the error model equilibrium point (0, ) with respect to , respectively.
Bringing into Equation (19), we have
where , , .
The linear discrete time-varying system is obtained by discretizing (20) as
where , T is the control period.
Finally, the system state prediction model is
where is the control sequence within the control time domain , is predicted time domain,
The MPC principle dictates that the optimal control output produced by the controller is the optimal solution to the objective function subject to constraints. Therefore, the selection of the objective function is a critical step in controller design. The system cost function is presented below.
where is the relaxation factor, is the penalty weights, and Q, R are state quantity tracking capability and control quantity weight matrices, respectively. It is worth noting that is introduced as a slack variable to relax hard constraints, providing a degree of freedom in situations where strict constraints may be infeasible. is a weight that determines the cost associated with violating constraints via the slack variable . A larger places more emphasis on minimizing constraint violations, effectively discouraging them unless absolutely necessary for feasibility. Conversely, a smaller permits more leniency in constraint violations.
Let . By bringing Equation (29) into Equation (33) and ignoring the constant term, the optimal control with constraints can be transformed into the standard quadratic form without constraints as follows:
where
Remark 1.
The first term in Equation (34) represents the system tracking performance, and the second term represents the system constraint on the control increment. During actual system operation, the system state volume constraint and the control volume constraint must also be taken into account. As a result, Equation (34) can be reformulated as a quadratic programming problem with constraints.
Solving Equation (38), the optimal sequence can be obtained.
where is optimal feedback control increment.
Next, the first value of the optimal feedback control increment sequence in the control time domain is used in the actual control.
where is the difference between the actual control and the reference control. Then, the final control quantity of the system is
3. Formation Control Design Based on Model Predictive Control
Path and speed planning is critical for the leader robot before the TCR can form a target formation. Proper planning not only ensures high-quality final placement but also reduces construction time and costs. In this section, we complete leader TCR motion path planning using a fifth-order polynomial curve. Additionally, we utilize the S-shaped velocity planning method to accomplish leader TCR velocity planning.
3.1. The Path Planning of Leader Traffic Cone Robot
Unlike traditional formation design ideas, this paper proposes a path planning strategy for TCRs based on the leader–follower method, where one TCR is designated as the leader and the remaining TCRs are designated as followers. Through the design of the follower TCRs’ formation and the motion planning of the leader TCR, it realizes the whole TCR formation control. As the follower TCRs maintain the same motion as the leader TCRs, the follower TCRs’ path planning can be ensured by the formation design.
During the placement of the TCRs in formation, the leader TCR can obtain the position of the upper and lower boundaries of the warning zone A and B at the moment T via GPS. In Figure 4, the leader TCR starts from point P and moves in formation at an optimal speed, arriving at point E to stop the placement.
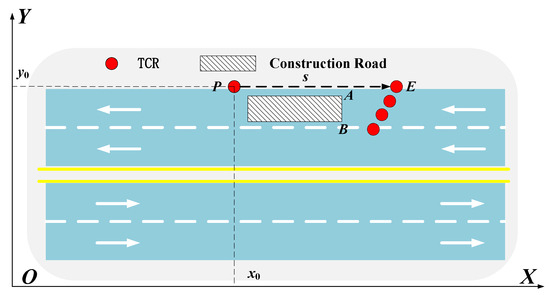
Figure 4.
Formation placement path of traffic cone robots.
From Figure 4, we can obtain information on the path of the leader TCR.
where s is the distance of the placement process of the TCR from the starting point, () is the horizontal and vertical coordinate of the starting point P.
From Figure 5, the following information is given about the leader’s path during the recovery condition.
where is the distance of the TCR recovery process from point E() is the horizontal and vertical coordinates of point E.
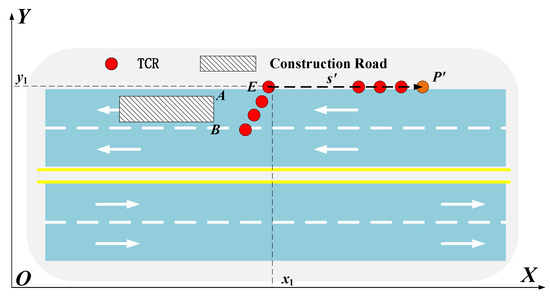
Figure 5.
Formation recovery path of traffic cone robots.
3.2. The Velocity Planning of Leader Traffic Cone Robot
In the placement (recovery) process, the driving speed of the TCR is a crucial factor for both construction efficiency and traffic safety. If the driving speed is too fast, it may pose safety hazards to passing vehicles, while driving too slow can affect the overall construction process. Therefore, maintaining a stable and appropriate moving speed is essential to ensure the success of the entire placement and recovery process.
In the field of velocity planning, there are several methods available such as trapezoidal velocity planning, five-polynomial S-shaped velocity planning, and seven-polynomial S-shaped velocity planning. In this study, the trapezoidal velocity planning method was adopted to determine the driving speed during the placement (recovery) process.
As shown in Figure 6, a complete trapezoidal velocity planning process contains three phases: uniform acceleration phase, uniform velocity phase, and uniform deceleration phase.
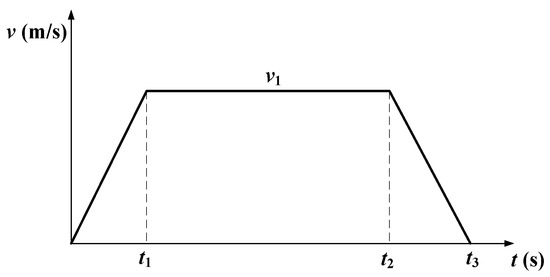
Figure 6.
Schematic diagram of trapezoidal velocity curve.
Next, the speed planning of the leader TCR is given as follows:
where is the initial velocity, is the velocity at moment , i = 1, 2, 3, and is maximum acceleration.
From the Figure 6, we can see that the uniform acceleration phase and the uniform deceleration phase are symmetrical, then we have
The uniform acceleration zone length , the uniform velocity zone length and the uniform deceleration zone length are given as
Let , m/s, and S = 5 m. Figure 7 shows the velocity plan for the entire formation trajectory.
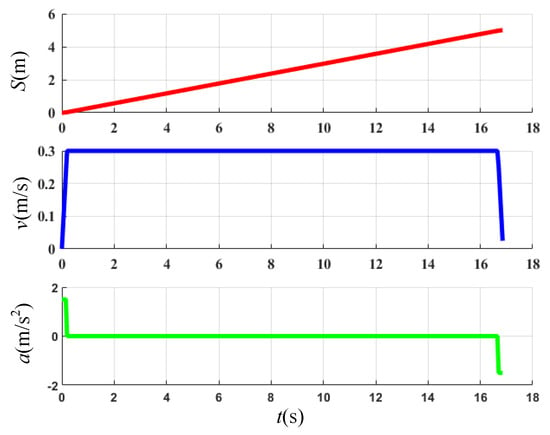
Figure 7.
Placement velocity planning chart of leader TCR.
Note that recovery placement velocity planning is similar to the placement process and is not repeated.
3.3. Linear Time-Varying MPC Design
The TCR formation control problem based on the leader–follower formation model can be decomposed into two sub-problems: trajectory tracking of the leader and formation following of the follower TCRs.
3.3.1. Trajectory Tracking Control Design for Leader TCR
The TCR formation control system is complex and requires high real-time requirements, and the nonlinear model predictive control is computationally intensive and difficult to meet controller real-time requirements. Therefore, this paper uses a linear time-varying model predictive control.
Rewrite the Equation (1) in the following form
where is the control input for the leader.
According to Equations (16)–(21), a linear discrete-time error model for the leader TCR can be obtained as follows:
where
Next, the optimal control sequence for the trajectory tracking of the leader TCR at k moments is given as follows:
Using the first value of the optimal feedback control increment sequence in the control time domain , we have
The final control of the leader TCR is then as follows:
where is the k moment to plan the leader TCR velocity.
3.3.2. Formation Tracking Control Design for Follower TCRs
Formation controller based on the leader–follower model ensures that each follower TCR maintains the desired formation with the leader to complete formation placement (recovery). This section presents a controller design based on MPC.
The kinematic Equantion (14) of the i-th follower TCR formation can be translated into the following form
where is the control input of the i-th follower the TCRs.
According to Equations (16)–(21), a linear discrete-time error model for the follower TCRs can be obtained as follows:
with
where
Next, the optimal control sequence for the trajectory tracking of the follower TCRs at k moments is given as follows:
Taking the first element of the control sequence as the feedback increment of the i-th follower TCR formation control, we have
The final control of the leader TCR is then as follows:
where is the k moment to plan the follower TCRs velocity.
To this end, the MPC controller flowchart is shown in Figure 8.
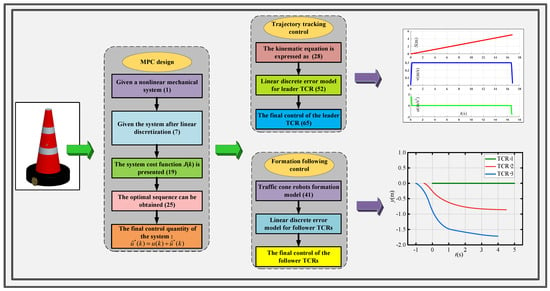
Figure 8.
The flowchart of the MPC controller.
4. Numerical Simulations
In this section, a pair of case studies are conducted to show the effectiveness of the proposed TCR method.
Case 1: The numerical simulation of the three TCRs under the formation placement condition.
The main parameters of the TCRs used for the simulation are given as follows: m, m, = rad, = rad,, = 0 rad, = 0.23 m, = 0.036 m, = 40, = 15, , , = 10, T = 0.05 s. The initial conditions of the TCRs are given as follows: = 0 m, = 0 m, = 0 m, m, m, = 0 m, m, = 0 m, = 0 m, and the leader TCR expectation position (5 m, 0 m).
Figure 9 illustrates the trajectory profile of the traffic cone robots’ (TCRs’) in-plane formation placement under the MPC controller. The TCRs maintain a diagonal formation from the starting position (0 m, 0 m) to the target position (5 m, 0 m). The speed of the TCRs is presented in Figure 10. The follower TCRs’ linear velocity fluctuates widely in the starting phase due to initial errors, but the velocity stabilizes at approximately 0.3 m/s after 10 s. The angular velocity gradually converges to 0 rad/s with time. Figure 11 presents the leader TCR-1’s tracking error results. The leader TCR-1 exhibited no initial position errors in either the x or y direction, and the initial heading error is 0.0002 rad. The heading error converged to zero within approximately 2 s of the simulation starting, indicating that the leader TCR-1 can accurately follow the desired placement trajectory in real time. Figure 12 shows the formation error of the follower TCRs, and the formation errors (formation distance error and formation angle error) converge to zero in about 10 s and remain stable during subsequent placement operations. These simulation results demonstrate the effectiveness of the control method in formation stabilization.
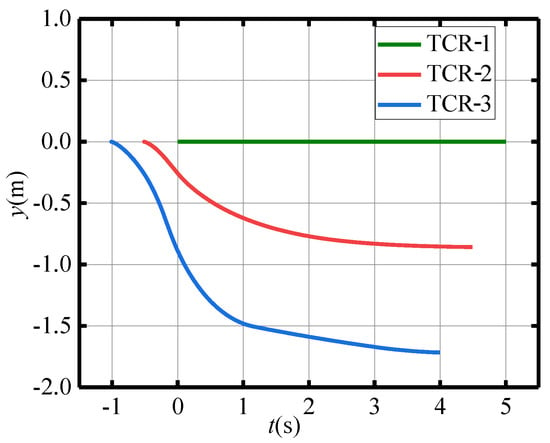
Figure 9.
Formation placement trajectory curve diagram about TCRs.
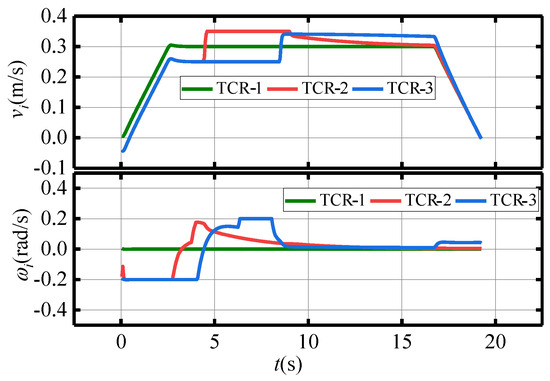
Figure 10.
Velocity graph of TCRs.
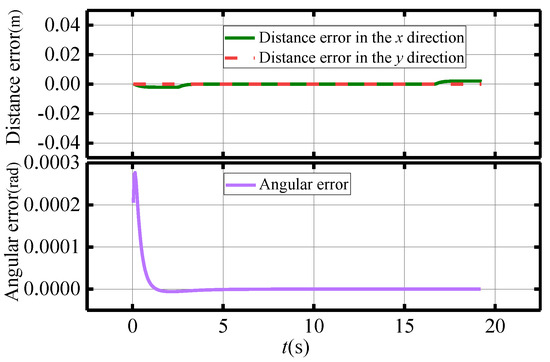
Figure 11.
Trajectory tracking error for formation placement of leader TCR.
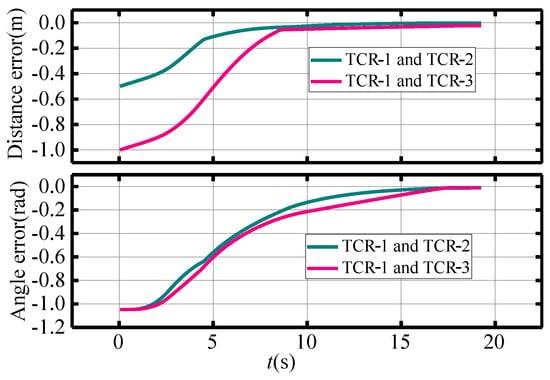
Figure 12.
Formation placement error of follower TCRs.
Case 2: The numerical simulation of the three TCRs under the formation recovery condition. The formation parameters are as follows: m, m, = = rad, = = 0 rad.
The initial conditions of the TCRs are specified as follows: = 5 m, = 0 m, = 0 m, = 4.5 m, m, = 0 m, = 3.59 m, m, and = 0 m, with the leader TCR expected to be positioned at (10 m, 0 m). The resulting trajectories of the TCRs are similar to those of case 1, with the formation recovery trajectories shown in Figure 13. Figure 14 and Figure 15 illustrate the velocities and formation recovery errors of the TCRs, respectively. As depicted in Figure 13, the MPC controller guides the TCRs from the placement position back to the emergency lane position. The TCRs experience some fluctuation in the formation recovery process due to initial position and angle errors, but the entire recovery process is smooth, and the maximum velocities remain within the specified upper limit of 0.3 m/s (0.3 rad/s), as shown in Figure 14. Furthermore, as demonstrated in Figure 15, the distance and angle errors of the leader TCR-1 and follower TCR-2 converge to 0 around 10 s, while the distance and angle errors of follower TCR-3 converge to 0 around 25 s, after which they remain stable. These results confirm that the proposed control method exhibits satisfactory performance even under recovery conditions.
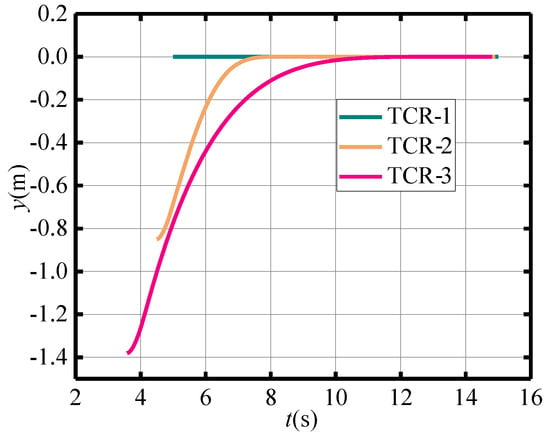
Figure 13.
Formation recovery trajectory curve diagram about TCRs.
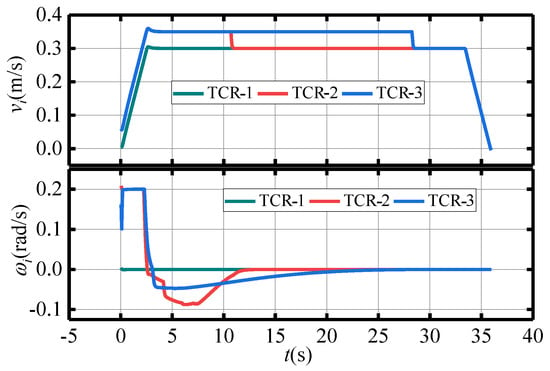
Figure 14.
Velocity graph of TCRs.
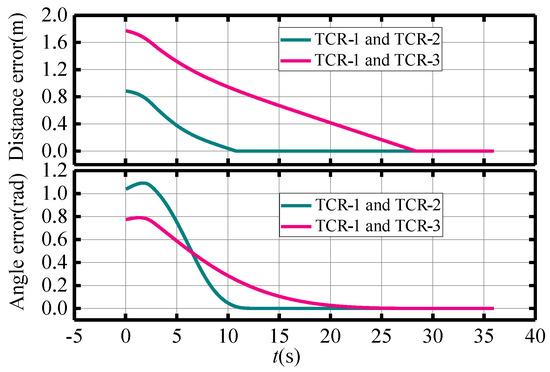
Figure 15.
Formation recovery error of follower TCRs.
5. Experiments
In this section, MATLAB 2020 b was used for developing and simulating the control algorithms, while ROS (robot operating system) is utilized for real-time communication and control of the TCRs. Specifically, MATLAB’s Robotics System Toolbox facilitated the integration with ROS, allowing us to design and test the MPC algorithms within MATLAB, convert them to C++, and then deploy these C++ algorithms to the TCR via ROS. Finally, these control algorithms are published to the relevant ROS topics. The TCR running ROS subscribes to these topics to receive commands. Additionally, sensor data from the TCRs were published on ROS topics. This enables the traffic cone robot formation placement and recovery task. Next, we demonstrate the effectiveness and practicality of the MPC controller designed in the previous sections by utilizing three TCRs in a formation to showcase its control performance.
5.1. Experiments
Figure 16 illustrates the experimental setup for the TCR, consisting of the mobile robot platform (IRobot), controller (Raspberry Pi), real-time kinematic (RTK) GPS sensors, and power supply. The PC computer serves as the monitoring layer, communicating with the Raspberry Pi through WiFi. The controllers communicate with each other and the computer via WiFi while also communicating with the RTK GPS through universal serial bus (USB) serial ports. The experimental procedure is as follows:
- (1)
- Connect the Raspberry Pi and PC via WIFI.
- (2)
- log in to Raspberry Pi remotely on PC through SSH, and start each TCR.
- (3)
- Start the parameter optimization node through the launch file.
- (4)
- Start the RTK GPS serial information reading node and start the trajectory display node through the launch file. This will convert the longitude, latitude, heading, speed, and other information output from both to the OXY plane coordinate system.
- (5)
- Start the TCR formation controller.
- (6)
- After the placement (recovery) operation is finished, stop the program and save the TCR’s trajectory information.
Figure 17 and Figure 18 show the experimental process diagrams of the TCRs in placement and recovery formations at t = 0 s, t = 10 s, and t = 20 s, respectively.

Figure 17.
Experimental scene of traffic cone robot placement conditions.

Figure 18.
Experimental scene of traffic cone robot recovery conditions.
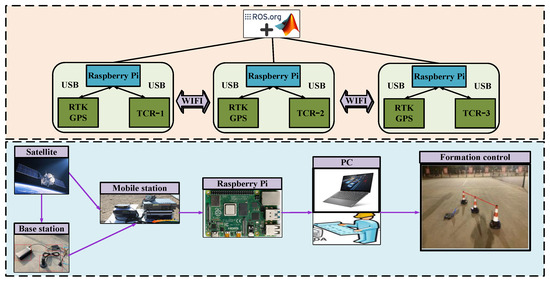
Figure 16.
Schematic diagram of experimental control principle of TCRs.
5.2. Experiment Result
The experimental setup is consistent with the simulation parameters. Figure 19, Figure 20, Figure 21, Figure 22 and Figure 23 display the experimental results for TCR placement and recovery. Figure 19 shows the trajectories of the leader and follower TCRs during formation placement, where the triangle symbol represents the start position and the star symbol represents the target position. Figure 20 shows that the distance error between the robots gradually converges to 0.1 m, achieving the desired formation of the leader–follower TCR system. Figure 21 depicts the time histories of the leader’s control inputs and , which meet the maximum system limits ( (−0.5 m/s, 0.5 m/s), (−0.5 rad/s, 0.5 rad/s)). Additionally, the recovery trajectories of the TCRs are shown in Figure 22, demonstrating an orderly return to the emergency lane position. Figure 23 illustrates the reasonable convergence of position errors for the three TCRs under the proposed formation tracking control. After 30 s, the error converges to a small neighborhood around −0.1 m due to GPS sensor error. The results demonstrate that the proposed control method still performs well in formation recovery tconditions.
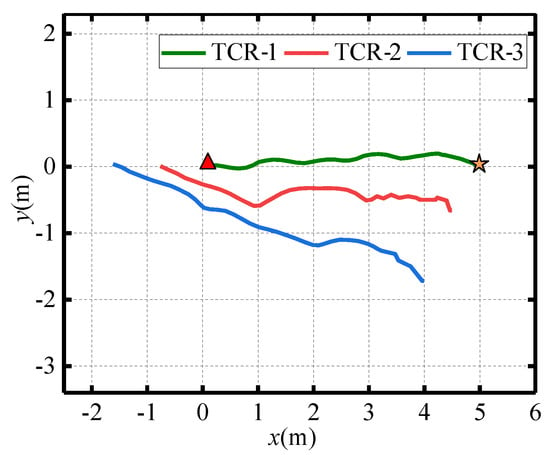
Figure 19.
The formation placement trajectory diagrams of the TCRs.
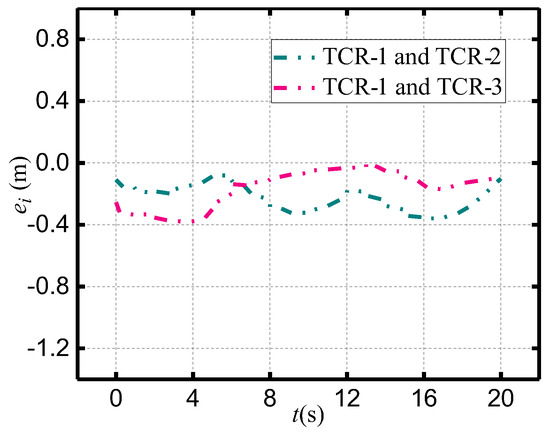
Figure 20.
Distance errors of TCRs.
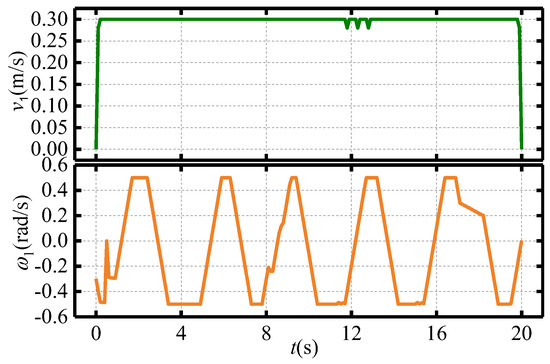
Figure 21.
The velocity diagrams of the leader TCR.
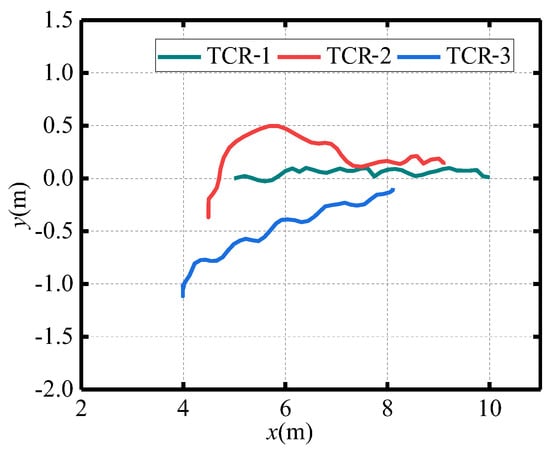
Figure 22.
The formation recovery trajectory diagrams of the TCRs.
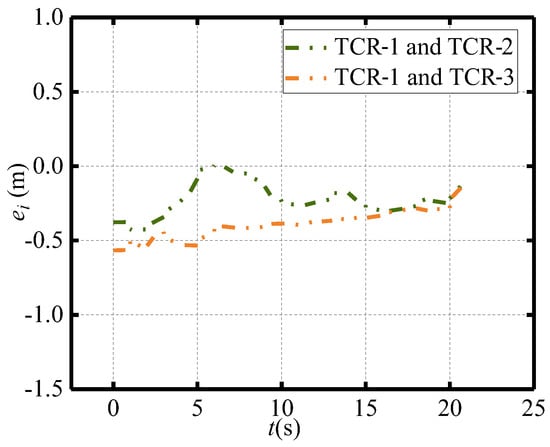
Figure 23.
Distance errors of the TCRs.
6. Conclusions
In this paper, we investigate the problem of formation placement and recovery in TCR systems. The formation control task is divided into two sub-tasks: motion planning for the lead TCR and formation control for the follower TCRs. The lead TCR undergoes path and velocity planning, and the resulting trajectory serves as a reference for the follower TCRs. Formation control design employs a time-varying MPC approach that linearizes and discretizes the formation kinematic model to maintain the formation while limiting the control inputs to meet the hardware requirements of the chassis ( (−0.5 m/s, 0.5 m/s), (−0.5 rad/s, 0.5 rad/s)). Simulations and experiments with TCRs demonstrate the effectiveness of the proposed formation placement and recovery control approach. Among them, the simulated distance error converges to 0 m, and the experimental distance error converges to about ±0.1 m (due to GPS accuracy), both of which satisfy the TCR formation requirements. In future work, we will develop a dynamic model for the TCRs based on the current kinematic model and incorporate road friction effects into the TCRs’ motion model. This refinement will involve examining how frictional forces impact formation control and trajectory tracking, thereby enhancing the practical applicability and robustness of our control strategies.
Author Contributions
Methodology, S.C.; Validation, S.J.; Writing—original draft, Z.L.; Writing—review and editing, M.Y. All authors have read and agreed to the published version of the manuscript.
Funding
National Key R D Program of China under Grant (2022YFE0123800), and Key Program for International S T Cooperation Projects of Hean under Grant (231111520200).
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to (the project was not completed and data confidentiality was required).
Conflicts of Interest
Zhiyong Li has received research grants from Henan Gaoyuan Maintenance Technology of Highway Co., Ltd. The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| TCR | traffic cone robot |
| KCLT | kinematic controller based on Lyapunov theory |
| DCSM | dynamic controller based on sliding mode |
| M-WMR | multiple-wheeled mobile robots |
| MPC | model predictive control |
| NMPC | nonlinear model predictive control |
| ATSMC | adaptive terminal sliding mode control |
| MIMO | multi-input multi-output |
| RTK | real-time kinematic |
| USB | universal serial bus |
| Nomenclature: | |
| Line velocity of the i-th TCR | |
| Angular velocity of the i-th TCR | |
| The desired follower TCR position posture | |
| The actual follower TCR position posture | |
| The actual distances between the follower and the leader | |
| The actual angles between the follower and the leader | |
| Difference between leader’s heading angle and follower’s heading angle | |
| k | The discrete time step |
| The system cost function | |
| The final control quantity | |
References
- Lee, H.S.; Jung, S. Line-up formation control of intelligent traffic cones. In Proceedings of the 2017 17th International Conference on Control, Automation and Systems (ICCAS), Jeju, Republic of Korea, 18–21 October 2017. [Google Scholar]
- Zhao, W.B.; Liu, H.; Lewis, F.L.; Wang, X.L. Data-driven optimal formation control for quadrotor team with unknown dynamics. IEEE Trans. Cybern. 2022, 52, 7889. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.; Zhu, Z.; Jing, X.; Lu, M.; Gu, Y. Magnetic driven double curved conical microhelical robot. Adv. Theory Simul. 2021, 4, 2100189. [Google Scholar] [CrossRef]
- Zhang, J.L.; Jiao, S.J.; Yi, X.G.; Wu, C.G. Adaptive robust control for uncertain underactuated mechanical systems. Adv. Theory Simul. 2023, 6, 2300323. [Google Scholar] [CrossRef]
- Do, K.D.; Pan, J. Nonlinear formation control of unicycle-type mobile robots. Robot Auton. Syst. 2007, 55, 191. [Google Scholar] [CrossRef]
- Zhang, Q.; Lapierre, L.; Xiang, X.B. Distributed control of coordinated path tracking for networked nonholonomic mobile vehicles. IEEE Trans. Ind. Informat. 2013, 8, 472. [Google Scholar] [CrossRef]
- Balch, T.; Arkin, R.C. Behavior-based formation control for multirobot teams. IEEE Trans. Robot Autom. 1998, 14, 926. [Google Scholar] [CrossRef]
- Monteiro, S.; Bicho, E. Attractor dynamics approach to formation control: Theory and application. Auton. Robot. 2010, 29, 331. [Google Scholar] [CrossRef]
- Lee, G.; Chwa, D. Decentralized behavior-based formation control of multiple robots considering obstacle avoidance. Intell. Serv. Robot 2018, 11, 127. [Google Scholar] [CrossRef]
- Cao, Y.C.; Stuart, D.; Ren, W.; Meng, Z.Y. Distributed containment control for multiple autonomous vehicles with double-integrator dynamics: Algorithms and experiments. IEEE Trans. Control Syst. Technol. 2011, 19, 929. [Google Scholar] [CrossRef]
- Shoja, S.; Baradarannia, M.; Hashemzadeh, F.; Badamchizadeh, M.; Bagheri, P. Surrounding control of nonlinear multi-agent systems with non-identical agents. ISA Trans. 2017, 70, 219. [Google Scholar] [CrossRef]
- Li, D.Y.; Ge, S.S.; He, W.; Ma, G.F.; Xie, L.H. Multilayer formation control of multi-agent systems. Automatica 2019, 109, 108558. [Google Scholar] [CrossRef]
- Zhang, J.L.; Zhao, R.Y.; Jiao, S.J. Optimization of robust formation tracking control for traffic cone robots with matching and mismatching uncertainties: A fuzzy-set theory-based approach. Expert Syst. Appl. 2023, 227, 120233. [Google Scholar] [CrossRef]
- Merheb, A.R.; Gazi, V.; Sezer-Uzol, N. Implementation studies of robot swarm navigation using potential functions and panel methods. IEEE/ASME Trans. Mechatronics 2016, 21, 2556. [Google Scholar] [CrossRef]
- Liu, X.M.; Ge, S.S.; Goh, C.H. Formation potential field for trajectory tracking control of multi-agents in constrained space. Int. J. Control 2017, 90, 2137. [Google Scholar] [CrossRef]
- Desai, J.P.; Ostrowski, J.P.; Kumar, V. Modeling and control of formations of nonholonomic mobile robots. IEEE Trans. Robot Autom. 2001, 17, 905. [Google Scholar] [CrossRef]
- Maghenem, M.A.; Loría, A.; Panteley, E. Cascades-based leader-follower formation tracking and stabilization of multiple nonholonomic vehicles. IEEE Trans. Autom. Control 2020, 65, 3639. [Google Scholar] [CrossRef]
- Wang, X.K.; Yu, Y.G.; Li, Z.K. Distributed sliding mode control for leader-follower formation flight of fixed-wing unmanned aerial vehicles subject to velocity constraints. Int J. Robust Nonlinear Control 2020, 31, 2110. [Google Scholar] [CrossRef]
- Zhao, Y.D.; Zhang, Y.Y.; Lee, J.Y. Lyapunov and sliding mode based leader–follower formation control for multiple mobile robots with an augmented distance-angle strategy. Int. J. Control Autom. Syst. 2019, 17, 1314. [Google Scholar] [CrossRef]
- Nair, R.R.; Behera, L.; Kumar, S. Event-triggered finite-time integral sliding mode controller for consensus-based formation of multirobot systems with disturbances. IEEE Trans. Control Syst. Technol. 2019, 27, 39. [Google Scholar] [CrossRef]
- Chwa, D. Tracking control of differential-drive wheeled mobile robots using a backstepping-like feedback linearization. IEEE Trans. Syst. Man Cybern. Syst. 2010, 40, 1285. [Google Scholar] [CrossRef]
- Kong, L.H.; He, W.; Yang, C.G.; Li, Z.J.; Sun, C.Y. Adaptive fuzzy control for coordinated multiple robots with constraint using impedance learning. IEEE Trans. Cybern. 2019, 49, 3052. [Google Scholar] [CrossRef] [PubMed]
- Xiao, H.Z.; Li, Z.J.; Chen, C.L.P. Formation control of leader–follower mobile robots’ systems using model predictive control based on neural-dynamic optimization. IEEE Trans. Ind. Electron. 2016, 63, 5752. [Google Scholar] [CrossRef]
- Lin, S.; Jia, R.; Yue, M.; Xu, Y. On composite leader–follower formation control for wheeled mobile robots with adaptive disturbance rejection. Appl Artif. Intell. 2019, 33, 1306. [Google Scholar] [CrossRef]
- Viadero-Monasterio, F.; Nguyen, A.-T.; Lauber, J.; Boada, M.J.L.; Boada, B.L. Event-triggered robust path tracking control considering roll stability under network-induced delays for autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 2023, 24, 14743. [Google Scholar] [CrossRef]
- Tian, Y.; Yao, Q.; Wang, C.; Wang, S.; Liu, J.; Wang, Q. Switchedmodel predictive controller for path tracking of autonomous vehicle considering rollover stability. Veh. Syst. Dyn. 2021, 60, 4166. [Google Scholar] [CrossRef]
- Wang, H.; Liu, B.; Ping, X.; An, Q. Path tracking control for autonomous vehicles based on an improved MPC. IEEE Access 2019, 7, 161064. [Google Scholar] [CrossRef]
- Samad, T. A survey on industry impact and challenges thereof. IEEE Control Syst. Mag. 2017, 37, 17. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).