Soft Robots: Computational Design, Fabrication, and Position Control of a Novel 3-DOF Soft Robot
Abstract
1. Introduction
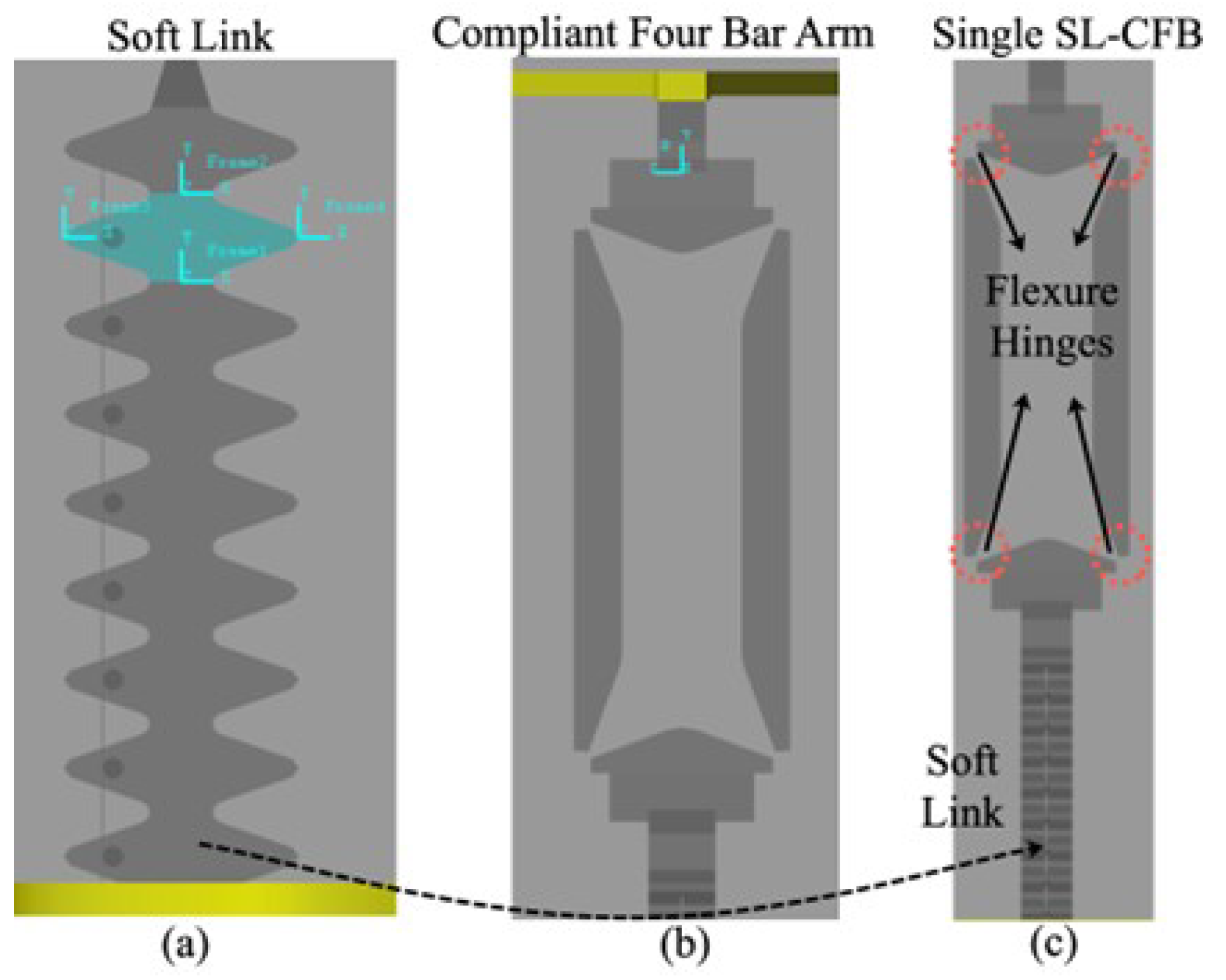
2. Design and Fabrication
3. Modeling the Kinematics
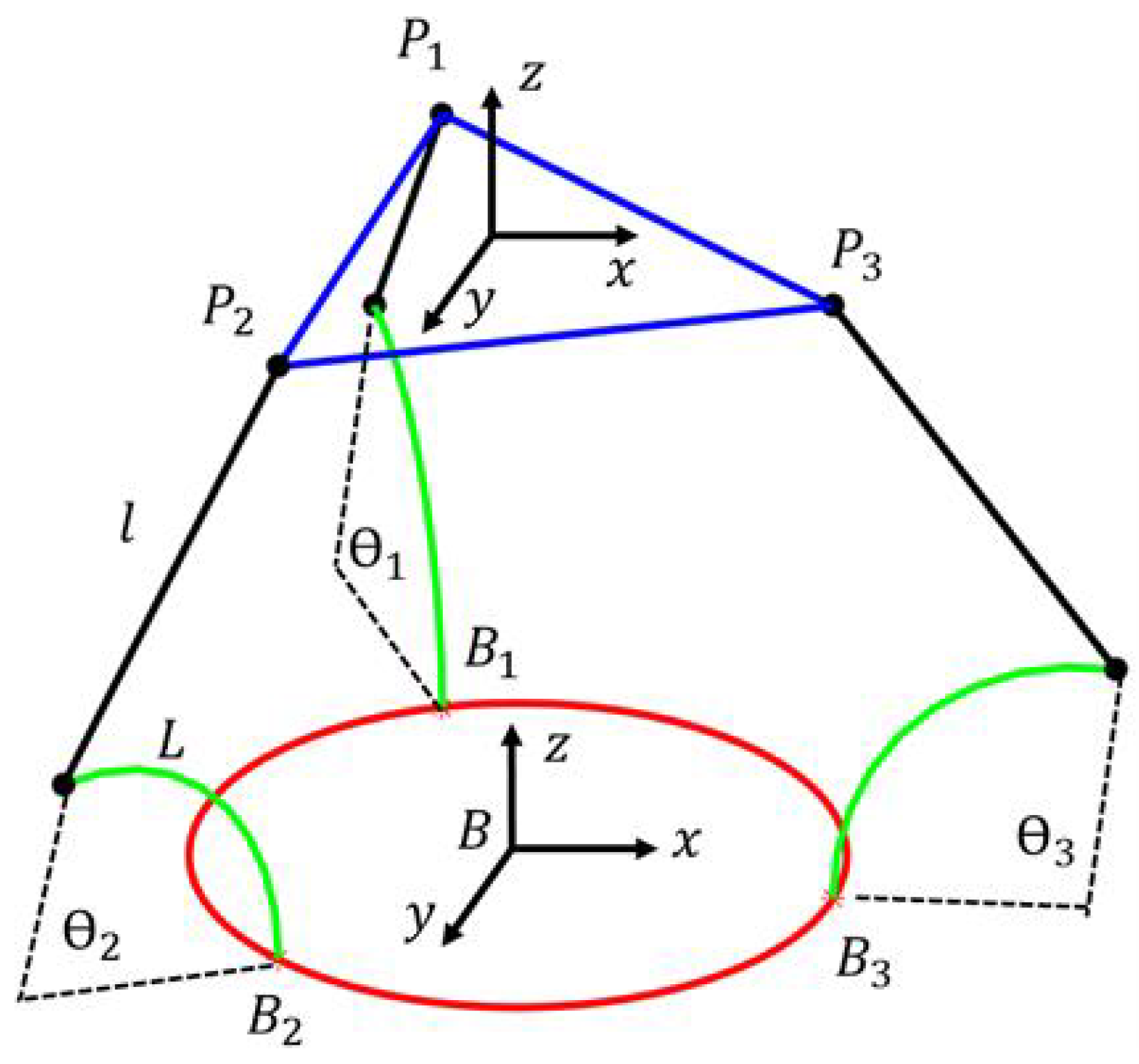
3.1. Analytic Kinematics
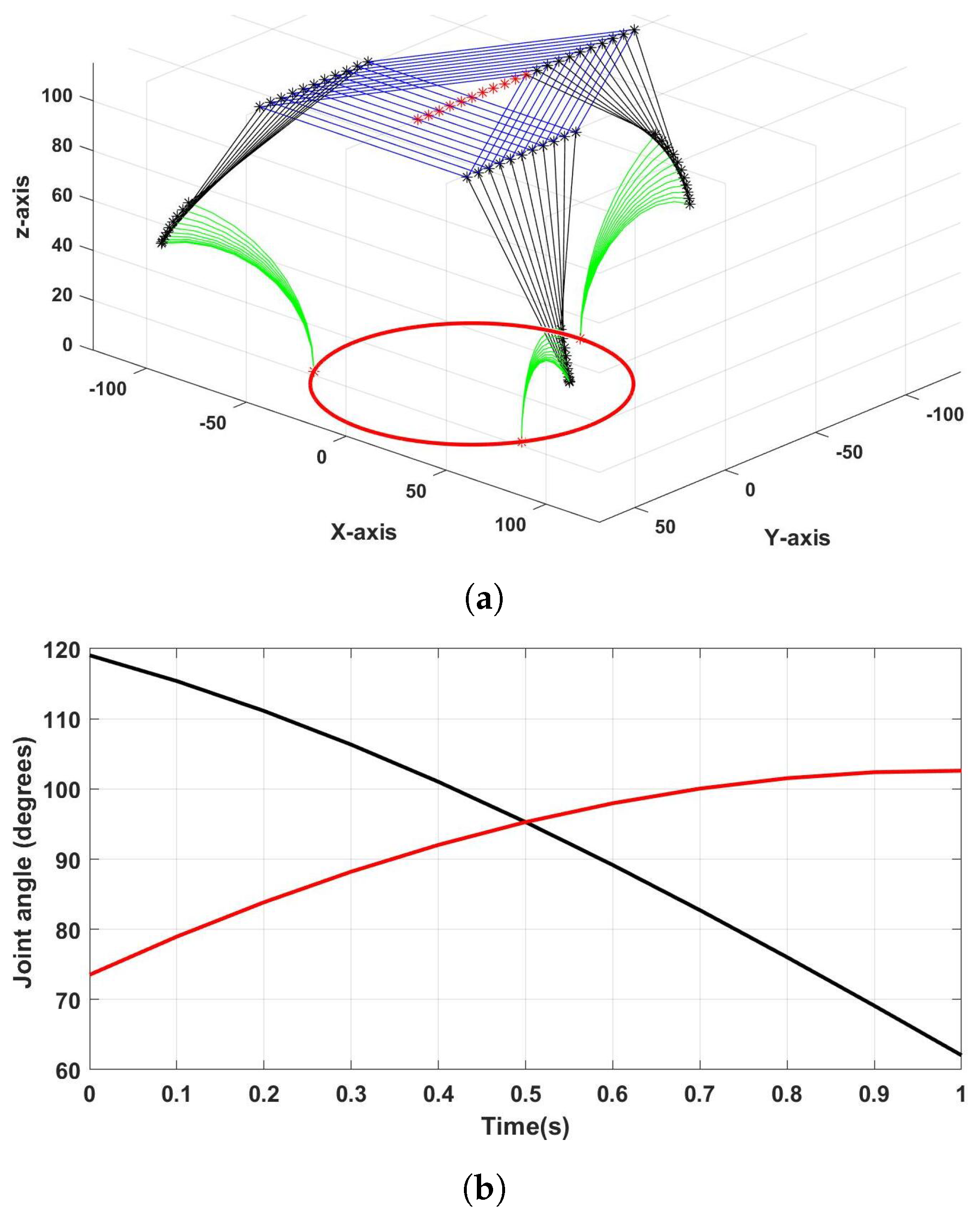
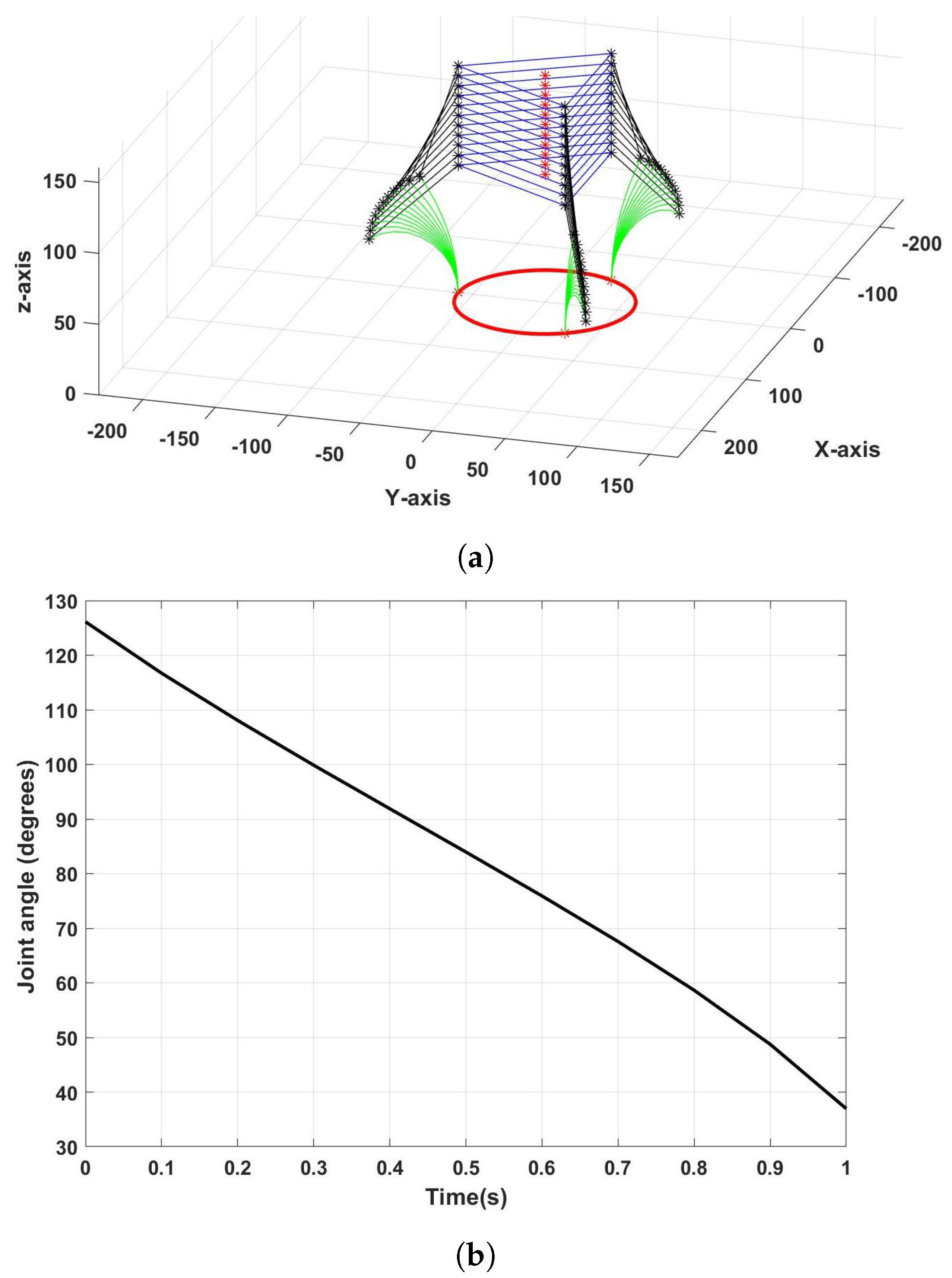
3.2. Numerical Kinematics
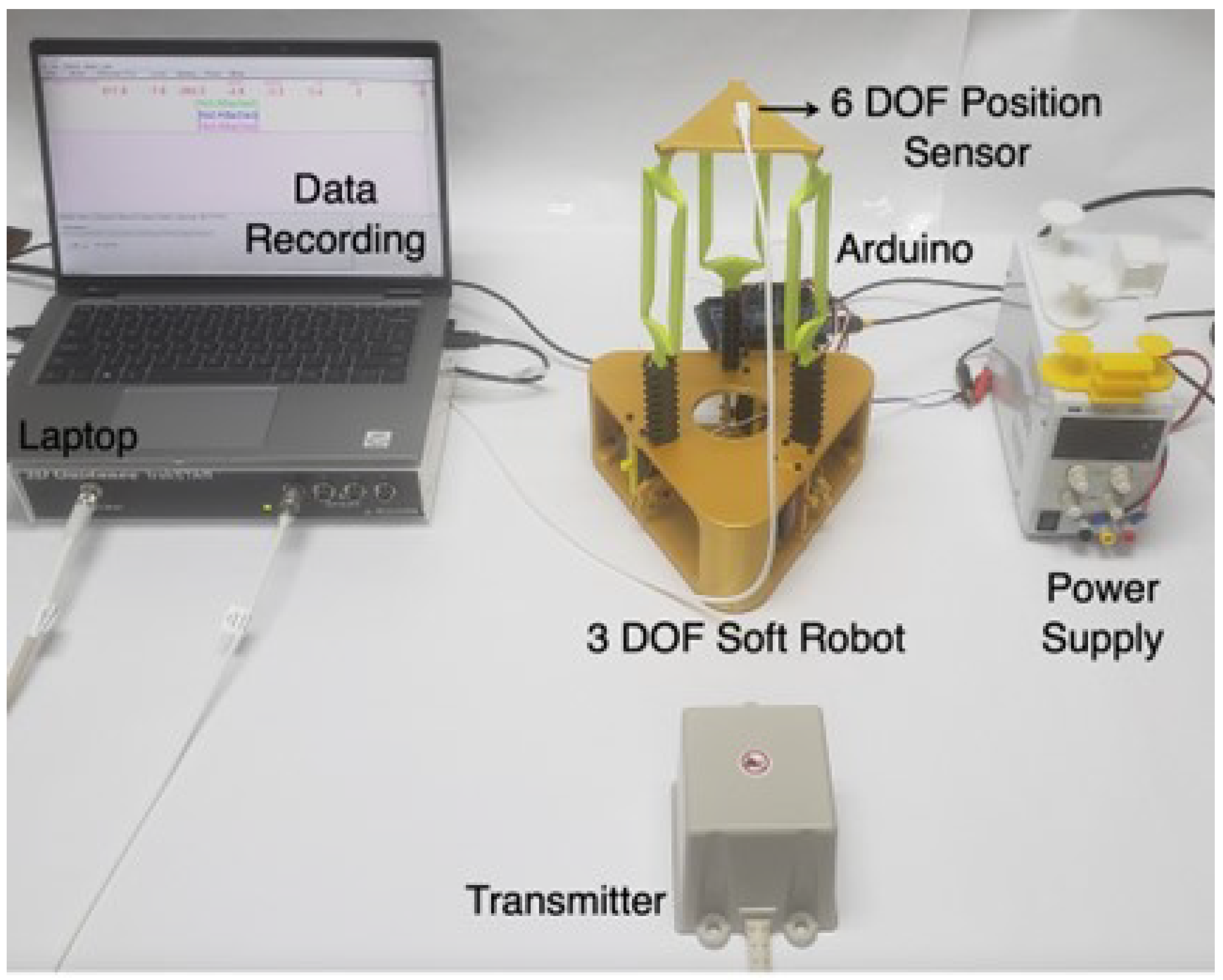
4. Soft Robot Position Control
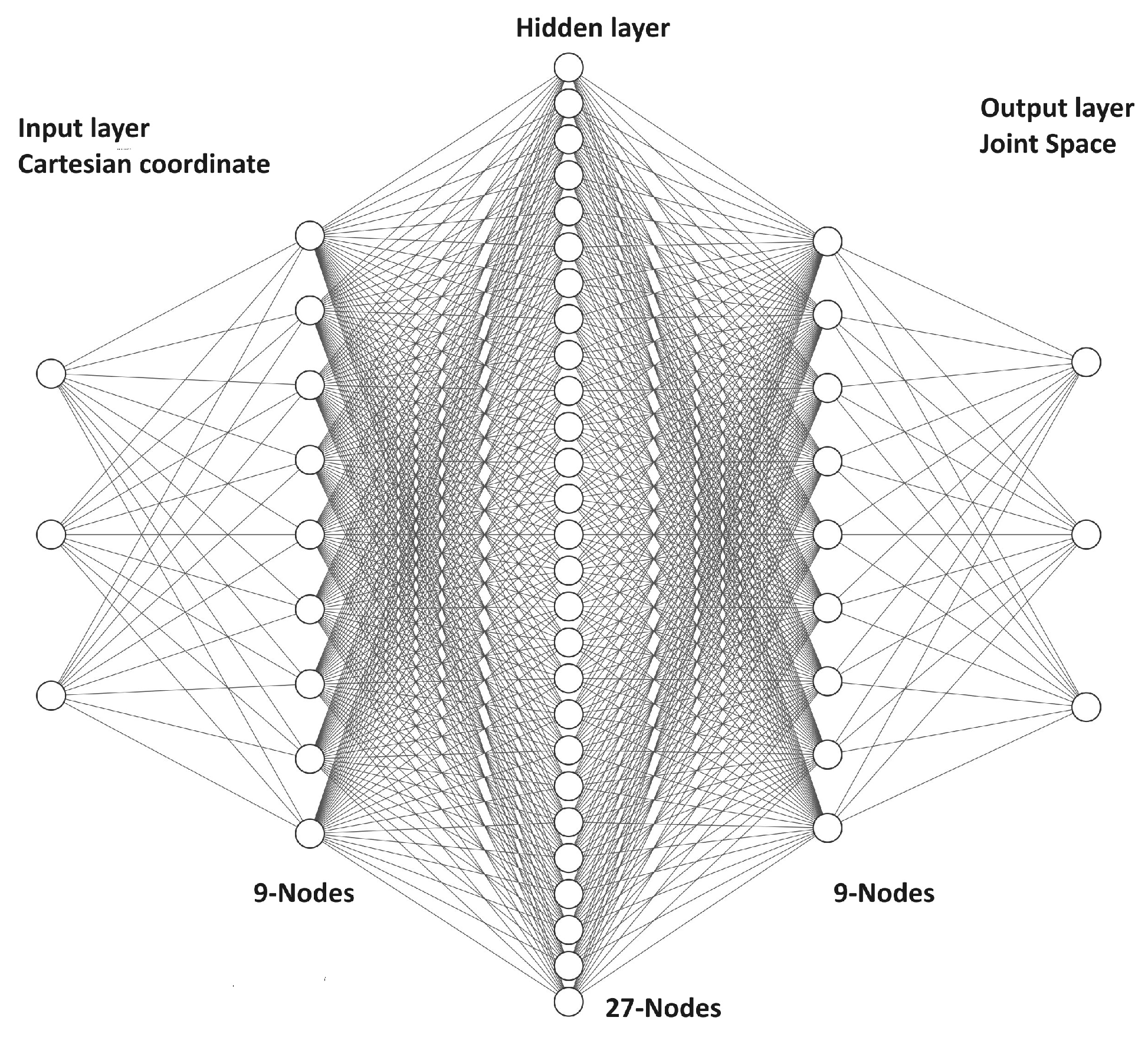
4.1. Data-Driven Approaches in Control
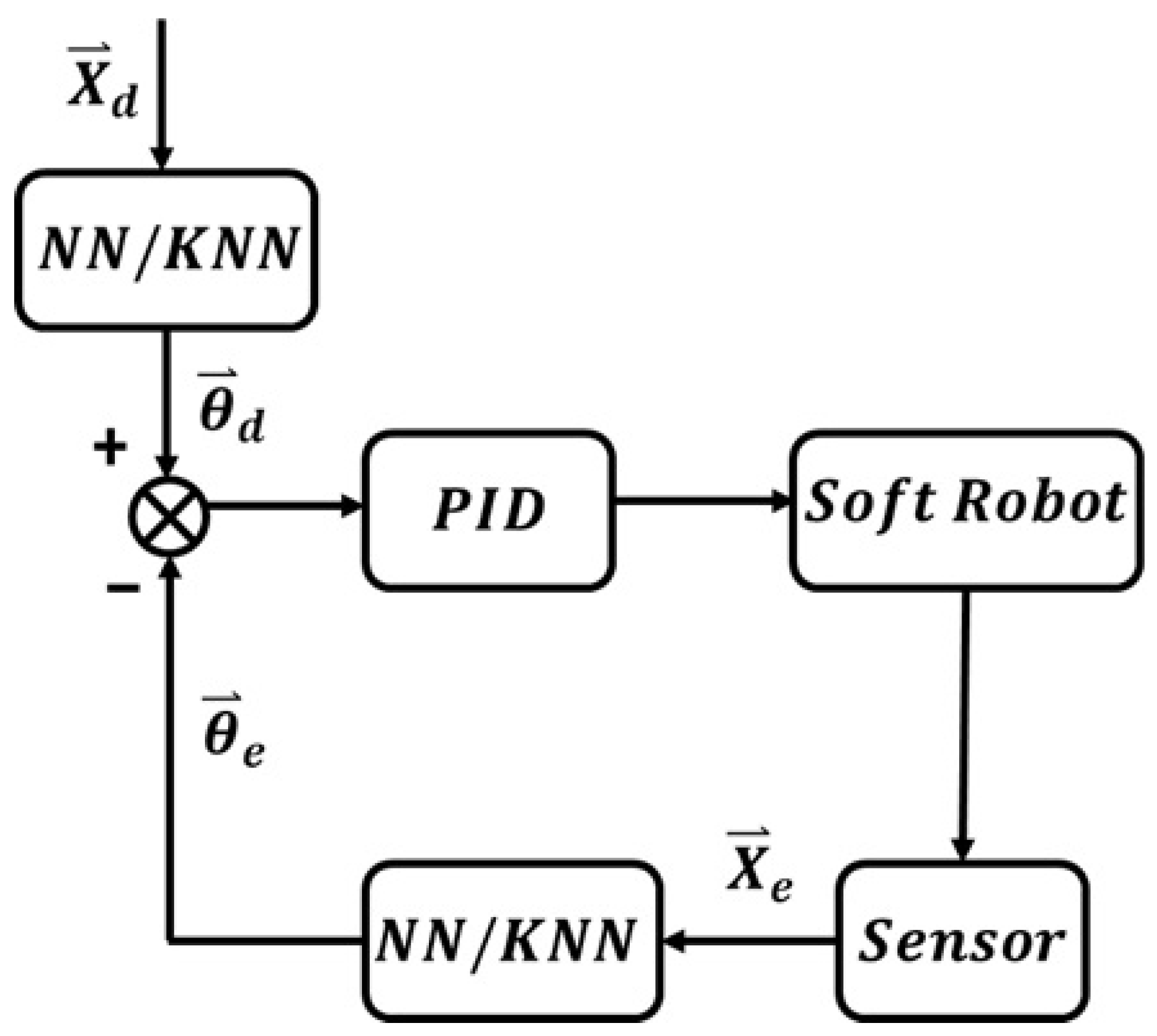
4.2. Closed-Loop Position Control
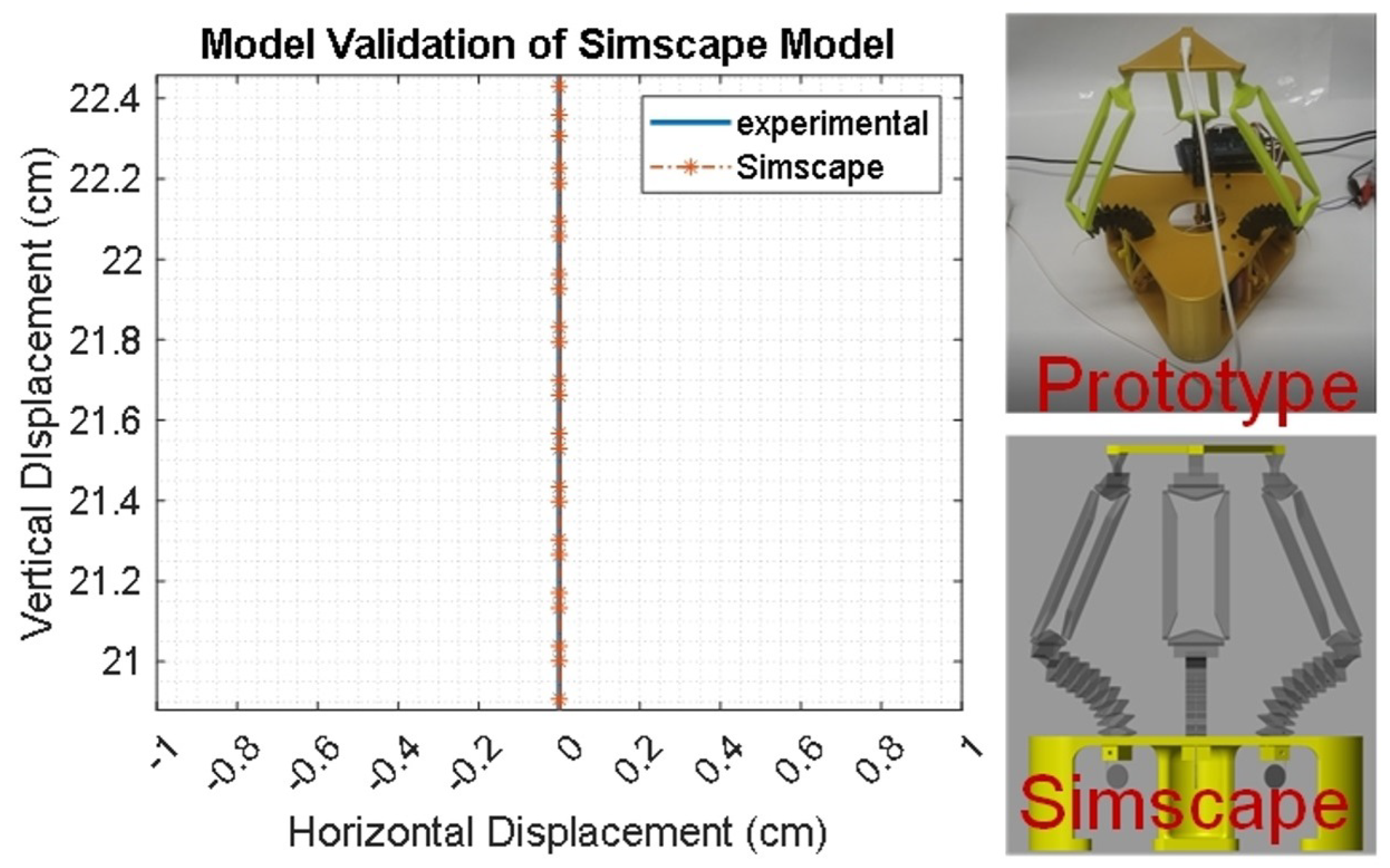
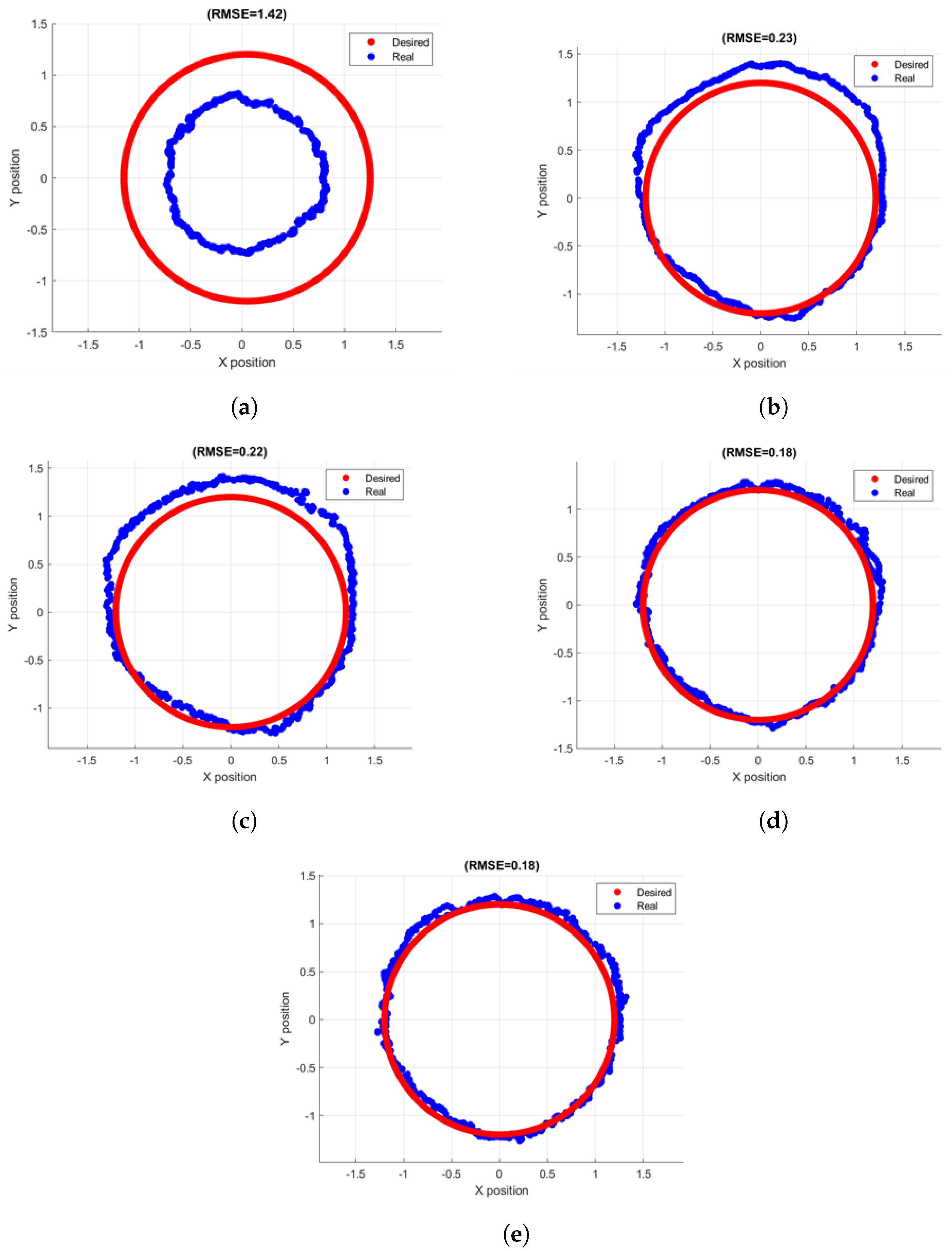
4.3. Experimental Position Control Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hawkes, E.W.; Majidi, C.; Tolley, M.T. Hard questions for soft robotics. Sci. Robot. 2021, 6, eabg6049. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Laschi, C.; Trimmer, B. Soft robotics: A bioinspired evolution in robotics. Trends Biotechnol. 2013, 31, 287–294. [Google Scholar] [CrossRef]
- Papendorp, S.; Ovando, A.; Gharaie, S.; Mosadegh, B.; Guerra-Zubiaga, D.; Alaie, S.; Ashuri, T.; Moghadam, A.A.A. Toward Development of Novel Remote Ultrasound Robotic System Using Soft Robotics Technology. J. Eng. Sci. Med. Diagn. Ther. 2024, 7, 021012. [Google Scholar] [CrossRef] [PubMed]
- Gilmore, J.; Abidoye, C.; Grace, D.; Voicu, R.C.; Ashuri, T.; Moghadam, A.A.A. Development of Novel Stewart Robot Equipped with 3D Printed Soft Actuators. In Proceedings of the SoutheastCon 2024, Atlanta, GA, USA, 15–24 March 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 960–965. [Google Scholar]
- Ashuri, T.; Armani, A.; Jalilzadeh Hamidi, R.; Reasnor, T.; Ahmadi, S.; Iqbal, K. Biomedical soft robots: Current status and perspective. Biomed. Eng. Lett. 2020, 10, 369–385. [Google Scholar] [CrossRef]
- Walker, J.; Zidek, T.; Harbel, C.; Yoon, S.; Strickland, F.S.; Kumar, S.; Shin, M. Soft robotics: A review of recent developments of pneumatic soft actuators. Actuators 2020, 9, 3. [Google Scholar] [CrossRef]
- Papendorp, S.; Iyun, O.; Schneider, C.; Tekes, A.; Ashuri, T.; Amiri Moghadam, A.A. Development of 3d Printed Soft Pneumatic Hand Motion Sensors. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Columbus, OH, USA, 30 October–3 November 2022; American Society of Mechanical Engineers: New York, NY, USA, 2022; Volume 86663, p. V004T05A067. [Google Scholar]
- Chen, G.; Yang, X.; Zhang, X.; Hu, H. Water hydraulic soft actuators for underwater autonomous robotic systems. Appl. Ocean Res. 2021, 109, 102551. [Google Scholar] [CrossRef]
- Katzschmann, R.K.; Marchese, A.D.; Rus, D. Hydraulic autonomous soft robotic fish for 3D swimming. In Proceedings of the Experimental Robotics: The 14th International Symposium on Experimental Robotics, Essaouira, Morocco, 15–18 June 2014; Springer: Berlin/Heidelberg, Germany, 2015; pp. 405–420. [Google Scholar]
- Katzschmann, R.K.; De Maille, A.; Dorhout, D.L.; Rus, D. Cyclic hydraulic actuation for soft robotic devices. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 3048–3055. [Google Scholar]
- Wu, S.; Baker, G.L.; Yin, J.; Zhu, Y. Fast Thermal Actuators for Soft Robotics. Soft Robot. 2021, 9, 1031–1039. [Google Scholar] [CrossRef]
- Hu, F.; Lyu, L.; He, Y. A 3D printed paper-based thermally driven soft robotic gripper inspired by cabbage. Int. J. Precis. Eng. Manuf. 2019, 20, 1915–1928. [Google Scholar] [CrossRef]
- Acevedo-Velazquez, A.I.; Keshtkar, N.; Mersch, J.; Katzer, K.; Cherif, C.; Zimmermann, M.; Gerlach, G.; Röbenack, K. Construction, modeling, and control of a three-beam prototype using interactive fiber rubber composites. PAMM 2023, 23, e202300198. [Google Scholar] [CrossRef]
- Song, K.; Kim, S.; Cha, Y. Soft electromagnetic actuator for assembly robots. Smart Mater. Struct. 2020, 29, 067001. [Google Scholar] [CrossRef]
- Ovando, A.; Papendorp, S.; Ashuri, T.; Amiri Moghadam, A.A. Development of a Novel Hybrid Soft Cable-Driven Parallel Robot. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, New Orleans, LA, USA, 29 October–2 November 2023; American Society of Mechanical Engineers: New York, NY, USA, 2023; Volume 87622, p. V005T06A059. [Google Scholar]
- Villeda-Hernandez, M.; Baker, B.C.; Romero, C.; Rossiter, J.M.; Dicker, M.P.; Faul, C.F. Chemically driven oscillating soft pneumatic actuation. Soft Robot. 2023, 10, 1159–1170. [Google Scholar] [CrossRef] [PubMed]
- Onal, C.D.; Chen, X.; Whitesides, G.M.; Rus, D. Soft mobile robots with on-board chemical pressure generation. In Proceedings of the Robotics Research: The 15th International Symposium ISRR, Flagstaff, AZ, USA, 9–12 December 2011; Springer: Berlin/Heidelberg, Germany, 2017; pp. 525–540. [Google Scholar]
- Liao, W.; Yang, Z. The integration of sensing and actuating based on a simple design fiber actuator towards intelligent soft robots. Adv. Mater. Technol. 2022, 7, 2101260. [Google Scholar] [CrossRef]
- Garcia, M.; Pena, P.; Tekes, A.; Moghadam, A.A.A. Development of Novel Three-Dimensional Soft Parallel Robot. In Proceedings of the SoutheastCon 2021, Atlanta, GA, USA, 10–13 March 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Hsiao, J.H.; Chang, J.Y.; Cheng, C.M. Soft medical robotics: Clinical and biomedical applications, challenges, and future directions. Adv. Robot. 2019, 33, 1099–1111. [Google Scholar] [CrossRef]
- Banerjee, H.; Tse, Z.T.H.; Ren, H. Soft robotics with compliance and adaptation for biomedical applications and forthcoming challenges. Int. J. Robot. Autom 2018, 33, 68–80. [Google Scholar] [CrossRef]
- Cianchetti, M.; Laschi, C.; Menciassi, A.; Dario, P. Biomedical applications of soft robotics. Nat. Rev. Mater. 2018, 3, 143–153. [Google Scholar] [CrossRef]
- Sitti, M. Miniature soft robots—Road to the clinic. Nat. Rev. Mater. 2018, 3, 74–75. [Google Scholar] [CrossRef]
- Oguntosin, V.; Harwin, W.S.; Kawamura, S.; Nasuto, S.J.; Hayashi, Y. Development of a wearable assistive soft robotic device for elbow rehabilitation. In Proceedings of the 2015 IEEE International Conference on Rehabilitation Robotics (ICORR), Singapore, 11–14 August 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 747–752. [Google Scholar]
- Manti, M.; Pratesi, A.; Falotico, E.; Cianchetti, M.; Laschi, C. Soft assistive robot for personal care of elderly people. In Proceedings of the 2016 6th IEEE International Conference on Biomedical Robotics and Biomechatronics (BioRob), Singapore, 26–29 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 833–838. [Google Scholar]
- Ansari, Y.; Manti, M.; Falotico, E.; Mollard, Y.; Cianchetti, M.; Laschi, C. Towards the development of a soft manipulator as an assistive robot for personal care of elderly people. Int. J. Adv. Robot. Syst. 2017, 14, 1729881416687132. [Google Scholar] [CrossRef]
- Shahid, T.; Gouwanda, D.; Nurzaman, S.G.; Gopalai, A.A. Moving toward soft robotics: A decade review of the design of hand exoskeletons. Biomimetics 2018, 3, 17. [Google Scholar] [CrossRef]
- Hawkes, E.W.; Blumenschein, L.H.; Greer, J.D.; Okamura, A.M. A soft robot that navigates its environment through growth. Sci. Robot. 2017, 2, eaan3028. [Google Scholar] [CrossRef]
- der Maur, P.A.; Djambazi, B.; Haberthür, Y.; Hörmann, P.; Kübler, A.; Lustenberger, M.; Sigrist, S.; Vigen, O.; Förster, J.; Achermann, F.; et al. Roboa: Construction and evaluation of a steerable vine robot for search and rescue applications. In Proceedings of the 2021 IEEE 4th International Conference on Soft Robotics (RoboSoft), New Haven, CT, USA, 12–16 April 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 15–20. [Google Scholar]
- Mintchev, S.; Zappetti, D.; Willemin, J.; Floreano, D. A soft robot for random exploration of terrestrial environments. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 7492–7497. [Google Scholar]
- Li, G.; Wong, T.W.; Shih, B.; Guo, C.; Wang, L.; Liu, J.; Wang, T.; Liu, X.; Yan, J.; Wu, B.; et al. Bioinspired soft robots for deep-sea exploration. Nat. Commun. 2023, 14, 7097. [Google Scholar] [CrossRef]
- Aracri, S.; Giorgio-Serchi, F.; Suaria, G.; Sayed, M.E.; Nemitz, M.P.; Mahon, S.; Stokes, A.A. Soft robots for ocean exploration and offshore operations: A perspective. Soft Robot. 2021, 8, 625–639. [Google Scholar] [CrossRef] [PubMed]
- Calanca, A.; Muradore, R.; Fiorini, P. A review of algorithms for compliant control of stiff and fixed-compliance robots. IEEE/ASME Trans. Mechatron. 2015, 21, 613–624. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, J.; Zhang, X.; Feng, Y.; Zeng, H.; Wang, L.; Feng, W. Light-driven bimorph soft actuators: Design, fabrication, and properties. Mater. Horizons 2021, 8, 728–757. [Google Scholar] [CrossRef] [PubMed]
- Moghadam, A.A.A.; Kouzani, A.; Torabi, K.; Kaynak, A.; Shahinpoor, M. Development of a novel soft parallel robot equipped with polymeric artificial muscles. Smart Mater. Struct. 2015, 24, 035017. [Google Scholar] [CrossRef]
- Abidoye, C.; Grace, D.; Contreras-Esquen, A.; Edwards, A.; Ashuri, T.; Tekes, A.; Amiri Moghadam, A.A. Development of a Novel 3-Universal-Spherical-Revolote Soft Parallel Robot. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Columbus, OH, USA, 30 October–3 November 2022; American Society of Mechanical Engineers: New York, NY, USA, 2022; Volume 86670, p. V005T07A022. [Google Scholar]
- Lindenroth, L.; Soor, A.; Hutchinson, J.; Shafi, A.; Back, J.; Rhode, K.; Liu, H. Design of a soft, parallel end-effector applied to robot-guided ultrasound interventions. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 3716–3721. [Google Scholar]
- Bryson, C.E.; Rucker, D.C. Toward parallel continuum manipulators. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 778–785. [Google Scholar]
- Hopkins, J.B.; Rivera, J.; Kim, C.; Krishnan, G. Synthesis and analysis of soft parallel robots comprised of active constraints. J. Mech. Robot. 2015, 7, 011002. [Google Scholar] [CrossRef]
- Lilge, S.; Nuelle, K.; Boettcher, G.; Spindeldreier, S.; Burgner-Kahrs, J. Tendon actuated continuous structures in planar parallel robots: A kinematic analysis. J. Mech. Robot. 2021, 13, 011025. [Google Scholar] [CrossRef]
- Nuelle, K.; Sterneck, T.; Lilge, S.; Xiong, D.; Burgner-Kahrs, J.; Ortmaier, T. Modeling, calibration, and evaluation of a tendon-actuated planar parallel continuum robot. IEEE Robot. Autom. Lett. 2020, 5, 5811–5818. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, Q. Design and testing of a soft parallel robot based on pneumatic artificial muscles for wrist rehabilitation. Sci. Rep. 2021, 11, 1273. [Google Scholar] [CrossRef] [PubMed]
- White, E.L.; Case, J.C.; Kramer-Bottiglio, R. A soft parallel kinematic mechanism. Soft Robot. 2018, 5, 36–53. [Google Scholar] [CrossRef]
- Huang, X.; Zhu, X.; Gu, G. Kinematic modeling and characterization of soft parallel robots. IEEE Trans. Robot. 2022, 38, 3792–3806. [Google Scholar] [CrossRef]
- Böttcher, G.; Lilge, S.; Burgner-Kahrs, J. Design of a reconfigurable parallel continuum robot with tendon-actuated kinematic chains. IEEE Robot. Autom. Lett. 2021, 6, 1272–1279. [Google Scholar] [CrossRef]
- Yan, W.; Chen, G.; Tang, S.; Zhang, Z.; Duan, X.; Wang, H. Design of a reconfigurable planar parallel continuum manipulator with variable stiffness. In Proceedings of the Intelligent Robotics and Applications: 14th International Conference, ICIRA 2021, Yantai, China, 22–25 October 2021; Proceedings, Part III 14. Springer: Berlin/Heidelberg, Germany, 2021; pp. 803–813. [Google Scholar]
- Yang, Z.; Zhu, X.; Xu, K. Continuum delta robot: A novel translational parallel robot with continuum joints. In Proceedings of the 2018 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Auckland, New Zealand, 9–12 July 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 748–755. [Google Scholar]
- Garcia, M.; McFall, K.; Tekes, A. Trajectory control of planar closed chain fully compliant mechanism. J. Mech. Sci. Technol. 2021, 35, 1711–1719. [Google Scholar] [CrossRef]
- Lin, H.; Tekes, A.; Tekes, C. Design, development and modelling of single actuated, compliant and symmetrical multi link hopping mechanism. J. Mech. Sci. Technol. 2020, 34, 555–563. [Google Scholar] [CrossRef]
- Tekes, A.; Lin, H.; McFall, K. Design, modelling and experimentation of a novel compliant translational dwell mechanism. J. Mech. Sci. Technol. 2019, 33, 3137–3145. [Google Scholar] [CrossRef]
- Muthusamy, P.K.; Garratt, M.; Pota, H.; Muthusamy, R. Real-time adaptive intelligent control system for quadcopter unmanned aerial vehicles with payload uncertainties. IEEE Trans. Ind. Electron. 2021, 69, 1641–1653. [Google Scholar] [CrossRef]
- Ashuri, T.; Vasquez Mayen, E.; Hamidi, R. A new statistical approach to enhance the performance of model-free optimal controls algorithms. In Proceedings of the 2018 Multidisciplinary Analysis and Optimization Conference, Atlanta, GA, USA, 25–29 June 2018; p. 3421. [Google Scholar]
- Tsavnin, A.; Efimov, S.; Zamyatin, S. Overshoot elimination for control systems with parametric uncertainty via a PID controller. Symmetry 2020, 12, 1092. [Google Scholar] [CrossRef]
- Azizkhani, M.; Godage, I.S.; Chen, Y. Dynamic control of soft robotic arm: A simulation study. IEEE Robot. Autom. Lett. 2022, 7, 3584–3591. [Google Scholar] [CrossRef]
- Costanzo, G.T.; Iacovella, S.; Ruelens, F.; Leurs, T.; Claessens, B.J. Experimental analysis of data-driven control for a building heating system. Sustain. Energy Grids Netw. 2016, 6, 81–90. [Google Scholar] [CrossRef]
- Ferri, G.; Munafo, A.; LePage, K.D. An autonomous underwater vehicle data-driven control strategy for target tracking. IEEE J. Ocean. Eng. 2018, 43, 323–343. [Google Scholar] [CrossRef]
- Ashuri, T.; Li, Y.; Hosseini, S.E. Recovery of energy losses using an online data-driven optimization technique. Energy Convers. Manag. 2020, 225, 113339. [Google Scholar] [CrossRef]
- Bruder, D.; Fu, X.; Gillespie, R.B.; Remy, C.D.; Vasudevan, R. Data-driven control of soft robots using Koopman operator theory. IEEE Trans. Robot. 2020, 37, 948–961. [Google Scholar] [CrossRef]
- Peng, X.; Cai, Y.; Li, Q.; Wang, K. Control rod position reconstruction based on K-Nearest Neighbor Method. Ann. Nucl. Energy 2017, 102, 231–235. [Google Scholar] [CrossRef]
- Xu, M.; Wang, P. Evidential KNN-based performance monitoring method for PID control system. In Proceedings of the 2020 5th International Conference on Mechanical, Control and Computer Engineering (ICMCCE), Harbin, China, 25–27 December 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 597–601. [Google Scholar]
- Chen, J.; Lau, H.Y. Learning the inverse kinematics of tendon-driven soft manipulators with K-nearest Neighbors Regression and Gaussian Mixture Regression. In Proceedings of the 2016 2nd International Conference on Control, Automation and Robotics (ICCAR), Hong Kong, China, 28–30 April 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 103–107. [Google Scholar]
- Xu, W.; Chen, J.; Lau, H.Y.; Ren, H. Data-driven methods towards learning the highly nonlinear inverse kinematics of tendon-driven surgical manipulators. Int. J. Med. Robot. Comput. Assist. Surg. 2017, 13, e1774. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Huang, P.; Ishibashi, Y.; Okuda, T.; Psannis, K.E. Effect of Neural Network on Robot Position Control Using Force Information. In Proceedings of the 2021 IEEE 9th International Conference on Information, Communication and Networks (ICICN), Xi’an, China, 25–28 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 545–549. [Google Scholar]
- Young, E.M.; Kuchenbecker, K.J. Implementation of a 6-DOF parallel continuum manipulator for delivering fingertip tactile cues. IEEE Trans. Haptics 2019, 12, 295–306. [Google Scholar] [CrossRef] [PubMed]
- Parsa, F.F.; Moghadam, A.A.A.; Ashuri, T. From Learning Agents to Agile Software: Reinforcement Learning’s Transformative Role in Requirements Engineering. In Proceedings of the SoutheastCon 2024, Atlanta, GA, USA, 15–24 March 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1627–1631. [Google Scholar]
- Coy, M.V.C.; Casallas, E.C. Training neural networks using reinforcement learning to reactive path planning. J. Appl. Eng. Sci. 2021, 19, 48–56. [Google Scholar]
- Chen, S.; Dong, J.; Ha, P.; Li, Y.; Labi, S. Graph neural network and reinforcement learning for multi-agent cooperative control of connected autonomous vehicles. Comput.-Aided Civ. Infrastruct. Eng. 2021, 36, 838–857. [Google Scholar] [CrossRef]
- Gillespie, M.T.; Best, C.M.; Townsend, E.C.; Wingate, D.; Killpack, M.D. Learning nonlinear dynamic models of soft robots for model predictive control with neural networks. In Proceedings of the 2018 IEEE International Conference on Soft Robotics (RoboSoft), Livorno, Italy, 24–28 April 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 39–45. [Google Scholar]
- Thuruthel, T.G.; Shih, B.; Laschi, C.; Tolley, M.T. Soft robot perception using embedded soft sensors and recurrent neural networks. Sci. Robot. 2019, 4, eaav1488. [Google Scholar] [CrossRef] [PubMed]
- Nadizar, G.; Medvet, E.; Nichele, S.; Pontes-Filho, S. An experimental comparison of evolved neural network models for controlling simulated modular soft robots. Appl. Soft Comput. 2023, 145, 110610. [Google Scholar] [CrossRef]
- Weerakoon, L.; Ye, Z.; Bama, R.S.; Smela, E.; Yu, M.; Chopra, N. Adaptive tracking control of soft robots using integrated sensing skins and recurrent neural networks. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 12170–12176. [Google Scholar]
- Shao, F.; Meng, W.; Ai, Q.; Xie, S.Q. Neural Network Adaptive Control of Hand Rehabilitation Robot Driven by Flexible Pneumatic Muscles. In Proceedings of the 2021 7th International Conference on Mechatronics and Robotics Engineering (ICMRE), Budapest, Hungary, 3–5 February 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 59–63. [Google Scholar]
- Bamgbose, S.O.; Li, X.; Qian, L. Neural Network Optimized Controller for Motion and Position Control in Autonomous Systems. In Proceedings of the 2018 IEEE 14th International Conference on Control and Automation (ICCA), Anchorage, AK, USA, 12–15 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 823–828. [Google Scholar]
- Majumder, A.; Sarkar, D.; Chakraborty, S.; Singh, A.; Roy, S.S.; Arora, A. Neural Network-Based Gain Scheduled Position Control of a Pneumatic Artificial Muscle. In Proceedings of the 2022 IEEE International Conference on Electronics, Computing and Communication Technologies (CONECCT), Bangalore, India, 8–10 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar]
- Ding, S.; Peng, J.; Hou, Y.; Lei, X. Neural Network-based Hybrid Position/Force Tracking Control for Flexible Joint Robot. In Proceedings of the 2020 IEEE International Systems Conference (SysCon), Montreal, QC, Canada, 24 August–20 September 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Wang, Y.; Yang, H.; Zhang, P. Position control of planar three-link underactuated manipulator based on wavelet neural network model. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–30 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 387–392. [Google Scholar]
- Siciliano, B.; Sciavicco, L.; Chiaverini, S.; Chiacchio, P.; Villani, L.; Caccavale, F. Jacobian-Based Algorithms: A Bridge between Kinematics and Control. In Proceedings of the Special Celebratory Symposium in the Honor of Professor Bernie Roth’s 70th Birthday; Citeseer. 2003; pp. 4–35. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=2f8e8dc8f8058912b9ef5a2c2c247247a326817f (accessed on 15 December 2023).
- Cheah, C.C.; Kawamura, S.; Arimoto, S. Feedback control for robotic manipulator with an uncertain Jacobian matrix. J. Robot. Syst. 1999, 16, 119–134. [Google Scholar] [CrossRef]
- Cheah, C.C.; Hirano, M.; Kawamura, S.; Arimoto, S. Approximate Jacobian control for robots with uncertain kinematics and dynamics. IEEE Trans. Robot. Autom. 2003, 19, 692–702. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garcia, M.; Esquen, A.-C.; Sabbagh, M.; Grace, D.; Schneider, E.; Ashuri, T.; Voicu, R.C.; Tekes, A.; Amiri Moghadam, A.A. Soft Robots: Computational Design, Fabrication, and Position Control of a Novel 3-DOF Soft Robot. Machines 2024, 12, 539. https://doi.org/10.3390/machines12080539
Garcia M, Esquen A-C, Sabbagh M, Grace D, Schneider E, Ashuri T, Voicu RC, Tekes A, Amiri Moghadam AA. Soft Robots: Computational Design, Fabrication, and Position Control of a Novel 3-DOF Soft Robot. Machines. 2024; 12(8):539. https://doi.org/10.3390/machines12080539
Chicago/Turabian StyleGarcia, Martin, Andrea-Contreras Esquen, Mark Sabbagh, Devin Grace, Ethan Schneider, Turaj Ashuri, Razvan Cristian Voicu, Ayse Tekes, and Amir Ali Amiri Moghadam. 2024. "Soft Robots: Computational Design, Fabrication, and Position Control of a Novel 3-DOF Soft Robot" Machines 12, no. 8: 539. https://doi.org/10.3390/machines12080539
APA StyleGarcia, M., Esquen, A.-C., Sabbagh, M., Grace, D., Schneider, E., Ashuri, T., Voicu, R. C., Tekes, A., & Amiri Moghadam, A. A. (2024). Soft Robots: Computational Design, Fabrication, and Position Control of a Novel 3-DOF Soft Robot. Machines, 12(8), 539. https://doi.org/10.3390/machines12080539







