A Prediction Model of Two-Sided Unbalance in the Multi-Stage Assembled Rotor of an Aero Engine
Abstract
1. Introduction
2. Methods
2.1. Measurement Definition of the Geometric Feature Parameters of a Single-Stage Rotor
2.2. Measurement Definition for the Mass Feature Parameters of a Single-Stage Rotor
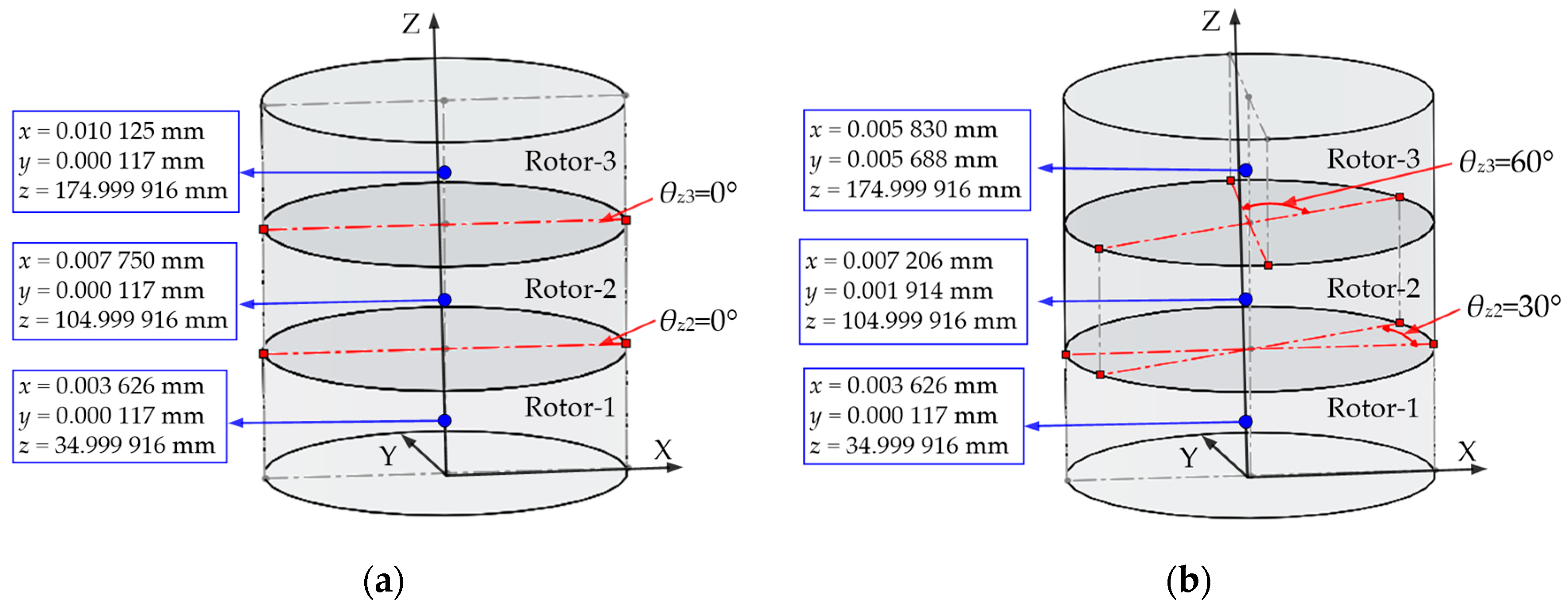
2.3. Coordinate Transfer of Multi-Stage Assembled Rotors
2.4. Mass Eccentricity Cumulative Errors of a Multi-Stage Rotor, Based on Its Actual Rotation Axis
2.5. Decomposition Principle of the Two-Sided Unbalance of a Multi-Stage Rotor
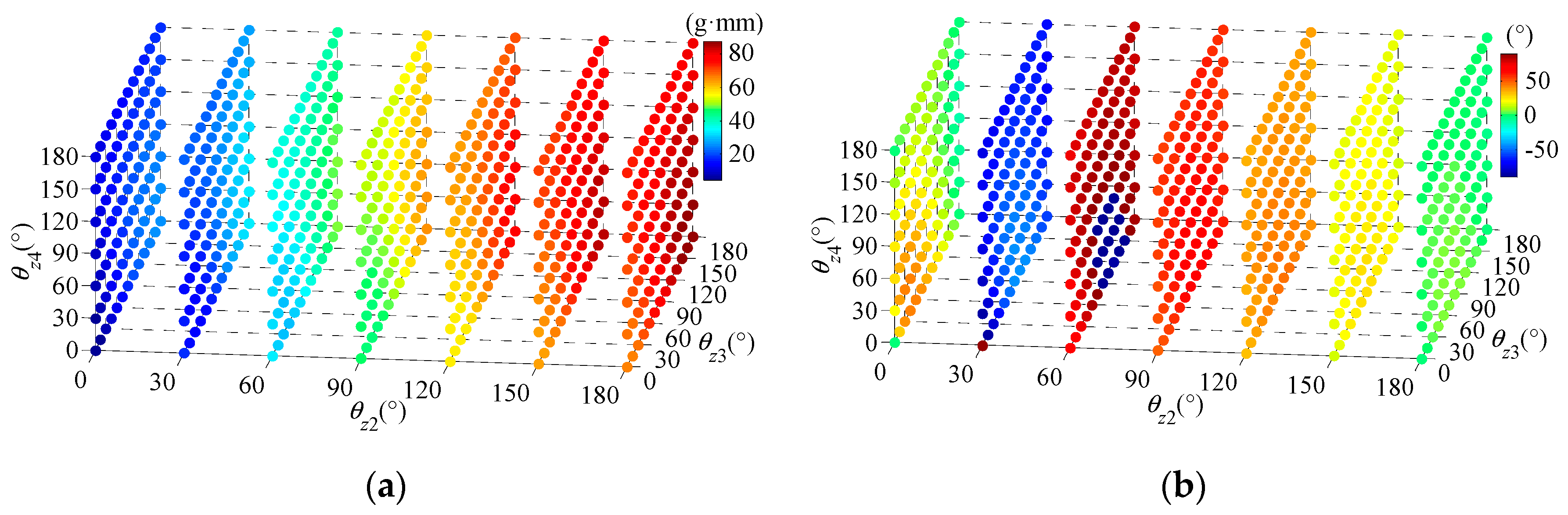
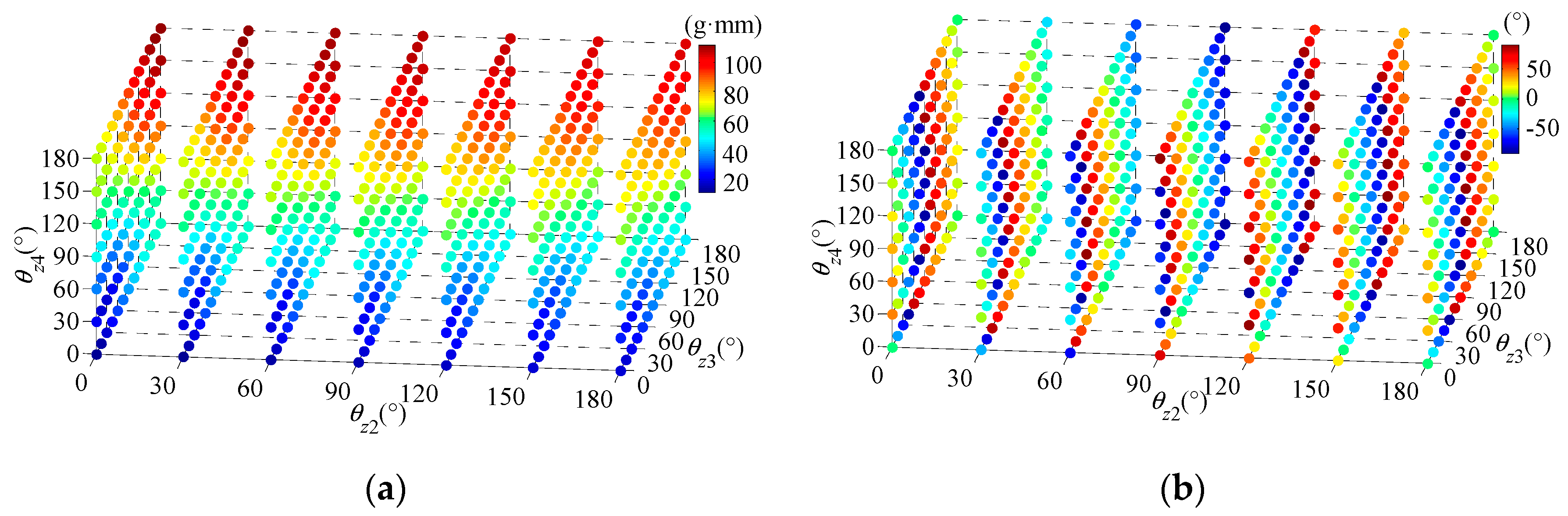
3. Simulation Analysis of the Two-Sided Unbalance of a Multi-Stage Rotor
4. Experimental Results and Discussion
4.1. Measurement of the Geometric Feature Parameters of a Four-Stage Rotor
4.2. Measurement of the Mass Feature Parameters of a Four-Stage Reduced-Scale Simulated Rotor
4.3. Testing and Analysis of the Two-Sided Unbalance for the Four-Stage Reduced-Scale Simulated Rotor
5. Conclusions
- According to the principle of homogeneous coordinate matrix transformations, the geometric and mass feature parameters of the rotors at each stage are unified to the same coordinate system, solving the problem of the asynchronous transmission of dual parameters.
- A linear parameter equation of the actual rotation axis of a multi-stage assembled rotor has been established, and this then reproduced the actual working conditions of the dynamic balance test. Therefore, the true two-side unbalance of a multi-stage assembled rotor can be accurately calculated.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.; Wang, W.; Wei, D. Unbalance response and stability analysis of a high-speed turbocharger bearing-rotor system. Tribol. Lett. 2022, 42, 620–631. [Google Scholar]
- Yang, W.; Liang, M.; Wang, L. Research on unbalance response characteristics of gas turbine blade-disk rotor system. J. Vibroeng. 2018, 20, 1676–1690. [Google Scholar] [CrossRef]
- Qiuxiao, W.; Fei, W. A new vibration mechanism of balancing machine for satellite-borne spinning rotors. Chin. J. Aeronaut. 2014, 27, 1318–1326. [Google Scholar]
- Dinggen, L.; Jiguang, C.; Junwen, W. The design and analysis of vibration structure of vertical dynamic balancing machine. Acta. Mech. Solida. Sin. 2004, 17, 11–17. [Google Scholar]
- Chen, Z.; Liu, Y.; Zhou, P. Assembly success rate calculation method for aero-engine based on improved taguchi method. J. Propuls. Technol. 2018, 39, 653–659. [Google Scholar]
- Wang, C.; Yu, H.; Zhang, W. Object-oriented aero-engine assembly models. Int. J. Internet Manuf. Serv. 2010, 2, 354–364. [Google Scholar] [CrossRef]
- Chen, Y.; Cui, J.; Sun, X. An unbalance optimization method for a multi-stage rotor based on an assembly error propagation model. Appl. Sci. 2021, 11, 887. [Google Scholar] [CrossRef]
- Hussain, T.; Yang, Z.; Popov, A. Straight-build assembly optimization: A method to minimize stage-by-stage eccentricity error in the assembly of axisymmetric rigid components (two-dimensional case study). J. Manuf. Sci. Eng. 2011, 133, 031014. [Google Scholar] [CrossRef]
- Hussain, T.; Mcwilliam, S.; Popov, A. Geometric error reduction in the assembly of axis-symmetric rigid components: A two-dimensional case study. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2012, 226, 1259–1274. [Google Scholar] [CrossRef]
- Hussain, T.; Yasinshaikh, G.; Shaikh, A. Variation propagation control in straight-build assemblies: 2d case study. Mehran Univ. Res. J. Eng. Technol. 2013, 32, 71–80. [Google Scholar]
- Yang, Z.; Popov, A.; Mcwilliam, S. Variation propagation control in mechanical assembly of cylindrical components. J. Manuf. Syst. 2012, 31, 162–176. [Google Scholar] [CrossRef]
- Yang, Z.; Hussain, T.; Popov, A. A comparison of different optimization techniques for variation propagation control in mechanical assembly. Mater. Sci. Eng. IOP 2011, 26, 012017. [Google Scholar] [CrossRef]
- Yang, Z.; Hussain, T.; Popov, A. Novel optimization technique for variation propagation control in an aero-engine assembly. J. Eng. Manuf. 2011, 225, 100–111. [Google Scholar] [CrossRef]
- Yang, Z.; Mcwilliam, S.; Popov, A. Dimensional variation propagation analysis in straight-build mechanical assemblies using a probabilistic approach. J. Manuf. Syst. 2013, 32, 348–356. [Google Scholar] [CrossRef]
- Shan, F.; Li, Z.; Zhu, B. Modeling and analysis of assembling deviation of typical aero-engine rotor parts. Manuf. Autom. 2015, 37, 100–103. (In Chinese) [Google Scholar]
- Meng, X.; Shan, F. Prediction of assembly quality of aero-engine rotor parts. Manuf. Autom. 2016, 38, 61–65. (In Chinese) [Google Scholar]
- Zhang, N.; Wu, Y.; Yang, R.; Xie, G. Digital simulation and analysis of assembly-deviation prediction based on measurement data. Appl. Sci. 2023, 13, 12193. [Google Scholar] [CrossRef]
- Wang, L.; Sun, C.; Tan, J. Improvement of location and orientation tolerances propagation control in cylindrical components assembly using stack-build assembly technique. Assem. Autom. 2015, 35, 358–366. [Google Scholar] [CrossRef]
- Sun, Y.; Guo, J.; Hong, J. Repair decision based on sensitivity analysis for aero-engine assembly. Int. J. Precis. Eng. Man. 2019, 20, 347–362. [Google Scholar] [CrossRef]
- Mu, X.; Wang, Y.; Yuan, B.; Sun, W.; Liu, C.; Sun, Q. A New assembly precision prediction method of aeroengine high-pressure rotor system considering manufacturing error and deformation of parts. J. Manuf. Syst. 2021, 61, 112–124. [Google Scholar] [CrossRef]
- Zhu, L.; Yang, Y.; Huang, H.; Bouzid, A.H.; Hong, J. A novel method to predict the concentricity of aero-engine rotor considering the assembly process of bolted flange joints. In Proceedings of the Pressure Vessels and Piping Conference, Las Vegas, NV, USA, 17–22 July 2022; American Society of Mechanical Engineers: New York, NY, USA, 2022; Volume 86151, p. V002T02A008. [Google Scholar]
- Shi, S.; Liu, J.; Gong, H.; Shao, N.; Anwer, N. Assembly accuracy analysis and phase optimization of aero-engine multistage rotors considering surface morphology and non-uniform contact deformation. Precis. Eng. 2024, 88, 595–610. [Google Scholar] [CrossRef]
- Zhang, B.; Lu, H.; Liu, S.; Yang, Y.; Sang, D. Aero-engine rotor assembly process optimization based on improved harris hawk algorithm. Aerospace 2023, 10, 28. [Google Scholar] [CrossRef]
- Zhang, X.; Fu, X.; Fu, B.; Du, H. Multi-objective optimization of aeroengine rotor assembly based on tensor coordinate transformation and NSGA-II. CIRP J. Manuf. Sci. Technol. 2024, 51, 190–200. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, M.; Sun, C. A method to minimize stage-by-stage initial unbalance in the aero engine assembly of multistage rotors. Aerosp. Sci. Technol. 2019, 85, 270–276. [Google Scholar] [CrossRef]
- Sun, C.; Li, C.; Liu, Y. Prediction method of concentricity and perpendicularity of aero engine multistage rotors based on PSO-BP neural network. IEEE Access 2019, 7, 132271–132278. [Google Scholar] [CrossRef]
- Sun, C.; Liu, Z.; Liu, Y. An adjustment method of geometry and mass centers for precision rotors assembly. IEEE Access 2019, 7, 169992–170002. [Google Scholar] [CrossRef]
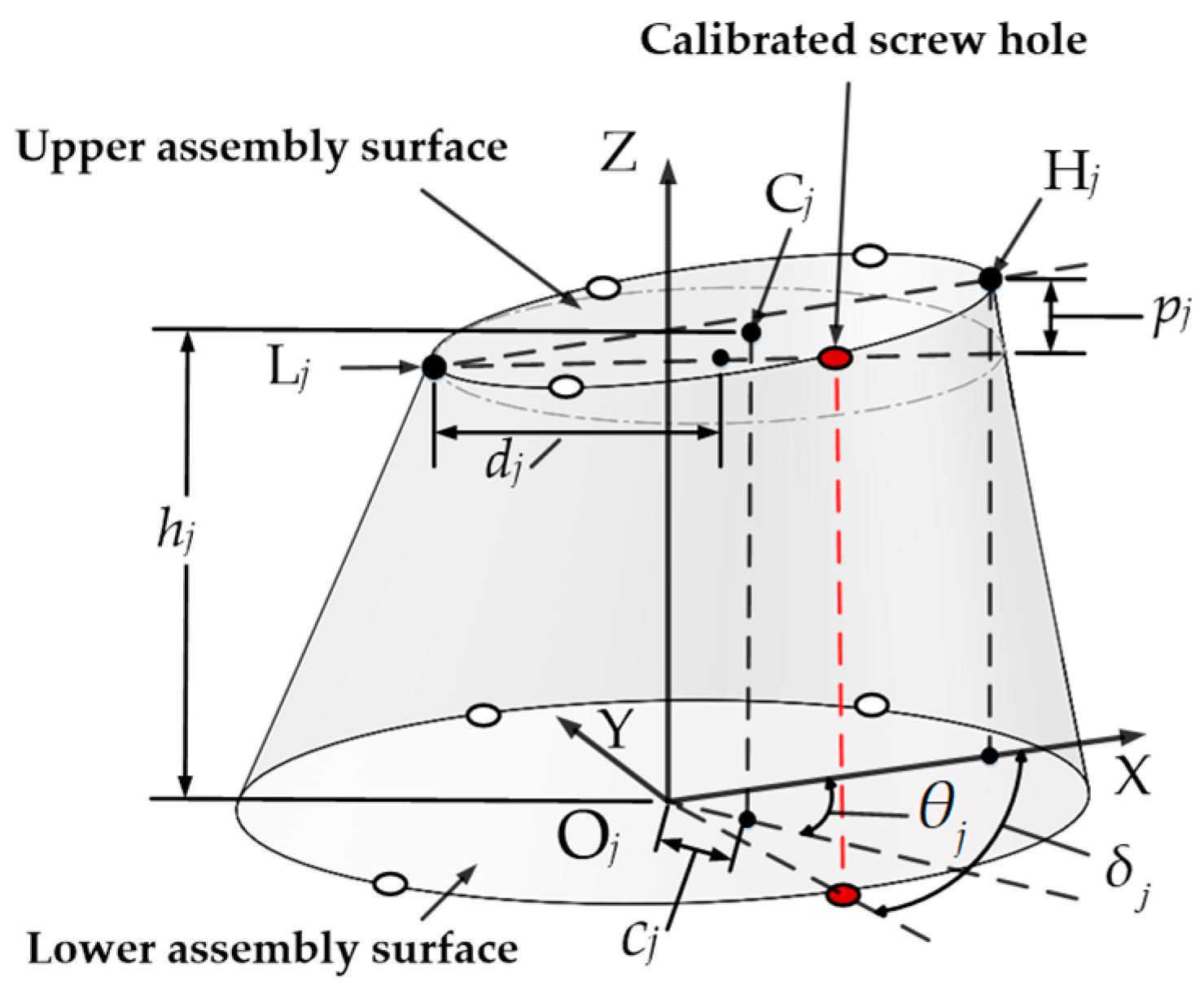













| Stage Number | cj (mm) | θj (°) | pj (mm) | hj (mm) | δj (°) | dj (mm) |
|---|---|---|---|---|---|---|
| 1 | 0.005 | 0 | 0.005 | 70 | 0 | 100 |
| 2 | 0.005 | 0 | 0.005 | 70 | 0 | 100 |
| 3 | 0.005 | 0 | 0.005 | 70 | 0 | 100 |
| Stage Number | Barycenter Coordinate Vector of the First Assembly State (mm) | Barycenter Coordinate Vector of the Second Assembly State (mm) |
|---|---|---|
| 1 | [0.003 626, 0.000 117, 34.999 160] | [0.003 626, 0.000 117, 34.999 160] |
| 2 | [0.007 751, 0.000 117, 104.999 916] | [0.007 207, 0.001 914, 104.999 916] |
| 3 | [0.010 126, 0.000 117, 174.999 916] | [0.005 830, 0.005 689, 174.999 916] |
| Stage Number | cj (mm) | θj (°) | pj (mm) | hj (mm) | δj (°) | dj (mm) |
|---|---|---|---|---|---|---|
| 1 | 0.02 | 0 | 0.02 | 70 | 0 | 25 |
| 2 | 0.02 | 90 | 0.02 | 138 | 90 | 51 |
| 3 | 0.02 | 180 | 0.02 | 115 | 180 | 17.5 |
| 4 | 0.02 | 270 | 0.02 | 60 | 270 | 17 |
| Stage Number | Unbalanced Mass Point Number | γjk (mm) | ljk (mm) | ujk (g) | φjk (°) |
|---|---|---|---|---|---|
| 1 | 1 | 21 | 2 | 0.5 | 0 |
| 2 | 34 | 63.5 | 0.5 | 0 | |
| 2 | 1 | 64 | 30 | 0.5 | 0 |
| 2 | 64 | 108 | 0.5 | 0 | |
| 3 | 1 | 41 | 25 | 0.5 | 0 |
| 2 | 96 | 107 | 0.5 | 0 | |
| 4 | 1 | 29 | 6.5 | 0.5 | 0 |
| 2 | 21 | 60 | 0.5 | 0 |
| Assembly Phase Sequence | Calculation Basis: Actual Rotation Axis | Calculation Basis: Longitudinal Axis of Datum Plane | ||
|---|---|---|---|---|
| UA (g·mm) ∠ ζA (°) | UB (g·mm) ∠ ζB (°) | UA (g·mm) ∠ ζA (°) | UB (g·mm) ∠ ζB (°) | |
| 1 | 14.46 ∠ −67 | 19.59 ∠ −53 | 34.01 ∠ −89 | 40.57 ∠ −69 |
| 2 | 34.04 ∠ 89 | 40.50 ∠ 69 | 19.53 ∠ 53 | 14.46 ∠ −67 |
| 3 | 18.25 ∠ 0 | 111.69 ∠ 0 | 62.70 ∠ −53 | 58.99 ∠ 11 |
| 4 | 4.51 ∠ 0 | 11.45 ∠ 0 | 55.46 ∠ −64 | 66.10 ∠ −10 |
| 5 | 85.10 ∠ 20 | 47.61 ∠ 32 | 33.47 ∠ 83 | 80.86 ∠ −7 |
| 6 | 63.43 ∠ 57 | 85.71 ∠ −68 | 4.50 ∠ 0 | 11.34 ∠ 0 |
| Stage Number | cj (mm) | θj (°) | pj (mm) | hj (mm) | δj (°) | dj (mm) |
|---|---|---|---|---|---|---|
| 1 | 0.015 3 | 108 | 0.013 0 | 70.322 5 | 21 | 25.016 0 |
| 2 | 0.094 4 | 216 | 0.023 5 | 137.963 1 | 261 | 50.929 6 |
| 3 | 0.096 3 | 34 | 0.035 1 | 114.896 6 | 177 | 17.509 5 |
| 4 | 0.049 6 | 85 | 0.019 4 | 60.113 0 | 99 | 17.023 9 |
| Stage Number | Unbalanced Mass Point Number | γjk (mm) | ljk (mm) | ujk (g) | φjk (°) |
|---|---|---|---|---|---|
| 1 | 1 | 21 | 2 | 0.26 | 71 |
| 2 | 34 | 63.5 | 0.23 | 233 | |
| 2 | 1 | 64 | 30 | 0.39 | 112 |
| 2 | 64 | 108 | 0.31 | 24 | |
| 3 | 1 | 41 | 25 | 0.28 | 96 |
| 2 | 96 | 107 | 0.53 | 113 | |
| 4 | 1 | 29 | 6.5 | 0.13 | 75 |
| 2 | 21 | 60 | 0.11 | 198 |
| Assembly Phase Sequences | UA (g·mm) | ζA (°) | UB (g·mm) | ζB (°) |
|---|---|---|---|---|
| θz2 = 30°, θz3 = 30°, θz4 = 30° | 18.41 | 110 | 45.55 | 106 |
| θz2 = 60°, θz3 = 60°, θz4 = 60° | 25.31 | 82 | 42.81 | 45 |
| θz2 = 90°, θz3 = 180°, θz4 = 180° | 31.02 | 57 | 65.43 | 67 |
| θz2 = 30°, θz3 = 60°, θz4 = 0° | 20.98 | 123 | 46.87 | 78 |
| θz2 = 0°, θz3 = 150°, θz4 = 90° | 27.65 | 153 | 58.90 | −4 |
| θz2 = 180°, θz3 = 0°, θz4 = 0° | 22.18 | 140 | 51.42 | −11 |
| Assembly Phase Sequences | UA (g·mm) | ζA (°) | UB (g·mm) | ζB (°) |
|---|---|---|---|---|
| θz2 = 30°, θz3 = 30°, θz4 = 30° | 19.89 | 115 | 46.70 | 107 |
| θz2 = 60°, θz3 = 60°, θz4 = 60° | 22.94 | 89 | 46.92 | 41 |
| θz2 = 90°, θz3 = 180°, θz4 = 180° | 29.88 | 50 | 68.68 | 62 |
| θz2 = 30°, θz3 = 60°, θz4 = 0° | 21.35 | 119 | 44.35 | 69 |
| θz2 = 0°, θz3 = 150°, θz4 = 90° | 26.65 | 147 | 59.57 | 2 |
| θz2 = 180°, θz3 = 0°, θz4 = 0° | 23.10 | 148 | 50.37 | −13 |
| Assembly Phase Sequences | UA (g·mm) | ζA (°) | UB (g·mm) | ζB (°) |
|---|---|---|---|---|
| θz2 = 30°, θz3 = 30°, θz4 = 30° | 29.94 | 2 | 56.71 | 70 |
| θz2 = 60°, θz3 = 60°, θz4 = 60° | 30.88 | 151 | 62.05 | 9 |
| θz2 = 90°, θz3 = 180°, θz4 = 180° | 26.67 | 113 | 65.20 | 45 |
| θz2 = 30°, θz3 = 60°, θz4 = 0° | 31.30 | 0 | 59.44 | 40 |
| θz2 = 0°, θz3 = 150°, θz4 = 90° | 29.15 | 17 | 71.04 | −14 |
| θz2 = 180°, θz3 = 0°, θz4 = 0° | 23.25 | 40 | 49.62 | 135 |
| Assembly Phase Sequences | Errors of UA (%) | Errors of ζA (%) | Errors of UB (%) | Errors of ζB (%) |
|---|---|---|---|---|
| θz2 = 30°, θz3 = 30°, θz4 = 30° | 8.0 | 1.4 | 2.5 | 0.3 |
| θz2 = 60°, θz3 = 60°, θz4 = 60° | −9.4 | 1.9 | 9.6 | −1.1 |
| θz2 = 90°, θz3 = 180°, θz4 = 180° | −3.7 | −1.9 | 5.0 | −1.4 |
| θz2 = 30°, θz3 = 60°, θz4 = 0° | 1.8 | −1.1 | −5.4 | −2.5 |
| θz2 = 0°, θz3 = 150°, θz4 = 90° | −3.6 | −1.7 | 1.1 | 1.7 |
| θz2 = 180°, θz3 = 0°, θz4 = 0° | 4.1 | 2.2 | −2.0 | −0.6 |
| Assembly Phase Sequences | Errors of UA (%) | Errors of ζA (%) | Errors of UB (%) | Errors of ζB (%) |
|---|---|---|---|---|
| θz2 = 30°, θz3 = 30°, θz4 = 30° | 62.6 | −30.0 | 24.5 | −10.0 |
| θz2 = 60°, θz3 = 60°, θz4 = 60° | 22.0 | 19.2 | 44.9 | −10.0 |
| θz2 = 90°, θz3 = 180°, θz4 = 180° | −14.0 | 15.6 | −0.4 | −6.1 |
| θz2 = 30°, θz3 = 60°, θz4 = 0° | 49.2 | −34.2 | 26.8 | −10.6 |
| θz2 = 0°, θz3 = 150°, θz4 = 90° | 5.4 | −37.8 | 20.6 | −2.8 |
| θz2 = 180°, θz3 = 0°, θz4 = 0° | 4.8 | −27.8 | −3.5 | 40.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, L.; Chen, Y. A Prediction Model of Two-Sided Unbalance in the Multi-Stage Assembled Rotor of an Aero Engine. Machines 2024, 12, 503. https://doi.org/10.3390/machines12080503
Song L, Chen Y. A Prediction Model of Two-Sided Unbalance in the Multi-Stage Assembled Rotor of an Aero Engine. Machines. 2024; 12(8):503. https://doi.org/10.3390/machines12080503
Chicago/Turabian StyleSong, Lingling, and Yue Chen. 2024. "A Prediction Model of Two-Sided Unbalance in the Multi-Stage Assembled Rotor of an Aero Engine" Machines 12, no. 8: 503. https://doi.org/10.3390/machines12080503
APA StyleSong, L., & Chen, Y. (2024). A Prediction Model of Two-Sided Unbalance in the Multi-Stage Assembled Rotor of an Aero Engine. Machines, 12(8), 503. https://doi.org/10.3390/machines12080503







