The Grinding and Correction of Face Gears Based on an Internal Gear Grinding Machine
Abstract
1. Introduction
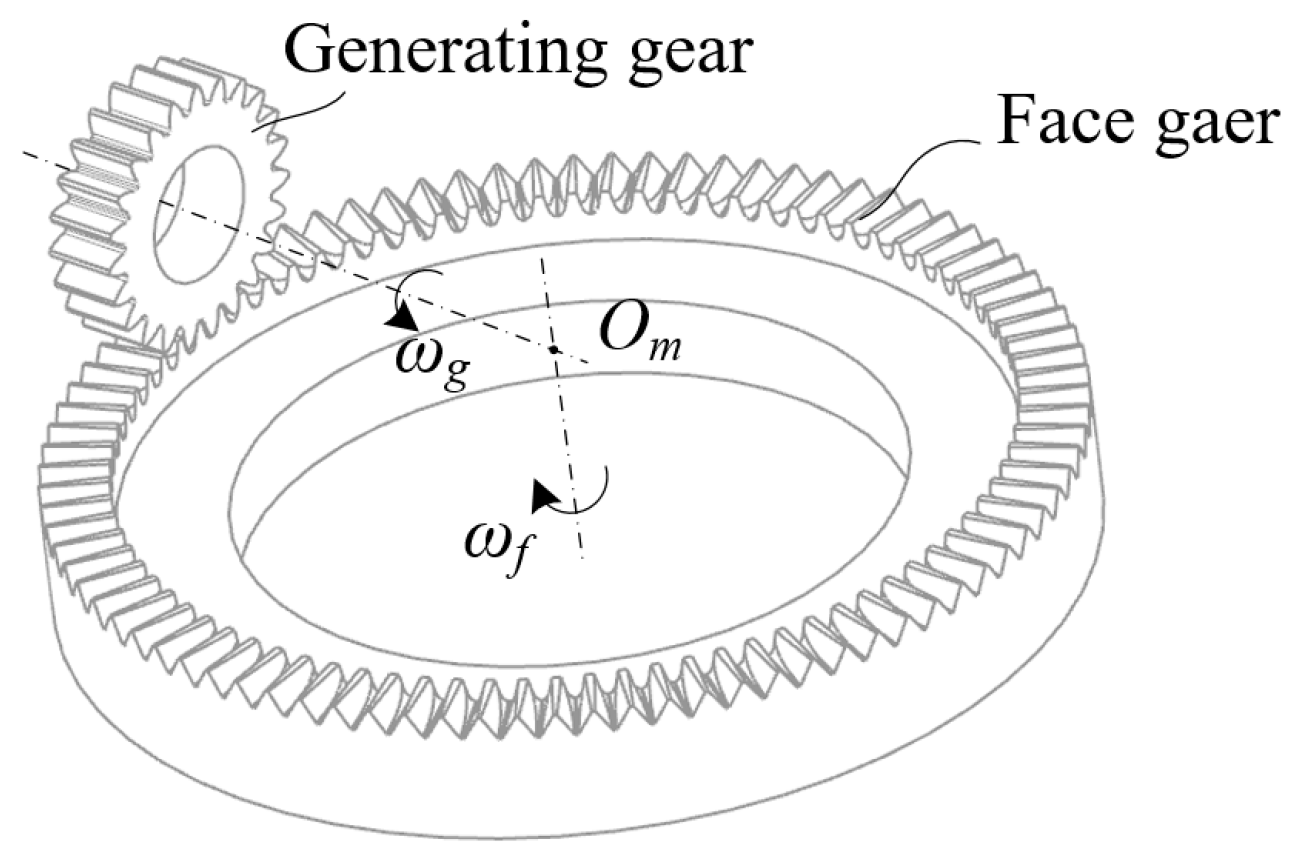
2. The Mechanism of Face Gear Formation
2.1. Generating Gear
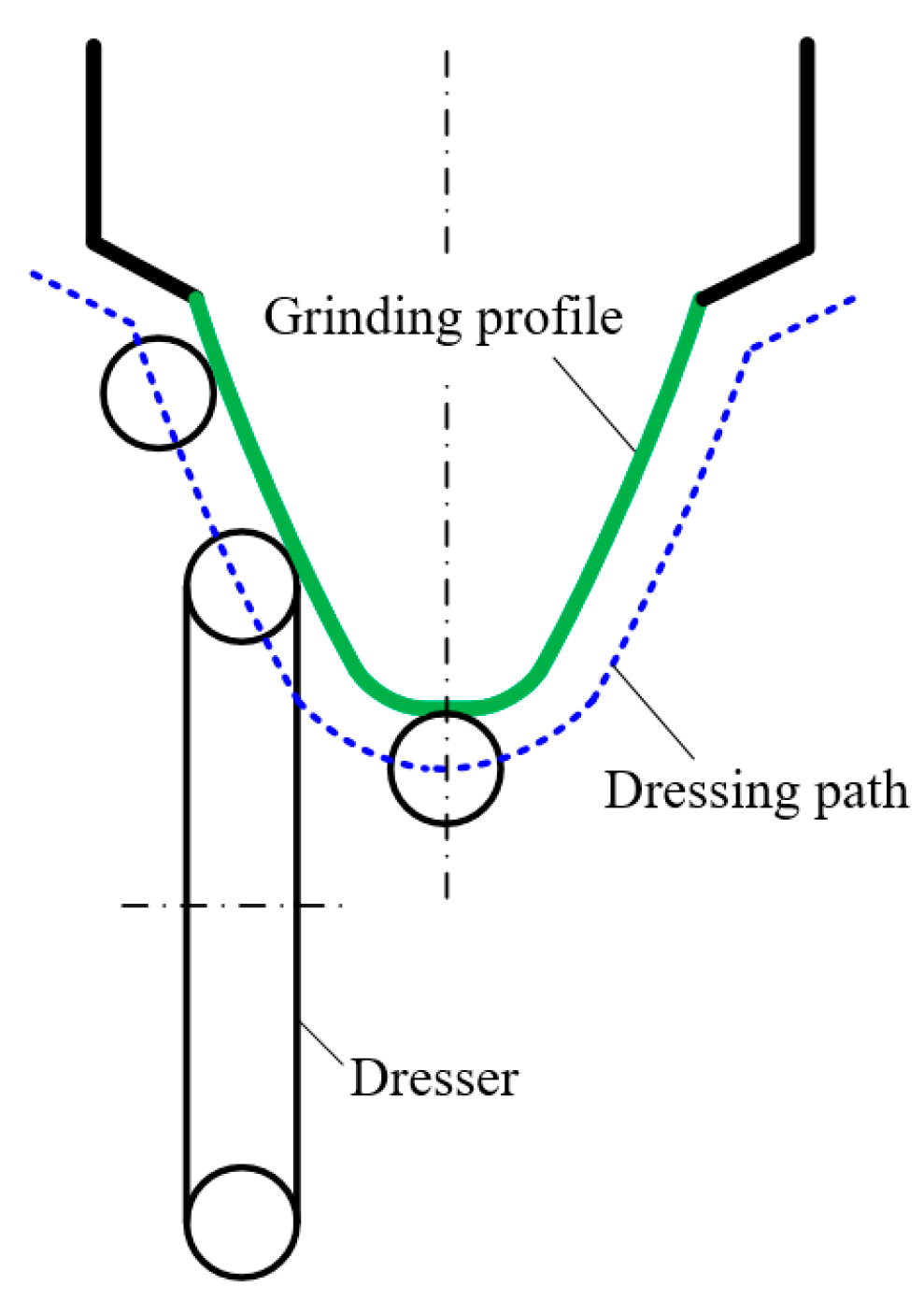
2.2. Motion of the Dish Wheel
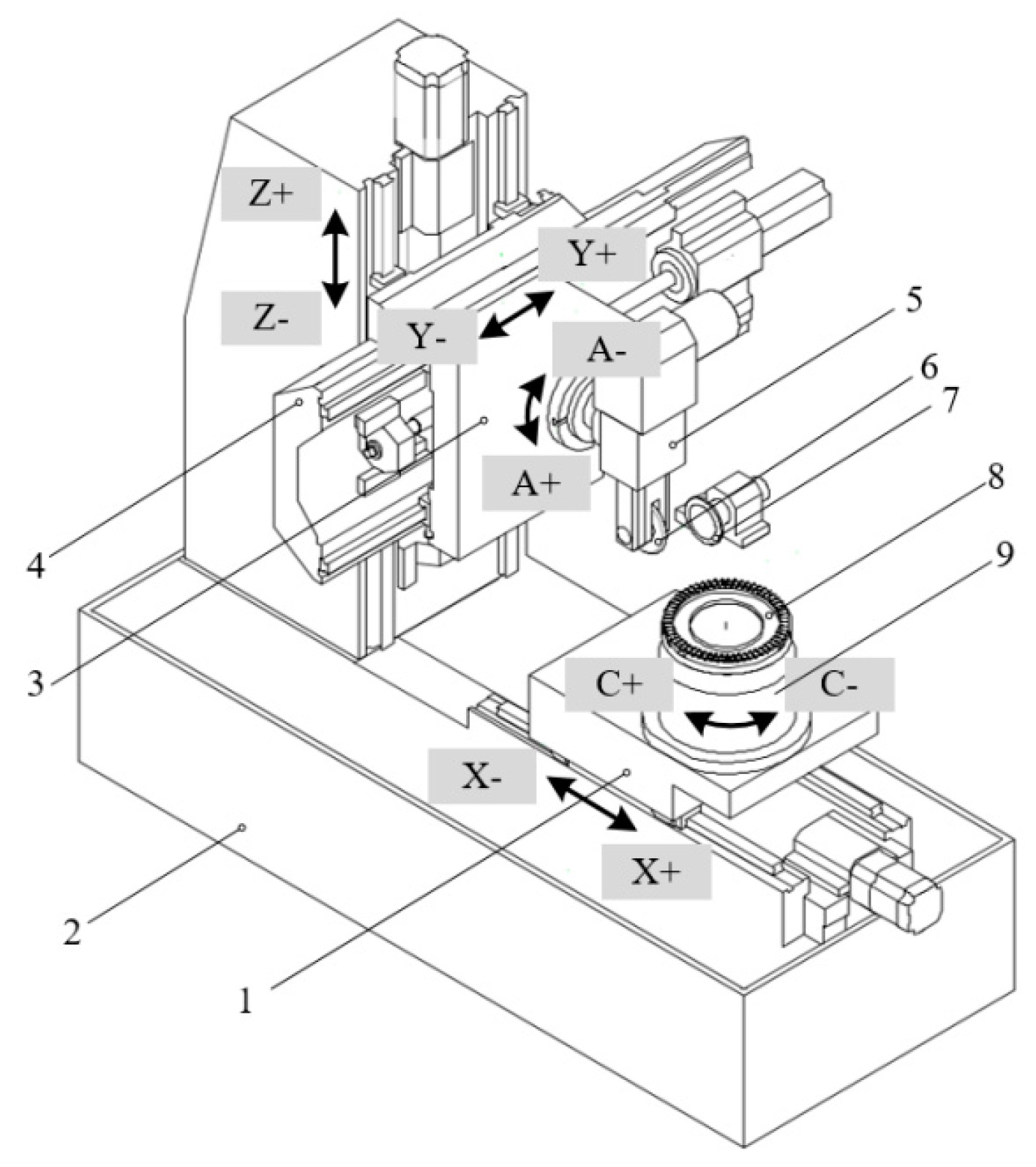
3. Grinding Strategy of the Gear Grinding Machine
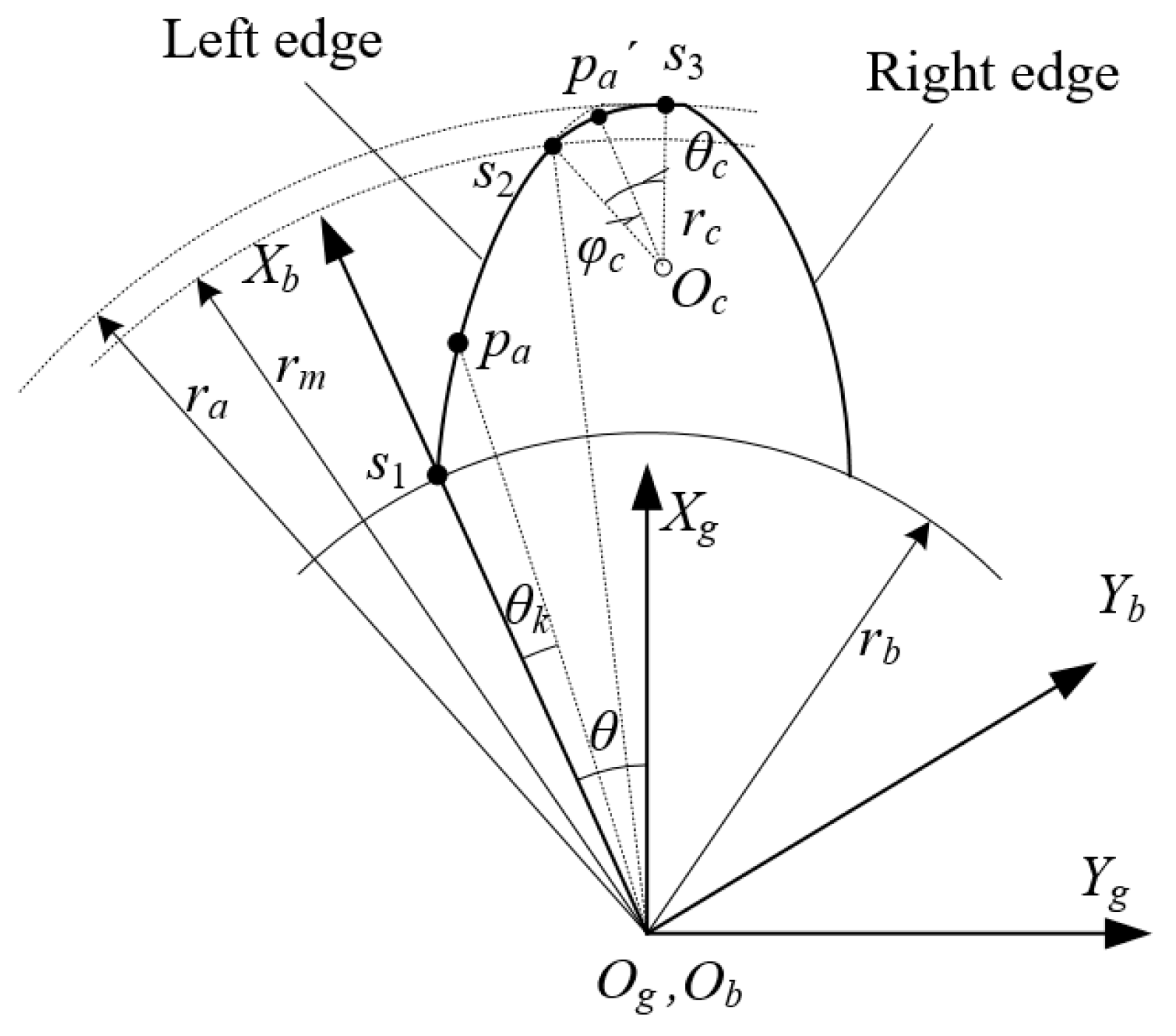
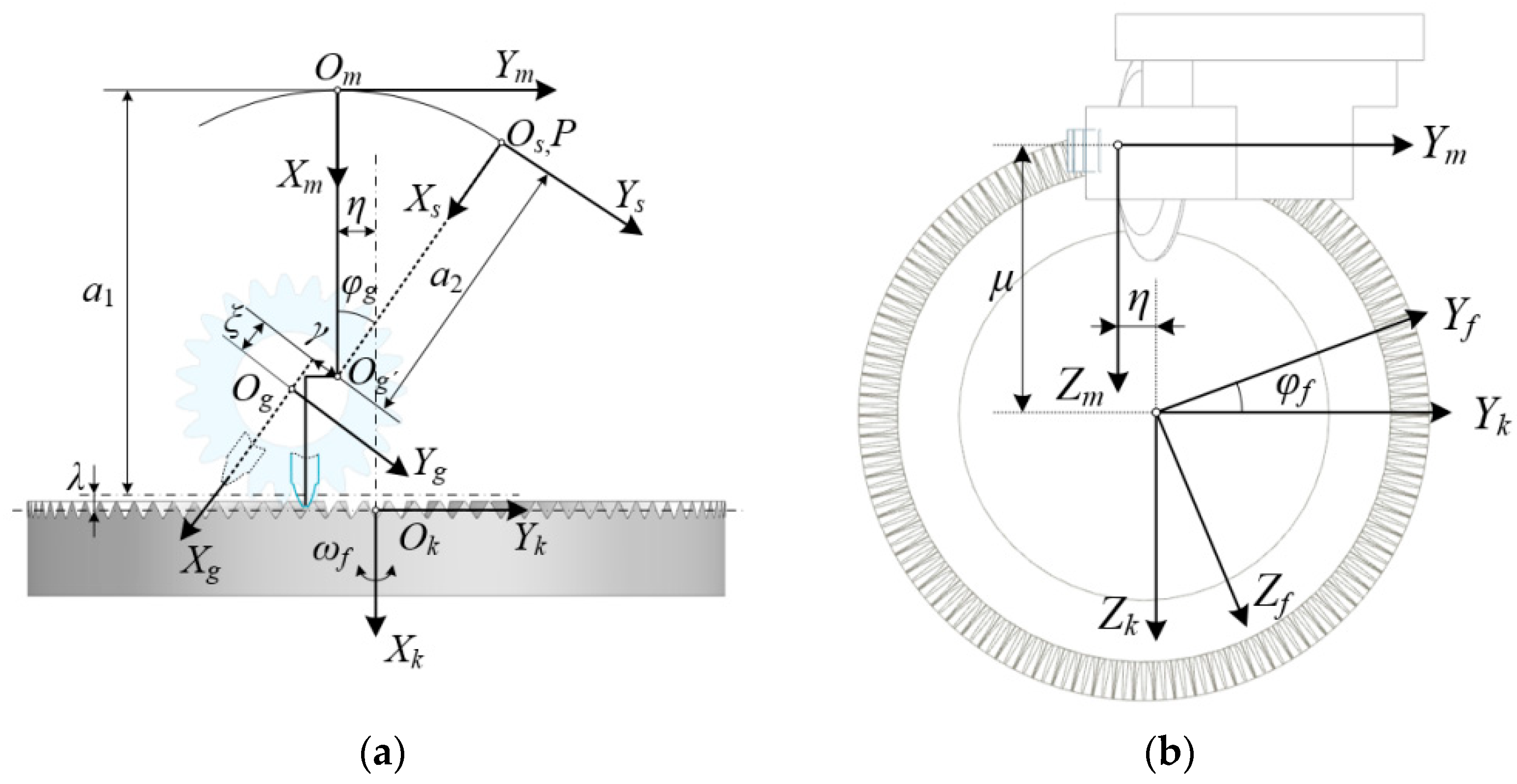
3.1. Motion Analysis of the Gear Grinding Machine
3.2. Error Source Analysis
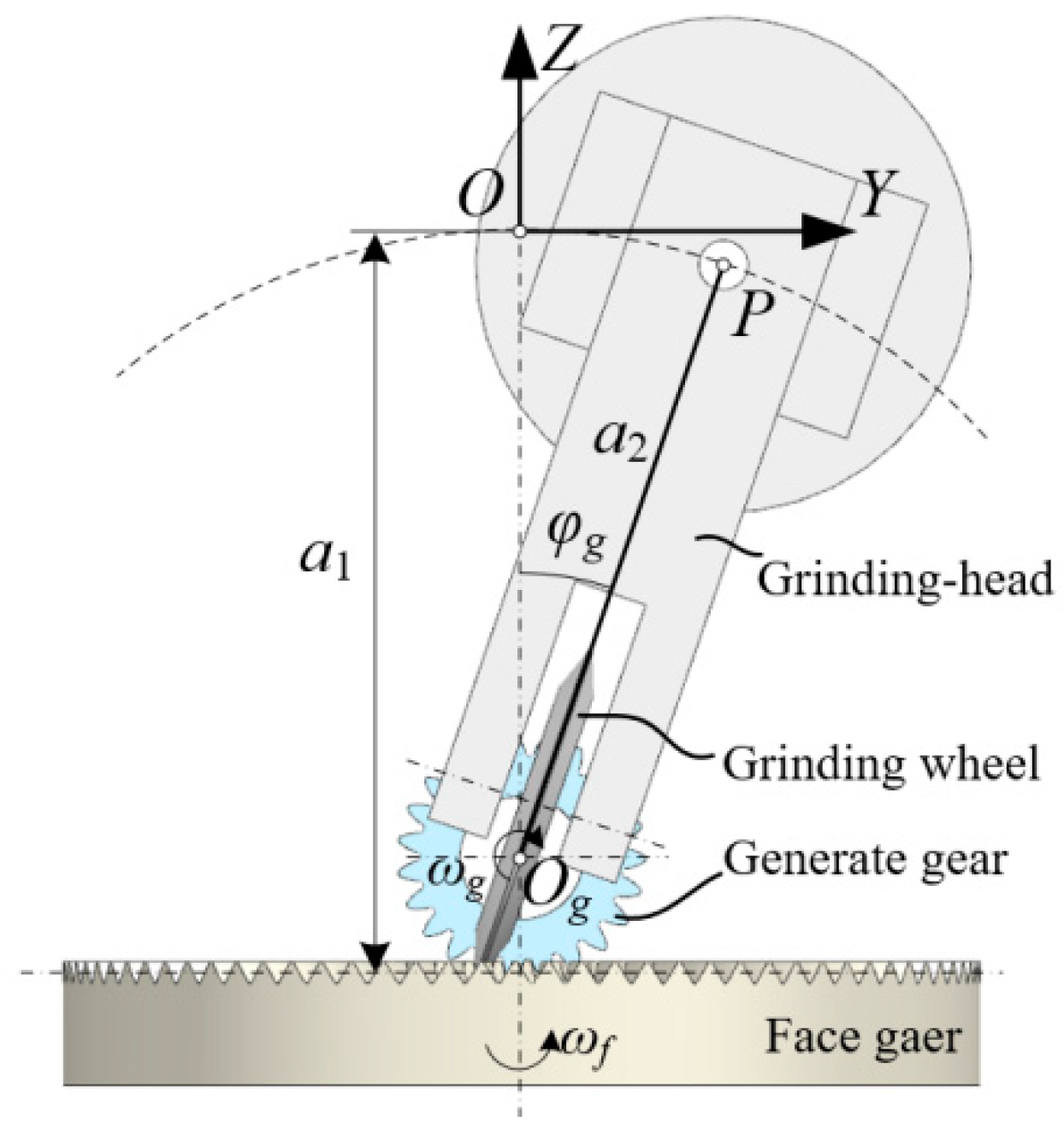
- The positional error caused by the lack of intersection between the rotational center of the grinding wheel head (Axis-A) and the face gear axis (Axis-C) can be recorded as η. This factor can be compensated by adjusting the position of Axis-Y during the grinding process.
- The positional error caused by the lack of positional coincidence between the center plane of the grinding wheel profile and the axis of the grinding wheel head (Axis-A) can be recorded as γ. This factor can be compensated by adjusting the coordinate offset of Axis-Y when dressing the grinding wheel.
- When the generating gear meshes with the face gear, the generating gear and the face gear are not in the theoretical position. The deviation between the theoretical mounting distance of the face gear and the actual installation distance can be recorded as λ. Because the reference cone angle of the face gear is 90°, this error factor can be compensated by adjusting the offset of Axis-Z.
- The designed rotation center of the generating gear does not coincide with the virtual rotation center of the generating gear generated by the motion axes of the grinding machine. The difference can be recorded as ξ. This results in the profile of the grinding wheel not rotating around the designed rotation center. This factor mainly comes from the manufacturing errors associated with the length of the grinding wheel head and the error of the diameter of the grinding wheel. This factor can be compensated by adjusting the setting value of a2 in the NC code.
4. Mathematical Modeling
4.1. Profile of the Grinding Wheel
4.2. Kinematic Model
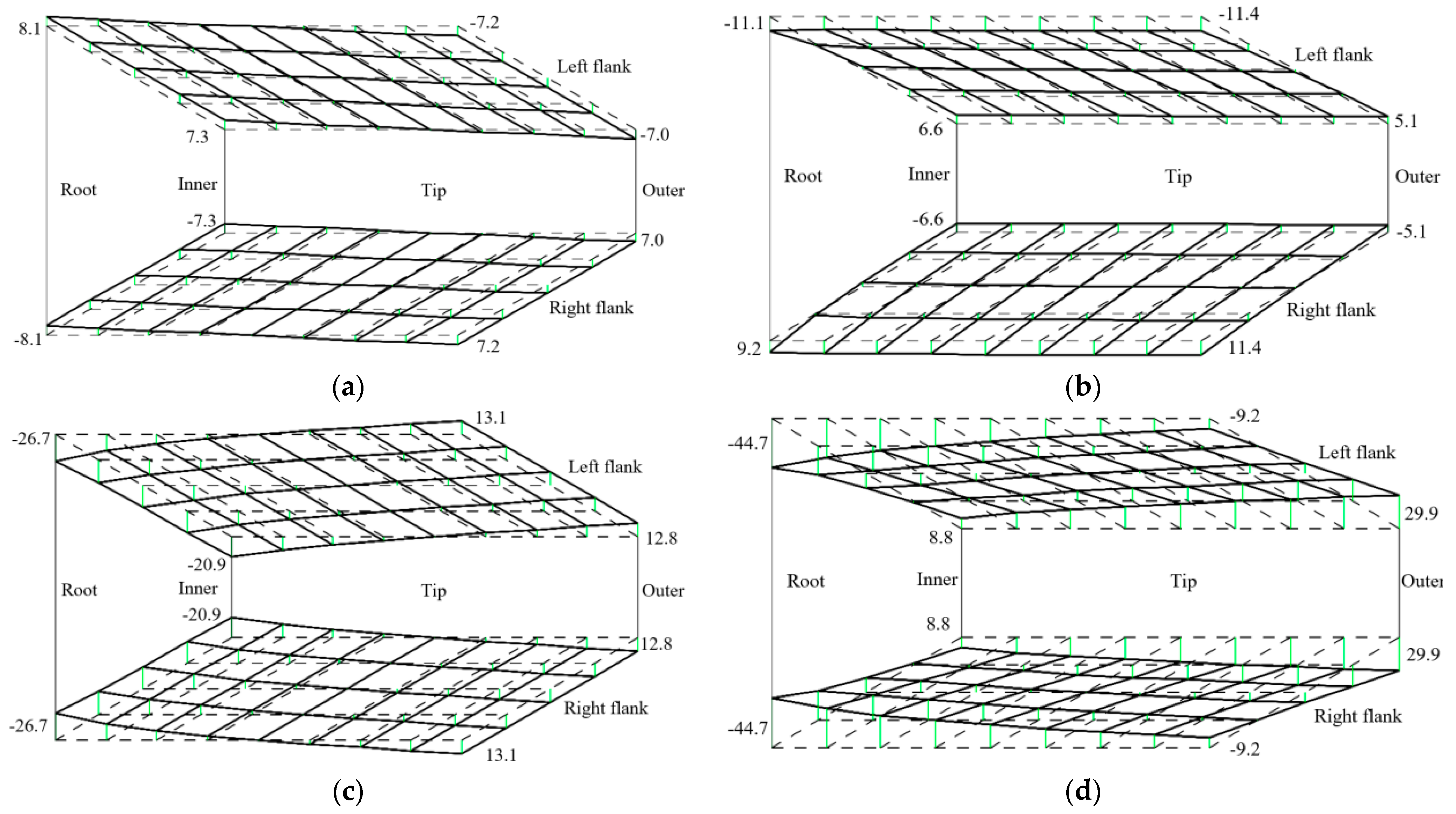
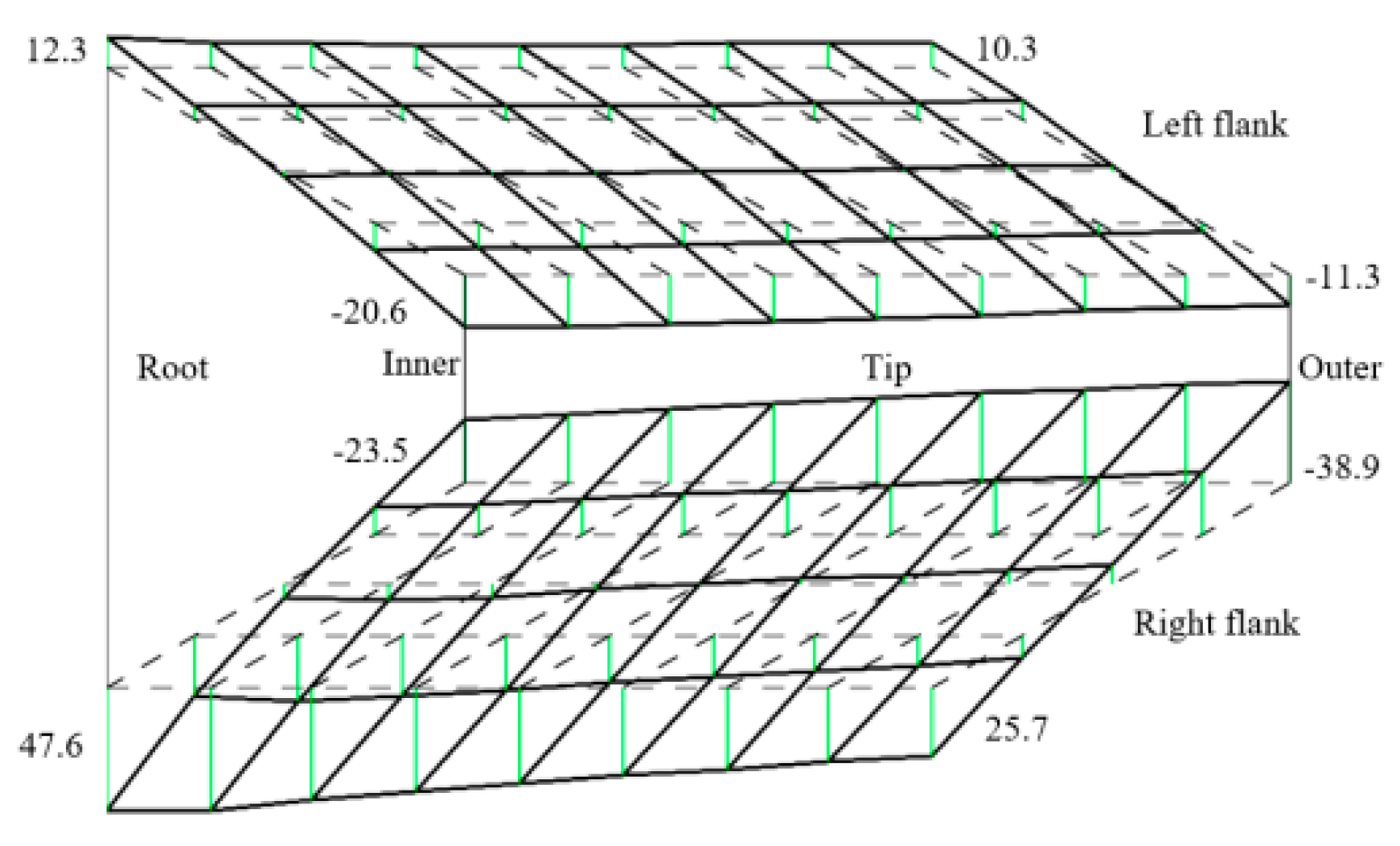
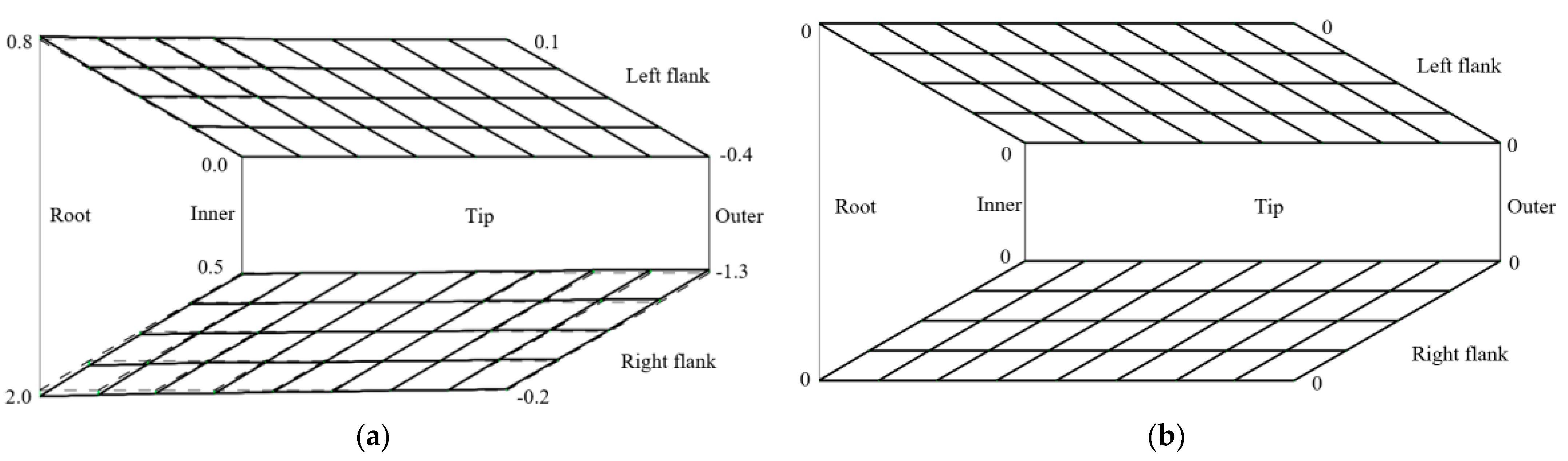
5. Analysis of the Tooth Surface Deviation
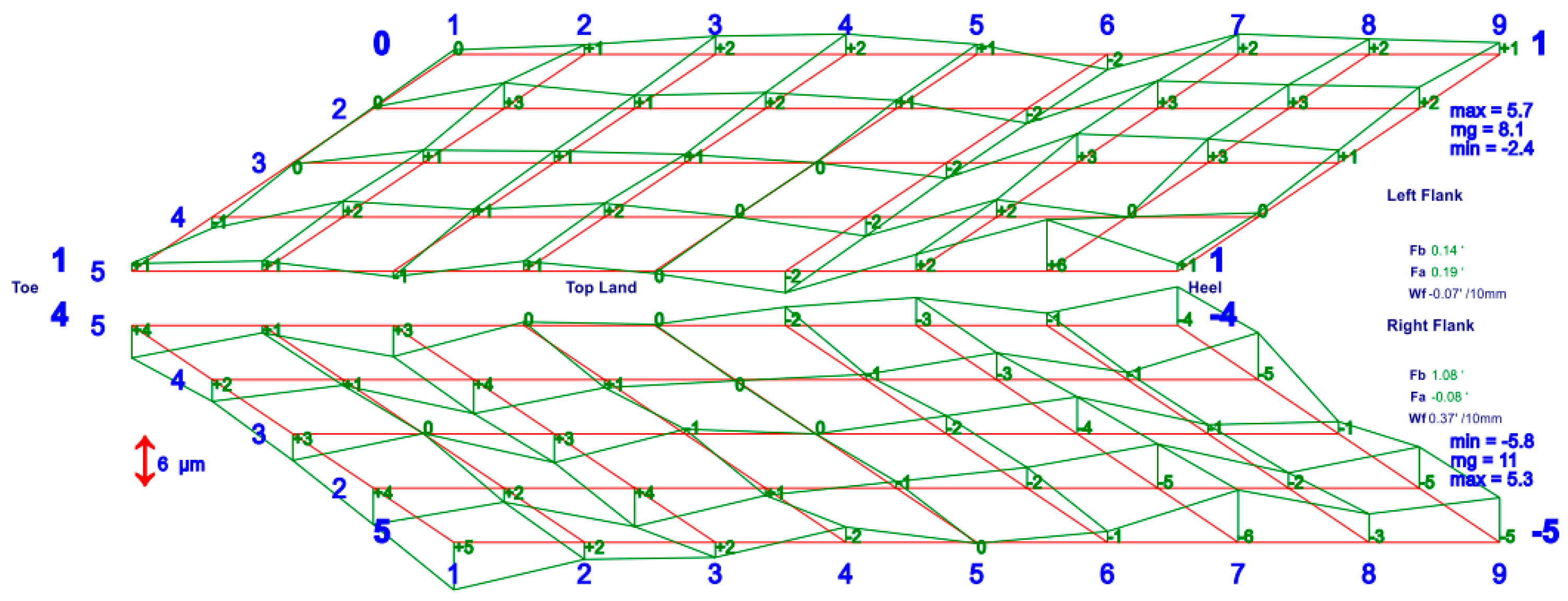
5.1. Distribution of the Deviation
5.2. Tooth Surface Correction Strategy
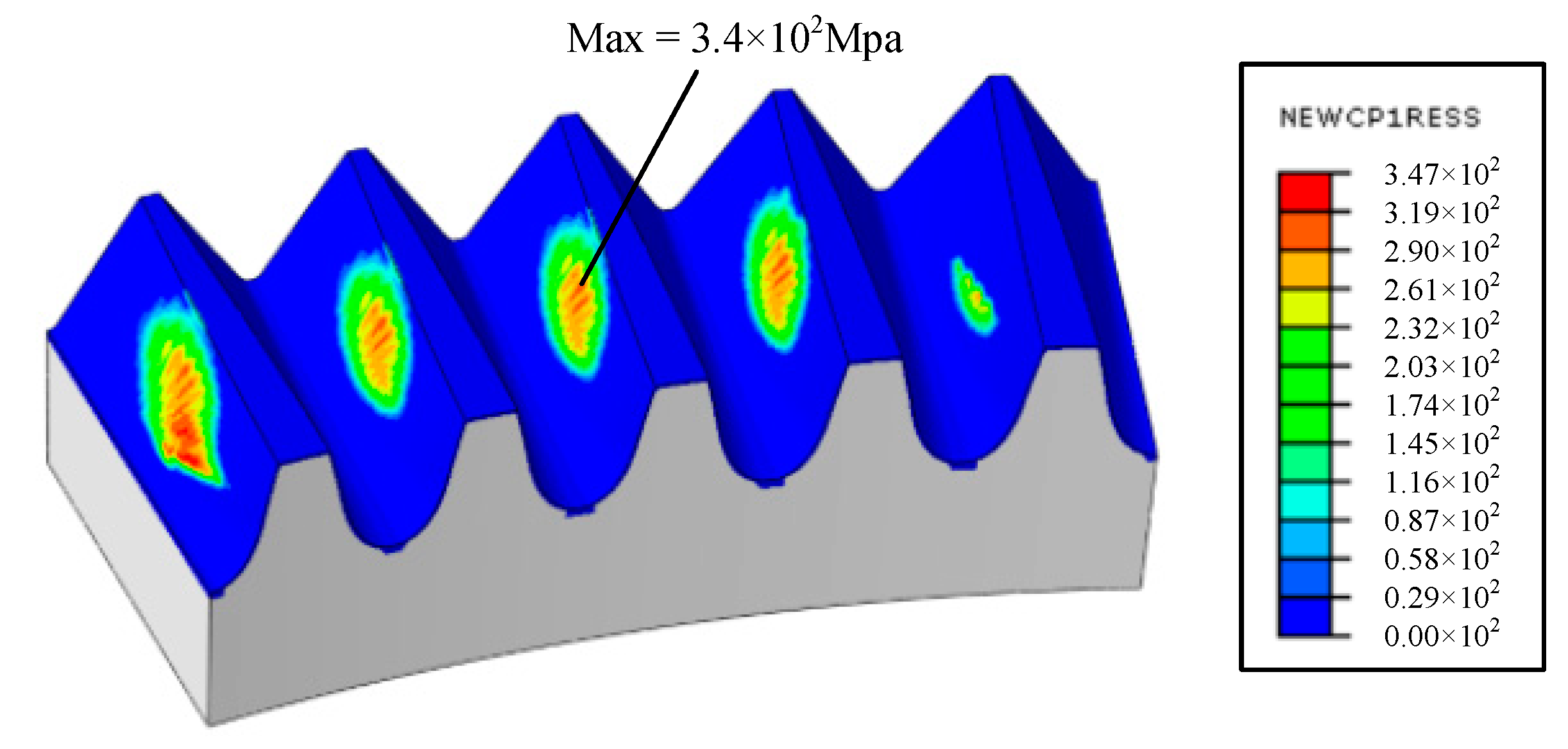
5.3. Contact Analysis
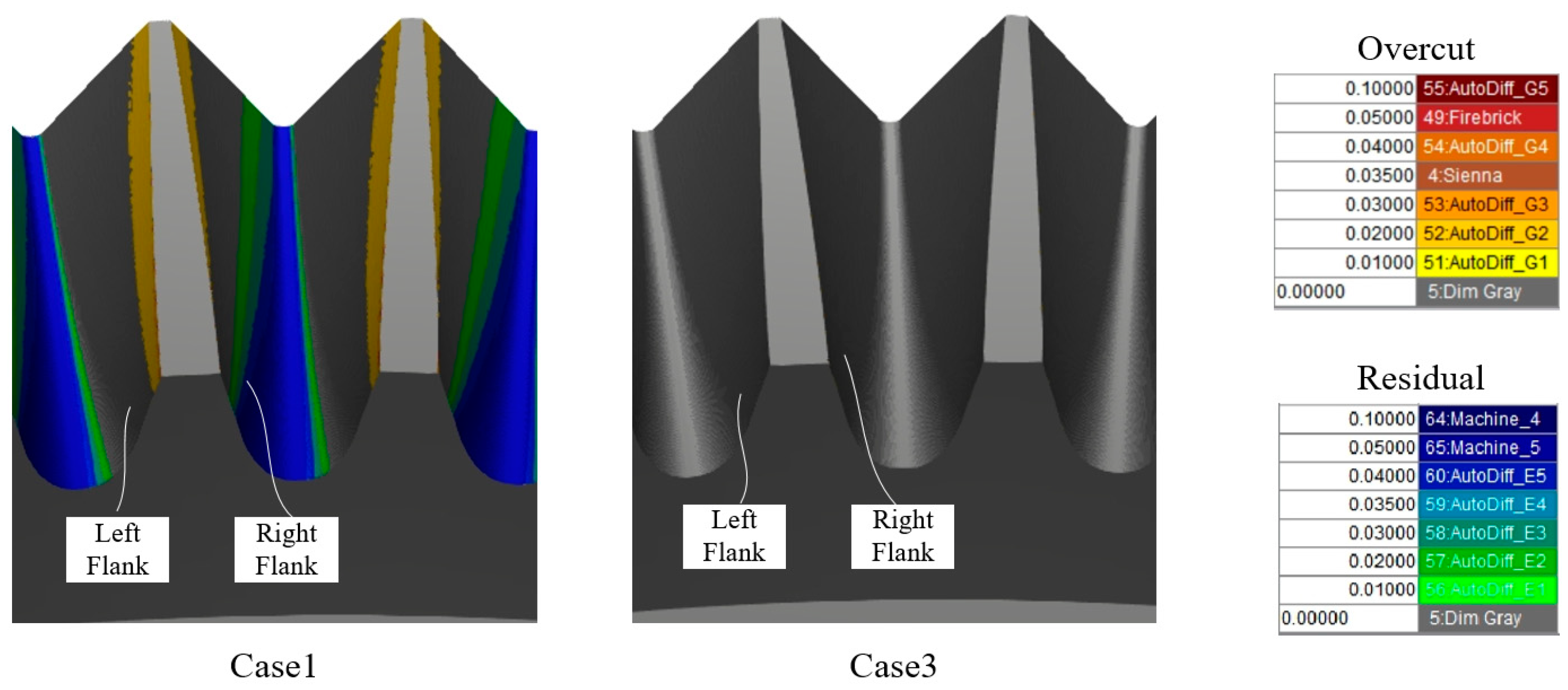
6. Experiment
7. Conclusions
- The grinding methods for face gears on an internal gear grinding machine were analyzed.
- A mathematical model containing positional errors of the machine tool was established, and this model can accurately predict the variation law of tooth surface deviations of face gears.
- A method in which a sensitivity matrix was used to adjust the grinding deviation of the tooth surface was developed. This method easily converged and could accurately calculate the adjustment parameters of the machine tool based on the distribution of the deviations in the tooth surface. The deviations in the tooth surface of the face gear were significantly reduced.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Heath, G.F.; Filler, R.; Tan, J. Development of Face Gear Technology for Industrial and Aerospace Power Transmission; Glenn Research Center: Cleveland, OH, USA, 2002; NASA/CR-2002-211320. [Google Scholar]
- Inoue, T.; Kurokawa, S. Influence of waveform components derived from the transmission error of a face gear pair on a fishing reel based on tactile sensibility. Precis. Eng. 2018, 51, 232–243. [Google Scholar] [CrossRef]
- Han, Z.; Jiang, C.; Deng, X. Machining and meshing analysis of face gears by power skiving. J. Adv. Mech. Des. Syst. Manuf. 2022, 16, JAMDSM0002. [Google Scholar] [CrossRef]
- Litvin, F.L.; Fuentes, A.; Zanzi, C.; Pontiggia, M.; Handschuh, R.F. Face-gear drive with spur involute pinion: Geometry, generation by a worm, stress analysis. Comput. Methods Appl. Mech. Eng. 2002, 191, 2785–2813. [Google Scholar] [CrossRef]
- Litvin, F.; Chen, Y.; Heath, G.; Sheth, V.; Chen, N. Apparatus and Method for Precision Grinding Face Gear. Patent number 6,146,253, 14 November 2000. Available online: https://www.freepatentsonline.com/6146253.html (accessed on 14 November 2000).
- Li, X.Z.; Zhu, R.P.; Li, Z.M.Q.; Li, F.J. Study on designing and dressing of worm for grinding process of face gear. Appl. Mech. Mater. 2011, 86, 475–478. [Google Scholar] [CrossRef]
- Tang, Z.; Zhou, Y.; Wang, S.; Zhu, J.; Tang, J. An innovative geometric error compensation of the multi-axis CNC machine tools with non-rotary cutters to the accurate worm grinding of spur face gears. Mech. Mach. Theory 2022, 169, 104664. [Google Scholar] [CrossRef]
- Zhou, Y.; Tang, J.; Zhou, H.; Yin, F. Multistep method for grinding face-gear by worm. J. Manuf. Sci. Eng. 2016, 138, 071013. [Google Scholar] [CrossRef]
- Shi, X.; Zhou, Y.; Tang, J.; Li, Z. An innovative generated approach to dressing the worm for grinding spur face gears. Manuf. Lett. 2020, 25, 26–29. [Google Scholar] [CrossRef]
- Shi, X.; Zhou, Y.; Zhang, W.; Tang, J. A new worm grinding method of face gears based on the optimization of dressing wheel profile. Forsch. Im Ingenieurwesen 2019, 83, 751–757. [Google Scholar] [CrossRef]
- Zhou, Y.S.; Tang, Z.W.; Shi, X.L.; Tang, J.Y.; Li, Z.-M.Q. Efficient and accurate worm grinding of spur face gears according to an advanced geometrical analysis and a closed-loop manufacturing process. J. Cent. South Univ. 2022, 29, 1–13. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Chu, X.M.; Zhao, W.J.; Wang, Z.; Su, G.Y.; Huang, Y.Z. A precision generating hobbing method for face gear with assembly spherical hob. J. Cent. South Univ. 2019, 26, 2704–2716. [Google Scholar] [CrossRef]
- Tang, J.Y.; Yin, F.; Chen, X.M. The principle of profile modified face-gear grinding based on disk wheel. Mech. Mach. Theory 2013, 70, 1–15. [Google Scholar] [CrossRef]
- Shen, Y.; Liu, X.; Li, D.; Li, Z. A method for grinding face gear of double crowned tooth geometry on a multi-axis CNC machine. Mech. Mach. Theory 2018, 121, 460–474. [Google Scholar] [CrossRef]
- Zhou, R.; Zhao, N.; Li, W.; Li, R.; Guo, G.; Guo, H. A grinding method of face gear mating with a conical spur involute pinion. Mech. Mach. Theory 2019, 141, 226–244. [Google Scholar] [CrossRef]
- Guo, H.; Peng, X.; Zhao, N.; Zhang, S. A CNC grinding method and envelope residual model for face gear. Int. J. Adv. Manuf. Technol. 2015, 79, 1689–1698. [Google Scholar] [CrossRef]
- Guo, H.; Gonzalez-Perez, I.; Fuentes-Aznar, A. Computerized generation and meshing simulation of face gear drives manufactured by circular cutters. Mech. Mach. Theory 2019, 133, 44–63. [Google Scholar] [CrossRef]
- Wang, Y.; Hou, L.; Lan, Z.; Zhang, G. Precision grinding technology for complex surface of aero face-gear. Int. J. Adv. Manuf. Technol. 2016, 86, 1263–1272. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Chu, X.; He, Y.; Zhang, W. Calculation model for surface roughness of face gears by disc wheel grinding. Int. J. Mach. Tools Manuf. 2017, 123, 76–88. [Google Scholar] [CrossRef]
- Ma, X.; Cai, Z.; Yao, B.; Chen, G.; Cai, S.; Liu, W. Prediction model for surface generation mechanism and roughness in face gear grinding. Int. J. Adv. Manuf. Technol. 2022, 120, 4423–4442. [Google Scholar] [CrossRef]
- Hermann, J. CONIFACE face gear cutting and grinding. Int. J. Gear Solut. 2010, 18, 39–47. [Google Scholar]
- Peng, X.L.; Niu, Q.Y.; Guo, W.; Fang, Z.D. A new method of motion rule synthesis for face gear manufacturing by plane-cutter. J. Mech. Des. 2017, 140, 023302. [Google Scholar] [CrossRef]
- Litvin, F.; Fuentes, A. Gear Geometry and Applied Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Ding, H.; Zhou, Y.; Tang, J.; Zhong, J.; Zhou, Z.; Wan, G. A novel operation approach to determine initial contact point for tooth contact analysis with errors of spiral bevel and hypoid gears. Mech. Mach. Theory 2017, 109, 155–170. [Google Scholar] [CrossRef]
- Peng, S.; Ding, H.; Tang, J. Accurate numerical computation of loaded tooth surface contact pressure and stress distributions for spiral bevel gears by considering time-varying meshing characteristics. Adv. Eng. Softw. 2019, 135, 102683. [Google Scholar] [CrossRef]
- Simon, V.V. Optimization of face-hobbed hypoid gears. Mech. Mach. Theory 2014, 77, 164–181. [Google Scholar] [CrossRef]





| Parameters | Values |
|---|---|
| Teeth number of the generating gear | zg = 24 |
| Module | m = 4 |
| Pressure angle | α = 25° |
| Teeth number of the face gear | zf = 86 |
| Inner diameter of the face gear | di = 320 mm |
| Outer diameter of the face gear | do = 370 mm |
| Radius of the grinding wheel | rG = 100 mm |
| Length of the grinding head | L = 350 mm |
| Dedendum of the face gear | hf = 5 mm |
| Factors | Case 1 | −X1 | Case 2 | −X2 | Case 3 |
|---|---|---|---|---|---|
| η | −0.1 | 0.095 | −0.005 | 0.005 | 0 |
| γ | 0.13 | −0.128 | 0.002 | −0.002 | 0 |
| λ | 0.06 | −0.062 | −0.002 | 0.002 | 0 |
| ξ | −0.11 | 0.108 | −0.002 | 0.002 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Z.; Jiang, C.; Deng, X.; Zhang, C.; Geng, L.; Feng, Y. The Grinding and Correction of Face Gears Based on an Internal Gear Grinding Machine. Machines 2024, 12, 496. https://doi.org/10.3390/machines12080496
Han Z, Jiang C, Deng X, Zhang C, Geng L, Feng Y. The Grinding and Correction of Face Gears Based on an Internal Gear Grinding Machine. Machines. 2024; 12(8):496. https://doi.org/10.3390/machines12080496
Chicago/Turabian StyleHan, Zhengyang, Chuang Jiang, Xiaozhong Deng, Congcong Zhang, Longlong Geng, and Yong Feng. 2024. "The Grinding and Correction of Face Gears Based on an Internal Gear Grinding Machine" Machines 12, no. 8: 496. https://doi.org/10.3390/machines12080496
APA StyleHan, Z., Jiang, C., Deng, X., Zhang, C., Geng, L., & Feng, Y. (2024). The Grinding and Correction of Face Gears Based on an Internal Gear Grinding Machine. Machines, 12(8), 496. https://doi.org/10.3390/machines12080496






