An Advanced Diagnostic Approach for Broken Rotor Bar Detection and Classification in DTC Controlled Induction Motors by Leveraging Dynamic SHAP Interaction Feature Selection (DSHAP-IFS) GBDT Methodology

Abstract

This paper introduces a sophisticated approach for identifying and categorizing broken rotor bars in direct torque-controlled (DTC) induction motors. DTC is implemented in industrial drive systems as a suitable control method to preserve torque control performance, which sometimes shows its impact on fault-representing frequencies. This is because of the DTC’s closed-loop control nature, whichtriesto reduce speed and torque ripples by changing the voltage profile. The proposed model utilizes the modified Shapley Additive exPlanations (SHAP) technique in combination with gradient-boosting decision trees (GBDT) to detect and classify the abnormalities in BRBs at diverse (0%, 25%, 50%, 75%, and 100%) loading conditions. To prevent overfitting of the proposed model, we used the adaptive fold cross-validation (AF-CV) technique, which can dynamically adjust the number of folds during the optimization process. By employing extensive feature engineering in the original dataset and then applying Shapely Additive exPlanations(SHAP)-based feature selection, our methodology effectively identifies informative features from signals (three-phase current, three-phase voltage, torque, and speed) and motor characteristics. The gradient-boosting decision tree (GBDT) classifier, trained using the given characteristics, extracts consistent and reliable classification performance under different loading circumstances and enables precise and accurate detection and classification of broken rotor bars. The proposed approach (SHAP-Fusion GBDT with AF-CV) is a major advancement in the field of machine learning in detecting motor anomalies at varying loading conditions and proved to be an effective mechanism for preventative maintenance and preventing faults in DTC-controlled induction motors byattaining an accuracy rate of 99% for all loading conditions.

1. Introduction

Induction motors (IMs) are considered extremely important pieces of electrical equipment because of their variety of applications, such as pumps, compressors, fans, conveyors, traction applications, etc. Moreover, their simple, cheap, reliable, and efficient construction makes them suitable for rough industrial environments with extensive duty cycles. Induction motors (IMs) experience various stresses due to mechanical, electrical, thermal, and environmental factors, each of which can contribute to the degradation of motor performance and increase the likelihood of faults such as broken rotor bars [1]. Many issues can arise in the motors due to these stresses, and the lack of clarity regarding these problems may result in a disastrous motor breakdown. To mitigate these issues, it is imperative to provide early detection and diagnosis techniques for identifying potential faults in the components of the IM. This will provide sufficient warning time before they reach the point of failure [2]. Usually, broken rotor bars account for 10% of induction motor defects, making this one of the most frequently occurring problems. In closed-loop control systems, detecting faults may present difficulties because of several interlinked state variables. Field-oriented control (FOC) and direct torque control (DTC), two prevalent control methods, are renowned for their efficacy and feasibility. 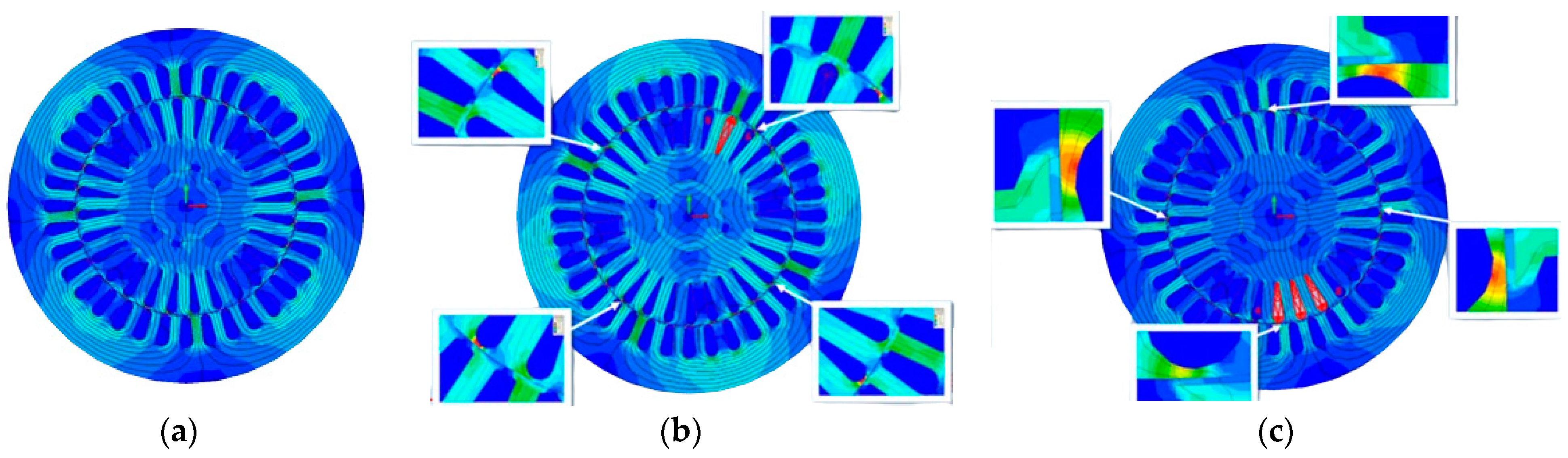The occurrence of a high-frequency factor in the stator current spectrum of DTC-fed squirrel cage induction motors (SCIM) is due to the influence of DTC’s control settings and switching frequencies [3,4]. Additionally, the amplitude of the phase current’s sideband near the source frequency is influenced by the control structure. The FEM analysis and cross-sectional view of the induction motor utilized in this investigation to analyze BRBs are depicted in Figure 1. It is evident that the flux density around the broken bars increases and puts the neighboring bars under increased magnetic stress, making them vulnerable too.

Approximately 85% of all electrical machines are squirrel cage induction motors (SQIMs) due to their reliability, robustness, and cost-effectiveness. Typically, variable-frequency drives (VFDs) or AC drives with adjustable speeds are the preferred methods for powering these induction motors, providing efficient and flexible control over their operation [5]. Overall, faults in induction motors can be broadly classified into electrical and mechanical categories. On the electrical side, approximately 30–40% of faults are associated with the stator, while 5–10% occur on the rotor side. Mechanical faults, which constitute about 40–50% of the total, often involve issues with components such as bearings and air gaps [6,7]. Rotor failures are caused by several different forces acting on them. The rotor bars can be affected due to thermal, electric, mechanical, and environmental factors. When there is a broken rotor bar (BRB), the torque and speed ripples increase, and the effective value is decreased. This may increase the vibrations affecting the other parts of the machine as well [8]. How to find and fix faults is an important part of protecting AC drives so that the problems mentioned above don’t happen. The MCSA method depends on specific frequencies in the current spectrum of the stator that serve as indicators of fault, such as broken rotor bars indicating frequencies described by Equation (1).

$$f_{brb}=(1\pm 2Ks)f_s$$

(1)

where $f_s$ is the supply frequency, K is an integer, and s denotes the rotor slip.

The authors in [9] introduced a third-order energy operator (TOEO) that utilizes a demodulated current signal to detect damaged rotor bars in low-load induction machines. In [10], the authors suggested an approach based on time domain-based analysis of incipient faults that occurred in broken rotor bars byemploying electromagnetic signatures. In [11], the authors proposed artificial neural networks (ANNs) with Hilbert transform to diagnose bearing faults in induction machines through motor current signature analysis based on theirunique spectral signature. In [12], the authors utilized the fast Fourier transform (FFT) for analyzing and understanding patterns in healthy and faulty signals based on single-current acquisition to diagnose bearing faults. In [13,14], the authors suggested an FFT that helps to detect and segregate various faults and their severity by analyzing components near the fundamental frequency. In [15,16], the authors employed FFT with advanced signal processing techniques like STFT and WT to diagnose abnormal conditions in bearings by orthogonal matching. In [17], the authors suggested convolutional neural networks (CNNs) and motor current signature analysis (MCSA) during transient states to diagnose abnormal conditions in bearings in induction motors. In [18], the authors suggested a reliable approach to diagnosing early bearing faults by employing the inverse thresholding technique through non-stationary assessment of fault frequencies in induction machines. Alternatively, multiple studies suggest utilizing continuous or discrete wavelet transforms (CWTs and DWTs) [19,20] to analyze signals that are both stationary and non-stationary in the time-frequency domain. Moreover, techniques like MUSIC transform [21,22], the stator current envelope [23], the maximum covariance [24], and the zoom-FFT techniques [25] are widely available in the literature.

In [26,27], the authors suggested a novel and effective signal processing method for the fast Fourier transform (FFT) to identify broken bar faults by utilizing the Goertzel algorithm. In [28], the authors utilized stator currents, voltages, or stray flux by focusing on specific frequency components for diagnosing broken rotor bars. In [29], the authors utilized stock well transform by employing maximum magnitude and phase angle obtained through S-transform to diagnose bearing conditions of the shaft side and fan side in induction motors. In [30,31], the authors proposed the application of wavelet-based transforms and Wigner–Ville distributions for fault identification in inverter-driven induction motors to diagnose bearing faults. However, their effectiveness in detecting induction motors powered by inverters is uncertain due to the presence of cross-terms and varying time-frequency resolutions, as highlighted in [32]. In [33,34], the authors employed the short-time Fourier transform (STFT), a straightforward approach for time-frequency analysis, to accurately trace harmonics associated with damaged rotor bars in induction machines. The authors in [35] employed variational mode decomposition (VMD) and also the empirical wavelet transform (EWT) for the detection of broken rotor bar faults at different operational conditions. The methodology proposed by the authors [36] uses the adaptive slope transform (AST) combined with the Chirplet transform (CT) to detect and classify abnormal conditions of broken rotor bars (BRBs) in grid-fed (DTC) induction motors. The authors in [37,38] suggested the application of ensemble empirical mode decomposition (EEMD) as a better choice to diagnose broken rotor bars in inverter-driven induction motors. The instant speed during MME was also monitored for the diagnosis of BRB faults in induction motors powered by inverters [39,40]. The authors in [41] suggested the precise identification of BRB faults that are influenced by control dynamics and load variations, although explainability in the field of machine learning is now becoming an important technique for selecting hidden features from datasets.

After the advancements in the fields of machine learning and deep learning, many feature extraction and selection methodologies wereintroduced to search for the best features from a dataset, and SHAP is considered thebest feature selection technique to trace the informative attributes. This technique can handle large volumes of operations in data management to optimize their data center processes. In [42], the author’s introduceda new technique named SHAP as a feature selection mechanism, utilizing a game theoretic approach and attaining better outcomes than existing techniques. In [43], the authors suggested the convolutional neural network CNN to diagnose broken rotor bars using continuous wavelet transform to generate time-frequency images in induction motors. In [44], the proposed convolutional neural network uses thefinite element method FEM to trace incipient bearing faults in DTC control induction machines. In [32], authors proposed multiple machine-learning algorithms named DT, ANN, and deep learning models to diagnose bearing faults based on comparison methodologies. In [45], the authors make use of sparse autoencoders with multi-layer perception to detect bearing faults based on motor current signature analysis. In [46], the authors proposed amachine learning model named random forest to detect failure modes of machines in different sections based on Shapely Additive exPlanations and prove its validity on different experimental datasets. In [47], the authors proposed a hybrid ML algorithm deep neural network DNN with gradient-boosting decision tree GBDT and feature selection based on SHAP values and achieved remarkable breakthroughs in diagnosing problems related to the medical field. In [48], the authors proposed an improved version of the SHAP technique named Kernel SHAP to detect abnormalities in multiple fields through autoencoders. In [49], the authors proposed a novel framework using different boosting algorithms like XGBoost, AdaBoost, and LightGBM for diagnosing compressive strength predictions in concrete using the Shapely Additive exPlanations (SHAP) approach. In [50], the authors utilized Shapely Additive exPlanations on real operations of DC data streams obtained from accelerometers to evaluate their performance through MAE, MPAE, and RMSE assessment metrics and find excellent outcomes.In [51], authors proposed an efficient feature selection technique named Shapely Additive exPlanations for the diagnosis of bearing faults in induction machines using an ML algorithm support vector machine. In [52], the authors employed Shapely Additive exPlanations on the time series SAR dataset for the prediction of spatial landscapes utilizing different machine learning algorithms.

SHapely Additive exPlanations (SHAP)

Shapley Additive exPlanations (SHAP) is an additive approach utilized for interpreting machine learning models by quantifying the contribution of each feature to the model’s predictions. It was first introduced by Lundberg and Lee in 2017 and is specifically built for explainable AI (XAI) [53]. As stated above, SHAP measures the Shapley values of the input features, i.e., the average marginal contribution of feature values across all possible features set in the model. It is the same thing assharing a gift evenly among friends based on our contributions. SHAP values help you determine the rank of importance of the prediction for each feature of your dataset. Looking at these numbers quantifies which variables matter most when you want to know what your model is telling you and which ones do notmatter at all. This enabled better and more streamlined models while also not compromising performance, resulting in abetter choice of features. SHAP values are a statistically applicable way of ranking features based on significance. The Shapley value estimation of the jth feature with i combinations of features, target feature x, j index, data streams D with matrix X, and predictive model f is calculated as follows:

$${\varnothing }_{ij}=f^{*}\left(x+j\right)-f^{*}\left(x-j\right)$$

(2)

where ${\varnothing }_{ij}$ denotes the average Shapley value of the j-th feature through the ith feature, $f^{*}\left(x+j\right)$ is the prediction for target x with a random number, including the j-th feature, and the group of features absent of the j-th feature is denoted as fˆ(xj). The equation is as follows to calculate the Shapley value of the j-th feature, which is the target, x, in general:

$${\varnothing }_j(x)={\displaystyle \frac{1}{n}}\sum _{k=1}^n({\varnothing }_{ij})$$

(3)

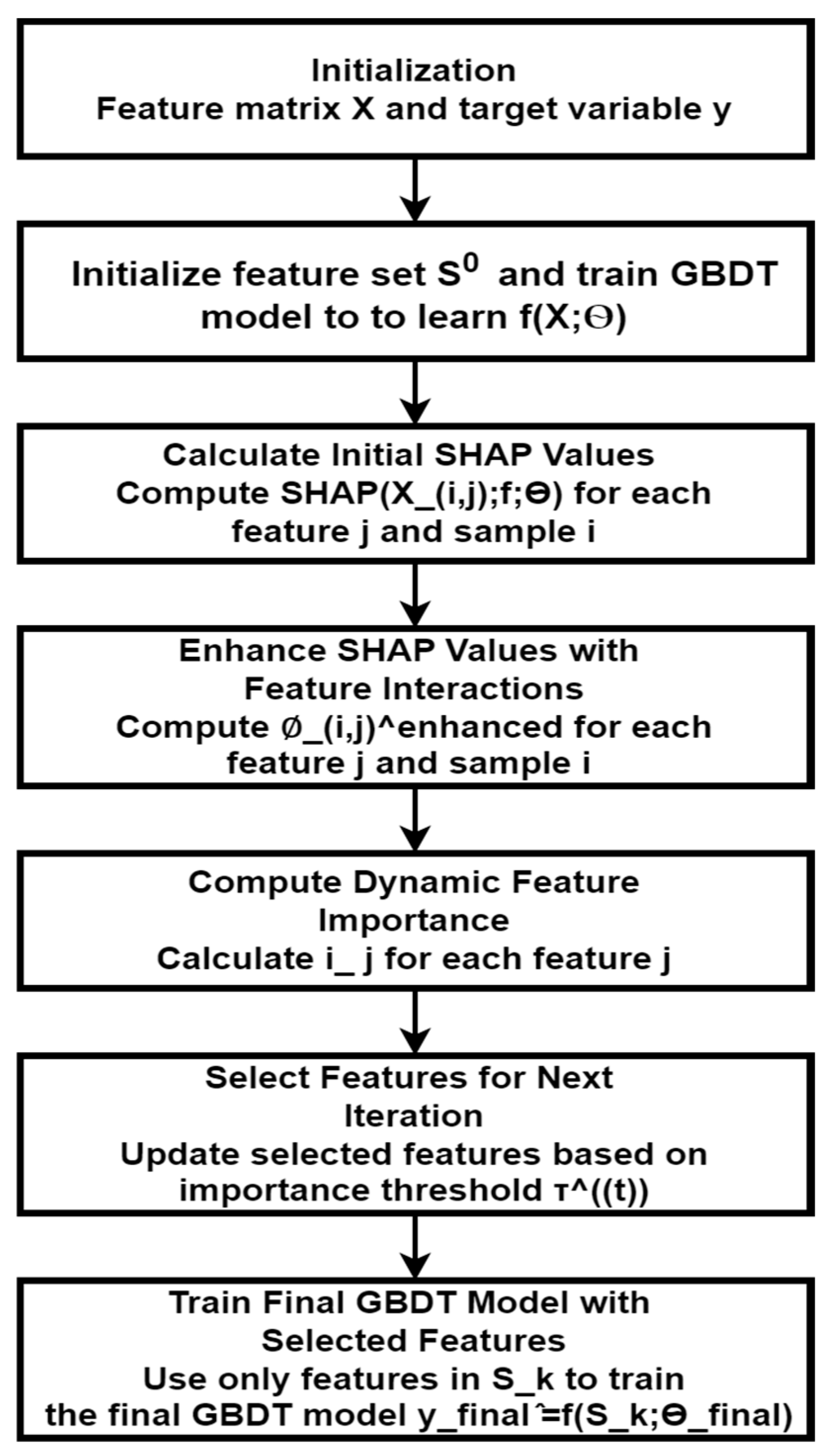
The significance of every attribute is calculated consistently and is ranked according to their Shapley rate in a predetermined arrangement. The model is subsequently trained to utilize the most significant attribute, as demonstrated in the subsequent iterations, starting from the top and progressing until the most favorable attribute subset is recognized.

• 1st interaction: $k_1$ = $f_1$
• 2nd interaction: $k_2$ = $f_1{f}_2$
• 3rd interaction: $k_3$ = $f_1{f}_2{f}_3$, $\dots \dots \dots f_n$
• Ultimately, the objective problem can be effectively modeled by identifying and utilizing the optimal feature subset.

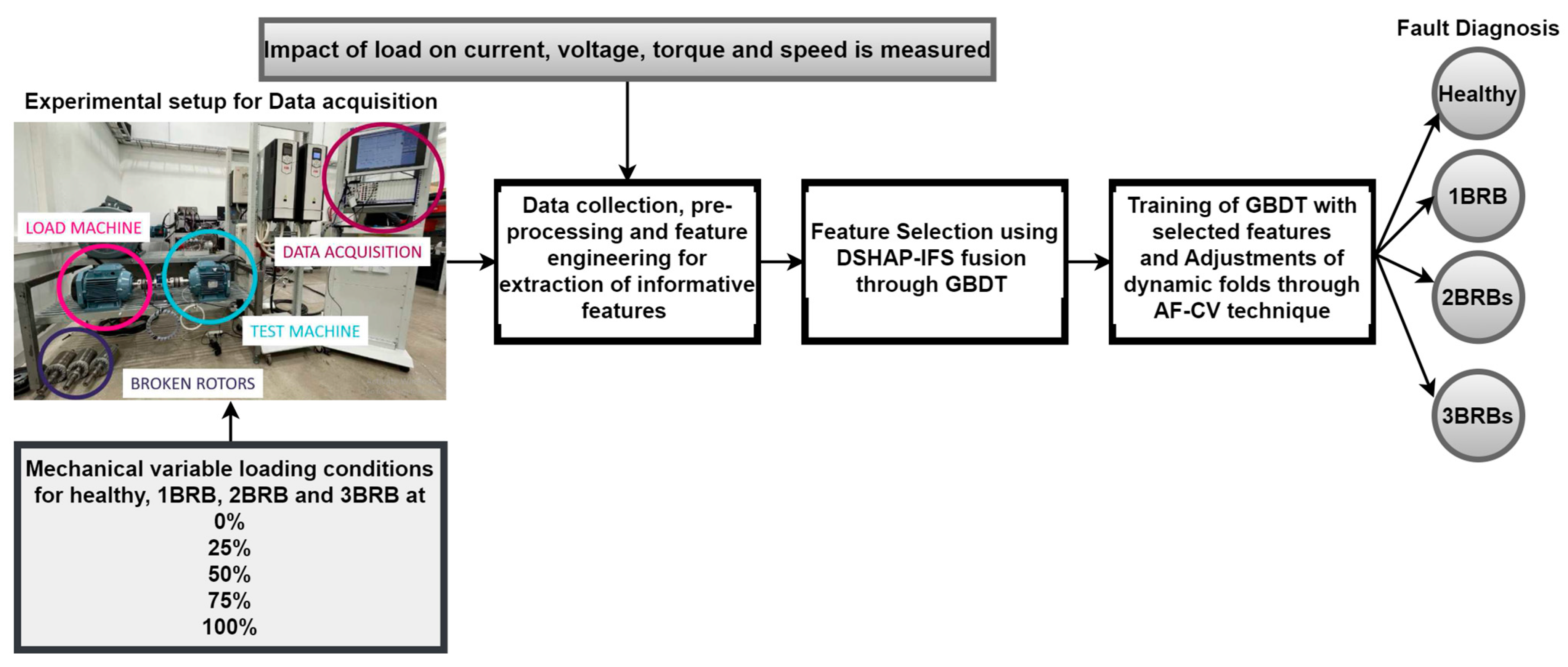
In this paper, dynamic SHAP interaction feature selection (DSHAP-IFS) with gradient-boosted decision trees (GBDT) is introduced—an innovative technique for feature selection by exploiting interactions among features to improve the model performance. Like a house built on the foundation of GBDT, DSHAP-IFS increases the importance of feature selection and contributes insight into the importance of the feature in the dataset. Through the iterative refinement of feature selection, by dynamically augmenting SHAP values, DSHAP-IFS can capture the subtle correlations among features, enabling further enhancement of model interpretability and predictive performance. This methodology helps identify the critical features that make a model work so that the learned model can be applied more rigorously to predict output for a variety of different applications. The main objectives and contributions of this article are given below:

• Introduction of a sophisticated method leveraging SHAP-fusion GBDT for precise detection and classification of BRBs in DTC-controlled induction motors.
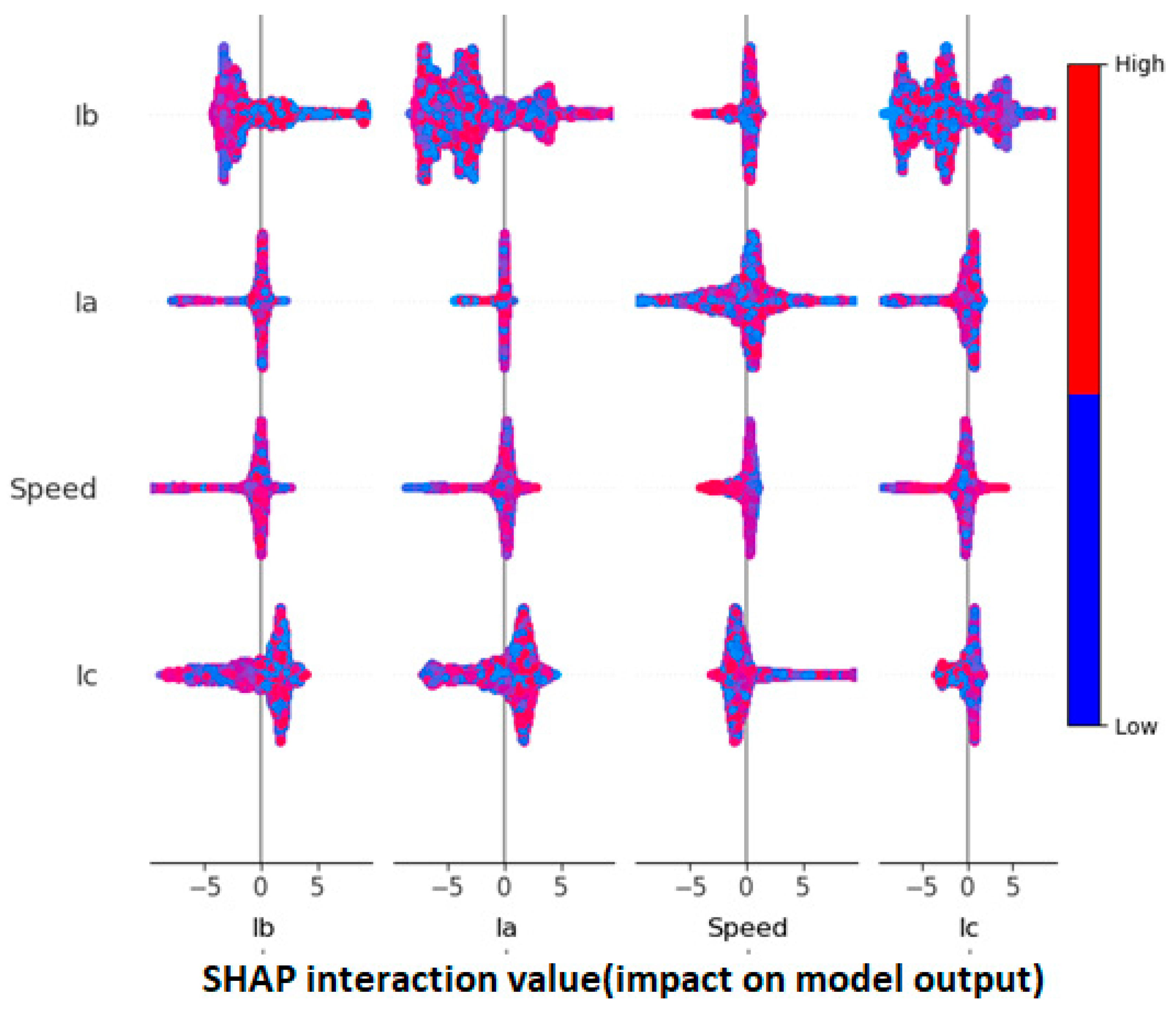
• Application of extensive feature engineering and SHAP-based feature selection to extract informative features from electrical signals (current, voltage, torque, speed) and motor characteristics.
• Explore the impact of SHAP-based feature selection on model interpretability and understanding of the underlying mechanisms driving BRB detection and classification in DTC-controlled induction motors.
• To ensure that the proposed method performs reliably under diverse loading conditions (0%, 25%, 50%, 75%, and 100%) and attains a high accuracy rate (99%) in the detection and classification of broken rotor bars.
• Application of adaptive fold cross-validation to reduce the overfitting in which the number of folds is changed during the optimization process.
• Demonstration of consistent and reliable classification performance of the GBDT classifier under varying loading conditions, ensuring accurate detection and classification of BRBs across different operational scenarios.
• Significance in advancing the field of machine learning for motor anomaly detection by achieving an impressive accuracy rate of 99% for all loading conditions, thereby contributing to the development of preventative maintenance strategies and enhancing the dependability of DTC-controlled induction motors.

2. Detection and Classification of Anomalies in Induction Motors: Analysis of Electrical Signatures in Healthy and Faulty States, with Emphasis on Broken Rotor Bars

This work focuses on the detection of problems in induction motors by analyzing electrical signals, with particular attention on identifying broken rotor bars. The objective was to obtain a precise representation of the motor’s performance, particularly in identifying any damaged rotor bars. In a healthy motor, the phase current, phase voltage, speed, and torque should exhibit a smooth and sinusoidal waveform. Furthermore, when the rotor bars of the motor are broken, an extra harmonic component is generated around the left sideband (LSB) and right side band (RSB)around the fundamental component at 50 Hz in the current, voltage, speed, and torque, which can be used to detect the failure in loaded conditions. Below is a brief explanation of the healthy and faulty states for phase current, voltage, torque, and speed: The following Equations (2)–(9) represent the healthy and faulty equations for current, voltage, speed, and torque and are given below:

2.1. Current Analysis

Takethe healthycondition of a motor as ℎ and the defective state (namely, a broken rotor bar) as brb. The mathematical representations for current (I), voltage (V), speed (N), and torque (T) in both healthy and malfunctioning situations are as follows:

2.1.1. Healthy Condition

In a healthy state, take the phase current $I_{ph}$ that is utilized to describe the sinusoidal function:

$$I_{ph}=I_m\sin (\omega t+\varnothing )$$

(4)

2.1.2. Faulty Condition

In a faulty state, take the phase current $I_{ph}$ that is used to represent an additional harmonic fault-induced current component:

$$I_{ph}=I_m\sin (\omega t+\varnothing )+I_f\sin ({\omega }_f\mathrm{t}+{\varnothing }_f)$$

(5)

The amplitude of the fault-induced current is represented by $I_f$, the fault frequency is denoted as ${\omega }_f$, and the phase angle of the fault component is indicated by ${\varnothing }_f$. This equation demonstrates that the failure contributes a novel frequency component to the current signal.

2.2. Voltage Analysis

2.2.1. Healthy Condition

Take voltage $V_{rh}$ in that can be characterized by the following equation when it is in a healthy state:

$$V_{rh}=I_{rh}\left(R_r+j{X}_r\right)+I_{mh}\left(j{X}_m\right)$$

(6)

where $I_{mh}$ represents the magnetizing current, $R_r$ represents the rotor resistance, $X_m$ represents the magnetizing reactance, and $I_{rh}$ represents the rotor current.

2.2.2. Faulty Condition

In a faulty state (broken rotor bars), the voltage in the rotor can be described by:

$$V_{rbrb}=I_{rbrb}\left(R_r+j{X}_r\right)+I_{mbrb}\left(j{X}_m\right)$$

(7)

The rotor current and magnetizing current with broken rotor bars are $I_{rbrb}$ and $I_{mbrb}$, respectively.

2.3. Speed Analysis

2.3.1. Healthy Condition

Take $N_h$ to represent the rotor speed in a healthy state of motor:

$$N_h=\left(1-S_h\right).{\displaystyle \frac{120f}{P}}$$

(8)

The variables in the equation are represented as follows: $S_h$ represents the slip, $f$ for frequency, and $P$ for the number of poles. This equation represents the relationship between the speed of the rotor, the slip, the frequency, and the number of poles in an optimal state.

2.3.2. Faulty Condition

In a faulty state (broken rotor bars), the rotor speed $N_{brb}$ can be described as:

$$N_{brb}=\left(1-S_{brb}\right){\displaystyle \frac{120f_{brb}}{P}}+N_f\mathrm{Sin} (2{\omega }_s\mathrm{t}+{\varnothing }_n)$$

(9)

Under faulty conditions, $f_{brb}$ represents frequency, $S_{brb}$ represents slip, $N_f$ represents the amplitude of fault-induced speed oscillation, ${\omega }_s$ represents synchronous speed frequency, t represents time, and ${\varnothing }_n$ represents fault component phase angle.

2.4. Torque Analysis

2.4.1. Healthy Condition

In the healthy state, $T_h$ can be described as:

$$T_h={\displaystyle \frac{3}{2\pi }}{\displaystyle \frac{P}{S_h}}{\displaystyle \frac{V_{sh}^2}{R_s}}{\displaystyle \frac{S_h}{S_h^2+{(X_s+X_m)}^2}}$$

(10)

In which $P$illustrates the no. of poles, $S_h$ is the slip, $R_s$ is the rotor resistance, $X_s$ is the stator resistance and $X_m$ shows the magnetizing reactance.

2.4.2. Faulty Condition

In faulty state (broken rotor bars), $T_{brb}$ can be described as:

$$T_{brb}={\displaystyle \frac{3}{2\pi }}{\displaystyle \frac{P}{S_{brb}}}{\displaystyle \frac{V_{sbrb}^2}{R_s}}{\displaystyle \frac{S_{brb}}{S_{brb}^2+{(X_s+X_m)}^2}}$$

(11)

where, $S_{brb}$ is the slip under faulty condition, and $V_{sbrb}^2$ are the stator voltages under faulty circumstances. This equation shows how the torque is affected by the presence of broken rotor bars, reflecting changes in the motor’s performance due to the fault.

3. Dynamic SHAP Interaction Feature Selection (DSHAP-IFS) with GBDT

Our research introduces DSHAP-IFS, a novel feature selection technique designed for identifying abnormalities in motor systems. DSHAP-IFS combine SHAP (SHapley Additive exPlanations) values with gradient-boosting decision trees (GBDT). DSHAP-IFS is designed to interact with several electrical signal features, such as current, voltage, speed, and torque, and accurately determine the dynamic significance of these aspects. Selection of effectors: The process refines feature selection iteratively by enhancing SHAP values through feature interactions, hence indicating the features chosen for model training. GBDT is utilized by DSHAP-IFS to accurately detect intricate feature interactions and non-linear relationships within electrical signals. This leads to enhanced modeling accuracy and increased interpretability of the model. Hence, the method given offers a comprehensive understanding of the significance of the features necessary for identifying and choosing important features from the dataset. This knowledge might be valuable in improving the effectiveness of using the dataset to detect abnormalities in motor systems. The proposed approach is shown in Algorithm 1.

Algorithm 1. DSHAP-IFS

Input features ▪ Feature matrix X∈$R^{n\ast 8}$ containing features [Va, Vb, Vc, Ia, Ib, Ic, torque, speed] ▪ Target vector Y ∈${\{0,1\}}^n$ representing Fault types ▪ Iterations: number of iterations for the feature selection process ▪ K: top number of features to be selected Output ▪ $\mathrm{Reduced} \mathrm{feature} \mathrm{matrix} X\_S_k$$, \mathrm{Final} \mathrm{GBDT} \mathrm{model} y\_final$ Initialization ▪ $S^0$ = {Va, Vb, Vc, Ia, Ib, Ic, torque, speed} ▪ $\mathrm{Train} \mathrm{the} \mathrm{GBDT} \mathrm{model}: \widehat{y}=f(X;$Ѳ) ▪ Calculate initial SHAP values: ▪ For each feature j in {Va, Vb, Vc, Ia, Ib, Ic, torque, speed} and each sample i in {1, 2, 3, …, n} through ▪ ${\varnothing }_{i,j}=SHAP(X_{i,j};f; \mathsf{\theta })$: 2. Iterative feature selection ▪ For t = 0 to iterations ▪ Enhance SHAP values with interactions: ▪ $\mathrm{For} \mathrm{each} \mathrm{feature} j \mathrm{in} S^{(t-1)}$ $${\varnothing }_{i,j}^{enhancements}={\varnothing }_{i,j}+\sum _{k\ne j}interaction({\varnothing }_{i,j},{\varnothing }_{i,k})$$ (12) 3. Compute dynamic feature importance $$I_j={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n|{\varnothing }_{i,j}^{enhanced}|$$ (13) ▪ Calculate the average absolute enhanced values. 4. Select features for the next iteration $$S^{(t+1)}=\{j\in N|I_j^{\left(t\right)}\ge {\tau }^{\left(t\right)}\}$$ (14) ▪ $\mathrm{Define} \mathrm{threshold} {\tau }^{\left(t\right)}$ and update the selected features. ▪ $\mathrm{Combine} \mathrm{SHAP} \mathrm{values} \mathrm{to} \mathrm{rank} \mathrm{features} I_j$ and choose the top k attributes with the highest priority values: $$S_k=\{j_1,j_2,\dots ,j_k\},\mathrm{where}, I_{j1>}{I}_{j2>},\dots , I_{jk}$$ (15) ▪ $\mathrm{Train} \mathrm{the} \mathrm{final} \mathrm{GBDT} \mathrm{model} \mathrm{using} \mathrm{only} \mathrm{the} \mathrm{selected} \mathrm{features} S_k$$\mathrm{and} \mathrm{introduce} \mathrm{the} X_{sk}$ be the reduced feature matrix containing only the selected features. $$\widehat{y_{final}}=f(S_k;{\mathsf{\theta }}_{final})$$ (16) 5. Return ▪ $X\_S_k$ ▪ $y\_final$ End algorithm

By capturing more complex feature correlations, dynamic augmentation of SHAP value via feature interactions makes this method distinctive. This strategy can improve feature selection and model performance by providing a more holistic understanding of feature significance. After finding the faulty features in the instantaneous spectrum, the algorithm for selecting and extracting strong features was implemented in the subsequent steps.

• DSHAP-IFS is a novel feature selection technique that leverages the SHAP (Shapley Additive exPlanations) values in combination with gradient-boosting decision trees (GBDT).
• DSHAP-IFS dynamically adjusts the importance of features based on their interaction with other features, allowing for more accurate and comprehensive feature selection.
• By integrating with GBDT, DSHAP-IFS can effectively handle complex feature interactions and non-linear relationships within the data.
• DSHAP-IFS follows an iterative process to enhance feature selection, iteratively updating the importance of features based on their interactions and selecting the top features for model training.
• The combination of DSHAP-IFS with GBDT results in improved model performance by selecting the most relevant features and capturing complex feature interactions.
• One of the main advantages of DSHAP-IFS is that it provides a comprehensive perspective on feature importance, considering not only individual feature importance but also their interactions, hence leading to more robust and interpretable models. A flowchart of DSHAP-IFS is shown in Figure 2.

4. Proposed Technique DSHAP-IFS Model Performance Evaluation Criteria

In analyseslike regression, the model error refers to the inconsistency between the observed assessment in a sample and the values predicted by the regression model. The model’s performance was assessed using the following evaluation criteria:

• Mean Absolute Error (MAE): MAE is just the sum of the difference between the predicted and actual (predicted–actual) values. It gives a clear idea of how our model is performing, irrespective of the bias of the errors.

$$MAE={\displaystyle \frac{1}{n}}{\displaystyle \frac{{\sum }_{i=1}^n|\widehat{y_i}-y_i|}{n}}$$

(17)

• RMSE (Root Mean Squared Error): The RMSE calculates the square root of the average of squared differences between predicted and actual analysis. It puts heavy weight on larger errors than the mean absolute error.

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{(\widehat{y_i}-y_i)}^2}$$

(18)

• MAPE (Mean Absolute Percentage Error): MAPE is the mean absolute percentage error, which is the simplest, and in the machine learning world, it is the amount of error between the predicted values and the true value. It is a comparative measure and expresses accuracy as a percentage.

$$MAPE={\displaystyle \frac{100}{n}}{\sum }_{i=1}^n\left|{\displaystyle \frac{\widehat{y_i}-y_i}{y_i}}\right|$$

(19)

Table 1. Comparison of feature selection techniques with proposed DSHAP-IFS.

Feature Selection Approach	MAE	RMSE	MAPE	Execution Time (s)
Permutation importance	0.612	0.0453	0.039	106.34
LIME	0.577	0.423	0.032	147.83
BORUTA	0.321	0.243	0.021	132.98
MOMI	0.342	0.369	0.018	111.43
LASSO	0.443	0.345	0.029	157.23
SHAP	0.0387	0.401	0.024	102.86
Proposed DSHAP-IFS	0.0317	0.221	0.0031	82.34

shows the summary of different feature selection (FS) methods, consisting of Permutation Importance, LIME, BORUTA, MOMI, LASSO, SHAP, and the introduced DSHAP-IFS approach. The feature importance we calculated uses an algorithm called Permutation Importance to measure the importance of a feature by observing the performance of models run after shuffling (randomizing) feature values. LIME approximates complex model predictions with interpretable models, and this offers local interpretability. The importance of other features is determined by BORUTA against random probes. MOMI simply gives greedy information on which features are leading to the model being more complex (MOMI is a model-agnostic algorithm). LASSO promotes sparsenessin the models by penalizing the coefficients of the features. Interpreting model predictions with SHAP values, the RESHAP-IFS method adds SHAP values togradient-boosting decision trees to improve feature selection. It surpasses all competing methods in accuracy as well as execution time, suggesting it is a promising solution for FS tasks.

Figure 3 shows the DSHAP-IFS feature importance plot, which provides a robust approach to interpreting machine learning model predictions by estimating the contribution of each feature to individual predictions. The graph shows Ib as the top feature from the dataset; red values show high-importance features, and blue values show low-importance features. Observations on the plot provide additional information about which features were important, helping understand the contribution of different input variables to model outcomes and supporting decision-making when deploying and improving the model.

5. Gradient-Boosting Decision Trees Approach

Gradient-boosting decision trees (GBDT) is a machine learning architecture used for regression and classification tasks by generating a prediction model by merging multiple weak prediction models, usually decision trees. The forest of trees grows based on the idea that each new tree learns from the mistakes made by the previous trees and makes corrections accordingly. Ensemble learning refers to the utilization of various machine learning techniques to perform predictive modeling. Gradient-boosting decision trees (GBDT) is an ensemble technique that aims to minimize bias and variation by aggregating the predictions of numerous base estimators [42]. For any dataset having d dimensions and n examples $\mathrm{D}=\left\{\left({\mathrm{x}}_{\mathrm{i},}{\mathrm{y}}_{\mathrm{i}}\right)\right\},$(${\mathrm{x}}_{\mathrm{i}}\mathsf{ϵ}{\mathrm{R}}^{\mathrm{d}},{\mathrm{y}}_{\mathrm{i}}\mathsf{ϵ}$ R, I = 1, 2, 3,…, n), the output F is forecasted as the addition of K additive functions, which is expressed as

$$F_x=\sum _{m=0}^M{\beta }_{m}h(x;\{{R_{lm}}_I^L\left\}\right)$$

(20)

In which h shows a tree by L nodes, and $R_{lm}$ denotes the partitioned region defined by the terminal node l of the m-th tree expansion coefficients M0 are jointly fitted to the training data set with ${\beta }_{m}h$ by minimizing a regularized objective function.

$$\zeta =\sum _i^n\psi (y_i,F(x_i\left)\right)$$

(21)

where $\psi$ a differentiable function for loss that is selected as the squared error this investigation and loss function is minimized by iteratively incorporating leaf nodes that generate the steepest descent, which is mathematically expressed as:

$${\gamma }_{lm}=arg \underset{\gamma }{\min }\sum _{x_i\mathsf{\epsilon }{\mathrm{R}}_{\mathrm{l}\mathrm{m}}}^N\psi (y_i,F_{m-1}\left(x_i\right)+\gamma )$$

(22)

$$F_m\left(x\right)=F_{m-1}\left(x\right)+v{\gamma }_{lm}\left(x_iϵR_{lm}\right)$$

(23)

where the shrinkage factor is $v$ for the range of (0, 1] that regulates the learning rate of the training procedure. Empirically, small attributes of $v$ are advantageous for the model’s preservation and, as a result, contribute to its generalization capability. In conclusion, GBDT is an effective and versatile ensemble learning approach that continues the building of models by iteratively building trees that correct the errors made earlier. It tackles the problem as a single optimization problem to be minimized with gradient descent, which makes it applicable to a very large range of regression and classification tasks. At the heart of the mathematical basis of GBDT, one computes the gradients, fits decision trees to residuals (RFT), and iteratively updates the model to improve performance.

6. Optimized Hyperparameters for Gradient-Boosted Decision Trees: Balancing Model Complexity and Overfitting

Table 2. Optimized hyperparameters for gradient-boosted decision trees (GBDT).

Parameters	Functions of Parameters	Default Value
n_estimators	The precise number of iterations	150
learning_rate	Max depth of every tree to define the learning rate of gradient boosting	0.01
max_depth	Maximum depth of each tree	5
min_samples_split	Minimum No. of samples required to split a node	2
min_samples_leaf	Minimum No. of samples required at a leaf node	7
max_features	Number of features to consider for each split	sqrt
subsample	The fraction of samples used for fitting each tree	0.9
loss	Loss function	deviance
criterion	When performing branching, calculate the impurity index of a weak estimate.	“Friedman_mse”

describes the optimal hyperparameters for the gradient-boosted decision trees (GBDT) tuning, which is designed to balance model complexity and reduce overfitting. The number of estimators (n_estimators), the learning rate (learning_rate), the maximum tree depth (max_depth), the minimum number of samples required to split a node (min_samples_split) and to be a leaf (min_samples_leaf), and the fraction of samples to be used for tree fitting (subsample) are all critical parameters. The loss function, criterion, and max_features hyperparameters are also set to specify the number of features to consider the loss function, and criterion for node separation, respectively. In GBDT models, such parameters ensure a balance between the model complexity and generalization performance per iteration.

7. Experimental Setup for Data Collection and Acquisition

Two identical machines were positioned back-to-back on a shared mechanical base to ensure precise measurements. One of these machines functioned as the load motor, outfitted with an industrial inverter to refine slip precision and control. To minimize its impact, the load-side inverter operated in scalar mode rather than DTC mode. Data collection encompassed various control contexts, including grid-fed, scalar, and direct torque control (DTC). DTC, representing an advanced drive control technique, holds promise for replacing conventional pulse width modulation (PWM) drives. Phase currents were meticulously measured at a sampling frequency of 20 KHz to yield detailed insights. Alternatively, power was supplied to the motor through an industrial inverter operating in direct current mode. Data collection involved diverse conditions, encompassing both healthy states and those featuring one, two, and three damaged rotor bars. The dataset comprised information from induction machines, capturing both normal and damaged rotor bar scenarios. This dataset formed the basis for training machine learning models tailored for fault detection that were categorized into healthy (no broken rotor bar) and faulty data, specifying instances with 1 BRB, 2 BRB, and 3 BRB. The training dataset consisted of 1.2 million samples at a frequency of 20 KHz, each representing a distinct scenario. Additionally, 300,000 samples were reserved for validation purposes. Figure 4 illustrates the healthy and faulty broken rotor bars that are artificially created by the drill to collect data. Figure 4 and Figure 5 showcases the rotors with broken rotor bars and the back-to-back connection of test and loading machines. Meanwhile, Figure 6 outlines the step-by-step procedure of the suggested technique for detecting and classifying abnormalities in BRBs. The parameters of the test machine are given in

Table 3. Main parameters and specifications of the motor under investigation.

Sr.No	Parameter	Symbol	Value
1	Pole Configuration	P	4
2	Phases	$\varnothing$	3
3	Connection	$∆$/Y	Delta/star
4	Stator slots	$N_s$	36 (non-skewed)
5	Rotor slots	$n_r$	28 (skewed)
6	Terminal voltage	$V_s$	690V/400V @ 50 Hz
7	Rated current	$I$	8.8A/13.5A
8	Rated power	$P_r$	7.5 kW @ 50 Hz
9	Rated slip	S	0.0667
10	Rated speed	$N_r$	1500rpm@50Hz

.

Dataset Statistics

The dataset provides comprehensive statistics for detecting broken rotor bars in direct torque-controlled (DTC) induction motors under varying loading conditions. It is organized by fault type, with each fault type monitored at five different loading conditions: 0%, 25%, 50%, 75%, and 100%. Data collection is consistent across all conditions, with a sampling frequency set at 20 kHz. For the healthy condition, the dataset includes 8250 samples, with 1650 samples collected per loading condition. This category represents the motor’s normal operational state without any faults, providing a baseline for comparison. The dataset consists of 8250 samples of motors operating with a single broken rotor bar and consistently dispersed across five different loading conditions. This guarantees a comprehensive description of the motor’s performance across all operational loads. The dataset for two damaged rotor bars consists of 8250 samples, which are used to analyze the behavior under varying levels of the loading parameter. The 3 BRB category comprises an equivalent number of samples, specifically 8250 samples, taken simultaneously under identical loading conditions and sampling frequencies. The dataset comprises a total of 33,000 samples, with an equal distribution across the four fault types (healthy, 1 BRB, 2 BRB, and 3 BRB) and five loading circumstances. Each fault type and loading condition combination includes 1650 samples, ensuring a balanced dataset for robust training and evaluation of machine learning models. The high-resolution data captured at a sampling frequency of 20 kHz is critical for accurately detecting and diagnosing motor faults, providing valuable insights for preventative maintenance and fault prediction in DTC-controlled induction motors. The details of dataset statistics is shown in

Table 4. Class labels and the related conditions for a dataset of DTC-controlled induction motors for BRB diagnosis.

Sr.No	Fault Type	No. of Samples Per Loading Condition	Total Samples	Sampling Frequency (KHz)	Loading Condition (%)	Fault Label
1	Healthy	1650	8250	20	0, 25, 50, 75, 100	Healthy
2	One BRB	1650	8250	20	0, 25, 50, 75, 100	1 BRB
3	Two BRB	1650	8250	20	0, 25, 50, 75, 100	2 BRB
4	Three BRB	1650	8250	20	0, 25, 50, 75, 100	3 BRB

.

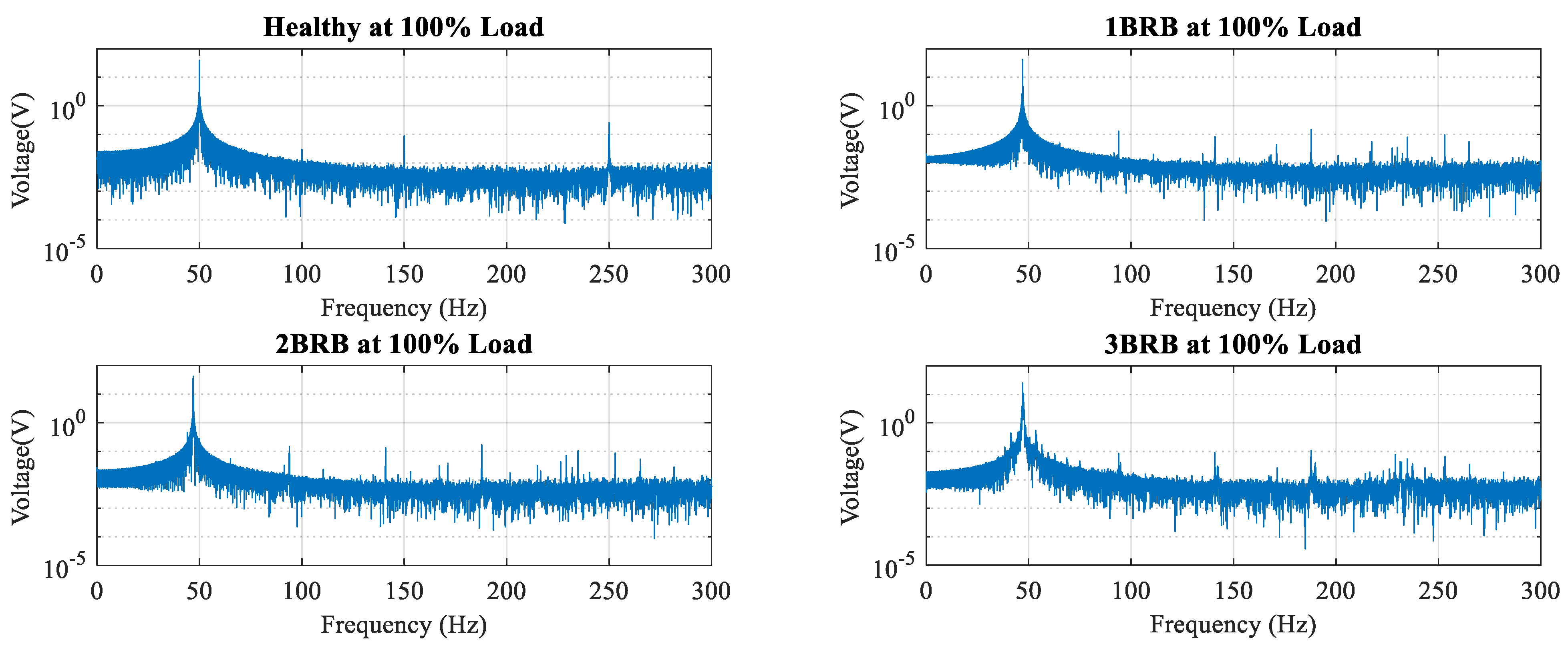
8. Results and Discussion

Figure 6, Figure 7, Figure 8 and Figure 9 represent the frequency spectrum of the motor’s current, voltage, speed, and torque underdifferent loading circumstances. As the system load progressively rises from 0% to 100%, many parameters, including current, voltage, torque, and speed, undergo alterations in their spectral characteristics. These changes are evident as a rise in the occurrence of harmonics surrounding the primary frequency component, usually seen at about 50 Hz in the current and voltage signal spectrum. More specifically, these harmonics represent sidebands known as the left-side band (LSB) and right-side band (LSB) around the center frequency. The left-side band is the lower frequency, and the right-side band is the higher frequency. The appearance and strengthening of these harmonics in the signal spectrum demonstrate the impact of load variation on the electrical system, which is of great importance for understanding the system’s behavior and performance in different operating conditions. The fast Fourier transform (FFT) analysis of current, voltage, speed, and torque signals for different conditions (healthy, 100% load, 1 BRB, 2 BRB, and 3 BRB phase unbalance) is an indispensable tool to investigate the operating performance and fault conditions of induction motors. Whenever the motor is healthy and operating at full load, the FFT will also show the highest frequency components for the normal motor mode of operation. Introducing one broken rotor bar (BRB) results in additional frequency components indicative of the fault, with further changes observed in the presence of two or three broken rotor bars. By comparing the FFT results across different conditions, characteristic frequency signatures of rotor bar faults emerge, enabling effective diagnosis and assessment of fault severity in induction motors, thereby facilitating condition monitoring and maintenance strategies for optimal motor performance and reliability. In the context of induction motor operation, as the load increases from 0% to 100%, the amplitude of harmonics around the fundamental component tends to increase. The fundamental component, typically appearing at 50Hz in power systems operating at 50 Hz, represents the primary frequency associated with the motor’s rotational speed. This phenomenon can be attributed to the non-linear behavior of the motor under varying load conditions, which leads to the generation of additional harmonics in the current, voltage, speed, and torque signals. As the load increases, the motor experiences greater magnetic flux variations and saturation effects, resulting in non-sinusoidal waveforms with enhanced harmonic content. This observation is consistent with the principles of electrical machinery and power system analysis, where load variations impact the spectral characteristics of motor signals due to changes in operating conditions and system dynamics. Such findings contribute to the academic understanding of motor behavior and provide insights into the effects of load variations on harmonic distortion in induction motors, offering implications for motor performance assessment and condition monitoring strategies in practical applications. Figure 7, Figure 8, Figure 9 and Figure 10 illustrate the frequency domain analysis of current, voltage, torque, and speed signals for healthy, 1 BRB, 2 BRB, and 3 BRB at different full-load scenarios.

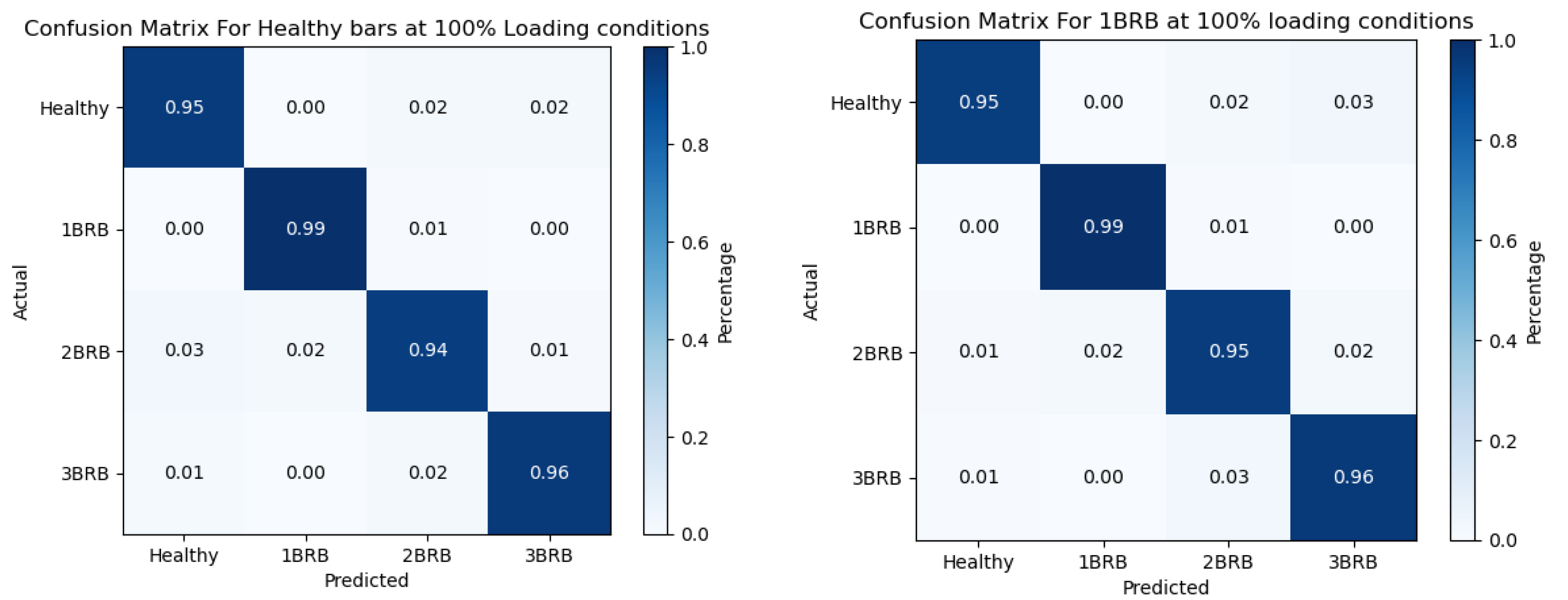
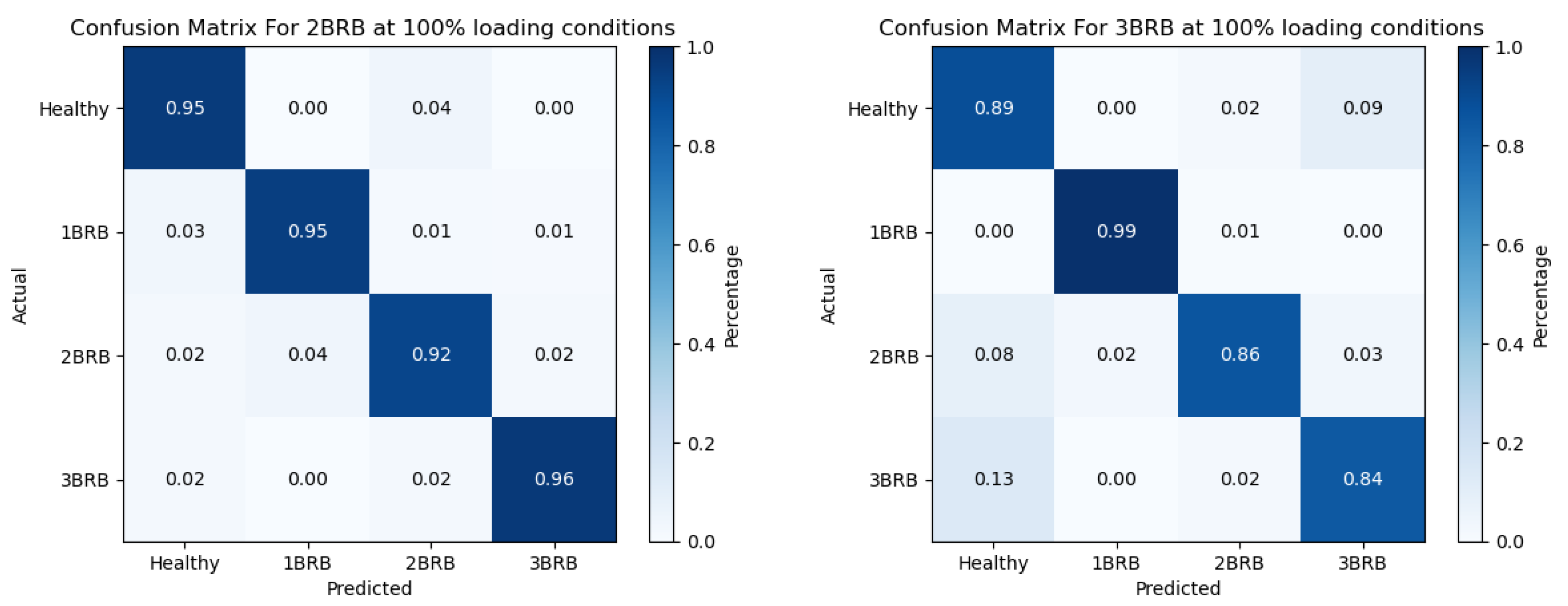
The confusion matrix illustrates the classification performance of a machine learning model in distinguishing between healthy and faulty rotor bar conditions in induction motors operating at 100% load. Therefore, a properly functioning and robust system would be the most precise, as it correctly identified the highest percentage of healthy rotor bars as healthy. The classification accuracy diminishes as the fault severity escalates from 1 BRB to 2 BRB and 3 BRB, indicating greater difficulty in determining the presence and kind of rotor bar faults. The expected performance of the model can be assessed using the confusion matrix, which provides a concise overview of the true positive, true negative, false positive, and false negative classifications of rotor bar circumstances. An in-depth analysis of the confusion matrix will be conducted to gain a comprehensive understanding of the model’s ability to detect and categorize various fault scenarios. This analysis aims to improve fault diagnosis and condition monitoring strategies for induction motors operating under diverse load conditions. Figure 11 shows the confusion matrix analysis for a healthy state and faulty states (1 BRB, 2 BRBs, and 3 BRBs) at 100% loading circumstances.

A ROC curve describes the classification model’s ability to differentiate between normal and defective rotor bar conditions in induction motors. The curves are presented for three fault levels: 1 BRB, 2 BRB, and 3 BRB. A receiver operating characteristic (ROC) curve illustrates the relationship between the sensitivity (true positive rate) and the specificity (1—false positive rate) of a classification model when the threshold for classifying data points varies. The ROC curves in this study assess the model’s capacity to correctly identify true-positive cases while minimizing false-positive detections across various fault scenarios. An ideal classification model will have an ROC curve that roughly aligns with the upper-left corner of the plot, indicating a high level of sensitivity and a low rate of false positives. By analyzing the ROC curves of healthy and faulty rotor bars, we may obtain vital information about the model’s capacity to effectively identify rotor bar faults of different levels of severity in various operating settings. Figure 12 shows the receiver operating characteristic curves for a healthy state: 1 BRB, 2BR, and 3 BRB at 100% loading conditions.

Table 5. Performance measures for healthy bars under various loading conditions.

Load (%)	Accuracy	Precision	Recall	F1 Score
At 0% Load	1.00	0.9638	0.9639	0.9639
At 25% Load	1.00	0.9646	0.9647	0.9647
At 50% Load	1.00	0.966	0.9662	0.9661
At 75% Load	1.00	0.9652	0.9654	0.9653
At 100% Load	1.00	0.9638	0.9639	0.9639

,

Table 6. Performance measures for 1 BRB under various loading conditions.

Load (%)	Accuracy	Precision	Recall	F1 Score
At 0% Load	0.9978	0.9638	0.9639	0.9639
At 25% Load	0.9971	0.9646	0.9647	0.9647
At 50% Load	0.9961	0.9660	0.9662	0.9661
At 75% Load	0.9968	0.9652	0.9654	0.9653
At 100% Load	0.9965	0.9638	0.9639	0.9639

,

Table 7. Performance measures for 2 BRBs under various loading conditions.

Load (%)	Accuracy	Precision	Recall	F1 Score
At 0% Load	0.9865	0.9642	0.9639	0.9642
At 25% Load	0.9745	0.9641	0.9637	0.9639
At 50% Load	0.9853	0.9639	0.9639	0.9637
At 75% Load	0.9843	0.9642	0.9636	0.9631
At 100% Load	0.9798	0.9642	0.9631	0.9633

and

Table 8. Performance measures for 3 BRBs under various loading conditions.

Load (%)	Accuracy	Precision	Recall	F1 Score
At 0% Load	0.9764	0.9444	0.9421	0.9411
At 25% Load	0.9843	0.9442	0.9433	0.9418
At 50% Load	0.9647	0.9443	0.9427	0.9423
At 75% Load	0.9764	0.9441	0.9431	0.9412
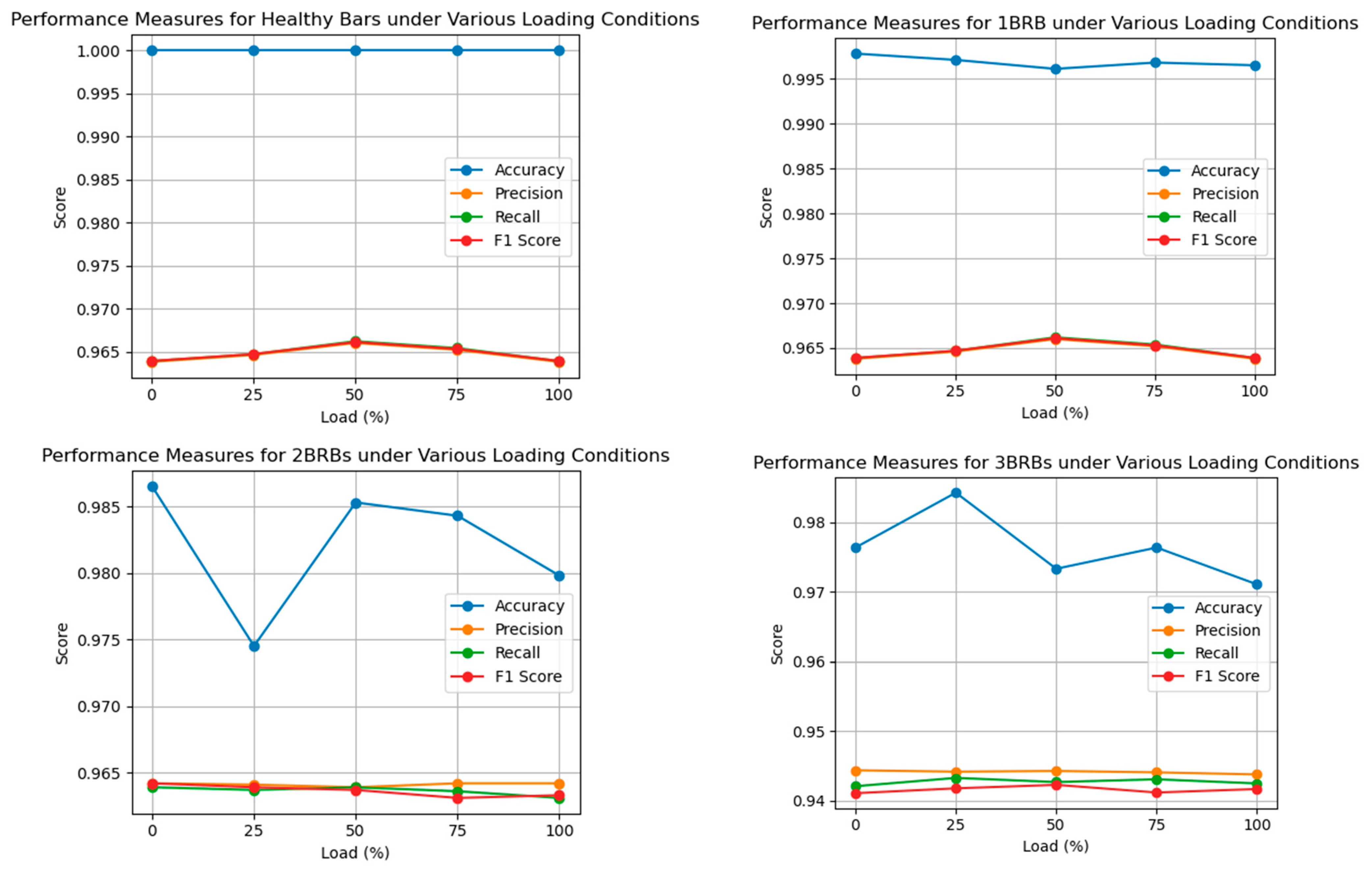
At 100% Load	0.9867	0.9438	0.9425	0.9417

demonstrate the performance metrics for the intact rotor bars and various fault scenarios (1 BRB, 2 BRBs, and 3 BRBs) when the induction motor operates at different load levels ranging from 0% to 100%. The tables collectively illustrate the classification model’s performance metrics—accuracy, precision, recall, and F1 score—under various loading conditions for healthy rotor bars and rotor bars with one, two, and three broken bars (1 BRB, 2 BRBs, and 3 BRBs). For healthy rotor bars, the model demonstrates exceptional performance, achieving perfect accuracy and high precision, recall, and F1 scores across all load levels. The consistent achievement of performance measures with accuracy levels exceeding 99% for healthy rotor bars signifies that the model possesses the capability to accurately and precisely classify these bars amidst varying loads. Specifically, the accuracy falls a bit when looking at the 1 BRB conditions, but the precision, recall, and F1 scores are consistent and high, showing the model is working relatively well. Weight fall of the fault impact increases to 2 BRBs, down accuracy to 2 BRBs, and the minimized precision, recall, and F1 scores alsoshowthat the difficulty of fault detection rises from healthy to faulty conditions. For 4BRBs, the performance of the proposed model drops significantly due to even lower precision, recall, and F1 scores as well as reduced accuracy compared to 3 BRBs, indicating that this model faces more difficulties in identifying and classifying severe faults under stress conditions. These requirements highlight the importance of developing powerful algorithms that not only work effectively for a wide range of fault scenarios but also ensure that high performance is maintained, hence enabling good fault diagnostics and condition monitoring in real industrial machinery. We employ these tables to assess the performance of powerful fault-tracing algorithms on real industrial machinery. Makarov and Goresky highlight the importance of operational conditions and fault severity in the establishment of successful fault diagnosis and condition monitoring schemes.

The performance measures during the detection and classification of 3 BRBs (broken rotor bars) in direct torque-controlled (DTC) induction motors under different loading conditions are illustrated in Figure 13. The rows correspond to a percentage of load from 0% to 100%. Accuracy, precision, recall, and F1 score: These are the metrics that will be used to calculate the performance of the classification model. 0% load: It means that the model indicates the actual condition 98.64% of the time, whetherthe part is healthy or faulty. Consequently, we have obtained high test accuracy, e.g., precision, recall, and F1 score metrics show consistent performance, ranging from 94.11% to 94.38%. In general, the results presented show that the approach using dynamic SHAP feature selection with GBDT can decently identify cracked rotor bars in DTC induction motors at different load conditions. The high accuracy, precision, recall, and F1 score metrics highlight the reliability of the classification model, enlarging itsin predicting maintenance and fault prevention of industrial drive systems.

9. Conclusions and Future Recommendations

This research presents an improved and advanced diagnostic approach for the detection and classification of broken rotor bars in direct torque-controlled (DTC) induction motors by leveraging the dynamic SHAP interaction feature selection (DSHAP-IFS) methodology in conjunction with gradient-boosting decision trees (GBDT). The suggested technique represents significant efficiency in identifying and classifying the rotor bar defects under various loading conditions (0%, 25%, 50%, 75%, and 100%). Through extensive feature engineering and the application of improved SHAP-based feature selection, the methodology effectively isolates informative features from current, voltage, speed, torque, and motor characteristics, leading to high-performance classification. The results indicate a remarkable accuracy rate of 99% across all loading scenarios, showcasing the potential of this approach for reliable fault detection and condition monitoring in industrial machinery. This method not only enhances the precision of fault diagnosis but also contributes to the sustainability and operational efficiency of induction motors by enabling proactive maintenance strategies. The proposed SHAP-fusion GBDT approach marks a significant advancement in machine learning applications for motor anomaly detection, providing a robust solution for ensuring the dependability and longevity of DTC-controlled induction motors. It also improves the reliability of DTC-controlled induction motors. The effective use of the SHAP-Fusion GBDT approach in this study paves the way for its use in other fault diagnosis and predictive maintenance in various process sectors. Machine learning can be utilized alongside advanced feature selection techniques such as SHAP, allowing for the practical implementation of data-driven approaches to improve operational efficiency and system reliability, allowing for future development and expansion. The following list outlines several future recommendations that will help researchers proceed with the work for the proposed methodology:

• Investigate the integration of real-time monitoring capabilities into the diagnostic framework to enable proactive fault mitigation strategies.
• Explore the scalability and computational efficiency of the SHAP-Fusion GBDT methodology for deployment in large-scale industrial environments.
• Conduct further research to enhance the interpretability of SHAP-based feature selection and its implications for understanding the diagnostic process.
• Extend the evaluation of the diagnostic approach to different motor types, operating conditions, and fault severities to enhance its versatility and applicability.
• Investigate the potential integration of predictive maintenance capabilities to enable predictive fault detection and maintenance scheduling.