Investigation of the Electrical Impedance Signal Behavior in Rolling Element Bearings as a New Approach for Damage Detection
Abstract
1. Introduction
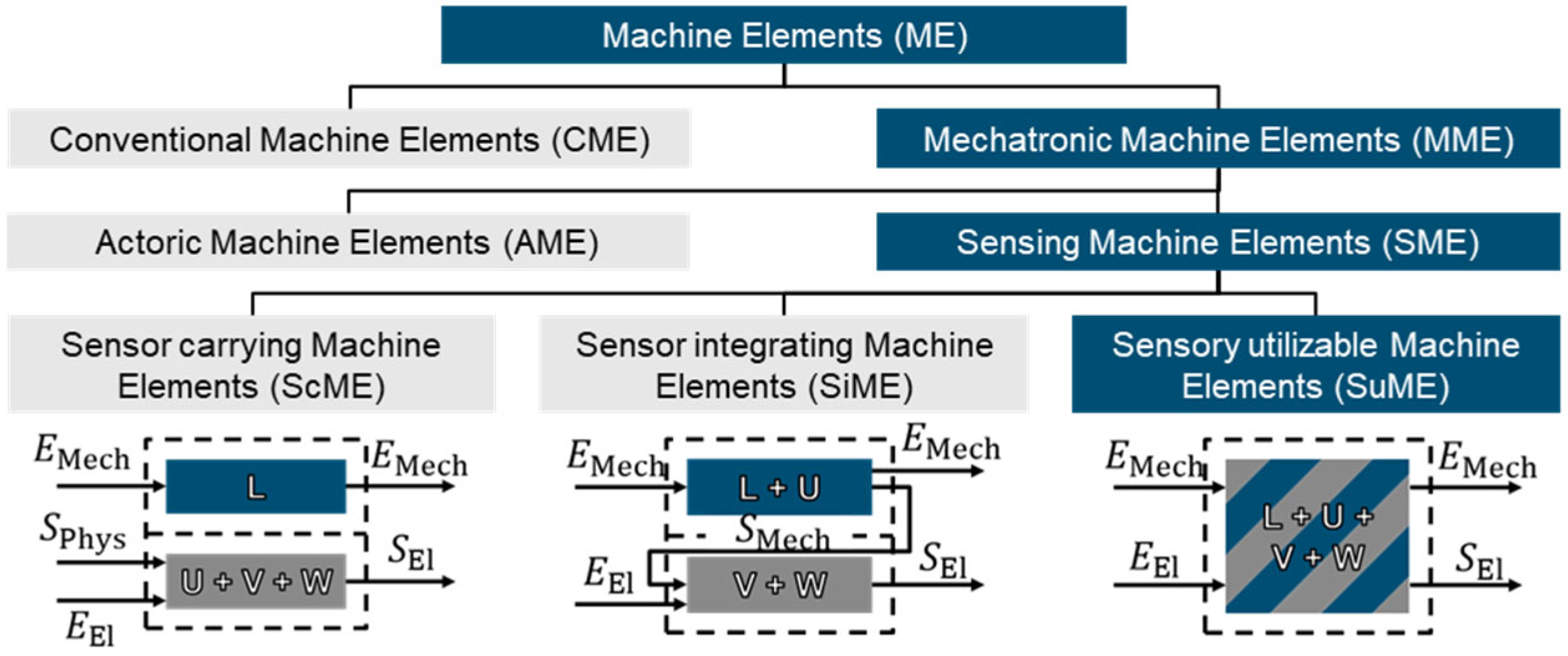
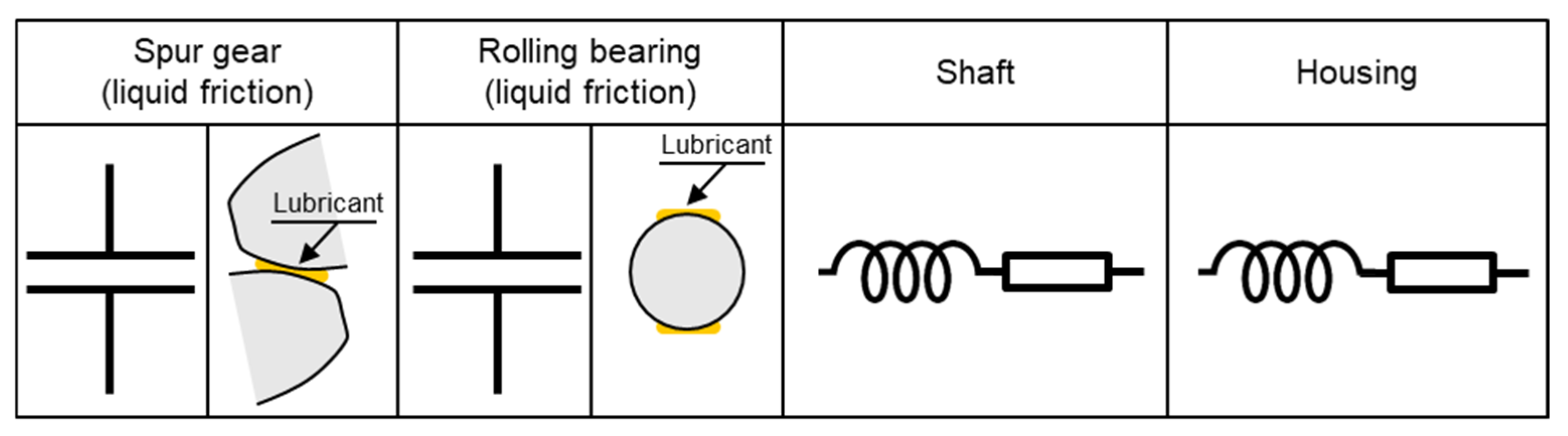
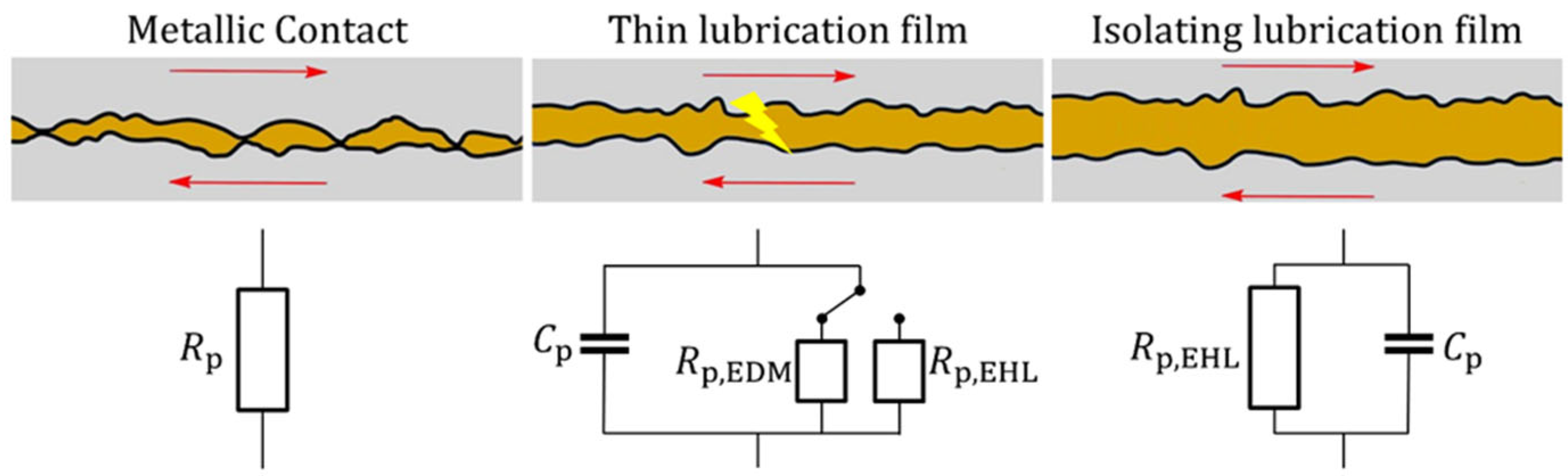
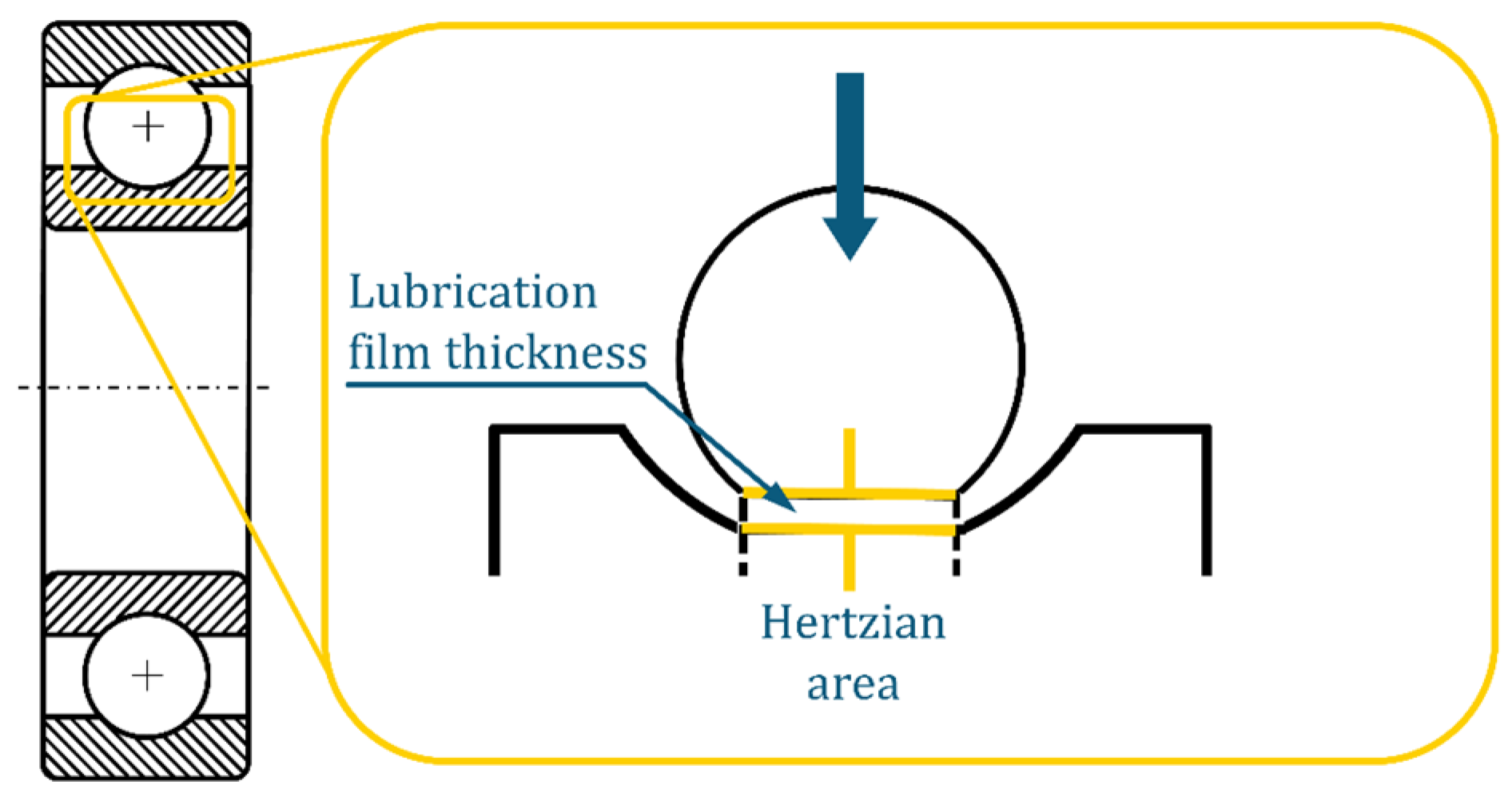
1.1. Electrical Properties of Rolling Element Bearings
1.2. Impedance-Based Condition Monitoring of Rolling Element Bearings
- How can impedance signals and their features be modified to optimize the impedance-based early damage detection for rolling element bearings?
- How does the impedance signal feature change under combined axial and radial load?
- How do impedance signal features behave for different bearing types in case of point contact?
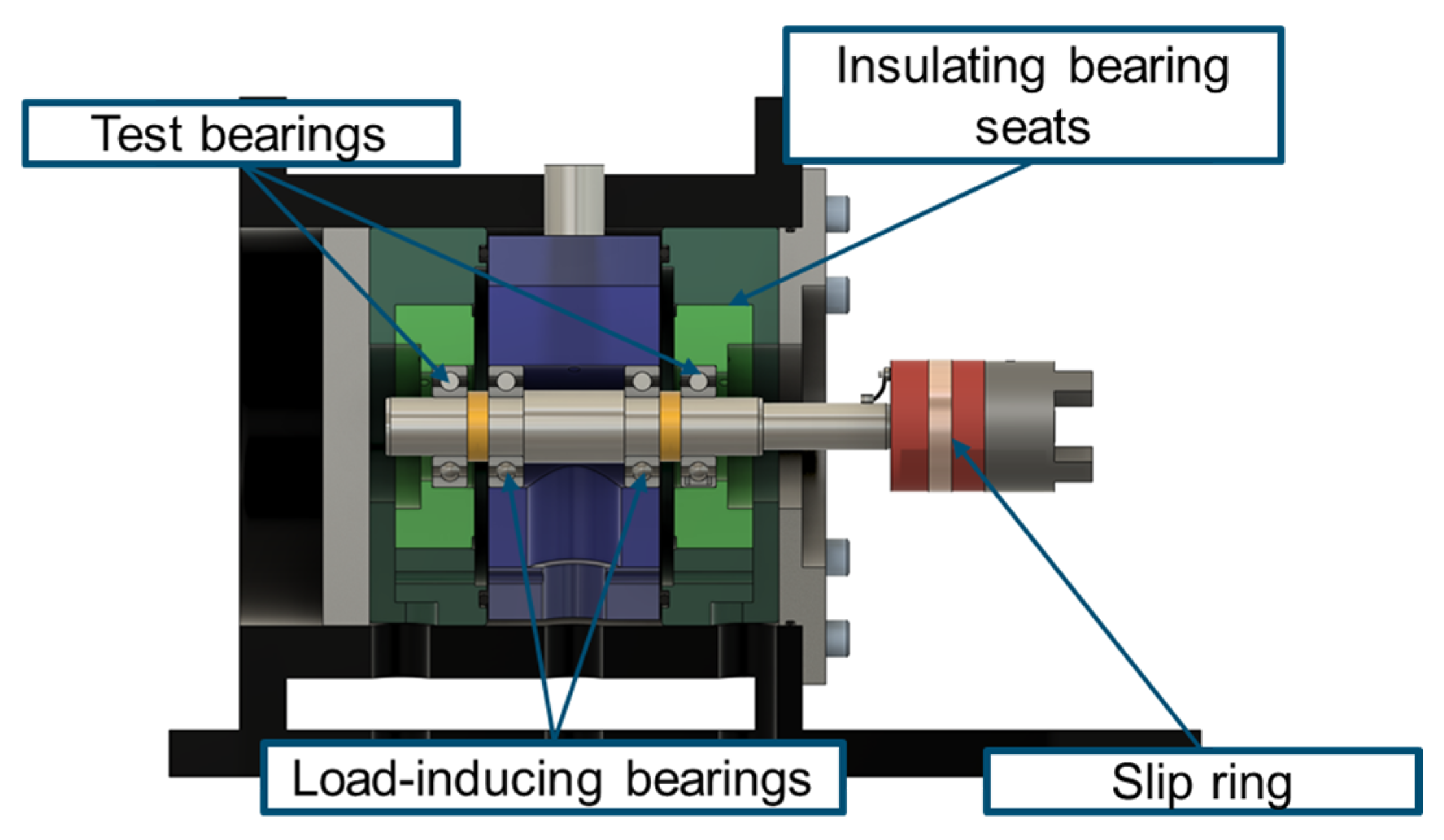
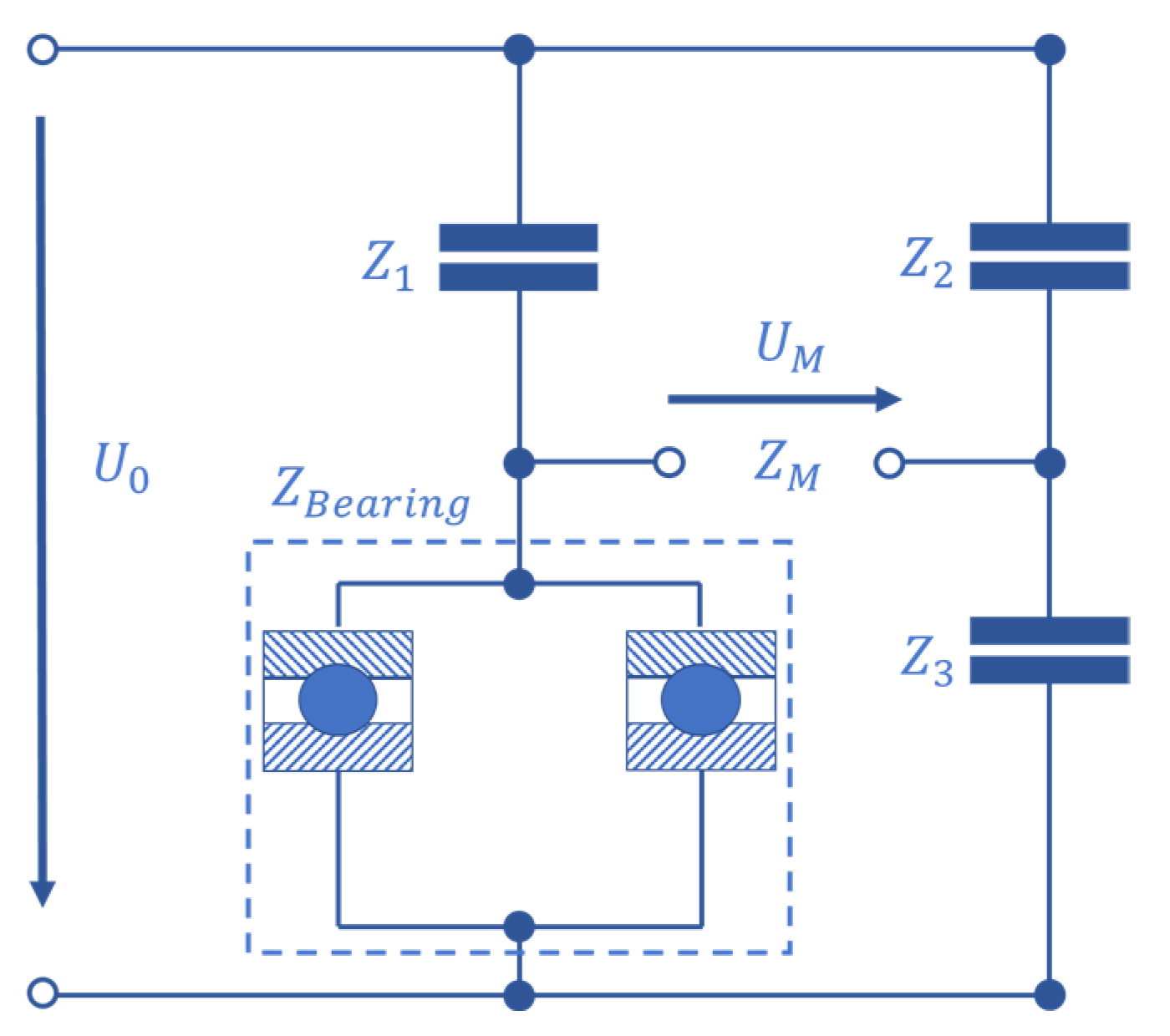
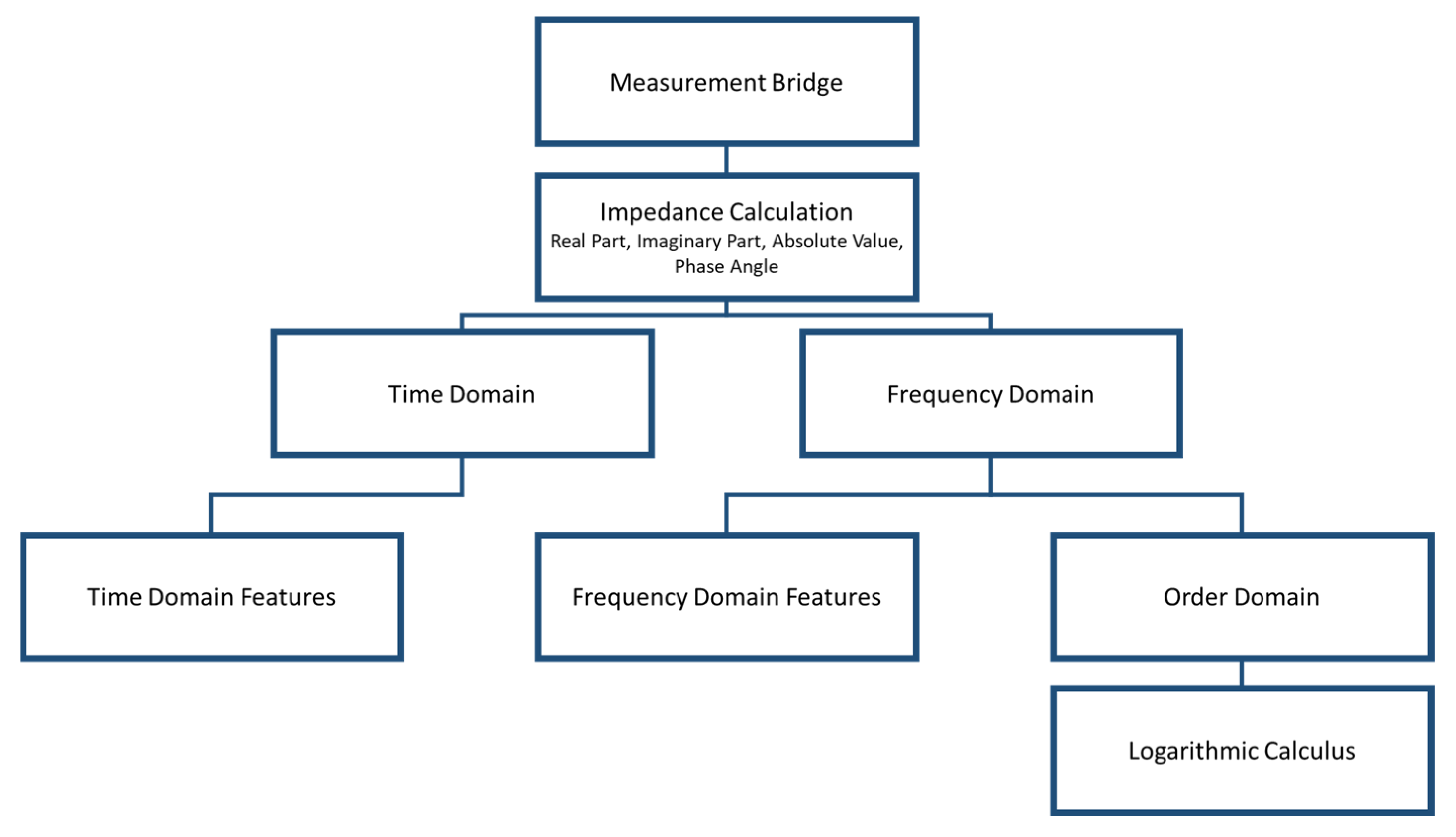
2. Materials and Methods
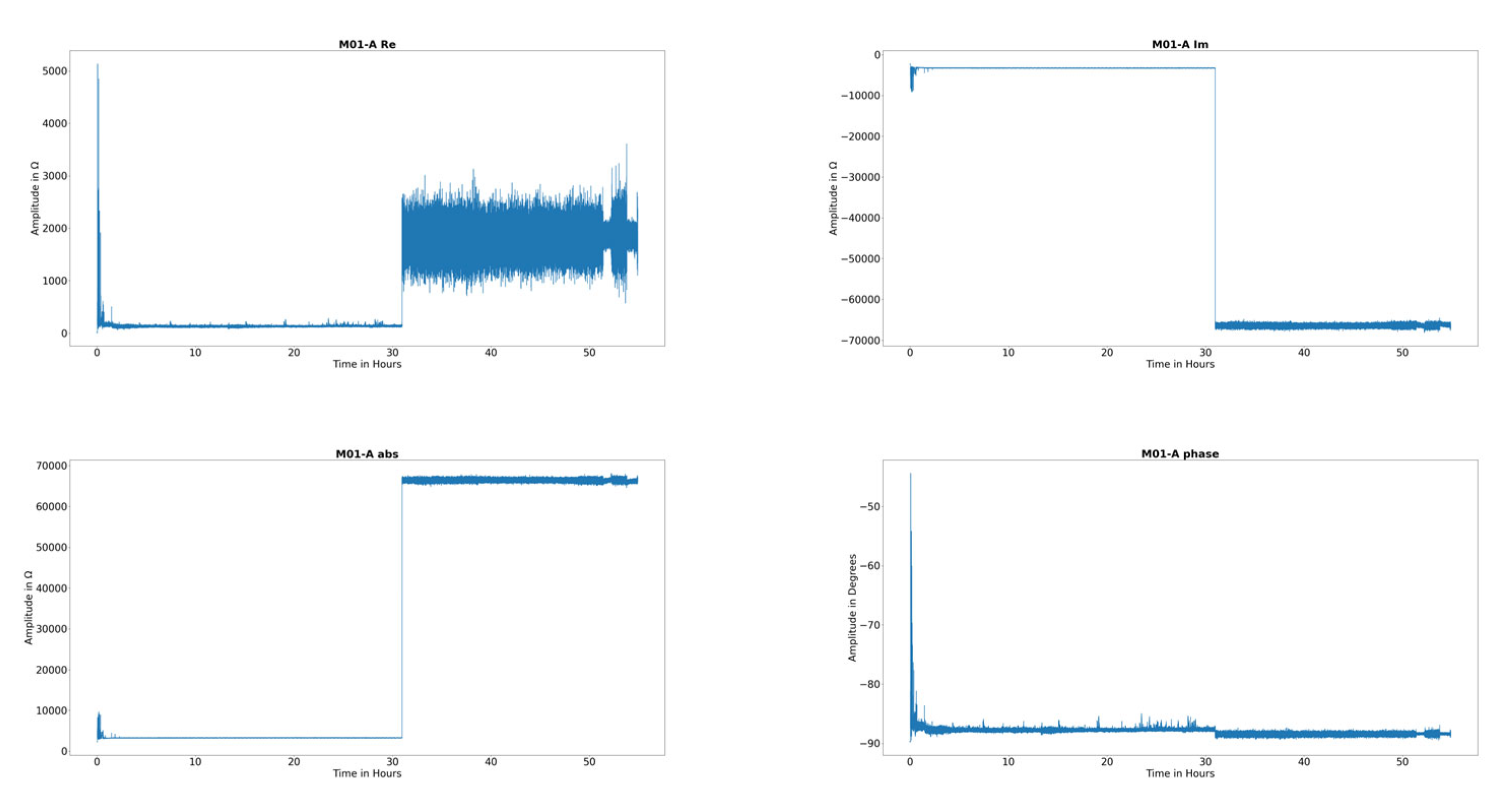
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Davies, A. Handbook of Condition Monitoring; Chapman & Hall: London, UK, 1998. [Google Scholar] [CrossRef]
- Cameron, J.R.; Thomson, W.T.; Dow, A.B. Vibration and current monitoring for detecting airgap eccentricity in large induction motors. IEE Proc. B Electr. Power Appl. 1986, 133, 155–163. [Google Scholar] [CrossRef]
- Jardine, A.K.; Lin, D.; Banjevic, D. A review on machinery diagnostics and prognostics implementing condition-based maintenance. Mech. Syst. Signal Process. 2006, 20, 1483–1510. [Google Scholar] [CrossRef]
- Schaeffler Monitoring Services GmbH. Condition Monitoring Praxis: Handbuch zur Schwingungs-Zustandsüberwachung von Maschinen und Anlagen; 1. Auflage; Vereinigte Fachverlage GmbH: Mainz, Germany, 2019; ISBN 978-3-7830-0419-9. [Google Scholar]
- Harris, T.A. Rolling Bearing Analysis, 4th ed.; Wiley: New York, NY, USA, 2001; ISBN 0-471-35457-0. [Google Scholar]
- Randall, R.B. Vibration-Based Condition Monitoring: Industrial, Aerospace and Automotive Applications; Wiley: Chichester, UK, 2011; ISBN 978-0-470-97765-1. [Google Scholar]
- Schenk, M. (Ed.) Instandhaltung technischer Systeme: Methoden und Werkzeuge zur Gewährleistung eines sicheren und wirtschaftlichen Anlagenbetriebs; Springer: Berlin, Germany, 2010; ISBN 978-3-642-03948-5. [Google Scholar]
- Łuczak, D. Machine Fault Diagnosis through Vibration Analysis: Time Series Conversion to Grayscale and RGB Images for Recognition via Convolutional Neural Networks. Energies 2024, 17, 1998. [Google Scholar] [CrossRef]
- Bienefeld, C.; Becker-Dombrowsky, F.M.; Shatri, E.; Kirchner, E. Investigation of Feature Engineering Methods for Domain-Knowledge-Assisted Bearing Fault Diagnosis. Entropy 2023, 25, 1278. [Google Scholar] [CrossRef] [PubMed]
- Lei, Y. Intelligent Fault Diagnosis and Remaining Useful Life Prediction of Rotating Machinery; Elsevier: Oxford, UK, 2016; ISBN 978-0-12-811534-3. [Google Scholar]
- Lei, Y.; He, Z.; Zi, Y. A new approach to intelligent fault diagnosis of rotating machinery. Expert Syst. Appl. 2008, 35, 1593–1600. [Google Scholar] [CrossRef]
- Akpudo, U.E.; Hur, J.-W. A feature fusion-based prognostics approach for rolling element bearings. J. Mech. Sci. Technol. 2020, 34, 4025–4035. [Google Scholar] [CrossRef]
- Bienefeld, C.; Vogt, A.; Kacmar, M.; Kirchner, E. Feature-Engineering für die Zustandsüberwachung von Wälzlagern mittels maschinellen Lernens. TuS 2021, 68, 5–11. [Google Scholar] [CrossRef]
- Miller, J.L.; Kitaljevich, D. In-line oil debris monitor for aircraft engine condition assessment. In Proceedings of the 2000 IEEE Aerospace Conference. Proceedings (Cat. No.00TH8484), Big Sky, MT, USA, 25 March 2000; pp. 49–56. [Google Scholar] [CrossRef]
- Thomson, W.T.; Barbour, A. On-line current monitoring and application of a finite element method to predict the level of static airgap eccentricity in three-phase induction motors. IEEE Trans. Energy Convers. 1998, 13, 347–357. [Google Scholar] [CrossRef]
- Engelhardt, R.A. Uncertainty Mode and Effects Analysis—Heuristische Methodik zur Analyse und Beurteilung von Unsicherheiten in technischen Systemen des Maschinenbaus. Ph.D. Dissertation, Technische Universität Darmstadt, Darmstadt, Germany, 2012. [Google Scholar]
- Vorwerk-Handing, G. Erfassung systemspezifischer Zustandsgrößen—Physikalische Effektkataloge zur systematischen Identifikation potentieller Messgrößen. Ph.D. Dissertation, Technische Universität Darmstadt, Darmstadt, Germany, 2020. [Google Scholar]
- Furtmann, A.; Tischmacher, H.; Poll, G. Extended HF equivalent model of a drive train. In International Conference on Electrical Machines (ICEM): SwissTech Convention Center, Lausanne, Switzerland, 4–7 September 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 2244–2250. ISBN 978-1-5090-2538-1. [Google Scholar]
- Furtmann, A.; Poll, G. Evaluation of Oil-Film Thickness Along the Path of Contact in a Gear Mesh by Capacitance Measurement. Tribol. Online 2016, 11, 189–194. [Google Scholar] [CrossRef]
- Becker-Dombrowsky, F.M.; Hausmann, M.; Welzbacher, P.; Harder, A.; Kirchner, E. Systematic identification of disturbance factors on electric characteristics of mechanical gearboxes. Forsch. Ingenieurwes 2023, 87, 399–410. [Google Scholar] [CrossRef]
- Furtmann, A. Elektrisches Verhalten von Maschinenelementen im Antriebsstrang. Ph.D. Dissertation, Gottfried Wilhelm Leibniz Universität Hannover, Hannover, Germany, 2017. [Google Scholar]
- Prashad, H. Tribology in Electrical Environments; Elsevier: Amsterdam, The Netherlands; London, UK, 2006; ISBN 978-0-444-51880-4. [Google Scholar]
- Prashad, H. Theoretical evaluation of impedance, capacitance and charge accumulation on roller bearings operated under electrical fields. Wear 1988, 125, 223–239. [Google Scholar] [CrossRef]
- Muetze, A. Bearing Currents in Inverter-Fed AC-Motors. Ph.D. Dissertation, Technische Universität Darmstadt, Darmstadt, Germany, 2003. [Google Scholar]
- Gemeinder, Y. Lagerimpedanz und Lagerschädigung bei Stromdurchgang in umrichtergespeisten elektrischen Maschinen. Ph.D. Dissertation, Technische Universität Darmstadt, Darmstadt, Germany, 2016. [Google Scholar]
- Martin, G. Die Wälzlagerimpedanz als Werkzeug zur Untersuchung von Oberflächenabweichungen in Wälzlagern. Ph.D. Dissertation, Technische Universität Darmstadt, Darmstadt, Germany, 2021. [Google Scholar]
- Schirra, T. Phänomenologische Betrachtung der sensorisch nutzbaren Effekte am Wälzlager: Einfluss unbelasteter Wälzkörper auf die elektrische Impedanz. Ph.D. Dissertation, Technische Universität Darmstadt, Darmstadt, Germany, 2020. [Google Scholar]
- Harder, A.; Zaiat, A.; Becker-Dombrowsky, F.M.; Puchtler, S.; Kirchner, E. Investigation of the Voltage-Induced Damage Progression on the Raceway Surfaces of Thrust Ball Bearings. Machines 2022, 10, 832. [Google Scholar] [CrossRef]
- Schirra, T.; Martin, G.; Vogel, S.; Kirchner, E. Ball bearings as sensors for systematical combination of load and failure monitoring. In Design 2018: Proceedings of the 15th International Design Conference, May 2018, Dubrovnik, Croatia; Marjanović, D., Štorga, M., Škec, S., Bojčetić, N., Pavković, N., Eds.; Faculty of Mechanical Engineering and Naval Architecture, University of Zagreb: Zagreb, Croatia, 2018; pp. 3011–3022. ISBN 978-953-7738-59-4. [Google Scholar]
- Tuomas, R.; Isaksson, O. Measurement of lubrication conditions in a rolling element bearing in a refrigerant environment. Ind. Lubr. Tribol. 2009, 61, 91–99. [Google Scholar] [CrossRef]
- Shi, H.; Zhang, H.; Huo, D.; Yu, S.; Su, J.; Xie, Y.; Li, W.; Ma, L.; Chen, H.; Sun, Y. An Ultrasensitive Microsensor Based on Impedance Analysis for Oil Condition Monitoring. IEEE Trans. Ind. Electron. 2022, 69, 7441–7450. [Google Scholar] [CrossRef]
- Zeng, L.; Wang, W.; Rogers, F.; Zhang, H.; Zhang, X.; Yang, D. A High Sensitivity Micro Impedance Sensor Based on Magnetic Focusing for Oil Condition Monitoring. IEEE Sens. J. 2020, 20, 3813–3821. [Google Scholar] [CrossRef]
- Becker-Dombrowsky, F.M.; Kirchner, E. Electrical impedance based condition monitoring of machine elements—A systematic review. Front. Mech. Eng. 2024, 10, 1412137. [Google Scholar] [CrossRef]
- Cen, H.; Bai, D.; Chao, Y.; Li, Y.; Li, R. EHL film thickness in rolling element bearings evaluated by electrical capacitance method: A review. Tribol.—Mater. Surf. Interfaces 2021, 15, 55–77. [Google Scholar] [CrossRef]
- Clarke, A.; Weeks, I.; Evans, H.P.; Snidle, R.W. An investigation into mixed lubrication conditions using electrical contact resistance techniques. Tribol. Int. 2016, 93, 709–716. [Google Scholar] [CrossRef]
- Dyson, A. Investigation of the Discharge-Voltage Method of Measuring the Thickness of Oil Films Formed in a Disc Machine under Conditions of Elastohydrodynamic Lubrication. Proc. Inst. Mech. Eng. 1966, 181, 633–652. [Google Scholar] [CrossRef]
- Jablonka, K.; Glovnea, R.; Bongaerts, J. Evaluation of EHD films by electrical capacitance. J. Phys. D Appl. Phys. 2012, 45, 385301. [Google Scholar] [CrossRef]
- Maruyama, T.; Maeda, M.; Nakano, K. Lubrication Condition Monitoring of Practical Ball Bearings by Electrical Impedance Method. Tribol. Online 2019, 14, 327–338. [Google Scholar] [CrossRef]
- Maruyama, T.; Radzi, F.; Sato, T.; Iwase, S.; Maeda, M.; Nakano, K. Lubrication Condition Monitoring in EHD Line Contacts of Thrust Needle Roller Bearing Using the Electrical Impedance Method. Lubricants 2023, 11, 223. [Google Scholar] [CrossRef]
- Maruyama, T.; Nakano, K. In Situ Quantification of Oil Film Formation and Breakdown in EHD Contacts. Tribol. Trans. 2018, 61, 1057–1066. [Google Scholar] [CrossRef]
- Schirra, T.; Martin, G.; Puchtler, S.; Kirchner, E. Electric impedance of rolling bearings—Consideration of unloaded rolling elements. Tribol. Int. 2021, 158, 106927. [Google Scholar] [CrossRef]
- Becker-Dombrowsky, F.M.; Koplin, Q.S.; Kirchner, E. Individual Feature Selection of Rolling Bearing Impedance Signals for Early Failure Detection. Lubricants 2023, 11, 304. [Google Scholar] [CrossRef]
- Chevallier, E.; Boudimbou, J.C.; Bouzerar, R.; Garcia, T.; Bolaers, F.; Chiementin, X. Monitoring of roller bearings: Electrical vs vibrational analysis. preprint 2023. [Google Scholar] [CrossRef]
- Martin, G.; Becker, F.M.; Kirchner, E. A novel method for diagnosing rolling bearing surface damage by electric impedance analysis. Tribol. Int. 2022, 170, 107503. [Google Scholar] [CrossRef]
- Schnabel, S.; Marklund, P.; Minami, I.; Larsson, R. Monitoring of Running-in of an EHL Contact Using Contact Impedance. Tribol. Lett. 2016, 63, 35. [Google Scholar] [CrossRef]
- Dahlke, H. Handbuch Wälzlager-Technik: Bauarten, Gestaltung, Betrieb; Springer Fachmedien: Wiesbaden, Germany, 1994; ISBN 978-3-663-01973-2. [Google Scholar]
- Deutsches Institut für Normung e.V. Wälzlager: Dynamische Tragzahlen und Nominelle Lebensdauer; 21.100.20 (281); Deutsches Institut für Normung e.V.: Berlin, Germany, 2021. [Google Scholar]
- Soviany, S.; Soviany, C. Feature Engineering. In Principles of Data Science, 1st ed.; Arabnia, H.R., Daimi, K., Stahlbock, R., Soviany, C., Heilig, L., Brüssau, K., Eds.; Springer International Publishing, Imprint Springer: Cham, Swizerland, 2020; pp. 79–103. ISBN 978-3-030-43981-1. [Google Scholar]
- Puchtler, S.; van der Kuip, J.; Kirchner, E. Analyzing Ball Bearing Capacitance Using Single Steel Ball Bearings. Tribol. Lett. 2023, 71. [Google Scholar] [CrossRef]
- Heemskerk, R.S.; Vermeiren, K.N.; Dolfsma, H. Measurement of Lubrication Condition in Rolling Element Bearings. ASLE Trans. 1982, 25, 519–527. [Google Scholar] [CrossRef]
- Jablonka, K.; Glovnea, R.; Bongaerts, J. Quantitative measurements of film thickness in a radially loaded deep-groove ball bearing. Tribol. Int. 2018, 119, 239–249. [Google Scholar] [CrossRef]

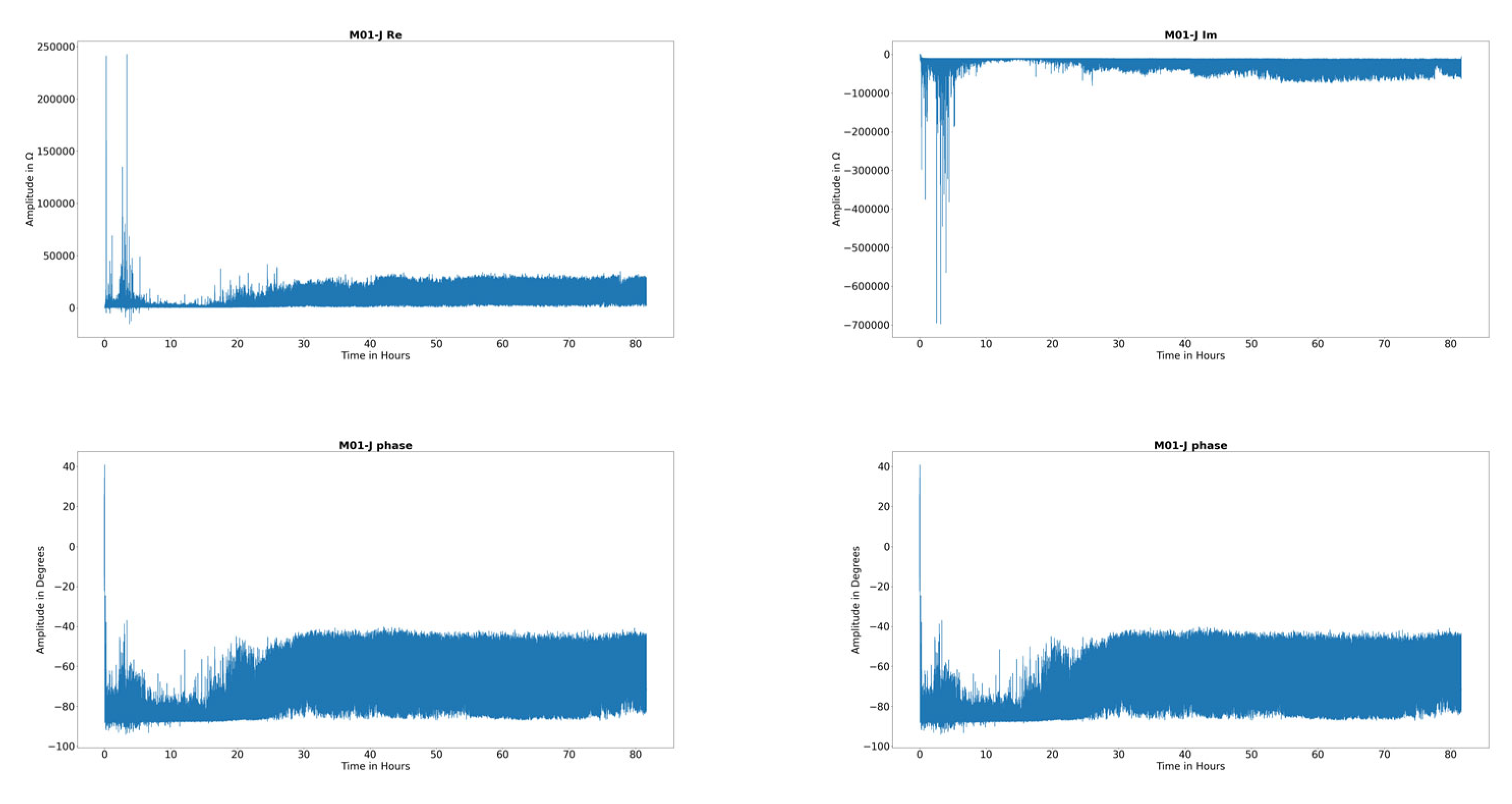
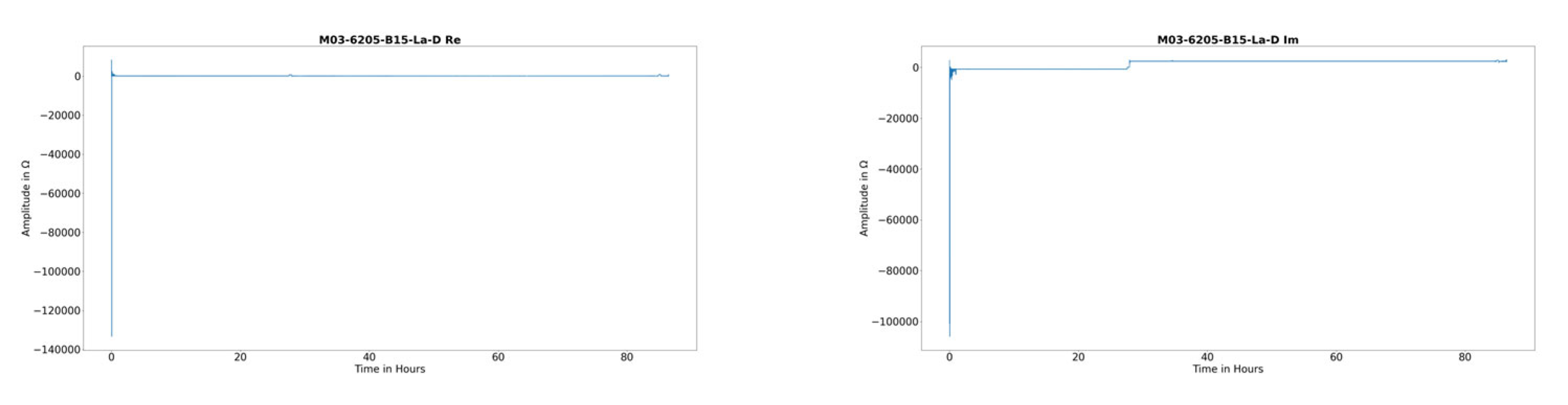
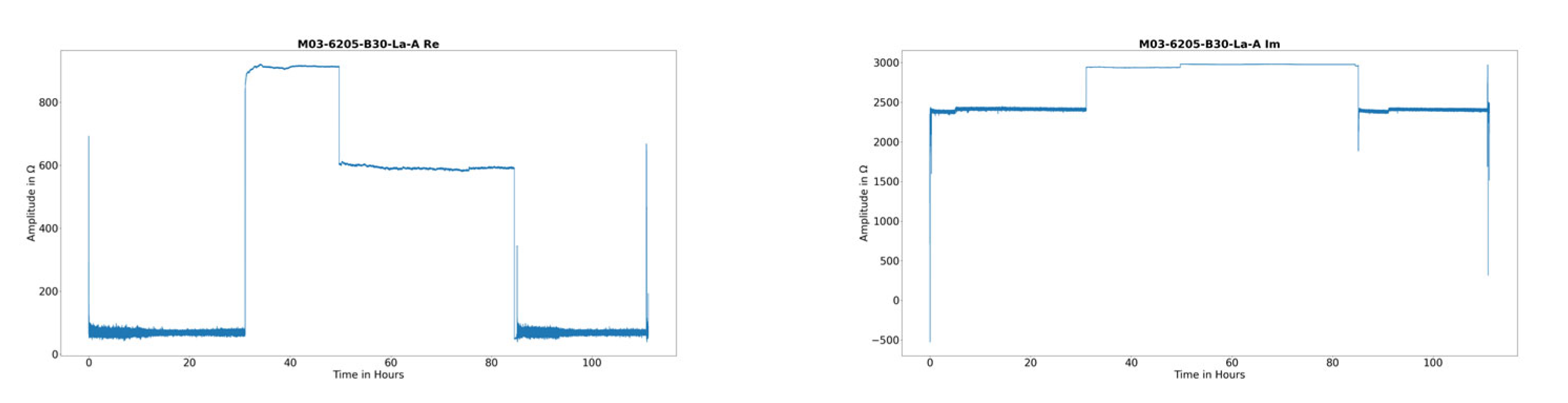
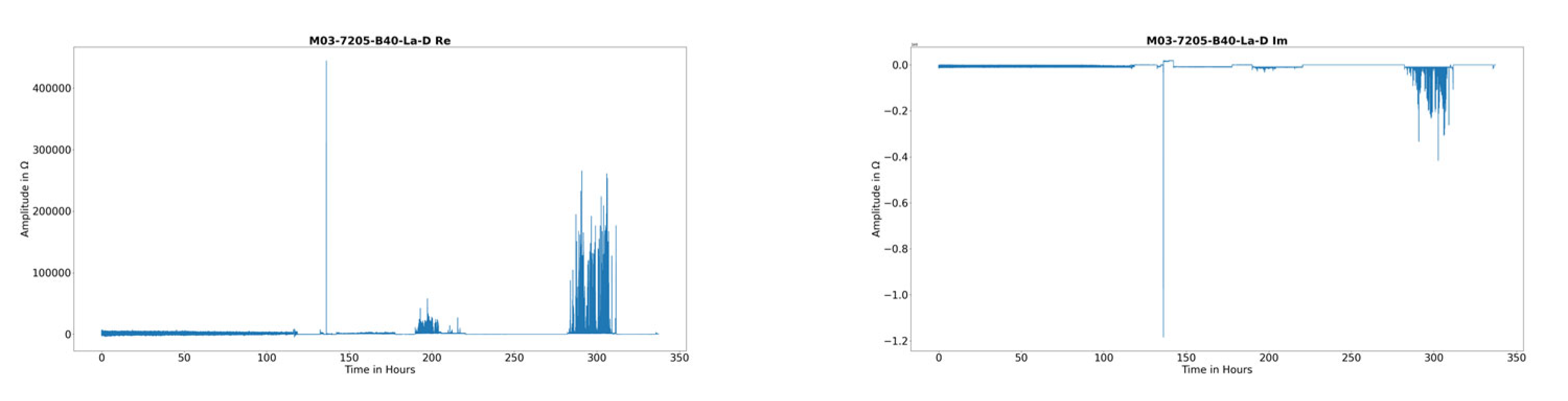
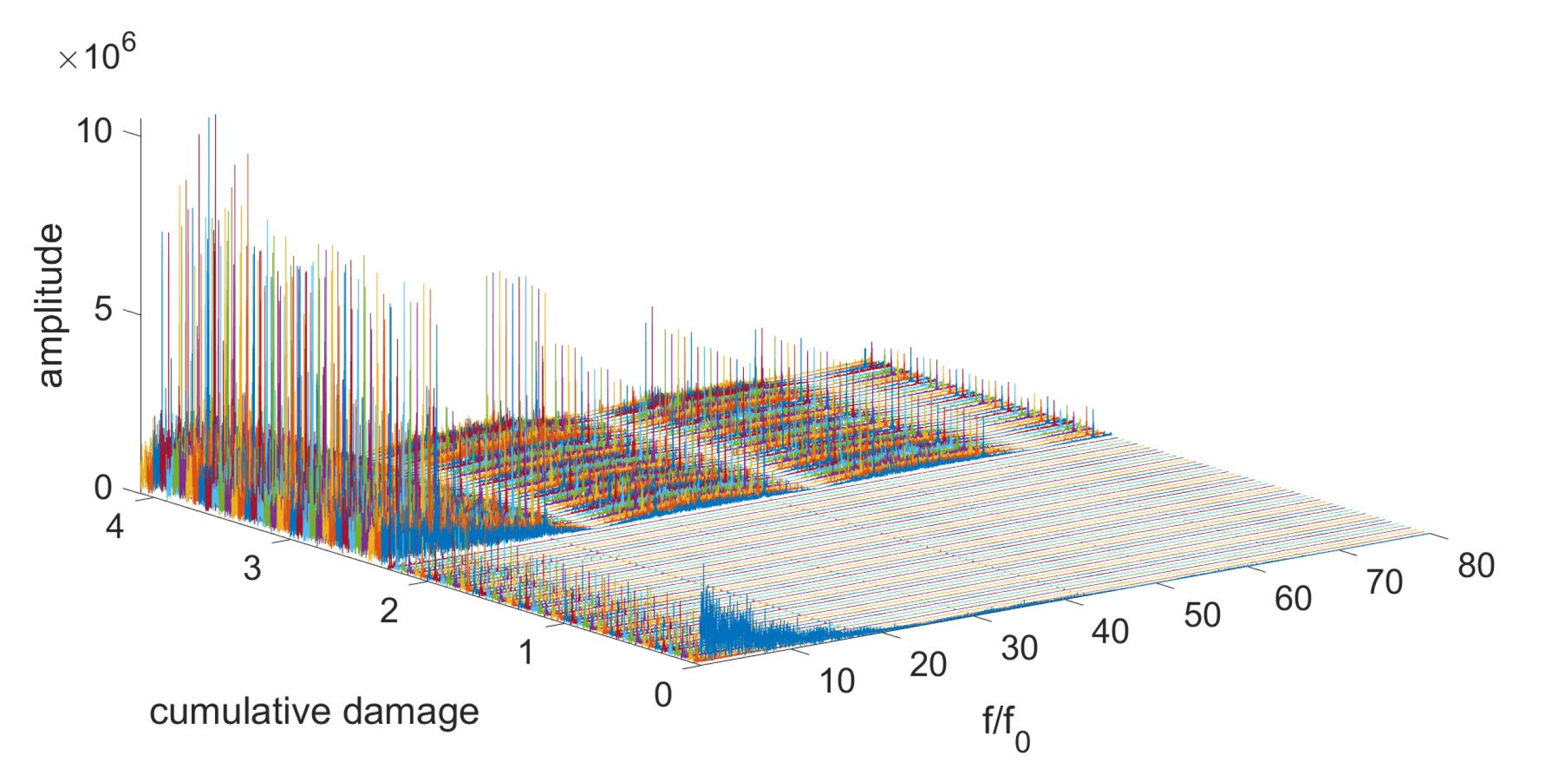
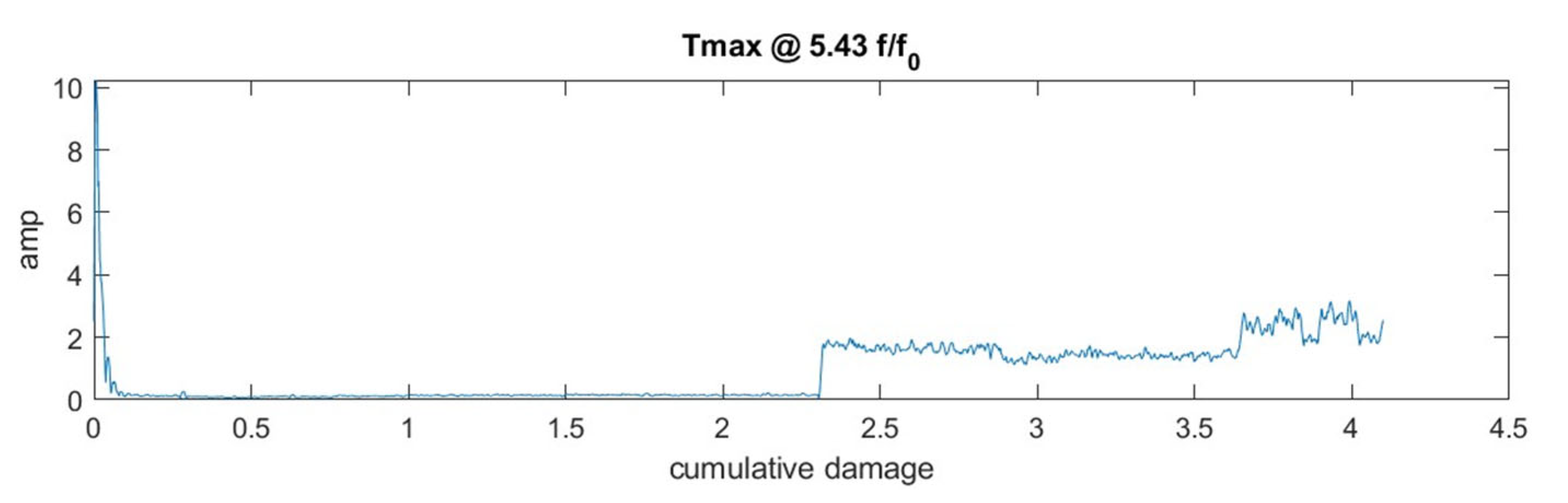


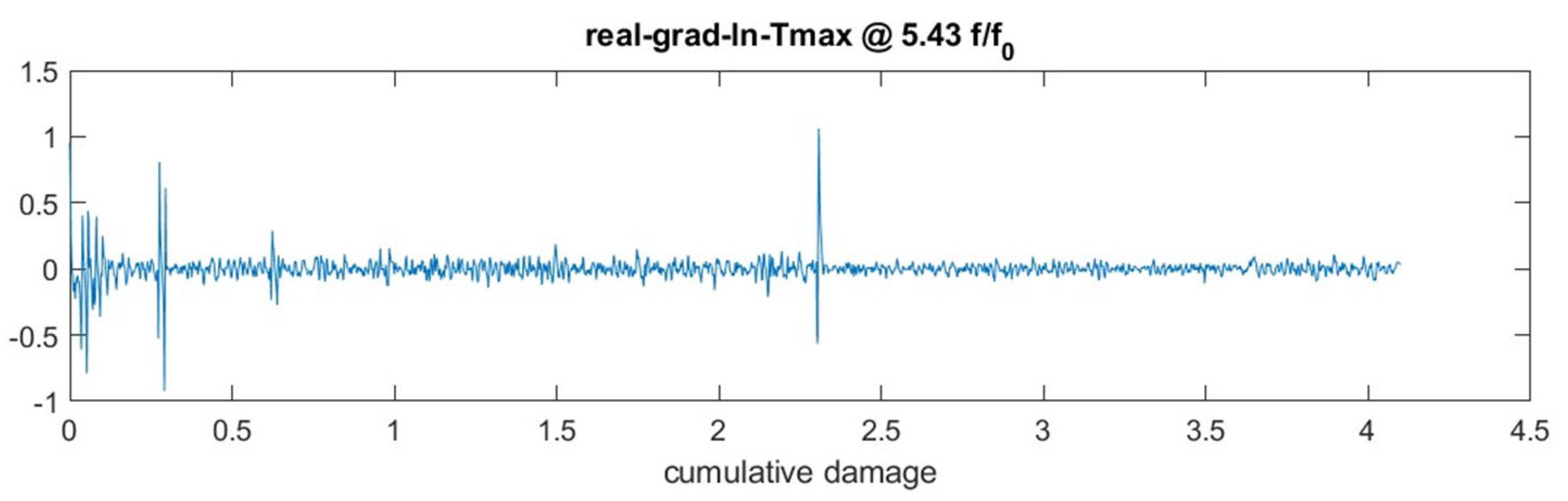
| Bearing Type | Amount of Fatigue Tests | Speed | C/P | Load angle β | Oil Temperature | ||
|---|---|---|---|---|---|---|---|
| FAG 6205 C C3 | 13 | 5000 rpm | 1.6 | 0° | 9375 N | 0 N | 60° |
| FAG 6205 C C3 | 5 | 5000 rpm | 1.6 | 15° | 9375 N | 2512 N | 60° |
| FAG 6205 C C3 | 5 | 5000 rpm | 1.6 | 30° | 9076 N | 5240 N | 60° |
| FAG 7205 B XL | 5 | 5000 rpm | 1.6 | 40° | 4410 N | 3700 N | 60° |
| FAG 7205 B XL | 5 | 5000 rpm | 1.6 | 55° | 3515 N | 5020 N | 60° |
| Number | Formula | Number | Formula |
|---|---|---|---|
| T1 | F1 | ||
| T2 | F2 | ||
| T3 | F3 | ||
| T4 | F4 | ||
| T5 | F5 | ||
| T6 | F6 | ||
| T7 | F7 | ||
| T8 | F8 | ||
| T9 | F9 | ||
| T10 | F10 | ||
| T11 | F11 | ||
| T12 | F12 | ||
| T13 | F13 | ||
| T14 | F14 | ||
| T15 | F15 | ||
| T16 | |||
| T17 | with sampling period |
| Feature | FAG 6205 C C3, β = 15° | FAG 6205 C C3, β = 30° |
|---|---|---|
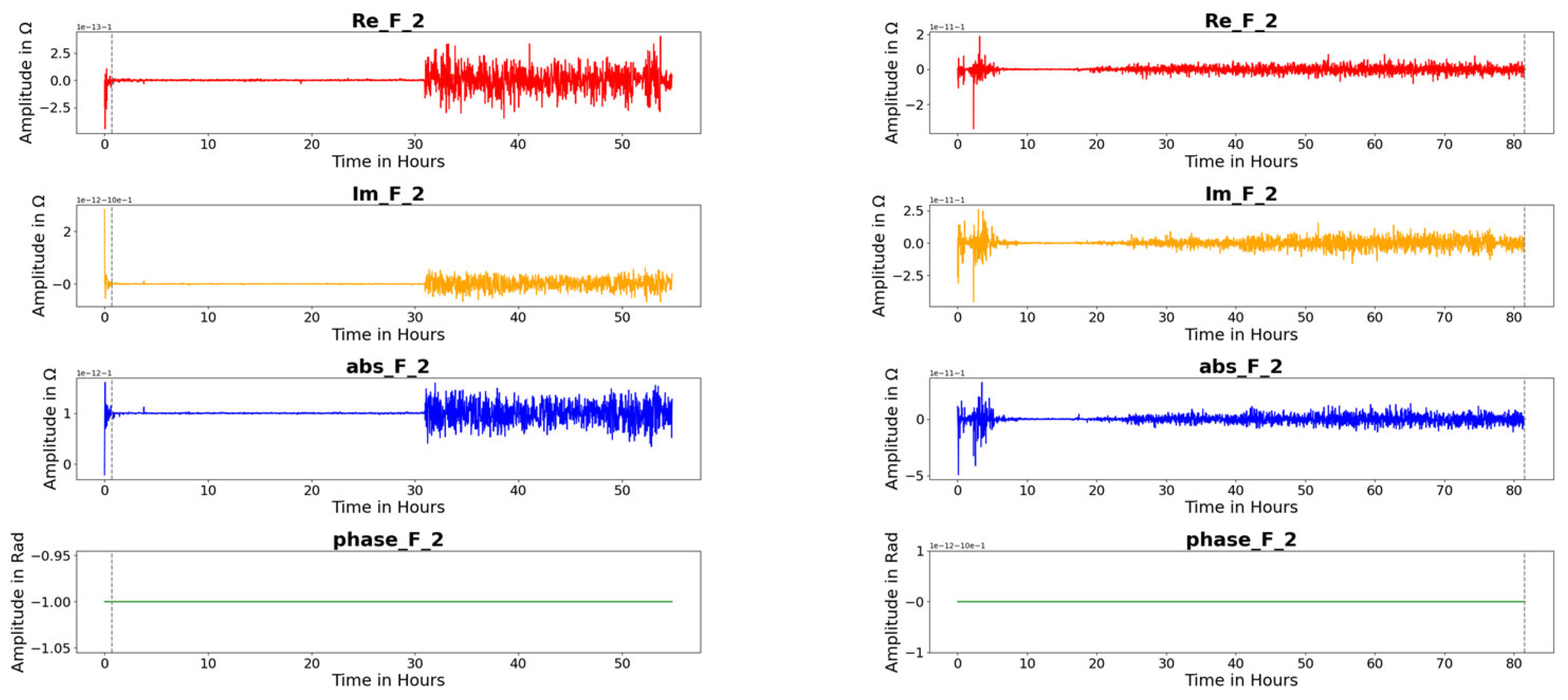
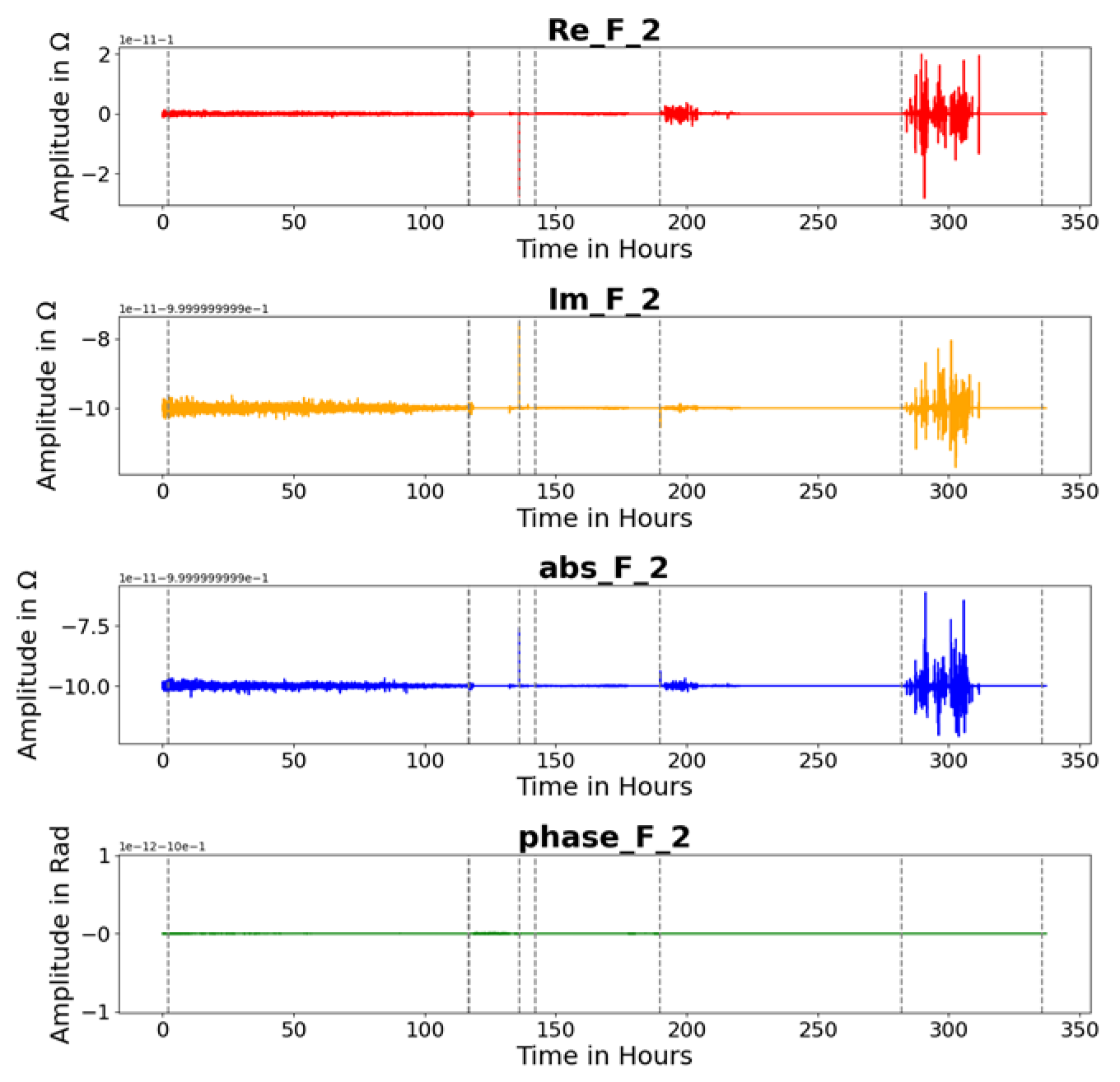
| Feature F 2 | 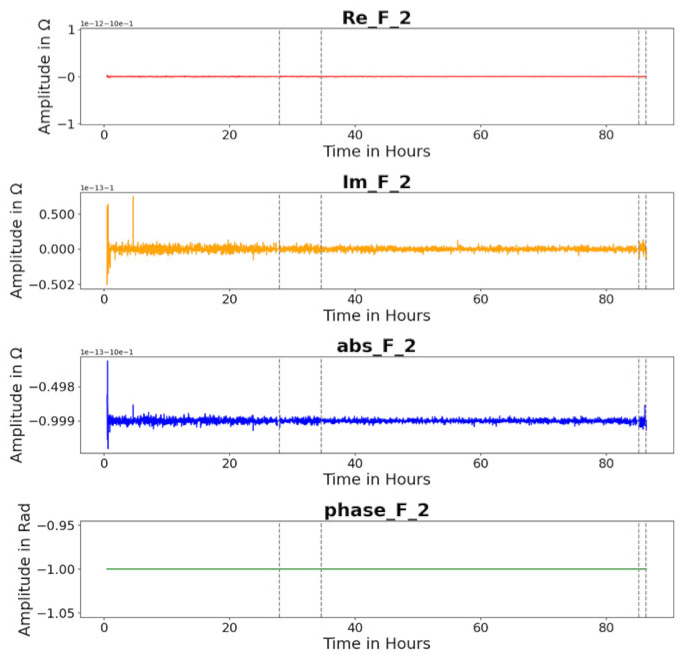 | 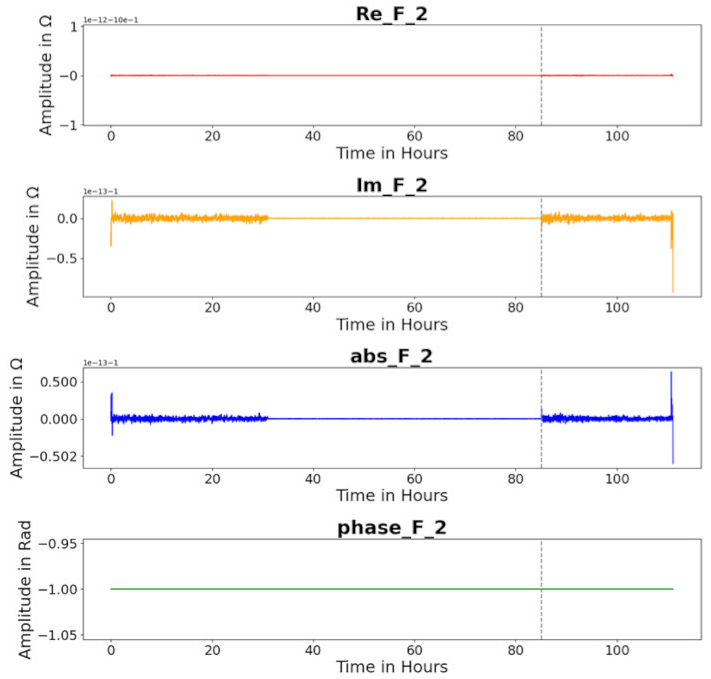 |
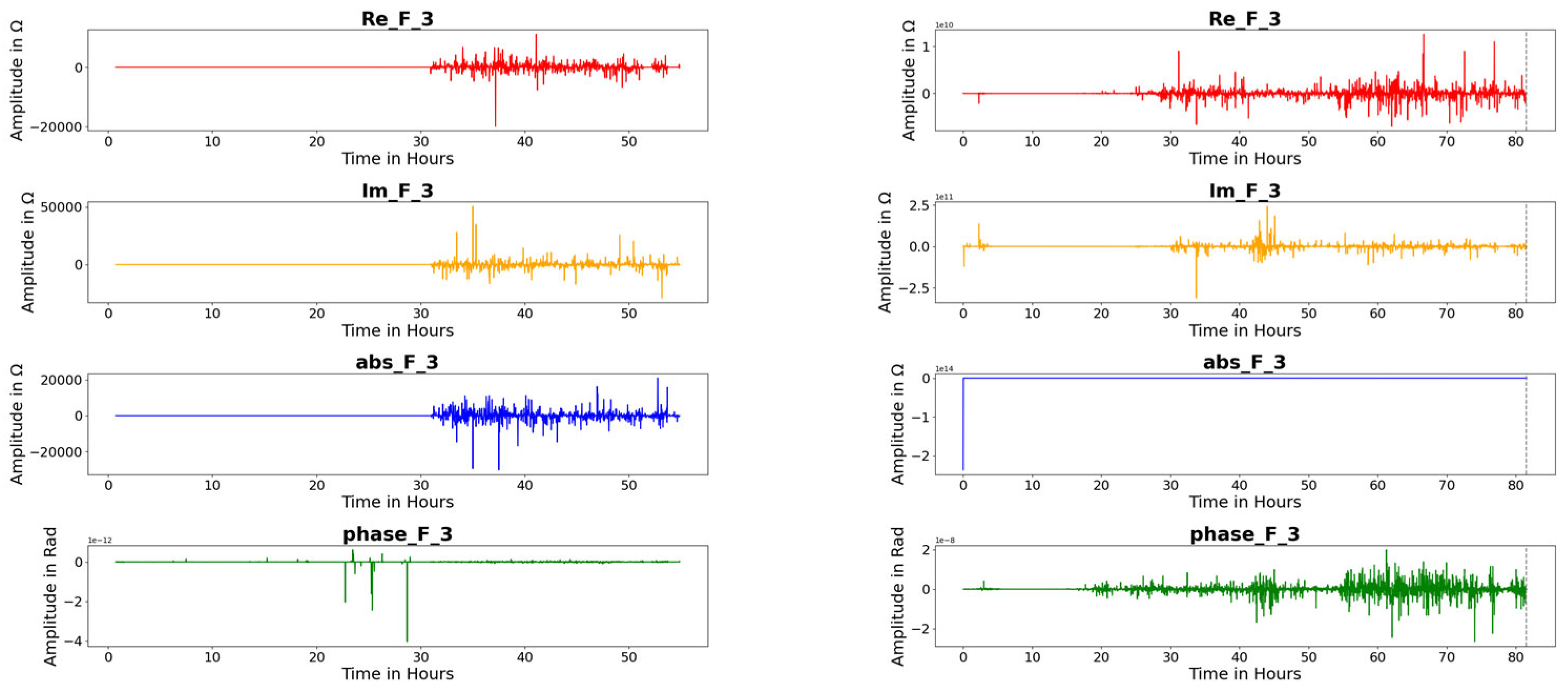
| Feature F 3 | 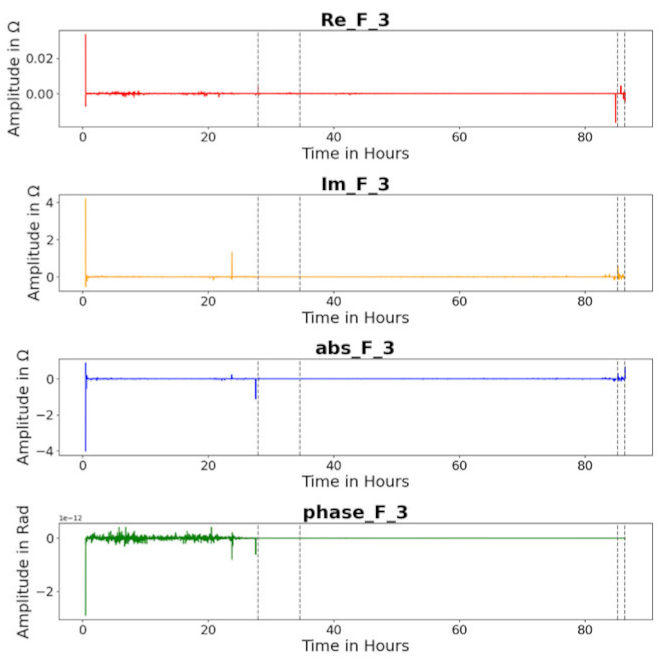 | 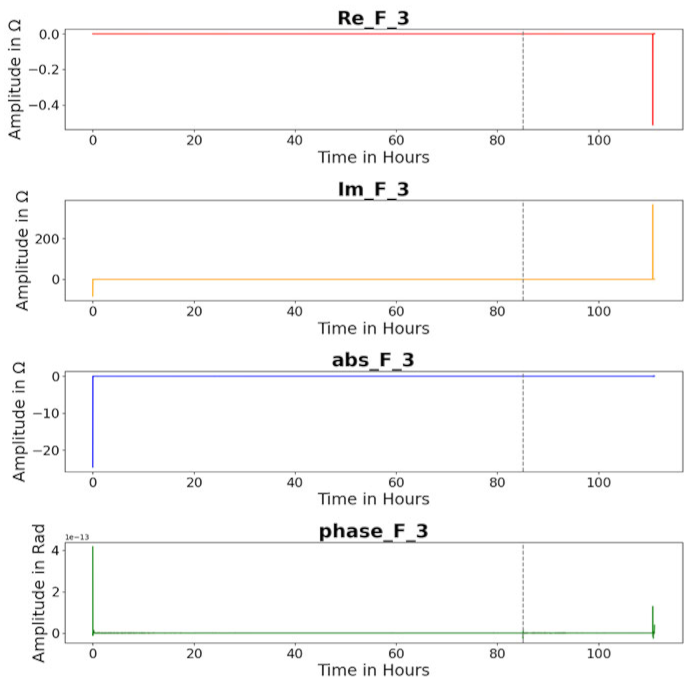 |
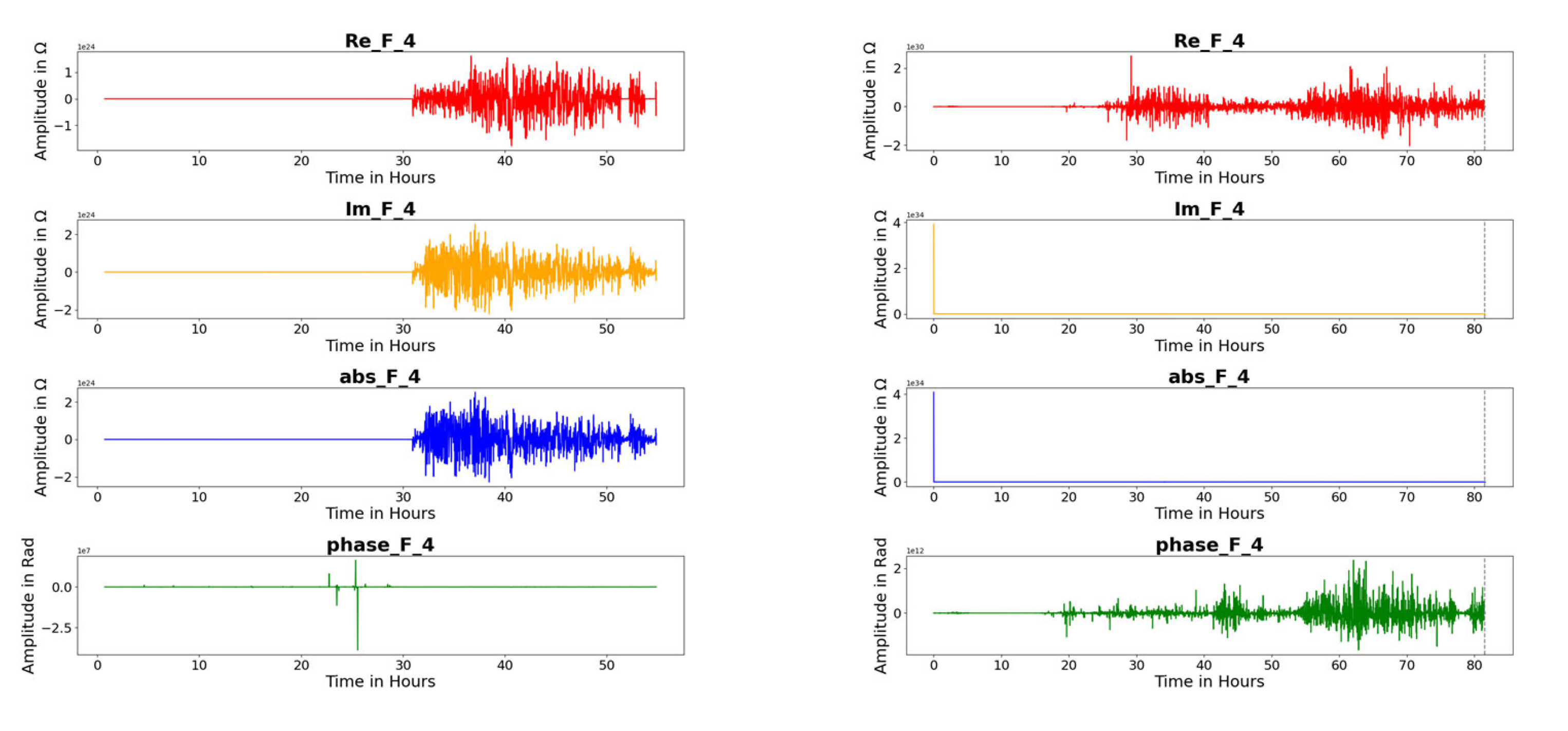
| Feature F 4 | 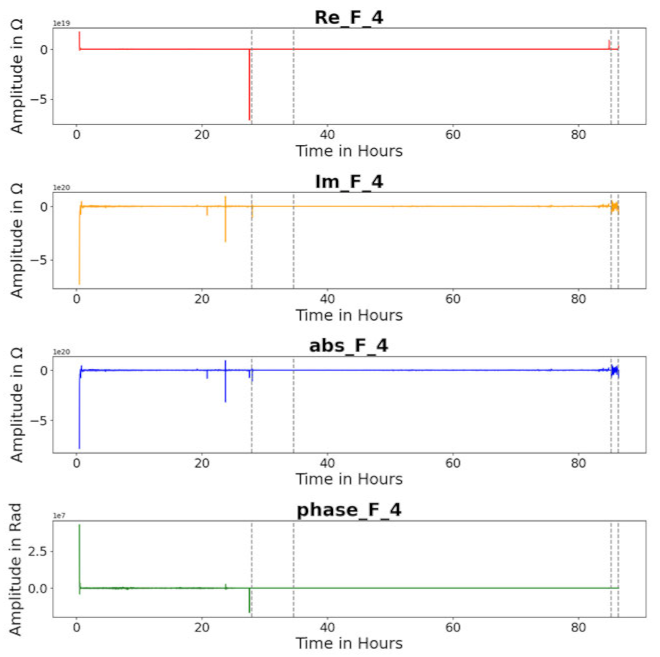 |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Becker-Dombrowsky, F.M.; Schink, J.; Frischmuth, J.; Kirchner, E. Investigation of the Electrical Impedance Signal Behavior in Rolling Element Bearings as a New Approach for Damage Detection. Machines 2024, 12, 487. https://doi.org/10.3390/machines12070487
Becker-Dombrowsky FM, Schink J, Frischmuth J, Kirchner E. Investigation of the Electrical Impedance Signal Behavior in Rolling Element Bearings as a New Approach for Damage Detection. Machines. 2024; 12(7):487. https://doi.org/10.3390/machines12070487
Chicago/Turabian StyleBecker-Dombrowsky, Florian Michael, Johanna Schink, Julian Frischmuth, and Eckhard Kirchner. 2024. "Investigation of the Electrical Impedance Signal Behavior in Rolling Element Bearings as a New Approach for Damage Detection" Machines 12, no. 7: 487. https://doi.org/10.3390/machines12070487
APA StyleBecker-Dombrowsky, F. M., Schink, J., Frischmuth, J., & Kirchner, E. (2024). Investigation of the Electrical Impedance Signal Behavior in Rolling Element Bearings as a New Approach for Damage Detection. Machines, 12(7), 487. https://doi.org/10.3390/machines12070487







