Design of Mixing Device Shafts Based on a Proposed Calculation Method Supported by Finite Element Method Analysis

Abstract

The elasticity of bearings as well as their clearance have an essential influence on the total arrow and, therefore, on their own pulsation. In most of the literature, this elasticity is neglected in the calculation of shaft deflections. In some work, the elasticity of the bearings has been taken into account when calculating the deflection of the mixing device shaft, but this has been carried out on the basis of a high degree of customization: the behavior of the bearings has been considered linearly elastic, which does not correspond to reality because according to the elastic response of the bearing, it is a nonlinear function of the radial displacement. When the shaft of a mixing device operates in a pressure vessel, at the outlet of the pressure vessel, the shaft is provided with a sealing device, which can be considered a third bearing. This aspect is also not taken into account in the calculation of the shaft’s deflection, which leads to a certain degree of error in its determination. This study aims to highlight the influence of the elasticity of the bearings and the sealing device on the stiffness of the shaft and to propose a method that supports a calculation program for calculating the elastic line of a vertical cantilever shaft, considering the role played by the bearings in the case that they behave nonlinearly and the sealing device as the third bearing. This problem was solved both by applying our own method and with the help of the FEM.

1. Introduction

As a result of the interaction between the medium and the vessel mixing device system [1,2,3,4,5,6,7,8], forces and moments are generated [1,2,3,4,5,9], which differ both in their formation mechanisms [10,11,12,13,14,15,16,17] and in their behavior in time and space [18,19,20,21,22,23,24,25]: the centrifugal force, gyroscopic moment, forces created by the mixer and shaft masses, transmission force, forces in the bearings, bearing force of the shaft and mixer, torsional moment, periodic forces caused by the fluid flow, axial hydrodynamic force of the mixer, transverse hydrodynamic force, inertia hydrodynamic force, damping hydrodynamic force [26,27,28], and forces caused by turbulence [29,30,31,32,33,34,35,36,37].

With the shaft loading of the mixing device being complex and the operating regime being characterized by random variations in the regime parameters [2,29,30,31,33], it is difficult to establish an exact theoretical approach in terms of shaft calculation [4,5,9,38]. For this reason, simplified loading models of the shaft mixer system have been established over time.

The calculation of the shaft of a mixing device only partially takes into account the actual state of loading [33,34], and there is not currently a uniform methodology for calculating these shafts [3,6].

Neglecting certain factors [23,39] and using theoretical loading models led to very complicated theoretical relations [22,29] and final results with some degree of error [7].

The elasticity of the bearings as well as their clearance have an essential influence on their total deflection and implicitly as well as on their own pulsation [4,37]. In most specialized papers [5,29], the elasticity of the bearings is neglected in the calculation of shaft deformations [4,9,37]. Lately, however, the attention of specialists has been drawn to the influence of the elastic characteristics of the bearings on shaft deformations [4,5,9,10,11,29,37].

In some papers [9,10,29], the elasticity of the bearings has been taken into account for calculating the deflection of the mixing device shaft, but this was carried out on the basis of a high degree of particularization: the behavior of the bearings was considered linearly elastic [9,10,29]. This particularization induces a certain error in the final obtained results because, according to [24,29], the elastic reaction of the bearing is a nonlinear function of the radial displacement [37].

On the other hand, the shaft of a mixing device is considered a cantilever shaft on two bearings [25,26,27,28,40], neglecting the consequences of the existence of the sealing device when it exists [8,9,29,37].

In reality, the sealing device has a stiffening effect on the shaft [12,29]. This effect is particularly noticeable on elastic shafts, and it is more pronounced on shafts without a bearing in the sealing device [5,9,12,29]. Due to the presence of the sealing device, the shaft deflection can be reduced, which leads to an increase in the critical speed.

It is also known that the improper design of the shaft of a mixing device can lead to inadequate shaft stiffness [23,29], resulting in the destruction of the sealing device in a very short time, with corresponding economic consequences [13,19,20]. However, the presence of the sealing device in the calculation of the shaft of the mixing device is very rarely found in the literature [14,15,16,17,18].

In view of the above, the purpose of this paper is presented below.

• To establish a method for calculating the elastic line of a vertical cantilever shaft supported on two bearings with the following:

  -

  Consideration of the clearance in the bearings in the case of nonlinear elastic behavior;

  -

  Additional stiffening introduced by the presence of the sealing device.

• To calculate the elastic line of a vertical cantilever shaft supported on two bearings using FEM with the following:

  -

  Consideration of the clearance in the bearings in the case of nonlinear elastic behavior;

  -

  Additional stiffening introduced by the presence of the sealing device.

2. Design Data/Work Hypotheses

This study aims to highlight the stiffening effect of the seal device on the shaft and the influence of bearing elasticity on shaft stiffness.

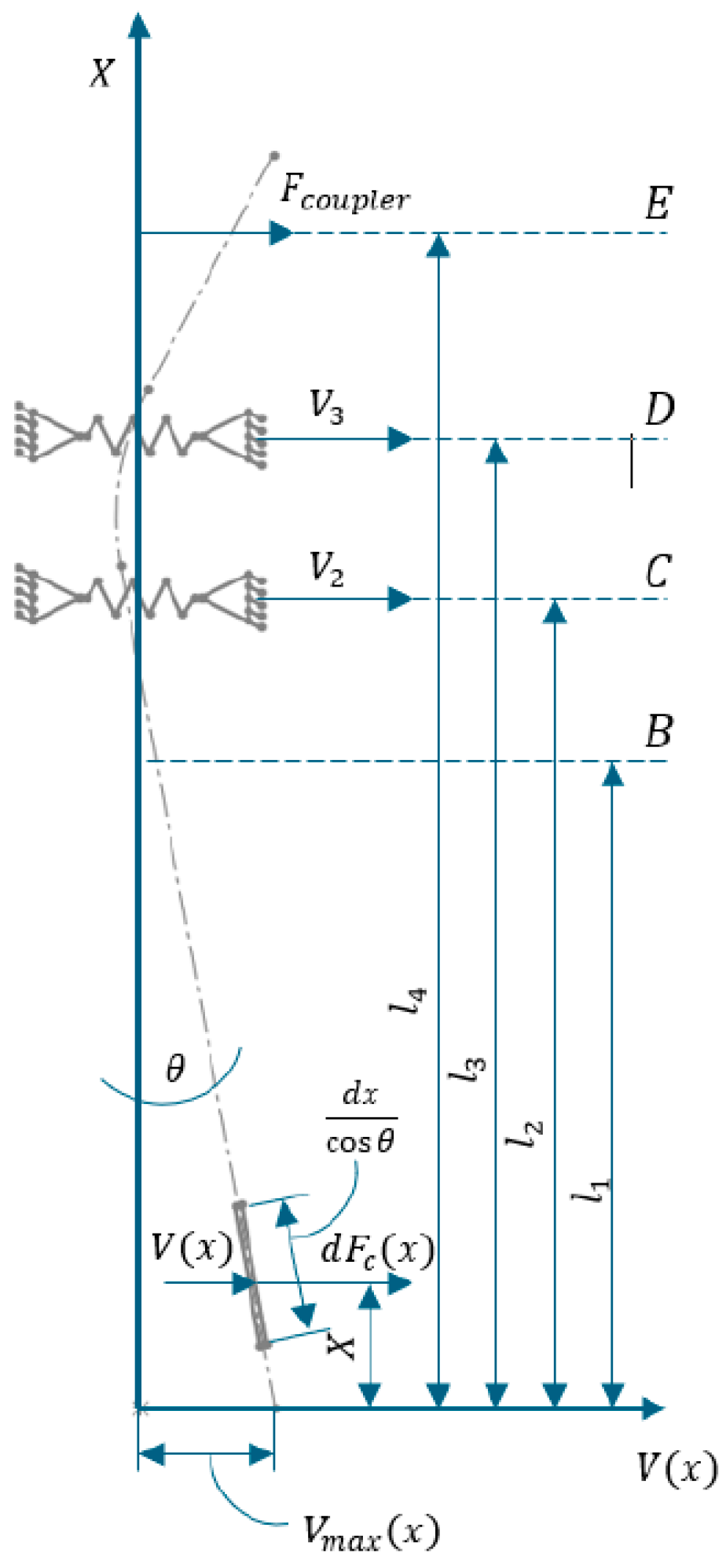
Thus, two distinct cases will be considered: the shaft of a mixing device with a vertical cantilever and no sealing device (AFDE—Figure 1) and the shaft of a mixing device with a vertical cantilever and a sealing device (ACDE)—Figure 2.

For each of the two cases (AFDE and ACDE), a steel shaft with a full circular cross-section, supported on two supports or three supports (if the sealing device is considered the third support), with a concentrated load at the end (the mixer), shall be considered.

Each of the two cases was solved for three speeds—n = 400 rpm, n = 640 rpm, and n = 1008 rpm—with the specification that the speeds were set according to the experimental stand [32,33] on which the validation of the theoretical results was carried out. Each case was assigned three work environments: air, water, and oil.

The shaft of the mixing device has a diameter of 10 mm and a length of 450 mm, and it is made of steel, 18 MoCN 15.

According to the actual values, corresponding to the experimental stand, the following dimensions were used:

• -

  For the shaft without a sealing device (AFDE), the cantilever length of the shaft, lc = 390 mm, and the distance between bearings, lr = 45 mm;

  -

  For the shaft with a sealing device (ACDE), the cantilever length of the shaft, lc = 340 mm, the distance between bearings, lr = 45 mm, and the length of the shaft between the lower bearing and the sealing device, lc,e = 50 mm.

Two radial ball bearings (of the same type) of type 6000 with a ball diameter of Dw = 4.7665 mm and with the number of balls, z = 7 were used.

The seal contains felt rings, whose stiffness was determined separately in the laboratory/taken from the database of the SolidWorks Premium 2023 SP0.1 software platform.

A symmetrical axial mixer with m = 0.1 kg was mounted at the end of the shaft console.

The force that stresses the shaft when it bends is considered the centrifugal force, determined by the residual unbalance, for which the following relation is used:

$$F_c=m_t{r}_d{\omega }^2,$$

(1)

where r_d is the distance between the geometric center and the mass center (residual imbalance), and m_t is the equivalent mass of the mixer.

$$m_t=m_a+m_b,$$

(2)

where m_a is the mixer mass and m_b is the concentrated mass of the shaft considered at the mass center of the mixer.

According to [31], for a shaft on two supports with a single mixer in the cantilever, it can be written that

$$m_b=q{M}_a,$$

(3)

where M_a is the mass of the whole shaft and q is the distribution factor of the shaft mass, which, according to [38], can be calculated with the following formula:

$$q={\displaystyle \frac{12}{{\left(4.6-3x\right)}^4{x}^2\left(x+3\right)}}, x={\displaystyle \frac{l}{l_r+l_c}},$$

(4)

Calculation hypotheses for determining shaft deformations:

-

The lunation and rotations of the planes normal to the shaft axis, which delimit a volume element, are neglected—Figure 3;

-

The load in the coupler is neglected;

-

The study is carried out under the conditions of the validity of the Bernoulli–Navier law (the cross-sectional planes of the unloaded shaft also remain plane after deformation) and of the Lowe–Kirchhoff law (the surface normal before deformation also remains normal after deformation);

-

The mixer attached to the shaft is axially symmetrical;

-

Temperature-induced deformations of the shaft are neglected;

-

The shaft material behaves linearly elastically according to Hooke’s law;

-

The shaft, made of homogeneous and isotropic material with a circular cross-section, is supported at the upper end; it is assumed to be ideal and rectilinear under a load so that the initial curvature is assumed to be zero;

-

The mounting elasticities of the bearing are permanent, symmetrical, and circular;

-

The effects of the axial force (displacements along the x-axis) and gyroscopic momentum are neglected;

-

The shaft is linear with a constant diameter d;

-

The filler material is considered linear elastic, and it behaves according to Hooke’s law;

-

The filler material completely fills the seal housing, the shaft is perfectly cylindrical and smooth, and the deformation of the shaft and seal housing under the action of the sealing pressure is negligible.

Consideration of the influence of the working environment on shaft deformations and its own pulsation, respectively, was carried out by considering the hydrodynamic mass of the mixer and addressed by the authors of the paper [38].

3. Calculation Method for a Vertical Cantilever Shaft with a Single Mixer without a Sealing Device (AFDE)

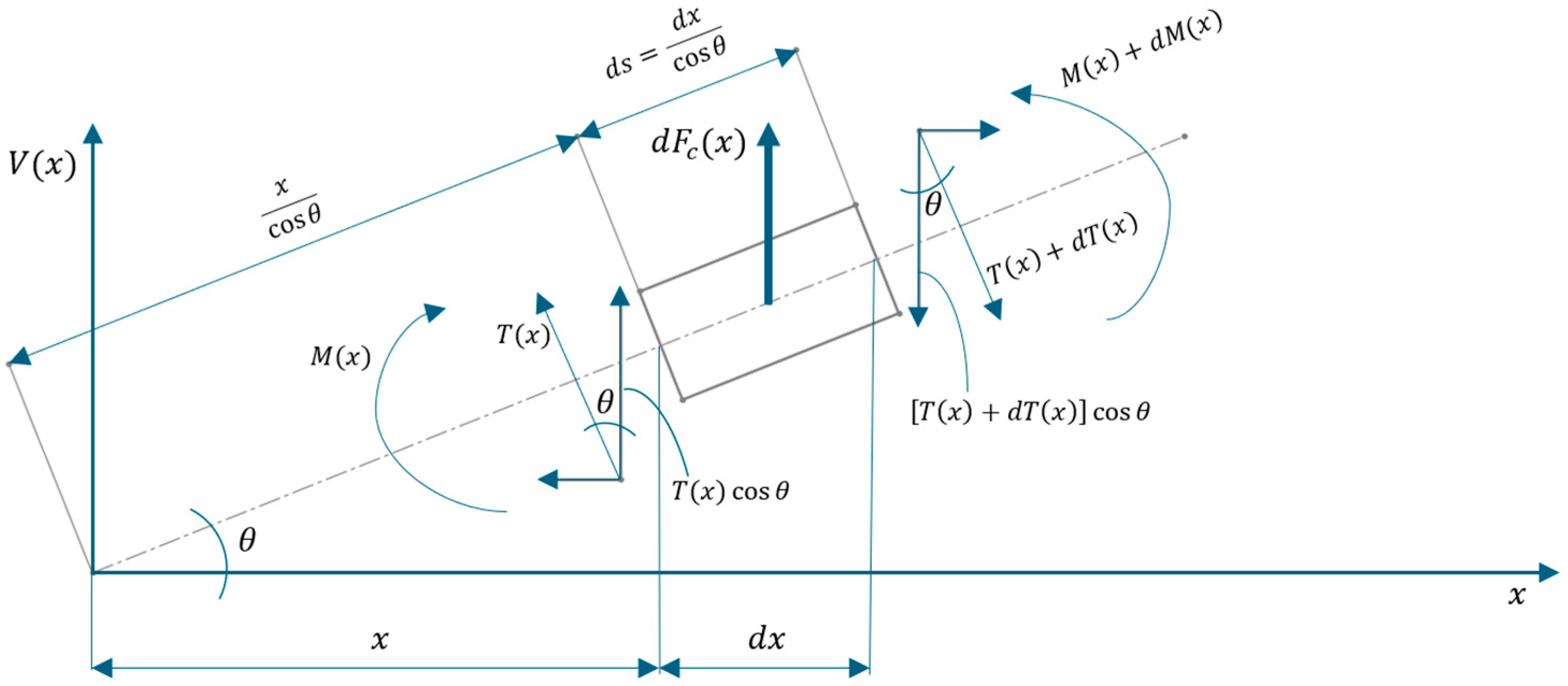
A volume element from a shaft is considered—Figure 1 and Figure 3—with a constant cross-section with an area A and a moment of inertia Iz made of a material of density ρ. The shaft rotates with an angular velocity ω, and, as a result of its bending stress, it has the arrow v(x) in the current section x.

The volume element is loaded by the loads M(x), T(x), M(x) + dM(x), and T(x) + dT(x) in the cross-sections at its ends and by the centrifugal force of its mass. The centrifugal force is considered to be concentrated in the center of mass, which rotates on a circle of radius r(x); it has the following expression:

$$d{F}_c\left(x\right)=dm{\omega }^{2}r\left(x\right),$$

(5)

in which it is approximated that r(x) ≈ v(x), and so

$$d{F}_c\left(x\right)=dm{\omega }^{2}v\left(x\right).$$

(6)

The mass element can be written as dm = $\rho$ dV, where dV = A ds, and the shaft length element is

$$ds={\displaystyle \frac{dx}{cos\theta }}.$$

For small values of the displacements, v(x), there are small values for the angle θ, so $\cos \theta \approx 1$ can be considered, and then the centrifugal force can be written in the following form:

$$d{F}_c\left(x\right)\cong \rho A{\omega }^{2}v\left(x\right)dx.$$

(7)

From the equilibrium equations of the volume element (the projection of forces on the v(x) axis and the moments with respect to the section on the right), we obtain

$$T\left(x\right)cos\theta +d{F}_c\left(x\right)-\left[T\left(x\right)-dT\left(x\right)\right]cos\theta =0,$$

(8)

and

$$M\left(x\right)-\left[M\left(x\right)-dM\left(x\right)\right]+T\left(x\right){\displaystyle \frac{dx}{cos\theta }}+d{F}_c\left(x\right){\displaystyle \frac{dx}{2}}=0.$$

(9)

Considering, as above, cos $\theta$ = 1, and neglecting in Equation (9) the last product as diverging to infinity at higher orders, relations (8) and (9), become

$$dT\left(x\right)=d{F}_c\left(x\right),$$

(10)

$${\displaystyle \frac{dM\left(x\right)}{d\left(x\right)}}=T\left(x\right),$$

(11)

According to [31], the differential equation (Euler) of the axis for the deformed beam has the following expression:

$${\displaystyle \frac{d^{2}v\left(x\right)}{d{x}^2}}=-{\displaystyle \frac{1}{E{I}_z}}M\left(x\right),$$

(12)

Derived from this relation, it follows that

$${\displaystyle \frac{d^{3}v\left(x\right)}{d{x}^3}}=-{\displaystyle \frac{1}{E{I}_z}}{\displaystyle \frac{dM\left(x\right)}{d\left(x\right)}},$$

(13)

Or, taking into account Equation (11),

$${\displaystyle \frac{d^{3}v\left(x\right)}{d{x}^3}}=-{\displaystyle \frac{1}{E{I}_z}}T\left(x\right).$$

(14)

From a new derivation and considering Equation (10), Equation (3) takes the following form:

$${\displaystyle \frac{d^{4}v\left(x\right)}{d{x}^4}}=-{\displaystyle \frac{1}{E{I}_z}}{\displaystyle \frac{d{F}_c\left(x\right)}{dx}}.$$

(15)

From relations (7) and (15), it follows that

$${\displaystyle \frac{d^{4}v\left(x\right)}{d{x}^4}}=-{\displaystyle \frac{1}{E{I}_z}}A\rho {\omega }^{2}v\left(x\right)dx.$$

(16)

The following notation is introduced:

$$\alpha =\sqrt[4]{{\displaystyle \frac{A\rho {\omega }^2}{4E{I}_z}}}.$$

(17)

With this notation, relation (16) takes the following form:

$${\displaystyle \frac{d^{4}v\left(x\right)}{d{x}^4}}+4{\alpha }^{4}v\left(x\right)=0,$$

(18)

which is a fourth-order, linear, homogeneous differential equation with constant coefficients. Its characteristic equation is as follows:

$$r^4+4{\alpha }^4=0.$$

(19)

The roots of this equation are

$$r_{\mathrm{1,2}}=\alpha \pm i\alpha \mathrm{a}\mathrm{n}\mathrm{d} r_{\mathrm{3,4}}=\alpha \pm i\alpha .$$

(20)

The general solution of the differential Equation (18) is

$$v\left(x\right)=e^{-\alpha x}\left(C_{5}sin\alpha x+C_{6}cos\alpha x\right)+e^{\alpha x}(C_{7}sin\alpha x+C_{8}cos\alpha x).$$

(21)

The calculation algorithm given by relations (5)–(21) applies to both zone $2, \mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h} x_2\in \left[0,l_2\right],$ and zones 3 and 4, with $x_3\in \left[l_2, l_3\right] and x_4\in \left[l_3, l_4\right], respectively.$

Similarly, for zone 3, with $x_3\in \left[l_2, l_3\right]$, and for zone 4, with $x_4\in \left[l_3, l_4\right]$, as shown in Figure 1, this leads to a non-homogeneous system of 14 equations with 14 unknowns (the integration constants and V₂ and V₃).

The determination of the integration constants from the system obtained by the above algorithm is carried out by setting the boundary conditions. The boundary conditions for Equations (12) and (14) are written as

$$M\left(x\right)=-E{I}_z{v}^{″}\left(x\right) ,$$

(22)

$$T\left(x\right)=-E{I}_z{v}^{″’}\left(x\right).$$

(23)

In most cases, in this calculation algorithm, the elasticity of the bearings is neglected. Even if it is taken into account, it is considered according to linear elasticity laws, which do not correspond to reality.

According to [24], the following nonlinear relation between the load, Q, and the deformation, $\delta ,$ of the bearing (in the case of elastic contact stress) is used:

$$Q=k_r{\delta }^n,$$

(24)

Based on relation (24), the “intrinsic elasticity” of the bearing is correlated with its deformation, and the reaction in the bearing can be written as follows:

$$V=k_r{\left(v\left(x\right)\right)}^n,$$

(25)

where k_r is the stiffness factor of the bearing, and v(x) is the arrow in the analyzed bearing.

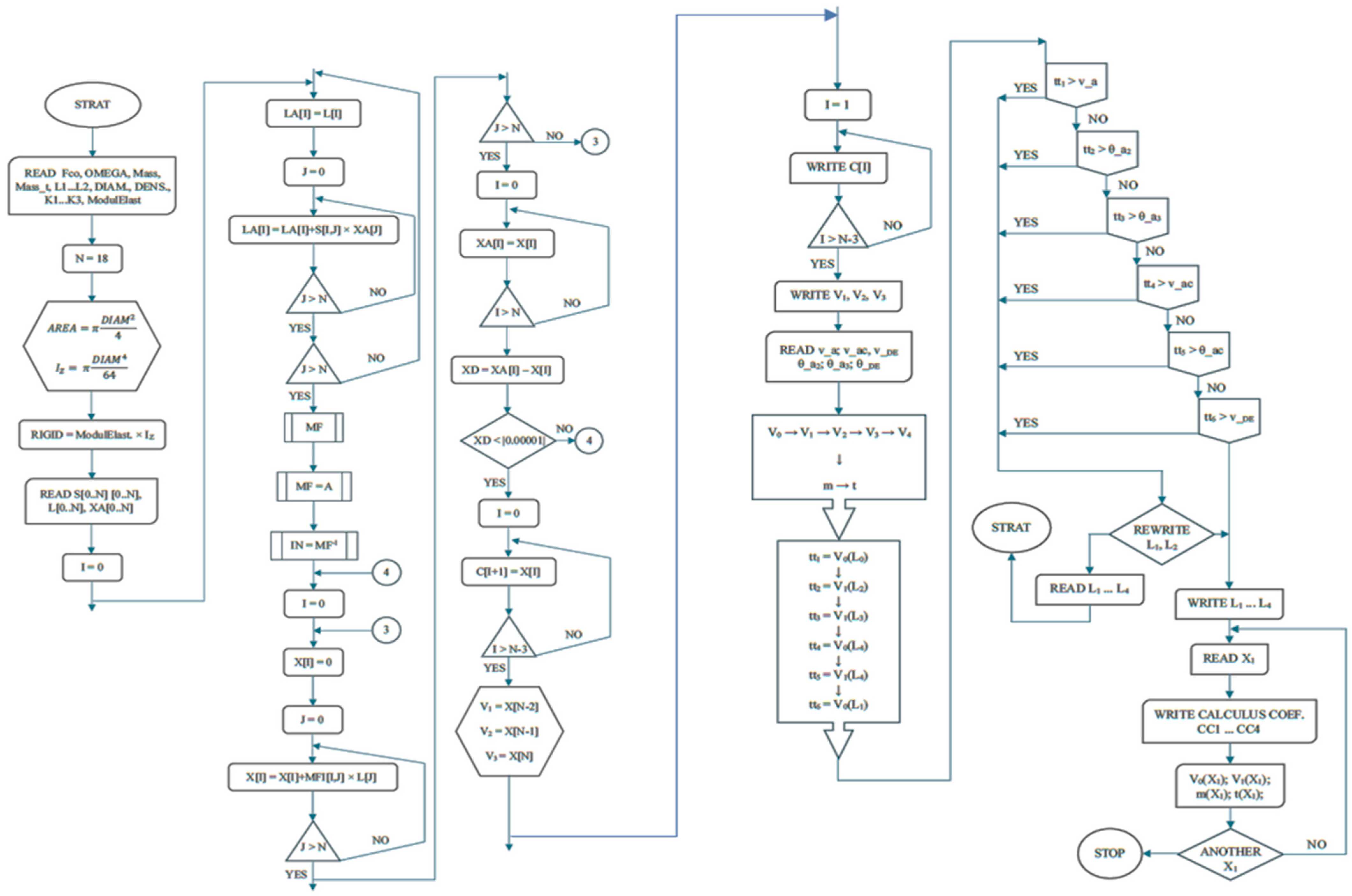
Based on the theory of numerical computation for solving nonlinear systems, the solving of the system thus obtained is extremely laborious. As a result, the authors developed their own computational program for solving the system.

The linearization of the system was carried out by two numerical analysis methods: the least-squares method and the Newton method. Accordingly, two variants of the calculation program were developed, the logical scheme of which is shown in Figure 4.

In addition to solving the system, the calculation programs also determine the deflections, shear force, and bending moment in any selected section of the shaft.

4. Calculation Method for a Vertical Cantilever Shaft with a Single Mixer on Three Supports with a Sealing Device

The type of sealing device used was soft-filled (felt).

The elastic force produced in the filler of the sealing device undergoing deformation, $∆r$, is

$$F_{DE}=k_u∆r_u,$$

(26)

where k_u is the elasticity constant of the filling material, and $∆r_u={\epsilon }_{\theta ,u}{r}_u$, where $r_u={\displaystyle \frac{d_1}{2}}+{\displaystyle \frac{c}{2}}$ and

$${\epsilon }_{\theta ,u}={\displaystyle \frac{E_u}{1-{\mu }_u^2}}\left[{\sigma }_{\theta }-{\mu }_u^2\left({\sigma }_x+{\sigma }_r\right)\right].$$

(27)

The reaction of the sealing device, considered the third support, is written according to relation (28):

$$V=k_{u}v\left(x\right).$$

(28)

The calculation algorithm given by relations (5) and (21) was applied on zone 1, with $x_1\in \left[0,l_1\right]$, zone 2, with $x_2\in \left[l_1,l_2\right],$ and zone 3 and 4, with $x_3\in \left[l_2, l_3\right]$ and $x_4\in \left[l_3, l_4\right]$, respectively, similar to the procedure for the vertical cantilevered shaft with a single mixer on two supports without a sealing device.

Similar to the previous case, the determination of the constants C₁–C₁₆ was carried out by setting the boundary conditions.

5. Logical Scheme

The initial variables were F_co, $\omega , m, l_1, l_2, l_3, l_4, \rho , k_1, k_2, {and k}_3$.

-

A, I_z, and stiffness were calculated;

-

Two systems of 14 equations and 19 equations, respectively, were solved as follows:

• Linearization of the system—method of least squares;
• Linearization of the system—Newton’s method;

-

The constants C₅–C₁₆ and C₁–C₁₆, respectively, were determined;

-

The arrow and the angular deflection were determined;

-

The shear force and bending moment were determined;

-

The deformation values with permissible values at the priority intersection points were compared;

-

If the conditions were not verified, new values for the initial data were given (Figure 4).

6. Conclusions on the Proposed Calculation Method

6.1. Novelty of the Method

Although it is well known that, in reality, there are consequences of the presence of the sealing device, this fact has not been considered in the literature for determining shaft deformations depending on the presence of this device.

The classical calculation for determining reactions, the shear force, the bending moment, and deformations, as presented in the literature, is carried out considering the bearings as rigid bearings. In some of the literature, however, the influence of the elasticity of the bearings on the shaft deflection of a mixing device is specified.

The elastic characteristics of the bearings are imposed by the oil film between the moving parts of the bearings and the elasticity of the bearing cages (the “intrinsic elasticity” of the bearing). Even when this effect has been taken into account, most research has considered the effect of elastic reactions on the deformations and critical angular velocity of a flexible shaft on which a disk of mass m is mounted according to linear laws.

It has been observed, however, that the elastic response of the support is a nonlinear function of the radial displacement.

In comparison with the presented methods from the literature and those used in the design of mixing device shafts, the method proposed by these authors takes into account real loading conditions: the nonlinear elasticity of the bearings and the stiffening effect of the seal device on the mixing device shaft, respectively.

6.2. Advantages of the Method

The advantages of the method are as follows:

-

The real load case of the nonlinear elasticity of the bearings is considered;

-

The influence of the sealing device on shaft deflections, shear force, and bending moment is considered;

-

The deflection in the seal zone is a function of the elastic characteristics of the filler material;

-

A quick calculation of deformations is possible in any section of interest of the shaft (the end of the cantilever, seal, bearings, coupling);

-

The calculation program can be further extended for the stepped shaft, the determination of the stress state in any section of interest of the shaft, and the calculation of a shaft with two or more mixers mounted on it.

Knowing the deformations and aiming to reduce them ensures the smooth operation of the mixing device and, at the same time avoids, premature wear or even damage to the sealing device, bearings, or coupling.

6.3. Disadvantages of the Method

The disadvantages of the method are as follows:

-

It is necessary to calculate the stiffness of the bearings and the spring constant of the sealing device in advance. However, specialized software is now available for these calculations.

-

The accuracy of the results depends on the calculation (determination) of F_co—Figure 1 and Figure 2—which is itself an approximate calculation.

-

Both the method of least squares and the Newton method, used in solving nonlinear systems, are approximate calculation methods.

-

This method can only be applied to soft-filled sealing devices. It cannot be used for other types of sealing devices.

-

The method can only be applied to an axially symmetrical mixer.

7. Solving the Problem Using the Finite Element Method

To carry out the study by means of finite element analysis, the SolidWorks Simulation module was used, which is part of the SolidWorks Add-Ins application complex of the SolidWorks Premium 2023 SP0.1 software platform.

The type of analysis addressed in this study is of a linear static structural type based on a solid mesh, which allows for thermal influences. The solver selection setting was automatic (the default state of the module). Measurement units were set to SI units (MKS); lengths were measured in mm, temperature was measured in Celsius, angular velocity was measured in Hertz, and stresses/pressure were measured in N/mm² (MPa).

The materials used and the yield criteria considered were Linear Elastic Isotropic and Max von Mises Stress.

The components’ interaction between the analyzed assemblies was considered a global contact interaction type (no penetration—surface-to-surface). A solid curvature-based mesh with 29 Jacobian points was also used. The element size was 5.2 mm with a tolerance of 0.25 mm. This produced a total of 29,252 nodes, with 20,964 elements having a maximum aspect ratio of 56.3%, of which 82.6% elements had an aspect ratio < 3. The percentage of distorted elements was, on average, 0.036%.

To solve the problem with the help of the SolidWorks Simulation program, the same design data were used as in the case of solving the problem with the author’s proposed theoretical method, previously presented.

8. Comparison of the Results Obtained by Applying Our Own Method with Those Resulting from Applying the FEM

It should be noted that the following notations were used to create the diagrams:

-

Shaft without sealing device—AFDE;

-

Shaft with sealing device—ACDE;

-

Results obtained by the finite element method—FEM;

-

Theoretical results for which the linearization of the systems was obtained by the Newton method—T. Newton;

-

Theoretical results for which the linearization of the systems was carried out by the least-squares method—T. Cmmp;

-

Mixer mass of 0.1 kg—m

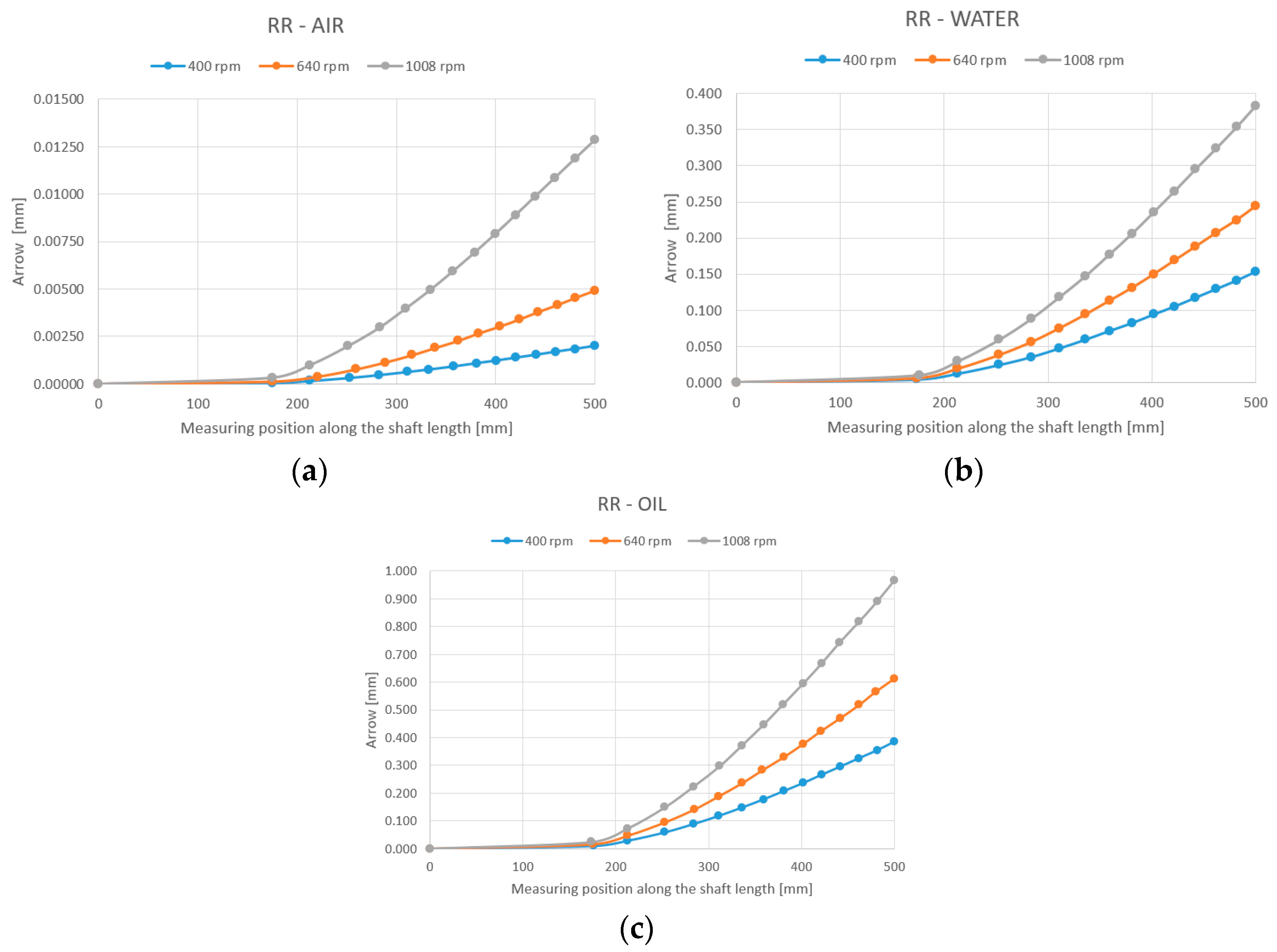
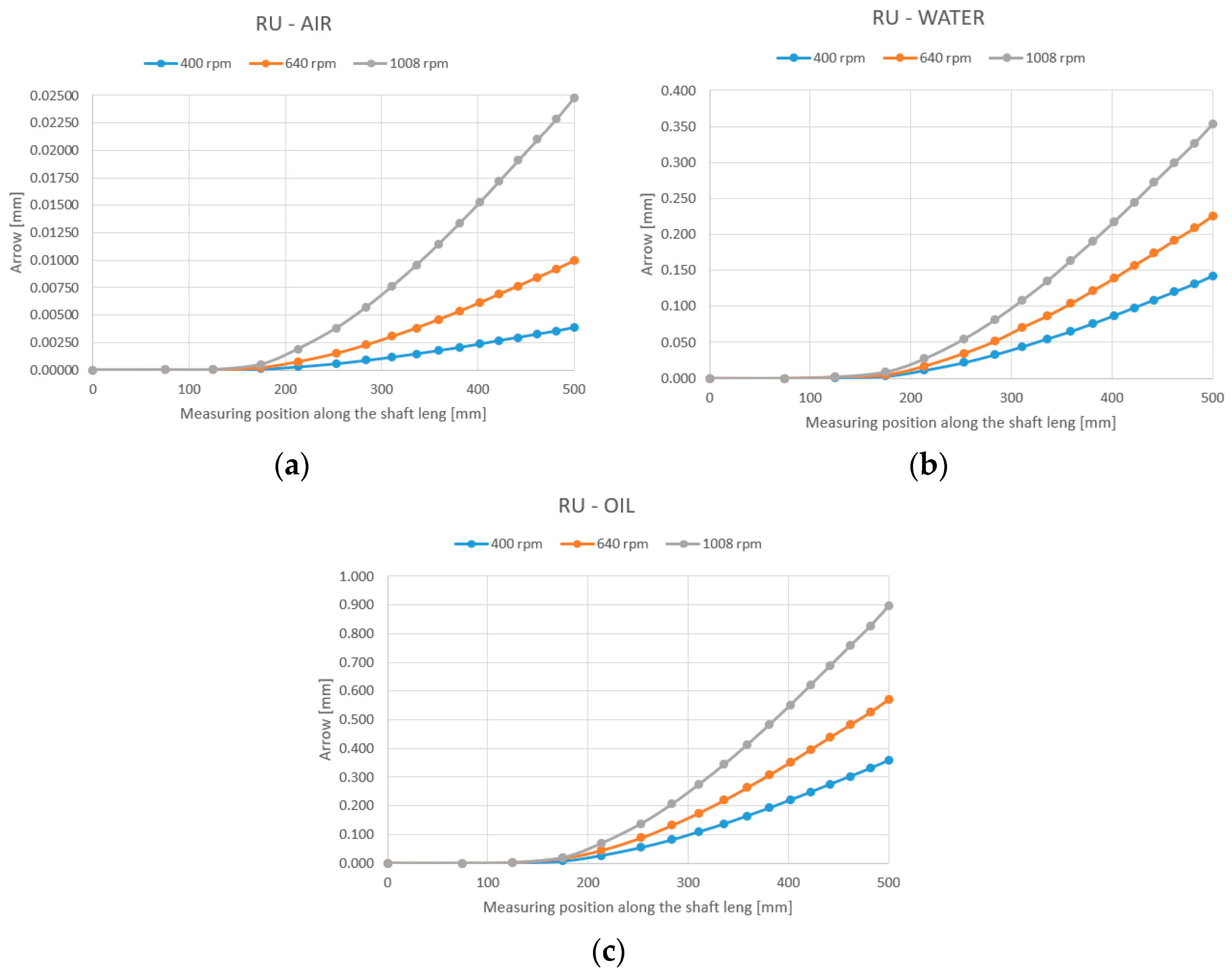
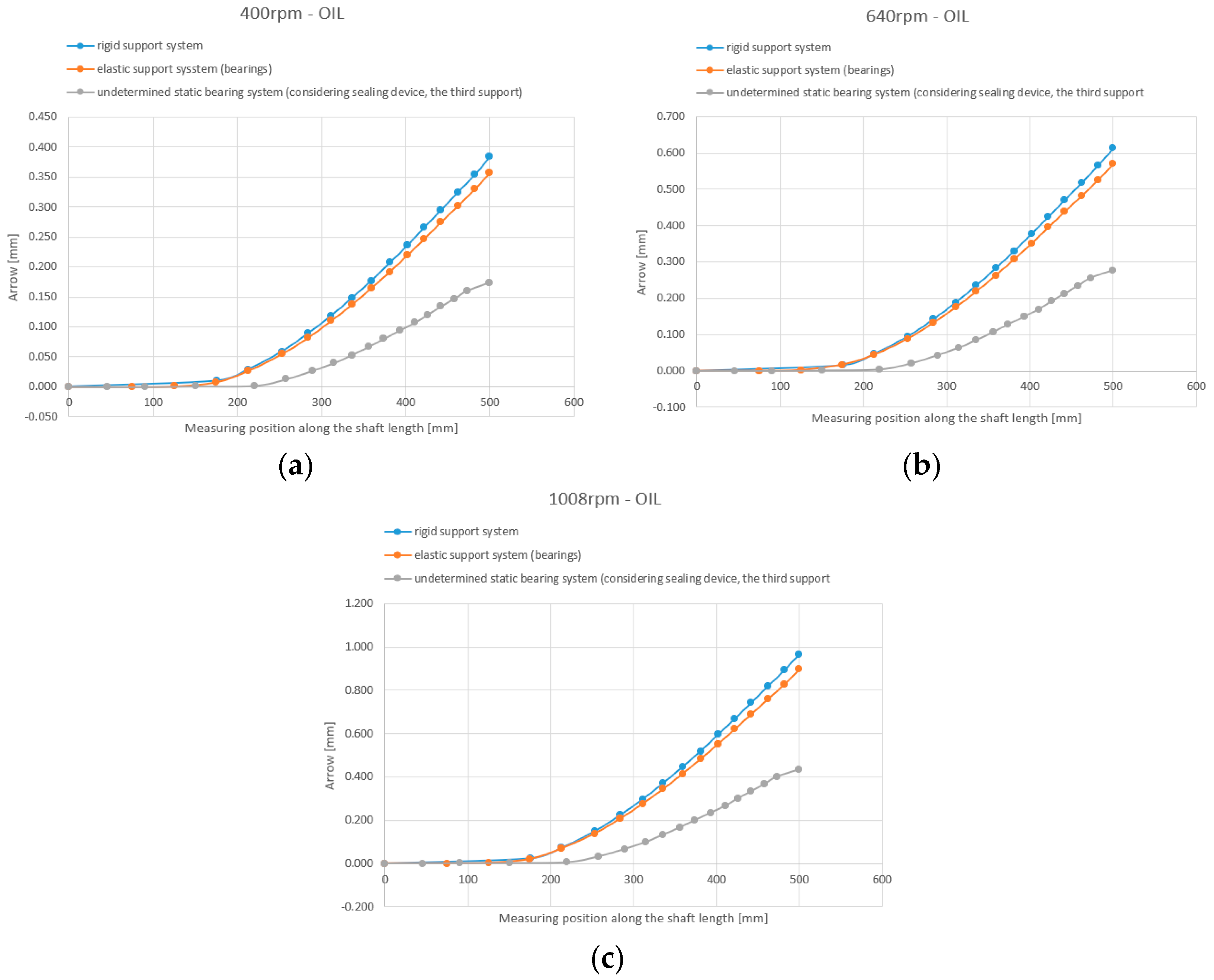
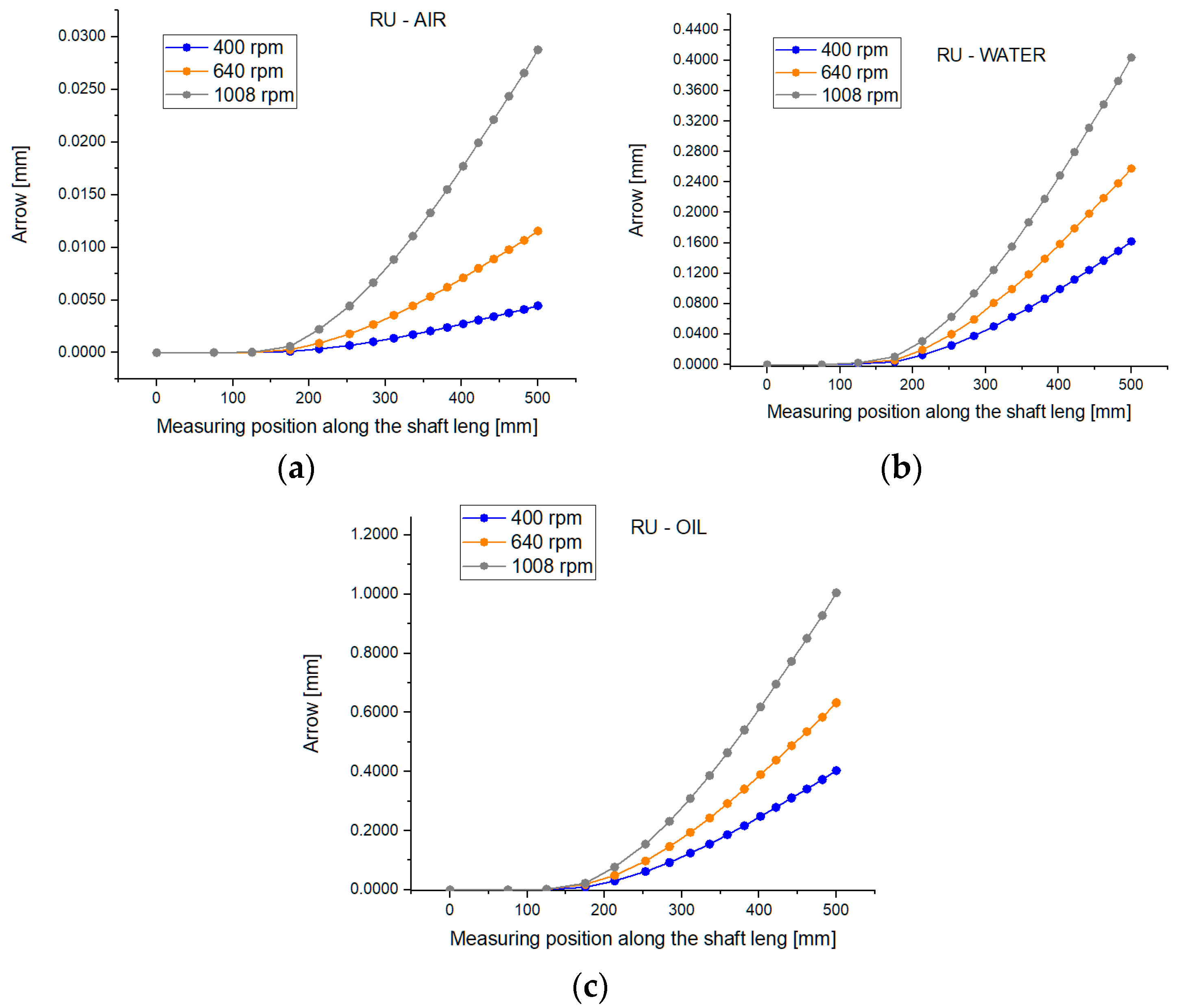
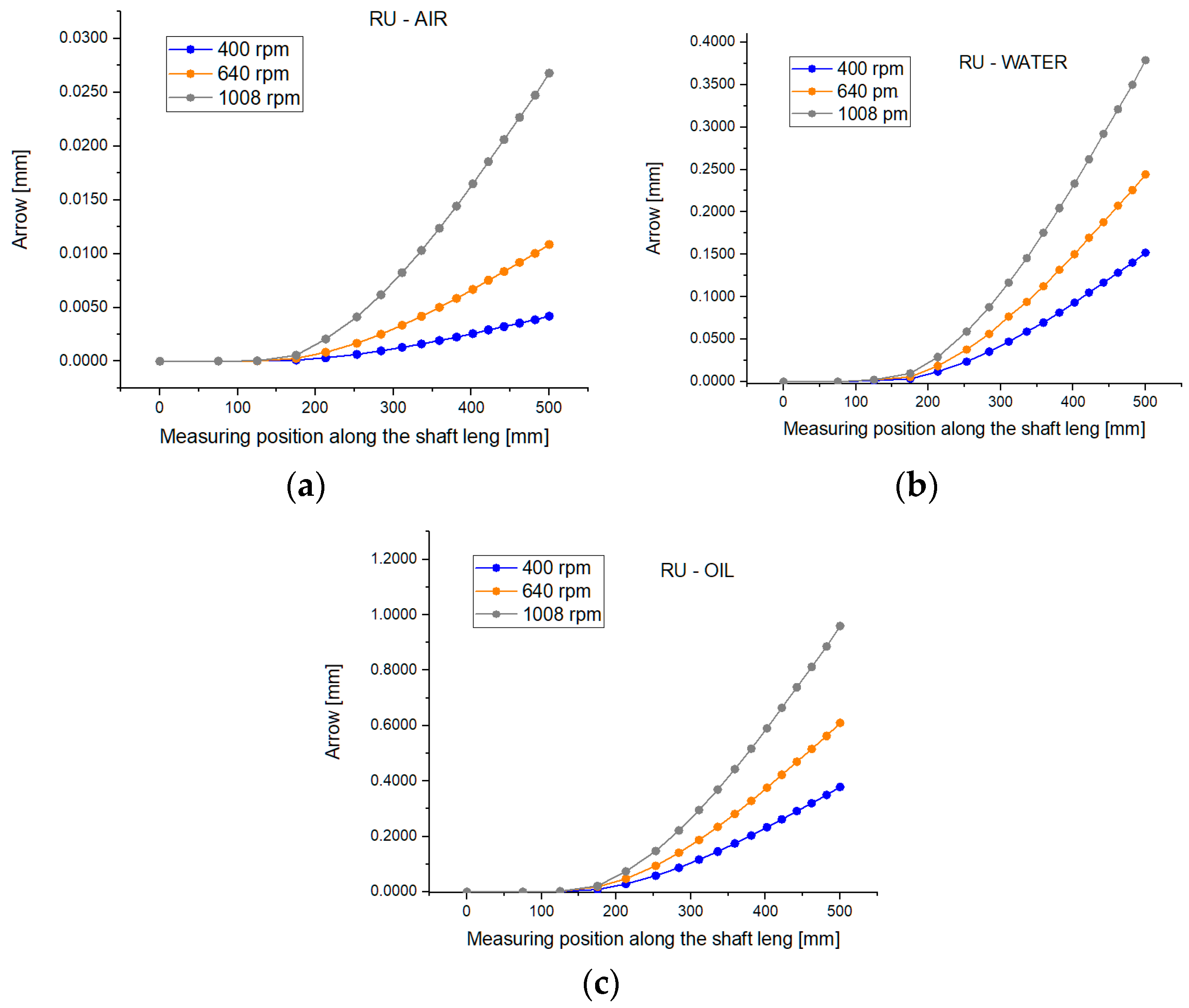
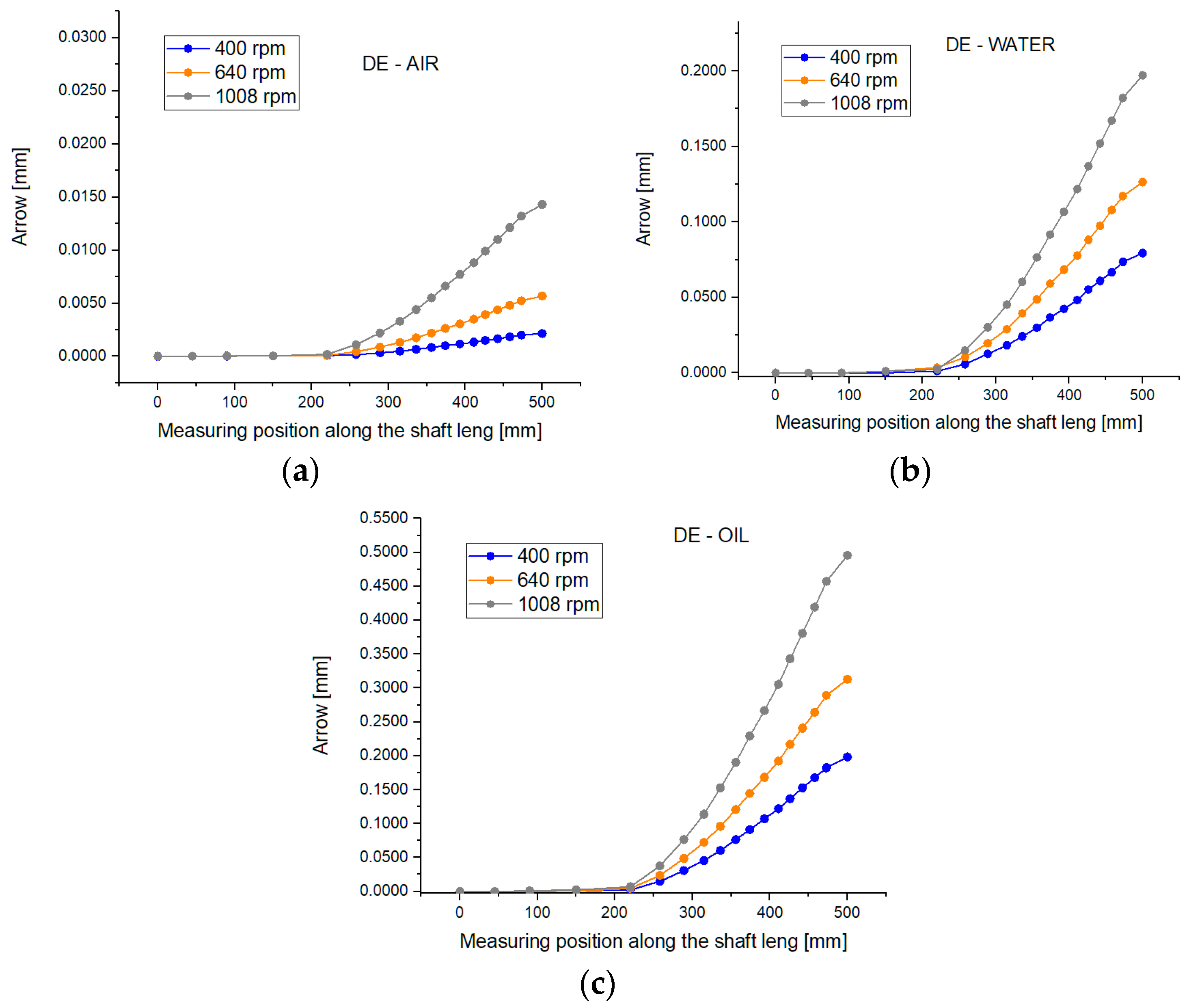
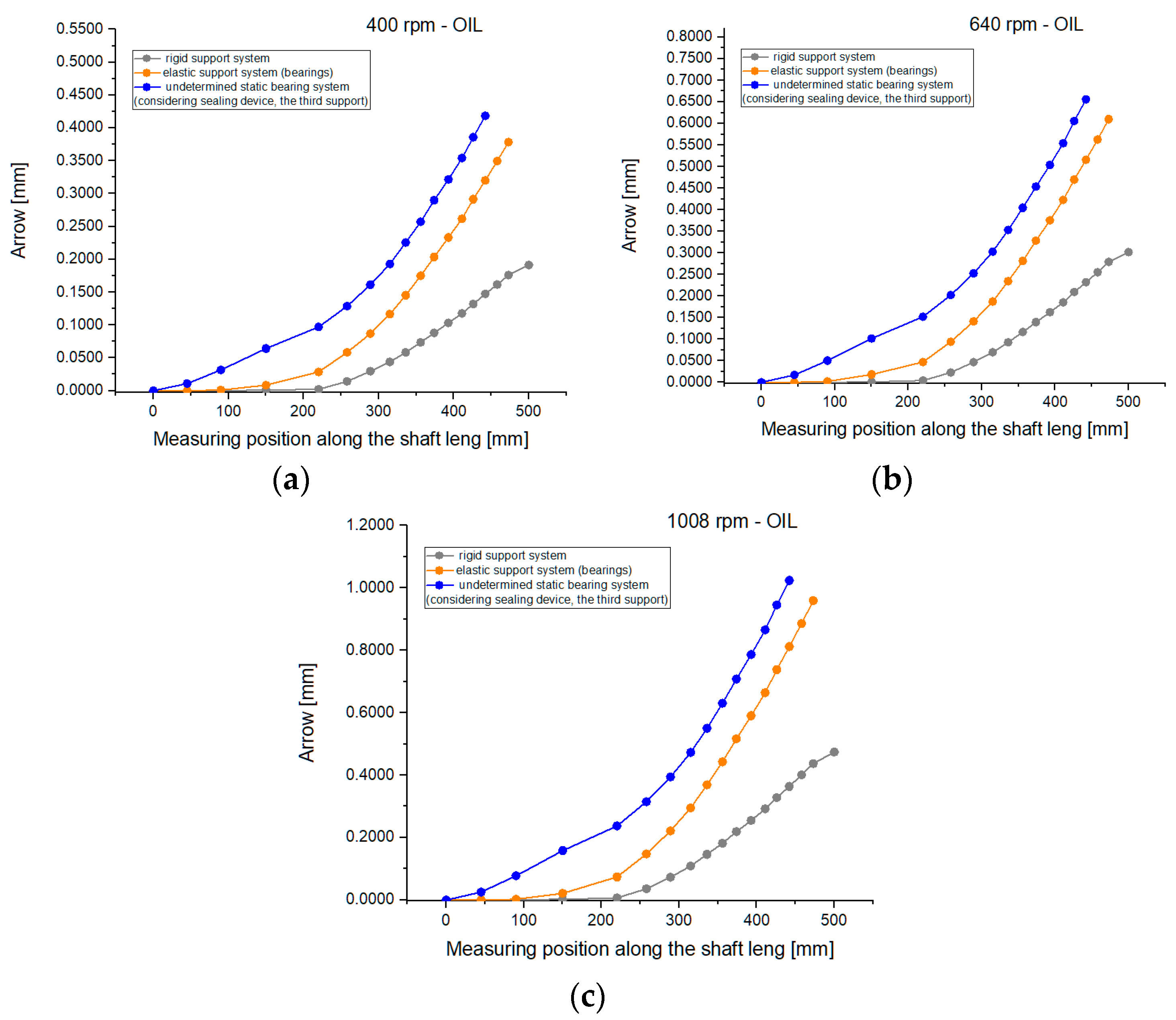
As can be seen theoretically and experimentally, shaft deformations are strongly influenced by both the working environment and the speed, as seen in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14. Based on the theoretical and experimental studies carried out, it was found that the shaft deflection, when mixing takes place in water, is larger than that when the shaft rotates in air because the hydrodynamic mass increases (Figure 6a,b, Figure 7a,b, Figure 9a,b, Figure 10a,b, Figure 11a,b and Figure 12a,b). The shaft deflection decreases, however, when the viscosity of the working medium increases (compared to water) because the amount of damping increases (Figure 6c, Figure 7c, Figure 9c, Figure 10c, Figure 11c, and Figure 12c).

It was found, both theoretically and experimentally, that the presence of the sealing device leads to an accentuated decrease in the shaft deflection, which leads to an increase in the fundamental pulsation, p₁, which is a very important aspect for shafts working at p > p₁ (elastic shaft).

For more conclusive evidence of the stiffening effect of the sealing device, the following diagrams were created: Figure 7, Figure 8, Figure 11, Figure 12, Figure 13 and Figure 14.

It was found that the theoretically determined arrow values are higher than the experimentally determined ones.

Both the proposed theoretical calculations are satisfactory from an engineering point of view, but the Newton method is preferred, as it leads to the smallest deviations from the experimentally determined values.

It should also be highlighted that, as can be seen from the diagrams in Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14, the data obtained through theoretical methods are not described by linear functions, as expected in the case of experimental determination, under static conditions for the arrows. This is explained, however, by the fact that the systems (AFDE and ACDE), which are nonlinear and non-homogeneous, were linearized using approximate numerical analysis methods.

9. Supporting Theoretical Results with Experimental Results

On the topic presented in the paper, the authors also conducted experimental research, which was the aim of other published papers [26,29,34,38,40].

Based on previous tests, in order to improve the accuracy of the data collected, an experimental installation with very high rigidity was used, making it almost impossible to pick up vibrations other than those induced by the working environment of the mixing device.

The bearing system was created by means of a cassette containing two bearings (of the same type) of radial ball bearing type 6000, with a ball diameter of D_w = 4.7665 mm, the number of balls being z = 7, and the same values of bearing characteristics that were used in the theoretical calculations.

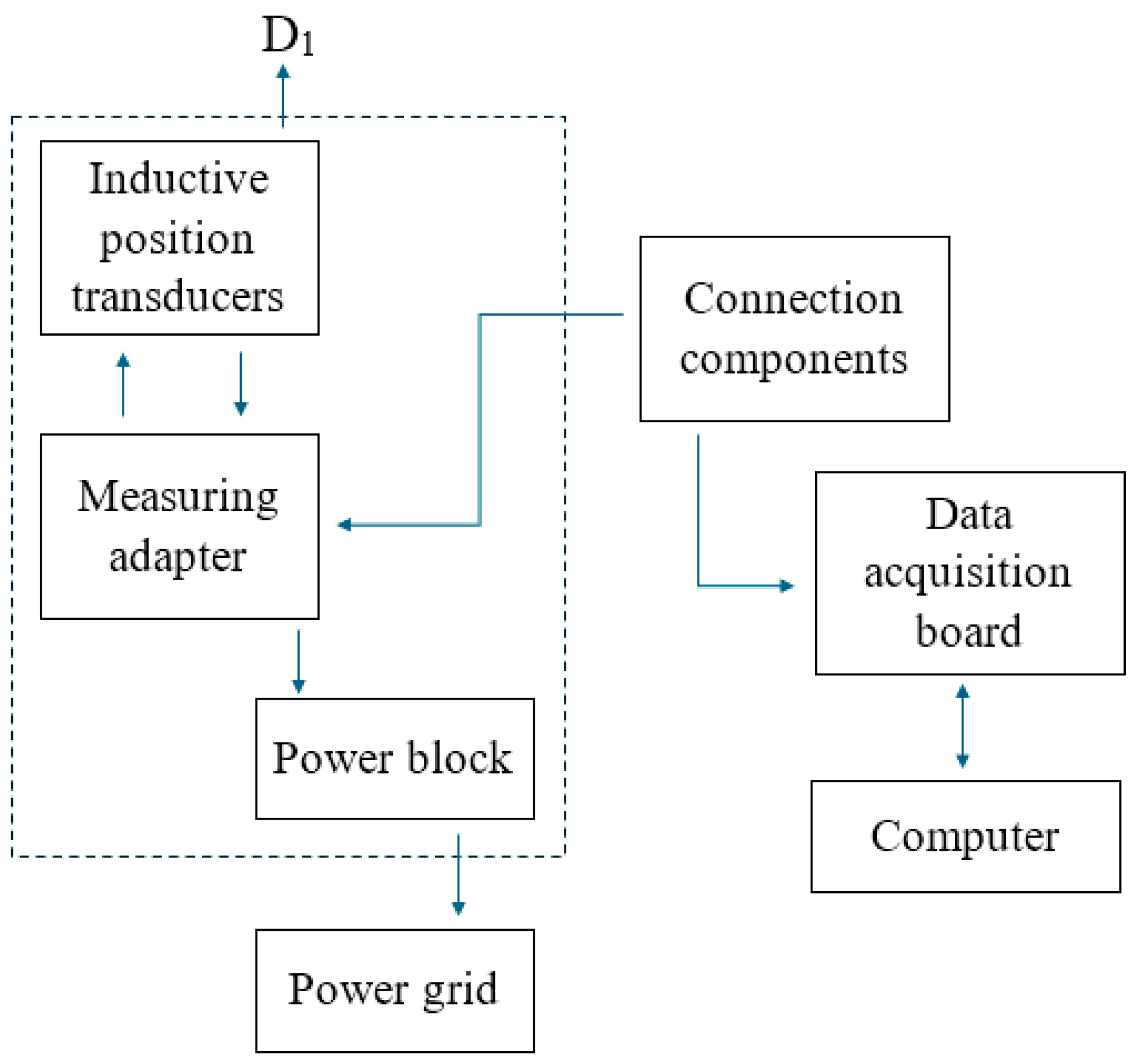
Inductive position transducers of type PR 9373 were used for the measurements.

A data acquisition board (Figure 15) connected to a computer was used for data collection and interpretation, which, using appropriate software, recorded and processed the measurement data.

The signal applied to the data acquisition board was amplified, sequenced, and discretized.

For data acquisition, Lab View software was used, specialized for graphical programming in the field of virtual instrumentation, with which any electronic measuring instrument can be graphically programmed and virtually realized.

The block scheme for the virtual tool consists of the following:

-

The configuration module, AI CONFIG, which recognizes the data acquisition board by means of the “device” number, sets the channels on which signals are collected, “acquisition channels (15:0)”, and sets the number of scans the programmer requests.

-

The start module, AI START, which commands the start of data scanning and allows the choice of the scanning rate which the programmer or user of the virtual instrument wants.

-

The data reading module, AI READ, which reads the collected data, depending on the number of channels chosen, the number of scans, and the scan rate set. It performs data filtering to remove noise superimposed on the useful signal due to the rotational movement of the shaft and transmits the processing result to graphic interface processing.

-

The data erasure block, AI CLEAR, which clears the data from the buffer following a scan and allows a new data collection process to start.

-

The error block, ERROR ?!, which signals the existence of a hard or soft error during the program run and data acquisition.

Based on this block scheme, a graphical control panel is automatically built for the virtual instrument, with which different values can be set for the number of scans, the number of channels on which data are acquired, etc. The front panel of the virtual instrument consists of digital switches for setting the number of channels, the scan rate, and the amount of scanned data.

As a result of conducting the experimental research, it was found that

-

The theoretically determined arrow values are higher than the experimentally determined ones.

-

Both the proposed theoretical calculations are satisfactory from an engineering point of view, but the Newton method is preferred, as it leads to the smallest deviations from the experimentally determined values.

10. Further Derived Research Directions

Further derived research directions include the following:

-

The shear force and bending moment in any section can be calculated in the same program; the program can then be extended to determine the stress state.

-

The determination of deformations as a function of the working medium (through the hydrodynamic mass, mh) and as a function of the working speed (through ω).

Applying the same calculation algorithm as presented above, the accuracy of the results can be increased if the real case of the stepped shaft is considered. In this case, it is sufficient to introduce an equivalent moment of inertia—Equation (29)—in the relations presented above:

$$I_{z,e}={\displaystyle \frac{\sum _{i=1}^n{I}_i{l}_i}{l}},$$

(29)

where l $=\sum _{i=1}^n{l}_i$ and n is the number of shaft steps.

Thus, for a given speed, the constant α in relation (17) becomes α_i, calculated with the following relation:

$$\alpha =∜{\displaystyle \frac{A\rho {\omega }^2}{4E{I}_{z,e}}}.$$

(30)

11. Conclusions

In designing mixing devices, taking into account the shaft deformations is an important step towards more accurate calculation and, therefore, towards increased reliability in the operation of the whole system.

With the results presented in this paper, it is supported that the classical method, which ignores the obvious stiffening effect of the seal, can be replaced by the proposed method of calculating the shaft of the mixing device as a statically determined shaft. In the classical method, even if the shaft is considered static and undetermined, considering the presence of the sealing device as well, the bearings and the sealing device were considered rigid bearings; if the bearings were considered elastic bearings, the effect of the elastic reaction was considered according to linear laws.

This paper, through the provided calculation method, solves the problem of shaft deformations in the case of the presence of a sealing device, as an elastic element, under the conditions of considering the nonlinear elasticity of the bearings.

With the help of the calculation program provided by the authors, the shear force and bending moment in any section can also be calculated, thus also providing the possibility of determining the stress state.

Although in the calculation algorithm presented in this paper, the case of a shaft with a constant cross-section was used, like in our own experimental installation, it is possible, if practical conditions require, to easily apply this in the case of the stepped shaft as well. For this, it is only necessary to use the equivalent moment of inertia as in the initial program data.

The authors believe that the accuracy of the results would have been better if they had also been able to solve the problem of accurately determining the cantilever loading force on the shaft. It is also considered that the numerical computation methods (the method of least squares and Newton’s method) used at this stage of research in solving nonlinear systems introduce a certain degree of approximation into the results.

However, a satisfactory approximation of experimentally obtained deformation values compared to the theoretically obtained ones (using both the proper method and the FEM) was observed. The proposed calculation method provides a satisfactory calculation in the context of engineering.

Based on comparative analysis, the authors recommend the software program based on the Newton method, finding that in this case, the differences between the theoretical and experimental results are the smallest [2,5,9,22,26,28,29].

It can be said, therefore, that both the established calculation relation and the calculation program can constitute real support in the activity of design engineers, with the calculation program offering the possibility of quickly determining deformations, as well as the cutting force and bending moment in sections of most interest in the shaft (console end, sealing device, bearings, coupling) and, generally, in any section. On the other hand, by determining shaft deformations at the design stage, their variation can be noticed, thus avoiding premature wear or even damage to the seal device, bearing, or coupling.