The Control of Handling Stability for Four-Wheel Steering Distributed Drive Electric Vehicles Based on a Phase Plane Analysis
Abstract
1. Introduction
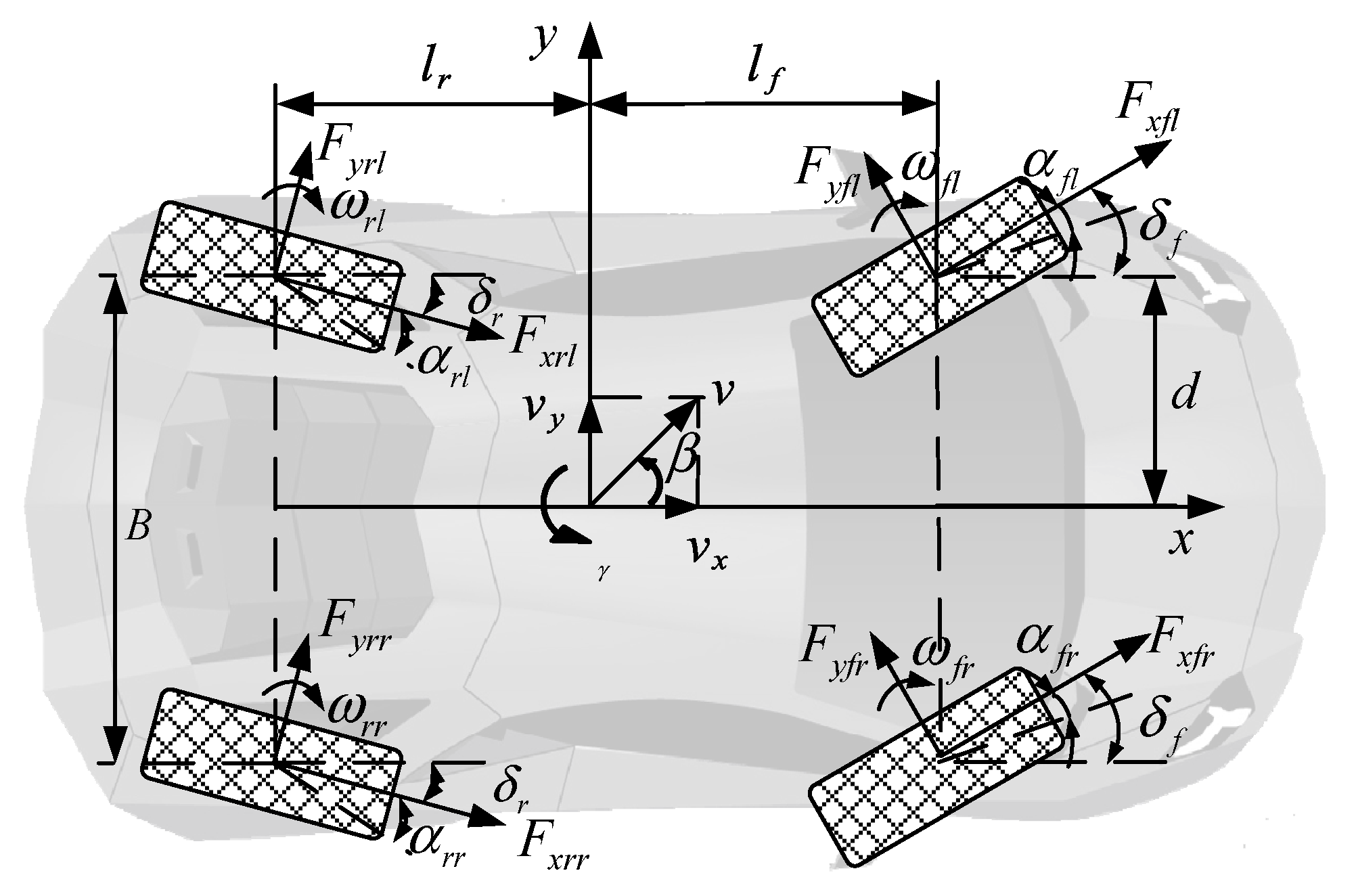
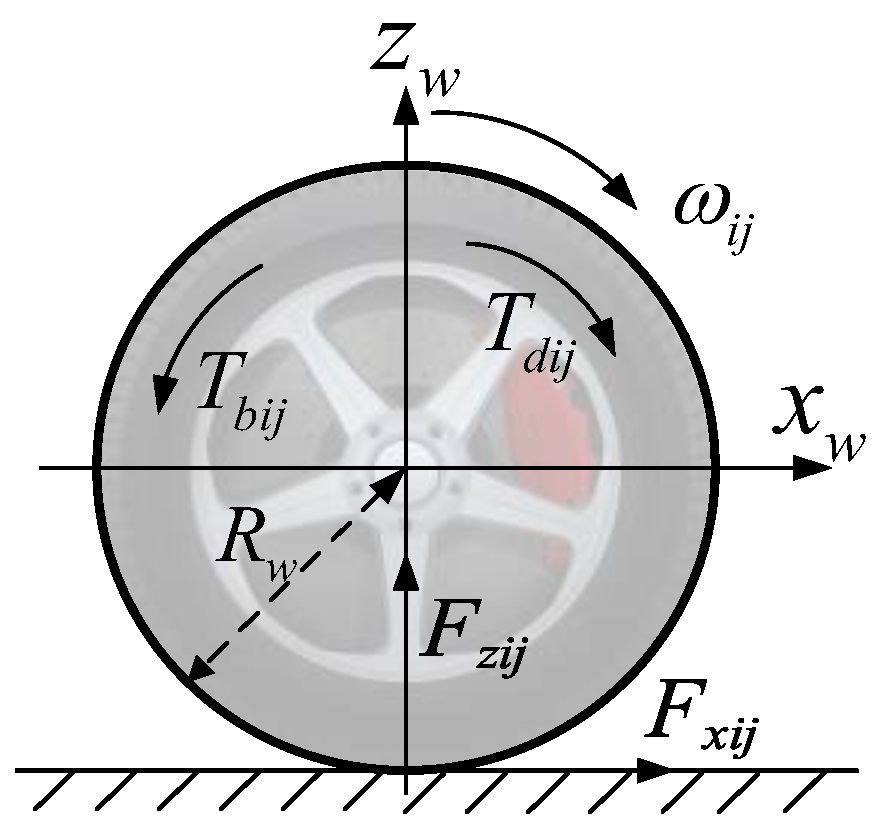
2. Vehicle System Modeling
2.1. Nonlinear 7 DOF Model of Four-Wheel Steering
2.2. Tire Model
2.3. Linear 2-DOF Model of Four-Wheel Steering
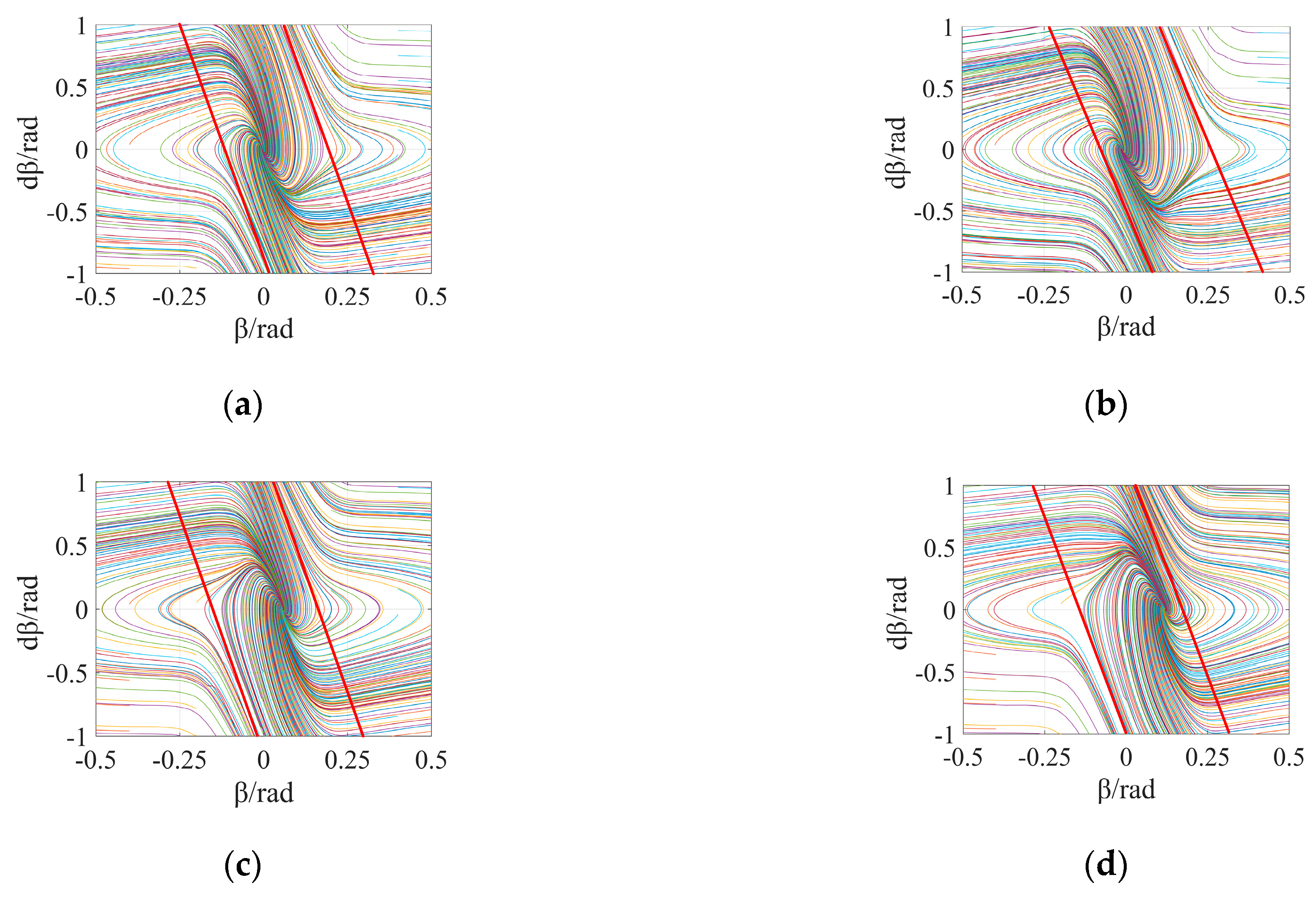
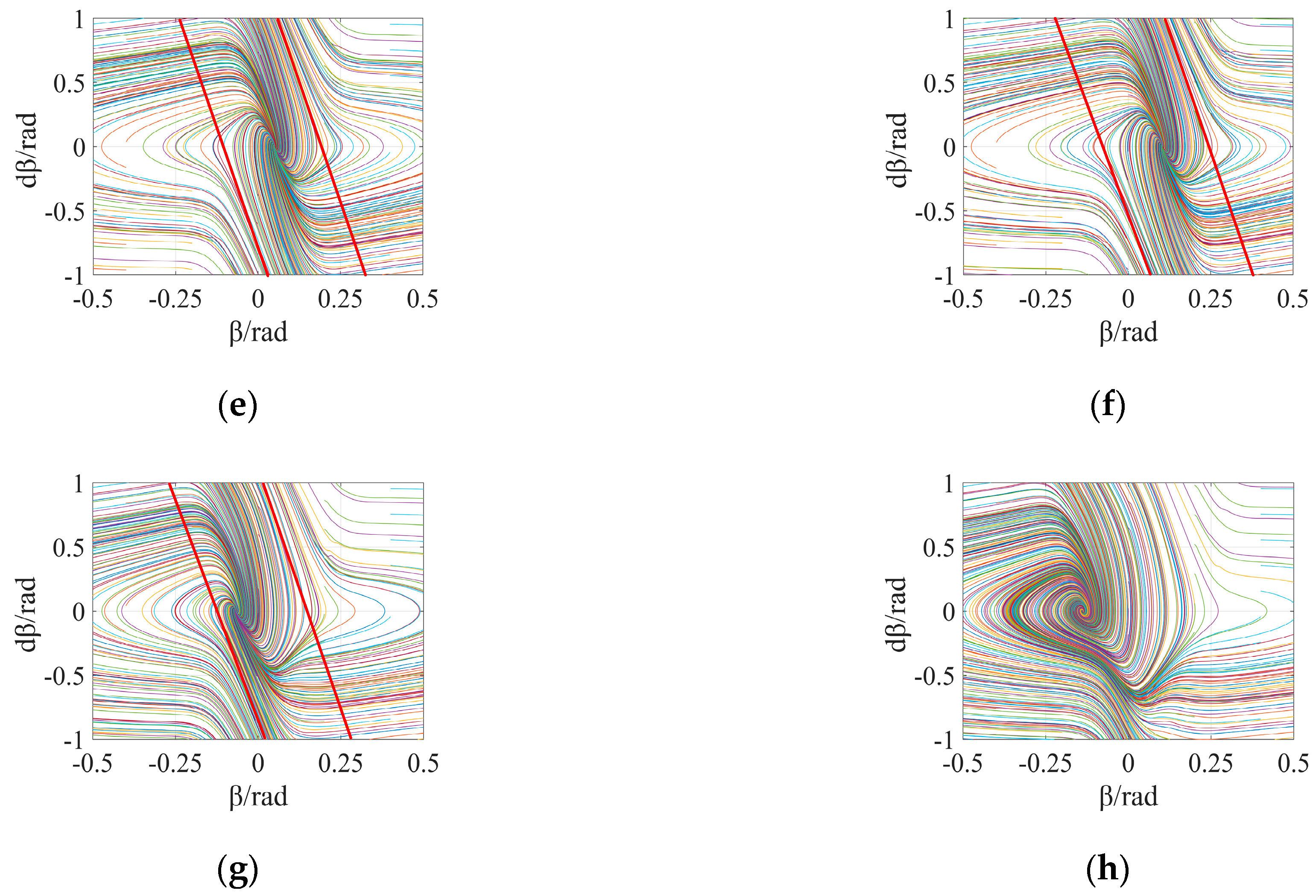
3. Phase Plane Analysis
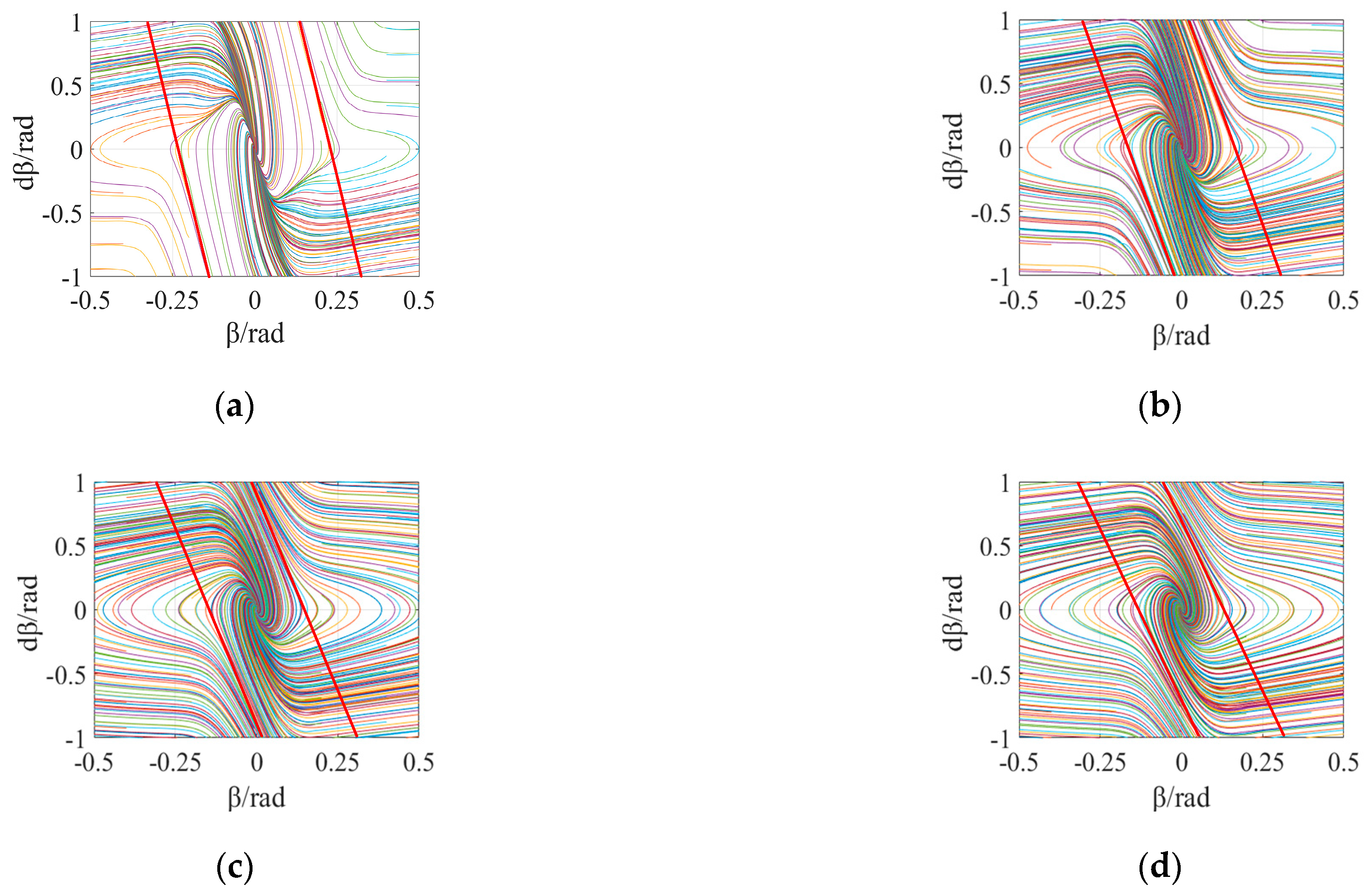
3.1. Phase Plane Stable Region Division
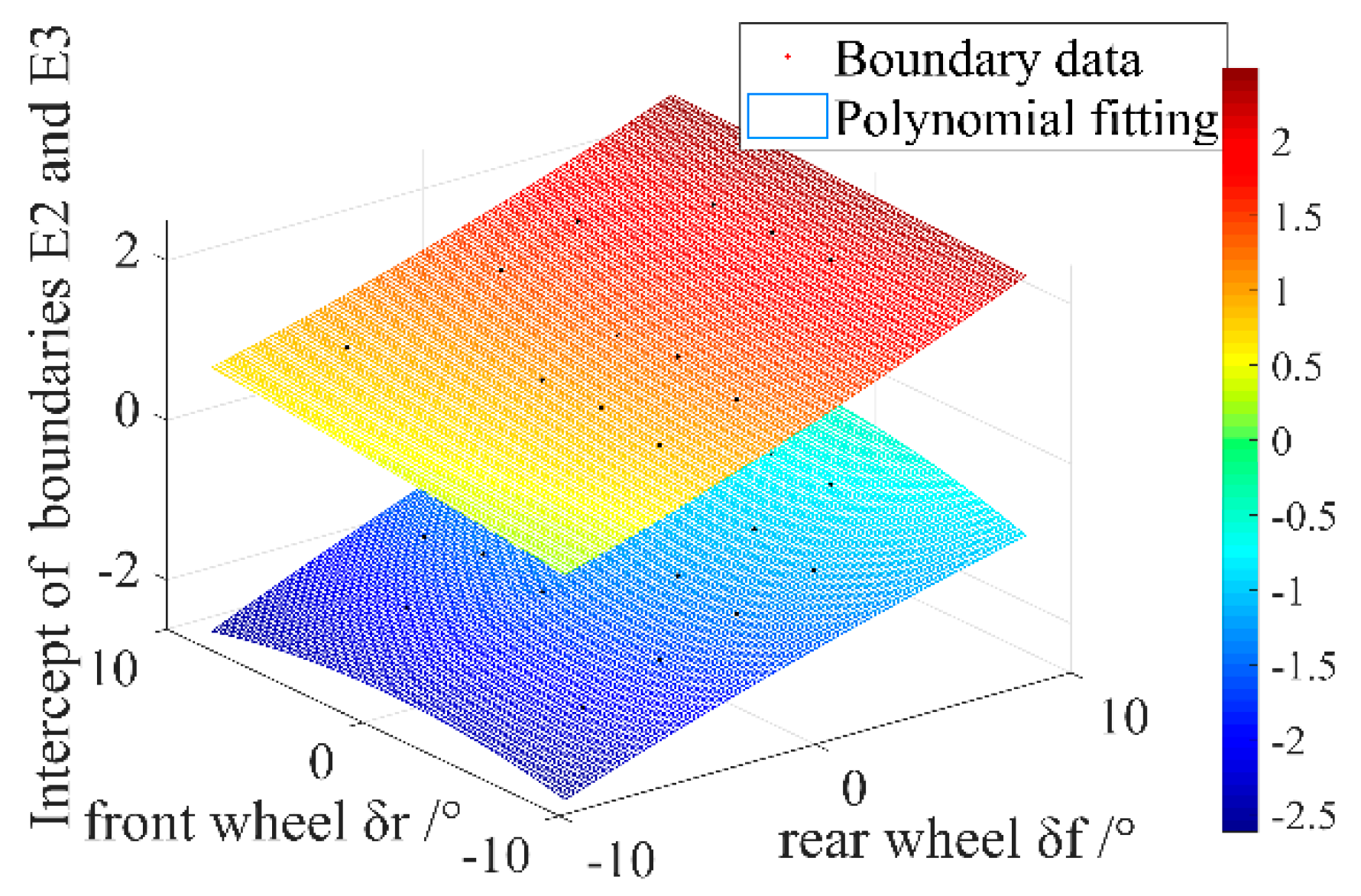
3.2. Stability Boundary Model
4. Hierarchical Stability Control Design
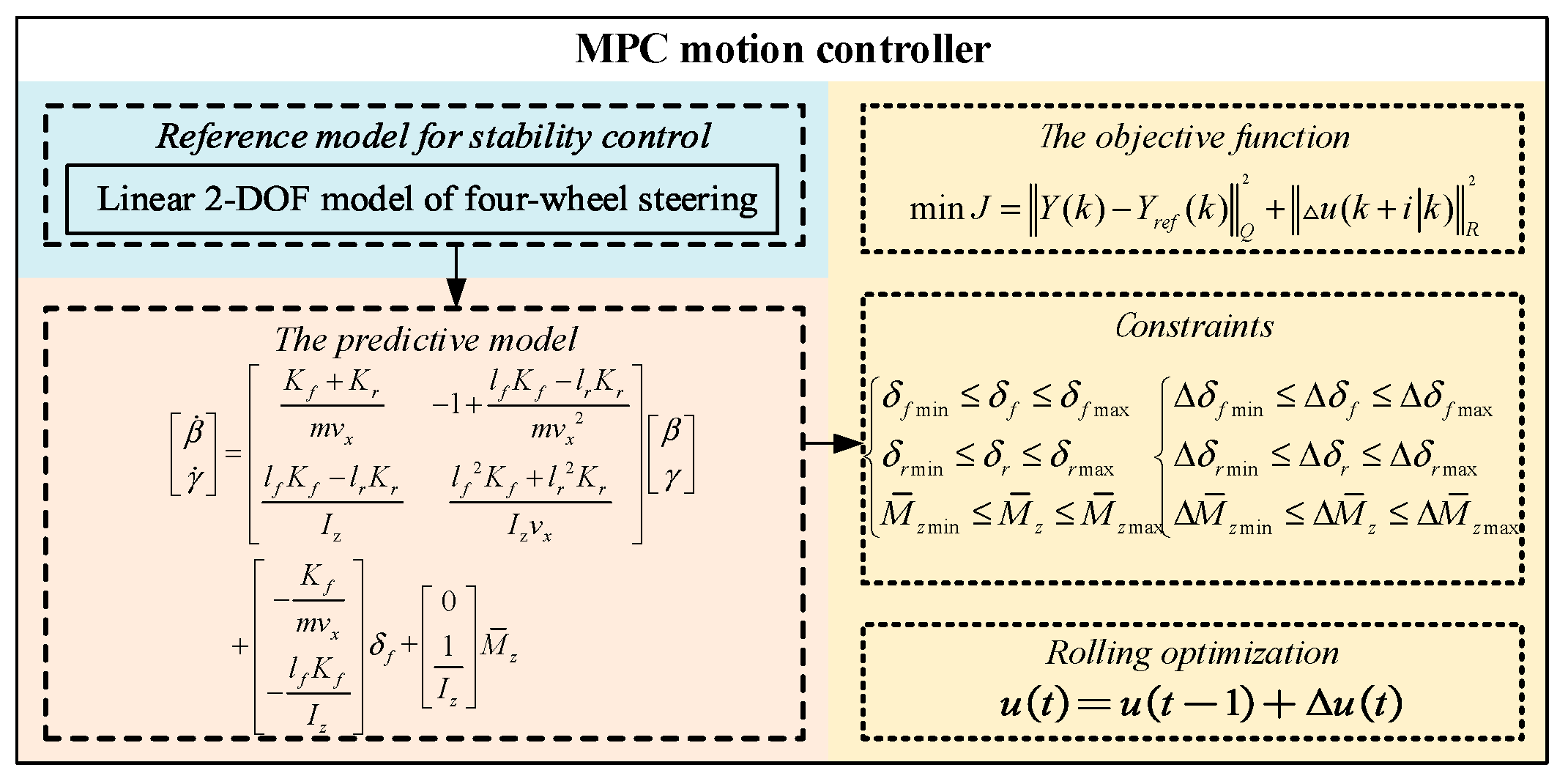
4.1. Control System Framework
4.2. Upper Motion Controller
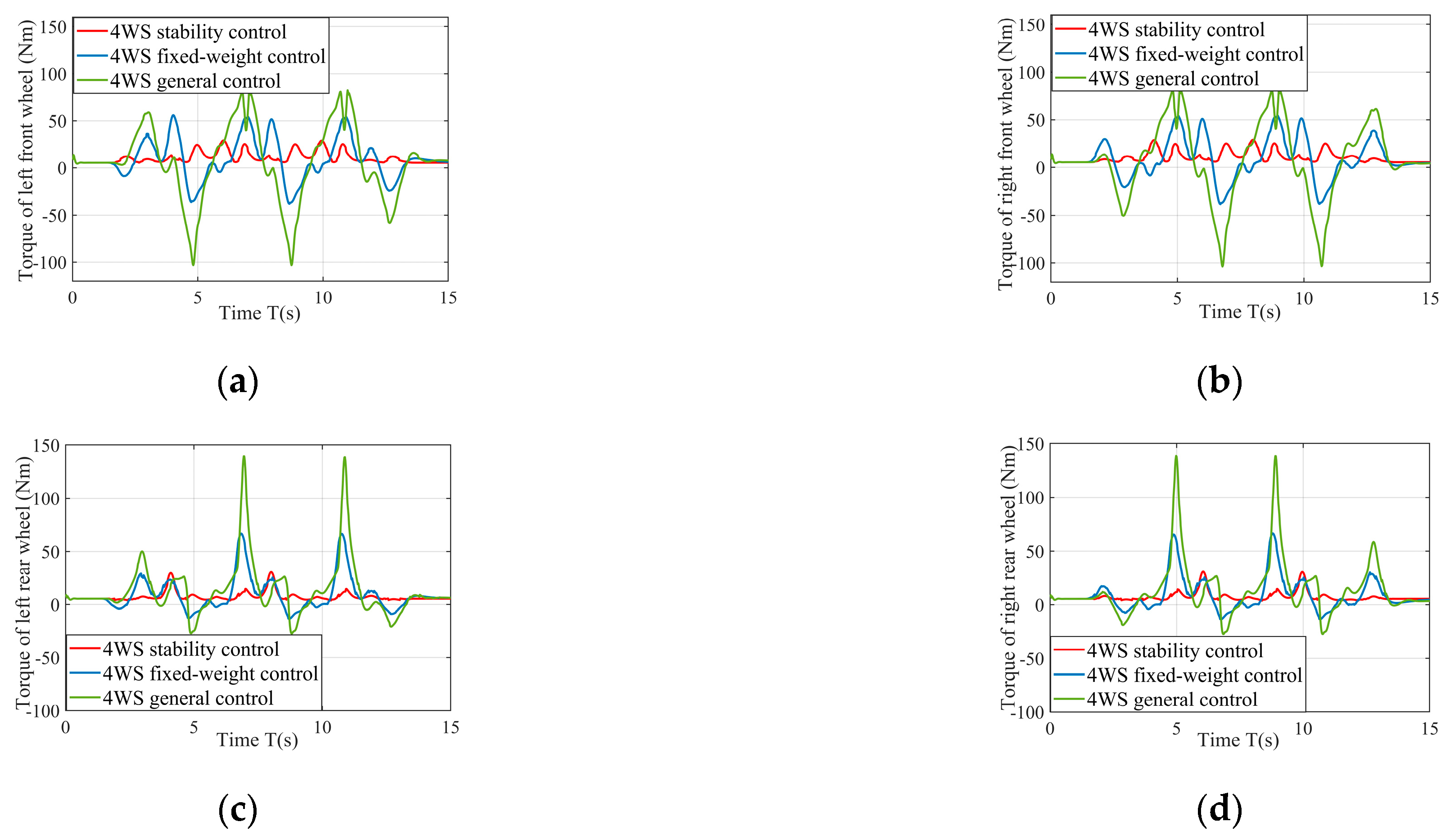
4.3. Lower Torque Distribution Controller
5. Simulation and Results
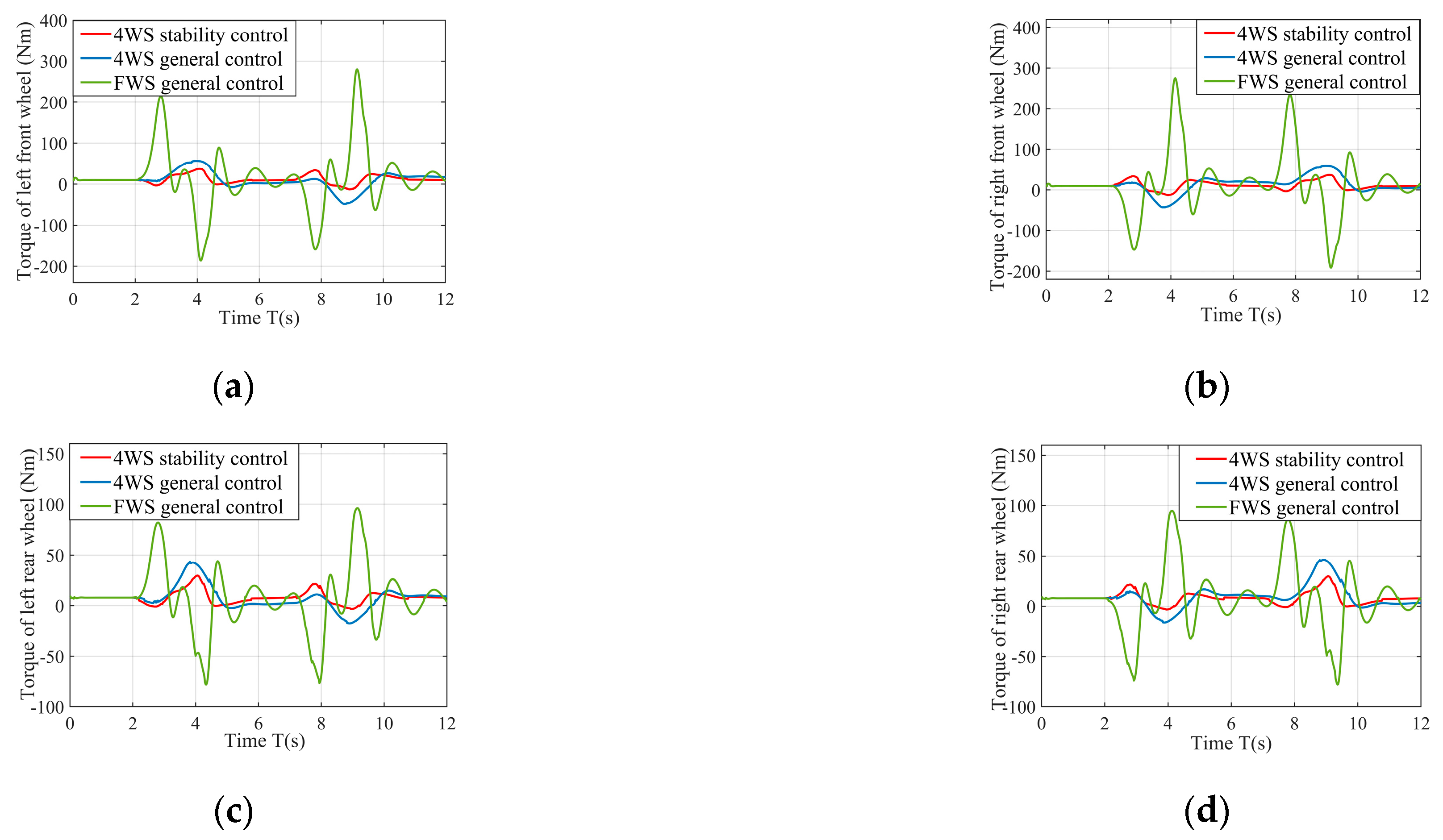
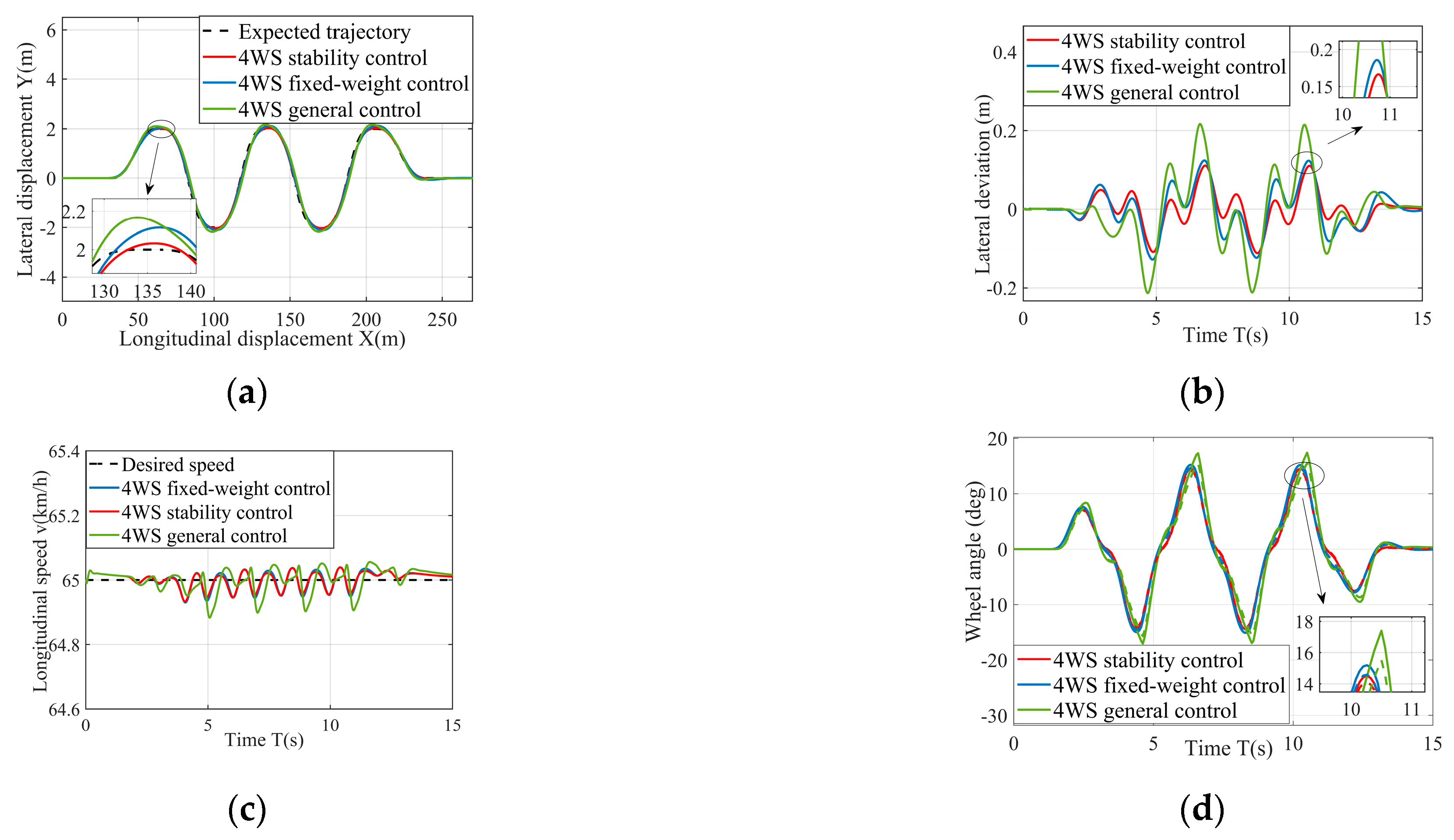
5.1. Double Lane Change Condition Simulation
5.2. Serpentine Working Condition Simulation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fu, W.; Liu, Y.; Zhang, X. Research on Accurate Motion Trajectory Control Method of Four-Wheel Steering AGV Based on Stanley-PID Control. Sensors 2023, 23, 7219. [Google Scholar] [CrossRef]
- Lai, F.; Huang, C. Path tracking and stability integrated control of intelligent vehicles under steering collision avoidance. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2023, 237, 1868–1884. [Google Scholar] [CrossRef]
- Su, L.; Wang, Z.; Chen, C. Torque vectoring control system for distributed drive electric bus under complicated driving conditions. Assem. Autom. 2022, 42, 1–18. [Google Scholar] [CrossRef]
- Liang, Z.; Shen, M.; Zhao, J.; Li, Z.; Ding, Z. Adaptive Sliding Mode Fault Tolerant Control for Autonomous Vehicle with Unknown Actuator Parameters and Saturated Tire Force Based on the Center of Percussion. IEEE Trans. Int. Transp. Syst. 2023, 24, 11595–11606. [Google Scholar] [CrossRef]
- Lei, Y.; Wen, G.; Fu, Y.; Li, X.; Hou, B.; Geng, X. Trajectory-following of a 4WID-4WIS vehicle via feedforward–backstepping sliding-mode control. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2022, 236, 322–333. [Google Scholar] [CrossRef]
- Lu, M.; Xu, Z. Integrated Handling and Stability Control with AFS and DYC for 4WID–EVs via Dual Sliding Mode Control. Autom. Control Comp. Sci. 2021, 55, 243–252. [Google Scholar]
- Silva, F.; Silva, L.; Eckert, J.; Yamashita, R.; Lourenco, M. Parameter influence analysis in an optimized fuzzy stability control for a four-wheel independent-drive electric vehicle. Control Eng. Pract. 2021, 120, 105000. [Google Scholar] [CrossRef]
- Zhang, D.; Song, Q.; Wang, G.; Liu, C. A Novel Longitudinal Speed Estimator for Four-Wheel Slip in Snowy Conditions. Appl. Sci. 2021, 11, 2809. [Google Scholar] [CrossRef]
- Zheng, H.; Yang, S.; Li, B. Optimization Control for 4WIS Electric Vehicle Based on the Coincidence Degree of Wheel Steering Centers. SAE Int. J. Veh. Dyn. Stab. NVH 2018, 2, 169–184. [Google Scholar] [CrossRef]
- Xu, T.; Zhao, Y.; Wang, Q.; Deng, H.; Lin, F. An Adaptive Inverse Model Control Method of Vehicle Yaw Stability with Active Front Steering Based on Adaptive RBF Neural Networks. IEEE Trans. Veh. Technol. 2023, 72, 13873–13887. [Google Scholar] [CrossRef]
- Botes, W.; Botha, T.; Els, P. Real-time lateral stability and steering characteristic control using non-linear model predictive control. Veh. Syst. Dyn. 2023, 61, 1063–1085. [Google Scholar] [CrossRef]
- Tan, Q.; Qiu, C.; Huang, J.; Yin, Y.; Zhang, X.; Liu, H. Path tracking control strategy for off-road 4WS4WD vehicle based on robust model predictive control. Rob. Autonom. Syst. 2022, 158, 104267. [Google Scholar] [CrossRef]
- Zhang, N.; Wang, J.; Li, Z.; Xu, N.; Ding, H.; Zhang, Z.; Guo, K.; Xu, H. Coordinated Optimal Control of AFS and DYC for Four-Wheel Independent Drive Electric Vehicles Based on MAS Model. Sensors 2023, 23, 3505. [Google Scholar] [CrossRef] [PubMed]
- Hang, P.; Chen, X. Integrated chassis control algorithm design for path tracking based on four-wheel steering and direct yaw-moment control. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2019, 233, 625–641. [Google Scholar] [CrossRef]
- Wang, C.; Heng, B.; Zhao, W. Yaw and lateral stability control for four-wheel-independent steering and four-wheel-independent driving electric vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 409–422. [Google Scholar] [CrossRef]
- Hang, P.; Xia, X.; Chen, X. Handling Stability Advancement With 4WS and DYC Coordinated Control: A Gain-Scheduled Robust Control Approach. IEEE Trans. Veh. Technol. 2021, 70, 3164–3174. [Google Scholar] [CrossRef]
- Taghavifar, H.; Hu, C.; Taghavifar, L.; Qin, Y.; Na, J.; Wei, C. Optimal robust control of vehicle lateral stability using damped least-square backpropagation training of neural networks. Neurocomputing 2020, 384, 256–267. [Google Scholar] [CrossRef]
- Tian, J.; Ding, J.; Zhang, C.; Luo, S. Four-Wheel Differential Steering Control of IWM Driven EVs. IEEE Access 2020, 8, 152963–152974. [Google Scholar] [CrossRef]
- Ge, L.; Shan, Z.; Ma, F.; Han, Z.; Guo, K. Simultaneous Stability and Path Following Control for 4WIS4WID Autonomous Vehicles Based on Computationally Efficient Offset Free MPC. Int. J. Control Autom. Syst. 2023, 21, 2782–2796. [Google Scholar] [CrossRef]
- Shi, K.; Yuan, X.; He, Q. Double-layer Dynamic Decoupling Control System for the Yaw Stability of Four Wheel Steering Vehicle. Int. J. Control Autom. Syst. 2019, 17, 1255–1263. [Google Scholar] [CrossRef]
- Marino, R.; Cinili, F. Input-output decoupling control by measurement feedback in four-wheel-steering vehicles. IEEE Trans. Control Syst. Technol. 2019, 17, 1163–1172. [Google Scholar] [CrossRef]
- Park, J.Y.; Na, S.; Cha, H.; Yi, K. Direct Yaw Moment Control with 4WD Torque-Vectoring for Vehicle Handling Stability and Agility. Int. J. Automot. Technol. 2022, 23, 555–565. [Google Scholar] [CrossRef]
- Wu, H.; Li, Y. Coordination Control of Path Tracking and Stability for 4WS Autonomous Vehicle. In Proceedings of the 2020 International Conference on Electromechanical Control Technology and Transportation (ICECTT), Nanchang, China, 15–17 May 2020; pp. 343–348. [Google Scholar]
- Wang, Q.; Zhao, Y.; Deng, Y.; Xu, H.; Deng, H.; Lin, F. Optimal Coordinated Control of ARS and DYC for Four-Wheel Steer and In-Wheel Motor Driven Electric Vehicle With Unknown Tire Model. IEEE Trans. Veh. Technol. 2020, 69, 10809–10819. [Google Scholar] [CrossRef]
- Sakhnevych, A.; Arricale, V.M.; Bruschetta, M.; Censi, A.; Mion, E.; Picotti, E.; Frazzoli, E. Investigation on the Model-Based Control Performance in Vehicle Safety Critical Scenarios with Varying Tyre Limits. Sensors 2021, 21, 5372. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Shu, H.; Chen, X.; Luo, S. Direct-yaw-moment control of four-wheel-drive electrical vehicle based on lateral tyre–road forces and sideslip angle observer. IET Int. Trans. Syst. 2019, 13, 303–312. [Google Scholar] [CrossRef]
- Yakub, F.; Mori, Y. Comparative study of autonomous path-following vehicle control via model predictive control and linear quadratic control. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2015, 229, 1695–1714. [Google Scholar] [CrossRef]
- Dong, Q.; Ji, X.; Liu, Y.; Liu, Y. Gain-Scheduled Steering and Braking Coordinated Control in Path Tracking of Intelligent Heavy Vehicles. ASME. J. Dyn. Sys. Meas. Control 2022, 144, 101006. [Google Scholar] [CrossRef]
- Yakub, F.; Muhammad, P.; Toh, H.T.; Talip, M.; Mori, Y. Explicit controller of a single truck stability and rollover mitigation. J. Mech. Sci. Technol. 2018, 32, 4373–4381. [Google Scholar] [CrossRef]
- Zhai, L.; Wang, C.; Hou, Y.; Hou, R.; Yuh, M.; Zhang, X. Two-level optimal torque distribution for handling stability control of a four hub-motor independent-drive electric vehicle under various adhesion conditions. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2022, 237, 544–559. [Google Scholar] [CrossRef]










| 6, 6 | 1.970 | −0.552 |
| 6, 3 | 1.973 | −0.490 |
| 3, 6 | 1.682 | −0.938 |
| 3, 3 | 1.573 | −0.816 |
| 3, 0 | 1.502 | −0.936 |
| 0, 3 | 1.198 | −1.219 |
| 0, 0 | 1.217 | −1.217 |
| 0, −3 | 1.308 | −1.213 |
| −3, 0 | 0.936 | −1.502 |
| −3, −3 | 0.931 | −1.629 |
| −6, −3 | 0.497 | −1.973 |
| −3, −6 | 0.823 | −1.641 |
| −6, −6 | 0.447 | −1.970 |
| 0.2 | 0.241 | −0.241 |
| 0.3 | 0.445 | −0.445 |
| 0.4 | 0.588 | −0.588 |
| 0.5 | 0.711 | −0.711 |
| 0.6 | 0.878 | −0.878 |
| 0.7 | 1.109 | −1.109 |
| 0.8 | 1.217 | −1.217 |
| 120 | −4.608 |
| 110 | −4.950 |
| 100 | −5.205 |
| 90 | −5.329 |
| 80 | −5.647 |
| 70 | −5.935 |
| 60 | −6.297 |
| 50 | −6.785 |
| 40 | −7.342 |
| Vehicle Parameters | Value |
|---|---|
| Vehicle mass | 1523 kg |
| Wheelbase | 2.548 m |
| Distance from CG to front axle | 1.163 m |
| Distance from CG to rear axle | 1.385 m |
| Track width | 1.530 m |
| Vehicle yaw moment of inertia | 2023 kg·m3 |
| Wheel inertia moment | 0.95 kg·m3 |
| Tire rolling radius | 0.354 m |
| Frontal area | 1.95 m2 |
| Wind resistance coefficient | 0.3 |
| Height of CG | 0.472 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Song, Q. The Control of Handling Stability for Four-Wheel Steering Distributed Drive Electric Vehicles Based on a Phase Plane Analysis. Machines 2024, 12, 478. https://doi.org/10.3390/machines12070478
Wang G, Song Q. The Control of Handling Stability for Four-Wheel Steering Distributed Drive Electric Vehicles Based on a Phase Plane Analysis. Machines. 2024; 12(7):478. https://doi.org/10.3390/machines12070478
Chicago/Turabian StyleWang, Guanfeng, and Qiang Song. 2024. "The Control of Handling Stability for Four-Wheel Steering Distributed Drive Electric Vehicles Based on a Phase Plane Analysis" Machines 12, no. 7: 478. https://doi.org/10.3390/machines12070478
APA StyleWang, G., & Song, Q. (2024). The Control of Handling Stability for Four-Wheel Steering Distributed Drive Electric Vehicles Based on a Phase Plane Analysis. Machines, 12(7), 478. https://doi.org/10.3390/machines12070478





