A Comparative Study of Pole–Slot Combination with Fractional Slot Concentrated Winding in Outer Rotor Permanent Magnet Synchronous Generator for Hybrid Drone System
Abstract
1. Introduction
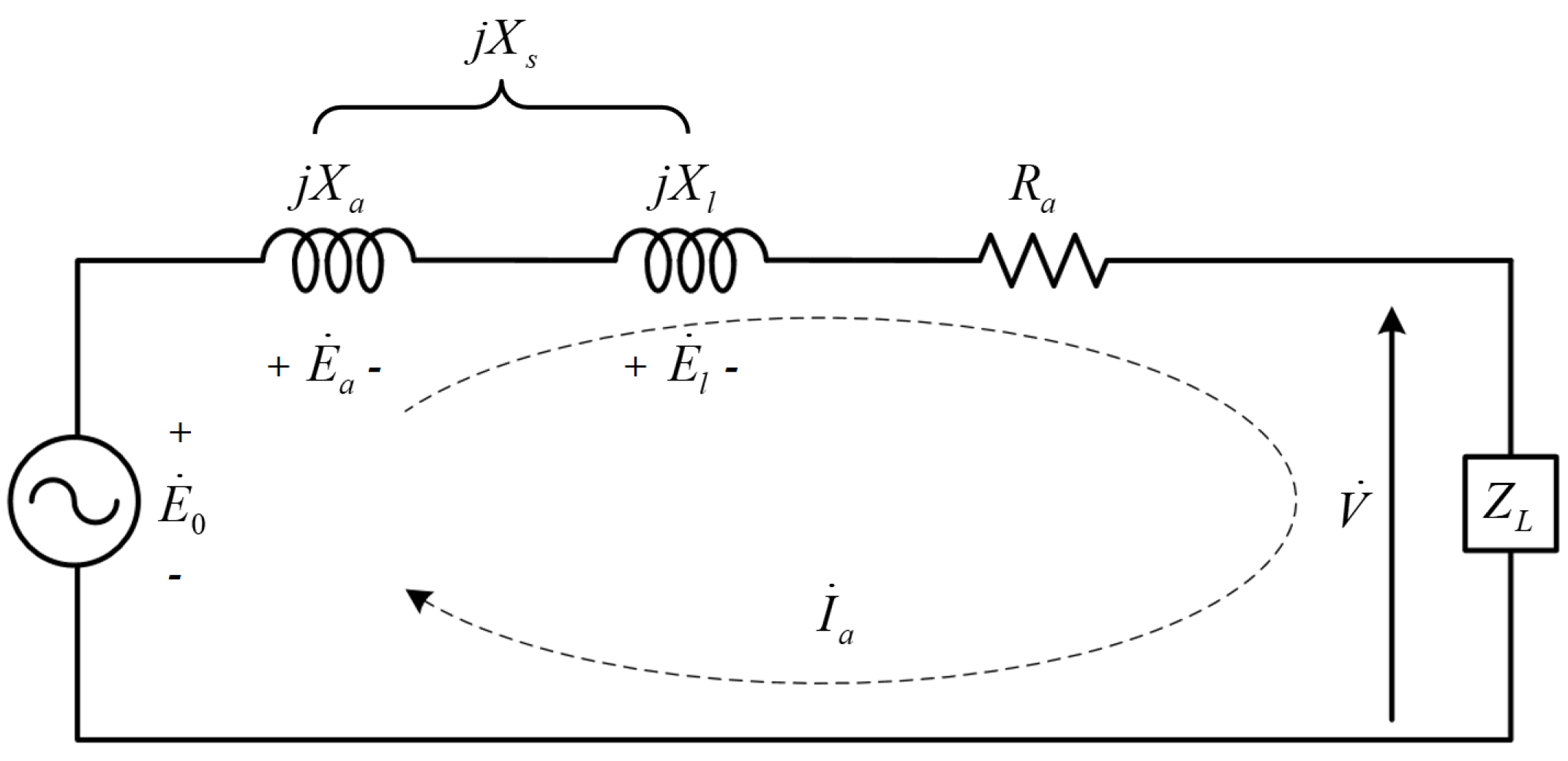
2. Principle and Equivalent Circuit of PMSG
3. Comparison of ORPMSG Models
3.1. Constraints of Comparison Models
3.2. Comparison Models of Pole–Slot Combinations for ORPMSG
- The larger the winding coefficient, the higher the BEMF and torque generated.
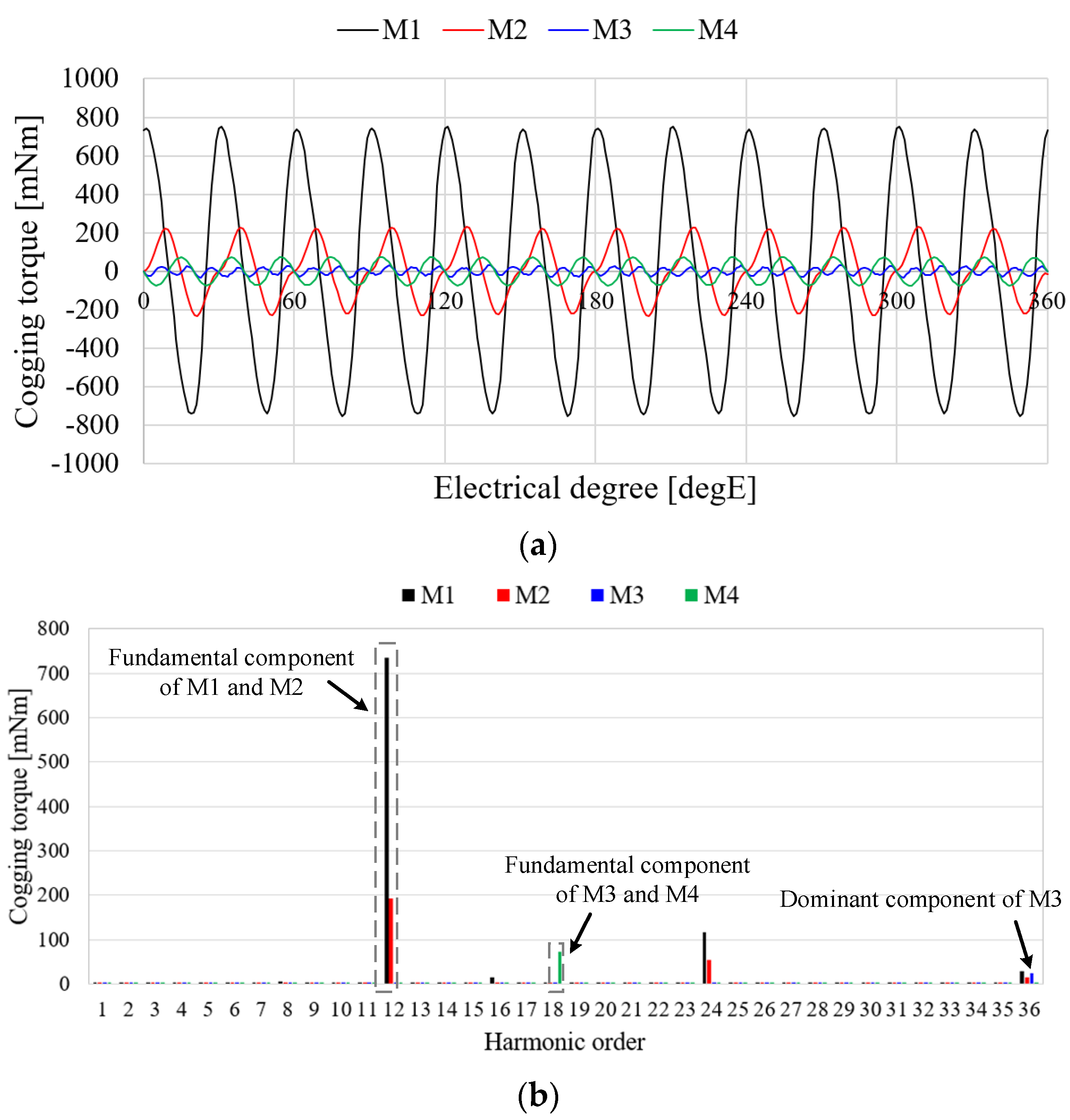
- The least common multiple (LCM) of the poles and slots is proportional to the cogging torque frequency. In general, the frequency of the cogging torque can increase, and the magnitude of the cogging torque can reduce as the LCM increases.
- Fractional slot machines contain fewer harmonics than do integer slot machines [34].
4. Comparison of the Characteristics of the Pole–Slot Combination
4.1. No-Load Characteristic
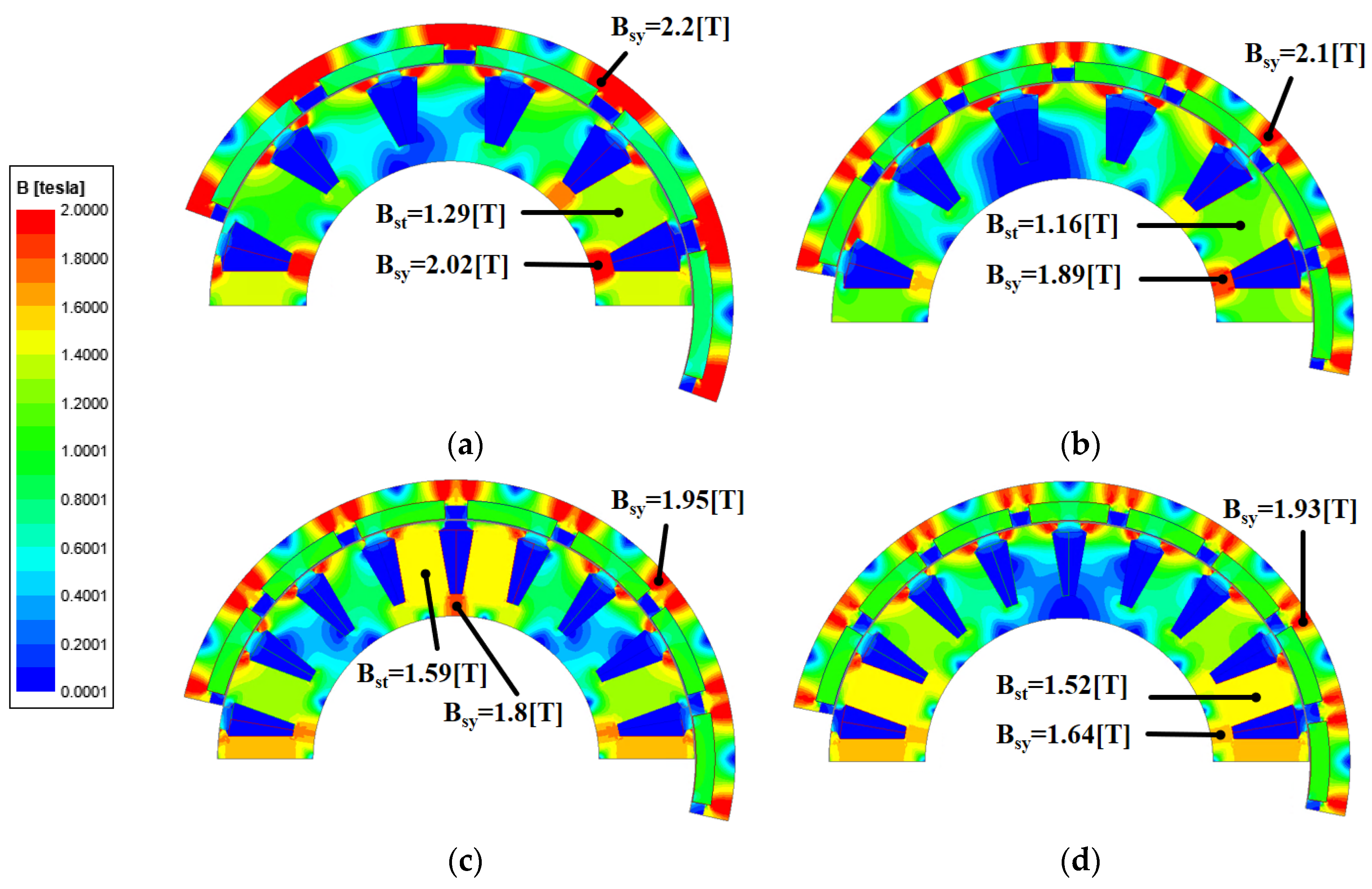
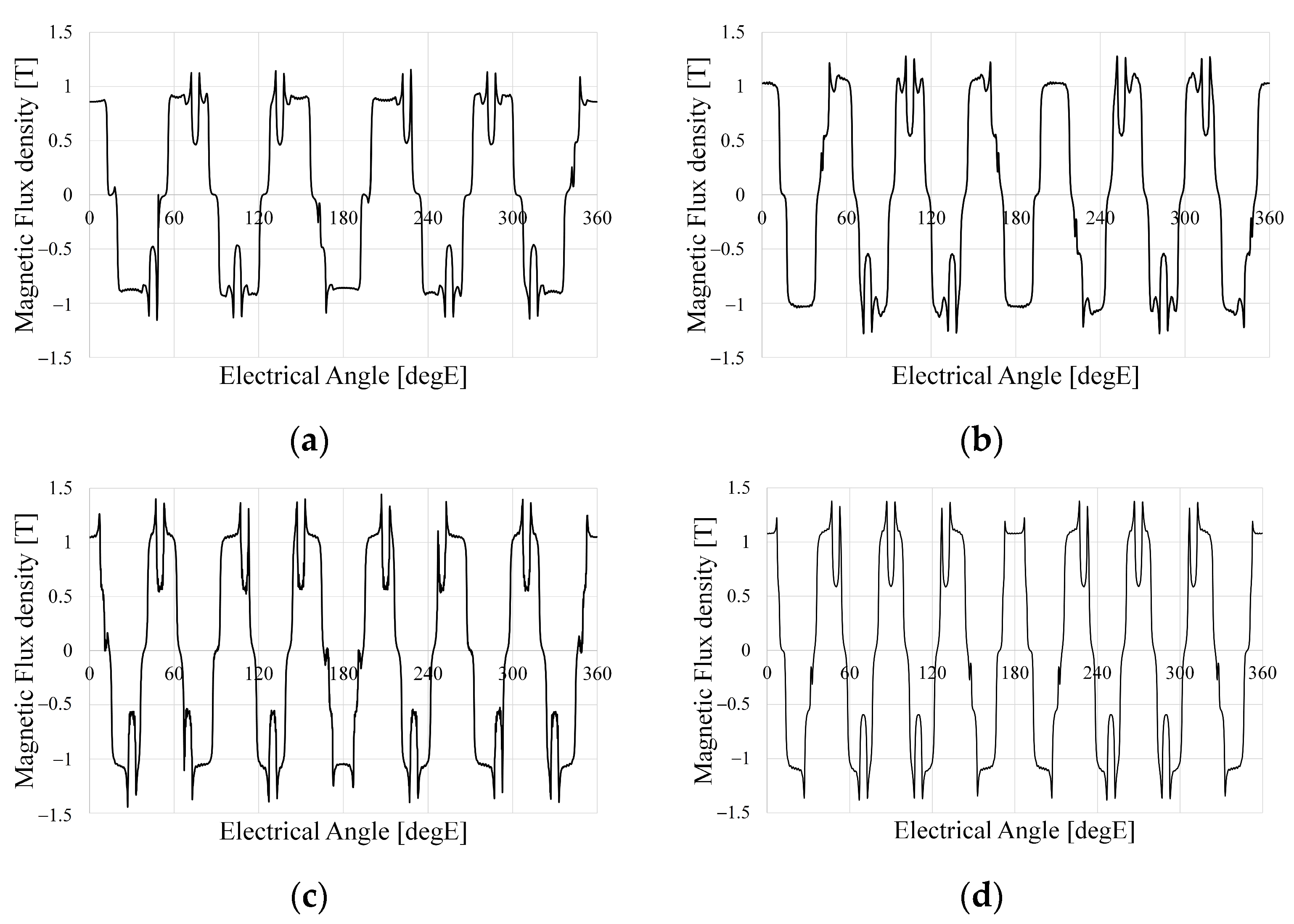
4.1.1. Airgap Magnetic Flux Density
4.1.2. Cogging Torque
4.1.3. Line to Line Voltage
4.2. On-Load Characteristic
4.2.1. Torque Characteristics by Sinusoidal Current
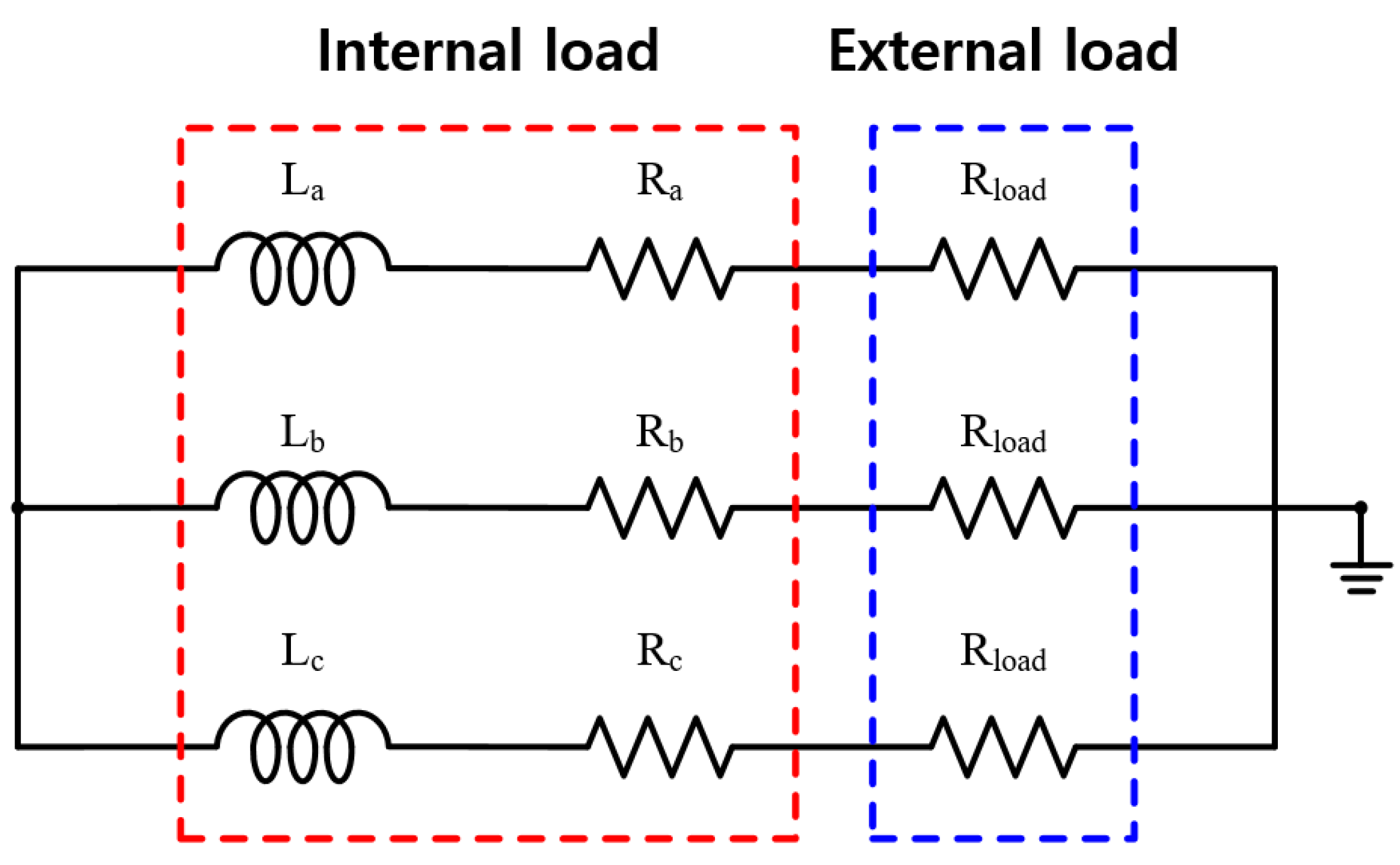
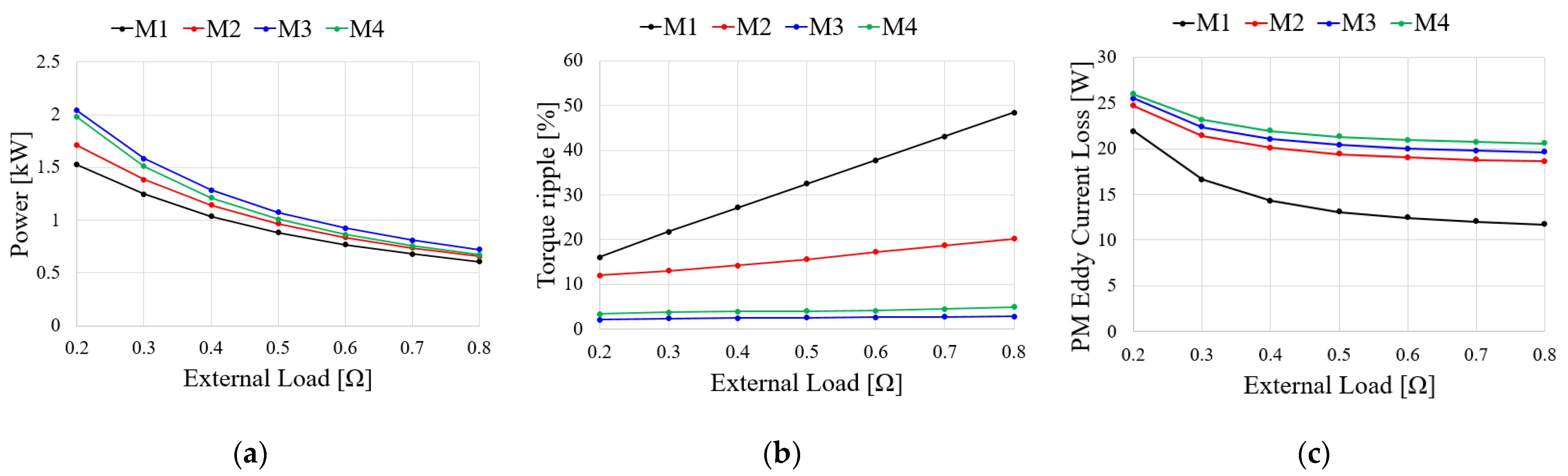
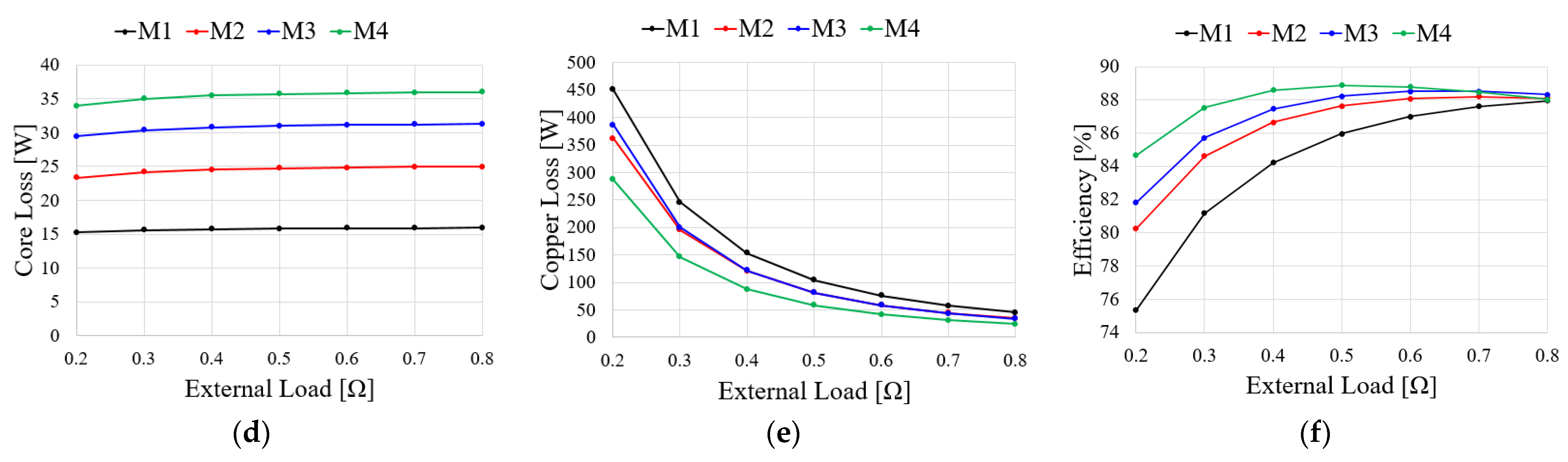
4.2.2. Generator Characteristic for External Resistance Load
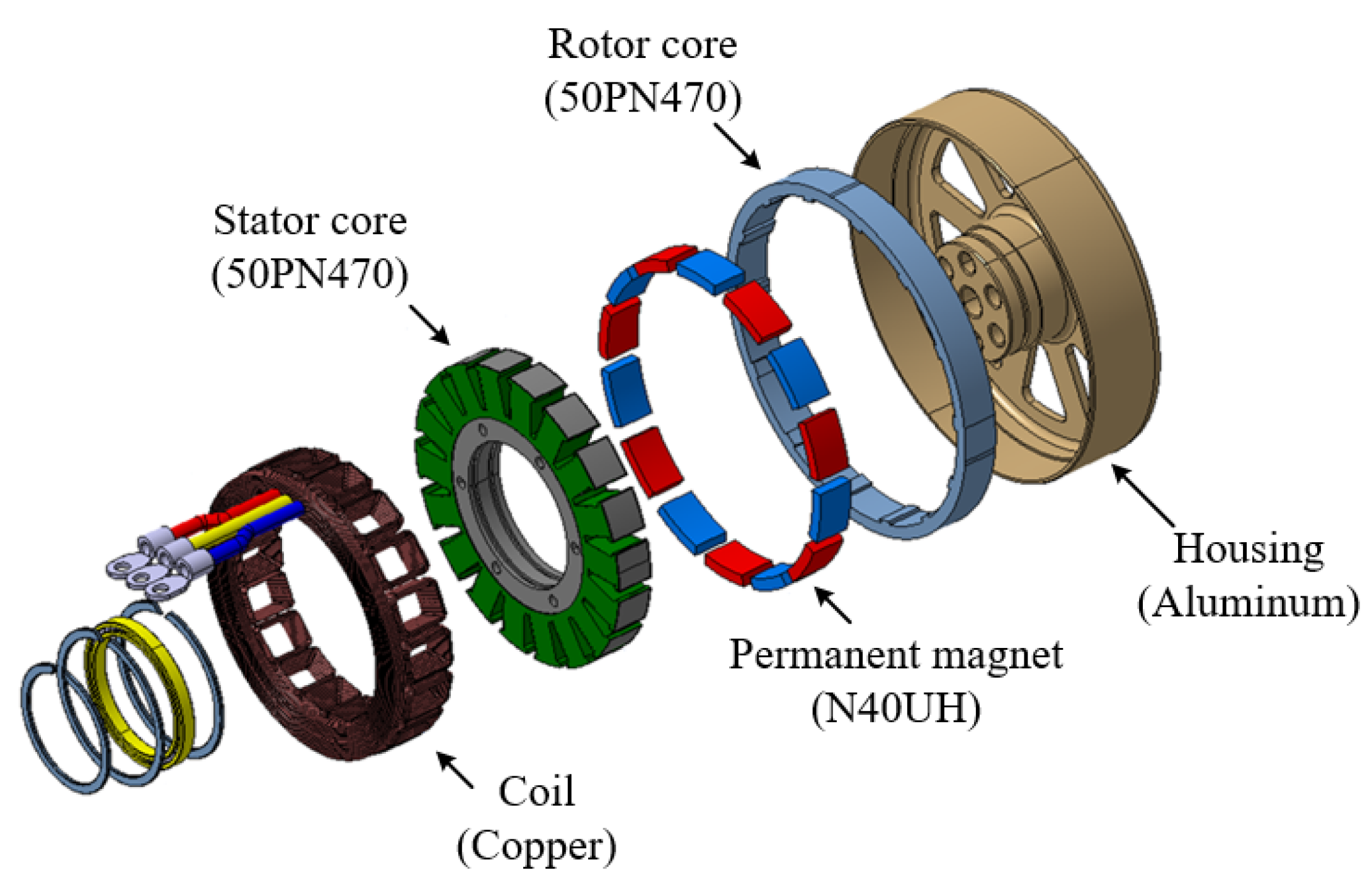
5. Manufacture and Experiment Verification
5.1. Manufacture of Prototype and Experiment Environment
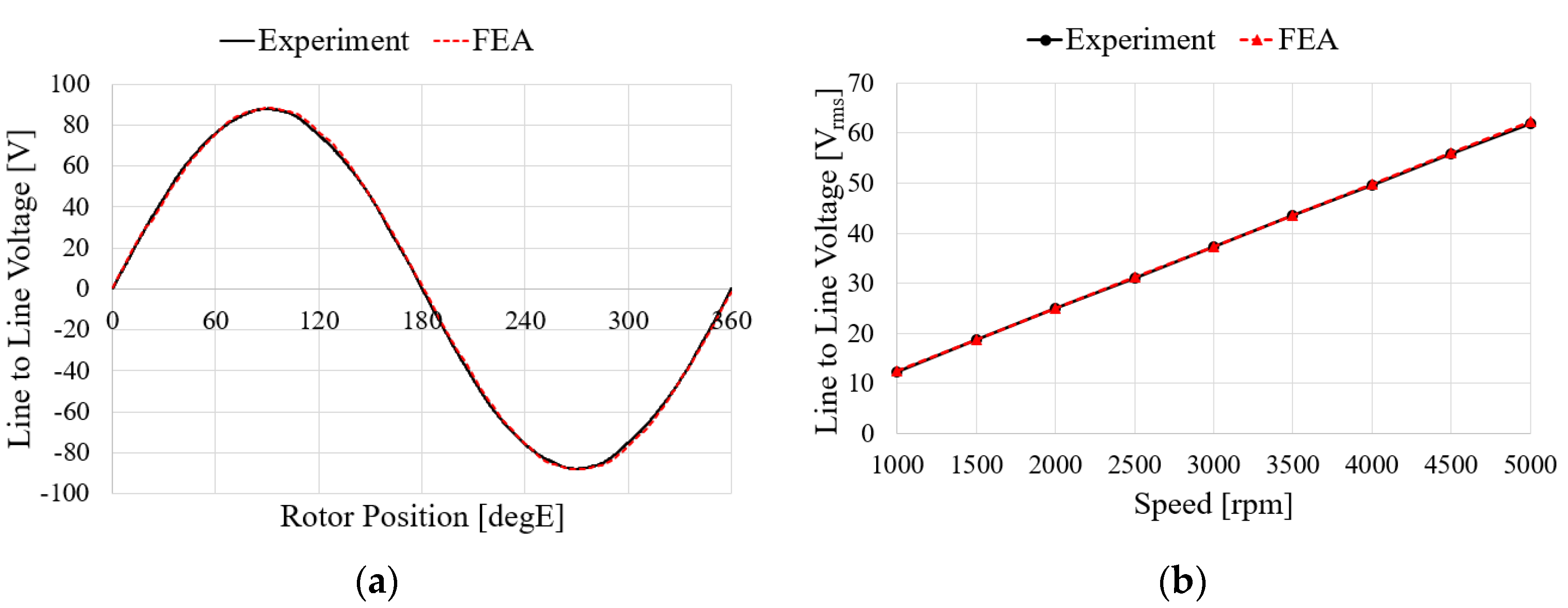
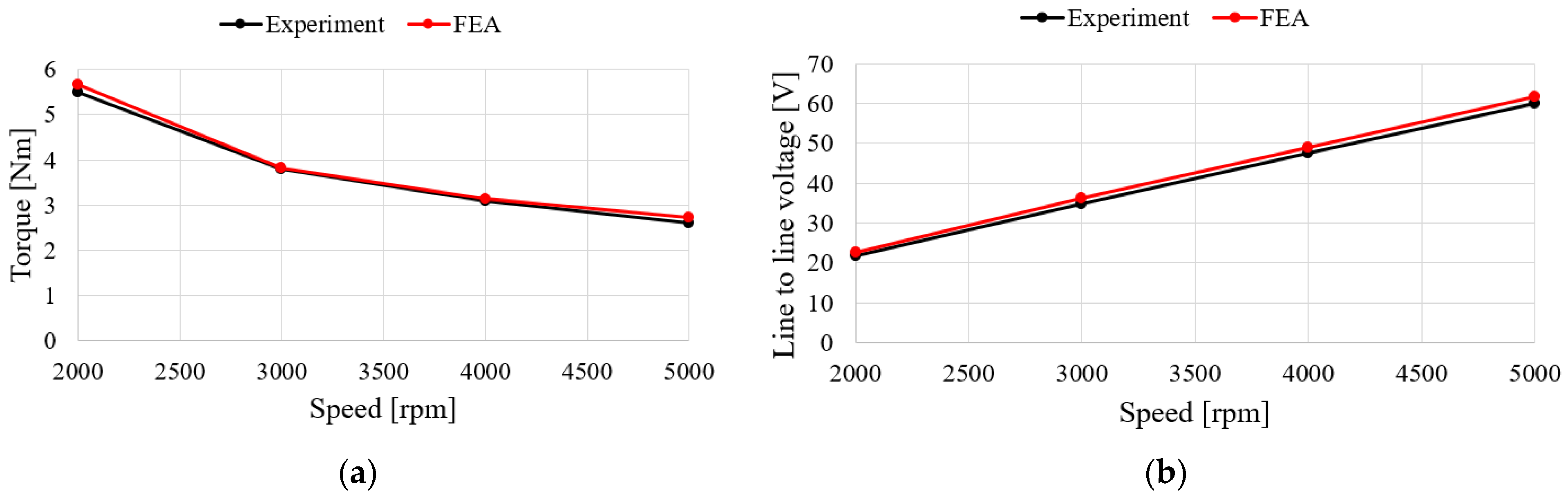
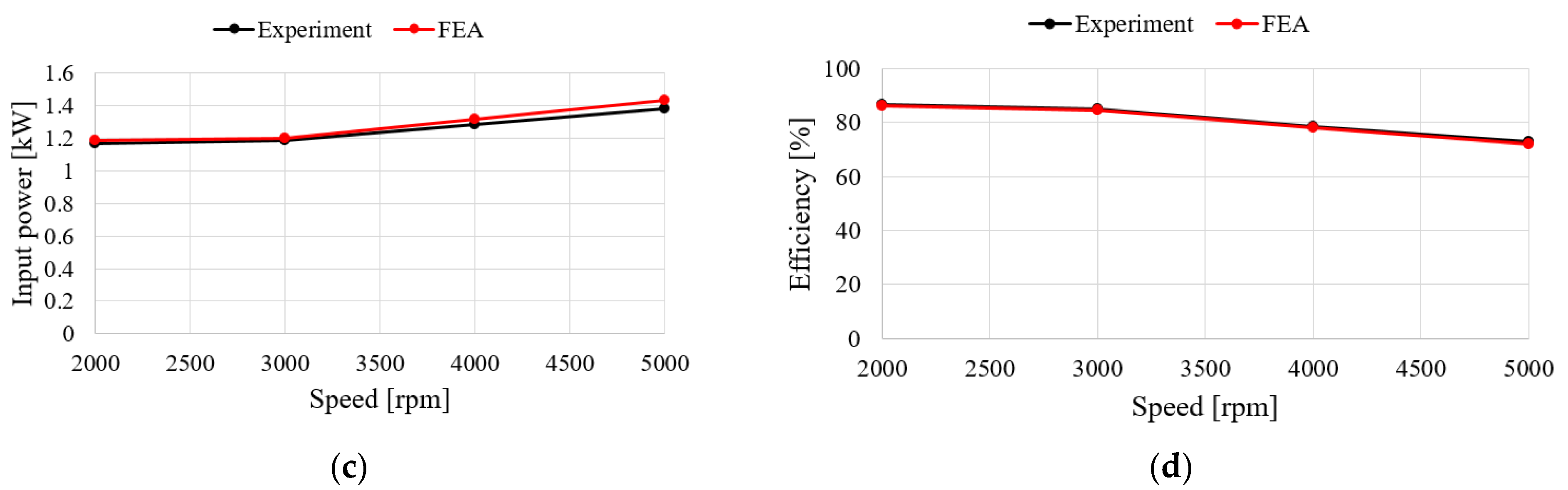
5.2. Performance Verification Comparison of FEA and Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Benarbia, T.; Kyamakya, K. A Literature Review of Drone-Based Package Delivery Logistics Systems and Their Implementation Feasibility. Sustainability 2022, 14, 360. [Google Scholar] [CrossRef]
- Rosser, J.C., Jr.; Vignesh, V.; Terwilliger, B.A.; Parker, B.C. Surgical and Medical Applications of Drones: A Comprehensive Review. JSLS 2018, 22, e2018.00018. [Google Scholar] [CrossRef]
- de Jong, S.M. Grand Challenges in Earth Observation Using Unpiloted Airborne Systems. Front. Remote Sens. 2020, 1, 601737. [Google Scholar] [CrossRef]
- ITF. Ready for Take Off? Integrating Drones into the Transport System; ITF Research Reports; OECD Publishing: Paris, France, 2021. [Google Scholar]
- Shahmoradi, J.; Talebi, E.; Roghanchi, P.; Hassanalian, M. A Comprehensive Review of Applications of Drone Technology in the Mining Industry. Drones 2020, 4, 34. [Google Scholar] [CrossRef]
- Emimi, M.; Khaleel, M.; Alkrash, A. The Current Opportunities and Challenges in Drone Technology. Int. J. Electr. Eng. Sustain. 2023, 1, 74–89. [Google Scholar]
- González-Jorge, H.; Martínez-Sánchez, J.; Bueno, M.; Arias, A.P. Unmanned Aerial Systems for Civil Applications: A Review. Drones 2017, 1, 2. [Google Scholar] [CrossRef]
- Vergouw, B.; Nagel, H.; Bondt, G.; Custers, B. Drone Technology: Types, Payloads, Applications, Frequency Spectrum Issues and Future Developments. Inf. Technol. Law Ser. 2016, 27, 21–45. [Google Scholar]
- Alwateer, M.; Loke, S.W. Emerging Drone Services: Challenges and Societal Issues. IEEE Technol. Soc. Mag. 2020, 39, 47–51. [Google Scholar] [CrossRef]
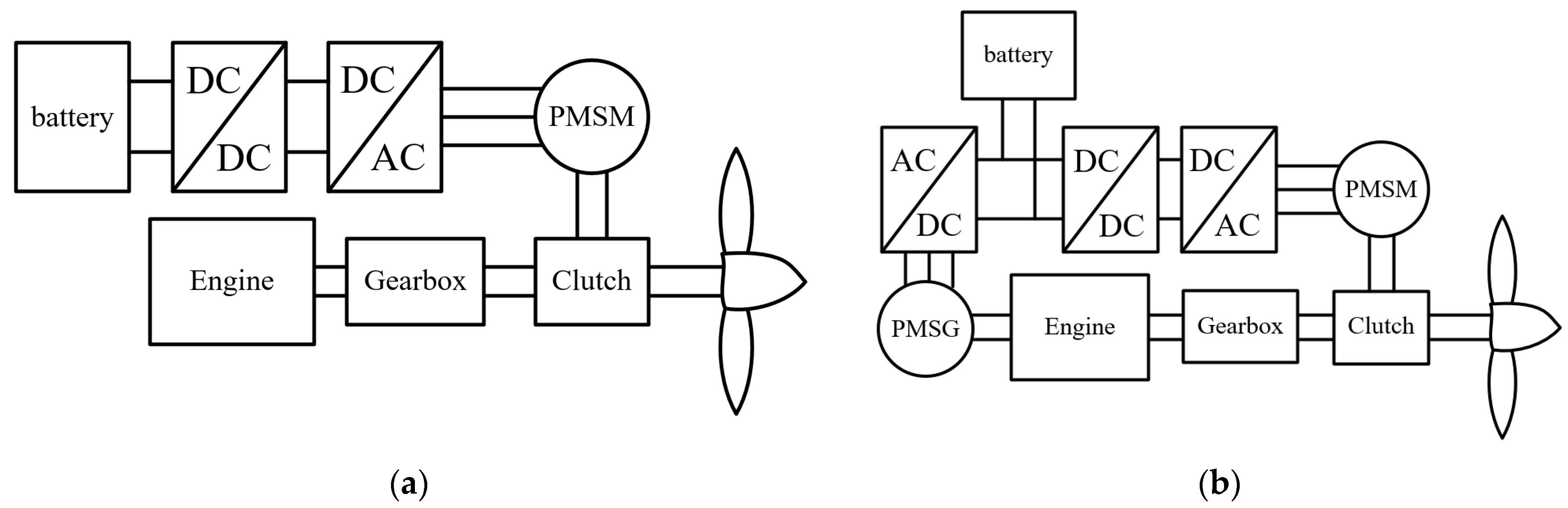
- Yang, X.; Pei, X. 15-Hybrid system for powering unmanned aerial vehicles: Demonstration and study cases. In Hybrid Energy System; Academic Press: Cambridge, MA, USA, 2022; pp. 439–473. [Google Scholar]
- Viswanathan, V.; Epstein, A.H.; Chiang, Y.M.; Takeuchi, E.; Bradley, M.; Langford, J.; Winter, M. The challenges and opportunities of battery-powered flight. Nature 2022, 601, 519–525. [Google Scholar] [CrossRef]
- Dannier, A.; Del Pizzo, A.; Di Noia, L.P.; Spina, I. Sizing Procedure of PMSMs for Hybrid Parallel Aircraft Propulsion. In Proceedings of the 2018 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Nottingham, UK, 7–9 November 2018. [Google Scholar]
- Jeong, K.S.; Lee, W.Y.; Kim, C.S. Energy management strategies of a fuel cell/battery hybrid system using fuzzy logics. J. Power Sources 2005, 145, 319–326. [Google Scholar] [CrossRef]
- Goh, C.S.; Kuan, J.R.; Danner, A. A fully solar-powered quadcopter able to achieve controlled flight out of the ground effect. Photovoltaics 2019, 27, 869–878. [Google Scholar] [CrossRef]
- Boukoberine, M.N.; Donateo, T.; Benbouzid, M. Optimized Energy Management Strategy for Hybrid Fuel Cell Powered Drones in Persistent Missions Using Real Flight Test Data. IEEE Trans. Energy Convers. 2022, 37, 2080–2091. [Google Scholar] [CrossRef]
- Park, J.H.; Lyu, H.G.; Lee, H.T. Power System Optimization for Electric Hybrid Unmanned Drone. J. Korean Soc. Aeronaut. Space Sci. 2019, 47, 300–308. [Google Scholar]
- Reyner, C.; Hartono, F. The development and testing of 2.4 kW lightweight hybrid power generator unit for multirotor. AIP Conf. Proc. 2023, 2941, 020045. [Google Scholar]
- Xiao, C.; Wang, B.; Wang, C.; Yan, Y. Design of a novel fully-active PEMFC-Lithium battery hybrid power system based on two automatic ON/OFF switches for unmanned aerial vehicle applications. Energy Convers. Manag. 2023, 292, 117417. [Google Scholar] [CrossRef]
- Nurrohaman, M.F.; Titalim, B.A.; Utama, T.H.; Adiprawita, W. Design and Implementation of On-board Hybrid Generator for Rotary Wing Drone. In Proceedings of the 2019 International Conference on Electrical Engineering and Informatics (ICEEI), Bandung, Indonesia, 9–10 July 2019. [Google Scholar]
- Li, S.; Gu, C.; Zhao, P.; Cheng, S. A novel hybrid propulsion system configuration and power distribution strategy for light electric aircraft. Energy Convers. Manag. 2021, 238, 114171. [Google Scholar] [CrossRef]
- Zhang, X.; Bowman, C.L.; O’Connell, T.C.; Haran, K.S. Large electric machines for aircraft electric propulsion. IET Electr. Power Appl. 2019, 12, 767–779. [Google Scholar] [CrossRef]
- Boukoberine, M.N.; Zhou, Z.; Benbouzid, M. A critical review on unmanned aerial vehicles power supply and energy management: Solutions, strategies, and prospects. Appl. Energy 2019, 255, 113823. [Google Scholar] [CrossRef]
- Nøland, J.K.; Leandro, M.; Suul, J.A.; Molinas, M. High-Power Machines and Starter-Generator Topologies for More Electric Aircraft: A Technology Outlook. IEEE Access 2020, 8, 130104–130123. [Google Scholar] [CrossRef]
- Reddy, P.B.; El-Refaie, A.M.; Huh, K.K.; Tangudu, J.K.; Jahns, T.M. Comparison of Interior and Surface PM Machines Equipped with Fractional-Slot Concentrated Windings for Hybrid Traction Applications. IEEE Trans. Energy Convers. 2012, 27, 593–602. [Google Scholar] [CrossRef]
- EL-Refaie, A.M. Fractional-Slot Concentrated-Windings Synchronous Permanent Magnet Machines: Opportunities and Challenges. IEEE Trans. Ind. Electron. 2010, 57, 107–121. [Google Scholar] [CrossRef]
- Dogan, H.; Wurtz, F.; Foggia, A.; Garbuio, L. Analysis of Slot-Pole Combination of Fractional-Slots PMSM for Embedded Applications. In Proceedings of the International Aegean Conference on Electrical Machines and Power Electronics and Electromotion, Istanbul, Turkey, 8–10 September 2011. [Google Scholar]
- Mamur, H.; Sahin, C.; Karacor, M.; Bhuiyan, M.R.A. Design and fabrication of an outer rotor permanent magnet synchronous generator with fractional winding for micro-wind turbines. IET 2020, 14, 2273–2282. [Google Scholar]
- Kim, S.Y.; Cho, J.H.; Lee, S.T.; Lee, S.G. Study of Characteristics According to Pole–Slot Combination of Fractional Slot Concentrated Winding Permanent Magnet Synchronous Motor. J. Electr. Eng. Technol. 2024, 2093–7423. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, Z.Q.; Gan, C.; Brockway, S.; Hilton, C. Comparison of optimal slot/pole number combinations in fractional slot permanent magnet synchronous machines having similar slot and pole numbers. IET 2019, 2019, 4585–4589. [Google Scholar]
- Miller, T.J.E. Brushless Permanent-Magnet and Reluctance Motor Drives; Oxford University Press: Oxford, UK, 1989; ISBN 0-19-859369-4. [Google Scholar]
- Kim, D.H.; Kim, K.S.; Yang, I.J.; Lee, J.; Kim, W.H. Alternative Bridge Spoke Permanent Magnet Synchronous Generator Design for Wind Power Generation Systems. IEEE Access 2021, 9, 152819–152828. [Google Scholar] [CrossRef]
- Park, Y.; Kim, H.; Jang, H.; Ham, S.H.; Lee, J.; Jung, D.H. Efficiency Improvement of Permanent Magnet BLDC With Halbach Magnet Array for Drone. IEEE Trans. Appl. Supercond. 2020, 3, 5201405. [Google Scholar] [CrossRef]
- Lee, C.-S.; Kim, H.-J. Induced EMF THD Reduction Design of Permanent Magnet Synchronous Generators for Diesel Engine Generators. Processes 2021, 9, 986. [Google Scholar] [CrossRef]
- Bianchi, N.; Fornasiero, E. Impact of MMF Space Harmonic on Rotor Losses in Fractional-Slot Permanent-Magnet Machines. IEEE Trans. Energy Convers. 2009, 24, 323–328. [Google Scholar] [CrossRef]
- Bianchi, N. Permanent magnet synchronous motors. In Industrial Electronics Handbooks, 2nd ed.; Power Electronics and Motor Drives; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Refaie, A.M.; Jahns, T.M. Optimal flux weakening in surface PM machines using fractional-slot concentrated windings. IEEE Trans. Ind. Appl. 2005, 41, 790–800. [Google Scholar] [CrossRef]
- Zhu, L.; Zhu, Z.Q.; Chan, C.C. Analytical Methods for Minimizing Cogging Torque in Permanent-Magnet Machines. IEEE Trans. Magn. 2009, 45, 2023–2031. [Google Scholar] [CrossRef]
- Ouamara, D.; Dubas, F. Permanent-Magnet Eddy-Current Losses: A Global Revision of Calculation and Analysis. Math. Comput. Appl. 2019, 24, 67. [Google Scholar] [CrossRef]






| Content | Value | Unit |
|---|---|---|
| Rated speed | 2000 | rpm |
| Rated power | 1 | kW |
| Battery voltage @ 5000 rpm | 48 | Vdc |
| Required voltage @ 5000 rpm | 57 | V |
| Rotor outer/inner diameter | 148.8/128 | mm |
| Stator outer/inner diameter | 127/76.24 | mm |
| Length of airgap | 0.5 | mm |
| Stack length | 15 | mm |
| Pole arc ratio | 0.8 | - |
| Total volume of PM | 1671 | mm3 |
| Slot opening | 6 | mm |
| Total slot area | 1917 | mm2 |
| Slot fill factor | 40 | % |
| Material of PM | N40UH | - |
| Material of rotor and stator core | 50PN470 | - |
| Content | M1 | M2 | M3 | M4 |
|---|---|---|---|---|
| Pole/slot | 10P12S | 14P12S | 14P18S | 16P18S |
| LCM of poles and slots | 60 | 84 | 126 | 144 |
| GCD of pole pairs and slots | 1 | 1 | 1 | 2 |
| Winding factor | 0.933 | 0.933 | 0.902 | 0.945 |
| Number of serial turns per phase | 104 | 88 | 96 | 84 |
| Content | M1 | M2 | M3 | M4 | Unit |
|---|---|---|---|---|---|
| Electrical period | 30 | 30 | 20 | 20 | degE |
| Fundamental harmonic order | 12 | 12 | 18 | 18 | - |
| Content | M1 | M2 | M3 | M4 | Unit |
|---|---|---|---|---|---|
| Phase voltage (fundamental) | 48.2 | 48.9 | 51 | 48.5 | Vmax |
| Line to line voltage (fundamental) | 83.4 | 84.8 | 88.4 | 84 | Vmax |
| Phase voltage THD | 5.36 | 9.17 | 2.21 | 5.75 | % |
| Line to line voltage THD | 2.22 | 4.71 | 0.36 | 0.52 | % |
| Content | M1 | M2 | M3 | M4 | Unit |
|---|---|---|---|---|---|
| Rated current | 30 | Arms | |||
| Torque | 5.92 | 6.03 | 6.29 | 5.99 | Nm |
| Torque ripple | 26.7 | 10.13 | 1.53 | 3.29 | % |
| Content | Speed (rpm) | Current (Arms) | Torque (Nm) | Output Voltage (V) | Input Power (kW) | Output Power (kW) | Efficiency (%) |
|---|---|---|---|---|---|---|---|
| Experiment | 2000 | 27.4 | 5.5 | 21.8 | 1.16 | 0.90 | 86.32 |
| 3000 | 17.2 | 3.8 | 34.9 | 1.19 | 0.95 | 84.7 | |
| 4000 | 12.7 | 3.1 | 47.5 | 1.28 | 0.97 | 78.52 | |
| 5000 | 10 | 2.6 | 60.1 | 1.38 | 0.98 | 72.88 | |
| FEA | 2000 | 27.4 | 5.63 | 22.7 | 1.19 | 1.02 | 86.09 |
| 3000 | 17.5 | 3.79 | 36.1 | 1.2 | 1.01 | 84.51 | |
| 4000 | 12.7 | 3.06 | 49.0 | 1.31 | 1.03 | 78.21 | |
| 5000 | 9.99 | 2.64 | 61.7 | 1.43 | 1.03 | 72.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.; Lee, J.; Kim, H. A Comparative Study of Pole–Slot Combination with Fractional Slot Concentrated Winding in Outer Rotor Permanent Magnet Synchronous Generator for Hybrid Drone System. Machines 2024, 12, 464. https://doi.org/10.3390/machines12070464
Kim J, Lee J, Kim H. A Comparative Study of Pole–Slot Combination with Fractional Slot Concentrated Winding in Outer Rotor Permanent Magnet Synchronous Generator for Hybrid Drone System. Machines. 2024; 12(7):464. https://doi.org/10.3390/machines12070464
Chicago/Turabian StyleKim, Jeongwon, Ju Lee, and Hyunwoo Kim. 2024. "A Comparative Study of Pole–Slot Combination with Fractional Slot Concentrated Winding in Outer Rotor Permanent Magnet Synchronous Generator for Hybrid Drone System" Machines 12, no. 7: 464. https://doi.org/10.3390/machines12070464
APA StyleKim, J., Lee, J., & Kim, H. (2024). A Comparative Study of Pole–Slot Combination with Fractional Slot Concentrated Winding in Outer Rotor Permanent Magnet Synchronous Generator for Hybrid Drone System. Machines, 12(7), 464. https://doi.org/10.3390/machines12070464






