Analytical Modeling of Eddy Current Losses and Thermal Analysis of Non-Uniform-Air-Gap Combined-Pole Permanent Magnet Motors for Electric Vehicles

Abstract

In order to solve the problem of large eddy current losses and high temperature rises caused by a large number of permanent magnets, a new type of combined-magnetic-pole permanent magnet motor is proposed in this paper. The sinusoidally distributed subdomain model of a non-uniform-air-gap rotor was established using the Laplace equation, and the analytical expression of eddy current losses in the rotor in a uniform air gap and non-uniform air gap was derived. The effect of the rotor’s eccentricity on eddy current losses was obtained. According to the characteristics of the distributed winding of the non-uniform-air-gap combined-pole permanent magnet motor, an equivalent treatment was performed to obtain the equivalent thermal conductivity value; to establish an equivalent thermal network model of the motor; determine the temperature of each component of the motor; and verify the correctness of the thermal network model through magnetothermal bidirectional coupling. Finally, an experimental platform was set up to carry out temperature rise experiments on the two prototypes. The experimental results show that a non-uniform-air-gap rotor structure can effectively reduce a rotor’s eddy current losses and motor temperature rise, as well as verify the accuracy of the analytical model’s calculation results.

1. Introduction

In order to solve the energy crisis and environmental pollution problems caused by internal combustion engine vehicles, automobile companies and research institutes in various countries have decided upon energy conservation and emissions reduction as the main development plan for future vehicles [1,2]. Due to electric vehicles having the characteristics of low pollution, zero emission, high energy efficiency, and diversified energy sources, the development of various new energy vehicles represented by electric vehicles has become an effective way to solve many problems caused by traditional fuel vehicles [3]. An electric drive system is the key part of electric vehicles, and its performance directly affects the power and economy of electric vehicles. Compared with a switched reluctance motor, an induction motor, and a brushless DC motor, a permanent magnet synchronous motor has the advantages of a high power density, high overload capacity, and high efficiency, and has been widely used in electric vehicle power drive systems. However, for the permanent magnet motor, the magnetic energy generated by the permanent magnet and the stator tooth slot produces a tooth slot effect, resulting in a high harmonic content in the motor’s magnetic field, which produces a large number of eddy current losses and harmonic losses on the fixed rotor and permanent magnet. The loss is the heat source, and this loss causes the internal temperature of the motor to rise [4,5]. In addition, since the armature winding of the permanent magnet motor needs to be embedded in the stator slot, the heat source is relatively concentrated, which causes heat dissipation difficulties in the motor when the heat increases. Too high a temperature rise in the permanent magnet motor reduces the performance of the magnetic material, and even leads to irreversible demagnetization of the permanent magnet. Therefore, accurate analysis of the temperature rise distribution of the permanent magnet motor can reduce the heat output. It is very important to improve the power density of electric vehicle drive systems.

In recent years, many researchers at home and abroad have carried out a lot of research on the calculation methods and influencing factors of motor temperature rises. In [5], the authors analyzed the two-dimensional temperature field of a motor, ignoring the distribution and change in the motor along the axis. In [6], the authors used the equivalent thermal network method and the finite element method to calculate the stable temperature rise and transient temperature rise of an electric vehicle motor under rated working conditions, respectively, and verified the adaptability and compatibility of the two methods. In [2], the effect of rotor pole optimization on the loss and temperature rise of an interior permanent magnet synchronous motor was studied, and then verified using finite element magnetothermal coupling analysis. However, the processing cost of an irregular permanent magnet is high. In [7,8], the method of permanent magnet segmentation was adopted to reduce the eddy current loss and lower the temperature rise. In addition, some studies have used the method of unequal turn winding and stator yoke setting of the magnetic bridge to reduce the eddy current loss and motor temperature rise, but these methods complicate the motor manufacturing process [5,9]. In [10], a double three-phase winding was used to suppress the high harmonic content in the armature field of permanent magnet motors with 10 poles and 12 slots; the motor structure was more complicated, and the reliability was reduced. In [11], the authors proposed a three-dimensional numerical hybrid calculation method based on the combination of the static three-dimensional finite element method and the three-dimensional finite difference method. The calculation accuracy of this method is relatively high, but the modeling is relatively complex and requires finite element pre-processing. Meanwhile, this method can only consider the eddy current loss of a rectangular permanent magnet, and its flexibility is also limited to a certain extent. In [12], the authors studied the effects of the surface slot depth, slot mode, and number of slots on eddy current losses of permanent magnets, and the results showed that the slot depth is related to the penetration depth of higher harmonics; too deep a slot not only further restrains eddy current losses, but also reduces the rotor strength. In [13], the authors used a three-dimensional temperature field model for thermal analysis of the motor, but it did not accurately calculate various losses that can affect the results of the thermal analysis. In [14], the authors conducted thermal analysis of a permanent magnet motor using a combination of the centralized parameter thermal network method and the numerical method; however, the influence of the temperature change on the properties and temperature of the permanent magnet material was not considered. To sum up, most of the existing literature use numerical calculation methods and finite element methods to analyze the loss and temperature rise of a built-in single-pole permanent magnet motor, while few studies have used the magnetothermal bidirectional coupling method to analyze the built-in combined-pole permanent magnet motor. In addition, existing studies have been conducted on the basis of uniform air gaps, and no relevant study has been found that explores the influence of non-uniform air gaps on eddy current losses and temperature rise.

This paper introduces the structure and magnetic circuit characteristics of an interior combined-pole permanent magnet motor, and analyzes the electromagnetic characteristics of a non-uniform-air-gap permanent magnet motor and the mechanism of eddy current loss. By establishing the sinusoidal distribution subdomain model of the non-uniform air gap and using the Fourier decomposition method and the Laplace equation, we derive the analytical expression of the motor’s eddy current loss, in order to determine the eddy current loss under different rotor eccentricity values. The principle of the low eddy current loss of a permanent magnet motor with a non-uniform-air-gap rotor structure is described. In addition, an equivalent thermal network model of the motor is established, and three-dimensional unidirectional and bidirectional magnetothermal coupling finite element models of the motor are established. The loss is accurately transferred to each part of the motor for thermal analysis, and the motor’s temperature rise in different analysis methods is compared. Two prototypes are produced, and an experimental platform is set up for testing. The research in this paper provides a reference method for loss analysis and temperature rise analysis of interior permanent magnet motors.

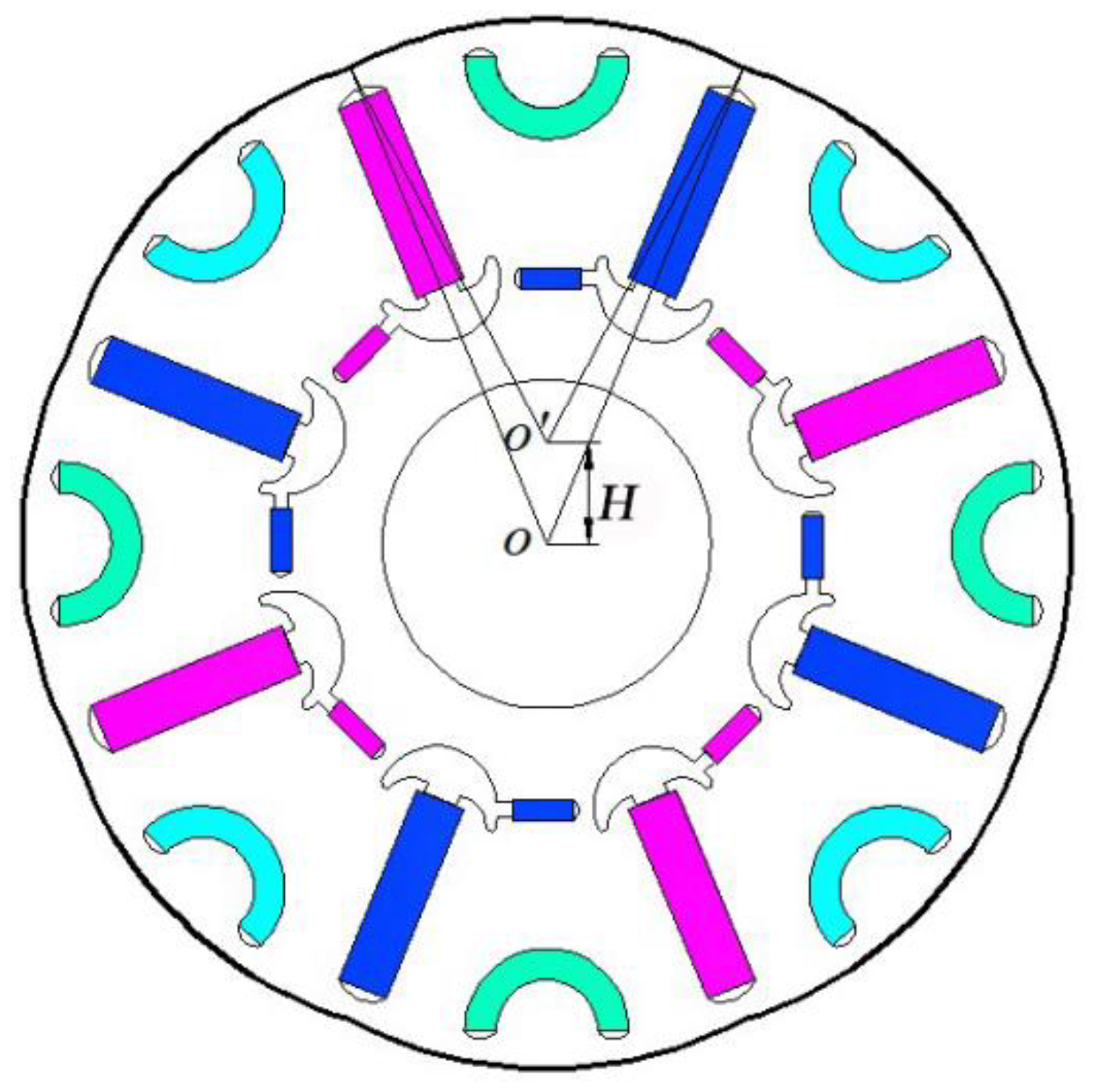
2. Structural Parameters of Permanent Magnet Motors

The interior tangential and double-radial permanent magnet motor (ITRPMM) proposed in this paper is shown in Figure 1. Each magnetic pole on the rotor structure is composed of a tangential magnetic field rectangular permanent magnet (TRPM), a radial magnetic field rectangular permanent magnet (RRPM), and a semicircular radial magnetic field permanent magnet (SRPM).

According to the performance requirements of a permanent magnet motor for electric vehicles, the structural parameters of the ITRPMM were determined using an empirical formula, as shown in

Table 1. Structural parameters of a new type of ITRPMM.

Parameter	Value	Parameter	Value
Rated voltage/(V)	60	Rated speed/(r·min)	3000
Rated power/(kW)	3	Outer diameter of rotor/(mm)	89
Number of pole pairs	4	Interior diameter of rotor/(mm)	30
Slots	36	Axial length/(mm)	60
Inner diameter of stator/(mm)	90	Number of turns per slot	11
Outer diameter of stator/(mm)	145	Volume of permanent magnet/(mm3)	72,000

. The structure diagram of the ITRPMM is shown in Figure 1.

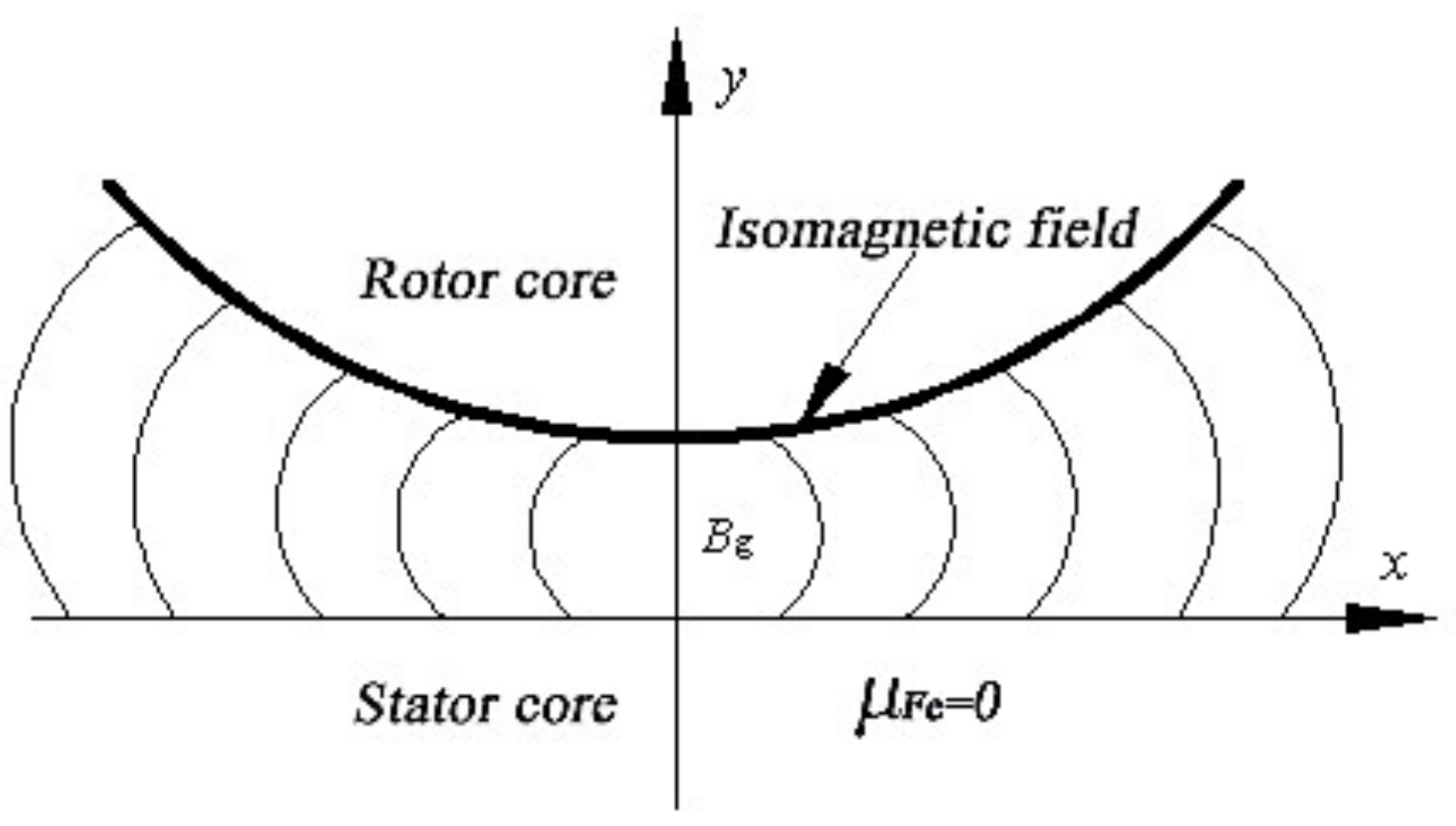
3. Establishment of a Subdomain Model of the Sinusoidal Distribution of a Non-Uniform Air Gap

Currently, the research on permanent magnet motors by experts and scholars at home and abroad is based on the fixed rotor axis coincidence (that is, a uniform air gap). The rotor shape of the uniform air gap structure is a standard circle, and the outer circle of the rotor and the rotating shaft are centered at point o. In order to study the influence of a non-uniform air gap on the motor’s output characteristics, a non-uniform-air-gap motor model was established, as shown in Figure 2. The outer circle of the rotor was composed of 8 arc segments, with different centers than the outer circle of the stator. The rotor eccentricity H = oo′, the size of which could be used to measure the eccentricity of the non-uniform air gap.

According to the geometric relationship, the formula of rotor eccentricity varying with the air gap length is derived as follows:

$$H=\sqrt{{\left(R_1-\delta \right)}^2+2\delta R_2\cos \alpha -R_2^2}$$

(1)

where R₁ is the inner diameter of the stator, R₂ is the outer diameter of the rotor, δ is the length of the air gap, and α is the circumference angle of the motor.

When the motor is unloaded, the current in the armature winding is 0, and the air gap magnetic field is an irrotational field. In this case, the scalar magnetic potential satisfies the Laplace equation, and a rectangular coordinate system can be established to solve the problem, as shown in Figure 3, where Bg is irrotational field air gap flux density, and the irrotational field permeability of the stator core and the rotor core is ${\mu }_{\mathrm{Fe}}$.

In a two-dimensional rectangular coordinate system, the Laplace equation is used to solve the scalar magnetic potential equation [15]:

$$\mathrm{\Omega }={\displaystyle \sum _{k=1}^{\infty }(A_k}\cos m_{k}x+B_k\sin m_{k}x)(C_k\mathrm{sh}{m}_{k}y+D_k\mathrm{ch}{m}_{k}y)$$

(2)

where Ω is the magnetic potential, and A_k, B_k, C_k, D_k, and m_k are constants determined by the boundary conditions.

Assuming ${\mu }_{\mathrm{Fe}}=\infty$, the boundary conditions can be expressed as follows:

When y = 0, Ω = 0

(3)

$$\mathrm{When} \mathrm{y}=\mathsf{\delta }, \mathrm{\Omega }={\mathrm{\Omega }}_0$$

(4)

Assuming that the surface magnetic field of the stator core is sinusoidal, when y = 0,we have the following:

$$B_y=-B_{\mathrm{g}}\cos \frac{\mathsf{\pi }}{\tau }x$$

(5)

where B_y is the magnetic density component of the air gap along the y axis, and $\tau$ is the polar distance of the rotor.

By substituting Equation (3) into Equation (2), we can deduce the following:

$${\displaystyle \sum _{k=1}^{\infty }(A_k\cos m_k}x+B_K\sin m_{k}x)D_k=0$$

(6)

According to Equation (6), D_k = 0. Therefore, Equation (2) becomes the following:

$$\mathrm{\Omega }={\displaystyle \sum _{k=1}^{\infty }({A_k}^{’}\cos m_k}x+{B_K}^{’}\sin m_{k}x)\mathrm{sh}{m}_{k}y$$

(7)

where ${A_k}^{’}=\frac{B_{\mathrm{g}}}{{\mu }_0{m}_k}$, $m_k=\frac{\mathsf{\pi }}{\tau }$ and ${B_k}^{’}=0$.

According to the second formula of the boundary conditions, that is, Equation (4), the magnetic density of the air gap at y = 0 can be obtained as follows:

$$B_{y(y=0)}=-B_{\mathrm{g}}\cos \frac{\mathsf{\pi }}{\tau }x$$

(8)

By substituting Equation (8) into Equation (7), we obtain the following:

$$\mathrm{\Omega }=\frac{B_{\mathrm{g}}\tau }{{\mu }_0\mathsf{\pi }}\cos \frac{\mathsf{\pi }}{\tau }x\mathrm{sh}\frac{\mathsf{\pi }}{\tau }y$$

(9)

Using Equation (4), the magnetic potential at y = δ on the surface of the rotor core can be obtained as follows:

$$\mathrm{\Omega }=\frac{B_{\mathrm{g}}\tau }{{\mu }_0\mathsf{\pi }}\cos \frac{\mathsf{\pi }}{\tau }x\mathrm{sh}\frac{\mathsf{\pi }}{\tau }\delta$$

(10)

When the central position of the rotor core x = 0 and y = δ₀, we can obtain the following:

$$\mathrm{\Omega }=\frac{B_{\mathrm{g}}\tau }{{\mu }_0\mathsf{\pi }}\cos \frac{\mathsf{\pi }}{\tau }x\mathrm{sh}\frac{\mathsf{\pi }}{\tau }{\delta }_0$$

(11)

Dividing Equations (10) and (11), we obtain the following:

$$\mathrm{sh}\frac{\mathsf{\pi }}{\tau }\delta =\frac{\mathrm{sh}\frac{\mathsf{\pi }}{\tau }{\delta }_0}{\cos \frac{\mathsf{\pi }}{\tau }x}$$

(12)

After sorting out Equation (12), the formula for the non-uniform air gap length can be obtained as follows:

$$\delta =\frac{\tau }{\mathsf{\pi }}{\mathrm{sh}}^{-1}\left(\frac{\mathrm{sh}\frac{\mathsf{\pi }}{\tau }{\delta }_0}{\cos \frac{\mathsf{\pi }}{\tau }x}\right)$$

(13)

By substituting Equation (13) into Equation (1), the relationship between the non-uniform air gap and rotor eccentricity can be expressed as follows:

$$\delta =\frac{(R_1^2-R_2^2)-H^2}{2R_1+2R_2\cos \alpha +\frac{\tau }{\pi }{\mathrm{sh}}^{-1}(\frac{\mathrm{sh}\frac{\pi }{\tau }{\delta }_0}{\cos \frac{\pi }{\tau }})}$$

(14)

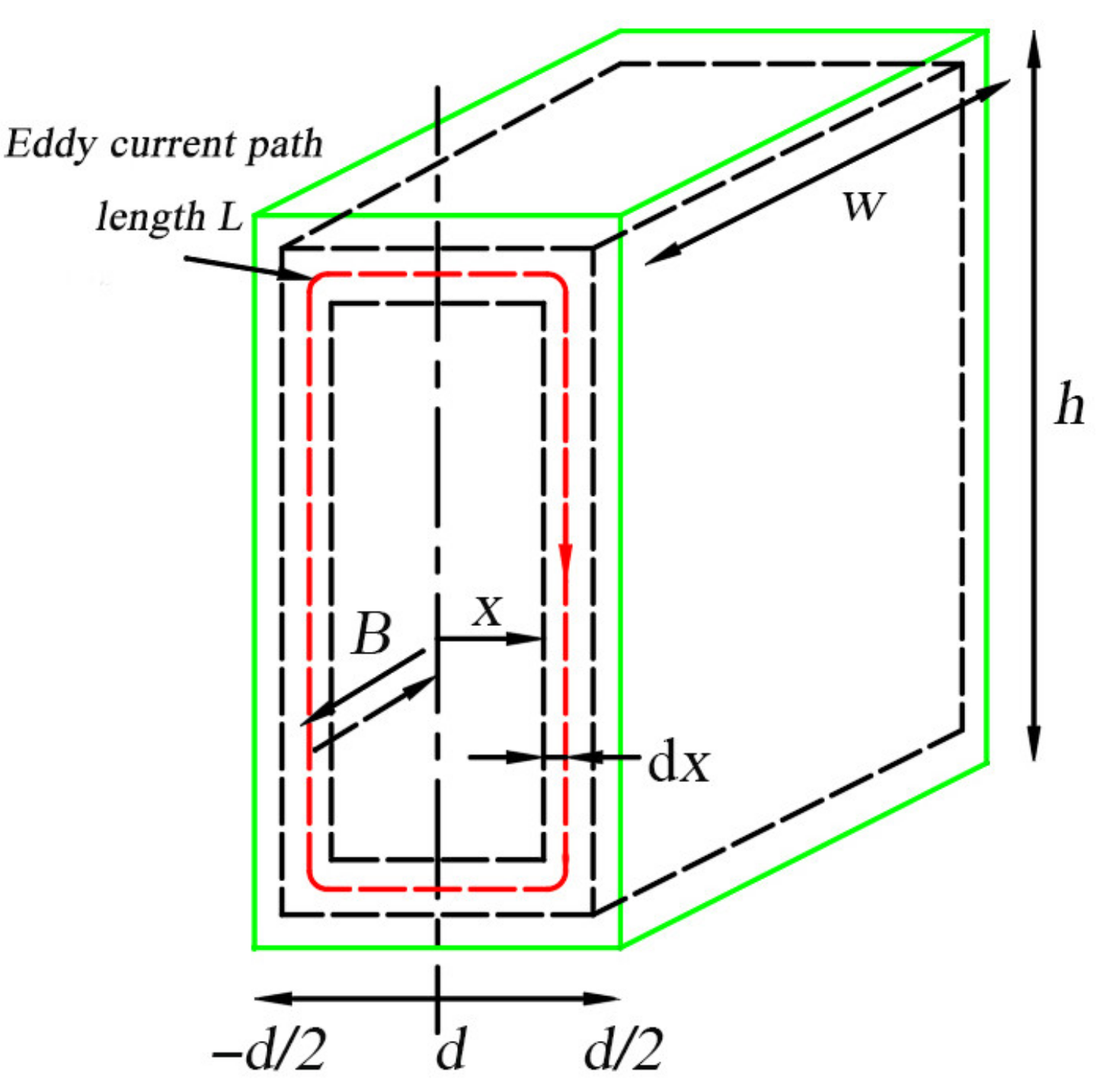
4. Establishment of an Analytical Model for Eddy Current Losses in the Rotor Core

Currently, the cores of permanent magnet rotors are mostly made of a laminated silicon steel sheet. It is assumed that eddy current losses in the rotor core exist only in each silicon steel sheet. In this paper, an eddy current loss model of a silicon steel sheet was established [16], as shown in Figure 4.

When the magnetic flux density B passes through the silicon steel sheet with resistivity ρ in the direction shown by the arrow in Figure 4, the eddy current loss P_E generated by the silicon steel sheet can be calculated as follows:

$$P_{\mathrm{E}}={\displaystyle {\int }_0^{\frac{d}{2}}\mathrm{d}}{P}_{\mathrm{E}}=\frac{w}{2}{\displaystyle {\int }_0^{\frac{d}{2}}{E}^2}\mathrm{d}x$$

(15)

where dP_E is the differential of eddy current loss at a given power, and E is the effective value of the induced voltage on the eddy current flux circuit, which can be calculated as follows:

$$E=2\pi f·B\sqrt{2}h$$

(16)

where $f$ is the motor frequency.

By substituting Equation (16) into Equation (15), we obtain the following:

$$P_{\mathrm{Fe}}=\frac{V{\pi }^2{f}^2{d}^2{B}^2}{6\rho }$$

(17)

where V is the volume of the silicon steel sheet, and V = d·w·h.

When the main performance indicators of the permanent magnet motor are determined, the aforementioned parameters can be calculated. Therefore, to reduce the rotor’s eddy current losses, it is necessary to start from the magnetic flux density B of the rotor core into the silicon steel sheet. It is difficult to determine the magnetic flux of the rotor core due to its different values at different positions. In this research, the relationship between the main air gap magnetic flux density B_r and the rotor core magnetic flux density B is expressed as follows:

$$B_{\mathrm{r}}=\sigma ·B$$

(18)

where $\sigma$ is the magnetic leakage coefficient, which refers to the ratio of the total flux ${\varphi }_{\mathrm{m}}$ provided by the permanent magnet to the total flux of the air gap entering the armature ${\varphi }_{\delta }$, $\sigma =\frac{{\varphi }_{\mathrm{m}}}{{\varphi }_{\delta }}$.

Then, the main air gap flux density B_r distributed radially along the rotor surface can be calculated as follows:

$$B_{\mathrm{r}}=F(x)·\lambda (x)$$

(19)

where $F(x)$ is the magnetomotive force of the magnetic field of the rotor in the air gap, and $\lambda (x)$ is the permeability of the air gap distributed radially along the rotor surface.

Using Fourier decomposition of $F(x)$ and $\lambda (x)$, the expression of the magnetic density of the main air gap after Fourier transformation can be obtained as follows:

$$\begin{array}{c}B(\theta ,t)=F_v(\theta ,t)·\lambda (\theta ,t)\\ \hspace{1em}\hspace{1em} \hspace{0.17em}={\displaystyle \sum _v\frac{f_v}{k_g}}{\mathrm{\Lambda }}_0\cos (v\theta -\omega t)+{\displaystyle \sum _{v_z}\frac{f_0}{k_g}}{\mathrm{\Lambda }}_k\cos (v_z\theta -\omega t)+{\displaystyle \sum _{v_z}{k}_g\frac{f_v}{2}}{\mathrm{\Lambda }}_k\cos (v_z\theta -\omega t)\end{array}$$

(20)

where $F_v(\theta ,t)$ is the magnetomotive force in the main air gap after Fourier decomposition; $\lambda (\theta ,t)$ is the permeability of the air gap after Fourier decomposition; $f_v$ is the harmonic amplitude of the stator magnetomotive force; $k_g$ is the magnetic saturation coefficient of the motor; ${\mathrm{\Lambda }}_0$ is the invariant part of the air gap magnetic permeability, ${\mathrm{\Lambda }}_0=\frac{{\mu }_0}{\delta K_c}$; K_c is the Carter coefficient, $K_c=\frac{\tau }{\tau -\gamma \delta }$; $\gamma$ is the coefficient; $f_0$ is the fundamental amplitude of the magnetomotive force; v is the number of harmonic poles of the stator magnetomotive force; v_z is the number of harmonic poles of the stator teeth; $\omega$ is the rotational angular velocity of the fundamental wave of the stator magnetomotive force; and ${\mathrm{\Lambda }}_k$ is the harmonic amplitude of the rotor surface air gap permeability.

Sorting out Equation (20), we obtain the following:

$$\begin{array}{c}{B}_{\mathrm{r}}={\displaystyle \sum _v\frac{f_v}{k_g}}{\mathrm{\Lambda }}_0\cos (v\theta -\omega t)+{\displaystyle \sum _{v_z}\frac{f_0}{k_g}}{\mathrm{\Lambda }}_k\cos (v_z\theta -\omega t)+{\displaystyle \sum _{v_z}{k}_g\frac{f_v}{2}}{\mathrm{\Lambda }}_k\cos (v_z\theta -\omega t)\\ \hspace{1em}={\displaystyle \sum _v\frac{f_v}{k_g}}·\frac{{\mu }_0(\tau -\gamma \delta )}{\delta \tau }\cos (v\theta -\omega t)+C\end{array}$$

(21)

where $C={\displaystyle \sum _{v_z}\frac{f_0}{k_g}}{\mathrm{\Lambda }}_k\cos (v_z\theta -\omega t)+{\displaystyle \sum _{v_z}{k}_g\frac{f_v}{2}}{\mathrm{\Lambda }}_k\cos (v_z\theta -\omega t)$.

By substituting Equations (20) and (14) into Equation (16), the relationship between eddy current losses and rotor eccentricity can be obtained as follows:

$$\begin{array}{c}{P}_{\mathrm{Fe}}=\frac{V{\pi }^2{f}^2{d}^2{\left[{\displaystyle \sum _v\frac{f_v}{k_g}}·\frac{{\mu }_0(\tau -\gamma \delta )}{\delta \tau }\cos (v\theta -\omega t)+C\right]}^2}{6\rho {\sigma }^2}\\ \hspace{1em} =\frac{V{\pi }^2{f}^2{d}^2{\left[{\displaystyle \sum _v\frac{f_v}{k_g}}·\frac{{\mu }_0[\tau -\gamma \frac{(R_1^2-R_2^2)-H^2}{2R_1+2R_2\cos \alpha +\frac{\iota }{\pi }{\mathrm{sh}}^{-1}(\mathrm{sh}\frac{\pi }{\tau }){(\cos \frac{\pi }{\tau })}^{-1}}]}{\frac{\tau ·[(R_1^2-R_2^2)-h^2]}{2R_1+2R_2\cos \alpha +\frac{\tau }{\pi }{\mathrm{sh}}^{-1}(\mathrm{sh}\frac{\pi }{\tau }){(\cos \frac{\pi }{\tau })}^{-1}}}\cos (v\theta -\omega t)+C\right]}^2}{6\rho {\sigma }^2}\end{array}$$

(22)

The eddy current losses of permanent magnet motors with uniform and non-uniform air gaps were calculated using the finite element method (using Ansys Maxwell 2021 software) and the model analysis method, respectively, as shown in Figure 5. According to the motor’s size and position, the rotor eccentricity was set to vary from 0 mm to 10 mm. We can see that with an increase in the rotor eccentricity, the peak value of eddy current loss did not increase or decrease linearly but approached a parabola, and when the rotor eccentricity was 4 mm, the minimum eddy current loss occurred at 27 W. The results of finite element analysis are in good agreement with analytical calculations, which verifies the correctness of the eddy current loss model of a non-uniform-air-gap combined-pole permanent magnet motor.

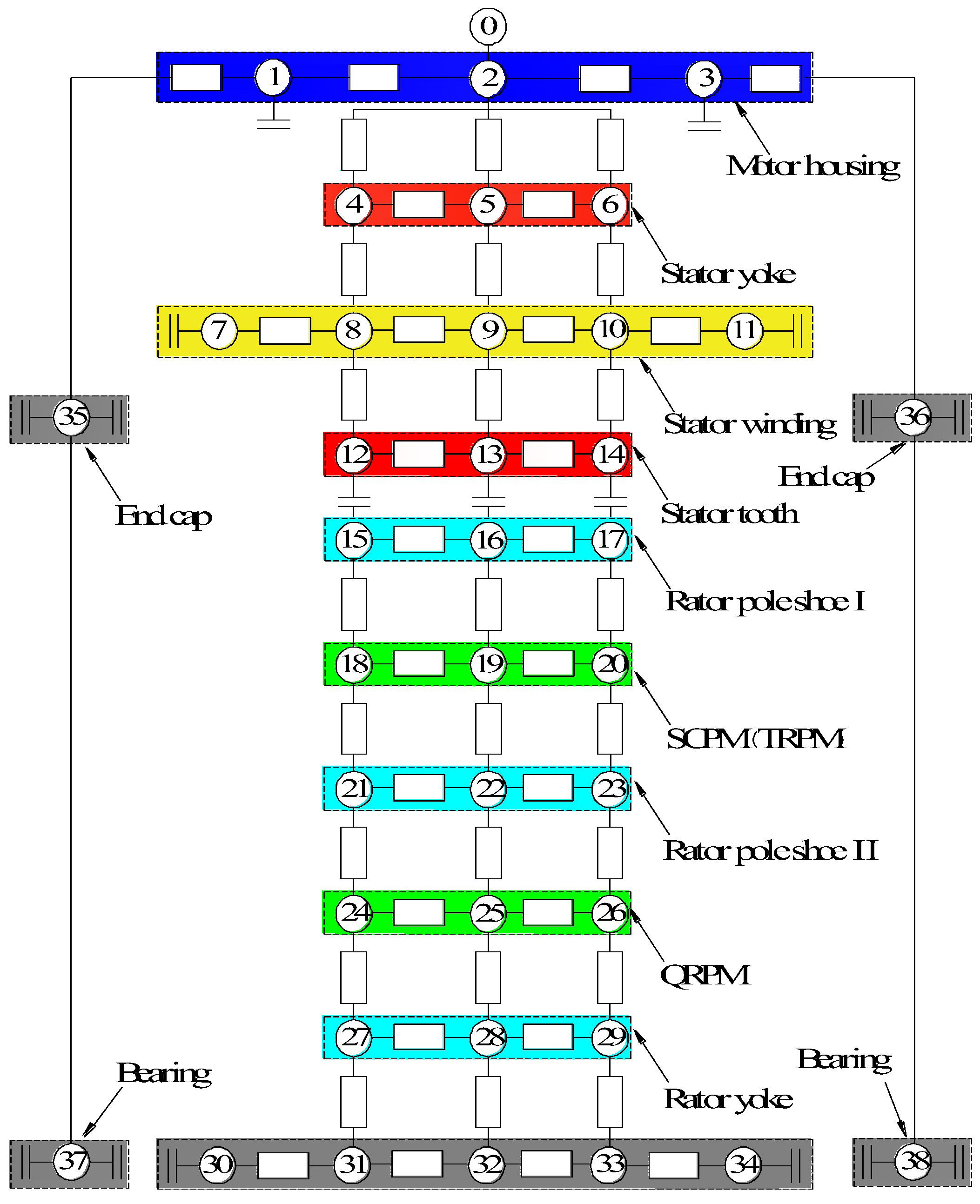
5. Establishment of an Equivalent Thermal Network Model

5.1. Equivalent Thermal Network Model

In designing permanent magnet motors, the motor’s internal temperature field defense and the influence of external heat dissipation on each part of the motor are problems that cannot be ignored. Thermal path analysis shows that many factors affect the motor’s temperature rise and directly affect the accuracy of the motor’s temperature rise meter. The equivalent thermal network method, which uses network topology as a calculation tool to model and analyze the motor’s temperature locally and as a whole, is widely used in practice due to its simple calculation process [17,18].

In order to facilitate the establishment of an equivalent thermal network, the following assumptions were made before establishing the model: (1) the skin effect of the winding in the stator slot of the motor is ignored; (2) the distribution of heat sources inside the motor is uniform, and the stray losses of the motor are concentrated in the stator teeth; and (3) the heat inside the motor is exchanged only through thermal conduction and convection, ignoring the influence of thermal radiation.

The shape of each part of the motor is mainly cylindrical or cuboid. For example, the heat fin on the shell, composed of radial and tangential permanent magnet steel, is rectangular, while the semicircular permanent magnet, the fixed rotor core, and the motor shell can be regarded as cylindrical. The thermal conductivity and thermal resistance of the motor parts can be obtained using the equations given next.

The thermal resistance equation of cuboid components is as follows:

$$R_{\mathrm{j}}=\frac{L_{\mathrm{c}}}{{\lambda }_{\mathrm{j}}{S}_{\mathrm{j}}}$$

(23)

where L_c is the heat transfer length of cuboid components, S_j is the contact area of cuboid components, and ${\lambda }_{\mathrm{j}}$ is the thermal conductivity of the cuboid material.

The thermal resistance equation of cylindrical components is as follows:

$$R_y=\frac{L_y}{{\lambda }_{\mathrm{T}}{S}_{\mathrm{dx}}}=\frac{\ln (\frac{r_w}{r_n})}{2{\lambda }_{\mathrm{T}}\pi }$$

(24)

where R_y is the radial thermal conductivity resistance of cylindrical components, r_w is the outer radius of cylindrical components, r_n is the inner radius of cylinder components, S_dx is the contact area or equivalent heat dissipation area between the components and the cooling fluid, and ${\lambda }_{\mathrm{T}}$ is the thermal conductivity of cylindrical components.

The thermal conductivity λ, specific heat capacity c, and density $\mathsf{\rho }$ of each component material of the ITRPMM proposed in this paper are shown in

Table 2. Material parameters of each component of the ITRPMM.

Component (Material)	λ /(W/m·K)	c /(J/kg·K)	$\mathbf{\rho }$/(kg·m−3)
Stator winding (copper)	379	383	8954
Stator and rotor (silicon steel)	40.6	426	7700
Permanent magnet (N35UH)	7.6	4600	7500
Shaft (steel)	46	4800	7850
Motor housing (aluminum)	230	8800	2700
Air gap (air)	0.026	1.4	1293

.

According to the aforementioned thermal conductivity and thermal resistance modeling theorem, the nodes of the ITRPMM were divided, and the circumferential half of the motor was dissected and analyzed because the motor is symmetrical. Figure 6 shows the simplified equivalent thermal network calculation model.

As can be seen in Figure 6, the materials of each component of the motor were used as influencing factors to divide the motor into 38 regions. These 38 calculation regions were divided into nodes at each position to simulate the real state of the heat conduction path, with node 0 as the external environment node, nodes 1–3 as motor casing nodes, nodes 4–6 as stator yoke nodes, nodes 7–11 as stator winding nodes, nodes 12–14 as stator tooth nodes, nodes 15–17 as rotor frontal nodes, nodes 18–20 as semicircular or tangential rectangular permanent magnet nodes, nodes 21–23 as the rotor between the radial rectangular magnet and the semicircular permanent magnet, nodes 24–26 as radial rectangular permanent magnets nodes, nodes 27–19 as nodes of the rotor core with radial permanent magnets, nodes 30–34 as rotor shaft nodes, nodes 35–36 as nodes of the motor’s front and rear air cavities, and node 37 as the main air gap node.

5.2. Equivalent Model of Armature Winding

Usually, in the motor’s armature winding, wires in the slot arrangement are irregular, and the insulation material distribution is not uniform, as shown in Figure 7a; thus, part of the heat in the stator slot in the direction of heat transfer cannot be accurately calculated. In order to simplify the calculation, the thermal field model of the stator slot was equated as follows: all of the copper wires in the slot, the insulating film, and the residual air gap between the wires were regarded as one heat conductor, while the slot insulation was regarded as another heat conductor for the calculation. The armature winding model after equating is shown in Figure 7b.

The thicknesses of the copper wires, insulating varnish, and insulating paper in the different heat transfer directions are different and converted. According to the slot width and depth, the equivalent thermal coefficient of the armature winding in the stator slot along the axial direction can be calculated using Equation (25):

$${\lambda }_{xi}={\displaystyle \sum _{i=1}^n{l}_x}/({\displaystyle \sum _{x=1}^n\frac{l_x}{{\lambda }_{xi}}})$$

(25)

where l_x is the thickness of the copper wire and insulating paper along the x direction, and λ_xi is the thermal conductivity of the copper wire and insulating paper.

The equivalent thermal conductivity of the armature winding in the stator slot along the radial direction can be calculated using Equation (26):

$${\lambda }_{yi}={\displaystyle \sum _{y=1}^n{l}_y}/({\displaystyle \sum _{y=1}^n\frac{l_y}{{\lambda }_{yi}}})$$

(26)

where l_y is the thickness of the copper wire and insulating paper along the y direction, and λ_yi is the thermal conductivity of the copper wire and insulating paper.

5.3. Calculation Results of the Equivalent Thermal Network Model

According to the principle of heat balance, the heat generated by each unit of the motor and the incoming heat should be equal to the heat output from the unit under the steady-state condition. The heat balance equations for the equivalent network nodes of an ITRPMM can be listed with the following matrix expression:

$$\mathrm{\Delta }G·\mathrm{\Delta }T=\mathrm{\Delta }P$$

(27)

where $\mathrm{\Delta }G$ is the thermal conductivity matrix, $\mathrm{\Delta }T$ is the node temperature matrix, and $\mathrm{\Delta }P$ is the heat source matrix.

Assuming that the external ambient temperature is 25 °C (room temperature), according to the motor’s heat dissipation conditions determined before, the temperature rise of the permanent magnet motor was calculated using the established equivalent thermal network model, in order to obtain the temperature rise of each node inside the motor. Next, the temperature rise of each component of the permanent magnet motor was averaged to ultimately solve the temperature rise problem of that component.

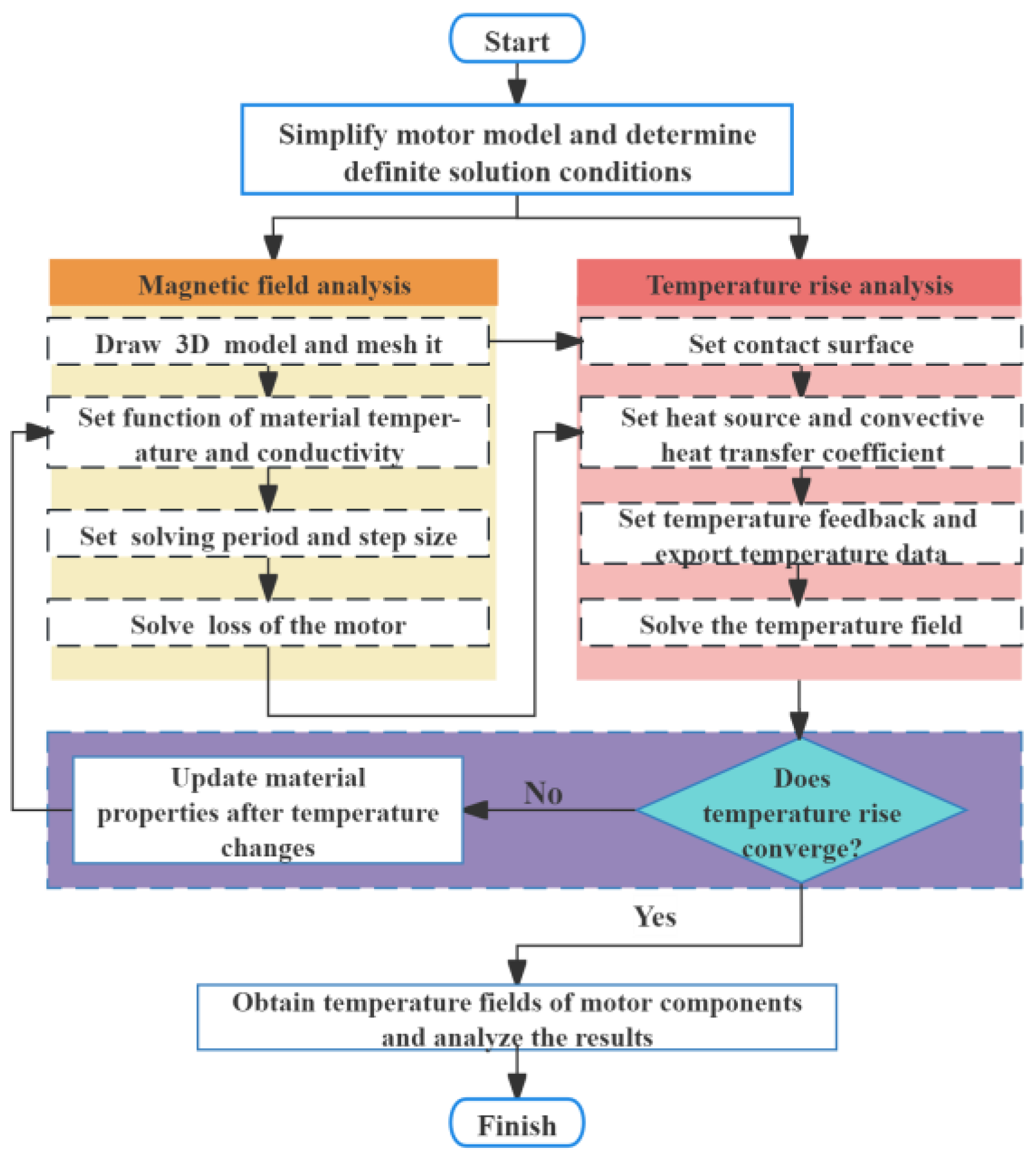
6. Magnetothermal Bidirectional Coupling Finite Element Simulation Analysis

The problems of loss and temperature rise of a permanent magnet motor are a coupled problem. The magnitude of loss causes a change in the temperature rise, and the temperature rise of the motor affects the permanent magnet’s remanent magnetism and coercivity, which, in turn, affects losses in the motor. For permanent magnet motors applied to electric vehicles, the rated thermal load is higher during load operation, and when the temperature exceeds the demagnetization temperature of the permanent magnet, irreversible demagnetization occurs, which reduces the service life of permanent magnet motors. Therefore, accurate calculation of the temperature field directly affects the reliability of the motor.

Using an equivalent thermal network to analyze the motor, the model can be simplified and solved quickly. Although the calculation is quick, the equivalent thermal network method cannot directly obtain the temperature distribution of each part of the motor. If any component is more complex, the equivalent thermal network method is difficult to use and the precision is not high. In order to carry out further thermal analysis of the motor and verify the calculation results of the equivalent thermal network, magnetothermal coupling simulation of the motor was performed. In addition, in order to improve the accuracy of the calculation, a three-dimensional field was used in the electromagnetic characteristic analysis and thermodynamic simulation of the motor.

The use of magnetothermal coupling finite element analysis can save simulation time, while providing better computational accuracy. Generally, there are two schemes for electromagnetic field and temperature field coupling: unidirectional coupling and bidirectional coupling [19,20]. In unidirectional coupling, electromagnetic field and temperature field calculations are carried out separately, and the results of the electromagnetic field are directly used in the calculation of the temperature field. Bidirectional coupling involves mutual transfer of data to conduct electromagnetic field analysis (loss is calculated as the heat source of the temperature field) and temperature field analysis (the temperature used for electromagnetic field analysis of the material properties is calculated) at the same time, with closed-loop transmission of the data for many iterations until the temperature reaches the set error range, or the maximum number of iterations is reached. In order to calculate the temperature field of the motor more accurately, the two-way coupling method was used, and the magnetothermal bidirectional coupling model is schematically shown in Figure 8.

According to the magnetothermal bidirectional coupling flowchart, finite element simulation analysis (using Ansys Workbench 2021 software) of the ITRPMM with a uniform air gap and a non-uniform air gap was carried out, and the temperature distribution diagram of the permanent magnet motor was obtained, as shown in Figure 9 and Figure 10, respectively.

In order to verify the correctness of the equivalent thermal network modeling and analysis results established through our research, the analysis results of each component of the motor were compared with the average value of the simulation results, as shown in

Table 3. Average temperature rise for each motor component at the steady state.

Component Name	Equivalent Thermal Network Method/ (°C)	Simulation Value of Uniform Air Gap/ (°C)	Simulation Value of Non-Uniform Air Gap/ (°C)
Motor housing	84.6	90.5	82.5
Stator yoke	86.5	88.42	81.3
Armature winding	90.3	96.65	83.5
Stator teeth	91.8	93.75	80.5
SCPM	85.6	84.17	79.23
TRPM	83.5	84.27	77.32
Rotor core	82.1	83.71	76.85
RRPM	81.8	82.76	79.78
Shaft	77.8	79.68	76.56

. Comparative analysis shows that the results of the equivalent thermal network method are basically the same as the simulation results, and the maximum error area exists in the armature winding. This is due to the fact that the armature winding has a long axial length, the equivalent thermal network method is less accurate, and the armature winding is made of copper, which transmits heat faster, so the average value of the calculation is more inaccurate.

7. Experimental Validation

In order to verify the validity of the established eddy current loss model of the ITRPMM and the accuracy of the calculation results of the bidirectional magnetothermal coupling method, two prototypes were test-fabricated. Other things being equal, the experimental results of the permanent magnet motor were compared and analyzed for rotor eccentricities of 0 mm and 4 mm. The results are shown in Figure 11a,b. Two rotor structures shared the same stator and armature winding for experimental testing, as shown in Figure 11c. The PT100 thermistor was pre-buried at the end of the armature winding and in the stator slot of the motor to build the test platform of the interior non-uniform-air-gap combined-pole PM motor, as shown in Figure 11d.

The experimental platform in Figure 11d was used to test the two prototypes. When a prototype is tested, the DC bus current of the motor controller is gradually increased, so that the motor speed keeps rising and the motor phase current reaches its limit value. Next, as the brake load increases, the motor speed decreases, and signals are detected and collected by the sensor. Finally, the output characteristic curve of the permanent magnet motor is displayed on the upper computer, as shown in Figure 12. When the two motors adopted the same control strategy, the maximum output torque of the non-uniform-air-gap motor was 34 N·m, while the maximum output torque of the uniform-air-gap motor was 33.4 N·m. This is because the non-uniform-air-gap motor can reduce the temperature rise, give full play to the magnetic properties of the permanent magnet, and improve the output torque.

The temperature rise test of the prototype using a thermal imager at 3000 r/min is shown in Figure 13, and the steady-state temperature cloud diagram of the prototype is shown in Figure 14. The maximum temperature of the motor housing was 89.5 °C when the temperature rise was stable, and the maximum temperature rise of the motor housing was 90.747 °C in the bidirectional magnetothermal coupling simulation results. The simulation results were in good agreement with the experimental results, which proves the accuracy of bidirectional magnetothermal coupling.

Through the motor temperature test experiment, the motor temperature rise test curve was obtained, as shown in Figure 15. When the uniform-air-gap permanent magnet motor ran for 120 min under the no-load condition, the test value of the stator winding temperature tending toward the steady state was 54 °C, while the steady-state temperature test value under the rated load condition was 96 °C. When the non-uniform-air-gap PM motor was run for 120 min at no load, the steady-state temperature test value was 52 °C, while the steady-state temperature test value under the rated load condition was 89 °C, which is consistent with the theoretical calculations as well as the simulation results. The experimental results showed that the permanent magnet motor with a non-uniform-air-gap rotor structure can effectively reduce the temperature rise of the armature winding, and the temperature difference between the non-uniform-air-gap and uniform-air-gap permanent magnet motors is larger under the rated load condition, which verifies the correctness of the three-dimensional magnetothermal bidirectional three-dimensional coupling model.

In our research, the no-load back electromotive force (EMF) test was carried out on the prototype using the two-machine towing feedback method. The experimental platform of the prototype built is shown in Figure 16. For the experimental test, a permanent magnet motor with a rated power of 5 kW, a rated voltage of 72 V, and a rated speed of 3000 r/min was used as the pilot motor, and the operating frequency and synchronous speed of the pilot motor were the same as those of the test motor.

Under the rated speed, the waveforms of the no-load back electromotive force measured by the two prototypes are shown in Figure 17. When the motor had a non-uniform air gap, the waveform of the back EMF was more similar to the sine law and had a smoother curve, indicating that when the rotor eccentricity is 4 mm, the high-order harmonic content of the magnetic density of the air gap is less, thus verifying the correctness of the theoretical analysis method. When the air gap was uniform, the amplitude of the no-load back EMF was 48 V, and when the air gap was non-uniform, the amplitude of the no-load back EMF was 51 V. These findings show that the design of the non-uniform air gap is beneficial for enhancing the amplitude of the back EMF, because the design improves the peak value of the motor’s air gap magnetic density when other conditions remain unchanged.

Fourier decomposition was performed on the measured no-load back EMF waveform, and the harmonic amplitudes of the no-load back EMF of the two prototypes were obtained, as shown in Figure 18. The fundamental amplitude of the non-uniform-air-gap motor was 50 V, the 3rd harmonic amplitude was 6.6 V, the 5th harmonic amplitude was 3.2 V, the 7th harmonic amplitude was 2.2 V, the 9th harmonic amplitude was 1.8 V, the 11th harmonic amplitude was 1 V, the 13th harmonic amplitude was 0.6 V, and the 15th harmonic amplitude was 0.25 V. However, the fundamental amplitude of the uniform-air-gap motor was 48 V, the 3rd harmonic amplitude was 9 V, the 5th harmonic amplitude was 4 V, the 7th harmonic amplitude was 2 V, the 9th harmonic amplitude was 1.4 V, the 11th harmonic amplitude was 1.2 V, the 13th harmonic amplitude was 0.8 V, and the 15th harmonic amplitude was 0.25 V. The no-load back EMF waveform distortion rate of the non-uniform-air-gap motor was 15.9%, and the no-load back EMF waveform distortion rate of the uniform-air-gap motor was 21.8%, which shows that the design of the non-uniform-air-gap structure can effectively reduce the high harmonic content of the back electromotive force, reduce the eddy current loss and motor temperature rise, and improve the power density of the motor, indicating that it is more suitable for driving the motors for electric vehicles.

8. Conclusions

(1)

We propose a new type of interior combined-pole permanent magnet motor for electric vehicles. Through the establishment of a sinusoidal subdomain model of the non-uniform-air-gap distribution and eddy current loss model, the analytical expression between rotor eccentricity and eddy current loss was derived. It was determined that when the ITRPMM rotor eccentricity is 4 mm, the waveform of the back EMF is more similar to the sine law. The content of higher harmonics in the air gap and the eddy current losses are the least.

(2)

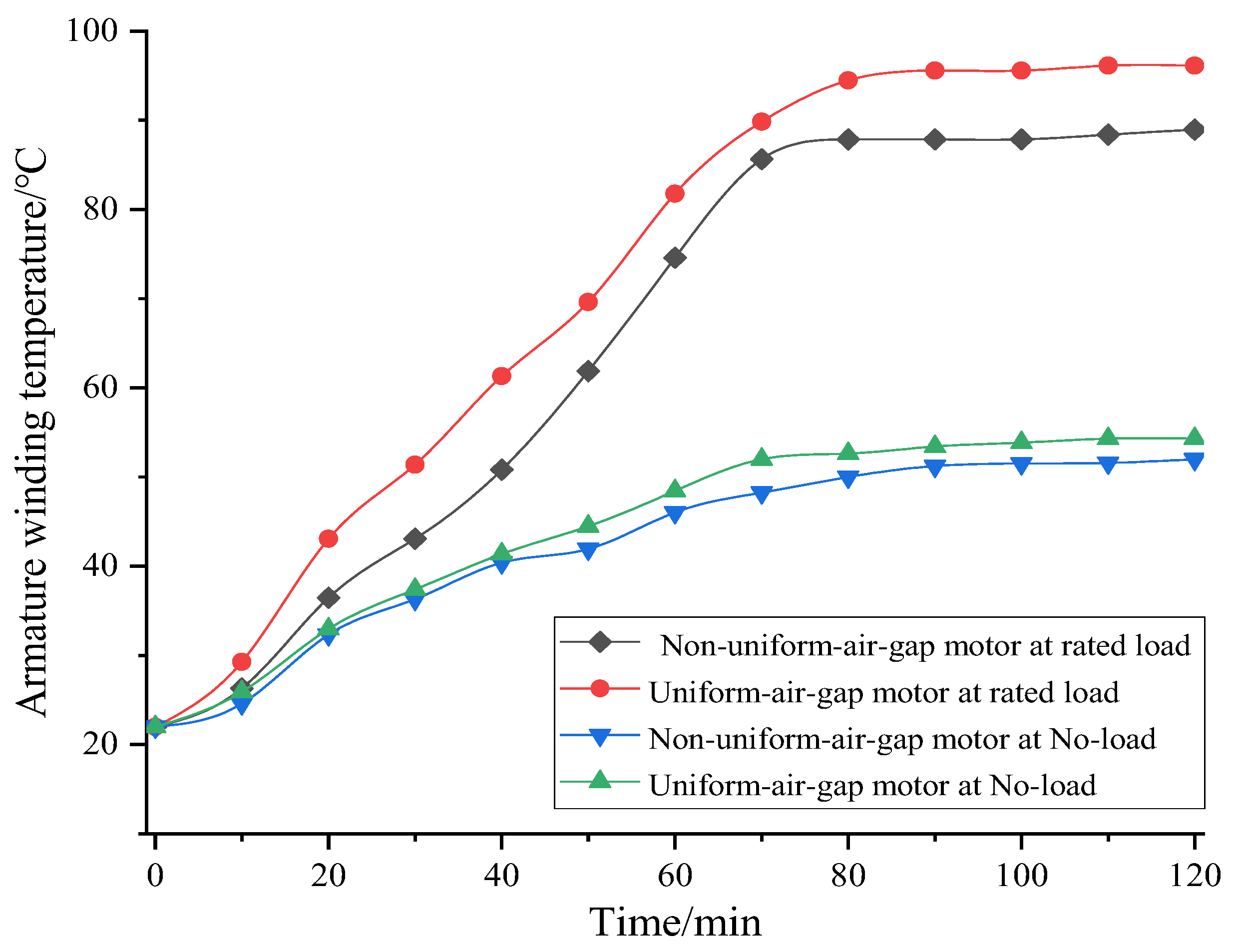
The equivalent thermal network model of the ITRPMM was established, the temperature rise matrix expression of the ITRPMM was obtained, and the temperature rise of each node of the motor was calculated. Finite element simulations of the uniform-air-gap and non-uniform-air-gap permanent magnet motors were verified using the magnetothermal bidirectional coupling method. When the permanent magnet motor adopts a non-uniform air gap structure, the temperature rise of each component significantly reduces. The calculation results of the equivalent thermal network method are between the simulation results of the uniform-air-gap and non-uniform-air-gap permanent magnet motors, and the armature winding is the component with the largest error in the calculation results of the analytical and finite element methods.

(3)

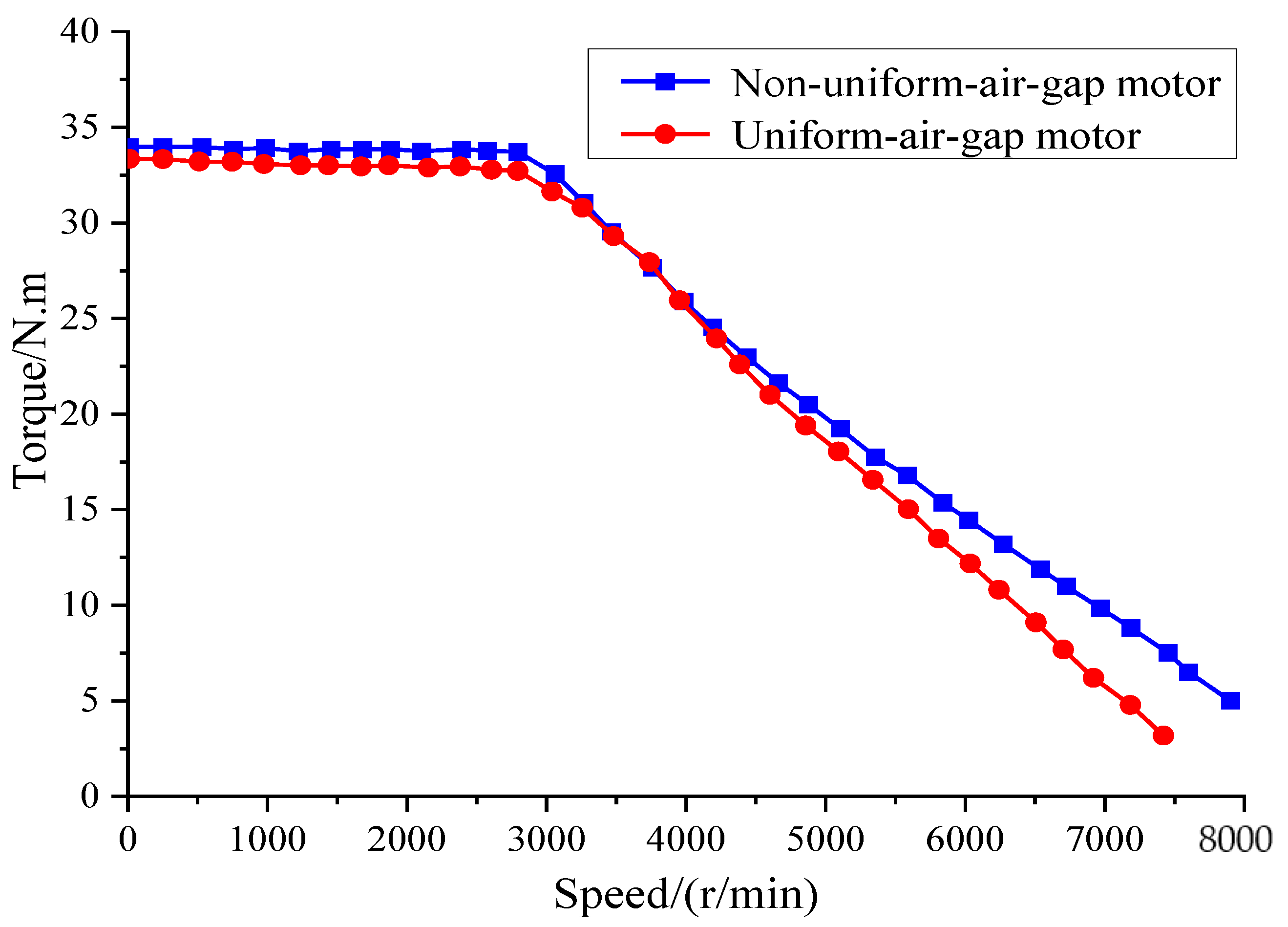
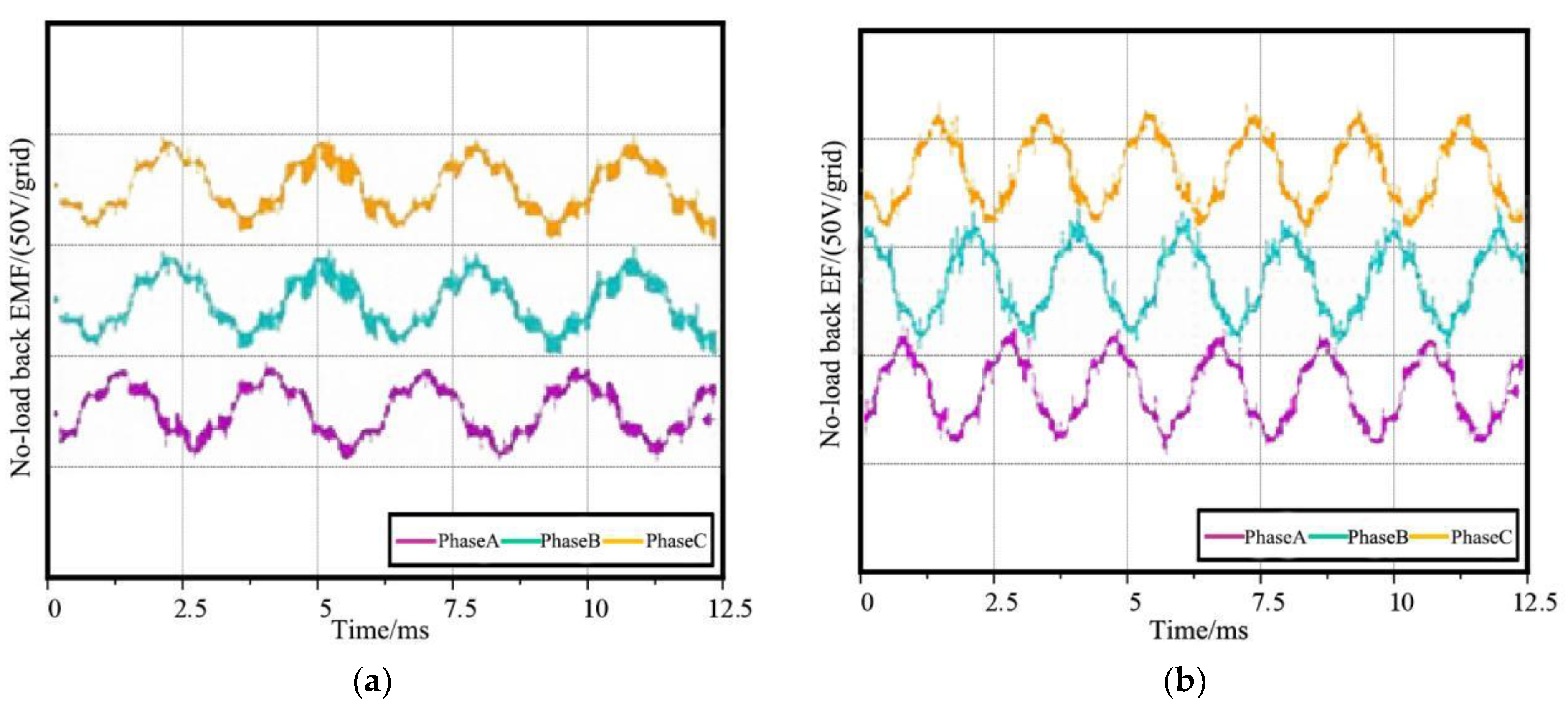
The prototype experiment showed that the permanent magnet motor with a non-uniform air gap structure can effectively reduce the rotor eddy current losses, and the no-load back EMF waveform distortion rate of the non-uniform-air-gap motor is 15.9%, while the no-load back EMF waveform distortion rate of the uniform-air-gap motor is 21.8%. Meanwhile, the non-uniform-air-gap motor can reduce the motor temperature rise and increase the output torque of the motor. When the two motors adopt the same control strategy, the maximum output torque of the non-uniform-air-gap motor is 34 N·m, while that of the uniform-air-gap motor is 33.4 N·m, which is conducive to improving the power density of the motor and is more suitable for permanent magnet motors for electric vehicles.