Objective Evaluation of Motion Cueing Algorithms for Vehicle Driving Simulator Based on Criteria Importance through Intercriteria Correlation (CRITIC) Weight Method Combined with Gray Correlation Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Visual–Vestibular Interaction Model and Evaluation Scheme
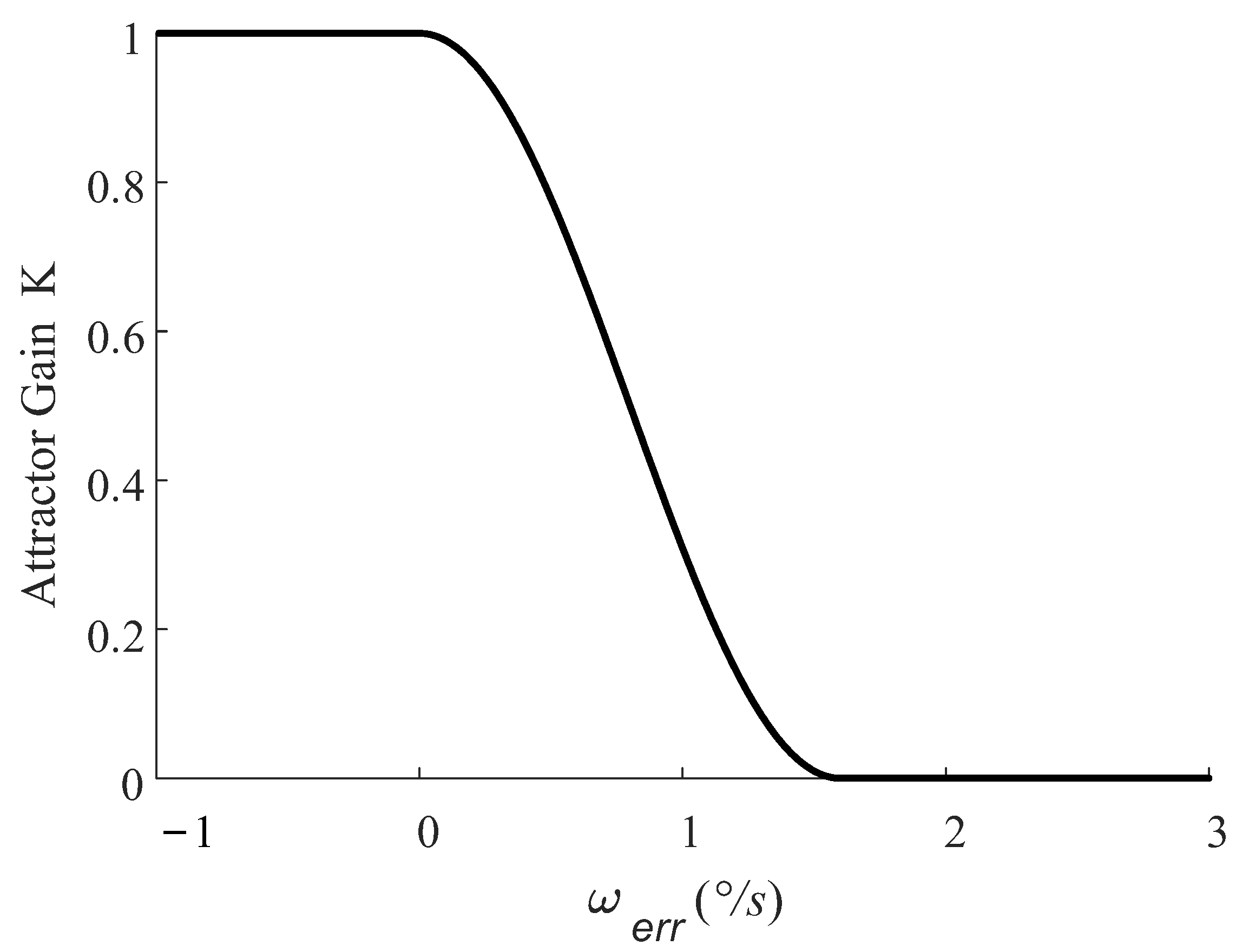
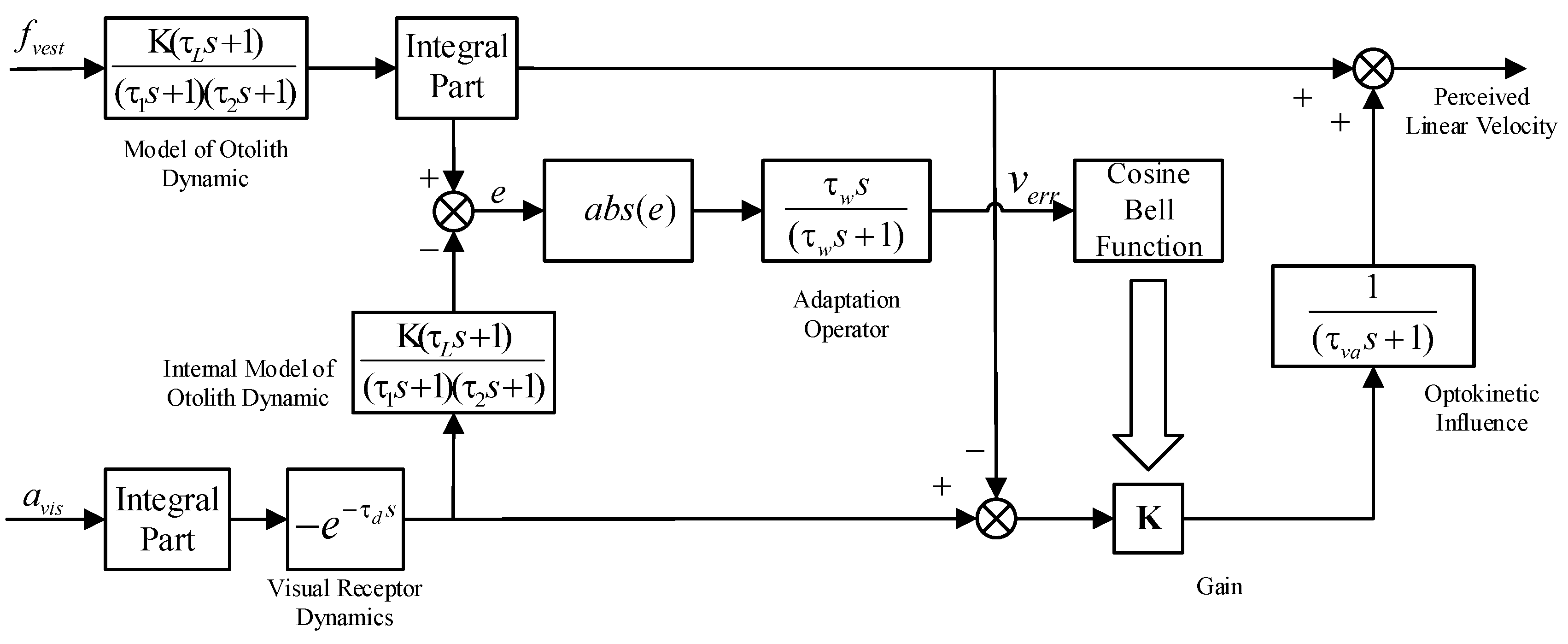
2.1.1. Visual–Vestibular Interaction Model
2.1.2. Model of Tilting Angle Perception of Head
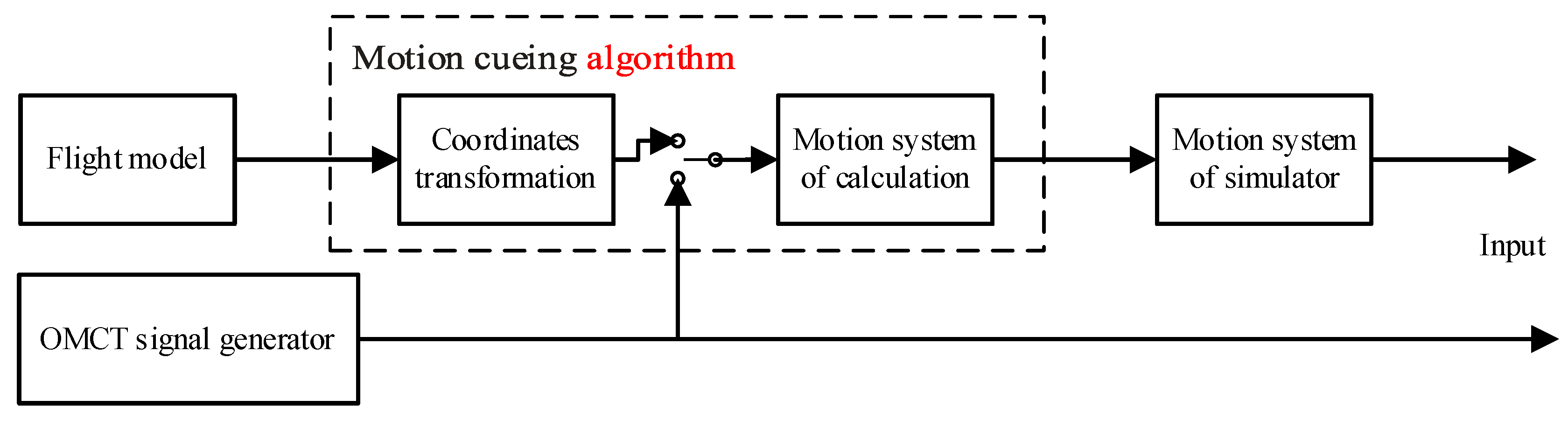
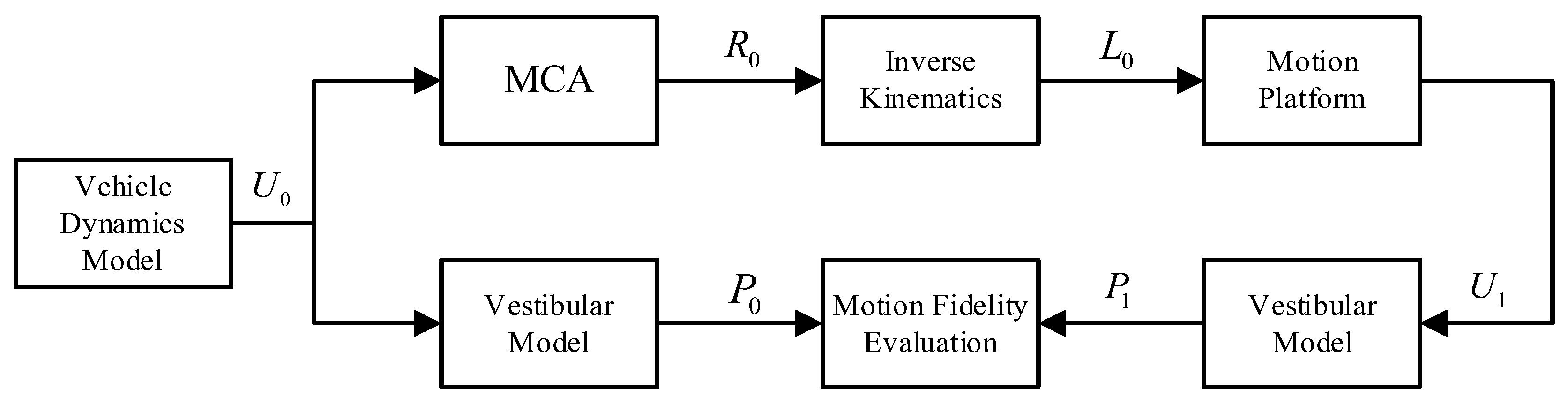
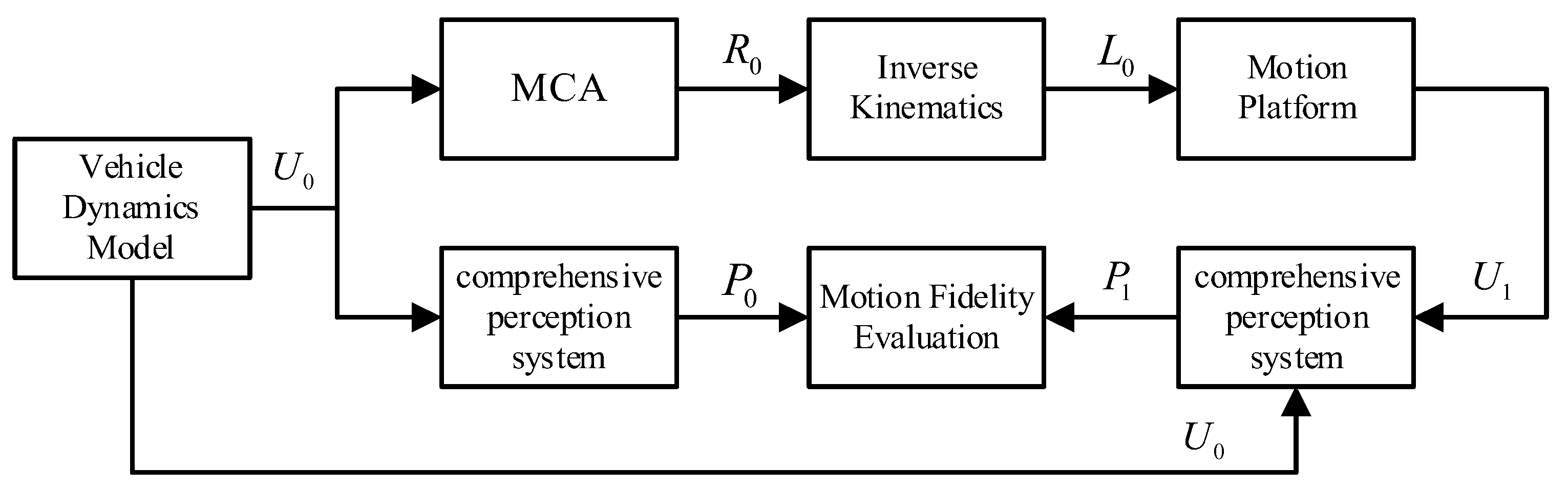
2.1.3. Improved Scheme of MCA Perceptual Fidelity Evaluation
2.2. Establishment of the Evaluation Indicator System
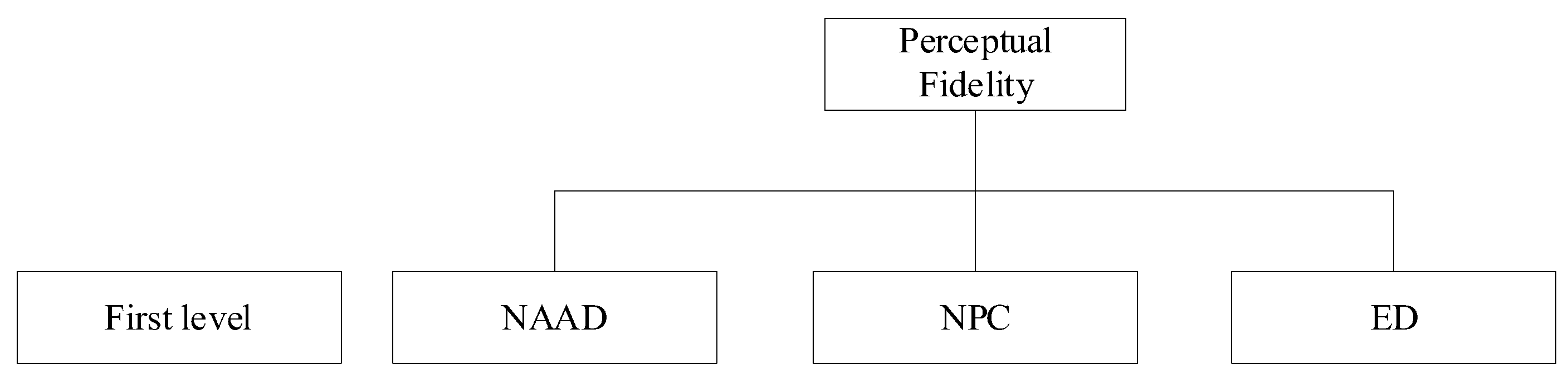
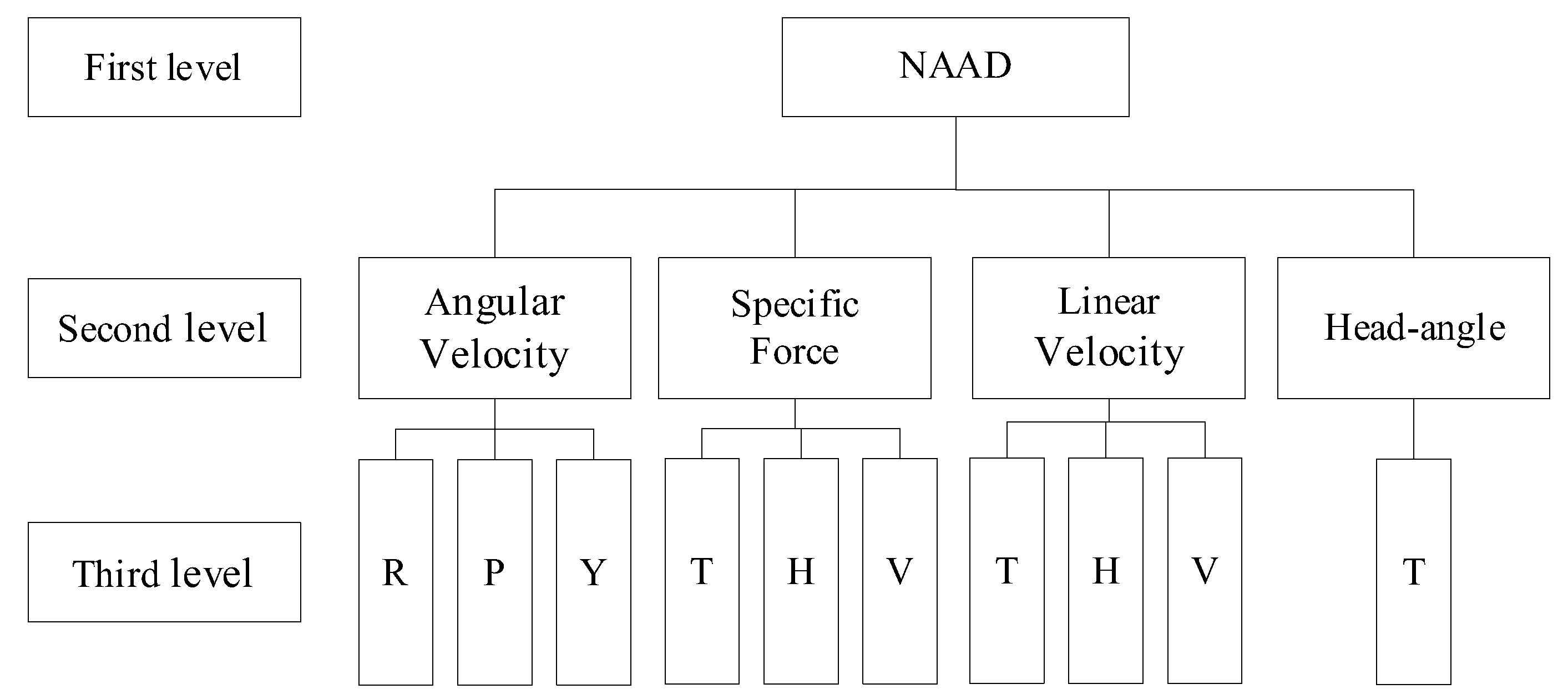
2.2.1. Key Performance Indicators
2.2.2. Weights of Indicators at the First Level
2.2.3. Criteria Importance through Intercriteria Correlation (CRITIC)
2.2.4. The Method of Gray Relational Analysis
2.2.5. Determine Combined Weights
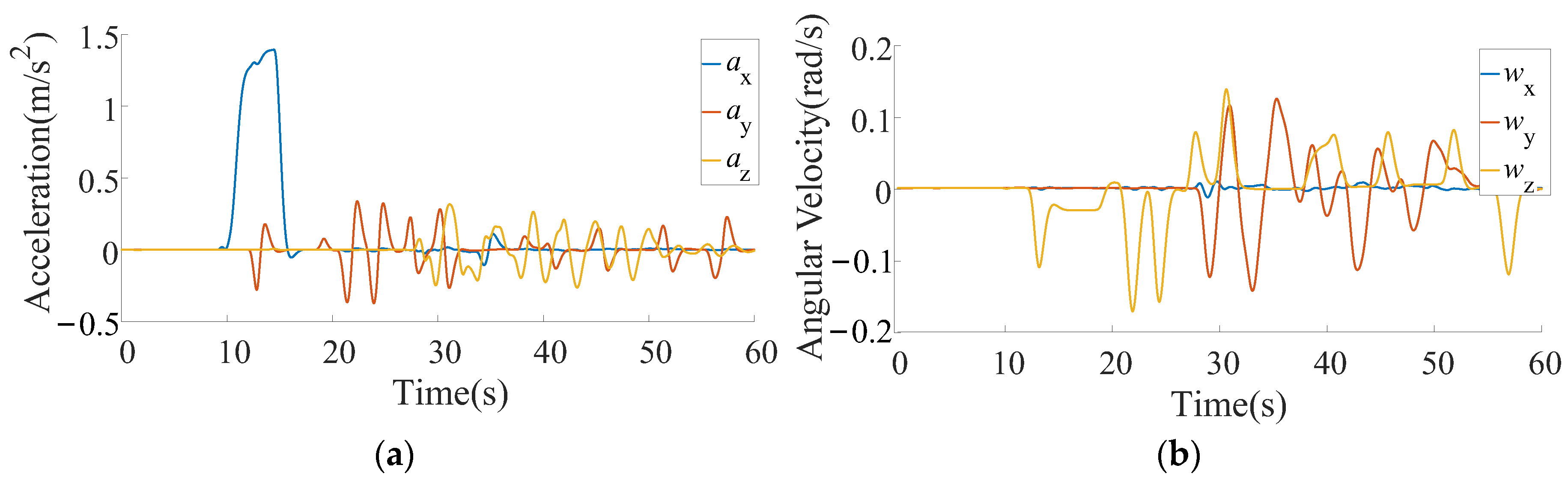
2.3. Example Analysis
3. Results
3.1. Apparatus and the MCAs
3.2. Experimental Procedure
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kwon, S.-J.; Kim, M.-S. A Study on Improvement of Motion Sensation for a Vehicle Driving Simulator Based on Specific Force Gain and Tilt Angle Scale Method. Appl. Sci. 2022, 12, 9473. [Google Scholar] [CrossRef]
- Conrad, B.; Schmidt, S.F. Motion Drive Signals for Piloted Flight Simulators; No. NASA-CR-1601; NASA: Washington, DC, USA, 1970.
- Parrish, R.V.; Dieudonne, J.E.; Bowles, R.L.; Martin, D.J. Coordinated adaptive filters for motion simulators. J. Aircr. 1975, 12, 44–50. [Google Scholar] [CrossRef]
- Sivan, R.; Ish-Shalom, J.; Huang, J.K. An optimal control approach to the design of moving flight simulators. IEEE Trans. Syst. Man Cybern. 1982, 12, 818–827. [Google Scholar] [CrossRef]
- Asadi, H.; Mohamed, S.; Nahavandi, S. Incorporating human perception with the motion washout filter using fuzzy logic control. IEEE/ASME Trans. Mechatron. 2015, 20, 3276–3284. [Google Scholar] [CrossRef]
- Mehmet, D.; Gilles, R.; Andras, K.; Marc, B.; Nadia, M. Model-based predictive motion cueing strategy for vehicle driving simulators. Control. Eng. Pract. 2009, 17, 995–1003. [Google Scholar]
- Zhu, D.; Duan, S.; Fang, D. Development of Cueing Algorithm Based on “Closed-Loop” Control for Flight Simulator Motion System. Wuhan Univ. J. Nat. Sci. 2019, 24, 376–382. [Google Scholar] [CrossRef]
- Ellensohn, F.; Venrooij, J.; Schwienbacher, M.; Rixen, D. Experimental evaluation of an optimization-based motion cueing algorithm. Transp. Res. Part F Traffic Psychol. Behav. 2019, 62, 115–125. [Google Scholar] [CrossRef]
- Casas-Yrurzum, S.; Portalés-Ricart, C.; Morillo-Tena, P. On the objective evaluation of motion cueing in vehicle simulations. IEEE Trans. Intell. Transp. Syst. 2021, 22, 3001–3012. [Google Scholar] [CrossRef]
- Advani, S.; Hosman, R.; Potter, M. Objective motion fidelity qualification in flight training simulators. In Proceedings of the AIAA Modeling and Simulation Technologies Conference and Exhibit, Hilton Head, SC, USA, 20–23 August 2007; pp. 1018–1030. [Google Scholar]
- Wei, C.; Wang, J.; Ying, X.; Shang, H.; Chao, J. Credibility evaluation of motion simulation based on visual-vestibular perception coherence. Space Med. Med. Eng. 2017, 30, 66–72. [Google Scholar]
- Hess, R.A.; Siwakosit, W. Assessment of flight simulator fidelity in multiaxis tasks including visual cue quality. J. Aircr. 2001, 38, 607–614. [Google Scholar] [CrossRef]
- Zeyada, Y.; Hess, R.A. Modeling human pilot cue utilization with applications to simulator fidelity assessment. J. Aircr. 2000, 37, 588–597. [Google Scholar] [CrossRef] [PubMed]
- Casas, S.; Coma, I.; Portalés, C.; Fernández, M. Towards a simulation-based tuning of motion cueing algorithms. Simul. Model. Pract. Theory 2016, 67, 137–154. [Google Scholar] [CrossRef]
- Zacharias, G. Motion Sensation Dependence on Visual and Vestibular Cues. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1977. [Google Scholar]
- Telban, R.; Cardullo, F. An integrated model of human motion perception with visual-vestibular interaction. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, Montreal, QC, Canada, 9 August 2001. [Google Scholar]
- Markkula, G.; Romano, R.; Waldram, R.; Giles, O.; Mole, C.; Wilkie, R. Modelling visual-vestibular integration and behavioural adaptation in the driving simulator. Transp. Res. Part F Traffic Psychol. Behav. 2019, 66, 310–323. [Google Scholar] [CrossRef]
- Dehouck, T.L.; Mulder, M.; van Paassen, M.M. The effects of simulator motion filter settings on pilot manual control behaviour. In Proceedings of the AIAA Modeling and Simulation Technologies Conference and Exhibit, Keystone, CO, USA, 21–24 August 2006. [Google Scholar]
- Gum, D.R. Modeling of the Human Force and Motion-Sensing Mechanisms; Technical Report; AFHRL-TR-72-54; Air Force Human Resources Lab: Dayton, OH, USA, 1973. [Google Scholar]
- Duc-An, P.; Duc-Toan, N. A novel motion cueing algorithm integrated multi-sensory system–vestibular and proprioceptive system. Proceedings of the Institution of Mechanical Engineers, Part K. J. Multi-Body Dyn. 2020, 234, 256–271. [Google Scholar]
- Aminzadeh, M.; Mahmoodi, A.; Sabzehparvar, M. Optimal motion-cueing algorithm using motion system kinematics. Eur. J. Control 2012, 18, 363–375. [Google Scholar] [CrossRef]
- Asadi, H.; Mohamed, S.; Zadeh, D.R.; Nahavandi, S. Optimisation of nonlinear motion cueing algorithm based on genetic algorithm. Veh. Syst. Dyn. 2015, 53, 526–545. [Google Scholar] [CrossRef]
- Qazani, M.R.C.; Asadi, H.; Nahavandi, S. A motion cueing algorithm based on model predictive control using terminal conditions in urban driving scenario. IEEE Syst. J. 2021, 15, 445–453. [Google Scholar] [CrossRef]
- Casas, S.; Coma, I.; Riera, J.V.; Fernández, M. Motion-cuing algorithms: Characterization of users’ perception. Hum. Factors 2015, 57, 144–162. [Google Scholar] [CrossRef] [PubMed]
- Luo, N.; He, M.; Gao, H. Comprehensive evaluation method for a distribution network based on improved AHP-CRITIC combination weighting and an extension evaluation model. Power Syst. Prot. Control 2021, 49, 86–96. [Google Scholar]
- Guan, L.; Gao, Z.; Tu, M.; Li, X.; Jiang, J. An evaluation method of power market operation efficiency based on Grey Relational Analysis of entropy weight method. In Proceedings of the IEEE Sustainable Power and Energy Conference: Energy Transition and Energy Internet (iSPEC 2020), Chengdu, China, 23–25 November 2020; pp. 1114–1120. [Google Scholar]
- Peng, X.; Garg, H. Intuitionistic fuzzy soft decision making method based on CoCoSo and CRITIC for CCN cache placement strategy selection. Artif. Intell. Rev. 2022, 55, 1567–1604. [Google Scholar] [CrossRef]





| Type | Advantages | Disadvantages |
|---|---|---|
| CMCA | Fewer parameters, fast calculation. | Fixed parameters, poor applicability. |
| AMCA | Filter parameters can be adjusted in real time. | The stability is poor, and the optimization efficiency is low. |
| OMCA | Human perception error is considered for the first time. | The parameters are fixed, and the calculation is complicated. |
| FMCA | Regulators are plentiful and flexible. | The algorithm structure is complex. |
| MPC-MCA | Parameters and constraints have a more intuitive relationship. | It is highly dependent on human perception model, which is not perfect. |
| Indicator | Correlation | Coefficient | Average | Weight |
|---|---|---|---|---|
| NAAD | 0.123 | 0.218 | 0.1705 | 0.17 |
| NPC | 0.425 | 0.495 | 0.460 | 0.47 |
| ED | 0.347 | 0.357 | 0.352 | 0.36 |
| Second Level | CRITIC Weight | GRA Weight | Combined Weight | Third Level | CRITIC Weight | GRA Weight | Combined Weight |
|---|---|---|---|---|---|---|---|
| Angular Velocity | 0.3784 | 0.2277 | 0.3031 | R | 0.2858 | 0.4074 | 0.3466 |
| P | 0.2826 | 0.2831 | 0.2829 | ||||
| Y | 0.4315 | 0.3095 | 0.3705 | ||||
| Specific Force | 0.0591 | 0.3415 | 0.2003 | H | 0.5138 | 0.2867 | 0.4002 |
| T | 0.2768 | 0.2873 | 0.2821 | ||||
| V | 0.2095 | 0.4260 | 0.3177 | ||||
| Linear Velocity | 0.2775 | 0.2414 | 0.2594 | H | 0.2627 | 0.3333 | 0.2980 |
| T | 0.3208 | 0.2760 | 0.2984 | ||||
| V | 0.4166 | 0.3907 | 0.4036 | ||||
| Head Angle | 0.2850 | 0.1894 | 0.2372 | ||||
| Second Level | CRITIC Weight | GRA Weight | Combined Weight | Third Level | CRITIC Weight | GRA Weight | Combined Weight |
|---|---|---|---|---|---|---|---|
| Angular Velocity | 0.3127 | 0.2330 | 0.2729 | R | 0.7947 | 0.3048 | 0.5498 |
| P | 0.0931 | 0.3603 | 0.2267 | ||||
| Y | 0.1122 | 0.3349 | 0.2235 | ||||
| Specific Force | 0.4044 | 0.2600 | 0.3322 | H | 0.9067 | 0.2877 | 0.5972 |
| T | 0.0501 | 0.3439 | 0.1969 | ||||
| V | 0.0433 | 0.3685 | 0.2059 | ||||
| Linear Velocity | 0.1626 | 0.2791 | 0.2209 | H | 0.6965 | 0.3262 | 0.5114 |
| T | 0.2202 | 0.2980 | 0.2591 | ||||
| V | 0.0833 | 0.3758 | 0.2295 | ||||
| Head Angle | 0.1203 | 0.2278 | 0.1740 | ||||
| Second Level | CRITIC Weight | GRA Weight | Combined Weight | Third Level | CRITIC Weight | GRA Weight | Combined Weight |
|---|---|---|---|---|---|---|---|
| Angular Velocity | 0.0974 | 0.2572 | 0.1774 | R | 0.5154 | 0.3067 | 0.4110 |
| P | 0.3879 | 0.2904 | 0.3392 | ||||
| Y | 0.0967 | 0.4030 | 0.2498 | ||||
| Specific Force | 0.2400 | 0.2756 | 0.2578 | H | 0.7089 | 0.2977 | 0.5033 |
| T | 0.2549 | 0.3135 | 0.2842 | ||||
| V | 0.0363 | 0.3888 | 0.2125 | ||||
| Linear Velocity | 0.2092 | 0.2737 | 0.2414 | H | 0.2094 | 0.3833 | 0.2963 |
| T | 0.0667 | 0.3744 | 0.2206 | ||||
| V | 0.7239 | 0.2423 | 0.4831 | ||||
| Head Angle | 0.4535 | 0.1934 | 0.3234 | ||||
| CMCA (a) | CMCA (b) | CMCA (c) | CMCA (d) | CMCA (e) | |
|---|---|---|---|---|---|
| Participant 1 | 7 | 6.5 | 7.5 | 8 | 8 |
| Participant 2 | 6 | 5 | 6 | 7 | 8 |
| Participant 3 | 6 | 5 | 7 | 8 | 9 |
| Participant 4 | 5 | 6.5 | 7 | 8 | 8.5 |
| Participant 5 | 4 | 7 | 5 | 6 | 7 |
| Participant 6 | 4 | 6 | 5 | 5.5 | 6 |
| Participant 7 | 5.5 | 6 | 6 | 7 | 8 |
| Participant 8 | 6 | 6.5 | 7 | 8 | 8.5 |
| Participant 9 | 5 | 5.5 | 7 | 6 | 7.5 |
| Participant 10 | 6 | 8.5 | 6.5 | 7 | 7.5 |
| The average | 5.45 | 6.25 | 6.40 | 7.05 | 7.80 |
| The MCAs | CMCA (a) | CMCA (b) | CMCA (c) | CMCA (d) | CMCA (e) |
|---|---|---|---|---|---|
| Subjective evaluation results | 0.165 | 0.190 | 0.194 | 0.214 | 0.237 |
| Objective evaluation results | 0.207 | 0.202 | 0.200 | 0.199 | 0.192 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, X.; Chen, X.; Jiao, Y.; Zhang, L. Objective Evaluation of Motion Cueing Algorithms for Vehicle Driving Simulator Based on Criteria Importance through Intercriteria Correlation (CRITIC) Weight Method Combined with Gray Correlation Analysis. Machines 2024, 12, 344. https://doi.org/10.3390/machines12050344
Jiang X, Chen X, Jiao Y, Zhang L. Objective Evaluation of Motion Cueing Algorithms for Vehicle Driving Simulator Based on Criteria Importance through Intercriteria Correlation (CRITIC) Weight Method Combined with Gray Correlation Analysis. Machines. 2024; 12(5):344. https://doi.org/10.3390/machines12050344
Chicago/Turabian StyleJiang, Xue, Xiafei Chen, Yiyang Jiao, and Lijie Zhang. 2024. "Objective Evaluation of Motion Cueing Algorithms for Vehicle Driving Simulator Based on Criteria Importance through Intercriteria Correlation (CRITIC) Weight Method Combined with Gray Correlation Analysis" Machines 12, no. 5: 344. https://doi.org/10.3390/machines12050344
APA StyleJiang, X., Chen, X., Jiao, Y., & Zhang, L. (2024). Objective Evaluation of Motion Cueing Algorithms for Vehicle Driving Simulator Based on Criteria Importance through Intercriteria Correlation (CRITIC) Weight Method Combined with Gray Correlation Analysis. Machines, 12(5), 344. https://doi.org/10.3390/machines12050344





