In order to verify the effectiveness of CNN-BiLSTM method in predicting the RUF, the PHM08 dataset was used to test the performance of multiple prediction models such as LSTM, BiLSTM, multi-layer LSTM and CNN-BiLSTM. Meanwhile, the number of LSTM layers, learning rate, time window size, the number of hidden layer neurons, the maximum number of iterations and the number of training samples were optimized to improve the prediction performance of CNN BiLSTM model. To ensure the consistency of the experiments, the experimental equipment used in this paper was a general PC with Intel(R) Core(TM) i7-8750 CPU and 16 GB of operating memory.
4.2. Result Analysis
First, comparing LSTM and BiLSTM prediction models. Initialize the parameters of the LSTM and BiLSTM models. Set the number of hidden layer neurons to 50, the size of the time window to 50, the maximum number of iterations to 200 and the number of training samples to 200. The learning rate optimization algorithm is Adam, and the activation function is ReLU. The mean absolute error (MAE) is selected as the loss function, and the early stopping method is added to the model to reduce the training time of the model and prevent over fitting. The final prediction results use MAE, root mean square error (RMSE) and R-Square (R
2) as the evaluation criteria, respectively. The MAE, RMSE and R
2 can be expressed as:
In which, yi, ŷi and are the theoretical value, predicted value and actual average value of RUL, respectively.
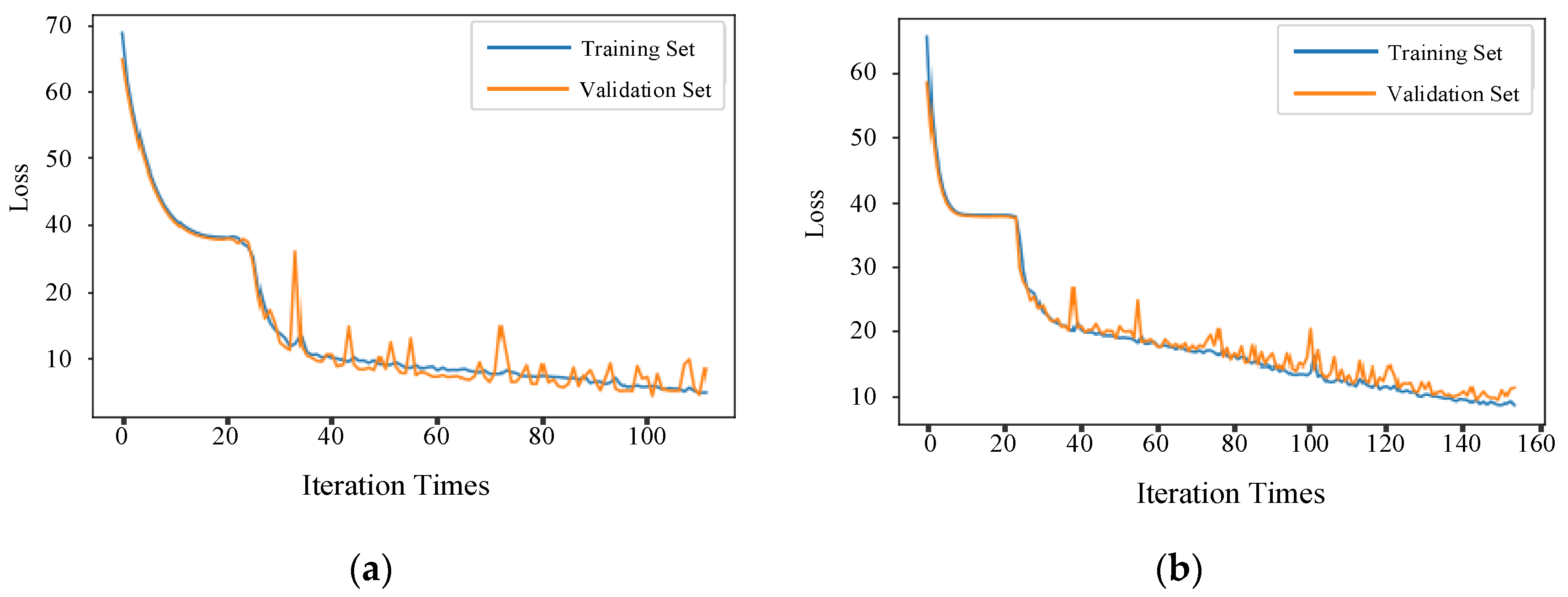
The loss function comparison results of the LSTM model and BiLSTM model are shown in
Figure 8. When using the LSTM model, the model stops training after 113 iterations, while the BiLSTM model stops training after 157 iterations due to the more complex network structure. Compared with LSTM, BiLSTM takes longer to train, but the loss decreases more, and the convergence effect is better.
Using MAE, RMSE and R
2 to evaluate the prediction results. In order to eliminate the influence of error, the average value of three prediction results is taken for statistical analysis, and the final evaluation results are shown in
Table 4. Using BiLSTM can achieve a better prediction effect.
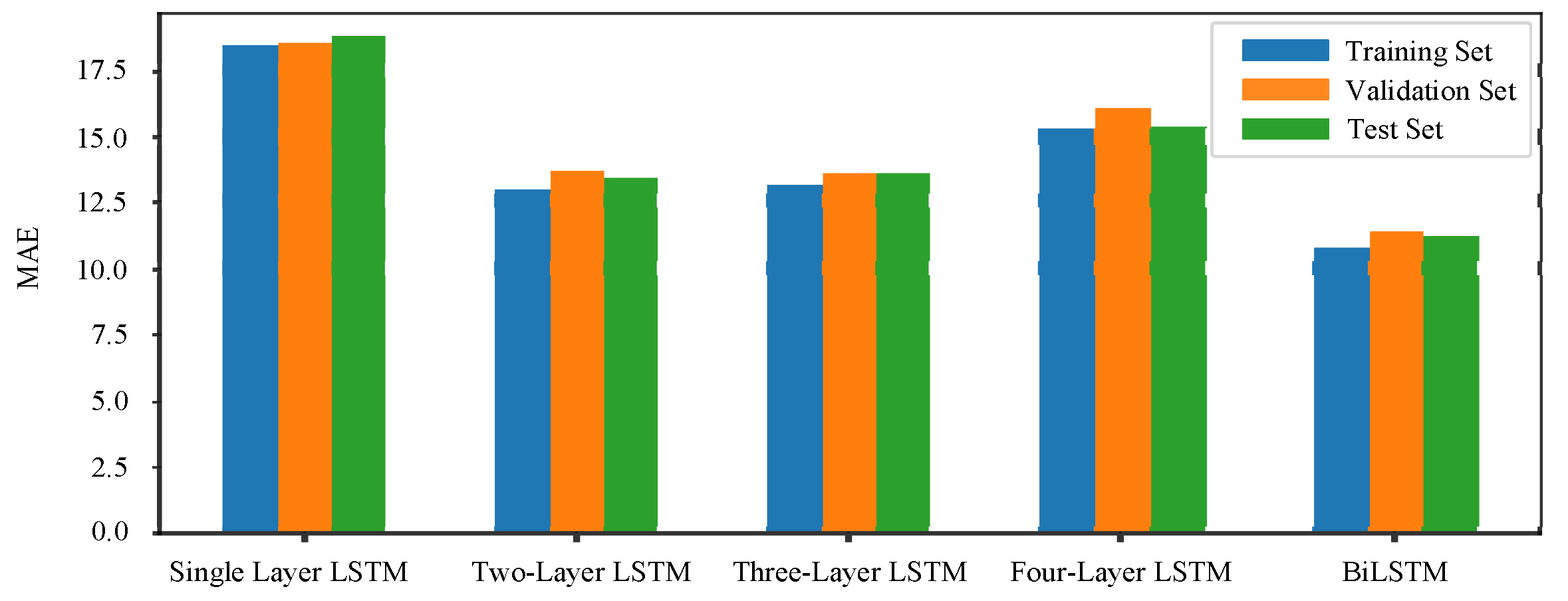
In general, stacking multiple LSTMs may also improve the performance of the LSTM model. To explore the performance of a multi-layer LSTM and BiLSTM, a total of five sets of models for one to four layers of LSTM and BiLSTM are compared using the above datasets. Each model experiment is run three times and the average is taken to obtain the final MAE, as shown in
Figure 9.
It can be found that the MAE value of a two-layer LSTM is lower than that of single-layer LSTM. However, when the LSTM layers continue to stack to the third or fourth layers, the MAE value does not change much compared with that of the two-layer LSTM. A small number of stacked LSTM network structures will improve the predictive accuracy of the RUL regression model, but the predictive accuracy of the model tends to stabilize as the LSTM layers continue to increase. The MAE of BiLSTM is lower than that of multi-layer LSTM. Therefore, in the RUL forecasting problem, the BiLSTM structure can better mine valuable time information from raw data than the multi-layer LSTM network structure, and the regression forecasting effect is better.
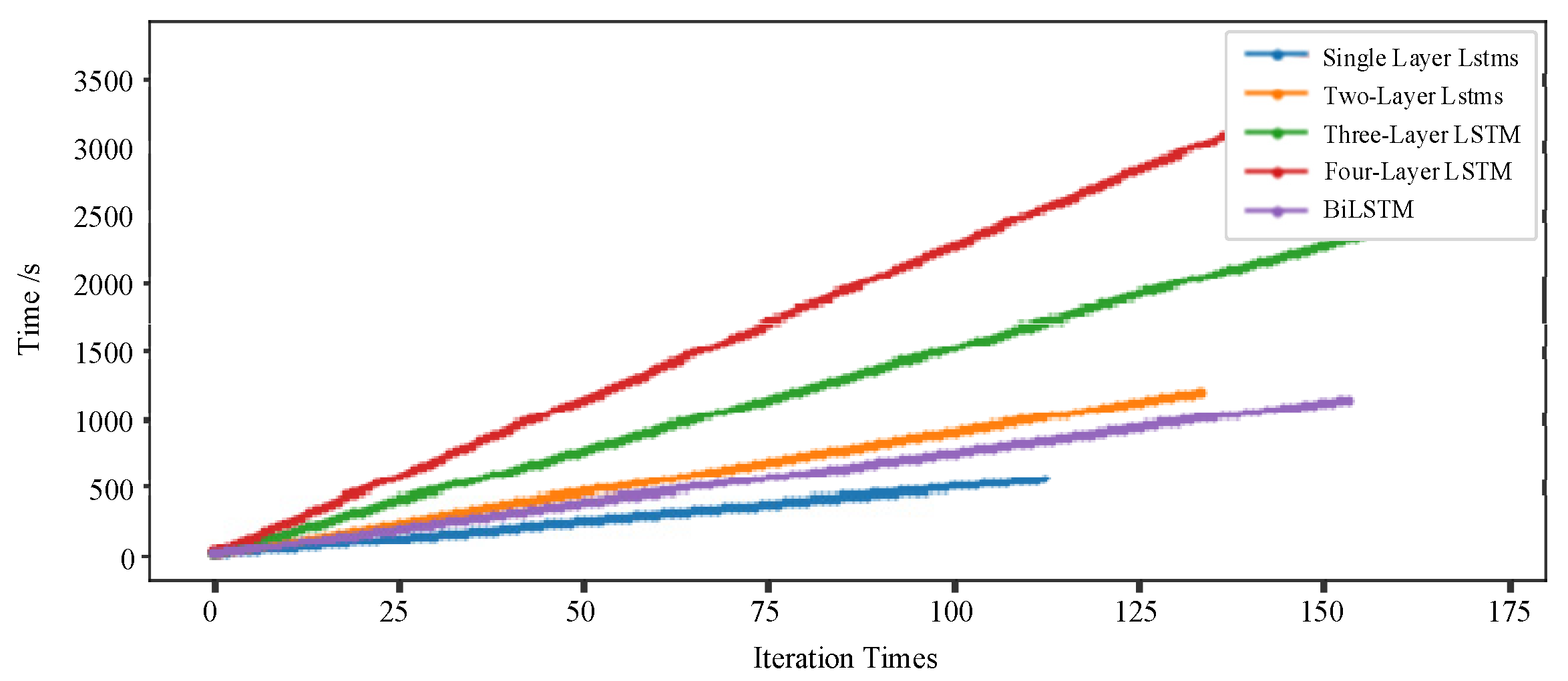
During the training, it is found that with LSTM stacking and network structure complicating, the regression model becomes more and more difficult to converge, and the prediction time increases. The training time of BiLSTM model is shorter than that of stacked LSTM, which is shown in
Figure 10.
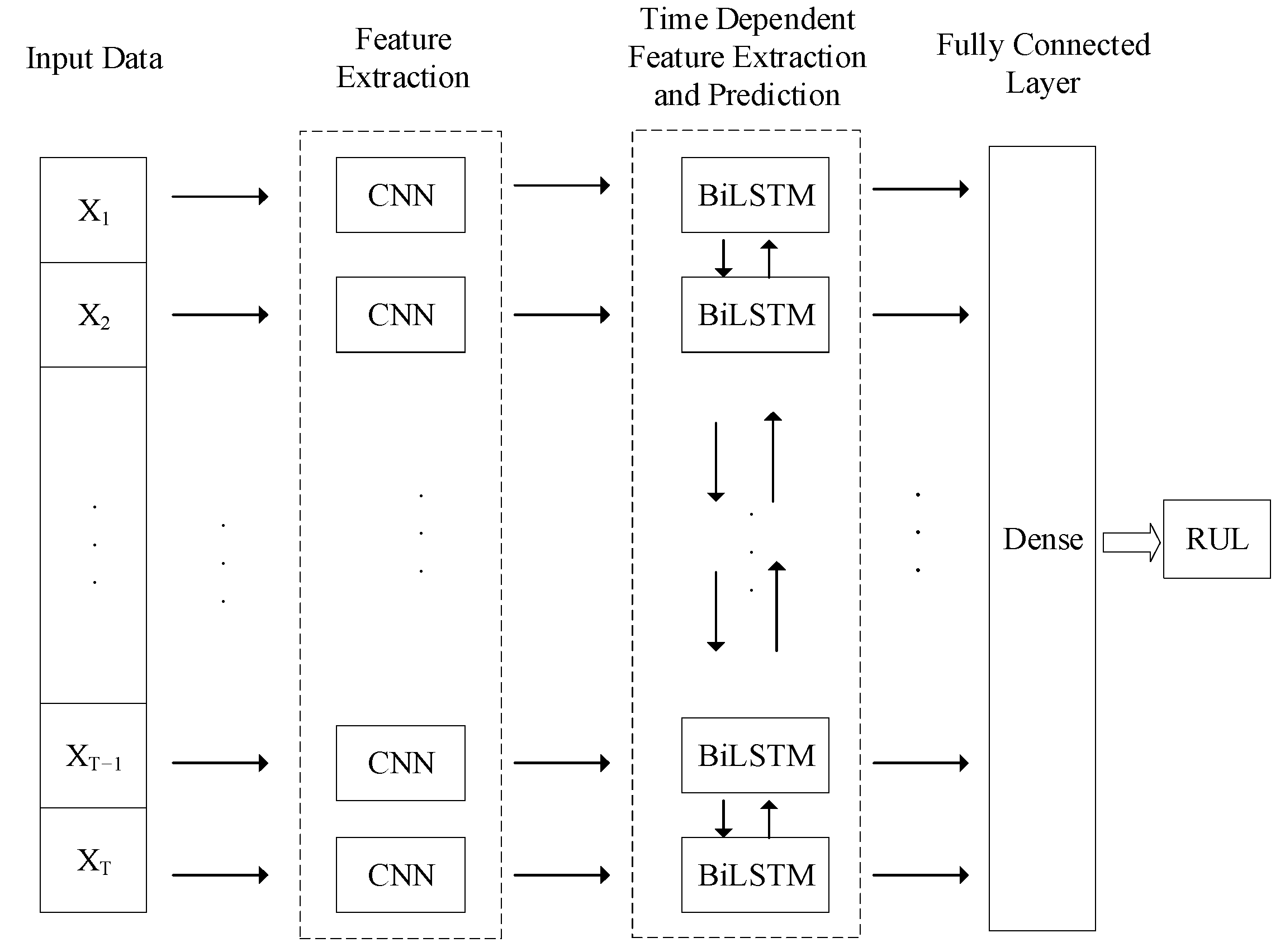
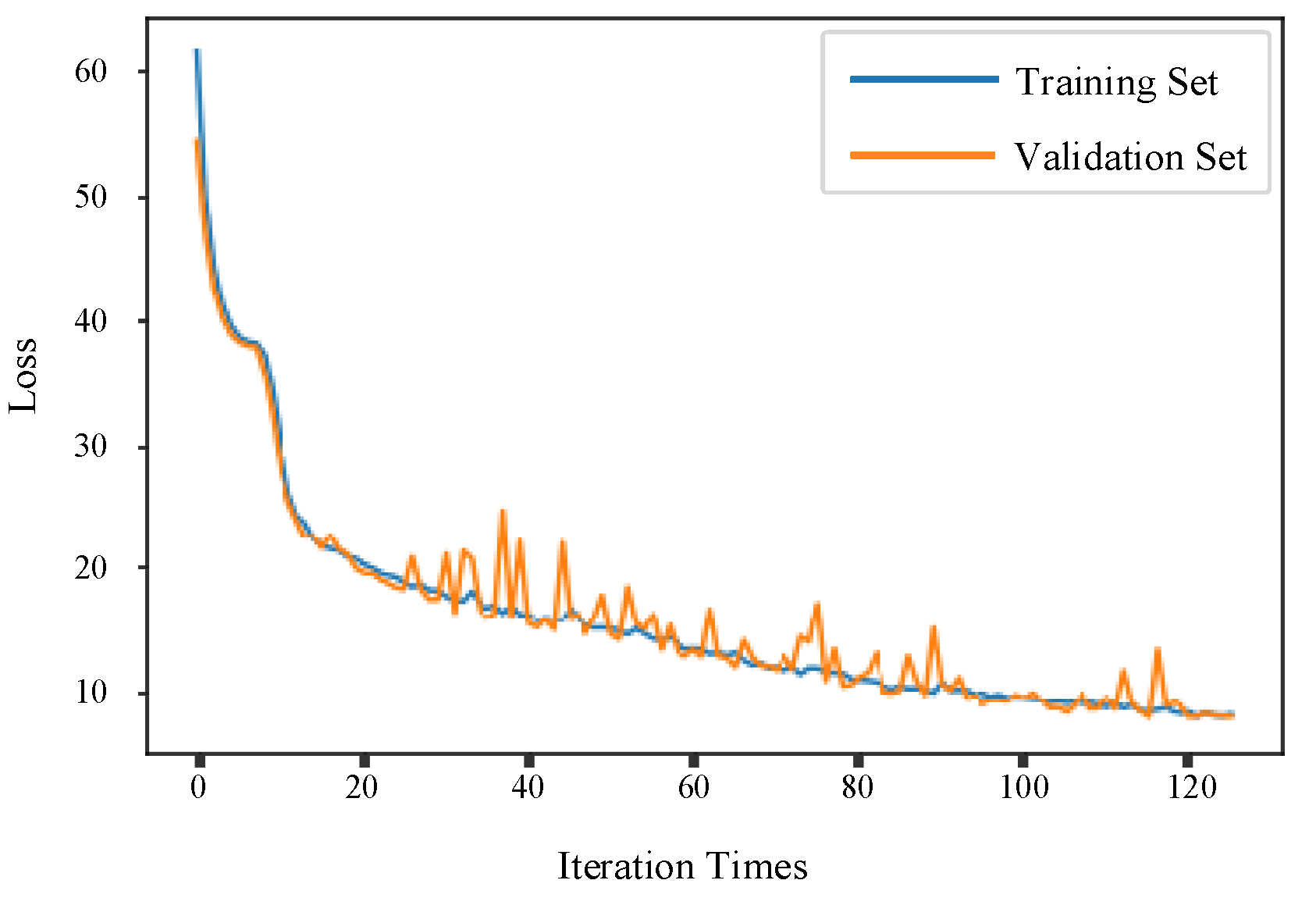
In order to further improve the BiLSTM feature extraction ability, a convolution layer and a maximum pooling layer are added to the BiLSTM to extract deep spatial features and retain the best features in the original data. The new model called CNN-BiLSTM stops iterating at 126 times. The loss function of CNN-BiLSTM decreases faster and fluctuates less than that of BiLSTM for the training set and verification set, as shown in
Figure 11.
The average evaluation results of the CNN-BiLSTM model are shown in
Table 5. The prediction effect has been significantly improved after improving BiLSTM with CNN.
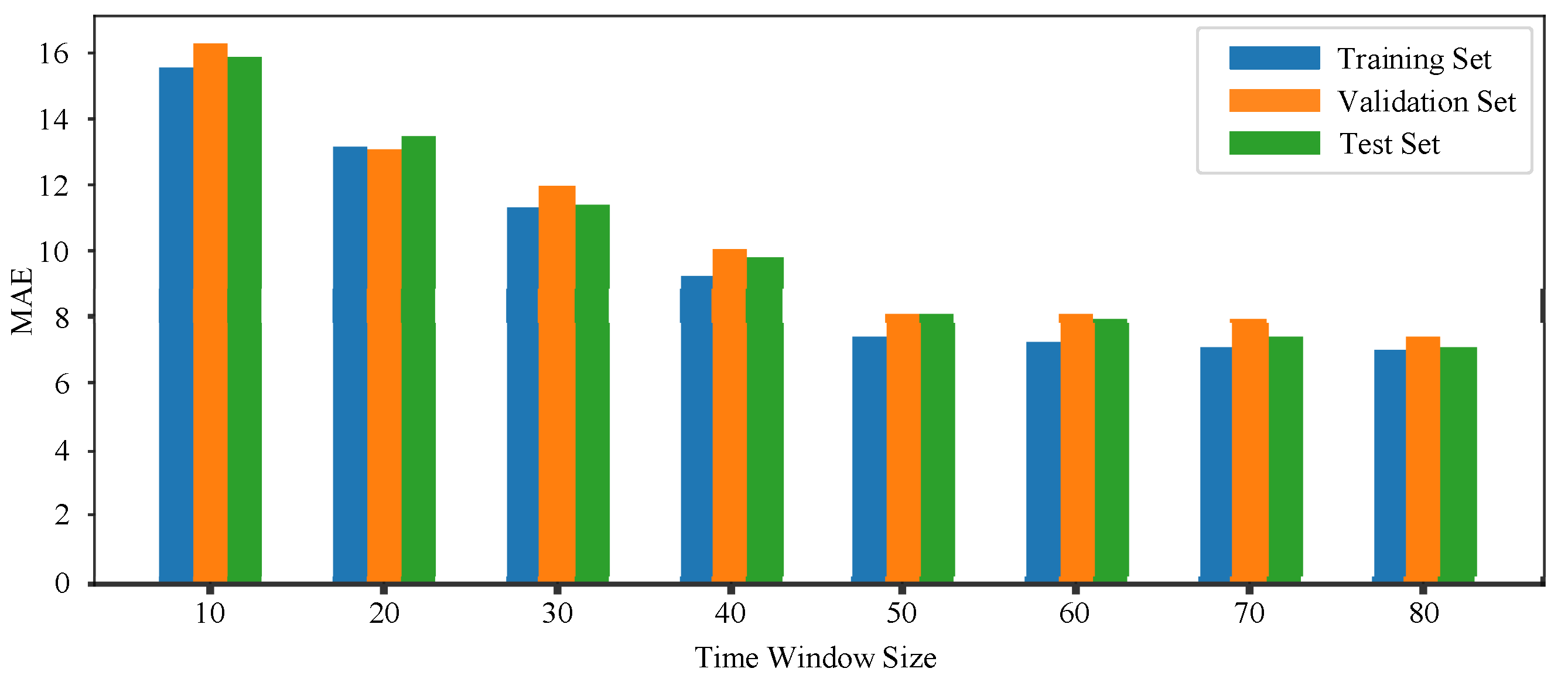
For optimizing the CNN-BiLSTM hyperparameters, the influence of different time window sizes is verified on the prediction performance of the model. The time window sizes 10, 20, 30, 40, 50, 60, 70, and 80 are used in comparative experiments, respectively. Each size experiment is run three times, and MAE takes the average of three sets of experimental results, as shown in
Figure 12.
It is observed that when the time window size increases from 10 to 50, the MAE of the prediction error decreases rapidly. When the time window size exceeds 50, the MAE decline is not obvious. So, in the subsequent model prediction performance test, the time window size of the prediction model is set to 50.
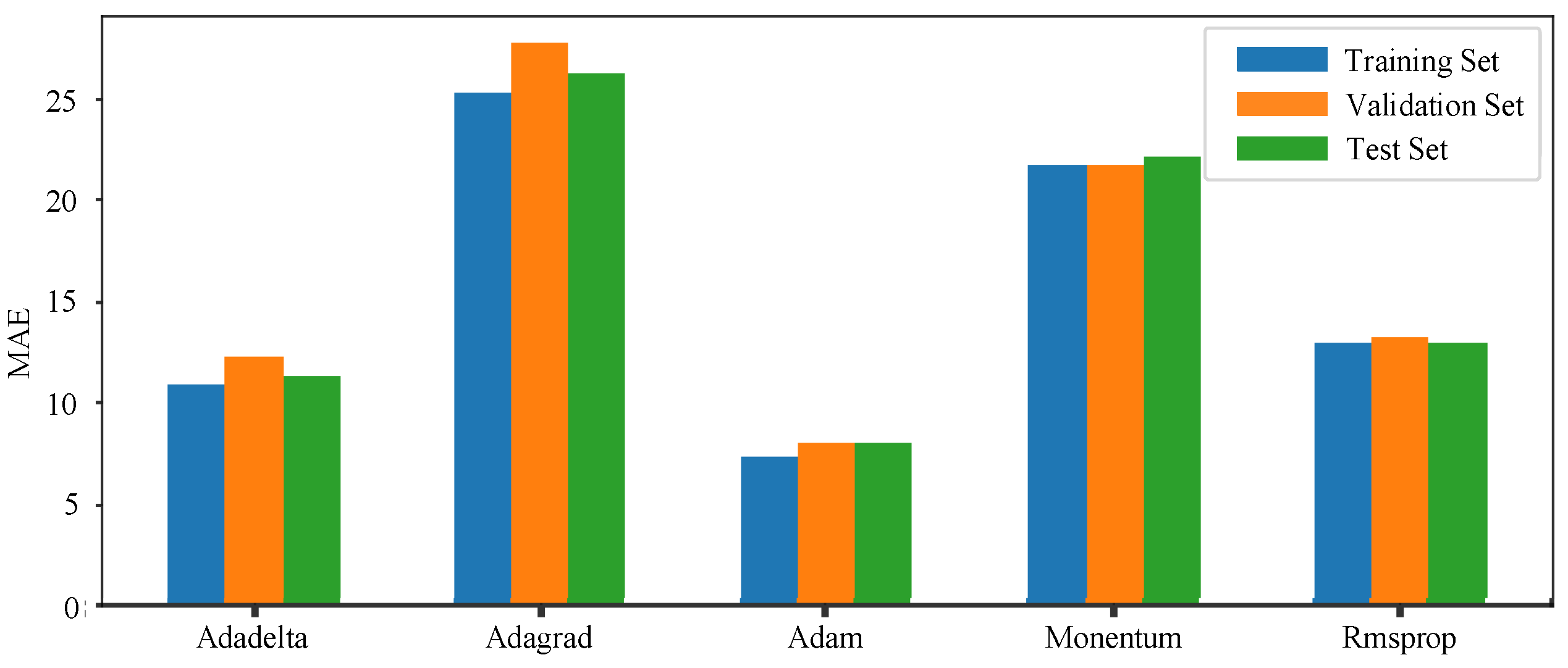
The comparison experiments of different algorithms are carried out for the learning rate optimization. The result is shown in
Figure 13, which indicates that the Adam is a more suitable learning rate optimization algorithm.
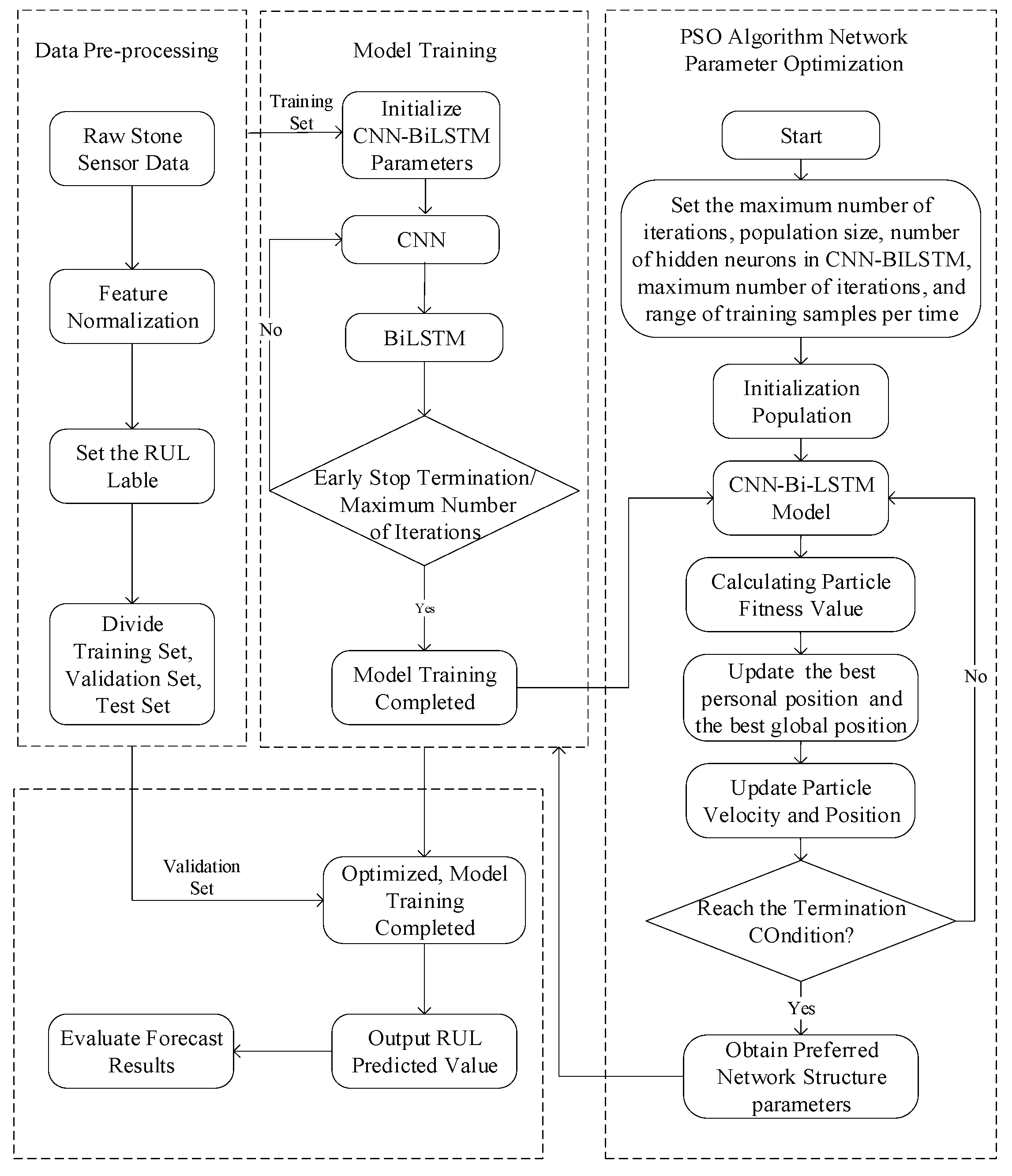
Use PSO to optimize the number of neurons in the hidden layer of the model, the maximum number of iterations, and the number of training samples. The value range of three variables are set as the following: number of hidden layer neurons is in [1, 200], maximum number of iterations is in [100, 500] and number of training samples is in [50, 500]. The vector formed by these three parameters is regarded as the particle position in PSO, and the number of particles is 50, the inertia factor is 0.5 and acceleration factor is 2. The MAE of CNN-BiLSTM is used as the fitness value of PSO. The MAE value of the training set on the CNN-BiLSTM model is 7.34 before PSO optimization. In order to reduce the training time of the model, stop training when the optimized MAE is less than 5 or the number of iterations reaches the maximum 200.
After PSO optimization, the hyperparameters of the model are: the number of hidden layer neurons is 64, the maximum number of iterations is 287 and the number of training samples is 254. By comparing the various evaluation metrics, the prediction results of the improved PSO-CNN-BiLSTM model are shown in
Table 6. Finally, when comparing the performance of LSTM, BiLSTM, CNN-BiLSTM and PSO-CNN-BiLSTM models on the test set, the PSO-CNN-BiLSTM model exhibits more excellent prediction results, as shown in
Table 7.
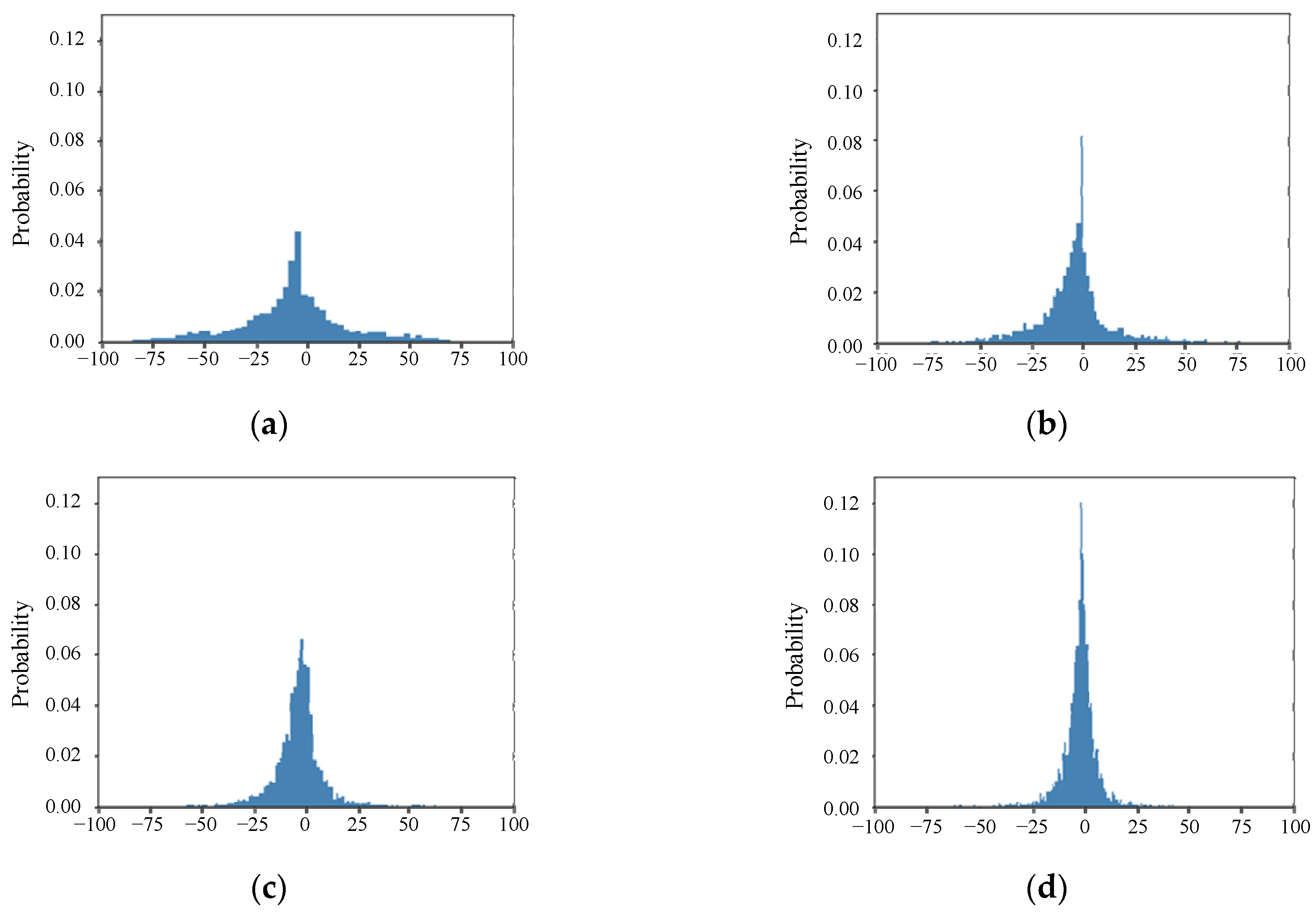
The prediction error distribution of the four models LSTM, BiLSTM, CNN-BiLSTM and PSO-CNN-BiLSTM on the test set is shown in
Figure 14. The PSO-CNN-BiLSTM model has the smallest error and the best prediction effect.
Input the data of 218 pieces of equipment into four models LSTM, BiLSTM, CNN-BiLSTM and PSO-CNN-BiLSTM, respectively, to obtain the comparison between the predicted value and the true value of the model. The results are shown in
Figure 15. Each sawtooth wave in the figure represents the complete life cycle of a turbine engine from start to failure. The orange line represents the true value, and the blue line represents the predicted value.
Comparing the results of the four models, the prediction results of PSO-CNN-BiLSTM are the closest to the true values, followed by CNN-BiLSTM, and then BiLSTM. LSTM has the worst prediction effect. In order to compare the prediction performance of the four models in detail, the RUL of one of the 218 devices is predicted by using the models. The results are shown in
Figure 16. The prediction result of the PSO-CNN-BiLSTM model with adjusted network hyperparameters is closer to the true value.
In order to evaluate the performance of the model proposed in this paper on test data, the quality of the model is measured using the Score function proposed in the International PHM Conference in the PHM08 Data Challenge [
35]. The scoring function is shown in Equation (18), which (Score) is an asymmetric function that penalizes more heavily when the prediction is late than when the prediction is early. Specifically, when the model-estimated remaining useful life (RUL) is lower than the actual value, the penalty is relatively light and is unlikely to trigger a serious system failure because there is still enough time for equipment maintenance. However, if the model-estimated RUL exceeds the actual value, maintenance schedules will be delayed, which may increase the risk of system failure, and therefore the penalty in this case will be more severe. This asymmetric scoring mechanism is intended to guide the model to be more cautious in its predictions in order to avoid potential risks due to inaccuracies in maintenance schedules.
where
and
represent the predicted and actual RUL of the
ith sample in the test dataset.
We have computed the prediction results of our lifetime prediction model using a specific scoring function (Equation (18)) and made a comparison with CNN, LSTM and other lifetime prediction methods in the literature.
Table 8 shows the score results.
After comparing the scores with other residual lifetime prediction methods, our proposed PSO-CNN-BiLSTM model is better at predicting the PHM08 dataset.