Abstract
The traditional PID controller in quadrotor UAVs has poor performance, a large overshoot, and a long adjustment time, which limit its stability and accuracy in practical applications. In order to solve this problem, an improved whale optimization fuzzy PID control strategy based on CRICLE chaos map initialization is proposed, and a detailed simulation analysis was carried out using MATLAB software (MATLAB R2022B). Firstly, to more realistically reflect quadrotor UAVs’ flight behavior, a dynamic simulation model was established, and the dynamics and kinematic characteristics of the aircraft were considered. Then, CRICLE chaotic mapping initialization was introduced to improve the global search ability of the whale optimization algorithm and to effectively initialize the parameters of the fuzzy PID controller. This improved initialization method helped to speed up the convergence process and improve the stability of the control system. In the simulation experiments, we compared the performance indicators of the improved CRICLE chaotic mapping initialization whale optimization fuzzy PID controller to the traditional PID and fuzzy PID controllers, including overshoot, adjustment time, etc. The results show that the proposed control strategy has better performance than the traditional PID and fuzzy PID controllers, significantly reduces overshoot, and achieves a significant improvement in adjustment time. Therefore, the improved CRICLE chaotic mapping initialization whale optimization fuzzy PID control strategy proposed in this study provides an effective solution for improving the performance of the quadrotor control system and has practical application potential.
1. Introduction
A UAV has a simple structure and strong terrain adaptability, does not need complex operations to change the circular rotation distance of the rotor, and only requires the speed of the rotor to be changed to alter the trajectory of the flight. UAVs can also perform a wide range of movements, giving them a wide range of applications, including precision agriculture [1], managing forest fires [2], urban transportation [3], crime detection [4], express delivery [5], etc.
Furthermore, the work by Israel Domínguez et al. [6] demonstrates the development of a low-cost quadrotor experimental platform, specifically detailing a methodology for implementing an observer-based Proportional Integral Derivative (PID) controller. This emphasizes the critical need for practical, real-world testing environments to evaluate and refine control algorithms, ensuring their reliability under actual operating conditions despite inherent system nonlinearities and disturbances.
Addressing another sophisticated application, M. Eusebia Guerrero-Sánchez and colleagues tackled [7] the challenge of safely and efficiently transporting cable-suspended payloads with quadrotors. Utilizing an Interconnection and Damping Assignment Passivity-Based Control (IDA-PBC) approach, they developed a robust control strategy that effectively attenuates swing, enhancing payload stability during transport. This method showcases the adaptability of UAVs to complex tasks where dynamic uncertainties and parametric variability are significant factors.
UAVs are nonlinear systems with complex dynamic behavior, so it is important to determine how to design the controller and which control strategies can reduce delays, enhance the vehicle’s robustness, increase the control quality, and reduce the control error. The existing UAV controllers can be roughly divided into linear robust controllers, nonlinear controllers, and intelligent controllers. Among them, linear robust control technology is older and more classic, and it has been widely used in many fields due to its simplicity of implementation and flexibility of parameter adjustment. However, traditional linear control methods face numerous limitations when dealing with the underactuated nonlinear characteristics [8] of quadrotor UAVs. In order to overcome these limitations, researchers have carried out in-depth research and made improvements to this control method. For example, Ivan Gonzalez-Hernandez et al. [9] proposed an integral-based sliding mode controller to improve the altitude control performance of quadrotor UAVs; however, it still belongs to the linear control category. Further advancing UAV control technology, Roger Miranda-Colorado and Luis T. Aguilar [10] have developed a robust PID control methodology specifically for quadrotors that not only enhances trajectory tracking and regulation tasks but also incorporates a power reduction methodology. This novel approach uses the cuckoo search algorithm for controller-gains tuning and designs trajectories that minimize jerk, thus reducing power demand even under parametric uncertainty and aerodynamical disturbances. In addition to enhancing control precision, reducing power consumption is also critical for improving UAV efficiency and operational longevity. Roger Miranda-Colorado and colleagues [11] have addressed this by developing a methodology that integrates trajectory design with controller-gains tuning using a cuckoo search algorithm. Their approach, employing a terminal sliding modes controller analyzed via strict Lyapunov functions, has demonstrated notable reductions in power consumption while maintaining robust performance against aerodynamic disturbances and parametric uncertainties, does not thoroughly explore more complex nonlinear control or adaptive control strategies, and shows obvious limitations when dealing with systems that have significant nonlinear characteristics and dynamic uncertainties.
Xiao Liang et al. [12] proposed a novel nonlinear control method based on backward control, which was specially designed for the transportation system of quadrotor UAVs; it not only considers the nonlinear characteristics of the system but also addresses the challenges caused by external interference and the internal dynamic uncertainty of the system. However, it does not adapt well to unforeseen changes in system dynamics or external disturbances.
Roger Miranda-Colorado et al. [13] discussed a variable-gain sliding mode control strategy based on Lyapunov’s theory to improve the robustness of the quadcopter to external disturbances and changes in internal parameters. However, nonlinear controllers are less flexible when it comes to modeling inaccurate or unforeseen changes in system dynamics. In contrast to intelligent or adaptive controllers, it is not suitable for systems with high uncertainty or rapidly changing conditions.
Muhammad Awais Sattar and Abdulla Ismail [14] proposed an adaptive fuzzy PID control method that combines PID control, fuzzy logic, and an adaptive control strategy to improve the adaptability and control performance of quadrotor UAVs in complex dynamic environments. The basic motion of the quadrotor UAV was controlled, and the effectiveness of the proposed control strategy was verified via a simulation.
In the Adaptive Dynamic Reconfiguration Control (ADRC) framework, the tuning of the extended state observer (ESO) parameters and the nonlinear state error feedback (NLSEF) control law is critical. Due to the complexity of these adjustments, a range of optimization techniques are essential for their precise calibration. Therefore, to fine-tune these parameters effectively, it is essential to integrate the fuzzy predictions, rules, and strategies of adaptation optimization methods. Researchers have adopted different strategies to enhance the performance of PID controllers. To achieve accurate control, one researcher implemented an auto-coupling PID controller (SC-PID) by constructing a nonlinear mathematical model and deriving the transfer function of each channel of the attitude loop. On the other hand, some researchers rely on the deep knowledge base and rule set of the expert system to optimize the parameters of PID controllers. Based on a comprehensive analysis of system performance and response, this method enables the dynamic adjustment of PID parameters to adapt to changing flight environments and conditions, aiming to improve the accuracy and robustness of controllers. In intelligent controllers, there are many algorithms inspired by nature that employ adaptive parameters, such as PID algorithms based on neural networks [15], genetic algorithms [16,17,18,19], hybrid genetic algorithms [20], etc.
To optimize their systems control effect, Li Wei et al. [21] proposed an improved particle swarm optimization algorithm to imitate the social behavior of bird hunting and fish swimming. In addition, many scientists have used this algorithm for the optimization of drone controllers [22,23,24,25,26,27,28,29,30,31]. Tri Kuntoro Priyambodo et al. [32] explored a method for finding the input parameters of a PID control system through an ant colony optimization algorithm that finds the shortest path from the nest to food based on the colony’s ability. Using a multi-objective variant of the bat algorithm, Nitish Katal and Parvesh Kumar [33] designed a fractional-order PID controller for the robust flight control of unmanned aerial vehicles (UAVs). The optimization function was formulated as a mixed sensitivity problem to ensure robust behavior. Its controller ensured a good tracking and robustness margin, ensuring a robust response in the presence of uncertainty.
Therefore, an optimization algorithm based on animal behavior has the advantages of strong global search ability, high robustness, easy implementation and parallelization, adaptability, and a wide application range. Compared to the above-mentioned optimization algorithms, the whale optimization algorithm (WOA) provides a novel search strategy that simulates the encirclement, spiral, and fast dash mechanisms in whale predation behavior and has the advantages of simple operation and fewer control parameter requirements, especially when dealing with the optimization problems of high-complexity systems such as quadrotor UAVs.
However, the whale algorithm suffers from the problem of early convergence, which means that the population converges to a disadvantaged maximum. In particular, due to the low initial population diversity, the algorithm can easily fall into the local optimal solution such that the global optimal solution of the problem cannot be reached.
To address this issue, chaotic mapping is introduced to compensate for the shortcomings of the standard whale optimization algorithm. Combined with fuzzy forecasting, this not only fully leverages fuzzy logic to manage the complexity and uncertainties of quadrotor UAV systems but also employs chaotic sequences from chaotic systems to enhance search space diversity and accelerate convergence. By applying chaos to the swarm’s historical optima, it assists in escaping local optima, thereby improving the algorithm’s global search capability. The automatic adjustment of PID controller parameters via the whale optimization algorithm enables dynamic optimal parameter selection, and the integration of fuzzy control and convergence speed enhances the controller’s adaptability, boosting the system’s overall performance. This novel intelligent controller is better suited for navigating systems with complex variations and changing environments.
The innovative aspects of this study include the following:
To address the low convergence accuracy and slow convergence speed issues associated with the traditional whale optimization algorithm (WOA), an initial population diversity strategy combining logical chaos mapping and skewed tent mapping is proposed.
The CRICLE modification enhances the conventional whale algorithm. By utilizing the whale algorithm to optimize the fuzzy PID in comparison to the conventional PID, it was discovered that the chaotic whale optimization algorithm’s fuzzy PID controller exhibits superior performance.
2. Quadrotor Dynamic Equation
2.1. Preliminary Definition of the Controller
Despite its symmetrical appearance, a drone is a nonlinear dynamic system with four inputs and six outputs. A competent controller should ensure that the drone stabilizes quickly upon reaching its predetermined position. Quadcopters are composed of four rotors placed at 90-degree intervals, achieving balance by rotating two rotors clockwise and the other two counter-clockwise. This configuration is crucial for maintaining balance and control during flight.
2.2. Definition of a Mixed-Coordinate System
At present, the mainstream research divides the body structure of UAVs into “+”-shaped and “X”-shaped, which present different aerodynamics and control dynamics and have a significant impact on their performance and application applicability. The “+” configuration features arms aligned with the drone’s frontal axis, facilitating intuitive yaw adjustment as the thrust is directly aligned with the drone’s direction. This setup improves forward flight efficiency by reducing air resistance, which is critical for linear trajectory missions. However, it complicates roll and pitch maneuvers, requiring different thrusts on the motors diagonally opposite each other, which may limit the UAV’s maneuverability.
On the contrary, the X configuration has arms in a diagonal direction, ensuring balanced maneuverability on all flight axes (yaw, pitch, and roll), which is attributed to the symmetrical distribution of propulsion. This layout not only supports agile and stable flight dynamics but also optimizes payload distribution and sensor placement, providing an unobstructed forward view that is critical for surveillance and FPV flight. The inherent design of the X configuration, despite slightly increasing the complexity of yaw control, significantly enhances the overall agility and application versatility of the quadcopter.
Our UAVs use a “+” configuration due to its wide applicability and inherent advantages in solving specific control system challenges, despite obvious difficulties, such as delayed control responses and the robustness of control strategies under variable flight conditions. These challenges are exacerbated by the unique dynamic nature of the + configuration, but our chaos whale optimization algorithm fuzzy PID controller overcomes them with propellers that are directly aligned with the drone’s fuselage axis, introducing complexity in achieving the precise control of yaw, pitch, and roll motion. This complexity requires the development of advanced control algorithms that are able to compensate for the inherent time delay and ensure the stability of the drone in different operating scenarios and its responsiveness to control inputs. Our novel controller aims to address these nuanced control issues, leveraging the configuration’s simple design to innovate powerful control solutions. Our choice is driven by the potential to enhance drone performance through customized control strategies designed to address specific aerodynamic and control dynamic issues within the “+ configuration.”
Subsequently, we establish a coordinate system (Figure 1) and formulate a dynamic equation, making the following assumptions:
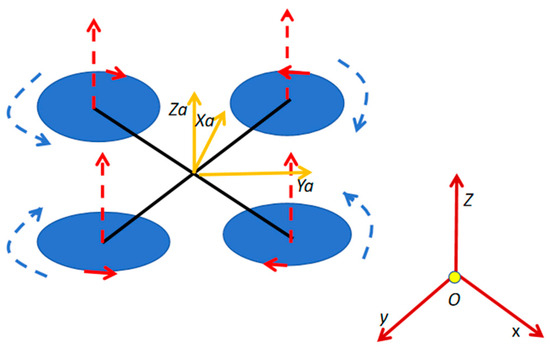
Figure 1.
UAV model and its coordinate system.
- The drone’s center of mass and body origin coincide at one point in the coordinate system.
- The drone’s mass is uniformly distributed, with perfect structural symmetry, excluding elastic variations.
- Gyroscopic effects and friction forces acting on the drone’s body are ignored.
- The Earth’s curvature is disregarded, and a flat Earth surface is assumed to simplify the model.
Given the strong coupling and underactuated nature of UAVs, modeling necessitates the initial determination of coordinate systems, including both the body and geographic coordinate systems.
In Figure 1, the geographical coordinate system is denoted by red lines, while the body coordinate system is represented by yellow lines. Within the body coordinate system, the three axes are labeled Xa, Ya, and Za. The system’s origin is positioned at the center of gravity of the body, with the Xa axis aligned parallel to the body and oriented in the direction of the body’s motion in the positive direction. The Za axis is perpendicular to the Xa axis and directed upwards, ensuring that the thrust component F1 along the Za axis is naturally positive, opposing the direction of gravitational force g. This configuration allows the control algorithm to directly compare thrust and gravity since both forces have components in the same direction within the body’s coordinate system. Thus, situated within the body’s vertical plane of symmetry, the Ya axis is perpendicular to the OXaZa plane.
The inertial frame (I) is defined as the geographical coordinate system with the Earth’s center as its origin point. The positive direction of the X-axis points eastward from the origin, while the Y-axis points northward. The Z-axis is perpendicular to the OXY plane, extending towards the sky.
2.3. The Establishment of the Model Equation
Firstly, we create a mathematical model of the six degrees of freedom and use them to design the controller for the inner and outer loops:
In order to model the dynamics of the quadrotor UAV, we first consider its six degrees of freedom. These degrees of freedom describe all the possible motions of the UAV in space: three translational motions (vertical lift, lateral side-to-side movement, and forward–backward translation) and three rotational motions (rotation around three main axes, i.e., roll, pitch, and yaw). These six degrees of freedom correspond to the six output variables of the UAV state, which are as follows:
x, y, z: These are the coordinates of the position in the ground coordinate system.
ϕ, θ, ψ: These correspond to the roll, pitch, and yaw angles of the UAV, respectively.
The input variable is the total lift generated by the four rotor blades F1 and three moments around the body spindle F2, F3, F4. Now, we use the constant of proportionality KT to represent the thrust–rotor speed (W) relationship and KM to express the relationship between torque and speed. The moments of inertia are represented by Jx, Jy, and Jz expression, and the distance from the motor to the center of the body is denoted by d.
Next, we establish the rotation matrix as the transformation matrix equation between two coordinate systems. The conversion from the geographic coordinate system to the body coordinate system V (vehicle frame) can be accomplished through rotation about the yaw angle. The transformation involving yaw α, pitch β, and roll γ can be represented by transformation matrix A [34] as follows:
Next, we utilize Newton’s second law to formulate the linear dynamic equations [35,36], obtaining the acceleration components in each direction.
Here, T represents the lift force, and M is the mass of the drone.
Then, by applying Newton’s second law and transforming it through rotation matrix A, we obtain the linear velocity equations [36,37]. The components of speed in the ground coordinate system are as follows:
˙represent the speed along the X, Y, and Z axes of the ground coordinate system, respectively. Ultimately, these speed components will be used to update the drone’s velocity and position within the ground coordinate system.
Next, we represent the drone’s angular dynamics using the Euler equations of motion [38]:
Here, represent the angular velocities around the X, Y, and Z axes, respectively. Since the equations obtained above are nonlinear and interdependent, numerical methods such as the Euler method or the Runge–Kutta method can be used to approximate the integration of these equations at each time step Δt.
We choose the Euler method for numerical integration.
Here γn, βn, and αn are the angular velocities at the current time step, while γn+1, βn+1, and αn+1 are the angular velocities at the next time step. This process is repeated throughout the simulation time, resulting in a time series of angular velocities.
Finally, we establish a nonlinear dynamic model [39,40]. Since the state equations describe all the dynamic behaviors of the drone, including linear dynamics (position and velocity) and angular dynamics (attitude and angular velocity), by combining the previous equations, we obtain the linear state equations and angular dynamic state equations.
Based on Newton’s laws of mechanics and the laws of rotational dynamics, we can construct a mathematical model describing the motion of a quadrotor drone:
In the equation of linear velocity (Equation (6)), represent the rate of change of the position vector (X, Y, Z) in the ground coordinate system; Φ, θ, and ψ are Euler angles, representing roll, pitch, and yaw, respectively; F1 is the total lift produced by the rotors; M is the mass of the quadrotor drone; and G is the acceleration due to gravity.
For the equation of angular velocity (Equation (7)), ˙α˙, ˙β˙, and ˙γ˙ represent the rate of change of the yaw, pitch, and roll angular velocities, respectively; Jx, Jy, and Jz are the moments of inertia about the body’s X, Y, and Z axes, respectively; d is the distance from the motor to the body center; and F2, F3, and F4 are the distances from the motor to the body center.
2.4. Parameter Determination
In the process of deduction and refinement for learning, significant experimentation is required to ascertain the values of the model parameters. Given that the control system demands lower resources at this stage, the choice of fuzzy logic for the control system is deemed reasonable. Notably, the thrust function determined through this experimental mechanism aligns more closely with a cubic function derived from parabolic trajectory analyses. The parameters extracted from this identification process are as follows:
Below is how each parameter is obtained and their role in computations and the program:
The way M is obtained is “Measured using a scale”. In the dynamic model in MATLAB, mass plays a vital role in calculating the thrust required for lift and maneuvering through the thrust equation. It directly affects the calculation of acceleration in translational motion equations and impacts the controller’s compensation for gravity.
L is derived from measurements of the physical UAV. It is crucial in the controller’s calculation of torques generated by the motors, which decides the quadrotor’s rotation and stability. It is used to calculate the moments for pitch, roll, and yaw adjustments in the rotational dynamics equations.
J_x, J_y, J_z are obtained using bifilar pendulum tests. These parameters are used to determine the angular accelerations in the simulation’s Euler equations of motion. They are critical for accurately modeling the UAV’s rotational dynamics and for the PID controller to stabilize angular motions.
D is measured from the UAV’s structure. It impacts the calculation of moments and thus the control inputs needed for attitude control. It is used in torque calculations where longer lever arms equate to greater turning forces for the same amount of motor torque.
KT is determined through thrust tests with a dynamometer. It allows the conversion of motor RPM into physical thrust values in the simulation model, which is used by the optimization algorithm to adjust the PID gains for precise altitude control.
KM, similar to KT, is discovered through motion testing. It helps in adjusting motor control inputs within the whale optimization algorithm to fine-tune the PID controller’s performance.
G is the acceleration due to gravity. It is a fixed input in the control system equations, factored into the lift force calculations to maintain the UAV in the air and to correct for the gravitational pull during flight maneuvers.
K_D is experimentally determined through computational fluid dynamics simulations. It is integrated into the dynamic model to account for the resistance experienced by the rotating parts, affecting the UAV’s energy efficiency and the PID controller’s response to rotational commands.
B_a is obtained through empirical testing, measuring the resistance to rotation at different speeds. It is included in the simulation to ensure that the controller compensates for these frictional forces when maintaining stable flight or when changing directions.
K_t is obtained from motor testing; this constant is essential for the control algorithms that manage motor speed. It is used to accurately translate control inputs into motor torques, which is crucial for maintaining desired thrust levels and for maneuvering the UAV.
K_v is also obtained from motor testing; the k_v value is used in the motor control subsystem of the UAV’s simulation model. It helps the optimization algorithm to understand the relationship between voltage and the resulting motor speed, thus enabling precise speed control for stable flight.
L_a is usually measured in an electrical way, and it is used in the electrical modeling of the motor in the UAV control system to determine the current consumption and the phase difference between voltage and current. This affects the PID controller’s ability to accurately adjust the motor speed in a variety of operations.
I_g is directly measured using a bifilar pendulum setup; it is crucial in the control system for predicting the response of the rotors to the control inputs. It affects the dynamics of how quickly a rotor can accelerate or decelerate, which in turn influences the UAV’s agility and stability.
R_a is measured using electrical instruments. It plays a role in efficiency calculations.
γ_2 is derived by fitting empirical thrust data to a polynomial model; this coefficient refines the thrust model by accounting for nonlinearities in thrust force generation. The simulation allows for more accurate prediction and control of the UAV’s vertical acceleration and deceleration, which is crucial for tasks such as landing or avoiding obstacles.
γ_3 is also derived by fitting empirical thrust data to a polynomial model; like γ_2, this higher-order coefficient provides even finer control over thrust force modeling. It is used by the controller to ensure an accurate representation of the UAV’s lift dynamics, especially under different loads and speed changes.
Next, we propose a control strategy based on the ground coordinate system position vectors (, , ) along with the rates of change of the roll, pitch, and yaw angular velocities (˙α˙, ˙β˙, ˙γ˙). The designed controller [41] regulates the rate of change of the position vector through an outer loop, while the inner loop targets the angular velocities of yaw, pitch, and roll. The input to the controller is based on the difference between the actual and desired values, with the output being the corresponding control quantity required to achieve precise control. Next, we will detail the design process of the controller, including the selection and optimization of parameters. The controller uses the deviation between actual and target values as the input to generate appropriate control signals as outputs, enabling precise adjustment of the system.
3. Structure of the Control System
3.1. Design of Control System
We developed a fuzzy PID controller design method based on the whale optimization algorithm, tailored to the nonlinear kinematic characteristics of quadrotor UAVs. Our approach includes a cascaded control architecture, where the inner loop is responsible for attitude control—specifically the angles of roll (ϕ), pitch (θ), and yaw (ψ)—while the outer loop manages position control, targeting displacement at the x, y, and z coordinates. The control system uses the difference between the desired and actual positions as the input for the outer loop controller, which then calculates the necessary lift. Simultaneously, the desired angles output by the outer loop and the actual angles from the inner loop are used to compute angular errors. These errors serve as inputs for the inner loop controller, which then determines the input torques required to maneuver the quadrotor drone. This integrated approach enables the comprehensive management of the drone’s six degrees of freedom, including both orientation and displacement. In the subsequent sections, we will elucidate the application of different controllers in the inner and outer loops and elaborate on the results of these implementations.
Figure 2 illustrates the configuration of the control system.
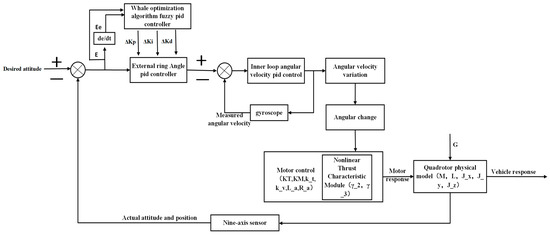
Figure 2.
The control system.
Figure 2 shows M, l, J_x, J_y, J_z, d, KT, KM, G, γ_2, γ_3. These parameters are defined in Table 1, representing the mass of the quadcopter UAV, the distance from each rotor to the center of gravity, the moment of inertia around the X-axis, the moment of inertia around the Y-axis, the moment of inertia around the Z-axis, the distance from the motor to the center of the body, the thrust constant of the rotor, the torque constant of the rotor, the gravitational acceleration, and the second- and third-order thrust coefficients. Kp, Ki, and Kd represent the proportional, integral, and derivative gain of the PID controller, respectively. Ee could represent the external error or environmental error that affects the attitude and position of the UAV. E generally stands for the error signal, which is the difference between the desired attitude (or position) and the actual attitude (or position). This error signal is often the input to the control system.

Table 1.
Control system parameter table.
denotes the derivative of the error over time, which reflects the rate of change of the error. It is a term often used in PID (Proportional–Integral–Derivative) control systems, where it contributes to the D-component, providing a prediction of future errors based on the current rate of change.
The diagram outlines a control system for a quadrotor UAV that achieves precise control and robustness to interference by integrating error feedback into real-time adjustments, ensuring that the UAV can effectively respond to changes in its environment and maintain its intended flight path.
3.2. Design of Fuzzy PID Controller
In this part, we detail the adaptive tuning method of the PID controller, which uses fuzzy PID to autotune the parameters and optimizes the command response ability of the controller through the incremental PID strategy. The output of the controller is generated using the following formula:
Here, Kp, Ki, and Kd denote the proportional gain, integral gain, and differential gain, respectively, and are modulated in the following proportions.
In this equation, u(t) denotes the control drive; e(t) is the error signal; Kp0, Ki0, and Kd0 represent the basic gain of the PID controller; and δKp, δKi, and δKd are adjusted according to the requirements. This adaptive approach enables the controller to adapt to fluctuations in system dynamics and external disturbances, maintaining stability and performance efficiency.
In this study, a control method combining fuzzy PID control and the whale optimization algorithm is adopted, and its structure is shown in Figure 3. The chaotic whale can adjust the δKp, δKi, and δKd of the PID controller, and then, the controller can control the controlled object. We conclude that combining chaotic mapping, the whale algorithm, the fuzzy rule, and PID control has a good control effect.
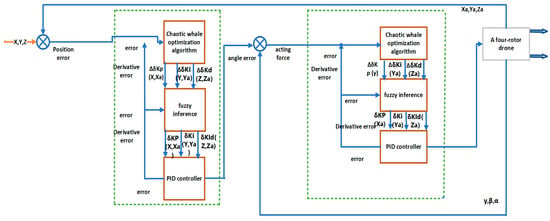
Figure 3.
Whale optimization algorithm fuzzy PID control flow chart.
The design of the fuzzy control rules in this study is described in Table 2.

Table 2.
Fuzzy control rule table.
In the fuzzy control presented in this article, there are typically two inputs: the error (E) and the rate of change of the error (EC), along with one output, which is the gain of the control signal. Table 2 encompasses a set of rules for three fuzzy controllers, targeting the proportional gain (Kp), integral gain (Ki), and differential gain (Kd). Each cell’s values, such as PB, PM, ZO, NS, NM, and NB, represent the linguistic variables of the fuzzy sets, corresponding to distinct fuzzy logic rules.
The significance of each fuzzy logic rule is as follows:
NB (Negative Big): A significant negative number, indicating a large and negative error or a large and negative rate of change of error.
NM (Negative Medium): A medium negative number, implying a moderate and negative error or a moderate and negative rate of change of error.
NS (Negative Small): A small negative number, suggesting a small and negative error or a small and negative rate of change of error.
ZO (Zero): Zero, meaning the error is near zero, or the rate of change of error is near zero.
PS (Positive Small): A small positive number, signifying a small and positive error or a small and positive rate of change of error.
PM (Positive Medium): A medium positive number, denoting a moderate and positive error or a moderate and positive rate of change of error.
PB (Positive Big): A significant positive number, indicating a large and positive error or a large and positive rate of change of error.
For instance, if the error (E) is a large positive number (PB), and the rate of change of error (EC) is also a large positive number (PB), then the proportional gain (Kp) might be set to a medium negative number (NM), meaning the controller may reduce the output to attempt to minimize this large positive error.
3.3. Whale Algorithm-Optimized Fuzzy Control Rules
In the design of a fuzzy PID controller based on the whale optimization algorithm (WOA), the number of control rules increases significantly due to the complexity of the seven fuzzy state variables and the dual-input–triple-output system. Specifically, with a fuzzy logic approach, the number of control rules alone can be in the hundreds. Determining these rules often relies on the experience and knowledge of experts and can be a daunting task. To solve this problem, a whale optimization algorithm is introduced in this study to optimize the rule set in the fuzzy controller.
Given that the ITAE (Integral of Time-weighted Absolute Error) takes into account the product of the absolute error and time, it emphasizes the system’s performance in the presence of long-standing errors in contrast to other performance metrics, such as Mean Absolute Error (MAE) or Mean Squared Error (MSE). This emphasis is due to ITAE’s calculation where the longer the error persists, the greater its impact on the overall performance metric. This weighting method effectively penalizes large errors persisting over time, encouraging the control system to reduce errors more rapidly and achieve a steady state quickly. Moreover, ITAE reduces reliance on expert experience, making the optimization process more objective and reliable. In multi-input multi-output systems, each output directly affects performance, and ITAE allows for a balanced consideration of the long-term performance of each output, thereby finding an optimized overall solution in complex control systems. In short, ITAE provides an effective means of balancing long-term performance and rapid system responsiveness. In this study, when designing the fuzzy PID controller using the Chaotic Mapping Whale Optimization Algorithm (WOA), considering the potential high complexity and the potentially large number of control rules, utilizing ITAE as the performance criterion simplifies the controller design. It quantifies the control system’s response to errors over time and provides a clear objective function, enabling the whale optimization algorithm to explicitly pursue a control strategy that reduces long-term errors throughout the optimization process.
Therefore, in this study, we use integration time multiplied by the absolute error (ITAE) as a performance criterion to evaluate the optimization process. This criterion is achieved by calculating the time integration of the error of the control quantities X1 and X2. In the whale optimization algorithm, the fitness function is defined as , where H(t) denotes the control error. The goal of optimization is to maximize this fitness function, which means that the larger the value of the fitness function, the better the control performance achieved.
3.4. Whale Algorithm
3.4.1. Conventional Whale Optimization Algorithm
The traditional whale optimization algorithm (WOA) is a biomimetic optimization algorithm proposed by Mirjalili and Lewis in 2016 [42] to mimic the social behavior and hunting mechanisms of humpback whales. It has been applied in various fields, including in control systems such as fuzzy PID (proportional–integral–derivative) controllers for stabilizing quadcopter UAVs. In this case, the WOA can optimize the parameters of the PID controller to improve performance and stability.
The algorithm functions by simulating the bubble-net hunting strategy of humpback whales, which is described below.
Encircling prey: Whales locate and encircle their prey before starting the bubble-net feeding method. Mathematically, this behavior is modeled as
In this equation, is the position vector of the target, which is the best solution found so far, is the whale’s position vector, and are coefficients that help determine the nature of the whale’s movement toward the prey or target, t is the current iteration, and is the calculated distance vector between the whale’s position and the target’s position.
Bubble-net attacking method (exploitation phase): This phase includes two approaches: shrinking encirclement and spiral position update.
Shrinking encirclement mechanism: This is achieved by decreasing the value of in the equation.
Spiral position update: The spiral equation between the whale and the prey (optimal solution) is defined as
In the scenario described above, is the distance between the whale and its prey. The constant b is used to define the spiral shape, and l is a random number within the range of [−1, 1].
Searching for prey (exploration phase): To simulate the random search for prey, the WOA utilizes the vector , where the position of the search agents is updated when , allowing the whales to search outside the region of the current best solution. This mechanism ensures global optimization capability and exploration of the search space.
Parameter adaptation: The algorithm adaptively adjusts the parameters throughout the optimization process to balance exploration and exploitation, ensuring that the algorithm converges to the global optimum.
In the context of quadcopter control, the WOA is generally used to optimize the PID control parameters (Kp, Ki, and Kd) to achieve the desired performance criteria, such as minimum overshoot, settling time, and steady-state errors. The optimization process is as follows:
- Define the cost function based on the dynamic response characteristics of the quadcopter.
- Initialize the population of the candidate solution (whales) using random PID parameters.
- Iteratively apply the WOA step to adjust the PID parameters to the optimal set of minimized cost functions.
This approach makes it possible to design a quadcopter control system that adaptively responds to changes in dynamics and external disturbances, thereby enhancing stability and maneuverability.
3.4.2. Chaotic Mapping-Optimized Whale Algorithm
The chaos mapping-enhanced whale optimization algorithm represents a simple method for tuning the PID controller, which is essential for achieving the expected dynamic response in the control system. Its rationale relies on the use of complex models of chaos theory to diversify the initial population of potential solutions, enabling a more thorough exploration of the solution space. The enhanced mathematical foundation is built on top of the application of logic mapping, expressed as . When the parameter value is within a certain range, it becomes more refined due to its chaotic behavior. By merging chaotic sequences, the algorithm is unlikely to succumb to the local optimal trap, which is a common drawback of traditional time-loss methods. This results in a more robust and reliable PID controller, as the optimization process explores all possible parameter settings, ensuring the responsiveness and stability of the control system.
In practice, the chaotic WOA first generates initial populations using chaotic sequences [43] to ensure good distribution in the latent solution space. Each individual in the population represents a set of PID parameters. The algorithm then iteratively updates each individual’s position in the population using the original WOA equation and chaotic sequences to navigate to the optimal PID parameter set. This process involves evaluating the performance of each group using a predefined cost function that reflects the expected outcomes of the control system, such as minimal overshoot, fast settling time, and low steady-state error.
The use of chaotic mapping to initialize the whale optimization algorithm (WOA) has several advantages over the traditional WOA. Due to its inherent irregularity and stochasticity, chaotic mapping can more uniformly cover the search space, avoiding the convergence of candidate solutions to local optima. This results in a more diverse initial population, which enhances the global search capability and could more rapidly converge to the global optimum. Thus, incorporating chaotic mapping into the WOA can enhance the algorithm’s ability to escape from local minima, enable a more thorough exploration of the solution space, and help solve complex optimization problems such as tuning PID controllers.
Therefore, we integrate chaotic mapping into the optimization process, aiming to enhance the performance and reliability of the PID controller by boosting global search capabilities and preventing premature convergence.
4. Simulation and Results Analysis
4.1. Semi-Physical Simulation
This study utilized a hardware-in-the-loop simulation method to conduct flight stability experiments on a quadrotor drone to evaluate the robustness, control precision, and latency optimization offered by our fuzzy controller based on the chaotic map-enhanced whale optimization algorithm. The use of a Raspberry Pi provides powerful computing capabilities for the drone. Its onboard Ubuntu system allows users to freely modify the interface settings between the Raspberry Pi and the drone. By programming the Raspberry Pi, control algorithms can be directly written into the ROS system. Through Pixhawk, the quadrotor can be flown along a predetermined trajectory, ultimately achieving the effect of trajectory tracking. As shown in Figure 4.
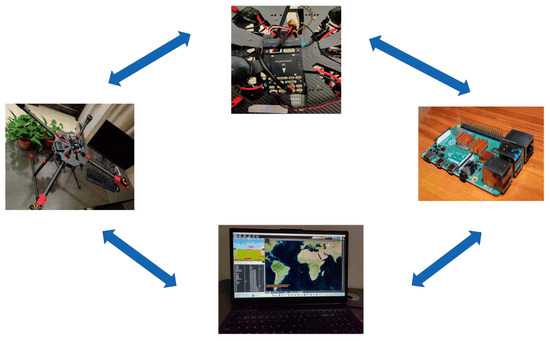
Figure 4.
Simulation test platform.
The main hardware components and their uses are as follows:
- 1.
- A host machine with a virtual machine installed: runs Ubuntu 22.04 and the ROS system.
- 2.
- Pixhawk V6X (Holybro from China): an advanced flight controller that controls the drone.
- 3.
- Raspberry Pi 4B (From the United Kingdom): runs external control programs and system integration and sends external control commands or network signals to the flight controller.
- 4.
- Flycolor X-Cross 80a HV3 5-12S 32bit ESC (Electronic Speed Controller) ( Flycolor From America): receives signals from the flight controller, processes them, and drives the rotation of the motors.
- 5.
- RCINPOWER G6215-330 Brushless Motor: (SUNNYSKY, From Zhongshan City, China) rotates to propel the propeller blades, providing upward lift for the drone.
- 6.
- A 25,000 mAh 6S solid-state battery (MAD from China): powers the drone.
- 7.
- H16 pro remote control (CUAV from China) (including the receiver), with the receiver installed on the aircraft and the remote control manually operated: controls the plane.
- 8.
- TAROT X4 960 MM carbon fiber (Overfly is from Wenzhou, China) frame: the main support structure for the drone.
- 9.
- NEO v3 Pro Positioning Module: (CUAV from China) offers high precision, real-time positioning capabilities, and other autonomous navigation systems.
- 10.
- S1 LIDAR (SLAMKIT from China Shanghai) with a ranging radius of 40 m: provides resistance to strong light exposure.
- 11.
- Dual-axis visual obstacle avoidance: a dual-axis visual obstacle avoidance system with 1080 P resolution for two-dimensional obstacle detection and avoidance.
- 12.
- UBEC: (HOBBYWING from China): provides a stable power supply for the Raspberry Pi.
- 13.
- Ammeter: provides a reliable power supply to the flight controller while detecting real-time voltage levels.
4.2. Closed-Loop System Stability
The whale optimization algorithm (WOA) and fuzzy control PID applied to quadrotor UAVs have shown promising stability results due to their robustness in dealing with interference and achieving precise control, especially in trajectory tracking and altitude control. Here are three studies that demonstrate the effectiveness and stability of these methods in quadcopter UAV applications.
One research paper integrated the WOA to optimize PID controller parameters, successfully reducing overshoot and improving response times in UAV flight dynamics [41].
Fuzzy Control PID: Implementation of fuzzy control alongside PID in quadrotor UAVs has shown improved handling of uncertainties and disturbances, leading to more stable flight patterns [44]. Research on combining fuzzy logic with PID control for UAVs emphasized enhanced stability and error minimization during complex flight maneuvers [45].
Next, we added chaos mapping using tools such as MATLABR2022b and Simulink to effectively demonstrate in a controlled virtual environment. The simulation can model the complex dynamics and control system so as to analyze the behavior and control strategy of the drone under various conditions in detail, and the results show that our closed-loop system is theoretically stable.
4.3. Discussion of Simulation and Results
To verify the effectiveness of the proposed method, the design of a controller is described, and simulation experiments are performed comparing the advantages and disadvantages of the three types of controllers under the same conditions, all numerical simulations run on a computer equipped with an AMD Ryzen 7 4800 H with Radeon Graphics 2.90 GHz processor and 32.0 GB, operating system Windows 11 Home Chinese Version, using MATLAB R2020b for programming and data processing. All UAV parameters are the same, as shown in Table 1. The controllers are a fuzzy PID controller optimized by a whale optimization algorithm enhanced by chaos mapping, a conventional fuzzy PID controller, and a traditional PID controller. The experimental conditions were as follows: the initial state of the UAV was set to zero, the simulation time was set to 20 s, the displacement target set point was 1 m, while the target set point for roll and pitch angles was 0°, and the yaw angle was 30°.
The simulation results are described below.
The simulation results show that the improved whale optimization algorithm can offer faster convergence speed and better stability in managing the displacement response of complex control systems, representing a new solution for optimizing control systems. Additionally, this study analyzes its related parameters.
In Figure 5, (a), (b) and (c) represent responses in the x, y, and z directions over time, respectively. Figure 5 and Table 3 demonstrate that our algorithm consistently achieves lower overshoot and faster settling time across all three types of displacement responses. Notably, in the Y-axis displacement, the overshoot reaches an optimal solution of zero, significantly enhancing the aircraft’s stability and positioning accuracy, reducing battery energy consumption for overshoot correction, and ultimately decreasing the risk of flight accidents. According to the evaluation standards in the field of engineering control, it is also evident that the chaotic map-enhanced whale optimization algorithm substantially improves the response time and control precision in displacement responses. This lays a solid foundation for applying this controller in various drone operations requiring low latency and high robustness, such as precision positioning and rapid obstacle avoidance.
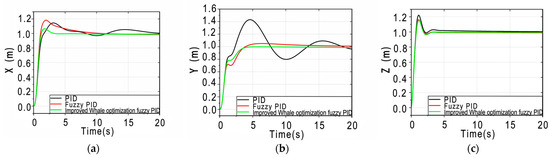
Figure 5.
Comparison of three controllers for displacement response.

Table 3.
Comparison of the displacement of the three controllers.
As shown in Figure 6, (a)–(c) represent the response of the control system over ϕ, θ, ψ, respectively, over time. As shown in Table 4.The simulation results show that the improved whale optimization algorithm offers faster convergence speed and improved stability in addressing the angular response of complex control systems. This represents a new solution for the optimization of control systems. Additionally, this study further analyzes its related parameters.
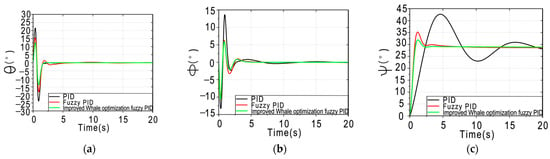
Figure 6.
Comparison of the angular response of the three controllers.

Table 4.
Comparison of the angles of the three controllers.
Regarding angle responses, our controller performs better, showing superior values and performance in terms of not only its settling time, overshoot, and undershoot but also its steady-state error, which is essentially zero. This indicates that the controller optimized by the chaotic whale algorithm can achieve more precise expected outputs and maintain its predetermined direction and path without drifting.
4.4. Anti-Interference Property
Similarly, we introduced a sinusoidal disturbance with an amplitude of 0.001 and a frequency of 1 radian/s to simulate external disturbances that have periodicity or occur at specific frequencies. This was utilized to further assess the robustness and dynamic response characteristics of the three drone control systems when faced with such specific frequency disturbances.
As shown in Figure 7, (a)–(f) is to control the position response and Angle response of the system over time under sinusoidal in terferencethe fuzzy PID controller optimized by the chaotic whale algorithm outperforms other controllers in terms of overshoot, settling time, and steady-state error even under sinusoidal disturbances. Furthermore, it exhibits significantly better performance in terms of the frequency and amplitude of oscillations. For example, the conventional PID shows high-frequency oscillations between 3 and 7 s on the roll axis, and the fuzzy PID exhibits high-frequency oscillations from 2.5 to 5 s on the pitch axis. Additionally, the amplitude of the PID reaches nearly 0.6 m on the Y-axis and 20° on the yaw axis. These oscillations under disturbance not only imply differences in the system’s stability and efficiency but also indicate severe wear on the drone and safety risks due to low control performance under disturbances. In summary, the chaotic map-enhanced whale-optimized fuzzy PID also demonstrates significant performance in terms of disturbance rejection.
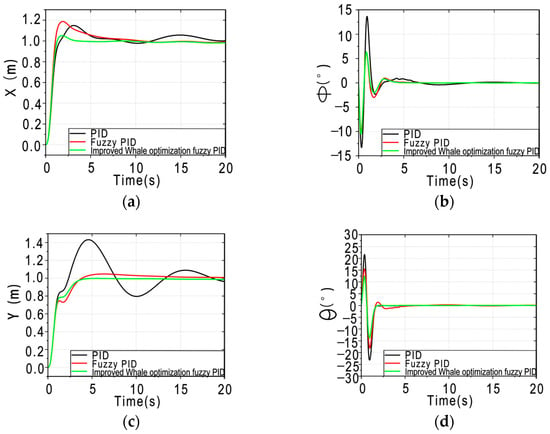
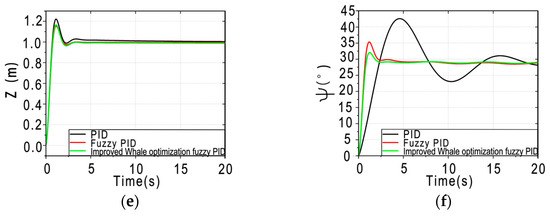
Figure 7.
Comparison of the three controllers in the case of sinusoidal interference.
5. Conclusions
In this study, in order to address the low convergence accuracy and slow convergence speed of the traditional WOA, the initial population diversity of logical chaos mapping was proposed. According to the optimization algorithm’s formula, to establish a dynamic model, we used CRICLE to improve the traditional whale algorithm, resulting in the proposed chaotic whale algorithm fuzzy PID controller. The simulation experiments were carried out using MatlabR2022b SIMULINK, and the following conclusions were drawn.
- Compared to the fuzzy PID and ordinary PID, the chaotic mapping-based whale optimization algorithm fuzzy PID gives the control system higher control accuracy and stronger robustness.
- Compared to the fuzzy PID and ordinary PID, the whale optimization algorithm fuzzy PID based on chaotic mapping performs better in an interference environment.
- The research in this paper will have better applications in drones that require high precision and robustness, such as agricultural drones for pesticide spraying and aerial drones for avoiding skyscrapers. It significantly improves the operational efficiency and safety of drones in complex environments through the integration of chaotic mapping and whale optimization algorithms.
Author Contributions
Conceptualization, Y.Z. (Yixuan Zhang); methodology, Y.Z. (Yixuan Zhang); software, Y.Z. (Yixuan Zhang); validation, Y.Z. (Yixuan Zhang); formal analysis, Y.Z. (Yixuan Zhang); investigation, Y.Z. (Yixuan Zhang); resources, F.L.; data curation, Y.Z. (Yixuan Zhang), Y.Z. (Yihe Zhang) and Z.Z.; writing—original draft preparation, Y.Z. (Yixuan Zhang); writing—review and editing, Y.Z. (Yixuan Zhang) and S.P.; visualization, Y.Z. (Yixuan Zhang); supervision, F.L. and S.P.; project administration, S.P. and F.L.; funding acquisition, F.L. and S.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Key Research and Development Project of Shanxi Province, grant number “202202140601021”, and the Agricultural High-Quality Development Science and Technology Support Project, grant number “TYGC23-10”.
Data Availability Statement
The datasets used or analyzed during the current study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Radoglou-Grammatikis, P.; Sarigiannidis, P.; Lagkas, T.; Moscholios, I. A Compilation of UAV Applications for Precision Agriculture. Comput. Netw. 2020, 172, 107148. [Google Scholar] [CrossRef]
- Chen, X.; Hopkins, B.; Wang, H.; O’neill, L.; Afghah, F.; Razi, A.; Fulé, P.; Coen, J.; Rowell, E.; Watts, A. Wildland Fire Detection and Monitoring Using a Drone-collected RGB/IR Image Dataset. IEEE Access 2022, 10, 121301–121317. [Google Scholar] [CrossRef]
- Dawam, E.S.; Feng, X.; Li, D. Autonomous Arial Vehicles in Smart Cities: Potential Cyber-physical Threats. In Proceedings of the 2018 IEEE 20th International Conference on High Performance Computing and Communications; IEEE 16th International Conference on Smart City; IEEE 4th International Conference on Data Science and Systems (HPCC/SmartCity/DSS), Arlington, VA, USA, 28–30 June 2018. [Google Scholar]
- Shmelova, T.; Lazorenko, V.; Bondarev, D.; Burlaka, O. Group Flights of Unmanned Aviation Vehicles for Smart Cities. In Proceedings of the 2019 9th International Conference on Advanced Computer Information Technologies (ACIT), Ceske Budejovice, Czech Republic, 5–7 June 2019; pp. 230–233. [Google Scholar]
- Samouh, F.; Gluza, V.; Djavadian, S.; Meshkani, S.; Farooq, B. Multimodal Autonomous Last-mile Delivery System Design and Application. In Proceedings of the 2020 IEEE International Smart Cities Conference (ISC2), Piscataway, NJ, USA, 28 September–1 October 2020; pp. 1–7. [Google Scholar]
- Domínguez, I.; Miranda-Colorado, R.; Aguilar, L.T.; Mercado-Ravell, D.A. A methodology for setting-up a low-cost quadrotor experimental platform. Control. Eng. Pract. 2024, 143, 105803. [Google Scholar] [CrossRef]
- Guerrero-Sánchez, M.E.; Mercado-Ravell, D.A.; Lozano, R.; García-Beltrán, C.D. Swing-attenuation for a quadrotor transporting a cable-suspended payload. ISA Trans. 2017, 68, 433–449. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, Y. The Design of the Four Rotor Unmanned Aircraft Control Algorithm. In Proceedings of the 2017 29th Chinese Control And Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 5146–5150. [Google Scholar]
- Gonzalez-Hernandez, I.; Salazar, S.; Lopez, R.; Lozano, R. Altitude Control Improvement for a Quadrotor UAV Using Integral Action in a Sliding-mode Controller. In Proceedings of the 2016 International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016; pp. 711–716. [Google Scholar]
- Miranda-Colorado, R.; Aguilar, L.T. Robust PID control of quadrotors with power reduction analysis. ISA Trans. 2020, 98, 47–62. [Google Scholar] [CrossRef]
- Miranda-Colorado, R.; Aguilar, L.T.; Herrero-Brito José, E. Reduction of power consumption on quadrotor vehicles via trajectory design and a controller-gains tuning stage. Aerosp. Sci. Technol. 2018, 78, 280–296. [Google Scholar] [CrossRef]
- Liang, X.; Fang, Y.; Sun, N. A Novel Nonlinear Backstepping-based Control Approach for Quadrotor Unmanned Aerial Vehicle Transportation Systems. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; pp. 884–889. [Google Scholar]
- Miranda-Colorado, R.; Domínguez, I.; Aguilar, L.T. Variable-gain Sliding Mode Control for Quadrotor Vehicles: Lyapunov-based Analysis and Finite-time Stability. Int. J. Control. 2023. [Google Scholar] [CrossRef]
- Sattar; Muhammad; Ismail, A. Adaptive Fuzzy Pid Control of a Quadrotor Uav, 2017. Available online: https://www.researchgate.net/publication/320273294_Adaptive_Fuzzy_PID_Control_of_a_Quadrotor_UAV (accessed on 1 January 2024).
- Mobarez, E.N.; Sarhan, A.; Ashry, M. Fractional Order PID Based on a Single Artificial Neural Network Algorithm for Fixed Wing UAVs. In Proceedings of the 2019 15th International Computer Engineering Conference (ICENCO), Cairo, Egypt, 29–30 September 2019; pp. 1–7. [Google Scholar]
- Yu, X.; Yan, L.; Guan, Z.; Wu, Y.; Peng, F.; Yan, F. Control of Fixed-wing UAV Using Optimized PID Controller with the Adaptive Genetic Algorithm. In Proceedings of the 2022 IEEE International Conference on Real-Time Computing and Robotics (RCAR), Guiyang, China, 17–22 July 2022. [Google Scholar]
- Gaur, M.; Chaudhary, H.; Khatoon, S.; Singh, R. Genetic Algorithm Based Trajectory Stabilization of Quadrotor. In Proceedings of the 2016 Second International Innovative Applications of Computational Intelligence on Power, Energy and Controls with their Impact on Humanity (CIPECH), Ghaziabad, India, 18–19 November 2016; pp. 29–33. [Google Scholar]
- Lin, F.; Duan, H.; Qu, X. PID Control Strategy for UAV Flight Control System Based on Improved Genetic Algorithm Optimization. In Proceedings of the 26th Chinese Control and Decision Conference (2014 CCDC), Changsha, China, 31 May–2 June 2014; pp. 92–97. [Google Scholar]
- Feng, Q.; Yu, J. Research on UAV Adaptive Control Method Based on Genetic Programming. In Proceedings of the 2021 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; pp. 2150–2154. [Google Scholar]
- Sun, Q.; Xu, H. Adaptive Control Method of UAV Intelligent Rudder Based on Hybrid Genetic Algorithm. In Proceedings of the 2021 33rd Chinese Control and Decision Conference (CCDC), Kunming, China, 22–24 May 2021. [Google Scholar]
- Li, G.; Wei, P.; Yang, W.; Gao, R. Research on Improved Particle Swarm Optimized Fuzzy PID Control for Quad-rotor UAV. In Proceedings of the 2021 China Automation Congress (CAC), Beijing, China, 22–24 October 2021. [Google Scholar]
- Lu, X.; Zhang, X.; Jia, S.; Shan, J. Design of Quadrotor Hovering Controller Based on Improved Particle Swarm Optimization. In Proceedings of the 2017 10th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 9–10 December 2017. [Google Scholar]
- Lu, J.; Yang, Y.; Jin, X. Quadrotor Inverted Pendulum Control Based on Improved Particle Swarm Optimization. In Proceedings of the 2021 China Automation Congress (CAC), Beijing, China, 22–24 October 2021. [Google Scholar]
- Boubertakh, H.; Bencharef, S.; Labiod, S. PSO-based PID Control Design for the Stabilization of a Quadrotor. In Proceedings of the 3rd International Conference on Systems and Control, Algiers, Algeria, 29–31 October 2013; pp. 514–517. [Google Scholar]
- Altan, A. Performance of Metaheuristic Optimization Algorithms Based on Swarm Intelligence in Attitude and Altitude Control of Unmanned Aerial Vehicle for Path Following. In Proceedings of the 2020 4th International Symposium on Multidisciplinary Studies and Innovative Technologies (ISMSIT), Istanbul, Turkey, 22–24 October 2020; pp. 1–6. [Google Scholar]
- Wang, Y.; Chenxie, Y.; Tan, J.; Wang, C.; Wang, Y.; Zhang, Y. Fuzzy Radial Basis Function Neural Network PID Control System for a Quadrotor UAV Based on Particle Swarm Optimization. In Proceedings of the 2015 IEEE International Conference on Information and Automation, Lijiang, China, 8–10 August 2015; pp. 2580–2585. [Google Scholar]
- Housny, H.; Chater, E.A.; Fadil, H.E. Fuzzy PID Control Tuning Design Using Particle Swarm Optimization Algorithm for a Quadrotor. In Proceedings of the 2019 5th International Conference on Optimization and Applications (ICOA), Kenitra, Morocco, 25–26 April 2019; pp. 1–6. [Google Scholar]
- Jun, W.; Xiong-Dong, Y.; Yu-Yang, T. Fault-tolerant Control Design of Quadrotor UAV Based on CPSO. In Proceedings of the 2018 IEEE 4th International Conference on Control Science and Systems Engineering (ICCSSE), Wuhan, China, 24–26 August 2018; pp. 279–283. [Google Scholar]
- Mac, T.T.; Copot, C.; Duc, T.T.; De Keyser, R. AR.Drone UAV Control Parameters Tuning Based on Particle Swarm Optimization Algorithm. In Proceedings of the 2016 IEEE International Conference on Automation, Quality and Testing, Robotics (AQTR), Cluj-Napoca, Romania, 19–21 May 2016; pp. 1–6. [Google Scholar]
- Liu, X.; Zhao, D.; Wu, Y. Application of Improved PSO in PID Parameter Optimization of Quad-rotor. In Proceedings of the 2015 12th International Computer Conference on Wavelet Active Media Technology and Information Processing (ICCWAMTIP), Chengdu, China, 18–20 December 2015; pp. 443–447. [Google Scholar]
- Liu, T.; Chen, Y.; Chen, Z.; Wu, H.; Cheng, L. Adaptive Fuzzy Fractional Order PID Control for 6-DOF Quad-rotor. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; pp. 2158–2163. [Google Scholar]
- Priyambodo, T.K.; Putra, A.E.; Dharmawan, A. Optimizing Control Based on Ant Colony Logic for Quadrotor Stabilization. In Proceedings of the 2015 IEEE International Conference on Aerospace Electronics and Remote Sensing Technology (ICARES), Bali, Indonesia, 3–5 December 2015; pp. 1–4. [Google Scholar]
- Katal, N.; Kumar, P.; Narayan, S. Design of PIλDμ Controller for Robust Flight Control of a UAV Using Multi-objective Bat Algorithm. In Proceedings of the 2015 2nd International Conference on Recent Advances in Engineering & Computational Sciences (RAECS), Chandigarh, India, 21–22 December 2015; pp. 1–5. [Google Scholar]
- Abdulkareem, A.; Oguntosin, V.; Popoola, O.M.; Idowu, A.A.; He, X. Modeling and Nonlinear Control of a Quadcopter for Stabilization and Trajectory Tracking. J. Eng. 2022, 2022, 2449901. [Google Scholar]
- Rinaldi, M.; Primatesta, S.; Guglieri, G. A Comparative Study for Control of Quadrotor UAVs. Appl. Sci. 2023, 13, 3464. [Google Scholar] [CrossRef]
- Pi, C.-H.; Ye, W.-Y.; Cheng, S. Robust Quadrotor Control Through Reinforcement Learning with Disturbance Compensation. Appl. Sci. 2021, 11, 3257. [Google Scholar] [CrossRef]
- Musa, S. Techniques for Quadcopter Modelling & Design: A Review. J. Unmanned Syst. Technol. 2018, 5, 66–75. [Google Scholar]
- Bouaiss, O.; Mechgoug, R.; Ajgou, R. Modeling, Control and Simulation of Quadrotor UAV. Presented at the 2020 1st International Conference on Communications, Control Systems and Signal Processing (CCSSP), El Oued, Algeria, 16–17 May 2020. [Google Scholar]
- Boualem, N.; Abderrezak, G.; Akram, A.; Lotfi, M. Fault Tolerant Attitude Estimation Strategy for a Quadrotor UAV under Total Sensor Failure. J. Control. Eng. Appl. Inform. 2023, 25, 79–89. [Google Scholar]
- Svacha, J.; Paulos, J.; Loianno, G.; Kumar, V. IMU-Based Inertia Estimation for a Quadrotor Using Newton-Euler Dynamics. IEEE Robot. Autom. Lett. 2020, 5, 3861–3867. [Google Scholar] [CrossRef]
- Sheta, A.; Braik, M.; Maddi, D.R.; Mahdy, A.; Aljahdali, S.; Turabieh, H. Optimization of PID Controller to Stabilize Quadcopter Movements Using Meta-heuristic Search Algorithms. Appl. Sci. 2021, 11, 6492. [Google Scholar] [CrossRef]
- Seyedali, M.; Andrew, L. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar]
- Rohr, N.; Ruggli, O.; Hanne, T.; Dornberger, R. Extending the Whale Optimization Algorithm with Chaotic Local Search. Presented at the 2020 7th International Conference on Soft Computing & Machine Intelligence (ISCMI), Stockholm, Sweden, 19–22 November 2020; pp. 28–33. [Google Scholar]
- Melo, A.G.; Andrade, F.A.A.; Guedes, I.P.; Carvalho, G.F.; Zachi, A.R.L.; Pinto, M.F. Fuzzy Gain-Scheduling PID for UAV Position and Altitude Controllers. Sensors 2022, 22, 2173. [Google Scholar] [CrossRef] [PubMed]
- Sangyam, T.; Laohapiengsak, P.; Chongcharoen, W.; Nilkhamhang, I. Path tracking of UAV using self-tuning PID controller based on fuzzy logic. In Proceedings of the SICE Annual Conference 2010, Taipei, Taiwan, 18–21 August 2010; pp. 1265–1269. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).