Autonomous Vehicle Decision and Control through Reinforcement Learning with Traffic Flow Randomization
Abstract
1. Introduction
2. Microscopic Traffic Flow
2.1. Rule-Based Microscopic Traffic Flow
2.1.1. IDM Car-Following Model
2.1.2. SL2015 Lane-Changing Model
2.2. LimSim High-Fidelity Microscopic Traffic Flow
2.2.1. Trajectory Generation
Lateral Trajectory Generation
Longitudinal Trajectory Generation
2.2.2. Optimal Trajectory Selection
3. Domain Randomization for Rule-Based Microscopic Traffic Flow
4. Simulation Experiment
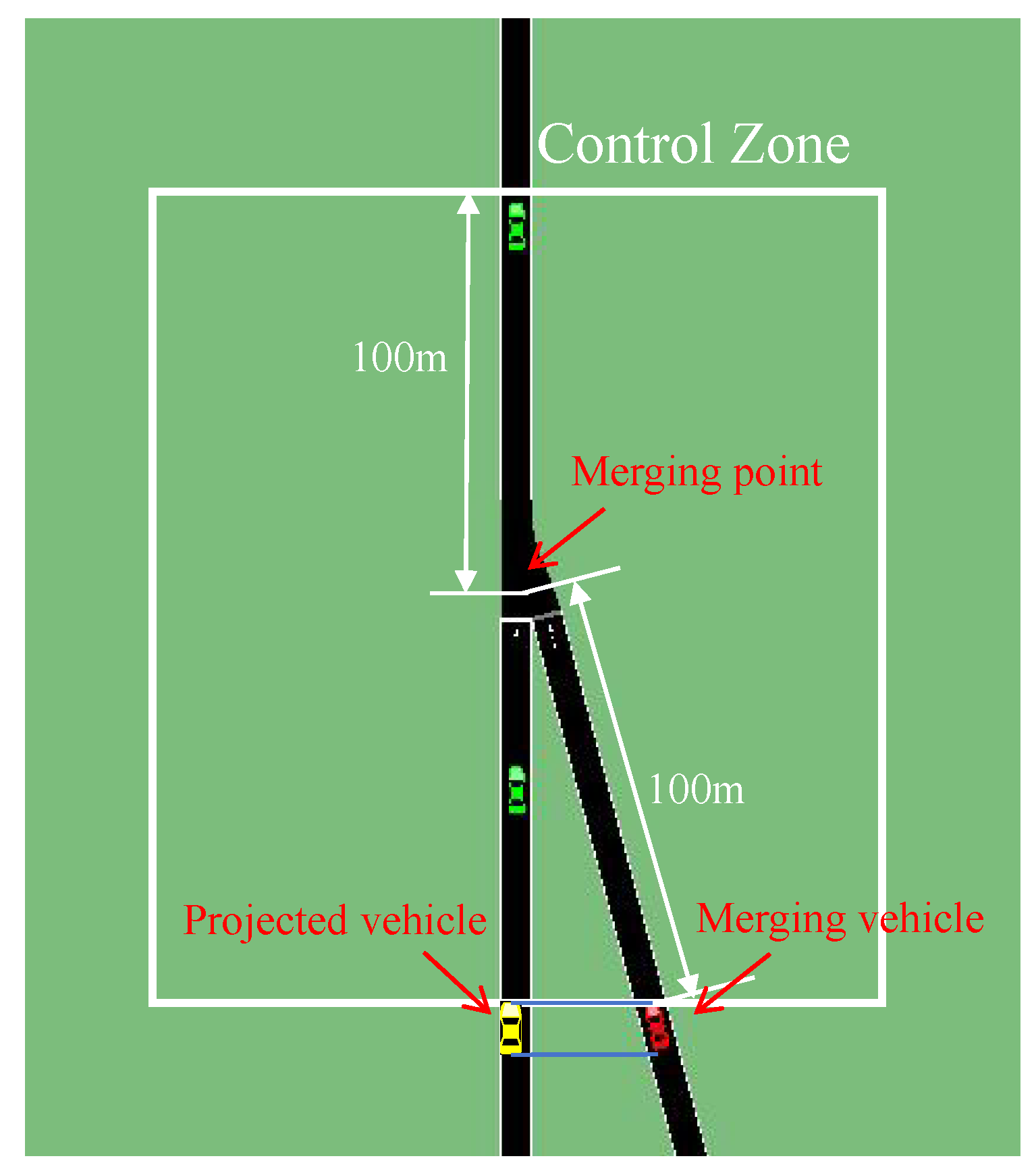
4.1. Merging
4.1.1. Merging Environment
State
Action
Reward
4.1.2. Soft Actor–Critic
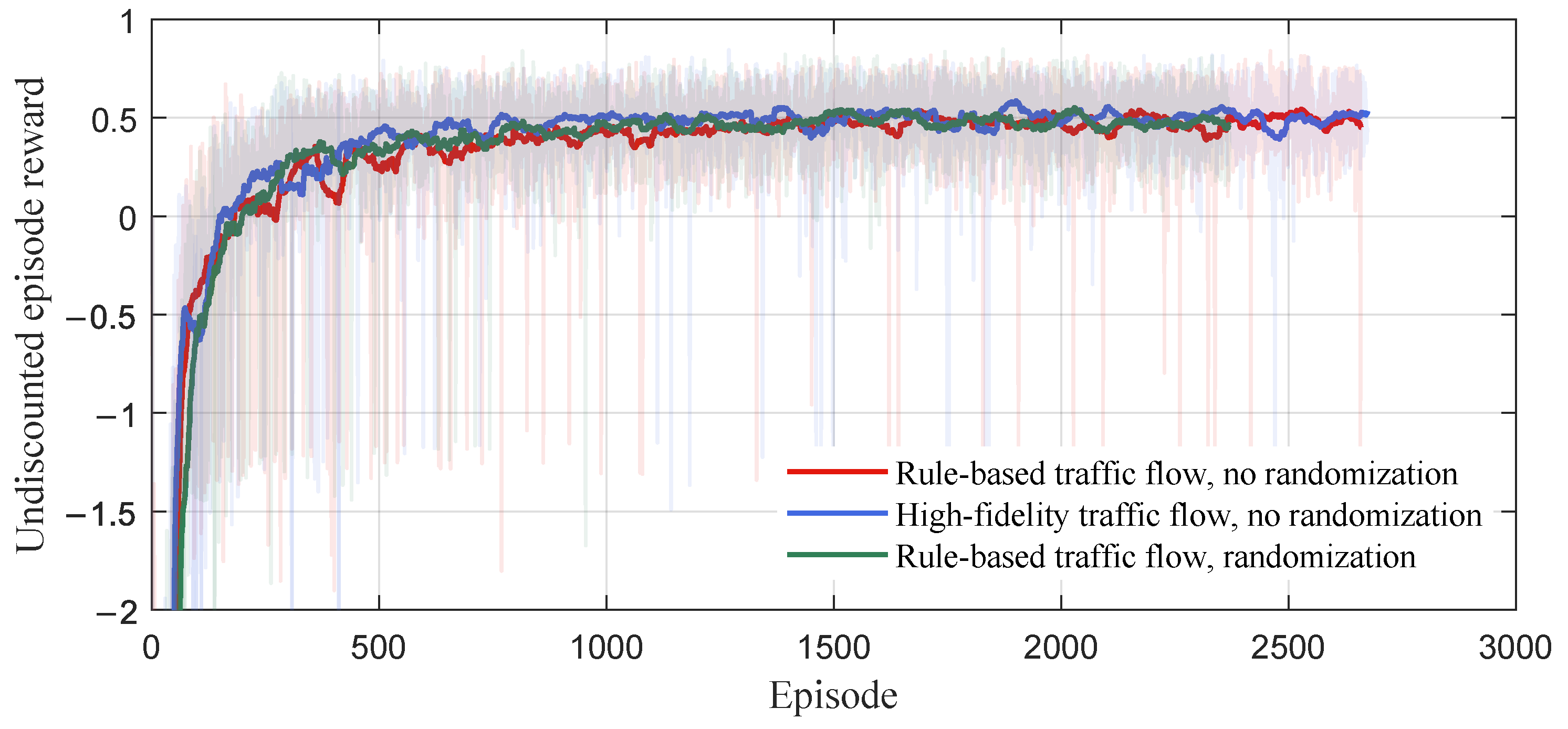
4.1.3. Results under Different Microscopic Traffic Flows
Training
Testing
Comparison and Analysis
4.1.4. Generalization Results for Increased Traffic Densities
4.1.5. Ablation Study
4.2. Freeway
4.2.1. Freeway Environment
State
Action
Reward
4.2.2. Parameterized Soft Actor–Critic
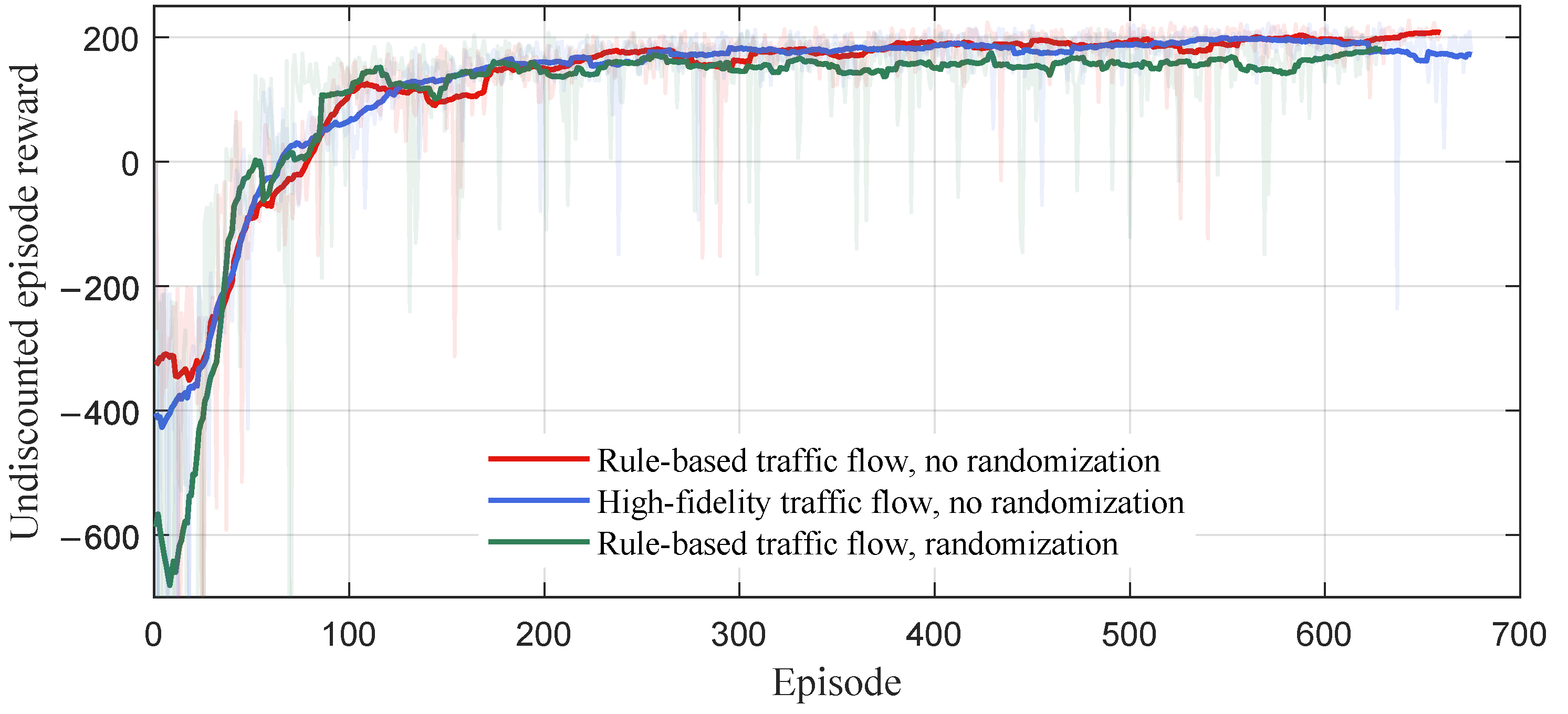
4.2.3. Results under Different Microscopic Traffic Flows
Training
Testing
Comparison and Analysis
4.2.4. Generalization Results for Increased Traffic Densities
4.2.5. Ablation Study
5. Conclusions
- The policy trained under the condition of domain-randomized rule-based microscopic traffic flow is able to maintain high rewards and success rates when tested with different microscopic traffic flows. However, the policy trained under the condition of microscopic traffic flow without randomization or high-fidelity microtraffic flow performs significantly worse when tested under microscopic traffic flows that are different from those of training. This indicates that domain randomization enables reinforcement learning agents to adapt to different types of traffic flow.
- The policy trained under the condition of domain-randomized rule-based microscopic traffic flow performs well when tested under high-fidelity microscopic traffic flow with different traffic densities. The policy trained under microscopic traffic flow without randomization decreases significantly with increasing traffic density. This indicates that the domain-randomized traffic flow possesses strong generalization to changes in traffic density.
- Although high-fidelity microscopic traffic flow is close to real microscopic traffic flows, the results show that not only does it considerably increase simulation time but policies trained under the condition of microscopic traffic flow also do not generalize well to different microscopic flows. Therefore, high-fidelity microscopic traffic flow is more suitable for testing rather than training.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Le Vine, S.; Zolfaghari, A.; Polak, J. Autonomous cars: The tension between occupant experience and intersection capacity. Transp. Res. Part C Emerg. Technol. 2015, 52, 1–14. [Google Scholar] [CrossRef]
- Sallab, A.E.; Abdou, M.; Perot, E.; Yogamani, S. Deep reinforcement learning framework for autonomous driving. arXiv 2017, arXiv:1704.02532. [Google Scholar] [CrossRef]
- Hoel, C.J.; Wolff, K.; Laine, L. Automated speed and lane change decision making using deep reinforcement learning. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 2148–2155. [Google Scholar]
- Ye, Y.; Zhang, X.; Sun, J. Automated vehicle’s behavior decision making using deep reinforcement learning and high-fidelity simulation environment. Transp. Res. Part C Emerg. Technol. 2019, 107, 155–170. [Google Scholar] [CrossRef]
- Ye, F.; Cheng, X.; Wang, P.; Chan, C.Y.; Zhang, J. Automated lane change strategy using proximal policy optimization-based deep reinforcement learning. In Proceedings of the 2020 IEEE Intelligent Vehicles Symposium (IV), Las Vegas, NV, USA, 19 October–13 November 2020; pp. 1746–1752. [Google Scholar]
- Lin, Y.; McPhee, J.; Azad, N.L. Anti-jerk on-ramp merging using deep reinforcement learning. In Proceedings of the 2020 IEEE Intelligent Vehicles Symposium (IV), Las Vegas, NV, USA, 19 October–13 November 2020; pp. 7–14. [Google Scholar]
- Peng, J.; Zhang, S.; Zhou, Y.; Li, Z. An Integrated Model for Autonomous Speed and Lane Change Decision-Making Based on Deep Reinforcement Learning. IEEE Trans. Intell. Transp. Syst. 2022, 23, 21848–21860. [Google Scholar] [CrossRef]
- Mirchevska, B.; Blum, M.; Louis, L.; Boedecker, J.; Werling, M. Reinforcement learning for autonomous maneuvering in highway scenarios. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium, Los Angeles, CA, USA, 11–14 June 2017. [Google Scholar]
- Treiber, M.; Hennecke, A.; Helbing, D. Congested traffic states in empirical observations and microscopic simulations. Phys. Rev. E 2000, 62, 1805. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Zeng, W.; Urtasun, R.; Yumer, E. Deep structured reactive planning. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 4897–4904. [Google Scholar]
- Huang, X.; Rosman, G.; Jasour, A.; McGill, S.G.; Leonard, J.J.; Williams, B.C. TIP: Task-informed motion prediction for intelligent vehicles. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 11432–11439. [Google Scholar]
- Punzo, V.; Simonelli, F. Analysis and comparison of microscopic traffic flow models with real traffic microscopic data. Transp. Res. Rec. 2005, 1934, 53–63. [Google Scholar] [CrossRef]
- Tessler, C.; Efroni, Y.; Mannor, S. Action robust reinforcement learning and applications in continuous control. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 6215–6224. [Google Scholar]
- Wang, J.X.; Kurth-Nelson, Z.; Tirumala, D.; Soyer, H.; Leibo, J.Z.; Munos, R.; Blundell, C.; Kumaran, D.; Botvinick, M. Learning to reinforcement learn. arXiv 2016, arXiv:1611.05763. [Google Scholar]
- Andrychowicz, O.M.; Baker, B.; Chociej, M.; Jozefowicz, R.; McGrew, B.; Pachocki, J.; Petron, A.; Plappert, M.; Powell, G.; Ray, A.; et al. Learning dexterous in-hand manipulation. Int. J. Robot. Res. 2020, 39, 3–20. [Google Scholar] [CrossRef]
- Sheckells, M.; Garimella, G.; Mishra, S.; Kobilarov, M. Using data-driven domain randomization to transfer robust control policies to mobile robots. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 3224–3230. [Google Scholar]
- Sun, Q.; Huang, X.; Williams, B.C.; Zhao, H. InterSim: Interactive traffic simulation via explicit relation modeling. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 11416–11423. [Google Scholar]
- Feng, L.; Li, Q.; Peng, Z.; Tan, S.; Zhou, B. Trafficgen: Learning to generate diverse and realistic traffic scenarios. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 3567–3575. [Google Scholar]
- Wenl, L.; Fu, D.; Mao, S.; Cai, P.; Dou, M.; Li, Y.; Qiao, Y. LimSim: A long-term interactive multi-scenario traffic simulator. In Proceedings of the 2023 IEEE 26th International Conference on Intelligent Transportation Systems (ITSC), Bilbao, Spain, 24–28 September 2023; pp. 1255–1262. [Google Scholar]
- Zheng, O.; Abdel-Aty, M.; Yue, L.; Abdelraouf, A.; Wang, Z.; Mahmoud, N. CitySim: A drone-based vehicle trajectory dataset for safety oriented research and digital twins. arXiv 2022, arXiv:2208.11036. [Google Scholar] [CrossRef]
- Werling, M.; Ziegler, J.; Kammel, S.; Thrun, S. Optimal trajectory generation for dynamic street scenarios in a frenet frame. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, Alaska, 3–8 May 2010; pp. 987–993. [Google Scholar]
- Berrazouane, M.; Tong, K.; Solmaz, S.; Kiers, M.; Erhart, J. Analysis and initial observations on varying penetration rates of automated vehicles in mixed traffic flow utilizing sumo. In Proceedings of the 2019 IEEE International Conference on Connected Vehicles and Expo (ICCVE), Graz, Austria, 4–8 November 2019; pp. 1–7. [Google Scholar]
- Kusari, A.; Li, P.; Yang, H.; Punshi, N.; Rasulis, M.; Bogard, S.; LeBlanc, D.J. Enhancing SUMO simulator for simulation based testing and validation of autonomous vehicles. In Proceedings of the 2022 IEEE Intelligent Vehicles Symposium (IV), Aachen, Germany, 5–9 June 2022; pp. 829–835. [Google Scholar]
- Krajzewicz, D.; Erdmann, J.; Behrisch, M.; Bieker, L. Recent development and applications of SUMO-Simulation of Urban MObility. Int. J. Adv. Syst. Meas. 2012, 5, 128–138. [Google Scholar]
- Wegener, A.; Piórkowski, M.; Raya, M.; Hellbrück, H.; Fischer, S.; Hubaux, J.P. TraCI: An interface for coupling road traffic and network simulators. In Proceedings of the 11th Communications and Networking Simulation Symposium, Ottawa, ON, Canada, 14–17 April 2008; pp. 155–163. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Hartikainen, K.; Tucker, G.; Ha, S.; Tan, J.; Kumar, V.; Zhu, H.; Gupta, A.; Abbeel, P.; et al. Soft actor-critic algorithms and applications. arXiv 2018, arXiv:1812.05905. [Google Scholar]
- Lin, Y.; Liu, X.; Zheng, Z.; Wang, L. Discretionary Lane-Change Decision and Control via Parameterized Soft Actor-Critic for Hybrid Action Space. arXiv 2024, arXiv:2402.15790. [Google Scholar] [CrossRef]

| Parameter | Default Value | Randomization Interval |
|---|---|---|
| 4 | ||
| T | 1 s | s |
| 2.6 m/s2 | m/s2 | |
| −4.5 m/s2 | m/s2 | |
| 8.33 m/s | m/s | |
| lcSpeedGain | 1 | |
| lcAssertive | 1 |
| Parameter | Value |
|---|---|
| Weight for merging midway | |
| Weight for penalizing first following’s braking | |
| Weight for penalizing jerk | |
| Maximum allowed speed difference | 5 m/s |
| Maximum allowed jerk value | 3 m/s3 |
| Traffic Flows for Training | |||||
|---|---|---|---|---|---|
| Rule-Based, No Randomization | High-Fidelity, No Randomization | Rule-Based, Randomization | |||
| Testing | rule-based, | Average reward | 0.0058 | 0.0002 | −0.0018 |
| no randomization | Success rate | 98.50% | 76.40% | ||
| high-fidelity, | Average reward | 0.0029 | 0.0055 | −0.0069 | |
| no randomization | Success rate | 95.20% | 97.50% | ||
| rule-based, | Average reward | −0.0089 | −0.0065 | ||
| randomization | Success rate | 56.00% | 66.70% | ||
| Traffic Density for Testing under High-Fidelity Traffic Flow | |||||
|---|---|---|---|---|---|
| Training under rule-based traffic flow (ϕ = 0.56) | no randomization | Average reward | 0.0039 | 0.0017 | 0.0006 |
| Success rate | 95.90% | 93.30% | 91.90% | ||
| randomization | Average reward | −0.0001 | −0.0002 | −0.0001 | |
| Success rate | 98.20% | 98.50% | 98.20% | ||
| Training under Rule-Based Traffic Flow | Traffic Flows for Testing | ||
|---|---|---|---|
|
Rule-Based, Randomization |
High-Fidelity, No Randomization | ||
| randomization—no | Average reward | 0.0049 | −0.0023 |
| Success rate | 99.90% | 95.60% | |
| randomization—no | Average reward | 0.0018 | −0.0049 |
| Success rate | 92.50% | 94.10% | |
| randomization—no | Average reward | 0.0038 | −0.0038 |
| Success rate | 97.30% | 97.70% | |
| randomization—no | Average reward | 0.0025 | −0.0026 |
| Success rate | 94.20% | 96.80% | |
| randomization—no | Average reward | −0.0070 | 0.0016 |
| Success rate | 65.00% | 93.70% | |
| no randomization | Average reward | −0.0089 | 0.0029 |
| Success rate | 56.00% | 95.20% | |
| randomization—all parameters | Average reward | 0.0057 | −0.0069 |
| Success rate | 99.30% | 98.20% | |
| Parameters | Value | Weights | Value |
|---|---|---|---|
| m/s2 | |||
| 2.6 m/s2 | |||
| 16.89 m/s | |||
| 8.89 m/s | |||
| 25 m | 1 | ||
| 2.5 m |
| Traffic Flows for Training | |||||
|---|---|---|---|---|---|
|
Rule-Based, No Randomization |
High-Fidelity, No Randomization |
Rule-Based, Randomization | |||
| Testing | rule-based, | Average reward | 200.50 | 205.32 | 197.15 |
| no randomization | Success rate | 100% | 99.70% | ||
| high-fidelity, | Average reward | 187.10 | 208.85 | 202.48 | |
| no randomization | Success rate | 98.90% | 99.60% | 99.90% | |
| rule-based, | Average reward | 126.27 | 160.06 | 186.72 | |
| randomization | Success rate | 80.40% | 89.00% | 99.40% | |
| Traffic Density for Testing under High-Fidelity Traffic Flow | |||||
|---|---|---|---|---|---|
| Training under rule-based traffic flow (ϕ = 0.14) | no randomization | Average speed | 16.39 | 15.89 | 15.77 |
| Average reward | 187.10 | 189.85 | 109.49 | ||
| Success rate | 98.90% | 93.90% | 66.50% | ||
| randomization | Average speed | 15.83 | 15.42 | 15.17 | |
| Average reward | 202.48 | 197.48 | 191.51 | ||
| Success rate | 99.90% | 99.80% | 99.90% | ||
| Training under Rule-Based Traffic Flow | Traffic Flows for Testing | ||
|---|---|---|---|
| Rule-Based, Randomization | High-Fidelity, No Randomization | ||
| randomization—no | Average reward | 170.46 | 187.65 |
| Success rate | 97.20% | 99.90% | |
| randomization—no | Average reward | 169.62 | 178.95 |
| Success rate | 98.50% | 99.60% | |
| randomization—no | Average reward | 181.49 | 202.52 |
| Success rate | 98.30% | 99.90% | |
| randomization—no | Average reward | 170.72 | 185.81 |
| Success rate | 99.40% | 100% | |
| randomization—no | Average reward | 96.99 | 150.10 |
| Success rate | 89.90% | 99.50% | |
| randomization—no lcSpeedGain | Average reward | 132.04 | 156.61 |
| Success rate | 100% | 100% | |
| randomization—no lcAssertive | Average reward | 173.71 | 188.57 |
| Success rate | 97.70% | 99.90% | |
| no randomization | Average reward | 126.27 | 187.10 |
| Success rate | 80.40% | 98.90% | |
| randomization—all parameters | Average reward | 186.72 | 202.48 |
| Success rate | 99.40% | 99.90% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.; Xie, A.; Liu, X. Autonomous Vehicle Decision and Control through Reinforcement Learning with Traffic Flow Randomization. Machines 2024, 12, 264. https://doi.org/10.3390/machines12040264
Lin Y, Xie A, Liu X. Autonomous Vehicle Decision and Control through Reinforcement Learning with Traffic Flow Randomization. Machines. 2024; 12(4):264. https://doi.org/10.3390/machines12040264
Chicago/Turabian StyleLin, Yuan, Antai Xie, and Xiao Liu. 2024. "Autonomous Vehicle Decision and Control through Reinforcement Learning with Traffic Flow Randomization" Machines 12, no. 4: 264. https://doi.org/10.3390/machines12040264
APA StyleLin, Y., Xie, A., & Liu, X. (2024). Autonomous Vehicle Decision and Control through Reinforcement Learning with Traffic Flow Randomization. Machines, 12(4), 264. https://doi.org/10.3390/machines12040264







