Design and Control of a Climbing Robot for Autonomous Vertical Gardening
Abstract
1. Introduction
2. Materials and Methods
2.1. Green Wall Design
2.2. Robot Mechanical Design
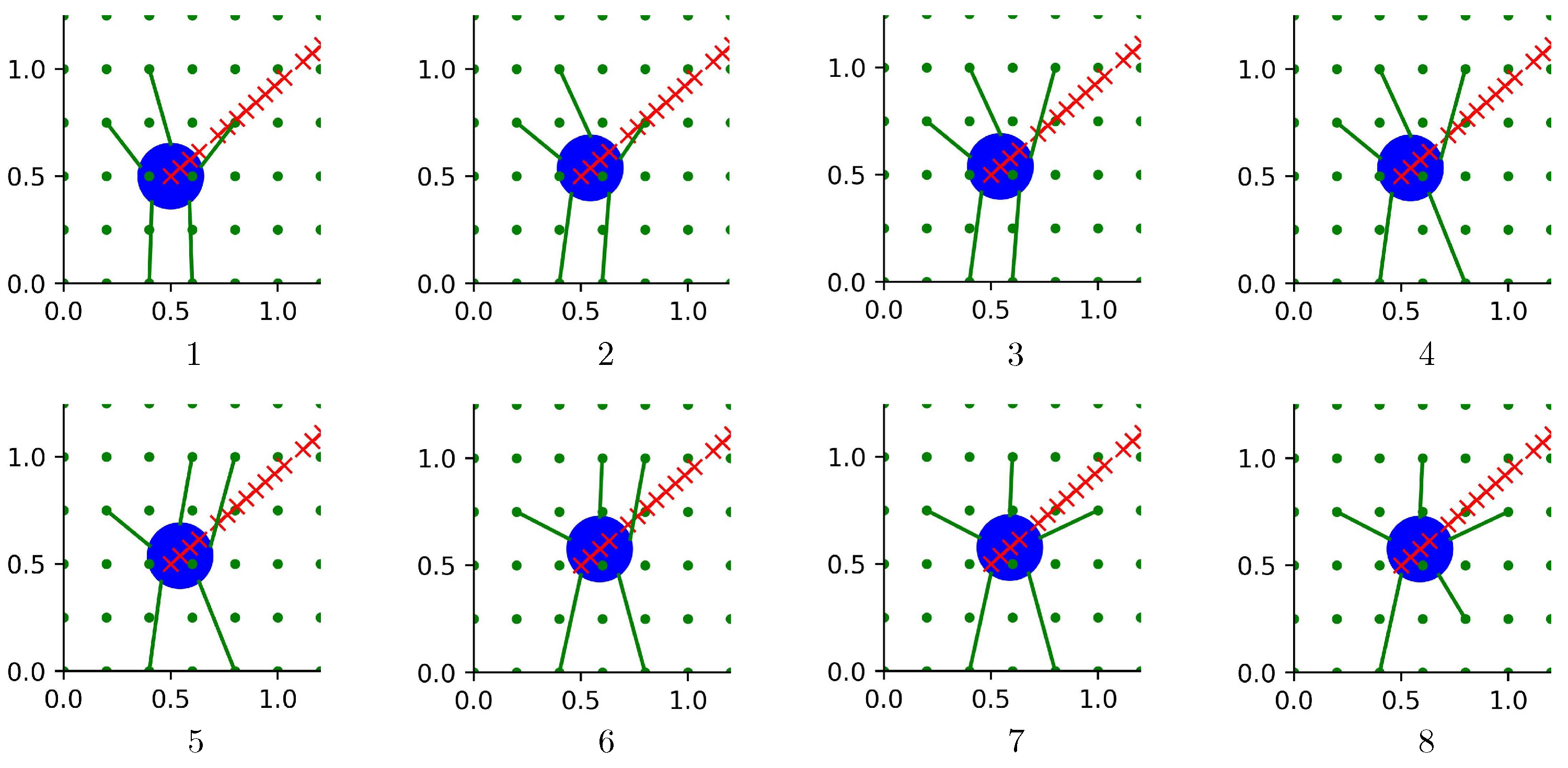
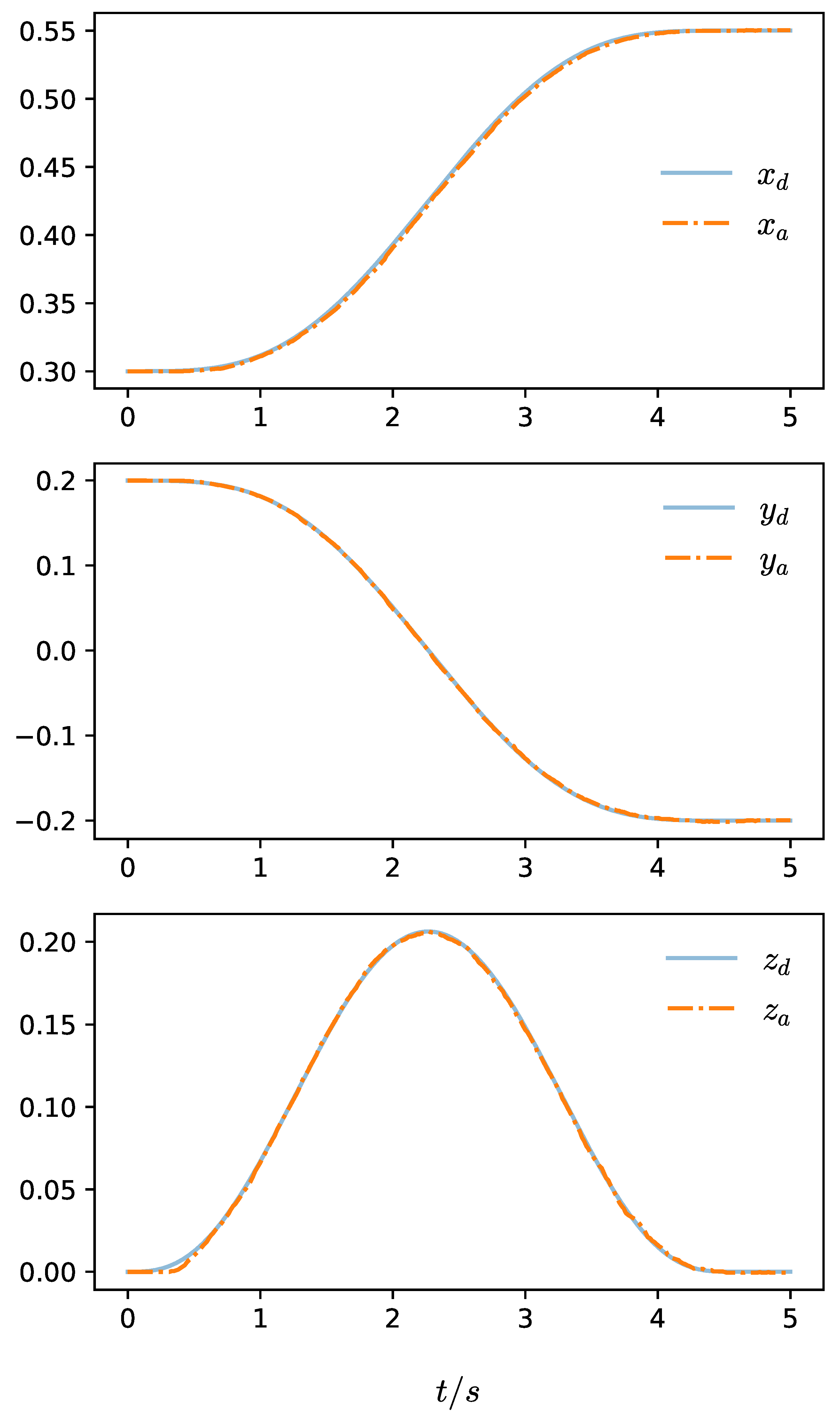
2.3. Motion Planning
2.4. Kinematic Analysis
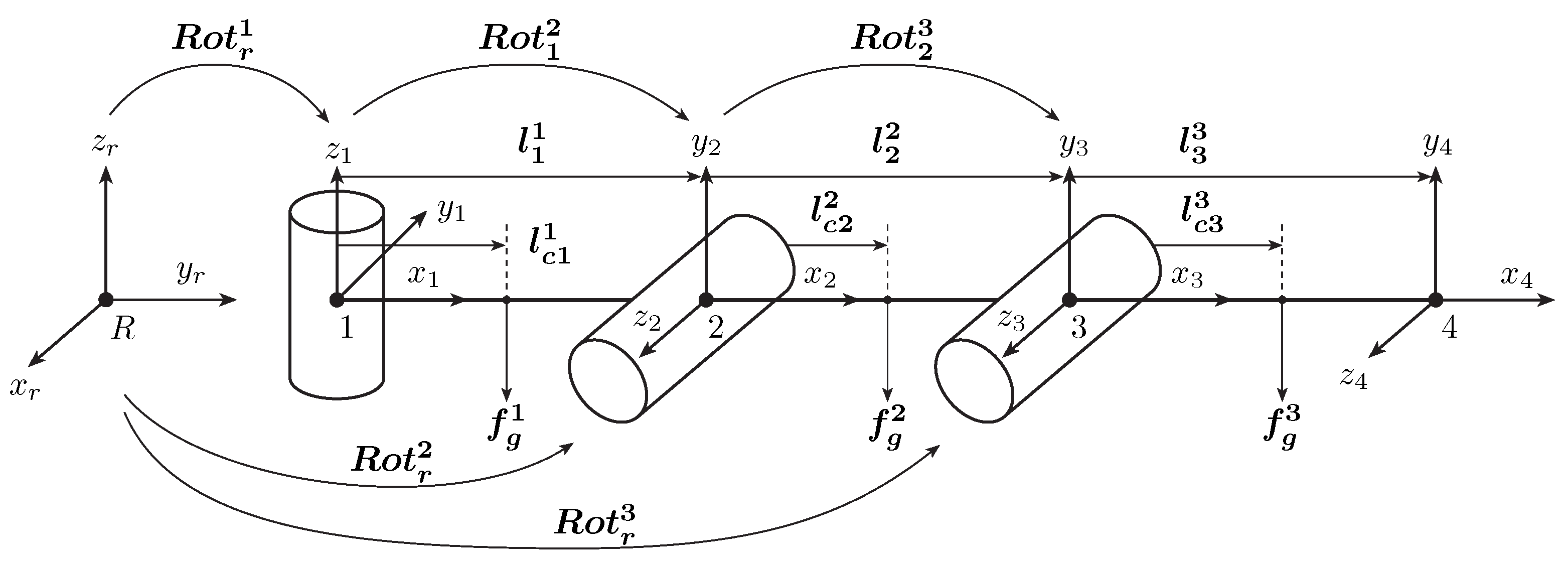
2.5. Robot Dynamics
2.5.1. Determining the Force on the End-Effector
- -
- torques of the previous segment,
- -
- forces of the previous segment, which through the lever represented by the length of the current segment (), cause torques in the joint,
- -
- torque in the joint, which is a result of the force of gravity and the lever represented by the distance between the joint and the center of gravity of the segment ().
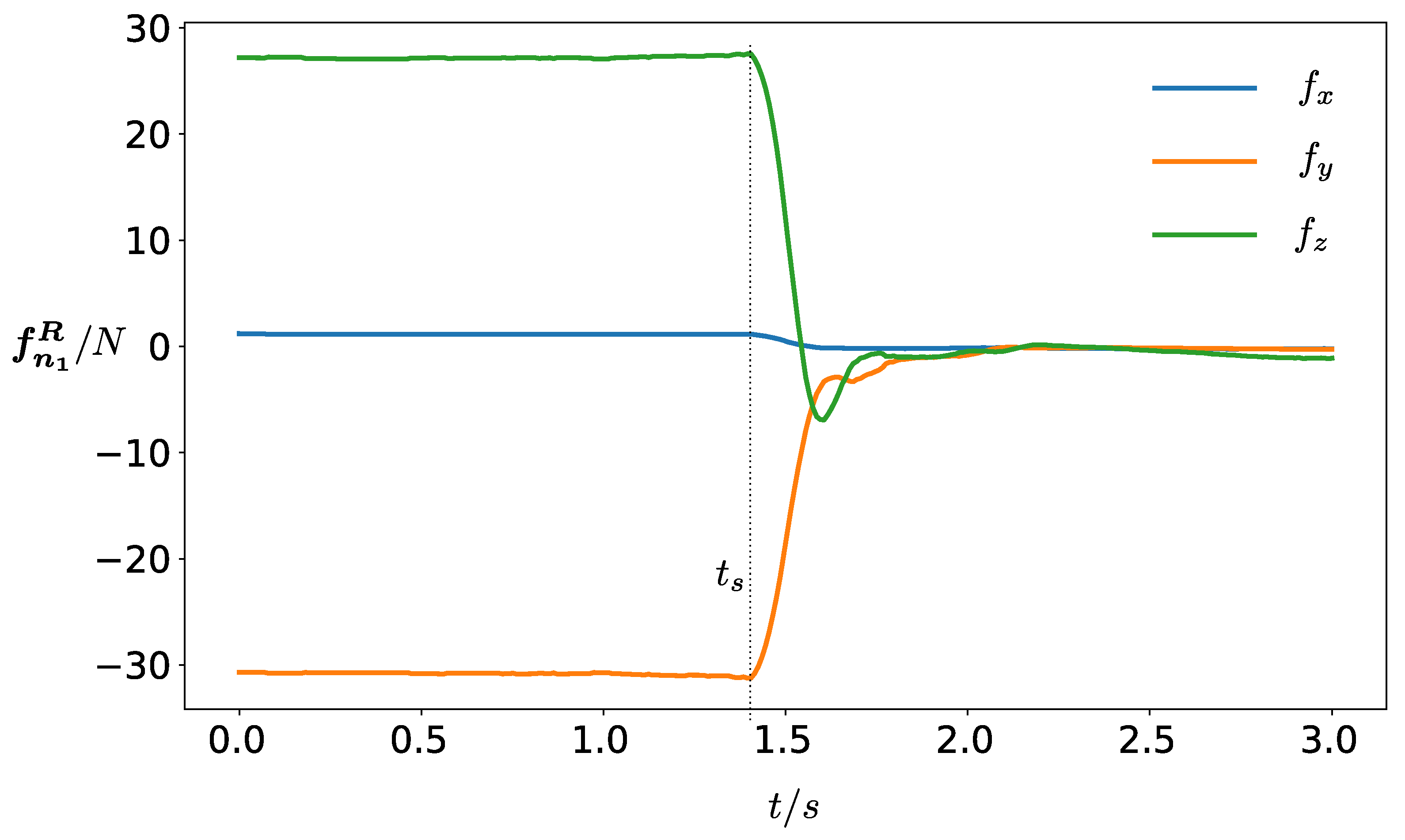
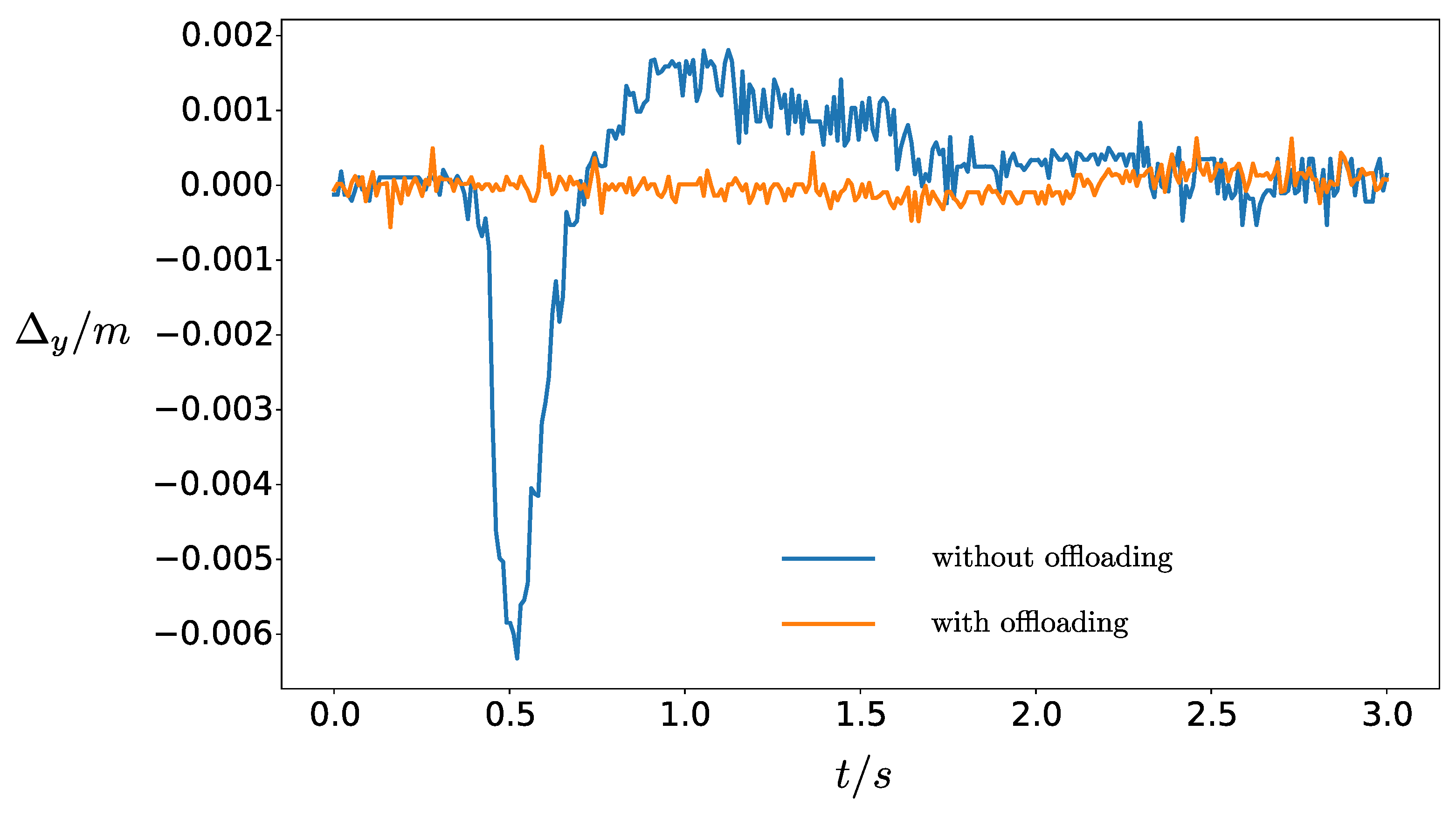
2.5.2. Optimal Distribution of Torques and Offloading of Each Individual Leg
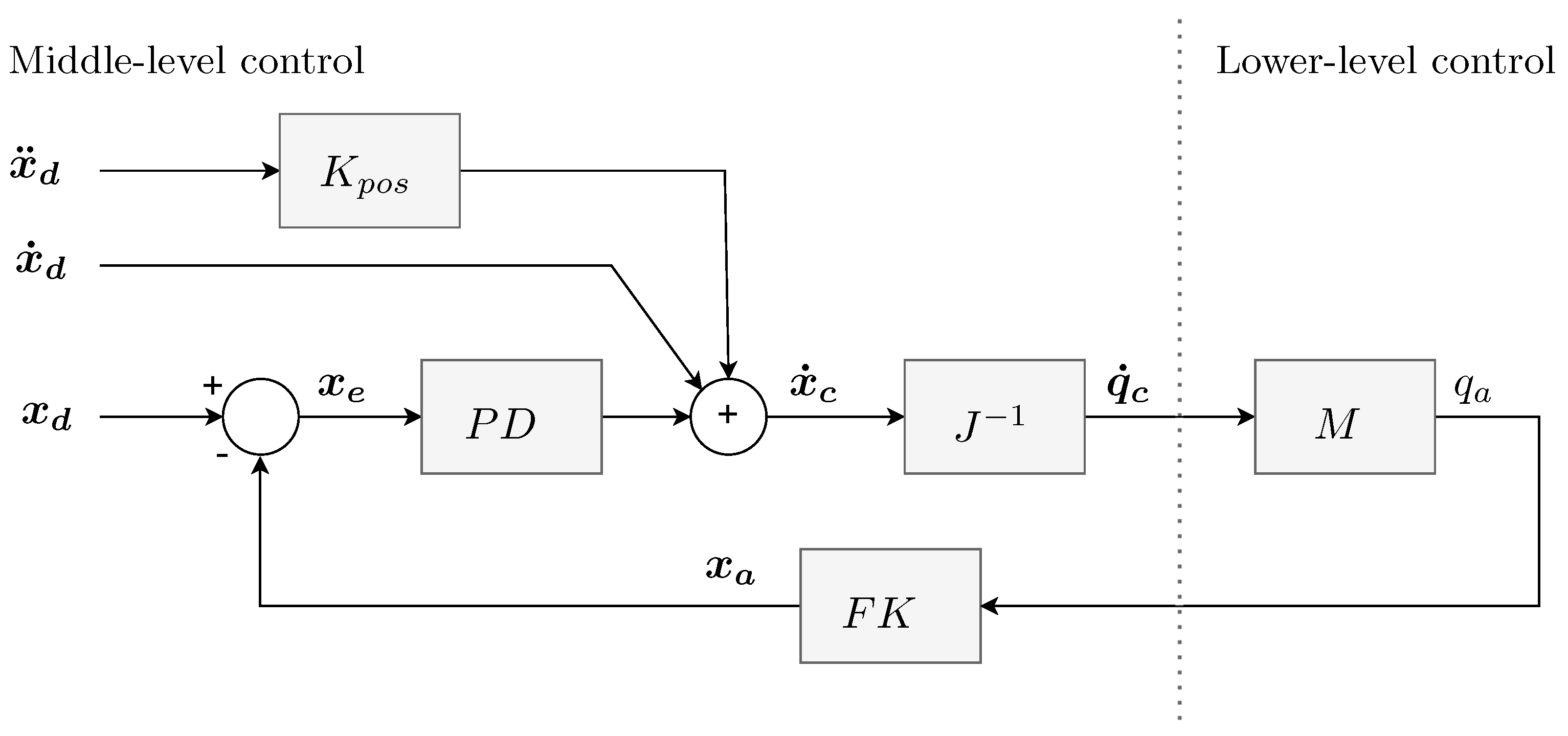
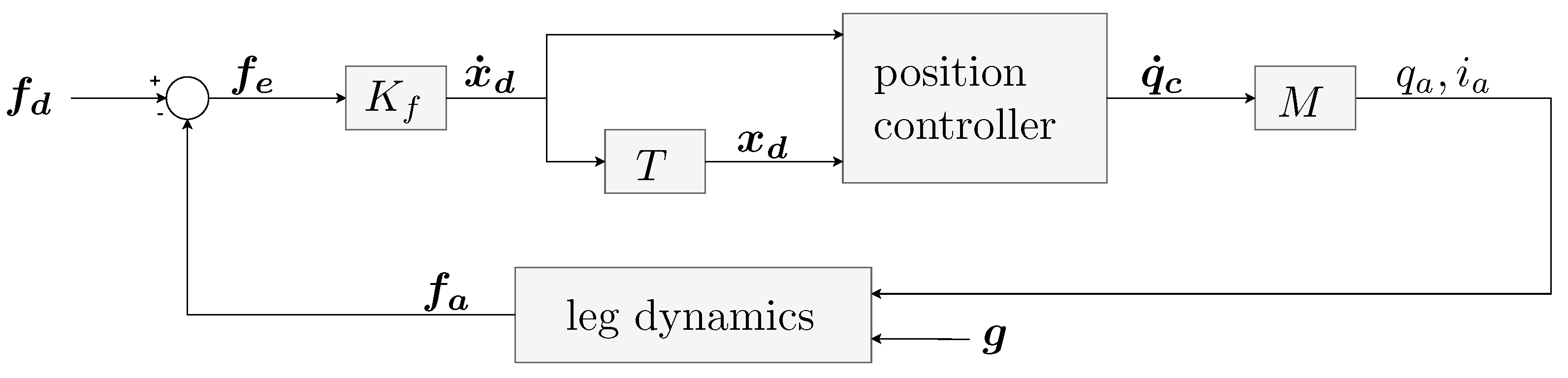
2.6. Robot Control
- the movement of the spider’s body
- force redistribution over all the legs
- movement of a single leg
- approach to the hold and attachment of the leg to the wall
- auxiliary single -leg movements for watering the plants or recharging the water reservoir
- position control mode,
- force control mode,
- velocity control mode.
2.6.1. Position Control Mode
2.6.2. Force Control Mode
2.6.3. Velocity Control Mode
3. Results
4. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fang, Y.; Wang, S.; Bi, Q.; Cui, D.; Yan, C. Design and Technical Development of Wall-Climbing Robots: A Review. J. Bionic Eng. 2022, 19, 877–901. [Google Scholar] [CrossRef]
- Tao, B.; Gong, Z.; Ding, H. Climbing robots for manufacturing. Natl. Sci. Rev. 2023, 10, nwad042. [Google Scholar] [CrossRef] [PubMed]
- Klančar, G.; Zdešar, A.; Blažič, S.; Škrjanc, I. Chapter 1—Introduction to Mobile Robotics. In Wheeled Mobile Robotics; Klančar, G., Zdešar, A., Blažič, S., Škrjanc, I., Eds.; Butterworth-Heinemann: Oxford, UK, 2017; pp. 1–11. [Google Scholar] [CrossRef]
- Chen, S.; Cao, Y.; Sarparast, M.; Yuan, H.; Dong, L.; Tan, X.; Cao, C. Soft Crawling Robots: Design, Actuation, and Locomotion. Adv. Mater. Technol. 2020, 5, 1900837. [Google Scholar] [CrossRef]
- Bellicoso, C.D.; Bjelonic, M.; Wellhausen, L.; Holtmann, K.; Günther, F.; Tranzatto, M.; Fankhauser, P.; Hutter, M. Advances in real-world applications for legged robots. J. Field Robot. 2018, 35, 1311–1326. [Google Scholar] [CrossRef]
- Schmidt, D.; Berns, K. Climbing robots for maintenance and inspections of vertical structures—A survey of design aspects and technologies. Robot. Auton. Syst. 2013, 61, 1288–1305. [Google Scholar] [CrossRef]
- Bisht, R.S.; Pathak, P.M.; Panigrahi, S.K. Design and development of a glass façade cleaning robot. Mech. Mach. Theory 2022, 168, 104585. [Google Scholar] [CrossRef]
- Eto, H.; Asada, H.H. Development of a Wheeled Wall-Climbing Robot with a Shape-Adaptive Magnetic Adhesion Mechanism. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 9329–9335. [Google Scholar] [CrossRef]
- Vidoni, R.; Gasparetto, A. Efficient force distribution and leg posture for a bio-inspired spider robot. Robot. Auton. Syst. 2011, 59, 142–150. [Google Scholar] [CrossRef]
- Silva, M.F.; Machado, J.A.T.; Tar, J.K. A Survey of Technologies for Climbing Robots Adhesion to Surfaces. In Proceedings of the 2008 IEEE International Conference on Computational Cybernetics, Stara Lesna, Slovakia, 27–29 November 2008; pp. 127–132. [Google Scholar] [CrossRef]
- Pack, R.; Christopher, J.; Kawamura, K. A Rubbertuator-based structure-climbing inspection robot. In Proceedings of the International Conference on Robotics and Automation, Albuquerque, NM, USA, 25–25 April 1997; Volume 3, pp. 1869–1874. [Google Scholar] [CrossRef]
- Ge, D.; Tang, Y.; Ma, S.; Matsuno, T.; Ren, C. A Pressing Attachment Approach for a Wall-Climbing Robot Utilizing Passive Suction Cups. Robotics 2020, 9, 26. [Google Scholar] [CrossRef]
- Unver, O.; Uneri, A.; Aydemir, A.; Sitti, M. Geckobot: A gecko inspired climbing robot using elastomer adhesives. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, 2006. ICRA 2006, Orlando, FL, USA, 15–19 May 2006; pp. 2329–2335. [Google Scholar] [CrossRef]
- Kim, S.; Spenko, M.; Trujillo, S.; Heyneman, B.; Mattoli, V.; Cutkosky, M.R. Whole body adhesion: Hierarchical, directional and distributed control of adhesive forces for a climbing robot. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Rome, Italy, 10–14 April 2007; pp. 1268–1273. [Google Scholar] [CrossRef]
- Wang, Z.; Bao, G.; Zhang, L.; Yang, Q. Development and control of flexible pneumatic wall-climbing robot. J. Cent. South Univ. Technol. 2009, 16, 961–970. [Google Scholar] [CrossRef]
- Minor, M.; Dulimarta, H.; Danghi, G.; Mukherjee, R.; Tummala, R.L.; Aslam, D. Design, implementation, and evaluation of an under-actuated miniature biped climbing robot. In Proceedings of the 2000 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2000) (Cat. No.00CH37113), Takamatsu, Japan, 31 October–5 November 2000; Volume 3, pp. 1999–2005. [Google Scholar] [CrossRef]
- Haynes, G.; Khripin, A.; Lynch, G.; Amory, J.; Saunders, A.; Rizzi, A.; Koditschek, D. Rapid pole climbing with a quadrupedal robot. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 2767–2772. [Google Scholar] [CrossRef]
- Nguyen, S.T.; Pham, A.Q.; Motley, C.; La, H.M. A Practical Climbing Robot for Steel Bridge Inspection. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 9322–9328. [Google Scholar] [CrossRef]
- Webster, C.; Kong, F.H.; Fitch, R. Bio-inspired 2D Vertical Climbing with a Novel Tripedal Robot. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 1239–1246. [Google Scholar] [CrossRef]
- Balaguer, C.; Gimenez, A.; Jardon, A. Climbing Robots Mobility for Inspection and Maintenance of 3D Complex Environments. Auton. Robot. 2005, 18, 157–169. [Google Scholar] [CrossRef]
- Kim, H.; Kang, T.; Loc, V.G.; Choi, H.R. Gait Planning of Quadruped Walking and Climbing Robot for Locomotion in 3D Environment. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 2733–2738. [Google Scholar] [CrossRef]
- Guan, Y.; Jiang, L.; Zhu, H.; Zhou, X.; Cai, C.; Wu, W.; Li, Z.; Zhang, H.; Zhang, X. Climbot: A modular bio-inspired biped climbing robot. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 1473–1478. [Google Scholar] [CrossRef]
- Chen, X.; Watanabe, K.; Kiguchi, K.; Izumi, K. Optimal Force Distribution for the Legs of a Quadruped Robot. Mach. Intell. Robot. Control 1999, 1, 87–94. [Google Scholar]
- Huang, W.K.; Xiao, J.L.; Zeng, F.L.; Lu, P.W.; Lin, G.J.; Hu, W.; Lin, X.Y.; Wu, Y. A Quadruped Robot with Three-Dimensional Flexible Legs. Sensors 2021, 21, 4907. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Zong, C.; Pancheri, F.; Chen, T.; Lueth, T.C. Design of topology optimized compliant legs for bio-inspired quadruped robots. Sci. Rep. 2023, 13, 4875. [Google Scholar] [CrossRef] [PubMed]
- Khalil, W. Dynamic Modeling of Robots Using Newton-Euler Formulation. In Informatics in Control, Automation and Robotics; Cetto, J.A., Ferrier, J.L., Filipe, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 3–20. [Google Scholar]
- Schaal, S.; Ijspeert, A.; Billard, A. Computational approaches to motor learning by imitation. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 2003, 358, 537–547. [Google Scholar] [CrossRef] [PubMed]
- Seriani, S.; Scalera, L.; Gasparetto, A.; Gallina, P. A new family of magnetic adhesion based wall-climbing robots. Mech. Mach. Sci. 2019, 68, 223–230. [Google Scholar] [CrossRef]
- Fang, G.; Cheng, J. Advances in Climbing Robots for Vertical Structures in the Past Decade: A Review. Biomimetics 2023, 8, 47. [Google Scholar] [CrossRef] [PubMed]


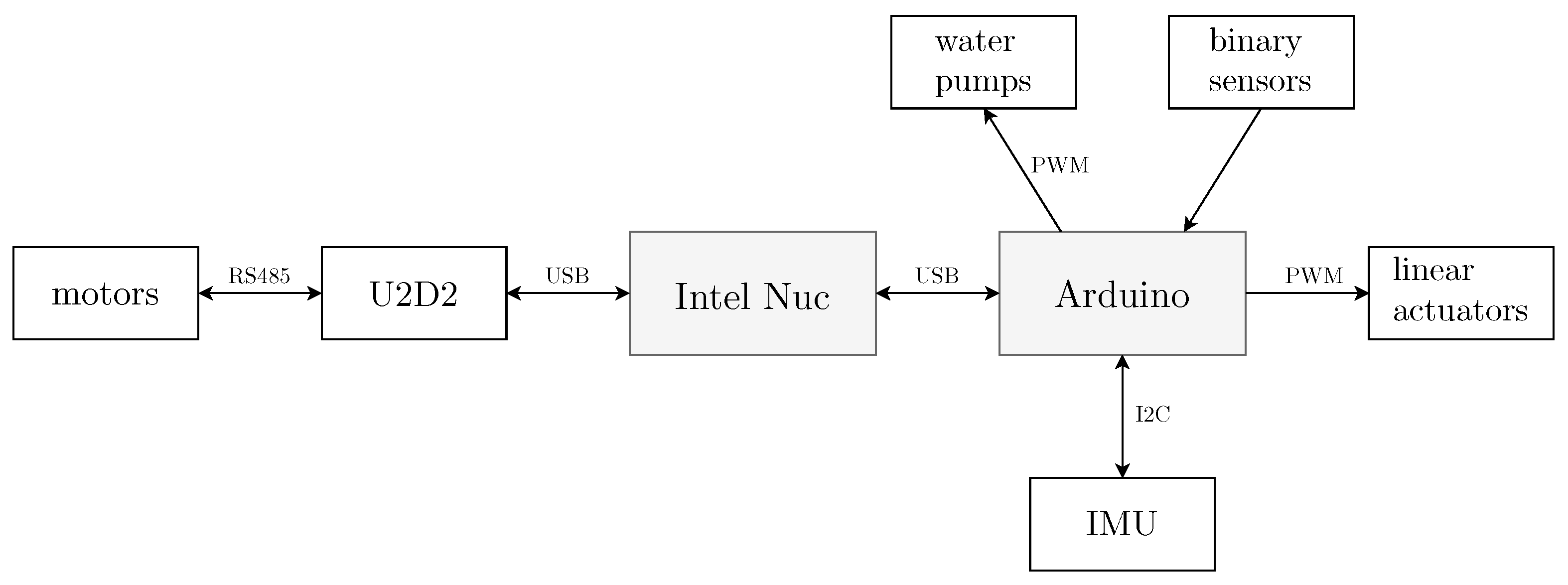



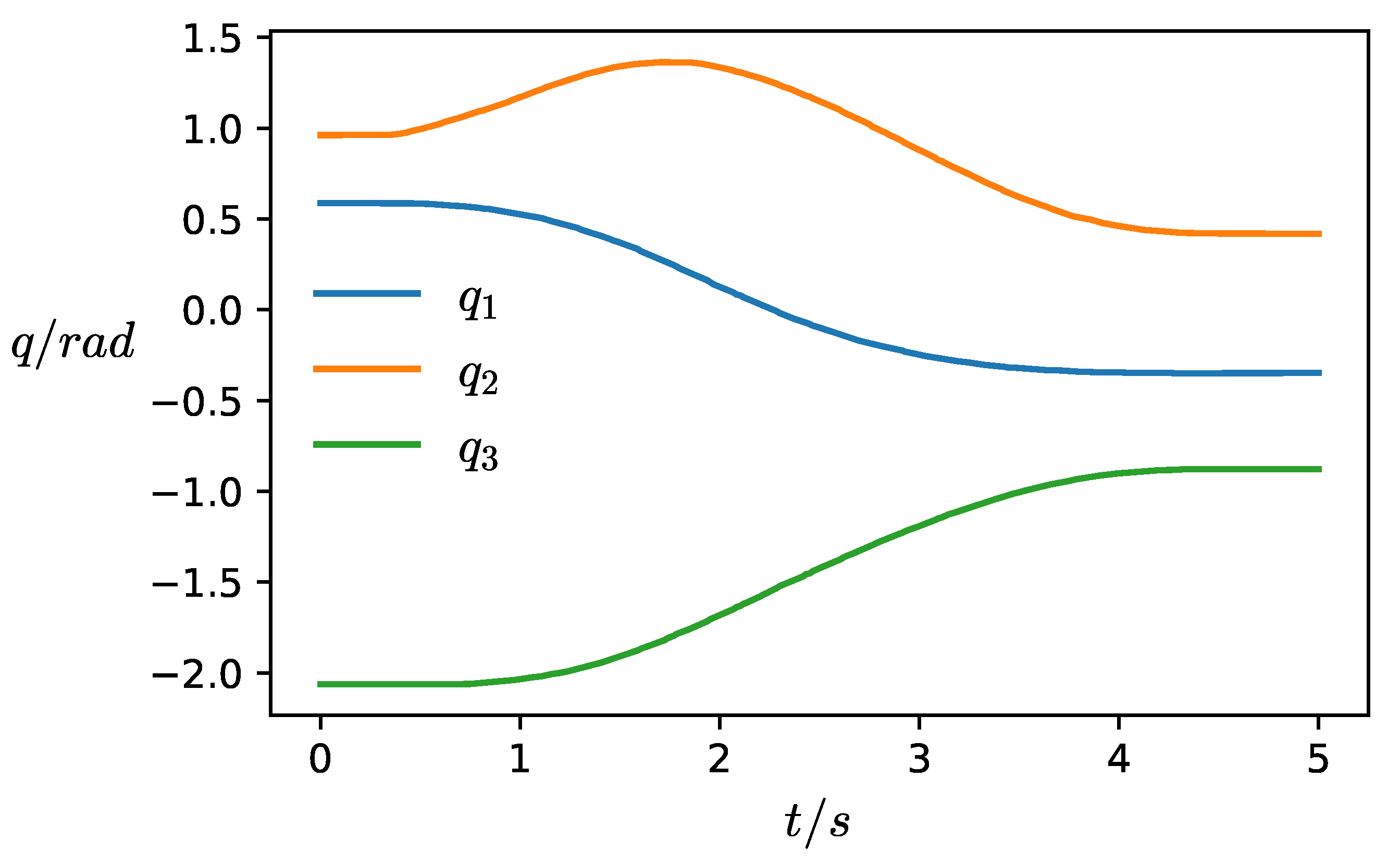


| Hardware Component | Part Name, Manufacturer |
|---|---|
| Main processing unit | Intel NUC 11 NUC11PAHi7 (Intel corporation, Santa Clara, CA, USA) |
| Peripherals control board | Arduino Nano (Arduino S.r.l., 20900 Monza (MB), Italy) |
| Motors for locomotion | Dynamixel XM430-W350-R (ROBOTIS Co., Seoul, Republic of Korea) |
| Linear motors for grippers | Actuonix L12-30-50-12-I (Micro Linear Actuators & Servos—Actuonix Motion Devices, Victoria, BC, Canada) |
| Serial to RS485 converter | U2D2 (ROBOTIS Co., Seoul, Republic of Korea) |
| Inertial measurement unit (IMU) | GY-521 MPU6050 (InvenSense, San Jose, CA, USA) |
| Segment | Length | Mass |
|---|---|---|
| First segment | 6.4 cm | 57 g |
| Second segment | 30 cm | 620 (670) g |
| Third segment | 27.6 cm | 270 g |
| Description | Data |
|---|---|
| Number of all leg movements | 7949 |
| Number of successful 1st moves | 6604 (83%) |
| Number of successful 1st moves for each leg | 1: 74%; 2: 85%: 3: 98%; 4: 83%; 5: 78% |
| Human intervention needed | 49 (0.6%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jamšek, M.; Sajko, G.; Krpan, J.; Babič, J. Design and Control of a Climbing Robot for Autonomous Vertical Gardening. Machines 2024, 12, 141. https://doi.org/10.3390/machines12020141
Jamšek M, Sajko G, Krpan J, Babič J. Design and Control of a Climbing Robot for Autonomous Vertical Gardening. Machines. 2024; 12(2):141. https://doi.org/10.3390/machines12020141
Chicago/Turabian StyleJamšek, Marko, Gal Sajko, Jurij Krpan, and Jan Babič. 2024. "Design and Control of a Climbing Robot for Autonomous Vertical Gardening" Machines 12, no. 2: 141. https://doi.org/10.3390/machines12020141
APA StyleJamšek, M., Sajko, G., Krpan, J., & Babič, J. (2024). Design and Control of a Climbing Robot for Autonomous Vertical Gardening. Machines, 12(2), 141. https://doi.org/10.3390/machines12020141








