Modeling of Chatter Stability for the Robot Milling of Natural Marble
Abstract
:1. Introduction
2. Experimental Design
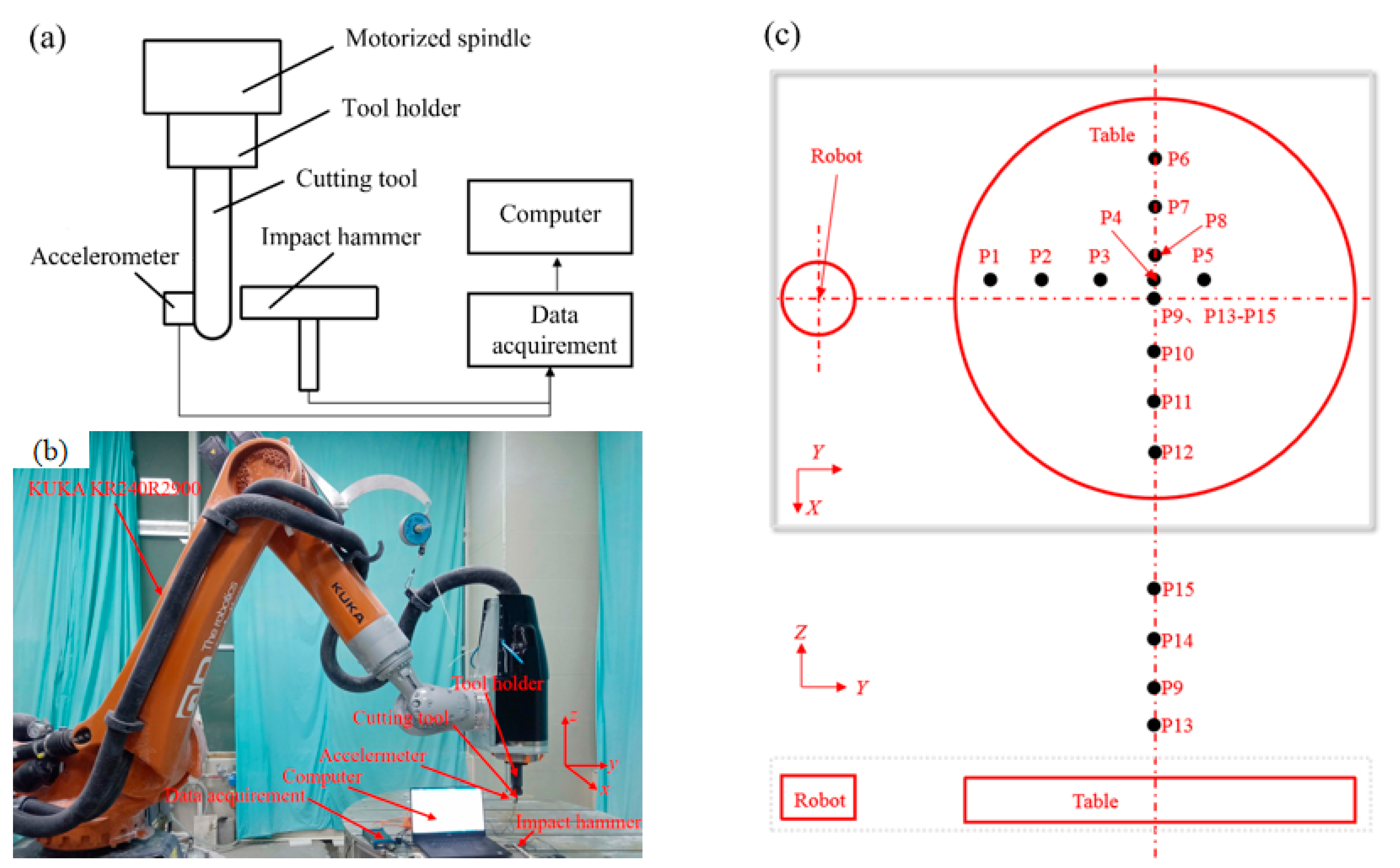
2.1. Description of the Robot Milling System
2.2. Experiments for the Identification of Milling Force Coefficients
2.3. Experiments for the Identification of Modal Parameters
2.4. Experiments for the Accuracy Verification of the Established Chatter Model
3. Modeling of Chatter Stability
3.1. Model of the Milling Force Coefficients
3.2. Model of Chatter Stability
4. Results and Discussion
4.1. Identification of Milling Force Coefficients and Modal Parameters
4.2. Identification of Modal Parameters
4.3. Accuracy Verification of the Established Chatter Model
4.4. Effect of Milling Parameters and Position on Chatter Stability
4.4.1. Effect of Milling Parameters on Chatter Stability
4.4.2. Effect of Milling Position on Chatter Stability
4.5. Industrial Applications
5. Conclusions
- An accurate chatter stability model for the robot milling of natural marble can be established based on the zeroth-order approximation method.
- With an increase in the radial cutting depth, the minimum critical axial cutting depth decreases sharply and then stabilizes, and the area of the absolute stable zone decreases sharply, while the conditional stable zone area increases slightly.
- With the stability lobe diagram of 0 mm in the X-direction as the reference, the stability lobe diagram for the coordinate values of −600 mm in the X-direction moves toward the upper and left directions, which improves the stability of the robot milling system.
- The stability lobe diagram for the coordinate values of 400 mm in the X-direction slightly moves toward the upper direction, which enhances the stability of the robot milling system.
- As the milling cutter moves in the positive Y-direction, the minimum critical axial cutting depth is constant, and the peak of the stability lobe diagram increases significantly, which makes the robot milling system more stable. The peak of the stability lobe diagram rises obviously and then declines when the milling cutter moves along the negative Y-direction.
- As the milling cutter moves upward, the minimum critical axial cutting depth declines then increases, while the peak of the stability lobe diagram decreases continuously, which worsens the stability of the robot milling system.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tian, H.; Pang, B.; Liu, J.; Meng, D.; Dang, X. Influence of different position modal parameters on milling chatter stability of orthopedic surgery robots. Sci. Rep. 2024, 14, 10581. [Google Scholar] [CrossRef] [PubMed]
- Liao, W.; Zheng, K.; Sun, L.; Dong, S.; Zhang, L. Review on chatter stability in robotic machining for large complex components. Acta Aeronaut. Astronaut. Sin. 2022, 43, 026061. [Google Scholar]
- Wu, J.; Tang, X.; Xin, S.; Wang, C.; Peng, F.; Yan, R. Research on the directionality of end dynamic compliance dominated by milling robot body structure and milling vibration suppression. Robot. Comput.-Integr. Manuf. 2024, 85, 102631. [Google Scholar] [CrossRef]
- Nie, W.; Zheng, M.; Zhang, W.; Liu, Y.; Bi, Y. Analytical prediction of chatter stability with the effect of multiple delays for variable pitch end mills and optimization of pitch parameters. Int. J. Adv. Manuf. Technol. 2022, 124, 2645–2658. [Google Scholar] [CrossRef]
- Liu, Z.; Deng, Z.; Yi, L.; Ge, J.; Yang, P. A review of research on robot machining chatter. Int. J. Adv. Manuf. Technol. 2024, 135, 49–79. [Google Scholar] [CrossRef]
- Pan, Z.; Zhang, H.; Zhu, Z.; Wang, J. Chatter analysis of robotic machining process. J. Mater. Process. Technol. 2006, 173, 301–309. [Google Scholar] [CrossRef]
- Cordes, M.; Hintze, W.; Altintas, Y. Chatter stability in robotic milling. Robot. Comput.-Integr. Manuf. 2019, 55, 11–18. [Google Scholar] [CrossRef]
- Cen, L.; Melkote, S.N. CCT-based mode coupling chatter avoidance in robotic milling. J. Manuf. Process. 2017, 29, 50–61. [Google Scholar] [CrossRef]
- Ji, Y.; Liu, R. Research on the influence of cutter overhang length on robotic milling chatter stability. Sci. Rep. 2024, 14, 24838. [Google Scholar] [CrossRef]
- Mao, S.-H.; Ye, S.-T.; Jiang, Y.-R.; Shen, C.-Q.; Zhang, X.-J.; Yan, S.-J.; Ding, H. On the existence of mode-coupling chatter in robotic milling based on chatter type indicators extracted by dynamic mode decomposition. Mech. Syst. Signal Process. 2024, 220, 111591. [Google Scholar] [CrossRef]
- Yang, B.; Guo, K.; Zhou, Q.; Sun, J. Early chatter detection in robotic milling under variable robot postures and cutting parameters. Mech. Syst. Signal Process. 2023, 186, 109860. [Google Scholar] [CrossRef]
- Altintaş, Y.; Budak, E. Analytical Prediction of Stability Lobes in Milling. CIRP Ann. 1995, 44, 357–362. [Google Scholar] [CrossRef]
- Budak, E.; Altintas, Y. Analytical prediction of chatter stability in milling-Part I general formulation. J. Dyn. Syst. Meas. Control ASME 1998, 120, 22–30. [Google Scholar] [CrossRef]
- Hao, D.; Wang, W.; Liu, Z.; Yun, C. Experimental study of stability prediction for high-speed robotic milling of aluminum. J. Vib. Control 2020, 26, 387–398. [Google Scholar] [CrossRef]
- Li, M.; Huang, D.; Yang, X. Chatter stability prediction and detection during high-speed robotic milling process based on acoustic emission technique. Int. J. Adv. Manuf. Technol. 2021, 117, 1589–1599. [Google Scholar] [CrossRef]
- Guihong, S.; Zhiqiang, L.; Yuchao, D.; Yi, Y.; Sichen, C.; Zirui, G.; Haoran, Z.; Zhibing, L.; Tianyang, Q.; Xibin, W. Stability prediction for robotic milling based on tool tip frequency response prediction by considering the interface stiffness of spindle-tool system. J. Sound Vib. 2024, 585, 118471. [Google Scholar] [CrossRef]
- Chen, S.; Liang, Z.; Du, Y.; Gao, Z.; Zheng, H.; Liu, Z.; Qiu, T.; Wang, X. Early chatter identification based on optimized VMD with multi-band information fusion and compression method in robotic milling process. Chin. J. Aeronaut. 2024, 37, 464–484. [Google Scholar] [CrossRef]
- Lei, Y.; Hou, T.; Ding, Y. Prediction of the Posture-Dependent Tool Tip Dynamics in Robotic Milling Based on Multi-Task Gaussian Process Regressions. Robot. Comput.-Integr. Manuf. 2023, 81, 102508. [Google Scholar] [CrossRef]
- Tunc, L.T.; Stoddart, D. Tool path pattern and feed direction selection in robotic milling for increased chatter-free material removal rate. Int. J. Adv. Manuf. Technol. 2017, 89, 2907–2918. [Google Scholar] [CrossRef]
- Li, J.; Li, B.; Shen, N.; Qian, H.; Guo, Z. Effect of the cutter path and the workpiece clamping position on the stability of the robotic milling system. Int. J. Adv. Manuf. Technol. 2016, 89, 2919–2933. [Google Scholar] [CrossRef]
- Xin, S.; Peng, F.; Tang, X.; Yan, R.; Li, Z.; Wu, J. Research on the influence of robot structural mode on regenerative chatter in milling and analysis of stability boundary improvement domain. Int. J. Mach. Tools Manuf. 2022, 179, 103918. [Google Scholar] [CrossRef]
- Mann, B.P.; Edes, B.T.; Easley, S.J.; Young, K.A.; Ma, K. Chatter vibration and surface location error prediction for helical end mills. Int. J. Mach. Tools Manuf. 2008, 48, 350–361. [Google Scholar] [CrossRef]
- Mejri, S.; Gagnol, V.; Le, T.-P.; Sabourin, L.; Ray, P.; Paultre, P. Dynamic characterization of machining robot and stability analysis. Int. J. Adv. Manuf. Technol. 2015, 82, 351–359. [Google Scholar] [CrossRef]













| No. | Rotation Speed n (r/min) | Feed per Cutting Edge fz (mm/z) | Axial Cutting Depth ap (mm) |
|---|---|---|---|
| 1 | 8000 | 0.05 | 5 |
| 2 | 8000 | 0.10 | 5 |
| 3 | 8000 | 0.15 | 5 |
| 4 | 8000 | 0.05 | 6 |
| 5 | 8000 | 0.10 | 6 |
| 6 | 8000 | 0.15 | 6 |
| No. | X (mm) | Y (mm) | Z (mm) | No. | X (mm) | Y (mm) | Z (mm) |
|---|---|---|---|---|---|---|---|
| P1 | −19.5 | 1262.61 | 474.4 | P9 | 0 | 2000.07 | 474.4 |
| P2 | −19.5 | 1598.97 | 474.4 | P10 | 200 | 2000.07 | 474.4 |
| P3 | −19.5 | 1874.79 | 474.4 | P11 | 400 | 2000.07 | 474.4 |
| P4 | −19.5 | 2000.07 | 474.4 | P12 | 600 | 2000.07 | 474.4 |
| P5 | −19.5 | 2249.98 | 474.4 | P13 | 0 | 2000.07 | 350 |
| P6 | −600 | 2000.07 | 474.4 | P14 | 0 | 2000.07 | 600 |
| P7 | −400 | 2000.07 | 474.4 | P15 | 0 | 2000.07 | 800 |
| P8 | −200 | 2000.07 | 474.4 | ||||
| No. | Rotation Speed n (r/min) | Feed per Cutting Edge fz (mm/z) | Axial Cutting Depth ap (mm) | Radial Cutting Depth ae (mm) |
|---|---|---|---|---|
| Exp. A | 7500 | 0.15 | 7.5 | 5 |
| Exp. B | 8100 | 0.15 | 5 | 5 |
| No. | Fx (N) | Fy (N) | Fz (N) |
|---|---|---|---|
| 1 | 364.76 | −1070.83 | 188.60 |
| 2 | 393.59 | −1213.78 | 159.83 |
| 3 | 476.95 | −1459.49 | 157.52 |
| 4 | 412.45 | −1225.90 | 183.56 |
| 5 | 611.19 | −1648.38 | 271.77 |
| 6 | 640.45 | −1750.91 | 263.71 |
| ap (mm) | Fxe (N) | Fxc (N) | Fye (N) | Fyc (N) | Fze (N) | Fzc (N) |
|---|---|---|---|---|---|---|
| 5 | 299.57 | 1121.94 | −859.37 | −3886.60 | 199.73 | −310.82 |
| 6 | 326.69 | 2280.04 | −1016.72 | −5250.08 | 159.53 | 801.54 |
| Ktc (N/mm2) | Krc (N/mm2) | Kac (N/mm2) | Kte (N/mm) | Kre (N/mm) | Kae (N/mm) | |
|---|---|---|---|---|---|---|
| ap = 5 mm | 1554.64 | 350.28 | 347.33 | 125.06 | 53.49 | 22.24 |
| ap = 6 mm | 1755.71 | 851.55 | 160.76 | 117.33 | 45.01 | 26.47 |
| Average values | 1655.18 | 600.91 | 254.04 | 121.20 | 49.25 | 24.35 |
| X-Direction | Y-Direction | |||||
|---|---|---|---|---|---|---|
| No. | ω (Hz) | ζ (%) | K (m × N−1) | ω (Hz) | ζ (%) | K (m × N−1) |
| P1 | 820.933 | 2.998 | 1.91 × 107 | 1013.055 | 1.985 | 2.31 × 107 |
| P2 | 821.002 | 3.012 | 1.90 × 107 | 1023.628 | 2.565 | 1.83 × 107 |
| P3 | 826.240 | 2.919 | 1.91 × 107 | 1032.886 | 2.100 | 2.70 × 107 |
| P4 | 820.806 | 2.445 | 2.33 × 107 | 1034.235 | 3.041 | 1.96 × 107 |
| P5 | 821.849 | 2.910 | 1.85 × 107 | 1023.213 | 2.564 | 2.29 × 107 |
| P6 | 823.993 | 3.149 | 1.54 × 107 | 841.072 | 5.143 | 1.12 × 107 |
| P7 | 826.148 | 2.39 | 2.05 × 107 | 1026.979 | 3.228 | 1.81 × 107 |
| P8 | 827.741 | 2.711 | 1.78 × 107 | 1021.630 | 2.963 | 1.91 × 107 |
| P9 | 825.026 | 3.467 | 1.40 × 107 | 1026.290 | 1.974 | 2.69 × 107 |
| P10 | 824.849 | 3.203 | 1.55 × 107 | 1029.159 | 2.596 | 1.98 × 107 |
| P11 | 890.224 | 7.238 | 9.72 × 106 | 1031.791 | 3.082 | 1.72 × 107 |
| P12 | 822.235 | 2.374 | 2.42 × 107 | 1027.256 | 2.552 | 1.86 × 107 |
| P13 | 827.779 | 2.908 | 1.83 × 107 | 1025.587 | 2.378 | 1.99 × 107 |
| P14 | 823.028 | 2.997 | 1.76 × 107 | 1023.510 | 2.977 | 1.83 × 107 |
| P15 | 825.123 | 2.478 | 2.00 × 107 | 1034.081 | 3.221 | 1.97 × 107 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, J.; Huang, H.; Huang, S.; Yin, F. Modeling of Chatter Stability for the Robot Milling of Natural Marble. Machines 2024, 12, 942. https://doi.org/10.3390/machines12120942
Huang J, Huang H, Huang S, Yin F. Modeling of Chatter Stability for the Robot Milling of Natural Marble. Machines. 2024; 12(12):942. https://doi.org/10.3390/machines12120942
Chicago/Turabian StyleHuang, Jixiang, Hui Huang, Shengui Huang, and Fangchen Yin. 2024. "Modeling of Chatter Stability for the Robot Milling of Natural Marble" Machines 12, no. 12: 942. https://doi.org/10.3390/machines12120942
APA StyleHuang, J., Huang, H., Huang, S., & Yin, F. (2024). Modeling of Chatter Stability for the Robot Milling of Natural Marble. Machines, 12(12), 942. https://doi.org/10.3390/machines12120942






