Dynamic Response of Electromechanical Coupled Motor Gear System with Gear Tooth Crack
Abstract
1. Introduction
2. Electromechanical Coupling Modeling of MGS
2.1. Equivalent Circuit Model of PMSM
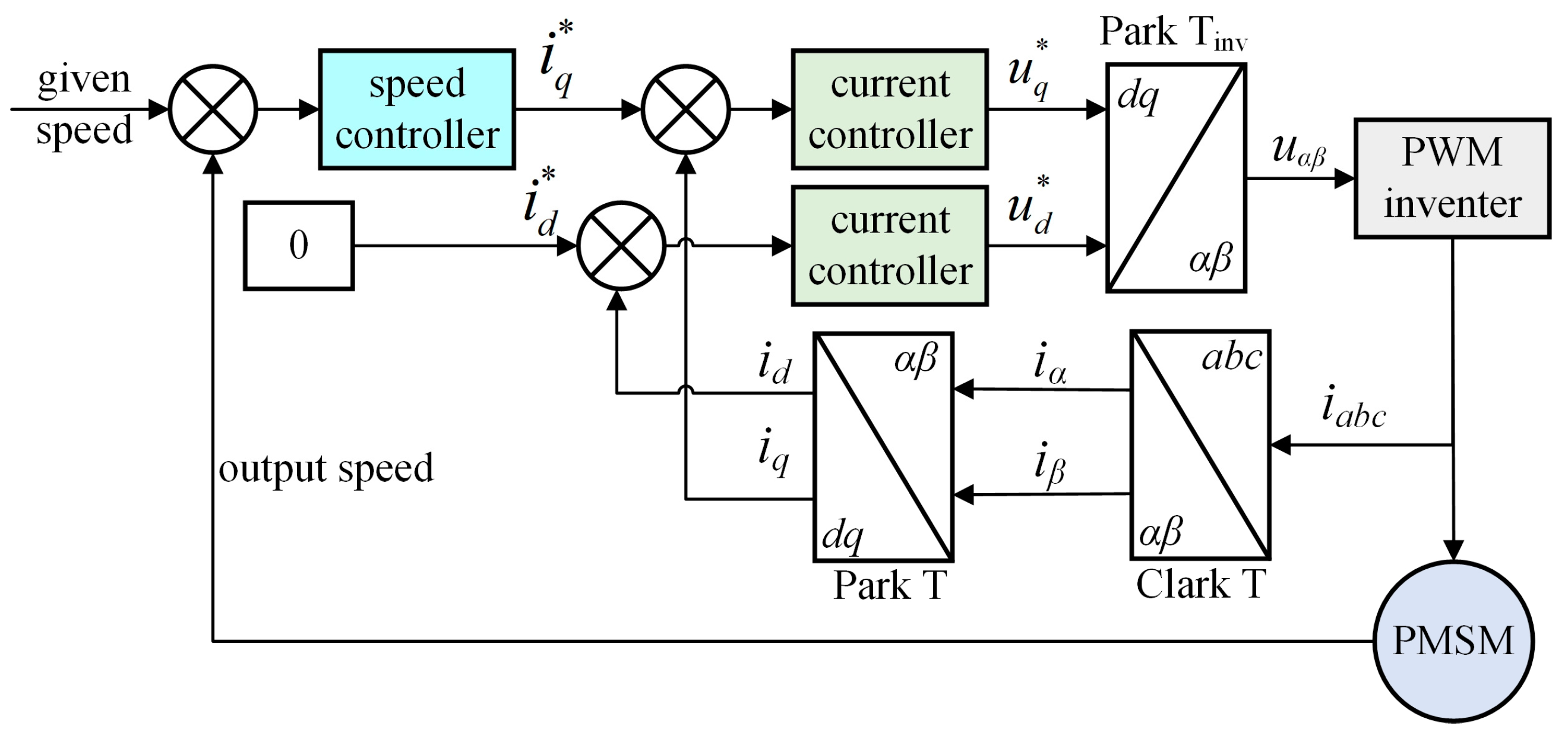
2.2. Vector-Control of Motor
- (1)
- Review of PI speed controller
- (2)
- Review of PI current controller
- (3)
- Review of SMC speed controller
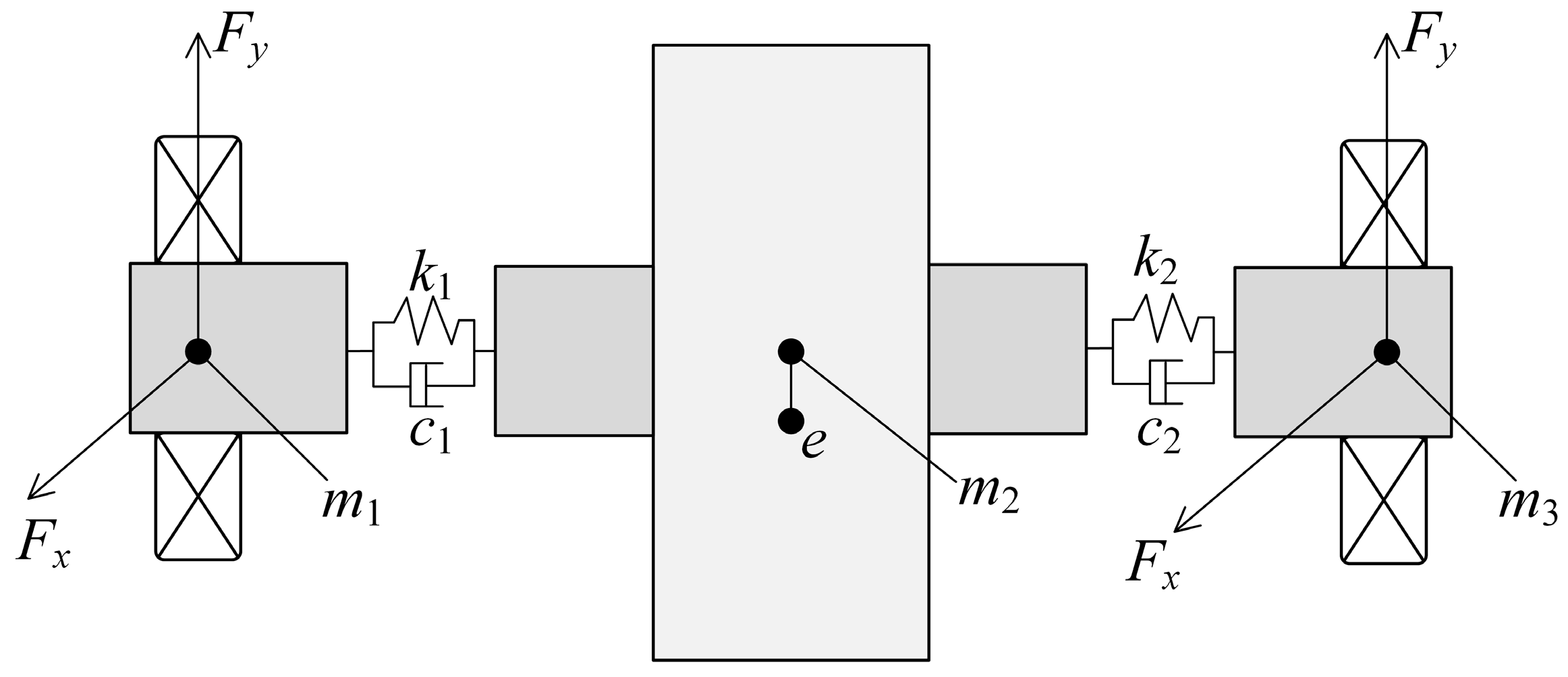
2.3. Mechanical Model of Motor Rotor
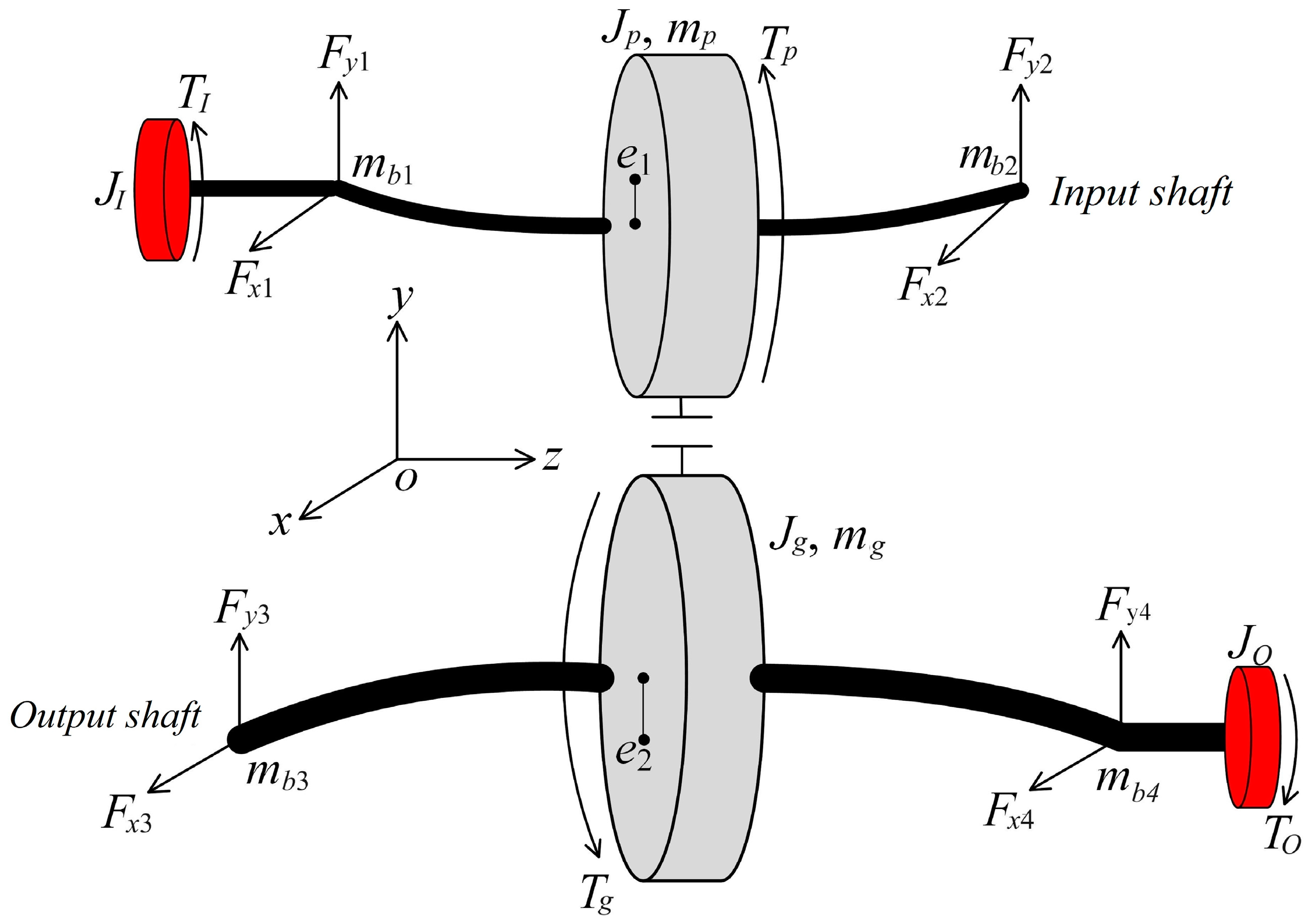
2.4. Dynamic Model of GTS
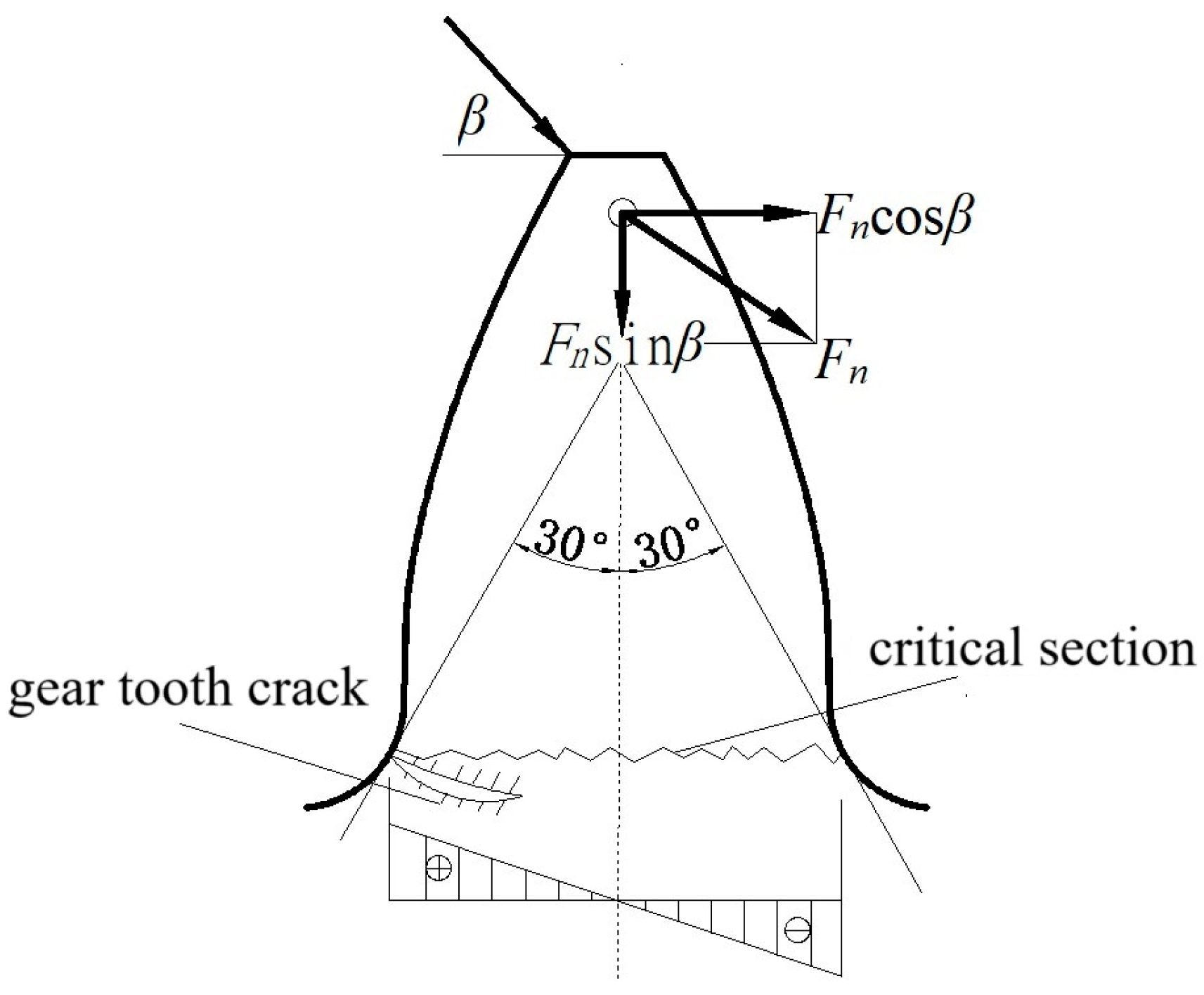
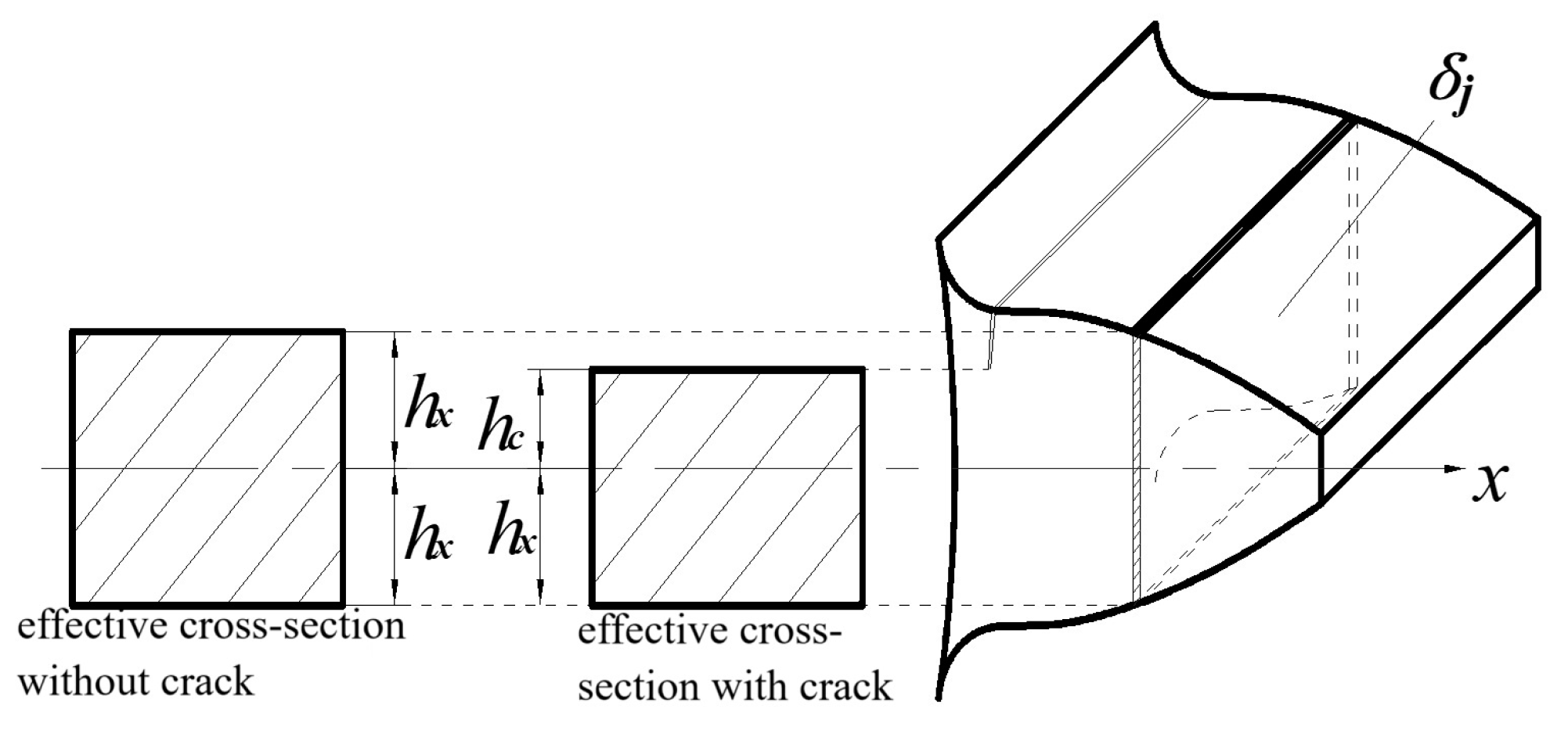
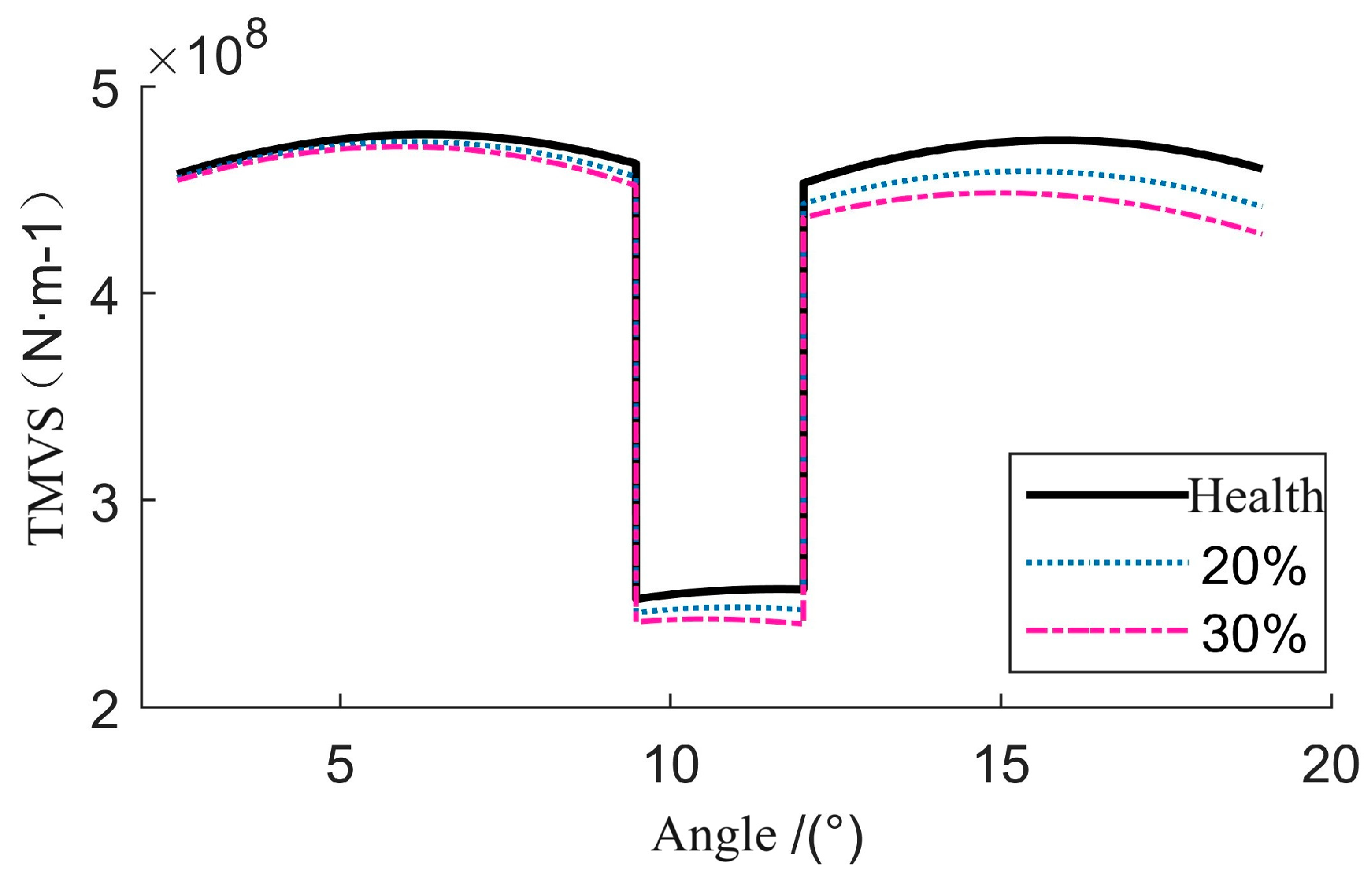
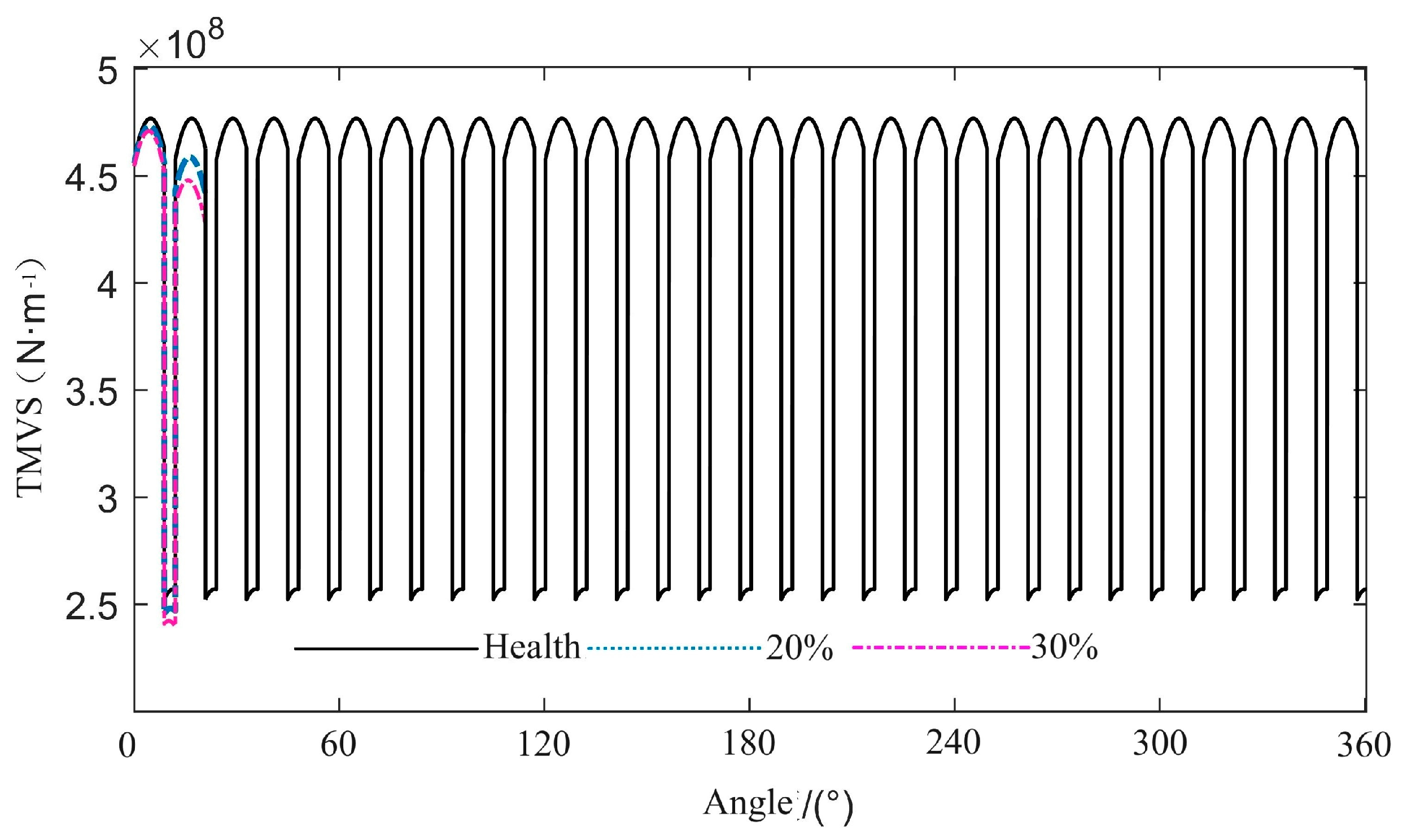
2.5. TVMS Considering Tooth Crack
- Double-tooth engagement: Initially, the cracked tooth engages in double-tooth engagement, maintaining contact with the preceding gear tooth.
- Transition to single-tooth engagement: As the engagement progresses, the cracked tooth transitions into a single-tooth engagement state.
- Reversion to double-tooth engagement: Upon the engagement of the subsequent gear tooth, the cracked tooth reverts to a double-tooth engagement configuration.
3. Verification of the Proposed Model
3.1. Introduction of Experimental Platform
3.2. Model Verification
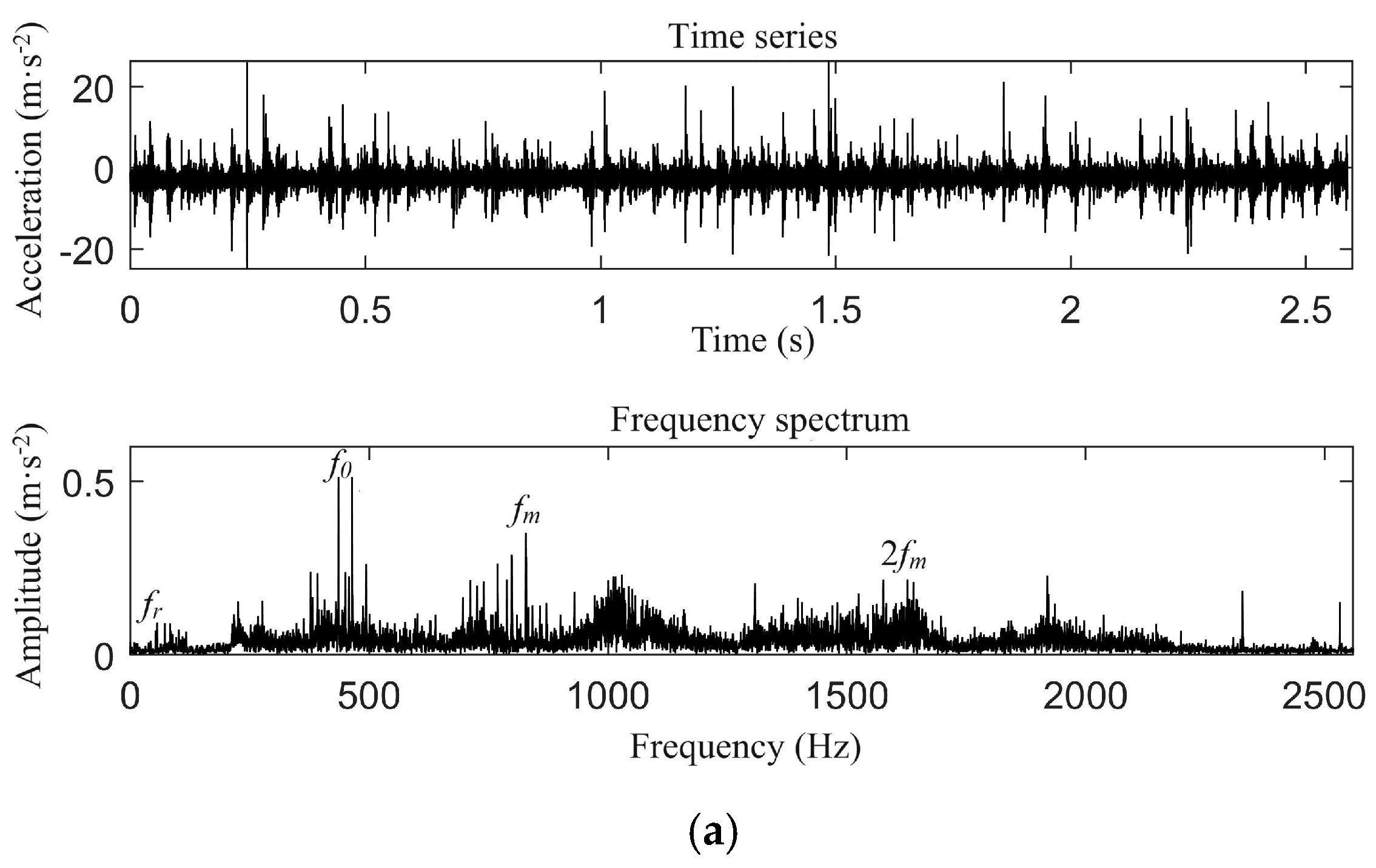
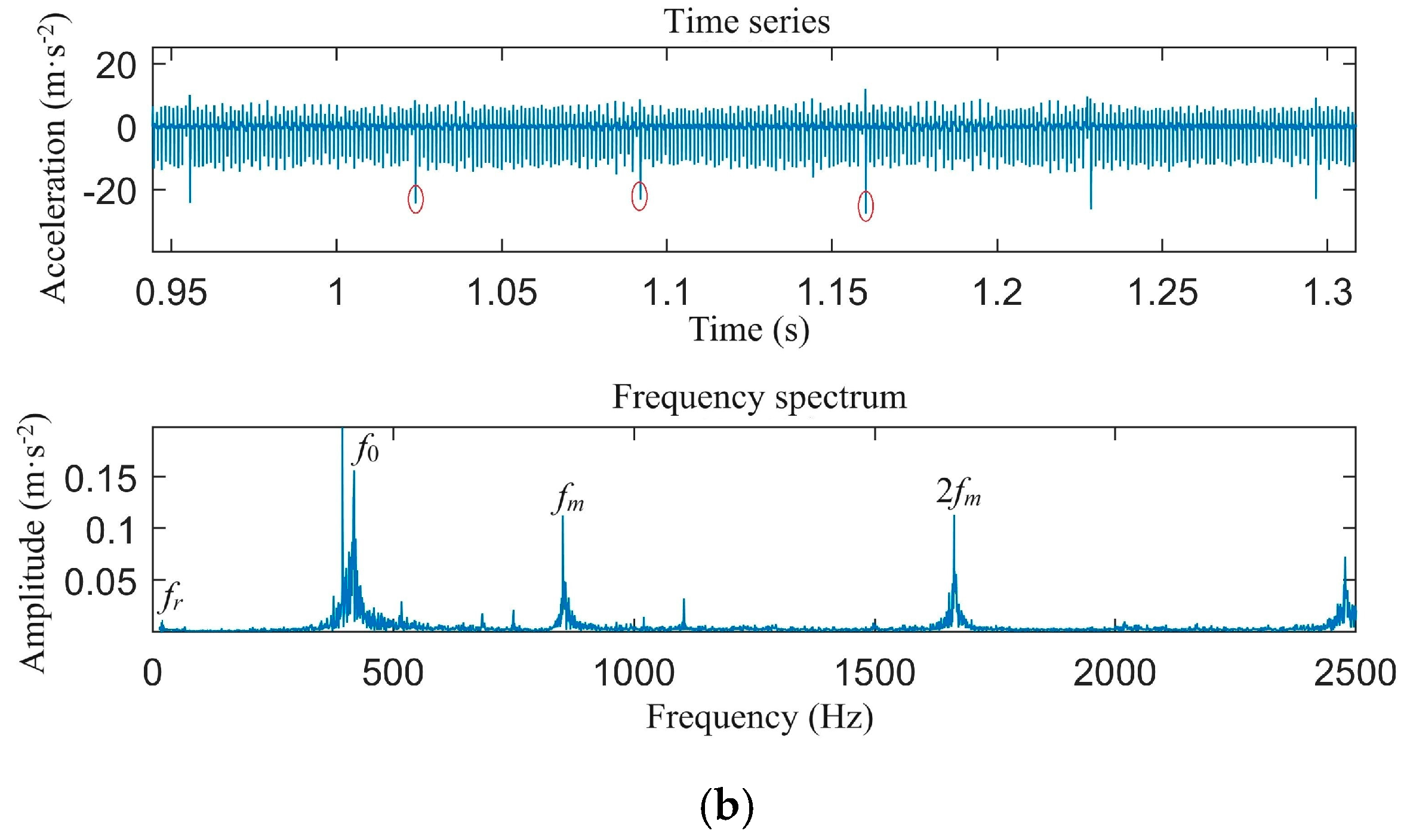
- Similarity in Time-Domain Signal: Both the simulation and experimental results display harmonic vibration patterns, suggesting that the simulation model accurately represents the system dynamics.
- Difference in Fluctuation Amplitude: The experimental results exhibit larger vibration acceleration amplitudes compared to the simulation, likely due to the complexities inherent in the real-world experimental setup.
- Consistency in Frequency Components: Both the simulation and experimental results identify the same primary frequency components, including the rotational frequency (fr), meshing frequency (fm), and twice of meshing frequency (2fm).
- Comparison of Sideband Components: The simulation results display fewer sidebands around the primary frequency components than the experimental results, highlighting the idealized conditions of the simulation model.
- Simulation of Tooth Root Cracks: In a healthy system, the rotational frequency components are minimal. However, with a tooth root crack, the time-domain graph exhibits periodic harmonics, and the rotational frequency becomes more pronounced in the frequency spectrum.
4. Electromechanical Coupling Dynamics Simulation
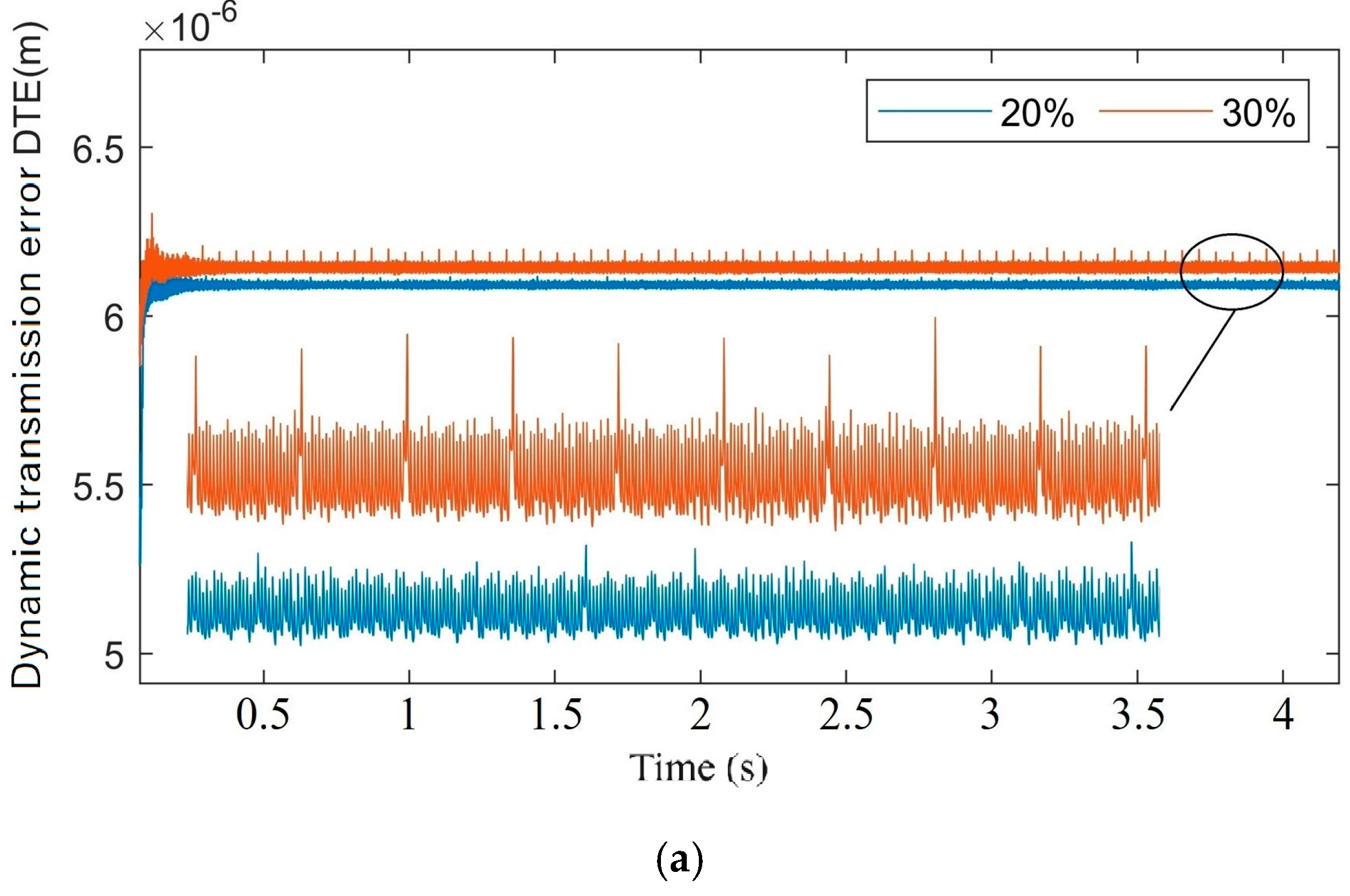
4.1. The Effect of Cracks on Gear Dynamics
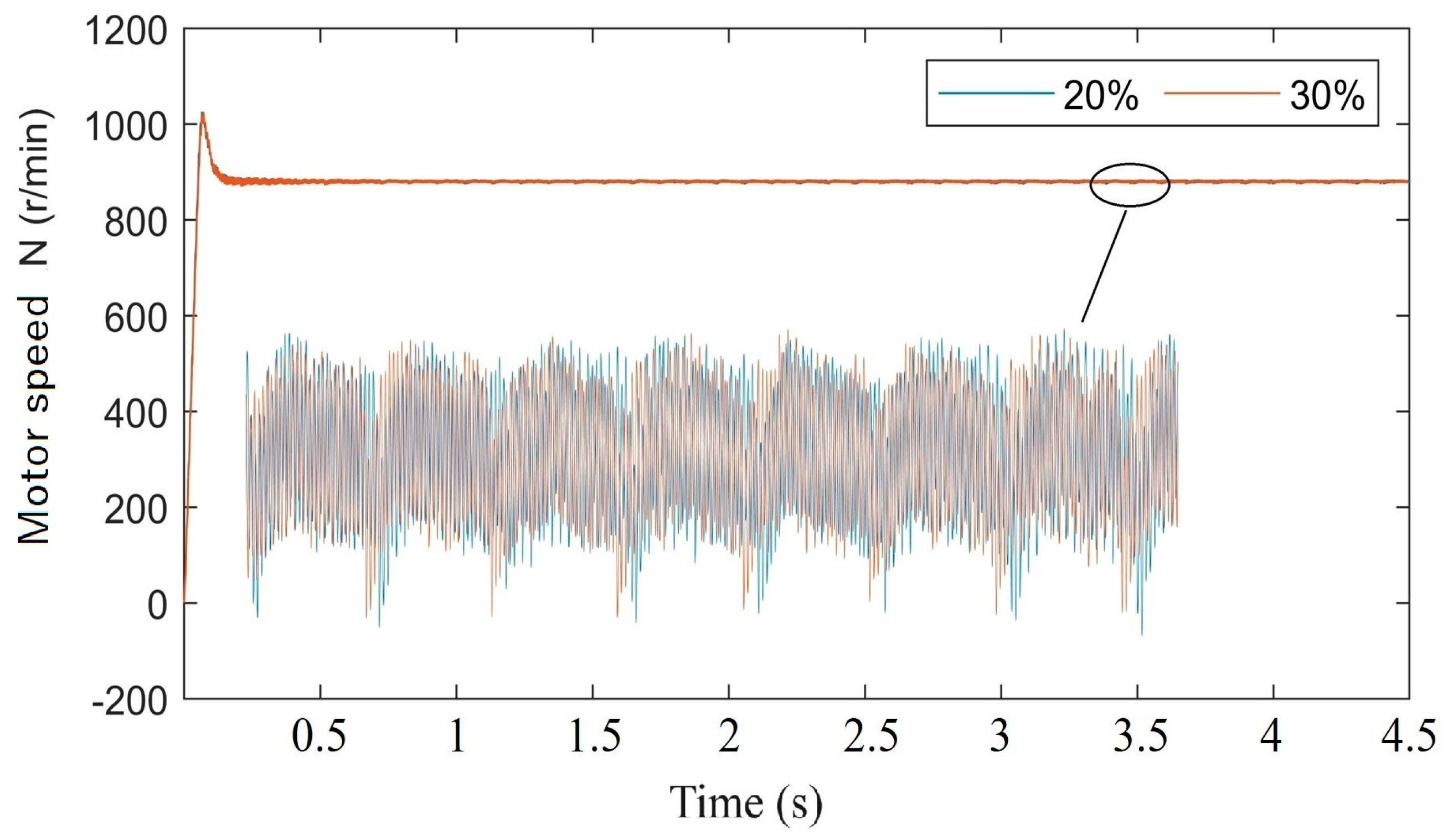
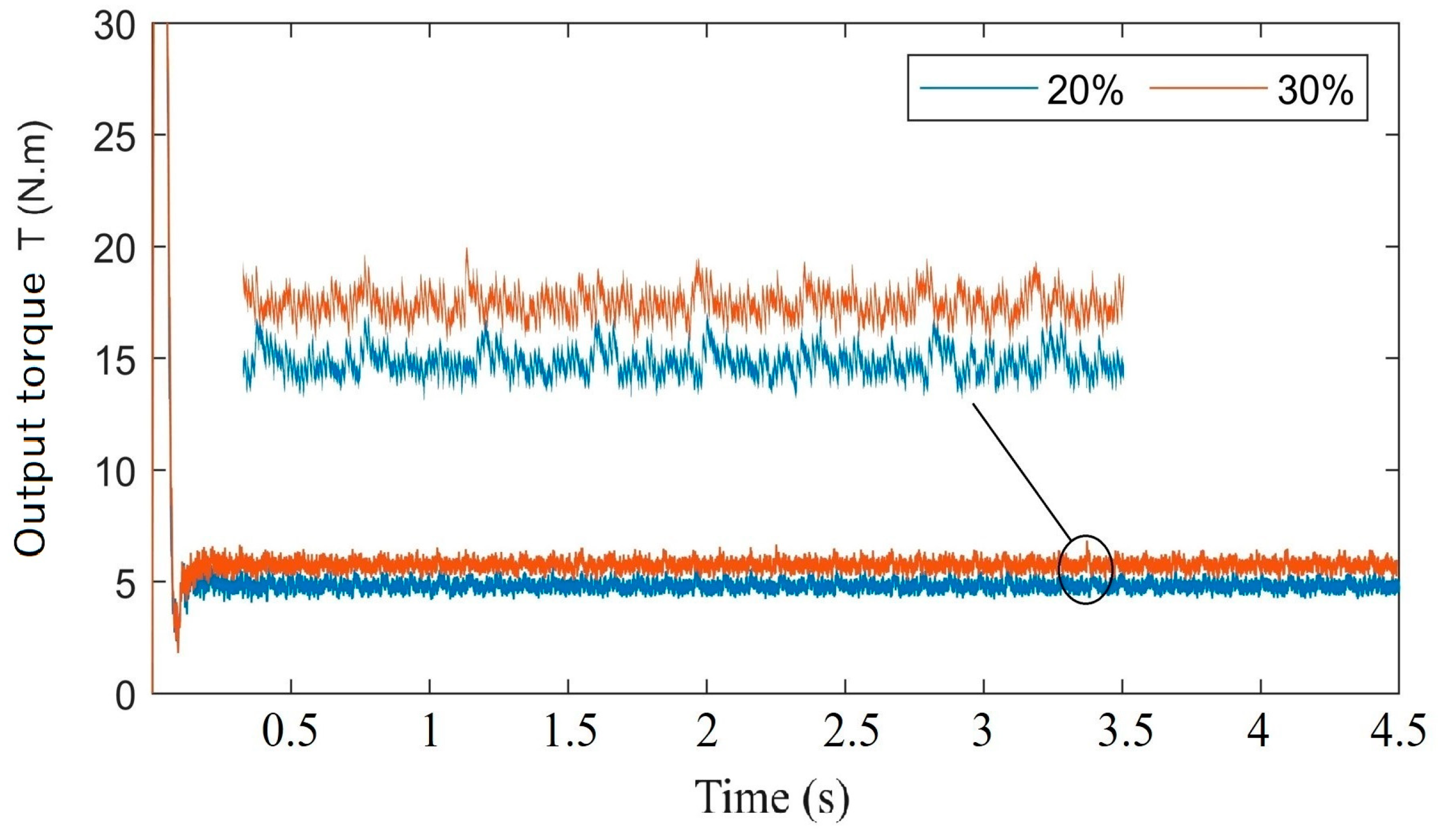
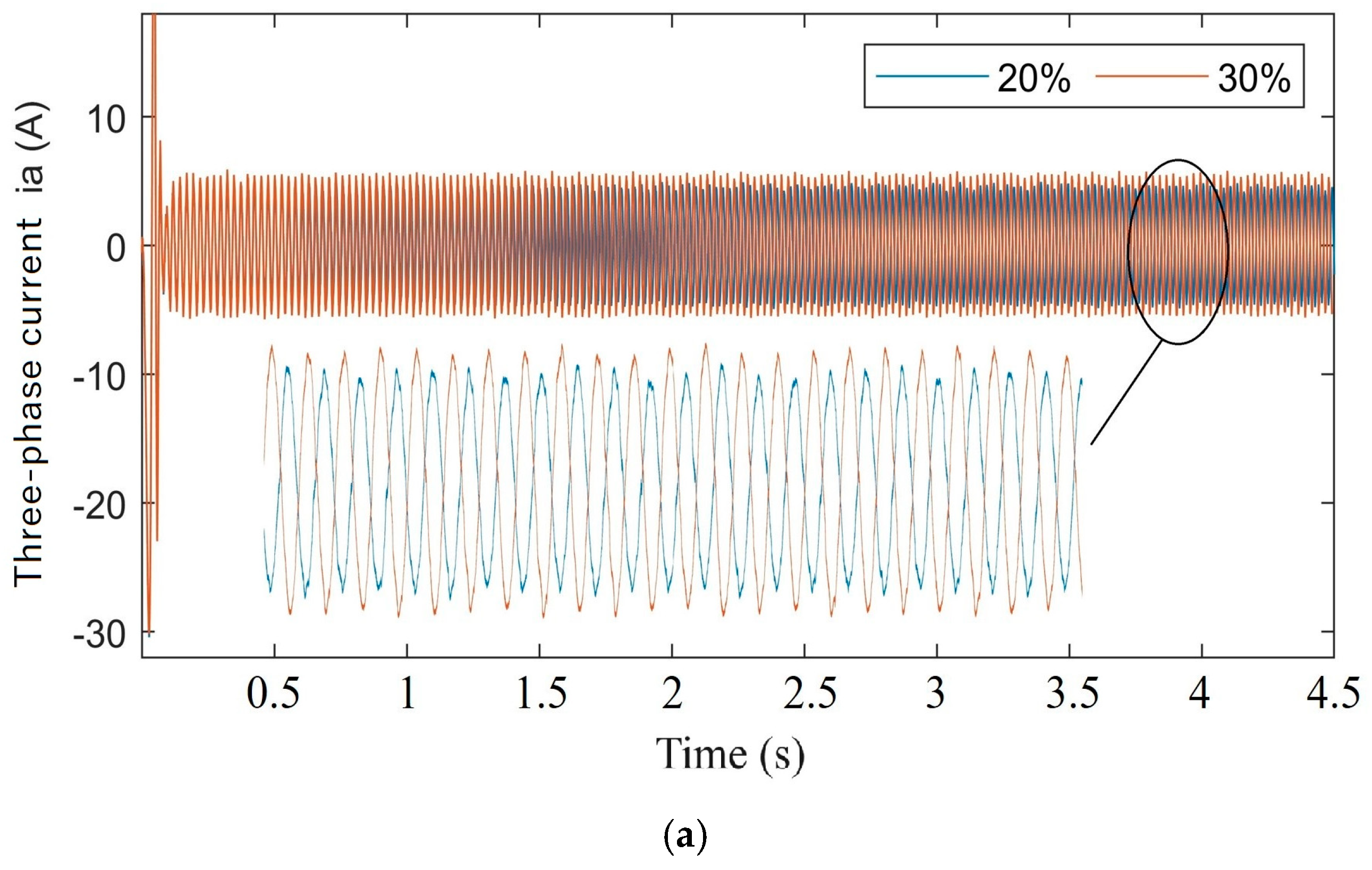
4.2. The Effect of Cracks on Motor Dynamics
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Calculation of TVMS
- Local Deformation (δL): Resulting from contact between the teeth.
- 2.
- Gear Body Contribution (δFB): The effect of the gear body on tooth deflection.
- 3.
- Fillet Deflection (δFF): In the direction of the applied tooth load.
- 4.
- Basic Deflection (δB): Includes bending, shearing, and axial deformation of the tooth as a beam.
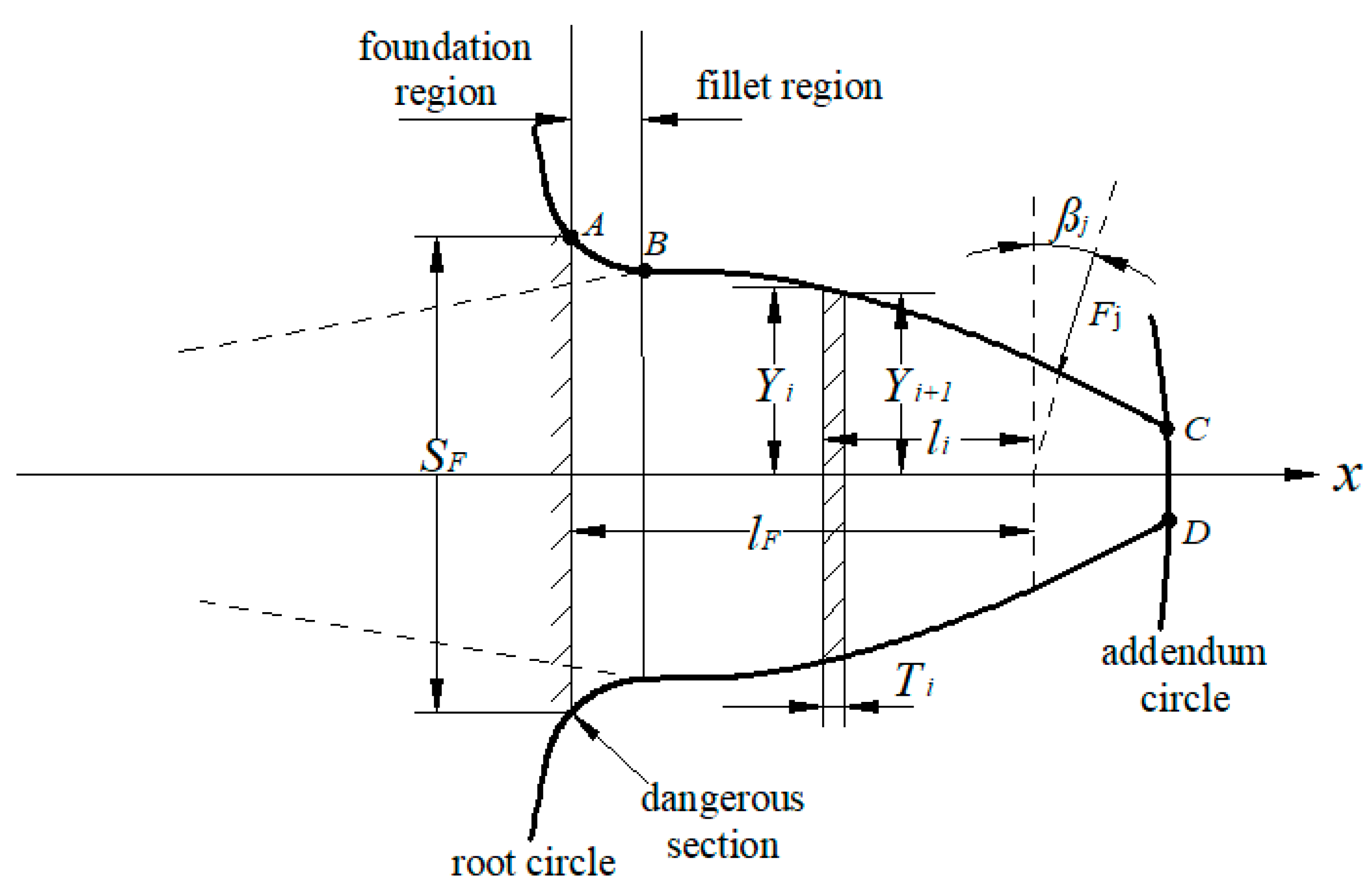
Appendix B. Calculation of Other Nonlinear Parameters in GTS
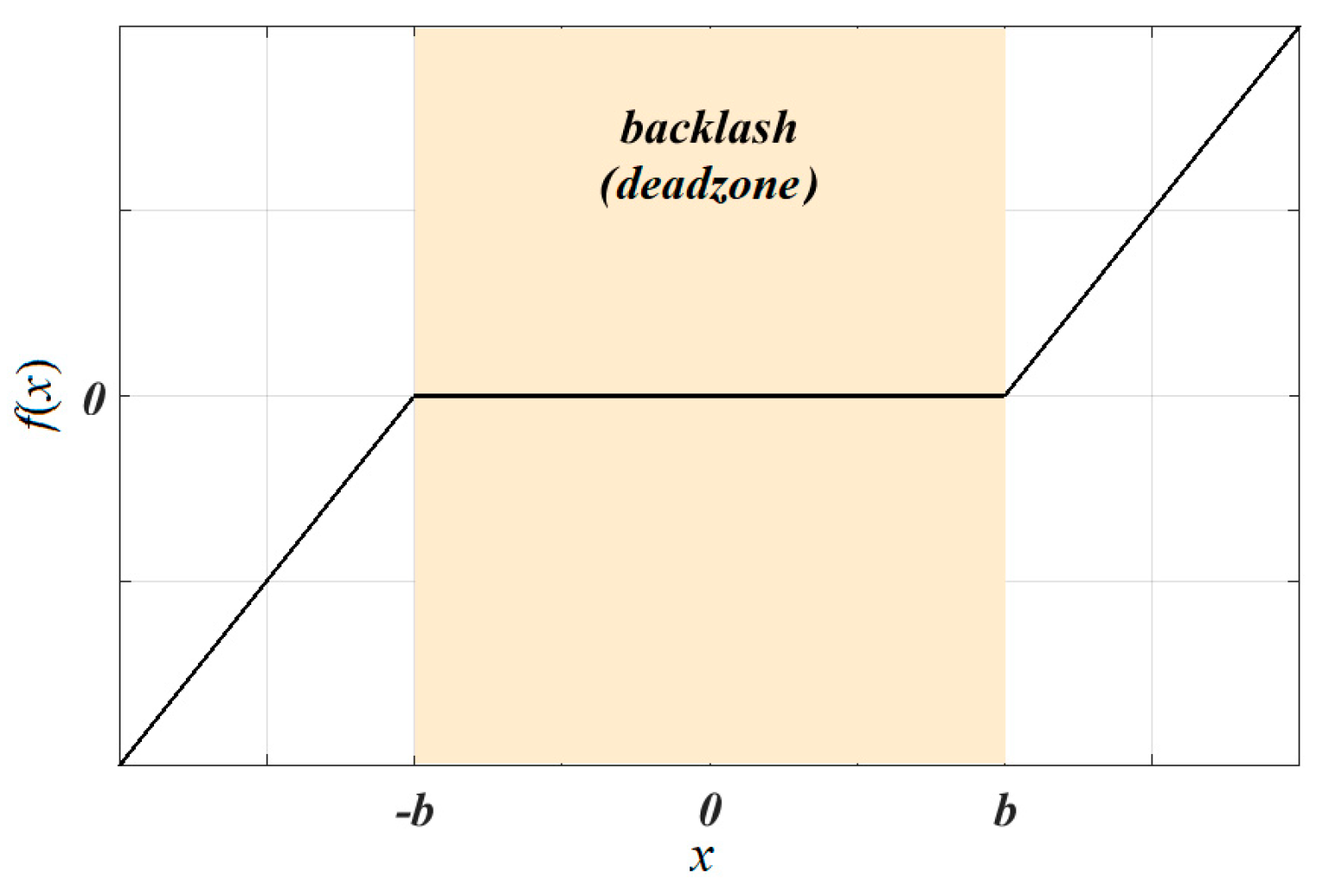
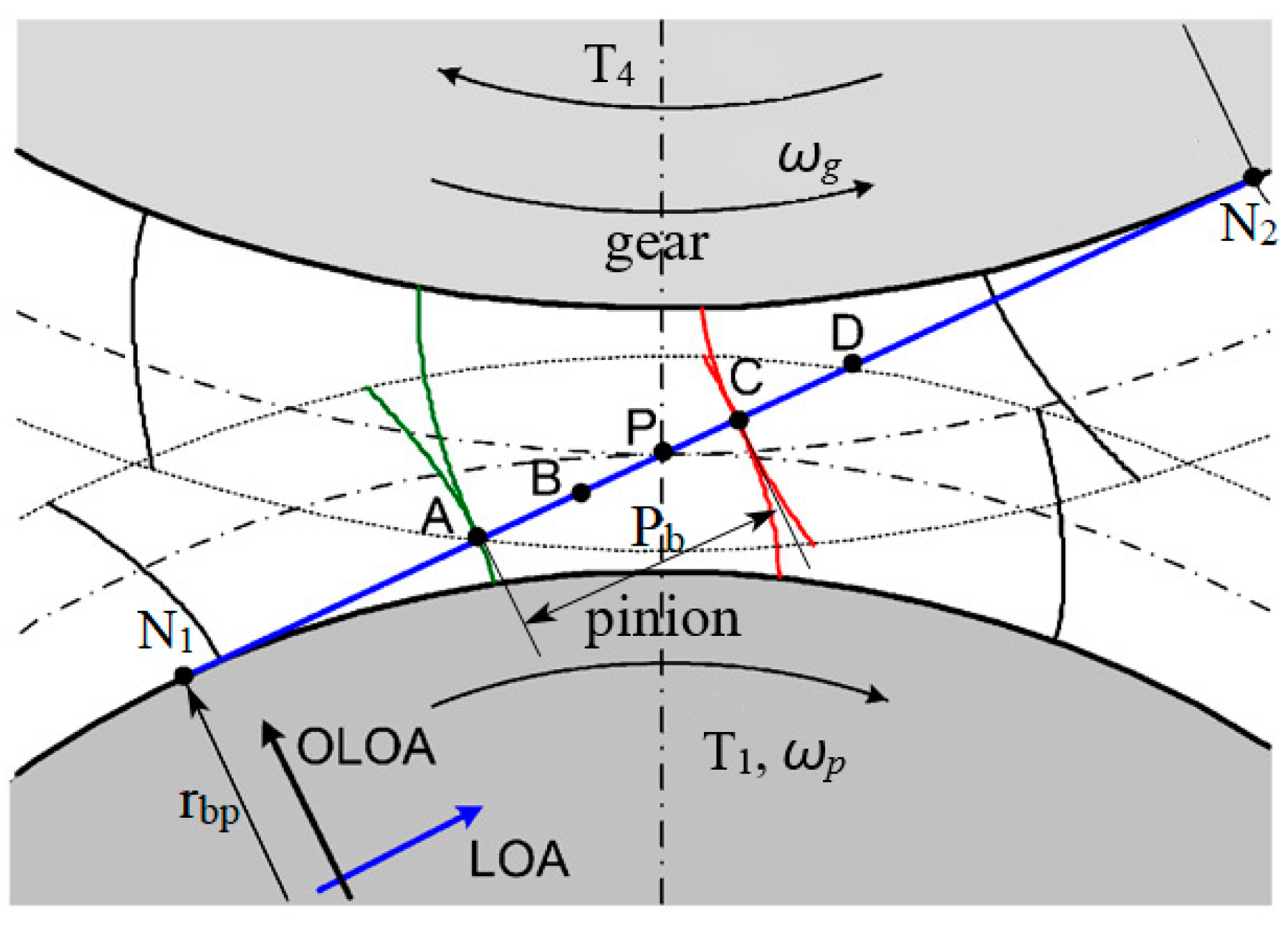
References
- Mohammed, O.D.; Rantatalo, M. Gear fault models and dynamics-based modelling for gear fault detection—A review. Eng. Fail. Anal. 2020, 117, 104798. [Google Scholar] [CrossRef]
- Cooley, C.G.; Parker, R.G. A review of planetary and epicyclic gear dynamics and vibrations research. Appl. Mech. Rev. 2014, 66, 040804. [Google Scholar] [CrossRef]
- Husain, I.; Ozpineci, B.; Islam, S.; Gurpinar, E.; Su, G.J.; Yu, W.; Chowdhury, S.; Xue, L.; Rahman, D.; Sahu, R. Electric drive technology trends, challenges, and opportunities for future electric vehicles. Proc. IEEE 2021, 109, 1039–1059. [Google Scholar] [CrossRef]
- Zhu, L.Y.; Yang, W.J.; Gou, X.F.; Li, Z.F. Dynamic characteristics of spur gear pair considering meshing impact and multi-state meshing. Meccanica 2023, 58, 619–642. [Google Scholar] [CrossRef]
- Szolc, T.; Konowrocki, R.; Michajłow, M.; Pręgowska, A. An investigation of the dynamic electromechanical coupling effects in machine drive systems driven by asynchronous motors. Mech. Syst. Signal Process. 2014, 49, 118–134. [Google Scholar] [CrossRef]
- Liu, C.; Wang, L.; Zhang, T.; Chen, X.; Ge, S. Electromechanical dynamic analysis for powertrain of off-grid switched-reluctance wind turbine hydrogen production system. Renew. Energy 2023, 208, 214–228. [Google Scholar] [CrossRef]
- Chen, R.; Qin, D.; Liu, C. Dynamic modelling and dynamic characteristics of wind turbine transmission gearbox-generator system electromechanical-rigid-flexible coupling. Alex. Eng. J. 2023, 65, 307–325. [Google Scholar] [CrossRef]
- Jiang, S.; Li, W.; Wang, Y.; Yang, X.; Xu, S. Study on electromechanical coupling torsional resonance characteristics of gear system driven by PMSM: A case on shearer semi-direct drive cutting transmission system. Nonlinear Dyn. 2021, 104, 1205–1225. [Google Scholar] [CrossRef]
- Kumar, V.; Rai, A.; Mukherjee, S.; Sarangi, S.A. Lagrangian approach for the electromechanical model of single-stage spur gear with tooth root cracks. Eng. Fail. Anal. 2021, 129, 105662. [Google Scholar] [CrossRef]
- Ryali, L.; Talbot, D. A dynamic gear load distribution model for epicyclic gear sets with a structurally compliant planet carrier. Mech. Mach. Theory 2023, 181, 105225. [Google Scholar] [CrossRef]
- Zghal, B.; Graja, O.; Dziedziech, K.; Chaari, F.; Jablonski, A.; Barszcz, T.; Haddar, M. A new modeling of planetary gear set to predict modulation phenomenon. Mech. Syst. Signal Process. 2019, 127, 234–261. [Google Scholar] [CrossRef]
- Hao, L.; Li, W.; Zhang, X. Impact of Gear Modification on Gear Dynamic Characteristics. J. Fail. Anal. Prev. 2023, 23, 853–864. [Google Scholar] [CrossRef]
- Zhang, C.; Wei, J.; Hou, S.; Zhang, J. Scaling law of gear transmission system obtained from dynamic equation and finite element method. Mech. Mach. Theory 2021, 159, 104285. [Google Scholar] [CrossRef]
- Zhou, C.; Jiang, X.; Su, J.; Liu, Y.; Hou, S. Injection lubrication for high-speed helical gears using the overset mesh method and experimental verification. Tribol. Int. 2022, 173, 107642. [Google Scholar] [CrossRef]
- Jedliński, Ł. Influence of gear eccentricity with non-parallel axis on the dynamic behaviour of a gear unit using a gear slice model with 26 degrees of freedom. Adv. Sci. Technol. Res. J. 2024, 18, 88–102. [Google Scholar] [CrossRef]
- Bartelmus, W. Gearbox dynamic multi-body modelling for condition monitoring under the case of varying operating condition. J. Coupled Syst. Multiscale Dyn. 2014, 2, 224–237. [Google Scholar] [CrossRef]
- Sakaridis, E.; Spitas, V.; Spitas, C. Non-linear modeling of gear drive dynamics incorporating intermittent tooth contact analysis and tooth eigenvibrations. Mech. Mach. Theory 2019, 136, 307–333. [Google Scholar] [CrossRef]
- Gong, H.; Shu, R.; Xiong, Y.; Xie, Z.; Huang, J.; Tan, R.; Yin, Q.; Zou, Z. Dynamic response analysis of a motor–gear transmission system considering the rheological characteristics of magnetorheological fluid coupling. Nonlinear Dyn. 2023, 111, 13781–13806. [Google Scholar] [CrossRef]
- Fateh, F.; White, W.N.; Gruenbacher, D. Torsional vibrations mitigation in the drivetrain of DFIG-based grid-connected wind turbine. IEEE Trans. Ind. Appl. 2017, 53, 5760–5767. [Google Scholar] [CrossRef]
- Féki, N.; Clerc, G.; Velex, P. Gear and motor fault modeling and detection based on motor current analysis. Electr. Power Syst. Res. 2013, 95, 28–37. [Google Scholar] [CrossRef]
- Lu, W.; Zhang, Y. Research on the effect of tooth root defects on the motor-multistage gear transmission system. Mech. Based Des. Struct. Mach. 2024, 53, 1561–1583. [Google Scholar] [CrossRef]
- Ge, S.; Hou, S.; Zhang, Z.; Wang, H.; Li, W. Electromechanical coupling dynamics of dual-motor electric drive system of hybrid electric vehicles. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024, 09544070241230703. [Google Scholar] [CrossRef]
- Marzebali, M.H.; Kia, S.H.; Henao, H.; Capolino, G.A.; Faiz, J. Planetary gearbox torsional vibration effects on wound-rotor induction generator electrical signatures. IEEE Trans. Ind. Appl. 2016, 52, 4770–4780. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, V.; Chandan, P.U.; Sarangi, S. Electromechanical Modelling and Multi Faults Diagnosis of Straight Bevel Gear Pair with Experimental Validation. J. Vib. Eng. Technol. 2024, 12, 79–92. [Google Scholar] [CrossRef]
- Han, Q.; Jiang, Z.; Kong, Y.; Wang, T.; Chu, F. Motor current model for detecting localized defects in planet rolling bearings. IEEE Trans. Ind. Electron. 2022, 70, 9483–9494. [Google Scholar] [CrossRef]
- Ouyang, T.; Wang, G.; Cheng, L.; Wang, J.; Yang, R. Comprehensive diagnosis and analysis of spur gears with pitting-crack coupling faults. Mech. Mach. Theory 2022, 176, 104968. [Google Scholar] [CrossRef]
- Molaie, M.; Samani, F.S.; Zippo, A.; Iarriccio, G.; Pellicano, F. Spiral bevel gears: Bifurcation and chaos analyses of pure torsional system. Chaos Solit. Fractals 2023, 177, 114179. [Google Scholar] [CrossRef]
- Sang, M.; Huang, K.; Xiong, Y.; Han, G.; Cheng, Z. Dynamic modeling and vibration analysis of a cracked 3K-II planetary gear set for fault detection. Mech. Sci. 2021, 12, 847–861. [Google Scholar] [CrossRef]
- Chai, N.; Yang, M.; Ni, Q.; Xu, D. Gear fault diagnosis based on dual parameter optimized resonance-based sparse signal decomposition of motor current. IEEE Trans. Ind. Appl. 2018, 54, 3782–3792. [Google Scholar] [CrossRef]
- El Yousfi, B.; Soualhi, A.; Medjaher, K.; Guillet, F. Electromechanical modeling of a motor–gearbox system for local gear tooth faults detection. Mech. Syst. Signal Process. 2022, 166, 108435. [Google Scholar] [CrossRef]
- Sheng, L.; Sun, Q.; Li, W.; Ye, G. Research on gear crack fault diagnosis model based on permanent magnet motor current signal. ISA Trans. 2023, 135, 188–198. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, J.; Wang, K.; Liu, P. Nonlinear dynamic responses of locomotive excited by rail corrugation and gear time-varying mesh stiffness. Transport 2022, 37, 383–397. [Google Scholar] [CrossRef]
- Ottewill, J.R.; Ruszczyk, A.; Broda, D. Monitoring tooth profile faults in epicyclic gearboxes using synchronously averaged motor currents: Mathematical modeling and experimental validation. Mech. Syst. Signal Process. 2017, 84, 78–99. [Google Scholar] [CrossRef]
- Liu, X.; Hou, M. Dynamic Characteristic Analysis of Permanent Magnet Toroidal Motor. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 7174–7179. [Google Scholar]
- Ullah, K.; Guzinski, J.; Mirza, A.F. Critical review on robust speed control techniques for permanent magnet synchronous motor (PMSM) speed regulation. Energies 2022, 15, 1235. [Google Scholar] [CrossRef]
- Parvez, M.; Elias, M.F.M.; Rahim, N.A.; Blaabjerg, F.; Abbott, D.; Al-Sarawi, S.F. Comparative study of discrete PI and PR controls for single-phase UPS inverter. IEEE Access 2020, 8, 45584–45595. [Google Scholar] [CrossRef]
- Kim, H.; Sikanen, E.; Nerg, J.; Sillanpää, T.; Sopanen, J.T. Unbalanced magnetic pull effects on rotor dynamics of a high-speed induction generator supported by active magnetic bearings—Analysis and experimental verification. IEEE Access 2020, 8, 212361–212370. [Google Scholar] [CrossRef]
- Tsuha, N.A.H.; Cavalca, K.L. Stiffness and damping of elastohydrodynamic line contact applied to cylindrical roller bearing dynamic model. J. Sound Vib. 2020, 481, 115444. [Google Scholar] [CrossRef]
- Salah, A.A.; Dorrell, D.G.; Guo, Y. A review of the monitoring and damping unbalanced magnetic pull in induction machines due to rotor eccentricity. IEEE Trans. Ind. Appl. 2019, 55, 2569–2580. [Google Scholar] [CrossRef]
- Yao, Z.; Wang, J.; Zhao, Y. Dynamic responses and control of geared transmission system based on multibody modeling methodology. J. Vib. Control 2023, 29, 543–561. [Google Scholar] [CrossRef]
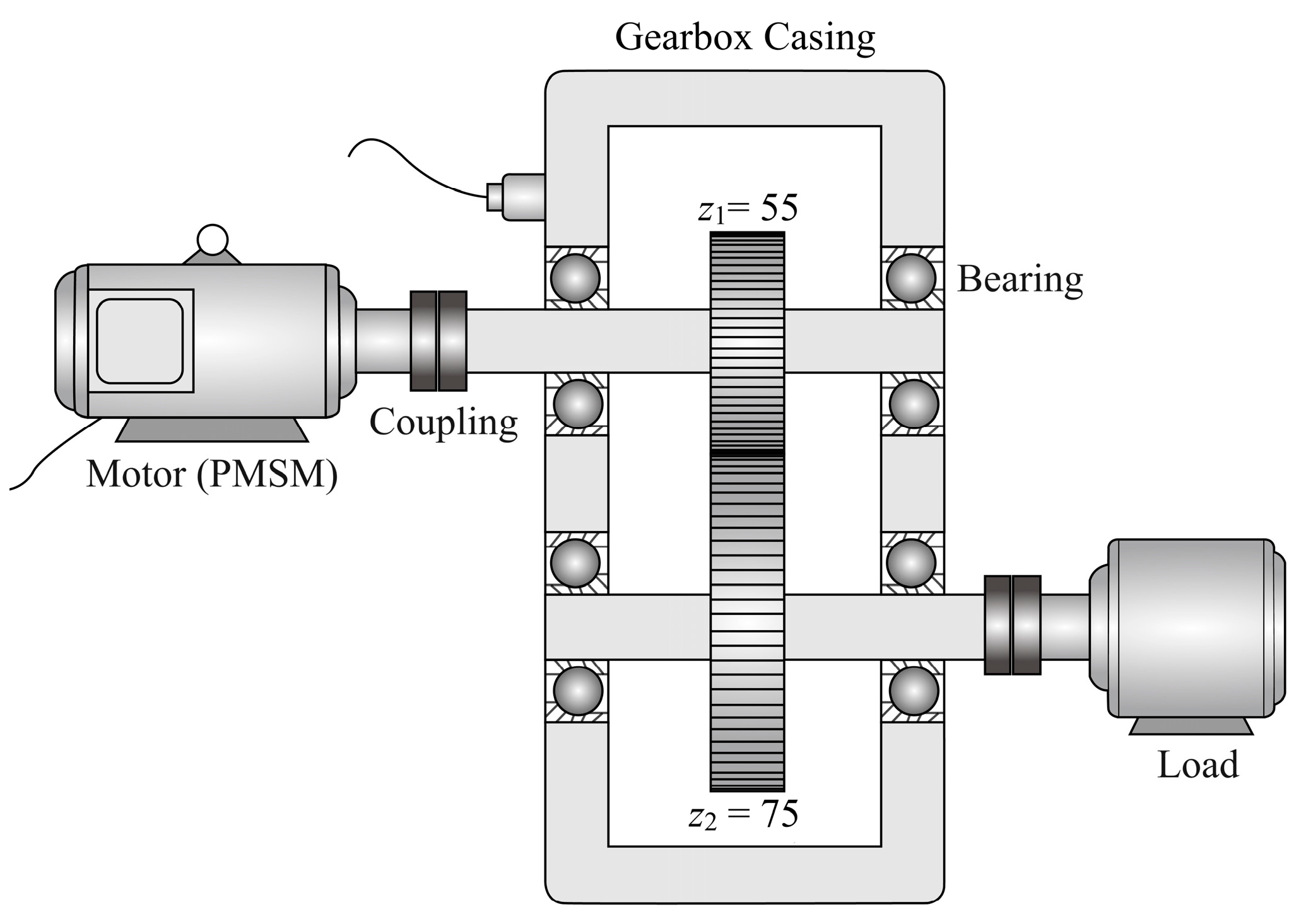






| Motor | Symbol | ||
|---|---|---|---|
| Number of Pole Pairs | np | 3 | |
| Flux Linkage (Wb) | ϕf | 0.175 | |
| Stator Resistance (Ω) | R | 2.875 | |
| Moment of Inertia (kg·m2) | J | 0.008 | |
| Stator Inductance (mH) | Ld, Lq | 8.5 | 8.5 |
| Gear | Symbol | Pinion | Gear |
| Number of teeth | z1, z2 | 55 | 75 |
| Mass (kg) | mp, mg | 2.328 | 3.937 |
| Moment of inertia (kg∙m2) | Jp, Jg | 0.0195 | 0.0614 |
| Modules (mm) | m | 2 | |
| Tooth width (mm) | B | 20 | |
| Pressure angle (deg) | α | 20 | |
| Pitch (mm) | Pn | 5.9 | |
| Contact ratio | ε | 1.797 | |
| Addendum coefficient | 1 | ||
| Tip clearance coefficient | λ | 0.25 | |
| Elastic modulus (Pa) | E | 210 G | |
| Poisson’s ratio | ν | 0.28 | |
| Mass density (kg·m−3) | ρ | 7800 | |
| Parameter | Symbol | Input Shaft | Output Shaft |
|---|---|---|---|
| Transverse stiffness (N/m) | kpx, kgy | 3 × 108 | 2 × 108 |
| Transverse damping (N∙s/m) | cgx, cgy | 1.1 × 103 | 0.9 × 103 |
| Torsional stiffness (N∙m/rad) | kI, kO | 9 × 106 | 7 × 106 |
| Torsional damping (N∙m∙s/rad) | cI, cO | 17 | 11 |
| Outer radius of the bearing (m) | R1, R2 | 0.09 | 0.04 |
| Inner radius of the bearing (m) | r1, r2 | 0.05 | 0.02 |
| Bearing clearance (mm) | γ01, γ02 | 0.02 | 0.05 |
| Number of bearing rollers | N1, N2 | 14 | 18 |
| Contact stiffness of supports (N/m3/2) | kb1, kb2 | 1.334 × 1010 | 1.056 × 1010 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, Z.; Lin, T.; Chen, Q.; Ren, H. Dynamic Response of Electromechanical Coupled Motor Gear System with Gear Tooth Crack. Machines 2024, 12, 918. https://doi.org/10.3390/machines12120918
Yao Z, Lin T, Chen Q, Ren H. Dynamic Response of Electromechanical Coupled Motor Gear System with Gear Tooth Crack. Machines. 2024; 12(12):918. https://doi.org/10.3390/machines12120918
Chicago/Turabian StyleYao, Zhaoyuan, Tianliang Lin, Qihuai Chen, and Haoling Ren. 2024. "Dynamic Response of Electromechanical Coupled Motor Gear System with Gear Tooth Crack" Machines 12, no. 12: 918. https://doi.org/10.3390/machines12120918
APA StyleYao, Z., Lin, T., Chen, Q., & Ren, H. (2024). Dynamic Response of Electromechanical Coupled Motor Gear System with Gear Tooth Crack. Machines, 12(12), 918. https://doi.org/10.3390/machines12120918






