Novel Dual Parallel-Connected-Pump Hydraulic System and Error Allocation Strategy for Segment Assembly
Abstract
1. Introduction
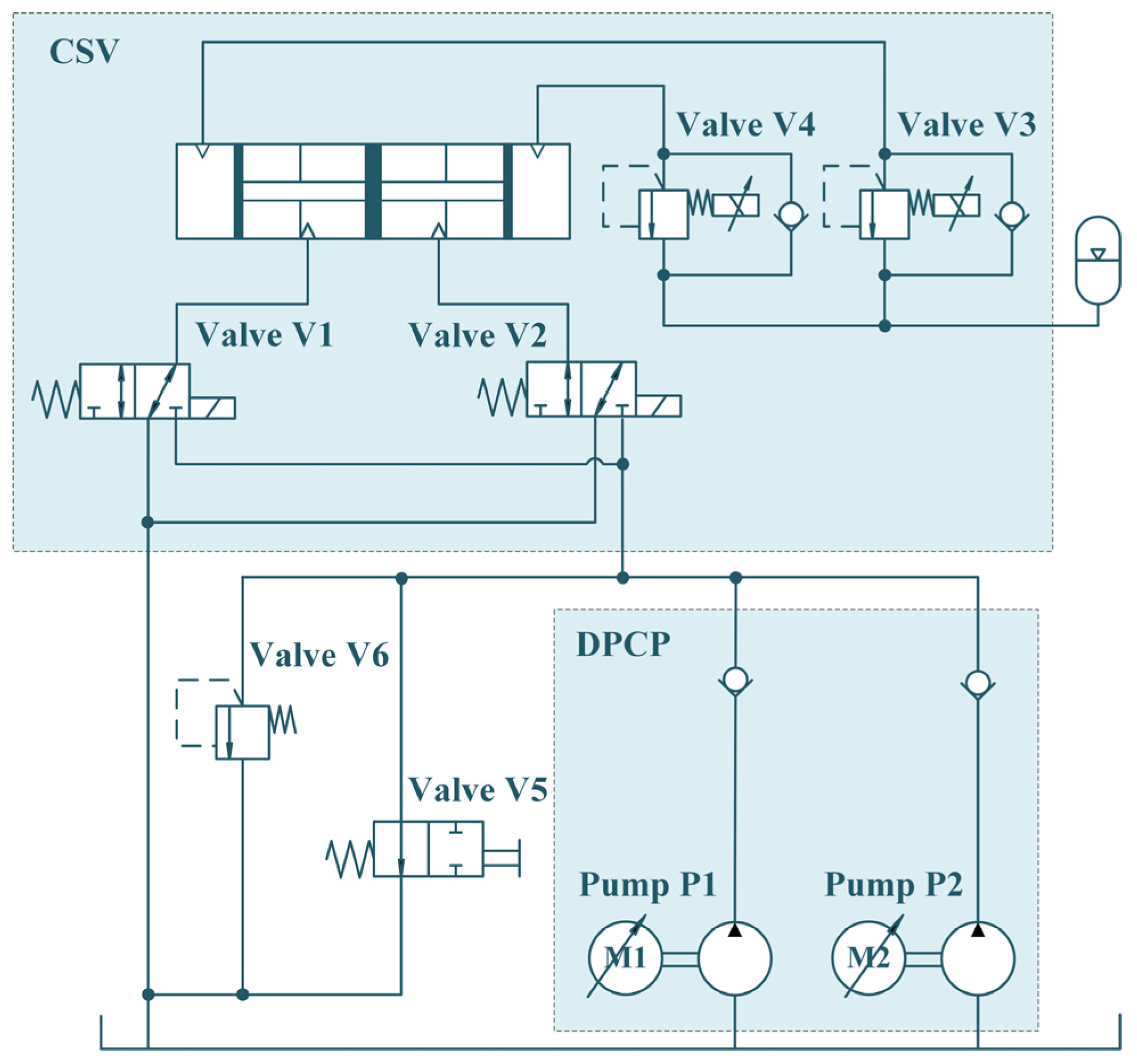
2. Design of Parallel-Connected-Pump Hydraulic System
3. Comparative Experiments
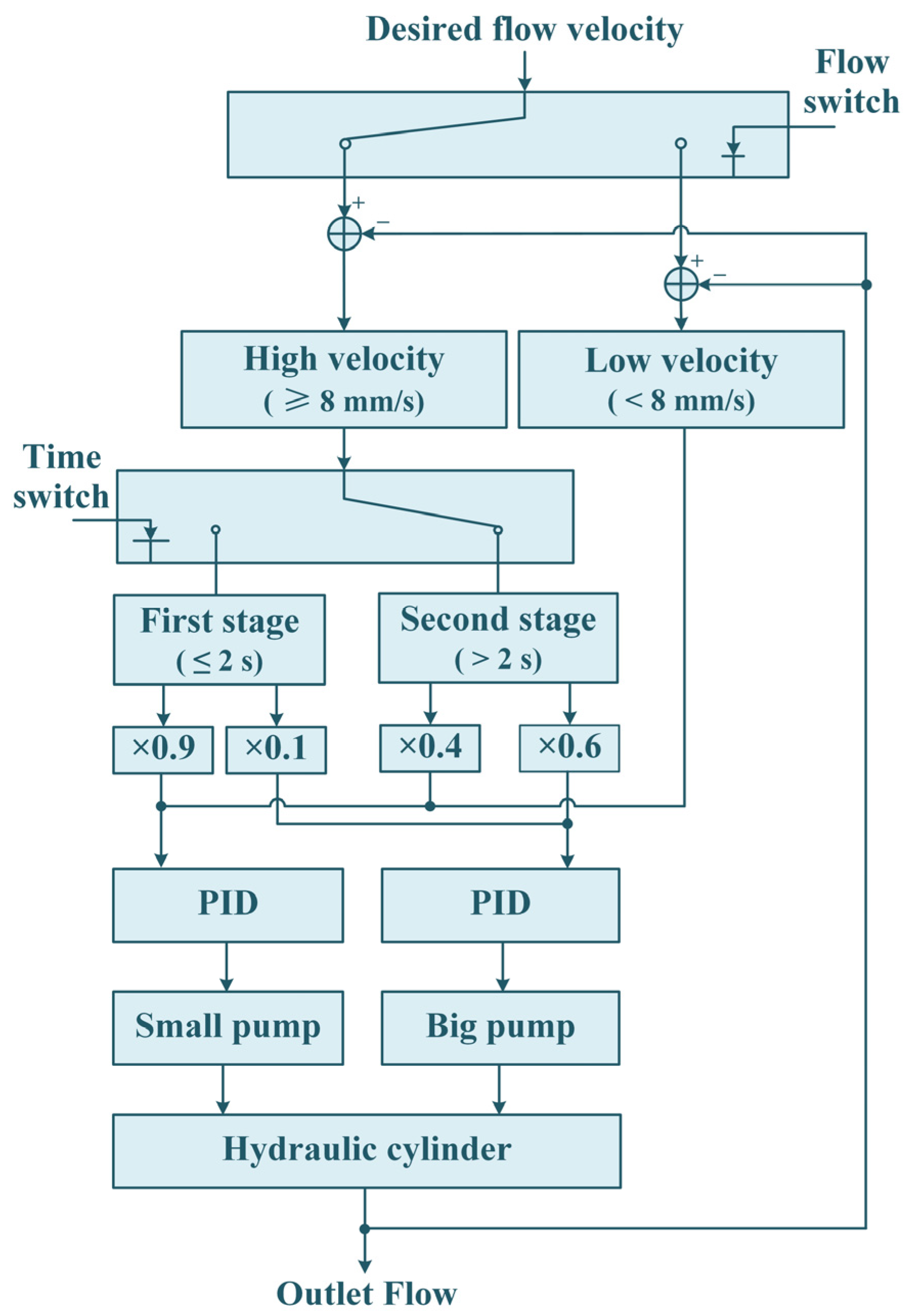
4. Two-Level Error Allocation Strategy
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hong, K.R.; Du, Y.L.; Kui, C.; Feng, H.H.; Jia, L.H.; Xu, F. Full-face tunnel boring machines (Shields/TBMs) in China: History, achievements, and prospects. Tunn. Constr. 2022, 42, 739–756. (In Chinese) [Google Scholar]
- Zheng, Z.; Luo, K.D.; Tan, X.Z.; Jia, L.H.; Xie, M.R.; Xie, H.B.; Jiang, L.J.; Gong, G.F.; Yang, H.Y.; Han, D. Autonomous steering control for tunnel boring machines. Autom. Constr. 2024, 159, 105259. [Google Scholar] [CrossRef]
- Zheng, Z.; Wang, F.; Gong, G.F.; Yang, H.Y.; Han, D. Intelligent technologies for construction machinery using data-driven methods. Autom. Constr. 2023, 147, 104711. [Google Scholar] [CrossRef]
- Lyu, L.; Liang, X.; Guo, J. Synchronization Control of a Dual-Cylinder Lifting Gantry of Segment Erector in Shield Tunneling Machine under Unbalance Loads. Machines 2021, 9, 152–174. [Google Scholar] [CrossRef]
- Li, Y.S.; Sun, Q.; Zhang, L.M.; Wang, Z.Y.; Feng, W.Q. Online multi-objective optimization for tunnel boring machine segment assembly considering stress concentration. Autom. Constr. 2023, 156, 105127. [Google Scholar] [CrossRef]
- Zhang, W.J.; Yang, Y.; Zhang, C.; Zhang, G.L.; He, L.C.; Lyu, J.R. Dynamic Autonomous Deviation Correction of Super-large Diameter Shield Tunnel Rings Based on Multi-objective Control Techniques. China J. Highw. Transp. 2023, 36, 231–234. [Google Scholar]
- Liu, C.Y.; Wu, J.; Jiang, X.L.; Gu, Y.F.; Xie, L.Q.; Huang, Z.R. Automatic assembly of prefabricated components based on vision-guided robot. Autom. Constr. 2024, 162, 105385. [Google Scholar] [CrossRef]
- Tshimbombo, T.; Perry, M.; Dow, H.; McAlorum, J.; Hoy, C.; Litina, C. Automated Manufacturing of tunnel segment. In Proceedings of the Conference on Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems, Long Beach, CA, USA, 13–16 March 2023. [Google Scholar]
- Du, C.D.; Du, Y.H.; Huang, X.F. Control Technology for Segment Dislocation and Attitude of Large-Diameter Shield Tunnels. Tunn. Constr. 2024, 44, 1510–1519. (In Chinese) [Google Scholar]
- Xie, P.; Chen, K.; Zhu, Y.; Luo, H. Dynamic parametric modeling of shield tunnel: A WebGL-based framework for assisting shield segment assembly point selection. Tunn. Undergr. Space Technol. 2023, 142, 105395. [Google Scholar] [CrossRef]
- Hu, M.; Sun, J.C.; Wu, B.J.; Wu, H.M.; Xu, Z.J. Shield Tunnel (Segment) Uplift Prediction and Control Based on Interpretable Machine Learning. Sustainability 2024, 16, 910. [Google Scholar] [CrossRef]
- Zheng, M.; Lan, M.; Zhu, C.L.; Lin, D.S.; Zhang, W.H. Overall Design for a Tunnel Segment Assembly System of Shield Machine Based on Virtual Reality Technology. In Proceedings of the 2019 IEEE International Conference on Architecture, Construction, Environment and Hydraulics (ICACEH), Xiamen, China, 20–22 December 2019. [Google Scholar]
- Guo, W.T.; Guo, W.Z.; Gao, F.; Mo, P.X. Innovative Group-Decoupling Design of a Segment Erector Based on GF Set Theory. Chin. J. Mech. Eng. 2013, 26, 264–274. [Google Scholar] [CrossRef]
- Yuan, Y.C.; Zhang, Y. Building of Fine-tuning Mechanism Posture and Kinematics Model for Shield Segment Erector. In Proceedings of the 2nd International Conference on Chemical, Material and Metallurgical Engineering (ICCMME 2012), Kunming, China, 15–16 December 2013. [Google Scholar]
- Wang, L.; Gong, G.; Yang, H.; Yang, X.; Hou, D. The Development of a High-Speed Segment Erecting System for Shield Tunneling Machine. IEEE ASME Trans. Mechatron. 2013, 18, 1713–1723. [Google Scholar] [CrossRef]
- Cui, G.; Zhang, D.; Zhou, H.; Zhang, Y. Operating dexterity optimization and analysis of a 3-DOF parallel manipulator for a tunnel segment assembly system. Int. J. Mech. Mater. Des. 2015, 11, 277–285. [Google Scholar] [CrossRef]
- Sun, H.; Tao, J.F.; Qin, C.J.; Dong, C.; Xu, S.; Zhuang, Q.W.; Liu, C.L. Multi-objective trajectory planning for segment assembly robots using a B-spline interpolation- and infeasible-updating non-dominated sorting-based method. Appl. Soft Comput. 2024, 152, 111216. [Google Scholar] [CrossRef]
- Zhang, Y.W.; Wei, B.; Cui, G.H.; Wang, N. Local Stiffness and Dexterity Analysis of a 3-SPS-S Orientation Fine-Tuning Manipulator for Segment Assembly Robots in Shield Tunneling Machines. Appl. Mech. Mater. 2012, 128, 904–908. [Google Scholar] [CrossRef]
- Shi, H.; Gong, G.; Yang, H. Drive system design and error analysis of the 6 degrees of freedom segment erector of shield tunneling machine. Front. Mech. Eng. 2011, 6, 369. [Google Scholar] [CrossRef]
- Zyada, Z.; Hasegawa, Y.; Fukuda, T. Multi-directional assembly of tunnel segments using a force controlled parallel link robot with fuzzy compensation. In Proceedings of the SICE 2003 Annual Conference (IEEE Cat. No.03TH8734), Fukui, Japan, 4–6 August 2003. [Google Scholar]
- Sun, W.; Du, J.N.; Wang, L.T.; Ma, H.H. High speed and low impact control method for electro-hydraulic system of segment erector in tunnel boring machine. J. Zhejiang Univ. Eng. Sci. 2017, 51, 1948–1958. (In Chinese) [Google Scholar]
- Zhou, Y.; Wang, Y.; Ding, L.; Love, P.E.D. Utilizing IFC for shield segment assembly in underground tunneling. Autom. Constr. 2018, 93, 178–191. [Google Scholar] [CrossRef]
- Kosuge, K.; Takeo, K.; Taguchi, D.; Fukuda, T.; Murakami, H. Task-oriented force control of parallel link robot for the assembly of segments of a shield tunnel excavation system. IEEE ASME Trans. Mechatron. 1996, 1, 250–258. [Google Scholar] [CrossRef]
- Wei, Q.; Tao, J.F.; Sun, H.; Liu, C.L. Mechanism Surrogate Based Model Predictive Control of Hydraulic Segment Assembly Robot with Sliding Friction. In Proceedings of the Intelligent Robotics and Applications, Hangzhou, China, 6 October 2023. [Google Scholar]
- Sun, H.; Tao, J.F.; Qin, C.J.; Yu, H.G.; Xu, S.; Zhuang, Q.W.; Liu, C.L. Optimal Energy Consumption and Response Capability Assessment for Hydraulic Servo Systems Containing Counterbalance Valves. J. Mech. Des. 2023, 145, 053501. [Google Scholar] [CrossRef]
- Sun, H.; Tao, J.F.; Qin, C.J.; Yu, H.G.; Liu, C.L. Dynamics Modeling and Bifurcation Analysis for Valve-Controlled Hydraulic Cylinder System Containing Counterbalance Valves. J. Vib. Eng. Technol. 2021, 9, 1941–1957. [Google Scholar] [CrossRef]
- Li, M.J.; Wei, J.H.; Fang, J.H.; Shi, W.Z.; Guo, K. Fuzzy impedance control of an electro-hydraulic actuator with an extended disturbance observer. Front. Inf. Technol. Electron. Eng. 2019, 20, 1221–1233. [Google Scholar] [CrossRef]
- Li, M.J.; Shi, W.Z.; Wei, J.H.; Fang, J.H.; Guo, K.; Zhang, Q. Parallel Velocity Control of an Electro-Hydraulic Actuator With Dual Disturbance Observers. IEEE Access 2019, 7, 56631–56641. [Google Scholar] [CrossRef]
- Long, M.; Hu, A.M.; Gao, Z.G.; He, X.J. Velocity and Load Characteristics Analysis of Pump-Control-Motor Hydraulic Drive System. In Proceedings of the International Conference on Manufacturing Engineering and Automation, Guangzhou, China, 7–9 December 2011. [Google Scholar]
- Zhu, T.; Xie, H.; Yang, H. Design and tracking control of an electro-hydrostatic actuator for a disc cutter replacement manipulator. Autom. Constr. 2022, 142, 104480. [Google Scholar] [CrossRef]
- Xiang, Y.S.; Li, R.Y.; Brach, C.; Liu, X.L.; Geimer, M. A Novel Algorithm for Hydrostatic-Mechanical Mobile Machines with a Dual-Clutch Transmission. Energies 2022, 15, 2095. [Google Scholar] [CrossRef]
- Xiang, Y.S.; Mutschler, S.; Brix, N.; Brach, C.; Geimer, M. Optimization of hydrostatic-mechanical transmission control strategy by means of torque control. In Proceedings of the 12th International Fluid Power Conference, Dresden, Germany, 12–14 October 2020. [Google Scholar]
- Mutschler, S.; Brix, N.; Xiang, Y.S. Torque Control for Mobile Machines. In Proceedings of the 11th International Fluid Power Conference, Aachen, Germany, 19–21 March 2018. [Google Scholar]
- Helian, B.B.; Chen, Z.; Yao, B. Precision Motion Control of a Servomotor-Pump Direct-Drive Electrohydraulic System With a Nonlinear Pump Flow Mapping. IEEE Trans. Ind. Electron. 2020, 67, 8638–8648. [Google Scholar] [CrossRef]
- Chen, Z.; Helian, B.B.; Zhou, Y.; Geimer, M. An integrated trajectory planning and motion control strategy of a variable rotational speed pump-controlled electro-hydraulic actuator. IEEE ASME Trans. Mechatron. 2022, 28, 588–597. [Google Scholar] [CrossRef]
- Lin, X.Z.; Xu, J.; Yu, J.C.; Zhang, X.L.; Zheng, Y.L.; Li, S.; Du, H. High-performance steering tracking control of open circuit variable-speed pump-controlled steering system for heavy-duty vehicles based on flow nonlinearity compensation. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024, 1–20. [Google Scholar] [CrossRef]








| Velocity (×mm/s) | Methods | ‖e‖mean (×mm) | ‖e‖max (×mm) |
|---|---|---|---|
| 1 | C1 | 0.179 | 0.602 |
| C2 | 0.463 | 1.069 | |
| 2 | C1 | 0.277 | 1.175 |
| C2 | 0.607 | 1.496 | |
| 3 | C1 | 0.364 | 1.669 |
| C2 | 0.630 | 1.496 | |
| 4 | C1 | 0.603 | 1.957 |
| C2 | 0.933 | 1.978 | |
| 5 | C1 | 0.472 | 2.657 |
| C2 | 1.135 | 2.802 | |
| 6 | C1 | 0.467 | 2.657 |
| C2 | 1.492 | 3.985 |
| Velocity (×mm/s) | Methods | ‖e‖mean (×mm) | ‖e‖max (×mm) |
|---|---|---|---|
| 7 | C1 | 1.744 | 4.027 |
| C2 | 2.388 | 6.106 | |
| 8 | C1 | 6.933 | 10.421 |
| C2 | 2.559 | 8.597 |
| Methods | ‖e‖mean (×mm) | ‖e‖max (×mm) |
|---|---|---|
| C1 | 6.933 | 10.421 |
| C2 | 2.559 | 8.597 |
| C3 | 1.412 | 3.818 |
| Velocity (×mm/s) | Second Proportion | ‖e‖mean (×mm) | ‖e‖max (×mm) |
|---|---|---|---|
| 9 | A1 | 1.589 | 5.208 |
| A2 | 1.094 | 3.662 | |
| A3 | 1.939 | 4.851 | |
| 10 | A1 | 1.614 | 4.807 |
| A2 | 1.352 | 4.540 | |
| A3 | 2.011 | 5.036 | |
| 11 | A1 | 1.974 | 6.580 |
| A2 | 1.555 | 5.799 | |
| A3 | 2.400 | 5.476 | |
| 12 | A1 | 2.167 | 8.054 |
| A2 | 1.699 | 7.007 | |
| A3 | 2.452 | 8.690 |
| Velocity (×mm/s) | Switch Timestamp (×s) | ‖e‖mean (×mm) | ‖e‖max (×mm) |
|---|---|---|---|
| 9 | S1 | 1.403 | 4.104 |
| S2 | 1.094 | 3.662 | |
| S3 | 2.005 | 4.314 | |
| 10 | S1 | 1.661 | 5.231 |
| S2 | 1.352 | 4.540 | |
| S3 | 1.971 | 5.121 | |
| 11 | S1 | 1.603 | 6.047 |
| S2 | 1.555 | 5.799 | |
| S3 | 2.147 | 6.770 | |
| 12 | S1 | 2.090 | 7.286 |
| S2 | 1.699 | 7.007 | |
| S3 | 2.092 | 7.479 |
| Velocity (×mm/s) | Methods | ‖e‖mean (×mm) | ‖e‖max (×mm) |
|---|---|---|---|
| 9 | C2 | 3.835 | 10.352 |
| C3 | 1.094 | 3.662 | |
| 10 | C2 | 4.740 | 12.767 |
| C3 | 1.352 | 4.540 | |
| 11 | C2 | 6.457 | 14.818 |
| C3 | 1.555 | 5.799 | |
| 12 | C2 | 9.827 | 17.728 |
| C3 | 1.699 | 7.007 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, L.; Zheng, Z.; Zhu, K.; Gong, G.; Yang, H.; Han, D. Novel Dual Parallel-Connected-Pump Hydraulic System and Error Allocation Strategy for Segment Assembly. Machines 2024, 12, 913. https://doi.org/10.3390/machines12120913
Jiang L, Zheng Z, Zhu K, Gong G, Yang H, Han D. Novel Dual Parallel-Connected-Pump Hydraulic System and Error Allocation Strategy for Segment Assembly. Machines. 2024; 12(12):913. https://doi.org/10.3390/machines12120913
Chicago/Turabian StyleJiang, Lijie, Zhe Zheng, Kaihao Zhu, Guofang Gong, Huayong Yang, and Dong Han. 2024. "Novel Dual Parallel-Connected-Pump Hydraulic System and Error Allocation Strategy for Segment Assembly" Machines 12, no. 12: 913. https://doi.org/10.3390/machines12120913
APA StyleJiang, L., Zheng, Z., Zhu, K., Gong, G., Yang, H., & Han, D. (2024). Novel Dual Parallel-Connected-Pump Hydraulic System and Error Allocation Strategy for Segment Assembly. Machines, 12(12), 913. https://doi.org/10.3390/machines12120913





