Multi-Objective Optimization Design of Dual-Spindle Component Based on Coupled Thermal–Mechanical–Vibration Collaborative Analysis
Abstract
1. Introduction
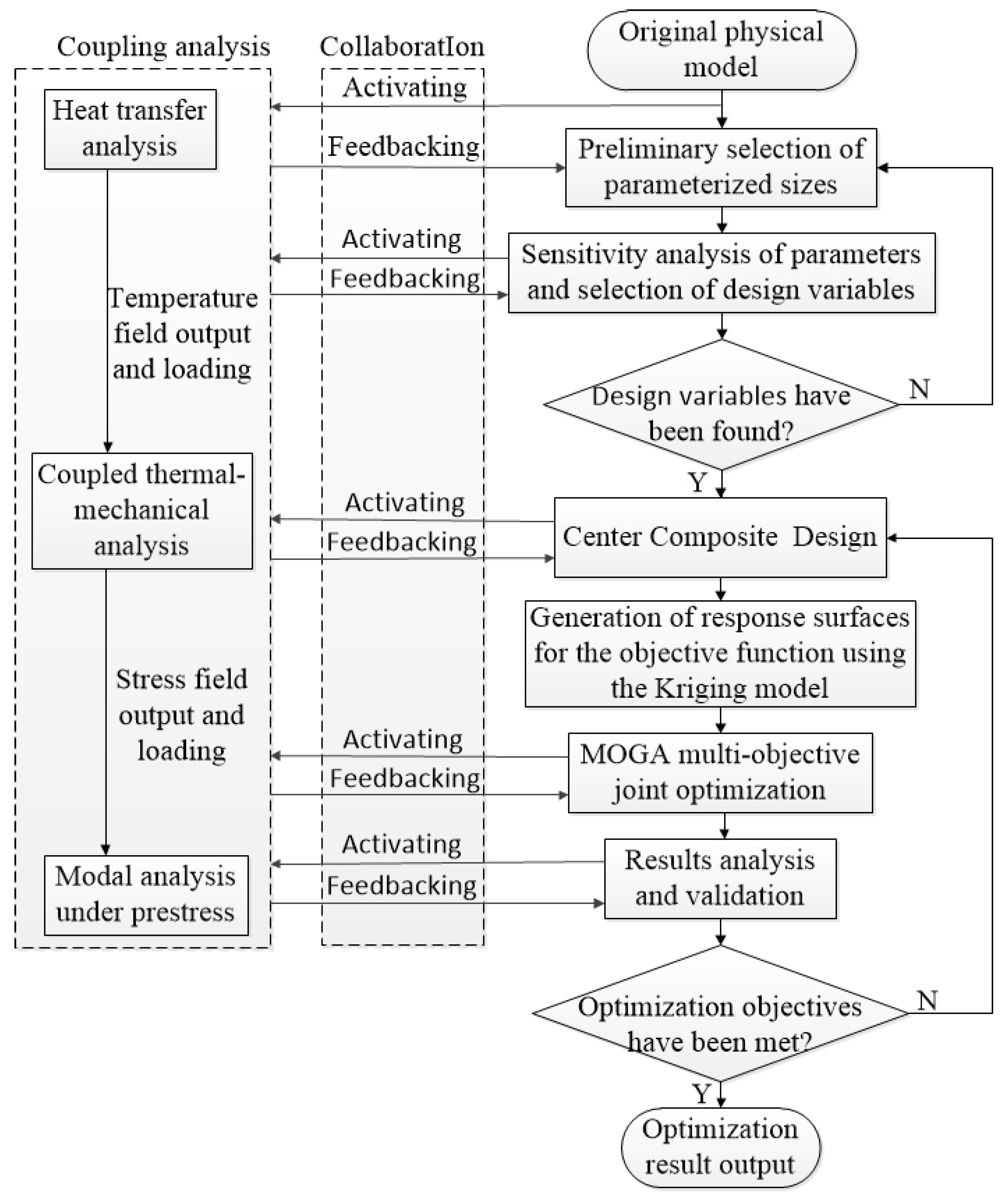
2. Optimization Method Based on Coupling Collaborative Analysis
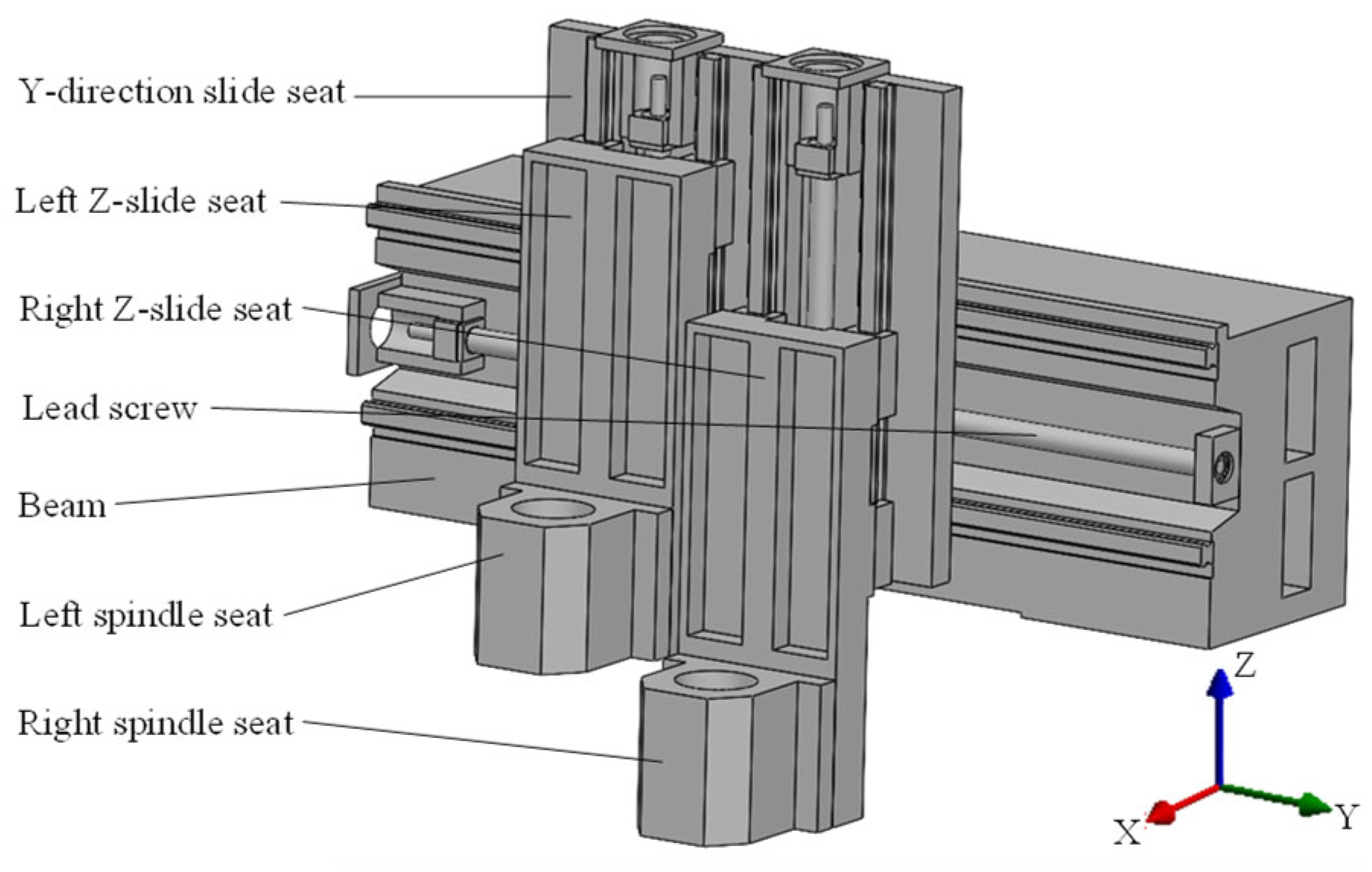
3. Load Analysis for Spindle Component of CNC Machine Tool
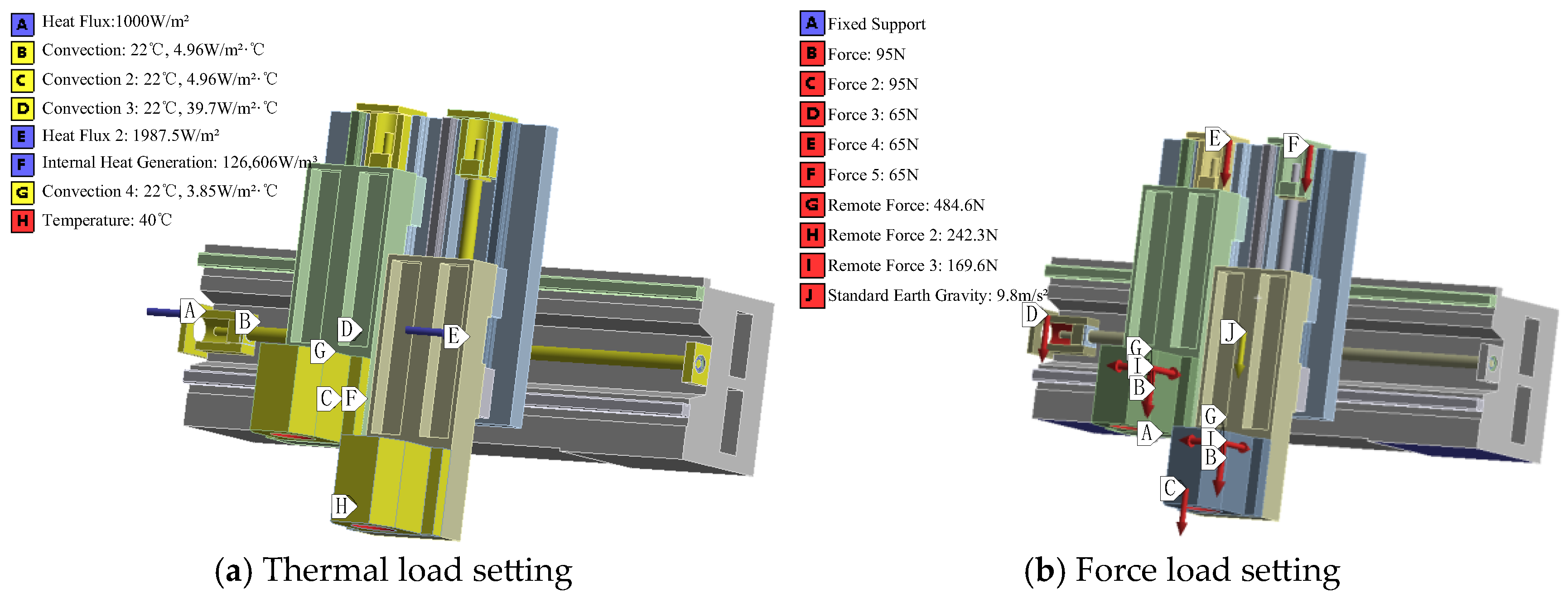
3.1. Thermal Load Calculation
3.2. Force Load Calculation
4. Coupled Thermal–Mechanical–Vibration Analysis and Design Variable Selection
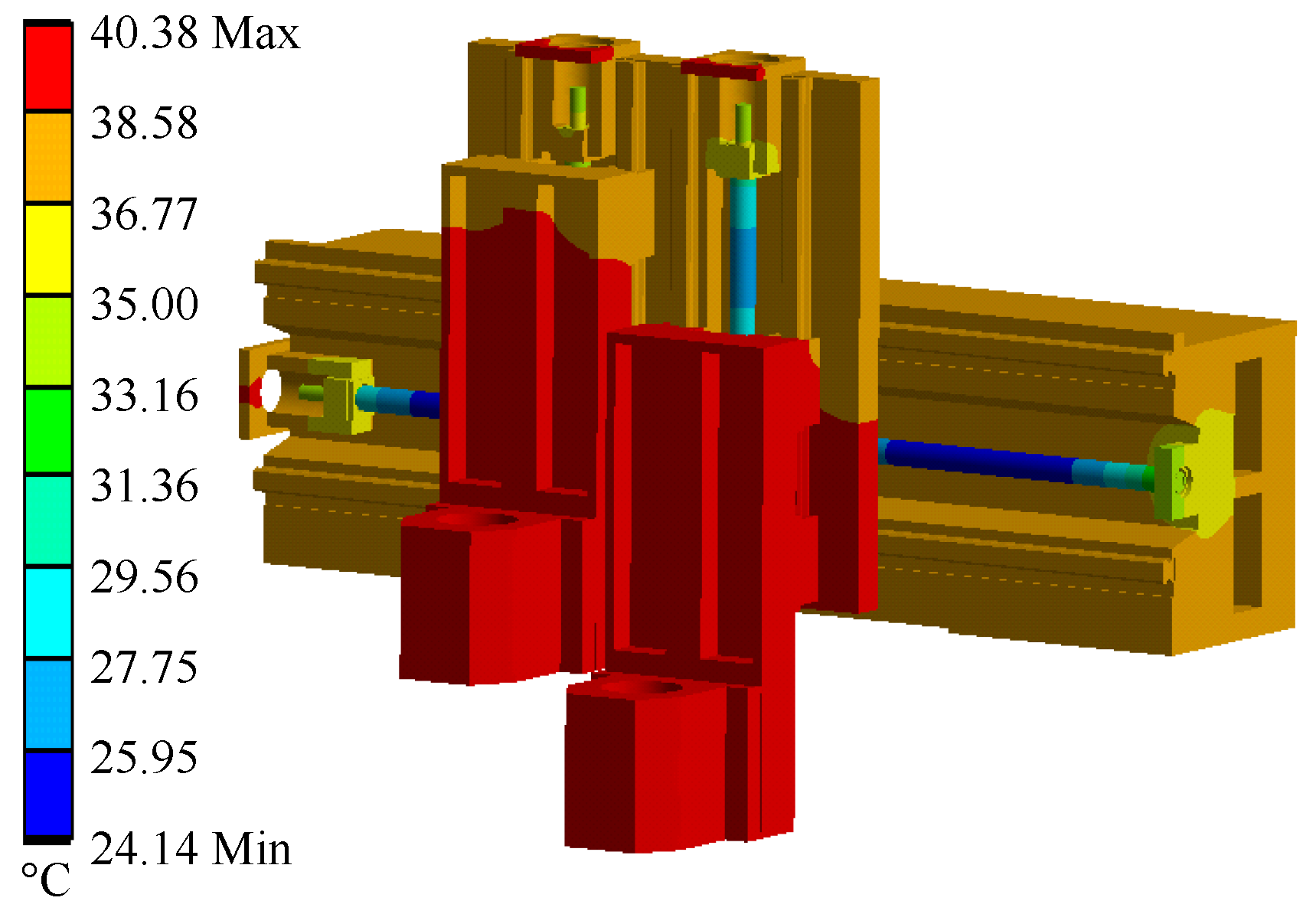
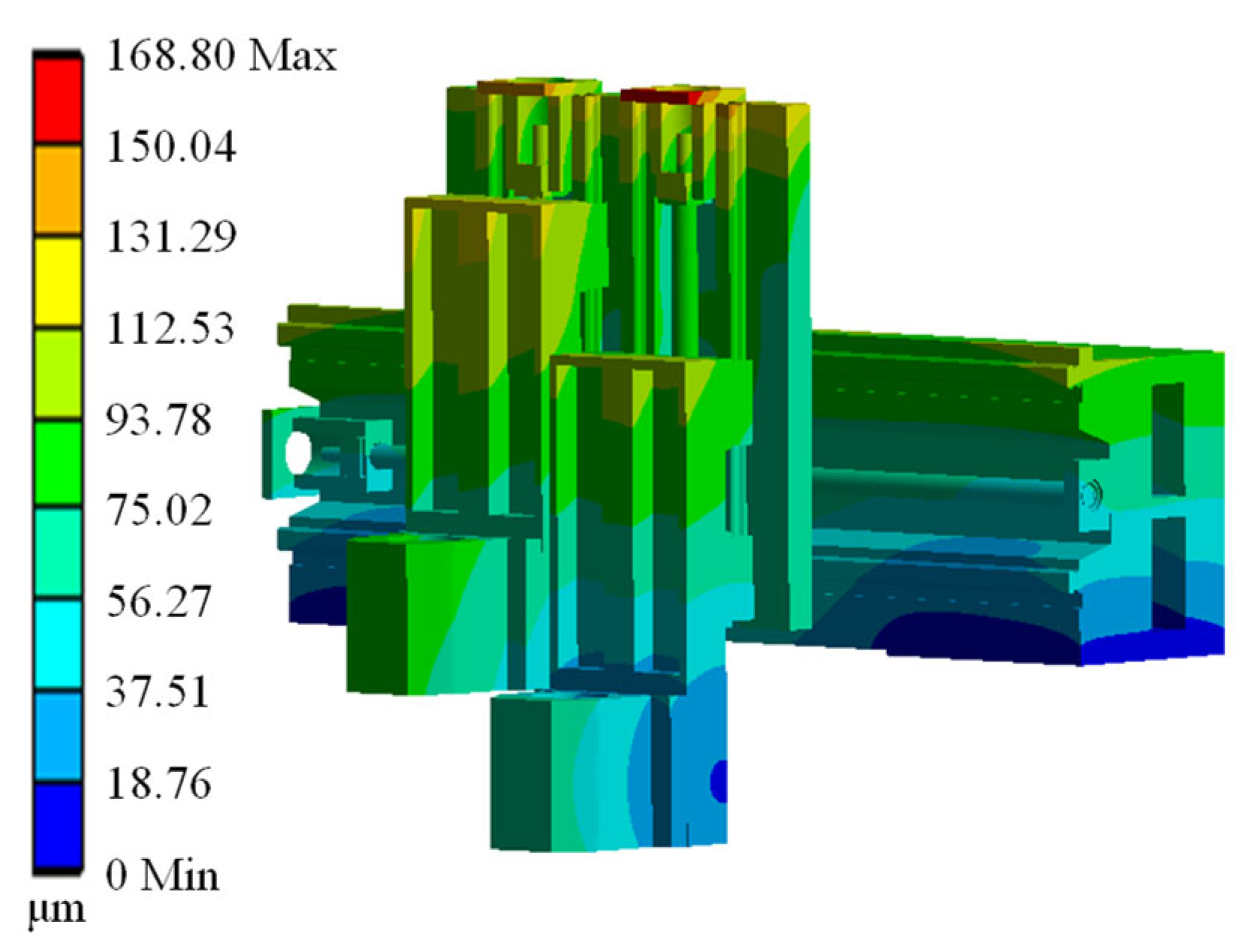
4.1. Coupling Analysis
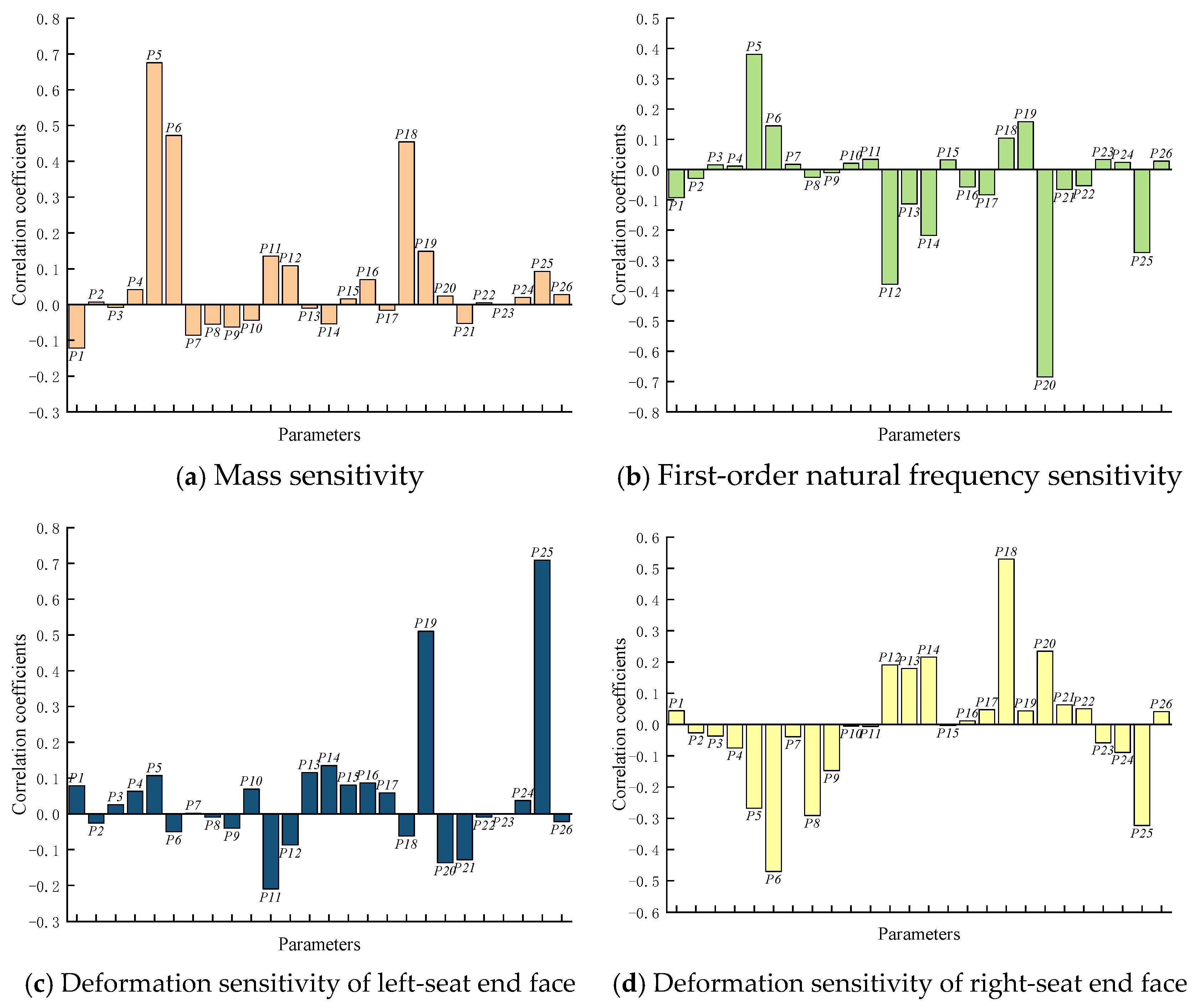
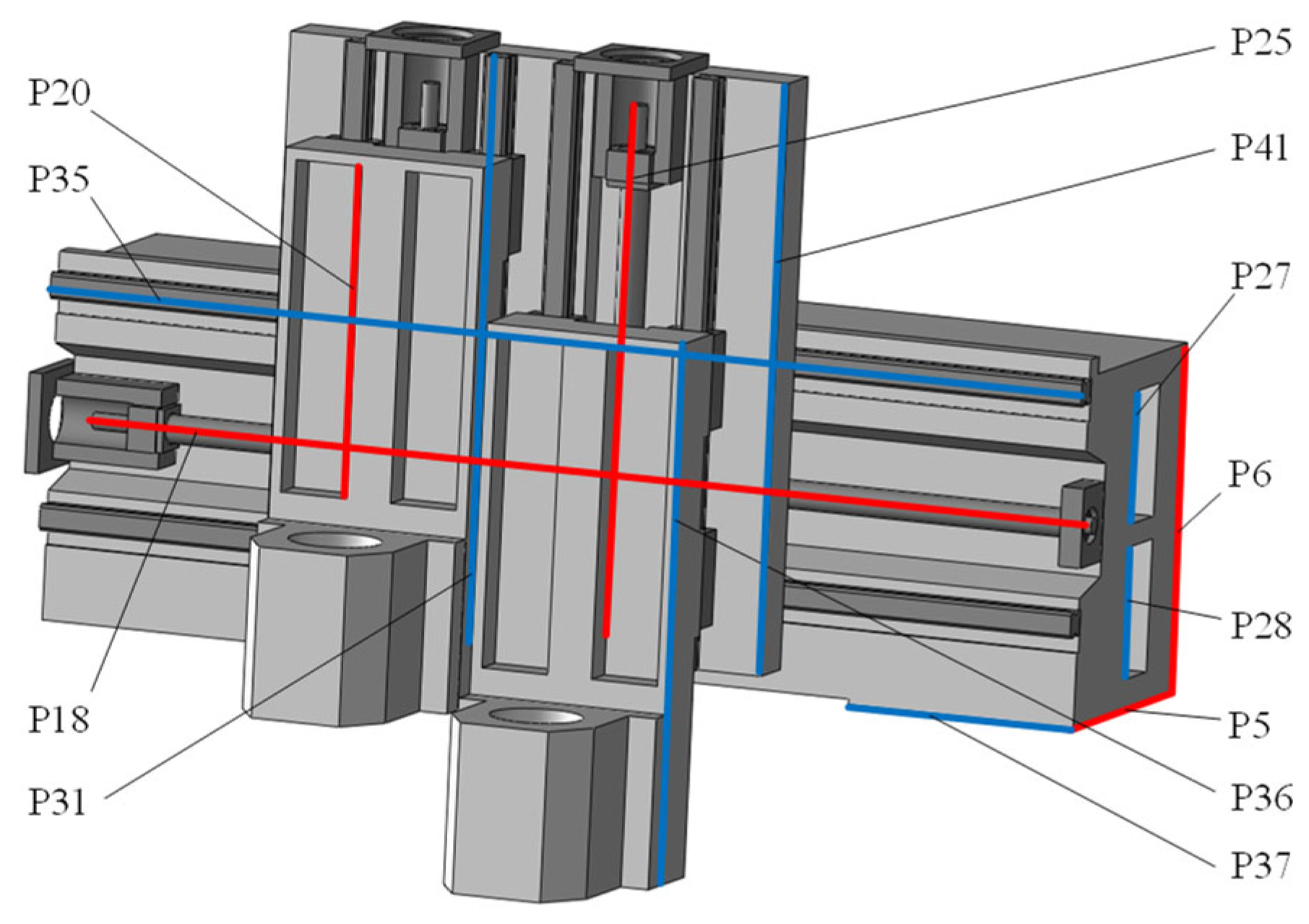
4.2. Parameter Sensitivity Analysis and Design Variable Selection
5. Response Surface Building and Optimization Design
5.1. Central Composite Design
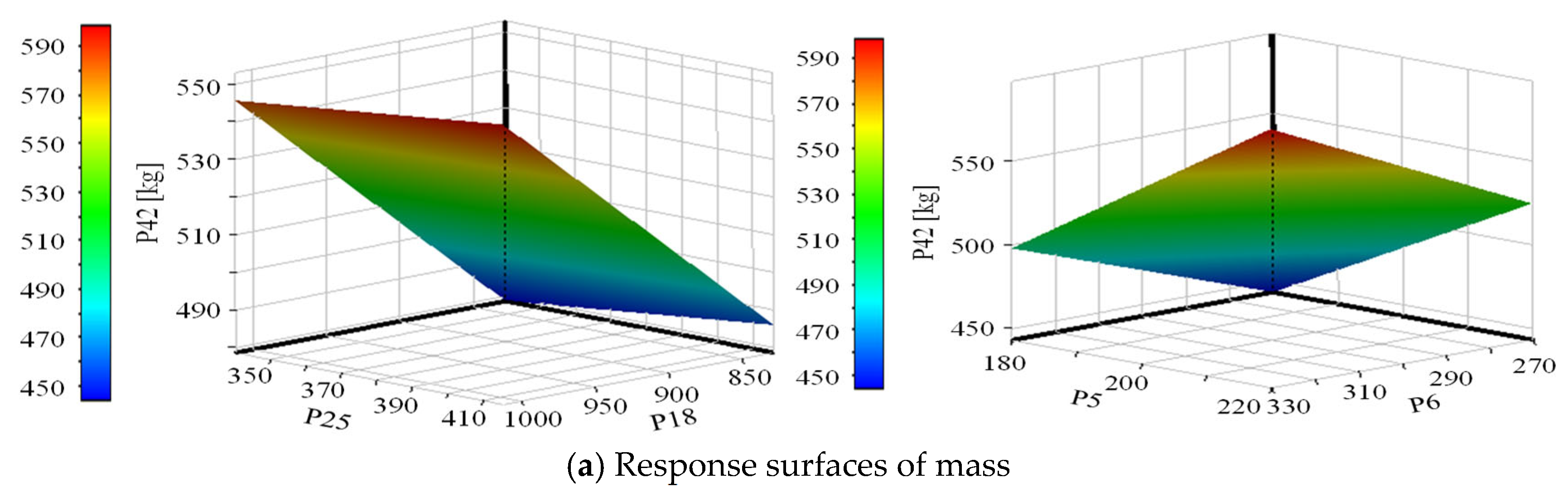
5.2. Response Surface Modeling
5.3. Analysis of Optimization Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.T.; Wang, D.; Zhang, S.; Tang, Z.; Wang, L.; Liu, Y. Design and development of a five-axis machine tool with high accuracy, stiffness and efficiency for aero-engine casing manufacturing. Chin. J. Aeronaut. 2022, 35, 485–496. [Google Scholar] [CrossRef]
- Lajili, M.; Chanal, H.; Bouzgarrou, B.C. Machine tool architecture selection at the preliminary design stage: Application to hard material machining. J. Comput. Des. Eng. 2020, 7, 657–667. [Google Scholar] [CrossRef]
- O’Toole, L.; Fang, F.Z. Optimal tool design in micro-milling of difficult-to-machine materials. Adv. Manuf. 2023, 11, 222–247. [Google Scholar] [CrossRef] [PubMed]
- Yuksel, E.; Erturk, A.S.; Budak, E. A Hybrid Contact Implementation Framework for Finite Element Analysis and Topology Optimization of Machine Tools. J. Manuf. Sci. Eng.-Trans. Asme 2020, 142, 081001. [Google Scholar] [CrossRef]
- Huang, W. Multi-Step Optimization Design of Weak Structural Parts of Machine Tools. Master’s Thesis, Shanghai Jiao Tong University, Shanghai, China, 2021. [Google Scholar]
- Liu, S.H.; Du, Y.B.; Lin, M. Study on lightweight structural optimization design system for gantry machine tool. Concurr. Eng.-Res. Appl. 2019, 27, 170–185. [Google Scholar] [CrossRef]
- Ding, Y.Y.; Rui, X.; Chang, Y.; Lu, H.; Chen, Y.; Ding, J.; Shehzad, A.; Chen, G.; Gu, J. Optimal design of the dynamic performance of the ultra-precision fly cutting machine tool. Int. J. Adv. Manuf. Technol. 2023, 124, 567–585. [Google Scholar] [CrossRef]
- Yang, J.S.; Zhou, Z.W.; Lin, X.L.; Deng, X.L.; Wang, J.C.; Zheng, Y.N. Multi-objective joint optimization design of high-precision turn-milling compound machine tool bed based on nonparametric regression response surface method. Manuf. Technol. Mach. Tool 2024, 5, 128–133. [Google Scholar]
- Chang, T.H.; Chen, S.L.; Kang, C.A.; Inasaki, I. Design optimization of the linkage dimension for a hybrid-type parallel kinematic machine tool. Proc. Inst. Mech. Eng. Part K-J. Multi-Body Dyn. 2002, 216, 143–156. [Google Scholar] [CrossRef]
- Zhai, L.X.; Sun, J.J.; Ma, X.; Han, W.T.; Luo, X.S. Thermal-structure coupling analysis and multi-objective optimization of motor rotor in MSPMSM. Chin. J. Aeronaut. 2019, 32, 1733–1747. [Google Scholar] [CrossRef]
- Chen, G.; Guo, S.J.; Ding, Q.Q.; Su, Z.; Tang, S.F. SHO-LSTM predictive modeling of spindle thermal error of CNC lathe. Adv. Eng. Sci. 2024, 56, 277–288. [Google Scholar]
- Guo, Z.Z.; Zhang, Y.S.; Liu, S.H. The Finite Element Analysis and the Multi-Objective Optimization Design of Spindle Systems of CNC Gantry Machine Tools. Key Eng. Mater. 2016, 693, 243–250. [Google Scholar] [CrossRef]
- Ouyang, X.L.; Xu, R.N.; Jiang, P.X. Three-equation local thermal non-equilibrium model for transient heat transfer in porous media: The internal thermal conduction effect in the solid phase. Int. J. Heat Mass Transf. 2017, 115, 1113–1124. [Google Scholar] [CrossRef]
- Zhang, C. Study on Thermal-Structural Coupling Simulation Analysis of Spacecraft. Master’s Thesis, Shanghai Jiao Tong University, Shanghai, China, 2021. [Google Scholar]
- Deng, X.L.; Fu, J.Z.; He, Y.; Chen, Z.C. Multi-physics coupling thermal characteristics of precision CNC machine tool spindle system. J. Zhejiang Univ. (Eng. Sci.) 2013, 47, 1863–1870. [Google Scholar]
- Wu, S.; Liu, T.; Liu, X.; Li, C.; Wang, C. Analysis of dynamic characteristic field of five-axis machine tool based on Kriging method. J. Vib. Meas. Diagn. 2022, 42, 68–75. [Google Scholar]
- Zhao, W.L. Research on Thermal-Mechanical Coupling Analysis and Optimization Design of Large CNC Machine Tool Workbench. Master’s Thesis, Hainan University, Haikou, China, 2021. [Google Scholar]
- Li, Z.J.; Zhao, C.Y.; Wen, B.C.; Lu, Z.C. Heat Source Rate Identification and Thermal Error Predictions of Ball Screw Feed Drive System for CNC Machine Tools. J. Northeast. Univ. 2019, 40, 1305–1309. [Google Scholar]
- Shen, J.X.; Xu, P.; Yu, Y.H.; Zheng, S.X. Optimization design and comprehensive performance analysis of BFPC machine tool gantry frame assembly. J. Mech. Eng. 2019, 55, 127–135. [Google Scholar] [CrossRef]
- Huang, H.Q.; Liu, H.L.; Wang, Y.; Huang, H.W.; Jiang, L.L. Stress-strain and modal analysis of marine centrifugal pump rotor based on fluid-solid coupling. Trans. Chin. Soc. Agric. Eng. 2014, 30, 98–105. [Google Scholar]
- Ye, H.; Gao, Y.; Liu, J.; Zhang, J.; Li, L.; Liu, X.B.; Liu, S.C.; Dong, G.X.; Jiang, F.L.; Guo, J.H. Optimization of Beam Dynamic Characteristics Based on Vibration Velocity and Noise. J. Hunan Univ. Nat. Sci. 2024, 51, 219–226. [Google Scholar]
- Amman, M.; Rashid, T.; Ali, A. Fermatean fuzzy multi-criteria decision-making based on Spearman rank correlation coefficient. Granul. Comput. 2023, 8, 2005–2019. [Google Scholar] [CrossRef]
- Zhang, D.H.; Yang, Y.C.; Liu, Y.M.; He, J. Hybrid DC line pilot protection method based on EMD and Spearman correlation coefficient. Power Syst. Prot. Control 2021, 49, 1–11. [Google Scholar]
- Issa, M.A.; Abidin, Z.Z.; Sobri, S.; Abdul-Rashid, S.; Mahdi, M.A.; Ibrahim, N.A.; Pudza, M.Y. Fabrication, characterization and response surface method optimization for quantum efficiency of fluorescent nitrogen-doped carbon dots obtained from carboxymethylcellulose of oil palms empty fruit bunch. Chin. J. Chem. Eng. 2020, 28, 584–592. [Google Scholar] [CrossRef]
- Liu, J.; Wang, K.L.; Lu, S.Q.; Li, X.; Huang, W.J.; Zeng, Q.; Zhou, T.; Wang, Z.Q. Optimization of deformation process parameters of Ti_2AlNb-based alloy based on response surface method. Rare Met. Mater. Eng. 2023, 52, 3581–3589. [Google Scholar]
- Deng, C.; Miao, J.; Yang, S.; Yin, G.; Wei, B. The Spatial Cutting Stability of CNC Machine Tool Based on Kriging Model. J. Vib. Meas. Diagn. 2019, 39, 495–502. [Google Scholar]
- Veerakumar, R.; Raul, V.; Liu, Y.; Wang, X.; Leifsson, L.; Hu, H. Metamodeling-based parametric optimization of DBD plasma actuation to suppress flow separation over a wind turbine airfoil model. Acta Mech. Sin. 2020, 36, 260–274. [Google Scholar] [CrossRef]
- Wan, Y.F.; Sun, W.L.; Wang, H.W.; Xu, T.T.; Wang, B.J. Lightweight design of wind turbine spindle based on Kriging model and MOGA algorithm. Acta Energiae Solaris Sin. 2022, 43, 388–395. [Google Scholar]
- Zhang, Y.M.; Bao, F.X.; Qi, P.N. Modeling method for thermal characteristics of ball screw nut pair. China Mech. Eng. 2020, 31, 2486–2490, 2496. [Google Scholar]
- Yang, X.F.; Shi, Y.; Xu, Y.; Li, Z.R. Influence of screw-nut preload on thermal characteristics of machine tool feed system. Mod. Manuf. Eng. 2019, 117–123. [Google Scholar]
- Shao, L.Z. Thermal Deformation Analysis and Structural Optimization of Five-Axis Gantry Machining Center. Master’s Thesis, Southeast University, Nanjing, China, 2018. [Google Scholar]
- Yang, X.; Zeng, L.W.; Chen, P.; Li, B. Complex heat flow characteristics and multi-dimensional control strategy of dry-cutting hobbing machine. China Mech. Eng. 2022, 33, 623–629. [Google Scholar]
- Jin, Y.L.; Yu, Q.; Wang, D.D.; Cheng, Y.; Zhang, X.M. Research on convective heat transfer coefficient of ball screw in machining center. Mach. Tool Hydraul. 2020, 48, 37–39. [Google Scholar]
- Lai, K.X.; Cao, H.J.; Li, H.C.; Li, B.J.; Huang, D.S. Coupling evaluation for material removal and thermal control on precision milling machine tools. Front. Mech. Eng. 2022, 17, 12. [Google Scholar] [CrossRef]
- Chang, J.T.; Liu, Y.; Kong, X.G.; Li, X.W.; Chen, Q.; Su, X. Prediction method of cutting force under variable working conditions based on geometric features of workpiece. J. Xidian Univ. 2022, 49, 154–165. [Google Scholar]
- Guo, R.L.; Deng, W.Q.; Li, D.L. Optimization design and performance analysis of CNC machine tool composite structure bed based on grey theory. J. Lanzhou Univ. Technol. 2021, 47, 53–58. [Google Scholar]
- Chen, Y.I.; Qiu, Z.H.; Guo, J.K.; H, J.; Liu, Z.G. An optimization method for the quality of basic large parts of machine tools in the conceptual design stage. J. Xi’an Jiaotong Univ. 2017, 51, 105–114. [Google Scholar]

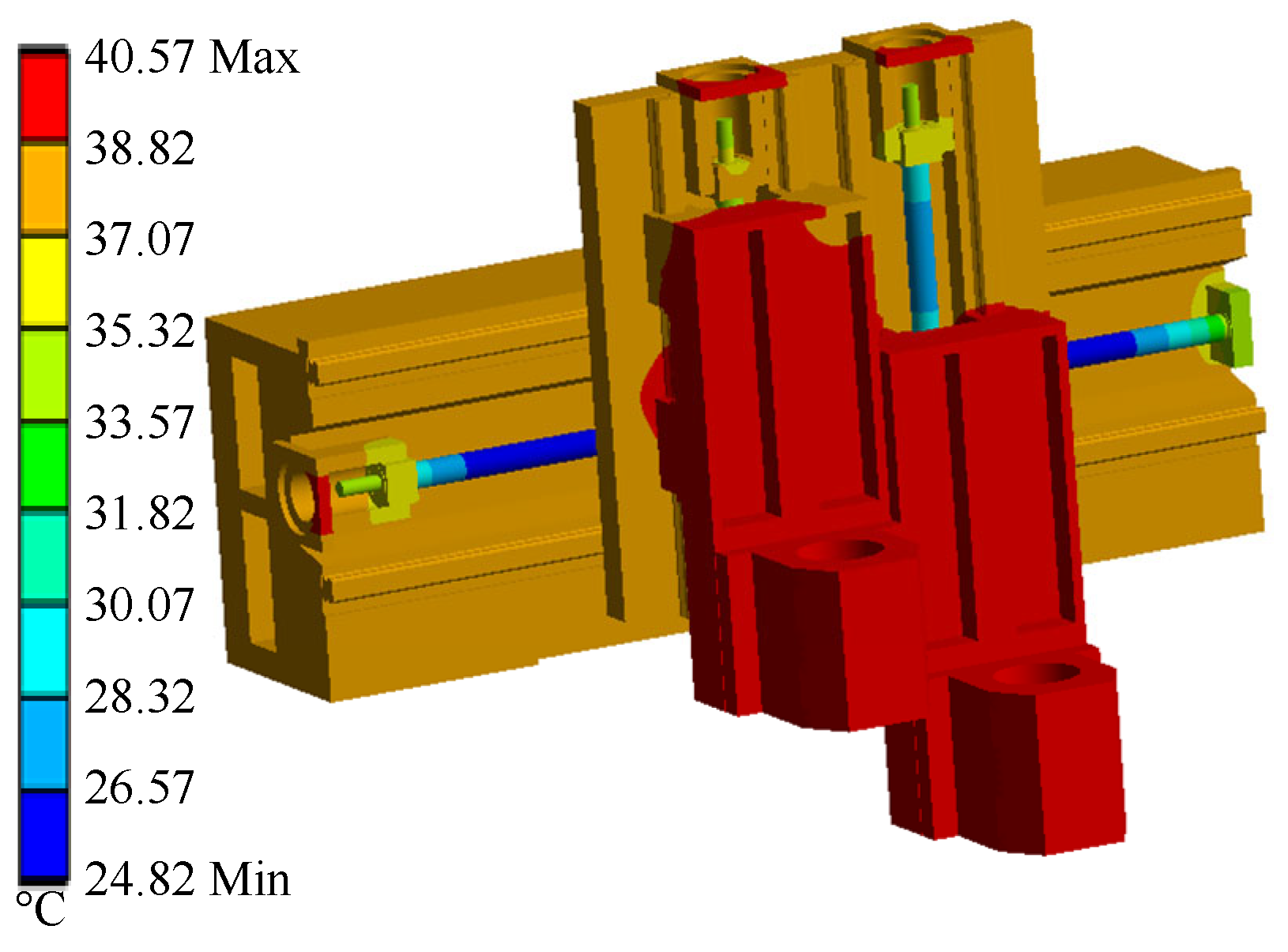
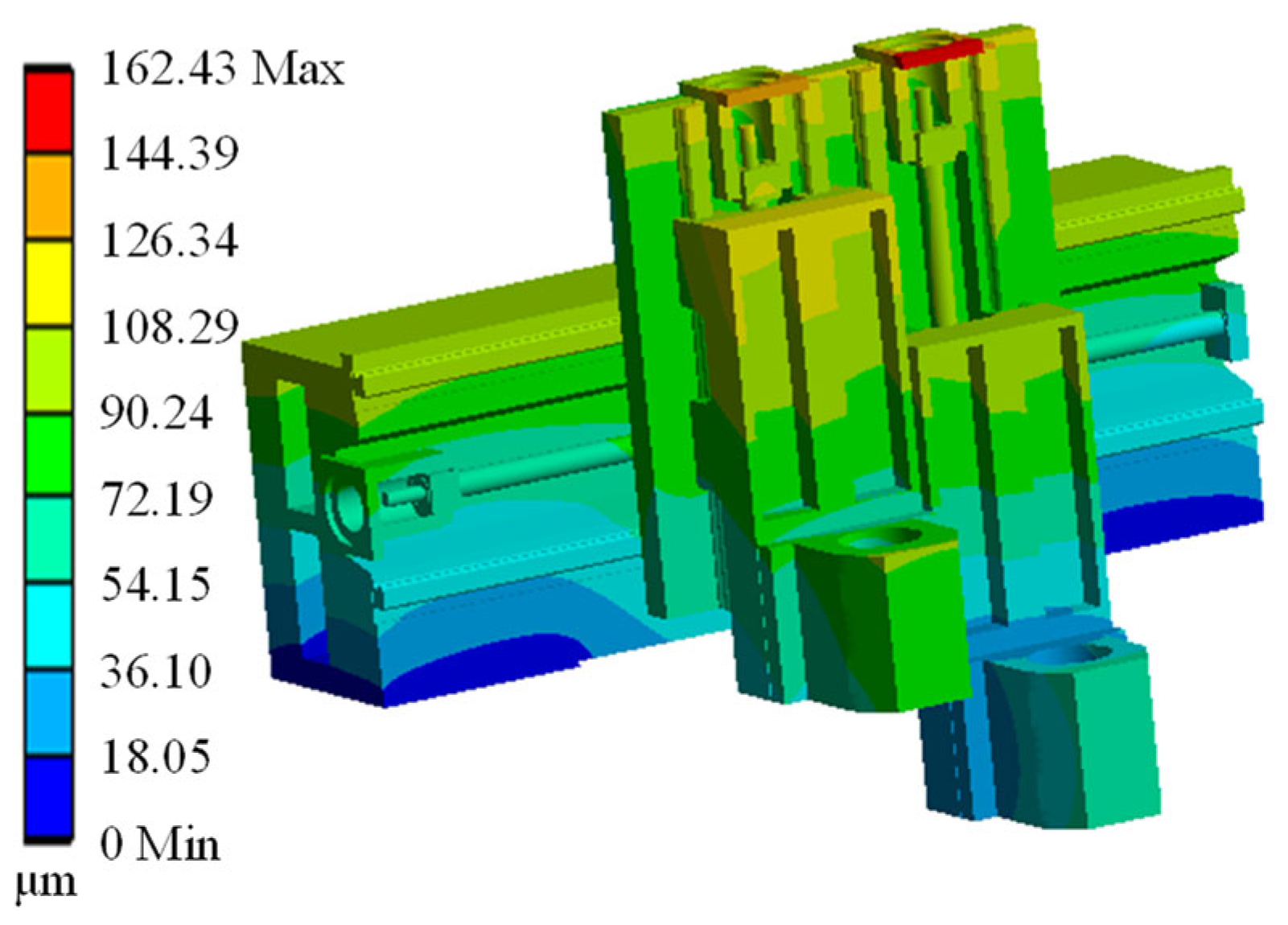


| Materials | Density/ (kg/m3) | Elastic Modulus /MPa | Poisson Ratio | Thermal Conductivity/(W/(m·K)) | Thermal Expansion Coefficient /(°C−1(10−5)) |
|---|---|---|---|---|---|
| HT300 | 7300 | 13,000 | 0.25 | 50 | 1.2 |
| 45 (modulated) | 7850 | 210,000 | 0.31 | 48 | 1.15 |
| Cronidur 30 | 7670 | 210,000 | 0.30 | 14.5 | 1.05 |
| Design Variables | Associated Parameters | Correlation Relationships |
|---|---|---|
| P5 | Null | Null |
| P6 | P27, P28 | P27= (P6 − 2 × P4 − P3)/2 + 12.5 = P28 |
| P18 | P35, P36 | P35 = P18 + 122, P36 = (P18−818)/2 |
| P20 | P37 | P37 = P12 + P20 + P22 + 20 |
| P25 | P31, P41 | P31 = P25 + 142 = p41 |
| Serial Number | P5/mm | P6/mm | P18/mm | P20/mm | P25/mm | Mass/kg | First-Order Natural Frequency /Hz | Thermal–Mechanical Coupling Deformation of the Left End Face /μm | Thermal–Mechanical Coupling Deformation of the Right End Face /μm |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 200 | 300 | 920 | 300 | 378 | 515.85 | 178.36 | 80.09 | 65.26 |
| 2 | 180 | 300 | 920 | 300 | 378 | 470.60 | 169.23 | 78.49 | 68.58 |
| 3 | 220 | 300 | 920 | 300 | 378 | 561.11 | 185.29 | 82.04 | 63.18 |
| 4 | 200 | 270 | 920 | 300 | 378 | 483.89 | 173.60 | 81.52 | 69.06 |
| 5 | 200 | 330 | 920 | 300 | 378 | 547.81 | 180.46 | 80.12 | 60.49 |
| 6 | 200 | 300 | 828 | 300 | 378 | 482.34 | 176.48 | 81.88 | 60.03 |
| 7 | 200 | 300 | 1012 | 300 | 378 | 549.37 | 179.54 | 79.79 | 71.77 |
| 8 | 200 | 300 | 920 | 270 | 378 | 512.70 | 191.98 | 82.81 | 62.55 |
| 9 | 200 | 300 | 920 | 330 | 378 | 519.01 | 161.81 | 78.11 | 69.02 |
| 10 | 200 | 300 | 920 | 300 | 340.2 | 512.18 | 180.04 | 74.49 | 70.92 |
| 11 | 200 | 300 | 920 | 300 | 415.8 | 519.53 | 169.87 | 91.90 | 61.46 |
| 12 | 194.33 | 291.49 | 893.93 | 291.49 | 388.71 | 485.58 | 176.33 | 83.61 | 63.45 |
| 13 | 205.66 | 291.49 | 893.93 | 291.49 | 367.28 | 507.78 | 185.29 | 79.73 | 64.32 |
| 14 | 194.33 | 308.50 | 893.93 | 291.49 | 367.28 | 500.35 | 181.88 | 78.27 | 63.27 |
| 15 | 205.66 | 308.50 | 893.93 | 291.49 | 388.71 | 528.14 | 183.11 | 84.76 | 60.20 |
| 16 | 194.33 | 291.49 | 946.06 | 291.49 | 367.28 | 501.31 | 181.09 | 78.33 | 69.89 |
| 17 | 205.66 | 291.49 | 946.06 | 291.49 | 388.71 | 528.94 | 182.09 | 83.88 | 65.42 |
| 18 | 194.33 | 308.50 | 946.06 | 291.49 | 388.71 | 521.31 | 179.12 | 82.71 | 64.19 |
| 19 | 205.66 | 308.50 | 946.06 | 291.49 | 367.28 | 546.27 | 188.13 | 78.80 | 65.20 |
| 20 | 194.33 | 291.49 | 893.93 | 308.50 | 367.28 | 485.29 | 171.64 | 77.47 | 68.04 |
| 21 | 205.66 | 291.49 | 893.93 | 308.50 | 388.71 | 511.65 | 172.73 | 83.33 | 63.75 |
| 22 | 194.33 | 308.50 | 893.93 | 308.50 | 388.71 | 504.22 | 170.40 | 82.05 | 62.67 |
| 23 | 205.66 | 308.50 | 893.93 | 308.50 | 367.28 | 527.85 | 177.59 | 78.13 | 63.86 |
| 24 | 194.33 | 291.49 | 946.06 | 308.50 | 388.71 | 505.18 | 169.53 | 81.61 | 68.84 |
| 25 | 205.66 | 291.49 | 946.06 | 308.50 | 367.28 | 528.64 | 176.54 | 78.13 | 69.99 |
| 26 | 194.33 | 308.50 | 946.06 | 308.50 | 367.28 | 521.01 | 174.15 | 76.59 | 69.22 |
| 27 | 205.66 | 308.50 | 946.06 | 308.50 | 388.71 | 550.14 | 175.07 | 82.25 | 64.52 |
| Performance | Mass/kg | First-Order Natural Frequency/Hz | Thermal–Mechanical Coupling Deformation of the Left End Face/μm | Thermal–Mechanical Coupling Deformation of the Right end Face/μm | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Point 1 | Point 2 | Point 3 | Point 1 | Point 2 | Point 3 | Point 1 | Point 2 | Point 3 | Point 1 | Point 2 | Point 3 | |
| Fitting values | 464.29 | 464.52 | 464.82 | 185.19 | 185.47 | 185.25 | 75.19 | 75.21 | 75.12 | 58.80 | 58.91 | 58.98 |
| Validation values | 464.42 | 464.63 | 464.95 | 185.05 | 185.37 | 185.15 | 75.90 | 75.88 | 75.78 | 59.29 | 59.39 | 59.47 |
| Correlation coefficients | 0.9997 | 0.9998 | 0.9997 | 0.9992 | 0.9995 | 0.9995 | 0.9906 | 0.9912 | 0.9912 | 0.9917 | 0.9919 | 0.9918 |
| Performance | Mass /kg | First-Order Natural Frequency/Hz | Thermal–Mechanical Coupling Deformation of the Left End Face/μm | Thermal–Mechanical Coupling Deformation of the Right End Face/μm | Temperature/°C |
|---|---|---|---|---|---|
| Original values | 515.86 | 178.36 | 80.10 | 65.27 | 40.384 |
| Optimized values | 464.02 | 185.31 | 75.86 | 59.41 | 40.568 |
| Rate of change/% | 10.1 | 3.9 | 5.3 | 9.0 | 0.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, X.; Xie, Y.; Deng, X.; Tian, J.; Han, Y.; Wang, P. Multi-Objective Optimization Design of Dual-Spindle Component Based on Coupled Thermal–Mechanical–Vibration Collaborative Analysis. Machines 2024, 12, 885. https://doi.org/10.3390/machines12120885
Lin X, Xie Y, Deng X, Tian J, Han Y, Wang P. Multi-Objective Optimization Design of Dual-Spindle Component Based on Coupled Thermal–Mechanical–Vibration Collaborative Analysis. Machines. 2024; 12(12):885. https://doi.org/10.3390/machines12120885
Chicago/Turabian StyleLin, Xiaoliang, Yiming Xie, Xiaolei Deng, Jing Tian, Yue Han, and Peng Wang. 2024. "Multi-Objective Optimization Design of Dual-Spindle Component Based on Coupled Thermal–Mechanical–Vibration Collaborative Analysis" Machines 12, no. 12: 885. https://doi.org/10.3390/machines12120885
APA StyleLin, X., Xie, Y., Deng, X., Tian, J., Han, Y., & Wang, P. (2024). Multi-Objective Optimization Design of Dual-Spindle Component Based on Coupled Thermal–Mechanical–Vibration Collaborative Analysis. Machines, 12(12), 885. https://doi.org/10.3390/machines12120885






