Development of a Virtual Telehandler Model Using a Bond Graph
Abstract
1. Introduction
2. Multiphysics Modelling
2.1. Mathematical Formulations and Multibody System Simulation (MBS)
- -
- Category A comprises general-purpose software widely used for multibody system simulation, including ADAMS, SIMPACK, RECURDyn, ALTAIR Motion Solve, and Samcef Mecano. These tools are often part of larger platforms or simulation portfolios, such as HEXAGON, 3DEXPERIENCE, and ALTAIR, which support complex multiphysics simulations.
- -
- Category B consists of programs initially focused on the dynamics of physical or multidomain systems but have since incorporated expanded functionalities, including bond graph methods. Examples include MODELICA (Dymola, SimulationX), SIMCenter AMESim, MAPLESim, 20-SIM, MathWorks (MATLAB, Simulink), etc.
- (1)
- (2)
- (3)
- (4)
- (5)
- (6)
2.2. Model Description
3. Telehandler Modelling Using Scalar and Vectorial Bond Graphs
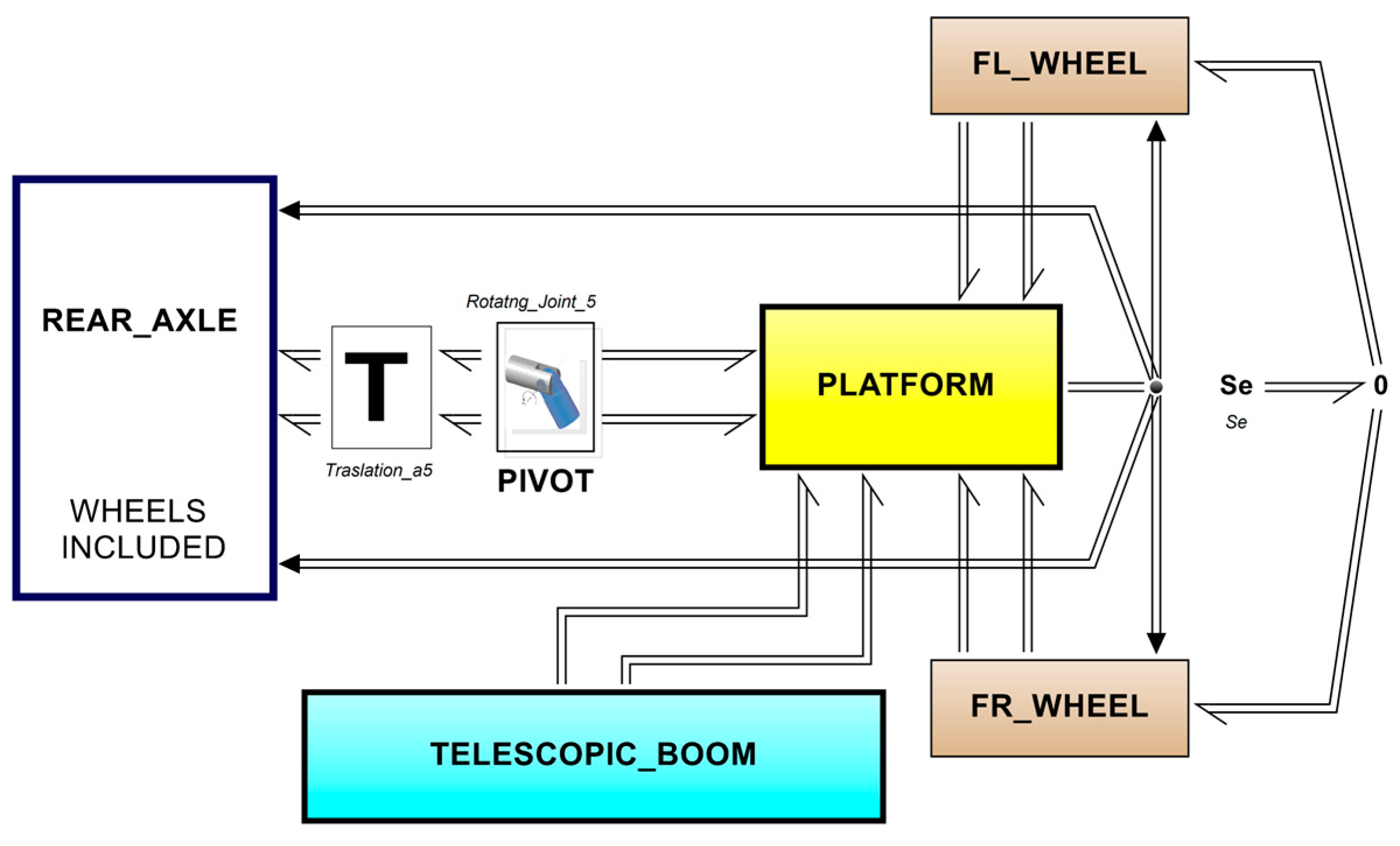
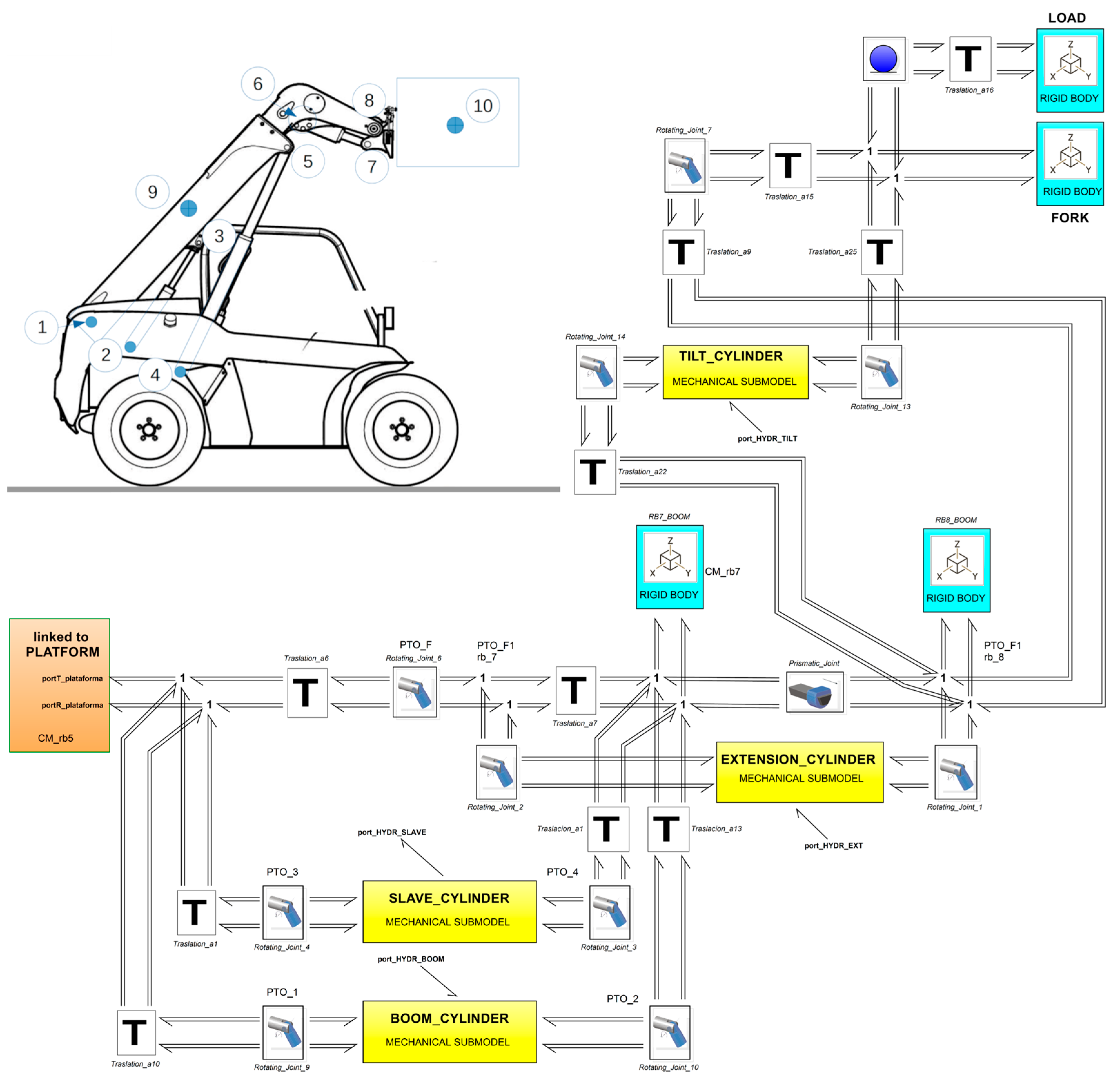
3.1. Telehandler Model (3D Bond Graph)
Mechanical Domain Modelling
- Platform submodel
- 2.
- Rear Axle submodel
- 3.
- Wheel and Soil/Tire Interaction Submodel
- 4.
- Telescopic arm system
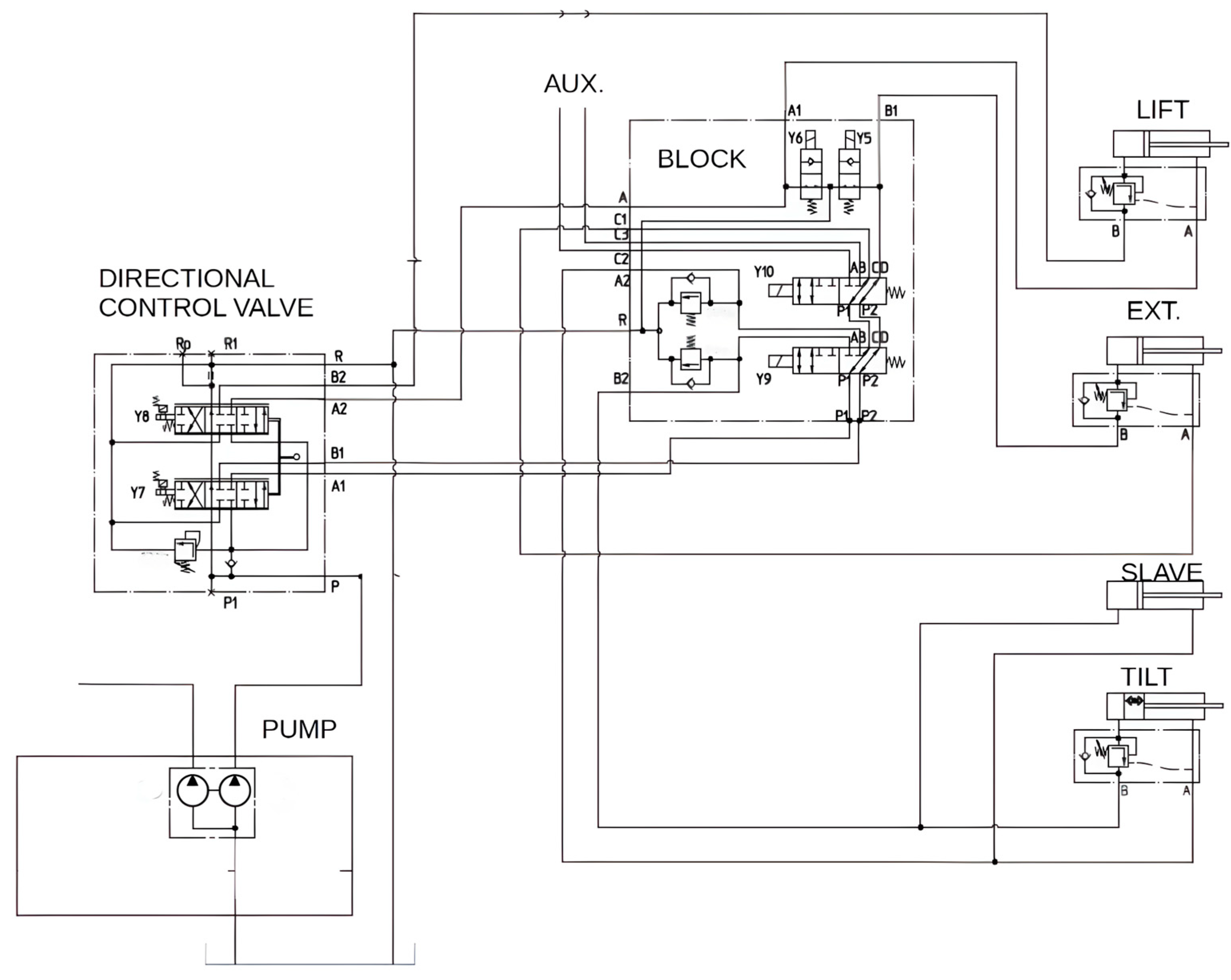
3.2. Hydraulic Domain Modelling
4. Experimental Test
4.1. Experimental Methodology
- Tests to determine the ground reaction forces on the four wheels under different operating conditions of the machine. The results of these tests will be used to validate the virtual model from a mechanical perspective.
- Tests on some specific functionalities of the machine, such as the self-levelling of the attachment fork. The experimental results will allow for the validation of the virtual model from a hydraulic perspective.
4.1.1. Tests to Determine the Ground Reaction Forces (Mechanical Domain)
4.1.2. Tests to Determine the Functionality Performance (Hydraulic Domain)
4.2. Experimental vs. Numerical Results: A Critical Examination of Their Validity and Model Limitations
- Mechanical domain
- 2.
- Hydraulic domain
5. Conclusions and Final Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Priora, G. Monitor and Control System of the Dynamic Stability on a Telescopic Handler with Telemetry and Experimental Data. Master’s Thesis, Politecnico di Torino (Italy), Torino, Italy, 2019. [Google Scholar]
- Machinery Regulation (UE) 2023/1230. Available online: https://eur-lex.europa.eu/eli/reg/2023/1230/oj (accessed on 14 June 2023).
- CEN/TS 1459-8:2018 (MAIN); Rough-Terrain Trucks—Safety Requirements and Verification—Part 8: Variable-Reach Tractors. Asociación Española de Normalización: Madrid, Spain, 2018.
- CEN/EN 15000:2008; Safety of Industrial Trucks. Self-Propelled Variable Reach Trucks. Specification, Performance and Test Requirements for Longitudinal Load Moment Indicators and Longitudinal Load Moment Limiters. Asociación Española de Normalización: Madrid, Spain, 2018.
- ISO 22915-14:2023; Industrial Truck—Verification of Stability. Part 14: Rough-Terrain Variable-Reach Trucks. International Organization for Standardization: Geneva, Switzerland, 2023.
- ISO 10896-1:2020; Rough-Terrain Trucks—Safety Requirements and Verification. Part 1: Variable-Reach Trucks. International Organization for Standardization: Geneva, Switzerland, 2020.
- Safe Use of Telehandlers in Construction; Good Practice Guide, 2nd ed.; Reference No. CPA 1101; Construction Plant-Hire Association: London, UK; Health Safety Executive (HSE): Merseyside, UK, 2015.
- Hunter, A.G.M. A review of research into machine stability on slopes. Saf. Sci. 1993, 16, 325–339. [Google Scholar] [CrossRef]
- Bietresato, M.; Mazzetto, F. Stability Tests of Agricultural and Operating Machines by Means of an Installation composed by a Rotating Platform with Four Weighting Quadrants. Appl. Sci. 2020, 10, 3786. [Google Scholar] [CrossRef]
- Urkullu, G. Integración de las Ecuaciones de la Dinámica de Sistemas Multicuerpo Mediante Diferencias Centrales de Orden dos. Ph.D. Thesis, Universidad del País Vasco—Euskal Herriko Unibertsitatea, Leioa, España, 2019. [Google Scholar]
- Garcia-Vallejo, D.; Mayo, J.; Escalona, J.L.; Domínguez, J. Three-Dimensional Formulation of Rigid-Flexible Multibody Systems with Flexible Beam Elements; Multibody System Dynamics 20: Singapore, 2008; pp. 1–28. [Google Scholar]
- Beater, P.; Otter, M. Multi domain simulation: Mechancis and hydraulics of an excavator. In Proceedings of the Conference: 3rd International Modelica Conference, Linköping, Sweden, 3–4 November 2003; The Modelica Association: Linköping, Sweden, 2003. [Google Scholar]
- Patil, A.; Radle, M. Hydraulic and multibody combined simulations for electric forklift design using modelica. Int. J. Eng. Sci. Technol. 2022, 10, 27–35. [Google Scholar] [CrossRef]
- Altare, G. Analisi e Modellazione del Circuito Idraulico di un Miniescavatore. Master’s Thesis, Politecnico di Torino, Torino, Italy, 2009. [Google Scholar]
- Altare, G.; Lovuolo, F.; Nervegna, N.; Rundo, M. Coupled Simulation of a Telehandler Forks Handling Hydraulics. Int. J. Fluid Power 2012, 13, 15–28. [Google Scholar] [CrossRef]
- Casoli, P.; Alvin, A. Modelling of an Excavator Pump Nonlinear Model and Structural Linkage/Mechanical Model. In Proceedings of the 12th Scandinavian International Conference on Fluid Power, Tampere, Finland, 18–20 May 2011; pp. 25–40. [Google Scholar]
- Prabhu, S.M. Model-Based Design for Off-Highway Machine Systems Development; SAE: Warrendale, PA, USA, 2007. [Google Scholar] [CrossRef]
- Jhala, H.S. A Multibody Simulation Approach to Identify Critical Instability Scenarios of a Forklift Truck. Master Automotive Technology. Master’s Thesis, Eindhoven University Technology, Eindhoven, The Netherlands, 2023. [Google Scholar]
- Hong, T.D.; Pham, M.Q.; Tram, S.C.; Tram, L.Q.; Nguyen, T.T. A comparative study on kinetics and dynamics of two dump truck lifting mechanisms using Matlab Simscape. Theor. Appl. Mech. Lett. 2024, 14, 100502. [Google Scholar] [CrossRef]
- Roccatello, A.; Mancò, S.; Nervegna, N. Modelling a Variable Displacement Axial Piston Pump in a Multibody Simulation Environment. J. Dyn. Sys. Meas. Control 2007, 29, 456–469. [Google Scholar] [CrossRef]
- Sapietova, A.; Saga, M.; Novak, P. Multi software platform for solving of multibody systems synthesis. Commun. Sci. Lett. Univ. Zilina 2012, 14, 43–48. [Google Scholar] [CrossRef]
- Prescot, W. Using multibody dynamics solvers in a Multiphysics environment. Multibody Dynamics. In Proceedings of the ECCOMAS Thematic Conference, Warsaw, Poland, 29 June–2 July 2009. [Google Scholar]
- Zi, B.; Zhang, L.; Zhang, D.; Qian, S. Modelling, analysis, and co-simulation of cable parallel manipulators for multiple cranes. Proc. IMechE Part C J. Mech. Eng. Sci. 2015, 229, 1693–1707. [Google Scholar] [CrossRef]
- Zhang, Z.; Xiao, B. Research on dual-wheel independent-drive control of electric forklift based on optimal slip ratio. Sci. Prog. 2020, 103, 927836. [Google Scholar] [CrossRef]
- Khadim, Q.; Kaikko, E.-P.; Puolatie, E.; Mikkola, A. Targeting the user experience in the development of mobile machinery using real-time multibody simulation. Adv. Mech. Eng. 2020, 12, 923176. [Google Scholar] [CrossRef]
- Parlapanis, C.; Müller, D.; Frontull, M. Modelling of the work functionality of a hydraulic actuated telescopic handler. IFAC Pap. Online 2022, 55, 253–258. [Google Scholar] [CrossRef]
- Marjamäki, H.; Mäkinen, J. Modelling telescopic boom. The plan case: Part I. Comput. Struct. 2003, 9, 1597–1609. [Google Scholar] [CrossRef]
- Marjamäki, H.; Mäkinen, J. Modelling a telescopic boom—The 3D case: Part II. Comput. Struct. 2006, 84, 2001–2015. [Google Scholar] [CrossRef]
- Zhao, T.; Qi, Z.; Wang, T. Dynamic Contact Analysis of Flexible Telescopic Boom Systems with Moving Boundary. Mathematics 2024, 12, 2496. [Google Scholar] [CrossRef]
- Repetzki, S.; Koppler, R.; Lamprecht, C.; Pipiorke, J. Vehicle dynamics of a telescopic handler. ATZ Heavy Duty Worldw. 2016, 9, 30–35. [Google Scholar] [CrossRef]
- Klopper, R. Fahrschwingungs analyse eines Teleskopladers mittels Mehrkörper simulations software—SimulationX. Driving Vibration Analysis of a Telescopic Handler Using Multibody Simulation Software. Master’s Thesis, Management Centre Innsbruck, Innsbruck, Austria, 2015. [Google Scholar]
- Park, Y.; Chang, P.H. Vibration control of a telescopic handler using time delay control and command less input shaping technique. Control Eng. Pract. 2020, 12, 769–780. [Google Scholar] [CrossRef]
- Monacelli, G.; Largo, S.; D’Aria, R. Virtual stability simulation of a telescopic handler machine according to the standard UNI EN 1459. In Proceedings of the European Altair Technology Conference, Turin, Italy, 22–24 April 2013. [Google Scholar]
- Guo, H.; Mu, X.; Du, F.; Kai, L. Lateral Stability Analysis of Telehandlers Based on Multibody Dynamics; Wseas Transactions on Applied and Theoretical Mechanics; E-ISSN: Paris, France, 2016; Volume 11, pp. 2224–3429. [Google Scholar]
- Somà, A.; Bruzzese, F.; Mocera, F.; Viglietti, E. Hybridization factor and performance of hybrid electric telehandler vehicle. IEEE Trans. Ind. Appl. 2016, 52, 5130–5138. [Google Scholar] [CrossRef]
- Reich, T.; Nagel, P.; Geimer, M. Beurteilung des Einsparpotentials eines hybriden Teleskopladers mithilfe eines Rollenprüfstandes. In Proceedings of the Kolloquium Mobilhydraulik Braunschweig, Braunschweig, Germany, 6–7 October 2014; Inst. Für Mobile Maschinen und Nutzfahrzeuge: Braunschweig, Germany, 2014. [Google Scholar]
- Hansen, R.H.; Andersen, T.O.; Pedersen, H.C. Development and implementation of an advanced power management algorithm for electronic load sensing on a telehandler, In Proceedings of the Bath/ASME Symposium on Fluid Power and Motion Control, Bath, UK, 15–17 September 2010.
- Činkelj, J.; Kamnik, R.; Čepon, P.; Mihelj, M.; Munih, M. Closed-loop control of hydraulic telescopic handler. Autom. Constr. 2010, 19, 954–963. [Google Scholar] [CrossRef]
- Craig, J.J. Introduction to Robotics: Mechanics and Control; Pearson Prentice Hall: Hoboken, NJ, USA, 2005; ISBN 0131236296. [Google Scholar]
- Borutzky, W. Bond Graph Methodology: Development and Analysis of Multidisciplinary Dynamic System Models; Springer Science & Business Media: Berlin/Heidelberg, Germany,, 2010; ISBN 13: 9781848828810. [Google Scholar]
- Romero, G. Procedimientos Optimizados Utilizando Métodos Simbólicos Para la Simulación de Sistemas Dinámicos Mediante Bond-GraphBond-Graph. Ph.D. Thesis, Universidad Politécnica de Madrid, España, Spain, 2005. [Google Scholar]
- Bos, A.M. Modelling Multibody Systems in Terms of Multibond Graphs with Application to a Motor Cycle. 90-9001442-X. Ph.D. Thesis, Universiteit Twente, Enschcde, The Netherlands, 1986. [Google Scholar]
- Tiernego, M.J.L.; Bos, A.M. Modelling the dynamics and kinematics of mechanical systems with MultiBond Graphs. Special issue on physical structure in modelling. J. Frankl. Inst. 1985, 319, 37–50. [Google Scholar] [CrossRef]
- Karnopp, D.; Rosenberg, R.; Perelson, A.S. System Dynamics: A Unified Approach. IEEE Trans. Syst. Man Cybern. 1976, SMC-6, 724. [Google Scholar] [CrossRef]
- Marquis-Favre, M.; Wilfrid and Scavarda, S. Alternative Causality Assignment Procedures in Bond Graph for Mechanical Systems. J. Dyn. Syst. Meas. Control. Trans. ASME 2002, 124, 457–463. [Google Scholar] [CrossRef]
- Zeid, A.; Chung, C.-H. Bond Graph modelling of multibody systems: A library of three-dimensional joints. J. Frankl. Inst. 1992, 4, 605–636. [Google Scholar] [CrossRef]
- Cellier, F.E.; Nebot, A. The Modelica Bond Graph Library. In Proceedings of the 4th International Modelica Conference, Hamburg Germany, 7–8 March 2005; p. 10. [Google Scholar]
- Zimmer, D.; François, E.C. The Modelica multi-Bond Graph library. In Proceedings of the 5th International Modelica Conference, Vienna, Austria, 4–5 September 2006. [Google Scholar]
- Filippini, G.; Nigro, N.; Junco, S. Vehicle dynamics simulation using Bond Graphs. In Proceedings of the International Modelling and Simulation Multiconference, Bueno Aires, Argentina, 8–10 February 2007. [Google Scholar]
- Boudon, B.; Dang, T.T.; Margetts, R.; Borutzky, W.; Malburet, F. Simulation methods of rigid holonomic multibody systems with Bond Graphs. Adv. Mech. Eng. 2019, 11, 1–29. [Google Scholar] [CrossRef]
- De las Heras, S.; Codina, E. Modelización de Sistemas Fluidos Mediante Bondgraph. Ph.D. Thesis, Universidad Politécnica de Madrid, Madrid, Spain, 1997. ISBN 84-605-7035-5. [Google Scholar]
- Pacejka, H.B. Tire and Vehicle Dynamics; Butterworth-Heinemann: Oxford, UK, 2012. [Google Scholar] [CrossRef]
- Merrit, H.E. Hydraulic Control Systems; John Wiley & Sons: Hoboken, NJ, USA, 1967; ISBN 0-471-59617-5. [Google Scholar]
- Borghi, M.; Milani, M.; Poaluzzi, R. Influence of Notch Shape and Number of Notches on the Metering Characteristics of Hydraulic Spool Valves. Int. J. Fluid Power 2005, 6, 5–18. [Google Scholar] [CrossRef]
- Lines, J.A.; Murphy, K. The radial damping of agricultural tractor tires. J. Terramechanics 1991, 28, 229–241. [Google Scholar] [CrossRef]
- Lines, J.A.; Murphy, K. The stiffness of agricultural tractor tires. J. Terramechanics 1991, 28, 49–64. [Google Scholar] [CrossRef]
- Berne, L.J.; Raush, G.; Roquet, P.; Gámez-Montero, P.J.; Codina, E. Graphic Method to Evaluate Power Requirements of a Hydraulic System Using Load-Holding Valves. Energies 2022, 15, 4558. [Google Scholar] [CrossRef]
























| Longitudinal Stability Compromised by the Following: | Lateral Stability Compromised by the Following: | ||||
|---|---|---|---|---|---|
| Action | Cause | Action | Cause | ||
| Load raising/lowering movement | Boom lifting/Extension | Gravitational force | Load transportation | Vehicle braking | Inertial force |
| Load lowering | Sudden boom braking | Inertial force | Travelling on uneven surfaces | Potholes, bumps, ramps, slopes | Gravitational/inertial force |
| Load transportation | Vehicle braking | Inertial force | Specific eccentric loads | Gravitational/inertial force | |
| Travelling on uneven surfaces | Potholes, bumps, ramps, slopes | Gravitational/inertial force | Suspended load | Gravitational/inertial force | |
| Suspended load | Gravitational/inertial force | Wind | External force | ||
| (a) | (b) | ||||
| CM (m) | Moment of Inertia, IIG (kg m2) | |||||||
|---|---|---|---|---|---|---|---|---|
| Rigid Body | Denomination | Mass (kg) | x | y | z | IIG1 (kg m2) | IIG2 (kg m2) | IIG3 (kg m2) |
| Left front wheel | RB1 | 40.0 | 0.000 | 0.628 | 0.360 | 1.0 | 1.0 | 2.2 |
| Right front wheel | RB2 | 40.0 | 0.000 | −0.628 | 0.360 | 1.0 | 1.0 | 2.2 |
| Left rear wheel | RB3 | 40.0 | −1.750 | 0.628 | 0.360 | 1.0 | 1.0 | 2.2 |
| Right rear wheel | RB4 | 40.0 | −1.750 | −0.628 | 0.360 | 1.0 | 1.0 | 2.2 |
| Platform (motor, axle, cardan, transfer box, oil tank, chassis) | RB5 | 2096.0 | −1.250 | 0.014 | 0.710 | 121.0 | 1032.0 | 1085.0 |
| Rear axle | RB6 | 113.0 | −1.741 | 0.010 | 0.362 | 0.8 | 12.6 | 12.6 |
| Boom | RB7 | 147.0 | −0.809 | −0.476 | 1.130 | 37.5 | 37.5 | 3.0 |
| Mobile boom | RB8 | 165.0 | −0.203 | −0.383 | 0.927 | 76.0 | 76.0 | 6.4 |
| Attachment (tablier, rocker, two forks) | RB9 | 178.0 | 0.938 | 0.000 | 0.102 | 2.0 | 2.0 | 3.5 |
| Load | RB10 | 640.0 | 1.177 | 0.000 | 0.514 | 266.0 | 266.0 | 266.0 |
| Housing lift cylinder | RB11 | 25.5 | −0.805 | −0.476 | 0.858 | 1.5 | 1.5 | 0.2 |
| Piston lift cylinder | RB12 | 25.5 | −0.805 | −0.476 | 0.858 | 1.5 | 1.5 | 0.2 |
| Housing compensation cylinder | RB13 | 9.0 | −1.325 | −0.476 | 1.079 | 0.3 | 0.3 | 0.1 |
| Piston compensation cylinder | RB14 | 9.0 | −1.325 | −0.476 | 1.079 | 0.3 | 0.3 | 0.1 |
| Housing flip cylinder | RB15 | 14.5 | 0.250 | −0.260 | 0.611 | 0.3 | 0.3 | 0.1 |
| Piston flip cylinder | RB16 | 14.5 | 0.250 | −0.260 | 0.611 | 0.3 | 0.3 | 0.1 |
| Housing steering cylinder | RB17 | 6.5 | −1.872 | 0.000 | 0.439 | 0.3 | 0.3 | 0.1 |
| Piston steering cylinder | RB18 | 6.5 | −1.872 | 0.000 | 0.439 | 0.3 | 0.3 | 0.1 |
| Left steering rod | RB19 | 2.0 | −1.872 | 0.412 | 0.439 | 0.1 | 0.1 | 0.1 |
| Right steering rod | RB20 | 2.0 | −1.872 | −0.412 | 0.439 | 0.1 | 0.1 | 0.1 |
| Left carrier | RB21 | 3.0 | −1.787 | 0.455 | 0.450 | 0.5 | 0.5 | 0.2 |
| Right carrier | RB22 | 3.0 | −1.787 | −0.455 | 0.450 | 0.5 | 0.5 | 0.2 |
| Table (Hydraulic Parameters) | Value | Units |
|---|---|---|
| Oil density | 875 | kg/m3 |
| Oil bulk modulus | 17.500 | bar |
| Oil kinematic viscosity | 46 | cSt |
| Pump maximum displacement | 12 | cm3/rev |
| Pump volumetric efficiency | 0,93 | |
| Pump hydraulic–mechanical efficiency | 0,96 | |
| Relief valve cracking pressure | 210 | bar |
| Overcentre valve ratio (CEB) (*) | 4:1 | |
| Overcentre pressure setting | 275 | bar |
| Directional control valve block (*) | 202 | serie |
| Viscous friction coefficient | 50 | N/m/s |
| Cylinder leakage coefficient | 0.01 | L/min/bar |
| Piston diameter of the boom hydraulic cylinder | 100 | mm |
| Rod diameter of boom hydraulic cylinder | 55 | mm |
| Travel of boom hydraulic cylinder | 689 | mm |
| Piston diameter of the extension hydraulic cylinder | 60 | mm |
| Rod diameter of extension hydraulic cylinder | 40 | mm |
| Travel of extension hydraulic cylinder | 1.239 | mm |
| Piston diameter of the fork hydraulic cylinder | 100 | mm |
| Rod diameter of fork hydraulic cylinder | 60 | mm |
| Travel of fork hydraulic cylinder | 268 | mm |
| Piston diameter of the slave hydraulic cylinder | 75 | mm |
| Rod diameter of slave hydraulic cylinder | 45 | mm |
| Travel of slave hydraulic cylinder | 344 | mm |
| Engine power | 19 | kW |
| Torque | 92.6/1700 | Nm/rpm |
| Engine speed | 2.300 | rpm (max) |
| Instrumentation | Characteristics | Reference |
|---|---|---|
| Position: 2 inclinometers | 2 inclinometers (I) to measure fork levelling −45° to 45° and 4 to 20 mA | SICK TMM55E-PMH045 |
| 3 extensometers (X) to measure boom extension. 0 to 1500 mm and 0 to 10 V | Micro epsilon, WDS-1500-P60-SR-U | |
| Accelerometers: 7 accelerometers | 7 lineal accelerometers, 3 axes, ranging from 3 g and 6 g | SparkFun, Triple Axis Accelerometer—MMA7260Q (6 g)/Analogue devices, ADXL335 Small, Low Power, 3-Axis ± 3 g |
| Loading: 2 weighing equipment | 2 electronic weighing system with visor. Used to weigh vehicle’s axles and total weight. Composed of two portable platforms of the WWS series and weighing terminal with touch screen and integrated printer. | DINI ARGEO USBCKR-1, portable kit. Wired version |
| Flow: 1 flowmeter | A flowmeter (Q) 0 to 300 L/min., 4 to 20 mA | HYDAC EVS 3100-A-0300-000 |
| Pressure: 13 pressure transducers (P) | 13 pressure transducers (P) of two types: 3 of 0–400 bar and 10 of 0–250 bar. 4 to 20 mA | WIKA, MH3 with connector M12 |
| Temperature: 1 sensor (T) | A PT 100 (T) temperature sensor and temperature transmitter (converts PT100 signal to a 4 to 20 mA electrical signal). Temperature transmitter ranges: 0 to 250 °C and 4 to 20 mA | Temperature transmitter model: Wika T20.10.100 |
| Other analogue signals | Analogue input signals of Delta Equipment: Voltage signal from 0 V at low level and 10 V at high level | 3 Triggers: one for the National Instruments Equip., one for the load cell, and one for the 3-way flow regulating valve solenoid signal |
| Experimental Equipment | Characteristics | Reference |
|---|---|---|
| Equipment 1 data acquisition | Equipment for accelerometer signals data acquisition | National Instruments USB-6343 |
| Laptop 1 | LabVIEW for acquisition of accelerometer signals | LabVIEW 2021 and NI software |
| Equipment 2 data acquisition | Data acquisition from hydraulic, position and temperature transducers and sensors | Delta RMC200 |
| Laptop 2 | Delta RMC Tools Software for acquisition signals from pressure, flow, temperature, and position sensors | Delta RMC Tools Software |
| Laptop 3 | To acquire data from the rear axle load cell of machine | |
| Digital camera | To record videos | Sony RX100 IV |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Puras, B.; Raush, G.; Freire, J.; Filippini, G.; Roquet, P.; Tirado, M.; Casadesús, O.; Codina, E. Development of a Virtual Telehandler Model Using a Bond Graph. Machines 2024, 12, 878. https://doi.org/10.3390/machines12120878
Puras B, Raush G, Freire J, Filippini G, Roquet P, Tirado M, Casadesús O, Codina E. Development of a Virtual Telehandler Model Using a Bond Graph. Machines. 2024; 12(12):878. https://doi.org/10.3390/machines12120878
Chicago/Turabian StylePuras, Beatriz, Gustavo Raush, Javier Freire, Germán Filippini, Pedro Roquet, Manel Tirado, Oriol Casadesús, and Esteve Codina. 2024. "Development of a Virtual Telehandler Model Using a Bond Graph" Machines 12, no. 12: 878. https://doi.org/10.3390/machines12120878
APA StylePuras, B., Raush, G., Freire, J., Filippini, G., Roquet, P., Tirado, M., Casadesús, O., & Codina, E. (2024). Development of a Virtual Telehandler Model Using a Bond Graph. Machines, 12(12), 878. https://doi.org/10.3390/machines12120878






