Dynamic Performance Analysis of Gas Film Floating Ring Seals Based on the Reynolds–Bernoulli Small-Perturbation Model
Abstract
:1. Introduction
2. RBSP Model
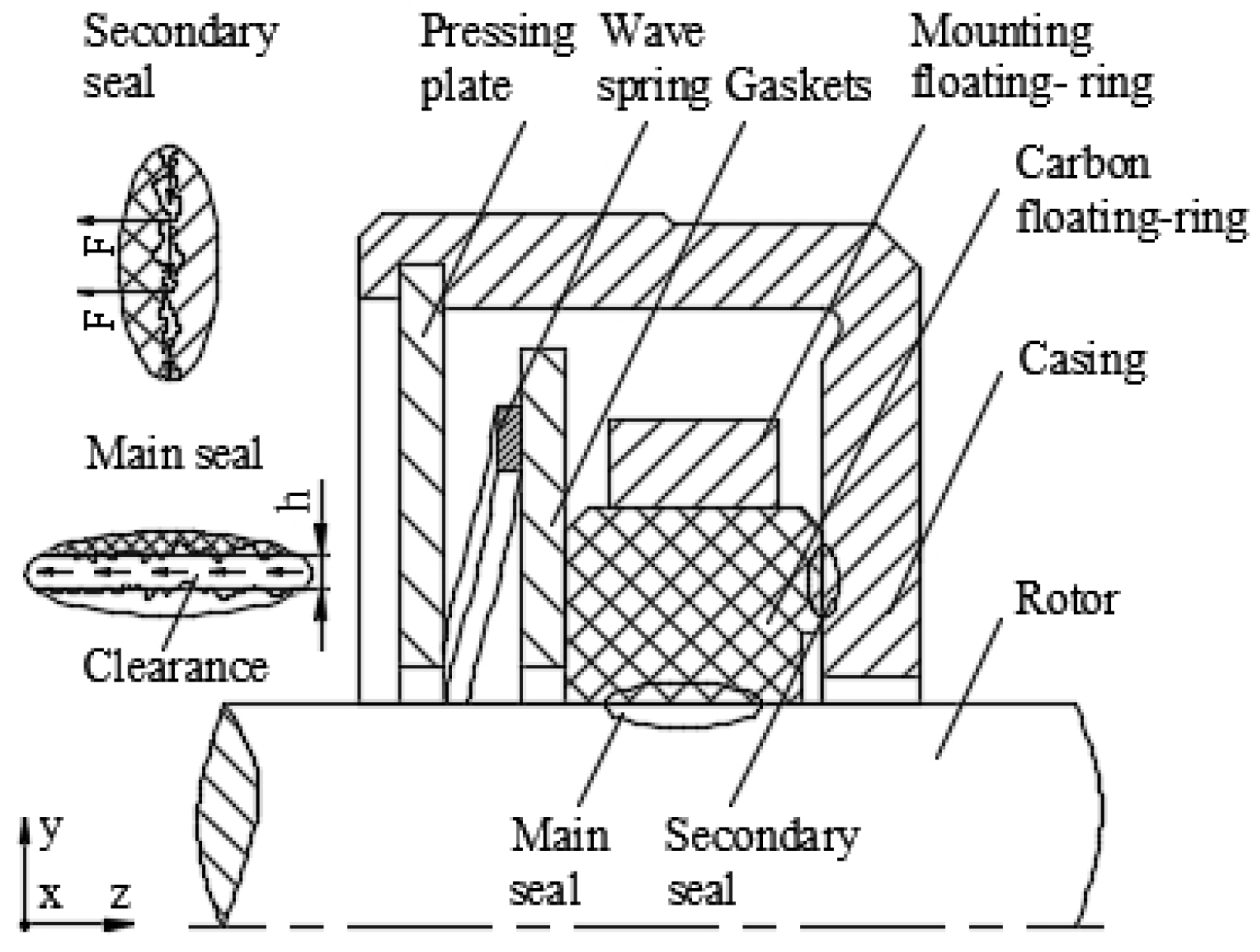
2.1. Structure and Working Principle
2.2. Reynolds–Bernoulli Gas Film Control Equation
2.3. Dynamic Characteristic Equations Based on the Small-Perturbation Method
2.4. Dynamic Pressure Control Equations
2.5. Dynamic Boundary Conditions Based on the R-B Equation
3. Analytical Models and Calculations
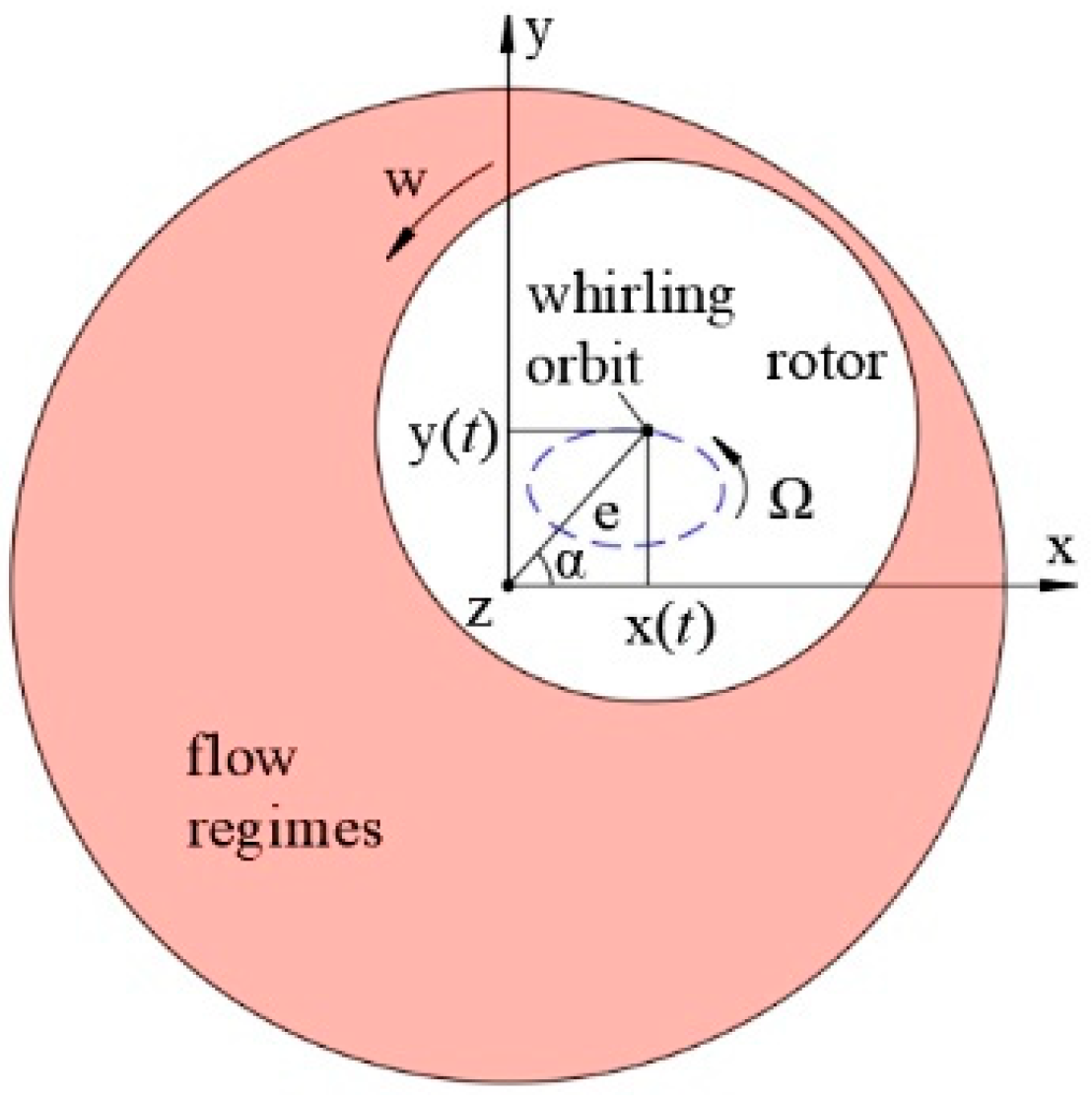
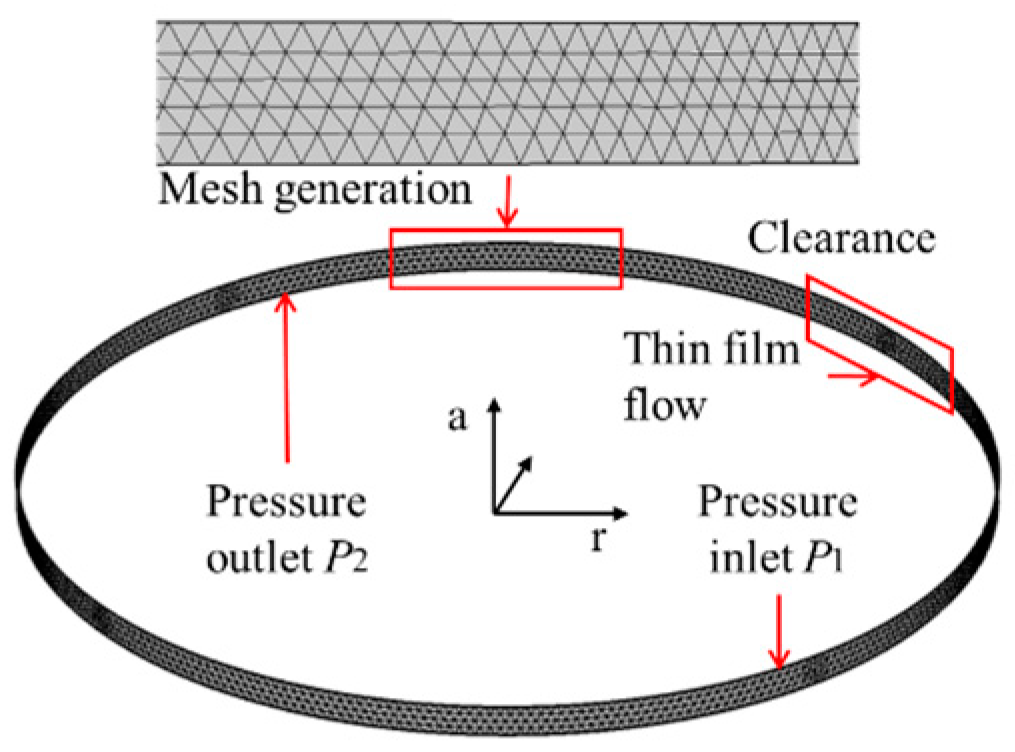
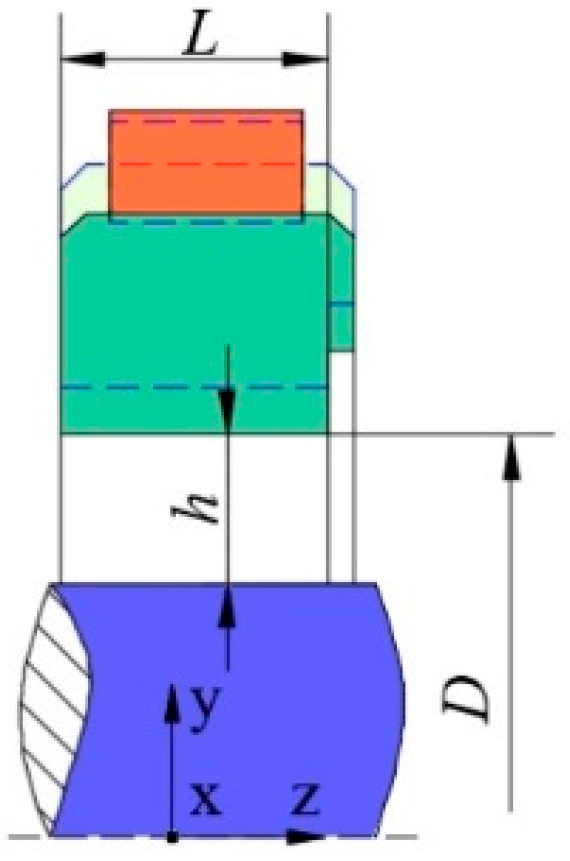
3.1. Analytical Modeling
3.2. Analysis of Calculation Results
4. Floating Ring Seal Performance Analysis
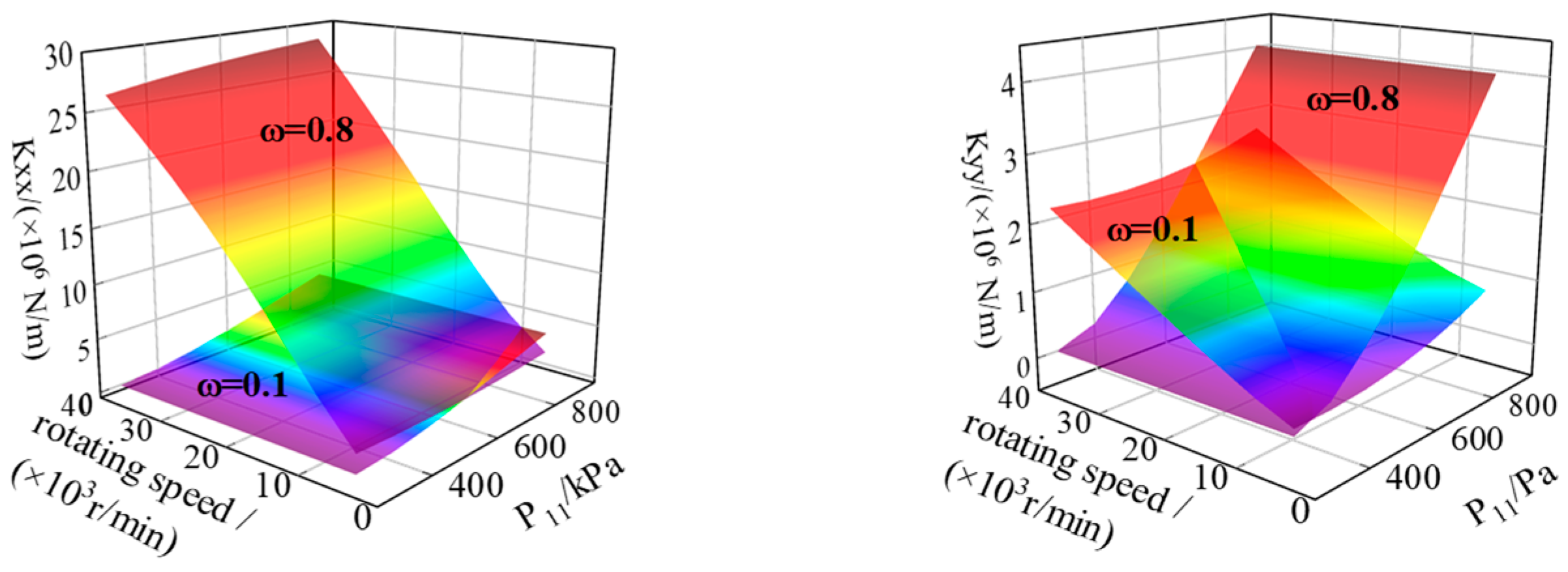
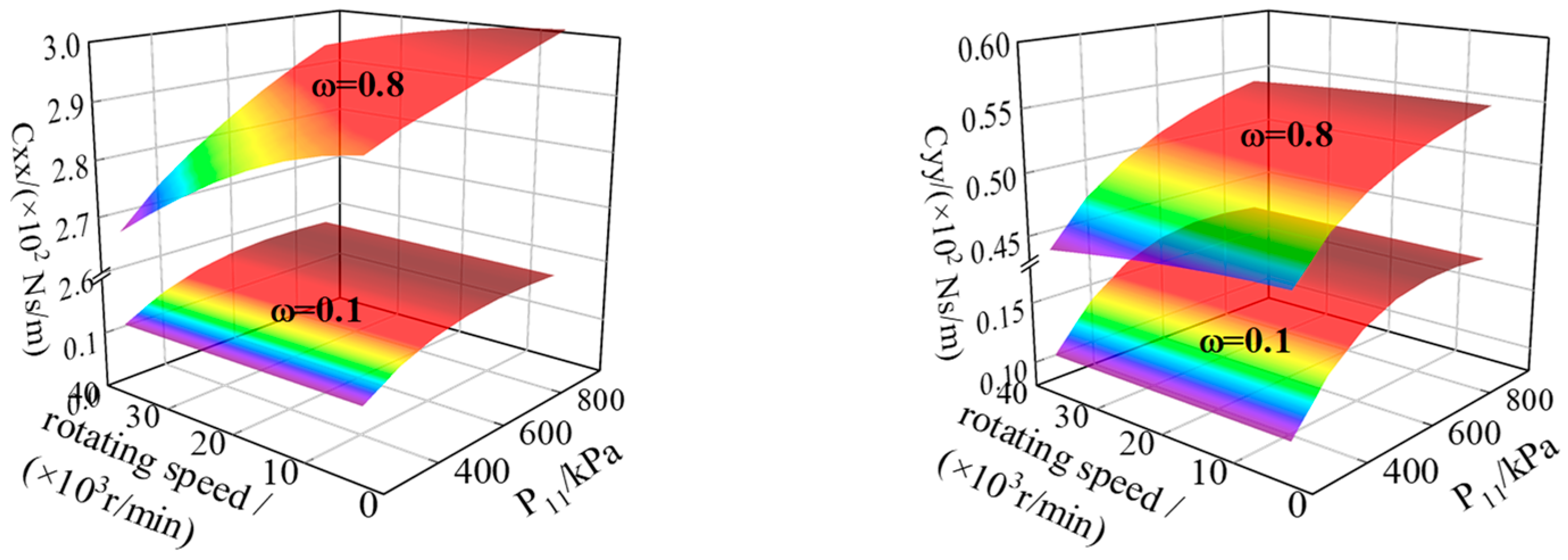
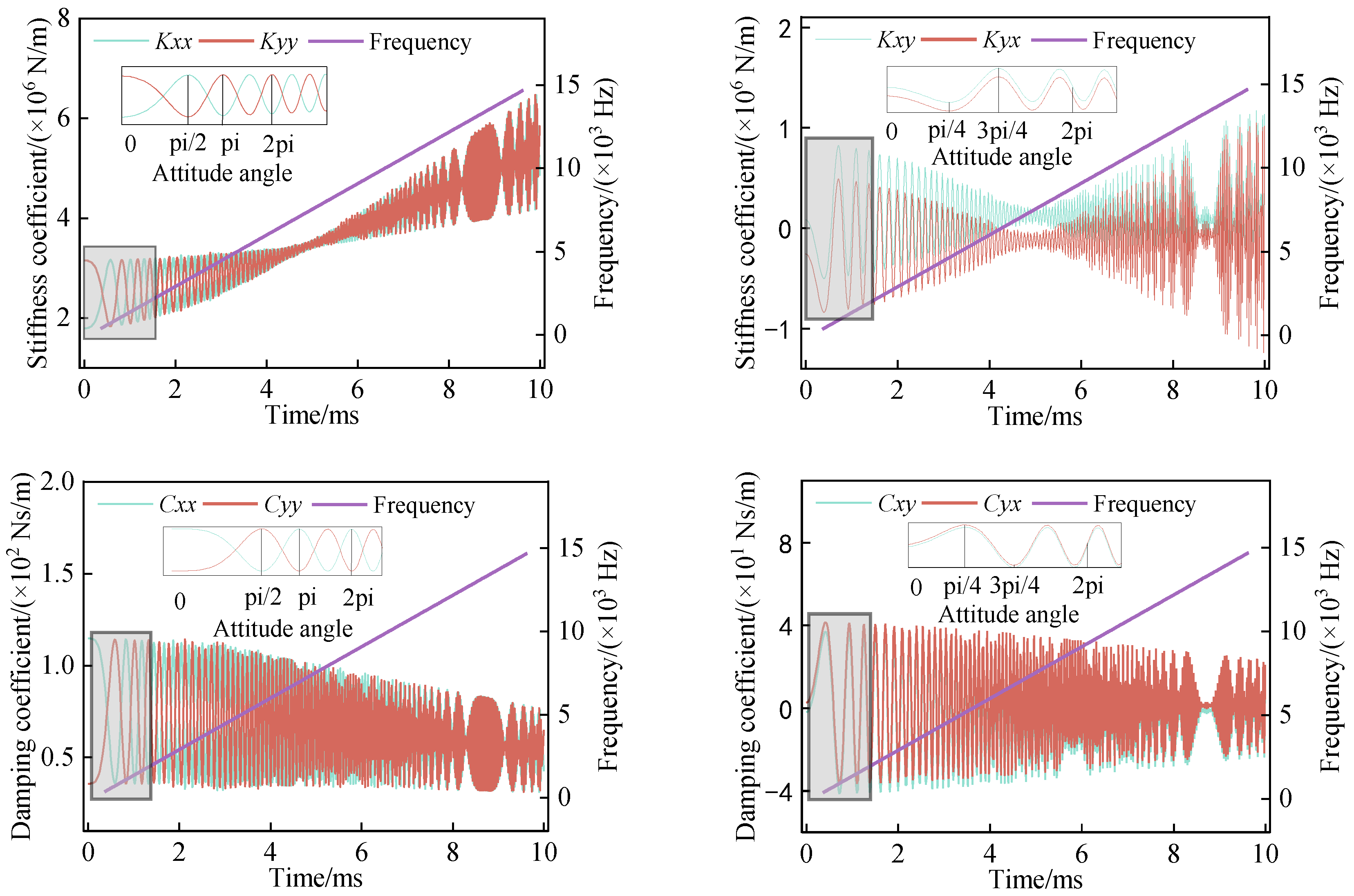
4.1. Dynamic Performance Analysis
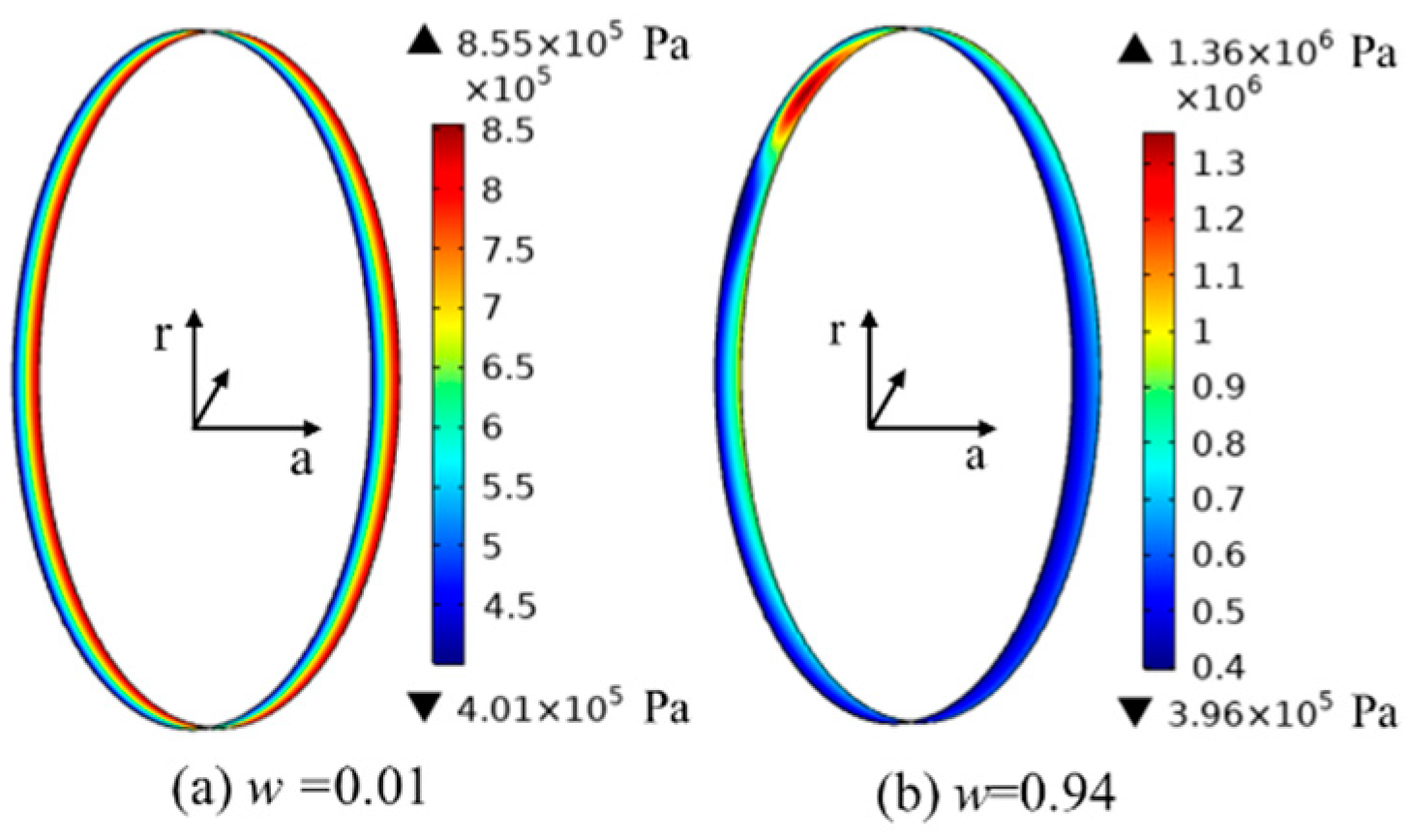
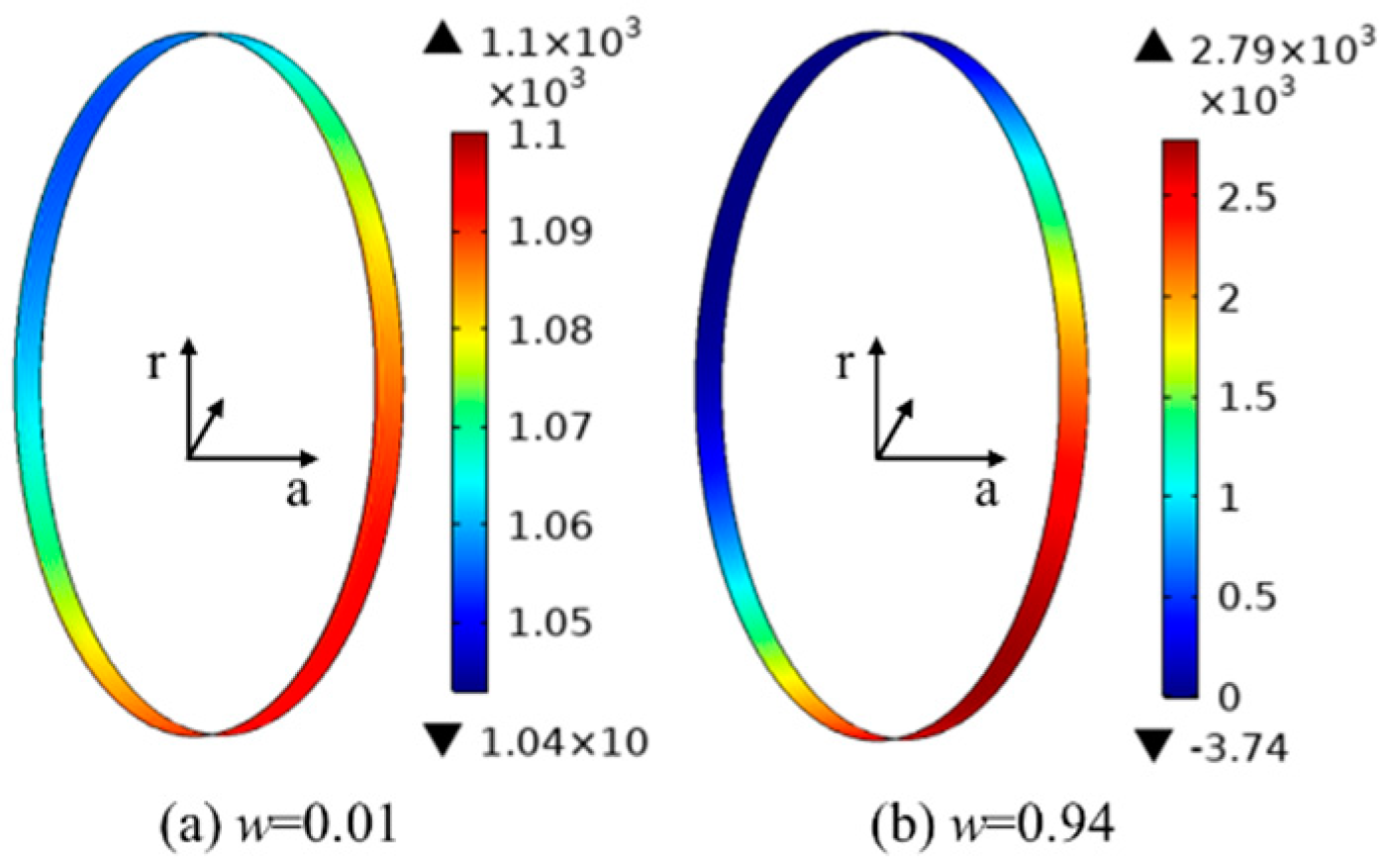
4.2. Steady-State Performance Analysis
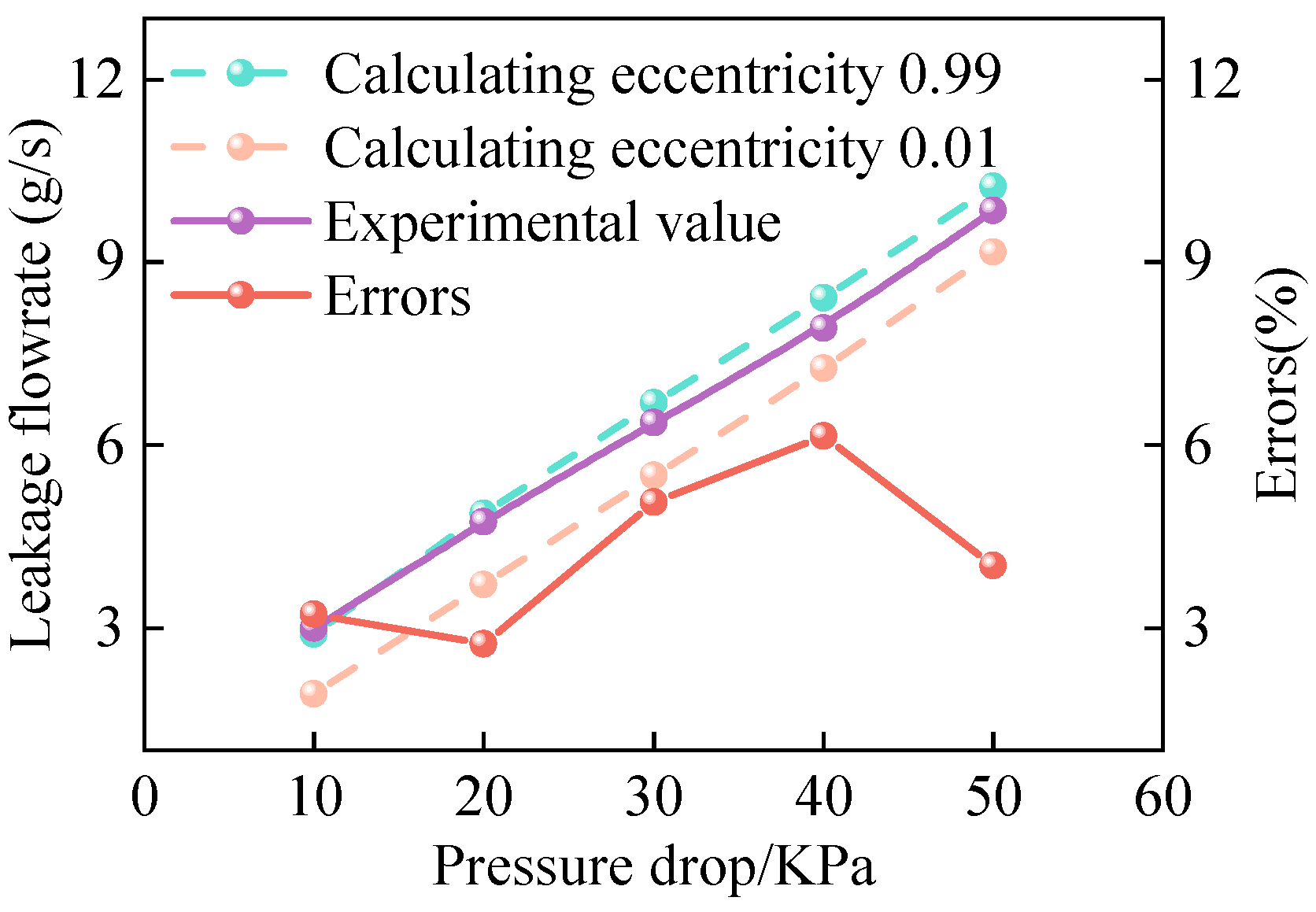
4.3. R-B Model Test Validation
5. Conclusions
- (1)
- The differential pressure effect of Poiseuille flow and the dynamic pressure effect of Couette flow are the two primary factors that enable the floating ring to overcome resistance and establish a non-contact seal. Additionally, the uneven distribution of pressure in Couette flow may be responsible for the oscillating motion of the floating ring.
- (2)
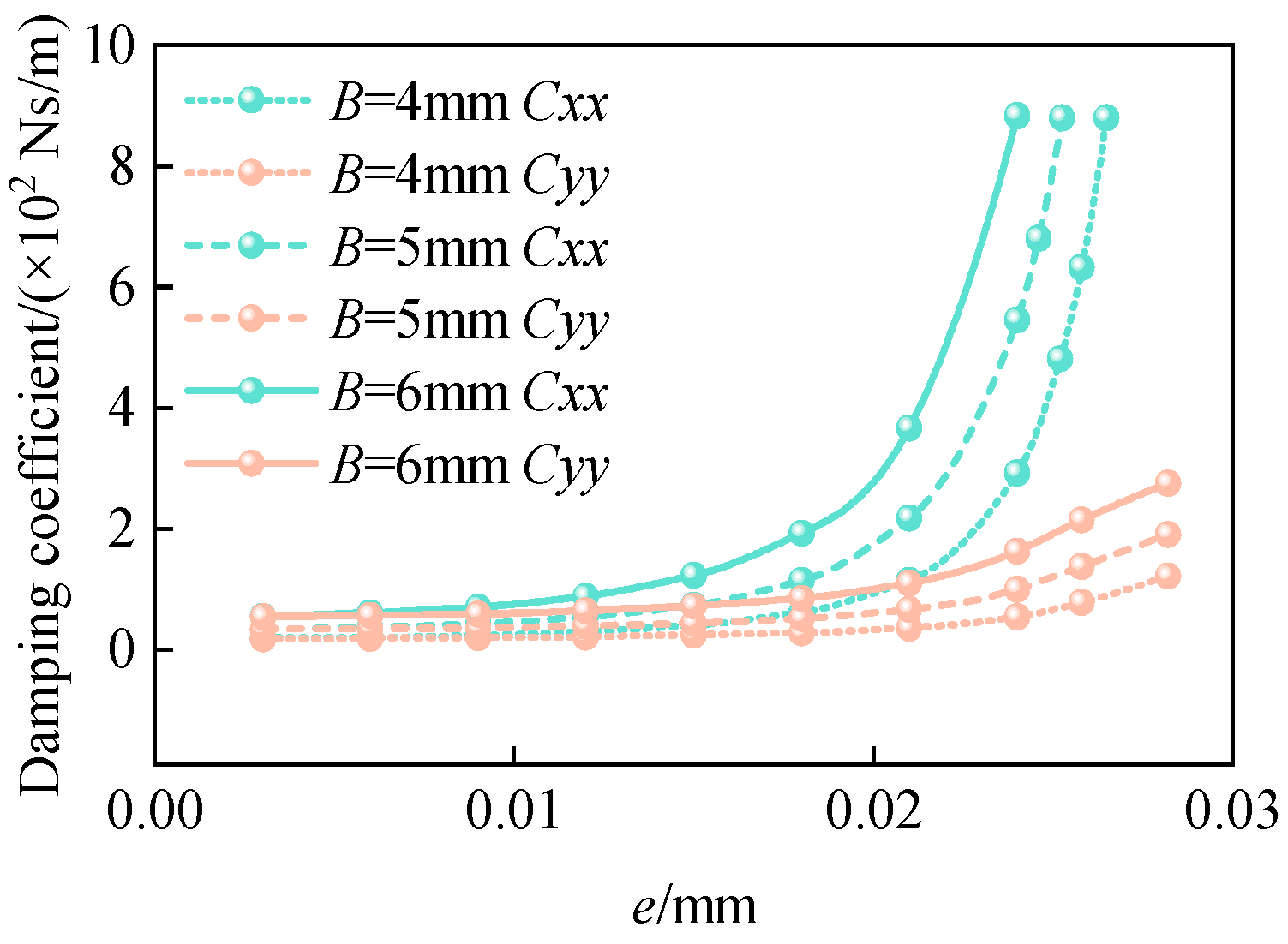
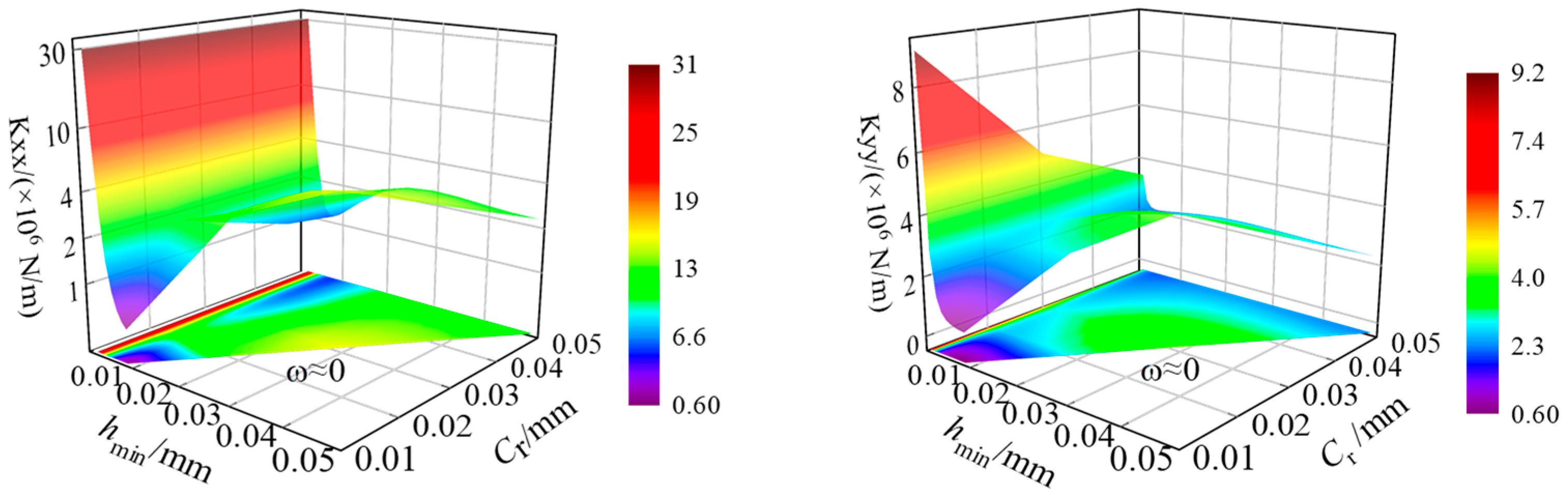
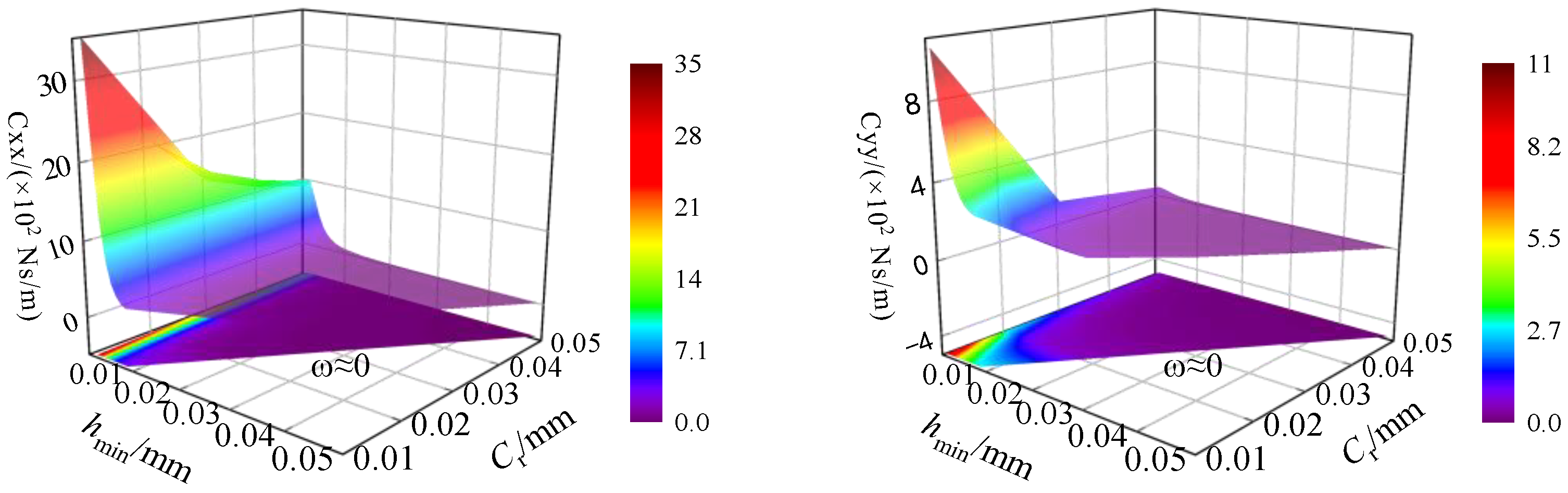
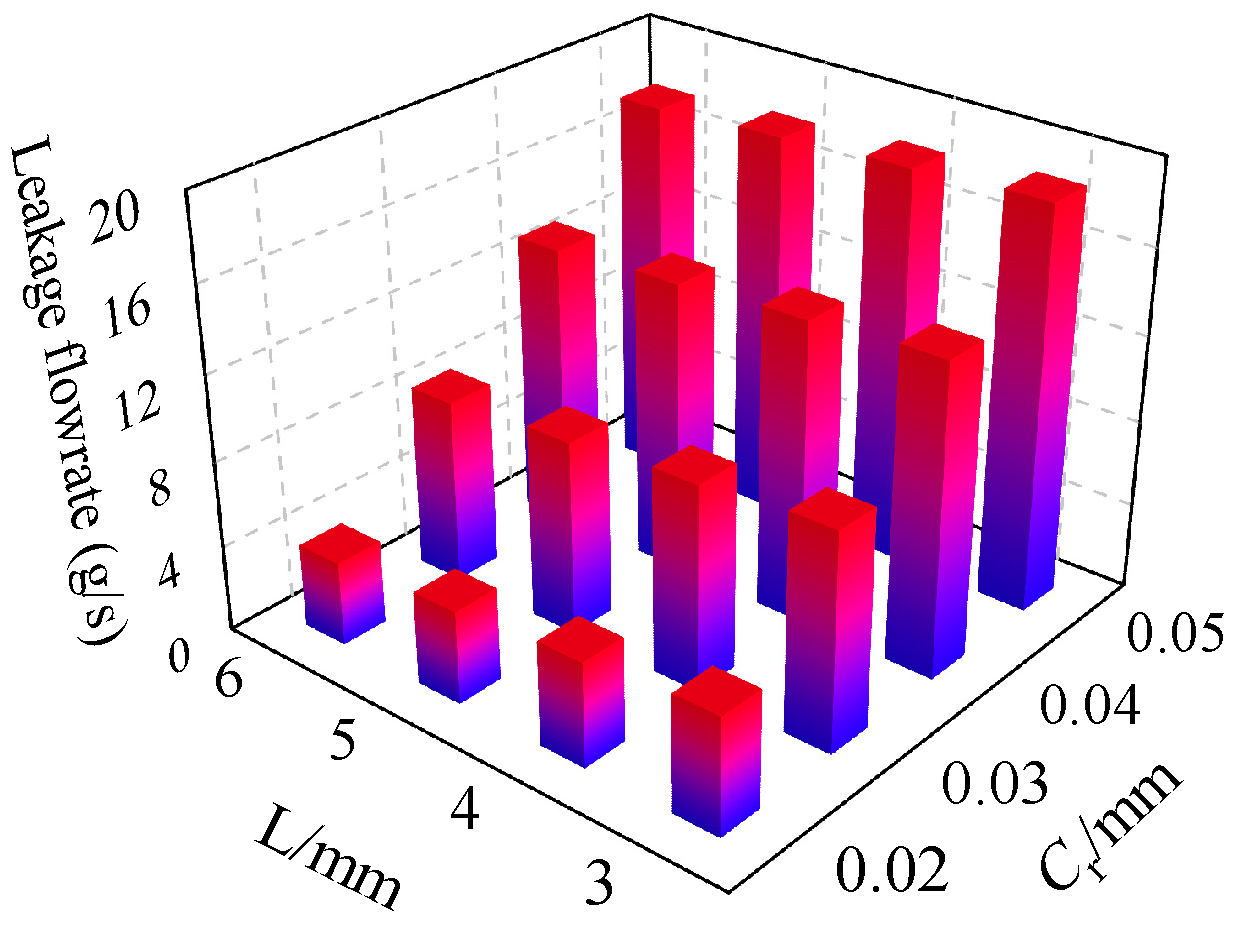
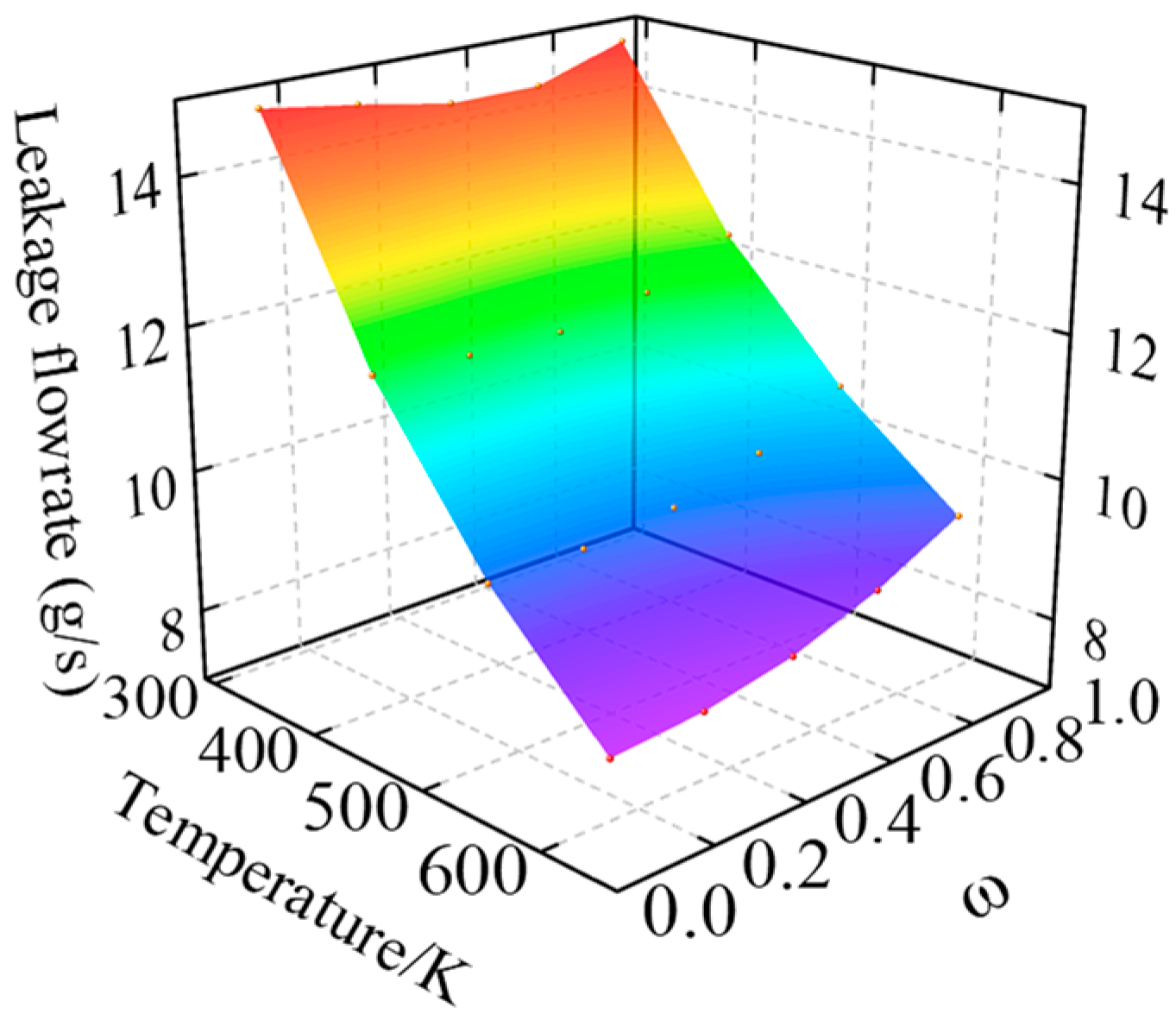
- When the minimum film thickness is greater than 0.005 mm, the pressure difference effect of Poiseuille flow dominates, and as the eccentricity increases, the dynamic pressure effect of Couette flow is significantly enhanced. A sealing radial clearance of 0.03 mm and a larger floating ring width exhibit better dynamic performance of the gas film.
- (3)
- Enhancing the differential pressure effect of Poiseuille flow and improving the pressure distribution of Couette flow are key focuses for further improving the sealing performance of the floating ring.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| damping coefficient [Ns/m] | |
| radial clearance [mm] | |
| diameter of gas film [mm] | |
| eccentricity [mm] | |
| film thickness [mm] | |
| critical film thickness [mm] | |
| minimum film thickness [mm] | |
| stiffness coefficient [N/m] | |
| Width of gas film [mm] | |
| average molar mass of the gas | |
| film pressure [Pa] | |
| inlet pressure [Pa] | |
| upstream pressure [Pa] | |
| outlet pressure [Pa] | |
| downstream pressure [Pa] | |
| molar gas constant | |
| radius of gas film [mm] | |
| time [s] | |
| velocity [m/s] | |
| axial flow velocity [m/s] | |
| relative eccentricity | |
| vibration in the x, y direction | |
| perturbation displacements | |
| perturbation velocities | |
| attitude angle | |
| air viscosity [] | |
| excitation frequency [Hz] | |
| combined standard deviation | |
| standard deviations of carbon | |
| standard deviations of casing | |
| whirl frequency [Hz] | |
| pressure loss coefficient | |
| density [kg/m3] | |
| Reynolds number |
References
- Jia, J.N.; Chen, Z.; Li, J.M.; Dong, G.G.; Hao, J. Structure and development of floating ring seals. Machinery 2007, 34, 1–3. [Google Scholar]
- Xia, P.; Liu, Z.S. Effects of structure elasticity on leakage and rotordynamic coefficients of floating ring seals. J. Propuls. Technol. 2017, 38, 2815. [Google Scholar]
- Zhang, J.Y.; Wang, L.H.; Su, X. Studies on leakage characteristics of floating ring seal based on reynolds equations and fluid numerical analysis. Machinery 2017, 44, 21–26. [Google Scholar]
- Chen, Z.; Gao, C.Y.; Fan, W.C. Simulation of flow field in a floating-ring seal and modification of its leakage rate expression. J. Sichuan Univ. (Eng. Sci. Ed.) 2016, 48, 208–214. [Google Scholar]
- Hu, T.X.; Zhou, K.; Wang, X.Y.; Li, N.; Zou, H.Y. Numerical calculation and experiment on leakage characteristics of floating ring seal. J. Aerosp. Power 2020, 35, 888–896. [Google Scholar]
- Hu, T.X.; Wang, X.Y.; Zhou, K.; Li, Q.F.; Zou, H.Y. Effects of temperature on leakage characteristics of floating ring seal. J. Propuls. Technol. 2022, 43, 200846. [Google Scholar]
- Anbarsooz, M.; Amiri, M.; Erfanian, A.; Benini, E. Effects of the ring clearance on the aerodynamic performance of a CO2 centrifugal compressors annular seal: A numerical study. Tribol. Int. 2022, 170, 107501. [Google Scholar] [CrossRef]
- Duan, W.; Chu, F.; Kim, C.-H.; Lee, Y.B. A bulk-flow analysis of static and dynamic characteristics of floating ring seals. Tribol. Int. 2007, 40, 470–478. [Google Scholar] [CrossRef]
- Wang, S.P.; Ding, X.X.; Ding, J.H.; Wang, J.M. Steady-State Characteristics of Spiral Groove Floating Ring Gas-film Seal Considering Temperature-Viscosity Effect. J. Appl. Fluid Mech. 2023, 16, 891–904. [Google Scholar]
- Tokunaga, Y.; Inoue, H.; Hiromatsu, J.; Iguchi, T.; Kuroki, Y.; Uchiumi, M. Rotor dynamic characteristics of floating ring seals in rocket turbopumps. Int. J. Fluid Mach. Syst. 2016, 9, 194–204. [Google Scholar] [CrossRef]
- Song, Z.; Li, S.; Chen, X.; Liu, Z.; Zhao, T.; Huang, B. Study on the Service Performance of a Two-Stage Floating-Ring Isolation Seal for a High-Speed Turbopump with a Cryogenic Medium. Machines 2023, 11, 373. [Google Scholar] [CrossRef]
- Hori, Y. Hydrodynamic Lubrication; Springer: Tokyo, Japan, 2006. [Google Scholar]
- Fukui, S.; Kaneko, R. A database for interpolation of poiseuille flow rates for high knudsen number lubrication problems. J. Tribol. 1990, 112, 78–83. [Google Scholar] [CrossRef]
- Wang, X.H.; Ding, X.X.; Li, N.; Zhang, Z.M.; Si, J.X. Finite element analysis and experimental verification of fractal wear on floating ring seal end faces. CIESC J. 2023, 74, 4956. [Google Scholar]
- He, Z.; Guo, Y.; Si, J.; Li, N.; Jia, L.; Zou, Y.; Wang, H. Numerical Optimization Analysis of Floating Ring Seal Performance Based on Surface Texture. Lubricants 2024, 12, 241. [Google Scholar] [CrossRef]
- Zhao, H.; Jiang, J.Y.; Sun, D.; Wang, S.; Li, Y. Numerical study on static and dynamic characteristics of an integral floating ring seal with shallow groove dynamic pressure. J. Aerosp. Power 2024, 39, 91–101. [Google Scholar]
- Mariot, A.; Arghir, M.; Hélies, P.; Dehouve, J. Experimental analysis of floating ring annular seals and comparisons with theoretical predictions. J. Eng. Gas Turbines Power 2016, 138, 042503. [Google Scholar] [CrossRef]
- Bae, J.H.; Kwak, H.D.; Heo, S.J.; Choi, C.H.; Choi, J.S. Numerical and experimental study of nose for Lox floating ring seal in turbopump. Aerospace 2022, 9, 667. [Google Scholar] [CrossRef]
- Arghir, M.; Nguyen, M.H.; Tonon, D.; Dehouve, J. Analytic modeling of floating ring annular seals. J. Eng. Gas Turbines Power 2012, 134, 052507. [Google Scholar] [CrossRef]
- Banakh, L.Y.; Barmina, O.V. Rotor system oscillations under the rotor rotation inside floating elements. J. Mach. Manuf. Reliab. 2018, 47, 6–12. [Google Scholar] [CrossRef]

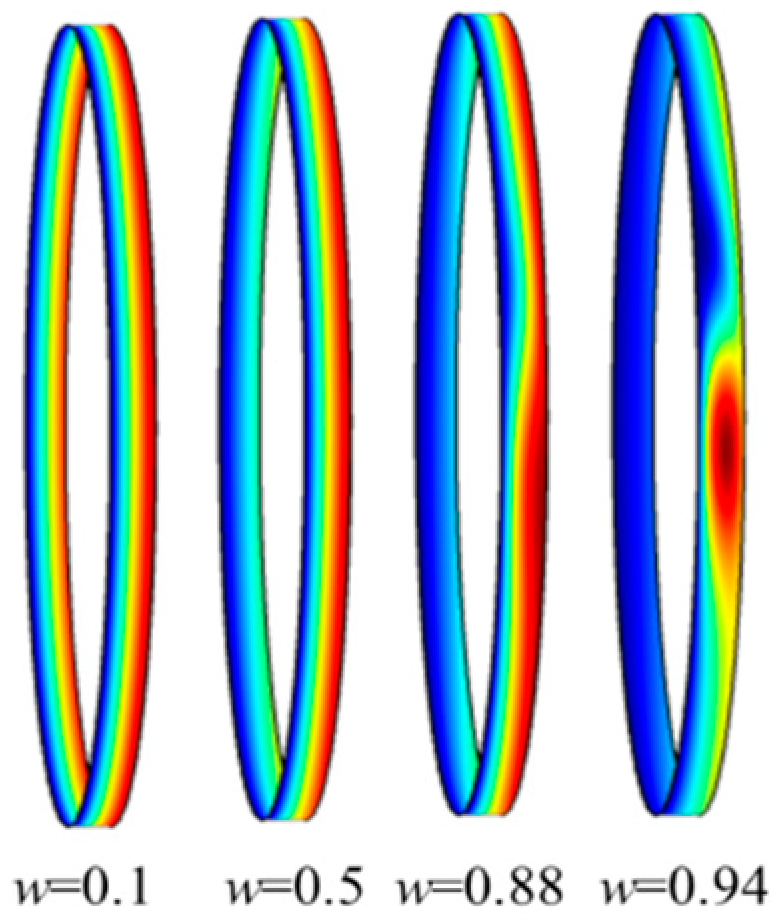
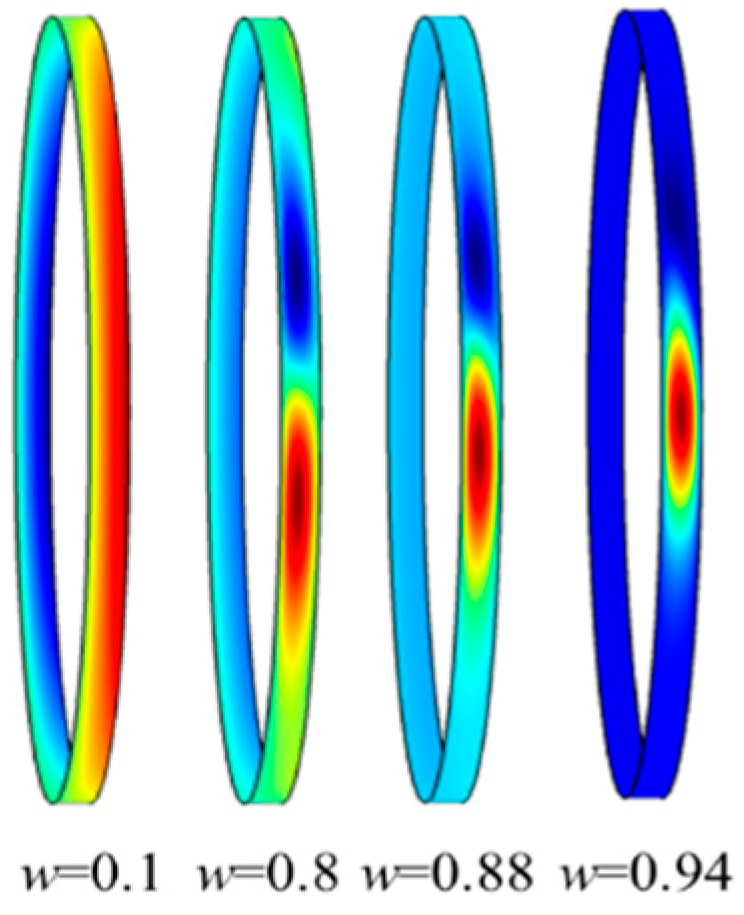
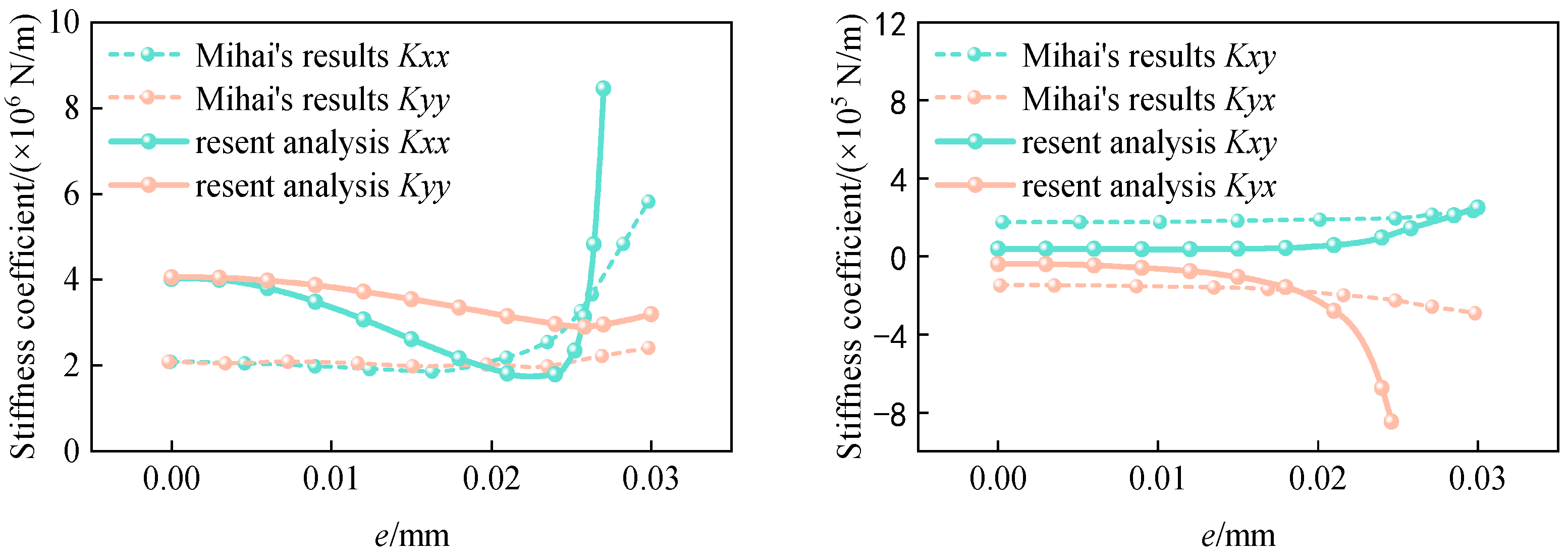

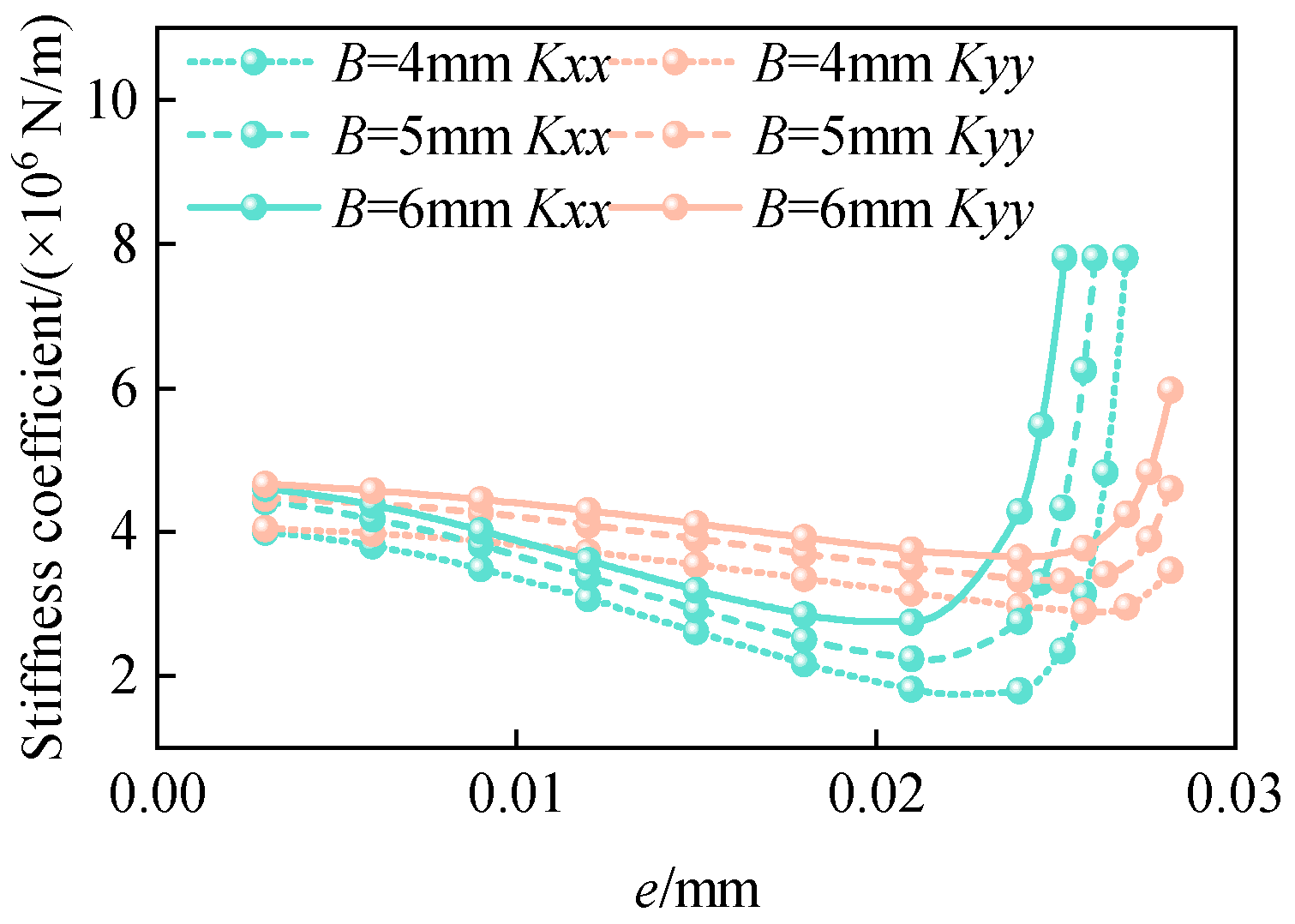



| Number of Grids | 472 | 900 | 1776 | 2836 |
|---|---|---|---|---|
| 1.797 | 1.802 | 1.804 | 1.804 | |
| 1.146 | 1.146 | 1.146 | 1.146 |
| Upstream pressure P11/kPa | 17 | 33 | 52 | 71 | 95 |
| Downstream pressure P22/kPa | 7 | 13 | 22 | 31 | 45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, S.; Ma, R.; Li, S.; Li, S. Dynamic Performance Analysis of Gas Film Floating Ring Seals Based on the Reynolds–Bernoulli Small-Perturbation Model. Machines 2024, 12, 860. https://doi.org/10.3390/machines12120860
Zhu S, Ma R, Li S, Li S. Dynamic Performance Analysis of Gas Film Floating Ring Seals Based on the Reynolds–Bernoulli Small-Perturbation Model. Machines. 2024; 12(12):860. https://doi.org/10.3390/machines12120860
Chicago/Turabian StyleZhu, Shuhai, Runmei Ma, Shuangxi Li, and Shicong Li. 2024. "Dynamic Performance Analysis of Gas Film Floating Ring Seals Based on the Reynolds–Bernoulli Small-Perturbation Model" Machines 12, no. 12: 860. https://doi.org/10.3390/machines12120860
APA StyleZhu, S., Ma, R., Li, S., & Li, S. (2024). Dynamic Performance Analysis of Gas Film Floating Ring Seals Based on the Reynolds–Bernoulli Small-Perturbation Model. Machines, 12(12), 860. https://doi.org/10.3390/machines12120860




