An Advanced Approach for Predicting Workpiece Surface Roughness Using Finite Element Method and Image Processing Techniques
Abstract
1. Introduction
2. Finite Element Modelling of Turning Process
2.1. Material Constitutive Modelling for Cutting
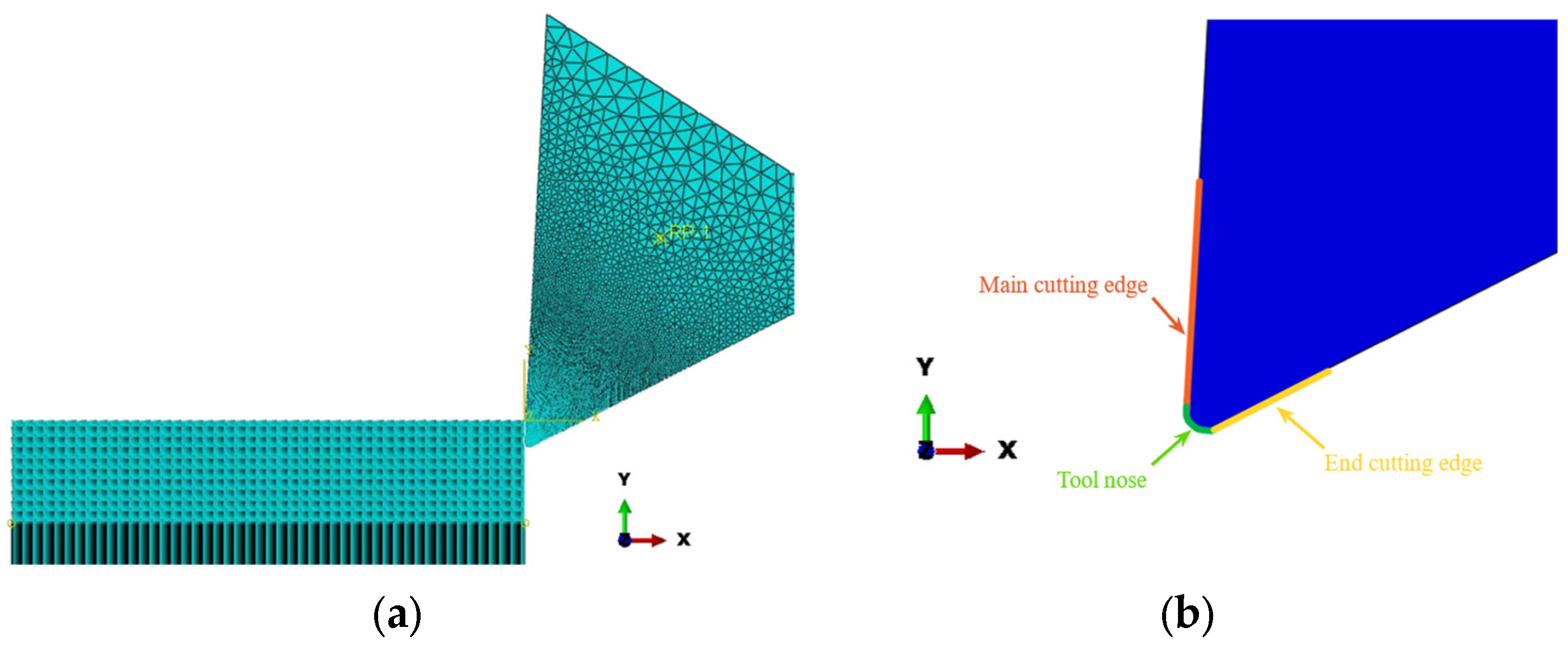
2.2. Turning FE Model Construction
3. Methodology Description
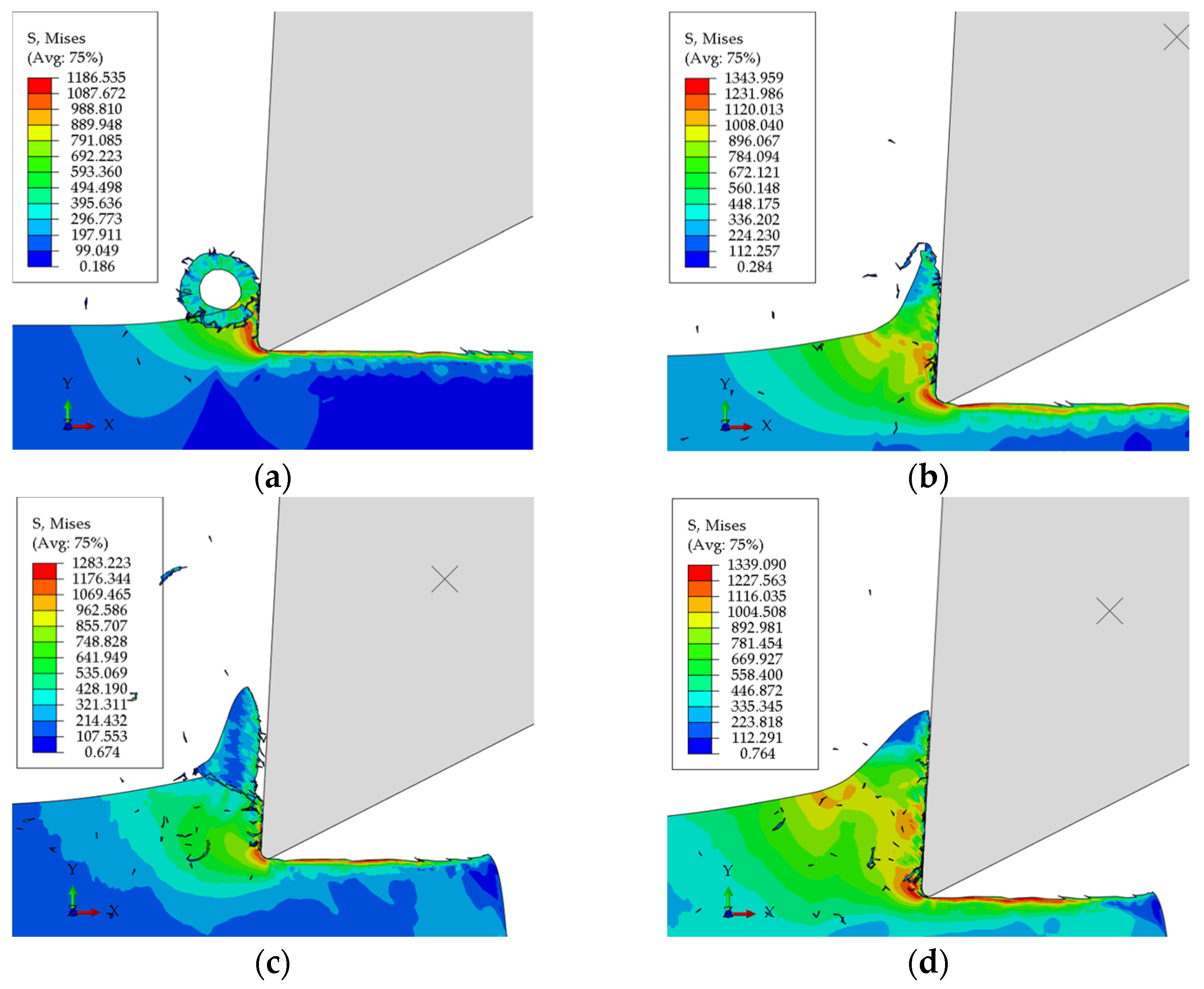
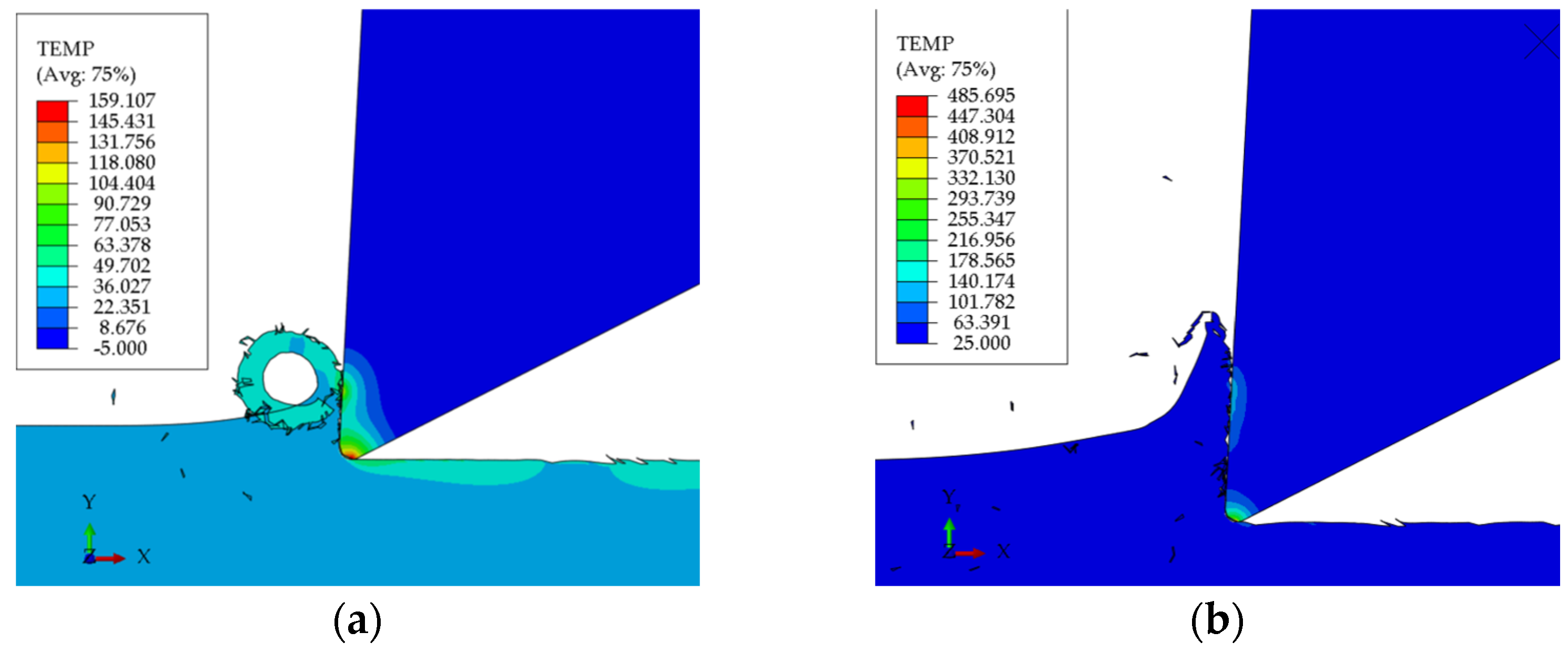
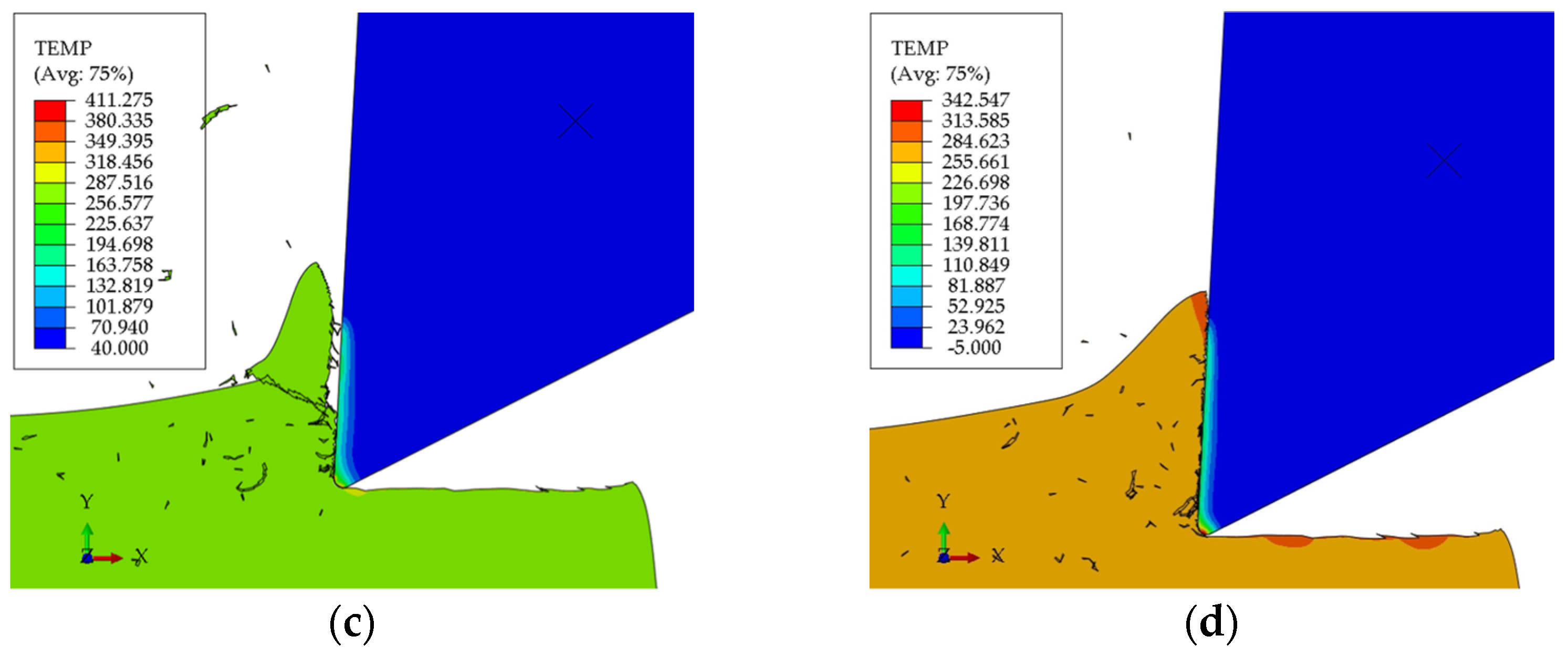
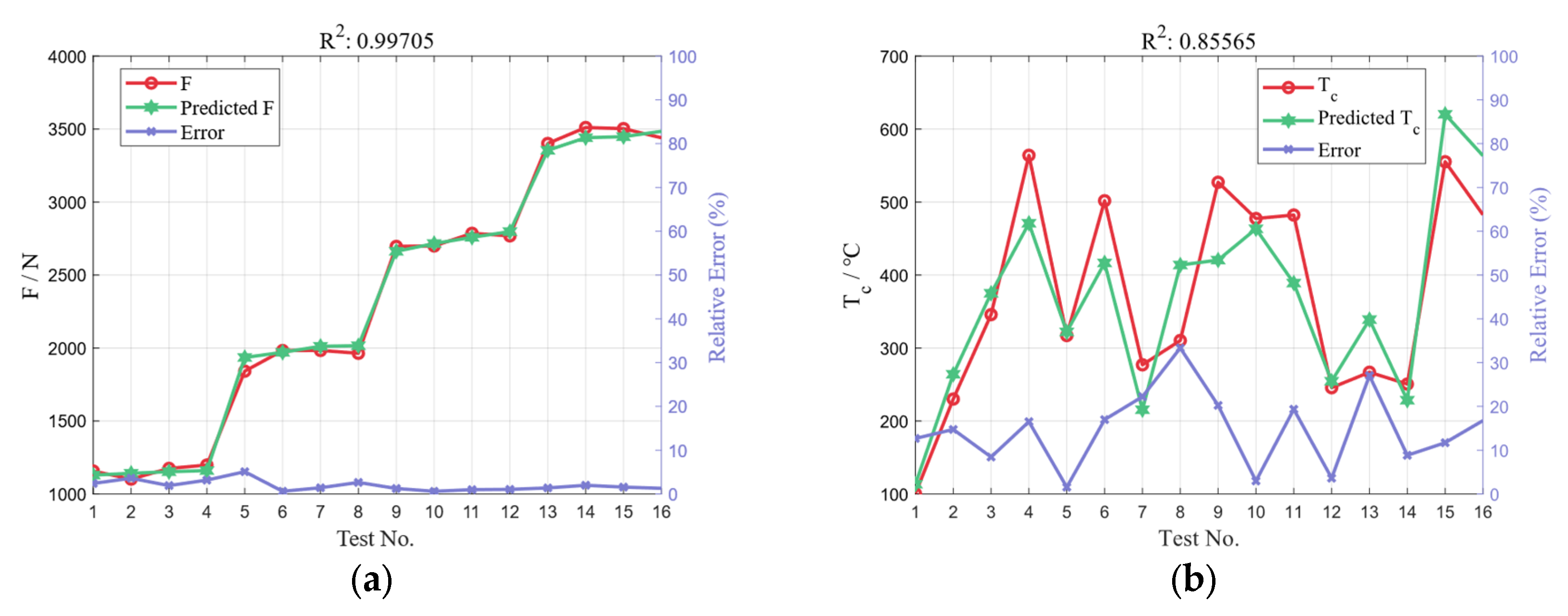
3.1. Cutting Forces and Temperatures Analysis
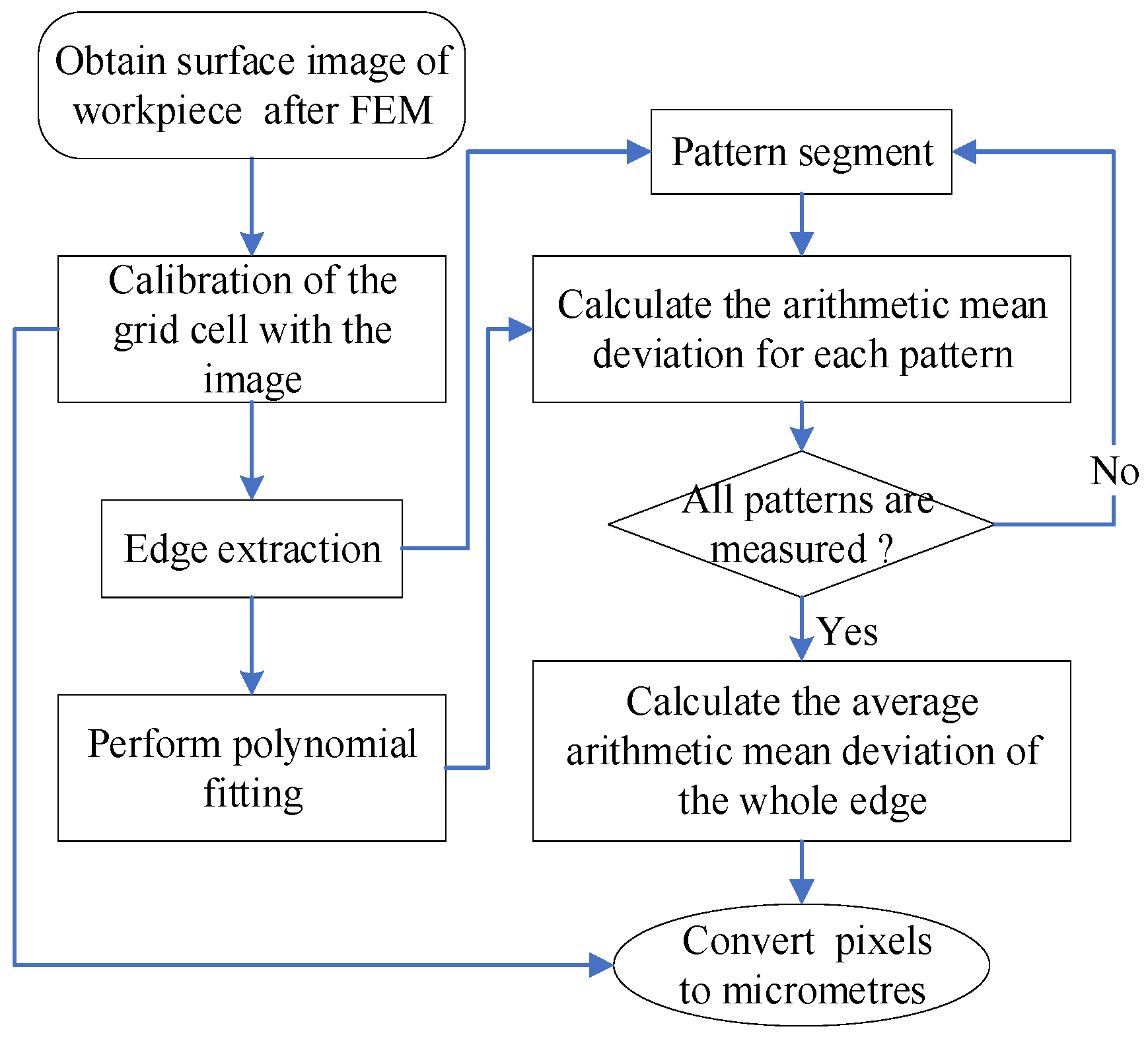
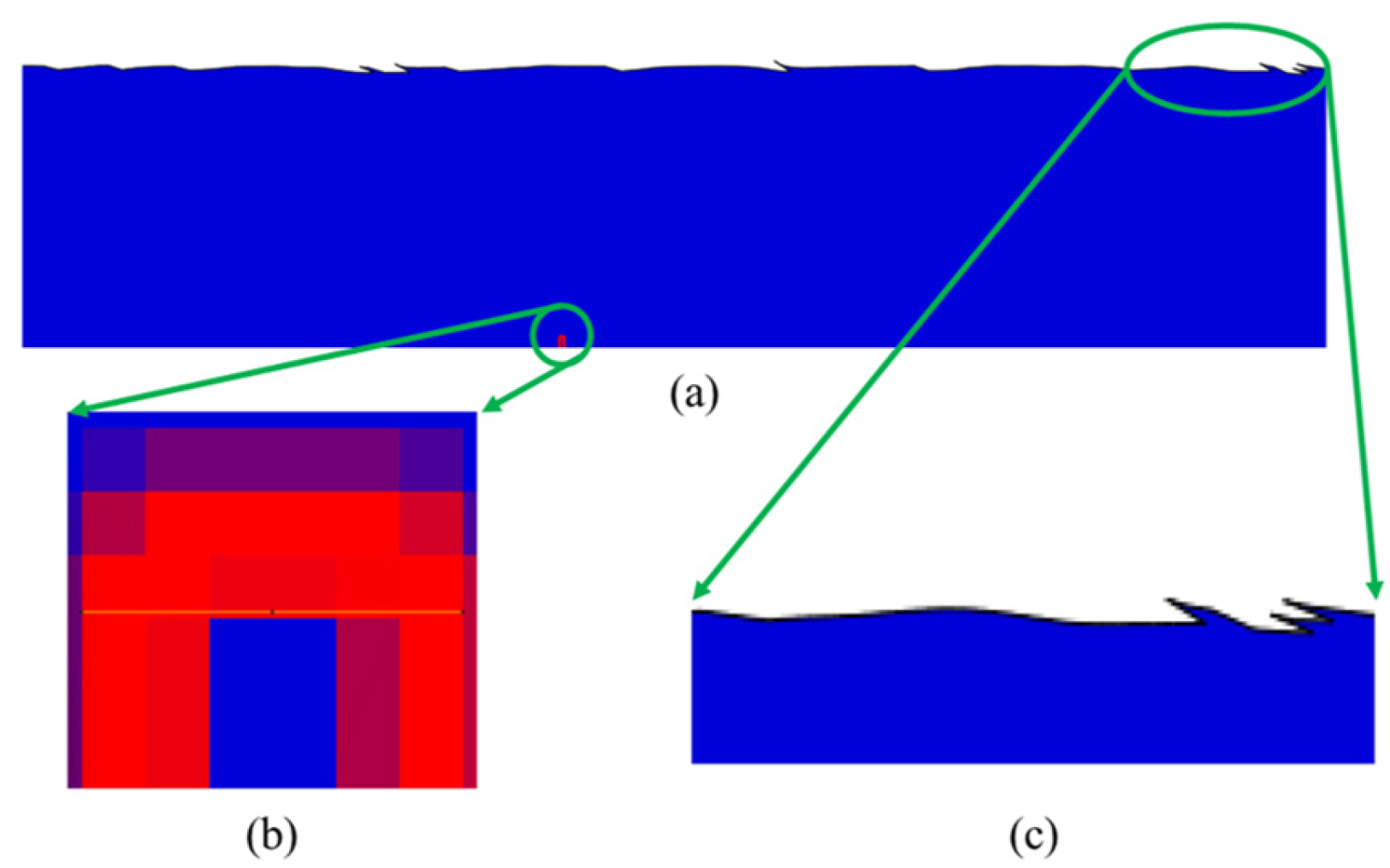
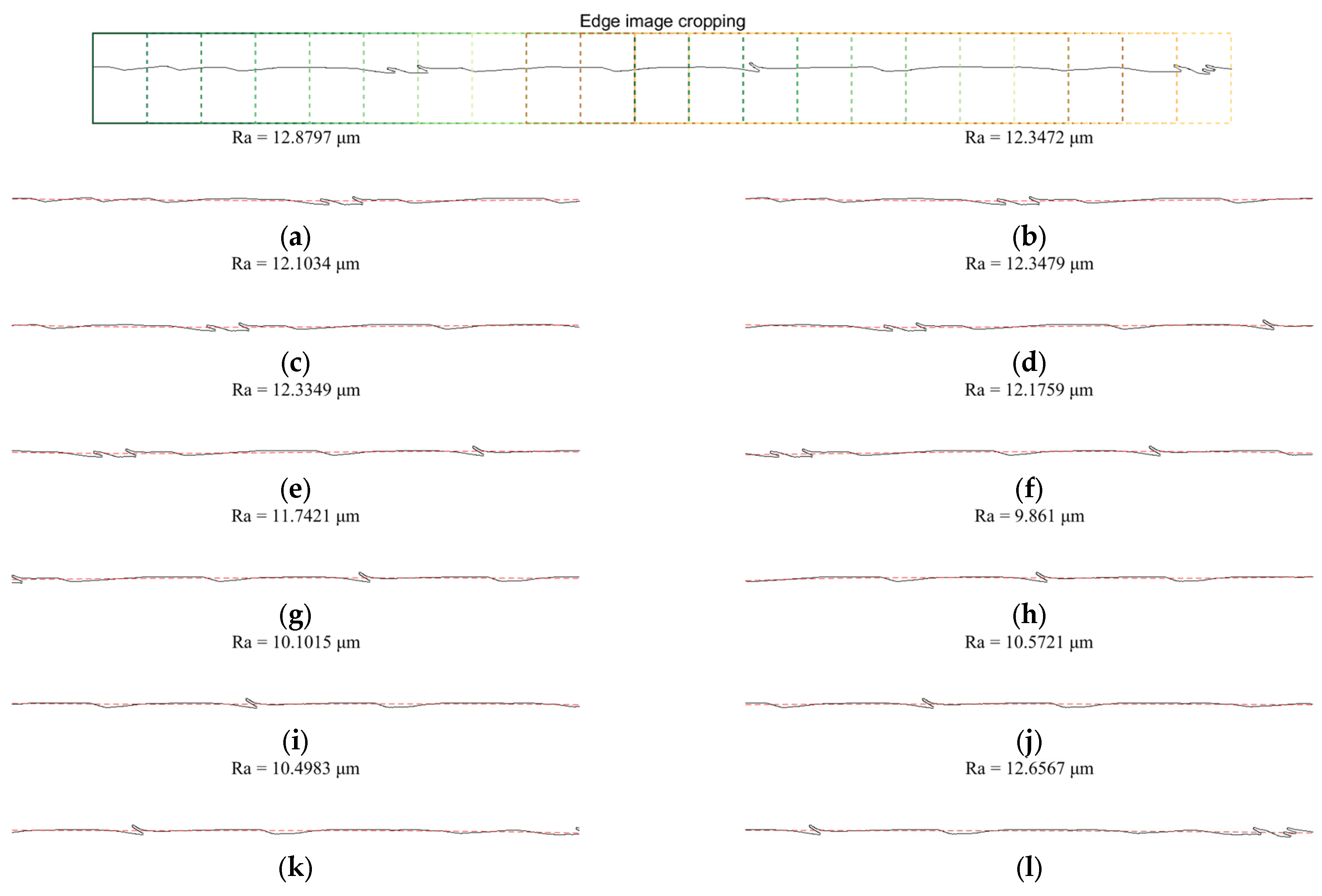
3.2. Workpiece Surface Characteristic Extraction
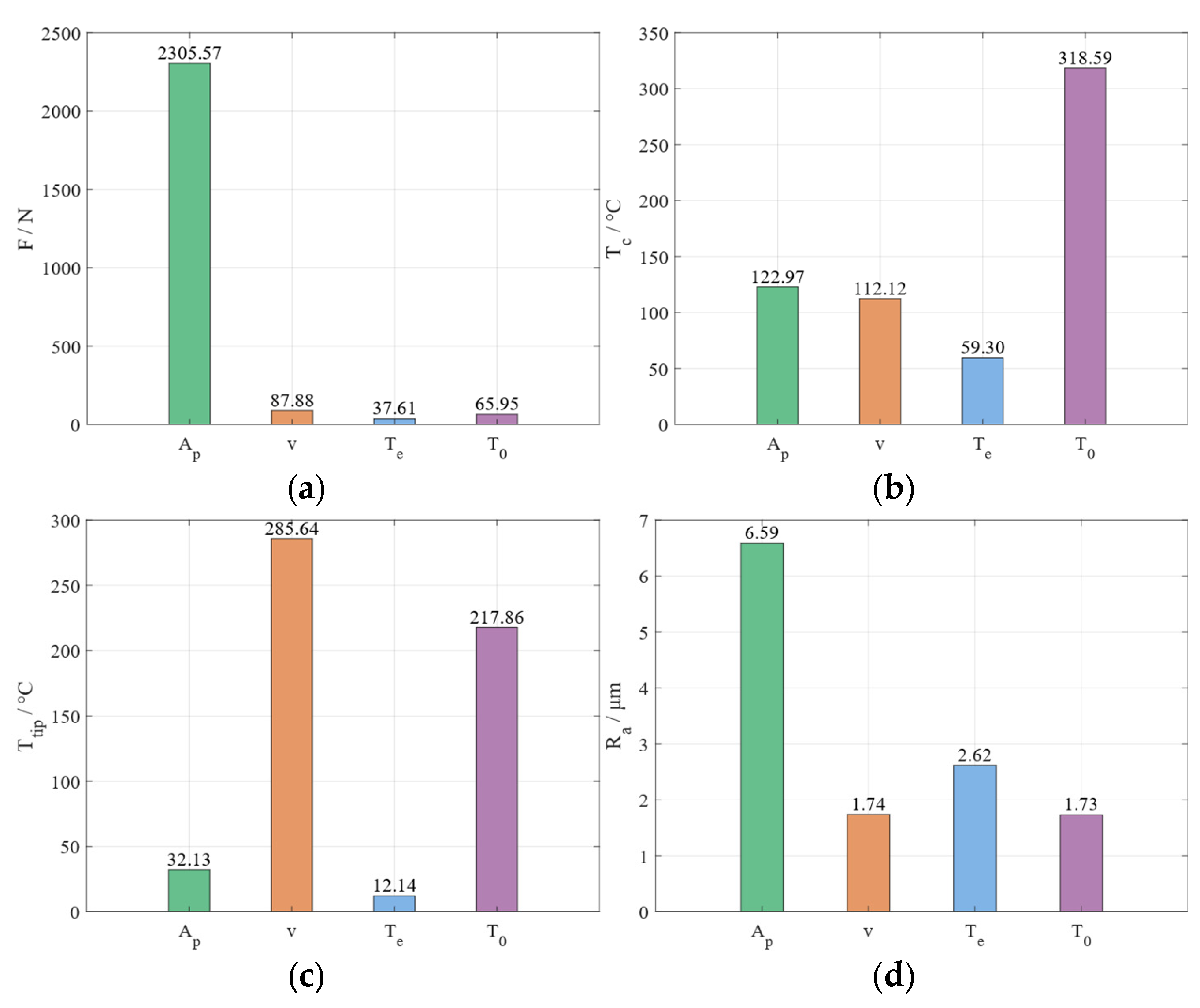
3.3. Range Analysis
3.4. Multiple Linear Regression Analysis
4. Turning Experiment Verification
4.1. Turning Operation Description
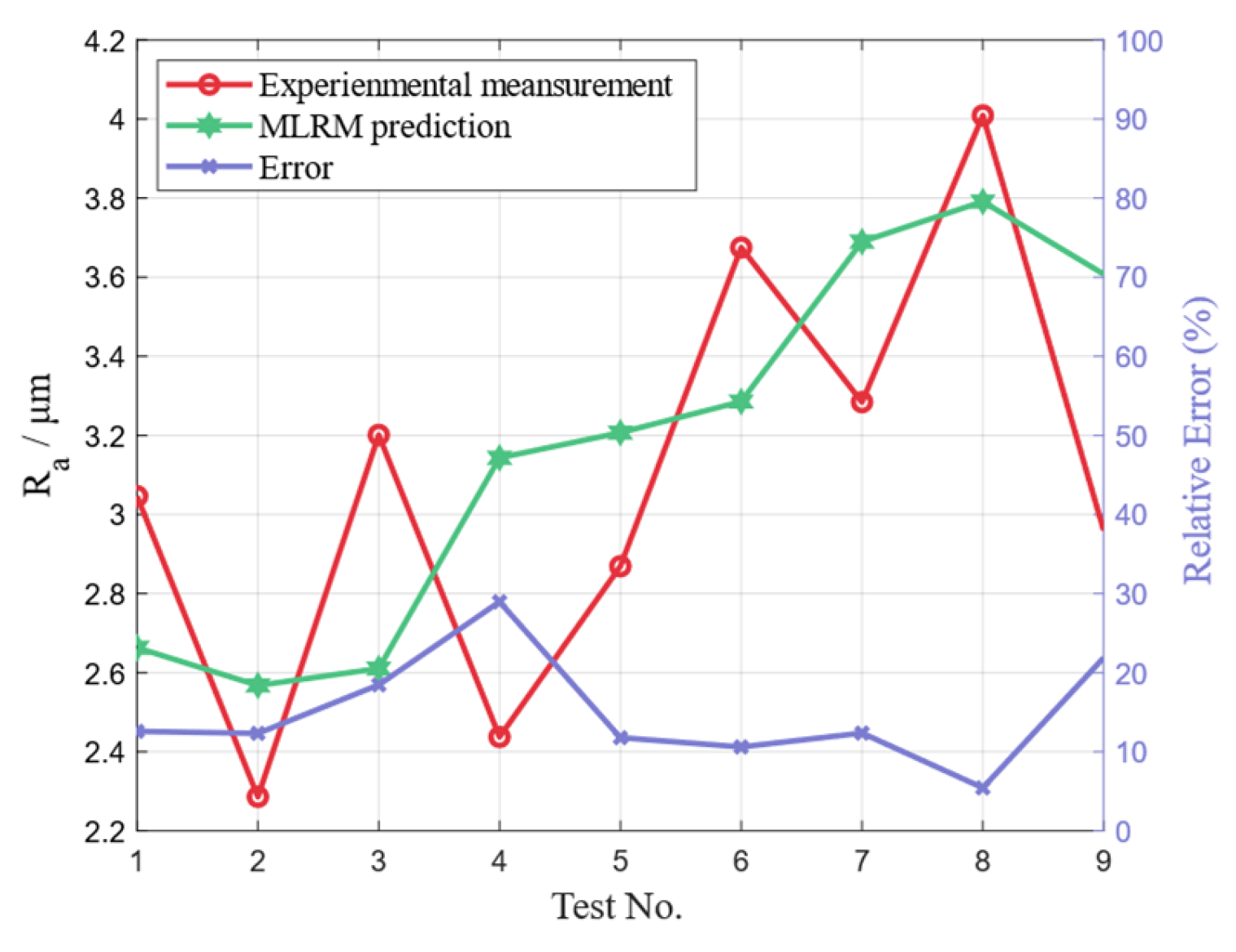
4.2. Workpiece Surface Roughness Measurement
4.3. Experiment Result Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bian, H.; Wang, Z.; Zhang, H.; Bu, X.; Lu, H.; Luo, K.; Lu, J. Response Surface Methodology-Based Optimization of Parameters and Cutting Quality of 22MnB5 Plates by UV Picosecond Laser Layered Cutting. Opt. Laser Technol. 2024, 177, 111197. [Google Scholar] [CrossRef]
- Cui, Z.; Liu, H.; Wu, L.; Cao, Z.; Zong, W. Cutting Force and Surface Quality in Ultra-Precision Milling of Oxygen-Free Copper under Different Cutting Strategies. J. Manuf. Process. 2024, 131, 2420–2442. [Google Scholar] [CrossRef]
- Wu, P.; He, Y.; Li, Y.; He, J.; Liu, X.; Wang, Y. Multi-Objective Optimisation of Machining Process Parameters Using Deep Learning-Based Data-Driven Genetic Algorithm and TOPSIS. J. Manuf. Syst. 2022, 64, 40–52. [Google Scholar] [CrossRef]
- Wang, L.; Yue, C.; Liu, X.; Li, M.; Xu, Y.; Liang, S.Y. Conventional and Micro Scale Finite Element Modeling for Metal Cutting Process: A Review. Chin. J. Aeronaut. 2023, 37, 199–232. [Google Scholar] [CrossRef]
- Nomani, J.; Polishetty, A.; Hilditch, T.; Littlefair, G. Developing a 2D Finite Element Cutting Model Based on Individual Phases in Orthogonal Cutting of Two-Phase Duplex Stainless Steel. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Li, C.; Shi, D.; Li, B.; Wang, H.; Feng, G.; Gu, F.; Ball, A.D. Modelling the Dynamics of a CNC Spindle for Tool Condition Identification Based on On-Rotor Sensing. Mech. Mach. Sci. 2023, 117, 1057–1071. [Google Scholar] [CrossRef]
- Vijayaraghavan, V.; Garg, A.; Gao, L.; Vijayaraghavan, R.; Lu, G. A Finite Element Based Data Analytics Approach for Modeling Turning Process of Inconel 718 Alloys. J. Clean. Prod. 2016, 137, 1619–1627. [Google Scholar] [CrossRef]
- Ye, G.G.; Jiang, M.Q.; Xue, S.F.; Ma, W.; Dai, L.H. On the Instability of Chip Flow in High-Speed Machining. Mech. Mater. 2018, 116, 104–119. [Google Scholar] [CrossRef]
- Yue, C.; Liu, X.; Liu, Z.; Xie, N.; Wang, Y. Tool Optimization for Splicing Die Milling Processes Based on Finite Element Simulation. Chin. Mech. Eng. 2020, 31, 2085–2094. [Google Scholar]
- Muhammad, R.; Roy, A.; Silberschmidt, V.V. Finite Element Modelling of Conventional and Hybrid Oblique Turning Processes of Titanium Alloy. Procedia CIRP 2013, 8, 510–515. [Google Scholar] [CrossRef]
- Okokpujie, I.P.; Tartibu, L.K.; Chima, P.C.; Ogundipe, A.T. A Finite Element Based Investigation of Tool Wear Rate via Machining of Al6061 Alloys Using Deform-3D. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Gok, K. Development of Three-Dimensional Finite Element Model to Calculate the Turning Processing Parameters in Turning Operations. Measurement 2015, 75, 57–68. [Google Scholar] [CrossRef]
- Fetecau, C.; Stan, F. Study of Cutting Force and Surface Roughness in the Turning of Polytetrafluoroethylene Composites with a Polycrystalline Diamond Tool. Measurement 2012, 45, 1367–1379. [Google Scholar] [CrossRef]
- Pan, L.; Wu, Z.R.; Fang, L.; Song, Y.D. Investigation of Surface Damage and Roughness for Nickel-Based Superalloy GH4169 under Hard Turning Processing. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2020, 234, 679–691. [Google Scholar] [CrossRef]
- Jia, S.; Wang, S.; Li, S.; Cai, W.; Liu, Y.; Bai, S.; Li, Z.S. Integrated Multi-Objective Optimization of Rough and Finish Cutting Parameters in Plane Milling for Sustainable Machining Considering Efficiency, Energy, and Quality. J. Clean. Prod. 2024, 471, 143406. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, K.; Xue, H.; Li, J.; Li, Y. Anisotropic Mechanism of Monocrystalline Silicon on Surface Quality in Precision Diamond Wire Saw Cutting. Mater. Sci. Semicond. Process 2025, 185, 108961. [Google Scholar] [CrossRef]
- Li, K.; Wang, X.; Gu, L. Magnetic Field Assisted Blasting Erosion Arc Machining (M-BEAM): A Novel Efficient and Quality Improved Machining Method for Inconel 718. J. Manuf. Process. 2024, 131, 233–244. [Google Scholar] [CrossRef]
- Wang, P.; Tao, H.; Qi, J.; Li, P. Machining Quality Prediction of Complex Thin-Walled Parts Using Multi-Task Dual Domain Adaptive Deep Transfer Learning. Adv. Eng. Inform. 2024, 62, 102640. [Google Scholar] [CrossRef]
- Liu, C.; Xu, W.; Niu, T.; Chen, Y. Roughness Evolution of Constrained Surface Based on Crystal Plasticity Finite Element Model and Coupled Eulerian-Lagrangian Method. Comput. Mater. Sci. 2022, 201, 110900. [Google Scholar] [CrossRef]
- Ma, X.; Zhao, J.; Du, W.; Zhang, X.; Jiang, Z. Analysis of Surface Roughness Evolution of Ferritic Stainless Steel Using Crystal Plasticity Finite Element Method. J. Mater. Res. Technol. 2019, 8, 3175–3187. [Google Scholar] [CrossRef]
- Yang, J.; Wang, X.; Kang, M. Finite Element Simulation of Surface Roughness in Diamond Turning of Spherical Surfaces. J. Manuf. Process. 2018, 31, 768–775. [Google Scholar] [CrossRef]
- Zhang, X.; Zheng, G.; Cheng, X.; Li, Y.; Li, L.; Liu, H. 2D Fractal Analysis of the Cutting Force and Surface Profile in Turning of Iron-Based Superalloy. Measurement 2020, 151, 107125. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, S.; Chen, H.; Zou, J.; Ma, L.; Yin, G. Study on Surface Quality and Subsurface Damage Mechanism of Nickel-Based Single-Crystal Superalloy in Precision Turning. J. Manuf. Process. 2023, 99, 230–242. [Google Scholar] [CrossRef]
- Zheng, G.; Xu, R.; Cheng, X.; Zhao, G.; Li, L.; Zhao, J. Effect of Cutting Parameters on Wear Behavior of Coated Tool and Surface Roughness in High-Speed Turning of 300M. Measurement 2018, 125, 99–108. [Google Scholar] [CrossRef]
- Liu, W.; Yang, X.; Zhang, P.; Chen, Y. Prediction Model of Surface Roughness of 7055 Aluminum Alloy after High Speed Cutting. Ordnance Mater. Sci. Eng. 2015, 38, 1–4. [Google Scholar] [CrossRef]
- Xi, Y.; Bermingham, M.; Wang, G.; Dargusch, M. FEA Modelling of Cutting Force and Chip Formation in Thermally Assisted Machining of Ti6Al4V Alloy. Mater. Sci. Forum 2013, 765, 343–347. [Google Scholar] [CrossRef]
- GB/T 700-2006; Carbon Structural Steels. ISO 630:1995, Structural Steels-Plates, Wide Flats, Bars, Sections and Profiles, NEQ. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China: Beijing, China, 2006.
- ISO 21920-2:2021; Geometrical Product Specifications (GPS)—Surface Texture: Profile—Part 2: Terms, Definitions and Surface Texture Parameters. ISO: Geneva, Switzerland, 2021.
- Lin, L.; Zhi, X.D.; Fan, F.; Meng, S.J.; Su, J.J. Determination of Parameters of Johnson-Cook Models of Q235B Steel. J. Vib. Shock 2014, 33, 153–158. [Google Scholar]
- Zhang, Y.; Jia, Y.; Wang, S.S.Y. An Improved Nearly-Orthogonal Structured Mesh Generation System with Smoothness Control Functions. J. Comput. Phys. 2012, 231, 5289–5305. [Google Scholar] [CrossRef]
- Garimella, R.V. Mesh Data Structure Selection for Mesh Generation and FEA Applications. Int. J. Numer. Methods Eng. 2002, 55, 451–478. [Google Scholar] [CrossRef]
- Smolenicki, D.; Boos, J.; Kuster, F.; Roelofs, H.; Wyen, C.F. In-Process Measurement of Friction Coefficient in Orthogonal Cutting. CIRP Ann. Manuf. Technol. 2014, 63, 97–100. [Google Scholar] [CrossRef]
- Usluer, E.; Emiroğlu, U.; Yapan, Y.F.; Kshitij, G.; Khanna, N.; Sarıkaya, M.; Uysal, A. Investigation on the Effect of Hybrid Nanofluid in MQL Condition in Orthogonal Turning and a Sustainability Assessment. Sustain. Mater. Technol. 2023, 36, e00618. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, M.; Liu, K.; Zhang, J. Optimization of Surface Roughness and Machining Parameters for Turning Superalloy GH4169 under High-Pressure Cooling. Surf. Topogr. 2021, 9, 045045. [Google Scholar] [CrossRef]
- Li, C.; Zou, Z.; Duan, W.; Liu, J.; Gu, F.; Ball, A.D. Characterizing the Vibration Responses of Flexible Workpieces during the Turning Process for Quality Control. Appl. Sci. 2023, 13, 12611. [Google Scholar] [CrossRef]
- Cui, Z.; Ni, J.; He, L.; Su, R.; Wu, C.; Xue, F.; Sun, J. Assessment of Cutting Performance and Surface Quality on Turning Pure Polytetrafluoroethylene. J. Mater. Res. Technol. 2022, 20, 2990–2998. [Google Scholar] [CrossRef]
- Liu, C.; Huang, Z.; Huang, S.; He, Y.; Yang, Z.; Tuo, J. Surface Roughness Prediction in Ball Screw Whirlwind Milling Considering Elastic-Plastic Deformation Caused by Cutting Force: Modelling and Verification. Measurement 2023, 220, 113365. [Google Scholar] [CrossRef]
- Meraz, M.; Alvarez-Ramirez, J.; Rodriguez, E. Multivariate Rescaled Range Analysis. Phys. A Stat. Mech. Its Appl. 2022, 589. [Google Scholar] [CrossRef]
- Çelik, Y.H.; Fidan, Ş. Analysis of Cutting Parameters on Tool Wear in Turning of Ti-6Al-4V Alloy by Multiple Linear Regression and Genetic Expression Programming Methods. Measurement 2022, 200, 111638. [Google Scholar] [CrossRef]
- Black, S.C.; Chiles, V.; Lissaman, A.J.; Martin, S.J. Turning and Milling. In Principles of Engineering Manufacture, 3rd ed.; Butterworth-Heinemann: Oxford, UK, 1996; pp. 316–371. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The Coefficient of Determination R-Squared Is More Informative than SMAPE, MAE, MAPE, MSE and RMSE in Regression Analysis Evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- GB/T 1031-2009; Geometrical Product Specifications(GPS)-Surface Texture: Profile Method-Surface Roughness Parameters and Their Values. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China: Beijing, China, 2009.


| Yield Stress ) | Stress–Strain Data Fitting Parameters ) | Strain Sensitivity Parameters C | Stress–Strain Data Fitting | Temperature Softening Parameters | Material Melting Point Temperature | Initial Temperature |
|---|---|---|---|---|---|---|
| 244.8 | 899.7 | 0.014 | 0.94 | 0.757 | 1521.85 | 25 |
| C | Si | Mn | P | S |
|---|---|---|---|---|
| 0.20 | 0.35 | 1.4 | 0.045 | 0.045 |
| ) | ) | ) |
|---|---|---|
| 7800 | 43 | 212,000 |
| ) | Conductivity ) | Expansion ) | ) | ) |
|---|---|---|---|---|
| 92 | 33 | 7.8 | 2 | 92 |
| Factors (H) | Dependent Variable (M) | ||||||
|---|---|---|---|---|---|---|---|
| ) | ) | P) | |||||
| 1 | 0.5 | 23 | −5 | 25 | 1156.882 | 100.598 | 335.875 |
| 2 | 0.5 | 40 | 10 | 150 | 1102.146 | 230.063 | 569.11 |
| 3 | 0.5 | 57 | 25 | 275 | 1174.938 | 345.761 | 767.819 |
| 4 | 0.5 | 73 | 40 | 400 | 1198.121 | 564.005 | 954.454 |
| 5 | 1 | 23 | 10 | 275 | 1841.327 | 317.102 | 494.456 |
| 6 | 1 | 40 | −5 | 400 | 1982.513 | 501.765 | 661.162 |
| 7 | 1 | 57 | 40 | 25 | 1983.465 | 276.969 | 693.212 |
| 8 | 1 | 73 | 25 | 150 | 1963.750 | 310.250 | 747.441 |
| 9 | 1.5 | 23 | 25 | 400 | 2696.075 | 527.120 | 621.308 |
| 10 | 1.5 | 40 | 40 | 275 | 2699.128 | 477.400 | 553.558 |
| 11 | 1.5 | 57 | −5 | 150 | 2785.703 | 482.18 | 689.275 |
| 12 | 1.5 | 73 | 10 | 25 | 2768.397 | 245.600 | 690.892 |
| 13 | 2 | 23 | 40 | 150 | 3401.107 | 266.800 | 414.796 |
| 14 | 2 | 40 | 25 | 25 | 3510.446 | 250.580 | 504.199 |
| 15 | 2 | 57 | 10 | 400 | 3502.793 | 555.200 | 858.687 |
| 16 | 2 | 73 | −5 | 275 | 3440.002 | 482.550 | 905.883 |
| Test No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
() | 7.698 | 5.600 | 4.829 | 5.865 | 12.267 | 11.042 | 6.118 | 11.635 |
| Test No. | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
() | 10.423 | 10.711 | 9.442 | 7.010 | 8.972 | 12.682 | 15.2528 | 13.428 |
| Factor | ) | |||
|---|---|---|---|---|
| Level | ||||
| Level 1 | 1 | 127.2345 | 0.07 | |
| Level 2 | 2 | 152.6814 | 0.14 | |
| Level 3 | 3 | 178.1283 | 0.21 | |
| Test No. | ) | |||
|---|---|---|---|---|
| 1 | 1 | 127.235 | 0.07 | 2.696 |
| 2 | 1 | 178.129 | 0.14 | 1.936 |
| 3 | 1 | 152.681 | 0.21 | 2.851 |
| 4 | 2 | 178.128 | 0.07 | 2.0873 |
| 5 | 2 | 152.681 | 0.14 | 2.519 |
| 6 | 2 | 127.235 | 0.21 | 3.325 |
| 7 | 3 | 152.681 | 0.07 | 2.934 |
| 8 | 3 | 127.235 | 0.14 | 3.659 |
| 9 | 3 | 178.128 | 0.21 | 2.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.; Li, C.; Zou, Z.; Han, Q.; Li, B.; Gu, F.; Ball, A.D. An Advanced Approach for Predicting Workpiece Surface Roughness Using Finite Element Method and Image Processing Techniques. Machines 2024, 12, 827. https://doi.org/10.3390/machines12110827
Chen T, Li C, Zou Z, Han Q, Li B, Gu F, Ball AD. An Advanced Approach for Predicting Workpiece Surface Roughness Using Finite Element Method and Image Processing Techniques. Machines. 2024; 12(11):827. https://doi.org/10.3390/machines12110827
Chicago/Turabian StyleChen, Taoming, Chun Li, Zhexiang Zou, Qi Han, Bing Li, Fengshou Gu, and Andrew D. Ball. 2024. "An Advanced Approach for Predicting Workpiece Surface Roughness Using Finite Element Method and Image Processing Techniques" Machines 12, no. 11: 827. https://doi.org/10.3390/machines12110827
APA StyleChen, T., Li, C., Zou, Z., Han, Q., Li, B., Gu, F., & Ball, A. D. (2024). An Advanced Approach for Predicting Workpiece Surface Roughness Using Finite Element Method and Image Processing Techniques. Machines, 12(11), 827. https://doi.org/10.3390/machines12110827








